लम्प्ड पैरामीटर कार्डियोवस्कुलर प्रतिरूप
लम्प्ड पैरामीटर कार्डियोवस्कुलर प्रतिरूप शून्य-आयामी गणितीय प्रतिरूप है जिसका उपयोग कार्डियोवास्कुलर प्रणाली के हेमोडायनामिक्स का वर्णन करने के लिए किया जाता है। भौतिक अर्थ वाले पैरामीटर्स के समुच्चय को देखते हुए (उदाहरण के लिए रक्त प्रवाह का प्रतिरोध), यह सम्पूर्ण हृदय प्रणाली में रक्तचाप या प्रवाह दर में परिवर्तन का अध्ययन करने की अनुमति देता है।[1][2] पैरामीटर्स को संशोधित करके, किसी विशिष्ट हृदय रोग के प्रभावों का अध्ययन करना संभव है। उदाहरण के लिए, उच्च रक्तचाप को प्रतिरूप के धमनी प्रतिरोधों को बढ़ाते हुए तैयार किया गया है।[1]
लम्प्ड पैरामीटर प्रतिरूप का उपयोग शून्य-आयामी स्थान के माध्यम से त्रि-आयामी स्थान (कार्डियोवास्कुलर प्रणाली) के हेमोडायनामिक्स का अध्ययन करने के लिए किया जाता है जो पाइप और विद्युत परिपथ के मध्य समानता का लाभ उठाता है। तीन से शून्य आयामों में कमी कार्डियोवास्कुलर प्रणाली को विभिन्न डिब्बों में विभाजित करके की जाती है, जिनमें से प्रत्येक प्रणाली के विशिष्ट घटक का प्रतिनिधित्व करता है, उदाहरण के लिए दायाँ आलिंद या प्रणालीगत धमनियाँ है। प्रत्येक कम्पार्टमेंट प्रतिरोध या संधारित्र, जैसे सरल परिपथ घटकों से बना होता है, जबकि रक्त प्रवाह रक्तचाप (वोल्टेज ड्रॉप) के अनुसार किरचॉफ के नियमों के अनुसार परिपथ के माध्यम से बहने वाली धारा के जैसे व्यवहार करता है।[2]
लम्प्ड पैरामीटर प्रतिरूप में सामान्य अंतर समीकरणों की प्रणाली सम्मिलित होती है जो हृदय कक्षों की मात्रा के समय में विकास और रक्त वाहिकाओं के माध्यम से रक्तचाप और प्रवाह का वर्णन करती है।[3]
प्रतिरूप विवरण
लम्प्ड पैरामीटर प्रतिरूप में सामान्य अंतर समीकरणों की प्रणाली होती है जो द्रव्यमान और गति के संरक्षण के सिद्धांतों का पालन करती है। प्रतिरूप को विद्युत सादृश्य का उपयोग करके प्राप्त किया जाता है जहां धारा रक्त प्रवाह का प्रतिनिधित्व करता है, वोल्टेज दबाव अंतर का प्रतिनिधित्व करता है, विद्युत प्रतिरोध संवहनी प्रतिरोध और (अनुभाग और रक्त वाहिका की लंबाई द्वारा निर्धारित), कैपेसिटेंस की भूमिका निभाता है संवहनी (फिजियोलॉजी) अनुपालन की भूमिका (बढ़ते ट्रांसम्यूरल दबाव के साथ पोत को विस्तारित करने और मात्रा बढ़ाने की क्षमता, जो पोत की दीवार के दो किनारों के मध्य दबाव में अंतर है) और प्रेरण रक्त जड़ता का प्रतिनिधित्व करता है। प्रत्येक हृदय कक्ष को इलास्टेंस के माध्यम से तैयार किया जाता है जो हृदय की मांसपेशियों की सिकुड़न और अनलोड की गई मात्रा का वर्णन करता है, जो कि शून्य-दबाव पर कक्ष में निहित रक्त की मात्रा है। हृदय वाल्व को डायोड के रूप में तैयार किया गया है। प्रतिरूप के पैरामीटर प्रतिरोध, कैपेसिटेंस, इंडक्टेंस और इलास्टेंस हैं। प्रणाली के अज्ञात प्रत्येक हृदय कक्ष के अंदर रक्त की मात्रा, परिसंचरण के प्रत्येक डिब्बे के अंदर रक्त दबाव और प्रवाह हैं। साधारण अंतर समीकरणों की प्रणाली को अस्थायी विवेक के लिए संख्यात्मक विधि के माध्यम से समाधान किया जाता है, उदाहरण के लिए, रनगे-कुट्टा विधि है।[3]
हृदय प्रणाली को विभिन्न भागों में विभाजित किया गया है:
- चार हृदय कक्ष: बाएँ, दाएँ आलिंद और बाएँ, दाएँ निलय;
- प्रणालीगत परिसंचरण जिसे धमनियों, शिराओं में विभाजित किया जा सकता है, यदि आवश्यक हो, विभिन्न रक्त वाहिकाओं के लिए अन्य डिब्बों में किया जा सकता है।
- फुफ्फुसीय परिसंचरण जिसे धमनियों, शिराओं और, यदि आवश्यक हो, विभिन्न रक्त वाहिकाओं के लिए अन्य भागों में विभाजित किया जा सकता है।
बाएं आलिंद और निलय और दाएँ आलिंद और निलय के नीचे की ओर चार हृदय वाल्व होते हैं: क्रमशः माइट्रल वाल्व, महाधमनी, त्रिकुस्पीड वाल्व और फुफ्फुसीय वाल्व आदि।[3]
फुफ्फुसीय और प्रणालीगत परिसंचरण का विभाजन निश्चित नहीं है, उदाहरण के लिए, यदि अध्ययन की रुचि प्रणालीगत केशिकाओं में है, तो प्रणालीगत केशिकाओं के लिए कम्पार्टमेंट लेखांकन को लम्प्ड पैरामीटर प्रतिरूप में जोड़ा जा सकता है। प्रत्येक डिब्बे को विंडकेसल परिपथ द्वारा विशिष्ट डिब्बे के आधार पर तत्वों की संख्या के साथ वर्णित किया गया है। प्रतिरूप के सामान्य अंतर समीकरण विंडकेसल परिपथ और किरचॉफ के नियमों से प्राप्त होते हैं।[4]
निम्नलिखित में विशिष्ट लम्प्ड पैरामीटर प्रतिरूप पर ध्यान केंद्रित किया जाएगा। जिन भागों पर विचार किया गया है वे चार हृदय कक्ष, प्रणालीगत और फुफ्फुसीय धमनियां और वेंस हैं।[5]
हृदय कक्ष समीकरण
चार हृदय कक्षों से संबंधित पैरामीटर निष्क्रिय और सक्रिय इलास्टेंस हैं (जहां सबस्क्रिप्ट विभिन्न हैं और यदि इलास्टेंस क्रमशः दाएं आलिंद या वेंट्रिकल या बाएं आलिंद या वेंट्रिकल को संदर्भित करते हैं) और अनलोड किए गए आयतन हृदय कक्षों की गतिशीलता का वर्णन समय-निर्भर इलास्टेंस द्वारा किया जाता है:[5]
जहाँ आवधिक (हृदय की धड़कन की अवधि के साथ) समय पर निर्भर कार्य को जो हृदय की धड़कन के समय हृदय के सक्रियण चरणों का लेखा-जोखा रखता है। उपरोक्त समीकरण से, निष्क्रिय इलास्टेंस हृदय कक्ष के न्यूनतम इलास्टेंस का प्रतिनिधित्व करता है, जबकि योग और इसका अधिकतम इलास्टेंस समय-निर्भर इलास्टेंस विशिष्ट हृदय कक्ष के अंदर दबाव की गणना निम्नानुसार करने की अनुमति देता है:[5]
जहाँ हृदय कक्ष में निहित रक्त की मात्रा है और प्रत्येक कक्ष के लिए मात्रा निम्नलिखित सामान्य अंतर समीकरणों का समाधान है जो हृदय कक्ष से जुड़े आवक और जावक रक्त प्रवाह के लिए उत्तरदायी हैं:[5]
जहाँ और क्रमशः माइट्रल, महाधमनी, ट्राइकसपिड और फुफ्फुसीय वाल्व के माध्यम से प्रवाह होते हैं और क्रमशः फुफ्फुसीय और प्रणालीगत वेंस के माध्यम से प्रवाह होते हैं।[5]
वाल्व समीकरण
वाल्वों को डायोड के रूप में तैयार किया जाता है और वाल्वों में रक्त प्रवाह अपस्ट्रीम और डाउनस्ट्रीम डिब्बे के मध्य दबाव जम्प पर निर्भर करता है:[5]
जहां प्रत्येक हृदय कक्ष के अंदर का दबाव पिछले अनुभाग में परिभाषित किया गया है, और प्रणालीगत और फुफ्फुसीय धमनी डिब्बे के अंदर समय-निर्भर दबाव हैं और दबाव बढ़ने के आधार पर वाल्व में प्रवाह होता है:[5]
जहां और वाल्वों के क्रमशः संवृत और विवृत होने पर उनके प्रतिरोध होते हैं।[5]
सर्कुलेशन कम्पार्टमेंट समीकरण
रक्त वाहिकाओं के प्रत्येक डिब्बे को प्रतिरोध, कैपेसिटेंस और इंडक्टेंस के संयोजन की विशेषता होती है। उदाहरण के लिए, धमनी प्रणालीगत परिसंचरण को तीन पैरामीटर्स द्वारा वर्णित किया जा सकता है और जो धमनी प्रणालीगत प्रतिरोध, धारिता और अधिष्ठापन का प्रतिनिधित्व करता है। प्रणालीगत धमनी परिसंचरण का वर्णन करने वाले सामान्य अंतर समीकरण हैं:[5]
जहां प्रणालीगत धमनी डिब्बे में रक्त प्रवाह है और शिराओं के डिब्बे के अंदर का दबाव है।[5]
समान संकेतन वाले अनुरूप समीकरण रक्त परिसंचरण का वर्णन करने वाले अन्य डिब्बों के लिए मान्य हैं।[5]
साधारण अंतर समीकरण प्रणाली
ऊपर वर्णित समीकरणों को एकत्र करने पर निम्नलिखित प्रणाली प्राप्त होती है:[5]
अंतिम बार पहले दो समीकरण क्रमशः बाएं आलिंद और निलय में आयतन से संबंधित हैं। तीसरे से छठे तक के समीकरण प्रणालीगत धमनी और शिरापरक प्रणालियों के दबाव और प्रवाह से संबंधित हैं। अंतिम समीकरण दाहिने हृदय और फुफ्फुसीय परिसंचरण से समान रूप से संबंधित हैं। प्रणाली प्रत्येक अज्ञात के लिए प्रारंभिक नियमों के साथ पूर्ण हो गया है।[5]
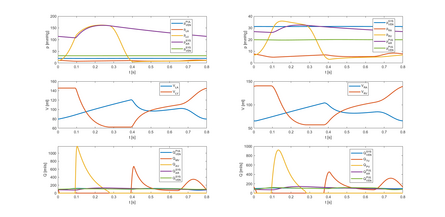
गणितीय दृष्टिकोण से, समस्या की सुव्यवस्थितता कॉची-लिप्सचिट्ज़ प्रमेय का परिणाम है, इसलिए इसका समाधान उपस्थित है और यह अद्वितीय है। प्रणाली का समाधान साधारण अंतर समीकरणों के लिए संख्यात्मक विधि के माध्यम से अनुमानित किया जाता है। संख्यात्मक अनुकरण की गणना इससे अधिक के लिए की जानी है हृदय की धड़कन (अंतिम बार) गतिशील प्रणाली के सीमा चक्र तक पहुंचने के लिए हृदय की धड़कनों की संख्या और हृदय गति पर निर्भर करता है, जिससे समाधान हृदय चक्र की आवधिकता का अनुकरण करने वाले आवधिक कार्य के समान व्यवहार किया जाता है।[5]
आगामी विकास
ऊपर वर्णित प्रतिरूप विशिष्ट लम्प्ड पैरामीटर प्रतिरूप है। इसे आवश्यकतानुसार किसी भी डिब्बे के अंदर डिब्बे या परिपथ घटकों को जोड़ने या हटाने में सरलता से संशोधित किया जा सकता है। नए या संशोधित डिब्बों को नियंत्रित करने वाले समीकरण पूर्व के जैसे किर्चॉफ़ के नियम हैं।[4]
श्वसन प्रणाली के लिए लम्प्ड पैरामीटर प्रतिरूप जोड़कर कार्डियोवस्कुलर लम्प्ड पैरामीटर प्रतिरूप को बढ़ाया जा सकता है। जहां तक हृदय प्रणाली का विचार है, श्वसन प्रणाली को विभिन्न भागों में विभाजित किया गया है, उदाहरण के लिए, स्वरयंत्र, ग्रसनी या श्वासनली है।[6] इसके अतिरिक्त, कार्डियोपल्मोनरी प्रतिरूप को रक्त ऑक्सीजनेशन के अध्ययन के लिए प्रतिरूप के साथ जोड़ा जा सकता है, उदाहरण के लिए, रक्त संतृप्ति का स्तर आदि।[7][8]
कई पैरामीटर प्रतिरूप हैं और प्रतिरूप का चयन कार्य या शोध के उद्देश्य पर निर्भर करता है। जटिल प्रतिरूप विभिन्न गतिशीलता का वर्णन कर सकते हैं, किंतु जटिलता में वृद्धि से अंतर समीकरणों की प्रणाली का समाधान करने के लिए बड़ी कम्प्यूटेशनल व्यय की आवश्यकता होती है।[9][10][11]
लम्प्ड पैरामीटर प्रतिरूप के कुछ 0-डी डिब्बों को इसके द्वारा प्रतिस्थापित किया जा सकता है -आयामी घटक () ज्यामितीय रूप से हृदय प्रणाली के विशिष्ट घटक का वर्णन करने के लिए (उदाहरण के लिए, बाएं वेंट्रिकल के 0-डी डिब्बे को इसके 3-डी प्रतिनिधित्व द्वारा प्रतिस्थापित किया जा सकता है)। परिणामस्वरूप, समीकरणों की प्रणाली में आयामी घटकों का वर्णन करने के लिए आंशिक अंतर समीकरण भी सम्मिलित होंगे और इसे संख्यात्मक रूप से समाधान करने के लिए बड़ी कम्प्यूटेशनल व्यय की आवश्यकता होगी।[12][13]
यह भी देखें
- ब्लड वेसल
- विवेक
- सीमित तत्व विधि
- हृदय
- लुम्प्ड-एलिमेंट प्रतिरूप
- प्रतिरूप ऑर्डर में कमी
संदर्भ
- ↑ 1.0 1.1 Shim, Eun Bo; Sah, Jong Youb; Youn, Chan Hyun (2004). "लम्प्ड पैरामीटर विधि का उपयोग करके हृदय प्रणाली की गतिशीलता का गणितीय मॉडलिंग". The Japanese Journal of Physiology (in English). 54 (6): 545–553. doi:10.2170/jjphysiol.54.545. ISSN 0021-521X. PMID 15760487.
- ↑ 2.0 2.1 Shi, Yubing; Lawford, Patricia; Hose, Rodney (2011). "हृदय प्रणाली में रक्त प्रवाह के शून्य-डी और 1-डी मॉडल की समीक्षा". BioMedical Engineering OnLine (in English). 10 (1): 33. doi:10.1186/1475-925X-10-33. ISSN 1475-925X. PMC 3103466. PMID 21521508.
- ↑ 3.0 3.1 3.2 Shim, Eun Bo; Sah, Jong Youb; Youn, Chan Hyun (2004). "लम्प्ड पैरामीटर विधि का उपयोग करके हृदय प्रणाली की गतिशीलता का गणितीय मॉडलिंग". The Japanese Journal of Physiology (in English). 54 (6): 545–553. doi:10.2170/jjphysiol.54.545. ISSN 0021-521X. PMID 15760487.
- ↑ 4.0 4.1 Shi, Yubing; Lawford, Patricia; Hose, Rodney (2011). "हृदय प्रणाली में रक्त प्रवाह के शून्य-डी और 1-डी मॉडल की समीक्षा". BioMedical Engineering OnLine (in English). 10 (1): 33. doi:10.1186/1475-925X-10-33. ISSN 1475-925X. PMC 3103466. PMID 21521508.
- ↑ 5.00 5.01 5.02 5.03 5.04 5.05 5.06 5.07 5.08 5.09 5.10 5.11 5.12 5.13 Dedè, Luca; Regazzoni, Francesco; Vergara, Christian; Zunino, Paolo; Guglielmo, Marco; Scrofani, Roberto; Fusini, Laura; Cogliati, Chiara; Pontone, Gianluca; Quarteroni, Alfio (2021). "Modeling the cardiac response to hemodynamic changes associated with COVID-19: a computational study". Mathematical Biosciences and Engineering (in English). 18 (4): 3364–3383. doi:10.3934/mbe.2021168. hdl:2434/843779. ISSN 1551-0018. PMID 34198390. S2CID 234973850.
- ↑ Ngo, Chuong; Dahlmanns, Stephan; Vollmer, Thomas; Misgeld, Berno; Leonhardt, Steffen (2018-06-01). "मनुष्यों में कार्डियोपल्मोनरी हेमोडायनामिक इंटरैक्शन का अध्ययन करने के लिए एक ऑब्जेक्ट-ओरिएंटेड कम्प्यूटेशनल मॉडल". Computer Methods and Programs in Biomedicine (in English). 159: 167–183. doi:10.1016/j.cmpb.2018.03.008. ISSN 0169-2607. PMID 29650311. S2CID 4802953.
- ↑ Albanese, Antonio; Cheng, Limei; Ursino, Mauro; Chbat, Nicolas W. (2016-04-01). "An integrated mathematical model of the human cardiopulmonary system: model development". American Journal of Physiology. Heart and Circulatory Physiology (in English). 310 (7): H899–H921. doi:10.1152/ajpheart.00230.2014. ISSN 0363-6135. PMID 26683899.
- ↑ Lu, K.; Clark, J. W.; Ghorbel, F. H.; Ware, D. L.; Bidani, A. (2001-12-01). "एक मानव कार्डियोपल्मोनरी सिस्टम मॉडल वलसाल्वा पैंतरेबाज़ी के विश्लेषण के लिए लागू किया गया". American Journal of Physiology. Heart and Circulatory Physiology (in English). 281 (6): H2661–H2679. doi:10.1152/ajpheart.2001.281.6.H2661. ISSN 0363-6135. PMID 11709436. S2CID 8246967.
- ↑ De Lazzari, C.; Darowski, M.; Ferrari, G.; Pisanelli, D.M.; Tosti, G. (2006). "हेमोपम्प उपकरण और कृत्रिम वेंटिलेशन की परस्पर क्रिया के अध्ययन में मॉडलिंग". Computers in Biology and Medicine (in English). 36 (11): 1235–1251. doi:10.1016/j.compbiomed.2005.08.001. PMID 16202402.
- ↑ Shi, Yubing; Korakianitis, Theodosios (2006). "बाएं हृदय की विफलता और इन-सीरीज़ पल्सटाइल वेंट्रिकुलर असिस्ट डिवाइस के साथ कार्डियोवास्कुलर डायनेमिक्स का संख्यात्मक सिमुलेशन". Artificial Organs (in English). 30 (12): 929–948. doi:10.1111/j.1525-1594.2006.00326.x. ISSN 0160-564X. PMID 17181834.
- ↑ Heldt, Thomas; Shim, Eun B.; Kamm, Roger D.; Mark, Roger G. (2002-03-01). "ऑर्थोस्टेटिक तनाव के प्रति हृदय संबंधी प्रतिक्रिया का कम्प्यूटेशनल मॉडलिंग". Journal of Applied Physiology (in English). 92 (3): 1239–1254. doi:10.1152/japplphysiol.00241.2001. ISSN 8750-7587. PMID 11842064.
- ↑ Blanco, Pablo J.; Feijóo, Raúl A. (2010). "A 3D-1D-0D Computational Model for the Entire Cardiovascular System". Mecánica Computacional (in English). 29 (59): 5887–5911.
- ↑ Baillargeon, Brian; Rebelo, Nuno; Fox, David D.; Taylor, Robert L.; Kuhl, Ellen (2014). "The Living Heart Project: A robust and integrative simulator for human heart function". European Journal of Mechanics - A/Solids (in English). 48: 38–47. Bibcode:2014EJMS...48...38B. doi:10.1016/j.euromechsol.2014.04.001. PMC 4175454. PMID 25267880.
अग्रिम पठन
- Bazilevs, Yuri; Takizawa, Kenji; Tezduyar, Tayfun E. (2013). Computational fluid-structure interaction: methods and applications. Wiley series in computational mechanics. Chichester: Wiley. ISBN 978-0-470-97877-1.
- Quarteroni, Alfio; Dede', Luca; Manzoni, Andrea; Vergara, Christian (2019). Mathematical modelling of the human cardiovascular system: data, numerical approximation, clinical applications. Cambridge monographs on applied and computational mathematics. New York, NY: Cambridge University Press. ISBN 978-1-108-61609-6.
- Hirschvogel, Marc; Bassilious, Marina; Jagschies, Lasse; Wildhirt, Stephen M.; Gee, Michael W. (2017). "A monolithic 3D-0D coupled closed-loop model of the heart and the vascular system: Experiment-based parameter estimation for patient-specific cardiac mechanics: 3D-0D coupled closed-loop model of the heart". International Journal for Numerical Methods in Biomedical Engineering (in English). 33 (8): e2842. doi:10.1002/cnm.2842. PMID 27743468. S2CID 36252500.