समोत्पाद (आइसोक्वेंट)
व्यष्टि अर्थशास्त्र में समोत्पाद (आइसोक्वेंट) (मात्रा और ग्रीक शब्द आइसो से लिया गया है, जिसका अर्थ है बराबर), बिंदुओं के समुच्चय के माध्यम से खींची गई एक समोच्च (कॉन्टूर) रेखा है, जिस पर दो या दो से अधिक निविष्ट की मात्रा को परिवर्तित करते समय समान मात्रा में उत्पादन प्राप्त है।[1][2] एक समोत्पाद पर x और y अक्ष दो प्रासंगिक निविष्ट को निरूपित करते हैं, जो सामान्यतः श्रम, पूंजी, भूमि या संगठन जैसे उत्पादन का एक कारक होता है। समोत्पाद को "सम-उत्पाद वक्र", या "समान उत्पाद वक्र" के रूप में भी जाना जाता है।
समोत्पाद बनाम अनधिमान वक्र
जबकि किसी अनधिमान वक्र प्रतिचित्रण उपभोक्ताओं की उपयोगिता-अधिकतमीकरण समस्या को हल करने में सहायता करता है, समोत्पाद प्रतिचित्रण लागत-न्यूनतमीकरण और उत्पादकों के लाभ और निर्गत (उत्पादन) अधिकतमीकरण की समस्या से संबंधित है। अनधिमान वक्र इसके अतिरिक्त समोत्पाद वक्रों से भिन्न होते हैं, जिसमें वे उपयोगिता का एक यथार्थ माप प्रदान नहीं कर सकते हैं, जैसे यह केवल एक आधार रेखा के लिए प्रासंगिक है। जबकि, समोत्पाद से, उत्पाद को भौतिक इकाइयों में यथार्थ रूप से मापा जा सकता है, और यह वास्तव में जितना समोत्पाद 1 समोत्पाद 2 से अधिक होता है, से जाना जाता है।
समोत्पाद की प्रकृति और व्यावहारिक उपयोग
प्रबंधकीय अर्थशास्त्र में, समोत्पाद सामान्यतः पूंजी-श्रम ग्राफ में समलागत वक्र के साथ खींचा जाता है, जो उत्पादन फलन में पूंजी और श्रम के बीच तकनीकी व्यापार को दर्शाता है, और दोनों निविष्ट के घटते सीमांत प्रतिफल को दर्शाता है। प्रबंधकीय अर्थशास्त्र में, समोत्पाद की इकाई सामान्यतः पूंजीगत लागत का नेट है। जैसे, तकनीकी प्रतिस्थापन (एमआरटीएस) की सीमांत प्रतिफल दरों के संचालन के कारण स्वभाव से समोत्पाद नीचे की ओर झुके हुए हैं।[3][4] एक समोत्पाद की प्रवणता उस दर को दर्शाता है जिस पर निविष्ट एक्स को निविष्ट वाई के लिए प्रतिस्थापित किया जा सकता है।[5] यह अवधारणा एमआरटीएस है, इसलिए एमआरटीएस = समोत्पाद की प्रवणता। इस प्रकार, समोत्पाद वक्र जितना अधिक तीव्र होगा, एमआरटीएस उतना ही अधिक होगा। चूंकि एमआरटीएस को कम होना चाहिए, इसलिए समोत्पाद्स को उनके मूल के उत्तल होना चाहिए। दूसरे स्थिरांक को धारण करते हुए एक आगत को जोड़ने से अंतत: सीमान्त उत्पादन घटने लगता है।
समोत्पाद की समोच्च रेखा दो निविष्ट के प्रत्येक संयोजन का प्रतिनिधित्व करती है जो संसाधनों (जैसे बजट, या समय) के व्यवसाय-संघों के उपयोग को पूरी तरह से अधिकतम करती है। संसाधनों के पूर्ण अधिकतमीकरण को सामान्यतः 'कुशल' माना जाता है। उत्पादन के कारकों का कुशल आवंटन तभी होता है जब दो समोत्पाद वक्र एक-दूसरे को स्पर्श करते हैं। यदि कोई व्यवसाय-संघ कंटूर लाइन के बाईं ओर उत्पादन करती है, तो व्यवसाय-संघ को अक्षमता से संचालन करने वाला माना जाता है, क्योंकि वे अपने उपलब्ध संसाधनों का अधिकतम उपयोग नहीं कर रहे हैं।[6] एक व्यवसाय-संघ कंटूर लाइन के दायीं ओर तब तक उत्पादन नहीं कर सकती जब तक कि वे अपनी सीमाओं से अधिक न हों।
समोत्पाद के एक परिवार को समोत्पाद प्रतिचित्रण द्वारा दर्शाया जा सकता है, एक ग्राफ जो कई समोत्पाद को जोड़ता है, प्रत्येक उत्पादन की एक अलग मात्रा का प्रतिनिधित्व करता है। एक समोत्पाद प्रतिचित्रण, समोत्पाद जोड़े के बीच बढ़ती या घटती दूरी के आधार पर घटते या बढ़ते रिटर्न को इंगित कर सकता है। उत्पादन में वृद्धि के रूप में निश्चित उत्पादन वृद्धि। [7] यदि उत्पादन बढ़ने के साथ-साथ उन समोत्पाद वक्रों के बीच की दूरी बढ़ती है, तो व्यवसाय-संघ का उत्पादन फलन पैमाने के ह्रासमान प्रतिफल को प्रदर्शित करता है, दोनों निविष्टों को दोगुना करने से पिछले समोत्पाद के दोगुने से कम उत्पादन वाले समोत्पाद पर प्लेसमेंट होगा। इसके विपरीत, यदि उत्पादन बढ़ने के साथ-साथ दूरी कम हो रही है, तो व्यवसाय-संघ को पैमाने के बढ़ते प्रतिफल का अनुभव हो रहा है, दोनों निविष्टों को दोगुना करने से मूल समोत्पाद के दोगुने से अधिक उत्पादन के साथ एक समोत्पाद पर प्लेसमेंट होता है। एक व्यवसाय-संघ उस जानकारी का उपयोग करना चुन सकती है जो समोत्पाद अनुमापी प्रतिफल पर प्रदान करती है, संसाधनों को आवंटित करने के तरीके के बारे में जानकारी के रूप में इसका उपयोग करके।[8]
यह जानना कि संसाधनों का आवंटन कैसे किया जाता है, प्रबंधकीय अर्थशास्त्र के लिए प्रासंगिक अवधारणा है। अप्राप्यता के इस विषय को रेखांकन से दर्शाने के लिए समोत्पाद्स उपयोगी हो सकते हैं। वे दिखाते हैं कि प्रश्न में व्यवसाय-संघ के पास समान स्तर के उत्पादन का उत्पादन करने के लिए दो अलग-अलग निविष्ट (ग्राफ़ में x और y) के बीच स्थानापन्न करने की क्षमता है (देखें: ग्राफ़ C)। वे दो वस्तुओं के विभिन्न मात्रा संयोजनों का भी प्रतिनिधित्व करते हैं जो एक बजट बाधा का पालन करते हैं। इस प्रकार, उन्हें एक उपकरण के रूप में उपयोग किया जा सकता है जिससे प्रबंधन को उत्पादन और लाभ दुविधाओं, जैसे कि लागत या अपशिष्ट न्यूनतमीकरण, और राजस्व और उत्पादन अधिकतमीकरण के बारे में बेहतर सूचित निर्णय लेने में सहायता मिलती है।
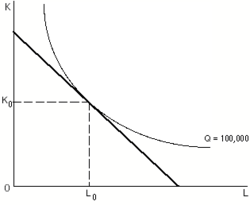
एक व्यवसाय-संघ किसी दिए गए उत्पाद का उत्पादन करने के लिए, समलागत वक्रों और समोत्पादों को मिलाकर, और प्रथम अनुक्रम की शर्तों का पालन करके, निविष्ट का न्यूनतम लागत संयोजन निर्धारित कर सकता है।[3] न्यूनतम लागत संयोजन वह होता है जहां सीमांत उत्पादों का अनुपात कारक कीमतों के अनुपात के बराबर होता है। इस बिंदु पर, समोत्पाद की प्रवणता, और समलागत की प्रवणता बराबर होगा (ग्राफ डी का चौराहा देखें)। एक व्यवसाय-संघ को कम से कम लागत संयोजन का उत्पादन करने के लिए प्रोत्साहन मिलता है क्योंकि यह इस बिंदु पर है, वांछित उत्पादन की संबंधित लागत कम से कम हो जाती है।[9]
अनधिमान वक्रों की तरह, दो समोत्पाद वक्र कभी एक-दूसरे को पार नहीं कर सकते हैं। इसके अतिरिक्त, निविष्ट का हर संभव संयोजन एक समोत्पाद पर है। अंत में, एक समोत्पाद परिणाम के ऊपर या दाईं ओर निविष्ट का कोई भी संयोजन उच्च स्तर के उत्पादन का प्रतिनिधित्व करता है, और इसके विपरीत। यद्यपि एक निविष्ट का सीमांत उत्पाद घटता है क्योंकि आप अन्य सभी निविष्टों को स्थिर रखते हुए निविष्ट की मात्रा बढ़ाते हैं, सीमांत उत्पाद कभी भी अनुभवजन्य रूप से देखी गई सीमा में ऋणात्मक नहीं होता है क्योंकि एक तर्कसंगत व्यवसाय-संघ उत्पादन को कम करने के लिए निविष्ट में कभी वृद्धि नहीं करेगी।
समोत्पाद की आकृतियाँ
यदि दो निविष्ट सही स्थानापन्न हैं, तो उत्पन्न समोत्पाद प्रतिचित्रण को रेखाचित्र में दर्शाया गया है। ए; उत्पादन के दिए गए स्तर Q3 के साथ, निविष्ट X को निविष्ट Y द्वारा अपरिवर्तित दर पर प्रतिस्थापित किया जा सकता है। सही स्थानापन्न आदानों को उत्पादन फलन में एक दूसरे के लिए प्रतिस्थापित किए जाने पर प्रतिफल की घटती हुई सीमांत दरों का अनुभव नहीं होता है।
यदि दो निविष्ट पूर्ण पूरक हैं, तो समोत्पाद प्रतिचित्रण रेखाचित्र का रूप ले लेता है। बी; उत्पादन के एक स्तर Q3 के साथ, निविष्ट X और निविष्ट Y को केवल समोत्पाद में किंक पर होने वाले निश्चित अनुपात में कुशलता से जोड़ा जा सकता है। व्यवसाय-संघ अधिकतम लाभ प्राप्त करने के लिए आवश्यक अनुपात में दो आगतों को संयोजित करेगी।
उत्पादन के दिए गए स्तर के लिए लागत-न्यूनतमीकरण समस्या को हल करने के लिए समोत्पाद्स को सामान्यतः समलागत लाइनों के साथ जोड़ा जाता है। शीर्ष आकृति में दिखाए गए विशिष्ट स्थिति में, सुचारू रूप से वक्रित समोत्पाद के साथ, निविष्ट की निश्चित इकाई लागत वाली एक व्यवसाय-संघ के पास समलागत वक्र होंगे जो रैखिक और नीचे की ओर प्रवणता वाले हैं, एक समोत्पाद और एक समलागत वक्र के बीच स्पर्शरेखा का कोई भी बिंदु उस समोत्पाद से जुड़े उत्पादन स्तर के उत्पादन के लिए लागत को कम करने वाले निविष्ट संयोजन का प्रतिनिधित्व करता है। समोत्पाद्स और समलागत्स (निविष्ट कीमतों को स्थिर रखने के साथ) के स्पर्शरेखा बिंदुओं को मिलाने वाली रेखा को विस्तार पथ कहा जाता है।[10]
गैर उत्तलता
तकनीकी प्रतिस्थापन की घटती सीमांत दर की धारणा के तहत, और इसलिए प्रतिस्थापन की एक धनात्मक और परिमित लोच, मूल के उत्तल है। स्थानीय रूप से गैर-उत्तल समोत्पाद हो सकता है यदि निविष्ट में से किसी एक में पर्याप्त रूप से मजबूत अनुमापी प्रतिफल हो। इस स्थिति में, प्रतिस्थापन की एक ऋणात्मक लोच है - निविष्ट ए से निविष्ट बी के अनुपात में वृद्धि के रूप में, बी के सापेक्ष ए का सीमांत उत्पाद घटने के बजाय बढ़ता है।
गैर-उत्तल समोत्पाद मूल्य परिवर्तन के जवाब में निविष्ट मिश्रण को कम करने वाले मूल्य में बड़े और असंतत परिवर्तन उत्पन्न करने के लिए प्रवण होता है। उदाहरण के लिए उस स्थिति पर विचार करें जहां समोत्पाद वैश्विक रूप से गैर उत्तल है, और समलागत वक्र रैखिक है। इस स्थिति में निविष्ट का न्यूनतम लागत मिश्रण एक कोने का समाधान होगा, और इसमें केवल एक निविष्ट सम्मिलित होगा (उदाहरण के लिए निविष्ट ए या निविष्ट बी)। किस निविष्ट का उपयोग करना है, यह चुनाव सापेक्ष कीमतों पर निर्भर करेगा। कुछ महत्वपूर्ण मूल्य अनुपात पर, इष्टतम निविष्ट मिश्रण सभी निविष्ट ए से सभी निविष्ट बी में स्थानांतरित हो जाएगा और इसके विपरीत सापेक्ष कीमतों में एक छोटे से बदलाव के जवाब में होगा।
यह भी देखें
- व्यष्टि अर्थशास्त्र
- उत्पादन, लागत और मूल्य निर्धारण
- उत्पादन सिद्धांत मूल बातें
- तकनीकी प्रतिस्थापन की सीमांत दर
- लर्नर आरेख
- बजट बाध्यता
इस पेज में लापता आंतरिक लिंक की सूची
- इनडीफरन्स कर्व
- उत्पादन प्रकार्य
- तकनीकी प्रतिस्थापन की सीमांत दर
- पैमाने पर करने के लिए रिटर्न
- बजट बाध्यता
- पहले आदेश की स्थिति
संदर्भ
- ↑ Varian, Hal R. (1992). सूक्ष्म आर्थिक विश्लेषण (Third ed.). Norton. ISBN 0-393-95735-7.
- ↑ Chiang, Alpha C. (1984). गणितीय अर्थशास्त्र के मौलिक तरीके (Third ed.). McGraw-Hill. pp. 359–363. ISBN 0-07-010813-7.
- ↑ 3.0 3.1 www2.econ.iastate.edu http://www2.econ.iastate.edu/classes/econ101/choi/ch11d.htm. Retrieved 2021-04-25.
{{cite web}}: Missing or empty|title=(help) - ↑ "आइसोक्वेंट्स". www.economics.utoronto.ca. Retrieved 2021-04-25.
- ↑ "उत्पादन कार्य" (PDF). UCLA. n.d. Retrieved 25 April 2021.
{{cite web}}: CS1 maint: url-status (link) - ↑ Arrow, K. J.; Chenery, H. B.; Minhas, B. S.; Solow, R. M. (1961). "पूंजी-श्रम प्रतिस्थापन और आर्थिक दक्षता". The Review of Economics and Statistics. 43 (3): 225–250. doi:10.2307/1927286. ISSN 0034-6535. JSTOR 1927286.
- ↑ Kwatiah, Natasha (2016-03-02). "आइसोक्वेंट दृष्टिकोण के संदर्भ में पैमाने के प्रतिफल के नियम". Economics Discussion (in English). Retrieved 2021-04-25.
- ↑ "आइसोक्वेंट की खोज". ResearchGate (in English). Retrieved 2021-04-25.
- ↑ "विस्तार पथ, रिजलाइन और इनपुट का न्यूनतम लागत संयोजन" (PDF). Eagri. n.d. Retrieved 2021-04-25.
{{cite web}}: CS1 maint: url-status (link) - ↑ Salvatore, Dominick (1989). Schaum's outline of theory and problems of managerial economics, McGraw-Hill, ISBN 978-0-07-054513-7