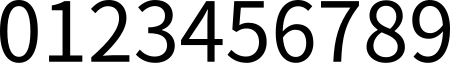अरबी अंक

From Vigyanwiki
Revision as of 12:20, 8 December 2022 by alpha>Artiverma
This article is about the symbols only. For the numerical system, see Decimal. For symbols used in Arab Script, see Eastern Arabic numerals. For other uses, see अरबी अंक (disambiguation).

Numbers written from 0 to 9
स्रोत संस टाइपफेस में सेट अरबी अंक
Part of a series on
Numeral systems
Place-value notation
Hindu-Arabic numerals
East Asian systems
Contemporary
Historic
Other systems
Ancient
Post-classical
Contemporary
By radix/base
Common radices/bases
Non-standard radices/bases
Sign-value notation
Non-alphabetic
Alphabetic
List of numeral systems

अरबी अंक दस संख्यात्मक अंक हैं: 0, 1, 2, 3, 4, 5, 6, 7, 8 तथा 9. वे दशमलव संख्या लिखने के लिए सबसे अधिक उपयोग किए जाने वाले प्रतीक हैं। उनका उपयोग अन्य प्रणालियों जैसे अष्टभुजाकार में संख्या लिखने के लिए, और पहचानकर्ता लिखने के लिए जैसे कंप्यूटर प्रतीकों, ट्रेडमार्क या लाइसेंस प्लेट के लिए भी किया जाता है। शब्द का अर्थ प्रायः एक दशमलव संख्या होता है, विशेष रूप से जब रोमन अंकों के विपरीत होता है।

उन्हें पश्चिमी अरबी अंक, ग़ुबार अंक, हिंदू-अरबी अंक भी कहा जाता है।[disputed (for: No indication this term means this subset of digit symbols)  – discuss][1] पश्चिमी अंक, लैटिन अंक या यूरोपीय अंक।[2] ऑक्सफोर्ड इंग्लिश डिक्शनरी पूर्वी अरबी अंकों को संदर्भित करने के लिए उन्हें पूरी तरह से पूंजीकृत अरबी अंकों के साथ अलग करती है।[3] शब्द संख्या या अंक या अंक प्रायः केवल इन प्रतीकों का अर्थ करते हैं, चूंकि यह केवल संदर्भ से अनुमान लगाया जा सकता है।

यह बेजाइया के एलजीरिया शहर में था कि इतालवी लोगों के विद्वान फिबोनैकी ने पहली बार अंकों का सामना किया; पूरे यूरोप में उन्हें ज्ञात कराने में उनका काम महत्वपूर्ण था। यूरोपीय व्यापार, पुस्तकों और उपनिवेशवाद ने दुनिया भर में अरबी अंकों को अपनाने को लोकप्रिय बनाने में मदद की। लैटिन वर्णमाला के समकालीन प्रसार से परे अंकों का दुनिया भर में उपयोग पाया गया है, और लेखन प्रणालियों में आम हो गया है जहां अन्य अंक प्रणालियां पहले सम्मिलित थीं, जैसे कि चीनी अंक और जापानी अंक ।

इतिहास

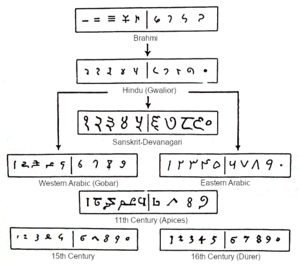
उत्पत्ति

भारतीय अंकों का अरबी अंकों में विकास और यूरोप में उनका अंगीकरण

यूरोप और अमेरिका में अंकों को सामान्यतः अरबी अंकों के रूप में जाना जाता है, इसका कारण यह है कि वे 10 वीं शताब्दी में स्पेन और उत्तरी अफ्रीका के अरबी बोलने वालों द्वारा यूरोप में प्रस्तुत किए गए थे, जो तब लीबिया से मोरक्को तक के अंकों का उपयोग कर रहे थे। अरबी प्रायद्वीप के पूर्वी भाग में, अरब पूर्वी अरबी अंकों या मशरिकी अंकों का उपयोग कर रहे थे: ٠ ١ ٢ ٣ ٤ ٥ ٦ ٧ ٨ ٩[lower-alpha 1][4]

अली इब्न अहमद अल-नसावी | अल-नसावी ने 11वीं शताब्दी के प्रारम्भ में लिखा था कि गणितज्ञ अंकों के रूप पर सहमत नहीं थे, लेकिन उनमें से अधिकांश स्वयं को उन रूपों के साथ प्रशिक्षित करने के लिए सहमत हुए थे जिन्हें अब पूर्वी अरबी अंकों के रूप में जाना जाता है।[5] उपलब्ध लिखित अंकों के सबसे पुराने प्रतिरूप मिस्र से हैं और 873-874 सीई तक के हैं। वे अंक 2 के तीन रूपों और अंक 3 के दो रूपों को दिखाते हैं, और ये विविधताएं उन भिन्नताओं का संकेत देती हैं जिन्हें बाद में पूर्वी अरबी अंकों और पश्चिमी अरबी अंकों के रूप में जाना जाने लगा।[6] 10वीं शताब्दी के बाद से माघरेब और अल-अंडालस में पश्चिमी अरबी अंकों का उपयोग किया जाने लगा।[7] पश्चिमी अरबी अंक रूपों में निरंतरता की कुछ मात्रा 10वीं शताब्दी से चली आ रही है, जो 976 से सेविले का इसिडोर के एटिमोलोगिया की लैटिन पांडुलिपि में और 12वीं और 13वीं शताब्दी में गेरबर्टियन अबेकस में, टोलेडो शहर से अनुवाद की शुरुआती पांडुलिपियों में पाई गई थी। , स्पेन।[4]

गणना मूल रूप से एक डस्ट बोर्ड (तख़्त, लैटिन: टैबुला) का उपयोग करके की जाती थी, जिसमें एक स्टाइलस के साथ प्रतीकों को लिखना और उन्हें मिटाना सम्मिलित था। ऐसा प्रतीत होता है कि धूल बोर्ड के उपयोग ने शब्दावली में भी एक विचलन प्रस्तुत किया है: जबकि हिंदू गणना को पूर्व में हिसाब अल-हिंदी कहा जाता था, इसे पश्चिम में हिसाब अल-ग़ुबर कहा जाता था (शाब्दिक रूप से, धूल के साथ गणना)।[8] पश्चिम में अंकों को स्वयं अश्कल अल-ग़ुबर (धूल के आंकड़े) या क़लम अल-ग़ुबर (धूल के अक्षर) के रूप में संदर्भित किया जाता था।[9] अबुल-हसन अल-उक्लिदिसी | अल-उक्लिदिसी ने बाद में बिना बोर्ड और मिटाए स्याही और कागज के साथ गणना की एक प्रणाली का आविष्कार किया।[10] एक लोकप्रिय मिथक का दावा है कि प्रतीकों को उनके कोणों की संख्या के माध्यम से उनके संख्यात्मक मान को इंगित करने के लिए डिज़ाइन किया गया था, लेकिन इसका कोई सबूत सम्मिलित नहीं है, और मिथक 4 के बाद किसी भी अंक के साथ सामंजस्य स्थापित करना मुश्किल है।[11]


गोद लेना और फैलाना

पश्चिम में पहले अरबी अंक स्पेन में कोडेक्स एल्बेल्डेंसिस में दिखाई दिए।

पश्चिम में 1 से 9 तक के अंकों का पहला उल्लेख 976 के कोड विजिलनस में पाया जाता है, स्पेन में पुरातनता से 10 वीं शताब्दी तक की अवधि को कवर करने वाले विभिन्न ऐतिहासिक दस्तावेजों का एक प्रबुद्ध पांडुलिपि संग्रह।[12] अन्य ग्रंथों से पता चलता है कि 1 से 9 तक की संख्याएं कभी-कभी एक प्लेसहोल्डर द्वारा पूरक होती हैं जिसे अंग्रेजी में नंबर 0 के लिए नाम के रूप में जाना जाता है, जिसे सर्कल या पहिया के रूप में दर्शाया जाता है, जो 0 के लिए अंतिम प्रतीक की याद दिलाता है। शून्य के लिए अरबी शब्द सिफर है (صفر), लैटिन में सिफ्रा के रूप में लिप्यंतरित, और अंग्रेजी शब्द सिफर की उत्पत्ति।

980 के दशक से, औरिलैक के गेरबर्ट (बाद में, पोप सिल्वेस्टर II) ने यूरोप में अंकों के ज्ञान का प्रसार करने के लिए अपनी स्थिति का उपयोग किया। गेरबर्ट ने अपनी युवावस्था में बार्सिलोना में अध्ययन किया। वह फ्रांस लौटने के बाद बार्सिलोना के लुपिटस से यंत्र से संबंधित गणितीय ग्रंथों का अनुरोध करने के लिए जाना जाता था।[12]

पश्चिम में अरबी अंकों का स्वागत धीरे-धीरे और गुनगुना था, क्योंकि अन्य अंक प्रणालियां पुराने रोमन नंबरों के अलावा परिचालित थीं। एक अनुशासन के रूप में, अरबी अंकों को अपने स्वयं के लेखन के हिस्से के रूप में अपनाने वाले पहले खगोलविद और ज्योतिषी थे, जो 12 वीं शताब्दी के मध्य बवेरिया से जीवित पांडुलिपियों से प्रमाणित थे। पैडरबोर्न के रेनहर (1140-1190) ने अपने पाठ कॉम्पोटस एमेंडैटस में ईस्टर की तिथियों की अधिक आसानी से गणना करने के लिए अपने कैलेंड्रिकल तालिकाओं में अंकों का उपयोग किया।[13]


इटली

लिबर अबाची का एक पृष्ठ। दाईं ओर की सूची फाइबोनैचि संख्याओं को दिखाती है: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377। 2, 8, और 9 पूर्वी अरबी से अधिक अरबी अंकों के समान हैं। अंक या भारतीय अंक

लियोनार्डो फाइबोनैचि, पीसा गणराज्य के एक गणितज्ञ, जिन्होंने बेजैया (बगिया), अल्जीरिया में अध्ययन किया था, ने अपनी 1202 पुस्तक अबेकस की किताब के साथ यूरोप में हिंदू-अरबी अंक प्रणाली को बढ़ावा दिया:

जब मेरे पिता, जिन्हें उनके देश द्वारा सार्वजनिक नोटरी के रूप में नियुक्त किया गया था, जो वहां जाने वाले पिसान व्यापारियों के लिए काम कर रहे बेजाई में थे, प्रभारी थे, उन्होंने मुझे अपने पास बुलाया, जबकि मैं अभी भी एक बच्चा था, और एक आँख थी उपयोगिता और भविष्य की सुविधा के लिए, मुझे वहाँ रहने और लेखा के स्कूल में निर्देश प्राप्त करने की इच्छा थी। वहां, जब मुझे उल्लेखनीय शिक्षण के माध्यम से भारतीयों के नौ प्रतीकों की कला से परिचित कराया गया, तो कला के ज्ञान ने मुझे बहुत जल्द सबसे ज्यादा प्रसन्न किया और मैं इसे समझ गया।

लिबर अबाची ने स्थितीय संख्यात्मक प्रणाली के विशाल लाभों को प्रस्तुत किया, और यह व्यापक रूप से प्रभावशाली था। जैसा कि फाइबोनैचि ने अंकों के लिए बेजाइआ के प्रतीकों का उपयोग किया था, इन प्रतीकों को भी उसी निर्देश में पेश किया गया था, जो अंततः उनके व्यापक रूप से अपनाने के लिए अग्रणी था।[14] फाइबोनैचि की शुरूआत 12वीं और 13वीं सदी की यूरोप की वाणिज्यिक क्रांति के साथ हुई, जो इटली में केंद्रित थी। रोमन और अन्य संख्यात्मक प्रणालियों की तुलना में स्थितीय संकेतन का उपयोग तेज और अधिक जटिल गणितीय कार्यों (जैसे मुद्रा रूपांतरण) के लिए किया जा सकता है। वे बड़ी संख्याओं को भी संभाल सकते थे, एक अलग गणना उपकरण की आवश्यकता नहीं थी, और उपयोगकर्ता को पूरी प्रक्रिया को दोहराए बिना गणना की जांच करने की अनुमति दी।[14]हालांकि स्थितीय संकेतन ने ऐसी संभावनाएं खोलीं जो पिछली प्रणालियों द्वारा बाधित थीं, देर से मध्ययुगीन इतालवी व्यापारियों ने रोमन अंकों (या अन्य गणना उपकरण) का उपयोग करना बंद नहीं किया। बल्कि, अरबी अंक एक अतिरिक्त उपकरण बन गया जिसका उपयोग दूसरों के साथ किया जा सकता था।[14]


यूरोप

अरबी अंकों का उपयोग सिखाने वाला एक जर्मन पाण्डुलिपि पृष्ठ (हंस तलहोफर थॉट, 1459)। इस समय, अंकों का ज्ञान अभी भी व्यापक रूप से गूढ़ के रूप में देखा जाता था, और तलहोफर ने उन्हें हिब्रू वर्णमाला और ज्योतिष के साथ प्रस्तुत किया।
जीन-एटिने मोंटूक्ला द्वारा कई रूपों में अंकों की तालिका, 1757

14वीं शताब्दी के अंत में अरबी अंकों का उपयोग करने वाले कुछ ही ग्रंथ इटली के बाहर दिखाई दिए। इससे पता चलता है कि व्यावसायिक व्यवहार में अरबी अंकों का उपयोग, और उनके द्वारा प्रदान किया गया महत्वपूर्ण लाभ, 15वीं शताब्दी के अंत तक आभासी इतालवी एकाधिकार बना रहा।[14]यह आंशिक रूप से भाषा के कारण हो सकता है - हालांकि फाइबोनैचि के लिबर अबाची को लैटिन में लिखा गया था, इतालवी अबेकस परंपराओं को मुख्य रूप से इतालवी भाषा में लिखा गया था जो अबेकस स्कूलों या व्यक्तियों के निजी संग्रह में प्रसारित हुआ था। गैर-इतालवी मर्चेंट बैंकरों के लिए व्यापक जानकारी तक पहुँच प्राप्त करना संभवतः कठिन था।

छापाखाना के आविष्कार से अंकों की यूरोपीय स्वीकृति में तेजी आई और 15वीं शताब्दी के दौरान वे व्यापक रूप से जाने गए। ल्यों जैसे वित्त और व्यापार के अन्य केंद्रों में उनका उपयोग लगातार बढ़ता गया।[15] मध्य युग में ग्रेट ब्रिटेन में उनके उपयोग के प्रारंभिक साक्ष्य में शामिल हैं: 1396 से एक समान घंटे का होरेरी चतुर्थांश (उपकरण),[16] इंग्लैंड में, हीथफील्ड और वाल्ड्रॉन चर्च, ससेक्स के टॉवर पर 1445 का एक शिलालेख; ब्रे, बर्कशायर चर्च, बर्कशायर के लकड़ी के लिच-गेट पर 1448 का एक शिलालेख; और Piddletrenthide चर्च, डोर्सेट में घंटाघर के दरवाजे पर 1487 का एक शिलालेख; और स्कॉटलैंड में एल्गिन, मोरे कैथेड्रल में हंटली के पहले अर्ल की कब्र पर 1470 का शिलालेख।[17] मध्य यूरोप में, हंगरी के राजा लैडिसलॉस मरणोपरांत ने अरबी अंकों का उपयोग शुरू किया, जो पहली बार 1456 के एक शाही दस्तावेज़ में दिखाई देते हैं।[18] 16वीं शताब्दी के मध्य तक, वे अधिकांश यूरोप में आम उपयोग में थे। रोमन अंक ज्यादातर हमारे भगवान के वर्ष में वर्षों के अंकन के लिए और घड़ी के चेहरों पर संख्याओं के लिए उपयोग में बने रहे।[citation needed] अन्य अंक (जैसे पूर्वी अरबी) वस्तुतः अज्ञात थे।[citation needed]


रूस

अरबी अंकों की शुरुआत से पहले, प्रारंभिक सिरिलिक वर्णमाला से प्राप्त सिरिलिक अंक, दक्षिण स्लाव और पूर्वी स्लाव स्लाविक लोगों द्वारा उपयोग किए जाते थे। प्रणाली का उपयोग रूस में 18 वीं शताब्दी के अंत तक किया गया था, हालांकि इसे औपचारिक रूप से 1699 में महान पीटर द्वारा आधिकारिक उपयोग में बदल दिया गया था।[19] माना जाता है कि अल्फ़ान्यूमेरिकल सिस्टम से पीटर के स्विच के कारण पश्चिम की नकल करने की उनकी इच्छा से परे हैं। इतिहासकार पीटर ब्राउन परिवर्तन के लिए समाजशास्त्रीय, सैन्यवादी और शैक्षणिक कारणों के लिए तर्क देते हैं। व्यापक, सामाजिक स्तर पर, रूसी व्यापारी, सैनिक और अधिकारी तेजी से पश्चिम के समकक्षों के संपर्क में आए और अरबी अंकों के सांप्रदायिक उपयोग से परिचित हो गए। पीटर द ग्रेट ने भी 1697 से 1698 तक पीटर द ग्रेट के ग्रैंड एम्बेसी के दौरान पूरे उत्तरी यूरोप में गुप्त यात्रा की और इस समय के दौरान अनौपचारिक रूप से पश्चिमी गणित के संपर्क में आने की संभावना थी।[20] गति में वस्तुओं के गुणों की गणना के मामले में सिरिलिक संख्यात्मक प्रणाली भी कम थी, जैसे तोपखाने के प्रक्षेपवक्र और परवलयिक उड़ान पैटर्न। बोलिस्टीक्स के बढ़ते विज्ञान में यह अरबी अंकों के साथ गति बनाए रखने में असमर्थ था, जबकि जॉन नेपियर जैसे पश्चिमी गणितज्ञ 1614 से इस विषय पर प्रकाशित कर रहे थे।[21]


चीन

युआन राजवंश (1271-1368) से संबंधित चीन से फारसी/अरबी अंकों में ऑर्डर 6 जादू वर्ग के साथ लोहे की प्लेट।

चीनी अंक जो स्थितीय संकेतन का उपयोग करते थे (जैसे कि गिनती की छड़ें और सूज़ौ अंक) अरबी अंकों के प्रारम्भ से पहले चीन में उपयोग में थे,[22][23] कुछ को मध्यकालीन चीन में मुस्लिम हुई लोगों द्वारा प्रस्तुत किया गया था। 17 वीं शताब्दी के प्रारम्भ में, यूरोपीय शैली के अरबी अंक स्पेनिश और पुर्तगालीजेसुइट्स द्वारा प्रस्तुत किए गए थे।[24][25][26]


एनकोडिंग

दस अरबी अंकों को इलेक्ट्रिक, रेडियो और डिजिटल संचार जैसे मोर्स कोड के लिए डिज़ाइन किए गए लगभग हर वर्ण सेट में एन्कोड किया गया है।

वे एएससीII में 0x30 से 0x39 की स्थिति में एन्कोड किए गए हैं। मास्क (कंप्यूटिंग) निचले चार बाइनरी बिट्स (या अंतिम हेक्साडेसिमल अंक लेते हुए) अंक का मान देता है, शुरुआती कंप्यूटरों पर पाठ को संख्याओं में बदलने में बहुत मदद करता है। ये पद यूनिकोड में विरासत में मिले थे।[27] ईबीसीडीआईसी ने विभिन्न मूल्यों का इस्तेमाल किया, लेकिन अंकों के मूल्य के बराबर 4 बिट्स भी कम थे।

ASCII Binary ASCII Octal ASCII Decimal ASCII Hex Unicode EBCDIC
Hex
0 0011 0000 060 48 30 U+0030 DIGIT ZERO F0
1 0011 0001 061 49 31 U+0031 DIGIT ONE F1
2 0011 0010 062 50 32 U+0032 DIGIT TWO F2
3 0011 0011 063 51 33 U+0033 DIGIT THREE F3
4 0011 0100 064 52 34 U+0034 DIGIT FOUR F4
5 0011 0101 065 53 35 U+0035 DIGIT FIVE F5
6 0011 0110 066 54 36 U+0036 DIGIT SIX F6
7 0011 0111 067 55 37 U+0037 DIGIT SEVEN F7
8 0011 1000 070 56 38 U+0038 DIGIT EIGHT F8
9 0011 1001 071 57 39 U+0039 DIGIT NINE F9


अन्य अंकों के साथ तुलना

Symbol Used with scripts Numerals
0 1 2 3 4 5 6 7 8 9 many Arabic numerals
𑁦 𑁧 𑁨 𑁩 𑁪 𑁫 𑁬 𑁭 𑁮 𑁯 Brahmi Brahmi numerals
० १ २ ३ ४ ५ ६ ७ ८ ९ Devanagari Devanagari numerals
০ ১ ২ ৩ ৪ ৫ ৬ ৭ ৮ ৯ Bengali–Assamese Bengali numerals
੦ ੧ ੨ ੩ ੪ ੫ ੬ ੭ ੮ ੯ Gurmukhi Gurmukhi numerals
૦ ૧ ૨ ૩ ૪ ૫ ૬ ૭ ૮ ૯ Gujarati Gujarati numerals
୦ ୧ ୨ ୩ ୪ ୫ ୬ ୭ ୮ ୯ Odia Odia numerals
᱐ ᱑ ᱒ ᱓ ᱔ ᱕ ᱖ ᱗ ᱘ ᱙ Santali Santali numerals
𑇐 𑇑 𑇒 𑇓 𑇔 𑇕 𑇖 𑇗 𑇘 𑇙 Sharada Sharada numerals
௦ ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯ Tamil Tamil numerals
౦ ౧ ౨ ౩ ౪ ౫ ౬ ౭ ౮ ౯ Telugu Telugu script § Numerals
೦ ೧ ೨ ೩ ೪ ೫ ೬ ೭ ೮ ೯ Kannada Kannada script § Numerals
൦ ൧ ൨ ൩ ൪ ൫ ൬ ൭ ൮ ൯ Malayalam Malayalam numerals
෦ ෧ ෨ ෩ ෪ ෫ ෬ ෭ ෮ ෯ Sinhala Sinhala numerals
၀ ၁ ၂ ၃ ၄ ၅ ၆ ၇ ၈ ၉ Burmese Burmese numerals
༠ ༡ ༢ ༣ ༤ ༥ ༦ ༧ ༨ ༩ Tibetan Tibetan numerals
᠐ ᠑ ᠒ ᠓ ᠔ ᠕ ᠖ ᠗ ᠘ ᠙ Mongolian Mongolian numerals
០ ១ ២ ៣ ៤ ៥ ៦ ៧ ៨ ៩ Khmer Khmer numerals
๐ ๑ ๒ ๓ ๔ ๕ ๖ ๗ ๘ ๙ Thai Thai numerals
໐ ໑ ໒ ໓ ໔ ໕ ໖ ໗ ໘ ໙ Lao Lao script § Numerals
᮰ ᮱ ᮲ ᮳ ᮴ ᮵ ᮶ ᮷ ᮸ ᮹ Sundanese Sundanese numerals
꧐ ꧑ ꧒ ꧓ ꧔ ꧕ ꧖ ꧗ ꧘ ꧙ Javanese Javanese numerals
᭐ ᭑ ᭒ ᭓ ᭔ ᭕ ᭖ ᭗ ᭘ ᭙ Balinese Balinese numerals
٠ ١ ٢ ٣ ٤ ٥ ٦ ٧ ٨ ٩ Arabic Eastern Arabic numerals
۰ ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹ Persian / Dari / Pashto
۰ ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹ Urdu / Shahmukhi
- ፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ Ethio-Semitic Ge'ez numerals
〇 一 二 三 四 五 六 七 八 九 East Asia Chinese numerals


यह भी देखें

व्याख्यात्मक नोट्स

  1. ↑ Shown right-to-left, zero is on the right, nine on the left.


उद्धरण

  1. ↑ "अरबी अंक". American Heritage Dictionary. Houghton Mifflin Harcourt Publishing Company. 2020. Archived from the original on 21 November 2021. Retrieved 21 November 2021.
  2. ↑ Terminology for Digits Archived 26 October 2021 at the Wayback Machine. Unicode Consortium.
  3. ↑ "Arabic", Oxford English Dictionary, 2nd edition
  4. ↑ 4.0 4.1 Burnett, Charles (2002). Dold-Samplonius, Yvonne; Van Dalen, Benno; Dauben, Joseph; Folkerts, Menso (eds.). चीन से पेरिस तक: गणितीय विचारों का 2000 साल का प्रसारण (in English). Franz Steiner Verlag. pp. 237–288. ISBN 978-3-515-08223-5. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
  5. ↑ Kunitzsch 2003, p. 7: "Les personnes qui se sont occupées de la science du calcul n'ont pas été d'accord sur une partie des formes de ces neuf signes; mais la plupart d'entre elles sont convenues de les former comme il suit."
  6. ↑ Kunitzsch 2003, p. 5.
  7. ↑ Kunitzsch 2003, pp. 12–13: "While specimens of Western Arabic numerals from the early period—the tenth to thirteenth centuries—are still not available, we know at least that Hindu reckoning (called ḥisāb al-ghubār) was known in the West from the 10th century onward..."
  8. ↑ Kunitzsch 2003, p. 8.
  9. ↑ Kunitzsch 2003, p. 10.
  10. ↑ Kunitzsch 2003, pp. 7–8.
  11. ↑ Ifrah, Georges (1998). संख्याओं का सार्वभौमिक इतिहास: प्रागितिहास से कंप्यूटर के आविष्कार तक. Translated by David Bellos (from the French). London: Harvill Press. pp. 356–357. ISBN 9781860463242.
  12. ↑ 12.0 12.1 Nothaft, C. Philipp E. (3 May 2020). "मध्ययुगीन यूरोप के शैतानी सिफर: एक आधुनिक मिथक की उत्पत्ति पर". British Journal for the History of Mathematics. 35 (2): 107–136. doi:10.1080/26375451.2020.1726050. ISSN 2637-5451. S2CID 213113566.
  13. ↑ Herold, Werner (2005). "डेर "कंप्यूटस एमेंडेडस" डेस रेनहर वॉन पैडरबोर्न". ixtheo.de (in German). Archived from the original on 30 July 2022. Retrieved 29 July 2022.{{cite web}}: CS1 maint: unrecognized language (link)
  14. ↑ 14.0 14.1 14.2 14.3 Danna, Raffaele (12 July 2021). व्यावहारिक अंकगणित की यूरोपीय परंपरा में हिंदू-अरबी अंकों का प्रसार: एक सामाजिक-आर्थिक परिप्रेक्ष्य (13वीं-16वीं शताब्दी) (Doctoral thesis). University of Cambridge. doi:10.17863/cam.72497. Archived from the original on 27 July 2021. Retrieved 29 July 2022.
  15. ↑ Danna, Raffaele; Iori, Martina; Mina, Andrea (22 June 2022). "एक संख्यात्मक क्रांति: व्यावहारिक गणित का प्रसार और पूर्व-आधुनिक यूरोपीय अर्थव्यवस्थाओं का विकास". SSRN 4143442.
  16. ↑ "Qld फार्म शेड में 14वीं सदी की घड़ी मिली". ABC News. Archived from the original on 29 February 2012. Retrieved 10 November 2011.
  17. ↑ See G. F. Hill, The Development of Arabic Numerals in Europe, for more examples.
  18. ↑ Erdélyi: Magyar művelődéstörténet 1-2. kötet. Kolozsvár, 1913, 1918.
  19. ↑ Conatser Segura, Sylvia (26 May 2020). रूसी इतिहास में ऑर्थोग्राफ़िक सुधार और भाषा योजना (Honors thesis). Archived from the original on 30 July 2022. Retrieved 29 July 2022.
  20. ↑ Brown, Peter B. (2012). "सत्रहवीं शताब्दी की रूसी सभ्यता में मस्कोवाइट अंकगणित: क्या यह "पिछड़ापन" लेबल को त्यागने का समय नहीं है?". Russian History. 39 (4): 393–459. doi:10.1163/48763316-03904001. ISSN 0094-288X. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
  21. ↑ Lockwood, E. H. (October 1978). "गणितीय खोज 1600-1750, पी. एल. ग्रिफिथ्स द्वारा। पीपी 121. £2·75. 1977. आईएसबीएन 0 7223 1006 4 (स्टॉकवेल)". The Mathematical Gazette. 62 (421): 219. doi:10.2307/3616704. ISSN 0025-5572. JSTOR 3616704. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
  22. ↑ Shell-Gellasch, Amy (2015). बीजगणित संदर्भ में: परिचयात्मक बीजगणित उत्पत्ति से अनुप्रयोगों तक. J. B. Thoo. Baltimore. ISBN 978-1-4214-1728-8. OCLC 907657424.{{cite book}}: CS1 maint: location missing publisher (link)
  23. ↑ Uy, Frederick L. (January 2003). "चीनी संख्या प्रणाली और स्थानीय मान". Teaching Children Mathematics. 9 (5): 243–247. doi:10.5951/tcm.9.5.0243. ISSN 1073-5836. Archived from the original on 30 July 2022. Retrieved 29 July 2022.
  24. ↑ Helaine Selin, ed. (1997). गैर-पश्चिमी संस्कृतियों में विज्ञान, प्रौद्योगिकी और चिकित्सा के इतिहास का विश्वकोश. Springer. p. 198. ISBN 978-0-7923-4066-9. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
  25. ↑ Meuleman, Johan H. (2002). वैश्वीकरण के युग में इस्लाम: आधुनिकता और पहचान के प्रति मुस्लिम दृष्टिकोण. Psychology Press. p. 272. ISBN 978-0-7007-1691-3. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
  26. ↑ Peng Yoke Ho (2000). ली, क्यूई और शू: चीन में विज्ञान और सभ्यता का परिचय. Mineola, New York: Courier Dover Publications. p. 106. ISBN 978-0-486-41445-4. Archived from the original on 27 October 2015. Retrieved 18 October 2015.
  27. ↑ "यूनिकोड मानक, संस्करण 13.0" (PDF). unicode.org. Archived (PDF) from the original on 2 June 2001. Retrieved 1 September 2021.


सामान्य और उद्धृत स्रोत


अग्रिम पठन


इस पेज में लापता आंतरिक लिंक की सूची

  • स्रोत बिना
  • इटालियन लोग
  • लैटिन वर्णमाला का प्रसार
  • मोरक्को
  • अन्दलुस
  • शब्द-साधन
  • बार्सिलोना के ल्यूपिटस
  • पीसा गणराज्य
  • चतुर्भुज (साधन)
  • Ladislaus मरणोपरांत
  • स्लाव लोग
  • पीटर द ग्रेट का ग्रैंड एम्बेसी
  • युआन वंश

बाहरी संबंध

Wikimedia Commons has media related to:
Arabic numerals
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=अरबी_अंक&oldid=41647’