विश्व रेखा

किसी वस्तु की विश्व रेखा वो पथ है जिसे कोई वस्तु चतुर्विम समष्टि स्पेसटाइम में खोज करती है। यह आधुनिक भौतिक विज्ञान और विशेष रूप से सैद्धांतिक भौतिक विज्ञान में एक महत्वपूर्ण अवधारणा है।

एक विश्व रेखा की अवधारणा को "समय" द्वारा एक ग्रहपथ या एक प्रक्षेप पथ

(उदाहरण के लिए,एक ग्रह की 'अंतरिक्ष में ग्रहपथ' या सड़क पर कार के 'प्रक्षेपण') जैसी अवधारणाओं से अलग किया जाता है सामान्य तौर पर स्पेसटाइम के एक बड़े क्षेत्र को शामिल करता है,जिसमें अवधारणात्मक रूप से सीधे पथों को उनकी सापेक्षता के सिद्धांत या गुरुत्वाकर्षण की परस्पर क्रिया की और अधिक सटीक अवस्था दिखाने के लिए पुनर्गणना की जाती है।

विश्व रेखाओं का विचार भौतिक विज्ञान में उत्पन्न हुआ था और हरमन मिंकोव्स्की द्वारा अग्रणी किया गया था। यह शब्द अब सबसे अधिक बार सापेक्षता सिद्धांतों यानी, विशेष सापेक्षता और सामान्य सापेक्षता में उपयोग किया जाता है।

भौतिक विज्ञान में प्रयोग

भौतिक विज्ञान में, किसी वस्तु की एक विश्व रेखा (अंतरिक्ष में एक बिंदु के रूप में अनुमानित, उदाहरण के लिए,एक कण या पर्यवेक्षक) वस्तु के इतिहास के अनुरूप स्पेसटाइम घटनाओं का अनुक्रम है। स्पेसटाइम में विश्व रेखा एक विशेष प्रकार का वक्र है। विश्व रेखा स्पेसटाइम में एक समय-समान वक्र है। विश्व रेखा का प्रत्येक बिंदु एक घटना है जिसे उस समय और उस समय वस्तु की स्थानिक स्थिति के साथ अंकित किया जा सकता है।

उदाहरण के लिए,अंतरिक्ष में पृथ्वी की भ्रमण पथ लगभग एक वृत्त है, जो अंतरिक्ष में एक त्रि-आयामी (बंद) वक्र है: पृथ्वी प्रत्येक वर्ष सूर्य के सापेक्ष अंतरिक्ष में उसी बिंदु पर लौटती है। हालाँकि,यह एक अलग समय पर वहाँ पहुँचता है। पृथ्वी की विश्व रेखा स्पेसटाइम में घुमावदार है इसलिए उसी बिंदु पर वापस नहीं आती है।

स्पेसटाइम घटनाओं की पहचान करने वाली एक सतत और सुचारू समन्वय प्रणाली के साथ घटनाओं का संग्रह है। प्रत्येक घटना को चार संख्याओं द्वारा अंकित किया जा सकता है: एक समय समन्वय और तीन स्थान निर्देशांक; इस प्रकार स्पेसटाइम एक चार-आयामी स्थान है। स्पेसटाइम के लिए गणितीय शब्द एक चतुर्विम समष्टि है। इस धारणा को उच्च-आयामी स्थान पर भी लागू किया जा सकता है। चार आयामों के आसान दृष्टिकोण के लिए, दो अंतरिक्ष निर्देशांक अक्सर दबा दिए जाते हैं। घटना को तब मिंकोव्स्की आरेख में एक बिंदु द्वारा दर्शाया जाता है, जो कि एक विमान है जिसे आमतौर पर समय के समन्वय के साथ प्लॉट किया जाता है, कहते हैं $t$, ऊपर की ओर और अंतरिक्ष समन्वय करते हैं, कहते हैं $x$ क्षैतिज रूप से। जैसा कि एफ.आर. हार्वे द्वारा व्यक्त किया गया है।

स्पेसटाइम में एक वक्र M को एक कण की एक विश्व रेखा कहा जाता है यदि इसकी स्पर्शरेखा प्रत्येक बिंदु पर भविष्य के समय की तरह हो। वक्राकार लंबाई मापदंड को उचित समय कहा जाता है और आमतौर पर इसे t के रूप में दर्शाया जाता है। M की लंबाई कण का उचित समय कहलाती है। यदि विश्व रेखा M एक रेखाखंड है, तो कण को ​​निर्बाध गिरावट में कहा जाता है।

एक विश्व रेखा स्पेसटाइम में एक बिंदु के पथ का पता लगाती है। एक विश्व पत्रक स्पेसटाइम के माध्यम से यात्रा करने वाली एक-आयामी रेखा द्वारा खोजी गई समान द्वि-आयामी सतह है। एक खुली डोरी की विश्व शीट ढीले सिरों वाली एक पट्टी होती है और एक बंद डोरी एक ट्यूब के समान होती है।

एक बार जब वस्तु को केवल एक बिंदु के रूप में नहीं बल्कि विस्तारित मात्रा के रूप में अनुमानित किया जाता है,तो यह एक विश्व रेखा नहीं बल्कि एक विश्व ट्यूब का पता लगाता है।

घटनाओं का वर्णन करने के लिए एक उपकरण के रूप में विश्व रेखाएं

वर्ल्ड लाइन,वर्ल्डशीट और वर्ल्ड वॉल्यूम,क्योंकि वे प्राथमिक कण , स्ट्रिंग सिद्धांत और मेम्ब्रेन (एम-थ्योरी) से प्राप्त होते हैं।

एक-आयामी रेखा या वक्र को निर्देशांक द्वारा एक मापदंड के कार्य के रूप में दर्शाया जा सकता है। मापदंड का प्रत्येक मान स्पेसटाइम में एक बिंदु से मेल खाता है और मापदंड को अलग-अलग करके एक रेखा का पता लगाता है। गणितीय शब्दों में एक वक्र को चार समन्वय कार्यों द्वारा परिभाषित किया जाता है $x^{a}(\tau ),\;a=0,1,2,3$ (जहां पर $x^{0}$ आमतौर पर समय समन्वय को दर्शाता है) एक मापदंड के आधार पर $\tau$. स्पेसटाइम में एक समन्वय ग्रिड, वक्र का समूह है,जो चार में से तीन समन्वय कार्य को स्थिर करने पर प्राप्त होता है।

कभी-कभी, विश्व रेखा शब्द का प्रयोग स्पेसटाइम में किसी भी वक्र के लिए शिथिल रूप से किया जाता है। यह शब्दावली भ्रम पैदा करती है। अधिक ठीक से, एक विश्व रेखा स्पेसटाइम में एक वक्र है जो एक कण,पर्यवेक्षक या छोटी वस्तु के (समय) इतिहास का पता लगाती है। आमतौर पर किसी वस्तु या प्रेक्षक के उचित समय को वक्र मापदंड के रूप में लिया जाता है $\tau$ विश्व रेखा के साथ।

स्पेसटाइम वक्र के कुछ उदाहरण

तीन अलग-अलग विश्व रेखाएं विभिन्न स्थिर चार-वेगों पर यात्रा का प्रतिनिधित्व करती हैं। t समय और x दूरी है।

एक वक्र जिसमें एक क्षैतिज रेखा खंड (स्थिर समन्वय समय पर एक रेखा) होता है,स्पेसटाइम में एक छड़ का प्रतिनिधित्व कर सकता है और उचित अर्थों में एक विश्व रेखा नहीं होगी। मापदंड छड़ की लंबाई का पता लगाता है।

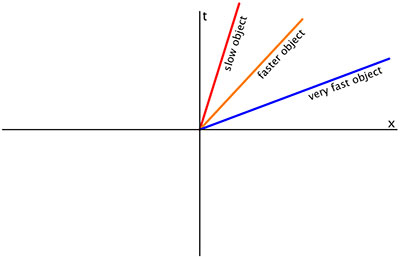
स्थिर स्थान समन्वय पर एक रेखा (ऊपर अपनाए गए सम्मेलन में एक लंबवत रेखा) अवशेष पर एक कण का प्रतिनिधित्व कर सकती है। एक झुकी हुई रेखा एक स्थिर समन्वय गति के साथ एक कण का प्रतिनिधित्व करती है। जितनी अधिक रेखा लंबवत से झुकी होती है,गति उतनी ही अधिक होती है।

दो विश्व रेखाएँ जो अलग-अलग शुरू होती हैं और फिर प्रतिच्छेद करती हैं, टकराव या संघट्टन का संकेत देती हैं। स्पेसटाइम में एक ही घटना से शुरू होने वाली दो विश्व रेखाएं, प्रत्येक अपने स्वयं के पथ का अनुसरण करती हैं, एक कण के दो अन्य में क्षति या एक कण के दूसरे द्वारा उत्सर्जन का प्रतिनिधित्व कर सकती हैं।

एक कण और एक पर्यवेक्षक की विश्व रेखाएं एक फोटॉन (प्रकाश का मार्ग) की विश्व रेखा से जुड़ी हो सकती हैं और एक कण द्वारा एक फोटॉन के उत्सर्जन को दर्शाने वाला आरेख बना सकती हैं जिसे बाद में पर्यवेक्षक द्वारा देखा जाता है या किसी अन्य कण द्वारा अवशोषित किया जाता है।

विश्व रेखा की स्पर्शरेखा सदिश: चतुर्वेग

चार समन्वय कार्य $x^{a}(\tau ),\;a=0,1,2,3$ एक विश्व रेखा को परिभाषित करना, एक वास्तविक परिवर्तन के वास्तविक कार्य हैं $\tau$ और सामान्य गणना में आसानी से विभेदित किया जा सकता है। एक मीट्रिक के अस्तित्व के बिना कोई एक बिंदु के बीच के अंतर के बारे में बात कर सकता है $p$ मापदंड मान पर वक्र पर $\tau _{0}$ और वक्र पर एक बिंदु का मापदंड ( $\tau _{0}+\Delta \tau$) थोड़ा दूर दर्शाता है। सीमा में $\Delta \tau \to 0$, इस अंतर से विभाजित $\Delta \tau$ एक वेक्टर को परिभाषित करता है, बिंदु पर विश्व रेखा का स्पर्शरेखा वेक्टर $p$. यह एक चतुर्विम समष्टि वेक्टर है, जिसे बिंदु में परिभाषित किया गया है $p$. यह वस्तु के सामान्य त्रिआयामी वेग से जुड़ा है और इसलिए इसे चतुर्वेग समष्टि कहा जाता है ${\vec {v}}$,।

$${\vec {v}}=\left(v^{0},v^{1},v^{2},v^{3}\right)=\left({\frac {dx^{0}}{d\tau }}\;,{\frac {dx^{1}}{d\tau }}\;,{\frac {dx^{2}}{d\tau }}\;,{\frac {dx^{3}}{d\tau }}\right)$$

जहां व्युत्पन्न बिंदु पर लिया जाता है $p$, तो $\tau =\tau _{0}$.

बिंदु p से जाने वाले सभी वक्रों में स्पर्शरेखा सदिश होती है,न कि केवल विश्व रेखाएँ। दो सदिशों का योग फिर से किसी अन्य वक्र पर स्पर्शरेखा सदिश होता है और एक अदिश से गुणा करने पर भी यही होता है। इसलिए, एक बिंदु p में सभी स्पर्शरेखा सदिश एक रैखिक स्थान को फैलाते हैं, जिसे बिंदु p पर स्पर्शरेखा स्थान कहा जाता है। उदाहरण के लिए, पृथ्वी की घुमावदार सतह की तरह द्विआयामी स्थान लेते हुए, एक विशिष्ट बिंदु पर इसका स्पर्शरेखा स्थान घुमावदार स्थान का समतल सन्निकटन होगा।

विशेष सापेक्षता में विश्व रेखाएं

घटनाओं के बीच अंतराल को मापने के साधन के बिना अब तक एक विश्व रेखा और स्पर्शरेखा वैक्टर की अवधारणा का वर्णन किया गया है। सामान्य गणित इस के अनुसार: विशेष सापेक्षता का सिद्धांत संभावित विश्व रेखाओं पर कुछ बाधाएं डालता है। विशेष सापेक्षता में स्पेसटाइम का वर्णन विशेष समन्वय प्रणालियों तक सीमित है जो गति नहीं करते हैं और इसलिए या तो घूमते नहीं हैं, संदर्भों को निष्क्रिय फ्रेम कहा जाता है। ऐसी समन्वय प्रणालियों में, प्रकाश की गति स्थिर होती है। स्पेसटाइम की संरचना एक द्विरेखीय रूप द्वारा निर्धारित की जाती है, जो प्रत्येक जोड़ी की घटनाओं के लिए एक वास्तविक संख्या देता है। द्विरैखीय स्थिति को कभी-कभी स्पेसटाइम मीट्रिक कहा जाता है, लेकिन अलग-अलग घटनाओं के परिणामस्वरूप कभी-कभी मान शून्य होता है, गणित के मीट्रिक रिक्त स्थान में मीट्रिक के विपरीत, द्विरैखिक स्पेसटाइम पर गणितीय मीट्रिक नहीं होता है।

स्वंतत्र रूप से गिरने वाले कणों/वस्तुओं की विश्व रेखाओं को जियोडेजिक्स कहा जाता है। विशेष सापेक्षता में ये मिंकोवस्की अंतरिक्ष में सीधी रेखाएं हैं।

अक्सर समय इकाइयों को इस तरह चुना जाता है कि प्रकाश की गति को एक निश्चित कोण पर रेखाओं द्वारा दर्शाया जा सके,आमतौर पर 45 डिग्री पर ऊर्ध्वाधर (समय) अक्ष के साथ एक कोन बनाते हैं। सामान्य तौर पर, स्पेसटाइम में उपयोगी वक्र तीन प्रकार के हो सकते हैं (अन्य प्रकार आंशिक रूप से एक और आंशिक रूप से दूसरे प्रकार के होंगे) ;

• 'प्रकाश-समान' वक्र,प्रत्येक बिंदु पर प्रकाश की गति वाले होते है। वे स्पेसटाइम में एक कोन बनाते हैं, इसे दो भागों में विभाजित किया जाता हैं। स्पेसटाइम में कोन त्रि-आयामी है,दो आयामों के साथ चित्रों में एक रेखा के रूप में दिखाई देता है, और एक स्थानिक आयाम के साथ चित्रों में कोन के रूप में दबाया जाता है।

एक प्रकाश शंकु का एक उदाहरण, अंतरिक्ष समय में एक बिंदु से आने और जाने वाली सभी संभावित प्रकाश किरणों की त्रि-आयामी सतह। यहाँ, इसे एक स्थानिक आयाम को दबा कर दर्शाया गया है।

एक तेजी से गतिमान पर्यवेक्षक (केंद्र) के प्रक्षेपवक्र (विश्व रेखा) के साथ क्षणिक रूप से सह-चलती जड़त्वीय फ्रेम। ऊर्ध्वाधर दिशा समय को इंगित करती है, जबकि क्षैतिज दूरी को इंगित करती है, धराशायी रेखा पर्यवेक्षक का स्पेसटाइम है। छोटे बिंदु स्पेसटाइम में विशिष्ट घटनाएँ हैं। ध्यान दें कि जब पर्यवेक्षक गति करता है तो क्षणिक रूप से सह-चलती जड़त्वीय फ्रेम कैसे बदलता है।

* समय के समान वक्र,जिनकी गति प्रकाश की गति से कम होती है। ये वक्र प्रकाश-समान वक्रों द्वारा परिभाषित कोन के भीतर आने चाहिए। सामान्य भाषा में: विश्व रेखाएं स्पेसटाइम में समय-समान वक्र हैं।

*अंतरिक्ष की तरह वक्र प्रकाश कोन के बाहर गिरते है। उदाहरण के लिए ऐसे वक्र किसी भौतिक वस्तु की लंबाई का वर्णन कर सकते हैं। एक बेलन की परिधि और छड़ की लंबाई अंतरिक्ष जैसे वक्र हैं।

विश्व रेखा पर दी गई घटना में, स्पेसटाइम में मिन्कोव्स्की स्पेस को तीन भागों में बांटा गया है।

• दी गई घटना का भविष्य उन सभी घटनाओं से बनता है जो भविष्य के प्रकाश कोन के भीतर स्थित समय-समान वक्रों के माध्यम से प्राप्त की जा सकती हैं।
• दी गई घटना का अतीत उन सभी घटनाओं से बनता है जो घटना को प्रभावित कर सकती हैं अर्थात,जो पिछले प्रकाश कोन के भीतर दी गई घटना से विश्व रेखाओं से जुड़ी हो सकती है।
  • दी गई घटना में प्रकाश कोन उन सभी घटनाओं से बनता है जिन्हें प्रकाश किरणों के माध्यम से घटना से जोड़ा जा सकता है। जब हम रात में आकाश का निरीक्षण करते हैं,तो हम मूल रूप से पूरे स्पेसटाइम के भीतर केवल पिछले प्रकाश कोन को देखते हैं।
• अन्यत्र दो प्रकाश शंकुओं के बीच का क्षेत्र है। एक पर्यवेक्षक के अन्यंत्र अंक उनके लिए दुर्गम हैं;अतीत में केवल बिंदु ही पर्यवेक्षक को संकेत भेज सकते हैं। सामान्य प्रयोगशाला अनुभव में,सामान्य इकाइयों और माप के तरीकों का उपयोग करते हुए, ऐसा लग सकता है कि हम वर्तमान को देखते हैं, लेकिन वास्तव में प्रकाश के फैलने में हमेशा देरी होती है। उदाहरण के लिए,हम सूर्य को वैसे ही देखते हैं जैसे वह लगभग 8 मिनट पहले था,न कि अभी जैसा है। गैलीलियन/न्यूटोनियन सिद्धांत में वर्तमान के विपरीत, अन्यत्र घना है; यह त्रिआयामी आयतन नहीं है, बल्कि चतुर्विम समष्टि क्षेत्र है।
  • हाइपरप्लेन समकालिक अन्यत्र में शामिल है, जो किसी दिए गए पर्यवेक्षक के लिए एक ऐसे स्थान द्वारा परिभाषित किया गया है जो उनकी विश्व रेखा के लिए अतिपर्वलिक-ऑर्थोगोनल है। यह वास्तव में त्रि-आयामी है, हालांकि यह आरेख में द्वि सतह होगा क्योंकि एक स्पष्ट चित्र बनाने के लिए एक आयाम को हटाना पड़ा था। यद्यपि प्रकाश कोन किसी दिए गए स्पेसटाइम बिंदु में सभी पर्यवेक्षकों के लिए समान होते हैं,अलग-अलग पर्यवेक्षकों,अलग-अलग वेगों के साथ, लेकिन स्पेसटाइम में बिंदु पर संयोग से,दुनिया की रेखाएं होती हैं जो उनके सापेक्ष वेगों द्वारा निर्धारित कोण पर एक दूसरे को पार करती हैं,और इस प्रकार उनके पास अलग-अलग एक साथ हाइपरप्लेन हैं।
  • वर्तमान का अर्थ अक्सर एकल स्पेसटाइम घटना पर माना जाता है।

समकालिक हाइपरप्लेन

एक विश्व रेखा के बाद से $w(\tau )\in R^{4}$ एक वेग निर्धारित करता है चतुर्विम समष्टि $v={\frac {dw}{d\tau }}$ वह समय की तरह है, मिंकोव्स्की रूप $\eta (v,x)$ एक रैखिक कार्य निर्धारित करता है $R^{4}\rightarrow R$ द्वारा $x\mapsto \eta (v,x).$ मान लीजिए N इस रैखिक क्रियात्मक का रिक्त स्थान है। तब N को V के संबंध में समकालिक हाइपरप्लेन कहा जाता है। समकालीन सापेक्षता एक कथन है जो N और V पर निर्भर करता है। वास्तव में, N के संबंध में V का ऑर्थोगोनल पूरक है η

जब दो विश्व रेखाएँ u और w संबंधित हैं ${\frac {du}{d\tau }}={\frac {dw}{d\tau }},$ फिर वे एक ही समकालिक हाइपरप्लेन साझा करते हैं। यह हाइपरप्लेन गणितीय रूप से मौजूद है, लेकिन सापेक्षता में भौतिक संबंधों में प्रकाश द्वारा सूचना की गति शामिल है। उदाहरण के लिए, कूलम्ब के नियम द्वारा वर्णित पारंपरिक विद्युत स्थैनिक बल को एक साथ हाइपरप्लेन में चित्रित किया जा सकता है,लेकिन देखरेख और बल के सापेक्ष संबंधों में मंद क्षमता शामिल है।

सामान्य सापेक्षता में विश्व रेखाएं

सामान्य सापेक्षता में विश्व रेखाओं का उपयोग मूल रूप से विशेष सापेक्षता के समान है, इस अंतर के साथ कि स्पेसटाइम वक्रता हो सकता है। एक मीट्रिक मौजूद है और इसकी गतिशीलता आइंस्टीन क्षेत्र समीकरणों द्वारा निर्धारित की जाती हैं और स्पेसटाइम में द्रव्यमान-ऊर्जा वितरण पर निर्भर होती है। मीट्रिक प्रकाश जैसा,अंतरिक्ष जैसा और समय जैसा वक्र को फिर से परिभाषित करता है। इसके अलावा, सामान्य सापेक्षता में, विश्व रेखाएं स्पेसटाइम में समयबद्ध वक्र होती हैं, जहां समयबद्ध वक्र प्रकाश कोन के भीतर आते हैं। हालांकि, जरूरी नहीं कि एक प्रकाश कोन समय अक्ष पर 45 डिग्री झुका हो। हालांकि,यह चुने हुए समन्वय प्रणाली की एक कलाकृति है, और सामान्य सापेक्षता की समन्वय स्वतंत्रता को दर्शाता है। कोई भी समयबद्ध वक्र एक उचित फ्रेम को स्वीकार करता है जिसका समय अक्ष उस वक्र से मेल खाता है, और, चूंकि कोई पर्यवेक्षक विशेषाधिकार प्राप्त नहीं है, इसलिए हमेशा एक स्थानीय समन्वय प्रणाली ढूंढ सकते हैं जिसमें प्रकाश कोन 45 डिग्री समय अक्ष पर झुका हुआ है। उदाहरण के लिए एडिंगटन-फिंकेलस्टीन निर्देशांक भी देखें।

स्वतंत्र कणों या वस्तुओं की विश्व रेखाओं (जैसे कि सूर्य के चारों ओर ग्रह या अंतरिक्ष में एक अंतरिक्ष यात्री) को जियोडेसिक्स कहा जाता है।

परिमाण क्षेत्र सिद्धांत में विश्व रेखाएं

परिमाण क्षेत्र सिद्धांत, वह ढांचा है जिसमें सभी आधुनिक कण भौतिकी का वर्णन परिमाणिक क्षेत्रों के सिद्धांत के रूप में वर्णित किया जाता है। हालांकि, इसकी व्यापक रूप से सराहना नहीं की गई, और यह फेनमैन के बाद से जाना जाता है जिसके अनुसार क्वांटम क्षेत्र सिद्धांतों को समान रूप से विश्व रेखाओं के संदर्भ में वर्णित किया जा सकता है। परिमाण क्षेत्र सिद्धांत का विश्व रेखा सूत्रीकरण गेज सिद्धांतों और विद्युत चुम्बकीय क्षेत्रों के गैर रेखीय प्रभावों का विवरण में विभिन्न गणनाओं के लिए विशेष रूप से उपयोगी साबित हुआ है।।

साहित्य में विश्व पंक्तियाँ

1884 में सी.एच.हिंटन ने एक निबंध लिखा चौथा आयाम क्या है?, जिसे उन्होंने एक वैज्ञानिक उपन्यास के रूप में प्रकाशित किया। उन्होंने लिखा है

तो फिर,चार-आयामी प्राणी स्वयं क्यों नहीं होने चाहिए,और हमारी क्रमिक स्थिति उन्हें त्रि-आयामी अंतरिक्ष के माध्यम से पारित करने के लिए कहती है जिसमें हमारी चेतना सीमित है।

मानव विश्व रेखाओं का एक लोकप्रिय विवरण जे.सी.फील्ड्स द्वारा टोरंटो विश्वविद्यालय में सापेक्षता के प्रारंभिक दिनों में दिया गया था। जैसा कि टोरंटो के वकील नॉर्मन रॉबर्टसन ने वर्णित किया है:

मुझे याद है [फ़ील्ड] रॉयल कैनेडियन संस्थान में शनिवार की शाम के एक संभाषण में व्याख्यान दे रहा था। यह एक गणितीय कल्पना होने के लिए विज्ञापित किया गया था — और यह था! अभ्यास का सार इस प्रकार था: उन्होंने माना कि, उनके जन्म के साथ, प्रत्येक इंसान के पास एक लंबा रेशा या धागे के साथ किसी प्रकार की आध्यात्मिक आभा होती है, जो जीवन भर उसके पीछे यात्रा करती है। फिर उन्होंने कल्पना में आगे बढ़कर उन जटिल उलझावों का वर्णन किया जो प्रत्येक व्यक्ति अन्य व्यक्तियों के साथ अपने संबंधों में शामिल हो गया,युवाओं की साधारण उलझनों की तुलना उन जटिल गांठों से की जो बाद के जीवन में विकसित होती हैं।

कर्ट वोनगुट ने अपने उपन्यास स्लॉटरहाउस-पांच में सितारों और लोगों की दुनिया का वर्णन किया है:

“बिली पिलग्रिम का कहना है कि ब्रह्मांड बहुत सारे चमकीले छोटे बिंदुओं की तरह नहीं दिखता है जो ट्रालफ़ामाडोर के प्राणियों के लिए है। प्राणी देख सकते हैं कि प्रत्येक तारा कहाँ है और कहाँ जा रहा है,ताकि आकाश दुर्लभ,चमकदार स्पेगेटी से भर जाए।और ट्रालफैमडोरियन मनुष्य को दो पैरों वाले प्राणियों के रूप में भी नहीं देखते हैं। बिली पिलग्रिम कहते हैं, वे उन्हें बड़े मिलपेड के रूप में देखते हैं - एक छोर पर बच्चों के पैर और दूसरी तरफ बूढ़े लोगों के पैर।

लगभग सभी वैज्ञानिक-कथा कहानियां विश्व रेखा की अवधारणा का सक्रिय रूप से उपयोग करती हैं। जैसे कि समय यात्रा को सक्षम करने के लिए, इस अवधारणा को एक रेखीय संरचना में फिट करने के लिए एक आयामी समयरेखा में अधिक सरलीकृत करती है,जो वास्तविकता के मॉडल में फिट नहीं होती है। ऐसी समय मशीनों को अक्सर तात्कालिक होने के रूप में चित्रित किया जाता है,इसकी सामग्री एक बार प्रस्थान करती है और अंतरिक्ष में एक ही शाब्दिक भौगोलिक बिंदु पर पहुंचती हैं। यह अक्सर एक निर्देश टिप्पणी के बिना,या अंतर्निहित धारणा के साथ किया जाता है कि निर्देश स्थानीय है। इसके लिए या तो सटीक टेलीपोर्टेशन की आवश्यकता होगी,क्योंकि एक घूर्णन ग्रह,गति वर्धन के अधीन होते है और यह एक निष्क्रिय फ्रेम नहीं है,या टाइम मशीन को उसी स्थान पर रहने के लिए, इसकी सामग्री जमी हुई है।

लेखक ओलिवर फ्रैंकलिन ने 2008 में वर्ल्ड लाइन्स नामक एक विज्ञान कथा कार्य प्रकाशित किया जिसमें उन्होंने आम लोगों के लिए परिकल्पना की एक सरल व्याख्या की।

लघु कहानी लाइफ लाइन में,लेखक रॉबर्ट ए.हेनलेन ने एक व्यक्ति की विश्व रेखा का वर्णन किया है:

वह एक पत्रकार के पास गया। मान लीजिए हम आपको एक उदाहरण के रूप में लेते हैं। आपका नाम रोजर्स है, है ना? बहुत अच्छी तरह से,रोजर्स,आप एक अंतरिक्ष-समय की घटना हैं जिसकी अवधि चार तरह से है। आप छह फीट लंबे नहीं हैं, आप लगभग बीस इंच चौड़े हैं और शायद दस इंच मोटे हैं। समय के साथ, आपके पीछे इस अंतरिक्ष-समय की घटना का विस्तार होता है,जो शायद उन्नीस-सोलह तक पहुंचता है, जिसमें से हम यहां समय अक्ष के समकोण पर एक अनुप्रस्थ काट हैं,और वर्तमान जितना मोटा। सबसे दूर एक बच्चा है, जो खट्टे दूध की महक और अपना नाश्ता बिब पर गिरा रहा है। दूसरे छोर पर, शायद, १९८० के दशक में कहीं एक बुजुर्ग आदमी है।

इस अंतरिक्ष-समय की घटना की कल्पना करें जिसे हम रोजर्स को एक लंबा गुलाबी कीड़ा कहते हैं, जो वर्षों से निरंतर है, एक छोर उसकी माँ के गर्भ में है,और दूसरा कब्र पर है ...

हेनलेन के मेथुसेलाह के बच्चे इस शब्द का उपयोग करते हैं, जैसा कि जेम्स ब्लिशो के समय का क्विन कुंक्स (बीप से विस्तारित) करता है।

5pb द्वारा निर्मित, स्टींस गेट नामक एक दृश्य उपन्यास, दुनिया की रेखाओं के स्थानांतरण पर आधारित एक कहानी बताता है। स्टीन्स; गेट विज्ञान साहसिक श्रृंखला का एक हिस्सा है। पूरी श्रृंखला में विश्व रेखाओं और अन्य भौतिक अवधारणाओं जैसे डिरैक सागर का भी उपयोग किया जाता है।

नील स्टीफेंसन के उपन्यास अनाथेम में आध्यात्मिक यथार्थवाद और नामवाद के बीच एक दार्शनिक बहस के बीच रात के खाने पर विश्वव्यापी चर्चा शामिल है।

एब्सोल्यूट च्वाइस विश्व रेखाओं को एक उप सतह और व्यवस्था उपकरण के रूप में दर्शाता है।

एक रणनीतिक युद्धाभ्यास के रूप में एक लगभग बंद समय-समान पथ को पूरा करने की कोशिश कर रहा एक अंतरिक्ष जहाज चार्ल्स स्ट्रॉस द्वारा पृष्ठभूमि वैयक्तिक विशेषता अंतरिक्ष का एक मुख्य सतह उपकरण बनाता है।

यह भी देखें

• विशिष्ट प्रकार की विश्व रेखाएं
  • जियोडेसिक्स
  • क्लोज्ड टाइमलाइक कर्व ्स
  • कारण संरचना#वक्र, वक्र जो विभिन्न प्रकार की विश्व रेखा का प्रतिनिधित्व करते हैं
  • आइसोट्रोपिक लाइन
• फेनमैन आरेख
• समय भूगोल

संदर्भ

• Minkowski, Hermann (1909), "Raum und Zeit" , Physikalische Zeitschrift, 10: 75–88

• Various English translations on Wikisource: Space and Time

• Ludwik Silberstein (1914) Theory of Relativity, p 130, Macmillan and Company.

• World lines article on h2g2.

• in depth text on world lines and special relativity