सतह प्रभार

सतह प्रभार एक द्वि-आयामी सतह है जिसमें गैर-शून्य विद्युत प्रभार होता है। ये विद्युत प्रभार इस 2-D सतह पर निरुद्ध हैं, और सतह पर प्रभार वितरण का वर्णन करने के लिए प्रति वर्ग मीटर (C•m−2) कूलम्ब में मापी गई सतह प्रभार घनत्व का उपयोग किया जाता है।विद्युत विभव एक सतही प्रभार पर निरंतर होता है और विद्युत क्षेत्र विच्छिन्न होता है, लेकिन अनंत नहीं होता; यह तब तक है जब तक कि सतह प्रभार में द्विध्रुव परत न हो। इसकी तुलना में, संभावित और विद्युत क्षेत्र दोनों किसी बिंदु प्रभार या रैखिक प्रभार पर अलग हो जाते हैं।

भौतिकी में, संतुलन पर, एक उपयुक्त संवाहक के आंतरिक भाग पर कोई प्रभार नहीं होता है; इसके अतिरिक्त, संवाहक का संपूर्ण प्रभार सतह पर रहता है। हालाँकि, यह केवल अनंत विद्युत प्रतिरोधकता और चालकता के उपयुक्त स्थिति पर लागू होता है; एक वास्तविक चालक का अधिकांश प्रभार चालक की सतह के सतही प्रभाव के अंदर रहता है। असंवाहक सामग्री के लिए, बाहरी विद्युत क्षेत्र के अनुप्रयोग पर, सामग्री में धनात्मक प्रभार और ऋणात्मक प्रभार विपरीत दिशाओं में थोड़ा आगे बढ़ेंगे, जिसके परिणामस्वरूप विस्तृत निकाय में ध्रुवीकरण घनत्व और सतह पर बाध्य प्रभार होता है।

रसायन विज्ञान में, कई अलग-अलग प्रक्रियाएं हैं जो एक सतह को प्रभारित कर सकती हैं, जिसमें आयनों का अवशोषण, प्राटॉनीकरण/अवक्षेपण और, जैसा कि ऊपर चर्चा की गई है, एक बाहरी विद्युत क्षेत्र का अनुप्रयोग सम्मिलित है। सतह प्रभार एक विद्युत क्षेत्र का उत्सर्जन करता है, जो कण प्रतिकर्षण और आकर्षण का कारण बनता है, जिससे कई कोलाइडल गुण प्रभावित होते हैं।

सतही प्रभार व्यावहारिक रूप से हमेशा कण की सतह पर दिखाई देता है जब इसे द्रव में रखा जाता है। अधिकांश तरल पदार्थों में आयन, धनात्मक (धनायन) और ऋणात्मक (आयन) होते हैं। ये आयन वस्तु की सतह के साथ परस्पर क्रिया करते हैं। इस परस्पर क्रिया से उनमें से कुछ का सतह पर अवशोषण हो सकता है। यदि अधिशोषित धनायनों की संख्या अधिशोषित ऋणायनों की संख्या से अधिक हो जाती है, तब सतह पर शुद्ध धनात्मक विद्युत प्रभार होगा।

सतह रासायनिक समूह का पृथक्करण (रसायन विज्ञान) एक अन्य संभावित क्रियाविधि है जो सतही प्रभार की ओर ले जाती है।

घनत्व

Main article: सतह प्रभार घनत्व

सतह प्रभार घनत्व को विद्युत प्रभार, q की मात्रा के रूप में परिभाषित किया गया है, जो दिए गए क्षेत्र A की सतह पर सम्मिलित है :

$$\sigma ={\frac {q}{A}}$$

संवाहक

गॉस के नियम के अनुसार, प्रयुक्त धारा को ले जाने वाले संतुलन पर एक संवाहक के आंतरिक भाग पर कोई प्रभार नहीं होता है। इसके अतिरिक्त, संवाहक का संपूर्ण प्रभार सतह पर रहता है, और समीकरण द्वारा व्यक्त किया जा सकता है:

$$\sigma =E\varepsilon _{0}$$

जहाँ E चालक पर प्रभार के कारण उत्पन्न विद्युत क्षेत्र है और $\varepsilon _{0}$ मुक्त स्थान की पारगम्यता है। यह समीकरण केवल पूर्ण रूप से बड़े क्षेत्र वाले संवाहकों के लिए परिशुद्ध है, लेकिन यह एक सदृश प्रदान करता है यदि E को संवाहक की सतह से एक पूर्ण रूप से छोटे यूक्लिडियन दूरी पर मापा जाता है।

कोलाइड्स और डूबी हुई वस्तुएं

मिश्रण	रासायनिक सूत्र	जीरो प्रभार का बिन्दु
टंगस्टन(VI) ऑक्साइड	WO3	0.2–0.5
सिलिकन कार्बाइड (अल्फा)	SiC	2–3.5
मैगनीज(IV) ऑक्साइड	MnO2	4–5
सिलिकॉन नाइट्राइड	Si3N4	6–7
थैलियम(I) ऑक्साइड	Tl2O	8
कॉपर(II) ऑक्साइड	CuO	9.5
निकेल(II) ऑक्साइड	NiO	10–11

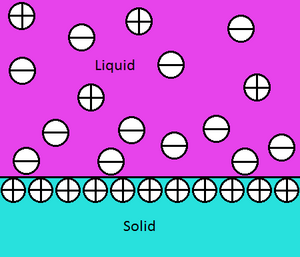
जब किसी सतह को विद्युत अपघट्य युक्त विलयन में डुबोया जाता है, तब यह शुद्ध सतह प्रभार विकसित करता है। यह प्रायः आयनिक अवशोषण के कारण होता है। जलीय विलयनों में सार्वभौमिक रूप से धनात्मक और ऋणात्मक आयन (क्रमश: धनायन और ऋणायन) होते हैं, जो सतह पर आंशिक प्रभारों के साथ परस्पर क्रिया करते हैं, सतह को अवशोषण करते हैं और इस प्रकार सतह को आयनित करते हैं और एक शुद्ध सतह प्रभार बनाते हैं। इस शुद्ध प्रभार के परिणामस्वरूप सतह विभव [L] होती है, जिसके कारण सतह प्रतिआयन के समूह से घिरा हुआ होता है, जो सतह से विलयन तक जाती है, और सामान्यतः कणों के बीच प्रतिकर्षण का परिणाम होता है। सामग्री में आंशिक प्रभार जितना बड़ा होता है, उससे अधिक आयन सतह पर अवशोषण कर लिए जाते हैं, और प्रतिआयन का समूह समान रूप से बड़ा होता है। विद्युत-अपघट्य की उच्च सांद्रता वाला एक विलयन भी प्रति-आयन समूह के आकार को बढ़ाता है। इस आयन/प्रतिवाद परत को विद्युतीय दोहरी परत के रूप में जाना जाता है।

एक विलयन का pH भी सतह के प्रभार को बहुत प्रभावित कर सकता है क्योंकि कणों की सतह पर सम्मिलित कार्यात्मक समूहों में प्रायः ऑक्सीजन या नाइट्रोजन हो सकते हैं, दो परमाणु जिन्हें प्रभार करने के लिए प्रोटोनित या अवक्षेपित किया जा सकता है। इस प्रकार, जैसे-जैसे हाइड्रोजन आयनों की सांद्रता परिवर्तित होती है, वैसे-वैसे कणों का सतही प्रभार भी परिवर्तित होता है। एक निश्चित pH पर, औसत सतही प्रभार शून्य के बराबर होगा; इसे शून्य प्रभार बिंदु (PZC) के रूप में जाना जाता है। सामान्य पदार्थों और उनसे जुड़े PZCs की सूची दाईं ओर दिखाई गई है।

अंतराफलक विभव

एक अन्तराफलक को दो अलग-अलग चरणों के बीच निर्मित सामान्य सीमा के रूप में परिभाषित किया जाता है, जैसे ठोस और गैस के बीच। विद्युत विभव, या प्रभार, किसी वस्तु की विद्युत क्षेत्र में स्थानांतरित विभव का परिणाम है। इस प्रकार एक अंतराफलक विभव को दो चरणों के बीच सामान्य सीमा पर स्थित प्रभार के रूप में परिभाषित किया जाता है (उदाहरण के लिए, एक प्रोटीन की सतह पर ग्लूटॉमिक अम्ल जैसे अमीनो अम्ल में इसकी पार्श्व श्रंखला कार्बोक्जिलिक अम्ल 4.1 से अधिक pH वाले वातावरण में अवक्षेपित हो सकती है। सतह पर एक प्रभारित अमीनो अम्ल उत्पन्न करता है, जो एक अंतराफलक विभव उपन्न करेगा)। विद्युतीय दोहरी परत के निर्माण के लिए अंतराफलक विभव जिम्मेदार है, जिसमें विद्युत-गतिक संवृति कहलाने वाले अनुप्रयोगों की एक विस्तृत श्रृंखला है। विद्युतीय दोहरी परत के सिद्धांत का विकास नीचे वर्णित है।

हेल्महोल्ट्ज़

मॉडल को 'विद्युतीय दोहरी परत' नाम दिया गया था जिसे सबसे पहले हरमन वॉन हेल्महोल्ट्ज़ ने पेश किया था। यह मानता है कि एक विलयन केवल विद्युत अपघट्य से बना है, इलेक्ट्रोड के पास कोई प्रतिक्रिया नहीं होती है जो इलेक्ट्रॉनों को स्थानांतरित कर सकती है, और केवल वैन डेर वाल का बल विलयन और इलेक्ट्रोड में आयनों के बीच सम्मिलित हैं। ये अन्तः क्रिया केवल इलेक्ट्रोड से जुड़े प्रभार घनत्व के कारण उत्पन्न होते हैं जो इलेक्ट्रोड की सतह पर इलेक्ट्रॉनों की अधिकता या कमी से उत्पन्न होते हैं। विद्युत तटस्थता बनाए रखने के लिए इलेक्ट्रोड के प्रभार को उसकी सतह के सदृश आयनों के पुनर्वितरण द्वारा संतुलित किया जाएगा। आकर्षित आयन इस प्रकार इलेक्ट्रोड के प्रभार को संतुलित करने वाली एक परत बनाते हैं। एक आयन इलेक्ट्रोड के पास जितनी निकटतम दूरी तक आ सकता है, वह आयन की त्रिज्या और एक व्यक्तिगत आयन के चारों ओर एक विलायकीयन क्षेत्र तक सीमित होगा। समस्त रूप से, प्रभार की दो परतें और इलेक्ट्रोड से बाहरी परत (बाहरी हेल्महोल्ट्ज़ सतह) के किनारे तक एक संभावित गिरावट देखी जाती है। उपरोक्त विवरण को देखते हुए, हेल्महोल्ट्ज़ मॉडल दो अलग-अलग प्रभार प्लेटों के साथ एक संधारित्र के प्रकृति के बराबर है, जिसके लिए प्लेटों से बढ़ती दूरी पर एक रैखिक संभावित गिरावट देखी जाती है।
हेल्महोल्त्ज़ मॉडल, जबकि अन्तराफलक के विवरण के लिए एक अच्छी नींव कई महत्वपूर्ण कारकों को ध्यान में नहीं रखती है: विलयन में प्रसार/मिश्रण, सतह पर अवशोषण की संभावना और विलायक द्विध्रुवीय क्षणों और इलेक्ट्रोड के बीच परस्पर क्रिया।

गौई-चैपमैन

एक दोहरी परत बनाने के लिए नकारात्मक प्रभार की कई परतें धनात्मक रूप से प्रभारित सतह के पास जमा हो जाती हैं।

गौई-चैपमैन सिद्धांत सतह विभव पर स्थिर सतह प्रभार के प्रभाव का वर्णन करता है। लुई जॉर्जेस गौई ने सुझाव दिया कि प्रभारित सतह पर अंतराफलक विभव को इसकी सतह से जुड़े कई आयनों की उपस्थिति और विलयन में विपरीत प्रभार के समान संख्या में आयनों की उपस्थिति के लिए अधीन किया जा सकता है। एक सकारात्मक सतह प्रभार एक दोहरी परत बनाएगा, क्योंकि विलयन में नकारात्मक आयन सकारात्मक सतह प्रभार को संतुलित करते हैं। प्रतिआयन कठोर रूप से संघटित नहीं होते हैं, लेकिन तरल चरण में फैल जाते हैं जब तक कि उनके विचलन द्वारा स्थापित प्रतिविभव इस प्रवृत्ति को प्रतिबंधित नहीं करती है। प्रतिआयनों की गतिज ऊर्जा, भाग में, परिणामी विसरित दोहरी परत के घनत्व को प्रभावित करेगी। C के बीच संबंध, सतह पर प्रतिआयन संकेन्द्रण, और $C_{o}$, बाहरी विलयन में प्रतिआयन संकेन्द्रण, बोल्टज़मान कारक है:

$$C=C_{0}e^{-{\frac {\psi ze}{k_{\mathrm {B} }T}}}$$

जहाँ z आयन पर प्रभार है, e प्रोटॉन का प्रभार है, k_B बोल्ट्जमैन स्थिरांक है और ψ प्रभारित सतह विभव है।

हालांकि यह सतह के सदृश अशुद्ध है, क्योंकि यह मानता है कि मोलीय एकाग्रता गतिविधि के बराबर है। यह भी मानता है कि आयनों को बिंदु प्रभारों के रूप में प्रतिरूपित किया गया था और बाद में संशोधित किया गया था। संशोधित गौई-चैपमैन सिद्धांत के रूप में जाना जाने वाला इस सिद्धांत का एक सुधार, निकटतम दृष्टिकोण के सतह के रूप में सतह के साथ उनकी परस्पर क्रिया के संबंध में आयनों के परिमित आकार को सम्मिलित करता है।

सतह विभव

सतह के प्रभार और सतह विभव के बीच के संबंध को ग्राहम समीकरण द्वारा व्यक्त किया जा सकता है, जो गौई-चैपमैन सिद्धांत से विद्युतीयता की स्थिति को मानते हुए प्राप्त किया गया है, जिसमें कहा गया है कि दोहरी परत का कुल प्रभार सतह के प्रभार के ऋणात्मक के बराबर होना चाहिए। एक आयामी पोइसन के समीकरण का उपयोग करना और यह मानते हुए कि, असीम रूप से बड़ी दूरी पर, संभावित प्रवणता 0 के बराबर है, ग्राहम समीकरण प्राप्त होता है:

$$\sigma ={\sqrt {8c_{0}\varepsilon \varepsilon _{0}k_{\mathrm {B} }N_{a}T}}\sinh \left({\frac {ze\psi _{0}}{2k_{\mathrm {B} }T}}\right)$$

कम विभव के स्थिति में, $\sinh(x)$ तक विस्तारित किया जा सकता है $\sinh(x)=x+x^{3}/3!+\cdots$ $\approx$ $x$, तथा $\lambda _{D}$ डेबी लंबाई के रूप में परिभाषित किया गया है। जो सरल अभिव्यक्ति की ओर ले जाता है:

$$\sigma ={\frac {\varepsilon \varepsilon _{0}\psi _{0}}{\lambda _{D}}}$$

स्टर्न

दोहरी परत का ओटो स्टर्न मॉडल अनिवार्य रूप से हेल्महोल्ट्ज़ और गौई-चैपमैन सिद्धांतो का संयोजन है। उनके सिद्धांत में कहा गया है कि आयनों का आकार सीमित होता है, इसलिए वे सतह पर कुछ नैनोमीटर से अधिक सदृश नहीं आ सकते हैं। स्टर्न परत के रूप में पहचानी जाने वाली दूरी के माध्यम से, आयनों को सतह पर संदर्भित एक बिंदु तक ले जाया जा सकता है, जहां आयन विस्तृत तरल से मिलते हैं, जिसे स्खलन सतह कहा जाता है। स्खलन सतह में संभावित Ψ घटकर जीटा विभव के रूप में जाना जाता है। हालांकि जीटा विभव एक मध्यवर्ती मूल्य है, जहां तक ​​​​विद्युत् स्थैतिक प्रतिकर्षण का संबंध है, इसे कभी-कभी सतह विभव से अधिक महत्वपूर्ण माना जाता है।

अनुप्रयोग

प्रभार की गई सतहें अत्यंत महत्वपूर्ण हैं और कई अनुप्रयोगों में उपयोग की जाती हैं। उदाहरण के लिए, बड़े कोलाइडल कणों के विलयन लगभग पूरी तरह से सतह के प्रभार के कारण प्रतिकर्षण पर निर्भर करते हैं जिससे वे बिखरे रहते है। यदि इन प्रतिकारक बलों को बाधित किया जाना था, संभवतया नमक या बहुलक के अतिरिक्त, कोलाइडल कण अब निलंबन को बनाए रखने में सक्षम नहीं होंगे और बाद में ऊर्ण पिंडन करेंगे।

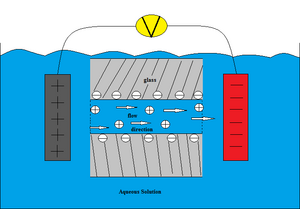
विद्युतगतिकी घटना

विद्युतगतिकी घटना एक दोहरी परत से उत्पन्न होने वाले विभिन्न प्रभावों को संदर्भित करती है। एक उल्लेखनीय उदाहरण वैद्युतकणसंचलन है, जहां एक माध्यम में निलंबित प्रभारित कण एक लागू विद्युत क्षेत्र के परिणामस्वरूप गति करेगा। वैद्युतकणसंचलन व्यापक रूप से आकार और प्रभार के आधार पर प्रोटीन जैसे अणुओं को अलग करने के लिए जैव रसायन में उपयोग किया जाता है। अन्य उदाहरणों में विद्युत असमस, अवसादन विभव और द्रवीभूत विभव सम्मिलित हैं।

प्रोटीन

प्रोटीन में प्रायः उनकी सतहों पर सम्मिलित समूह होते हैं जिन्हें pH के आधार पर आयनित या विआयनीकृत किया जा सकता है, जिससे प्रोटीन के सतही प्रभार को बदलना अपेक्षाकृत आसान हो जाता है। प्रोटीन की गतिविधि पर इसका विशेष रूप से महत्वपूर्ण प्रभाव पड़ता है जो एंजाइम या झिल्ली प्रवाहों के रूप में कार्य करता है, मुख्य रूप से, प्रोटीन की सक्रिय स्थल में एक विशिष्ट कार्यद्रव को बाँधने में सक्षम होने के लिए सही सतह प्रभार होना चाहिए।

आसंजक/विलेपन

प्रभारित सतहें प्रायः ऐसी सतहें बनाने में उपयोगी होती हैं जो कुछ अणुओं को अवशोषण नहीं कर पाएंगी (उदाहरण के लिए, क्षारकीय प्रोटीनों के अवशोषण को रोकने के लिए, एक सकारात्मक रूप से प्रभारित सतह का उपयोग किया जाना चाहिए)। बहुलक इस संबंध में बहुत उपयोगी हैं कि उन्हें क्रियाशील किया जा सकता है ताकि उनमें आयनीकरणीय समूह हों, जो एक जलीय विलयन में डूबे रहने पर एक सतह प्रभार प्रदान करने का काम करते हैं।