रुद्धोष्म प्रक्रम

ऊष्मप्रवैगिकी में, एक स्थिरोष्म प्रक्रिया (ग्रीक: एडियाबाटोस, अगम्य) एक प्रकार की उष्मागतिकीय प्रक्रिया है जो ऊष्मप्रवैगिकी प्रणाली और इसके पर्यावरण (प्रणालियों) के बीच ऊष्मा या द्रव्यमान को स्थानांतरित किए बिना होती है। समतापी प्रक्रिया के विपरीत, एक स्थिरोष्म प्रक्रिया केवल कार्य (ऊष्मागतिकी) के रूप में परिवेश में ऊर्जा स्थानांतरित करती है।Cite error: Closing </ref> missing for <ref> tag ऊष्मप्रवैगिकी में एक प्रमुख अवधारणा के रूप में स्थिरोष्म प्रक्रिया उस सिद्धांत का समर्थन करती है जो ऊष्मप्रवैगिकी के पहले नियम की व्याख्या करता है।

कुछ रासायनिक और भौतिक प्रक्रियाएं इतनी तेजी से होती हैं कि ऊर्जा प्रणाली में ऊष्मा के रूप में प्रवेश या बाहर नहीं निकल पाती है, जिससे एक सुविधाजनक स्थिरोष्म सन्निकटन हो जाता है।^[1] उदाहरण के लिए, रूद्धोष्म ज्वाला ताप इस सन्निकटन का उपयोग ज्वाला के तापमान की ऊपरी सीमा की गणना करने के लिए करता है, यह मानते हुए कि दहन अपने परिवेश में कोई ऊष्मा नहीं खोता है।

मौसम विज्ञान और समुद्र विज्ञान में, रूद्धोष्म शीतलन नमी या लवणता का संघनन पैदा करता है, द्रव खण्ड़ को अधिसंतृप्ति करता है। इसलिए, अधिकता को दूर किया जाना चाहिए। वहां, प्रक्रिया एक छद्म-स्थिरोष्म प्रक्रिया बन जाती है जिससे तरल पानी या नमक जो संघनित होता है उसे आदर्श तात्कालिक वर्षा द्वारा गठन पर हटा दिया जाता है। प्रच्छन्न-स्थिरोष्म प्रक्रिया को केवल विस्तार के लिए परिभाषित किया गया है क्योंकि एक संपीड़ित खण्ड़ ऊष्म हो जाता है और असंतृप्त रहता है।^[2]

विवरण

एक प्रणाली में या प्रणाली से ऊष्मा के हस्तांतरण के बिना एक प्रक्रिया, जिसमे Q = 0 हो, वह स्थिरोष्म कहलाती है, और इस तरह की प्रणाली को स्थिरोष्म रूप से पृथक कहा जाता है।^[3]^[4] सरलीकृत धारणा प्रायः बनाई जाती है कि एक प्रक्रिया स्थिरोष्म होती है। उदाहरण के लिए, एक यन्त्र के सिलेंडर के भीतर एक गैस (वायुरूप द्रव्य) का संपीड़न इतनी तेजी से होता है कि संपीड़न प्रक्रिया के समय के पैमाने पर, प्रणाली की ऊर्जा का थोड़ा सा हिस्सा ऊष्मा के रूप में परिवेश में स्थानांतरित कि या जा सकता है। भले ही सिलेंडर ऊष्मारोधी नहीं है और काफी प्रवाहकीय है, उस प्रक्रिया को स्थिरोष्म होने के लिए आदर्श बनाया गया है। ऐसी प्रणाली की विस्तार प्रक्रिया के लिए भी यही कहा जा सकता है।

रूद्धोष्म अलगाव की धारणा उपयोगी है और प्रायः प्रणाली के व्यवहार के एक अच्छे पहले सन्निकटन की गणना करने के लिए इस तरह के अन्य आदर्शों के साथ जोड़ा जाता है। उदाहरण के लिए, पियरे-साइमन लाप्लास के अनुसार, जब ध्वनि एक गैस में यात्रा करती है, तो माध्यम में ऊष्मा चालन के लिए कोई समय नहीं होता है, और इसलिए ध्वनि का प्रसार रूद्धोष्म होता है। ऐसी स्थिरोष्म प्रक्रिया के लिए, प्रत्यास्थता मापांक (यंग का मापांक) $E = γP$ के रूप में व्यक्त किया जा सकता है, जहाँ पर निरंतर दबाव ( $γ = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}Cp/Cv$ ) और स्थिर आयतन पर ताप क्षमता अनुपात $γ$ है और $P$ गैस का दबाव है।

रूद्धोष्म धारणा के विभिन्न अनुप्रयोग

एक बंद प्रणाली के लिए, ऊष्मप्रवैगिकी के पहले नियम को इस प्रकार लिखा जा सकता है: $Δ U = Q - W$ , जहाँ पर $Δ U$ प्रणाली की आंतरिक ऊर्जा के परिवर्तन को दर्शाता है, $Q$ उष्मा के रूप में इसमें जोड़ी गई ऊर्जा की मात्रा को, और $W$ तंत्र द्वारा अपने परिवेश पर किये गए कार्य को दर्शाता है।

यदि प्रणाली में ऐसी दृढ़ बाधाएँ हैं कि कार्य को अंदर या बाहर ( $W = 0$ ) स्थानांतरित नहीं किया जा सकता है, और बाधाएँ स्थिरोष्म नहीं हैं और ऊर्जा को ऊष्मा ( $Q > 0$ ) के रूप में जोड़ा जाता है, और कोई चरण परिवर्तन नहीं होता है, तो प्रणाली का तापमान बढ़ जाएगा।
यदि प्रणाली में ऐसी दृढ़ बाधाएँ हैं कि दबाव-आयतन का काम नहीं किया जा सकता है, परन्तु बाधाएँ ( $Q = 0$ ) स्थिरोष्म हैं, और ऊर्जा को समआयतनिक प्रक्रिया (स्थिर मात्रा) के रूप में जोड़ा जाता है जो घर्षण के रूप में काम करता है या प्रणाली के भीतर एक विस्कासी तरल पदार्थ ( $W < 0$ ) का विलोड़न करता है, और कोई चरण परिवर्तन नहीं होता है, तो प्रणाली का तापमान बढ़ जाएगा।
यदि प्रणाली की बाधाएँ स्थिरोष्म ( $Q = 0$ ) हैं परन्तु दृढ़ ( $W \neq 0$ ) नहीं, और, एक कल्पित आदर्श प्रक्रिया में, ऊर्जा को घर्षण रहित, गैर-विस्कासी दबाव-मात्रा कार्य के रूप में प्रणाली ( $W < 0$ ) में जोड़ा जाता है, और कोई चरण परिवर्तन नहीं होता है तो प्रणाली का तापमान बढ़ जाएगा। ऐसी प्रक्रिया को एक समऐन्ट्रॉपिक प्रक्रिया कहा जाता है और इसे प्रतिवर्ती कहा जाता है। आदर्श रूप से, यदि प्रक्रिया को उलट दिया गया तो ऊर्जा पूरी तरह से प्रणाली द्वारा किए गए कार्य के रूप में पुनर्प्राप्त की जा सकती है। यदि प्रणाली में एक संपीड़ित गैस होती है और मात्रा में कम हो जाती है, तो गैस की स्थिति की अनिश्चितता कम हो जाती है, और प्रतीत होता है कि प्रणाली की एंट्रॉपी कम हो जाएगी, परन्तु प्रणाली का तापमान बढ़ जाएगा क्योंकि प्रक्रिया समऐन्ट्रॉपिक ( $Δ S = 0$ ) है।
यदि प्रणाली की बाधाएँ स्थिरोष्म नहीं हैं, और ऊर्जा को ऊष्मा के रूप में स्थानांतरित किया जाता है, तो एंट्रॉपी को प्रणाली में ऊष्मा के साथ स्थानांतरित किया जाता है। ऐसी प्रक्रिया न तो स्थिरोष्म है और न ही समऐन्ट्रॉपिक, ऊष्मप्रवैगिकी के दूसरे नियम के अनुसार Q > 0, और ΔS > 0 है।

स्वाभाविक रूप से होने वाली स्थिरोष्म प्रक्रियाएं अपरिवर्तनीय हैं (एन्ट्रॉपी उत्पन्न होती है)।

स्थिरोष्म रूप से पृथक प्रणाली में कार्य के रूप में ऊर्जा के हस्तांतरण की कल्पना दो आदर्शीकृत चरम प्रकारों के रूप में की जा सकती है। इस तरह के एक प्रकार में, प्रणाली के भीतर कोई एन्ट्रापी उत्पन्न नहीं होता है (कोई घर्षण, विस्कासी अपव्यय, आदि), और कार्य केवल दबाव-आयतन कार्य होता है ( $P d V$ द्वारा निरूपित)। प्रकृति में, यह आदर्श प्रकार केवल सन्निकटत होता है क्योंकि यह एक असीम धीमी प्रक्रिया की मांग करता है और अपव्यय का कोई स्रोत नहीं होता है।

अन्य चरम प्रकार का कार्य समआयतनिक कार्य ( $d V = 0$ ) है, जिसके लिए प्रणाली के भीतर केवल घर्षण या विस्कासी अपव्यय के माध्यम से ऊर्जा को काम के रूप में जोड़ा जाता है। एक विलोडक जो चरण परिवर्तन के बिना, दृढ़ दीवारों के साथ स्थिरोष्म रूप से पृथक प्रणाली के विस्कासी तरल पदार्थ में ऊर्जा स्थानांतरित करता है, तरल पदार्थ के तापमान में वृद्धि का कारण बनता है, परन्तु वह काम पुनर्प्राप्त करने योग्य नहीं होता है। समआयतनिक कार्य अपरिवर्तनीय है।^[5] ऊष्मप्रवैगिकी का दूसरा नियम मानता है कि कार्य के रूप में ऊर्जा के हस्तांतरण की एक प्राकृतिक प्रक्रिया में हमेशा कम से कम समआयतनिक कार्य होता है और प्रायः ये दोनों चरम प्रकार के कार्य होते हैं। प्रत्येक प्राकृतिक प्रक्रिया अपरिवर्तनीय $Δ S > 0$ है, घर्षण या संलग्नशीलता हमेशा कुछ सीमा तक उपस्थित होती है।

स्थिरोष्म तापन और शीतलन

गैस का रूद्धोष्म संपीड़न गैस के तापमान में वृद्धि का कारण बनता है। दबाव, या वसंत के खिलाफ स्थिरोष्म विस्तार, तापमान में गिरावट का कारण बनता है। इसके विपरीत, मुक्त विस्तार एक आदर्श गैस के लिए एक समतापी प्रक्रिया है।

स्थिरोष्म तापन तब होता है जब गैस का दबाव उसके आस-पास के काम से बढ़ जाता है, उदाहरण के लिए, एक पिस्टन एक सिलेंडर के भीतर गैस को संपीड़ित करता है और तापमान बढ़ाता है जहां कई व्यावहारिक परिस्थितियों में दीवारों के माध्यम से संपीड़न समय ऊष्मा चालन की तुलना में धीमी हो सकती है। यह डीजल यंत्रों में व्यावहारिक अनुप्रयोग पाता है जो ईंधन वाष्प तापमान को प्रज्वलित करने के लिए पर्याप्त रूप से बढ़ाने के लिए संपीड़न आघात के दौरान ऊष्मा अपव्यय की कमी पर निर्भर करता है।

स्थिरोष्म तापन पृथ्वी के वायुमंडल में तब होता है जब एक वायु द्रव्यमान उतरता है, उदाहरण के लिए, एक अवरोही वायु, फोहेन वायु, या चिनूक वायु एक पर्वत श्रृंखला पर नीचे की ओर बहती है। जब वायु का एक खण्ड़ उतरता है तो खण्ड़ पर दबाव बढ़ जाता है। दबाव में इस वृद्धि के कारण, खण्ड़ का आयतन कम हो जाता है और इसका तापमान बढ़ जाता है क्योंकि वायु के खण्ड़ पर काम किया जाता है, इस प्रकार इसकी आंतरिक ऊर्जा में वृद्धि होती है, जो वायु के उस द्रव्यमान के तापमान में वृद्धि से प्रकट होती है। वायु का खण्ड़ केवल चालन या विकिरण (ऊष्मा) द्वारा ऊर्जा को धीरे-धीरे नष्ट कर सकता है, और पहले सन्निकटन के लिए इसे रूद्धोष्म रूप से पृथक माना जा सकता है और प्रक्रिया एक रूद्धोष्म प्रक्रिया है।

स्थिरोष्म शीतलन तब होता है जब स्थिरोष्म रूप से पृथक प्रणाली पर दबाव कम हो जाता है, जिससे यह विस्तार करने की अनुमति देता है, जिससे यह अपने परिवेश पर काम करता है। जब गैस के खण्ड़ पर लगाया गया दबाव कम हो जाता है, तो खण्ड़ में गैस को फैलने दिया जाता है; जैसे-जैसे आयतन बढ़ता है, तापमान गिरता है क्योंकि इसकी आंतरिक ऊर्जा घटती है। स्थिरोष्म शीतलन पृथ्वी के वायुमंडल में पर्वतीय उत्थापन और प्रतिपवन तरंग के साथ होता है, और यह छत्र (मौसम विज्ञान) या मसुराकार बादलों का निर्माण कर सकता है।

पर्वतीय क्षेत्रों में रूद्धोष्म शीतलन के कारण, सहारा रेगिस्तान के कुछ भागों में यदाकदा ही हिमपात होता है।^[6]

स्थिरोष्म शीतलन में तरल पदार्थ सम्मिलित नहीं होता है। एक तकनीक बहुत कम तापमान तक पहुँचने के लिए उपयोग की जाती है (पूर्ण शून्य से एक डिग्री के हज़ार और यहां तक कि मिलियन) स्थिरोष्म विचुंबकत्व के माध्यम से होती है, जहां एक चुंबकीय सामग्री पर चुंबकीय क्षेत्र में परिवर्तन का उपयोग स्थिरोष्म शीतलन प्रदान करने के लिए किया जाता है। इसके अतिरिक्त, एक विस्तारित ब्रह्मांड की सामग्री को एक स्थिरोष्म रूप से शीतल करने वाले द्रव के रूप में (पहले क्रम में) वर्णित किया जा सकता है।

आरोही द्रुतपुंज भी विस्फोट से पहले स्थिरोष्म शीतलन से गुजरता है, विशेष रूप से द्रुतपुंज की स्तिथि में महत्वपूर्ण है जो कि किंबरलाईट जैसी बड़ी गहराई से तेजी से बढ़ता है।

स्थलमंडल के नीचे पृथ्वी के संवाहक आवरण (दुर्बलतामंडल) में, आवरण का तापमान लगभग एक स्थिरोष्म है। उथली गहराई के साथ तापमान में साधारण दबाव में कमी के कारण होती है।^[7]

इस तरह के तापमान परिवर्तन को आदर्श गैस कानून, या वायुमंडलीय प्रक्रियाओं के लिए जलस्थैतिक समीकरण का उपयोग करके निर्धारित किया जा सकता है।

व्यवहार में, कोई भी प्रक्रिया वास्तव में रूद्धोष्म नहीं है। कई प्रक्रियाएं अभिरूचि की प्रक्रिया के समय के पैमाने और एक प्रणाली सीमा में ऊष्मा अपव्यय की दर में बड़े अंतर पर निर्भर करती हैं, और इस प्रकार एक स्थिरोष्म धारणा का उपयोग करके अनुमान लगाया जाता है। हमेशा कुछ ऊष्मा का नुकसान होता है, क्योंकि कोई सही विसंवाहक उपस्थित नहीं है।

आदर्श गैस (प्रतिवर्ती प्रक्रिया)

एक साधारण पदार्थ के लिए, एक स्थिरोष्म प्रक्रिया के दौरान जिसमें आयतन बढ़ता है, काम करने वाले पदार्थ की आंतरिक ऊर्जा घटनी चाहिए

एक उत्क्रमणीय (अर्थात्, कोई एन्ट्रापी पीढ़ी नहीं) रूद्धोष्म प्रक्रिया से गुजरने वाली एक आदर्श गैस के लिए गणितीय समीकरण को बहुविध प्रक्रिया समीकरण द्वारा दर्शाया जा सकता है^[1]: $PV^{\gamma }={\text{constant}},$

जहाँ पर $P$ दबाव है, $V$ मात्रा है, और $γ$ स्थिरोष्म सूचकांक या ताप क्षमता अनुपात के रूप में परिभाषित किया गया है

\gamma ={\frac {C_{P}}{C_{V}}}={\frac {f+2}{f}}.

यहां $C P$ निरंतर दबाव के लिए विशिष्ट ऊष्मा है, $C V$ स्थिर आयतन के लिए विशिष्ट ऊष्मा है, और $f$ स्वतंत्रता की घात (भौतिकी और रसायन विज्ञान) की संख्या है (3 एकलपरमाण्विक गैस के लिए, 5 द्विपरमाणुक गैस या कार्बन डाइऑक्साइड जैसे रैखिक अणुओं की गैस के लिए)।

एकपरमाणुक आदर्श गैस के लिए, $γ = 5 / 3$ , और एक डायटोमिक गैस के लिए (जैसे भूयाति और प्राणवायु, वायु के मुख्य घटक) $γ = 7 / 5$ है।^[8] ध्यान दें कि उपरोक्त सूत्र केवल पारम्परिक आदर्श गैसों पर लागू होता है (अर्थात, पूर्ण शून्य तापमान से ऊपर की गैसें) और बोस-आइंस्टीन या फर्मीओनिक घनीभूत नहीं।

$P$ और $V$ के बीच उपरोक्त संबंध को फिर से लिखने के लिए कोई भी आदर्श गैस कानून का उपयोग कर सकता है, जैसे ^[1]

P^{1-\gamma }T^{\gamma }={\text{constant}},

TV^{\gamma -1}={\text{constant}}.

जहाँ T निरपेक्ष या ऊष्मागतिक तापमान है।

स्थिरोष्म संपीड़न का उदाहरण

पेट्रोल यन्त्र में संपीड़न आघात का उपयोग स्थिरोष्म संपीड़न के उदाहरण के रूप में किया जा सकता है। प्रतिरूप धारणाएं निम्न हैं: सिलेंडर की असम्पीडित मात्रा एक लीटर (1L = 1000 cm³ = 0.001 m³); भीतर गैस केवल आणविक भूयाति और प्राणवायु से युक्त वायु है (इस प्रकार 5 डिग्री छूट के साथ एक डायटोमिक गैस, और इसी तरह $γ = 7 / 5$ ); यन्त्र का संपीड़न अनुपात 10:1 है (अर्थात, पिस्टन द्वारा असम्पीडित गैस की 1 L मात्रा 0.1 L तक कम हो जाती है); और असम्पीडित गैस लगभग कमरे के तापमान और दबाव (~27 °C, या 300 K के ऊष्म कमरे का तापमान, और 1 बार = 100 kPa का दबाव, यानी विशिष्ट समुद्र-स्तर वायुमंडलीय दबाव) पर होती है।

{\begin{aligned}&P_{1}V_{1}^{\gamma }=\mathrm {constant} _{1}=100\,000~{\text{Pa}}\times (0.001~{\text{m}}^{3})^{\frac {7}{5}}\\&=10^{5}\times 6.31\times 10^{-5}~{\text{Pa}}\,{\text{m}}^{21/5}=6.31~{\text{Pa}}\,{\text{m}}^{21/5},\end{aligned}}

इसलिए इस उदाहरण के लिए स्थिरोष्म स्थिरांक लगभग 6.31 Pa m^{4.2 है।}

गैस अब 0.1 L (0.0001 m³) आयतन, जिसे हम मानते हैं कि इतनी जल्दी होता है कि कोई भी ऊष्मा दीवारों के माध्यम से गैस में प्रवेश या बाहर नहीं निकलती है। रूद्धोष्म स्थिरांक समान रहता है, परन्तु परिणामी दबाव अज्ञात रहता है

P_{2}V_{2}^{\gamma }=\mathrm {constant} _{1}=6.31~{\text{Pa}}\,{\text{m}}^{21/5}=P\times (0.0001~{\text{m}}^{3})^{\frac {7}{5}},

अब हम अंतिम दबाव के लिए हल कर सकते हैं^[9]

P_{2}=P_{1}\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma }=100\,000~{\text{Pa}}\times {\text{10}}^{7/5}=2.51\times 10^{6}~{\text{Pa}}

या 25.1 स्तंभ। दबाव में यह वृद्धि सामान्य 10:1 संपीड़न अनुपात से अधिक है जो इंगित करेगा; ऐसा इसलिए है क्योंकि गैस न केवल संपीड़ित होती है, बल्कि गैस को संपीड़ित करने के लिए किए गए कार्य से इसकी आंतरिक ऊर्जा भी बढ़ जाती है, और मूल दबाव के 10 गुना की सरलीकृत गणना से जो परिणाम होगा, उससे अधिक दबाव में एक अतिरिक्त वृद्धि होगी।

आदर्श गैस नियम, PV = nRT (n मोल्स में गैस की मात्रा है और R उस गैस के लिए गैस स्थिरांक है) का उपयोग करके, हम यन्त्र सिलेंडर में संपीड़ित गैस के तापमान के लिए भी हल कर सकते हैं। हमारी प्रारंभिक शर्तें 100 kPa दबाव, 1 L आयतन और 300 K तापमान हैं, हमारा प्रायोगिक स्थिरांक (nR) है:

{\frac {PV}{T}}=\mathrm {constant} _{2}={\frac {10^{5}~{\text{Pa}}\times 10^{-3}~{\text{m}}^{3}}{300~{\text{K}}}}=0.333~{\text{Pa}}\,{\text{m}}^{3}{\text{K}}^{-1}.

हम जानते हैं कि संपीड़ित गैस $V$ = 0.1 L और $P$ = 2.51×10⁶ Pa है, तो हम तापमान के लिए हल कर सकते हैं:

T={\frac {PV}{\mathrm {constant} _{2}}}={\frac {2.51\times 10^{6}~{\text{Pa}}\times 10^{-4}~{\text{m}}^{3}}{0.333~{\text{Pa}}\,{\text{m}}^{3}{\text{K}}^{-1}}}=753~{\text{K}}.

यह 753 K, या 479 °C, या 896 °F का अंतिम तापमान होता है, जो कई ईंधनों के प्रज्वलन बिंदु से काफी ऊपर होता है। यही कारण है कि एक उच्च-संपीड़न यन्त्र के लिए विशेष रूप से तैयार किए गए ईंधन की आवश्यकता होती है जो स्वयं-प्रज्वलित न हो (जो तापमान और दबाव की इन स्थितियों के तहत संचालित होने पर यन्त्र को दस्तक दे सकता है), या एक मध्यशीतक के साथ एक अतिभरक दबाव को बढ़ावा देने के लिए परन्तु कम के साथ तापमान बढ़ना लाभदायक होगा। एक डीजल यन्त्र और भी अधिक विषम परिस्थितियों में काम करता है, जिसमें 16: 1 या उससे अधिक का संपीड़न अनुपात विशिष्ट होता है, ताकि एक बहुत ही उच्च गैस तापमान प्रदान किया जा सके, जो डाले किए गए ईंधन के तत्काल प्रज्वलन को सुनिश्चित करता है।

गैस का स्थिरोष्म मुक्त प्रसार

एक आदर्श गैस के स्थिरोष्म मुक्त विस्तार के लिए, गैस को एक आवरणयुक्त धारक में समाहित किया जाता है और फिर एक निर्वात में विस्तार करने की अनुमति दी जाती है। क्योंकि गैस के प्रसार के लिए कोई बाहरी दबाव नहीं है, प्रणाली द्वारा या प्रणाली पर किया गया कार्य शून्य है। चूँकि इस प्रक्रिया में कोई ऊष्मा अंतरण या कार्य सम्मिलित नहीं है, तो ऊष्मप्रवैगिकी के पहले नियम का अर्थ है कि प्रणाली का शुद्ध आंतरिक ऊर्जा परिवर्तन शून्य है। एक आदर्श गैस के लिए, तापमान स्थिर रहता है क्योंकि उस स्थिति में आंतरिक ऊर्जा केवल तापमान पर निर्भर करती है। चूंकि निरंतर तापमान पर, एन्ट्रापी आयतन के समानुपाती होती है, इसलिए इस स्तिथि में एन्ट्रापी बढ़ जाती है, इसलिए यह प्रक्रिया अपरिवर्तनीय है।

स्थिरोष्म तापन और शीतलन के लिए P-V संबंध की व्युत्पत्ति

स्थिरोष्म प्रक्रिया की परिभाषा यह है कि प्रणाली में ऊष्मा हस्तांतरण शून्य $δQ = 0$ है, फिर, ऊष्मप्रवैगिकी के पहले नियम के अनुसार,

dU+\delta W=\delta Q=0,

(a1)

जहाँ पर $dU$ प्रणाली की आंतरिक ऊर्जा में परिवर्तन है और $δW$ कार्य प्रणाली द्वारा किया जाता है। कोई काम ( $δW$ ) आंतरिक ऊर्जा $U$ की कीमत पर किया जाना चाहिए, चूंकि कोई ऊष्मा $δQ$ आसपास से सप्लाई नहीं की जा रही है। दबाव-मात्रा काम $δW$ प्रणाली द्वारा किया गया कार्य निम्न रूप में परिभाषित किया गया है

\delta W=P\,dV.

(a2)

हालांकि, $P$ स्थिरोष्म प्रक्रिया के दौरान स्थिर नहीं रहता है बल्कि इसके साथ $V$ बदल जाता है .

यह जानने की इच्छा है कि $dP$ के मूल्य कैसे हैं और $dV$ स्थिरोष्म प्रक्रिया आगे बढ़ने पर एक दूसरे से संबंधित होती है। एक आदर्श गैस के लिए (आदर्श गैस नियम को याद कीजिए $PV = nRT$ ) आंतरिक ऊर्जा किसके द्वारा दी जाती है

U=\alpha nRT=\alpha PV,

(a3)

जहाँ पर $α$ स्वतंत्रता की घात की संख्या 2 से विभाजित है, $R$ सार्वभौमिक गैस स्थिरांक है और $n$ प्रणाली में मोल्स की संख्या है (एक स्थिर)।

अवकलन समीकरण (a3) प्राप्त होता है

dU=\alpha nR\,dT=\alpha \,d(PV)=\alpha (P\,dV+V\,dP).

(a4)

समीकरण $dU = nC V dT$ (a4) को प्रायः व्यक्त किया जाता है क्योंकि $C V = αR$ .

अब निम्न प्राप्त करने के लिए समीकरण (a2) और (a4) को समीकरण (a1) में प्रतिस्थापित करें

-P\,dV=\alpha P\,dV+\alpha V\,dP,

$- P dV$ : खंडित कीजिये

-(\alpha +1)P\,dV=\alpha V\,dP,

और दोनों पक्षों को $PV$ से विभाजित करें :

-(\alpha +1){\frac {dV}{V}}=\alpha {\frac {dP}{P}}.

बाएँ और दाएँ पक्षों को $V 0$ से V और $P 0$ से P तक एकीकृत करने और पक्षों को क्रमशः बदलने के बाद,

\ln \left({\frac {P}{P_{0}}}\right)=-{\frac {\alpha +1}{\alpha }}\ln \left({\frac {V}{V_{0}}}\right).

दोनों पक्षों को प्रतिपादित करें, $γ$ से $α + 1 / α$ स्थानापन्न करें, ताप क्षमता अनुपात

\left({\frac {P}{P_{0}}}\right)=\left({\frac {V}{V_{0}}}\right)^{-\gamma },

और निम्न प्राप्त करने के लिए नकारात्मक चिह्न को हटा दें

\left({\frac {P}{P_{0}}}\right)=\left({\frac {V_{0}}{V}}\right)^{\gamma }.

इसलिए,

\left({\frac {P}{P_{0}}}\right)\left({\frac {V}{V_{0}}}\right)^{\gamma }=1,

और

P_{0}V_{0}^{\gamma }=PV^{\gamma }=\mathrm {constant} .

\Delta U=\alpha RnT_{2}-\alpha RnT_{1}=\alpha Rn\Delta T.

(b1)

इसी समय, इस प्रक्रिया के परिणामस्वरूप दबाव-आयतन परिवर्तन द्वारा किया गया कार्य बराबर होता है

W=\int _{V_{1}}^{V_{2}}P\,dV.

(b2)

चूँकि हमें प्रक्रिया के रूद्धोष्म होने की आवश्यकता है, निम्नलिखित समीकरण को सत्य होना चाहिए

\Delta U+W=0.

(b3)

पिछली व्युत्पत्ति द्वारा,

PV^{\gamma }={\text{constant}}=P_{1}V_{1}^{\gamma }.

(b4)

पुनर्व्यवस्थित (B 4) देता है

P=P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }.

इसे (B 2) में प्रतिस्थापित करना देता है

W=\int _{V_{1}}^{V_{2}}P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }\,dV.

समाकलित करने पर हमें कार्य का व्यंजक प्राप्त होता है,

W=P_{1}V_{1}^{\gamma }{\frac {V_{2}^{1-\gamma }-V_{1}^{1-\gamma }}{1-\gamma }}={\frac {P_{2}V_{2}-P_{1}V_{1}}{1-\gamma }}.

स्थानापन्न $γ = α + 1 / α$ दूसरे कार्यकाल में,

W=-\alpha P_{1}V_{1}^{\gamma }\left(V_{2}^{1-\gamma }-V_{1}^{1-\gamma }\right).

पुनर्व्यवस्थित,

W=-\alpha P_{1}V_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).

आदर्श गैस कानून का उपयोग करना और एक स्थिर मोलर मात्रा मानना (जैसा कि व्यावहारिक स्तिथियों में प्रायः होता है),

W=-\alpha nRT_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).

निरंतर सूत्र द्वारा,

{\frac {P_{2}}{P_{1}}}=\left({\frac {V_{2}}{V_{1}}}\right)^{-\gamma },

या

\left({\frac {P_{2}}{P_{1}}}\right)^{-{\frac {1}{\gamma }}}={\frac {V_{2}}{V_{1}}}.

$W$ के लिए पिछली अभिव्यक्ति में प्रतिस्थापित करना ,

W=-\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right).

इस व्यंजक और (b1) को (b3) में प्रतिस्थापित करने पर प्राप्त होता है

\alpha nR(T_{2}-T_{1})=\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right).

सरल बनाना,

T_{2}-T_{1}=T_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right),

{\frac {T_{2}}{T_{1}}}-1=\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1,

T_{2}=T_{1}\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}.

असतत सूत्र और कार्य अभिव्यक्ति की व्युत्पत्ति

एक प्रणाली की आंतरिक ऊर्जा में परिवर्तन, स्तिथि 1 से स्तिथि 2 तक मापा जाता है, और निम्न के बराबर होता है

इसी समय, इस प्रक्रिया के परिणामस्वरूप दबाव-आयतन परिवर्तन द्वारा किया गया कार्य बराबर होता है

W=\int _{V_{1}}^{V_{2}}P\,dV.

(c2)

चूँकि हमें प्रक्रिया के रूद्धोष्म होने की आवश्यकता है, निम्नलिखित समीकरण को सत्य होना चाहिए

\Delta U+W=0.

(c3)

पिछली व्युत्पत्ति द्वारा,

PV^{\gamma }={\text{constant}}=P_{1}V_{1}^{\gamma }.

(c4)

पुनर्व्यवस्थित (c4) देता है

P=P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }.

इसे (C 2) में प्रतिस्थापित करना देता है

W=\int _{V_{1}}^{V_{2}}P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }\,dV.

समाकलित करने पर हमें कार्य का व्यंजक प्राप्त होता है,

W=P_{1}V_{1}^{\gamma }{\frac {V_{2}^{1-\gamma }-V_{1}^{1-\gamma }}{1-\gamma }}={\frac {P_{2}V_{2}-P_{1}V_{1}}{1-\gamma }}.

स्थानापन्न $γ = α + 1 / α$ दूसरे कार्यकाल में,

W=-\alpha P_{1}V_{1}^{\gamma }\left(V_{2}^{1-\gamma }-V_{1}^{1-\gamma }\right).

पुनर्व्यवस्थित,

W=-\alpha P_{1}V_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).

आदर्श गैस कानून का उपयोग करना और एक स्थिर मोलर मात्रा मानना (जैसा कि व्यावहारिक स्तिथियों में प्रायः होता है),

W=-\alpha nRT_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).

निरंतर सूत्र द्वारा,

{\frac {P_{2}}{P_{1}}}=\left({\frac {V_{2}}{V_{1}}}\right)^{-\gamma },

या

\left({\frac {P_{2}}{P_{1}}}\right)^{-{\frac {1}{\gamma }}}={\frac {V_{2}}{V_{1}}}.

$W$ के लिए पिछली अभिव्यक्ति में प्रतिस्थापित करना ,

W=-\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right).

इस व्यंजक और (c1) को (c3) में प्रतिस्थापित करने पर प्राप्त होता है

\alpha nR(T_{2}-T_{1})=\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right).

सरल बनाना,

T_{2}-T_{1}=T_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right),

{\frac {T_{2}}{T_{1}}}-1=\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1,

T_{2}=T_{1}\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}.

स्थिरोष्म रेखांकन

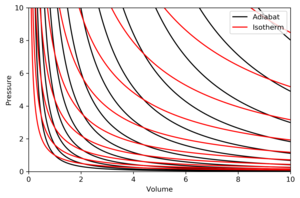
एक एडियाबैट आरेख में निरंतरएन्ट्रापी का एक वक्र है। P-V आरेख पर स्थिरोष्म के कुछ गुण दर्शाए गए हैं। इन गुणों को आदर्श गैसों के पारम्परिक व्यवहार से पढ़ा जा सकता है, केवल उस क्षेत्र को छोड़कर जहां PV छोटा हो जाता है (कम तापमान), जहां परिमाण प्रभाव महत्वपूर्ण हो जाते हैं।

प्रत्येक स्थिरोष्म स्पर्शोन्मुख रूप से V अक्ष और P अक्ष दोनों तक पहुँचता है (बिल्कुल समताप रेखा की तरह)।
प्रत्येक एडियाबैट प्रत्येक समताप वक्र को ठीक एक बार काटता है।
एक एडियाबैट एक समताप वक्र के समान दिखता है, अथवा इसके कि एक विस्तार के दौरान, एक एडियाबैट एक समताप वक्र की तुलना में अधिक दबाव खो देता है, इसलिए इसमें एक तेज झुकाव (अधिक ऊर्ध्वाधर) होता है।
यदि समताप रेखाएं उत्तर-पूर्व दिशा (45°) की ओर अवतल हैं, तो स्थिरोष्म पूर्व-उत्तर-पूर्व (31°) की ओर अवतल हैं।
यदि स्थिर विभवताप रेखा और समताप वक्र को क्रमशः एंट्रॉपी और तापमान के नियमित अंतराल पर चित्रित किया जाता है (जैसे समोच्च मानचित्र पर ऊंचाई), तो जैसे ही आंख धुरी (दक्षिण-पश्चिम की तरफ) की ओर बढ़ती है, यह देखती है कि समताप वक्र का घनत्व स्थिर रहता है, परन्तु यह देखता है कि स्थिर विभवताप रेखा का घनत्व बढ़ता है। अपवाद पूर्ण शून्य के बहुत करीब है, जहां स्थिर विभवताप रेखा का घनत्व तेजी से गिरता है और वे दुर्लभ हो जाते हैं (नर्नस्ट के प्रमेय देखें)।

सही आरेख एक P-V आरेख है जिसमें स्थिर विभवताप रेखा और समताप वक्र की अधिस्थापन है:

समताप रेखाएँ लाल वक्र हैं और स्थिरोष्म काली वक्र हैं।

स्थिर विभवताप रेखा समऐन्ट्रॉपिक हैं।

आयतन क्षैतिज अक्ष है और दबाव ऊर्ध्वाधर अक्ष है।

व्युत्पत्ति

स्थिरोष्म शब्द (/ˌædiəˈbætɪk/) प्राचीन ग्रीक शब्द ἀδιάβατος अगम्य (नदियों के जेनोफोन द्वारा प्रयुक्त) का अंग्रेजीकरण है।

यह विलियम जॉन मैक्कॉर्न रैंकिन (1866) द्वारा ऊष्मागतिक अर्थ में प्रयोग किया जाता है,^[10]^[11] और 1871 में जेम्स क्लर्क मैक्सवेल द्वारा अपनाया गया (स्पष्ट रूप से रैंकिन के लिए शब्द का श्रेय)।^[12]

व्युत्पत्ति संबंधी उत्पत्ति यहां ऊष्मा की असंभवता और दीवार के पार पदार्थ के हस्तांतरण से मेल खाती है।

ग्रीक शब्द ἀδιάβατος निजी अभावात्मक ἀ- (नहीं) और διαβατός से बना है, जो बदले में διά (के माध्यम से), और βαῖνειν (चलना, जाना, आना) से निकला है।^[13]

ऊष्मप्रवैगिकी सिद्धांत में वैचारिक महत्व

ऊष्मप्रवैगिकी के आरंभिक दिनों से ही स्थिरोष्म प्रक्रिया महत्वपूर्ण रही है। जूल के कार्य में यह महत्वपूर्ण था क्योंकि इसने ऊष्मा और कार्य की मात्राओं को लगभग सीधे संबंधित करने का एक तरीका प्रदान किया।

ऊर्जा दीवारों से घिरे ऊष्मागतिक प्रणाली में प्रवेश कर सकती है या छोड़ सकती है जो बड़े पैमाने पर स्थानांतरण को केवल ऊष्मा या काम के रूप में रोकती है। इसलिए, ऐसी प्रणाली में काम की मात्रा लगभग सीधे दो अंगों के चक्र में ऊष्मा के बराबर मात्रा से संबंधित हो सकती है। पहला अंग एक समआयतनिक स्थिरोष्म कार्य प्रक्रिया है जो प्रणाली की आंतरिक ऊर्जा को बढ़ाता है; दूसरा, एक समआयतनिक और निष्क्रिय ऊष्मा हस्तांतरण प्रणाली को उसकी मूल स्थिति में लौटाता है। तदनुसार, रैंकिन ने कैलोरीमेट्रिक मात्रा के स्थान पर कार्य की इकाइयों में ऊष्मा की मात्रा को मापा।^[14] 1854 में, रैंकिन ने एक मात्रा का उपयोग किया जिसे उन्होंने ऊष्मागतिक प्रणाली कहा जिसे बाद में एंट्रॉपी कहा गया, और उस समय उन्होंने ऊष्मा के संचरण के बिना वक्र के बारे में भी लिखा,^[15] जिसे उन्होंने बाद में स्थिरोष्म वक्र कहा।^[10]इसके दो समताप वक्राल अंगों के अतिरिक्त, कार्नोट के चक्र में दो स्थिरोष्म अंग हैं।

ऊष्मप्रवैगिकी की नींव के लिए, इसके वैचारिक महत्व पर ब्रायन द्वारा जोर दिया गया था,^[16] कैराथियोडोरी द्वारा,^[17]और बोर्न द्वारा।^[18] इसका कारण यह है कि उष्मामिति एक प्रकार के तापमान को पहले से ही ऊष्मप्रवैगिकी के पहले नियम के बयान से पहले परिभाषित करती है, जैसे कि अनुभवजन्य पैमानों पर आधारित है। इस तरह की पूर्वधारणा में अनुभवजन्य तापमान और पूर्ण तापमान के बीच अंतर करना सम्मिलित है। बल्कि, दूसरे नियम के वैचारिक आधार के रूप में उपलब्ध होने तक परम ऊष्मागतिक तापमान की परिभाषा को छोड़ देना सबसे अच्छा है।^[19]

अठारहवीं शताब्दी में, ऊर्जा के संरक्षण का नियम अभी तक पूरी तरह से तैयार या स्थापित नहीं हुआ था, और ऊष्मा की प्रकृति पर बहस हुई थी। इन समस्याओं के लिए एक दृष्टिकोण यह था कि उष्मामिति द्वारा मापी गई ऊष्मा को एक प्राथमिक पदार्थ के रूप में माना जाए जो मात्रा में संरक्षित है। उन्नीसवीं शताब्दी के मध्य तक, इसे ऊर्जा के एक रूप के रूप में मान्यता दी गई थी, और इसके द्वारा ऊर्जा के संरक्षण के नियम को भी मान्यता दी गई थी। वह विचार जिसने अंततः खुद को स्थापित किया, और वर्तमान में इसे सही माना जाता है, यह है कि ऊर्जा के संरक्षण का नियम एक प्राथमिक स्वयंसिद्ध है, और उस ऊष्मा का विश्लेषण परिणामी के रूप में किया जाना है। इस प्रकाश में, ऊष्मा किसी एक पिंड की कुल ऊर्जा का एक घटक नहीं हो सकती है क्योंकि यह एक स्तिथि कार्य नहीं है, बल्कि एक चर है जो दो पिंडों के बीच स्थानांतरण का वर्णन करता है। रूद्धोष्म प्रक्रिया महत्वपूर्ण है क्योंकि यह इस वर्तमान दृष्टिकोण का एक तार्किक घटक है।^[19]

स्थिरोष्म शब्द के अलग-अलग उपयोग

यह वर्तमान लेख सूक्ष्मदर्शीय ऊष्मप्रवैगिकी के दृष्टिकोण से लिखा गया है, और स्थिरोष्म शब्द का उपयोग इस लेख में ऊष्मागतिकी के पारंपरिक तरीके से किया गया है, जिसे रैंकिन द्वारा प्रस्तुत किया गया है। वर्तमान लेख में यह बताया गया है कि, उदाहरण के लिए, यदि गैस का संपीड़न तेजी से होता है, तो ऊष्मा हस्तांतरण के लिए बहुत कम समय होता है, तब भी जब गैस एक निश्चित दीवार से स्थिरोष्म रूप से पृथक नहीं होती है। इस अर्थ में, गैस का तेजी से संपीड़न कभी-कभी लगभग या शिथिल रूप से रूद्धोष्म कहा जाता है, हालांकि प्रायः समऐन्ट्रॉपिक से दूर होता है, तब भी जब गैस एक निश्चित दीवार द्वारा रूद्धोष्म रूप से पृथक नहीं होती है।

परिमाण यांत्रिकी और परिमाण सांख्यिकीय यांत्रिकी, हालाँकि, स्थिरोष्म शब्द का उपयोग बहुत अलग अर्थ में किया जाता है, एक ऐसा जो कई बार पारम्परिक ऊष्मागतिक अर्थ के विपरीत लग सकता है। परिमाण सिद्धांत में, स्थिरोष्म शब्द का अर्थ संभवतःसमऐन्ट्रॉपिक के पास, या संभवतःअर्ध-स्थैतिक के पास हो सकता है, परन्तु शब्द का उपयोग दो विषयों के बीच बहुत भिन्न है।

एक ओर, परिमाण सिद्धांत में, यदि संपीडन कार्य का एक विक्षुब्ध तत्व लगभग असीम रूप से धीरे-धीरे किया जाता है (अर्थात् अर्ध-स्थैतिक रूप से कहा जाता है), तो इसे रूद्धोष्म रूप से किया गया कहा जाता है। विचार यह है कि ईजेनफंक्शन के आकार धीरे-धीरे और लगातार बदलते हैं, ताकि कोई परिमाण कूद शुरू न हो, और परिवर्तन वस्तुतः उलटा हो। जबकि व्यवसाय संख्या अपरिवर्तित हैं, फिर भी एक-से-एक अनुरूप, पूर्व और बाद के संपीड़न, ईजेनस्टेट्स के ऊर्जा स्तरों में परिवर्तन होता है। इस प्रकार ऊष्मा हस्तांतरण के बिना और प्रणाली के भीतर यादृच्छिक परिवर्तन की शुरूआत के बिना काम का एक परेशान करने वाला तत्व किया गया है। उदाहरण के लिए, मैक्स बोर्न वास्तव में लिखते हैं, यह सामान्यतः 'स्थिरोष्म' स्तिथि है जिसके साथ हमें करना है: यानी सीमित स्तिथि जहां बाहरी बल (या एक दूसरे पर प्रणाली के हिस्सों की प्रतिक्रिया) बहुत धीमी गति से कार्य करता है। इस स्तिथि में, बहुत उच्च सन्निकटन के लिए

c_{1}^{2}=1,\,\,c_{2}^{2}=0,\,\,c_{3}^{2}=0,\,...\,,

अर्थात्, संक्रमण की कोई संभावना नहीं है, और अस्तव्यस्तता की समाप्ति के बाद प्रणाली प्रारंभिक अवस्था में है। इस तरह की धीमी अस्तव्यस्तता इसलिए प्रतिवर्ती है, क्योंकि यह पारम्परिक रूप से है।^[20]

दूसरी ओर, परिमाण सिद्धांत में, यदि संपीडक कार्य का एक विक्षुब्ध तत्व तेजी से किया जाता है, तो यह संक्रमण के क्षण के अभिन्न और समय-निर्भर अस्तव्यस्तता सिद्धांत के अनुसार, साथ ही साथ ईजेनस्टेट्स के व्यवसाय संख्या और ऊर्जा को बदलता है। ईजेनस्टेट्स के कार्यात्मक रूप को स्वयं परेशान करते हैं। उस सिद्धांत में, इस तरह के एक तेजी से परिवर्तन को स्थिरोष्म नहीं कहा जाता है, और इसके विपरीत प्रतिरूद्धोष्म शब्द लागू होता है।

हाल ही में किए गए अनुसंधान^[21] से पता चलता है कि अस्तव्यस्तता से अवशोषित शक्ति इन गैर-स्थिरोष्म संक्रमणों की दर से मेल खाती है। यह ऊष्मा के रूप में ऊर्जा हस्तांतरण की पारम्परिक प्रक्रिया से मेल खाती है, परन्तु परिमाण स्तिथि में सापेक्ष समय के पैमाने उलट जाते हैं। परिमाण स्थिरोष्म प्रक्रियाएं अपेक्षाकृत लंबे समय के पैमाने पर होती हैं, जबकि पारम्परिक स्थिरोष्म प्रक्रियाएं अपेक्षाकृत कम समय के पैमाने पर होती हैं। यह भी ध्यान दिया जाना चाहिए कि 'ऊष्मा' की अवधारणा (स्थानांतरित तापीय ऊर्जा की मात्रा के संदर्भ में) परिमाण स्तर पर टूट जाती है, और इसके स्थान पर ऊर्जा के विशिष्ट रूप (सामान्यतः विद्युत चुम्बकीय) पर विचार किया जाना चाहिए। परिमाण स्थिरोष्म प्रक्रिया में अस्तव्यस्तता से ऊर्जा का छोटा या नगण्य अवशोषण पारम्परिक ऊष्मागतिकी में स्थिरोष्म प्रक्रियाओं के परिमाण समधर्मी के रूप में पहचानने और शब्द के पुन: उपयोग के लिए एक अच्छा औचित्य प्रदान करता है।

इसके अतिरिक्त, वायुमंडलीय ऊष्मप्रवैगिकी में, एक प्रतिरूद्धोष्म प्रक्रिया वह है जिसमें ऊष्मा का आदान-प्रदान होता है।^[22]

पारम्परिक ऊष्मप्रवैगिकी में, इस तरह के तेजी से परिवर्तन को अभी भी रूद्धोष्म कहा जाएगा क्योंकि प्रणाली रूद्धोष्म रूप से पृथक है, और ऊष्मा के रूप में ऊर्जा का कोई हस्तांतरण नहीं होता है। संलग्नशीलता या अन्य एन्ट्रॉपी उत्पादन के कारण परिवर्तन की मजबूत अपरिवर्तनीयता, इस पारम्परिक उपयोग पर प्रभाव नहीं डालती है।

इस प्रकार सूक्ष्मदर्शीय ऊष्मप्रवैगिकी में गैस के एक द्रव्यमान के लिए, शब्दों का इतना उपयोग किया जाता है कि एक संपीड़न कभी-कभी शिथिल या लगभग रूद्धोष्म कहा जाता है यदि यह ऊष्मा हस्तांतरण से बचने के लिए पर्याप्त तेज़ है, भले ही प्रणाली स्थिरोष्म रूप से पृथक न हो। परन्तु परिमाण सांख्यिकीय सिद्धांत में, एक संपीड़न को स्थिरोष्म नहीं कहा जाता है यदि यह तीव्र है, भले ही प्रणाली शब्द के पारम्परिक ऊष्मप्रवैगिक अर्थों में रूद्धोष्म रूप से पृथक हो। जैसा कि ऊपर बताया गया है, दो विषयों में शब्दों का अलग-अलग उपयोग किया जाता है।

यह भी देखें

अग्नि पिस्टन
ऊष्मा विस्फोट

संबंधित भौतिकी विषय

ऊष्मप्रवैगिकी का पहला नियम
एंट्रॉपी (पारम्परिक ऊष्मप्रवैगिकी)
स्थिरोष्म चालकता
स्थिरोष्म ह्रासदर
कुल वायु का तापमान
चुंबकीय प्रशीतन
बेरी चरण

संबंधित ऊष्मागतिक प्रक्रियाएं

चक्रीय प्रक्रिया
समदाबी प्रक्रम
समएन्थैल्पिक प्रक्रिया
समऐन्ट्रॉपिक प्रक्रिया
समआयतनिक प्रक्रिया
समतापी प्रक्रिया
बहुदैशिक प्रक्रम
स्थैतिकवत् प्रक्रम

संदर्भ

↑ ^1.0 ^1.1 ^1.2 Bailyn, M. (1994), pp. 52–53.
↑ "pseudoadiabatic process". American Meteorological Society. Retrieved November 3, 2018.
↑ Tisza, L. (1966). Generalized Thermodynamics. Cambridge, MA: MIT Press. p. 48. (adiabatic partitions inhibit the transfer of heat and mass)
↑ Münster, A. (1970), p. 48: "mass is an adiabatically inhibited variable."
↑ Münster, A. (1970). Classical Thermodynamics. Translated by Halberstadt, E. S. London: Wiley–Interscience. p. 45. ISBN 0-471-62430-6.
↑ Knight, Jasper (31 January 2022). "Snowfall in the Sahara desert: an unusual weather phenomenon". The Conversation. Retrieved 3 March 2022.
↑ Turcotte and Schubert (2002). भूगतिकी. Cambridge: Cambridge University Press. pp. 185. ISBN 0-521-66624-4.
↑ Adiabatic Processes.
↑ Atkins, Peter; de Paula, Giulio (2006). Atkins' Physical Chemistry (8th ed.). W.H.Freeman. p. 48. ISBN 0-7167-8759-8.
↑ ^10.0 ^10.1 Rankine, W.J.McQ. (1866). On the theory of explosive gas engines, The Engineer, July 27, 1866; at page 467 of the reprint in Miscellaneous Scientific Papers, edited by W.J. Millar, 1881, Charles Griffin, London.
↑ Partington, J. R. (1949), An Advanced Treatise on Physical Chemistry., vol. 1, Fundamental Principles. The Properties of Gases, London: Longmans, Green and Co., p. 122
↑ Maxwell, J. C. (1871), Theory of Heat (first ed.), London: Longmans, Green and Co., p. 129
↑ Liddell, H.G., Scott, R. (1940). A Greek-English Lexicon, Clarendon Press, Oxford UK.
↑ Rankine, W.J.McQ. (1854). "On the geometrical representation of the expansive action of heat, and theory of thermodynamic engines". Proc. R. Soc. 144: 115–175. Miscellaneous Scientific Papers p. 339
↑ Rankine, W.J.McQ. (1854). "On the geometrical representation of the expansive action of heat, and theory of thermodynamic engines". Proc. R. Soc. 144: 115–175. Miscellaneous Scientific Papers p. 341.
↑ Bryan, G. H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications. Leipzig: B. G. Teubner.
↑ Cite error: Invalid <ref> tag; no text was provided for refs named Carathéodory
↑ Born, M. (1949). "Natural Philosophy of Cause and Chance". London: Oxford University Press. {{cite journal}}: Cite journal requires |journal= (help)
↑ ^19.0 ^19.1 Bailyn, M. (1994). "Chapter 3". A Survey of Thermodynamics. New York, NY: American Institute of Physics. ISBN 0-88318-797-3.
↑ Born, M. (1927). "Physical aspects of quantum mechanics". Nature. 119 (2992): 354–357. Bibcode:1927Natur.119..354B. doi:10.1038/119354a0. (Translation by Robert Oppenheimer.)
↑ Mandal, Anirban; Hunt, Katharine L. C. (2020-03-14). "Variance of the energy of a quantum system in a time-dependent perturbation: Determination by nonadiabatic transition probabilities". The Journal of Chemical Physics. 152 (10): 104110. Bibcode:2020JChPh.152j4110M. doi:10.1063/1.5140009. ISSN 0021-9606. PMID 32171229. S2CID 212731108.
↑ "diabatic process". American Meteorological Society. Retrieved 24 November 2020.

General

Silbey, Robert J.; et al. (2004). Physical chemistry. Hoboken: Wiley. p. 55. ISBN 978-0-471-21504-2.
Nave, Carl Rod. "Adiabatic Processes". HyperPhysics.
Thorngren, Dr. Jane R.. "Adiabatic Processes". Daphne – A Palomar College Web Server., 21 July 1995.Archived 2011-05-09 at the Wayback Machine.

बाहरी कड़ियाँ

Media related to रुद्धोष्म प्रक्रम at Wikimedia Commons

Article in HyperPhysics Encyclopaedia

[Bailyn_53-1] 1.0 ^1.1 ^1.2 Bailyn, M. (1994), pp. 52–53.

[2] "pseudoadiabatic process". American Meteorological Society. Retrieved November 3, 2018.

[3] Tisza, L. (1966). Generalized Thermodynamics. Cambridge, MA: MIT Press. p. 48. (adiabatic partitions inhibit the transfer of heat and mass)

[4] Münster, A. (1970), p. 48: "mass is an adiabatically inhibited variable."

[5] Münster, A. (1970). Classical Thermodynamics. Translated by Halberstadt, E. S. London: Wiley–Interscience. p. 45. ISBN 0-471-62430-6.

[6] Knight, Jasper (31 January 2022). "Snowfall in the Sahara desert: an unusual weather phenomenon". The Conversation. Retrieved 3 March 2022.

[7] Turcotte and Schubert (2002). भूगतिकी. Cambridge: Cambridge University Press. pp. 185. ISBN 0-521-66624-4.

[8] Adiabatic Processes.

[9] Atkins, Peter; de Paula, Giulio (2006). Atkins' Physical Chemistry (8th ed.). W.H.Freeman. p. 48. ISBN 0-7167-8759-8.

[Rankine_1866-10] 10.0 ^10.1 Rankine, W.J.McQ. (1866). On the theory of explosive gas engines, The Engineer, July 27, 1866; at page 467 of the reprint in Miscellaneous Scientific Papers, edited by W.J. Millar, 1881, Charles Griffin, London.

[Partington_122-11] Partington, J. R. (1949), An Advanced Treatise on Physical Chemistry., vol. 1, Fundamental Principles. The Properties of Gases, London: Longmans, Green and Co., p. 122

[12] Maxwell, J. C. (1871), Theory of Heat (first ed.), London: Longmans, Green and Co., p. 129

[13] Liddell, H.G., Scott, R. (1940). A Greek-English Lexicon, Clarendon Press, Oxford UK.

[14] Rankine, W.J.McQ. (1854). "On the geometrical representation of the expansive action of heat, and theory of thermodynamic engines". Proc. R. Soc. 144: 115–175. Miscellaneous Scientific Papers p. 339

[15] Rankine, W.J.McQ. (1854). "On the geometrical representation of the expansive action of heat, and theory of thermodynamic engines". Proc. R. Soc. 144: 115–175. Miscellaneous Scientific Papers p. 341.

[16] Bryan, G. H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications. Leipzig: B. G. Teubner.

[Carathéodory-17] Cite error: Invalid <ref> tag; no text was provided for refs named Carathéodory

[18] Born, M. (1949). "Natural Philosophy of Cause and Chance". London: Oxford University Press. {{cite journal}}: Cite journal requires |journal= (help)

[Bailyn_Ch_3-19] 19.0 ^19.1 Bailyn, M. (1994). "Chapter 3". A Survey of Thermodynamics. New York, NY: American Institute of Physics. ISBN 0-88318-797-3.

[20] Born, M. (1927). "Physical aspects of quantum mechanics". Nature. 119 (2992): 354–357. Bibcode:1927Natur.119..354B. doi:10.1038/119354a0. (Translation by Robert Oppenheimer.)

[21] Mandal, Anirban; Hunt, Katharine L. C. (2020-03-14). "Variance of the energy of a quantum system in a time-dependent perturbation: Determination by nonadiabatic transition probabilities". The Journal of Chemical Physics. 152 (10): 104110. Bibcode:2020JChPh.152j4110M. doi:10.1063/1.5140009. ISSN 0021-9606. PMID 32171229. S2CID 212731108.

[22] "diabatic process". American Meteorological Society. Retrieved 24 November 2020.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

Anonymous

Search

रुद्धोष्म प्रक्रम

Namespaces

More

Page actions

Contents

विवरण

रूद्धोष्म धारणा के विभिन्न अनुप्रयोग

स्थिरोष्म तापन और शीतलन

आदर्श गैस (प्रतिवर्ती प्रक्रिया)

स्थिरोष्म संपीड़न का उदाहरण

गैस का स्थिरोष्म मुक्त प्रसार

स्थिरोष्म तापन और शीतलन के लिए P-V संबंध की व्युत्पत्ति

असतत सूत्र और कार्य अभिव्यक्ति की व्युत्पत्ति

स्थिरोष्म रेखांकन

व्युत्पत्ति

ऊष्मप्रवैगिकी सिद्धांत में वैचारिक महत्व

स्थिरोष्म शब्द के अलग-अलग उपयोग

यह भी देखें

संदर्भ

बाहरी कड़ियाँ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

रुद्धोष्म प्रक्रम

विवरण

रूद्धोष्म धारणा के विभिन्न अनुप्रयोग

स्थिरोष्म तापन और शीतलन

आदर्श गैस (प्रतिवर्ती प्रक्रिया)

स्थिरोष्म संपीड़न का उदाहरण

गैस का स्थिरोष्म मुक्त प्रसार

स्थिरोष्म तापन और शीतलन के लिए P-V संबंध की व्युत्पत्ति

असतत सूत्र और कार्य अभिव्यक्ति की व्युत्पत्ति

स्थिरोष्म रेखांकन

व्युत्पत्ति

ऊष्मप्रवैगिकी सिद्धांत में वैचारिक महत्व

स्थिरोष्म शब्द के अलग-अलग उपयोग

यह भी देखें

संदर्भ

बाहरी कड़ियाँ

Navigation

Wiki tools

Page tools

Other projects

Categories