मेरोमॉर्फिक फलन

जटिल विश्लेषण के गणितीय क्षेत्र में, जटिल विमान के एक खुले सेट 'डी' पर एक मेरोमोर्फिक फ़ंक्शन एक फ़ंक्शन (गणित) है जो एक सेट के लिए 'डी' को छोड़कर के सभी पर होलोमॉर्फिक फ़ंक्शन है। पृथक बिंदुओं के, जो फ़ंक्शन के ध्रुव (जटिल विश्लेषण) हैं। यह शब्द ग्रीक भाषा मेरोस से आया है (विकि:μέρος|μέρος), जिसका अर्थ है भाग डी पर प्रत्येक मेरोमोर्फिक फ़ंक्शन को डी पर परिभाषित दो होलोमोर्फिक फ़ंक्शंस (भाजक 0 स्थिर नहीं) के बीच के अनुपात के रूप में व्यक्त किया जा सकता है: किसी भी ध्रुव को भाजक के शून्य के साथ मेल खाना चाहिए।

गामा समारोह पूरे जटिल विमान में मेरोमोर्फिक है।

अनुमानी विवरण

सहजता से, एक मेरोमोर्फिक फ़ंक्शन दो अच्छी तरह से व्यवहार (होलोमोर्फिक) कार्यों का अनुपात है। इस तरह के एक समारोह अभी भी अच्छी तरह से व्यवहार किया जाएगा, संभवतः उन बिंदुओं को छोड़कर जहां अंश का भाजक शून्य है। यदि हर में z पर शून्य है और अंश में नहीं है, तो फलन का मान अनंत तक पहुंच जाएगा; यदि दोनों भागों में z पर शून्य है, तो किसी को इन शून्यों के बहुपद के मूल की बहुलता (गणित) # गुणन की तुलना करनी चाहिए।

बीजगणितीय दृष्टिकोण से, यदि फ़ंक्शन का डोमेन सेट से जुड़ा हुआ है, तो मेरोमोर्फिक फ़ंक्शंस का सेट होलोमोर्फिक फ़ंक्शंस के सेट के अभिन्न डोमेन के अंशों का क्षेत्र है। यह परिमेय संख्याओं और पूर्णांकों के बीच संबंध के अनुरूप है।

पूर्व, वैकल्पिक उपयोग

अध्ययन के दोनों क्षेत्रों में जहां इस शब्द का प्रयोग किया गया है और 20वीं शताब्दी में शब्द का सटीक अर्थ बदल गया है। 1930 के दशक में, समूह सिद्धांत में, एक मेरोमोर्फिक फ़ंक्शन (या मेरोमोर्फ) समूह जी से स्वयं में एक फ़ंक्शन था जो समूह पर उत्पाद को संरक्षित करता था। इस फ़ंक्शन की छवि को G का ऑटोमोर्फिज़्म कहा जाता था। इसी तरह, एक होमोमोर्फिक फ़ंक्शन (या होमोमोर्फ) उन समूहों के बीच एक फ़ंक्शन था जो उत्पाद को संरक्षित करता था, जबकि एक होमोमोर्फिज़्म एक होमोमोर्फ की छवि थी। शब्द का यह रूप अब अप्रचलित है, और समूह सिद्धांत में संबंधित शब्द मेरोमोर्फ का अब उपयोग नहीं किया जाता है। एंडोमोर्फिज्म शब्द अब फ़ंक्शन के लिए ही उपयोग किया जाता है, फ़ंक्शन की छवि को कोई विशेष नाम नहीं दिया गया है।

एक मेरोमोर्फिक फ़ंक्शन अनिवार्य रूप से एक एंडोमोर्फिज्म नहीं है, क्योंकि इसके ध्रुवों पर जटिल बिंदु इसके डोमेन में नहीं हैं, लेकिन इसकी सीमा में हो सकते हैं।

गुण

चूंकि मेरोमोर्फिक फ़ंक्शन के ध्रुव अलग-थलग हैं, इसलिए अधिक से अधिक गणनीय हैं।ध्रुवों का समूह अनंत हो सकता है, जैसा कि फ़ंक्शन द्वारा उदाहरण दिया गया है

$$f(z)=\csc z={\frac {1}{\sin z}}.$$

हटाने योग्य विलक्षणता को खत्म करने के लिए विश्लेषणात्मक निरंतरता का उपयोग करके, मेरोमोर्फिक कार्यों को जोड़ा जा सकता है, घटाया जा सकता है, गुणा किया जा सकता है और भागफल $f/g$ तक बन सकता है $g(z)=0$ डी के जुड़े हुए स्थान पर। इस प्रकार, यदि डी जुड़ा हुआ है, तो मेरोमोर्फिक फ़ंक्शन एक क्षेत्र (गणित) बनाते हैं, वास्तव में जटिल संख्याओं का एक क्षेत्र विस्तार।

उच्च आयाम

कई जटिल चरों में, एक मेरोमोर्फिक फ़ंक्शन को स्थानीय रूप से दो होलोमोर्फिक फ़ंक्शन के भागफल के रूप में परिभाषित किया जाता है। उदाहरण के लिए, $f(z_{1},z_{2})=z_{1}/z_{2}$ द्वि-आयामी जटिल एफ़िन स्पेस पर एक मेरोमोर्फिक फ़ंक्शन है। यहाँ यह अब सच नहीं है कि प्रत्येक मेरोमॉर्फिक फ़ंक्शन को रीमैन क्षेत्र में मूल्यों के साथ एक होलोमोर्फिक फ़ंक्शन के रूप में माना जा सकता है: codimension दो की अनिश्चितता का एक सेट है (दिए गए उदाहरण में इस सेट में मूल शामिल हैं $(0,0)$).

आयाम एक के विपरीत, उच्च आयामों में कॉम्पैक्ट जटिल कई गुना मौजूद होते हैं, जिन पर कोई गैर-निरंतर मेरोमोर्फिक फ़ंक्शन नहीं होते हैं, उदाहरण के लिए, सबसे जटिल टोरस।

उदाहरण

• सभी तर्कसंगत कार्य,<ref name=Lang_1999>Lang, Serge (1999). जटिल विश्लेषण (4th ed.). Berlin; New York: Springer-Verlag. ISBN 978-0-387-98592-3.</रेफरी> उदाहरण के लिए
  $$f(z)={\frac {z^{3}-2z+10}{z^{5}+3z-1}},$$
  पूरे जटिल तल पर मेरोमोर्फिक हैं।
• कार्य
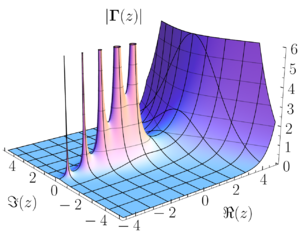
  $$f(z)={\frac {e^{z}}{z}}\quad {\text{and}}\quad f(z)={\frac {\sin {z}}{(z-1)^{2}}}$$
  साथ ही साथ गामा फ़ंक्शन और रीमैन जीटा फ़ंक्शन पूरे जटिल तल पर मेरोमोर्फिक हैं।* कार्यक्रम
  $$f(z)=e^{\frac {1}{z}}$$
  मूल, 0. को छोड़कर पूरे जटिल तल में परिभाषित किया गया है। हालांकि, 0 इस कार्य का ध्रुव नहीं है, बल्कि एक आवश्यक विलक्षणता है। इस प्रकार, यह कार्य पूरे जटिल विमान में मेरोमोर्फिक नहीं है। हालाँकि, यह मेरोमोर्फिक (यहां तक ​​​​कि होलोमोर्फिक) है $\mathbb {C} \setminus \{0\}$.
• जटिल लघुगणक समारोह
  $$f(z)=\ln(z)$$
  संपूर्ण जटिल तल पर मेरोमोर्फिक नहीं है, क्योंकि इसे केवल पृथक बिंदुओं के एक सेट को छोड़कर पूरे जटिल तल पर परिभाषित नहीं किया जा सकता है।* कार्यक्रम
  $$f(z)=\csc {\frac {1}{z}}={\frac {1}{\sin \left({\frac {1}{z}}\right)}}$$
  बिंदु के बाद से पूरे विमान में मेरोमोर्फिक नहीं है $z=0$ ध्रुवों का एक संचय बिंदु है और इस प्रकार यह एक पृथक विलक्षणता नहीं है।* कार्यक्रम
  $$f(z)=\sin {\frac {1}{z}}$$
  मेरोमोर्फिक भी नहीं है, क्योंकि इसमें 0 पर एक आवश्यक विलक्षणता है।

रीमैन सतहों पर

रीमैन की सतह पर, प्रत्येक बिंदु एक खुले पड़ोस को स्वीकार करता है जो जटिल तल के एक खुले उपसमुच्चय के लिए biholomorphism है। इस प्रकार प्रत्येक रीमैन सतह के लिए मेरोमोर्फिक फ़ंक्शन की धारणा को परिभाषित किया जा सकता है।

जब डी संपूर्ण रीमैन क्षेत्र है, मेरोमोर्फिक कार्यों का क्षेत्र जटिल क्षेत्र पर एक चर में तर्कसंगत कार्यों का क्षेत्र है, क्योंकि कोई यह साबित कर सकता है कि क्षेत्र पर कोई मेरोमोर्फिक फ़ंक्शन तर्कसंगत है। (यह तथाकथित बेहूदा सिद्धांत का एक विशेष मामला है।)

प्रत्येक रीमैन सतह के लिए, एक मेरोमोर्फिक फ़ंक्शन एक होलोमोर्फिक फ़ंक्शन के समान होता है जो रीमैन क्षेत्र के लिए मैप करता है और जो ∞ के बराबर निरंतर फ़ंक्शन नहीं होता है। ध्रुव उन सम्मिश्र संख्याओं के अनुरूप होते हैं जिन्हें ∞ से प्रतिचित्रित किया जाता है।

एक गैर-कॉम्पैक्ट रीमैन सतह पर, प्रत्येक मेरोमोर्फिक फ़ंक्शन को दो (वैश्विक रूप से परिभाषित) होलोमोर्फिक फ़ंक्शन के भागफल के रूप में महसूस किया जा सकता है। इसके विपरीत, एक कॉम्पैक्ट रीमैन सतह पर, प्रत्येक होलोमोर्फिक फ़ंक्शन स्थिर होता है, जबकि हमेशा गैर-निरंतर मेरोमोर्फिक फ़ंक्शन मौजूद होते हैं।

यह भी देखें

• चचेरे भाई की समस्या
• Mittag-Leffler's प्रमेय
• वीयरस्ट्रास गुणनखंड प्रमेय