स्थिर समय

भौतिकी और अभियांत्रिकी में स्थिर समय, सामान्यतः ग्रीक भाषा के पत्र द्वारा प्रथम-क्रम, एलटीआई प्रणाली सिद्धांत $τ$ (टाउ) निरूपित किया जाता है, रैखिक समय-अपरिवर्तनीय (एलटीआई) प्रणाली के चरण निवेश की प्रतिक्रिया को चिह्नित करने वाला प्राचल है।^[1] स्थिर समयांक प्रथम-क्रम एलटीआई प्रणाली की मुख्य विशेषता इकाई है।

समय अनुक्षेत्र में समय की प्रतिक्रिया को मालूम करने के लिए सामान्यतः विकल्प इकाई पग फलन के चरण प्रतिक्रिया या डिराक डेल्टा फलन निवेश के आवेग प्रतिक्रिया के माध्यम से होता है।^[2] आवृत्तिय अनुक्षेत्र में (उदाहरण के लिए, चरण प्रतिक्रिया के फूरियर रूपांतरण को देखते हुए, या निवेश का उपयोग जो समय का एक सरल ज्यावक्रीय फलन है) स्थिर समयांक पहले-क्रम के समय-अपरिवर्तनीय के तरंगधैर्य (संकेत आगे बढ़ाना) को भी निर्धारित करता है। प्रणाली वह आवृत्ति है जिस पर संकेत की शक्ति कम आवृत्तियों पर उसके आधे मान तक गिर जाती है।

तरंगधैर्य (संकेत प्रसंस्करण) प्रणाली - चुंबकीय कैसेट, रेडियो प्रेषित्र और रेडियो आदाता, रिकॉर्ड उपमार्ग, पुनर्प्रदर्शन उपकरण, और अंकीय निस्पंदन - की आवृत्ति प्रतिक्रिया को चिह्नित करने के लिए स्थिर समयांक का भी उपयोग किया जाता है जिसे प्रथम-क्रम एलटीआई प्रणाली द्वारा नमूना या अनुमानित किया जाता है। अन्य उदाहरणों में अभिन्न और यौगिक कार्रवाई नियंत्रक के लिए नियंत्रण प्रणाली में उपयोग होने वाला स्थिर समय सम्मलित है जो अधिकांशतः विद्युतीय के अतिरिक्त वायवीय होता है।

स्थिर समयांक उष्णता सम्बन्धी प्रणाली के लिए लम्प्ड प्रणाली विश्लेषण (ढेर क्षमता विश्लेषण विधि) की विशेषता है, जिसका उपयोग तब किया जाता है जब वस्तुएं संवहन शीतलन या वार्मिंग के प्रभाव में समान रूप से ठंडी या गर्म होती हैं।^[3] भौतिक रूप से, स्थिर समयांक प्रणाली की प्रतिक्रिया के लिए शून्य से क्षय होने के लिए आवश्यक अतीत समय यह दर्शाता है कि यदि प्रणाली प्रारंभिक दर पर क्षय करना जारी रखती है, तो क्षय की दर में प्रगतिशील परिवर्तन के कारण प्रतिक्रिया वास्तव के मूल्य में कमी हो जाती है $1 / e \approx 36.8%$ (पदध्वनि कमी से कहते हैं)। बढ़ती हुई प्रणाली में, प्रणाली की पदध्वनि प्रतिक्रिया तक पहुँचने के लिए स्थिर समय है $1 - 1 / e \approx 63.2%$ । इसके अंतिम (स्पर्शोन्मुख) मूल्य हैं(पदध्वनि वृद्धि से कहते हैं)। विघटनाभिक क्षय में स्थिर समयांक क्षय स्थिरांक (λ) से संबंधित होता है, और यह क्षय होने से पहले क्षय प्रणाली (जैसे एक परमाणु) के औसत जीवनकाल, या 36.8% परमाणुओं को छोड़कर सभी के लिए लगने वाले समय दोनों का प्रतिनिधित्व करता है। क्षय करने के लिए स्थिर समय अर्ध-जीवन से अधिक लंबा होना चाहिए, जो केवल 50% परमाणुओं के क्षय होने का समय है।

विभेदक समीकरण

पहले के आदेश एलटीआई प्रणाली की विशेषता विभेदक समीकरण है

\tau {\frac {dV}{dt}}+V=f(t)

जहाँ $τ$ घातीय क्षय स्थिरांक का प्रतिनिधित्व करता है और वी समय का कार्य टी है

V=V(t).

दायीं ओर का बल देने वाला कार्य ऍफ़(टी) समय के बाहरी परिचालन फलन का वर्णन करना, जिसे प्रणाली निवेश के रूप में माना जा सकता है, जिसके लिए वी(टी) प्रतिक्रिया है, या प्रणाली संकेत है। मौलिक उदाहरण के लिए ऍफ़(टी) हैं:

हीविसाइड अनुभाग फलन, जिसे अधिकांशतः निरूपित किया जाता है यू(टी):

u(t)={\begin{cases}0,&t<0\\1,&t\geq 0\end{cases}}

आवेग फलन, जिसे अधिकांशतः निरूपित किया जाता है $δ (t)$ , और ज्यावक्रीय निवेश फलन:

f(t)=A\sin(2\pi ft)

या

f(t)=Ae^{j\omega t},

जहाँ ए प्रणोदन फलन का आयाम है, ऍफ़ हर्ट्ज़ में आवृत्ति है, और $ω = 2 π f$ प्रति सेकंड रेडियंस में आवृत्ति है।

उदाहरण समाधान

प्रारंभिक मूल्य के साथ अंतर समीकरण का उदाहरण समाधान $V 0$ और कोई विवशतापूर्वक कार्य नहीं है

V(t)=V_{0}e^{-t/\tau }

जहाँ

V_{0}=V(t=0)

का प्रारंभिक मूल्य वी है। इस प्रकार, प्रतिक्रिया स्थिर समय के साथ घातीय क्षय $τ$ है।

चर्चा

कल्पना करना

V(t)=V_{0}e^{-t/\tau }.

इस व्यवहार को क्षयकारी घातीय कार्य कहा जाता है। समय

τ

(टाउ) को स्थिर समयांक के रूप में संदर्भित किया जाता है और इसका उपयोग इंगित करने के लिए कि घातीय फलन कितनी तेजी से घटता है (जैसा कि इस स्थितियों में) किया जाता है।

यहाँ:

टी समय है (सामान्यतः $टी > 0$ नियंत्रण अभियांत्रिकी में)
$V 0$ प्रारंभिक मूल्य है (नीचे विशिष्ट स्थितियों देखें)।

विशिष्ट स्थितियों

होने देना $t=0$ ; तब $V=V_{0}e^{0}$ , इसलिए $V=V_{0}$
होने देना $t=\tau$ ; तब $V=V_{0}e^{-1}\approx 0.37V_{0}$
होने देना $V=f(t)=V_{0}e^{-t/\tau }$ , इसलिए ${\textstyle \lim _{t\to \infty }f(t)=0}$
होने देना $t=5\tau$ ; तब $V=V_{0}e^{-5}\approx 0.0067V_{0}$

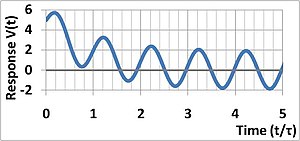
समय की अवधि के पश्चात निरंतर फलन पहुंचता $e -1$ है। इसके प्रारंभिक मूल्य का लगभग 37%, चार स्थितियों में, पांच बार स्थिरांक के पश्चात फलन अपने मूल के एक% से कम मान तक पहुँच जाता है। अधिकांशतः स्थितियों में यह एक% सीमा यह मानने के लिए पर्याप्त है कि फलन शून्य तक क्षय हो गया है। अंगूठे के नियम के रूप में, नियंत्रण अभियांत्रिकी में स्थिर प्रणाली वह है जो इस प्रकार के समग्र अवमंदित व्यवहार को प्रदर्शित करती है।

तरंगधैर्य से निरंतर समय का संबंध

साइन लहर प्रणोदन फलन के लिए प्रणाली की प्रतिक्रिया का उदाहरण। स्थिर समयांक की इकाइयों में समय अक्ष

τ

. प्रतिक्रिया नम हो जाती है और एक साधारण साइन लहर बन जाती है।

तरंगधैर्य की इकाइयों में प्रणाली बनाम आवृत्ति की आवृत्ति प्रतिक्रिया

f 3dB

. प्रतिक्रिया को एकता के शून्य आवृत्ति मान पर सामान्यीकृत किया जाता है, और तरंगधैर्य पर 1/√2 तक गिर जाता है।

मान लीजिए कि प्रणोदन फलन को ज्यावक्रीय के रूप में चुना गया है:

\tau {\frac {dV}{dt}}+V=f(t)=Ae^{j\omega t}.

(यूलर के सूत्र के आधार पर अंतिम परिणाम के वास्तविक या काल्पनिक भाग को लेकर वास्तविक कोसाइन या साइन लहर निवेश की प्रतिक्रिया प्राप्त की जाती है।) समय के लिए इस समीकरण का सामान्यतः समाधान $t \geq 0 s$ , मानते हुए $V (t = 0) = V 0$ है:

{\begin{aligned}V(t)&=V_{0}e^{-t/\tau }+{\frac {Ae^{-t/\tau }}{\tau }}\int _{0}^{t}\,dt'\ e^{t'/\tau }e^{j\omega t'}\\&=V_{0}e^{-t/\tau }+{\frac {1/\tau }{j\omega +1/\tau }}A\left(e^{j\omega t}-e^{-t/\tau }\right).\end{aligned}}

लंबे समय तक क्षयकारी घातांक नगण्य हो जाते हैं और स्थिर-अवस्था समाधान या दीर्घकालिक समाधान

V_{\infty }(t)={\frac {1/\tau }{j\omega +1/\tau }}Ae^{j\omega t}.

इस प्रतिक्रिया का परिमाण है:

|V_{\infty }(t)|=A{\frac {1}{\tau \left(\omega ^{2}+(1/\tau )^{2}\right)^{1/2}}}=A{\frac {1}{\sqrt {1+(\omega \tau )^{2}}}}.

सम्मेलन द्वारा, इस प्रणाली की तरंगधैर्य वह आवृत्ति है जहाँ $| V \infty | 2$ आधा मूल्य, या जहाँ तक गिर जाता है $ωτ = 1$ . यह सामान्यतः तरंगधैर्य (संकेत प्रसंस्करण) प्रथा है, जिसे आवृत्तियों रेंज के रूप में परिभाषित किया गया है, जहाँ बिजली आधे से भी कम (अधिकतम -3 dB) गिरती है। रेडियन/एस के अतिरिक्त हर्ट्ज़ में आवृत्ति का उपयोग करना ( $ω = 2 πf$ ):

f_{\mathrm {3dB} }={\frac {1}{2\pi \tau }}.

अंकन $f 3dB$ डेसिबल में शक्ति की अभिव्यक्ति से उपजा है और अवलोकन है कि आधी शक्ति के मूल्य में गिरावट के अनुरूप है $| V \infty |$ 1/2 या 3 डेसिबल के कारक द्वारा इस प्रकार स्थिर समयांक प्रणाली की तरंगधैर्य को निर्धारित करता है।

मनमाने ढंग से प्रारंभिक शर्तों के साथ पदध्वनि प्रतिक्रिया

दो भिन्न-भिन्न प्रारंभिक मूल्यों के लिए प्रणाली की चरण प्रतिक्रिया वी₀, अंतिम मान से ऊपर और शून्य पर लंबे समय तक प्रतिक्रिया स्थिर है, वी_∞. स्थिर समयांक की इकाइयों में समय अक्ष

\tau

है।

मान लीजिए कि प्रणोदन फलन को चरण निवेश के रूप में चुना गया है:

{\frac {dV}{dt}}+{\frac {1}{\tau }}V=f(t)=Au(t),

साथ यू(टी) हीविसाइड अनुभाग फलन समय के लिए इस समीकरण का सामान्यतः समाधान $t \geq 0 s$ , मानते हुए $V (t = 0) = V 0$ है:

V(t)=V_{0}e^{-t/\tau }+A\tau \left(1-e^{-t/\tau }\right).

(यह देखा जा सकता है कि यह प्रतिक्रिया है $ω \to 0$ ज्यावक्रीय निवेश के लिए उपरोक्त प्रतिक्रिया की सीमा है।)

लंबे समय का समाधान समय स्वतंत्र और प्रारंभिक स्थितियों से स्वतंत्र है:

V_{\infty }=A\tau .

आरंभिक स्थितियों की परवाह किए बिना समान प्रणाली के लिए स्थिर समयांक समान रहती है। सीधे तौर पर कहा जाए तो यह किसी भी प्रारंभिक बिंदु पर उस मूल्य के कितने करीब हो प्रणाली अपनी अंतिम स्थिर-स्थिति को दर पर प्राप्त करती है।

उदाहरण के लिए, विद्युत मोटर पर विचार जिसकी शुरुआत पहले क्रम के एलटीआई प्रणाली द्वारा अच्छी प्रकार से तैयार की गयी है। कल्पना करें कि जब आराम से प्रारंभ किया जाता है, तो मोटर लेती है 1/8 100 आरपीएम, या 63 आरपीएम की नाममात्र गति के 63% तक पहुँचने के लिए सेकंड का - 37 आरपीएम की कमी। फिर यह पता चलेगा कि अगले के पश्चात 1/8 सेकंड में, मोटर ने अतिरिक्त 23 आरपीएम को गति दी है, जो उस 37 आरपीएम अंतर के 63% के बराबर है। यह इसे 86 आरपीएम पर लाता है - अभी भी 14 आरपीएम कम है। एक तिहाई के पश्चात 1/8 सेकंड में, मोटर ने अतिरिक्त 9 आरपीएम (उस 14 आरपीएम अंतर का 63%) प्राप्त किया होगा, जो इसे 95 आरपीएम पर रखता है।

वास्तव में, किसी भी प्रारंभिक गति को देखते हुए s ≤ 100 RPM, 1/8 सेकंड के पश्चात इस विशेष मोटर ने अतिरिक्त लाभ 0.63 × (100 − s) आरपीएम. प्राप्त किया है।

उदाहरण

विद्युत परिपथों में स्थिर समयांक

संधारित्र तनाव चरण-प्रतिक्रिया।

प्रारंभ करनेवाला तनाव चरण-प्रतिक्रिया।

एकल अवरोध और प्रारंभ से बना आरएल परिपथ में, स्थिर समय $\tau$ (दूसरा में) है:

\tau ={\frac {L}{R}}

जहाँ आर विद्युत प्रतिरोध(ओम में) है और एल अधिष्ठापन है(हेनरी (यूनिट))।

इसी प्रकार, एकल अवरोध और संधारित्र से बना आरसी परिपथ, स्थिर समय $\tau$ (सेकंड में) है:

\tau =RC

जहाँ आर प्रतिरोध है(ओम में) और सी समाई है(फैराड में)।

विद्युत परिपथ अधिकांशतः इन उदाहरणों की तुलना में अधिक जटिल होते हैं, और कई बार स्थिरांक प्रदर्शित कर सकते हैं (कुछ उदाहरणों के लिए चरण प्रतिक्रिया और ध्रुव विभाजन देखें)। उन स्थितियों में जहाँ नकारात्मक प्रतिक्रिया प्रवर्धक उपलब्ध है, प्रणाली अस्थिर बढ़ते दोलनों को प्रदर्शित कर सकती है। इसके अतिरिक्त, बहुत कम आयाम उत्तेजनाओं के बिना, भौतिक विद्युत परिपथ संभवतः ही कभी सही मायने में रैखिक प्रणाली होती हैं, चूंकि, रैखिकता के सन्निकटन का व्यापक रूप से उपयोग किया जाता है।

अंकीय इलेक्ट्रॉनिक परिपथ में एक और माध्यम, ऍफ़ ओ फोर अधिकांशतः उपयोग किया जाता है। इसे समीकरण के माध्यम से स्थिर समय इकाइयों में परिवर्तित $5\tau ={\text{FO4}}$ किया जाता है।^[4]

उष्णता सम्बन्धी स्थिर समय

स्थिर समयांक उष्णता सम्बन्धी प्रणाली के लिए लुम्प्ड प्रणाली विश्लेषण (ढेर क्षमता विश्लेषण विधि) की विशेषता है, जिसका उपयोग तब किया जाता है जब संवहन (गर्मी हस्तांतरण) के प्रभाव में वस्तुओं को समान रूप से ठंडा या गर्म किया जाता हो। इन स्थितियों में, एक निश्चित समय पर शरीर से परिवेश में गर्मी हस्तांतरण शरीर और परिवेश के बीच तापमान के अंतर के समानुपाती होती है:^[5]

F=hA_{s}\left(T(t)-T_{a}\right),

जहाँ एच ऊष्मा अंतरण गुणांक है, और ए_अस सतह क्षेत्र है, टी तापमान फलन है, अर्थात, टी(टी) समय पर शरीर का तापमान है, और टी_ए निरंतर परिवेश का तापमान है। धनात्मक चिह्न इस सम्मेलन को इंगित करता है कि एफ सकारात्मक है जब शरीर गर्मी छोड़ रही है क्योंकि इसका तापमान परिवेश के तापमान से अधिक है (एफ एक बाहरी प्रवाह है)। यदि गर्मी परिवेश में लुप्त जाती है, तो इस गर्मी हस्तांतरण से शरीर के तापमान में गिरावट आती है:^[5]

\rho c_{p}V{\frac {dT}{dt}}=-F,

जहाँ ρ = घनत्व, c_p = विशिष्ट ऊष्मा और वि शरीर का आयतन है, ऋणात्मक संकेत तापमान में गिरावट को इंगित करता है जब गर्मी हस्तांतरण शरीर से बाहर की ओर होती है (अर्थात, जब एफ > 0)। गर्मी हस्तांतरण के लिए इन दो भावों की समानता करना,

\rho c_{p}V{\frac {dT}{dt}}=-hA_{s}\left(T(t)-T_{a}\right).

यह प्रथम-क्रम एलटीआई प्रणाली है जिसे इस रूप में डाला जा सकता है:

{\frac {dT}{dt}}+{\frac {1}{\tau }}T={\frac {1}{\tau }}T_{a},

साथ ही,

\tau ={\frac {\rho c_{p}V}{hA_{s}}}.

दूसरे शब्दों में, उच्च ताप क्षमता वाले बड़े द्रव्यमान ρV c_p तापमान में धीमे परिवर्तन (लंबे समय तक स्थिर टी) की ओर ले जाते हैं, जबकि बड़े सतह क्षेत्र ए_एस उच्च गर्मी हस्तांतरण एच के साथ अधिक तेजी से तापमान परिवर्तन (कम स्थिर समय टी) होता है।

परिचयात्मक अवकल समीकरण के साथ तुलना समय-परिवर्तित परिवेश तापमान टी के संभावित सामान्यीकरण का सुझाव देती है। चूंकि, चर ΔT ≡ (T − T) को प्रतिस्थापित करके सरल स्थिर परिवेश उदाहरण को बनाए रखना: ${\frac {d\Delta T}{dt}}+{\frac {1}{\tau }}\Delta T=0.$

जिन प्रणालियों के लिए शीतलन उपरोक्त घातीय समीकरण को संतुष्ट करता है, उन्हें न्यूटन के शीतलन के नियम को संतुष्ट करने के लिए कहा जाता है। इस समीकरण के समाधान से पता चलता है कि ऐसी प्रणालियों में, प्रणाली के तापमान और उसके परिवेश के बीच का अंतर ΔT समय टी के फलन के रूप में दिया जाता है:

\Delta T(t)=\Delta T_{0}e^{-t/\tau },

जहाँ डीटी₀ प्रारंभिक तापमान समय टी = 0 पर अंतर है। शब्दों में, शरीर ही तापमान को परिवेश के रूप में मानता है जो स्थिर समय द्वारा निर्धारित घातीय धीमे दर पर होता है।

जीव पदाथ-विद्य में स्थिर समयांक

उत्तेजनीय कोशिका जैसे मायोसाइट या स्नायु में, कला क्षमता का स्थिर समय $\tau$ है

\tau =r_{m}c_{m}

जहाँ आर_एम कला भर में प्रतिरोध है और सी_एम कला की समाई है।

कला के पार प्रतिरोध खुले आयन चैनलों की संख्या का कार्य है और समाई लिपिड बिलेयर के गुणों का कार्य है।

कला तनाव में वृद्धि और गिरावट का वर्णन करने के लिए स्थिर समयांक का उपयोग किया जाता है, जहाँ वृद्धि का वर्णन किया जाता है

V(t)=V_{\textrm {max}}\left(1-e^{-t/\tau }\right)

और पतन का वर्णन किया है

V(t)=V_{\textrm {max}}e^{-t/\tau }

जहाँ तनाव मिलीवोल्ट में है, समय सेकंड में है, और $\tau$ सेकेंड में है।

वी_max स्थिर क्षमता से अधिकतम तनाव परिवर्तन के रूप में परिभाषित किया गया है, जहाँ

V_{\textrm {max}}=r_{m}I

जहाँ आर_एम कला के पार प्रतिरोध है और मैं कला धारा है।

टी = के लिए सेटिंग $\tau$ उदय सेट के लिए V(t) 0.63V के बराबर है। इसका अर्थ है कि स्थिर समय V के 63% के पश्चात अतीत हुआ समय है_max तक पहुँच चुका है।

टी = के लिए सेटिंग $\tau$ फॉल सेट के लिए V(t) 0.37V के बराबर है, जिसका अर्थ है कि स्थिर समयांक वी के 37% तक गिरने के पश्चात अतीत हुआ समय है।

स्थिर समयांक जितना बड़ा होता है, स्नायु की क्षमता का उत्थान या पतन उतना ही धीमा होता है। लंबे समय के स्थिरांक का परिणाम लौकिक योग, या बार-बार संभावितों का बीजगणितीय योग हो सकता है। स्थानिक योग के माध्यम से तंत्रिका जीव विज्ञान में कम समय निरंतर एक संयोग का पता लगाता है।

घातीय क्षय

घातीय क्षय में, जैसे विघटनाभिक क्षय समस्थानिक, स्थिर समयांक को औसत जीवनकाल के रूप में व्याख्या किया जाता है। आधा जीवन टी_एचएल घातीय स्थिर समयांक से संबंधित $\tau$ द्वारा है,

T_{HL}=\tau \ln 2.

स्थिर समयांक के व्युत्क्रम को क्षय स्थिरांक कहा जाता है, और निरूपित किया जाता है $\lambda =1/\tau$ .

काल संबंधी ज्ञानेंद्री

स्थिर समय वह समय है जो एक काल संबंधी संवेदक को माप में तेजी से बदलाव का उत्तर देने में लगता है, और जब तक कि यह सामान्यतः संवेदक से अपेक्षित त्रुटिहीन सहिष्णुता के भीतर मूल्यों को माप नहीं ले पाता है।

यह अधिकांशतः तापमान, ओस-बिंदु तापमान, आर्द्रता और वायु के मापन पर लागू होता है। रेडियोसोंडे विशेष रूप से ऊंचाई में तेजी से वृद्धि के कारण प्रभावित होता हैं।

यह भी देखें

संदर्भ

↑ Béla G. Lipták (2003). इंस्ट्रूमेंट इंजीनियर्स हैंडबुक: प्रक्रिया नियंत्रण और अनुकूलन (4 ed.). CRC Press. p. 100. ISBN 978-0-8493-1081-2.</रेफरी><ref group="note">Concretely, a first-order LTI system is a system that can be modeled by a single first order differential equation in time. Examples include the simplest single-stage electrical RC circuits and RL circuits.
↑ Bong Wie (1998). Space vehicle dynamics and control. American Institute of Aeronautics and Astronautics. p. 100. ISBN 978-1-56347-261-9.
↑ GR North (1988). "Lessons from energy balance models". In Michael E. Schlesinger (ed.). Physically-based Modelling and Simulation of Climate and Climatic Change (NATO Advanced Study Institute on Physical-Based Modelling ed.). Springer. NATO. p. 627. ISBN 978-90-277-2789-3.
↑ Harris, D.; Sutherland, I. (2003). "Logical effort of carry propagate adders". The Thirty-Seventh Asilomar Conference on Signals, Systems & Computers, 2003. pp. 873–878. doi:10.1109/ACSSC.2003.1292037. ISBN 0-7803-8104-1. S2CID 7880203.
↑ ^5.0 ^5.1 Roland Wynne Lewis; Perumal Nithiarasu; K. N. Seetharamu (2004). Fundamentals of the finite element method for heat and fluid flow. Wiley. p. 151. ISBN 978-0-470-84789-3.

बाहरी संबंध

[Lipták-1] Béla G. Lipták (2003). इंस्ट्रूमेंट इंजीनियर्स हैंडबुक: प्रक्रिया नियंत्रण और अनुकूलन (4 ed.). CRC Press. p. 100. ISBN 978-0-8493-1081-2.</रेफरी><ref group="note">Concretely, a first-order LTI system is a system that can be modeled by a single first order differential equation in time. Examples include the simplest single-stage electrical RC circuits and RL circuits.

[Wie-2] Bong Wie (1998). Space vehicle dynamics and control. American Institute of Aeronautics and Astronautics. p. 100. ISBN 978-1-56347-261-9.

[NATO-3] GR North (1988). "Lessons from energy balance models". In Michael E. Schlesinger (ed.). Physically-based Modelling and Simulation of Climate and Climatic Change (NATO Advanced Study Institute on Physical-Based Modelling ed.). Springer. NATO. p. 627. ISBN 978-90-277-2789-3.

[4] Harris, D.; Sutherland, I. (2003). "Logical effort of carry propagate adders". The Thirty-Seventh Asilomar Conference on Signals, Systems & Computers, 2003. pp. 873–878. doi:10.1109/ACSSC.2003.1292037. ISBN 0-7803-8104-1. S2CID 7880203.

[Lewis-5] 5.0 ^5.1 Roland Wynne Lewis; Perumal Nithiarasu; K. N. Seetharamu (2004). Fundamentals of the finite element method for heat and fluid flow. Wiley. p. 151. ISBN 978-0-470-84789-3.

[1]

[2]

[3]

[4]

[5]

Anonymous

Search

स्थिर समय

Namespaces

More

Page actions

Contents