टेंट मैप
गणित में, मापदंड μ वाला टेंट मैप वास्तविक संख्या-मूल्य वाला एक फलन होता है जिसे fμ द्वारा परिभाषित किया जाता है
इसे यह नाम fμके एक फलन के ग्राफ़ के टेंट जैसे आकार के होने के कारण दिया गया था। 0 और 2 के भीतर मापदंड μ के मानों के लिए, fμ इकाई अंतराल [0, 1] को अपने आप में मैपित करता है, इस प्रकार यह उस पर एक भिन्न-समय गतिशील प्रणाली को परिभाषित करता है (समकक्ष, एक पुनरावृत्ति संबंध)। विशेष रूप से, पुनरावृत्त फलन एक बिंदु x0 [0, 1] में एक अनुक्रम उत्पन्न होता है:
जहां μ एक सकारात्मक वास्तविक स्थिरांक होता है। उदाहरण के लिए मापदंड μ = 2 का चयन करते हुए, फलन fμ के प्रभाव को इकाई अंतराल को दो भागों में मोड़ने के संचालन के परिणाम के रूप में देखा जा सकता है, फिर परिणामी अंतराल (गणित) [0, 1/2] को पुनः से अंतराल [0, 1] प्राप्त करने के लिए बढ़ाया जा सकता है। प्रक्रिया को दोहराते हुए, अंतराल का कोई भी बिंदु x0 ऊपर वर्णित अनुसार नई पश्चात की स्थिति ग्रहण करता है, जिससे [0, 1] में एक अनुक्रम xn उत्पन्न होता है।
टेंट मैप कि स्थिति बिट शिफ्ट मैप और लॉजिस्टिक मैप के r = 4 स्थिति में दोनों का एक गैर-रेखीय परिवर्तन होता है।
व्यवहार
मापदंड μ = 2 के साथ टेंट मैप और मापदंड r = 4 के साथ लॉजिस्टिक मैप स्थलीय रूप से संयुग्मित होता हैं,[1] और इस प्रकार दो मैपों का व्यवहार इस अर्थ में पुनरावृत्ति के तहत समान होता है।
μ के मूल्य के आधार पर, टेंट मैप पूर्वानुमानित से लेकर विशृंखल तक गतिशील व्यवहार की एक श्रृंखला प्रदर्शित करता है।
- यदि μ 1 से कम होता है तो बिंदु x = 0, x के सभी प्रारंभिक मानों के लिए प्रणाली का एक आकर्षक निश्चित बिंदु होता है अर्थात् प्रणाली x के किसी भी प्रारंभिक मान से x = 0 की ओर परिवर्तित हो जाएगा।
- यदि μ 1 है तो 1/2 से कम या उसके समान x के सभी मान प्रणाली के निश्चित बिंदु होते हैं।
- यदि μ 1 से अधिक है तो प्रणाली में दो निश्चित बिंदु होते हैं, एक 0 पर, और दूसरा μ/(μ + 1) पर। दोनों निश्चित बिंदु अस्थिर होते हैं, अर्थात किसी भी निश्चित बिंदु के समीप x का मान उसकी ओर जाने के अतिरिक्त उससे दूर चला जाएगा। उदाहरण के लिए, जब μ 1.5 है तो x = 0.6 पर एक निश्चित बिंदु होता है (चूंकि 1.5(1 − 0.6) = 0.6) परन्तु x = 0.61 से प्रारंभ करने पर हमें निम्न प्रकार से प्राप्त होता है
- यदि μ 1 और 2 के वर्गमूल के मध्य होता है तो प्रणाली μ − μ2 और μ/2 के मध्य अंतराल का एक समुच्चय मैपित करता है। अंतरालों का यह समुच्चय मैप का जूलिया समुच्चय होता है - अर्थात, यह इस मैप के अंतर्गत वास्तविक रेखा का सबसे छोटा अपरिवर्तनीय उपसमुच्चय होता है। यदि μ 2 के वर्गमूल से अधिक होता है, तो ये अंतराल विलीन हो जाते हैं, और जूलिया समुच्चय μ − μ2 से μ/2 तक संपूर्ण अंतराल होता है (द्विभाजन आरेख देखें)।
- यदि μ 1 और 2 के मध्य है तो अंतराल [μ − μ2/2, μ/2] में आवधिक और गैर-आवधिक दोनों बिंदु सम्मिलित होते हैं, यधपि सभी कक्षा (गतिशीलता) अस्थिर होती हैं (अर्थात् आस-पास के बिंदु कक्षाओं की ओर जाने के अतिरिक्त उनसे दूर जाते हैं)। μ बढ़ने पर लंबी लंबाई वाली कक्षाएँ दिखाई देती हैं। उदाहरण के लिए:
- यदि μ 2 के समान होता है तो प्रणाली अंतराल [0, 1] को स्वयं मैपित करता है। अब इस अंतराल के भीतर प्रत्येक कक्षा की लंबाई के साथ-साथ गैर-आवधिक बिंदु भी उपस्थित होता है। [0, 1] में आवर्त बिंदु सघन होता हैं, इसलिए मैप विशृंखलता सिद्धांत बन जाता है। वास्तव में, गतिशीलता गैर-आवधिक होगी यदि और मात्र यदि एक अपरिमेय संख्या हो। इसे बात पर ध्यान देकर देखा जा सकता है कि जब को बाइनरी संख्या अंकन में व्यक्त किया जाता है तो मैप क्या करता है: यह बाइनरी बिंदु को एक स्थान से दाईं ओर स्थानांतरित करता है; फिर, यदि बाइनरी बिंदु के बाईं ओर जो दिखाई देता है वह एक है तो यह सभी को शून्य में परिवर्तित कर देता है और इसके विपरीत (परिमित बाइनरी विस्तार की स्थिति में अंतिम बिट एक को छोड़कर); एक अपरिमेय संख्या से प्रारंभ होकर यह प्रक्रिया बिना दोहराए सदैव चलती रहती है। x के लिए अपरिवर्तनीय माप इकाई अंतराल पर एकसमान घनत्व होता है।[2] पर्याप्त रूप से लंबे अनुक्रम के लिए स्वत:सहसंबंध फलन {} सभी गैर-शून्य अंतरालों पर शून्य स्वत:सहसंबंध दिखाएगा।[3] इस प्रकार स्वत:सहसंबंध फलन का उपयोग करके इसे सफेद ध्वनि से भिन्न नहीं किया जा सकता है। ध्यान दें कि लॉजिस्टिक मैप का r = 4 स्थिति और टेंट मैप की स्थिति एक-दूसरे के समरूप होती हैं: तार्किक रूप से विकसित होने वाले चर को प्रदर्शित करते हुए , होमोमोर्फिज्म निम्न प्रकार होता है
- यदि μ 2 से अधिक है तो मैप का जूलिया समुच्चय वियोजित हो जाता है, और अंतराल [0, 1] के भीतर एक कैंटर समुच्चय में पृथक हो जाता है। जूलिया समुच्चय में अभी भी गैर-आवधिक और आवधिक दोनों बिंदुओं (किसी भी कक्षा की लंबाई के लिए कक्षाओं सहित) की अनंत संख्या सम्मिलित है, परन्तु [0, 1] के भीतर लगभग प्रत्येक बिंदु अब अंततः अनंत की ओर विचलन करेगा। कैनोनिकल कैंटर समुच्चय (इकाई पंक्ति के उपसमुच्चय से मध्य तिहाई को क्रमिक रूप से हटाकर प्राप्त किया गया) μ = 3 के लिए टेंट मैप का जूलिया समुच्चय होता है।
संख्यात्मक त्रुटियाँ
मापदंड m = 2.0 के लिए टेंट मैप की समय श्रृंखला जो संख्यात्मक त्रुटि दिखाती है: समय श्रृंखला का प्लॉट (पुनरावृत्तियों की संख्या के संबंध में x चर का प्लॉट) में उतार-चढ़ाव बंद हो जाता है और n = 50 के पश्चात कोई मान नहीं देखा जाता है। मापदंड m = 2.0, प्रारंभिक बिंदु यादृच्छिक होता है।
कक्षीय आरेख को आवर्धित करना
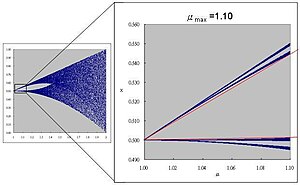
- कक्षीय आरेख को समीप से देखने पर पता चलता है कि μ ≈ 1 पर 4 भिन्न-भिन्न क्षेत्र होता हैं। आगे आवर्धन के लिए, 2 संदर्भ रेखाएं (लाल) टिप से उपयुक्त x तक निश्चित μ पर खींची जाती हैं (उदाहरण के लिए, 1.10) जैसा कि दिखाया गया है।
- संबंधित संदर्भ रेखाओं से मापी गई दूरी के साथ, आगे का विवरण मैप के ऊपरी और निचले भाग में दिखाई देता है। (कुछ μ पर कुल 8 भिन्न-भिन्न क्षेत्र)
असममित टेंट मैप
असममित टेंट मैप मूल रूप से एक विकृत, परन्तु फिर भी टुकड़े-टुकड़े रैखिक, टेंट मैप के स्थिति का संस्करण होता है। इसे निम्न प्रकार परिभाषित किया गया है
मापदंड के लिए . h> टेंट मैप की स्थिति की वर्तमान स्थिति है। एक क्रम {} में समान स्वत:सहसंबंध फलन होगा[3]जैसा कि प्रथम-क्रम स्वत:प्रतिगामी प्रक्रिया से डेटा {} के साथ स्वतंत्र और समान रूप से वितरित किया जाएगा। इस प्रकार एक असममित टेंट मैप के डेटा को, स्वत:सहसंबंध फलन का उपयोग करके, प्रथम-क्रम स्वत:प्रतिगामी प्रक्रिया द्वारा उत्पन्न डेटा से पृथक नहीं किया जा सकता है।
यह भी देखें
संदर्भ
- ↑ Conjugating the Tent and Logistic Maps, Jeffrey Rauch, University of Michigan
- ↑ Collett, Pierre, and Eckmann, Jean-Pierre, Iterated Maps on the Interval as Dynamical Systems, Boston: Birkhauser, 1980.
- ↑ 3.0 3.1 Brock, W. A., "Distinguishing random and deterministic systems: Abridged version," Journal of Economic Theory 40, October 1986, 168-195.