डेटा समानांतरता
समक्रमिक अभिकलित्र वातावरण में कई संसाधित्र में आँकडे़ समानांतरवाद समानांतर है। यह आँकडे़ को विभिन्न नोड्स में वितरित करने पर केंद्रित है, जो समानांतर में आँकडे़ पर काम करते हैं। समानांतर में प्रत्येक तत्व पर काम करके इसे सरणियों और मैट्रिक्स जैसी नियमित आँकडे़ संरचनाओं पर लागू किया जा सकता है। यह समांतरता के दूसरे रूप के रूप में कार्य समानता के विपरीत है।
'n' तत्वों की एक सरणी पर आँकडे़ समानांतर कार्य को सभी संसाधित्र के बीच समान रूप से विभाजित किया जा सकता है। आइए मान लें कि हम दिए गए सरणी के सभी तत्वों को योग करना चाहते हैं और एक अतिरिक्त संचालन के लिए समय Ta टाइम यूनिट है। अनुक्रमिक निष्पादन कि स्थिति में, प्रक्रिया द्वारा लिया जाने वाला समय n×Ta समय इकाइयां होगा क्योंकि यह एक सरणी के सभी तत्वों का योग करता है। दूसरी ओर, यदि हम इस कार्य को 4 संसाधित्र पर आँकडे़ समानांतर कार्य के रूप में निष्पादित करते हैं तो लगने वाला समय (n/4)×Ta + विलयन उपरिव्यय समय इकाइयों तक कम हो जाएगा। समानांतर निष्पादन के परिणामस्वरूप अनुक्रमिक निष्पादन पर 4 का गति वर्धन होता है। ध्यान देने वाली एक महत्वपूर्ण बात यह है कि आँकडे़ समानांतर क्रमादेशन मॉडल के प्रदर्शन के मूल्यांकन में संदर्भ की अवस्थिति एक महत्वपूर्ण भूमिका निभाती है। आँकडे़ की स्थानीयता क्रमादेश द्वारा निष्पादित मेमोरी एक्सेस के साथ-साथ कैश के आकार पर निर्भर करती है।
इतिहास
सोलोमन मशीन के विकास के साथ 1960 के दशक में आँकडे़ समानता की अवधारणा का दोहन प्रारंभ हुआ।[1] सोलोमन मशीन, जिसे वेक्टर संसाधित्र भी कहा जाता है, बड़े आँकडे़ ऐरे (लगातार समय के चरणों में कई आँकडे़ पर संचालन) पर काम करके गणितीय कार्यों के प्रदर्शन में तेजी लाने के लिए विकसित किया गया था। एक ही निर्देश का उपयोग करके एक ही समय में कई आँकडे़ पर संचालन करके आँकडे़ संचालन की संगामिति (अभिकलित्र विज्ञान) को भी चूषित किया गया। इन संसाधित्र को 'सरणी संसाधित्र' कहा जाता था।[2] 1980 के दशक में, शब्द पेश किया गया था [3] इस क्रमादेशन शैली का वर्णन करने के लिए, जिसका व्यापक रूप से C* जैसी आँकडे़ समानांतर भाषाओं में कनेक्शन मशीनो को क्रमादेश करने के लिए उपयोग किया जाता था। आज, ग्राफ़िक्स प्रोसेसिंग युनिट (जीपीयू) में आँकडे़ समानता का सबसे अच्छा उदाहरण है, जो एक ही निर्देश का उपयोग करके समष्टि और समय में कई आँकडे़ पर संचालन की दोनों तकनीकों का उपयोग करते हैं।
अधिकांश आँकडे़ समानांतर हार्डवेयर केवल एक निश्चित संख्या में समानांतर स्तरों का समर्थन करता है, अधिकांशत: केवल एक। इसका मतलब यह है कि एक समानांतर संचालन के अंदर पुनरावर्ती रूप से अधिक समानांतर संचालन प्रारंभ करना संभव नहीं है, और इसका मतलब है कि क्रमादेशर नीड़ित हार्डवेयर समानता का उपयोग नहीं कर सकते है। क्रमादेशन भाषा एनईएसएल सपाट समानांतर मशीनों पर एक नीड़ित आँकडे़-समानांतर क्रमादेशन मॉडल को लागू करने का एक प्रारंभिक प्रयास था, और विशेष रूप से समतल परिवर्तन को प्रारंभ किया, जो नीड़ित आँकडे़ समानता को फ्लैट आँकडे़ समानता में बदल देती है। यह कार्य अन्य भाषाओं जैसे कि आँकडे़ समानांतर हास्केल और फ़ुथर्क (क्रमादेशन भाषा) द्वारा जारी रखा गया था, चूंकि वर्तमान आँकडे़-समानांतर क्रमादेशन भाषाओं में मनमाने ढंग से नीड़ित आँकडे़ समानता व्यापक रूप से उपलब्ध नहीं है।
विवरण
निर्देशों के एक सेट (SIMD) को निष्पादित करने वाले बहु संसाधित्र प्रणाली में, आँकडे़ समानता तब प्राप्त होती है जब प्रत्येक संसाधित्र अलग-अलग वितरित आँकडे़ पर समान कार्य करता है। कुछ स्थितियों में, एकल निष्पादन थ्रेड सभी आँकडे़ पर संचालन को नियंत्रित करता है। दूसरों में, अलग-अलग थ्रेड संचालन को नियंत्रित करते हैं, लेकिन वे एक ही संकेतावली को निष्पादित करते हैं।
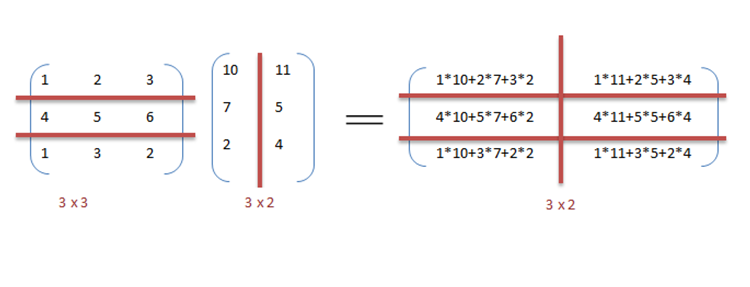
उदाहरण के लिए, आव्यूह गुणन और जोड़ को क्रमिक तरीके से विचार करें जैसा कि उदाहरण में चर्चा की गई है।
उदाहरण
नीचे गुणा और दो आव्यूहों के जोड़ के लिए अनुक्रमिक छद्म संकेतावली है जहां परिणाम मैट्रिक्स में संग्रहीत किया जाता है C. गुणा के लिए छद्म संकेतावली दो आव्यूहों के डॉट गुणनफल की गणना करता है A, B और C परिणाम को निर्गत मैट्रिक्स में संग्रहीत करता है।
यदि निम्नलिखित क्रमादेशों को क्रमिक रूप से क्रियान्वित किया जाता है, तो परिणाम की गणना करने में लगने वाला समय होगा (पंक्ति की लंबाई मानते हुए और दोनों आव्यूहों की स्तंभ लंबाई n हैं) और क्रमशः गुणा और जोड़ के लिए है।
// Matrix multiplication
for (i = 0; i < row_length_A; i++)
{
for (k = 0; k < column_length_B; k++)
{
sum = 0;
for (j = 0; j < column_length_A; j++)
{
sum += A[i][j] * B[j][k];
}
C[i][k] = sum;
}
}
// Array addition
for (i = 0; i < n; i++) {
c[i] = a[i] + b[i];
}
हम इसे तेजी से निष्पादित करने के लिए पूर्ववर्ती संकेतावली में आँकडे़ समानता का फायदा उठा सकते हैं क्योंकि अंकगणित परिपथ स्वतंत्र है। OpenMP का उपयोग करके मैट्रिक्स गुणन संकेतावली का समानांतरकरण प्राप्त किया जाता है। एक OpenMP निर्देश, omp समानांतर के लिए संकलक को समानांतर में परिपथ के लिए संकेतावली निष्पादित करने का निर्देश देता है। गुणन के लिए, हम मैट्रिक्स A और B को क्रमशः पंक्तियों और स्तंभों के साथ ब्लॉक में विभाजित कर सकते हैं। यह हमें मैट्रिक्स C में प्रत्येक तत्व की व्यक्तिगत रूप से गणना करने की अनुमति देता है जिससे कार्य समानांतर हो जाता है। उदाहरण के लिए: A[m x n] dot B [n x k] में समाप्त किया जा सकता है के अतरिक्त जब m*k संसाधित्र का उपयोग करके समानांतर में निष्पादित किया जाता है।
// Matrix multiplication in parallel
#pragma omp parallel for schedule(dynamic,1) collapse(2)
for (i = 0; i < row_length_A; i++){
for (k = 0; k < column_length_B; k++){
sum = 0;
for (j = 0; j < column_length_A; j++){
sum += A[i][j] * B[j][k];
}
C[i][k] = sum;
}
}
यह उदाहरण से देखा जा सकता है कि बहुत सारे संसाधित्र की आवश्यकता होगी क्योंकि मैट्रिक्स का आकार बढ़ता रहेगा। निष्पादन समय को कम रखना प्राथमिकता है लेकिन जैसे-जैसे मैट्रिक्स का आकार बढ़ता है, हमें ऐसी प्रणाली की जटिलता और उससे जुड़ी लागतों जैसी अन्य बाधाओं का सामना करना पड़ता है। इसलिए, प्रणाली में संसाधित्र की संख्या को सीमित करते हुए, हम अभी भी उसी सिद्धांत को लागू कर सकते हैं और दो मैट्रिक्स के उत्पाद की गणना करने के लिए आँकडे़ को बड़ी मात्रा में विभाजित कर सकते हैं।[4]
आँकडे़ समानांतर कार्यान्वयन में सरणियों को जोड़ने के लिए, दो केंद्रीय प्रसंस्करण इकाइयों (सीपीयू) A और B के साथ एक अधिक मामूली प्रणाली मान लें, सीपीयू A सरणियों के शीर्ष आधे से सभी तत्वों को जोड़ सकता है, जबकि सीपीयू B सभी तत्वों को जोड़ सकता है सरणियों का निचला आधा भाग। चूंकि दो संसाधित्र समानांतर में काम करते हैं, सरणी जोड़ने का काम अकेले एक सीपीयू का उपयोग करके सीरियल में एक ही संचालन करने का आधा समय लेगा।
क्रमादेश नीचे स्यूडोसंकेतावली में व्यक्त किया गया है—जो कुछ मनमाना संचालन लागू करता है, foo, सरणी में प्रत्येक तत्व पर d—आँकडे़ समानता दिखाता है:[nb 1]
यदि सीपीयू = A तब
if CPU = "a" then
lower_limit := 1
upper_limit := round(d.length / 2)
else if CPU = "b" then
lower_limit := round(d.length / 2) + 1
upper_limit := d.length
for i from lower_limit to upper_limit by 1 do
foo(d[i])
2 संसाधित्र प्रणाली पर निष्पादित एसपीएमडी प्रणाली में, दोनों सीपीयू संकेतावली को निष्पादित करेंगे।
प्रसंस्करण (कार्य समानांतरता) के विपरीत, आँकडे़ समांतरता आँकडे़ की वितरित (समानांतर) प्रकृति पर जोर देती है। अधिकांश वास्तविक कार्यक्रम कार्य समांतरता और आँकडे़ समांतरता के बीच निरंतरता पर कहीं गिर जाते हैं।
समांतरता के लिए कदम
अनुक्रमिक कार्यक्रम को समानांतर करने की प्रक्रिया को चार असतत चरणों में तोड़ा जा सकता है।[5]
| प्रकार | विवरण |
|---|---|
| अपघटन | कार्यक्रम को कार्यों में विभाजित किया जाता है जो सहमति की सबसे छोटी कारनामिक इकाई है। |
| समनुदेशन | प्रक्रियाओं को कार्य सौंपे जाते हैं। |
| वाद्यवृंदन | डेटा अभिगम, संचार, और प्रक्रियाओं का समन्वयन। |
| प्रतिचित्रिण | प्रक्रियाओं को संसाधित्र से जोड़ा जाता है। |
आँकडे़ समानता बनाम कार्य समानता
| डेटा समानांतरता | कार्य समानांतरता |
|---|---|
| एक ही संचालन एक ही डेटा के विभिन्न उपसमूहों पर किया जाता है। | अलग-अलग ऑपरेशन एक ही या अलग आंकड़े पर किए जाते हैं। |
| तुल्यकालिक अभिकलन | अतुल्यकालिक अभिकलन |
| स्पीडअप अधिक है क्योंकि डेटा के सभी सेटों पर केवल एक निष्पादन थ्रेड चल रहा है। | स्पीडअप कम है क्योंकि प्रत्येक संसाधित्र डेटा के समान या अलग सेट पर एक अलग थ्रेड या प्रक्रिया निष्पादित करेगा। |
| समांतरता की मात्रा इनपुट डेटा आकार के आनुपातिक होती है। | समांतरता की मात्रा स्वतंत्र कार्यों की संख्या के आनुपातिक होती है। |
| मल्टी संसाधित्र सिस्टम पर इष्टतम लोड संतुलन के लिए अभिकल्पित किया गया। | भार संतुलन हार्डवेयर और अनुसूचन कलन विधि की उपलब्धता पर निर्भर करता है जैसे स्थिर और गतिशील अनुसूचन। |
आँकडे़ समानता बनाम मॉडल समानता
| डेटा समानांतरता | मॉडल समानांतरता |
|---|---|
| प्रत्येक थ्रेड के लिए समान मॉडल का उपयोग किया जाता है लेकिन उनमें से प्रत्येक को दिया गया डेटा विभाजित और साझा किया जाता है। | प्रत्येक थ्रेड के लिए समान डेटा का उपयोग किया जाता है, और मॉडल को थ्रेड्स के बीच विभाजित किया जाता है। |
| यह छोटे नेटवर्क के लिए तेज़ है लेकिन बड़े नेटवर्क के लिए बहुत धीमा है क्योंकि बड़ी मात्रा में डेटा को एक साथ संसाधित्र के बीच स्थानांतरित करने की आवश्यकता होती है। | यह छोटे नेटवर्क के लिए धीमा और बड़े नेटवर्क के लिए तेज़ है। |
| डेटा समानता का आदर्श रूप से सरणी और मैट्रिक्स अभिकलन और दृढ़ तंत्रिका नेटवर्क में उपयोग किया जाता है | मॉडल समानता को गहन शिक्षा में अपने अनुप्रयोगों का पता चला |
मिश्रित आँकडे़ और कार्य समानता
आँकडे़ और कार्य समानता, एक ही अनुप्रयोग के लिए उन्हें एक साथ जोड़कर एक साथ लागू किया जा सकता है। इसे मिश्रित आँकडे़ और कार्य समानता कहा जाता है। मिश्रित समानता के लिए परिष्कृत अनुसूचन कलन विधि और सॉफ़्टवेयर समर्थन की आवश्यकता होती है। संचार धीमा होने और संसाधित्र की संख्या बड़ी होने पर यह समानता का सबसे अच्छा प्रकार है।[7]
मिश्रित आँकडे़ और कार्य समानता के कई अनुप्रयोग हैं। यह विशेष रूप से निम्नलिखित अनुप्रयोगों में प्रयोग किया जाता है:
- मिश्रित आँकडे़ और कार्य समानता वैश्विक जलवायु मॉडलिंग में अनुप्रयोगों को ढूंढती है। बड़े आँकडे़ समानांतर संगणनाएं पृथ्वी के वायुमंडल और महासागरों का प्रतिनिधित्व करने वाले आँकडे़ के ग्रिड बनाकर की जाती हैं और भौतिक प्रक्रियाओं के कार्य और मॉडल को अनुकरण करने के लिए कार्य समानांतरता को नियोजित किया जाता है।
- समय क्रम आधारित सर्किट सिमुलेशन में। आँकडे़ को विभिन्न उप-सर्किटों के बीच विभाजित किया जाता है और कार्यों से वाद्यवृंदन के साथ समानता हासिल की जाती है।
आँकडे़ समानांतर क्रमादेशन वातावरण
विभिन्न प्रकार के आँकडे़ समानांतर क्रमादेशन वातावरण आज उपलब्ध हैं, जिनमें से सबसे व्यापक रूप से उपयोग किए जाते हैं:
- संदेश पासिंग अंतरपृष्ठ: यह समानांतर अभिकलित्र के लिए एक क्रॉस-प्लेटफ़ॉर्म(कई ऑपरेटिंग सिस्टमस पर खुलने में समर्थ सॉफ्टवेर) संदेश पासिंग क्रमादेशन अंतरपृष्ठ है। यह उपयोगकर्ताओं को C, C ++ और फोरट्रान में सुबाह्य संदेश पासिंग क्रमादेश लिखने की अनुमति देने के लिए लाइब्रेरी कार्यों के शब्दार्थ को परिभाषित करता है।
- बहु-प्रसंस्करण[8] (ओपन एमपी): यह एक एप्लिकेशन क्रमादेशन अंतरपृष्ठ (एपीआई) है जो बहु संसाधित्र प्रणाली के कई प्लेटफॉर्म पर साझा मेमोरी क्रमादेशन मॉडल का समर्थन करता है।
- CUDA और OpenACC: CUDA और OpenACC (क्रमशः) समक्रमिक अभिकलित्र एपीआई प्लेटफॉर्म हैं जो एक सॉफ्टवेयर अभियन्ता को सामान्य प्रयोजन प्रसंस्करण के लिए जीपीयू की अभिकलनी इकाइयों का उपयोग करने की अनुमति देने के लिए अभिकल्पित किए गए हैं।
- थ्रेडिंग बिल्डिंग ब्लॉक्स और राफ्टलिब: दोनों खुले स्त्रोत क्रमादेशन वातावरण जो विषम संसाधनों में म / म ++ वातावरण में मिश्रित आँकडे़ / कार्य समानता को सक्षम करते हैं।
अनुप्रयोग
आँकडे़ समानांतरवाद भौतिकी, रसायन विज्ञान, जीव विज्ञान, भौतिक विज्ञान से लेकर संकेत संसाधन तक विभिन्न क्षेत्रों में अपने अनुप्रयोगों को पाता है। विज्ञान आण्विक गतिशीलता जैसे मॉडलों के अनुकरण के लिए आँकडे़ समानांतरता को लागू करता है,[9] संजीन आँकडे़ का अनुक्रम विश्लेषण [10] और अन्य भौतिक घटनाएँ। आँकडे़ समानता के लिए संकेत संसाधन में ड्राइविंग बल वीडियो एन्संकेतावलीिंग, इमेज और ग्राफिक्स प्रोसेसिंग, वायरलेस संचार हैं [11] कुछ नाम है।
यह भी देखें
टिप्पणियाँ
- ↑ Some input data (e.g. when
d.lengthevaluates to 1 androundrounds towards zero [this is just an example, there are no requirements on what type of rounding is used]) will lead tolower_limitbeing greater thanupper_limit, it's assumed that the loop will exit immediately (i.e. zero iterations will occur) when this happens.
संदर्भ
- ↑ "The Solomon Computer".
- ↑ "SIMD/Vector/GPU" (PDF). Retrieved 2016-09-07.
- ↑ Hillis, W. Daniel and Steele, Guy L., Data Parallel Algorithms Communications of the ACMDecember 1986
- ↑ Barney, Blaise. "समानांतर कंप्यूटिंग का परिचय". computing.llnl.gov. Archived from the original on 2013-06-10. Retrieved 2016-09-07.
- ↑ Solihin, Yan (2016). समानांतर वास्तुकला के मूल तत्व. Boca Raton, FL: CRC Press. ISBN 978-1-4822-1118-4.
- ↑ "How to Parallelize Deep Learning on GPUs Part 2/2: Model Parallelism". Tim Dettmers. 2014-11-09. Retrieved 2016-09-13.
- ↑ "The Netlib" (PDF).
- ↑ "ोपंम्प.ऑर्ग". openmp.org. Archived from the original on 2016-09-05. Retrieved 2016-09-07.
- ↑ Boyer, L. L; Pawley, G. S (1988-10-01). "बड़े पैमाने पर समानांतर कंप्यूटर का उपयोग करके जोड़ीदार बलों के साथ बातचीत करने वाले कणों के समूहों की आणविक गतिशीलता". Journal of Computational Physics. 78 (2): 405–423. Bibcode:1988JCoPh..78..405B. doi:10.1016/0021-9991(88)90057-5.
- ↑ Yap, T.K.; Frieder, O.; Martino, R.L. (1998). "जैविक अनुक्रम विश्लेषण में समानांतर संगणना". IEEE Transactions on Parallel and Distributed Systems. 9 (3): 283–294. CiteSeerX 10.1.1.30.2819. doi:10.1109/71.674320.
- ↑ Singh, H.; Lee, Ming-Hau; Lu, Guangming; Kurdahi, F.J.; Bagherzadeh, N.; Filho, E.M. Chaves (2000-06-01). "MorphoSys: an integrated reconfigurable system for data-parallel and computation-intensive applications". IEEE Transactions on Computers. 49 (5): 465–481. doi:10.1109/12.859540. ISSN 0018-9340.
- Hillis, W. Daniel and Steele, Guy L., Data Parallel Algorithms Communications of the ACM December 1986
- Blelloch, Guy E, Vector Models for Data-Parallel Computing MIT Press 1990. ISBN 0-262-02313-X