प्रकाशिकी एल्गोरिथ्म
| Part of a series on |
| Machine learning and data mining |
|---|
 |
समूहिंग संरचना की पहचान करने के लिए क्रम बिंदु (ओप्टिक्स) एक ऐसा एल्गोरिदम है जो स्थानिक डेटा में घनत्व-आधारित[1] समूह को खोजने के लिए उपयोगी है।यह एल्गोरिदम मिहाएल एंकर्स्ट, मार्कस एम. ब्रेयुनिग, हंस पीटर क्रिएगेल, और जोर्ग सैंडर द्वारा प्रस्तुत किया गया था।[2] इसकी मूल विचारधारा डीबीएससीएएन के समान है[3],परंतु यह डीबीएससीएएन की एक प्रमुख कमियों में से एक को पता करता है: भिन्न घनत्व वाले डेटा में मायने रखने वाले समूह्स का पता लगाने की समस्या होती हैं।इसके लिए, डेटाबेस के बिंदुओं ऐसे क्रमबद्ध किया जाता हैं कि जो स्थानिक रूप से निकटतम बिंदु होते हैं, वे क्रमबद्धीकरण में पड़ोसी बन जाते हैं।इसके अतिरिक्त, प्रत्येक बिंदु के लिए एक विशेष दूरी संग्रहीत की जाती है जो एक समूह के लिए स्वीकार्य घनत्व को प्रतिनिधित करती है, क्योंकी दोनों बिंदु एक ही समूह का हिस्सा बनें रहे। यह एक डेंड्रोग्राम के रूप में प्रतिष्ठित किया जाता है।
मूलभूत विचार
डीबीएससीएएन की तरह, ऑप्टिक्स को दो मापदंडों की आवश्यकता होती है: ε, जो अधिकतम दूरी (रेडियस) का वर्णन करता है जिसे ध्यान में लेने के लिए, और मिनिप्ट्स,, जो समूह बनाने के लिए आवश्यक बिंदुओं की संख्या का वर्णन करता है।एक बिंदु p एक मुख्य बिंदु होता है अगर उसके ε-पड़ोस में न्यूनतम से न्यूनतम मिनिप्ट्स, बिंदु पाए जाते हैं। डीबीएससीएएन के विपरीत, ऑप्टिक्स उन बिंदुओं पर भी विचार करता है जो अधिक सघनता से भरे समूह का हिस्सा हैं, इसलिए प्रत्येक बिंदु को एक मुख्य दूरी सौंपी जाती है जो मिनिप्ट्स,वां निकटतम बिंदु के लिए दूरी का वर्णन करती है:
एक दूसरे बिंदु o के रीचेबिलिटी-दूरी को एक बिंदु p से या तो o और p के मध्य की दूरी होती है, या p की कोर दूरी होती हैं, जो भी बड़ी होती है।
अगर p और o निकटतम पड़ोसी हैं, तो यही हमें मान लेना चाहिए कि p और o एक ही क्लस्टर का हिस्सा हैं।
यदि कोई पर्याप्त घनत्व वाला क्लस्टर (ε के संदर्भ में) उपलब्ध नहीं होता है, तो कोर दूरी और रीचेबिलिटी-दूरी अवर्णनीय होती हैं। पर्याप्त बड़े ε के लिए, यह कभी नहीं होता है, परंतु तब हर ε-नेबरहुड क्वेरी संपूर्ण डेटाबेस लौटाती है, जिससे रनटाइम होता है। इसलिए, ε मापदंड को उपयोग करके उन क्लस्टर्स के घनत्व को कम करने की आवश्यकता होती है जो अब और रुचिकर नहीं हैं, और एल्गोरिदम को तेजी से चलाने के लिए यह आवश्यक हैं।
यदि सख्त अर्थ में कहें, मापदंड ε आवश्यक नहीं है। यह सरल रूप से अधिकतम संभव मान पर सेट किया जा सकता है। यद्यपि, जब एक स्थानिक सूचकांक उपलब्ध होता है, तो यह जटिलता के संबंध में एक व्यावहारिक भूमिका निभाता है। ऑप्टिक्स को डीबीएससीएएन से पृथक होता है इस मापदंड को हटाकर, न्यूनतम से न्यूनतम एक्सटेंट तक, जहां केवल अधिकतम मान को देने की आवश्यकता होती है।
स्यूडोकोड
ऑप्टिक्स का मूल दृष्टिकोण डीबीएससीएएन के समान है, परंतु इसके स्थान पर जाने माने, परंतु अभी तक अप्रसंस्कृत क्लस्टर सदस्यों को एक सेट में रखने की अतिरिक्त, उन्हें प्राथमिकता कतार में रखा जाता है।
function ऑप्टिक्स(DB, ε, MinPts) is
for each point p of DB do
p.reachability-distance = UNDEFINED
for each unprocessed point p of DB do
N = getNeighbors(p, ε)
mark p as processed
output p to the ordered list
if core-distance(p, ε, MinPts) != UNDEFINED then
Seeds = empty priority queue
update(N, p, Seeds, ε, MinPts)
for each next q in Seeds do
N' = getNeighbors(q, ε)
mark q as processedरें
output q to the ordered list
if core-distance(q, ε, MinPts) != UNDEFINED do
update(N', q, Seeds, ε, MinPts)
अपडेट() के दौरान, प्राथमिकता कतार (प्रायोरिटी क्यू) "सीड्स" को और के -पड़ोस में से अपडेट किया जाता है:
function update(N, p, Seeds, ε, MinPts) is
coredist = core-distance(p, ε, MinPts)
for each o in N
if o is not processed then
new-reach-dist = max(coredist, dist(p,o))
if o.reachability-distance == UNDEFINED then // o is not in Seeds
o.reachability-distance = new-reach-dist
Seeds.insert(o, new-reach-dist)
else // o in Seeds, check for improvement
if new-reach-dist < o.reachability-distance then
o.reachability-distance = new-reach-dist
Seeds.move-up(o, new-reach-dist)
इसलिए ऑप्टिक्स एक विशेष क्रम में बिंदुओं को आउटपुट करता है, जो उनकी सबसे छोटी रीचैबिलिटी दूरी के साथ एनोटेट होता है (मूल एल्गोरिदम में, कोर दूरी भी निर्यात की जाती है,परंतु आगे की प्रक्रिया के लिए इसकी आवश्यकता नहीं है)।
क्लस्टर्स को निकालना
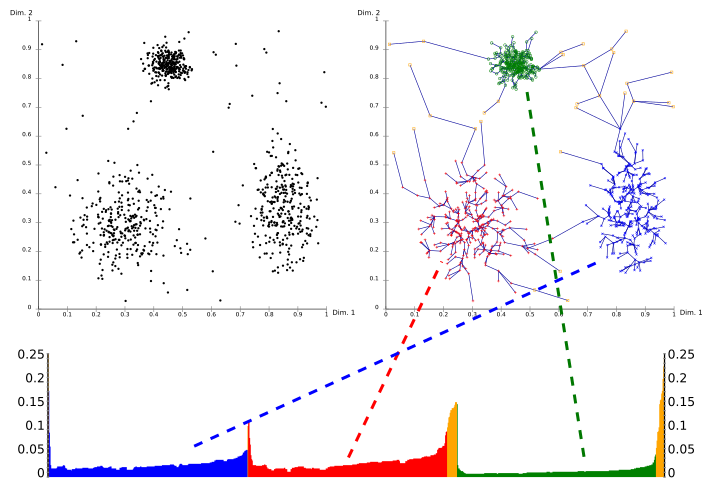 रीचैबिलिटी-प्लॉट (एक विशेष प्रकार का डेंड्रोग्राम) का उपयोग करके,
रीचैबिलिटी-प्लॉट (एक विशेष प्रकार का डेंड्रोग्राम) का उपयोग करके,
रीचेबिलिटी प्लॉट का उपयोग करके (एक विशेष प्रकार के डेन्ड्रोग्राम), क्लस्टर्स के वृद्धिकीय संरचना को आसानी से प्राप्त किया जा सकता है। यह एक 2D प्लॉट है, जिसमें ऑप्टिक्स द्वारा प्रसंस्कृत किए जाने वाले बिंदुओं के क्रमबद्धीकरण को x-अक्ष पर और रीचेबिलिटी दूरी को y-अक्ष पर दर्शाया जाता है। क्योंकि क्लस्टर्स में सम्मिलित बिंदुओं के पास उनके निकटतम पड़ोसी तक की दूरी बहुत न्यूनतम होती है, इसलिए रीचेबिलिटी प्लॉट में क्लस्टर्स वैलीज़ के रूप में प्रकट होते हैं। जितनी गहरी वैली, उतना ही घना या समृद्ध क्लस्टर होता है।
ऊपर दिए गए चित्र में इस संकेत का वर्णन है। इसमें ऊपर के बाएं कोने में, एक सिंथेटिक उदाहरण डेटा सेट दर्शाया गया है। ऊपर के दाएं हिस्से में, ऑप्टिक्स द्वारा उत्पन्न किया गया स्पैनिंग ट्री का दृश्य दर्शाया गया है, और नीचे का हिस्सा ऑप्टिक्स द्वारा गणना किए गए रीचेबिलिटी प्लॉट को दिखाता है। इस प्लॉट में रंग स्तर हैं, और इन्हें एल्गोरिदम द्वारा नहीं गणा गया है; लेकिन यह अच्छी तरह से दिखाता है कि प्लॉट में वैलीज़ किस तरह से ऊपर वाले डेटा सेट के क्लस्टर्स के साथ संबंधित होते हैं। इस चित्र में पीले बिंदुओं को नॉइज़ माना जाता है, और उनके रीचेबिलिटी प्लॉट में कोई वैली नहीं मिलती हैं। उन्हें सामान्यतः क्लस्टर्स के साथ संलग्न नहीं किया जाता है, केवल एक व्यावसायिक परिणाम में सर्वव्यापी "सभी डेटा" क्लस्टर के साथ नही जोड़ा जाता हैं।
इस प्लॉट से क्लस्टर्स को निकालने के लिए, इसे विज़ुअल निरीक्षण के उपरांत x-अक्ष पर रेंज का चयन करके हाथ से किया जा सकता है, y-अक्ष पर एक थ्रेशोल्ड चयन करके (परिणाम फिर एक डीबीएससीएएन क्लस्टरिंग परिणाम के समान होता है जिसमें एक समान और मिनिप्ट्स,मापदंड होते हैं; यहां एक 0.1 की मान अच्छे परिणाम देने के लिए उत्तम सिद्ध हो सकती है), या विभिन्न एल्गोरिदम्स द्वारा जो धरा, घुटन डिटेक्शन या स्थानिक अधिकतमों के माध्यम से वैलीज़ का पता लगाने का प्रयास करते हैं। इस तरह प्राप्त किए गए क्लस्टरिंग सामान्यतः वृद्धिकीय होते हैं, और इन्हें एकल डीबीएससीएएन चलने से प्राप्त नहीं किया जा सकता हैं।
जटिलता
डीबीएससीएएन की तरह, ऑप्टिक्स भी प्रत्येक बिंदु को एक बार प्रोसेस करता है और इस प्रोसेसिंग के दौरान एक ε-पड़ोसी क्वेरी का निष्पादन करता है। यदि किसी स्थानिक सूचकांक के साथ ε-पड़ोसी क्वेरी को रनटाइम में निष्पादित किया जा सकता है, तो कुल रनटाइम प्राप्त होता है। मूल ऑप्टिक्स पेपर के लेखकों ने रिपोर्ट किया है कि डीबीएससीएएन के तुलना में एक वास्तविक निरंतर मंदी गणकांश का अनुमानित कायम संक्रमण फैक्टर 1.6 है। ध्यान दें कि का मूल्य एल्गोरिथम की लागत पर भारी प्रभाव पड़ सकता है, क्योंकि अधिकतम मान किसी पड़ोसी क्वेरी की लागत को रैखिक संज्ञानात्मकता तक उठा सकता है।
विशेष रूप से, चुनना (डेटा सेट में अधिकतम दूरी से अधिक) संभव है,परंतु द्विघात जटिलता की ओर ले जाता है, क्योंकि प्रत्येक पड़ोस क्वेरी पूर्ण डेटा सेट लौटाती है। यहां तक कि जब कोई स्थानिक सूचकांक उपलब्ध नहीं होता है, तब भी ढेर के प्रबंधन में अतिरिक्त लागत आती है। इसलिए, डेटा सेट के लिए उचित रूप से चुना जाना चाहिए।
एक्सटेंशन
ऑप्टिक्स-ऑफ[4] ऑप्टिक्स पर आधारित एक विसंगति का पता लगाने वाला एल्गोरिदम है। मुख्य उपयोग एक अलग आउटलायर डिटेक्शन विधि का उपयोग करने की तुलना में कम लागत पर ऑप्टिक्स के उपस्रथितन से आउटलेर्स का निष्कर्षण है। स्थानीय बाह्य कारक का बेहतर ज्ञात संस्करण उन्हीं अवधारणाओं पर आधारित है।
डेली-क्लू,[5] डेंसिटी-लिंक-समूहिंग सिंगल-लिंकेज समूहिंग और ऑप्टिक्स के विचारों को जोड़ती है, जिससे मापदंड और ऑप्टिक्स की तुलना में प्रदर्शन में सुधार की प्रस्ताव देता है।
हायएससी[6] ऑप्टिक्स पर आधारित एक पदानुक्रमित उप-स्थान समूहिंग (अक्ष-समानांतर) विधि होती है।
हाईसीओ[7] ऑप्टिक्स पर आधारित एक पदानुक्रमित सहसंबंध समूहिंग एल्गोरिदम है।
व्यंजन[8] हाईएससी पर एक सुधार है जो अधिक जटिल पदानुक्रम पा सकता है।
फोप्टिक्स[9] यादृच्छिक अनुमानों का उपयोग करके तेज़ कार्यान्वयन करता है।
एचडीबीएसकैन*[10] डीबीएससीएएन के परिशोधन पर आधारित है, जो समूहों से सीमा-बिंदुओं को बाहर करता है और इस प्रकार हार्टिगन द्वारा घनत्व-स्तरों की मूल परिभाषा का अधिक सख्ती से पालन करता है।[11]
उपलब्धता
ओप्टिक्स, ओप्टिक्स-ओएफ, डीली-क्लू, हिस्क, हिको और डिश के जावा अनुमानित कार्यनीतियों के विभिन्न प्रस्तावनाएँ ईएलकी डेटा माइनिंग फ्रेमवर्क में उपलब्ध हैं (जिनमें कई दूरी फंक्शनों के लिए इंडेक्स त्वरण और जिएक्स निकासी विधि का स्वचालित क्लस्टर निकालने का समर्थन किया गया है)। अन्य जावा प्रस्तावनाएँ में वेका एक्सटेंशन सम्मिलित है (जिसमें जिएक्स क्लस्टर निकासी के लिए समर्थन नहीं है)।
आर पैकेज "dbscan" में ऑप्टिक्स का एक C++ प्रस्तावना सम्मिलित है (जिसमें रस्त्रीय डीबीस्कैन जैसे और जिएक्स क्लस्टर निकासी दोनों हैं) जिसमें केवल यूक्लिड दूरी के लिए इंडेक्स त्वरण के लिए के-डी ट्री का उपयोग होता है।
ऑप्टिक्स के पायथन अनुमानित कार्यनीतियाँ पायथन में पाइक्लस्टरिंग और स्किकिट-लर्न पुस्तकालय में उपलब्ध हैं। एचडीबीएसकैन* एचडीबीएसकैन पुस्तकालय में उपलब्ध है।
संदर्भ
- ↑ Kriegel, Hans-Peter; Kröger, Peer; Sander, Jörg; Zimek, Arthur (May 2011). "घनत्व-आधारित क्लस्टरिंग". Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. 1 (3): 231–240. doi:10.1002/widm.30. S2CID 36920706.
- ↑ Mihael Ankerst; Markus M. Breunig; Hans-Peter Kriegel; Jörg Sander (1999). OPTICS: Ordering Points To Identify the Clustering Structure. ACM SIGMOD international conference on Management of data. ACM Press. pp. 49–60. CiteSeerX 10.1.1.129.6542.
- ↑ Martin Ester; Hans-Peter Kriegel; Jörg Sander; Xiaowei Xu (1996). Evangelos Simoudis; Jiawei Han; Usama M. Fayyad (eds.). A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96). AAAI Press. pp. 226–231. CiteSeerX 10.1.1.71.1980. ISBN 1-57735-004-9.
- ↑ Markus M. Breunig; Hans-Peter Kriegel; Raymond T. Ng; Jörg Sander (1999). "OPTICS-OF: Identifying Local Outliers". Principles of Data Mining and Knowledge Discovery. Lecture Notes in Computer Science. Vol. 1704. Springer-Verlag. pp. 262–270. doi:10.1007/b72280. ISBN 978-3-540-66490-1. S2CID 27352458.
- ↑ Achtert, Elke; Böhm, Christian; Kröger, Peer (2006). "DeLi-Clu: Boosting Robustness, Completeness, Usability, and Efficiency of Hierarchical Clustering by a Closest Pair Ranking". In Ng, Wee Keong; Kitsuregawa, Masaru; Li, Jianzhong; Chang, Kuiyu (eds.). Advances in Knowledge Discovery and Data Mining, 10th Pacific-Asia Conference, PAKDD 2006, Singapore, April 9-12, 2006, Proceedings. Lecture Notes in Computer Science. Vol. 3918. Springer. pp. 119–128. doi:10.1007/11731139_16.
- ↑ Achtert, Elke; Böhm, Christian; Kriegel, Hans{-}Peter; Kröger, Peer; Müller{-}Gorman, Ina; Zimek, Arthur (2006). "Finding Hierarchies of Subspace Clusters". In Fürnkranz, Johannes; Scheffer, Tobias; Spiliopoulou, Myra (eds.). Knowledge Discovery in Databases: PKDD 2006, 10th European Conference on Principles and Practice of Knowledge Discovery in Databases, Berlin, Germany, September 18-22, 2006, Proceedings. Lecture Notes in Computer Science. Vol. 4213. Springer. pp. 446–453. doi:10.1007/11871637_42.
- ↑ Achtert, E.; Böhm, C.; Kröger, P.; Zimek, A. (2006). सहसंबंध समूहों के खनन पदानुक्रम. pp. 119–128. CiteSeerX 10.1.1.707.7872. doi:10.1109/SSDBM.2006.35. ISBN 978-0-7695-2590-7. S2CID 2679909.
{{cite book}}:|journal=ignored (help) - ↑ Achtert, Elke; Böhm, Christian; Kriegel, Hans{-}Peter; Kröger, Peer; Müller{-}Gorman, Ina; Zimek, Arthur (2007). "Detection and Visualization of Subspace Cluster Hierarchies". In Ramamohanarao, Kotagiri; Krishna, P. Radha; Mohania, Mukesh K.; Nantajeewarawat, Ekawit (eds.). Advances in Databases: Concepts, Systems and Applications, 12th International Conference on Database Systems for Advanced Applications, DASFAA 2007, Bangkok, Thailand, April 9-12, 2007, Proceedings. Lecture Notes in Computer Science. Vol. 4443. Springer. pp. 152–163. doi:10.1007/978-3-540-71703-4_15.
- ↑ Schneider, Johannes; Vlachos, Michail (2013). "यादृच्छिक अनुमानों के माध्यम से तेज़ पैरामीटर रहित घनत्व-आधारित क्लस्टरिंग". 22nd ACM International Conference on Information and Knowledge Management(CIKM).
- ↑ Campello, Ricardo J. G. B.; Moulavi, Davoud; Zimek, Arthur; Sander, Jörg (22 July 2015). "डेटा क्लस्टरिंग, विज़ुअलाइज़ेशन और आउटलायर डिटेक्शन के लिए पदानुक्रमित घनत्व अनुमान". ACM Transactions on Knowledge Discovery from Data. 10 (1): 1–51. doi:10.1145/2733381. S2CID 2887636.
- ↑ J.A. Hartigan (1975). क्लस्टरिंग एल्गोरिदम. John Wiley & Sons.