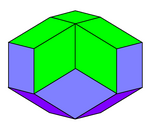
रोम्बिक आइकोसैहेड्रोन
| विषमकोण का आइकोसैहेड्रोन | |
|---|---|
| |
| प्रकार | ज़ोनोहेड्रोन |
| चेहरे के | 20 सर्वांगसम स्वर्ण रोम्बी |
| किनारों | 40 |
| कोने | 22 |
| प्रति शीर्ष पर फलक | 3, 4, या 5 |
| दोहरी बहुफलक | अनियमित चेहरे वाला पंचकोणीय जाइरोबिकुपोला |
| समरूपता | D5d = D5v, [2+,10], (2*5) |
| गुण | उत्तल, ज़ोनोहेड्रोन |
समचतुर्भुज आइकोसैहेड्रोन ऐसा बहुफलक आकार का चपटा गोलाकार क्षेत्र है। जिसके 20 फलक सर्वांगसमता (ज्यामिति) मुख्यतः स्वर्ण समचतुर्भुज के समान होते हैं,[1] इस प्रकार प्रत्येक शीर्ष पर 3, 4, या 5 फलक मिलते हैं। इसके 5 फलक (शीर्ष आकृति पर हरा) इसके 2 ध्रुवों में से प्रत्येक फलक पर मिलते हैं, ये 2 कोने 5-गुना समरूपता के अपने अक्ष पर स्थित रहते हैं, जो 2-गुना समरूपता के 5 अक्षों के विपरीत विषुवतीय किनारों के मध्य बिंदुओं के माध्यम से लंबवत होते हैं (इस प्रकार शीर्ष के चित्र पर उदाहरण के रूप में अधिकांश बाएँ हाथ और सबसे दाएँ हाथ के मध्य किनारे के रूप में रहते हैं)। इसके अन्य 10 फलक इसके भूमध्य रेखा का अनुसरण करते हैं, जिसके 5 फलक ऊपर की ओर और 5 नीचे की ओर रहते हैं, इन 10 समचतुर्भुजों में से प्रत्येक की 4 भुजाओं में से 2 भुजाएँ इस ज़िग-ज़ैग तिरछे बहुभुज के रूप में भूमध्य रेखा पर स्थित रहती हैं। इस कारण समचतुर्भुज आइकोसैहेड्रोन में 22 शीर्ष होते हैं। इसमें तीन आयामों में डायहेड्रल समरूपता है। D5d, [2+,10], (2*5) समरूपता समूह, क्रम 20; इस प्रकार इसमें समरूपता का केंद्र है, क्योंकि इसमें 5 भुजाएँ विषम स्थान पर रहती है।
इसके अतिरिक्त सभी फलक सर्वांगसम रहते हैं, समचतुर्भुज आइकोसैहेड्रॉन फलक संक्रमणीय अवस्था में नहीं रहते है, क्योंकि कोई यह भिन्नता कर सकता है कि कोई विशेष फलक भूमध्य रेखा के पास है या ध्रुव के पास इस फलक के चारों ओर के कोने की जांच करता है।
ज़ोनोहेड्रॉन
समचतुर्भुज आईकोसाहेड्रॉन मुख्य रूप से ज़ोनोहेड्रॉन है, जो नियमित रूप से त्रिकोणीय, नियमित पेंटागोनल, अपितु अनियमित चतुर्भुज फलकों के साथ पंचकोना जाइरोबिकोपोला के लिए दोहरी स्थिति उत्पन्न करता है।
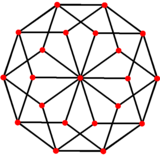
समचतुर्भुज आइकोसैहेड्रोन में 8 समानांतर किनारों के 5 समूह होते हैं, जिन्हें 8 फलकों के रूप में वर्णित किया गया है यहाँ पर समांतरोहेड्रॉन सामयिक प्रकार का एक उदाहरण प्रस्तुत किया गया हैं।
|
समचतुर्भुज आइकोसैहेड्रोन के किनारों को 5 समानांतर-सेटों में समूहीकृत किया जा सकता है, जो इस वायरफ्रेम ऑर्थोगोनल प्रोजेक्शन में देखा गया है। |
समचतुर्भुज आईकोसाहेड्रॉन 5 क्यूब से 3 आयामों के शीर्ष प्रथम प्रक्षेपण का उत्तल हल बनाता है। इस प्रकार 5-घन मानचित्र के 32 शीर्ष समचतुर्भुजीय आइकोसैहेड्रोन के 22 बाहरी शीर्षों में, शेष 10 आंतरिक शीर्षों के साथ एक पंचकोणीय प्रतिप्रिज्म बनाते हैं।
इसी प्रकार कोई 4-घन से हर्बल डोडेकाहेड्रॉन प्राप्त कर सकता है, और 6-घन से एक समचतुर्भुज ट्राईकॉन्टाहेड्रोन प्राप्त कर सकता है।
संबंधित पॉलीहेड्रा
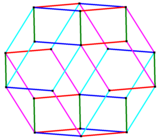
समचतुर्भुज आइकोसैहेड्रोन को 10 मध्य फलकों के एक बेल्ट को हटाकर समचतुर्भुज ट्राईकॉन्टाहेड्रोन से प्राप्त किया जा सकता है।
 एक समचतुर्भुज ट्राइकॉन्टाहेड्रॉन को एक लम्बी समचतुर्भुज आइकोसैहेड्रोन के रूप में देखा जा सकता है। |
 समचतुर्भुज आइकोसैहेड्रोन और समचतुर्भुज ट्राइकॉन्टाहेड्रोन में समान 10-गुना सममित लंबकोणीय प्रक्षेपण होता है। (*) |
(उदाहरण के लिए, बाई ओर की आकृति पर आप यह देख सकते हैं):
समचतुर्भुज ट्राइकॉन्टाहेड्रोन के 10 मध्य फलकों के (ऊर्ध्वाधर) बेल्ट का ऑर्थोगोनल प्रोजेक्शन सामान्य ऑर्थोगोनल प्रोजेक्शन का केवल क्षैतिज स्थिति में बाहरी नियमित के लिए डेकागन पर देखा जा सकता हैं।
संदर्भ
- ↑ Weisstein, Eric W. "रोम्बिक इकोसैहेड्रोन". mathworld.wolfram.com (in English). Retrieved 2019-12-20.
