संसूचन सीमा
संसूचन सीमा (LOD or LoD) सबसे कम संकेत है, या संकेत से निर्धारित (या निकाली गई) सबसे कम संगत मात्रा है, जिसे पर्याप्त आत्मविश्वास या सांख्यिकीय महत्व के साथ देखा जा सकता है। चूँकि, स्पष्ट सीमा(निर्णय का स्तर) यह तय करने के लिए प्रयोग किया जाता है कि निरंतर उतार-चढ़ाव वाले पृष्ठभूमि ध्वनि के ऊपर एक संकेत सांख्यिकीय महत्व इच्छानुसार रहता है और विभिन्न क्षेत्रों में दांव के आधार पर वैज्ञानिकों, सांख्यिकीविदों और नियामकों के बीच नीति और अधिकांशतः वाद-विवाद का विषय होता है।
विश्लेषणात्मक रसायन विज्ञान में महत्व
विश्लेषणात्मक रसायन शास्त्र में, संसूचन की सीमा, संसूचन की निचली सीमा, पहचान या विश्लेषणात्मक संवेदनशीलता की सीमा के लिए एलओडी भी कहा जाता है (संवेदनशीलता और विशिष्टता के साथ अस्पष्ट नहीं होना), किसी पदार्थ की सबसे कम मात्रा है जिसे अनुपस्थिति से अलग किया जा सकता है पदार्थ (एक रिक्त मान) एक निश्चित विश्वास अंतराल (सामान्यतः 99%) के साथ।[1][2][3] संसूचन की सीमा का अनुमान रिक्त के माध्य रिक्त के मानक विचलन, संभाव्य वर्गीकरण के ढलान (संवेदनशीलता और विशिष्टता) और एक परिभाषित विश्वास अंतराल (उदाहरण के लिए 3.2 इस इच्छानुसार मूल्य के लिए सबसे स्वीकृत मूल्य है) से लगाया जाता है।[4] एक और विचार जो संसूचन की सीमा को प्रभावित करता है वह है कच्चे विश्लेषणात्मक संकेत से एकाग्रता की भविष्यवाणी करने के लिए उपयोग किए जाने वाले नमूना की पर्याप्तता और स्पष्टता है ।[5]
एक रैखिक समीकरण के बाद अंशांकन प्लॉट से एक विशिष्ट उदाहरण के रूप में यहां सबसे सरल संभव मॉडल के रूप में लिया गया है:
जहां मापे गए सिग्नल से मेल खाता है (उदाहरण के लिए वोल्टेज, ल्यूमिनसेंस, ऊर्जा, आदि), "b" वह मान जिसमें सीधी रेखा निर्देशांक अक्ष को काटती है, "a" प्रणाली की संवेदनशीलता (अथार्त, ढलान) लाइन का, या मापे गए सिग्नल को निर्धारित की जाने वाली मात्रा से संबंधित कार्य ) और "x" सिग्नल से निर्धारित की जाने वाली मात्रा (जैसे तापमान, एकाग्रता, पीएच, आदि) का मान,[6] "x" के लिए एलओडी की गणना "x" मान के रूप में की जाती है जिसमें रिक्त स्थान "y" के औसत मान और इसके मानक विचलन "s" के "t" गुना के समान होता है (या, यदि शून्य है, तो) मापे गए न्यूनतम मान के अनुरूप मानक विचलन) जहां "t" चुना हुआ आत्मविश्वास मूल्य है (उदाहरण के लिए 95% के आत्मविश्वास के लिए इसे t = 3.2, माना जा सकता है, जो रिक्त की सीमा से निर्धारित होता है)।[4]
इस प्रकार, इस उपदेशात्मक उदाहरण में:
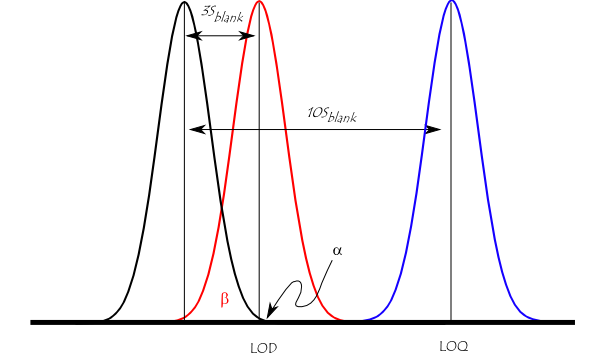
नीचे दिया गया आंकड़ा रिक्त पर सामान्य वितरण माप के लिए संभाव्यता घनत्व कार्य दिखाकर रिक्त स्थान, संसूचन की सीमा (एलओडी ) और परिमाण की सीमा (एलओक्यू) के बीच संबंध को दर्शाता है, एलओडी पर 3 × मानक विचलन के रूप में परिभाषित किया गया है। रिक्त, और एलओक्यू पर रिक्त के 10 × मानक विचलन के रूप में परिभाषित किया गया है। एलओडी पर एक संकेत के लिए, टाइप I और टाइप II त्रुटियाँ (गलत सकारात्मक और झूठे नकारात्मक की संभावना) छोटी (1%) है। चूँकि टाइप I और टाइप II त्रुटियां (मिथ्या सकारात्मक और मिथ्या नकारात्मक की संभावना) एक नमूने के लिए 50% है जिसकी एलओडी (लाल रेखा) पर एकाग्रता है। इसका अर्थ है कि एक नमूने में एलओडी में अशुद्धता हो सकती है, किन्तु 50% संभावना है कि एक माप एलओडी से कम परिणाम देगा। एलओक्यू (नीली रेखा) पर, गलत नकारात्मक होने की न्यूनतम संभावना होती है।
साधन का संसूचन की सीमा
अधिकांश वैज्ञानिक उपकरण तब भी संकेत उत्पन्न करते हैं जब एक रिक्त (आव्यूह (रासायनिक विश्लेषण) विश्लेषण के बिना) का विश्लेषण किया जाता है। इस संकेत को ध्वनि स्तर कहा जाता है। आईडीएल विश्लेषण एकाग्रता है जो ध्वनि स्तर के मानक विचलन से तीन गुना अधिक संकेत उत्पन्न करने के लिए आवश्यक है। यह अनुमानित आईडीएल पर 8 या अधिक मानकों का विश्लेषण करके व्यावहारिक रूप से मापा जा सकता है और फिर उन मानकों की मापी गई सांद्रता से मानक विचलन की गणना की जा सकती है।
संसूचन की सीमा (शुद्ध और व्यावहारिक रसायन के अंतर्राष्ट्रीय संघ के अनुसार) विश्लेषण की सबसे छोटी सांद्रता या पदार्थ की सबसे छोटी निरपेक्ष मात्रा है, जिसमें अभिकर्मक रिक्त के बार-बार माप से उत्पन्न होने वाले सिग्नल की तुलना में सांख्यिकीय रूप से काफी बड़ा संकेत होता है।
गणितीय रूप से, संसूचन की सीमा पर विश्लेषण का संकेत () द्वारा दिया गया है:
जहाँ , कई बार मापे गए रिएजेंट ब्लैंक के लिए सिग्नल का माध्य मान है, और अभिकर्मक ब्लैंक के सिग्नल के लिए ज्ञात मानक विचलन है।
संसूचन की सीमा को परिभाषित करने के लिए अन्य दृष्टिकोण भी विकसित किए गए हैं। परमाणु अवशोषण स्पेक्ट्रोस्कोपी में सामान्यतः इस तत्व के एक पतला समाधान का विश्लेषण करके और किसी दिए गए तरंग दैर्ध्य पर संबंधित अवशोषण को रिकॉर्ड करके एक निश्चित तत्व के लिए संसूचन की सीमा निर्धारित की जाती है। माप 10 बार दोहराया जाता है। रिकॉर्ड किए गए अवशोषक संकेत के 3σ को प्रयोगात्मक स्थितियों के तहत विशिष्ट तत्व के लिए संसूचन की सीमा के रूप में माना जा सकता है: चयनित तरंग दैर्ध्य, लौ का प्रकार या ग्रेफाइट ओवन, रासायनिक आव्यूह, हस्तक्षेप करने वाले पदार्थों की उपस्थिति, उपकरण ...।
विधि का संसूचन की सीमा
अधिकांशतः केवल रासायनिक प्रतिक्रिया करने या विश्लेषण को प्रत्यक्ष विश्लेषण के लिए प्रस्तुत करने की तुलना में विश्लेषणात्मक पद्धति के लिए अधिक होता है। प्रयोगशाला में विकसित कई विश्लेषणात्मक विधि, विशेष रूप से इनमें एक उत्कृष्ट वैज्ञानिक उपकरण का उपयोग सम्मिलित है, विश्लेषण करने से पहले नमूना तैयार करने या नमूनों का पूर्व उपचार करने की आवश्यकता होती है। उदाहरण के लिए, एक नमूने को गर्म करना आवश्यक हो सकता है जिसे किसी विशेष धातु के लिए पहले एसिड (पाचन प्रक्रिया) के अतिरिक्त के साथ विश्लेषण किया जाना है। किसी दिए गए उपकरण के माध्यम से नमूना को विश्लेषण से पहले पतला या केंद्रित किया जा सकता है। विश्लेषण पद्धति में अतिरिक्त चरण त्रुटियों के लिए अतिरिक्त अवसर जोड़ते हैं। चूंकि संसूचन की सीमा त्रुटियों के संदर्भ में परिभाषित की गई है, यह स्वाभाविक रूप से मापी गई पहचान सीमा को बढ़ाएगी। इस वैश्विक पहचान सीमा (विश्लेषण पद्धति के सभी चरणों सहित) को विधि पहचान सीमा (एमडीएल) कहा जाता है। एमडीएल का निर्धारण करने का व्यावहारिक विधि पहचान की अपेक्षित सीमा के पास एकाग्रता के सात नमूनों का विश्लेषण करना है। मानक विचलन तब निर्धारित किया जाता है। एक पक्षीय छात्र का टी-वितरण निर्धारित मानक विचलन बनाम निर्धारित और गुणा किया जाता है। सात नमूनों के लिए (छह डिग्री की स्वतंत्रता के साथ) 99% विश्वास अंतराल के लिए टी मान 3.14 है। सात समान नमूनों का पूर्ण विश्लेषण करने के अतिरिक्त, यदि उपकरण संसूचन लिमिट ज्ञात है, तो एमडीएल का अनुमान उपकरण संसूचन लिमिट, या संसूचन के निचले स्तर को गुणा करके, उपकरण के साथ सैंपल सॉल्यूशन का विश्लेषण करने से पहले अशक्त पड़ने से लगाया जा सकता है। चूँकि यह अनुमान नमूना तैयार करने से उत्पन्न होने वाली किसी भी अनिश्चितता को अनदेखा करता है और इसलिए संभवतः वास्तविक एमडीएल को कम करके निर्णय करेगा।
प्रत्येक मॉडल की सीमा
सभी वैज्ञानिक विषयों में संसूचन की सीमा, या परिमाणीकरण की सीमा की समस्या का सामना करना पड़ता है। यह विभिन्न प्रकार की परिभाषाओं और प्रश्नों के समाधान के लिए विकसित समाधानों की विविधता की व्याख्या करता है। सरलतम स्थितियों में जैसे परमाणु और रासायनिक माप में, परिभाषाओं और दृष्टिकोणों को संभवतः स्पष्ट और सरलतम समाधान प्राप्त हुए हैं। जैव रासायनिक परीक्षणों में और कई अधिक जटिल कारकों के आधार पर जैविक प्रयोगों में, मिथ्या सकारात्मक और मिथ्या नकारात्मक प्रतिक्रियाओं वाली स्थिति को संभालने के लिए अधिक उत्कृष्ट है। कई अन्य विषयों में जैसे कि भू-रसायन, भूकंप विज्ञान, खगोल विज्ञान, वृक्षवलय कालक्रम , जलवायु विज्ञान, सामान्य रूप से जीवन विज्ञान, और कई अन्य क्षेत्रों में व्यापक रूप से गणना करना असंभव है, समस्या व्यापक है और एक ध्वनि (वर्णक्रमीय घटना) से संकेत निष्कर्षण से संबंधित है। इसमें जटिल सांख्यिकीय विश्लेषण प्रक्रियाएं सम्मिलित हैं और इसलिए यह उपयोग किए गए मॉडलों पर भी निर्भर करता है,[5] अनिश्चितता को संभालने और प्रबंधित करने के लिए की जाने वाली परिकल्पनाएं और सरलीकरण या अनुमान है जब डेटा रिज़ॉल्यूशन खराब होता है और अलग-अलग सिग्नल ओवरलैप होते हैं, तो पैरामीटर निकालने के लिए अलग-अलग विखंडन प्रक्रियाएं प्रयुक्त होती हैं। विभिन्न फेनोमेनोलॉजी (भौतिकी), गणितीय और सांख्यिकीय मॉडल का उपयोग भी पहचान की सीमा की स्पष्ट गणितीय परिभाषा को जटिल बना सकता है और इसकी गणना कैसे की जाती है। यह बताता है कि संसूचन की सीमा की धारणा की स्पष्ट गणितीय परिभाषा के बारे में आम सहमति क्यों कठिन है। चूँकि एक बात स्पष्ट है: इसके लिए सदैव पर्याप्त संख्या में डेटा (या संचित डेटा) और सांख्यिकीय रूप से महत्वपूर्ण होने के लिए एक कठोर सांख्यिकीय विश्लेषण की आवश्यकता होती है।
परिमाणीकरण की सीमा
परिमाणीकरण की सीमा (एलओक्यू, या एलओक्यू) एक संकेत (या एकाग्रता, गतिविधि, प्रतिक्रिया ...) का न्यूनतम मूल्य है जिसे स्वीकार्य स्पष्ट ता और स्पष्ट ता के साथ परिमाणित किया जा सकता है।
एलओक्यू वह सीमा है जिस पर दो अलग-अलग संकेतों/मूल्यों के बीच अंतर को एक उचित निश्चितता के साथ पहचाना जा सकता है, अथार्त जब संकेत पृष्ठभूमि से सांख्यिकीय रूप से भिन्न होता है। एलओक्यू प्रयोगशालाओं के बीच अधिक भिन्न हो सकता है, इसलिए सामान्यतः एक अन्य संसूचन की सीमा का उपयोग किया जाता है जिसे 'व्यावहारिक मात्राकरण सीमा' (पीक्यूएल) कहा जाता है।
यह भी देखें
- पृष्ठ भूमि ध्वनि
- पृष्ठभूमि विकिरण
- इलेक्ट्रॉनिक ध्वनि
- ध्वनि (वर्णक्रमीय घटना)
- केमोमेट्रिक्स
- गामा स्पेक्ट्रोस्कोपी#अंशांकन और पृष्ठभूमि विकिरण
- माल्मक्विस्ट पूर्वाग्रह
- पी-मान
- पी-मान का दुरुपयोग
- सांख्यिकीय महत्व
संदर्भ
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "detection limit". doi:10.1351/goldbook.L03540
- ↑ MacDougall D, Crummett WB, et al. (1980). "पर्यावरण रसायन विज्ञान में डेटा अधिग्रहण और डेटा गुणवत्ता मूल्यांकन के लिए दिशानिर्देश". Analytical Chemistry. 52 (14): 2242–49. doi:10.1021/ac50064a004.
- ↑ Saah AJ, Hoover DR (1998). "[Sensitivity and specificity revisited: significance of the terms in analytic and diagnostic language]". Ann Dermatol Venereol. 125 (4): 291–4. PMID 9747274.
- ↑ 4.0 4.1 Armbruster DA, Pry T (August 2008). "रिक्त की सीमा, पता लगाने की सीमा और परिमाण की सीमा". The Clinical Biochemist. Reviews. 29 Suppl 1 (1): S49–S52. PMC 2556583. PMID 18852857.
- ↑ 5.0 5.1 "आर: प्रत्येक मॉडल के लिए "डिटेक्शन" सीमा". search.r-project.org (in English). Retrieved 2022-01-04.
- ↑ Quesada-González D, Stefani C, González I, de la Escosura-Muñiz A, Domingo N, Mutjé P, Merkoçi A (September 2019). "सेल्युलोज नैनोफाइबर का उपयोग करके सोने के नैनोपार्टिकल-आधारित पार्श्व प्रवाह परीक्षणों पर सिग्नल वृद्धि". Biosensors & Bioelectronics. 141: 111407. doi:10.1016/j.bios.2019.111407. hdl:10261/201014. PMID 31207571. S2CID 190531742.
- ↑ Long, Gary L.; Winefordner, J. D. (1983), "Limit of detection: a closer look at the IUPAC definition", Anal. Chem., 55 (7): 712A–724A, doi:10.1021/ac00258a724
अग्रिम पठन
- Altshuler B, Pasternack B (1963-03-01). "Statistical measures of the lower limit of detection of a radioactivity counter". Health Physics. 9 (3): 293–298. doi:10.1097/00004032-196303000-00005. ISSN 0017-9078. PMID 14040764. Retrieved 2022-01-03.
- Currie LA (1968). "Limits for qualitative detection and quantitative determination. Application to radiochemistry". Analytical Chemistry. 40 (3): 586–593. doi:10.1021/ac60259a007. ISSN 0003-2700.
- Long GL, Winefordner JD (1983). "Limit of detection. A closer look at the IUPAC definition". Analytical Chemistry. 55 (7): 712A–724A. doi:10.1021/ac00258a001. ISSN 0003-2700.
- Armbruster DA, Pry T (August 2008). "Limit of blank, limit of detection and limit of quantitation". The Clinical Biochemist. Reviews. 29 Suppl 1 (Suppl 1): S49–S52. PMC 2556583. PMID 18852857.
- European Commission. Joint Research Centre. (2016). Guidance document on the estimation of LOD and LOQ for measurements in the field of contaminants in feed and food. Luxembourg: Publications Office. doi:10.2787/8931. ISBN 9789279617683. Retrieved 2022-01-03.
- "DIN 32645 – Chemical analysis – Decision limit, detection limit and determination limit under repeatability conditions – Terms, methods, evaluation. Technical standard. Deutsches Institut für Normung, Berlin (DIN 32645:2008-11) | Via Engineering360" (in German). Published by Beuth Verlag, a subsidiary of the DIN Group. doi:10.31030/1465413. Retrieved 2022-01-03.
{{cite web}}: CS1 maint: unrecognized language (link)
बाहरी संबंध
- Evans WC (21 February 2019). "Limit of Detection – Interactive Java applet to illustrate some basic ideas of the limit of detection problem". GeoGebra. Retrieved 2022-01-04.
- "The R Language". search.r-project.org (in English). Retrieved 2022-01-04.
- Garrett RG (2013-11-01). "The 'rgr' package for the R Open Source statistical computing and graphics environment – a tool to support geochemical data interpretation". Geochemistry: Exploration, Environment, Analysis. 13 (4): 355–378. doi:10.1144/geochem2011-106. ISSN 1467-7873. S2CID 129059022. Retrieved 2022-01-04.
- "R: "Detection" limit for each model". search.r-project.org (in English). Retrieved 2022-01-04.
- Deutsches Institut für Normung. "R: Calibration data from DIN 32645 (Package envalysis version 0.5.1)". search.r-project.org (in English). Retrieved 2022-01-04.
- Downloads of articles (a.o. harmonization of concepts by ISO and IUPAC) and an extensive list of references