अनुप्रस्थ तरंग

क्षैतिज दिशा में एक लोचदार माध्यम के माध्यम से फैलने वाली एक सरल (समतल) अनुप्रस्थ तरंग का चित्रण, जिसमें कण ऊर्ध्वाधर दिशा में विस्थापित होते हैं। सामग्री की केवल एक परत दिखाई गई है

एक साधारण प्रकाश तरंग में एक किरण के साथ विद्युत (लाल) और चुंबकीय (नीला) क्षेत्रों का चित्रण। किरण के लंबवत किसी भी समतल के लिए, प्रत्येक क्षेत्र का मान हमेशा समतल के सभी बिंदुओं पर समान होता है।

2d ग्रिड (अनुभवजन्य मॉडल) में अनुप्रस्थ गोलाकार तरंग का प्रसार

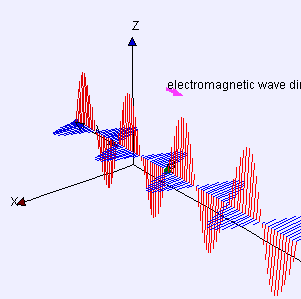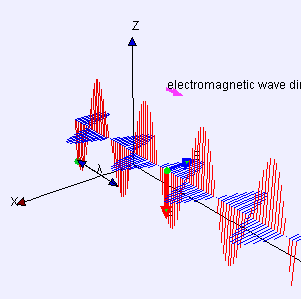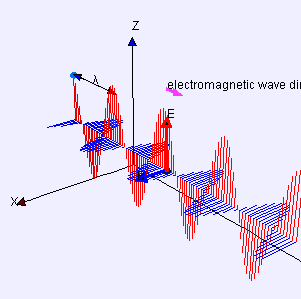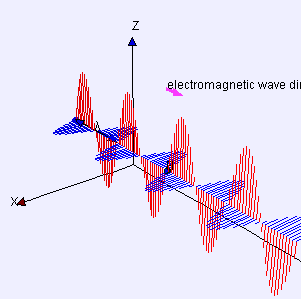
भौतिकी में, एक अनुप्रस्थ तरंग एक तरंग है जिसका दोलन तरंग के आगे बढ़ने की दिशा के लंबवत होते हैं। यह एक अनुदैर्ध्य तरंग के विपरीत है जो इसके दोलनों की दिशा में यात्रा करती है। जल तरंगें अनुप्रस्थ तरंग का उदाहरण हैं।

तरंगों द्वारा एक सरल उदाहरण दिया जाता है जो एक छोर को लंगर डालकर और दूसरे छोर को ऊपर और नीचे घुमाकर क्षैतिज लंबाई के तार पर बनाया जा सकता है। एक अन्य उदाहरण लहर तरंगें हैं जो एक ड्रम की झिल्ली पर निर्मित होती हैं। तरंगें उन दिशाओं में फैलती हैं जो झिल्ली तल के समानांतर होती हैं, लेकिन झिल्ली में प्रत्येक बिंदु स्वयं उस तल के लंबवत ऊपर और नीचे विस्थापित हो जाता है। प्रकाश एक अनुप्रस्थ तरंग का एक और उदाहरण है, जहां दोलन विद्युत क्षेत्र और चुंबकीय क्षेत्र हैं, जो प्रसार की दिशा का वर्णन करने वाली आदर्श प्रकाश किरणों के समकोण पर इंगित करते हैं।

उत्पन्न कतरनी तनाव के कारण अनुप्रस्थ तरंगें सामान्यतः लोच (भौतिकी) ठोस में होती हैं; इस स्थिति में दोलन तरंग के प्रसार के लंबवत दिशाओं में ठोस कणों का विस्थापन उनकी आराम की स्थिति से दूर होता है। ये विस्थापन सामग्री के स्थानीय कतरनी विरूपण के अनुरूप हैं। अतः इस प्रकृति की अनुप्रस्थ तरंग को अपरूपण तरंग कहते हैं। चूंकि तरल पदार्थ आराम के दौरान अपरूपण बलों का विरोध नहीं कर सकते हैं, तरल पदार्थों के थोक के अंदर अनुप्रस्थ तरंगों का प्रसार संभव नहीं है। भूकंप विज्ञान में, कतरनी तरंगों को द्वितीयक तरंगें या एस-तरंगें भी कहा जाता है।

अनुप्रस्थ तरंगें अनुदैर्ध्य तरंगों के विपरीत होती हैं, जहां लहर की दिशा में दोलन होते हैं। अनुदैर्ध्य तरंग का मानक उदाहरण गैसों, तरल पदार्थों या ठोस पदार्थों में एक ध्वनि तरंग या दबाव तरंग है, जिसके दोलनों के कारण उस सामग्री का संपीड़न और विस्तार होता है जिसके माध्यम से तरंग फैलती है। दबाव तरंगों को भूभौतिकी में प्राथमिक तरंगें या पी-तरंगें कहा जाता है।

गणितीय सूत्रीकरण

गणितीय रूप से, सबसे सरल प्रकार की अनुप्रस्थ तरंग एक समतल रैखिक रूप से ध्रुवीकृत sinusoidal होती है। यहाँ समतल का अर्थ है कि प्रसार की दिशा अपरिवर्तित है और पूरे माध्यम में समान है; ध्रुवीकरण (तरंगों) का अर्थ है कि विस्थापन की दिशा भी अपरिवर्तनीय है और पूरे माध्यम में समान है; और विस्थापन का परिमाण प्रसार की दिशा में केवल समय और स्थिति का एक ज्यावक्रीय फलन है।

ऐसी तरंग की गति को गणितीय रूप में इस प्रकार व्यक्त किया जा सकता है। चलो 'डी' प्रचार की दिशा (एक वेक्टर (गणित) इकाई लंबाई के साथ), और ओ माध्यम में कोई संदर्भ बिंदु। चलो यू दोलनों की दिशा हो ('डी के लिए लंबवत एक और इकाई-लंबाई वेक्टर)। माध्यम के किसी भी बिंदु 'p' और किसी भी समय 't' (सेकंड) पर एक कण का विस्थापन होगा

$$S(p,t)=Au\sin \left({\frac {t-(p-o){\frac {d}{v}}}{T}}+\phi \right)$$

जहाँ A तरंग का 'आयाम' या 'ताकत' है, T उसकी 'अवधि' है, v प्रसार की 'गति' है, और o पर φ इसका 'चरण' है। ये सभी प्राचल वास्तविक संख्याएँ हैं। प्रतीक • दो सदिशों के आंतरिक उत्पाद को दर्शाता है।

इस समीकरण से, तरंग d दिशा में यात्रा करती है और दोलन दिशा u के साथ आगे और पीछे होते हैं। लहर को यू दिशा में रैखिक रूप से ध्रुवीकृत कहा जाता है।

एक पर्यवेक्षक जो एक निश्चित बिंदु पी को देखता है, वहां कण को ​​एक सरल सरल हार्मोनिक गति (साइनसोइडल) गति में अवधि टी सेकंड के साथ, प्रत्येक अर्थ में अधिकतम कण विस्थापन ए के साथ दिखाई देगा; अर्थात्, प्रति सेकंड f = 1/T पूर्ण दोलन चक्र की 'आवृत्ति' के साथ। एक निश्चित समय t पर सभी कणों का एक स्नैपशॉट, d के लम्बवत् प्रत्येक तल पर सभी कणों के लिए समान विस्थापन दिखाएगा, क्रमिक तलों में विस्थापन के साथ एक साइनसोइडल पैटर्न बनाते हुए, प्रत्येक पूर्ण चक्र 'तरंग दैर्ध्य' द्वारा d के साथ विस्तारित होता है λ = वी टी = वी/एफ। पूरा पैटर्न गति V के साथ दिशा d में चलता है।

समान समीकरण समतलीय रूप से ध्रुवीकृत साइनसोइडल प्रकाश तरंग का वर्णन करता है, सिवाय इसके कि विस्थापन S(p, t) बिंदु p और समय t पर विद्युत क्षेत्र है। (चुंबकीय क्षेत्र को एक ही समीकरण द्वारा वर्णित किया जाएगा, लेकिन एक विस्थापन दिशा के साथ जो कि d और u दोनों के लंबवत है, और एक अलग आयाम है।)

लहर सुपरपोजिशन सिद्धांत == एक सजातीय रैखिक संयोजन माध्यम में, जटिल दोलनों (सामग्री या प्रकाश प्रवाह में कंपन) को कई सरल साइनसोइडल तरंगों की तरंग सुपरपोजिशन के रूप में वर्णित किया जा सकता है, या तो अनुप्रस्थ या अनुदैर्ध्य।

उदाहरण के लिए, एक वायलिन स्ट्रिंग के कंपन का विश्लेषण विभिन्न आवृत्तियों की कई अनुप्रस्थ तरंगों के योग के रूप में किया जा सकता है, जो स्ट्रिंग को या तो ऊपर या नीचे या बाएं से दाएं विस्थापित करती हैं। एक तालाब में तरंगों का विश्लेषण अनुप्रस्थ और अनुदैर्ध्य तरंगों (गुरुत्वाकर्षण तरंगों) के संयोजन के रूप में किया जा सकता है जो एक साथ फैलती हैं।

परिपत्र ध्रुवीकरण

यदि माध्यम रैखिक है और एक ही यात्रा दिशा d के लिए कई स्वतंत्र विस्थापन दिशाओं की अनुमति देता है, तो हम ध्रुवीकरण की दो परस्पर लंबवत दिशाओं को चुन सकते हैं, और किसी भी दिशा में रैखिक रूप से ध्रुवीकृत किसी भी तरंग को उन दो तरंगों के रैखिक संयोजन (मिश्रण) के रूप में व्यक्त कर सकते हैं।

एक ही आवृत्ति, वेग और यात्रा की दिशा वाली दो तरंगों के संयोजन से, लेकिन विभिन्न चरणों और स्वतंत्र विस्थापन दिशाओं के साथ, एक गोलाकार ध्रुवीकरण या अण्डाकार ध्रुवीकरण तरंग प्राप्त होती है। ऐसी तरंग में कण आगे और पीछे जाने के अतिरिक्त वृत्ताकार या अण्डाकार प्रक्षेपवक्र का वर्णन करते हैं।

यह समझने में मदद कर सकता है कि ऊपर वर्णित एक तंग स्ट्रिंग के साथ विचार प्रयोग को फिर से देखना। ध्यान दें कि आप अपने हाथ को ऊपर और नीचे की अतिरिक्त दाएं और बाएं घुमाकर भी डोरी पर तरंगें छोड़ सकते हैं। यह एक महत्वपूर्ण विषय है। दो स्वतंत्र (ऑर्थोगोनल) दिशाएँ हैं जिनमें तरंगें गति कर सकती हैं। (यह समकोण पर किसी भी दो दिशाओं के लिए सही है, ऊपर और नीचे और दाएं और बाएं को स्पष्टता के लिए चुना जाता है।) आपके हाथ को एक सीधी रेखा में ले जाकर लॉन्च की गई कोई भी तरंगें रैखिक रूप से ध्रुवीकृत तरंगें होती हैं।

लेकिन अब अपने हाथ को एक घेरे में घुमाने की कल्पना करें। आपकी गति से डोरी पर एक सर्पिल तरंग प्रक्षेपित होगी। आप अपने हाथ को एक साथ ऊपर और नीचे दोनों तरफ घुमा रहे हैं। अगल-बगल की गति का मैक्सिमा ऊपर और नीचे गति के मैक्सिमा से एक चौथाई तरंग दैर्ध्य (या सर्कल के चारों ओर एक चौथाई रास्ता, जो कि 90 डिग्री या π/2 रेडियन है) होता है। स्ट्रिंग के साथ किसी भी बिंदु पर, स्ट्रिंग का विस्थापन आपके हाथ के समान वृत्त का वर्णन करेगा, लेकिन तरंग के प्रसार की गति से विलंबित होगा। यह भी ध्यान दें कि आप अपने हाथ को दक्षिणावर्त वृत्त या वामावर्त वृत्त में ले जाना चुन सकते हैं। ये वैकल्पिक वृत्ताकार गतियाँ दाएँ और बाएँ गोलाकार ध्रुवीकृत तरंगें उत्पन्न करती हैं।

जिस सीमा तक आपका वृत्त अपूर्ण है, एक नियमित गति दीर्घवृत्त का वर्णन करेगी, और अण्डाकार रूप से ध्रुवीकृत तरंगें उत्पन्न करेगी। विलक्षणता के चरम पर आपका दीर्घवृत्त एक सीधी रेखा बन जाएगा, जो दीर्घवृत्त के प्रमुख अक्ष के साथ रैखिक ध्रुवीकरण का निर्माण करेगा। एक अण्डाकार गति को हमेशा असमान आयाम के दो ओर्थोगोनल रैखिक गतियों में विघटित किया जा सकता है और 90 डिग्री चरण से बाहर हो सकता है, जिसमें परिपत्र ध्रुवीकरण विशेष मामला होता है जहां दो रैखिक गतियों का एक ही आयाम होता है।

रबर के धागे पर यांत्रिक रूप से उत्पन्न परिपत्र ध्रुवीकरण, एक यांत्रिक ध्रुवीकरण फिल्टर द्वारा रैखिक ध्रुवीकरण में परिवर्तित हो जाता है।