एंटीना माप: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Antenna testing techniques}} | {{Short description|Antenna testing techniques}} | ||
एंटीना माप तकनीक [[एंटीना (रेडियो)]] के परीक्षण को संदर्भित करती है ताकि यह सुनिश्चित किया जा सके कि एंटीना विनिर्देशों को पूरा करती है या केवल इसे चिह्नित करने के लिए करते है। एंटेना के विशिष्ट पैरामीटर [[एंटीना लाभ|वृद्धि]], | '''''एंटीना माप''''' तकनीक [[एंटीना (रेडियो)]] के परीक्षण को संदर्भित करती है ताकि यह सुनिश्चित किया जा सके कि एंटीना विनिर्देशों को पूरा करती है या केवल इसे चिह्नित करने के लिए करते है। एंटेना के विशिष्ट पैरामीटर [[एंटीना लाभ|वृद्धि]], [[एंटीना बैंडविड्थ|बैंडविड्थ]], विकिरण पैटर्न, [[ दिशात्मक |किरण-पुंज विस्तार]], ध्रुवीकरण (तरंगें), और [[विद्युत प्रतिबाधा|प्रतिबाधा]] हैं। | ||
ऐन्टेना पैटर्न किसी दिए गए दिशा से समतल तरंग की घटना के लिए ऐन्टेना की प्रतिक्रिया है या किसी दिए गए दिशा में ऐन्टेना द्वारा प्रेषित तरंग की सापेक्ष शक्ति घनत्व है। व्युत्क्रम ऐन्टेना के लिए, ये दो पैटर्न समान हैं। [[एंटीना पैटर्न]] मापन तकनीकों की | ऐन्टेना पैटर्न किसी दिए गए दिशा से समतल तरंग की घटना के लिए ऐन्टेना की प्रतिक्रिया है या किसी दिए गए दिशा में ऐन्टेना द्वारा प्रेषित तरंग की सापेक्ष शक्ति घनत्व है। व्युत्क्रम ऐन्टेना के लिए, ये दो पैटर्न समान हैं। [[एंटीना पैटर्न]] मापन तकनीकों की समूह विकसित किया गया है। विकसित की गई पहली तकनीक सुदूर-क्षेत्र की परास थी, जहाँ परीक्षण के अंतर्गत एंटीना (एयूटी) को परास एंटीना के सुदूर-क्षेत्र में रखा जाता है। बड़े एंटेना के लिए सुदूर-क्षेत्र की परास बनाने के लिए आवश्यक आकार के कारण, निकट-क्षेत्र तकनीक विकसित की गई, जो ऐन्टेना के समीप की सतह पर क्षेत्र की माप की (सामान्य रूप से इसकी [[तरंग दैर्ध्य]] से 3 से 10 गुना होती है) स्वीकृति देती है। यह माप तब अनंत पर समान होने का अनुमान लगाया गया है। तीसरी सामान्य विधि सुसम्बद्ध परास है, जो परीक्षण के अंतर्गत एंटीना के पास क्षेत्र बनाने के लिए [[परावर्तक (एंटीना)]] का उपयोग करती है जो लगभग समतल तरंग की तरह दिखती है। | ||
== सुदूर-क्षेत्र | == सुदूर-क्षेत्र परास (एफएफ) == | ||
सुदूर-क्षेत्र की | सुदूर-क्षेत्र की परास मूल एंटीना माप तकनीक थी, और सबसे सरल थी; इसमें एंटीना को परीक्षण (एयूटी) के अंतर्गत[[ इंस्ट्रुमेंटेशन | यंत्र]] एंटीना से लंबी दूरी पर रखना सम्मिलित है। सामान्य रूप से, सुदूर-क्षेत्र की दूरी या फ्रौनहोफर दूरी <math>\ D_\mathsf{Frnh}\ ,</math> माना जाता है | ||
: <math>D_\mathsf{Frnh} = \frac{\ 2d^2\ }{\lambda}\ ,</math> | : <math>D_\mathsf{Frnh} = \frac{\ 2d^2\ }{\lambda}\ ,</math> | ||
जहाँ <math>\ d\ </math> किसी भी दिशा में एंटीना का सबसे चौड़ा व्यास है, और <math>\ \lambda\ </math> रेडियो तरंग की तरंग दैर्ध्य है।<ref>{{cite book |first=C.A. |last=Balanis |year=2005 |title=Antenna Theory: Analysis and design |edition=3rd |publisher=Wiley Interscience}}</ref> इस दूरी से परीक्षण के अंतर्गत एंटीना और मानक | जहाँ <math>\ d\ </math> किसी भी दिशा में एंटीना का सबसे चौड़ा व्यास है, और <math>\ \lambda\ </math> रेडियो तरंग की तरंग दैर्ध्य है।<ref>{{cite book |first=C.A. |last=Balanis |year=2005 |title=Antenna Theory: Analysis and design |edition=3rd |publisher=Wiley Interscience}}</ref> इस दूरी से परीक्षण के अंतर्गत एंटीना और मानक अभिग्राही एंटीना को अलग करने से दूर दूरी में एंटीना पैटर्न का उपयुक्त परिशुद्ध अनुमान प्राप्त करने के लिए पर्याप्त परीक्षण के अंतर्गत एंटीना में पता लगाने योग्य चरण भिन्नता कम हो जाती है। | ||
[[IEEE|विद्युत और इलेक्ट्रॉनिक्स इंजीनियर संस्थान]] ऐन्टेना मापन मानक (दस्तावेज़ आईडी विद्युत और इलेक्ट्रॉनिक्स इंजीनियर संस्थान-सॉफ्टवेयर अभियांत्रिकी शब्दावली का मानक शब्दकोष-149-1979), सुदूर-क्षेत्र | [[IEEE|विद्युत और इलेक्ट्रॉनिक्स इंजीनियर संस्थान]] ऐन्टेना मापन मानक (दस्तावेज़ आईडी विद्युत और इलेक्ट्रॉनिक्स इंजीनियर संस्थान-सॉफ्टवेयर अभियांत्रिकी शब्दावली का मानक शब्दकोष-149-1979), सुदूर-क्षेत्र परास और ग्राउंड-बाउंस परास (नीचे चर्चा की गई) दोनों के लिए माप और विभिन्न तकनीकों के लिए व्यवस्था का सुझाव देता है। | ||
== निकट क्षेत्र | == निकट क्षेत्र परास (एनएफ) == | ||
{{main|विद्युत चुम्बकीय निकट-क्षेत्र परीक्षण यंत्र}} | {{main|विद्युत चुम्बकीय निकट-क्षेत्र परीक्षण यंत्र}} | ||
=== समतलीय निकट क्षेत्र | === समतलीय निकट क्षेत्र परास === | ||
समतलीय | समतलीय निकट क्षेत्र माप समतलीय सतह पर छोटे से अन्वेषी एंटीना को जांच करके आयोजित किया जाता है। इन मापों को फिर फूरियर रूपांतरण के उपयोग से या अधिक विशेष रूप से लाप्लास रूपांतरण के लिए स्थिर प्रावस्था के रूप में जाना जाने वाला एक तरीका प्रयुक्त करके दूर-क्षेत्र में परिवर्तित कर दिया जाता है।<ref>''Asymptotic Behavior of Monodromy'', Springer Berlin / Heidelberg, 1991, {{ISBN|978-3-540-55009-9}}</ref> निकट क्षेत्र मापन में तीन मूल प्रकार की समतलीय जांच सम्मिलित हैं। | ||
====आयताकार तलीय क्रमवीक्षण==== | ====आयताकार तलीय क्रमवीक्षण==== | ||
अन्वेषी [[कार्तीय समन्वय प्रणाली]] में स्थानांतरण करती है और इसका रैखिक संचलन Δx = Δy = λ /2 की अधिकतम निकट-क्षेत्र प्रतिदर्श अंतराल के साथ | अन्वेषी [[कार्तीय समन्वय प्रणाली]] में स्थानांतरण करती है और इसका रैखिक संचलन Δx = Δy = λ /2 की अधिकतम निकट-क्षेत्र प्रतिदर्श अंतराल के साथ नियमित आयताकार प्रतिदर्श ग्रिड बनाता है। | ||
==== ध्रुवीय समतलीय क्रमवीक्षण ==== | ==== ध्रुवीय समतलीय क्रमवीक्षण ==== | ||
| Line 32: | Line 32: | ||
[[File:BipolarGrid.svg|210px]] | [[File:BipolarGrid.svg|210px]] | ||
=== बेलनाकार निकट-क्षेत्र | === बेलनाकार निकट-क्षेत्र परास === | ||
बेलनाकार निकट-क्षेत्र | बेलनाकार निकट-क्षेत्र परास परीक्षण के अंतर्गत एंटीना के समीप बेलनाकार सतह पर विद्युत क्षेत्र को मापती है। बेलनाकार [[हार्मोनिक्स]] का उपयोग इन मापों को सुदूर-क्षेत्र में परिवर्तित करने के लिए किया जाता है। | ||
[[File:CylindricalGrid.svg|210px]] | [[File:CylindricalGrid.svg|210px]] | ||
=== गोलाकार निकट-क्षेत्र | === गोलाकार निकट-क्षेत्र परास === | ||
गोलाकार निकट-क्षेत्र | गोलाकार निकट-क्षेत्र परास परीक्षण के अंतर्गत एंटीना के समीप गोलाकार सतह पर विद्युत क्षेत्र को मापती है। इन मापों को सुदूर-क्षेत्र में परिवर्तित करने के लिए गोलाकार हार्मोनिक्स का उपयोग किया जाता है | ||
== मुक्त आकाशीय | == मुक्त आकाशीय परास == | ||
विद्युत चुम्बकीय विकिरण प्रसार और सूचना प्रसार का सूत्र है: | विद्युत चुम्बकीय विकिरण प्रसार और सूचना प्रसार का सूत्र है: | ||
| Line 46: | Line 46: | ||
जहाँ {{mvar|D}} दूरी, {{mvar|P}} शक्ति और {{mvar|S}} गति को निरूपित करता है। | जहाँ {{mvar|D}} दूरी, {{mvar|P}} शक्ति और {{mvar|S}} गति को निरूपित करता है। | ||
समीकरण का अर्थ है कि संचार दूरी को दोगुना करने के लिए चार गुना सामर्थ्य की आवश्यकता होती है। इसका अर्थ यह भी है कि दोहरी सामर्थ्य दोहरी संचार गति (बिट दर) की स्वीकृति देती है। दोहरी सामर्थ्य लगभग | समीकरण का अर्थ है कि संचार दूरी को दोगुना करने के लिए चार गुना सामर्थ्य की आवश्यकता होती है। इसका अर्थ यह भी है कि दोहरी सामर्थ्य दोहरी संचार गति (बिट दर) की स्वीकृति देती है। दोहरी सामर्थ्य लगभग 3डेसीबल (या पूर्णतया {{nobr| {{math| 10×log{{sub|10}}(2) ≈ 3.0103000}} }}) वृद्धि है। स्वभावतः, वास्तविक विश्व में सभी प्रकार की अन्य घटनाएं हैं जो अनुमानित वितरित शक्ति को जटिल बनाती हैं, जैसे फ्रेनल अस्वीकार करना, पथ हानि, पृष्ठ भूमि रव इत्यादि। | ||
=== सुसम्बद्ध | === सुसम्बद्ध परास === | ||
सुसम्बद्ध एंटीना परीक्षण | सुसम्बद्ध एंटीना परीक्षण परास (सीएटीआर) सुविधा है जिसका उपयोग आवृति पर एंटीना प्रणाली के सुविधाजनक परीक्षण प्रदान करने के लिए किया जाता है जहां परीक्षण के अंतर्गत एंटीना के लिए सुदूर-क्षेत्र की दूरी प्राप्त करना पारंपरिक [[मुक्त स्थान|मुक्त आकाशीय]] विधियों का उपयोग करना असंभव होगा। इसका आविष्कार [[जॉर्जिया टेक रिसर्च इंस्टीट्यूट|जॉर्जिया तकनीकी अनुसंधान संस्थान]] में रिचर्ड सी जॉनसन ने किया था।<ref>{{cite press release |first=Lea |last=McLees |title=जीटीआरआई एंटीना विशेषज्ञ और इंजीनियरिंग मेंटर का निधन|periodical=The Whistle |type=obituary |publisher=[[Georgia Institute of Technology]] |url=https://smartech.gatech.edu/handle/1853/3890 |access-date=2011-11-09}}</ref> सुसम्बद्ध एंटीना परीक्षण परास स्रोत एंटीना का उपयोग करता है जो गोलाकार तरंगाग्र और एक या एक से अधिक द्वितीयक परावर्तकों को विकिरण गोलाकार तरंगाग्र को वांछित परीक्षण क्षेत्र के अंदर समतलीय तरंगाग्र में मिलाने के लिए उपयोग करता है। इसे पूरा करने के लिए विशिष्ट अभिव्यक्ति शृंगी भरण एंटीना और [[परवलयिक परावर्तक]] का उपयोग करता है। | ||
सुसम्बद्ध एंटीना परीक्षण परास का उपयोग [[माइक्रोवेव|सूक्ष्मतरंग]] और मिलीमीटर तरंग आवृत्तियों के लिए किया जाता है जहाँ <math>\ \frac{\ 2 D^2\ }{\lambda}\ </math> सुदूर-क्षेत्र की दूरी बड़ी है, जैसे उच्च-वृद्धि परावर्तक एंटेना के साथ होती है। आवश्यक परास का आकार पूर्ण आकार के सुदूर-क्षेत्र के अप्रतिघ्वनिक कक्ष के लिए आवश्यक आकार से बहुत कम हो सकता है, हालांकि विशेष रूप से डिज़ाइन किए गए सुसम्बद्ध एंटीना परीक्षण परास परावर्तक के निर्माण की कीमत परिशुद्ध सुनिश्चित करने की आवश्यकता के कारण अधिक हो सकती है परावर्तक सतह (सामान्य रूप से से कम {{nobr| {{sfrac|1|100}}[[wavelength|{{mvar|λ}}]] [[root mean square|{{sc|RMS}}]] }} सतह परिशुद्धता) और विवर्तित तरंगों से संरक्षित करने के लिए विशेष रूप से परावर्तक के कोर का संशोधन करने के लिए जो वांछित किरण पैटर्न में अन्तः क्षेप कर सकते हैं। | |||
=== उन्नत | === उन्नत परास === | ||
उन्नत परास में, परीक्षण के अंतर्गत एंटीना और मापने वाले एंटीना दोनों को जमीन से परावर्तित तरंगों से अन्तः क्षेप को कम करने के साधन के रूप में जमीन के ऊपर कई तरंग दैर्ध्य पर चढ़ाया जाता है। | |||
=== | === तिर्यक परास === | ||
तिर्यक् परास में, अभिग्राही एंटीना को परीक्षण के अंतर्गत एंटीना की तुलना में भू-तल से ऊपर लगाया जाता है या तो परास की पृथ्वी की सतह को परीक्षण के अंतर्गत एंटीना माउंट (धारक) से नीचे की ओर झुकाया जाता है या एंटीना को बहुत ऊंचे अवस्था पर रखा जाता है। झुकी हुई पृथ्वी (या तो वास्तविक या प्रभावी) अभिग्राही एंटीना के नीचे विकसित के लिए परावर्तित तरंगों को कोण बनाकर सममित तरंग प्रतिबिंब से अन्तः क्षेप को नष्ट करने या कम करने के उपकरण के रूप में कार्य करती है। सैद्धांतिक रूप में, समान तकनीक को अभिग्राही एंटीना के ऊपर पृथ्वी-परावर्तित अधिकांश तरंगों को विकसित करने के लिए प्रतिवर्त में प्रयुक्त किया जा सकता है। | |||
== एंटीना पैरामीटर == | == एंटीना पैरामीटर == | ||
{{see also| | {{see also|एंटीना (रेडियो) § विशेषताएँ}} | ||
ध्रुवीकरण | |||
ध्रुवीकरण के अतिरिक्त, उपरोक्त पैरामीटरों में स्थायी तरंग अनुपात सबसे आसानी से मापा जाता है। प्रतिबाधा को विशेष उपकरणों से मापा जा सकता है, क्योंकि यह सम्मिश्र संख्या स्थायी तरंग अनुपात से संबंधित है। विकिरण पैटर्न को मापने के लिए महत्वपूर्ण स्थान-रिक्ति सहित परिष्कृत व्यवस्था (एंटीना के दूर क्षेत्र में संवेदित्र लगाने के लिए पर्याप्त है, या एंटीना माप के लिए डिज़ाइन किया गया अप्रतिध्वनिक कक्ष), प्रयोग ज्यामिति का सावधानीपूर्वक अध्ययन, और माप के समय ऐन्टेना को घुमाने वाले विशेष माप उपकरण की आवश्यकता होती है। | |||
===विकिरण पैटर्न === | ===विकिरण पैटर्न === | ||
{{main| | {{main|विकिरण पैटर्न}} | ||
विकिरण पैटर्न ऐन्टेना द्वारा प्रेषित या प्राप्त सापेक्ष क्षेत्र | |||
विकिरण पैटर्न ऐन्टेना द्वारा प्रेषित या प्राप्त सापेक्ष क्षेत्र सामर्थ्य का चित्रमय चित्रण है, और पार्श्व खण्ड और पश्च खंड दिखाता है। चूंकि ऐन्टेना अंतरिक्ष में विकीर्ण होते हैं, ऐन्टेना का वर्णन करने के लिए प्रायः कई वक्र आवश्यक होते हैं। यदि ऐन्टेना का विकिरण अक्ष के बारे में सममित है (जैसा कि द्विध्रुव, कुंडलित ऐन्टेना और कुछ परवलयिक ऐन्टेना में होता है) अद्वितीय ग्राफ पर्याप्त है। | |||
प्रत्येक एंटीना आपूर्तिकर्ता/उपयोगकर्ता के पास अलग-अलग मानकों के साथ-साथ | प्रत्येक एंटीना आपूर्तिकर्ता/उपयोगकर्ता के पास अलग-अलग मानकों के साथ-साथ आलेखन प्रारूप भी होते हैं। प्रत्येक प्रारूप के अपने लाभ और हानि हैं। एंटीना के विकिरण पैटर्न को उन सभी बिंदुओं के स्थान के रूप में परिभाषित किया जा सकता है जहां प्रति इकाई सतह पर उत्सर्जित शक्ति समान होती है। प्रति इकाई सतह से निकलने वाली शक्ति विद्युत चुम्बकीय तरंग के वर्ग विद्युत क्षेत्र के समानुपाती होती है। विकिरण पैटर्न समान विद्युत क्षेत्र वाले बिंदुओं का स्थान है। इस प्रतिनिधित्व में, संदर्भ सामान्य रूप से उत्सर्जन का सबसे अच्छा कोण होता है। दिशा के कार्य के रूप में ऐन्टेना के प्रत्यक्ष लब्धि को चित्रित करना भी संभव है। प्राय: लब्धि को [[डेसीबल]] में दिया जाता है। | ||
रेखांकन कार्तीय (आयताकार) निर्देशांक या एक ध्रुवीय भूखंड का उपयोग करके चित्रित किया जा सकता है। यह अंतिम बीमविड्थ (किरण-पुंज विस्तार) को मापने के लिए उपयोगी है, जो कि समागम द्वारा, अधिकतम लब्धि के आसपास -3डेसीबल बिंदुओं पर कोण है। कार्तीय या ध्रुवीय निर्देशांक में और लघुगणकीय पैमाने की सीमाओं के चयन के साथ वक्र का आकार बहुत भिन्न हो सकता है। नीचे दिए गए चार आरेखण समान अर्ध-तरंग ऐन्टेना के विकिरण पैटर्न हैं। | |||
{| class="wikitable" | {| class="wikitable" | ||
| [[Image:RadPatt-lin.png|thumb|340px| | | [[Image:RadPatt-lin.png|thumb|340px|अर्ध-तरंग द्विध्रुवीय एंटीना का विकिरण पैटर्न रैखिक पैमाना।]] | ||
| [[Image:HWDipoleGain.svg|thumb|340px| | | [[Image:HWDipoleGain.svg|thumb|340px|अर्ध-तरंग द्विध्रुव का लब्धि पैमाना डीबीआई में है।]] | ||
|- | |- | ||
|[[Image:RadPatt-Cart.png|right|thumb|340px| | |[[Image:RadPatt-Cart.png|right|thumb|340px|अर्ध-तरंग द्विध्रुव का लब्धि कार्तीय प्रतिनिधित्व]] | ||
|[[Image:L-over2-rad-pat-per.jpg|thumb|340px|3D | |[[Image:L-over2-rad-pat-per.jpg|thumb|340px|अर्ध-तरंग द्विध्रुव एंटीना का 3D विकिरण पैटर्न।]] | ||
|} | |} | ||
=== दक्षता === | === दक्षता === | ||
{{main| | {{main| ऐन्टेना दक्षता}} | ||
दक्षता | |||
दक्षता एक एंटीना द्वारा वास्तव में विकीर्ण की गई शक्ति का संचारक से प्राप्त विद्युत शक्ति का अनुपात है। [[ डमी भार |मूक भार]] में 1:1 का स्थायी तरंग अनुपात हो सकता है, लेकिन 0 की दक्षता, क्योंकि यह ऊष्मा उत्पन्न करने के लिए सभी आपतित शक्ति को अवशोषित करता है, लेकिन कोई [[ आकाशवाणी आवृति | रेडियो आवृत्ति]] ऊर्जा विकीर्ण नहीं करता है [[स्थायी तरंग अनुपात]] ऐन्टेना की दक्षता का माप नहीं है। [[विकिरण प्रतिरोध]] ऐन्टेना द्वारा विकिरण के लिए नष्ट की गई शक्ति के कारण होने वाले विद्युत के प्रतिरोध का भाग है। दुर्भाग्य से, इसे प्रत्यक्ष रूप से मापा नहीं जा सकता है लेकिन कुल विद्युत प्रतिरोध का घटक है जिसमें हानि प्रतिरोध सम्मिलित है। हानि प्रतिरोध सुसंगत रेडियो तरंगों के अतिरिक्त ऐन्टेना सामग्री में ऊष्मा के लिए नष्ट हुई शक्ति का परिणाम है, इस प्रकार दक्षता कम हो जाती है। दक्षता (<math>\ \tilde{\eta}\ </math>) को रेडियो तरंगों (<math>\ P_\mathsf{rad}\ </math>) के रूप में सुसंगत रूप से विकिरित शक्ति के अनुपात के रूप में परिभाषित किया गया है। एंटीना द्वारा उपयोग की जाने वाली कुल शक्ति के लिए, जो सुसंगत रूप से विकिरित शक्ति (<math>\ P_\mathsf{rad}\ </math>) और उष्मा के रूप में विकिरित शक्ति (<math>\ P_\mathsf{loss}\ </math>) का योग होता है: | |||
:<math> \tilde{\eta} \equiv \frac{P_\mathsf{rad} }{\ P_\mathsf{rad} + P_\mathsf{loss}\ }\ </math> | :<math> \tilde{\eta} \equiv \frac{P_\mathsf{rad} }{\ P_\mathsf{rad} + P_\mathsf{loss}\ }\ </math> | ||
ऐन्टेना दक्षता भी गणितीय रूप से विकिरण प्रतिरोध | ऐन्टेना दक्षता भी गणितीय रूप से विकिरण प्रतिरोध (<math>\ R_\mathsf{rad}\ </math>) के समान होती है, जो कुल प्रतिरोध (विद्युत-दाब बिन्दु पर मापी गई प्रतिबाधा का वास्तविक भाग, जो प्रायः प्रभरण बिंदु होता है) से विभाजित होती है: | ||
:<math> \tilde{\eta} = \frac{R_\mathsf{rad} }{\ R_\mathsf{rad} + R_\mathsf{loss}\ }\ .</math> | :<math> \tilde{\eta} = \frac{R_\mathsf{rad} }{\ R_\mathsf{rad} + R_\mathsf{loss}\ }\ .</math> | ||
=== बैंडविड्थ === | === बैंडविड्थ === | ||
{{main| | {{main|एंटीना बैंडविड्थ}} | ||
आईईईई बैंडविड्थ को आवृत्तियों की | |||
विद्युत और इलेक्ट्रॉनिक्स इंजीनियर संस्थान (आईईईई) बैंडविड्थ को आवृत्तियों की परास के रूप में परिभाषित करता है जिसके अंदर ऐन्टेना का प्रदर्शन, कुछ विशेषताओं के संबंध में, निर्दिष्ट मानक के अनुरूप होता है।<ref>{{cite report |title=एंटेना के लिए शर्तों की IEEE मानक परिभाषाएँ|date=June 1993 |id=IEEE Std 145-1993 |pages=6, 21 |publisher=[[IEEE]] |url=http://ieeexplore.ieee.org/servlet/opac?punumber=2785}}</ref> दूसरे शब्दों में, बैंडविड्थ आवृत्तियों की श्रृंखला के माध्यम से ऐन्टेना की समग्र प्रभावशीलता पर निर्भर करता है, इसलिए इन सभी मापदंडों को एंटीना की बैंडविड्थ समर्थता को पूरी तरह से समझने के लिए समझा जाना चाहिए। यह परिभाषा व्यावहारिक परिभाषा के रूप में काम कर सकती है, हालांकि, व्यवहार में, बैंडविड्थ सामान्य रूप से प्रेरित की आवृत्ति विस्तार पर स्थायी तरंग अनुपात या विकीर्ण शक्ति जैसी विशेषता को मापकर निर्धारित की जाती है। उदाहरण के लिए, स्थायी तरंग अनुपात बैंडविड्थ सामान्य रूप से आवृत्ति विस्तार को मापकर निर्धारित किया जाता है जहाँ स्थायी तरंग अनुपात 2:1 से कम होता है। प्रतिध्वनित एंटेना के लिए बैंडविड्थ का निर्धारण करने के लिए और प्रायः उपयोग किया जाने वाला मान {{nobr|−3 dB }}परावर्तनिक हानि मान है, चूंकि स्थायी तरंग अनुपात के कारण हानि−10·log<sub>10</sub>(2÷1) = −3.01000 dB है। | |||
=== दिशिकता === | |||
{{main| दिशिकता}} | |||
ऐन्टेना दिशिकता अधिकतम विकिरण [[तीव्रता (भौतिकी)]] (शक्ति प्रति इकाई सतह) का अनुपात है जो ऐन्टेना द्वारा अधिकतम दिशा में विकीर्ण होती है और परिकल्पित [[आइसोट्रोपिक एंटीना|समदैशिक एंटीना]] द्वारा विकिरित तीव्रता से विभाजित होती है जो उस ऐन्टेना के समान समग्र शक्ति को विकीर्ण करती है। उदाहरण के लिए, परिकल्पनात्मक ऐन्टेना जिसमें गोलार्ध (1/2 गोला) का विकिरणित पैटर्न था, उसकी 2 की दिशिकता होगी। दिशिकता आयाम रहित अनुपात है और इसे संख्यात्मक रूप से या [[डेसिबल]] (डीबी) में व्यक्त किया जा सकता है। दिशिकता [[निर्देश लाभ|निर्देश]] लब्धि के शिखर मान के समान है; इन मानो को [[एंटीना दक्षता]] के संबंध में निर्दिष्ट किए बिना निर्दिष्ट किया जाता है, इस प्रकार शक्ति लब्धि (या केवल "लब्धि") से भिन्न होता है जिसका मूल्य एंटीना की दक्षता से कम हो जाता है। | |||
=== | === लब्धि === | ||
{{main| | {{main|ऐन्टेना लाब्धि}} | ||
लब्धि पैरामीटर के रूप में किसी दिए गए एंटीना की दिशिकता को मापता है। कम लब्धि वाला एंटीना सभी दिशाओं में समान रूप से विकिरण उत्सर्जित करता है, जबकि एक उच्च-लब्धि एंटीना विशेष दिशाओं में अधिमानतः विकीर्ण होगा। एक परिकल्पित समदैशिक एंटीना द्वारा समान दूरी पर विकिरणित प्रबलता (भौतिकी) से विभाजित यादृच्छिक दूरी पर एंटीना द्वारा दी गई दिशा में तीव्रता (शक्ति प्रति इकाई सतह) के अनुपात के रूप में परिभाषित किया गया है। : | |||
:<math>\ G = {\left({P \over S}\right)_\mathsf{ant} \over \left({P \over S}\right)_\mathsf{iso}}\ </math> | :<math>\ G = {\left({P \over S}\right)_\mathsf{ant} \over \left({P \over S}\right)_\mathsf{iso}}\ </math> | ||
हम | हम <nowiki>''परिकल्पनात्मक''</nowiki> लिखते हैं क्योंकि पूर्ण समदैशिक एंटीना का निर्माण नहीं किया जा सकता है। लब्धि आयामहीन संख्या (इकाइयों के बिना) है। | ||
ऐन्टेना का लाभ | ऐन्टेना का लाभ निष्क्रिय घटना है - ऐन्टेना द्वारा विद्युत नहीं जोड़ी जाती है, लेकिन समदैशिक ऐन्टेना द्वारा प्रेषित की तुलना में निश्चित दिशा में अधिक विकीर्ण शक्ति प्रदान करने के लिए सिर्फ पुनर्वितरित किया जाता है। यदि ऐन्टेना का कुछ दिशाओं में एक से अधिक वृद्धि होती है, तो अन्य दिशाओं में इसकी वृद्धि एक से कम होनी चाहिए क्योंकि ऐन्टेना द्वारा ऊर्जा का संरक्षण किया जाता है। लब्धि निर्धारित करते समय एंटीना डिजाइनर को एंटीना के लिए अनुप्रयोग को ध्यान में रखना चाहिए। उच्च-लब्धि वाले एंटेना में लंबी दूरी और अपेक्षाकृत अधिकतम सिग्नल गुणवत्ता का लाभ होता है, लेकिन किसी विशेष दिशा में सावधानी से प्रयोजन होना चाहिए। कम लब्धि वाले एंटेना की परास कम होती है, लेकिन एंटीना का उन्मुखीकरण महत्वहीन होता है। उदाहरण के लिए, अंतरिक्ष यान पर डिश एंटीना उच्च-लब्धि उपकरण है (प्रभावी होने के लिए ग्रह पर इंगित किया जाना चाहिए), जबकि लैपटॉप कंप्यूटर में विशिष्ट [[Wifi|वाईफाई]] एंटीना कम-लब्धि होती है (जब तक आधार केंद्र परास के अंदर है), ऐन्टेना अंतरिक्ष में किसी भी अभिविन्यास में हो सकता है)। | ||
== भौतिक पृष्ठभूमि == | == भौतिक पृष्ठभूमि == | ||
[[Image:radiation1.png|right|frame|मापा विद्युत क्षेत्र विकीर्ण | [[Image:radiation1.png|right|frame|मापा विद्युत क्षेत्र विकीर्ण <math>\scriptstyle{r'\over c}</math> सेकंड पहले किया गया था।]]विद्युत आवेश द्वारा निर्मित [[विद्युत क्षेत्र]] <math>\scriptstyle{q}</math> है | ||
::<math>\vec E={-q\over 4\pi \varepsilon_\circ}\left[{\vec e_{r'}\over r'^2}+ | ::<math>\vec E={-q\over 4\pi \varepsilon_\circ}\left[{\vec e_{r'}\over r'^2}+ | ||
{r'\over c}{d\ \over dt}\left({\vec e_{r'}\over r'^2}\right) + | {r'\over c}{d\ \over dt}\left({\vec e_{r'}\over r'^2}\right) + | ||
| Line 114: | Line 119: | ||
जहाँ: | जहाँ: | ||
* <math>\scriptstyle{c}</math> निर्वात में [[प्रकाश की गति]] है। | * <math>\scriptstyle{c}</math> निर्वात में [[प्रकाश की गति]] है। | ||
* <math>\scriptstyle{\varepsilon_\circ }</math> | * <math>\scriptstyle{\varepsilon_\circ }</math> मुक्त आकाशीय की पारगम्यता है। | ||
* <math>\scriptstyle{r'}</math> | * <math>\scriptstyle{r'}</math> प्रेक्षण बिंदु से दूरी (वह स्थान जहाँ <math>\scriptstyle{\vec E}</math> का मूल्यांकन किया जाता है) उस बिंदु तक जहाँ आवेश <math>\scriptstyle{r'\over c}</math> सेकंड से पहले जब माप किया जाता है। | ||
* <math>\textstyle{\vec e_{r'}}</math> अवलोकन बिंदु से निर्देशित इकाई वेक्टर है (वह स्थान जहां <math>\scriptstyle{\vec E}</math> मूल्यांकन किया जाता है) उस बिंदु तक | * <math>\textstyle{\vec e_{r'}}</math> अवलोकन बिंदु से निर्देशित इकाई वेक्टर है (वह स्थान जहां <math>\scriptstyle{\vec E}</math> का मूल्यांकन किया जाता है) उस बिंदु तक जहाँ आवेश <math>\scriptstyle{r'\over c}</math> सेकंड से पहले जब माप किया जाता है। | ||
इस | इस सूत्र में "प्रवेशिका" प्रकट होती है क्योंकि विद्युत चुम्बकीय संकेत प्रकाश की गति से संचरण करता है। संकेतों को उस बिंदु से आने के रूप में देखा जाता है जहां वे उत्सर्जित हुए थे न कि उस बिंदु से जहां प्रेक्षण के समय उत्सर्जक है। जो तारे हम आकाश में देखते हैं वे अब वहां नहीं होते जहां हम उन्हें देखते हैं। हम उनकी वर्तमान स्थिति को भविष्य में देखेंगे; आज हम जिन तारों को देखते हैं उनमें से कुछ सम्मिलित नहीं हैं। | ||
सूत्र में पहला शब्द [[मंद समय]] के साथ सिर्फ | सूत्र में पहला शब्द [[मंद समय|मंदित समय]] के साथ सिर्फ विद्युत् स्थैतिक क्षेत्र है। | ||
दूसरा शब्द ऐसा है जैसे कि प्रकृति इस तथ्य की स्वीकृति देने की | दूसरा शब्द ऐसा है जैसे कि प्रकृति इस तथ्य की स्वीकृति देने की प्रयास कर रही थी कि प्रभाव मंद (फेनमैन) है। | ||
तीसरा शब्द एकमात्र ऐसा शब्द है जो एंटेना के सुदूर क्षेत्र के लिए | तीसरा शब्द एकमात्र ऐसा शब्द है जो एंटेना के सुदूर क्षेत्र के लिए अधीन है। | ||
पहले दो पद समानुपातिक | पहले दो पद समानुपातिक <math>\textstyle{1\over r^2}</math>हैं। केवल तीसरा आनुपातिक <math>\textstyle{1\over r}</math> है। | ||
एंटीना के पास, सभी शर्तें महत्वपूर्ण हैं। हालाँकि, यदि दूरी | एंटीना के पास, सभी शर्तें महत्वपूर्ण हैं। हालाँकि, यदि दूरी अपेक्षाकृत अधिक बड़ी है, तो पहले दो पद नगण्य हो जाते हैं और केवल तीसरा शेष रहता है: | ||
::<math>\vec E={-q\over 4\pi \varepsilon c^2_\circ}{d^2\ \over dt^2}\left(\vec e_{r'}\right)=-q10^{-7}{d^2\ \over dt^2}\left(\vec e_{r'}\right)\, </math> | ::<math>\vec E={-q\over 4\pi \varepsilon c^2_\circ}{d^2\ \over dt^2}\left(\vec e_{r'}\right)=-q10^{-7}{d^2\ \over dt^2}\left(\vec e_{r'}\right)\, </math> | ||
[[Image:Rediation2.png|right|frame|विद्युत क्षेत्र | [[Image:Rediation2.png|right|frame|विद्युत क्षेत्र विद्युत धारा के एक तत्व द्वारा विकीर्ण होता है। धारा का तत्व, विद्युत क्षेत्र वेक्टर <math>\scriptstyle{\vec E_\theta}</math> और <math>\textstyle{r}</math> समान तल पर हैं।]]यदि आवेश q ज्यावक्रीय गति में आयाम <math>\scriptstyle{\ell_\circ}</math> और स्पंदन <math>\scriptstyle{\omega}</math> के साथ है, तो आवेश द्वारा विकिरित शक्ति है: | ||
:: <math>P= {q^2\omega^4\ell_\circ^2 \over 12\pi\varepsilon_\circ c^3}</math> वाट। | :: <math>P= {q^2\omega^4\ell_\circ^2 \over 12\pi\varepsilon_\circ c^3}</math> वाट। | ||
ध्यान दें कि विकिरणित शक्ति आवृत्ति की | ध्यान दें कि विकिरणित शक्ति आवृत्ति की चतुर्थ शक्ति के समानुपाती होती है। कम आवृत्तियों की तुलना में उच्च आवृत्तियों पर विकीर्ण करना कहीं अधिक आसान है। यदि आवेशों की गति धाराओं के कारण होती है, तो यह दिखाया जा सकता है कि विद्युत क्षेत्र छोटी लंबाई <math>\scriptstyle{d\ell}</math> द्वारा विकिरित (छोटा) विद्युत क्षेत्र एक संचालक का समय परिवर्ती धारा <math>\scriptstyle{I}</math> प्रवाहित करने वाला है | ||
::<math>dE_\theta(t+\textstyle{r\over c})=\displaystyle{-d\ell \sin\theta \over 4\pi\varepsilon_\circ c^2 r}{dI\over dt}\,</math> | ::<math>dE_\theta(t+\textstyle{r\over c})=\displaystyle{-d\ell \sin\theta \over 4\pi\varepsilon_\circ c^2 r}{dI\over dt}\,</math> | ||
इस समीकरण के बाईं ओर | इस समीकरण के बाईं ओर संचालक की छोटी लंबाई से निकलने वाली विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र है। अनुक्रमणिका <math>\scriptstyle{\theta}</math> स्मरण कराता है कि क्षेत्र स्रोत की रेखा के लंबवत है। और <math>\scriptstyle{t+{r\over c}}</math> h स्मरण कराता है कि यह प्रेक्षित क्षेत्र है <math>\scriptstyle{{r\over c}}</math> सेकंड धारा व्युत्पन्न पर मूल्यांकन के बाद देखा गया है। कोण <math>\scriptstyle{\theta}</math> धारा की दिशा और उस बिंदु की दिशा के बीच का कोण है जहां क्षेत्र को मापा जाता है। | ||
विद्युत क्षेत्र और विकीर्ण शक्ति वर्तमान तत्व के लंबवत विमान में अधिकतम होती है। वे धारा की दिशा में शून्य हैं। | विद्युत क्षेत्र और विकीर्ण शक्ति वर्तमान तत्व के लंबवत विमान में अधिकतम होती है। वे धारा की दिशा में शून्य हैं। | ||
| Line 141: | Line 145: | ||
केवल समय-परिवर्तनशील धाराएँ विद्युत चुम्बकीय शक्ति विकीर्ण करती हैं। | केवल समय-परिवर्तनशील धाराएँ विद्युत चुम्बकीय शक्ति विकीर्ण करती हैं। | ||
यदि | यदि धारा ज्यावक्रीय है, तो इसे जटिल रूप में लिखा जा सकता है, उसी तरह प्रतिबाधाओं के लिए उपयोग किया जाता है। केवल वास्तविक भाग भौतिक रूप से अर्थपूर्ण है: | ||
::<math>I=I_\circ e^{j\omega t}</math> | ::<math>I=I_\circ e^{j\omega t}</math> | ||
जहाँ: | जहाँ: | ||
* <math>\scriptstyle{I_\circ}</math> | * <math>\scriptstyle{I_\circ}</math> धारा का आयाम है। | ||
* <math>\scriptstyle{{\omega = 2\pi f}}</math> कोणीय आवृत्ति है। | * <math>\scriptstyle{{\omega = 2\pi f}}</math> कोणीय आवृत्ति है। | ||
*<math>\scriptstyle{j = \sqrt{-1}}</math> | *<math>\scriptstyle{j = \sqrt{-1}}</math> | ||
धारा के तत्व द्वारा विकीर्ण विद्युत चुम्बकीय तरंग का (छोटा) विद्युत क्षेत्र है: | |||
::<math>dE_\theta(t+\textstyle{{r\over c}})=\displaystyle{-d\ell j\omega \over 4\pi\varepsilon_\circ c^2} {\sin\theta \over r} e^{j\omega t}\,</math> | ::<math>dE_\theta(t+\textstyle{{r\over c}})=\displaystyle{-d\ell j\omega \over 4\pi\varepsilon_\circ c^2} {\sin\theta \over r} e^{j\omega t}\,</math> | ||
और समय | और समय <math>\textstyle{t}\,</math>के लिए: | ||
::<math>dE_\theta(t)={-d\ell j\omega \over 4\pi\varepsilon_\circ c^2} {\sin\theta \over r} e^{j\left(\omega t-{\omega\over c}r\right)}\,</math> | ::<math>dE_\theta(t)={-d\ell j\omega \over 4\pi\varepsilon_\circ c^2} {\sin\theta \over r} e^{j\left(\omega t-{\omega\over c}r\right)}\,</math> | ||
तारों द्वारा निर्मित एंटीना द्वारा विकीर्ण विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र विद्युत धारा के सभी छोटे तत्वों द्वारा विकिरित सभी विद्युत क्षेत्रों का योग होता है। यह जोड़ इस तथ्य से जटिल है कि प्रत्येक विद्युत क्षेत्र की दिशा और प्रावस्था सामान्य रूप से भिन्न होते हैं। | तारों द्वारा निर्मित एंटीना द्वारा विकीर्ण विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र विद्युत धारा के सभी छोटे तत्वों द्वारा विकिरित सभी विद्युत क्षेत्रों का योग होता है। यह जोड़ इस तथ्य से जटिल है कि प्रत्येक विद्युत क्षेत्र की दिशा और प्रावस्था सामान्य रूप से भिन्न होते हैं। | ||
== | == अभिग्रहण में एंटीना मापदंडों की गणना == | ||
किसी दिए गए दिशा में | किसी दिए गए दिशा में लब्धि और दी गई [[आवृत्ति]] पर प्रतिबाधा समान होती है जब ऐन्टेना का उपयोग संचरण या अभिग्रहण में किया जाता है। | ||
विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र सभी विद्युत | विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र सभी विद्युत संचालकों में प्रत्येक छोटे खंड में छोटे से [[वोल्टेज|विद्युत दाब]] को प्रेरित करता है। प्रेरित विद्युत दाब विद्युत क्षेत्र और संचालक की लंबाई पर निर्भर करता है। विद्युत दाब खंड और विद्युत क्षेत्र के सापेक्ष अभिविन्यास पर भी निर्भर करता है। | ||
प्रत्येक छोटा | प्रत्येक छोटा विद्युत दाब धारा को प्रेरित करता है और ये धाराएं ऐन्टेना विद्युत प्रतिबाधा के छोटे से भाग के माध्यम से प्रसारित होती हैं। उन सभी धाराओं और विभव का परिणाम सन्निकट से बहुत दूर है। हालांकि, [[पारस्परिकता (विद्युत चुंबकत्व)]] का उपयोग करके, यह प्रमाणित करना संभव है कि अभिग्राही एंटीना के थेवेनिन समकक्ष परिपथ है: | ||
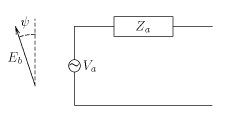
[[Image:Equiv-receiv-antenna.jpg|left|अभिग्राही ऐन्टेना का समतुल्य परिपथ।]] | [[Image:Equiv-receiv-antenna.jpg|left|अभिग्राही ऐन्टेना का समतुल्य परिपथ।]] | ||
<math>V_a={\sqrt{R_a\ G_a\ } \lambda \cos \psi\over2\sqrt{\pi Z_\circ}}E_b</math> | <math>V_a={\sqrt{R_a\ G_a\ } \lambda \cos \psi\over2\sqrt{\pi Z_\circ}}E_b</math> | ||
*<math>\scriptstyle{V_a}</math> थेवेनिन समतुल्य परिपथ | *<math>\scriptstyle{V_a}</math> थेवेनिन समतुल्य परिपथ विभव है। | ||
*<math>\scriptstyle{Z_a}</math> थेवेनिन समकक्ष | *<math>\scriptstyle{Z_a}</math> थेवेनिन समकक्ष परिपथ प्रतिबाधा है और ऐन्टेना प्रतिबाधा के समान है। | ||
*<math>\scriptstyle{R_a}</math> ऐन्टेना प्रतिबाधा की श्रृंखला प्रतिरोधक | *<math>\scriptstyle{R_a}</math> ऐन्टेना प्रतिबाधा की श्रृंखला प्रतिरोधक <math>\scriptstyle{Z_a}\,</math> भाग है। | ||
*<math>\scriptstyle{G_a}</math> विद्युत चुम्बकीय तरंगों के आगमन की दिशा में ऐन्टेना (उत्सर्जन के समान) का प्रत्यक्ष | *<math>\scriptstyle{G_a}</math> विद्युत चुम्बकीय तरंगों के आगमन की दिशा में ऐन्टेना (उत्सर्जन के समान) का प्रत्यक्ष वृद्धि है। | ||
*<math>\scriptstyle{\lambda}</math> तरंग दैर्ध्य है। | *<math>\scriptstyle{\lambda}</math> तरंग दैर्ध्य है। | ||
*<math>\scriptstyle{E_b}</math> आने वाली विद्युत चुम्बकीय तरंग के विद्युत क्षेत्र का परिमाण है। | *<math>\scriptstyle{E_b}</math> आने वाली विद्युत चुम्बकीय तरंग के विद्युत क्षेत्र का परिमाण है। | ||
*<math>\scriptstyle{\psi}</math> ऐन्टेना के साथ आने वाली तरंग के विद्युत क्षेत्र के गलत संरेखण का कोण है। | *<math>\scriptstyle{\psi}</math> ऐन्टेना के साथ आने वाली तरंग के विद्युत क्षेत्र के गलत संरेखण का कोण है। द्विध्रुवीय ऐन्टेना के लिए, अधिकतम प्रेरित विद्युत दाब तब प्राप्त होता है जब विद्युत क्षेत्र द्विध्रुव के समानांतर होता है। यदि ऐसा नहीं होता है और वे कोण <math>\scriptstyle{\psi}</math> द्वारा गलत संरेखित होते हैं प्रेरित विद्युत दाब <math>\scriptstyle{\cos\psi}</math> से गुणा किया जाएगा। | ||
* <math> \scriptstyle{Z_\circ=\sqrt{{\mu_\circ \over \varepsilon_\circ}}= 376.730313461\ \Omega}</math> | * <math> \scriptstyle{Z_\circ=\sqrt{{\mu_\circ \over \varepsilon_\circ}}= 376.730313461\ \Omega}</math> सार्वभौमिक स्थिरांक है जिसे निर्वात प्रतिबाधा या मुक्त आकाशीय प्रतिबाधा कहा जाता है। | ||
किसी भी प्रकार के एंटीना के लिए समतुल्य | किसी भी प्रकार के एंटीना के लिए समतुल्य परिपथ और दाईं ओर सूत्र मान्य हैं। यह द्विध्रुवीय एंटीना, [[पाश एंटीना]], परवलयिक एंटीना या [[एंटीना सरणी (विद्युत चुम्बकीय)]] भी हो सकता है। | ||
इस सूत्र से निम्नलिखित परिभाषाओं को सिद्ध करना आसान है: | इस सूत्र से निम्नलिखित परिभाषाओं को सिद्ध करना आसान है: | ||
:: एंटीना प्रभावी लंबाई<math> = \displaystyle{{{\sqrt{R_aG_a}\lambda\cos\psi\over\sqrt{\pi Z_\circ}}}} \,</math> | :: एंटीना प्रभावी लंबाई<math> = \displaystyle{{{\sqrt{R_aG_a}\lambda\cos\psi\over\sqrt{\pi Z_\circ}}}} \,</math> | ||
वह लंबाई है, जिसे प्राप्त तरंग के विद्युत क्षेत्र से गुणा करके, थेवेनिन समकक्ष एंटीना | वह लंबाई है, जिसे प्राप्त तरंग के विद्युत क्षेत्र से गुणा करके, थेवेनिन समकक्ष एंटीना परिपथ का विद्युत दाब दिया जाता है। | ||
:: अधिकतम उपलब्ध शक्ति<math>=\displaystyle{{G_a\lambda^2\over 4\pi Z_\circ}E_b^2} \,</math> | :: अधिकतम उपलब्ध शक्ति<math>=\displaystyle{{G_a\lambda^2\over 4\pi Z_\circ}E_b^2} \,</math> | ||
अधिकतम शक्ति है जो | अधिकतम शक्ति है जो एंटीना आने वाली विद्युत चुम्बकीय तरंग से निकाल सकता है। | ||
:: | :: अनुप्रस्थ परिच्छेद या प्रभावी प्रग्रहण सतह<math> = \displaystyle{{G_a\over4\pi}\lambda^2} \,</math> | ||
वह सतह है जो आने वाली | वह सतह है जो आने वाली तरंग की प्रति इकाई सतह की शक्ति से गुणा करके अधिकतम उपलब्ध विद्युत देती है। | ||
विद्युत चुम्बकीय क्षेत्र से ऐन्टेना द्वारा निकाली जा सकने वाली अधिकतम शक्ति केवल ऐन्टेना के लाभ और वर्ग तरंग दैर्ध्य | विद्युत चुम्बकीय क्षेत्र से ऐन्टेना द्वारा निकाली जा सकने वाली अधिकतम शक्ति केवल ऐन्टेना के लाभ और वर्ग तरंग दैर्ध्य <math>\scriptstyle{\lambda}</math> पर निर्भर करती है, यह एंटीना के आयामों पर निर्भर नहीं करता है। | ||
समकक्ष | समकक्ष परिपथ का उपयोग करके, यह दिखाया जा सकता है कि एंटीना निवेश प्रतिबाधा से अनुरूप वाले भार के साथ समाप्त होने पर एंटीना द्वारा अधिकतम शक्ति अवशोषित हो जाती है। इसका तात्पर्य यह भी है कि समरूप वाली परिस्थितियों में, अभिग्राही एंटीना द्वारा पुन: विकिरित शक्ति की मात्रा अवशोषित शक्ति के समान होती है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[एंटीना मॉडलिंग]] | * [[एंटीना मॉडलिंग]] | ||
* मुक्त | * मुक्त आकाशीय | ||
* [[मुक्त स्थान का प्रतिबाधा]] | * [[मुक्त स्थान का प्रतिबाधा|मुक्त आकाशीय प्रतिबाधा]] | ||
* निकट और दूर का | * निकट और दूर का क्षेत्र | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 203: | Line 207: | ||
*{{cite magazine |last=Brown |first=F. W. |title=How to Measure Antenna Gain |date=November 1964 |magazine=[[CQ Amateur Radio|CQ]] |page=40}} | *{{cite magazine |last=Brown |first=F. W. |title=How to Measure Antenna Gain |date=November 1964 |magazine=[[CQ Amateur Radio|CQ]] |page=40}} | ||
{{DEFAULTSORT:Antenna Measurement}} | {{DEFAULTSORT:Antenna Measurement}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page|Antenna Measurement]] | ||
[[Category:Created On 24/03/2023]] | [[Category:Citation Style 1 templates|M]] | ||
[[Category:Collapse templates|Antenna Measurement]] | |||
[[Category:Created On 24/03/2023|Antenna Measurement]] | |||
[[Category:Lua-based templates|Antenna Measurement]] | |||
[[Category:Machine Translated Page|Antenna Measurement]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Antenna Measurement]] | |||
[[Category:Pages with script errors|Antenna Measurement]] | |||
[[Category:Short description with empty Wikidata description|Antenna Measurement]] | |||
[[Category:Sidebars with styles needing conversion|Antenna Measurement]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Antenna Measurement]] | |||
[[Category:Templates based on the Citation/CS1 Lua module|Antenna Measurement]] | |||
[[Category:Templates generating COinS|Cite magazine]] | |||
[[Category:Templates generating microformats|Antenna Measurement]] | |||
[[Category:Templates that add a tracking category|Antenna Measurement]] | |||
[[Category:Templates that are not mobile friendly|Antenna Measurement]] | |||
[[Category:Templates that generate short descriptions|Antenna Measurement]] | |||
[[Category:Templates using TemplateData|Antenna Measurement]] | |||
[[Category:Wikipedia fully protected templates|Cite magazine]] | |||
[[Category:Wikipedia metatemplates|Antenna Measurement]] | |||
[[Category:एंटेना (रेडियो)|Antenna Measurement]] | |||
Latest revision as of 16:10, 13 April 2023
एंटीना माप तकनीक एंटीना (रेडियो) के परीक्षण को संदर्भित करती है ताकि यह सुनिश्चित किया जा सके कि एंटीना विनिर्देशों को पूरा करती है या केवल इसे चिह्नित करने के लिए करते है। एंटेना के विशिष्ट पैरामीटर वृद्धि, बैंडविड्थ, विकिरण पैटर्न, किरण-पुंज विस्तार, ध्रुवीकरण (तरंगें), और प्रतिबाधा हैं।
ऐन्टेना पैटर्न किसी दिए गए दिशा से समतल तरंग की घटना के लिए ऐन्टेना की प्रतिक्रिया है या किसी दिए गए दिशा में ऐन्टेना द्वारा प्रेषित तरंग की सापेक्ष शक्ति घनत्व है। व्युत्क्रम ऐन्टेना के लिए, ये दो पैटर्न समान हैं। एंटीना पैटर्न मापन तकनीकों की समूह विकसित किया गया है। विकसित की गई पहली तकनीक सुदूर-क्षेत्र की परास थी, जहाँ परीक्षण के अंतर्गत एंटीना (एयूटी) को परास एंटीना के सुदूर-क्षेत्र में रखा जाता है। बड़े एंटेना के लिए सुदूर-क्षेत्र की परास बनाने के लिए आवश्यक आकार के कारण, निकट-क्षेत्र तकनीक विकसित की गई, जो ऐन्टेना के समीप की सतह पर क्षेत्र की माप की (सामान्य रूप से इसकी तरंग दैर्ध्य से 3 से 10 गुना होती है) स्वीकृति देती है। यह माप तब अनंत पर समान होने का अनुमान लगाया गया है। तीसरी सामान्य विधि सुसम्बद्ध परास है, जो परीक्षण के अंतर्गत एंटीना के पास क्षेत्र बनाने के लिए परावर्तक (एंटीना) का उपयोग करती है जो लगभग समतल तरंग की तरह दिखती है।
सुदूर-क्षेत्र परास (एफएफ)
सुदूर-क्षेत्र की परास मूल एंटीना माप तकनीक थी, और सबसे सरल थी; इसमें एंटीना को परीक्षण (एयूटी) के अंतर्गत यंत्र एंटीना से लंबी दूरी पर रखना सम्मिलित है। सामान्य रूप से, सुदूर-क्षेत्र की दूरी या फ्रौनहोफर दूरी माना जाता है
जहाँ किसी भी दिशा में एंटीना का सबसे चौड़ा व्यास है, और रेडियो तरंग की तरंग दैर्ध्य है।[1] इस दूरी से परीक्षण के अंतर्गत एंटीना और मानक अभिग्राही एंटीना को अलग करने से दूर दूरी में एंटीना पैटर्न का उपयुक्त परिशुद्ध अनुमान प्राप्त करने के लिए पर्याप्त परीक्षण के अंतर्गत एंटीना में पता लगाने योग्य चरण भिन्नता कम हो जाती है।
विद्युत और इलेक्ट्रॉनिक्स इंजीनियर संस्थान ऐन्टेना मापन मानक (दस्तावेज़ आईडी विद्युत और इलेक्ट्रॉनिक्स इंजीनियर संस्थान-सॉफ्टवेयर अभियांत्रिकी शब्दावली का मानक शब्दकोष-149-1979), सुदूर-क्षेत्र परास और ग्राउंड-बाउंस परास (नीचे चर्चा की गई) दोनों के लिए माप और विभिन्न तकनीकों के लिए व्यवस्था का सुझाव देता है।
निकट क्षेत्र परास (एनएफ)
समतलीय निकट क्षेत्र परास
समतलीय निकट क्षेत्र माप समतलीय सतह पर छोटे से अन्वेषी एंटीना को जांच करके आयोजित किया जाता है। इन मापों को फिर फूरियर रूपांतरण के उपयोग से या अधिक विशेष रूप से लाप्लास रूपांतरण के लिए स्थिर प्रावस्था के रूप में जाना जाने वाला एक तरीका प्रयुक्त करके दूर-क्षेत्र में परिवर्तित कर दिया जाता है।[2] निकट क्षेत्र मापन में तीन मूल प्रकार की समतलीय जांच सम्मिलित हैं।
आयताकार तलीय क्रमवीक्षण
अन्वेषी कार्तीय समन्वय प्रणाली में स्थानांतरण करती है और इसका रैखिक संचलन Δx = Δy = λ /2 की अधिकतम निकट-क्षेत्र प्रतिदर्श अंतराल के साथ नियमित आयताकार प्रतिदर्श ग्रिड बनाता है।
ध्रुवीय समतलीय क्रमवीक्षण
आयताकार क्रमवीक्षण विधि का अधिक जटिल समाधान समतल ध्रुवीय क्रमवीक्षण विधि है।
द्वि-ध्रुवीय तलीय क्रमवीक्षण
द्वि-ध्रुवीय तकनीक समतल ध्रुवीय विन्यास के समान है।
बेलनाकार निकट-क्षेत्र परास
बेलनाकार निकट-क्षेत्र परास परीक्षण के अंतर्गत एंटीना के समीप बेलनाकार सतह पर विद्युत क्षेत्र को मापती है। बेलनाकार हार्मोनिक्स का उपयोग इन मापों को सुदूर-क्षेत्र में परिवर्तित करने के लिए किया जाता है।
गोलाकार निकट-क्षेत्र परास
गोलाकार निकट-क्षेत्र परास परीक्षण के अंतर्गत एंटीना के समीप गोलाकार सतह पर विद्युत क्षेत्र को मापती है। इन मापों को सुदूर-क्षेत्र में परिवर्तित करने के लिए गोलाकार हार्मोनिक्स का उपयोग किया जाता है
मुक्त आकाशीय परास
विद्युत चुम्बकीय विकिरण प्रसार और सूचना प्रसार का सूत्र है:
जहाँ D दूरी, P शक्ति और S गति को निरूपित करता है।
समीकरण का अर्थ है कि संचार दूरी को दोगुना करने के लिए चार गुना सामर्थ्य की आवश्यकता होती है। इसका अर्थ यह भी है कि दोहरी सामर्थ्य दोहरी संचार गति (बिट दर) की स्वीकृति देती है। दोहरी सामर्थ्य लगभग 3डेसीबल (या पूर्णतया 10×log10(2) ≈ 3.0103000 ) वृद्धि है। स्वभावतः, वास्तविक विश्व में सभी प्रकार की अन्य घटनाएं हैं जो अनुमानित वितरित शक्ति को जटिल बनाती हैं, जैसे फ्रेनल अस्वीकार करना, पथ हानि, पृष्ठ भूमि रव इत्यादि।
सुसम्बद्ध परास
सुसम्बद्ध एंटीना परीक्षण परास (सीएटीआर) सुविधा है जिसका उपयोग आवृति पर एंटीना प्रणाली के सुविधाजनक परीक्षण प्रदान करने के लिए किया जाता है जहां परीक्षण के अंतर्गत एंटीना के लिए सुदूर-क्षेत्र की दूरी प्राप्त करना पारंपरिक मुक्त आकाशीय विधियों का उपयोग करना असंभव होगा। इसका आविष्कार जॉर्जिया तकनीकी अनुसंधान संस्थान में रिचर्ड सी जॉनसन ने किया था।[3] सुसम्बद्ध एंटीना परीक्षण परास स्रोत एंटीना का उपयोग करता है जो गोलाकार तरंगाग्र और एक या एक से अधिक द्वितीयक परावर्तकों को विकिरण गोलाकार तरंगाग्र को वांछित परीक्षण क्षेत्र के अंदर समतलीय तरंगाग्र में मिलाने के लिए उपयोग करता है। इसे पूरा करने के लिए विशिष्ट अभिव्यक्ति शृंगी भरण एंटीना और परवलयिक परावर्तक का उपयोग करता है।
सुसम्बद्ध एंटीना परीक्षण परास का उपयोग सूक्ष्मतरंग और मिलीमीटर तरंग आवृत्तियों के लिए किया जाता है जहाँ सुदूर-क्षेत्र की दूरी बड़ी है, जैसे उच्च-वृद्धि परावर्तक एंटेना के साथ होती है। आवश्यक परास का आकार पूर्ण आकार के सुदूर-क्षेत्र के अप्रतिघ्वनिक कक्ष के लिए आवश्यक आकार से बहुत कम हो सकता है, हालांकि विशेष रूप से डिज़ाइन किए गए सुसम्बद्ध एंटीना परीक्षण परास परावर्तक के निर्माण की कीमत परिशुद्ध सुनिश्चित करने की आवश्यकता के कारण अधिक हो सकती है परावर्तक सतह (सामान्य रूप से से कम 1/100[[wavelength|λ]] RMS सतह परिशुद्धता) और विवर्तित तरंगों से संरक्षित करने के लिए विशेष रूप से परावर्तक के कोर का संशोधन करने के लिए जो वांछित किरण पैटर्न में अन्तः क्षेप कर सकते हैं।
उन्नत परास
उन्नत परास में, परीक्षण के अंतर्गत एंटीना और मापने वाले एंटीना दोनों को जमीन से परावर्तित तरंगों से अन्तः क्षेप को कम करने के साधन के रूप में जमीन के ऊपर कई तरंग दैर्ध्य पर चढ़ाया जाता है।
तिर्यक परास
तिर्यक् परास में, अभिग्राही एंटीना को परीक्षण के अंतर्गत एंटीना की तुलना में भू-तल से ऊपर लगाया जाता है या तो परास की पृथ्वी की सतह को परीक्षण के अंतर्गत एंटीना माउंट (धारक) से नीचे की ओर झुकाया जाता है या एंटीना को बहुत ऊंचे अवस्था पर रखा जाता है। झुकी हुई पृथ्वी (या तो वास्तविक या प्रभावी) अभिग्राही एंटीना के नीचे विकसित के लिए परावर्तित तरंगों को कोण बनाकर सममित तरंग प्रतिबिंब से अन्तः क्षेप को नष्ट करने या कम करने के उपकरण के रूप में कार्य करती है। सैद्धांतिक रूप में, समान तकनीक को अभिग्राही एंटीना के ऊपर पृथ्वी-परावर्तित अधिकांश तरंगों को विकसित करने के लिए प्रतिवर्त में प्रयुक्त किया जा सकता है।
एंटीना पैरामीटर
ध्रुवीकरण के अतिरिक्त, उपरोक्त पैरामीटरों में स्थायी तरंग अनुपात सबसे आसानी से मापा जाता है। प्रतिबाधा को विशेष उपकरणों से मापा जा सकता है, क्योंकि यह सम्मिश्र संख्या स्थायी तरंग अनुपात से संबंधित है। विकिरण पैटर्न को मापने के लिए महत्वपूर्ण स्थान-रिक्ति सहित परिष्कृत व्यवस्था (एंटीना के दूर क्षेत्र में संवेदित्र लगाने के लिए पर्याप्त है, या एंटीना माप के लिए डिज़ाइन किया गया अप्रतिध्वनिक कक्ष), प्रयोग ज्यामिति का सावधानीपूर्वक अध्ययन, और माप के समय ऐन्टेना को घुमाने वाले विशेष माप उपकरण की आवश्यकता होती है।
विकिरण पैटर्न
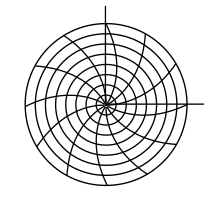
विकिरण पैटर्न ऐन्टेना द्वारा प्रेषित या प्राप्त सापेक्ष क्षेत्र सामर्थ्य का चित्रमय चित्रण है, और पार्श्व खण्ड और पश्च खंड दिखाता है। चूंकि ऐन्टेना अंतरिक्ष में विकीर्ण होते हैं, ऐन्टेना का वर्णन करने के लिए प्रायः कई वक्र आवश्यक होते हैं। यदि ऐन्टेना का विकिरण अक्ष के बारे में सममित है (जैसा कि द्विध्रुव, कुंडलित ऐन्टेना और कुछ परवलयिक ऐन्टेना में होता है) अद्वितीय ग्राफ पर्याप्त है।
प्रत्येक एंटीना आपूर्तिकर्ता/उपयोगकर्ता के पास अलग-अलग मानकों के साथ-साथ आलेखन प्रारूप भी होते हैं। प्रत्येक प्रारूप के अपने लाभ और हानि हैं। एंटीना के विकिरण पैटर्न को उन सभी बिंदुओं के स्थान के रूप में परिभाषित किया जा सकता है जहां प्रति इकाई सतह पर उत्सर्जित शक्ति समान होती है। प्रति इकाई सतह से निकलने वाली शक्ति विद्युत चुम्बकीय तरंग के वर्ग विद्युत क्षेत्र के समानुपाती होती है। विकिरण पैटर्न समान विद्युत क्षेत्र वाले बिंदुओं का स्थान है। इस प्रतिनिधित्व में, संदर्भ सामान्य रूप से उत्सर्जन का सबसे अच्छा कोण होता है। दिशा के कार्य के रूप में ऐन्टेना के प्रत्यक्ष लब्धि को चित्रित करना भी संभव है। प्राय: लब्धि को डेसीबल में दिया जाता है।
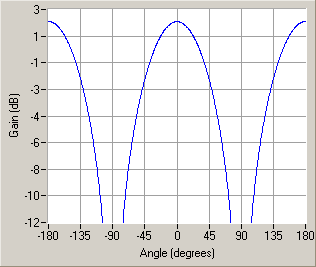
रेखांकन कार्तीय (आयताकार) निर्देशांक या एक ध्रुवीय भूखंड का उपयोग करके चित्रित किया जा सकता है। यह अंतिम बीमविड्थ (किरण-पुंज विस्तार) को मापने के लिए उपयोगी है, जो कि समागम द्वारा, अधिकतम लब्धि के आसपास -3डेसीबल बिंदुओं पर कोण है। कार्तीय या ध्रुवीय निर्देशांक में और लघुगणकीय पैमाने की सीमाओं के चयन के साथ वक्र का आकार बहुत भिन्न हो सकता है। नीचे दिए गए चार आरेखण समान अर्ध-तरंग ऐन्टेना के विकिरण पैटर्न हैं।
दक्षता
दक्षता एक एंटीना द्वारा वास्तव में विकीर्ण की गई शक्ति का संचारक से प्राप्त विद्युत शक्ति का अनुपात है। मूक भार में 1:1 का स्थायी तरंग अनुपात हो सकता है, लेकिन 0 की दक्षता, क्योंकि यह ऊष्मा उत्पन्न करने के लिए सभी आपतित शक्ति को अवशोषित करता है, लेकिन कोई रेडियो आवृत्ति ऊर्जा विकीर्ण नहीं करता है स्थायी तरंग अनुपात ऐन्टेना की दक्षता का माप नहीं है। विकिरण प्रतिरोध ऐन्टेना द्वारा विकिरण के लिए नष्ट की गई शक्ति के कारण होने वाले विद्युत के प्रतिरोध का भाग है। दुर्भाग्य से, इसे प्रत्यक्ष रूप से मापा नहीं जा सकता है लेकिन कुल विद्युत प्रतिरोध का घटक है जिसमें हानि प्रतिरोध सम्मिलित है। हानि प्रतिरोध सुसंगत रेडियो तरंगों के अतिरिक्त ऐन्टेना सामग्री में ऊष्मा के लिए नष्ट हुई शक्ति का परिणाम है, इस प्रकार दक्षता कम हो जाती है। दक्षता () को रेडियो तरंगों () के रूप में सुसंगत रूप से विकिरित शक्ति के अनुपात के रूप में परिभाषित किया गया है। एंटीना द्वारा उपयोग की जाने वाली कुल शक्ति के लिए, जो सुसंगत रूप से विकिरित शक्ति () और उष्मा के रूप में विकिरित शक्ति () का योग होता है:
ऐन्टेना दक्षता भी गणितीय रूप से विकिरण प्रतिरोध () के समान होती है, जो कुल प्रतिरोध (विद्युत-दाब बिन्दु पर मापी गई प्रतिबाधा का वास्तविक भाग, जो प्रायः प्रभरण बिंदु होता है) से विभाजित होती है:
बैंडविड्थ
विद्युत और इलेक्ट्रॉनिक्स इंजीनियर संस्थान (आईईईई) बैंडविड्थ को आवृत्तियों की परास के रूप में परिभाषित करता है जिसके अंदर ऐन्टेना का प्रदर्शन, कुछ विशेषताओं के संबंध में, निर्दिष्ट मानक के अनुरूप होता है।[4] दूसरे शब्दों में, बैंडविड्थ आवृत्तियों की श्रृंखला के माध्यम से ऐन्टेना की समग्र प्रभावशीलता पर निर्भर करता है, इसलिए इन सभी मापदंडों को एंटीना की बैंडविड्थ समर्थता को पूरी तरह से समझने के लिए समझा जाना चाहिए। यह परिभाषा व्यावहारिक परिभाषा के रूप में काम कर सकती है, हालांकि, व्यवहार में, बैंडविड्थ सामान्य रूप से प्रेरित की आवृत्ति विस्तार पर स्थायी तरंग अनुपात या विकीर्ण शक्ति जैसी विशेषता को मापकर निर्धारित की जाती है। उदाहरण के लिए, स्थायी तरंग अनुपात बैंडविड्थ सामान्य रूप से आवृत्ति विस्तार को मापकर निर्धारित किया जाता है जहाँ स्थायी तरंग अनुपात 2:1 से कम होता है। प्रतिध्वनित एंटेना के लिए बैंडविड्थ का निर्धारण करने के लिए और प्रायः उपयोग किया जाने वाला मान −3 dB परावर्तनिक हानि मान है, चूंकि स्थायी तरंग अनुपात के कारण हानि−10·log10(2÷1) = −3.01000 dB है।
दिशिकता
ऐन्टेना दिशिकता अधिकतम विकिरण तीव्रता (भौतिकी) (शक्ति प्रति इकाई सतह) का अनुपात है जो ऐन्टेना द्वारा अधिकतम दिशा में विकीर्ण होती है और परिकल्पित समदैशिक एंटीना द्वारा विकिरित तीव्रता से विभाजित होती है जो उस ऐन्टेना के समान समग्र शक्ति को विकीर्ण करती है। उदाहरण के लिए, परिकल्पनात्मक ऐन्टेना जिसमें गोलार्ध (1/2 गोला) का विकिरणित पैटर्न था, उसकी 2 की दिशिकता होगी। दिशिकता आयाम रहित अनुपात है और इसे संख्यात्मक रूप से या डेसिबल (डीबी) में व्यक्त किया जा सकता है। दिशिकता निर्देश लब्धि के शिखर मान के समान है; इन मानो को एंटीना दक्षता के संबंध में निर्दिष्ट किए बिना निर्दिष्ट किया जाता है, इस प्रकार शक्ति लब्धि (या केवल "लब्धि") से भिन्न होता है जिसका मूल्य एंटीना की दक्षता से कम हो जाता है।
लब्धि
लब्धि पैरामीटर के रूप में किसी दिए गए एंटीना की दिशिकता को मापता है। कम लब्धि वाला एंटीना सभी दिशाओं में समान रूप से विकिरण उत्सर्जित करता है, जबकि एक उच्च-लब्धि एंटीना विशेष दिशाओं में अधिमानतः विकीर्ण होगा। एक परिकल्पित समदैशिक एंटीना द्वारा समान दूरी पर विकिरणित प्रबलता (भौतिकी) से विभाजित यादृच्छिक दूरी पर एंटीना द्वारा दी गई दिशा में तीव्रता (शक्ति प्रति इकाई सतह) के अनुपात के रूप में परिभाषित किया गया है। :
हम ''परिकल्पनात्मक'' लिखते हैं क्योंकि पूर्ण समदैशिक एंटीना का निर्माण नहीं किया जा सकता है। लब्धि आयामहीन संख्या (इकाइयों के बिना) है।
ऐन्टेना का लाभ निष्क्रिय घटना है - ऐन्टेना द्वारा विद्युत नहीं जोड़ी जाती है, लेकिन समदैशिक ऐन्टेना द्वारा प्रेषित की तुलना में निश्चित दिशा में अधिक विकीर्ण शक्ति प्रदान करने के लिए सिर्फ पुनर्वितरित किया जाता है। यदि ऐन्टेना का कुछ दिशाओं में एक से अधिक वृद्धि होती है, तो अन्य दिशाओं में इसकी वृद्धि एक से कम होनी चाहिए क्योंकि ऐन्टेना द्वारा ऊर्जा का संरक्षण किया जाता है। लब्धि निर्धारित करते समय एंटीना डिजाइनर को एंटीना के लिए अनुप्रयोग को ध्यान में रखना चाहिए। उच्च-लब्धि वाले एंटेना में लंबी दूरी और अपेक्षाकृत अधिकतम सिग्नल गुणवत्ता का लाभ होता है, लेकिन किसी विशेष दिशा में सावधानी से प्रयोजन होना चाहिए। कम लब्धि वाले एंटेना की परास कम होती है, लेकिन एंटीना का उन्मुखीकरण महत्वहीन होता है। उदाहरण के लिए, अंतरिक्ष यान पर डिश एंटीना उच्च-लब्धि उपकरण है (प्रभावी होने के लिए ग्रह पर इंगित किया जाना चाहिए), जबकि लैपटॉप कंप्यूटर में विशिष्ट वाईफाई एंटीना कम-लब्धि होती है (जब तक आधार केंद्र परास के अंदर है), ऐन्टेना अंतरिक्ष में किसी भी अभिविन्यास में हो सकता है)।
भौतिक पृष्ठभूमि
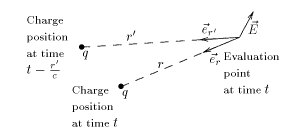
विद्युत आवेश द्वारा निर्मित विद्युत क्षेत्र है
जहाँ:
- निर्वात में प्रकाश की गति है।
- मुक्त आकाशीय की पारगम्यता है।
- प्रेक्षण बिंदु से दूरी (वह स्थान जहाँ का मूल्यांकन किया जाता है) उस बिंदु तक जहाँ आवेश सेकंड से पहले जब माप किया जाता है।
- अवलोकन बिंदु से निर्देशित इकाई वेक्टर है (वह स्थान जहां का मूल्यांकन किया जाता है) उस बिंदु तक जहाँ आवेश सेकंड से पहले जब माप किया जाता है।
इस सूत्र में "प्रवेशिका" प्रकट होती है क्योंकि विद्युत चुम्बकीय संकेत प्रकाश की गति से संचरण करता है। संकेतों को उस बिंदु से आने के रूप में देखा जाता है जहां वे उत्सर्जित हुए थे न कि उस बिंदु से जहां प्रेक्षण के समय उत्सर्जक है। जो तारे हम आकाश में देखते हैं वे अब वहां नहीं होते जहां हम उन्हें देखते हैं। हम उनकी वर्तमान स्थिति को भविष्य में देखेंगे; आज हम जिन तारों को देखते हैं उनमें से कुछ सम्मिलित नहीं हैं।
सूत्र में पहला शब्द मंदित समय के साथ सिर्फ विद्युत् स्थैतिक क्षेत्र है।
दूसरा शब्द ऐसा है जैसे कि प्रकृति इस तथ्य की स्वीकृति देने की प्रयास कर रही थी कि प्रभाव मंद (फेनमैन) है।
तीसरा शब्द एकमात्र ऐसा शब्द है जो एंटेना के सुदूर क्षेत्र के लिए अधीन है।
पहले दो पद समानुपातिक हैं। केवल तीसरा आनुपातिक है।
एंटीना के पास, सभी शर्तें महत्वपूर्ण हैं। हालाँकि, यदि दूरी अपेक्षाकृत अधिक बड़ी है, तो पहले दो पद नगण्य हो जाते हैं और केवल तीसरा शेष रहता है:
यदि आवेश q ज्यावक्रीय गति में आयाम और स्पंदन के साथ है, तो आवेश द्वारा विकिरित शक्ति है:
- वाट।
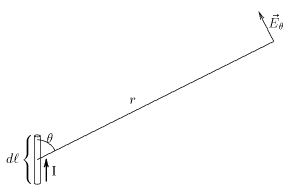
ध्यान दें कि विकिरणित शक्ति आवृत्ति की चतुर्थ शक्ति के समानुपाती होती है। कम आवृत्तियों की तुलना में उच्च आवृत्तियों पर विकीर्ण करना कहीं अधिक आसान है। यदि आवेशों की गति धाराओं के कारण होती है, तो यह दिखाया जा सकता है कि विद्युत क्षेत्र छोटी लंबाई द्वारा विकिरित (छोटा) विद्युत क्षेत्र एक संचालक का समय परिवर्ती धारा प्रवाहित करने वाला है
इस समीकरण के बाईं ओर संचालक की छोटी लंबाई से निकलने वाली विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र है। अनुक्रमणिका स्मरण कराता है कि क्षेत्र स्रोत की रेखा के लंबवत है। और h स्मरण कराता है कि यह प्रेक्षित क्षेत्र है सेकंड धारा व्युत्पन्न पर मूल्यांकन के बाद देखा गया है। कोण धारा की दिशा और उस बिंदु की दिशा के बीच का कोण है जहां क्षेत्र को मापा जाता है।
विद्युत क्षेत्र और विकीर्ण शक्ति वर्तमान तत्व के लंबवत विमान में अधिकतम होती है। वे धारा की दिशा में शून्य हैं।
केवल समय-परिवर्तनशील धाराएँ विद्युत चुम्बकीय शक्ति विकीर्ण करती हैं।
यदि धारा ज्यावक्रीय है, तो इसे जटिल रूप में लिखा जा सकता है, उसी तरह प्रतिबाधाओं के लिए उपयोग किया जाता है। केवल वास्तविक भाग भौतिक रूप से अर्थपूर्ण है:
जहाँ:
- धारा का आयाम है।
- कोणीय आवृत्ति है।
धारा के तत्व द्वारा विकीर्ण विद्युत चुम्बकीय तरंग का (छोटा) विद्युत क्षेत्र है:
और समय के लिए:
तारों द्वारा निर्मित एंटीना द्वारा विकीर्ण विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र विद्युत धारा के सभी छोटे तत्वों द्वारा विकिरित सभी विद्युत क्षेत्रों का योग होता है। यह जोड़ इस तथ्य से जटिल है कि प्रत्येक विद्युत क्षेत्र की दिशा और प्रावस्था सामान्य रूप से भिन्न होते हैं।
अभिग्रहण में एंटीना मापदंडों की गणना
किसी दिए गए दिशा में लब्धि और दी गई आवृत्ति पर प्रतिबाधा समान होती है जब ऐन्टेना का उपयोग संचरण या अभिग्रहण में किया जाता है।
विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र सभी विद्युत संचालकों में प्रत्येक छोटे खंड में छोटे से विद्युत दाब को प्रेरित करता है। प्रेरित विद्युत दाब विद्युत क्षेत्र और संचालक की लंबाई पर निर्भर करता है। विद्युत दाब खंड और विद्युत क्षेत्र के सापेक्ष अभिविन्यास पर भी निर्भर करता है।
प्रत्येक छोटा विद्युत दाब धारा को प्रेरित करता है और ये धाराएं ऐन्टेना विद्युत प्रतिबाधा के छोटे से भाग के माध्यम से प्रसारित होती हैं। उन सभी धाराओं और विभव का परिणाम सन्निकट से बहुत दूर है। हालांकि, पारस्परिकता (विद्युत चुंबकत्व) का उपयोग करके, यह प्रमाणित करना संभव है कि अभिग्राही एंटीना के थेवेनिन समकक्ष परिपथ है:
- थेवेनिन समतुल्य परिपथ विभव है।
- थेवेनिन समकक्ष परिपथ प्रतिबाधा है और ऐन्टेना प्रतिबाधा के समान है।
- ऐन्टेना प्रतिबाधा की श्रृंखला प्रतिरोधक भाग है।
- विद्युत चुम्बकीय तरंगों के आगमन की दिशा में ऐन्टेना (उत्सर्जन के समान) का प्रत्यक्ष वृद्धि है।
- तरंग दैर्ध्य है।
- आने वाली विद्युत चुम्बकीय तरंग के विद्युत क्षेत्र का परिमाण है।
- ऐन्टेना के साथ आने वाली तरंग के विद्युत क्षेत्र के गलत संरेखण का कोण है। द्विध्रुवीय ऐन्टेना के लिए, अधिकतम प्रेरित विद्युत दाब तब प्राप्त होता है जब विद्युत क्षेत्र द्विध्रुव के समानांतर होता है। यदि ऐसा नहीं होता है और वे कोण द्वारा गलत संरेखित होते हैं प्रेरित विद्युत दाब से गुणा किया जाएगा।
- सार्वभौमिक स्थिरांक है जिसे निर्वात प्रतिबाधा या मुक्त आकाशीय प्रतिबाधा कहा जाता है।
किसी भी प्रकार के एंटीना के लिए समतुल्य परिपथ और दाईं ओर सूत्र मान्य हैं। यह द्विध्रुवीय एंटीना, पाश एंटीना, परवलयिक एंटीना या एंटीना सरणी (विद्युत चुम्बकीय) भी हो सकता है।
इस सूत्र से निम्नलिखित परिभाषाओं को सिद्ध करना आसान है:
- एंटीना प्रभावी लंबाई
वह लंबाई है, जिसे प्राप्त तरंग के विद्युत क्षेत्र से गुणा करके, थेवेनिन समकक्ष एंटीना परिपथ का विद्युत दाब दिया जाता है।
- अधिकतम उपलब्ध शक्ति
अधिकतम शक्ति है जो एंटीना आने वाली विद्युत चुम्बकीय तरंग से निकाल सकता है।
- अनुप्रस्थ परिच्छेद या प्रभावी प्रग्रहण सतह
वह सतह है जो आने वाली तरंग की प्रति इकाई सतह की शक्ति से गुणा करके अधिकतम उपलब्ध विद्युत देती है।
विद्युत चुम्बकीय क्षेत्र से ऐन्टेना द्वारा निकाली जा सकने वाली अधिकतम शक्ति केवल ऐन्टेना के लाभ और वर्ग तरंग दैर्ध्य पर निर्भर करती है, यह एंटीना के आयामों पर निर्भर नहीं करता है।
समकक्ष परिपथ का उपयोग करके, यह दिखाया जा सकता है कि एंटीना निवेश प्रतिबाधा से अनुरूप वाले भार के साथ समाप्त होने पर एंटीना द्वारा अधिकतम शक्ति अवशोषित हो जाती है। इसका तात्पर्य यह भी है कि समरूप वाली परिस्थितियों में, अभिग्राही एंटीना द्वारा पुन: विकिरित शक्ति की मात्रा अवशोषित शक्ति के समान होती है।
यह भी देखें
- एंटीना मॉडलिंग
- मुक्त आकाशीय
- मुक्त आकाशीय प्रतिबाधा
- निकट और दूर का क्षेत्र
संदर्भ
- ↑ Balanis, C.A. (2005). Antenna Theory: Analysis and design (3rd ed.). Wiley Interscience.
- ↑ Asymptotic Behavior of Monodromy, Springer Berlin / Heidelberg, 1991, ISBN 978-3-540-55009-9
- ↑ McLees, Lea. "जीटीआरआई एंटीना विशेषज्ञ और इंजीनियरिंग मेंटर का निधन". The Whistle (obituary). Georgia Institute of Technology. Retrieved 2011-11-09.
- ↑ एंटेना के लिए शर्तों की IEEE मानक परिभाषाएँ (Report). IEEE. June 1993. pp. 6, 21. IEEE Std 145-1993.
अग्रिम पठन
- Brown, F. W. (November 1964). "How to Measure Antenna Gain". CQ. p. 40.