इलेक्ट्रॉनिक बैंड संरचना

ठोस भौतिकी अवस्था में, एक ठोस की इलेक्ट्रॉनिक बैंड संरचना (या बस बैंड संरचना) ऊर्जा स्तरों की सीमा का वर्णन करती है जो इलेक्ट्रॉनों के भीतर निहित होती है, साथ ही साथ ऊर्जा की सीमाएं भी हैं जो उनके पास नहीं होती हैं (उन्हें बैंड गैप्स कहा जाता है या निषिद्ध बैंड (forbidden bands))।

बैंड सिद्धांत (Band theory) इन बैंडों और बैंड अंतराल को प्राप्त करता है, जो परमाणुओं या अणुओं के एक बड़े, आवधिक जाली (periodic lattice) में एक इलेक्ट्रॉन के लिए अनुमत क्वांटम यांत्रिक तरंग कार्यों (wave functions) की जांच करता है। बैंड सिद्धांत (Band Theory) का सफलतापूर्वक उपयोग ठोस पदार्थों के कई भौतिक गुणों को समझाने के लिए किया गया है, जैसे कि विद्युत प्रतिरोधकता (electrical resistivity) और ऑप्टिकल अवशोषण (optical absorption), और सभी सॉलिड स्टेट डिवाइसेस (solid-state devices) की समझ की नींव बनाता है। जहाँ सॉलिड स्टेट डिवाइसेस से तात्पर्य ट्रांजिस्टर, सोलर सेल आदि से है।

क्यों बैंड और बैंड अंतराल होते हैं (Why bands and band gaps occur)

बड़ी संख्या में कार्बन परमाणुओं का एक काल्पनिक उदाहरण एक हीरे के क्रिस्टल को बनाने के लिए एक साथ लाया जा रहा है, जो इलेक्ट्रॉनिक बैंड संरचना के गठन का प्रदर्शन करता है। सही ग्राफ परमाणुओं के बीच रिक्ति के एक समारोह के रूप में ऊर्जा के स्तर को दिखाता है। जब बहुत दूर (ग्राफ के दाईं ओर) सभी परमाणुओं में एक ही ऊर्जा के साथ असतत वैलेंस ऑर्बिटल्स पी और एस होता है। हालांकि, जब परमाणु करीब आते हैं (बाईं ओर), उनके इलेक्ट्रॉन ऑर्बिटल्स स्थानिक रूप से ओवरलैप होने लगते हैं। ऑर्बिटल्स हाइब्रिडाइज़ करते हैं, और प्रत्येक परमाणु स्तर अलग -अलग ऊर्जाओं के साथ n स्तरों में विभाजित होता है, जहां n परमाणुओं की संख्या है। चूंकि n एक मैक्रोस्कोपिक आकार के क्रिस्टल में एक बहुत बड़ी संख्या है, इसलिए आसन्न स्तर ऊर्जावान रूप से एक साथ करीब हैं, प्रभावी रूप से एक निरंतर ऊर्जा बैंड बनाते हैं। वास्तविक डायमंड क्रिस्टल सेल आकार (ए द्वारा निरूपित) में, दो बैंड बनते हैं, जिसे वैलेंस और कंडक्शन बैंड कहा जाता है, जिसे 5.5 & nbsp; EV बैंड गैप द्वारा अलग किया जाता है। अंतर-परमाणु रिक्ति को और भी अधिक (जैसे, एक उच्च दबाव के तहत) कम करना बैंड संरचना को और संशोधित करता है।

बैंड के गठन का एनीमेशन और कैसे इलेक्ट्रॉनों ने उन्हें एक धातु और एक इन्सुलेटर में भर दिया

एक एकल पृथक परमाणु के इलेक्ट्रॉनों पर परमाणु ऑर्बिटल्स (atomic orbitals) पर कब्जा कर लेते है, जिनमें से प्रत्येक में असतत ऊर्जा स्तर (discrete energy level) होता है। जब दो या दो से अधिक परमाणु एक अणु (molecule) बनाने के लिए एक साथ जुड़ते हैं, तो उनके परमाणु ऑर्बिटल्स (atomic orbitals) ओवरलैप (overlap) और संकरण (hybridize) करते हैं।

इसी तरह, यदि समान परमाणुओं की एक बड़ी संख्या एक ठोस बनाने के लिए एक साथ आती है, जैसे कि एक क्रिस्टल जाली (crystal lattice), परमाणुओं के परमाणु ऑर्बिटल्स (atomic orbitals) पास के ऑर्बिटल्स के साथ ओवरलैप (overlap) करते हैं। प्रत्येक असतत ऊर्जा स्तर (discrete energy level) एन (N) स्तरों में विभाजित होता है, प्रत्येक एक अलग ऊर्जा के साथ। चूंकि ठोस के एक मैक्रोस्कोपिक टुकड़े (macroscopic piece) में परमाणुओं की संख्या एक बहुत बड़ी संख्या है (n ~ 10²² ) ऑर्बिटल्स की संख्या बहुत बड़ी है और इस प्रकार वे ऊर्जा में बहुत बारीकी से फैले हुए हैं (10⁻²² -eV के क्रम में)। आसन्न स्तरों की ऊर्जा एक साथ इतनी करीब है कि उन्हें एक निरंतरता (continuum), एक ऊर्जा बैंड (energy band) के रूप में माना जा सकता है।

बैंड का यह गठन ज्यादातर परमाणु में सबसे बाहरी इलेक्ट्रॉनों (वैलेंस इलेक्ट्रॉनों) की एक विशेषता है, जो रासायनिक संबंध (chemical bonding) और विद्युत चालकता (electrical conductivity) में शामिल हैं। आंतरिक इलेक्ट्रॉन ऑर्बिटल्स (inner electron orbitals) एक महत्वपूर्ण डिग्री (significant degree) तक ओवरलैप नहीं करते हैं, इसलिए उनके बैंड बहुत संकीर्ण होते हैं।

बैंड अंतराल (Band gaps) अनिवार्य रूप से ऊर्जा के किसी भी बैंड द्वारा कवर नहीं किए गए ऊर्जा के बचे हुए रेंज हैं, जो ऊर्जा बैंड की परिमित चौड़ाई (finite widths) का परिणाम है। बैंड में अलग -अलग चौड़ाई होती है, जिसमें परमाणु ऑर्बिटल्स में ओवरलैप की डिग्री के आधार पर चौड़ाई होती है, जिसमें से वे उत्पन्न होते हैं। दो आसन्न बैंड (Two adjacent bands) केवल ऊर्जा की सीमा (range of energy) को पूरी तरह से कवर करने के लिए पर्याप्त व्यापक (wide enough) नहीं हो सकते हैं। उदाहरण के लिए, कोर ऑर्बिटल्स (core orbitals) (जैसे 1s electrons) से जुड़े बैंड आसन्न परमाणुओं (adjacent atoms) के बीच छोटे ओवरलैप के कारण बेहद संकीर्ण हैं। नतीजतन, कोर बैंड (core bands) के बीच बड़े बैंड अंतराल (large band gaps) होते हैं। उच्च बैंड में अधिक ओवरलैप के साथ तुलनात्मक रूप से बड़े ऑर्बिटल्स शामिल होते हैं, उच्च ऊर्जा पर उत्तरोत्तर व्यापक (progressively wider) हो जाते हैं ताकि उच्च ऊर्जा पर कोई बैंड अंतराल (band gaps) न हो।

बुनियादी अवधारणाएं

मान्यताओं और बैंड संरचना सिद्धांत की सीमाएँ

बैंड सिद्धांत केवल एक ठोस के क्वांटम स्थिति के लिए एक अनुमान है, जो एक साथ बंधे कई समान परमाणुओं या अणुओं से युक्त ठोस पदार्थों पर लागू होता है।ये बैंड सिद्धांत को मान्य होने के लिए आवश्यक धारणाएं हैं:

• अनंत आकार की प्रणाली: बैंड के निरंतर होने के लिए, सामग्री के टुकड़े में बड़ी संख्या में परमाणु शामिल होने चाहिए।चूंकि सामग्री का एक मैक्रोस्कोपिक टुकड़ा 10 के क्रम पर होता है²² परमाणु, यह एक गंभीर प्रतिबंध नहीं है; बैंड सिद्धांत भी एकीकृत सर्किट में सूक्ष्म आकार के ट्रांजिस्टर पर लागू होता है। संशोधनों के साथ, बैंड संरचना की अवधारणा को उन प्रणालियों तक भी बढ़ाया जा सकता है जो केवल कुछ आयामों के साथ बड़े होते हैं, जैसे कि 2deg | दो-आयामी इलेक्ट्रॉन सिस्टम।
• सजातीय प्रणाली: बैंड संरचना एक सामग्री की एक आंतरिक संपत्ति है, जो मानता है कि सामग्री सजातीय है। व्यावहारिक रूप से, इसका मतलब है कि सामग्री का रासायनिक मेकअप पूरे टुकड़े में समान होना चाहिए।
• गैर-अंतःक्रिया: बैंड संरचना एकल इलेक्ट्रॉन राज्यों का वर्णन करती है। इन राज्यों का अस्तित्व यह मानता है कि इलेक्ट्रॉन एक स्थिर क्षमता में यात्रा करते हैं, बिना गतिशील रूप से जाली कंपन, अन्य इलेक्ट्रॉनों, फोटॉन, आदि के साथ बातचीत के बिना यात्रा करते हैं।

उपरोक्त मान्यताओं को कई महत्वपूर्ण व्यावहारिक स्थितियों में तोड़ा गया है, और बैंड संरचना के उपयोग को बैंड सिद्धांत की सीमाओं पर एक करीबी चेक रखने की आवश्यकता होती है:

• अमानवीयता और इंटरफेस: सतहों, जंक्शनों और अन्य अमानवीयता के पास, थोक बैंड संरचना बाधित है। न केवल स्थानीय छोटे पैमाने पर व्यवधान हैं (जैसे, सतह राज्य या बैंड गैप के अंदर डोपेंट राज्य), बल्कि स्थानीय चार्ज असंतुलन भी हैं। इन चार्ज असंतुलन में इलेक्ट्रोस्टैटिक प्रभाव होते हैं जो अर्धचालक, इंसुलेटर और वैक्यूम (डोपिंग, बैंड झुकने वाले) में गहराई से विस्तारित होते हैं।
• एक ही पंक्तियों के साथ, अधिकांश इलेक्ट्रॉनिक प्रभाव (कैपेसिटेंस, इलेक्ट्रिकल कंडक्टेंस, इलेक्ट्रिक-फील्ड स्क्रीनिंग) में सतहों और/या पास के इंटरफेस से गुजरने वाले इलेक्ट्रॉनों की भौतिकी शामिल होती है। इन प्रभावों का पूरा विवरण, एक बैंड संरचना चित्र में, इलेक्ट्रॉन-इलेक्ट्रॉन इंटरैक्शन के कम से कम एक अल्पविकसित मॉडल की आवश्यकता होती है (देखें अंतरिक्ष चार्ज, बैंड झुकने)।
• छोटे सिस्टम: उन प्रणालियों के लिए जो हर आयाम के साथ छोटे होते हैं (जैसे, एक छोटा अणु या एक क्वांटम डॉट), कोई निरंतर बैंड संरचना नहीं है। छोटे और बड़े आयामों के बीच क्रॉसओवर मेसोस्कोपिक भौतिकी का दायरा है।
• दृढ़ता से सहसंबद्ध सामग्री (उदाहरण के लिए, mott insulators) को केवल एकल-इलेक्ट्रॉन राज्यों के संदर्भ में समझा नहीं जा सकता है। इन सामग्रियों के इलेक्ट्रॉनिक बैंड संरचनाओं को खराब रूप से परिभाषित किया गया है (या कम से कम, विशिष्ट रूप से परिभाषित नहीं) और उनकी भौतिक स्थिति के बारे में उपयोगी जानकारी प्रदान नहीं कर सकते हैं।

क्रिस्टलीय समरूपता और वेववेक्टर (rystalline symmetry and wavevectors

)

अंजीर 1. विशेष समरूपता बिंदुओं के लिए लेबल दिखाते हुए एक चेहरे-केंद्रित क्यूबिक जाली का ब्रिलॉइन ज़ोन।

अंजीर 2. एसआई, जीई, जीएएएस और इनस के लिए बैंड संरचना प्लॉट तंग बाध्यकारी मॉडल के साथ उत्पन्न।ध्यान दें कि SI और GE अप्रत्यक्ष बैंड गैप सामग्री हैं, जबकि GAAS और INAs प्रत्यक्ष हैं।

Main articles: Bloch's theorem and Brillouin zone

See also: Symmetry in physics, Crystallographic point group, and Space group

बैंड संरचना गणना एक क्रिस्टल जाली (crystal lattice) की आवधिक प्रकृति (periodic nature) का लाभ उठाती है, इसकी समरूपता का शोषण (exploiting its symmetry) करती है। सिंगल-इलेक्ट्रॉन श्रोडिंगर समीकरण (Schrödinger equation) एक जाली-आवासीय क्षमता (lattice-periodic potential) में एक इलेक्ट्रॉन के लिए हल किया जाता है, जिससे ब्लोच इलेक्ट्रॉनों (Bloch electrons) को समाधान के रूप में दिया जाता है

$\psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} )$,

जहां k को वेववेक्टर (wavevector) कहा जाता है। K के प्रत्येक मान के लिए, बैंड इंडेक्स (band index) n द्वारा लेबल (labelled) किए गए श्रोडिंगर समीकरण (Schrödinger equation) के कई समाधान हैं, जो केवल ऊर्जा बैंड की संख्या में हैं। इन ऊर्जा स्तरों में से प्रत्येक K में परिवर्तन के साथ सुचारू रूप से विकसित होता है, जिससे अवस्था का एक सहज बैंड (smooth band of states) बनता है। प्रत्येक बैंड के लिए हम एक फ़ंक्शन को परिभाषित कर सकते हैं ई _n(के) (E_n(k)), जो उस बैंड में इलेक्ट्रॉनों के लिए फैलाव संबंध (dispersion relation) है।

वेववेक्टर (WaveVector),ब्रिलियन ज़ोन (Brillouin zone) के अंदर किसी भी मूल्य पर ले जाता है, जो कि वेववेक्टर (WaveVector) (पारस्परिक जाली)/(reciprocal lattice) स्थान में एक पॉलीहेड्रॉन (polyhedron) है जो क्रिस्टल की जाली से संबंधित है। ब्रिलियन ज़ोन (Brillouin zone) के बाहर वेववेक्टर (WaveVector) केवल उन अवस्थाओं के अनुरूप हैं जो ब्रिलियन ज़ोन (Brillouin zone) के भीतर उन अवस्थाओं के लिए भौतिक रूप से समान हैं। ब्रिलियन ज़ोन (Brillouin zone) में विशेष उच्च समरूपता बिंदु/रेखाएँ (symmetry points/lines) γ, Δ, λ, σ (चित्र 1 देखें) जैसे लेबल दिये गए हैं।

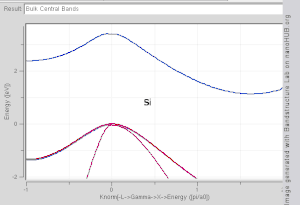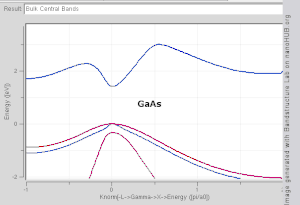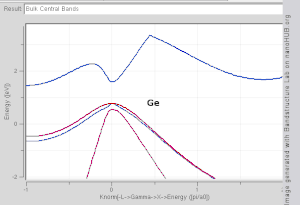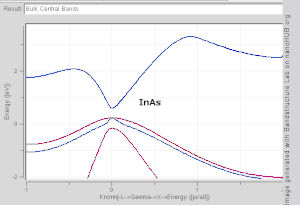
वेववेक्टर (WaveVector) के एक फलन के रूप में एक बैंड के आकार की कल्पना करना मुश्किल है, क्योंकि इसमें चार-आयामी स्थान (plot in four-dimensional space) में एक भूखंड की आवश्यकता होगी, E vs. k_x, k_y, k_{z,विज्ञान}साहित्य में 'बैंड संरचना भूखंडों' (band structure plots) को देखना सामान्य है जो E_n(k) के मानों (values) को दर्शाता है। बैंड संरचना को देखने के लिए एक और विधि, वेववेक्टर स्पेस (wavevector space) में एक निरंतर-ऊर्जा आइसोसुरफेस (constant-energy isosurface) की साजिश करना है, जो किसी विशेष मूल्य के बराबर ऊर्जा के साथ अवस्थाओं को दिखाता है। फर्मी स्तर (Fermi level) के बराबर ऊर्जा वाले राज्यों का आइसोसुरफेस (isosurface) को फर्मी सतह (Fermi level) के रूप में जाना जाता है।

बैंड गैप (band gap) के आसपास के अवस्थाओं के वेववेक्टर (WaveVector) का उपयोग करके ऊर्जा बैंड अंतराल (Energy band gaps) को वर्गीकृत किया जा सकता है:

• डायरेक्ट बैंड गैप: बैंड गैप के ऊपर निम्नतम-ऊर्जा अवस्था में k वही होता है जो बैंड गैप के नीचे उच्चतम-ऊर्जा अवस्था होती है।
• अप्रत्यक्ष बैंड गैप: बैंड गैप के ऊपर और नीचे की निकटतम अवस्थाओं में k का मान समान नहीं होता है।

विषमता: गैर-क्रिस्टलीय ठोस पदार्थों में बैंड संरचनाएं (Asymmetry: Band structures in non-crystalline solids)

यद्यपि इलेक्ट्रॉनिक बैंड संरचनाएं आमतौर पर क्रिस्टलीय (crystalline) सामग्री से जुड़ी होती हैं, क्वासी-क्रिस्टलीय (quasi-crystalline) और अनाकार ठोस (amorphous solids) भी बैंड अंतराल का प्रदर्शन कर सकते हैं। ये अध्ययन करने के लिए सैद्धांतिक रूप से कुछ अधिक कठिन हैं क्योंकि उनके पास एक क्रिस्टल की सरल समरूपता (simple symmetry of a crystal) की कमी है, और सामान्यतया एक सटीक फैलाव संबंध (precise dispersion relation) निर्धारित करना संभव नहीं है। नतीजतन, ठोस पदार्थों के इलेक्ट्रॉनिक बैंड संरचना पर लगभग सभी मौजूदा सैद्धांतिक कार्य (existing theoretical work) ने क्रिस्टलीय सामग्रियों (crystalline materials) पर ध्यान केंद्रित किया है।

अवस्था का घनत्व (Density of states)

Main article: Density of states

स्टेट्स फ़ंक्शन (states function) g(E) के घनत्व को E के निकट इलेक्ट्रॉन ऊर्जा के लिए प्रति इकाई आयतन, प्रति इकाई ऊर्जा में इलेक्ट्रॉनिक अवस्थाओं की संख्या के रूप में परिभाषित किया गया है।

बैंड थ्योरी (band theory) पर आधारित प्रभावों की गणना के लिए स्टेट्स फंक्शन (states function) का घनत्व महत्वपूर्ण है। फर्मी के गोल्डन रूल में (Fermi's Golden Rule), ऑप्टिकल अवशोषण (optical absorption) की दर की गणना के लिए, यह एक इलेक्ट्रॉन के लिए एक्सेबल इलेक्ट्रॉनों (excitable electrons) की संख्या और अंतिम अवस्था की संख्या दोनों प्रदान करता है। यह विद्युत चालकता (electrical conductivity) की गणना में दिखाई देता है जहां यह मोबाइल अवस्था (mobile states) की संख्या प्रदान करता है, और इलेक्ट्रॉन बिखरने की दरों (electron scattering rates) की गणना में जहां यह बिखरने के बाद अंतिम अवस्था की संख्या प्रदान करता है।

एक बैंड गैप (band gap) के अंदर ऊर्जा के लिए, g(E) = 0।

बैंड का भरना (Filling of bands)

Main articles: Fermi level and Fermi–Dirac statistics

संतुलन पर विभिन्न प्रकार की सामग्रियों में इलेक्ट्रॉनिक अवस्थाओं को भरना। यहां, ऊंचाई ऊर्जा है जबकि चौड़ाई सूचीबद्ध सामग्री में एक निश्चित ऊर्जा के लिए उपलब्ध राज्यों का घनत्व है। Tवह शेड फर्मी-डिराक वितरण (काला: सभी राज्य भर गए, सफेद: कोई राज्य नहीं भरा) का अनुसरण करता है। धातुएस और सेमीमेटलएस में फर्मी स्तर ई_F कम से कम एक बैंड के अंदर स्थित है।

इंसुलेटरएस और सेमीकंडक्टरएस में फर्मी स्तर एक बैंड गैप के अंदर होता है; हालाँकि, अर्धचालकों में बैंड इलेक्ट्रॉनों या होलएस के साथ थर्मली पॉप्युलेट होने के लिए फर्मी स्तर के काफी करीब होते हैं।

थर्मोडायनामिक संतुलन में (thermodynamic equilibrium), एक इलेक्ट्रॉन से भरी ऊर्जा ई (E) की स्थिति की संभावना फर्मी-डीरेक वितरण (Fermi–Dirac distribution) द्वारा दी गई है, एक थर्मोडायनामिक वितरण (thermodynamic distribution) जो पाउली बहिष्करण सिद्धांत (Pauli exclusion principle) को ध्यान में रखता है:

$f(E)={\frac {1}{1+e^{{(E-\mu )}/{k_{\rm {B}}T}}}}$

जहाँ पे:

*kBT बोल्ट्जमैन नियतांक Boltzmann's constant) और तापमान का उत्पाद है, और

• µ इलेक्ट्रॉनों की कुल रासायनिक क्षमता (total chemical potential) है, या फर्मी स्तर (अर्धचालक भौतिकी में, यह मात्रा अक्सर E_F को दर्शाती है)। एक ठोस का फ़र्मी स्तर सीधे उस ठोस पर वोल्टेज से संबंधित होता है, जैसा कि एक वोल्टमीटर (voltmeter) के साथ मापा जाता है। परंपरागत रूप से, बैंड संरचना भूखंडों (band structure plots) में फर्मी स्तर को ऊर्जा का शून्य (एक ऑर्बिटरी चॉइस (an arbitrary choice)) माना जाता है।

पदार्थ में इलेक्ट्रॉनों का घनत्व केवल अवस्था के घनत्व के समय फर्मी-डीरेक वितरण (Fermi–Dirac distribution) का अभिन्न अंग है:

$N/V=\int _{-\infty }^{\infty }g(E)f(E)\,dE$

यद्यपि बैंड की संख्या अनंत होती है और इस प्रकार अनंत संख्या में अवस्थाओं की संख्या होती है, लेकिन इन बैंडों में केवल एक परिमित संख्या )finite number) में इलेक्ट्रॉनों की संख्या होती है। इलेक्ट्रॉनों की संख्या के लिए पसंदीदा मूल्य इलेक्ट्रोस्टैटिक्स (consequence of electrostatics) का एक परिणाम है: यद्यपि किसी सामग्री की सतह को चार्ज किया जा सकता है, सामग्री का आंतरिक थोक (internal bulk of a material) चार्ज करना पसंद करता है। चार्ज तटस्थता (charge neutrality) की स्थिति का मतलब है कि एन/वी (N/V) को सामग्री में प्रोटॉन के घनत्व से मेल खाना चाहिए। ऐसा होने के लिए, सामग्री खुद को इलेक्ट्रोस्टिक रूप से समायोजित करती है, अपनी बैंड संरचना को ऊर्जा में ऊपर या नीचे स्थानांतरित करती है (जिससे जी (ई)/g(E) को स्थानांतरित कर दिया जाता है, जब तक कि यह फर्मी स्तर (Fermi level) के संबंध में सही संतुलन में न हो।

फर्मी स्तर (चालन बैंड, वैलेंस बैंड) के पास बैंड के नाम (Names of bands near the Fermi level (conduction band, valence band))

एक ठोस में अनुमत बैंड (allowed bands) की संख्या अनंत होती है, जैसे कि एक परमाणु में असीम रूप से कई ऊर्जा स्तर होते हैं। हालांकि, अधिकांश बैंडों में बहुत अधिक ऊर्जा होती है, और आमतौर पर सामान्य परिस्थितियों में अवहेलना (disregarded) होती है। इसके विपरीत, कोर ऑर्बिटल्स (जैसे 1 एस इलेक्ट्रॉनों)/ core orbitals (such as 1s electrons) से जुड़े बहुत कम ऊर्जा बैंड हैं। ये कम-ऊर्जा कोर बैंड (low-energy core bands) भी सामान्य परिस्थितियों में अवहेलना (disregarded) ही करते हैं क्योंकि वे हर समय इलेक्ट्रॉनों से भरे रहते हैं, और इसलिए निष्क्रिय होते हैं। इसी तरह, सामग्री में उनके बैंड संरचना (band structure) में कई बैंड अंतराल (band gaps) होते हैं।

सबसे महत्वपूर्ण बैंड और बैंड अंतराल (bands and band gaps)- जो इलेक्ट्रॉनिक्स और ऑप्टोइलेक्ट्रॉनिक्स (optoelectronics) के लिए प्रासंगिक हैं - वे फर्मी स्तर (Fermi level) के पास ऊर्जा वाले हैं। फ़र्मी स्तर (Fermi level) के पास बैंड और बैंड अंतराल (bands and band gaps) को विशेष नाम दिए गए हैं, जो सामग्री के आधार पर हैं:

• एक अर्धचालक (semiconductor) या बैंड इन्सुलेटर (band insulator) में, फर्मी स्तर एक बैंड गैप (band gap) से घिरा हुआ है, जिसे बैंड गैप (band gap) के रूप में संदर्भित किया जाता है (इसे बैंड संरचना में अन्य बैंड अंतराल से अलग करने के लिए)। बैंड गैप (band gap) के ऊपर निकटतम बैंड को चालन बैंड (conduction band) कहा जाता है, और बैंड गैप के नीचे के निकटतम बैंड को वैलेंस बैंड (valence band कहा जाता है। नाम वैलेंस बैंड (valence band) को रसायन विज्ञान के सादृश्य द्वारा गढ़ा (coined) गया था, क्योंकि अर्धचालक (और इंसुलेटर) में वैलेंस बैंड, वैलेंस ऑर्बिटल्स (valence orbitals) से बाहर बनाया गया है।
• एक धातु या अर्धधातु में, फर्मी स्तर (Fermi level) एक या अधिक अनुमत बैंड (allowed bands) के अंदर है। सेमीमेटल्स में बैंड को आमतौर पर कंडक्शन बैंड "conduction band" या वैलेंस बैंड "valence band" के रूप में संदर्भित किया जाता है, जो इस बात पर निर्भर करता है कि चार्ज ट्रांसपोर्ट (charge transport) अधिक इलेक्ट्रॉन-लाइक (electron-like) या होल-जैसे (hole-like), अर्धचालक के सादृश्य द्वारा (analogy to semiconductors)। हालांकि, कई धातुओं में, बैंड न तो इलेक्ट्रॉन की तरह होते हैं और न ही होल (hole) जैसे होते हैं, और अक्सर सिर्फ वैलेंस बैंड "valence band" कहा जाता है क्योंकि वे वैलेंस ऑर्बिटल्स (valence orbitals) से बने होते हैं। एक धातु की बैंड संरचना में बैंड अंतराल (band gaps) कम ऊर्जा भौतिकी के लिए महत्वपूर्ण नहीं है, क्योंकि वे फ़र्मी स्तर से बहुत दूर हैं।

क्रिस्टल में सिद्धांत (Theory in crystals)

ANSATZ एक आवधिक क्रिस्टल जाली (periodic crystal lattice) में इलेक्ट्रॉन तरंगों का विशेष मामला है, जो बलोच के प्रमेय (Bloch's theorem) का उपयोग करते हुए सामान्यतया विवर्तन के गतिशील सिद्धांत (dynamical theory of diffraction) में माना जाता है। प्रत्येक क्रिस्टल एक आवधिक संरचना (periodic structure) है जिसे एक ब्राविस जाली (Bravais lattice) द्वारा चित्रित किया जाता है, और प्रत्येक ब्राविस जाली (Bravais lattice) के लिए हम पारस्परिक जाली (reciprocal lattice) का निर्धारण कर सकते हैं, जो तीन पारस्परिक जाली वैक्टरों (three reciprocal lattice vectors) (b₁, b₂, b₃) के एक सेट में आवधिकता को घेरता (encapsulates) है। अब, किसी भी आवधिक संभावित V(r) जो प्रत्यक्ष जाली (direct lattice) के समान आवधिकता (periodicity) को साझा करते हैं, को एक फूरियर श्रृंखला (Fourier series) के रूप में विस्तारित किया जा सकता है, जिसके एकमात्र गैर-लुप्त (non-vanishing) होने वाले घटक पारस्परिक जाली वैक्टर (reciprocal lattice vectors) से जुड़े हैं। इसे विस्तार रूप में लिखा जा सकता है:

$V(\mathbf {r} )=\sum _{\mathbf {K} }{V_{\mathbf {K} }e^{i\mathbf {K} \cdot \mathbf {r} }}$

जहां k = K = m₁b₁ + m₂b₂ + m₃b₃ , जहां (m₁, m₂, m₃) पूर्णांक हैं।

इस सिद्धांत से, एक विशेष सामग्री की बैंड संरचना (band structure) की भविष्यवाणी करने का प्रयास किया जा सकता है, हालांकि इलेक्ट्रॉनिक संरचना गणना (electronic structure calculations) के लिए अधिकांश एब इनिटियो तरीके (ab initio methods) ऑब्जर्वड बैंड गैप (observed band gap) की भविष्यवाणी करने में विफल रहे हैं।

लगभग मुक्त इलेक्ट्रॉन सन्निकटन (Nearly free electron approximation)

Main articles: Nearly free electron model, Free electron model, and pseudopotential

लगभग मुक्त इलेक्ट्रॉन सन्निकटन में (nearly free electron approximation), इलेक्ट्रॉनों के बीच अन्योन्यक्रिया (interactions) को पूरी तरह से नजरअंदाज कर दिया जाता है। यह सन्निकटन (approximation) बलोच के प्रमेय (Bloch's Theorem) के उपयोग की अनुमति देता है, जिसमें कहा गया है कि आवधिक क्षमता (periodic potential) में इलेक्ट्रॉनों में तरंगों (wavefunctions) और ऊर्जा होती है जो कि पड़ोसी पारस्परिक जाली वैक्टर (neighboring reciprocal lattice vectors) के बीच एक निरंतर चरण बदलाव (constant phase shift) तक वेववेक्टर (wavevector) में आवधिक होते हैं। आवधिकता (periodicity) के परिणामों को बलोच के प्रमेय (Bloch's Theorem) द्वारा गणितीय रूप से वर्णित किया गया है, जिसमें कहा गया है कि ईजेनस्टेट वेवफंक्शन (eigenstate wavefunctions) का रूप है

${\Psi }_{n,\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n}(\mathbf {r} )$

जहां बलोच कार्य करता है $u_{n}(\mathbf {r} )$ क्रिस्टल जाली पर आवधिक है, यानी,

$u_{n}(\mathbf {r} )=u_{n}(\mathbf {r} -\mathbf {R} )$।

यहां इंडेक्स n एन-वें एनर्जी बैंड (n-th energy band) को संदर्भित करता है, वेववेक्टर 'के' (wavevector k) इलेक्ट्रॉन की गति की दिशा से संबंधित है, 'आर' (r) क्रिस्टल में स्थिति है, और 'आर' (R) एक परमाणु साइट का स्थान है।

NFE मॉडल विशेष रूप से धातुओं जैसे सामग्रियों में अच्छी तरह से काम करता है जहां पड़ोसी परमाणुओं के बीच की दूरी छोटी होती है। ऐसी सामग्रियों में पड़ोसी परमाणुओं पर परमाणु ऑर्बिटल्स (atomic orbitals) और क्षमता का ओवरलैप (overlap) अपेक्षाकृत बड़ा है। उस स्थिति में इलेक्ट्रॉन के तरंग फ़ंक्शन (wave function) को एक (संशोधित) प्लेन वेव द्वारा अनुमानित किया जा सकता है। एल्यूमीनियम जैसी धातु की बैंड संरचना भी खाली जाली सन्निकटन (empty lattice approximation) के करीब हो जाती है।

तंग बाध्यकारी मॉडल (Tight binding model)

Main article: Tight binding

लगभग मुक्त इलेक्ट्रॉन सन्निकटन (free electron approximation) के विपरीत चरम मानता है कि क्रिस्टल में इलेक्ट्रॉन घटक परमाणुओं की एक सभा की तरह व्यवहार करते हैं। यह टाइट बाइंडिंग मॉडल (tight binding model) समय-स्वतंत्र एकल इलेक्ट्रॉन श्रोडिंगर समीकरण (time-independent single electron Schrödinger equation) का समाधान मानता है $\Psi$ परमाणु ऑर्बिटल्स (atomic orbitals) के एक रैखिक संयोजन द्वारा अच्छी तरह से अनुमानित है $\psi _{n}(\mathbf {r} )$.

$\Psi (\mathbf {r} )=\sum _{n,\mathbf {R} }b_{n,\mathbf {R} }\psi _{n}(\mathbf {r} -\mathbf {R} )$,

जहां गुणांक $b_{n,\mathbf {R} }$ इस फॉर्म का सबसे अच्छा अनुमानित समाधान देने के लिए चुना जाता है। इंडेक्स एन (n) एक परमाणु ऊर्जा स्तर को संदर्भित करता है और 'आर' (R) एक परमाणु साइट को संदर्भित करता है। इस विचार का उपयोग करके एक अधिक सटीक दृष्टिकोण वनियर फंक्शन (Wannier functions) को नियोजित करता है, द्वारा परिभाषित किया गया है:

$a_{n}(\mathbf {r} -\mathbf {R} )={\frac {V_{C}}{(2\pi )^{3}}}\int _{\text{BZ}}d\mathbf {k} e^{-i\mathbf {k} \cdot (\mathbf {R} -\mathbf {r} )}u_{n\mathbf {k} }$;

जिसमें $u_{n\mathbf {k} }$ बलोच के प्रमेय (Bloch's theorem) का आवधिक हिस्सा (periodic part) है और इंटीग्रल ब्रिलोइन ज़ोन (Brillouin zone) पर है। यहाँ सूचकांक (n) क्रिस्टल में n-th ऊर्जा बैंड को संदर्भित करता है।परमाणु ऑर्बिटल्स की तरह, परमाणु साइटों (atomic sites) के पास वैनियर फ़ंक्शंस (Wannier functions) स्थानीयकृत (localized) होते हैं, लेकिन बलोच फ़ंक्शंस (Bloch functions) के संदर्भ में परिभाषित किया जा रहा है, वे क्रिस्टल क्षमता के आधार पर समाधानों से सटीक रूप से संबंधित हैं। विभिन्न परमाणु साइटों (atomic sites) 'आर' (R) पर वैनियर फ़ंक्शन (Wannier functions) ऑर्थोगोनल (orthogonal) हैं। वैनियर फ़ंक्शन (Wannier functions) का उपयोग n-th एनर्जी बैंड के लिए श्रोडिंगर सॉल्यूशन (Schrödinger solution) बनाने के लिए किया जा सकता है:

$\Psi _{n,\mathbf {k} }(\mathbf {r} )=\sum _{\mathbf {R} }e^{-i\mathbf {k} \cdot (\mathbf {R} -\mathbf {r} )}a_{n}(\mathbf {r} -\mathbf {R} )$।

टीबी मॉडल (TB model) परमाणु ऑर्बिटल्स और पड़ोसी परमाणुओं (neighbouring atoms) पर क्षमता के बीच सीमित ओवरलैप वाली सामग्रियों में अच्छी तरह से काम करता है। SI, GAAS, SiO₂जैसी सामग्रियों की बैंड संरचनाएं उदाहरण के लिए डायमंड को परमाणु sp³ ऑर्बिटल्स के आधार पर टीबी-हैमिल्टनियों (TB-Hamiltonians) द्वारा अच्छी तरह से वर्णित किया गया है। संक्रमण धातुओं में एक मिश्रित टीबी-एनएफई मॉडल (TB-NFE model) का उपयोग व्यापक एनएफई चालन बैंड (broad NFE conduction band) और संकीर्ण एम्बेडेड टीबी डी-बैंड (narrow embedded TB d-bands) का वर्णन करने के लिए किया जाता है।वानियर फलनों (Wannier functions) के परमाणु कक्षीय भाग (atomic orbital part) के रेडियल फलनों (radial functions) की गणना सबसे आसानी से स्यूडोपोटेंशियल विधियों (pseudopotential methods) के उपयोग द्वारा की जाती है। एनएफई (NFE), टीबी (TB) या संयुक्त एनएफई-टीबी (NFE-TB) बैंड संरचना, गणना, कभी -कभी स्यूडोपोटेंशियल तरीकों (pseudopotential methods) के आधार पर तरंग फ़ंक्शन (wave function) सन्निकटन (approximations) के साथ विस्तारित किया जाता है, अक्सर आगे की गणना के लिए एक आर्थिक शुरुआती बिंदु के रूप में उपयोग किया जाता है।

केकेआर मॉडल (KKR model)

Main article: Multiple scattering theory

केकेआर विधि (KKR method), जिसे मल्टीपल स्कैटरिंग थ्योरी "multiple scattering theory" या ग्रीन की फ़ंक्शन विधि (Green's function method) भी कहा जाता है, हैमिल्टन (Hamiltonian) के बजाय इनवर्स ट्रांजीशन मैट्रिक्स (inverse transition matrix) टी T के स्थिर मान ज्ञात करता है। कोरिंगा (Korringa), कोहन (Kohn) और रोस्टॉकर (Rostocker) द्वारा एक वैरिएशनल कार्यान्वयन (variational implementation) का सुझाव दिया गया था, और इसे अक्सर कोरिंगा -कोन -रोस्टोकर विधि (Korringa–Kohn–Rostoker method) के रूप में संदर्भित किया जाता है। केकेआर (KKR method) या ग्रीन के फंक्शन फॉर्मुलेशन (Green's function formulation) की सबसे महत्वपूर्ण विशेषताएं हैं (1) यह समस्या के दो पहलुओं को अलग करता है: संरचना (परमाणुओं की स्थिति) बिखरने (परमाणुओं की रासायनिक पहचान) से; और (2) ग्रीन के फ़ंक्शन (Green's functions) इलेक्ट्रॉनिक गुणों के एक स्थानीयकृत विवरण (localized description) के लिए एक प्राकृतिक दृष्टिकोण प्रदान करते हैं जो मिश्र धातुओं और अन्य अव्यवस्थित प्रणाली (disordered system) के लिए अनुकूलित (adapted) किए जा सकते हैं। परमाणु स्थितियों (atomic positions) पर इस सन्निकटन केंद्रों (approximation centers) का सबसे सरल रूप गैर-अतिव्यापी क्षेत्रों (मफिन टिन (muffin tins) के रूप में संदर्भित) है। इन क्षेत्रों के भीतर, एक इलेक्ट्रॉन द्वारा अनुभव की जाने वाली क्षमता को दिए गए नाभिक के बारे में गोलाकार रूप से सममित (spherically symmetric) होने का अनुमान लगाया गया है। शेष अंतरालीय क्षेत्र में (interstitial region), स्क्रीन की गई क्षमता (screened potential) को एक स्थिर के रूप में अनुमानित किया जाता है। परमाणु-केंद्रित क्षेत्रों (atom-centered spheres) और अंतरालीय क्षेत्र (interstitial region) के बीच क्षमता की निरंतरता (Continuity of the potential) लागू की जाती है।

घनत्व-कार्यात्मक सिद्धांत (Density-functional theory)

Main article: Density functional theory

See also: Kohn–Sham equations

हाल के भौतिकी साहित्य में, इलेक्ट्रॉनिक संरचनाओं और बैंड भूखंडों (band plots) के एक बड़े हिस्से की गणना घनत्व-कार्यात्मक सिद्धांत (डीएफटी) "density-functional theory" (DFT) का उपयोग करके की जाती है, जो एक मॉडल नहीं है, बल्कि एक सिद्धांत है, अर्थात्, एक सूक्ष्म प्रथम-सिद्धांत (microscopic first-principles theory) जो संघनित पदार्थ भौतिकी (condensed matter physics) का सिद्धांत है जो इलेक्ट्रॉनिक घनत्व (electronic density) के कार्यात्मक में एक विनिमय-सहसंबंध शब्द (exchange-correlation term) की शुरूआत के माध्यम से इलेक्ट्रॉन-इलेक्ट्रॉन कई-शरीर की समस्या से निपटने का प्रयास करता है। डीएफटी-गणना वाले बैंड (DFT-calculated bands) कई मामलों में प्रयोगात्मक रूप से माप बैंड (measured bands) के साथ पाए जाते हैं, उदाहरण के लिए कोण-हल किए गए फोटोइमिशन स्पेक्ट्रोस्कोपी (angle-resolved photoemission spectroscopy) (एआरपीईएस)/(ARPES)। विशेष रूप से, बैंड का आकार सामान्य तौर पर डीएफटी (DFT) द्वारा अच्छी तरह से पुन: पेश किया जाता है। लेकिन प्रयोग के परिणामों की तुलना में डीएफटी बैंड (DFT bands) में व्यवस्थित त्रुटियां (systematic errors) भी हैं। विशेष रूप से, डीएफटी (DFT) व्यवस्थित रूप से लगभग 30-40% इंसुलेटर (insulators) और अर्धचालक (semiconductors) में बैंड गैप को कम करता है।

यह आमतौर पर माना जाता है कि डीएफटी (DFT) केवल एक प्रणाली के जमीनी अवस्था गुणों (ground state properties) की भविष्यवाणी करने के लिए एक सिद्धांत है (जैसे कि कुल ऊर्जा, परमाणु संरचना, आदि), और यह कि एक्ससिटेड स्टेट प्रोपर्टीज (excited state properties) को डीएफटी (DFT) द्वारा निर्धारित नहीं किया जा सकता है। यह एक गलत धारणा है। सिद्धांत रूप में, डीएफटी (DFT) किसी भी सिस्टम की किसी भी संपत्ति (ग्राउंड स्टेट या एक्ससिटेड स्टेट) को निर्धारित कर सकता है जो एक कार्यात्मक है जो उस प्रोपर्टी के लिए ग्राउंड स्टेट डेन्सिटी (ground state density) को मैप करता है। यह होहेनबर्ग -कोन प्रमेय का सार है (This is the essence of the Hohenberg–Kohn theorem)। प्रयोग में, हालांकि, कोई ज्ञात कार्यात्मक मौजूद नहीं ( no known functional exists) है जो एक सामग्री के भीतर इलेक्ट्रॉनों की उत्तेजना ऊर्जा (excitation energies) के लिए ग्राउंड स्टेट डेन्सिटी (ground state density) को मैप करता है। इस प्रकार, साहित्य में एक डीएफटी बैंड प्लॉट (DFT band plot) के रूप में उद्धृत (quoted) किया गया है, डीएफटी कोहन-शम समीकरणों (DFT Kohn–Sham energies) का एक प्रतिनिधित्व है। कोहन-शम ऊर्जा (Kohn–Sham system), अर्थात्, एक काल्पनिक गैर-अंतःक्रियात्मक प्रणाली (fictive non-interacting system) की ऊर्जा, कोहन-शम प्रणाली (Kohn–Sham system), जिसकी कोई भौतिक व्याख्या नहीं है। कोहन -शम इलेक्ट्रॉनिक संरचना (Kohn–Sham electronic structure) को एक प्रणाली के वास्तविक, क्वासिपार्टिकल इलेक्ट्रॉनिक संरचना (quasiparticle electronic structure of a system) के साथ भ्रमित नहीं होना चाहिए, और कोहन -शम ऊर्जाओं (Kohn–Sham energies) के लिए कोई कोपमैन की प्रमेय (Koopmans' theorem) होल्डिंग (holding) नहीं है, जैसा कि हार्ट्री -फॉक ऊर्जा (Hartree–Fock energies) के लिए है, जिसे वास्तव में क्वासिपार्टिकल ऊर्जा (quasiparticle energies) के लिए एक अनुमान माना जा सकता है। इसलिए, सिद्धांत रूप में, कोहन-शम आधारित डीएफटी, (Kohn–Sham based DFT) एक बैंड सिद्धांत नहीं है, अर्थात, बैंड और बैंड-प्लॉट (band-plots) की गणना के लिए उपयुक्त सिद्धांत नहीं है। सिद्धांत रूप में समय-निर्भर घनत्व कार्यात्मक सिद्धांत (time-dependent DFT)| समय-निर्भर DFT (time-dependent DFT) का उपयोग वास्तविक बैंड संरचना की गणना करने के लिए किया जा सकता है, हालांकि व्यवहारिकता में यह अक्सर मुश्किल होता है। एक लोकप्रिय दृष्टिकोण हाइब्रिड फ़ंक्शंस (hybrid functionals) का उपयोग है, जिसमें हार्ट्री -फॉक सटीक एक्सचेंज (Hartree–Fock exact exchange) का एक हिस्सा शामिल है; यह अर्धचालकों के अनुमानित बैंडगैप्स में पर्याप्त सुधार करता है, लेकिन धातुओं और व्यापक-बैंडगैप सामग्री (wide-bandgap materials) के लिए कम विश्वसनीय है।

ग्रीन के फ़ंक्शन के तरीके और ab initio GW सन्निकटन (Green's function methods and the ab initio GW approximation)

Main articles: Green's function (many-body theory) and Green–Kubo relations

इलेक्ट्रॉन-इलेक्ट्रॉन इंटरैक्शन (electron-electron interaction) सहित बैंड की गणना करने के लिए मैनी बॉडी इफेक्ट्स (many-body effects), कोई भी तथाकथित ग्रीन के फ़ंक्शन (Green's function) (कई-बॉडी थ्योरी) का सहारा ले सकता है। वास्तव में, एक प्रणाली के ग्रीन के फंक्शन का ज्ञान (knowledge of the Green's function of a system) दोनों जमीन (कुल ऊर्जा) प्रदान करता है और एक्ससिटेड स्टेट ऑब्जरवेशन ऑफ द सिस्टम (excited state observables of the system) भी प्रदान करता है और सिस्टम के राज्य वेधशालाओं (state observables) को भी उत्साहित करता है। ग्रीन के कार्य (Green's function) के ध्रुव क़य्वासीप्रैक्टिकल (quasiparticle) ऊर्जा, जो एक ठोस के बैंड हैं। ग्रीन के फ़ंक्शन (Green's function) की गणना डायसन समीकरण (Dyson equation) को हल करके की जा सकती है, जब सिस्टम की आत्म-ऊर्जा (self-energy) ज्ञात होती है। ठोस जैसी वास्तविक प्रणालियों के लिए, आत्म-ऊर्जा (self-energy) एक बहुत ही जटिल मात्रा है और समस्या को हल करने के लिए आमतौर पर अनुमानों की आवश्यकता होती है। ऐसा ही एक सन्निकटन (approximations), GW सन्निकटन /(GW approximation) है, इसलिए गणितीय रूप से कहा जाता है गणितीय रूप से स्व-ऊर्जा ग्रीन के फ़ंक्शन G के उत्पाद Σ = GW और गतिशील रूप से स्क्रीन किए गए इंटरैक्शन (interaction) W के रूप में लेती है और इसे पूरी तरह से अब इनिसियो वे (ab initio way) से भी तैयार किया जा सकता है। जीडब्ल्यू सन्निकटन (GW approximation) प्रयोग के साथ समझौते में इंसुलेटर (insulators) और अर्धचालकों (semiconductors) के बैंड अंतराल (band gaps) प्रदान करता है, और इसलिए व्यवस्थित डीएफटी (systematic DFT underestimation) को कम करने के लिए।

डायनेमिक मीन-फील्ड थ्योरी (Dynamical mean-field theory)

Main article: Dynamical mean-field theory

यद्यपि लगभग मुक्त इलेक्ट्रॉन सन्निकटन (approximation) इलेक्ट्रॉन बैंड संरचनाओं के कई गुणों का वर्णन करने में सक्षम है, इस सिद्धांत का एक परिणाम यह है कि यह प्रत्येक यूनिट सेल (each unit cell) में समान संख्या में इलेक्ट्रॉनों की भविष्यवाणी करता है। यदि इलेक्ट्रॉनों की संख्या विषम है, तब हम उम्मीद करेंगे कि प्रत्येक यूनिट सेल में एक अयुग्मित इलेक्ट्रॉन (unpaired electron) है, और इस प्रकार वैलेंस बैंड (valence band) पूरी तरह से अधिकृत नहीं कर रहा है, जिससे सामग्री एक कंडक्टर (material a conductor) बन जाती है। हालांकि, सीओओ (CoO) जैसी सामग्री जिसमें प्रति यूनिट सेल में विषम संख्या होती है, इस परिणाम के साथ सीधे विरोध में, इंसुलेटर होते हैं। इस तरह की सामग्री को एक mott इन्सुलेटर (Mott insulator) के रूप में जाना जाता है, और विसंगति (inclusion) को समझाने के लिए विस्तृत इलेक्ट्रॉन-इलेक्ट्रॉन इंटरैक्शन (बैंड सिद्धांत में क्रिस्टल क्षमता पर केवल एक औसत प्रभाव के रूप में इलाज किया जाता है) को शामिल करने की आवश्यकता होती है। हबर्ड मॉडल (Hubbard model) एक अनुमानित सिद्धांत (approximate theory) है जिसमें इन इंटरैक्शन (interactions) को शामिल किया गया है। इसे तथाकथित डायनेमिक मीन-फील्ड थ्योरी (dynamical mean-field theory) के भीतर गैर-पर्टर्बिटिक (non-perturbatively) रूप से उपचारित (treated) किया जा सकता है, जो लगभग मुक्त इलेक्ट्रॉन सन्निकटन (free electron approximation) और परमाणु सीमा के बीच अंतर को कम करने का प्रयास करता है। औपचारिक रूप से, हालांकि, अवस्थाएं इस मामले में गैर-हस्तक्षेप (non-interacting) नहीं कर रहे हैं और एक बैंड संरचना की अवधारणा (concept of a band structure) इन मामलों का वर्णन करने के लिए पर्याप्त नहीं है।

अन्य (Others)

सैद्धांतिक ठोस अवस्था भौतिकी में बैंड संरचनाओं की गणना एक महत्वपूर्ण विषय है। ऊपर उल्लिखित मॉडलों के अलावा, अन्य मॉडलों में निम्नलिखित शामिल हैं:

• खाली जाली सन्निकटन (Empty lattice approximation): मुक्त स्थान के एक क्षेत्र की बैंड संरचना जिसे एक जाली में विभाजित किया गया है।
• k · P perturbation सिद्धांत (k·p perturbation theory): एक ऐसी तकनीक है जो एक बैंड संरचना को केवल कुछ मापदंडों के संदर्भ में वर्णित करने की अनुमति देती है। तकनीक का उपयोग सामान्य तौर पर अर्धचालक के लिए किया जाता है, और मॉडल में मापदंडों को अक्सर प्रयोग द्वारा निर्धारित किया जाता है।
• क्रोनिग-पेनी मॉडल (Kronig–Penney model), क्रोनिग-पेनी मॉडल, बैंड गठन के चित्रण के लिए उपयोगी एक आयामी आयताकार कुआं मॉडल (one-dimensional rectangular well model) सरल होते हुए भी, यह कई महत्वपूर्ण घटनाओं की भविष्यवाणी करता है, लेकिन मात्रात्मक नहीं है।
• हबर्ड मॉडल (Hubbard model)

बैंड संरचना को वेववेक्टर (wavevectors) के लिए सामान्यीकृत किया गया है जो जटिल संख्याएं हैं, जिसके परिणामस्वरूप एक जटिल बैंड संरचना (complex band structure) कहा जाता है, जो सतहों और इंटरफेस (interfaces) पर रुचि रखता है।

प्रत्येक मॉडल कुछ प्रकार के ठोस पदार्थों का बहुत अच्छी तरह से वर्णन करता है, और कुछ अन्य का खराब तरीके से। लगभग मुक्त इलेक्ट्रॉन मॉडल (nearly free electron model) धातुओं के लिए अच्छी तरह से काम करता है, लेकिन गैर-धातुओं (non-metals) के लिए खराब है। तंग बाइंडिंग मॉडल (tight binding model) आयनिक इंसुलेटर (ionic insulators) के लिए बेहद सटीक है, जैसे कि मेटल हलाइड लवण (जैसे NaCl)।

बैंड आरेख

यह समझने के लिए कि वास्तविक स्थान में फ़र्मी स्तर के सापेक्ष बैंड संरचना कैसे बदलती है, एक बैंड संरचना प्लॉट को अक्सर बैंड आरेख के रूप में पहली बार सरल बनाया जाता है।एक बैंड आरेख में ऊर्ध्वाधर अक्ष ऊर्जा है जबकि क्षैतिज अक्ष वास्तविक स्थान का प्रतिनिधित्व करता है।क्षैतिज रेखाएं ऊर्जा के स्तर का प्रतिनिधित्व करती हैं, जबकि ब्लॉक ऊर्जा बैंड का प्रतिनिधित्व करते हैं।जब इन आरेख में क्षैतिज रेखाएं धीमी हो जाती हैं, तो स्तर या बैंड की ऊर्जा दूरी के साथ बदल जाती है।आरेखित रूप से, यह क्रिस्टल सिस्टम के भीतर एक विद्युत क्षेत्र की उपस्थिति को दर्शाता है।बैंड आरेख एक दूसरे के संपर्क में रखने पर एक दूसरे से विभिन्न सामग्रियों के सामान्य बैंड संरचना गुणों से संबंधित होने में उपयोगी होते हैं।

यह भी देखें

• बैंड-गैप इंजीनियरिंग-एक सामग्री के बैंड संरचना को बदलने की प्रक्रिया
• बैंड संरचना के सिद्धांत में फेलिक्स बलोच- पियोनियर
• एलन हेरिस विल्सन- बैंड संरचना के सिद्धांत में पियोनियर

सामान्य ग्रंथ सूची

• Charles Kittel (1996). Introduction to Solid State Physics (Seventh ed.). New York: Wiley. ISBN 978-0-471-11181-8.

अग्रिम पठन

• Ashcroft, Neil and N. David Mermin, Solid State Physics, ISBN 0-03-083993-9
• Harrison, Walter A., Elementary Electronic Structure, ISBN 981-238-708-0
• Harrison, Walter A.; W. A. Benjamin Pseudopotentials in the theory of metals, (New York) 1966
• Marder, Michael P., Condensed Matter Physics, ISBN 0-471-17779-2
• Martin, Richard, Electronic Structure: Basic Theory and Practical Methods, ISBN 0-521-78285-6
• Millman, Jacob; Arvin Gabriel, Microelectronics, ISBN 0-07-463736-3, Tata McGraw-Hill Edition.
• Nemoshkalenko, V. V., and N. V. Antonov, Computational Methods in Solid State Physics, ISBN 90-5699-094-2
• Omar, M. Ali, Elementary Solid State Physics: Principles and Applications, ISBN 0-201-60733-6
• Singh, Jasprit, Electronic and Optoelectronic Properties of Semiconductor Structures Chapters 2 and 3, ISBN 0-521-82379-X
• Vasileska, Dragica, Tutorial on Bandstructure Methods (2008)

बाहरी संबंध

• Animation, applications and research about quantum physics and band theory (Université Paris Sud)