बलयुग्म (यांत्रिकी): Difference between revisions

Latest revision as of 18:00, 17 April 2023

यांत्रिकी में बलयुग्म परिणामी बल (या शुद्ध बल या योग) बलाघूर्ण के साथ बलों की प्रणाली है। किन्तु कोई परिणामी बल नहीं है।^[1]

एक उत्कृष्ठ शब्द बल बलयुग्म या शुद्ध क्षण है। इसका प्रभाव कोणीय गति प्रदान करना है। किन्तु कोई रैखिक गति नहीं है। कठोर वस्तु की गतिशीलता में बलयुग्म 'मुक्त सदिश स्थल' हैं। जिसका अर्थ है कि वस्तु पर उनके प्रभाव आवेदन के बिंदु से स्वतंत्र हैं।

बलयुग्म का परिणामी क्षण एक स्थिति होती है। बलयुग्म के पास गुण है कि वह संदर्भ बिंदु से स्वतंत्र है।

साधारण बलयुग्म

परिभाषा

बलयुग्म एक सभी बलों का युग्म है और परिमाण में बराबर, विपरीत दिशा में निर्देशित और लंबवत दूरी से विस्थापित होता है।

सबसे सरल प्रकार के बलयुग्म में दो समान और विपरीत बल होते हैं। जिनकी क्रिया रेखा मिलती जुलती है। इसे सिंपल कपल कहते हैं।^[1] बलों का एक मोड़ प्रभाव या क्षण होता है। जिसे अक्ष के बारे में टॉर्क कहा जाता है। जो बलों के विमान के लिए सामान्य (ज्यामिति) (लंबवत) होता है। बलयुग्म के बलाघूर्ण के लिए एसआई इकाई न्यूटन मीटर है।

यदि दो बल $F$ और $- F$ हैं। तो टॉर्क का यूक्लिडियन वेक्टर निम्न सूत्र द्वारा दिया जाता है:

\tau =Fd

जहाँ-

$\tau$ बलयुग्म का क्षण है।
$F$ बल का परिमाण है।
$d$ दो समानांतर बलों के बीच लंबवत दूरी (आघूर्ण) है।

टॉर्क का परिमाण $F • d$ के बराबर है। इकाई वेक्टर द्वारा दिए गए टॉर्क की दिशा ${\hat {e}}$ के साथ जो दो बलों वाले विमान के लंबवत है और धनात्मक वामावर्त बलयुग्म है। जब $d$ बलों के दो बिंदुओं के बीच सदिश के रूप में लिया जाता है तो टॉर्क का क्रॉस उत्पाद $d$ और $F$ है, अर्थात-

\mathbf {\tau } =|\mathbf {d} \times \mathbf {F} |.

संदर्भ बिंदु की स्वतंत्रता

किसी बल के प्रभाव को केवल एक निश्चित बिंदु $P$ के संबंध में परिभाषित किया जाता है। (यह पल के बारे में कहा जाता है $P$ ) और सामान्यतः जब $P$ बदल जाता है। तो बल का प्रभाव भी बदल जाता है। चूंकि बलयुग्म का प्रभाव (टॉर्क) संदर्भ बिंदु $P$ से स्वतंत्र है। कोई भी बिंदु वही प्रभाव देगा।^[1]दूसरे शब्दों में बलयुग्म किसी भी अधिक सामान्य बलाघूर्ण के विपरीत मुक्त सदिश है। (इस तथ्य को पियरे वैरिग्नन का सेकंड मोमेंट प्रमेय कहा जाता है।)^[2]इसका प्रमाण इस प्रकार है: माना कि बल सदिशों का एक समुच्चय $F 1$ , $F 2$ है। जो एक युग्म बनाते हैं। स्थिति वैक्टर के साथ (कुछ मूल के बारे में $P$ ) $r 1$ , $r 2$ , आदि, क्रमशः $P$ के बारे में बलाघूर्ण हैं-

M=\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\cdots

अब हम एक नया संदर्भ बिंदु चुनते हैं। जो $P'$ से भिन्न है। $P$ वेक्टर द्वारा $r$ नया बलाघूर्ण है।

M'=(\mathbf {r} _{1}+\mathbf {r} )\times \mathbf {F} _{1}+(\mathbf {r} _{2}+\mathbf {r} )\times \mathbf {F} _{2}+\cdots

अब क्रॉस उत्पाद की वितरण गुण का तात्पर्य है।

M'=\left(\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\cdots \right)+\mathbf {r} \times \left(\mathbf {F} _{1}+\mathbf {F} _{2}+\cdots \right).

चूंकि एक बल बलयुग्म की परिभाषा का अर्थ है।

\mathbf {F} _{1}+\mathbf {F} _{2}+\cdots =0.

इसलिए-

M'=\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\cdots =M

यह प्रमाणित करता है कि बलाघूर्ण संदर्भ बिंदु से स्वतंत्र है। जो इस बात का प्रमाण है कि बलयुग्म मुक्त सदिश है।

बल और बलयुग्म

द्रव्यमान के केंद्र से दूरी d पर कठोर वस्तु पर लगाए गए बल F का वही प्रभाव होता है। जो समान बल सीधे द्रव्यमान के केंद्र पर निर्धारित होता है और बलयुग्म Cℓ = Fd है। बलयुग्म के तल पर समकोण पर कठोर वस्तु का कोणीय त्वरण उत्पन्न करता है।^[3] द्रव्यमान के केंद्र में बल की दिशा में अभिविन्यास में बदलाव के बिना वस्तु को गति देता है। सामान्य प्रमेय हैं कि^[3] एक कठोर पिंड के किसी भी बिंदु O' पर कार्य करने वाला बल किसी भी बिंदु O पर समान और समानांतर बल F द्वारा प्रतिस्थापित किया जा सकता है और F के समानांतर बलों वाला बलयुग्म जिसका बलाघूर्ण M = Fd है, d का पृथक्करण है। इसके विपरीत बलयुग्म के तल में बलयुग्म और बल को उचित रूप से स्थित बल द्वारा प्रतिस्थापित किया जा सकता है।

किसी भी बलयुग्म को एक ही दिशा और बलाघूर्ण के समान विमान में किसी भी वांछित बल या किसी वांछित भुजा के द्वारा प्रतिस्थापित किया जा सकता है।^[3]

अनुप्रयोग

मैकेनिकल इंजीनियरिंग और भौतिक विज्ञान में बलयुग्म बहुत महत्वपूर्ण हैं। कुछ उदाहरण हैं:

किसी के हाथ से पेचकस पर लगने वाला बल।
पेचकश की नोक द्वारा पेंच के सिर पर लगाया गया बल।
कताई प्रोपेलर पर कार्य करने वाले बलों को खींचें।
एक समान विद्युत क्षेत्र में विद्युत द्विध्रुव पर बल।
अंतरिक्ष यान पर प्रतिक्रिया नियंत्रण प्रणाली।
स्टीयरिंग व्हील पर हाथों द्वारा लगाया गया बल।

यह भी देखें

संदर्भ

↑ ^1.0 ^1.1 ^1.2 Dynamics, Theory and Applications by T.R. Kane and D.A. Levinson, 1985, pp. 90-99: Free download
↑ Engineering Mechanics: Equilibrium, by C. Hartsuijker, J. W. Welleman, page 64 Web link
↑ ^3.0 ^3.1 ^3.2 Augustus Jay Du Bois (1902). इंजीनियरिंग के यांत्रिकी, खंड 1. Wiley. p. 186.

H.F. Girvin (1938) Applied Mechanics, §28 Couples, pp 33,4, Scranton Pennsylvania: International Textbook Company.

[Kane-1] 1.0 ^1.1 ^1.2 Dynamics, Theory and Applications by T.R. Kane and D.A. Levinson, 1985, pp. 90-99: Free download

[2] Engineering Mechanics: Equilibrium, by C. Hartsuijker, J. W. Welleman, page 64 Web link

[DuBois-3] 3.0 ^3.1 ^3.2 Augustus Jay Du Bois (1902). इंजीनियरिंग के यांत्रिकी, खंड 1. Wiley. p. 186.

[1]

[2]

[3]

@@ Line 1: / Line 1: @@
-{{Short description|Pair of equal and opposite forces acting along different lines of action of force on a rigid body}}{{Classical mechanics|cTopic=Fundamental concepts}}
+{{Short description|Pair of equal and opposite forces acting along different lines of action of force on a rigid body}}{{Classical mechanics|cTopic=मूलभूत सिद्धांत}}
-[[यांत्रिकी]] में बलयुग्म परिणामी बल (या [[शुद्ध बल]] या योग) बलाघूर्ण के साथ बलों की प्रणाली है। किन्तु कोई परिणामी बल नहीं है।<ref name=Kane>''Dynamics, Theory and Applications'' by T.R. Kane and D.A. Levinson, 1985, pp. 90-99: [http://ecommons.library.cornell.edu/handle/1813/638 Free download]</ref>
+[[यांत्रिकी]] में '''बलयुग्म''' परिणामी बल (या [[शुद्ध बल]] या योग) बलाघूर्ण के साथ बलों की प्रणाली है। किन्तु कोई परिणामी बल नहीं है।<ref name=Kane>''Dynamics, Theory and Applications'' by T.R. Kane and D.A. Levinson, 1985, pp. 90-99: [http://ecommons.library.cornell.edu/handle/1813/638 Free download]</ref>
-एक उत्कृष्ठ शब्द बल बलयुग्म या शुद्ध क्षण है। इसका प्रभाव कोणीय [[गति]] प्रदान करना है। किन्तु कोई रैखिक गति नहीं है। [[कठोर शरीर की गतिशीलता]] में बलयुग्म 'मुक्त [[सदिश स्थल]]' हैं। जिसका अर्थ है कि शरीर पर उनके प्रभाव आवेदन के बिंदु से स्वतंत्र हैं।
+एक उत्कृष्ठ शब्द बल बलयुग्म या शुद्ध क्षण है। इसका प्रभाव कोणीय [[गति]] प्रदान करना है। किन्तु कोई रैखिक गति नहीं है। [[कठोर शरीर की गतिशीलता|कठोर वस्तु की गतिशीलता]] में बलयुग्म 'मुक्त [[सदिश स्थल]]' हैं। जिसका अर्थ है कि वस्तु पर उनके प्रभाव आवेदन के बिंदु से स्वतंत्र हैं।
-बलयुग्म का परिणामी क्षण एक स्थिति  होती है। बलयुग्म के पास गुण है कि वह संदर्भ बिंदु से स्वतंत्र है।
+बलयुग्म का परिणामी क्षण एक स्थिति होती है। बलयुग्म के पास गुण है कि वह संदर्भ बिंदु से स्वतंत्र है।
 == साधारण बलयुग्म ==
@@ Line 14: / Line 14: @@
 सबसे सरल प्रकार के बलयुग्म में दो समान और विपरीत बल होते हैं। जिनकी क्रिया रेखा मिलती जुलती है। इसे सिंपल कपल कहते हैं।<ref name=Kane>''Dynamics, Theory and Applications'' by T.R. Kane and D.A. Levinson, 1985, pp. 90-99: [http://ecommons.library.cornell.edu/handle/1813/638 Free download]</ref> बलों का एक मोड़ प्रभाव या क्षण होता है। जिसे अक्ष के बारे में टॉर्क कहा जाता है। जो बलों के विमान के लिए [[सामान्य (ज्यामिति)]] (लंबवत) होता है। बलयुग्म के बलाघूर्ण के लिए एसआई इकाई [[न्यूटन मीटर]] है।
-यदि दो बल हैं {{mvar|F}} और {{math|−''F''}}, तो टॉर्क का [[यूक्लिडियन वेक्टर]] निम्न सूत्र द्वारा दिया जाता है:
+यदि दो बल {{mvar|F}} और {{math|−''F''}} हैं। तो टॉर्क का [[यूक्लिडियन वेक्टर]] निम्न सूत्र द्वारा दिया जाता है:
 <math display="block">\tau = F d </math>
-कहाँ
+जहाँ-
-*<math>\tau</math> बलयुग्म का क्षण है
+*<math>\tau</math> बलयुग्म का क्षण है।
-*{{mvar|F}} बल का परिमाण है
+*{{mvar|F}} बल का परिमाण है।
-*{{mvar|d}} दो समानांतर बलों के बीच लंबवत दूरी (आघूर्ण) है
+*{{mvar|d}} दो समानांतर बलों के बीच लंबवत दूरी (आघूर्ण) है।
-टॉर्क का परिमाण बराबर है {{math|''F'' • ''d''}}, [[ इकाई वेक्टर ]] द्वारा दिए गए टॉर्क की दिशा के साथ <math>\hat{e}</math>, जो दो बलों वाले विमान के लंबवत है और धनात्मक एक वामावर्त बलयुग्म है। कब {{mvar|d}} बलों की कार्रवाई के बिंदुओं के बीच एक सदिश के रूप में लिया जाता है, तो टोक़ का क्रॉस उत्पाद है {{mvar|d}} और {{mvar|F}}, अर्थात।
+टॉर्क का परिमाण {{math|''F'' • ''d''}} के बराबर है। [[ इकाई वेक्टर |इकाई वेक्टर]] द्वारा दिए गए टॉर्क की दिशा <math>\hat{e}</math> के साथ जो दो बलों वाले विमान के लंबवत है और धनात्मक वामावर्त बलयुग्म है। जब {{mvar|d}} बलों के दो बिंदुओं के बीच सदिश के रूप में लिया जाता है तो टॉर्क का क्रॉस उत्पाद {{mvar|d}} और {{mvar|F}} है, अर्थात-
-<math display="block"> \mathbf{\tau} = | \mathbf{d} \times \mathbf{F} | .</math>
+<math display="block"> \mathbf{\tau} = | \mathbf{d} \times \mathbf{F} | .</math><br />'''<big><u>संदर्भ बिंदु की स्वतंत्रता</u></big>'''
+किसी बल के प्रभाव को केवल एक निश्चित बिंदु {{mvar|P}} के संबंध में परिभाषित किया जाता है। (यह पल के बारे में कहा जाता है {{mvar|P}} ) और सामान्यतः जब {{mvar|P}} बदल जाता है। तो बल का प्रभाव भी बदल जाता है। चूंकि बलयुग्म का प्रभाव (टॉर्क) संदर्भ बिंदु {{mvar|P}} से स्वतंत्र है। कोई भी बिंदु वही प्रभाव देगा।<ref name="Kane" />दूसरे शब्दों में बलयुग्म किसी भी अधिक सामान्य बलाघूर्ण के विपरीत मुक्त सदिश है। (इस तथ्य को [[पियरे वैरिग्नन]] का सेकंड मोमेंट प्रमेय कहा जाता है।)<ref>''Engineering Mechanics: Equilibrium'', by C. Hartsuijker, J. W. Welleman, page 64 [https://books.google.com/books?id=oPhH90IWW60C&pg=PA64 Web link]</ref>इसका प्रमाण इस प्रकार है: माना कि बल सदिशों का एक समुच्चय {{math|'''F'''{{sub|1}}}}, {{math|'''F'''{{sub|2}}}} है। जो एक युग्म बनाते हैं। स्थिति वैक्टर के साथ (कुछ मूल के बारे में {{mvar|P}}) {{math|'''r'''{{sub|1}}}}, {{math|'''r'''{{sub|2}}}}, आदि, क्रमशः {{mvar|P}} के बारे में बलाघूर्ण हैं-
-== संदर्भ बिंदु की स्वतंत्रता ==
-किसी बल के क्षण को केवल एक निश्चित बिंदु के संबंध में परिभाषित किया जाता है {{mvar|P}} (यह पल के बारे में कहा जाता है {{mvar|P}} ) और, सामान्य तौर पर, जब {{mvar|P}} बदल जाता है, पल बदल जाता है। हालाँकि, बलयुग्म का क्षण (टोक़) संदर्भ बिंदु से स्वतंत्र है {{mvar|P}}: कोई भी बिंदु वही क्षण देगा।<ref name=Kane/>दूसरे शब्दों में, एक बलयुग्म, किसी भी अधिक सामान्य क्षणों के विपरीत, एक मुक्त सदिश है। (इस तथ्य को [[पियरे वैरिग्नन]] का सेकंड मोमेंट प्रमेय कहा जाता है।)<ref>''Engineering Mechanics: Equilibrium'', by C. Hartsuijker, J. W. Welleman, page 64 [https://books.google.com/books?id=oPhH90IWW60C&pg=PA64 Web link]</ref>
-इस दावे का प्रमाण इस प्रकार है: मान लीजिए बल सदिशों का एक समुच्चय है {{math|'''F'''{{sub|1}}}}, {{math|'''F'''{{sub|2}}}}, आदि जो एक जोड़ी बनाते हैं, स्थिति वैक्टर के साथ (कुछ मूल के बारे में {{mvar|P}}), {{math|'''r'''{{sub|1}}}}, {{math|'''r'''{{sub|2}}}}, आदि, क्रमशः। के बारे में क्षण {{mvar|P}} है
 :<math>M = \mathbf{r}_1\times \mathbf{F}_1 + \mathbf{r}_2\times \mathbf{F}_2 + \cdots</math>
-अब हम एक नया संदर्भ बिंदु चुनते हैं {{mvar|P'}} से भिन्न है {{mvar|P}} वेक्टर द्वारा {{math|'''r'''}}. नया क्षण है
+अब हम एक नया संदर्भ बिंदु चुनते हैं। जो {{mvar|P'}} से भिन्न है। {{mvar|P}} वेक्टर द्वारा {{math|'''r'''}} नया बलाघूर्ण है।
 :<math>M' = (\mathbf{r}_1+\mathbf{r})\times \mathbf{F}_1 + (\mathbf{r}_2+\mathbf{r})\times \mathbf{F}_2 + \cdots</math>
-अब क्रॉस उत्पाद की वितरण संपत्ति का तात्पर्य है
+अब क्रॉस उत्पाद की वितरण गुण का तात्पर्य है।
 :<math>M' = \left(\mathbf{r}_1\times \mathbf{F}_1 + \mathbf{r}_2\times \mathbf{F}_2 + \cdots\right) + \mathbf{r}\times \left(\mathbf{F}_1 + \mathbf{F}_2 + \cdots \right).</math>
-हालाँकि, एक बल बलयुग्म की परिभाषा का अर्थ है
+चूंकि एक बल बलयुग्म की परिभाषा का अर्थ है।
 :<math>\mathbf{F}_1 + \mathbf{F}_2 + \cdots = 0.</math>
-इसलिए,
+इसलिए-
 :<math>M' = \mathbf{r}_1\times \mathbf{F}_1 + \mathbf{r}_2\times \mathbf{F}_2 + \cdots = M</math>
-यह साबित करता है कि क्षण संदर्भ बिंदु से स्वतंत्र है, जो इस बात का प्रमाण है कि बलयुग्म एक मुक्त सदिश है।
+यह प्रमाणित करता है कि बलाघूर्ण संदर्भ बिंदु से स्वतंत्र है। जो इस बात का प्रमाण है कि बलयुग्म मुक्त सदिश है।
 == बल और बलयुग्म ==
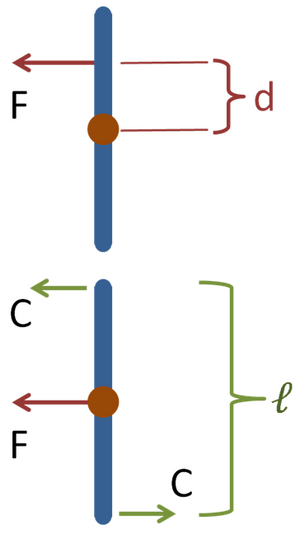
-[[File:Force and couple.PNG |thumb]]द्रव्यमान के केंद्र से दूरी d पर एक कठोर शरीर पर लगाए गए बल F का वही प्रभाव होता है जो समान बल सीधे द्रव्यमान के केंद्र पर लागू होता है और एक जोड़े Cℓ = Fd। बलयुग्म जोड़े के तल पर समकोण पर कठोर शरीर का [[कोणीय त्वरण]] उत्पन्न करता है।<ref name="DuBois">{{cite book |title=इंजीनियरिंग के यांत्रिकी, खंड 1|author=Augustus Jay Du Bois |url=https://archive.org/details/mechanicsengine01boisgoog |page=[https://archive.org/details/mechanicsengine01boisgoog/page/n233 186] |publisher=Wiley |year=1902}}
+[[File:Force and couple.PNG |thumb]]द्रव्यमान के केंद्र से दूरी d पर कठोर वस्तु पर लगाए गए बल F का वही प्रभाव होता है। जो समान बल सीधे द्रव्यमान के केंद्र पर निर्धारित होता है और बलयुग्म Cℓ = Fd है। बलयुग्म के तल पर समकोण पर कठोर वस्तु का [[कोणीय त्वरण]] उत्पन्न करता है।<ref name="DuBois">{{cite book |title=इंजीनियरिंग के यांत्रिकी, खंड 1|author=Augustus Jay Du Bois |url=https://archive.org/details/mechanicsengine01boisgoog |page=[https://archive.org/details/mechanicsengine01boisgoog/page/n233 186] |publisher=Wiley |year=1902}}
-</ref> द्रव्यमान के केंद्र में बल बल की दिशा में बल की दिशा में अभिविन्यास में बदलाव के बिना शरीर को गति देता है। सामान्य प्रमेय हैं:<ref name=DuBois/>: एक कठोर पिंड के किसी भी बिंदु O' पर कार्य करने वाला एक बल किसी भी बिंदु O पर समान और समानांतर बल F द्वारा प्रतिस्थापित किया जा सकता है और F के समानांतर बलों वाला एक बलयुग्म जिसका क्षण M = Fd है, d का पृथक्करण है ओ और ओ'। इसके विपरीत, बलयुग्म के तल में एक बलयुग्म और एक बल को उचित रूप से स्थित एक बल द्वारा प्रतिस्थापित किया जा सकता है।
+</ref> द्रव्यमान के केंद्र में बल की दिशा में अभिविन्यास में बदलाव के बिना वस्तु को गति देता है। सामान्य प्रमेय हैं कि<ref name=DuBois/> एक कठोर पिंड के किसी भी बिंदु O' पर कार्य करने वाला बल किसी भी बिंदु O पर समान और समानांतर बल F द्वारा प्रतिस्थापित किया जा सकता है और F के समानांतर बलों वाला बलयुग्म जिसका बलाघूर्ण M = Fd है, d का पृथक्करण है। इसके विपरीत बलयुग्म के तल में बलयुग्म और बल को उचित रूप से स्थित बल द्वारा प्रतिस्थापित किया जा सकता है।
-: किसी भी जोड़े को एक ही दिशा और क्षण के समान विमान में किसी भी वांछित बल या किसी वांछित भुजा के द्वारा प्रतिस्थापित किया जा सकता है।<ref name=DuBois/>
+: किसी भी बलयुग्म को एक ही दिशा और बलाघूर्ण के समान विमान में किसी भी वांछित बल या किसी वांछित भुजा के द्वारा प्रतिस्थापित किया जा सकता है।<ref name=DuBois/>
 == अनुप्रयोग ==
-[[मैकेनिकल इंजीनियरिंग]] और भौतिक विज्ञान में जोड़े बहुत महत्वपूर्ण हैं। कुछ उदाहरण हैं:
+[[मैकेनिकल इंजीनियरिंग]] और भौतिक विज्ञान में बलयुग्म बहुत महत्वपूर्ण हैं। कुछ उदाहरण हैं:
-* किसी के हाथ से पेचकस पर लगने वाला बल
+* किसी के हाथ से पेचकस पर लगने वाला बल।
-* पेचकश की नोक द्वारा पेंच के सिर पर लगाया गया बल
+* पेचकश की नोक द्वारा पेंच के सिर पर लगाया गया बल।
-* कताई [[प्रोपेलर]] पर कार्य करने वाले बलों को खींचें
+* कताई [[प्रोपेलर]] पर कार्य करने वाले बलों को खींचें।
 * एक समान विद्युत क्षेत्र में विद्युत द्विध्रुव पर बल।
-* एक अंतरिक्ष यान पर [[प्रतिक्रिया नियंत्रण प्रणाली]]।
+* अंतरिक्ष यान पर [[प्रतिक्रिया नियंत्रण प्रणाली]]।
 * [[स्टीयरिंग व्हील]] पर हाथों द्वारा लगाया गया बल।
@@ Line 61: / Line 57: @@
 * [[ट्रैक्शन (इंजीनियरिंग)]]
 * टॉर्क
-* [[पल (भौतिकी)]]
+* [[पल (भौतिकी)|बलाघूर्ण (भौतिकी)]]
-* ताकत
+* बल
 ==संदर्भ==
 {{reflist}}
 * H.F. Girvin (1938) ''Applied Mechanics'', §28 Couples, pp 33,4, Scranton Pennsylvania: International Textbook Company.
-[[Category: भौतिक मात्रा]] [[Category: यांत्रिकी]]
-[[Category: Machine Translated Page]]
 [[Category:Created On 21/03/2023]]
+[[Category:Lua-based templates]]
+[[Category:Machine Translated Page]]
+[[Category:Mechanics templates]]
+[[Category:Pages with empty portal template]]
+[[Category:Pages with script errors]]
+[[Category:Physics sidebar templates]]
+[[Category:Portal-inline template with redlinked portals]]
+[[Category:Templates Translated in Hindi]]
+[[Category:Templates Vigyan Ready]]
+[[Category:Templates that add a tracking category]]
+[[Category:Templates that generate short descriptions]]
+[[Category:Templates using TemplateData]]
+[[Category:भौतिक मात्रा]]
+[[Category:यांत्रिकी]]

Anonymous

Search

बलयुग्म (यांत्रिकी): Difference between revisions

Namespaces

More

Page actions

Latest revision as of 18:00, 17 April 2023

Contents

साधारण बलयुग्म

बल और बलयुग्म

अनुप्रयोग

यह भी देखें

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

बलयुग्म (यांत्रिकी): Difference between revisions

Latest revision as of 18:00, 17 April 2023

साधारण बलयुग्म

बल और बलयुग्म

अनुप्रयोग

यह भी देखें

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Categories