द्रव्यमान संतुलन: Difference between revisions
| Line 26: | Line 26: | ||
== निदर्शी उदाहरण == | == निदर्शी उदाहरण == | ||
साधारण उदाहरण अवधारणा को चित्रित कर सकता है। उस स्थिति पर विचार करें जिसमें टैंक में ठोस पदार्थों को निकालने के लिए घोल [[ स्थायीकरण टंकी |स्थायीकरण टंकी]] में प्रवाहित हो रहा है। टैंक में आंशिक रूप से जलमग्न [[कन्वेयर बेल्ट|वाहक पट्ट]] के माध्यम से तल पर ठोस एकत्र किए जाते हैं, और पानी अतिप्रवाह विसर्जन केंद्र के माध्यम से बाहर निकलता है। | |||
इस उदाहरण में दो पदार्थ हैं: ठोस और पानी है। पानी के अतिप्रवाह विसर्जन केंद्र में घोल प्रवेश द्वार की तुलना में ठोस पदार्थों के सापेक्ष पानी की बढ़ी हुई सांद्रता होती है, और वाहक पट्ट के बाहर निकलने से पानी के सापेक्ष ठोस पदार्थों की बढ़ी हुई सांद्रता होती है। | इस उदाहरण में दो पदार्थ हैं: ठोस और पानी है। पानी के अतिप्रवाह विसर्जन केंद्र में घोल प्रवेश द्वार की तुलना में ठोस पदार्थों के सापेक्ष पानी की बढ़ी हुई सांद्रता होती है, और वाहक पट्ट के बाहर निकलने से पानी के सापेक्ष ठोस पदार्थों की बढ़ी हुई सांद्रता होती है। | ||
| Line 38: | Line 38: | ||
मान लीजिए कि [[गारा|गारा प्रवेशिका]] संरचना (द्रव्यमान द्वारा) 50% ठोस और 50% पानी है, जिसमें {{val|100|ul=किग्रा|upl=मिनट}} बड़े स्तर पर प्रवाह होता है | माना जाता है कि टैंक स्थिर अवस्था में काम कर रहा है, और चूंकि संचयन शून्य है, इसलिए ठोस और पानी दोनों के लिए इनपुट और आउटपुट बराबर होना चाहिए। यदि हम जानते हैं कि घोल टैंक के लिए हटाने की दक्षता 60% है, तो पानी के विसर्जन केंद्र में सम्मिलित में होगा {{val|20|ul=किग्रा|upl=मिनट}} ठोस (40% गुना {{val|100|ul=किग्रा|upl=मिनट}} गुना 50% ठोस)। यदि हम संयुक्त ठोस और पानी की प्रवाह दर को मापते हैं, और पानी के {{val|65|ul=किग्रा|upl=मिनट}} विसर्जन केंद्र को दिखाया गया है, तो वाहिका पट्ट के माध्यम से निकलने वाले पानी की मात्रा {{val|5|ul=किग्रा|upl=मिनट}} होनी चाहिए | यह हमें पूरी तरह से यह निर्धारित करने की अनुमति देता है कि प्रणाली में द्रव्यमान को केवल सीमित जानकारी के साथ कैसे वितरित किया गया है और प्रणाली सीमाओं में द्रव्यमान संतुलन संबंधों का उपयोग कर रहा है। इस प्रणाली के द्रव्यमान संतुलन को सारणीबद्ध रूप में वर्णित किया जा सकता है: | मान लीजिए कि [[गारा|गारा प्रवेशिका]] संरचना (द्रव्यमान द्वारा) 50% ठोस और 50% पानी है, जिसमें {{val|100|ul=किग्रा|upl=मिनट}} बड़े स्तर पर प्रवाह होता है | माना जाता है कि टैंक स्थिर अवस्था में काम कर रहा है, और चूंकि संचयन शून्य है, इसलिए ठोस और पानी दोनों के लिए इनपुट और आउटपुट बराबर होना चाहिए। यदि हम जानते हैं कि घोल टैंक के लिए हटाने की दक्षता 60% है, तो पानी के विसर्जन केंद्र में सम्मिलित में होगा {{val|20|ul=किग्रा|upl=मिनट}} ठोस (40% गुना {{val|100|ul=किग्रा|upl=मिनट}} गुना 50% ठोस)। यदि हम संयुक्त ठोस और पानी की प्रवाह दर को मापते हैं, और पानी के {{val|65|ul=किग्रा|upl=मिनट}} विसर्जन केंद्र को दिखाया गया है, तो वाहिका पट्ट के माध्यम से निकलने वाले पानी की मात्रा {{val|5|ul=किग्रा|upl=मिनट}} होनी चाहिए | यह हमें पूरी तरह से यह निर्धारित करने की अनुमति देता है कि प्रणाली में द्रव्यमान को केवल सीमित जानकारी के साथ कैसे वितरित किया गया है और प्रणाली सीमाओं में द्रव्यमान संतुलन संबंधों का उपयोग कर रहा है। इस प्रणाली के द्रव्यमान संतुलन को सारणीबद्ध रूप में वर्णित किया जा सकता है: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+स्पष्टीकरण के लिए द्रव्यमान संतुलन | ||
! | ! | ||
! colspan="3" | | ! colspan="3" |प्रवाह | ||
|- | |- | ||
! | !पदार्थ | ||
! | !स्पष्टीकरण प्रवेशिका | ||
! | !स्पष्ट जल विसर्जन केंद्र | ||
! | !निष्काषित ठोस | ||
|- | |- | ||
! | !ठोस | ||
|50 | |50 किग्रा/मिनट | ||
|20 | |20 किग्रा/मिनट | ||
|30 | |30 किग्रा/मिनट | ||
|- | |- | ||
! | !जल | ||
|50 | |50 किग्रा/मिनट | ||
|45 | |45 किग्रा/मिनट | ||
|5 | |5 किग्रा/मिनट | ||
|- | |- | ||
! | !समग्र | ||
|100 | |100 किग्रा/मिनट | ||
|65 | |65 किग्रा/मिनट | ||
|35 | |35 किग्रा/मिनट | ||
|} | |} | ||
Revision as of 14:37, 11 April 2023
भौतिकी में, द्रव्यमान संतुलन, जिसे भौतिक संतुलन भी कहा जाता है, भौतिक प्रणालियों के विश्लेषण के लिए द्रव्यमान के संरक्षण का अनुप्रयोग है। प्रणाली में प्रवेश करने और छोड़ने वाली पदार्थ के लिए लेखांकन करके, बड़े स्तर पर प्रवाह की पहचान की जा सकती है जो इस तकनीक के बिना अज्ञात या मापना मुश्किल हो सकता है। प्रणाली के विश्लेषण में उपयोग किया जाने वाला सही संरक्षण नियम (भौतिकी) समस्या के संदर्भ पर निर्भर करता है, परन्तु सभी बड़े स्तर पर संरक्षण के आस-पास घूमते हैं, अर्थात वह पदार्थ गायब नहीं हो सकता है या बिना किसी कारण के नहीं बनाया जा सकता है।[1]: 59–62
इसलिए, बड़े स्तर पर संतुलन अभियांत्रिकी और पर्यावरण विश्लेषण में व्यापक रूप से उपयोग किया जाता है। उदाहरण के लिए, द्रव्यमान संतुलन सिद्धांत का उपयोग रासायनिक रिएक्टर को डिजाइन करने के लिए, रसायनों के उत्पादन के लिए वैकल्पिक प्रक्रियाओं का विश्लेषण करने के साथ-साथ प्रदूषण फैलाव और भौतिक प्रणालियों की अन्य प्रक्रियाओं के मॉडल के लिए किया जाता है। निकटता से संबंधित और पूरक विश्लेषण तकनीकों में संख्या संतुलन समीकरण, ऊर्जा लेखा और कुछ अत्यधिक जटिल एन्ट्रापी (उस ऊर्जा का परिणाम जो यांत्रिक ऊर्जा में परिवर्तिति नहीं हो सकती है) संतुलन सम्मिलित हैं। प्रशीतन चक्र जैसी प्रणालियों के जटिल डिजाइन और विश्लेषण के लिए इन तकनीकों की आवश्यकता होती है।
पर्यावरण की जांच में, बजट गणना का उपयोग बड़े स्तर पर संतुलन समीकरणों का वर्णन करने के लिए किया जाता है, जहां उनका उपयोग जांचने की डेटा (इनपुट और आउटपुट आदि की तुलना) के मूल्यांकन के लिए किया जाता है। जीव विज्ञान में, उपापचयी संगठन के लिए गतिशील ऊर्जा बजट सिद्धांत द्रव्यमान और ऊर्जा संतुलन का स्पष्ट उपयोग करता है।
परिचय
द्रव्यमान संतुलन के लिए उद्धृत सामान्य रूप वह द्रव्यमान है जो प्रणाली में प्रवेश करता है, द्रव्यमान के संरक्षण द्वारा, या तो प्रणाली को छोड़ देता है या प्रणाली के भीतर जमा हो जाता है।
गणितीय रूप से रासायनिक प्रतिक्रिया के बिना प्रणाली के लिए द्रव्यमान संतुलन इस प्रकार है:[1]: 59–62
कठोरता से उपरोक्त समीकरण रासायनिक प्रतिक्रियाओं वाले प्रणाली के लिए क्रियान्वित होता है यदि संतुलन समीकरण में प्रारूपों का कुल द्रव्यमान, यानी सिस्टम की सभी रासायनिक पदार्थों का योग कहा जाता है। रासायनिक अभिक्रिया के अभाव में आने और जाने वाली किसी भी रासायनिक प्रजाति की मात्रा समान होगी; यह प्रणाली में उपस्थित प्रत्येक प्रजाति के लिए समीकरण उत्पन्न देता है। चूँकि, यदि ऐसा नहीं है, तो प्रत्येक रासायनिक प्रजाति के उत्पादन या कमी (विलेय) की अनुमति देने के लिए द्रव्यमान संतुलन समीकरण में संशोधन किया जाना चाहिए। कुछ इस समीकरण में रासायनिक प्रतिक्रियाओं के लिए शब्द का उपयोग करते हैं, जो कमी के लिए ऋणात्मक और उत्पादन के लिए धनात्मक होगा। चूँकि, इस समीकरण के पारंपरिक रूप को धनात्मक उत्पादन शब्द (अर्थात प्रतिक्रिया का उत्पाद) और ऋणात्मक विलेय शब्द (उत्पादों का उत्पादन करने के लिए उपयोग किए जाने वाले अभिकारक) दोनों के लिए लिखा गया है। यद्यपि सभी प्रकार से शब्द प्रणाली पर कुल संतुलन के लिए उत्तरदायी होगा, यदि यह संतुलन समीकरण व्यक्तिगत प्रजाति पर क्रियान्वित किया जाना है और फिर पूरी प्रक्रिया, दोनों शब्द आवश्यक हैं। इस संशोधित समीकरण का उपयोग न केवल प्रतिक्रियाशील प्रणालियों के लिए किया जा सकता है, बल्कि जनसंख्या संतुलन के लिए भी किया जा सकता है जैसे कि कण यांत्रिकी समस्याओं में उत्पन्न होता है। समीकरण नीचे दिया गया है; ध्यान दें कि यह उस स्थिति में पहले के समीकरण को सरल बनाता है जब उत्पादन शब्द शून्य हो।[1]: 59–62
- परमाणु प्रतिक्रिया की अनुपस्थिति में, रासायनिक प्रतिक्रिया की उपस्थिति में भी अंदर और बाहर बहने वाले परमाणुओं की संख्या समान रहनी चाहिए।
- संतुलन बनाने के लिए, प्रणाली की सीमाओं को स्पष्ट रूप से परिभाषित किया जाना चाहिए।
- बड़े स्तर पर संतुलन भौतिक प्रणालियों पर कई स्तर पर लिया जा सकता है।
- बड़े स्तर पर संतुलन को स्थिर स्थिति की धारणा के साथ सरल बनाया जा सकता है, जिसमें संचय अवधि शून्य है।
निदर्शी उदाहरण
साधारण उदाहरण अवधारणा को चित्रित कर सकता है। उस स्थिति पर विचार करें जिसमें टैंक में ठोस पदार्थों को निकालने के लिए घोल स्थायीकरण टंकी में प्रवाहित हो रहा है। टैंक में आंशिक रूप से जलमग्न वाहक पट्ट के माध्यम से तल पर ठोस एकत्र किए जाते हैं, और पानी अतिप्रवाह विसर्जन केंद्र के माध्यम से बाहर निकलता है।
इस उदाहरण में दो पदार्थ हैं: ठोस और पानी है। पानी के अतिप्रवाह विसर्जन केंद्र में घोल प्रवेश द्वार की तुलना में ठोस पदार्थों के सापेक्ष पानी की बढ़ी हुई सांद्रता होती है, और वाहक पट्ट के बाहर निकलने से पानी के सापेक्ष ठोस पदार्थों की बढ़ी हुई सांद्रता होती है।
मान्यताओं
- स्थिर अवस्था
- अप्रतिक्रियाशील प्रणाली
विश्लेषण
मान लीजिए कि गारा प्रवेशिका संरचना (द्रव्यमान द्वारा) 50% ठोस और 50% पानी है, जिसमें 100 किग्रा/मिनट बड़े स्तर पर प्रवाह होता है | माना जाता है कि टैंक स्थिर अवस्था में काम कर रहा है, और चूंकि संचयन शून्य है, इसलिए ठोस और पानी दोनों के लिए इनपुट और आउटपुट बराबर होना चाहिए। यदि हम जानते हैं कि घोल टैंक के लिए हटाने की दक्षता 60% है, तो पानी के विसर्जन केंद्र में सम्मिलित में होगा 20 किग्रा/मिनट ठोस (40% गुना 100 किग्रा/मिनट गुना 50% ठोस)। यदि हम संयुक्त ठोस और पानी की प्रवाह दर को मापते हैं, और पानी के 65 किग्रा/मिनट विसर्जन केंद्र को दिखाया गया है, तो वाहिका पट्ट के माध्यम से निकलने वाले पानी की मात्रा 5 किग्रा/मिनट होनी चाहिए | यह हमें पूरी तरह से यह निर्धारित करने की अनुमति देता है कि प्रणाली में द्रव्यमान को केवल सीमित जानकारी के साथ कैसे वितरित किया गया है और प्रणाली सीमाओं में द्रव्यमान संतुलन संबंधों का उपयोग कर रहा है। इस प्रणाली के द्रव्यमान संतुलन को सारणीबद्ध रूप में वर्णित किया जा सकता है:
| प्रवाह | |||
|---|---|---|---|
| पदार्थ | स्पष्टीकरण प्रवेशिका | स्पष्ट जल विसर्जन केंद्र | निष्काषित ठोस |
| ठोस | 50 किग्रा/मिनट | 20 किग्रा/मिनट | 30 किग्रा/मिनट |
| जल | 50 किग्रा/मिनट | 45 किग्रा/मिनट | 5 किग्रा/मिनट |
| समग्र | 100 किग्रा/मिनट | 65 किग्रा/मिनट | 35 किग्रा/मिनट |
मास फीडबैक (रीसायकल)
बड़े पैमाने पर संतुलन उन प्रणालियों में किया जा सकता है जिनमें चक्रीय प्रवाह होता है। इन प्रणालियों में आउटपुट स्ट्रीम को एक इकाई के इनपुट में वापस फीड किया जाता है, अक्सर आगे के पुनर्संसाधन के लिए।[1]: 97–105
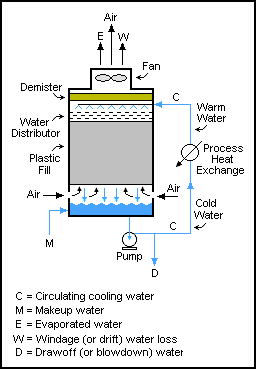
ऐसी प्रणालियाँ ग्राइंडिंग (अपघर्षक कटिंग) सर्किट में आम हैं, जहाँ अनाज को कुचला जाता है और फिर छलनी से केवल बारीक कणों को सर्किट से बाहर निकाला जाता है और बड़े कणों को रोलर मिल (ग्राइंडर) में वापस कर दिया जाता है। हालाँकि, रीसायकल प्रवाह किसी भी तरह से ठोस यांत्रिकी संचालन तक सीमित नहीं हैं; उनका उपयोग तरल और गैस प्रवाह में भी किया जाता है। ऐसा ही एक उदाहरण शीतलन टॉवर में है, जहां एक टावर के माध्यम से पानी को कई बार पंप किया जाता है, प्रत्येक पास में केवल थोड़ी मात्रा में पानी खींचा जाता है (ठोस निर्माण को रोकने के लिए) जब तक कि यह या तो वाष्पित न हो जाए या खींचे गए पानी से बाहर न निकल जाए। जल का द्रव्यमान संतुलन M = D + W + E है।
इनपुट उत्पादों के समग्र रूपांतरण को बढ़ाने में रीसायकल एड्स का उपयोग, जो कम प्रति-पास रूपांतरण प्रक्रियाओं (जैसे हैबर प्रक्रिया) के लिए उपयोगी है।
विभेदक द्रव्यमान संतुलन
एक मास बैलेंस भी गणना लिया जा सकता है। अवधारणा एक बड़े द्रव्यमान संतुलन के समान है, लेकिन यह एक सीमित प्रणाली के संदर्भ में किया जाता है (उदाहरण के लिए, कोई समय में सीमित मामले या अधिक सामान्य रूप से मात्रा पर विचार कर सकता है)। डिफरेंशियल मास बैलेंस का उपयोग डिफरेंशियल इक्वेशन उत्पन्न करने के लिए किया जाता है जो लक्ष्य प्रणाली को मॉडलिंग और समझने के लिए एक प्रभावी उपकरण प्रदान कर सकता है।
विभेदक जन संतुलन आमतौर पर दो चरणों में हल किया जाता है: सबसे पहले, अंतर समीकरणों को नियंत्रित करने का एक सेट प्राप्त किया जाना चाहिए, और फिर इन समीकरणों को विश्लेषणात्मक रूप से या कम ट्रैक्टेबल समस्याओं के लिए संख्यात्मक रूप से हल किया जाना चाहिए।
निम्नलिखित प्रणालियाँ अंतर द्रव्यमान संतुलन के अनुप्रयोगों के अच्छे उदाहरण हैं:
- आदर्श (हलचल) बैच रिएक्टर
- आदर्श टैंक रिएक्टर, जिसे निरंतर हलचल-टैंक रिएक्टर (CSTR) भी कहा जाता है
- आइडियल प्लग फ्लो रिएक्टर मॉडल (पीएफआर)
आदर्श बैच रिएक्टर
आदर्श पूरी तरह मिश्रित बैच रिएक्टर एक बंद प्रणाली है। इज़ोटेर्मल प्रक्रिया ग्रहण की जाती है, और मिश्रण एकाग्रता ढाल को रोकता है क्योंकि प्रतिक्रियाशील सांद्रता घट जाती है और समय के साथ उत्पाद सांद्रता बढ़ जाती है।[2]: 40–41 कई रसायन शास्त्र की पाठ्यपुस्तकें स्पष्ट रूप से मानती हैं कि अध्ययन की गई प्रणाली को एक बैच रिएक्टर के रूप में वर्णित किया जा सकता है जब वे प्रतिक्रिया कैनेटीक्स और रासायनिक संतुलन के बारे में लिखते हैं। किसी पदार्थ A का द्रव्यमान संतुलन बन जाता है
जहां आरA उस दर को दर्शाता है जिस पर पदार्थ A का उत्पादन होता है, V आयतन है (जो स्थिर हो सकता है या नहीं), nA पदार्थ A के मोल्स (n) की संख्या।
एक फेड-बैच रिएक्टर में कुछ अभिकारकों/अवयवों को लगातार या दालों में जोड़ा जाता है (पहले सभी अवयवों को मिलाकर दलिया बनाने की तुलना करें और फिर इसे उबलने दें, जिसे एक बैच रिएक्टर के रूप में वर्णित किया जा सकता है, या पहले केवल पानी और नमक मिलाकर और अन्य अवयवों को जोड़ने से पहले उस उबाल को बनाना, जिसे फेड-बैच रिएक्टर के रूप में वर्णित किया जा सकता है)। फेड-बैच रिएक्टरों के लिए मास बैलेंस थोड़ा और जटिल हो गया है।
प्रतिक्रियाशील उदाहरण
पहले उदाहरण में, हम दिखाएंगे कि हाइड्रोकार्बन-बेस ईंधन तेल के दहन के लिए वायु-ईंधन अनुपात और दहन उत्पाद गैस में प्रतिशत ऑक्सीजन के बीच संबंध बनाने के लिए द्रव्यमान संतुलन का उपयोग कैसे करें। सबसे पहले, सामान्य शुष्क हवा में होता है 0.2095 mol हवा के प्रति मोल ऑक्सीजन का, इसलिए एक तिल है O
2 में 4.773 mol शुष्क हवा। स्तुईचिओमेटरी दहन के लिए, हवा के द्रव्यमान और ईंधन तेल में प्रत्येक ज्वलनशील तत्व के द्रव्यमान के बीच संबंध हैं:
विशिष्ट विश्लेषणात्मक प्रक्रियाओं की सटीकता को ध्यान में रखते हुए, स्टोइकीओमेट्रिक दहन पर ईंधन के प्रति द्रव्यमान वायु के द्रव्यमान के लिए एक समीकरण है:
जहाँ wC, wH, wS, और wO ईंधन तेल में प्रत्येक तत्व के द्रव्यमान अंश को संदर्भित करता है, सल्फर SO2 और AFR को जलाता है।mass द्रव्यमान इकाइयों में वायु-ईंधन अनुपात को संदर्भित करता है।
के लिए {{val|1|ul=kg}86.1% C, 13.6% H, 0.2% O, और 0.1% S युक्त ईंधन तेल का हवा का स्टोइकोमेट्रिक द्रव्यमान है 14.56 kg, इसलिए AFR = 14.56। दहन उत्पाद द्रव्यमान तब है 15.56 kg. सटीक स्टोइकोमेट्री पर, O
2 अनुपस्थित होना चाहिए। 15 प्रतिशत अधिक हवा में, AFR = 16.75, और दहन उत्पाद गैस का द्रव्यमान है 17.75 kg, जिसमें है 0.505 kg अतिरिक्त ऑक्सीजन की। दहन गैस में इस प्रकार 2.84 प्रतिशत होता है O
2 द्रव्यमान द्वारा। प्रतिशत अतिरिक्त हवा और % के बीच संबंधO
2 दहन गैस में द्विघात समीकरणों द्वारा सटीक रूप से व्यक्त किया जाता है, जो 0-30 प्रतिशत अतिरिक्त हवा की सीमा से अधिक मान्य है:
दूसरे उदाहरण में, हम सामूहिक क्रिया के नियम का उपयोग रासायनिक संतुलन स्थिरांक के लिए व्यंजक प्राप्त करने के लिए करेंगे।
मान लें कि हमारे पास एक बंद रिएक्टर है जिसमें निम्न तरल चरण प्रतिवर्ती प्रतिक्रिया होती है:
पदार्थ A के लिए द्रव्यमान संतुलन बन जाता है
जैसा कि हमारे पास एक तरल चरण प्रतिक्रिया है, हम (आमतौर पर) एक स्थिर मात्रा मान सकते हैं और तब से हम पाते हैं
या
कई पाठ्य पुस्तकों में इसे प्रतिक्रिया दर की परिभाषा के रूप में निहित धारणा को निर्दिष्ट किए बिना दिया गया है कि हम केवल एक प्रतिक्रिया के साथ एक बंद प्रणाली में प्रतिक्रिया दर के बारे में बात कर रहे हैं। यह एक दुर्भाग्यपूर्ण गलती है जिसने कई छात्रों को वर्षों से भ्रमित किया है।
द्रव्यमान क्रिया के नियम के अनुसार अग्र अभिक्रिया दर को इस प्रकार लिखा जा सकता है
और पश्च प्रतिक्रिया दर के रूप में
जिस दर पर पदार्थ A का उत्पादन होता है वह इस प्रकार है
और चूंकि, संतुलन पर, ए की एकाग्रता स्थिर है, हम प्राप्त करते हैं
या, पुनर्व्यवस्थित
आदर्श टैंक रिएक्टर/लगातार उभारा टैंक रिएक्टर
निरंतर मिश्रित टैंक रिएक्टर एक खुली प्रणाली है जिसमें अभिकारकों की प्रभावशाली धारा और उत्पादों की प्रवाह धारा होती है।[2]: 41 एक झील को एक टैंक रिएक्टर के रूप में माना जा सकता है, और लंबे टर्नओवर समय वाली झीलें (उदाहरण के लिए कम फ्लक्स-टू-वॉल्यूम अनुपात के साथ) कई उद्देश्यों के लिए लगातार उत्तेजित (जैसे सभी मामलों में सजातीय) मानी जा सकती हैं। द्रव्यमान संतुलन तब बन जाता है
जहां क्यू0 और Q क्रमशः सिस्टम के अंदर और बाहर वॉल्यूमेट्रिक फ्लो को दर्शाता है और CA,0 और सीA प्रवाह और बहिर्वाह में क्रमशः ए की एकाग्रता। एक खुली व्यवस्था में हम कभी भी रासायनिक संतुलन तक नहीं पहुँच सकते। हालाँकि, हम एक गतिशील संतुलन तक पहुँच सकते हैं जहाँ सभी राज्य चर (तापमान, सांद्रता, आदि) स्थिर रहते हैं ().
उदाहरण
एक बाथटब पर विचार करें जिसमें कुछ नहाने का नमक घुला हो। अब हम बॉटम प्लग को अंदर रखते हुए और पानी भरते हैं। क्या होता है?
चूंकि कोई प्रतिक्रिया नहीं है, और चूंकि कोई बहिर्वाह नहीं है . जन संतुलन बन जाता है
या
हालांकि, कुल आयतन के लिए द्रव्यमान संतुलन का उपयोग करना, यह स्पष्ट है कि ओर वो . इस प्रकार हम प्राप्त करते हैं
ध्यान दें कि कोई प्रतिक्रिया नहीं है और इसलिए कोई प्रतिक्रिया दर या दर कानून शामिल नहीं है, और फिर भी . इस प्रकार हम यह निष्कर्ष निकाल सकते हैं कि प्रतिक्रिया दर को सामान्य तरीके से परिभाषित नहीं किया जा सकता है . किसी के बीच एक कड़ी से पहले पहले एक द्रव्यमान संतुलन लिखना चाहिए और प्रतिक्रिया दर पाई जा सकती है। हालाँकि, कई पाठ्यपुस्तकें प्रतिक्रिया दर को परिभाषित करती हैं
इस बात का उल्लेख किए बिना कि यह परिभाषा स्पष्ट रूप से मानती है कि सिस्टम बंद है, इसकी एक स्थिर मात्रा है और केवल एक प्रतिक्रिया है।
आदर्श प्लग फ्लो रिएक्टर (पीएफआर)
आदर्शीकृत प्लग फ्लो रिएक्टर एक खुली प्रणाली है जो एक ट्यूब जैसी होती है जिसमें प्रवाह की दिशा में कोई मिश्रण नहीं होता है लेकिन प्रवाह की दिशा में लंबवत सही मिश्रण होता है, जो अक्सर प्रवाह अशांत होने पर नदियों और पानी के पाइप जैसी प्रणालियों के लिए उपयोग किया जाता है। जब एक ट्यूब के लिए द्रव्यमान संतुलन बनाया जाता है, तो सबसे पहले ट्यूब के एक अतिसूक्ष्म भाग पर विचार किया जाता है और आदर्श टैंक रिएक्टर मॉडल का उपयोग करके उस पर द्रव्यमान संतुलन बनाया जाता है।[2]: 46–47 वह द्रव्यमान संतुलन प्राप्त करने के लिए संपूर्ण रिएक्टर आयतन पर अभिन्न है:
संख्यात्मक समाधान में, उदा। कंप्यूटर का उपयोग करते समय, आदर्श ट्यूब को अक्सर टैंक रिएक्टरों की एक श्रृंखला में अनुवादित किया जाता है, क्योंकि यह दिखाया जा सकता है कि पीएफआर श्रृंखला में हिलाए गए टैंकों की अनंत संख्या के बराबर है, लेकिन बाद वाले का विश्लेषण करना अक्सर आसान होता है, विशेष रूप से स्थिर अवस्था में .
अधिक जटिल समस्याएं
वास्तव में, रिएक्टर अक्सर गैर-आदर्श होते हैं, जिसमें सिस्टम का वर्णन करने के लिए उपरोक्त रिएक्टर मॉडल के संयोजन का उपयोग किया जाता है। न केवल रासायनिक प्रतिक्रिया दर, बल्कि द्रव्यमान अंतरण दर भी एक प्रणाली के गणितीय विवरण में महत्वपूर्ण हो सकती है, विशेष रूप से विषम प्रणालियों में। <रेफरी नाम = पेरी 1963 4-21>Perry, Robert H.; Chilton, Cecil H.; Kirkpatrick, Sidney D. (1963). Chemical Engineers' Handbook (fourth ed.). McGraw-Hill. pp. 4–21.</ref>
जैसा कि रासायनिक प्रतिक्रिया दर तापमान पर निर्भर करती है, यह अक्सर प्रणाली का पूरी तरह से वर्णन करने के लिए ऊर्जा लेखा (अक्सर एक पूर्ण ऊर्जा संतुलन के बजाय एक गर्मी संतुलन) के साथ-साथ बड़े पैमाने पर संतुलन बनाने के लिए आवश्यक होता है। ऊर्जा संतुलन के लिए एक अलग रिएक्टर मॉडल की आवश्यकता हो सकती है: एक प्रणाली जो द्रव्यमान के संबंध में बंद है, ऊर्जा के संबंध में खुली हो सकती है उदा। चूँकि ऊष्मा ऊष्मा चालन के माध्यम से प्रणाली में प्रवेश कर सकती है।
व्यावसायिक उपयोग
औद्योगिक प्रक्रिया संयंत्रों में, इस तथ्य का उपयोग करते हुए कि प्रक्रिया संयंत्र के किसी भी हिस्से में प्रवेश करने और छोड़ने वाले द्रव्यमान को संतुलित होना चाहिए, मापित प्रवाह को सही करने के लिए डेटा सत्यापन और सुलह एल्गोरिदम को नियोजित किया जा सकता है, बशर्ते कि सांख्यिकीय सामंजस्य और बहिष्करण की अनुमति देने के लिए प्रवाह माप की पर्याप्त अतिरेक मौजूद हो। पता लगाने योग्य गलत माप। चूंकि सभी वास्तविक विश्व मापित मानों में अंतर्निहित त्रुटि होती है, वित्तीय रिपोर्टिंग, अनुकूलन और विनियामक रिपोर्टिंग के लिए मापे गए मानों की तुलना में मिलान किए गए माप बेहतर आधार प्रदान करते हैं। इसे दैनिक आधार पर व्यावसायिक रूप से संभव बनाने के लिए सॉफ्टवेयर पैकेज मौजूद हैं।
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 Himmelblau, David M. (1967). केमिकल इंजीनियरिंग में बुनियादी सिद्धांत और गणना (2nd ed.). Prentice Hall.
- ↑ 2.0 2.1 2.2 Weber, Walter J., Jr. (1972). जल गुणवत्ता नियंत्रण के लिए भौतिक-रासायनिक प्रक्रियाएं. Wiley-Interscience. ISBN 0-471-92435-0.
{{cite book}}: CS1 maint: multiple names: authors list (link)
बाहरी संबंध
- Material Balance Calculations
- Material Balance Fundamentals
- The Material Balance for Chemical Reactors
- Material and energy balance
- Heat and material balance method of process control for petrochemical plants and oil refineries, United States Patent 6751527
- Morris, Arthur E.; Geiger, Gordon; Fine, H. Alan (2011). Handbook on Material and Energy Balance Calculations in Material Processing (3rd ed.). Wiley. ISBN 978-1-118-06565-5.