सिग्मॉइड फ़ंक्शन: Difference between revisions
No edit summary |
No edit summary |
||
| (6 intermediate revisions by 4 users not shown) | |||
| Line 2: | Line 2: | ||
[[File:Logistic-curve.svg|thumb|320px|right|[[ रसद वक्र | तर्कगणित वक्र]]]] | [[File:Logistic-curve.svg|thumb|320px|right|[[ रसद वक्र | तर्कगणित वक्र]]]] | ||
[[File:Error Function.svg|thumb|right|320px|[[त्रुटि समारोह|त्रुटि फलन]] का आलेख]] | [[File:Error Function.svg|thumb|right|320px|[[त्रुटि समारोह|त्रुटि फलन]] का आलेख]]सिग्माभ फलन एक गणितीय फलन है जिसमें एक विशेषता एस-आकार का वक्र या सिग्माभ वक्र होता है। | ||
सिग्माभ फलन का | सिग्माभ फलन का सामान्य उदाहरण [[रसद समारोह|तर्कगणित फलन]] है जो पहले चित्र में दिखाया गया है और सूत्र द्वारा परिभाषित किया गया है:<ref name="Han-Morag_1995" /> | ||
अन्य मानक सिग्माभ फलन उदाहरण अनुभाग में दिए गए हैं। कुछ क्षेत्रों में, विशेष रूप से [[कृत्रिम तंत्रिका नेटवर्क]] के संदर्भ में, सिग्माभ फलन शब्द का उपयोग तर्कगणित फलन के लिए | <math>S(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{e^x + 1}=1-S(-x).</math> | ||
अन्य मानक सिग्माभ फलन उदाहरण अनुभाग में दिए गए हैं। कुछ क्षेत्रों में, विशेष रूप से [[कृत्रिम तंत्रिका नेटवर्क]] के संदर्भ में, सिग्माभ फलन शब्द का उपयोग तर्कगणित फलन के लिए उपनाम के रूप में किया जाता है। | |||
सिग्माभ फलन के विशेष स्थितियों में [[गोम्पर्ट्ज़ वक्र]] (मॉडलिंग प्रणाली में उपयोग किया जाता है जो x के बड़े मानों पर संतृप्त होते है) और ओगी वक्र (कुछ बांधों के [[स्पिलवे|अधिप्लव मार्ग]] में उपयोग किया जाता है) सम्मिलित हैं। सिग्माभ फलनों में सभी [[वास्तविक संख्या|वास्तविक संख्याओं]] का प्रांत होता है, पुनरावृत्ति (प्रतिक्रिया) मान के साथ सामान्यतः एकदिष्ट रूप से बढ़ता है परन्तु घट सकता है। सिग्माभ फलनों प्रायः 0 से 1 की सीमा में पुनरावृत्ति मान (y अक्ष) दिखाते हैं। एक और सामान्यतः उपयोग की जाने वाली सीमा -1 से 1 तक होती है। | सिग्माभ फलन के विशेष स्थितियों में [[गोम्पर्ट्ज़ वक्र]] (मॉडलिंग प्रणाली में उपयोग किया जाता है जो x के बड़े मानों पर संतृप्त होते है) और ओगी वक्र (कुछ बांधों के [[स्पिलवे|अधिप्लव मार्ग]] में उपयोग किया जाता है) सम्मिलित हैं। सिग्माभ फलनों में सभी [[वास्तविक संख्या|वास्तविक संख्याओं]] का प्रांत होता है, पुनरावृत्ति (प्रतिक्रिया) मान के साथ सामान्यतः एकदिष्ट रूप से बढ़ता है परन्तु घट सकता है। सिग्माभ फलनों प्रायः 0 से 1 की सीमा में पुनरावृत्ति मान (y अक्ष) दिखाते हैं। एक और सामान्यतः उपयोग की जाने वाली सीमा -1 से 1 तक होती है। | ||
[[कृत्रिम न्यूरॉन]] के [[सक्रियण समारोह|सक्रियण फलन]] के रूप में तर्कगणित और [[अतिशयोक्तिपूर्ण स्पर्शरेखा|अतिपरवलय स्पर्शरेखीय]] फलनों सहित सिग्माभ फलनों की एक विस्तृत विविधता का उपयोग किया गया है। सिग्माभ वक्र आँकड़ों में [[संचयी वितरण कार्य|संचयी बंटन]] फलनों (जो 0 से 1 तक जाते हैं) के रूप में भी सामान्य हैं, जैसे कि [[रसद घनत्व|तर्कगणित घनत्व]] के अभिन्न अंग, [[सामान्य घनत्व]] और छात्र का | [[कृत्रिम न्यूरॉन]] के [[सक्रियण समारोह|सक्रियण फलन]] के रूप में तर्कगणित और [[अतिशयोक्तिपूर्ण स्पर्शरेखा|अतिपरवलय स्पर्शरेखीय]] फलनों सहित सिग्माभ फलनों की एक विस्तृत विविधता का उपयोग किया गया है। सिग्माभ वक्र आँकड़ों में [[संचयी वितरण कार्य|संचयी बंटन]] फलनों (जो 0 से 1 तक जाते हैं) के रूप में भी सामान्य हैं, जैसे कि [[रसद घनत्व|तर्कगणित घनत्व]] के अभिन्न अंग, [[सामान्य घनत्व]] और छात्र का t संचय घनत्व फलन। तर्कगणित सिग्माभ फलन व्युत्क्रमणीय है, और इसका व्युत्क्रम लॉजिट फलन है। | ||
== परिभाषा == | == परिभाषा == | ||
सिग्माभ फलन एक परिबद्ध फलन, विभेदक, वास्तविक फलन है जो सभी वास्तविक निविष्ट मानों के लिए परिभाषित किया गया है और प्रत्येक बिंदु पर एक गैर-ऋणात्मक व्युत्पन्न है<ref name="Han-Morag_1995" /> <ref name="yibei" /> और ठीक एक नतिपरिवर्तन बिंदु है। सिग्माभ फलन और सिग्माभ वक्र एक ही वस्तु को संदर्भित करते हैं। | |||
== गुण == | == गुण == | ||
सामान्यतः, एक सिग्माभ फलन [[मोनोटोनिक फ़ंक्शन|एकदिष्ट फलन]] होता है, और इसका पहला व्युत्पन्न होता है जो घंटाकार फलन होता है। इसके विपरीत, किसी भी निरंतर, गैर-ऋणात्मक, [[घंटी के आकार का कार्य|घंटाकार फलन]] (एक स्थानीय अधिकतम और कोई स्थानीय न्यूनतम, जब तक पतित न हो) सिग्माभी होगा। इस प्रकार कई सामान्य संचय बंटन के लिए संचयी बंटन फलन सिग्माभी हैं। ऐसा ही एक उदाहरण त्रुटि फलन है, जो | सामान्यतः, एक सिग्माभ फलन [[मोनोटोनिक फ़ंक्शन|एकदिष्ट फलन]] होता है, और इसका पहला व्युत्पन्न होता है जो घंटाकार फलन होता है। इसके विपरीत, किसी भी निरंतर, गैर-ऋणात्मक, [[घंटी के आकार का कार्य|घंटाकार फलन]] (एक स्थानीय अधिकतम और कोई स्थानीय न्यूनतम, जब तक पतित न हो) सिग्माभी होगा। इस प्रकार कई सामान्य संचय बंटन के लिए संचयी बंटन फलन सिग्माभी हैं। ऐसा ही एक उदाहरण त्रुटि फलन है, जो सामान्य बंटन के संचयी बंटन फलन से संबंधित है; दूसरा चाप स्पर्शरेखा फलन है, जो कॉची बंटन के संचयी बंटन फलन से संबंधित है। | ||
सिग्माभ फलन क्षैतिज स्पर्शोन्मुख की एक युग्म द्वारा <math>x \rightarrow \pm \infty</math> के रूप में व्यवरूद्ध है। | |||
सिग्माभ फलन किसी विशेष बिंदु से कम मानों के लिए उन्मुख फलन है, और यह उस बिंदु से अधिक मानों के लिए अवमुख फलन है: यहां कई उदाहरणों में, वह बिंदु 0 है। | सिग्माभ फलन किसी विशेष बिंदु से कम मानों के लिए उन्मुख फलन है, और यह उस बिंदु से अधिक मानों के लिए अवमुख फलन है: यहां कई उदाहरणों में, वह बिंदु 0 है। | ||
== उदाहरण == | == उदाहरण == | ||
[[File:Gjl-t(x).svg|thumb|320px|right|कुछ सिग्माभ फलनों की तुलना की। रेखाचित्र में सभी फलनों को सामान्यीकृत किया जाता है ताकि मूल में उनकी | [[File:Gjl-t(x).svg|thumb|320px|right|कुछ सिग्माभ फलनों की तुलना की। रेखाचित्र में सभी फलनों को सामान्यीकृत किया जाता है ताकि मूल में उनकी प्रवणता 1 हो।]] | ||
* तर्कगणित फलन | |||
<math display="block"> f(x) = \frac{1}{1 + e^{-x}} </math> | |||
* अतिपरवलय स्पर्शरेखीय (उपरोक्त तर्कगणित फलन का स्थानांतरित और सोपानी किया गया संस्करण) <math display="block"> f(x) = \tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}} </math> | * अतिपरवलय स्पर्शरेखीय (उपरोक्त तर्कगणित फलन का स्थानांतरित और सोपानी किया गया संस्करण) <math display="block"> f(x) = \tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}} </math> | ||
* [[आर्कटैंजेंट फ़ंक्शन|चाप स्पर्शरेखा फलन]] <math display="block"> f(x) = \arctan x </math> | * [[आर्कटैंजेंट फ़ंक्शन|चाप स्पर्शरेखा फलन]] <math display="block"> f(x) = \arctan x </math> | ||
| Line 29: | Line 34: | ||
* त्रुटि फलन <math display="block"> f(x) = \operatorname{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} \, dt </math> | * त्रुटि फलन <math display="block"> f(x) = \operatorname{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} \, dt </math> | ||
* [[सामान्यीकृत रसद समारोह|सामान्यीकृत तर्कगणित फलन]] <math display="block"> f(x) = \left(1 + e^{-x} \right)^{-\alpha}, \quad \alpha > 0 </math> | * [[सामान्यीकृत रसद समारोह|सामान्यीकृत तर्कगणित फलन]] <math display="block"> f(x) = \left(1 + e^{-x} \right)^{-\alpha}, \quad \alpha > 0 </math> | ||
* [[स्मूथस्टेप| | * [[स्मूथस्टेप|मृदु चरण]] फलन <math display="block"> f(x) = \begin{cases} | ||
{\displaystyle | {\displaystyle | ||
\left( \int_0^1 \left(1 - u^2\right)^N du \right)^{-1} \int_0^x \left( 1 - u^2 \right)^N \ du}, & |x| \le 1 \\ | \left( \int_0^1 \left(1 - u^2\right)^N du \right)^{-1} \int_0^x \left( 1 - u^2 \right)^N \ du}, & |x| \le 1 \\ | ||
| Line 38: | Line 43: | ||
* और अधिक सामान्य रूप में<ref name="Dunning-Kensler-Coudeville-Bailleux_2015" /> <math display="block"> f(x) = \frac{x}{\left(1 + |x|^{k}\right)^{1/k}} </math> | * और अधिक सामान्य रूप में<ref name="Dunning-Kensler-Coudeville-Bailleux_2015" /> <math display="block"> f(x) = \frac{x}{\left(1 + |x|^{k}\right)^{1/k}} </math> | ||
* शिफ्ट और सोपानी तक, कई सिग्माभ<math display="block"> f(x) = \varphi(\varphi(x, \beta), \alpha) , </math>की विशेष स्थिति हैं जहां<math display="block"> \varphi(x, \lambda) = \begin{cases} (1 - \lambda x)^{1/\lambda} & \lambda \ne 0 \\e^{-x} & \lambda = 0 \\ \end{cases} </math>ऋणात्मक शक्ति परिवर्तन का व्युत्क्रम है, और <math>\alpha < 1</math> और <math>\beta < 1</math> आकार पैरामीटर हैं।<ref name="grex" /> | * शिफ्ट और सोपानी तक, कई सिग्माभ<math display="block"> f(x) = \varphi(\varphi(x, \beta), \alpha) , </math>की विशेष स्थिति हैं जहां<math display="block"> \varphi(x, \lambda) = \begin{cases} (1 - \lambda x)^{1/\lambda} & \lambda \ne 0 \\e^{-x} & \lambda = 0 \\ \end{cases} </math>ऋणात्मक शक्ति परिवर्तन का व्युत्क्रम है, और <math>\alpha < 1</math> और <math>\beta < 1</math> आकार पैरामीटर हैं।<ref name="grex" /> | ||
*समतल अंतर्वेशन<ref>{{Cite web|url=https://www.youtube.com/watch?v=vD5g8aVscUI|title=Smooth Transition Function in One Dimension | Smooth Transition Function Series Part 1|via=www.youtube.com| date =16 August 2022|author=EpsilonDelta|at=13:29/14:04}}</ref> को (-1,1) के लिए सामान्यीकृत किया गया है और <math>n</math> शून्य पर | *समतल अंतर्वेशन<ref>{{Cite web|url=https://www.youtube.com/watch?v=vD5g8aVscUI|title=Smooth Transition Function in One Dimension | Smooth Transition Function Series Part 1|via=www.youtube.com| date =16 August 2022|author=EpsilonDelta|at=13:29/14:04}}</ref> को (-1,1) के लिए सामान्यीकृत किया गया है और <math>n</math> शून्य पर प्रवणता है: | ||
<math display="block">\begin{align}f(x) &= \begin{cases} | <math display="block">\begin{align}f(x) &= \begin{cases} | ||
{\displaystyle | {\displaystyle | ||
| Line 53: | Line 58: | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
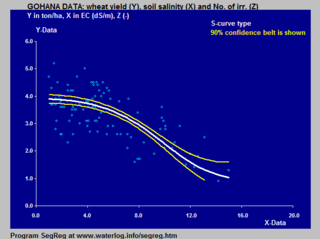
[[File:Gohana inverted S-curve.png|thumb|right|320px|गेहूं की उपज और मृदा लवणता के बीच संबंध को प्रतिरूपित करने के लिए प्रतिलोमित तर्कगणित एस-वक्र]]कई प्राकृतिक प्रक्रियाएं, जैसे कि जटिल प्रणाली [[ सीखने की अवस्था |अधिगमन वक्र]], लघु प्रारम्भ से | [[File:Gohana inverted S-curve.png|thumb|right|320px|गेहूं की उपज और मृदा लवणता के बीच संबंध को प्रतिरूपित करने के लिए प्रतिलोमित तर्कगणित एस-वक्र]]कई प्राकृतिक प्रक्रियाएं, जैसे कि जटिल प्रणाली [[ सीखने की अवस्था |अधिगमन वक्र]], लघु प्रारम्भ से प्रगति प्रदर्शित करती हैं जो समय के साथ एक चरमोत्कर्ष को गति देती है और पहुंचती है। जब एक विशिष्ट गणितीय मॉडल की कमी होती है, तो सिग्माभ फलन का उपयोग प्रायः किया जाता है।<ref name="Gibbs_2000" /> | ||
वैन जेनुचटेन-गुप्ता मॉडल एक प्रतिलोमित एस-वक्र पर आधारित है और [[मिट्टी की लवणता|मृदा लवणता]] के लिए फसल की उपज की प्रतिक्रिया पर लागू होते है। | वैन जेनुचटेन-गुप्ता मॉडल एक प्रतिलोमित एस-वक्र पर आधारित है और [[मिट्टी की लवणता|मृदा लवणता]] के लिए फसल की उपज की प्रतिक्रिया पर लागू होते है। | ||
| Line 59: | Line 64: | ||
कृषि में मॉडलिंग फसल प्रतिक्रिया में मृदा लवणता और मृदा में [[पानी की मेज|भौम जलस्तर]] की गहराई दोनों के लिए फसल उपज (गेहूं) की प्रतिक्रिया के लिए तर्कगणित एस-वक्र के अनुप्रयोग के उदाहरण दिखाए गए हैं। | कृषि में मॉडलिंग फसल प्रतिक्रिया में मृदा लवणता और मृदा में [[पानी की मेज|भौम जलस्तर]] की गहराई दोनों के लिए फसल उपज (गेहूं) की प्रतिक्रिया के लिए तर्कगणित एस-वक्र के अनुप्रयोग के उदाहरण दिखाए गए हैं। | ||
कृत्रिम तंत्रिका नेटवर्क में, दक्षता के अतिरिक्त कभी-कभी गैर- | कृत्रिम तंत्रिका नेटवर्क में, दक्षता के अतिरिक्त कभी-कभी गैर-मृदु फलनों का उपयोग किया जाता है; इन्हें [[ कठिन अवग्रह |जटिल सिग्माभ]] के रूप में जाना जाता है। | ||
[[ऑडियो सिग्नल प्रोसेसिंग|श्रव्य संकेत प्रक्रमण]] में, सिग्माभ फलनों का उपयोग [[एनालॉग सर्किटरी|अनुरूप परिपथिकी]] [[क्लिपिंग (ऑडियो)|कर्तन ( | [[ऑडियो सिग्नल प्रोसेसिंग|श्रव्य संकेत प्रक्रमण]] में, सिग्माभ फलनों का उपयोग [[एनालॉग सर्किटरी|अनुरूप परिपथिकी]] [[क्लिपिंग (ऑडियो)|कर्तन (श्रव्य]]) की ध्वनि का अनुकरण करने के लिए [[ webshaper |तरंग संरूपित्र]] [[स्थानांतरण प्रकार्य|स्थानांतरण प्रफलन]] के रूप में किया जाता है।<ref name="Smith_2010" /> | ||
[[जीव रसायन]] और [[ औषध |औषध विज्ञान]] में, [[हिल समीकरण (जैव रसायन)|हिल समीकरण (जैव रसायन]]) और हिल-लैंगमुइर समीकरण सिग्माभ फलन हैं। | [[जीव रसायन]] और [[ औषध |औषध विज्ञान]] में, [[हिल समीकरण (जैव रसायन)|हिल समीकरण (जैव रसायन]]) और हिल-लैंगमुइर समीकरण सिग्माभ फलन हैं। | ||
| Line 67: | Line 72: | ||
कंप्यूटर आलेख और वास्तविक समय प्रतिपादन में, कुछ सिग्माभ फलनों का उपयोग रंगों या ज्यामिति को दो मानों के बीच सुचारू रूप से और प्रत्यक्ष सन्धि या असंततता के बिना मिश्रित करने के लिए किया जाता है। | कंप्यूटर आलेख और वास्तविक समय प्रतिपादन में, कुछ सिग्माभ फलनों का उपयोग रंगों या ज्यामिति को दो मानों के बीच सुचारू रूप से और प्रत्यक्ष सन्धि या असंततता के बिना मिश्रित करने के लिए किया जाता है। | ||
पीएच पैमाने की | पीएच पैमाने की लघुगणकीय प्रकृति के कारण प्रबल अम्ल और प्रबल आधारों के बीच अनुमापन वक्र सिग्माभ आकार के होते है। | ||
[[एक प्रकार 3]] का उपयोग करके तर्कगणित फलन की कुशलता से गणना की जा सकती है।<ref name="Gustafson-Yonemoto_2017" /> | [[एक प्रकार 3|प्रकार 3]] का उपयोग करके तर्कगणित फलन की कुशलता से गणना की जा सकती है।<ref name="Gustafson-Yonemoto_2017" /> | ||
== यह भी देखें == | == यह भी देखें == | ||
{{div col|colwidth=30em}} | {{div col|colwidth=30em}} | ||
* [[चरण फलन]] | * [[चरण फलन]] | ||
| Line 108: | Line 112: | ||
* {{cite web|archive-url=https://web.archive.org/web/20220714181630/https://www.waterlog.info/sigmoid.htm|url-status=live |url=https://www.waterlog.info/sigmoid.htm |title=Fitting of logistic S-curves (sigmoids) to data using SegRegA|archive-date=14 July 2022 }} | * {{cite web|archive-url=https://web.archive.org/web/20220714181630/https://www.waterlog.info/sigmoid.htm|url-status=live |url=https://www.waterlog.info/sigmoid.htm |title=Fitting of logistic S-curves (sigmoids) to data using SegRegA|archive-date=14 July 2022 }} | ||
{{Differentiable computing}} | {{Differentiable computing}} | ||
[[Category: | [[Category:Collapse templates]] | ||
[[Category:Created On 10/04/2023]] | [[Category:Created On 10/04/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:कृत्रिम तंत्रिका प्रसार]] | |||
[[Category:प्राथमिक विशेष कार्य]] | |||
Latest revision as of 16:53, 27 April 2023

सिग्माभ फलन एक गणितीय फलन है जिसमें एक विशेषता एस-आकार का वक्र या सिग्माभ वक्र होता है।
सिग्माभ फलन का सामान्य उदाहरण तर्कगणित फलन है जो पहले चित्र में दिखाया गया है और सूत्र द्वारा परिभाषित किया गया है:[1]
अन्य मानक सिग्माभ फलन उदाहरण अनुभाग में दिए गए हैं। कुछ क्षेत्रों में, विशेष रूप से कृत्रिम तंत्रिका नेटवर्क के संदर्भ में, सिग्माभ फलन शब्द का उपयोग तर्कगणित फलन के लिए उपनाम के रूप में किया जाता है।
सिग्माभ फलन के विशेष स्थितियों में गोम्पर्ट्ज़ वक्र (मॉडलिंग प्रणाली में उपयोग किया जाता है जो x के बड़े मानों पर संतृप्त होते है) और ओगी वक्र (कुछ बांधों के अधिप्लव मार्ग में उपयोग किया जाता है) सम्मिलित हैं। सिग्माभ फलनों में सभी वास्तविक संख्याओं का प्रांत होता है, पुनरावृत्ति (प्रतिक्रिया) मान के साथ सामान्यतः एकदिष्ट रूप से बढ़ता है परन्तु घट सकता है। सिग्माभ फलनों प्रायः 0 से 1 की सीमा में पुनरावृत्ति मान (y अक्ष) दिखाते हैं। एक और सामान्यतः उपयोग की जाने वाली सीमा -1 से 1 तक होती है।
कृत्रिम न्यूरॉन के सक्रियण फलन के रूप में तर्कगणित और अतिपरवलय स्पर्शरेखीय फलनों सहित सिग्माभ फलनों की एक विस्तृत विविधता का उपयोग किया गया है। सिग्माभ वक्र आँकड़ों में संचयी बंटन फलनों (जो 0 से 1 तक जाते हैं) के रूप में भी सामान्य हैं, जैसे कि तर्कगणित घनत्व के अभिन्न अंग, सामान्य घनत्व और छात्र का t संचय घनत्व फलन। तर्कगणित सिग्माभ फलन व्युत्क्रमणीय है, और इसका व्युत्क्रम लॉजिट फलन है।
परिभाषा
सिग्माभ फलन एक परिबद्ध फलन, विभेदक, वास्तविक फलन है जो सभी वास्तविक निविष्ट मानों के लिए परिभाषित किया गया है और प्रत्येक बिंदु पर एक गैर-ऋणात्मक व्युत्पन्न है[1] [2] और ठीक एक नतिपरिवर्तन बिंदु है। सिग्माभ फलन और सिग्माभ वक्र एक ही वस्तु को संदर्भित करते हैं।
गुण
सामान्यतः, एक सिग्माभ फलन एकदिष्ट फलन होता है, और इसका पहला व्युत्पन्न होता है जो घंटाकार फलन होता है। इसके विपरीत, किसी भी निरंतर, गैर-ऋणात्मक, घंटाकार फलन (एक स्थानीय अधिकतम और कोई स्थानीय न्यूनतम, जब तक पतित न हो) सिग्माभी होगा। इस प्रकार कई सामान्य संचय बंटन के लिए संचयी बंटन फलन सिग्माभी हैं। ऐसा ही एक उदाहरण त्रुटि फलन है, जो सामान्य बंटन के संचयी बंटन फलन से संबंधित है; दूसरा चाप स्पर्शरेखा फलन है, जो कॉची बंटन के संचयी बंटन फलन से संबंधित है।
सिग्माभ फलन क्षैतिज स्पर्शोन्मुख की एक युग्म द्वारा के रूप में व्यवरूद्ध है।
सिग्माभ फलन किसी विशेष बिंदु से कम मानों के लिए उन्मुख फलन है, और यह उस बिंदु से अधिक मानों के लिए अवमुख फलन है: यहां कई उदाहरणों में, वह बिंदु 0 है।
उदाहरण
- तर्कगणित फलन
- अतिपरवलय स्पर्शरेखीय (उपरोक्त तर्कगणित फलन का स्थानांतरित और सोपानी किया गया संस्करण)
- चाप स्पर्शरेखा फलन
- गुडरमैनियन फलन
- त्रुटि फलन
- सामान्यीकृत तर्कगणित फलन
- मृदु चरण फलन
- कुछ बीजगणितीय फलन, उदाहरण के लिए
- और अधिक सामान्य रूप में[3]
- शिफ्ट और सोपानी तक, कई सिग्माभकी विशेष स्थिति हैं जहांऋणात्मक शक्ति परिवर्तन का व्युत्क्रम है, और और आकार पैरामीटर हैं।[4]
- समतल अंतर्वेशन[5] को (-1,1) के लिए सामान्यीकृत किया गया है और शून्य पर प्रवणता है:
अनुप्रयोग
कई प्राकृतिक प्रक्रियाएं, जैसे कि जटिल प्रणाली अधिगमन वक्र, लघु प्रारम्भ से प्रगति प्रदर्शित करती हैं जो समय के साथ एक चरमोत्कर्ष को गति देती है और पहुंचती है। जब एक विशिष्ट गणितीय मॉडल की कमी होती है, तो सिग्माभ फलन का उपयोग प्रायः किया जाता है।[6]
वैन जेनुचटेन-गुप्ता मॉडल एक प्रतिलोमित एस-वक्र पर आधारित है और मृदा लवणता के लिए फसल की उपज की प्रतिक्रिया पर लागू होते है।
कृषि में मॉडलिंग फसल प्रतिक्रिया में मृदा लवणता और मृदा में भौम जलस्तर की गहराई दोनों के लिए फसल उपज (गेहूं) की प्रतिक्रिया के लिए तर्कगणित एस-वक्र के अनुप्रयोग के उदाहरण दिखाए गए हैं।
कृत्रिम तंत्रिका नेटवर्क में, दक्षता के अतिरिक्त कभी-कभी गैर-मृदु फलनों का उपयोग किया जाता है; इन्हें जटिल सिग्माभ के रूप में जाना जाता है।
श्रव्य संकेत प्रक्रमण में, सिग्माभ फलनों का उपयोग अनुरूप परिपथिकी कर्तन (श्रव्य) की ध्वनि का अनुकरण करने के लिए तरंग संरूपित्र स्थानांतरण प्रफलन के रूप में किया जाता है।[7]
जीव रसायन और औषध विज्ञान में, हिल समीकरण (जैव रसायन) और हिल-लैंगमुइर समीकरण सिग्माभ फलन हैं।
कंप्यूटर आलेख और वास्तविक समय प्रतिपादन में, कुछ सिग्माभ फलनों का उपयोग रंगों या ज्यामिति को दो मानों के बीच सुचारू रूप से और प्रत्यक्ष सन्धि या असंततता के बिना मिश्रित करने के लिए किया जाता है।
पीएच पैमाने की लघुगणकीय प्रकृति के कारण प्रबल अम्ल और प्रबल आधारों के बीच अनुमापन वक्र सिग्माभ आकार के होते है।
प्रकार 3 का उपयोग करके तर्कगणित फलन की कुशलता से गणना की जा सकती है।[8]
यह भी देखें
- चरण फलन
- संकेत फलन
- हैविसाइड चरण फलन
- तर्कगणित प्रतिक्रमण
- लॉजिट
- निष्कोण फलन
- सोबोलेवा संशोधित अतिपरवलय स्पर्शरेखीय
- निष्कोण अधिकतम फलन
- स्विश फलन
- वीबुल बंटन
- फर्मी-डिराक सांख्यिकी
संदर्भ
- ↑ 1.0 1.1 Han, Jun; Morag, Claudio (1995). "The influence of the sigmoid function parameters on the speed of backpropagation learning". In Mira, José; Sandoval, Francisco (eds.). From Natural to Artificial Neural Computation. Lecture Notes in Computer Science. Vol. 930. pp. 195–201. doi:10.1007/3-540-59497-3_175. ISBN 978-3-540-59497-0.
- ↑ Ling, Yibei; He, Bin (December 1993). "Entropic analysis of biological growth models". IEEE Transactions on Biological Engineering. 40 (12): 1193–2000. doi:10.1109/10.250574. PMID 8125495.
- ↑ Dunning, Andrew J.; Kensler, Jennifer; Coudeville, Laurent; Bailleux, Fabrice (2015-12-28). "Some extensions in continuous methods for immunological correlates of protection". BMC Medical Research Methodology. 15 (107): 107. doi:10.1186/s12874-015-0096-9. PMC 4692073. PMID 26707389.
- ↑ "grex --- Growth-curve Explorer". GitHub. 9 July 2022. Archived from the original on 2022-08-25. Retrieved 2022-08-25.
- ↑ EpsilonDelta (16 August 2022). "Smooth Transition Function in One Dimension | Smooth Transition Function Series Part 1". 13:29/14:04 – via www.youtube.com.
- ↑ Gibbs, Mark N.; Mackay, D. (November 2000). "Variational Gaussian process classifiers". IEEE Transactions on Neural Networks. 11 (6): 1458–1464. doi:10.1109/72.883477. PMID 18249869. S2CID 14456885.
- ↑ Smith, Julius O. (2010). Physical Audio Signal Processing (2010 ed.). W3K Publishing. ISBN 978-0-9745607-2-4. Archived from the original on 2022-07-14. Retrieved 2020-03-28.
- ↑ Gustafson, John L.; Yonemoto, Isaac (2017-06-12). "Beating Floating Point at its Own Game: Posit Arithmetic" (PDF). Archived (PDF) from the original on 2022-07-14. Retrieved 2019-12-28.
अग्रिम पठन
- Mitchell, Tom M. (1997). Machine Learning. WCB McGraw–Hill. ISBN 978-0-07-042807-2.. (NB. In particular see "Chapter 4: Artificial Neural Networks" (in particular pp. 96–97) where Mitchell uses the word "logistic function" and the "sigmoid function" synonymously – this function he also calls the "squashing function" – and the sigmoid (aka logistic) function is used to compress the outputs of the "neurons" in multi-layer neural nets.)
- Humphrys, Mark. "Continuous output, the sigmoid function". Archived from the original on 2022-07-14. Retrieved 2022-07-14. (NB. Properties of the sigmoid, including how it can shift along axes and how its domain may be transformed.)
बाहरी संबंध
- "Fitting of logistic S-curves (sigmoids) to data using SegRegA". Archived from the original on 14 July 2022.