समान कण: Difference between revisions

From Vigyanwiki
(Created page with "{{Short description|Concept in quantum mechanics of perfectly substitutable particles}}{{Use American English|date=January 2019}}{{multiple issues| {{refimprove|date=September...")
 
No edit summary
Line 1: Line 1:
{{Short description|Concept in quantum mechanics of perfectly substitutable particles}}{{Use American English|date=January 2019}}{{multiple issues|
{{Short description|Concept in quantum mechanics of perfectly substitutable particles}}{{Statistical mechanics|cTopic=[कण सांख्यिकी{{!}}कण सांख्यिकी]}}
{{refimprove|date=September 2008}}
{{more footnotes|date=September 2008}}
}}


{{Statistical mechanics|cTopic=[[Particle statistics|Particle Statistics]]}}
[[क्वांटम यांत्रिकी|परिमाण यांत्रिकी]] [[मेसन|प्रक्रिया]], समान [[कण]] (जिन्हें अप्रभेद्य या अविवेकी कण भी कहा जाता है) ऐसे कण होते हैं जिन्हें सिद्धांत रूप में भी एक दूसरे से अलग नहीं किया जा सकता है। समान कणों की प्रजातियों में [[प्राथमिक कण]] (जैसे [[इलेक्ट्रॉन|विद्युदअणु]]), समग्र उप-परमाणु कण (जैसे [[परमाणु नाभिक]]), साथ ही परमाणु और [[अणु]] शामिल हैं, लेकिन इन तक सीमित नहीं हैं।अर्ध कण भी इसी प्रकार का व्यवहार करते हैं। हालांकि सभी ज्ञात अप्रभेद्य कण केवल परिमाण दायरे में मौजूद हैं, कणों के सभी संभावित प्रकारों की कोई विस्तृत सूची नहीं है और न ही प्रयोज्यता की स्पष्ट सीमा है, जैसा कि कण सांख्यिकी परिमाण सांख्यिकी में पता लगाया गया है।


[[क्वांटम यांत्रिकी]] [[मेसन]], समान [[कण]] (जिन्हें अप्रभेद्य या अविवेकी कण भी कहा जाता है) ऐसे कण होते हैं जिन्हें सिद्धांत रूप में भी एक दूसरे से अलग नहीं किया जा सकता है। समान कणों की प्रजातियों में [[प्राथमिक कण]] (जैसे [[इलेक्ट्रॉन]]), समग्र उप-परमाणु कण (जैसे [[परमाणु नाभिक]]), साथ ही परमाणु और [[अणु]] शामिल हैं, लेकिन इन तक सीमित नहीं हैं। [[क्वासिपार्टिकल]]्स भी इसी प्रकार का व्यवहार करते हैं। हालांकि सभी ज्ञात अप्रभेद्य कण केवल क्वांटम दायरे में मौजूद हैं, कणों के सभी संभावित प्रकारों की कोई विस्तृत सूची नहीं है और न ही प्रयोज्यता की स्पष्ट सीमा है, जैसा कि कण सांख्यिकी #Quantum सांख्यिकी में पता लगाया गया है।
समान कणों की दो मुख्य श्रेणियां हैं: बोसोन, जो परिमाण अवस्थाओं को साझा कर सकते हैं, और [[फर्मियन]], जो नहीं कर सकते (जैसा कि [[पाउली अपवर्जन सिद्धांत]] द्वारा वर्णित है)। फोटॉन, ग्लूऑन, [[फोनन]], [[हीलियम -4]] नाभिक और सभी मेसॉन [[बोसॉन]] के उदाहरण हैं। विद्युदअणु, [[ न्युट्रीनो ]], [[क्वार्क]], [[प्रोटॉन]], [[न्यूट्रॉन]] और [[हीलियम -3]] नाभिक फ़र्मियन के उदाहरण हैं।


समान कणों की दो मुख्य श्रेणियां हैं: बोसोन, जो क्वांटम अवस्थाओं को साझा कर सकते हैं, और [[फर्मियन]], जो नहीं कर सकते (जैसा कि [[पाउली अपवर्जन सिद्धांत]] द्वारा वर्णित है)। फोटॉन, ग्लूऑन, [[फोनन]], [[हीलियम -4]] नाभिक और सभी मेसॉन [[बोसॉन]] के उदाहरण हैं। इलेक्ट्रॉन, [[ न्युट्रीनो ]], [[क्वार्क]], [[प्रोटॉन]], [[न्यूट्रॉन]] और [[हीलियम -3]] नाभिक फ़र्मियन के उदाहरण हैं।
तथ्य यह है कि कण समान हो सकते हैं, [[सांख्यिकीय यांत्रिकी]] में महत्वपूर्ण परिणाम हैं, जहां गणना संभाव्यता सिद्धांत तर्कों पर निर्भर करती है, जो इस बात के प्रति संवेदनशील हैं कि अध्ययन की जा रही वस्तुएं समान हैं या नहीं। नतीजतन, समान कण अलग-अलग कणों से स्पष्ट रूप से भिन्न सांख्यिकीय व्यवहार प्रदर्शित करते हैं। उदाहरण के लिए, गिब्स के गिब्स विरोधाभास मिश्रण विरोधाभास के समाधान के रूप में कणों की अविभाज्यता को प्रस्तावित किया गया है।
 
तथ्य यह है कि कण समान हो सकते हैं, [[सांख्यिकीय यांत्रिकी]] में महत्वपूर्ण परिणाम हैं, जहां गणना संभाव्यता सिद्धांत तर्कों पर निर्भर करती है, जो इस बात के प्रति संवेदनशील हैं कि अध्ययन की जा रही वस्तुएं समान हैं या नहीं। नतीजतन, समान कण अलग-अलग कणों से स्पष्ट रूप से भिन्न सांख्यिकीय व्यवहार प्रदर्शित करते हैं। उदाहरण के लिए, गिब्स के गिब्स विरोधाभास # द मिक्सिंग पैराडॉक्स के समाधान के रूप में कणों की अविभाज्यता को प्रस्तावित किया गया है।


== कणों के बीच भेद ==
== कणों के बीच भेद ==


कणों के बीच भेद करने की दो विधियाँ हैं। पहली विधि कणों के आंतरिक भौतिक गुणों, जैसे [[द्रव्यमान]], विद्युत आवेश और [[स्पिन (भौतिकी)]] में अंतर पर निर्भर करती है। यदि मतभेद मौजूद हैं, तो संबंधित गुणों को मापकर कणों के बीच अंतर करना संभव है। हालाँकि, यह एक अनुभवजन्य तथ्य है कि एक ही प्रजाति के सूक्ष्म कणों में पूरी तरह से समान भौतिक गुण होते हैं। उदाहरण के लिए, ब्रह्माण्ड के प्रत्येक इलेक्ट्रॉन में बिल्कुल समान विद्युत आवेश होता है; यही कारण है कि प्राथमिक प्रभार जैसी किसी चीज के बारे में बात करना संभव है।
कणों के बीच भेद करने की दो विधियाँ हैं। पहली विधि कणों के आंतरिक भौतिक गुणों, जैसे [[द्रव्यमान]], विद्युत आवेश और [[स्पिन (भौतिकी)]] (चक्रण) में अंतर पर निर्भर करती है। यदि मतभेद मौजूद हैं, तो संबंधित गुणों को मापकर कणों के बीच अंतर करना संभव है। हालाँकि, यह एक अनुभवजन्य तथ्य है कि एक ही प्रजाति के सूक्ष्म कणों में पूरी तरह से समान भौतिक गुण होते हैं। उदाहरण के लिए, ब्रह्माण्ड के प्रत्येक विद्युदअणु में बिल्कुल समान विद्युत आवेश होता है; यही कारण है कि प्राथमिक प्रभार जैसी किसी चीज के बारे में बात करना संभव है।


भले ही कणों के समान भौतिक गुण हों, कणों के बीच अंतर करने के लिए एक दूसरी विधि बनी रहती है, जो प्रत्येक कण के प्रक्षेपवक्र को ट्रैक करना है। जब तक प्रत्येक कण की स्थिति को अनंत सटीकता के साथ मापा जा सकता है (यहां तक ​​कि जब कण टकराते हैं), तब तक कोई अस्पष्टता नहीं होगी कि कौन सा कण है।
भले ही कणों के समान भौतिक गुण हों, कणों के बीच अंतर करने के लिए एक दूसरी विधि बनी रहती है, जो प्रत्येक कण के प्रक्षेपवक्र को मार्ग  करना है। जब तक प्रत्येक कण की स्थिति को अनंत सटीकता के साथ मापा जा सकता है (यहां तक ​​कि जब कण टकराते हैं), तब तक कोई अस्पष्टता नहीं होगी कि कौन सा कण है।


दूसरे दृष्टिकोण के साथ समस्या यह है कि यह क्वांटम यांत्रिकी के सिद्धांतों के विपरीत है। क्वांटम सिद्धांत के अनुसार, माप के बीच की अवधि के दौरान कणों की निश्चित स्थिति नहीं होती है। इसके बजाय, वे [[ तरंग क्रिया ]] द्वारा नियंत्रित होते हैं जो प्रत्येक स्थिति में एक कण को ​​खोजने की संभावना देते हैं। जैसे-जैसे समय बीतता है, वेवफंक्शन फैलते हैं और ओवरलैप होते हैं। एक बार ऐसा हो जाने के बाद, बाद के माप में यह निर्धारित करना असंभव हो जाता है कि कौन से कण की स्थिति पहले मापी गई स्थिति के अनुरूप है। कणों को तब अप्रभेद्य कहा जाता है।
दूसरे दृष्टिकोण के साथ समस्या यह है कि यह परिमाण यांत्रिकी के सिद्धांतों के विपरीत है। परिमाण सिद्धांत के अनुसार, माप के बीच की अवधि के दौरान कणों की निश्चित स्थिति नहीं होती है। इसके बजाय, वे [[ तरंग क्रिया ]] द्वारा नियंत्रित होते हैं जो प्रत्येक स्थिति में एक कण को ​​खोजने की संभावना देते हैं। जैसे-जैसे समय बीतता है, तरंग के कार्य फैलते हैं और अधिव्यापन होते हैं। एक बार ऐसा हो जाने के बाद, बाद के माप में यह निर्धारित करना असंभव हो जाता है कि कौन से कण की स्थिति पहले मापी गई स्थिति के अनुरूप है। कणों को तब अप्रभेद्य कहा जाता है।


== क्वांटम यांत्रिक विवरण ==
== परिमाण यांत्रिक विवरण ==


=== सममित और विषम स्थिति ===
=== सममित और विषम स्थिति ===
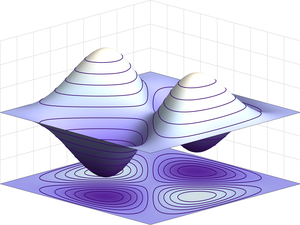
[[Image:Asymmetricwave2.png|right|thumb|एक अनंत वर्ग कुएं की क्षमता में (फर्मियोनिक) 2-कण अवस्था के लिए एंटीसिमेट्रिक वेवफंक्शन।]]
[[Image:Asymmetricwave2.png|right|thumb|एक अनंत वर्ग कुएं की क्षमता में (फर्मियोनिक) 2-कण अवस्था के लिए प्रतिसममित तरंग कार्य।]]
[[Image:Symmetricwave2.png|right|thumb|एक अनंत वर्ग कुएं की क्षमता में (बोसोनिक) 2-कण अवस्था के लिए सममित तरंग।]]क्वांटम यांत्रिकी के गणितीय सूत्रीकरण पर लेख में विकसित औपचारिकता का उपयोग करते हुए उपरोक्त चर्चा को ठोस बनाने के लिए एक उदाहरण निम्नलिखित है।
[[Image:Symmetricwave2.png|right|thumb|एक अनंत वर्ग कुएं की क्षमता में (बोसोनिक) 2-कण अवस्था के लिए सममित तरंग।]]परिमाण यांत्रिकी के गणितीय सूत्रीकरण पर लेख में विकसित औपचारिकता का उपयोग करते हुए उपरोक्त चर्चा को ठोस बनाने के लिए एक उदाहरण निम्नलिखित है।


चलो n एकल-कण अवस्थाओं को निर्दिष्ट करने के लिए (असतत) क्वांटम संख्याओं के एक पूर्ण सेट को निरूपित करते हैं (उदाहरण के लिए, एक बॉक्स समस्या में कण के लिए, n को वेवफंक्शन के परिमाणित तरंग वेक्टर के रूप में लें।) सरलता के लिए, एक प्रणाली पर विचार करें। दो कणों की जो एक दूसरे के साथ बातचीत नहीं कर रहे हैं। मान लीजिए कि एक कण n अवस्था में है<sub>1</sub>, और दूसरा राज्य n में है<sub>2</sub>. सिस्टम की क्वांटम स्थिति को अभिव्यक्ति द्वारा निरूपित किया जाता है
चलो n एकल-कण अवस्थाओं को निर्दिष्ट करने के लिए (असतत) परिमाण संख्याओं के एक पूर्ण समुच्चय को निरूपित करते हैं (उदाहरण के लिए, एक वर्ग समस्या में कण के लिए, n को तरंग कार्य के परिमाणित तरंग संवाहक  के रूप में लें।) सरलता के लिए, एक प्रणाली पर विचार करें। दो कणों की जो एक दूसरे के साथ बातचीत नहीं कर रहे हैं। मान लीजिए कि एक कण n अवस्था में है<sub>1</sub>, और दूसरा पद n में है<sub>2</sub>. सिस्टम की परिमाण स्थिति को अभिव्यक्ति द्वारा निरूपित किया जाता है


:<math> | n_1 \rang | n_2 \rang </math>
:<math> | n_1 \rang | n_2 \rang </math>
जहां टेन्सर उत्पाद का क्रम मायने रखता है (यदि <math> | n_2 \rang | n_1 \rang </math>, तो कण 1 राज्य n पर कब्जा कर लेता है<sub>2</sub> जबकि कण 2 राज्य n पर कब्जा कर लेता है<sub>1</sub>). यह [[टेंसर उत्पाद]] स्थान के लिए आधार बनाने का प्रामाणिक तरीका है <math>H \otimes H</math> व्यक्तिगत रिक्त स्थान से संयुक्त प्रणाली का। यह अभिव्यक्ति अलग-अलग कणों के लिए मान्य है, हालांकि, यह अप्रभेद्य कणों के लिए उपयुक्त नहीं है <math> |n_1\rang |n_2\rang</math> और <math>|n_2\rang |n_1\rang </math> कणों के आदान-प्रदान के परिणामस्वरूप आम तौर पर अलग-अलग अवस्थाएँ होती हैं।
जहां प्रदिश उत्पाद का क्रम मायने रखता है (यदि <math> | n_2 \rang | n_1 \rang </math>, तो कण 1 पद n पर अधिकृत कर लेता है<sub>2</sub> जबकि कण 2 पद n पर अधिकृत कर लेता है<sub>1</sub>). यह [[प्रदिश उत्पाद]] स्थान के लिए आधार बनाने का प्रामाणिक तरीका है <math>H \otimes H</math> व्यक्तिगत अंतरालक से संयुक्त प्रणाली का। यह अभिव्यक्ति अलग-अलग कणों के लिए मान्य है, हालांकि, यह अप्रभेद्य कणों के लिए उपयुक्त नहीं है <math> |n_1\rang |n_2\rang</math> और <math>|n_2\rang |n_1\rang </math> कणों के आदान-प्रदान के परिणामस्वरूप आम तौर पर अलग-अलग अवस्थाएँ होती हैं।


* कण 1 n पर कब्जा कर लेता है<sub>1</sub> स्थिति और कण 2 n पर कब्जा कर लेता है<sub>2</sub> राज्य ≠ कण 1 n पर कब्जा कर लेता है<sub>2</sub> स्थिति और कण 2 n पर कब्जा कर लेता है<sub>1</sub> राज्य ।
* कण 1 n पर अधिकृत कर लेता है<sub>1</sub> स्थिति और कण 2 n पर अधिकृत कर लेता है<sub>2</sub> पद ≠ कण 1 n पर अधिकृत कर लेता है<sub>2</sub> स्थिति और कण 2 n पर अधिकृत कर लेता है<sub>1</sub> पद ।


दो अवस्थाएँ शारीरिक रूप से केवल तभी समतुल्य होती हैं, जब वे एक जटिल चरण कारक द्वारा अधिक से अधिक भिन्न हों। दो अप्रभेद्य कणों के लिए, कण विनिमय से पहले की अवस्था विनिमय के बाद की अवस्था के भौतिक रूप से समतुल्य होनी चाहिए, इसलिए ये दोनों अवस्थाएँ एक जटिल चरण कारक द्वारा भिन्न होती हैं। यह तथ्य बताता है कि दो अप्रभेद्य (और गैर-अंतःक्रियात्मक) कणों के लिए एक स्थिति निम्नलिखित दो संभावनाओं द्वारा दी गई है: <ref>{{Cite web|url=http://www.tcm.phy.cam.ac.uk/~pdh1001/thesis/node14.html|title = 2.3 Identical particles}}</ref><ref>{{harvtxt|Tuckerman|2010|p=385}}</ref><ref>{{Cite book|title=परिचयात्मक क्वांटम यांत्रिकी|last=Liboff|first=Richard|publisher=Addison-Wesley|year=2003|isbn=978-0805387148|pages=597}}</ref>
दो अवस्थाएँ शारीरिक रूप से केवल तभी समतुल्य होती हैं, जब वे एक जटिल चरण कारक द्वारा अधिक से अधिक भिन्न हों। दो अप्रभेद्य कणों के लिए, कण विनिमय से पहले की अवस्था विनिमय के बाद की अवस्था के भौतिक रूप से समतुल्य होनी चाहिए, इसलिए ये दोनों अवस्थाएँ एक जटिल चरण कारक द्वारा भिन्न होती हैं। यह तथ्य बताता है कि दो अप्रभेद्य (और गैर-अंतःक्रियात्मक) कणों के लिए एक स्थिति निम्नलिखित दो संभावनाओं द्वारा दी गई है: <ref>{{Cite web|url=http://www.tcm.phy.cam.ac.uk/~pdh1001/thesis/node14.html|title = 2.3 Identical particles}}</ref><ref>{{harvtxt|Tuckerman|2010|p=385}}</ref><ref>{{Cite book|title=परिचयात्मक क्वांटम यांत्रिकी|last=Liboff|first=Richard|publisher=Addison-Wesley|year=2003|isbn=978-0805387148|pages=597}}</ref>
:<math> |n_1\rang |n_2\rang \pm |n_2\rang |n_1\rang </math>
:<math> |n_1\rang |n_2\rang \pm |n_2\rang |n_1\rang </math>
राज्यों जहां यह एक राशि है सममित के रूप में जाना जाता है, जबकि अंतर को शामिल करने वाले राज्यों को एंटीसिमेट्रिक कहा जाता है। अधिक पूरी तरह से, सममित राज्यों का रूप है
पदों जहां यह एक राशि है सममित के रूप में जाना जाता है, जबकि अंतर को शामिल करने वाले पदों को प्रतिसममित कहा जाता है। अधिक पूरी तरह से, सममित पदों का रूप है


:<math> |n_1, n_2; S\rang \equiv \mbox{constant} \times \bigg( |n_1\rang |n_2\rang + |n_2\rang |n_1\rang \bigg) </math>
:<math> |n_1, n_2; S\rang \equiv \mbox{constant} \times \bigg( |n_1\rang |n_2\rang + |n_2\rang |n_1\rang \bigg) </math>
जबकि एंटीसिमेट्रिक राज्यों का रूप है
जबकि प्रतिसममित पदों का रूप है


:<math> |n_1, n_2; A\rang \equiv \mbox{constant} \times \bigg( |n_1\rang |n_2\rang - |n_2\rang |n_1\rang \bigg) </math>
:<math> |n_1, n_2; A\rang \equiv \mbox{constant} \times \bigg( |n_1\rang |n_2\rang - |n_2\rang |n_1\rang \bigg) </math>
ध्यान दें कि यदि एन<sub>1</sub> और n<sub>2</sub> समान हैं, एंटीसिमेट्रिक अभिव्यक्ति शून्य देता है, जो एक राज्य वेक्टर नहीं हो सकता क्योंकि इसे सामान्यीकृत नहीं किया जा सकता है। दूसरे शब्दों में, एक से अधिक समान कण एक एंटीसिमेट्रिक स्थिति पर कब्जा नहीं कर सकते (एक एंटीसिमेट्रिक राज्य केवल एक कण द्वारा कब्जा कर लिया जा सकता है)। इसे पाउली अपवर्जन सिद्धांत के रूप में जाना जाता है, और यह परमाणुओं के रासायनिक गुणों और पदार्थ की स्थिरता के पीछे मूलभूत कारण है।
ध्यान दें कि यदि एन<sub>1</sub> और n<sub>2</sub> समान हैं, प्रतिसममित अभिव्यक्ति शून्य देता है, जो एक पद संवाहक  नहीं हो सकता क्योंकि इसे सामान्यीकृत नहीं किया जा सकता है। दूसरे शब्दों में, एक से अधिक समान कण एक प्रतिसममित स्थिति पर अधिकृत नहीं कर सकते (एक प्रतिसममित पद केवल एक कण द्वारा अधिकृत कर लिया जा सकता है)। इसे पाउली अपवर्जन सिद्धांत के रूप में जाना जाता है, और यह परमाणुओं के रासायनिक गुणों और पदार्थ की स्थिरता के पीछे मूलभूत कारण है।


=== एक्सचेंज समरूपता ===
=== विनिमय समरूपता ===


सममित और विषमतापूर्ण राज्यों का महत्व अंततः अनुभवजन्य साक्ष्य पर आधारित है। यह प्रकृति का एक तथ्य प्रतीत होता है कि समान कण मिश्रित समरूपता की अवस्थाओं पर कब्जा नहीं करते हैं, जैसे कि
सममित और विषमतापूर्ण पदों का महत्व अंततः अनुभवजन्य साक्ष्य पर आधारित है। यह प्रकृति का एक तथ्य प्रतीत होता है कि समान कण मिश्रित समरूपता की अवस्थाओं पर अधिकृत नहीं करते हैं, जैसे कि


:<math> |n_1, n_2; ?\rang = \mbox{constant} \times \bigg( |n_1\rang |n_2\rang + i |n_2\rang |n_1\rang \bigg) </math>
:<math> |n_1, n_2; ?\rang = \mbox{constant} \times \bigg( |n_1\rang |n_2\rang + i |n_2\rang |n_1\rang \bigg) </math>
वास्तव में इस नियम का एक अपवाद है, जिस पर बाद में चर्चा की जाएगी। दूसरी ओर, यह दिखाया जा सकता है कि सममित और एंटीसिमेट्रिक राज्य एक अर्थ में विशेष हैं, बहु-कण राज्यों की एक विशेष समरूपता की जांच करके जिसे विनिमय समरूपता के रूप में जाना जाता है।
वास्तव में इस नियम का एक अपवाद है, जिस पर बाद में चर्चा की जाएगी। दूसरी ओर, यह दिखाया जा सकता है कि सममित और प्रतिसममित पद एक अर्थ में विशेष हैं, बहु-कण पदों की एक विशेष समरूपता की जांच करके जिसे विनिमय समरूपता के रूप में जाना जाता है।


एक्सचेंज ऑपरेटर कहे जाने वाले रैखिक ऑपरेटर ''पी'' को परिभाषित करें। जब यह दो राज्य वैक्टरों के टेन्सर उत्पाद पर कार्य करता है, तो यह राज्य वैक्टरों के मूल्यों का आदान-प्रदान करता है:
विनिमय संक्रियक कहे जाने वाले रैखिक संक्रियक ''पी'' को परिभाषित करें। जब यह दो पद सदिश  के प्रदिश उत्पाद पर कार्य करता है, तो यह पद सदिश  के मूल्यों का आदान-प्रदान करता है:


:<math>P \bigg(|\psi\rang |\phi\rang \bigg) \equiv |\phi\rang |\psi\rang </math>
:<math>P \bigg(|\psi\rang |\phi\rang \bigg) \equiv |\phi\rang |\psi\rang </math>
P हर्मिटियन संकारक और एकात्मक संकारक दोनों है। क्योंकि यह एकात्मक है, इसे एक [[समरूपता (भौतिकी)]] के रूप में माना जा सकता है। इस समरूपता को कणों से जुड़े लेबलों के आदान-प्रदान के तहत समरूपता के रूप में वर्णित किया जा सकता है (यानी, एकल-कण हिल्बर्ट रिक्त स्थान के लिए)।
P हर्मिटियन संकारक और एकात्मक संकारक दोनों है। क्योंकि यह एकात्मक है, इसे एक [[समरूपता (भौतिकी)]] के रूप में माना जा सकता है। इस समरूपता को कणों से जुड़े नामपत्रों के आदान-प्रदान के तहत समरूपता के रूप में वर्णित किया जा सकता है (यानी, एकल-कण हिल्बर्ट अंतरालक के लिए)।


स्पष्ट रूप से, <math>P^2 = 1</math> (पहचान संचालक), इसलिए P के आइगेनमान +1 और -1 हैं। संबंधित [[eigenvector]]s सममित और एंटीसिमेट्रिक राज्य हैं:
स्पष्ट रूप से, <math>P^2 = 1</math> (पहचान संचालक), इसलिए P के अतिलक्षणिक अंतराल (अभिलक्षणिक मान ) +1 और -1 हैं। संबंधित [[अभिलक्षणिक सदिश]] सममित और प्रतिसममित पद हैं:


:<math>P|n_1, n_2; S\rang = + |n_1, n_2; S\rang</math>
:<math>P|n_1, n_2; S\rang = + |n_1, n_2; S\rang</math>
:<math>P|n_1, n_2; A\rang = - |n_1, n_2; A\rang</math>
:<math>P|n_1, n_2; A\rang = - |n_1, n_2; A\rang</math>
दूसरे शब्दों में, सममित और एंटीसिमेट्रिक राज्य अनिवार्य रूप से कण लेबल के आदान-प्रदान के तहत अपरिवर्तित होते हैं: हिल्बर्ट स्पेस में कहीं और घुमाए जाने के बजाय उन्हें केवल +1 या -1 के कारक से गुणा किया जाता है। यह इंगित करता है कि अप्रभेद्यता पर पहले की चर्चा के साथ कण लेबल का कोई भौतिक अर्थ नहीं है।
दूसरे शब्दों में, सममित और प्रतिसममित पद अनिवार्य रूप से कण नामपत्र के आदान-प्रदान के तहत अपरिवर्तित होते हैं: हिल्बर्ट अंतराल में कहीं और घुमाए जाने के बजाय उन्हें केवल +1 या -1 के कारक से गुणा किया जाता है। यह इंगित करता है कि अप्रभेद्यता पर पहले की चर्चा के साथ कण नामपत्र का कोई भौतिक अर्थ नहीं है।


यह याद किया जाएगा कि P हर्मिटियन है। नतीजतन, इसे सिस्टम के अवलोकन के रूप में माना जा सकता है, जिसका अर्थ है कि, सिद्धांत रूप में, यह पता लगाने के लिए एक माप किया जा सकता है कि कोई राज्य सममित या विषम है या नहीं। इसके अलावा, कणों की समानता इंगित करती है कि [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] को सममित रूप में लिखा जा सकता है, जैसे कि
यह याद किया जाएगा कि P हर्मिटियन है। नतीजतन, इसे सिस्टम के अवलोकन के रूप में माना जा सकता है, जिसका अर्थ है कि, सिद्धांत रूप में, यह पता लगाने के लिए एक माप किया जा सकता है कि कोई पद सममित या विषम है या नहीं। इसके अलावा, कणों की समानता इंगित करती है कि [[हैमिल्टनियन (क्वांटम यांत्रिकी)|हैमिल्टनियन (परिमाण यांत्रिकी)]] को सममित रूप में लिखा जा सकता है, जैसे कि


:<math>H = \frac{p_1^2}{2m} + \frac{p_2^2}{2m} + U(|x_1 - x_2|) + V(x_1) + V(x_2) </math>
:<math>H = \frac{p_1^2}{2m} + \frac{p_2^2}{2m} + U(|x_1 - x_2|) + V(x_1) + V(x_2) </math>
यह दिखाना संभव है कि ऐसे हैमिल्टन [[कम्यूटेटर]] को संतुष्ट करते हैं
यह दिखाना संभव है कि ऐसे हैमिल्टन [[रूपान्तरण संबंध]] को संतुष्ट करते हैं


:<math>\left[P, H\right] = 0</math>
:<math>\left[P, H\right] = 0</math>
[[हाइजेनबर्ग चित्र]] के अनुसार, इसका अर्थ है कि P का मान गति का एक स्थिरांक है। यदि क्वांटम राज्य प्रारंभिक रूप से सममित (एंटीसिमेट्रिक) है, तो सिस्टम विकसित होने पर यह सममित (एंटीसिमेट्रिक) रहेगा। गणितीय रूप से, यह कहता है कि राज्य वेक्टर पी के दो ईजेनस्पेस में से एक तक ही सीमित है, और पूरे हिल्बर्ट स्पेस में रेंज करने की अनुमति नहीं है। इस प्रकार, उस आइगेनस्पेस को सिस्टम के वास्तविक हिल्बर्ट स्पेस के रूप में भी माना जा सकता है। [[फॉक स्पेस]] की परिभाषा के पीछे यही विचार है।
[[हाइजेनबर्ग चित्र]] के अनुसार, इसका अर्थ है कि P का मान गति का एक स्थिरांक है। यदि परिमाण पद प्रारंभिक रूप से सममित ( प्रतिसममित) है, तो सिस्टम विकसित होने पर यह सममित ( प्रतिसममित) रहेगा। गणितीय रूप से, यह कहता है कि पद संवाहक  पी के दो अतिलक्षणिक अंतराल में से एक तक ही सीमित है, और पूरे हिल्बर्ट अंतराल में रेंज करने की अनुमति नहीं है। इस प्रकार, उस अतिलक्षणिक अंतराल को सिस्टम के वास्तविक हिल्बर्ट अंतराल के रूप में भी माना जा सकता है। [[फॉक स्पेस|फॉक अंतराल]] की परिभाषा के पीछे यही विचार है।


=== फर्मियंस और बोसोन ===
=== फर्मियंस और बोसोन ===


समरूपता या एंटीसिमेट्री का चुनाव कण की प्रजातियों द्वारा निर्धारित किया जाता है। उदाहरण के लिए, फोटॉनों या हीलियम-4 परमाणुओं का वर्णन करते समय सममित अवस्थाओं का हमेशा उपयोग किया जाना चाहिए, और इलेक्ट्रॉनों या प्रोटॉनों का वर्णन करते समय प्रतिसममित अवस्थाओं का उपयोग किया जाना चाहिए।
समरूपता या एंटीसिमेट्री का चुनाव कण की प्रजातियों द्वारा निर्धारित किया जाता है। उदाहरण के लिए, फोटॉनों या हीलियम-4 परमाणुओं का वर्णन करते समय सममित अवस्थाओं का हमेशा उपयोग किया जाना चाहिए, और विद्युदअणुों या प्रोटॉनों का वर्णन करते समय प्रतिसममित अवस्थाओं का उपयोग किया जाना चाहिए।


सममित अवस्था प्रदर्शित करने वाले कण बोसोन कहलाते हैं। कई समान बोसोन से बनी प्रणालियों के सांख्यिकीय गुणों के लिए सममित राज्यों की प्रकृति के महत्वपूर्ण परिणाम हैं। इन सांख्यिकीय गुणों को बोस-आइंस्टीन सांख्यिकी के रूप में वर्णित किया गया है।
सममित अवस्था प्रदर्शित करने वाले कण बोसोन कहलाते हैं। कई समान बोसोन से बनी प्रणालियों के सांख्यिकीय गुणों के लिए सममित पदों की प्रकृति के महत्वपूर्ण परिणाम हैं। इन सांख्यिकीय गुणों को बोस-आइंस्टीन सांख्यिकी के रूप में वर्णित किया गया है।


वे कण जो प्रतिसममित अवस्थाएँ प्रदर्शित करते हैं, फ़र्मियन कहलाते हैं। प्रतिसममिति पाउली बहिष्करण सिद्धांत को जन्म देती है, जो समान क्वांटम अवस्था को साझा करने से समान फर्मों को मना करती है। फर्मी-डिराक सांख्यिकी द्वारा कई समान फर्मों की प्रणालियों का वर्णन किया गया है।
वे कण जो प्रतिसममित अवस्थाएँ प्रदर्शित करते हैं, फ़र्मियन कहलाते हैं। प्रतिसममिति पाउली बहिष्करण सिद्धांत को जन्म देती है, जो समान परिमाण अवस्था को साझा करने से समान फर्मों को मना करती है। फर्मी-डिराक सांख्यिकी द्वारा कई समान फर्मों की प्रणालियों का वर्णन किया गया है।


[[पैरास्टैटिस्टिक्स]] भी संभव हैं।
[[पैरास्टैटिस्टिक्स]] भी संभव हैं।


कुछ द्वि-आयामी प्रणालियों में, मिश्रित समरूपता हो सकती है। इन विदेशी कणों को किसी के रूप में जाना जाता है, और वे भिन्नात्मक आँकड़ों का पालन करते हैं। किसी भी प्रकार के अस्तित्व के लिए प्रायोगिक साक्ष्य [[क्वांटम हॉल प्रभाव]] में मौजूद है, एक घटना जो द्वि-आयामी इलेक्ट्रॉन गैसों में देखी गई है जो [[MOSFET]]s की व्युत्क्रम परत बनाती है। एक [[ऋणायन]] प्रकार का आँकड़ा है, जिसे चोटी के आँकड़ों के रूप में जाना जाता है, जो [[ निटवेअर ]] के रूप में जाने जाने वाले कणों से जुड़े होते हैं।
कुछ द्वि-आयामी प्रणालियों में, मिश्रित समरूपता हो सकती है। इन विदेशी कणों को किसी के रूप में जाना जाता है, और वे भिन्नात्मक आँकड़ों का पालन करते हैं। किसी भी प्रकार के अस्तित्व के लिए प्रायोगिक साक्ष्य [[क्वांटम हॉल प्रभाव|परिमाण हॉल प्रभाव]] में मौजूद है, एक घटना जो द्वि-आयामी विद्युदअणु गैसों में देखी गई है जो [[MOSFET]]s की व्युत्क्रम परत बनाती है। एक [[ऋणायन]] प्रकार का आँकड़ा है, जिसे चोटी के आँकड़ों के रूप में जाना जाता है, जो [[ निटवेअर ]] के रूप में जाने जाने वाले कणों से जुड़े होते हैं।


[[स्पिन-सांख्यिकी प्रमेय]] समान कणों के विनिमय समरूपता को उनके स्पिन (भौतिकी) से संबंधित करता है। इसमें कहा गया है कि बोसोन में पूर्णांक स्पिन होता है, और फ़र्मियन में आधा-पूर्णांक स्पिन होता है। किसी के पास भिन्नात्मक स्पिन होती है।
[[स्पिन-सांख्यिकी प्रमेय]] समान कणों के विनिमय समरूपता को उनके स्पिन (भौतिकी) से संबंधित करता है। इसमें कहा गया है कि बोसोन में पूर्णांक स्पिन होता है, और फ़र्मियन में आधा-पूर्णांक स्पिन होता है। किसी के पास भिन्नात्मक स्पिन होती है।
Line 85: Line 80:
=== एन कण ===
=== एन कण ===


उपरोक्त चर्चा एन कणों के मामले में आसानी से सामान्यीकृत होती है। मान लीजिए कि क्वांटम संख्या n वाले N कण हैं<sub>1</sub>, एन<sub>2</sub>, ..., एन<sub>N</sub>. यदि कण बोसोन हैं, तो वे पूरी तरह से सममित स्थिति पर कब्जा कर लेते हैं, जो ''किसी भी दो'' कण लेबल के आदान-प्रदान के तहत सममित है:
उपरोक्त चर्चा एन कणों के मामले में आसानी से सामान्यीकृत होती है। मान लीजिए कि परिमाण संख्या n वाले N कण हैं<sub>1</sub>, एन<sub>2</sub>, ..., एन<sub>N</sub>. यदि कण बोसोन हैं, तो वे पूरी तरह से सममित स्थिति पर अधिकृत कर लेते हैं, जो ''किसी भी दो'' कण नामपत्र के आदान-प्रदान के तहत सममित है:


:<math>|n_1 n_2 \cdots n_N; S\rang = \sqrt{\frac{\prod_n m_n!}{N!}} \sum_p \left|n_{p(1)}\right\rang \left|n_{p(2)}\right\rang \cdots \left|n_{p(N)}\right\rang </math>
:<math>|n_1 n_2 \cdots n_N; S\rang = \sqrt{\frac{\prod_n m_n!}{N!}} \sum_p \left|n_{p(1)}\right\rang \left|n_{p(2)}\right\rang \cdots \left|n_{p(N)}\right\rang </math>
यहां, एन तत्वों पर अभिनय करने वाले क्रम[[परिवर्तन]] पी के तहत सभी अलग-अलग राज्यों में योग लिया जाता है। योग के लिए छोड़ा गया वर्गमूल एक [[सामान्यीकरण स्थिरांक]] है। मात्रा एम<sub>n</sub>N-कण अवस्था में प्रत्येक एकल-कण अवस्था n प्रकट होने की संख्या के लिए खड़ा है। ध्यान दें कि Σ<sub>n</sub> m<sub>n</sub> = एन।
यहां, एन तत्वों पर अभिनय करने वाले क्रम[[परिवर्तन]] पी के तहत सभी अलग-अलग पदों में योग लिया जाता है। योग के लिए छोड़ा गया वर्गमूल एक [[सामान्यीकरण स्थिरांक]] है। मात्रा एम<sub>n</sub>N-कण अवस्था में प्रत्येक एकल-कण अवस्था n प्रकट होने की संख्या के लिए खड़ा है। ध्यान दें कि Σ<sub>n</sub> m<sub>n</sub> = एन।


एक ही नस में, 'पूरी तरह से एंटीसिमेट्रिक स्टेट्स' पर कब्जा कर लेते हैं:
एक ही नस में, 'पूरी तरह से प्रतिसममित स्टेट्स' पर अधिकृत कर लेते हैं:


:<math>|n_1 n_2 \cdots n_N; A\rang = \frac{1}{\sqrt{N!}} \sum_p \operatorname{sgn}(p) \left|n_{p(1)}\right\rang \left|n_{p(2)}\right\rang \cdots \left|n_{p(N)}\right\rang\ </math>
:<math>|n_1 n_2 \cdots n_N; A\rang = \frac{1}{\sqrt{N!}} \sum_p \operatorname{sgn}(p) \left|n_{p(1)}\right\rang \left|n_{p(2)}\right\rang \cdots \left|n_{p(N)}\right\rang\ </math>
यहाँ, {{math|sgn(''p'')}} प्रत्येक क्रमचय के क्रमचय की समानता है (अर्थात <math>+1</math> अगर <math>p</math> पारदर्शिता की एक समान संख्या से बना है, और <math>-1</math> अगर विषम)। ध्यान दें कि नहीं है <math>\Pi_n m_n</math> शब्द, क्योंकि प्रत्येक एकल-कण अवस्था केवल एक बार फर्मीओनिक अवस्था में प्रकट हो सकती है। अन्यथा विषमता के कारण योग फिर से शून्य होगा, इस प्रकार यह शारीरिक रूप से असंभव स्थिति का प्रतिनिधित्व करता है। यह अनेक कणों के लिए पाउली अपवर्जन सिद्धांत है।
यहाँ, {{math|sgn(''p'')}} प्रत्येक क्रमचय के क्रमचय की समानता है (अर्थात <math>+1</math> अगर <math>p</math> पारदर्शिता की एक समान संख्या से बना है, और <math>-1</math> अगर विषम)। ध्यान दें कि नहीं है <math>\Pi_n m_n</math> शब्द, क्योंकि प्रत्येक एकल-कण अवस्था केवल एक बार फर्मीओनिक अवस्था में प्रकट हो सकती है। अन्यथा विषमता के कारण योग फिर से शून्य होगा, इस प्रकार यह शारीरिक रूप से असंभव स्थिति का प्रतिनिधित्व करता है। यह अनेक कणों के लिए पाउली अपवर्जन सिद्धांत है।


इन राज्यों को सामान्य किया गया है ताकि
इन पदों को सामान्य किया गया है ताकि


:<math> \lang n_1 n_2 \cdots n_N; S | n_1 n_2 \cdots n_N; S\rang = 1, \qquad \lang n_1 n_2 \cdots n_N; A | n_1 n_2 \cdots n_N; A\rang = 1. </math>
:<math> \lang n_1 n_2 \cdots n_N; S | n_1 n_2 \cdots n_N; S\rang = 1, \qquad \lang n_1 n_2 \cdots n_N; A | n_1 n_2 \cdots n_N; A\rang = 1. </math>
Line 102: Line 97:
=== माप ===
=== माप ===


मान लीजिए कि सममित (एंटीसिमेट्रिक) अवस्था में एन बोसोन (फर्मियन) की एक प्रणाली है
मान लीजिए कि सममित ( प्रतिसममित) अवस्था में एन बोसोन (फर्मियन) की एक प्रणाली है


:<math>|n_1 n_2 \cdots n_N; S/A \rang</math>
:<math>|n_1 n_2 \cdots n_N; S/A \rang</math>
और असतत वेधशालाओं के किसी अन्य सेट पर माप किया जाता है, मी। सामान्य तौर पर, यह कुछ परिणाम m देता है<sub>1</sub>एक कण के लिए, एम<sub>2</sub>दूसरे कण के लिए, और आगे। यदि कण बोसोन (फर्मियन) हैं, तो माप के बाद की स्थिति सममित (एंटीसिमेट्रिक) होनी चाहिए, अर्थात।
और असतत वेधशालाओं के किसी अन्य सेट पर माप किया जाता है, मी। सामान्य तौर पर, यह कुछ परिणाम m देता है<sub>1</sub>एक कण के लिए, एम<sub>2</sub>दूसरे कण के लिए, और आगे। यदि कण बोसोन (फर्मियन) हैं, तो माप के बाद की स्थिति सममित ( प्रतिसममित) होनी चाहिए, अर्थात।


:<math>|m_1 m_2 \cdots m_N; S/A \rang</math>
:<math>|m_1 m_2 \cdots m_N; S/A \rang</math>
Line 116: Line 111:
जो सत्यापित करता है कि कुल प्रायिकता 1 है। योग को m के क्रमित मानों तक सीमित रखना होगा<sub>1</sub>, ..., एम<sub>N</sub>यह सुनिश्चित करने के लिए कि प्रत्येक बहु-कण अवस्था को एक से अधिक बार नहीं गिना जाता है।
जो सत्यापित करता है कि कुल प्रायिकता 1 है। योग को m के क्रमित मानों तक सीमित रखना होगा<sub>1</sub>, ..., एम<sub>N</sub>यह सुनिश्चित करने के लिए कि प्रत्येक बहु-कण अवस्था को एक से अधिक बार नहीं गिना जाता है।


=== वेवफंक्शन प्रतिनिधित्व ===
=== तरंग कार्य प्रतिनिधित्व ===


अब तक, चर्चा में केवल असतत वेधशालाओं को शामिल किया गया है। इसे निरंतर अवलोकनीयों तक बढ़ाया जा सकता है, जैसे स्थिति (वेक्टर) x।
अब तक, चर्चा में केवल असतत वेधशालाओं को शामिल किया गया है। इसे निरंतर अवलोकनीयों तक बढ़ाया जा सकता है, जैसे स्थिति (संवाहक ) x।


याद रखें कि एक निरंतर अवलोकनीय का ईजेनस्टेट अवलोकन योग्य के मूल्यों की एक असीम श्रेणी का प्रतिनिधित्व करता है, अलग-अलग अवलोकनों के साथ एक मान नहीं। उदाहरण के लिए, यदि कोई कण |ψ⟩ अवस्था में है, तो उसके आयतन d के क्षेत्र में पाए जाने की संभावना<sup>3</sup>x किसी स्थिति x के आस-पास है
याद रखें कि एक निरंतर अवलोकनीय का ईजेनस्टेट अवलोकन योग्य के मूल्यों की एक असीम श्रेणी का प्रतिनिधित्व करता है, अलग-अलग अवलोकनों के साथ एक मान नहीं। उदाहरण के लिए, यदि कोई कण |ψ⟩ अवस्था में है, तो उसके आयतन d के क्षेत्र में पाए जाने की संभावना<sup>3</sup>x किसी स्थिति x के आस-पास है
Line 126: Line 121:


:<math> \lang x | x' \rang = \delta^3 (x - x') </math>
:<math> \lang x | x' \rang = \delta^3 (x - x') </math>
सममित और एंटीसिमेट्रिक मल्टी-पार्टिकल स्टेट्स का निर्माण पहले की तरह निरंतर ईजेनस्टेट्स से किया जा सकता है। हालाँकि, यह एक अलग सामान्यीकरण स्थिरांक का उपयोग करने के लिए प्रथागत है:
सममित और प्रतिसममित मल्टी-पार्टिकल स्टेट्स का निर्माण पहले की तरह निरंतर ईजेनस्टेट्स से किया जा सकता है। हालाँकि, यह एक अलग सामान्यीकरण स्थिरांक का उपयोग करने के लिए प्रथागत है: