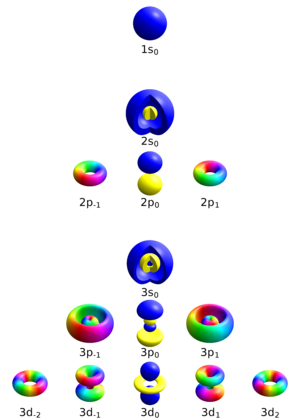सांख्यिक अंक: Difference between revisions

Revision as of 20:43, 29 April 2023

क्वांटम संख्या वाले हाइड्रोजन जैसे परमाणुओं के लिए एकल इलेक्ट्रॉन ऑर्बिटल्स

n = 1, 2, 3

(ब्लॉक),

ℓ

(पंक्तियां) और

m

(कॉलम)। घुमाव

s

दृश्यमान नहीं है, क्योंकि इसकी कोई स्थानिक निर्भरता नहीं है।

क्वांटम यांत्रिकी और रसायन विज्ञान में, क्वांटम संख्याएं क्वांटम प्रणाली की गतिशीलता में संरक्षित मात्रा के मूल्यों का वर्णन करती हैं। क्वांटम संख्याएँ ऑपरेटर (क्वांटम यांत्रिकी) के आइगेनमानों के अनुरूप होती हैं जो हैमिल्टनियन (क्वांटम यांत्रिकी) के साथ आवागमन करती हैं - ऐसी मात्राएँ जिन्हें प्रणालीकी ऊर्जा के रूप में एक ही समय में सटीकता के साथ जाना जा सकता है और उनके संबंधित आइगेनस्पेस। एक साथ, एक क्वांटम प्रणालीके सभी क्वांटम नंबरों का एक विनिर्देश पूरी तरह से प्रणालीकी एक आधार (रैखिक बीजगणित) स्थिति की विशेषता है, और सैद्धांतिक रूप से क्वांटम यांत्रिकी में एक साथ माप हो सकता है।

क्वांटम यांत्रिकी का एक महत्वपूर्ण पहलू ब्याज की कई अवलोकनीय मात्राओं का परिमाणीकरण (भौतिकी) है। विशेष रूप से, यह क्वांटम संख्या की ओर जाता है जो असतत गणित या अर्ध-पूर्णांक में मान लेता है; हालांकि वे कुछ मामलों में अनंत तक पहुंच सकते थे। यह क्वांटम यांत्रिकी को चिरसम्मत यांत्रिकी से अलग करता है, जहां द्रव्यमान, आवेश या संवेग जैसे प्रणालीको चिह्नित करने वाले मान, सभी निरंतर श्रेणी में होते हैं। क्वांटम संख्याएँ अक्सर विशेष रूप से परमाणुओं में इलेक्ट्रॉनों के ऊर्जा स्तर का वर्णन करती हैं, लेकिन अन्य संभावनाओं में कोणीय गति, स्पिन (भौतिकी), आदि सम्मिलित हैं। एक महत्वपूर्ण समूह फ्लेवर (कण भौतिकी) है - आंतरिक समरूपता क्वांटम संख्या जो एक कण के प्रकार और उसके निर्धारण मौलिक बलों के माध्यम से अन्य कणों के साथ पारस्परिक प्रभाव बनता है। किसी भी क्वांटम प्रणाली में एक या अधिक क्वांटम संख्याएँ हो सकती हैं; इस प्रकार सभी संभावित क्वांटम संख्याओं को सूचीबद्ध करना कठिन है।

किसी दिए गए प्रणालीके लिए आवश्यक क्वांटम संख्या

क्वांटम संख्याओं का मिलान एक प्रणाली से दूसरी प्रणाली में भिन्न होता है और इसका कोई सार्वभौमिक उत्तर नहीं है। इसलिए प्रत्येक प्रणाली का विश्लेषण करने के लिए इन मापदंडों को पाया जाना चाहिए। एक परिमाणित प्रणाली के लिए कम से कम एक क्वांटम संख्या की आवश्यकता होती है। किसी भी क्वांटम प्रणाली की गतिशीलता (अर्थात समय विकास) एक ऑपरेटर की राशि द्वारा हैमिल्टनियन (क्वांटम यांत्रिकी) के रूप में वर्णित है, $H$ . प्रणालीकी ऊर्जा के अनुरूप प्रणाली की एक क्वांटम संख्या है; यानी, हैमिल्टनियन के eigenvalues में से एक है। प्रत्येक रैखिक स्वतंत्रता ऑपरेटर के लिए एक क्वांटम संख्या भी होती है $O$ हेमिल्टनियन के साथ वह कम्युनिटी। कम्यूटिंग वेधशालाओं (सीएससीओ) का एक पूरा सेट जो हैमिल्टनियन के साथ यात्रा करता है, प्रणालीको उसके सभी क्वांटम नंबरों के साथ चित्रित करता है। क्वांटम संख्या और सीएससीओ के ऑपरेटरों के बीच एक-से-एक संबंध है, प्रत्येक क्वांटम संख्या के साथ इसके संबंधित ऑपरेटर के एक eigenvalues लेते हैं। अलग-अलग बेसिस (रैखिक बीजगणित) के परिणामस्वरूप जो मनमाने ढंग से आने वाले ऑपरेटरों का एक पूरा सेट बनाने के लिए चुना जा सकता है, अलग-अलग स्थितियों में एक ही प्रणाली के विवरण के लिए क्वांटम संख्याओं के विभिन्न सेटों का उपयोग किया जा सकता है।

परमाणु में इलेक्ट्रॉन

चार क्वांटम संख्याएँ परमाणु में एक इलेक्ट्रॉन का पूरी तरह से वर्णन कर सकती हैं:

स्पिन-ऑर्बिट इंटरेक्शन, स्पिन-ऑर्बिटल इंटरैक्शन, हालांकि, इन नंबरों से संबंधित है। इस प्रकार, प्रणालीका पूरा विवरण कम क्वांटम संख्याओं के साथ दिया जा सकता है, यदि इन आधार वैक्टरों के लिए ऑर्थोगोनल विकल्प बनाए जाते हैं।

विशिष्टता

एक प्रणाली में विभिन्न इलेक्ट्रॉनों की अलग-अलग क्वांटम संख्याएँ होंगी। उदाहरण के लिए, उच्चतम व्याप्त कक्षीय इलेक्ट्रॉन, वास्तविक विभेदक इलेक्ट्रॉन (अर्थात वह इलेक्ट्रॉन जो पिछले तत्व से एक तत्व को अलग करता है), या औफबाऊ सिद्धांत # मैडेलुंग ऊर्जा आदेश नियम के अनुसार विभेदक इलेक्ट्रॉन। लेण्टेनियुम में, एक और उदाहरण के रूप में, सम्मिलित इलेक्ट्रॉन 6s में हैं; 5डी; और 4f कक्षक, क्रमशः। इस मामले में प्रमुख क्वांटम संख्याएँ 6, 5 और 4 हैं।

सामान्य शब्दावली

यहाँ प्रयुक्त मॉडल चार क्वांटम संख्याओं का उपयोग करते हुए इलेक्ट्रॉनों का वर्णन करता है, $n$ , $ℓ$ , $m ℓ$ , $m s$ , जो की नीचे दिया गया है। परमाणु कण अवस्था (जैसे प्रोटॉन और न्यूट्रॉन) के प्राचीन विवरण में यह सामान्य नामकरण भी है। आण्विक कक्षाओं के क्वांटम विवरण के लिए अन्य क्वांटम संख्याओं की आवश्यकता होती है, क्योंकि हैमिल्टनियन (क्वांटम यांत्रिकी) और इसकी समरूपता अलग-अलग होती है।

प्रिंसिपल क्वांटम नंबर

मुख्य क्वांटम संख्या एक इलेक्ट्रॉन शेल इलेक्ट्रॉन शेल, या ऊर्जा स्तर का वर्णन करती है। का मान है $n$ 1 से लेकर उस परमाणु के सबसे बाहरी इलेक्ट्रॉन वाले शेल तक होता है, अर्थात^[1]

n = 1, 2, ...

उदाहरण के लिए, सीज़ियम (Cs) में, सबसे बाहरी वैलेंस (रसायन विज्ञान) इलेक्ट्रॉन ऊर्जा स्तर 6 के शेल में होता है, इसलिए सीज़ियम में एक इलेक्ट्रॉन हो सकता है $n$ मान 1 से 6 तक।

टाइम-इंडिपेंडेंट पोटेंशियल में कणों के लिए (देखें श्रोडिंगर इक्वेशन टाइम इंडिपेंडेंट|श्रोडिंगर इक्वेशन), यह भी लेबल करता है $n$ हेमिल्टनियन का वां आइगेनवेल्यू ( $H$ ), यानी ऊर्जा $E$ , कोणीय संवेग के कारण योगदान के साथ (शब्द सम्मिलित है $J 2$ ) छोड़ दिया। तो यह संख्या केवल इलेक्ट्रॉन और नाभिक के बीच की दूरी पर निर्भर करती है (अर्थात, रेडियल निर्देशांक $r$ ). से औसत दूरी बढ़ जाती है $n$ . इसलिए अलग-अलग प्रिंसिपल क्वांटम नंबर वाले क्वांटम स्टेट्स को अलग-अलग शेल से संबंधित कहा जाता है।

अज़ीमुथल क्वांटम संख्या

अज़ीमुथल क्वांटम संख्या, जिसे कोणीय संवेग क्वांटम संख्या या कक्षीय क्वांटम संख्या के रूप में भी जाना जाता है, इलेक्ट्रॉन शेल#उपकोशों (सबशेल्स) का वर्णन करता है, और संबंध के माध्यम से कक्षीय कोणीय गति का परिमाण देता है।

L 2 = ħ 2 ℓ (ℓ + 1)

रसायन विज्ञान और स्पेक्ट्रोस्कोपी में, $ℓ = 0$ को s कक्षीय कहा जाता है, $ℓ = 1$ , p कक्षीय, $ℓ = 2$ , d कक्षीय, और $ℓ = 3$ , f कक्षीय।

का मान है $ℓ$ 0 से लेकर $n - 1$ , तो पहला p कक्षीय ( $ℓ = 1$ ) दूसरे इलेक्ट्रॉन शेल में प्रकट होता है ( $n = 2$ ), पहला d कक्षीय ( $ℓ = 2$ ) तीसरे शेल में प्रकट होता है ( $n = 3$ ), और इसी तरह:^[2]

ℓ = 0, 1, 2,..., n - 1

में प्रांरम्भ होने वाली क्वांटम संख्या $n$ = 3,ℓ = 0, एक परमाणु के तीसरे इलेक्ट्रॉन शेल के s कक्षीय में इलेक्ट्रॉन का वर्णन करता है। रसायन विज्ञान में, यह क्वांटम संख्या बहुत महत्वपूर्ण है, क्योंकि यह एक परमाणु कक्षीय के आकार को निर्दिष्ट करती है और रासायनिक बंधनों और बंधन कोणों को दृढ़ता से प्रभावित करती है। अज़ीमुथल क्वांटम संख्या एक कक्षीय में मौजूद कोणीय नोड्स की संख्या को भी निरूपित कर सकती है। उदाहरण के लिए, p ऑर्बिटल्स के लिए, $ℓ = 1$ और इस प्रकार p ऑर्बिटल में कोणीय नोड्स की मात्रा 1 है।

कक्षीय का आकार अज़ीमुथल क्वांटम संख्या द्वारा भी दिया जाता है।

चुंबकीय क्वांटम संख्या

चुंबकीय क्वांटम संख्या उस उपधारा के भीतर विशिष्ट परमाणु कक्षीय (या बादल) का वर्णन करती है, और एक निर्दिष्ट अक्ष के साथ कक्षीय कोणीय गति का प्रक्षेपण करती है:

L z = m ℓ ħ

के मान $m ℓ$ से रेंज $- ℓ$ को $ℓ$ , पूर्णांक अंतराल के साथ।^[3]^{[page needed]}

एस उपधारा ( $ℓ = 0$ ) में केवल एक कक्षीय होता है, और इसलिए {{math|m_ℓ}एक s कक्षीय में एक इलेक्ट्रॉन का } हमेशा 0 होगा। p उपकोश ( $ℓ = 1$ ) में तीन ऑर्बिटल्स होते हैं (कुछ प्रणालियों में, तीन डम्बल के आकार के बादलों के रूप में चित्रित), इसलिए {{mvar|m_ℓ}एक p कक्षीय में एक इलेक्ट्रॉन का } -1, 0, या 1 होगा। d उपकोश ( $ℓ = 2$ ) में पाँच ऑर्बिटल्स होते हैं $m ℓ$ -2, -1, 0, 1 और 2 के मान।

स्पिन क्वांटम संख्या

स्पिन क्वांटम संख्या प्रत्येक कक्षीय के भीतर इलेक्ट्रॉन के आंतरिक स्पिन कोणीय गति का वर्णन करती है और कोणीय गति ऑपरेटर # स्पिन कोणीय गति का प्रक्षेपण देती है $S$ निर्दिष्ट अक्ष के साथ:

S z = m s ħ

.

सामान्य तौर पर, के मान $m s$ से रेंज $- s$ को $s$ , कहाँ $s$ स्पिन क्वांटम संख्या है, जो कण के आंतरिक स्पिन कोणीय गति से जुड़ी है:^[4]

m s = - s, - s + 1, - s + 2, ..., s - 2, s - 1, s

.

एक इलेक्ट्रॉन में स्पिन संख्या होती है $s = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/2$ , फलस्वरूप $m s$ ± होगा1/2, स्पिन अप और स्पिन डाउन स्टेट्स का जिक्र करते हुए। पाउली अपवर्जन सिद्धांत के कारण किसी भी व्यक्तिगत कक्षीय में प्रत्येक इलेक्ट्रॉन की अलग-अलग क्वांटम संख्याएँ होनी चाहिए, इसलिए एक कक्षीय में कभी भी दो से अधिक इलेक्ट्रॉन नहीं होते हैं।

नियम

के लिए कोई सार्वभौमिक निश्चित मान नहीं हैं $m ℓ$ और $m s$ . बल्कि, $m ℓ$ और $m s$ मान मनमानी हैं। इन स्थिरांकों के लिए विकल्पों पर एकमात्र प्रतिबंध यह है कि गणना या विवरण के एक विशेष सेट के भीतर उपयोग किए जाने वाले नामकरण योजनाबद्ध को सुसंगत होना चाहिए (उदाहरण के लिए एक पी ऑर्बिटल में पहले इलेक्ट्रॉन द्वारा कब्जा किए गए कक्षीय को इस रूप में वर्णित किया जा सकता है) $m ℓ = -1$ या $m ℓ = 0$ या $m ℓ = 1$ , लेकिन $m ℓ$ उस कक्षीय में अगले अयुग्मित इलेक्ट्रॉन का मान भिन्न होना चाहिए; फिर भी, $m ℓ$ फिर से अन्य कक्षकों में इलेक्ट्रॉनों को सौंपा जा सकता है $m ℓ = -1$ या $m ℓ = 0$ या $m ℓ = 1$ ).

इन नियमों का सारांश इस प्रकार है:

Name	Symbol	Meaning	Range of values	Value examples
Principal quantum number	$n$	shell	$1 \leq n$	$n = 1, 2, 3, \dots$
Azimuthal quantum number (angular momentum)	$ℓ$	subshell (s orbital is listed as 0, p orbital as 1 etc.)	$0 \leq ℓ \leq n - 1$	for $n = 3$ : $ℓ = 0, 1, 2$ (s, p, d)
Magnetic quantum number (projection of angular momentum)	$m ℓ$	Orbital (orientation of the orbital)	$- ℓ \leq m ℓ \leq ℓ$	for $ℓ = 2$ : $m ℓ = -2, -1, 0, 1, 2$
Spin quantum number	$m s$	spin of the electron (−1/2 = "spin down", 1/2 = "spin up")	$- s \leq m s \leq s$	for an electron $s = 1 / 2$ , so $m s = - 1 / 2, + 1 / 2$

उदाहरण: कार्बन (C) परमाणु के सबसे बाहरी वैलेंस (रसायन विज्ञान) इलेक्ट्रॉनों को संदर्भित करने के लिए उपयोग की जाने वाली क्वांटम संख्याएँ, जो 2p परमाणु कक्षीय में स्थित हैं, हैं; $n = 2$ (दूसरा इलेक्ट्रॉन शेल), $ℓ = 1$ (p कक्षीय इलेक्ट्रॉन कोश#उपकोश), $m ℓ = 1, 0, -1$ , $m s = 1 / 2$ (समानांतर स्पिन)।

स्पेक्ट्रोस्कोपी के परिणामों ने संकेत दिया कि अधिकतम दो इलेक्ट्रॉन एक कक्षीय पर कब्जा कर सकते हैं। हालांकि, हुंड के नियमों के अनुसार, दो इलेक्ट्रॉनों में कभी भी समान सटीक क्वांटम स्थिति नहीं हो सकती है और न ही क्वांटम संख्याओं का एक ही सेट हो सकता है, जो पाउली अपवर्जन सिद्धांत को संबोधित करता है। एक चौथा क्वांटम नंबर, जो दो संभावित मूल्यों के साथ स्पिन का प्रतिनिधित्व करता है, संघर्ष को हल करने के लिए एक तदर्थ धारणा के रूप में जोड़ा गया था; इस धारणा को बाद में सापेक्षवादी क्वांटम यांत्रिकी और प्रसिद्ध स्टर्न-गेरलाच प्रयोग के परिणामों से विस्तार से समझाया जाएगा।

पृष्ठभूमि

क्वांटम यांत्रिकी के पूरे इतिहास में कई अलग-अलग मॉडल प्रस्तावित किए गए हैं, लेकिन नामकरण की सबसे प्रमुख प्रणाली फ्रेडरिक डॉग, रॉबर्ट एस. मुल्लिकेन के हंड-मुल्लिकेन आणविक कक्षीय सिद्धांत और इरविन श्रोडिंगर | श्रोडिंगर, जॉन सी. स्लेटर के योगदान से उत्पन्न हुई है। और जॉन लेनार्ड-जोन्स। नामकरण की इस प्रणाली में नील्स बोह्र ऊर्जा स्तर, हंड-मुल्लिकेन कक्षीय सिद्धांत, और स्पेक्ट्रोस्कोपी और हुंड के नियमों के आधार पर इलेक्ट्रॉन स्पिन पर अवलोकन सम्मिलित थे।^[5]

कुल कोणीय संवेग संख्या

कण का कुल कोणीय संवेग

जब कोई स्पिन-ऑर्बिट इंटरेक्शन को ध्यान में रखता है, तो $L$ और $S$ ऑपरेटर अब हैमिल्टनियन (क्वांटम यांत्रिकी) के साथ क्रमविनिमेयता नहीं रखते हैं, और उनके आइगेनवेल्यू समय के साथ बदलते हैं। इस प्रकार क्वांटम संख्याओं का एक और सेट इस्तेमाल किया जाना चाहिए। इस सेट में सम्मिलित है^[6]^[7]

The total angular momentum quantum number:
$j = | ℓ \pm s |$

which gives the total angular momentum through the relation

$J 2 = ħ 2 j (j + 1)$
The projection of the total angular momentum along a specified axis:
$m j = - j, - j + 1, - j + 2, ..., j - 2, j - 1, j$

analogous to the above and satisfies

$m j = m ℓ + m s$ and $| m ℓ + m s | \leq j$
Parity
This is the eigenvalue under reflection: positive (+1) for states which came from even $ℓ$ and negative (−1) for states which came from odd $ℓ$ . The former is also known as even parity and the latter as odd parity, and is given by

$P = (-1) ℓ$

उदाहरण के लिए, निम्नलिखित 8 अवस्थाओं पर विचार करें, जो उनकी क्वांटम संख्या द्वारा परिभाषित हैं:

	$n$	$ℓ$	$m ℓ$	$m s$	$ℓ + s$	$ℓ - s$	$m ℓ + m s$
(1)	2	1	1	+1/2	3/2	~~1/2~~	3/2
(2)	2	1	1	−1/2	3/2	1/2	1/2
(3)	2	1	0	+1/2	3/2	1/2	1/2
(4)	2	1	0	−1/2	3/2	1/2	−1/2
(5)	2	1	−1	+1/2	3/2	1/2	−1/2
(6)	2	1	−1	−1/2	3/2	~~1/2~~	−3/2
(7)	2	0	0	+1/2	1/2	−1/2	1/2
(8)	2	0	0	−1/2	1/2	−1/2	−1/2

प्रणालीमें क्वांटम राज्यों को इन 8 राज्यों के रैखिक संयोजन के रूप में वर्णित किया जा सकता है। हालाँकि, स्पिन-ऑर्बिट इंटरैक्शन की उपस्थिति में, यदि कोई 8 राज्यों द्वारा एक ही प्रणाली का वर्णन करना चाहता है जो हैमिल्टनियन (क्वांटम यांत्रिकी) के आइजन्वेक्टर हैं (अर्थात प्रत्येक एक ऐसे राज्य का प्रतिनिधित्व करता है जो समय के साथ दूसरों के साथ मिश्रण नहीं करता है), हमें चाहिए निम्नलिखित 8 राज्यों पर विचार करें:

$j$	$m j$	parity
3/2	3/2	odd	coming from state (1) above
3/2	1/2	odd	coming from states (2) and (3) above
3/2	−1/2	odd	coming from states (4) and (5) above
3/2	−3/2	odd	coming from state (6) above
1/2	1/2	odd	coming from states (2) and (3) above
1/2	−1/2	odd	coming from states (4) and (5) above
1/2	1/2	even	coming from state (7) above
1/2	−1/2	even	coming from state (8) above

परमाणु कोणीय गति क्वांटम संख्या

परमाणु नाभिक में, प्रोटॉन और न्यूट्रॉन (न्यूक्लियॉन) की पूरी असेंबली में प्रत्येक न्यूक्लियॉन के कोणीय संवेग के कारण परिणामी कोणीय संवेग होता है, जिसे आमतौर पर निरूपित किया जाता है। $I$ . यदि न्यूट्रॉन का कुल कोणीय संवेग है $j n = ℓ + s$ और एक प्रोटॉन के लिए है $j p = ℓ + s$ (कहाँ $s$ प्रोटॉन और न्यूट्रॉन के लिए होता है 1/2 फिर से (नोट देखें)), फिर 'परमाणु कोणीय गति क्वांटम संख्या' $I$ द्वारा दिए गए हैं:

I = | j n - j p |, | j n - j p | + 1, | j n - j p | + 2, ..., (j n + j p) - 2, (j n + j p) - 1, (j n + j p)

नोट: परमाणु (और परमाणु) राज्यों के कक्षीय कोणीय संवेग सभी ħ के पूर्णांक गुणक हैं जबकि न्यूट्रॉन और प्रोटॉन के आंतरिक कोणीय संवेग अर्ध-पूर्णांक गुणक हैं। यह तुरंत स्पष्ट होना चाहिए कि न्यूक्लियंस के आंतरिक स्पिन का संयोजन उनकी कक्षीय गति के साथ हमेशा कुल स्पिन के लिए आधा-पूर्णांक मान देगा, $I$ , किसी भी सम-एक नाभिक के लिए किसी भी विषम-ए नाभिक और पूर्णांक मानों का।

संख्या के साथ समानता $I$ का उपयोग परमाणु कोणीय गति वाले राज्यों को लेबल करने के लिए किया जाता है, हाइड्रोजन (H), कार्बन (C), और सोडियम (Na) के कुछ समस्थानिकों के उदाहरण हैं;^[8]

¹ ₁H	$I$ = (1/2)⁺	⁹ ₆C	$I$ = (3/2)⁻	²⁰ ₁₁Na	$I$ = 2⁺
² ₁H	$I$ = 1⁺	¹⁰ ₆C	$I$ = 0⁺	²¹ ₁₁Na	$I$ = (3/2)⁺
³ ₁H	$I$ = (1/2)⁺	¹¹ ₆C	$I$ = (3/2)⁻	²² ₁₁Na	$I$ = 3⁺
		¹² ₆C	$I$ = 0⁺	²³ ₁₁Na	$I$ = (3/2)⁺
		¹³ ₆C	$I$ = (1/2)⁻	²⁴ ₁₁Na	$I$ = 4⁺
		¹⁴ ₆C	$I$ = 0⁺	²⁵ ₁₁Na	$I$ = (5/2)⁺
		¹⁵ ₆C	$I$ = (1/2)⁺	²⁶ ₁₁Na	$I$ = 3⁺

में असामान्य उतार-चढ़ाव का कारण $I$ , केवल एक न्यूक्लियॉन के अंतर से भी, प्रोटॉन और न्यूट्रॉन की विषम और सम संख्या के कारण होते हैं - न्यूक्लियॉन के जोड़े में शून्य का कुल कोणीय संवेग होता है (बिल्कुल ऑर्बिटल्स में इलेक्ट्रॉनों की तरह), एक विषम या सम संख्या में अयुग्मित न्यूक्लियॉन छोड़ते हैं। . कार्बनिक रसायन में एनएमआर स्पेक्ट्रोस्कोपी के संचालन के लिए परमाणु स्पिन की संपत्ति एक महत्वपूर्ण कारक है,^[7]और परमाणु चिकित्सा में एमआरआई,^[8]बाहरी चुंबकीय क्षेत्र के साथ बातचीत करने वाले परमाणु चुंबकीय क्षण के कारण।

प्राथमिक कण

प्राथमिक कणों में कई क्वांटम संख्याएँ होती हैं जिन्हें आमतौर पर उनके लिए आंतरिक कहा जाता है। हालांकि, यह समझा जाना चाहिए कि प्राथमिक कण कण भौतिकी के मानक मॉडल की क्वांटम अवस्थाएँ हैं, और इसलिए इन कणों की क्वांटम संख्याएँ इस मॉडल के हैमिल्टनियन (क्वांटम यांत्रिकी) से वही संबंध रखती हैं जो बोह्र की क्वांटम संख्याएँ हैं। परमाणु अपने हैमिल्टनियन (क्वांटम यांत्रिकी) को करता है। दूसरे शब्दों में, प्रत्येक क्वांटम संख्या समस्या की समरूपता को दर्शाती है। अंतरिक्ष समय और विकट: आंतरिक समरूपता के बीच अंतर करने के लिए क्वांटम क्षेत्र सिद्धांत में यह अधिक उपयोगी है।

स्पेसटाइम समरूपता से संबंधित विशिष्ट क्वांटम संख्याएं स्पिन (भौतिकी) (घूर्णी समरूपता से संबंधित), समता (भौतिकी), सी-समता और टी समता (स्पेसटाइम के पॉइनकेयर समरूपता से संबंधित) हैं। विशिष्ट आंतरिक समरूपता^{[clarification needed]} लेप्टान संख्या और बेरिऑन संख्या या विद्युत आवेश हैं। (इस तरह की क्वांटम संख्याओं की पूरी सूची के लिए स्वाद (कण भौतिकी) पर लेख देखें।)

गुणक क्वांटम संख्या

अधिकांश संरक्षित क्वांटम संख्याएँ योगात्मक होती हैं, इसलिए एक प्राथमिक कण प्रतिक्रिया में, प्रतिक्रिया के पहले और बाद में क्वांटम संख्याओं का योग समान होना चाहिए। हालाँकि, कुछ, जिन्हें आमतौर पर समता (भौतिकी) कहा जाता है, गुणक होते हैं; यानी, उनका उत्पाद संरक्षित है। सभी गुणात्मक क्वांटम संख्याएँ एक समरूपता (जैसे समता) से संबंधित होती हैं जिसमें समरूपता परिवर्तन को दो बार लागू करना कुछ भी नहीं करने के बराबर होता है (इनवोल्यूशन (गणित))।

यह भी देखें

संदर्भ

↑ Beiser, A. (1987). आधुनिक भौतिकी की अवधारणाएँ (4th ed.). McGraw-Hill (International). ISBN 0-07-100144-1.^{[page needed]}
↑ Atkins, P. W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. Vol. 1. Oxford University Press. ISBN 0-19-855129-0.^{[page needed]}
↑ Eisberg & Resnick 1985.
↑ Peleg, Y.; Pnini, R.; Zaarur, E.; Hecht, E. (2010). क्वांटम यांत्रिकी. Schuam's Outlines (2nd ed.). McGraw Hill (USA). ISBN 978-0-07-162358-2.^{[page needed]}
↑ Chemistry, Matter, and the Universe, R.E. Dickerson, I. Geis, W.A. Benjamin Inc. (USA), 1976, ISBN 0-19-855148-7
↑ Atkins, P. W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. Vol. 1. Oxford University Press. ISBN 0-19-855129-0.^{[page needed]}
↑ ^7.0 ^7.1 Atkins, P. W. (1977). Molecular Quantum Mechanics Part III: An Introduction to Quantum Chemistry. Vol. 2. Oxford University Press.^{[ISBN missing]}^{[page needed]}
↑ ^8.0 ^8.1 Krane, K. S. (1988). परिचयात्मक परमाणु भौतिकी. John Wiley & Sons. ISBN 978-0-471-80553-3.^{[page needed]}

अग्रिम पठन

Dirac, Paul A. M. (1982). Principles of quantum mechanics. Oxford University Press. ISBN 0-19-852011-5.
Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.
Halzen, Francis & Martin, Alan D. (1984). QUARKS AND LEPTONS: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2.
Eisberg, Robert Martin; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). John Wiley & Sons. ISBN 978-0-471-87373-0 – via Internet Archive.

बाहरी संबंध

[1] Beiser, A. (1987). आधुनिक भौतिकी की अवधारणाएँ (4th ed.). McGraw-Hill (International). ISBN 0-07-100144-1.^{[page needed]}

[2] Atkins, P. W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. Vol. 1. Oxford University Press. ISBN 0-19-855129-0.^{[page needed]}

[FOOTNOTEEisbergResnick1985-3] Eisberg & Resnick 1985.

[4] Peleg, Y.; Pnini, R.; Zaarur, E.; Hecht, E. (2010). क्वांटम यांत्रिकी. Schuam's Outlines (2nd ed.). McGraw Hill (USA). ISBN 978-0-07-162358-2.^{[page needed]}

[5] Chemistry, Matter, and the Universe, R.E. Dickerson, I. Geis, W.A. Benjamin Inc. (USA), 1976, ISBN 0-19-855148-7

[6] Atkins, P. W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. Vol. 1. Oxford University Press. ISBN 0-19-855129-0.^{[page needed]}

[Atkins_1977-7] 7.0 ^7.1 Atkins, P. W. (1977). Molecular Quantum Mechanics Part III: An Introduction to Quantum Chemistry. Vol. 2. Oxford University Press.^{[ISBN missing]}^{[page needed]}

[Krane_1988-8] 8.0 ^8.1 Krane, K. S. (1988). परिचयात्मक परमाणु भौतिकी. John Wiley & Sons. ISBN 978-0-471-80553-3.^{[page needed]}

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

@@ Line 1: / Line 1: @@
 {{Short description|Notation for conserved quantities in physics and chemistry}}
-{{Redirect|Q-number|the Q-theory concept|Q-analog|the number format|Q (number format)}}
 [[Image:Atomic orbitals n123 m-eigenstates.png|thumb|क्वांटम संख्या वाले हाइड्रोजन जैसे परमाणुओं के लिए एकल इलेक्ट्रॉन ऑर्बिटल्स {{math|1=''n'' = 1, 2, 3}} (ब्लॉक), {{mvar|{{ell}}}} (पंक्तियां) और {{mvar|m}} (कॉलम)। घुमाव {{mvar|s}} दृश्यमान नहीं है, क्योंकि इसकी कोई स्थानिक निर्भरता नहीं है।]]
 {{Quantum mechanics|fundamentals}}
-[[क्वांटम यांत्रिकी]] और [[रसायन विज्ञान]] में, क्वांटम संख्याएं [[ क्वांटम प्रणाली ]] की गतिशीलता में [[संरक्षित मात्रा]] के मूल्यों का वर्णन करती हैं। क्वांटम संख्याएँ [[ऑपरेटर (क्वांटम यांत्रिकी)]] के आइगेनमानों के अनुरूप होती हैं जो [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] के साथ आवागमन करती हैं - ऐसी मात्राएँ जिन्हें सिस्टम की ऊर्जा के रूप में एक ही समय में सटीकता के साथ जाना जा सकता है<ref group="note">specifically, observables <math>\widehat{A}</math>  that [[Commutator|commute]] with the Hamiltonian are [[simultaneously diagonalizable]] with it and so the eigenvalues <math>a</math> and the energy (eigenvalues of the Hamiltonian) are not limited by an [[Uncertainty principle|uncertainty relation]] arising from non-commutativity.</ref>—और उनके संबंधित आइगेनस्पेस। एक साथ, एक क्वांटम सिस्टम के सभी क्वांटम नंबरों का एक विनिर्देश पूरी तरह से सिस्टम की एक [[आधार (रैखिक बीजगणित)]] स्थिति की विशेषता है, और सैद्धांतिक रूप से क्वांटम यांत्रिकी में एक साथ माप हो सकता है।
+[[क्वांटम यांत्रिकी]] और [[रसायन विज्ञान]] में, क्वांटम संख्याएं [[ क्वांटम प्रणाली ]] की गतिशीलता में [[संरक्षित मात्रा]] के मूल्यों का वर्णन करती हैं। क्वांटम संख्याएँ [[ऑपरेटर (क्वांटम यांत्रिकी)]] के आइगेनमानों के अनुरूप होती हैं जो [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] के साथ आवागमन करती हैं - ऐसी मात्राएँ जिन्हें प्रणालीकी ऊर्जा के रूप में एक ही समय में सटीकता के साथ जाना जा सकता है और उनके संबंधित आइगेनस्पेस। एक साथ, एक क्वांटम प्रणालीके सभी क्वांटम नंबरों का एक विनिर्देश पूरी तरह से प्रणालीकी एक [[आधार (रैखिक बीजगणित)]] स्थिति की विशेषता है, और सैद्धांतिक रूप से क्वांटम यांत्रिकी में एक साथ माप हो सकता है।
-क्वांटम यांत्रिकी का एक महत्वपूर्ण पहलू ब्याज की कई अवलोकनीय मात्राओं का [[परिमाणीकरण (भौतिकी)]] है।<ref group="note">Many observables have discrete [[Spectrum of an operator|spectra (sets of eigenvalues)]] in quantum mechanics, so the quantities can only be measured in discrete (often integer) values.</ref> विशेष रूप से, यह क्वांटम संख्या की ओर जाता है जो असतत गणित या अर्ध-पूर्णांक में मान लेता है; हालांकि वे कुछ मामलों में अनंत तक पहुंच सकते थे। यह क्वांटम यांत्रिकी को [[शास्त्रीय यांत्रिकी]] से अलग करता है, जहां द्रव्यमान, आवेश या संवेग जैसे सिस्टम को चिह्नित करने वाले मान, सभी निरंतर श्रेणी में होते हैं। क्वांटम संख्याएँ अक्सर विशेष रूप से परमाणुओं में इलेक्ट्रॉनों के [[ऊर्जा स्तर]] का वर्णन करती हैं, लेकिन अन्य संभावनाओं में कोणीय गति, [[स्पिन (भौतिकी)]], आदि शामिल हैं। एक महत्वपूर्ण परिवार [[स्वाद (कण भौतिकी)]] है - [[आंतरिक समरूपता]] क्वांटम संख्या जो एक कण के प्रकार और उसके निर्धारण [[मौलिक बल]]ों के माध्यम से अन्य कणों के साथ बातचीत। किसी भी क्वांटम प्रणाली में एक या अधिक क्वांटम संख्याएँ हो सकती हैं; इस प्रकार सभी संभावित क्वांटम संख्याओं को सूचीबद्ध करना कठिन है।
+क्वांटम यांत्रिकी का एक महत्वपूर्ण पहलू ब्याज की कई अवलोकनीय मात्राओं का [[परिमाणीकरण (भौतिकी)]] है। विशेष रूप से, यह क्वांटम संख्या की ओर जाता है जो असतत गणित या अर्ध-पूर्णांक में मान लेता है; हालांकि वे कुछ मामलों में अनंत तक पहुंच सकते थे। यह क्वांटम यांत्रिकी को  [[शास्त्रीय यांत्रिकी|चिरसम्मत यांत्रिकी]] से अलग करता है, जहां द्रव्यमान, आवेश या संवेग जैसे प्रणालीको चिह्नित करने वाले मान, सभी निरंतर श्रेणी में होते हैं। क्वांटम संख्याएँ अक्सर विशेष रूप से परमाणुओं में इलेक्ट्रॉनों के [[ऊर्जा स्तर]] का वर्णन करती हैं, लेकिन अन्य संभावनाओं में कोणीय गति, [[स्पिन (भौतिकी)]], आदि सम्मिलित हैं। एक महत्वपूर्ण समूह [[स्वाद (कण भौतिकी)|फ्लेवर (कण भौतिकी)]] है - [[आंतरिक समरूपता]] क्वांटम संख्या जो एक कण के प्रकार और उसके निर्धारण [[मौलिक बल]]ों के माध्यम से अन्य कणों के साथ पारस्परिक प्रभाव बनता है। किसी भी क्वांटम प्रणाली में एक या अधिक क्वांटम संख्याएँ हो सकती हैं; इस प्रकार सभी संभावित क्वांटम संख्याओं को सूचीबद्ध करना कठिन है।
-== किसी दिए गए सिस्टम के लिए आवश्यक क्वांटम संख्या ==
+== किसी दिए गए प्रणालीके लिए आवश्यक क्वांटम संख्या ==
-{{Main|Quantum system}}
+{{Main|क्वांटम प्रणाली}}
-क्वांटम संख्याओं का मिलान एक प्रणाली से दूसरी प्रणाली में भिन्न होता है और इसका कोई सार्वभौमिक उत्तर नहीं है। इसलिए प्रत्येक प्रणाली का विश्लेषण करने के लिए इन मापदंडों को पाया जाना चाहिए। एक परिमाणित प्रणाली के लिए कम से कम एक क्वांटम संख्या की आवश्यकता होती है। किसी भी क्वांटम प्रणाली की गतिशीलता (अर्थात समय विकास) एक [[ ऑपरेटर की राशि ]] द्वारा हैमिल्टनियन (क्वांटम यांत्रिकी) के रूप में वर्णित है, {{mvar|H}}. सिस्टम की ऊर्जा के अनुरूप सिस्टम की एक क्वांटम संख्या है; यानी, हैमिल्टनियन के [[eigenvalue]]s में से एक। प्रत्येक [[ रैखिक स्वतंत्रता ]] ऑपरेटर के लिए एक क्वांटम संख्या भी होती है {{mvar|O}} हेमिल्टनियन के साथ वह कम्युनिटी। कम्यूटिंग वेधशालाओं (CSCO) का एक पूरा सेट जो हैमिल्टनियन के साथ यात्रा करता है, सिस्टम को उसके सभी क्वांटम नंबरों के साथ चित्रित करता है। क्वांटम संख्या और सीएससीओ के ऑपरेटरों के बीच एक-से-एक संबंध है, प्रत्येक क्वांटम संख्या के साथ इसके संबंधित ऑपरेटर के एक eigenvalues लेते हैं। अलग-अलग बेसिस (रैखिक बीजगणित) के परिणामस्वरूप जो मनमाने ढंग से आने वाले ऑपरेटरों का एक पूरा सेट बनाने के लिए चुना जा सकता है, अलग-अलग स्थितियों में एक ही प्रणाली के विवरण के लिए क्वांटम संख्याओं के विभिन्न सेटों का उपयोग किया जा सकता है।
+क्वांटम संख्याओं का मिलान एक प्रणाली से दूसरी प्रणाली में भिन्न होता है और इसका कोई सार्वभौमिक उत्तर नहीं है। इसलिए प्रत्येक प्रणाली का विश्लेषण करने के लिए इन मापदंडों को पाया जाना चाहिए। एक परिमाणित प्रणाली के लिए कम से कम एक क्वांटम संख्या की आवश्यकता होती है। किसी भी क्वांटम प्रणाली की गतिशीलता (अर्थात समय विकास) एक [[ ऑपरेटर की राशि ]] द्वारा हैमिल्टनियन (क्वांटम यांत्रिकी) के रूप में वर्णित है, {{mvar|H}}. प्रणालीकी ऊर्जा के अनुरूप प्रणाली की एक क्वांटम संख्या है; यानी, हैमिल्टनियन के [[eigenvalue]]s में से एक है। प्रत्येक [[ रैखिक स्वतंत्रता | रैखिक स्वतंत्रता]] ऑपरेटर के लिए एक क्वांटम संख्या भी होती है {{mvar|O}} हेमिल्टनियन के साथ वह कम्युनिटी। कम्यूटिंग वेधशालाओं (सीएससीओ) का एक पूरा सेट जो हैमिल्टनियन के साथ यात्रा करता है, प्रणालीको उसके सभी क्वांटम नंबरों के साथ चित्रित करता है। क्वांटम संख्या और सीएससीओ के ऑपरेटरों के बीच एक-से-एक संबंध है, प्रत्येक क्वांटम संख्या के साथ इसके संबंधित ऑपरेटर के एक eigenvalues लेते हैं। अलग-अलग बेसिस (रैखिक बीजगणित) के परिणामस्वरूप जो मनमाने ढंग से आने वाले ऑपरेटरों का एक पूरा सेट बनाने के लिए चुना जा सकता है, अलग-अलग स्थितियों में एक ही प्रणाली के विवरण के लिए क्वांटम संख्याओं के विभिन्न सेटों का उपयोग किया जा सकता है।
 == परमाणु में इलेक्ट्रॉन ==
-चार क्वांटम संख्याएँ एक परमाणु में एक इलेक्ट्रॉन का पूरी तरह से वर्णन कर सकती हैं:
+चार क्वांटम संख्याएँ परमाणु में एक इलेक्ट्रॉन का पूरी तरह से वर्णन कर सकती हैं:
 *[[मुख्य क्वांटम संख्या]] ({{mvar|n}})
@@ Line 20: / Line 19: @@
 * [[स्पिन क्वांटम संख्या]] ({{mvar|m<sub>s</sub>}})
-स्पिन-ऑर्बिट इंटरेक्शन | स्पिन-ऑर्बिटल इंटरैक्शन, हालांकि, इन नंबरों से संबंधित है। इस प्रकार, सिस्टम का पूरा विवरण कम क्वांटम संख्याओं के साथ दिया जा सकता है, यदि इन आधार वैक्टरों के लिए ऑर्थोगोनल विकल्प बनाए जाते हैं।
+स्पिन-ऑर्बिट इंटरेक्शन, स्पिन-ऑर्बिटल इंटरैक्शन, हालांकि, इन नंबरों से संबंधित है। इस प्रकार, प्रणालीका पूरा विवरण कम क्वांटम संख्याओं के साथ दिया जा सकता है, यदि इन आधार वैक्टरों के लिए ऑर्थोगोनल विकल्प बनाए जाते हैं।
 === विशिष्टता ===
-एक प्रणाली में विभिन्न इलेक्ट्रॉनों की अलग-अलग क्वांटम संख्याएँ होंगी। उदाहरण के लिए, उच्चतम व्याप्त कक्षीय इलेक्ट्रॉन, वास्तविक विभेदक इलेक्ट्रॉन (अर्थात वह इलेक्ट्रॉन जो पिछले तत्व से एक तत्व को अलग करता है), या औफबाऊ सिद्धांत # मैडेलुंग ऊर्जा आदेश नियम के अनुसार विभेदक इलेक्ट्रॉन। [[लेण्टेनियुम]] में, एक और उदाहरण के रूप में, शामिल इलेक्ट्रॉन 6s में हैं; 5डी; और 4f कक्षक, क्रमशः। इस मामले में प्रमुख क्वांटम संख्याएँ 6, 5 और 4 हैं।
+एक प्रणाली में विभिन्न इलेक्ट्रॉनों की अलग-अलग क्वांटम संख्याएँ होंगी। उदाहरण के लिए, उच्चतम व्याप्त कक्षीय इलेक्ट्रॉन, वास्तविक विभेदक इलेक्ट्रॉन (अर्थात वह इलेक्ट्रॉन जो पिछले तत्व से एक तत्व को अलग करता है), या औफबाऊ सिद्धांत # मैडेलुंग ऊर्जा आदेश नियम के अनुसार विभेदक इलेक्ट्रॉन। [[लेण्टेनियुम]] में, एक और उदाहरण के रूप में,  सम्मिलित  इलेक्ट्रॉन 6s में हैं; 5डी; और 4f कक्षक, क्रमशः। इस मामले में प्रमुख क्वांटम संख्याएँ 6, 5 और 4 हैं।
 === सामान्य शब्दावली ===
-यहाँ प्रयुक्त मॉडल चार क्वांटम संख्याओं का उपयोग करते हुए इलेक्ट्रॉनों का वर्णन करता है, {{mvar|n}}, {{mvar|{{ell}}}}, {{mvar|m<sub>{{ell}}</sub>}}, {{mvar|m<sub>s</sub>}}, नीचे दिया गया। परमाणु कण राज्यों (जैसे प्रोटॉन और न्यूट्रॉन) के शास्त्रीय विवरण में यह सामान्य नामकरण भी है। आण्विक कक्षाओं के क्वांटम विवरण के लिए अन्य क्वांटम संख्याओं की आवश्यकता होती है, क्योंकि हैमिल्टनियन (क्वांटम यांत्रिकी) और इसकी समरूपता अलग-अलग होती है।
+यहाँ प्रयुक्त मॉडल चार क्वांटम संख्याओं का उपयोग करते हुए इलेक्ट्रॉनों का वर्णन करता है, {{mvar|n}}, {{mvar|{{ell}}}}, {{mvar|m<sub>{{ell}}</sub>}}, {{mvar|m<sub>s</sub>}},  जो की नीचे दिया गया है। परमाणु कण अवस्था (जैसे प्रोटॉन और न्यूट्रॉन) के  प्राचीन विवरण में यह सामान्य नामकरण भी है। आण्विक कक्षाओं के क्वांटम विवरण के लिए अन्य क्वांटम संख्याओं की आवश्यकता होती है, क्योंकि हैमिल्टनियन (क्वांटम यांत्रिकी) और इसकी समरूपता अलग-अलग होती है।
 ==== प्रिंसिपल क्वांटम नंबर ====
-{{Main|Principal quantum number}}
+{{Main|मुख्य क्वांटम संख्या}}
-{{See also|electron shell}}
+{{See also|इलेक्ट्रॉन शेल}}
-प्रिंसिपल क्वांटम संख्या एक [[इलेक्ट्रॉन कवच]] इलेक्ट्रॉन खोल, या ऊर्जा स्तर का वर्णन करती है। का मान है {{mvar|n}} 1 से लेकर उस परमाणु के सबसे बाहरी इलेक्ट्रॉन वाले शेल तक होता है, अर्थात<ref>{{cite book|title=आधुनिक भौतिकी की अवधारणाएँ|edition=4th |first=A. |last=Beiser |publisher=McGraw-Hill (International) |date=1987 |ISBN=0-07-100144-1}}{{page needed|date=November 2019}}</ref>
+मुख्य क्वांटम संख्या एक [[इलेक्ट्रॉन कवच|इलेक्ट्रॉन शेल]] इलेक्ट्रॉन शेल, या ऊर्जा स्तर का वर्णन करती है। का मान है {{mvar|n}} 1 से लेकर उस परमाणु के सबसे बाहरी इलेक्ट्रॉन वाले शेल तक होता है, अर्थात<ref>{{cite book|title=आधुनिक भौतिकी की अवधारणाएँ|edition=4th |first=A. |last=Beiser |publisher=McGraw-Hill (International) |date=1987 |ISBN=0-07-100144-1}}{{page needed|date=November 2019}}</ref>
 :{{math|1=''n'' = 1, 2, ...}}
-उदाहरण के लिए, [[सीज़ियम]] (Cs) में, सबसे बाहरी [[वैलेंस (रसायन विज्ञान)]] इलेक्ट्रॉन ऊर्जा स्तर 6 के खोल में होता है, इसलिए सीज़ियम में एक इलेक्ट्रॉन हो सकता है {{mvar|n}} मान 1 से 6 तक।
+उदाहरण के लिए, [[सीज़ियम]] (Cs) में, सबसे बाहरी [[वैलेंस (रसायन विज्ञान)]] इलेक्ट्रॉन ऊर्जा स्तर 6 के शेल में होता है, इसलिए सीज़ियम में एक इलेक्ट्रॉन हो सकता है {{mvar|n}} मान 1 से 6 तक।
-टाइम-इंडिपेंडेंट पोटेंशियल में कणों के लिए (देखें श्रोडिंगर इक्वेशन#टाइम इंडिपेंडेंट|श्रोडिंगर इक्वेशन), यह भी लेबल करता है {{mvar|n}} हेमिल्टनियन का वां आइगेनवेल्यू ({{mvar|H}}), यानी ऊर्जा {{mvar|E}}, कोणीय संवेग के कारण योगदान के साथ (शब्द शामिल है {{math|'''J'''<sup>2</sup>}}) बाहर छोड़ दिया। तो यह संख्या केवल इलेक्ट्रॉन और नाभिक के बीच की दूरी पर निर्भर करती है (अर्थात, रेडियल निर्देशांक {{math|'''r'''}}). से औसत दूरी बढ़ जाती है {{math|'''n'''}}. इसलिए अलग-अलग प्रिंसिपल क्वांटम नंबर वाले क्वांटम स्टेट्स को अलग-अलग शेल से संबंधित कहा जाता है।
+टाइम-इंडिपेंडेंट पोटेंशियल में कणों के लिए (देखें श्रोडिंगर इक्वेशन टाइम इंडिपेंडेंट|श्रोडिंगर इक्वेशन), यह भी लेबल करता है {{mvar|n}} हेमिल्टनियन का वां आइगेनवेल्यू ({{mvar|H}}), यानी ऊर्जा {{mvar|E}}, कोणीय संवेग के कारण योगदान के साथ (शब्द सम्मिलित है {{math|'''J'''<sup>2</sup>}}) छोड़ दिया। तो यह संख्या केवल इलेक्ट्रॉन और नाभिक के बीच की दूरी पर निर्भर करती है (अर्थात, रेडियल निर्देशांक {{math|'''r'''}}). से औसत दूरी बढ़ जाती है {{math|'''n'''}}. इसलिए अलग-अलग प्रिंसिपल क्वांटम नंबर वाले क्वांटम स्टेट्स को अलग-अलग शेल से संबंधित कहा जाता है।
 ==== अज़ीमुथल क्वांटम संख्या ====
-{{Main|Azimuthal quantum number}}
+{{Main|अज़ीमुथल क्वांटम संख्या}}
-{{See also|electron shell#Subshells}}
+{{See also|इलेक्ट्रॉन शेल#सबशेल्स}}
-अज़ीमुथल क्वांटम संख्या, जिसे कोणीय संवेग क्वांटम संख्या या कक्षीय क्वांटम संख्या के रूप में भी जाना जाता है, इलेक्ट्रॉन खोल#उपकोशों का वर्णन करता है, और संबंध के माध्यम से कक्षीय कोणीय गति का परिमाण देता है।
+अज़ीमुथल क्वांटम संख्या, जिसे कोणीय संवेग क्वांटम संख्या या कक्षीय क्वांटम संख्या के रूप में भी जाना जाता है, इलेक्ट्रॉन शेल#उपकोशों (सबशेल्स) का वर्णन करता है, और संबंध के माध्यम से कक्षीय कोणीय गति का परिमाण देता है।
 :{{math|1=''L''<sup>2</sup> {{=}} ''ħ''<sup>2</sup> ''{{ell}}'' (''{{ell}}'' + 1)}}
-रसायन विज्ञान और स्पेक्ट्रोस्कोपी में, {{math|1=''{{ell}}'' = 0}} को कक्षीय कहा जाता है, {{math|1=''{{ell}}'' = 1}}, पी कक्षीय, {{math|1=''{{ell}}'' = 2}}, डी कक्षीय, और {{math|1=''{{ell}}'' = 3}}, च कक्षीय।
+रसायन विज्ञान और स्पेक्ट्रोस्कोपी में, {{math|1=''{{ell}}'' = 0}} को s कक्षीय कहा जाता है, {{math|1=''{{ell}}'' = 1}}, p कक्षीय, {{math|1=''{{ell}}'' = 2}}, d कक्षीय, और {{math|1=''{{ell}}'' = 3}}, f कक्षीय।
-का मान है {{mvar|{{ell}}}} 0 से लेकर {{math|''n'' − 1}}, तो पहला p कक्षीय ({{math|1=''{{ell}}'' = 1}}) दूसरे इलेक्ट्रॉन शेल में प्रकट होता है ({{math|1=''n'' = 2}}), पहला d कक्षीय ({{math|1=''{{ell}}'' = 2}}) तीसरे खोल में प्रकट होता है ({{math|1=''n'' = 3}}), और इसी तरह:<ref>{{cite book|title=Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry|volume=1|first=P. W.|last=Atkins|publisher=Oxford University Press|date=1977|ISBN=0-19-855129-0}}{{page needed|date=February 2019}}</ref>
+का मान है {{mvar|{{ell}}}} 0 से लेकर {{math|''n'' − 1}}, तो पहला p कक्षीय ({{math|1=''{{ell}}'' = 1}}) दूसरे इलेक्ट्रॉन शेल में प्रकट होता है ({{math|1=''n'' = 2}}), पहला d कक्षीय ({{math|1=''{{ell}}'' = 2}}) तीसरे शेल में प्रकट होता है ({{math|1=''n'' = 3}}), और इसी तरह:<ref>{{cite book|title=Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry|volume=1|first=P. W.|last=Atkins|publisher=Oxford University Press|date=1977|ISBN=0-19-855129-0}}{{page needed|date=February 2019}}</ref>
 :{{math|1=''{{ell}}'' = 0, 1, 2,..., ''n'' − 1}}
-में शुरू होने वाली क्वांटम संख्या {{mvar|n}} = 3,{{ell}} = 0, एक परमाणु के तीसरे इलेक्ट्रॉन खोल के एस कक्षीय में एक इलेक्ट्रॉन का वर्णन करता है। रसायन विज्ञान में, यह क्वांटम संख्या बहुत महत्वपूर्ण है, क्योंकि यह एक [[परमाणु कक्षीय]] के आकार को निर्दिष्ट करती है और [[रासायनिक बंध]]नों और [[बंधन कोण]]ों को दृढ़ता से प्रभावित करती है। अज़ीमुथल क्वांटम संख्या एक कक्षीय में मौजूद कोणीय नोड्स की संख्या को भी निरूपित कर सकती है। उदाहरण के लिए, पी ऑर्बिटल्स के लिए, {{math|1=''{{ell}}'' = 1}} और इस प्रकार एपी ऑर्बिटल में कोणीय नोड्स की मात्रा 1 है।
+में प्रांरम्भ  होने वाली क्वांटम संख्या {{mvar|n}} = 3,{{ell}} = 0, एक परमाणु के तीसरे इलेक्ट्रॉन शेल के s कक्षीय में इलेक्ट्रॉन का वर्णन करता है। रसायन विज्ञान में, यह क्वांटम संख्या बहुत महत्वपूर्ण है, क्योंकि यह एक [[परमाणु कक्षीय]] के आकार को निर्दिष्ट करती है और [[रासायनिक बंध]]नों और [[बंधन कोण]]ों को दृढ़ता से प्रभावित करती है। अज़ीमुथल क्वांटम संख्या एक कक्षीय में मौजूद कोणीय नोड्स की संख्या को भी निरूपित कर सकती है। उदाहरण के लिए, p ऑर्बिटल्स के लिए, {{math|1=''{{ell}}'' = 1}} और इस प्रकार p ऑर्बिटल में कोणीय नोड्स की मात्रा 1 है।
 कक्षीय का आकार अज़ीमुथल क्वांटम संख्या द्वारा भी दिया जाता है।
 ====चुंबकीय क्वांटम संख्या====
-{{Main|Magnetic quantum number}}
+{{Main|चुंबकीय क्वांटम संख्या}}
-{{See also|atomic orbital}}
+{{See also|परमाणु कक्षीय}}
 चुंबकीय क्वांटम संख्या उस उपधारा के भीतर विशिष्ट परमाणु कक्षीय (या बादल) का वर्णन करती है, और एक निर्दिष्ट अक्ष के साथ कक्षीय कोणीय गति का प्रक्षेपण करती है:
@@ Line 97: / Line 98: @@
 | [[Spin quantum number]] || {{mvar|m<sub>s</sub>}}|| spin of the electron (−{{sfrac|1|2}} = "spin down", {{sfrac|1|2}} = "spin up") || {{math|−''s'' ≤ ''m<sub>s</sub>'' ≤ ''s''}} || for an electron {{math|1=''s'' = {{sfrac|1|2}}}}, <br /> so {{math|1=''m<sub>s</sub>'' = −{{sfrac|1|2}}, +{{sfrac|1|2}}}}
 |}
-उदाहरण: [[कार्बन]] (C) परमाणु के सबसे बाहरी वैलेंस (रसायन विज्ञान) [[इलेक्ट्रॉन]]ों को संदर्भित करने के लिए उपयोग की जाने वाली क्वांटम संख्याएँ, जो 2p परमाणु कक्षीय में स्थित हैं, हैं; {{math|1=''n'' = 2}} (दूसरा इलेक्ट्रॉन खोल), {{math|1=''{{ell}}'' = 1}} (p कक्षीय इलेक्ट्रॉन कोश#उपकोश), {{math|1=''m<sub>{{ell}}</sub>'' = 1, 0, −1}}, {{math|1=''m<sub>s</sub>'' = {{sfrac|1|2}}}} (समानांतर स्पिन)।
+उदाहरण: [[कार्बन]] (C) परमाणु के सबसे बाहरी वैलेंस (रसायन विज्ञान) [[इलेक्ट्रॉन]]ों को संदर्भित करने के लिए उपयोग की जाने वाली क्वांटम संख्याएँ, जो 2p परमाणु कक्षीय में स्थित हैं, हैं; {{math|1=''n'' = 2}} (दूसरा इलेक्ट्रॉन शेल), {{math|1=''{{ell}}'' = 1}} (p कक्षीय इलेक्ट्रॉन कोश#उपकोश), {{math|1=''m<sub>{{ell}}</sub>'' = 1, 0, −1}}, {{math|1=''m<sub>s</sub>'' = {{sfrac|1|2}}}} (समानांतर स्पिन)।
 [[स्पेक्ट्रोस्कोपी]] के परिणामों ने संकेत दिया कि अधिकतम दो इलेक्ट्रॉन एक कक्षीय पर कब्जा कर सकते हैं। हालांकि, हुंड के नियमों के अनुसार, दो इलेक्ट्रॉनों में कभी भी समान सटीक क्वांटम स्थिति नहीं हो सकती है और न ही क्वांटम संख्याओं का एक ही सेट हो सकता है, जो पाउली अपवर्जन सिद्धांत को संबोधित करता है। एक चौथा क्वांटम नंबर, जो दो संभावित मूल्यों के साथ स्पिन का प्रतिनिधित्व करता है, संघर्ष को हल करने के लिए एक तदर्थ धारणा के रूप में जोड़ा गया था; इस धारणा को बाद में सापेक्षवादी क्वांटम यांत्रिकी और प्रसिद्ध स्टर्न-गेरलाच प्रयोग के परिणामों से विस्तार से समझाया जाएगा।
 === पृष्ठभूमि ===
-क्वांटम यांत्रिकी के पूरे इतिहास में कई अलग-अलग मॉडल प्रस्तावित किए गए हैं, लेकिन नामकरण की सबसे प्रमुख प्रणाली [[फ्रेडरिक डॉग]], रॉबर्ट एस. मुल्लिकेन के हंड-मुल्लिकेन [[आणविक कक्षीय]] सिद्धांत और इरविन श्रोडिंगर | श्रोडिंगर, जॉन सी. स्लेटर के योगदान से उत्पन्न हुई है। और [[जॉन लेनार्ड-जोन्स]]। नामकरण की इस प्रणाली में [[नील्स बोह्र]] ऊर्जा स्तर, हंड-मुल्लिकेन कक्षीय सिद्धांत, और स्पेक्ट्रोस्कोपी और हुंड के नियमों के आधार पर इलेक्ट्रॉन स्पिन पर अवलोकन शामिल थे।<ref>Chemistry, Matter, and the Universe, R.E. Dickerson, I. Geis, W.A. Benjamin Inc. (USA), 1976, {{ISBN|0-19-855148-7}}</ref>
+क्वांटम यांत्रिकी के पूरे इतिहास में कई अलग-अलग मॉडल प्रस्तावित किए गए हैं, लेकिन नामकरण की सबसे प्रमुख प्रणाली [[फ्रेडरिक डॉग]], रॉबर्ट एस. मुल्लिकेन के हंड-मुल्लिकेन [[आणविक कक्षीय]] सिद्धांत और इरविन श्रोडिंगर | श्रोडिंगर, जॉन सी. स्लेटर के योगदान से उत्पन्न हुई है। और [[जॉन लेनार्ड-जोन्स]]। नामकरण की इस प्रणाली में [[नील्स बोह्र]] ऊर्जा स्तर, हंड-मुल्लिकेन कक्षीय सिद्धांत, और स्पेक्ट्रोस्कोपी और हुंड के नियमों के आधार पर इलेक्ट्रॉन स्पिन पर अवलोकन  सम्मिलित  थे।<ref>Chemistry, Matter, and the Universe, R.E. Dickerson, I. Geis, W.A. Benjamin Inc. (USA), 1976, {{ISBN|0-19-855148-7}}</ref>
@@ Line 110: / Line 111: @@
 {{Further|Clebsch–Gordan coefficients}}
 {{See also|Azimuthal quantum number#Total angular momentum of an electron in the atom}}
-जब कोई स्पिन-ऑर्बिट इंटरेक्शन को ध्यान में रखता है, तो {{mvar|L}} और {{mvar|S}} ऑपरेटर अब हैमिल्टनियन (क्वांटम यांत्रिकी) के साथ [[ क्रमविनिमेयता ]] नहीं रखते हैं, और उनके आइगेनवेल्यू समय के साथ बदलते हैं। इस प्रकार क्वांटम संख्याओं का एक और सेट इस्तेमाल किया जाना चाहिए। इस सेट में शामिल है<ref>{{cite book|title=Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry |volume=1 |first=P. W. |last=Atkins |publisher=Oxford University Press |date=1977 |ISBN=0-19-855129-0}}{{page needed|date=February 2019}}</ref><ref name="Atkins 1977">{{cite book|title=Molecular Quantum Mechanics Part III: An Introduction to Quantum Chemistry |volume=2 |first=P. W. |last=Atkins |publisher=Oxford University Press |date=1977}}{{ISBN missing}}{{page needed|date=February 2019}}</ref>
+जब कोई स्पिन-ऑर्बिट इंटरेक्शन को ध्यान में रखता है, तो {{mvar|L}} और {{mvar|S}} ऑपरेटर अब हैमिल्टनियन (क्वांटम यांत्रिकी) के साथ [[ क्रमविनिमेयता ]] नहीं रखते हैं, और उनके आइगेनवेल्यू समय के साथ बदलते हैं। इस प्रकार क्वांटम संख्याओं का एक और सेट इस्तेमाल किया जाना चाहिए। इस सेट में  सम्मिलित  है<ref>{{cite book|title=Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry |volume=1 |first=P. W. |last=Atkins |publisher=Oxford University Press |date=1977 |ISBN=0-19-855129-0}}{{page needed|date=February 2019}}</ref><ref name="Atkins 1977">{{cite book|title=Molecular Quantum Mechanics Part III: An Introduction to Quantum Chemistry |volume=2 |first=P. W. |last=Atkins |publisher=Oxford University Press |date=1977}}{{ISBN missing}}{{page needed|date=February 2019}}</ref>
 {{ordered list
@@ Line 163: / Line 164: @@
 |  2 ||  0 ||   0  ||  −{{sfrac|1|2}} || {{sfrac|1|2}} || −{{sfrac|1|2}} ||  −{{sfrac|1|2}}
 |}
-सिस्टम में क्वांटम राज्यों को इन 8 राज्यों के रैखिक संयोजन के रूप में वर्णित किया जा सकता है। हालाँकि, स्पिन-ऑर्बिट इंटरैक्शन की उपस्थिति में, यदि कोई 8 राज्यों द्वारा एक ही प्रणाली का वर्णन करना चाहता है जो हैमिल्टनियन (क्वांटम यांत्रिकी) के [[आइजन्वेक्टर]] हैं (अर्थात प्रत्येक एक ऐसे राज्य का प्रतिनिधित्व करता है जो समय के साथ दूसरों के साथ मिश्रण नहीं करता है), हमें चाहिए निम्नलिखित 8 राज्यों पर विचार करें:
+प्रणालीमें क्वांटम राज्यों को इन 8 राज्यों के रैखिक संयोजन के रूप में वर्णित किया जा सकता है। हालाँकि, स्पिन-ऑर्बिट इंटरैक्शन की उपस्थिति में, यदि कोई 8 राज्यों द्वारा एक ही प्रणाली का वर्णन करना चाहता है जो हैमिल्टनियन (क्वांटम यांत्रिकी) के [[आइजन्वेक्टर]] हैं (अर्थात प्रत्येक एक ऐसे राज्य का प्रतिनिधित्व करता है जो समय के साथ दूसरों के साथ मिश्रण नहीं करता है), हमें चाहिए निम्नलिखित 8 राज्यों पर विचार करें:
 :{| class="wikitable"
 ! {{math|''j''}} ||  {{math|1=''m<sub>j</sub>''}} || parity ||

v t e Electron configuration
Electron shell Atomic orbital Quantum mechanics Introduction to quantum mechanics
Quantum numbers	[[Principal quantum number\|Principal quantum number ( $n$ )]] [[Azimuthal quantum number\|Azimuthal quantum number ( $ℓ$ )]] [[Magnetic quantum number\|Magnetic quantum number ( $m$ )]] [[Spin quantum number\|Spin quantum number ( $s$ )]]
Ground-state configurations	Periodic table (electron configurations) Electron configurations of the elements (data page)
Electron filling	Pauli exclusion principle Hund's rule Aufbau principle
Electron pairing	Electron pair Unpaired electron
Bonding participation	Valence electron Core electron
Electron counting rules	Octet rule 18-electron rule

v t e Quantum mechanics
Background	Introduction History Timeline Classical mechanics Old quantum theory Glossary
Fundamentals	Born rule Bra–ket notation Complementarity Density matrix Energy level Ground state Excited state Degenerate levels Zero-point energy Entanglement Hamiltonian Interference Decoherence Measurement Nonlocality Quantum state Superposition Tunnelling Scattering theory Symmetry in quantum mechanics Uncertainty Wave function Collapse Wave–particle duality
Formulations	Formulations Heisenberg Interaction Matrix mechanics Schrödinger Path integral formulation Phase space
Equations	Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations	Interpretations Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Many-worlds Objective collapse Quantum logic Relational Transactional Von Neumann-Wigner
Experiments	Bell's inequality Davisson–Germer Delayed-choice quantum eraser Double-slit Franck–Hertz Mach–Zehnder interferometer Elitzur–Vaidman Popper Quantum eraser Stern–Gerlach Wheeler's delayed choice
Science	Quantum biology Quantum chemistry Quantum chaos Quantum cosmology Quantum differential calculus Quantum dynamics Quantum geometry Quantum measurement problem Quantum stochastic calculus Quantum spacetime
Technology	Quantum algorithms Quantum amplifier Quantum bus Quantum cellular automata Quantum finite automata Quantum channel Quantum circuit Quantum complexity theory Quantum computing Timeline Quantum cryptography Quantum electronics Quantum error correction Quantum imaging Quantum image processing Quantum information Quantum key distribution Quantum logic Quantum logic gates Quantum machine Quantum machine learning Quantum metamaterial Quantum metrology Quantum network Quantum neural network Quantum optics Quantum programming Quantum sensing Quantum simulator Quantum teleportation
Extensions	Casimir effect Quantum statistical mechanics Quantum field theory History Quantum gravity Relativistic quantum mechanics
Related	Schrödinger's cat in popular culture Quantum mysticism
Category Physics portal Commons

Anonymous

Search

सांख्यिक अंक: Difference between revisions

Namespaces

More

Page actions

Revision as of 20:43, 29 April 2023

Contents

किसी दिए गए प्रणालीके लिए आवश्यक क्वांटम संख्या

परमाणु में इलेक्ट्रॉन

विशिष्टता

सामान्य शब्दावली

प्रिंसिपल क्वांटम नंबर

अज़ीमुथल क्वांटम संख्या

चुंबकीय क्वांटम संख्या

स्पिन क्वांटम संख्या

नियम

पृष्ठभूमि

कुल कोणीय संवेग संख्या

कण का कुल कोणीय संवेग

परमाणु कोणीय गति क्वांटम संख्या

प्राथमिक कण

गुणक क्वांटम संख्या

यह भी देखें

टिप्पणियाँ

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

सांख्यिक अंक: Difference between revisions

Revision as of 20:43, 29 April 2023

किसी दिए गए प्रणालीके लिए आवश्यक क्वांटम संख्या

परमाणु में इलेक्ट्रॉन

विशिष्टता

सामान्य शब्दावली

प्रिंसिपल क्वांटम नंबर

अज़ीमुथल क्वांटम संख्या

चुंबकीय क्वांटम संख्या

स्पिन क्वांटम संख्या

नियम

पृष्ठभूमि

कुल कोणीय संवेग संख्या

कण का कुल कोणीय संवेग

परमाणु कोणीय गति क्वांटम संख्या

प्राथमिक कण

गुणक क्वांटम संख्या

यह भी देखें

टिप्पणियाँ

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories