एफ़िन लाई बीजगणित

गणित में, एफ़िन लाई बीजगणित अनंत-आयामी लाई बीजगणित है, जो परिमित-आयामी सरल लाई बीजगणित से विहित फैशन में निर्मित होता है। एफ़िन लाई बीजगणित को देखते हुए, नीचे वर्णित अनुसार, संबंधित एफ़िन केएसी-मूडी बीजगणित भी बना सकता है। विशुद्ध रूप से गणितीय दृष्टिकोण से, एफ़िन लाई बीजगणित रोचक हैं क्योंकि उनके प्रतिनिधित्व सिद्धांत, परिमित-आयामी अर्ध-सरल लाई बीजगणित के प्रतिनिधित्व सिद्धांत के जैसे, सामान्य केएसी-मूडी बीजगणित की तुलना में अधिक उत्तम समझा जाता है। जैसा कि विक्टर केएसी द्वारा देखा गया है, एफ़िन लाई बीजगणित के निरूपण के लिए वर्ण सूत्र कुछ संयुक्त पहचान, मैकडोनाल्ड पहचान का अर्थ है।

एफ़िन लाई बीजगणित स्ट्रिंग सिद्धांत और द्वि-आयामी अनुरूप क्षेत्र सिद्धांत में महत्वपूर्ण भूमिका निभाते हैं जिस प्रकार से वे निर्मित होते हैं: साधारण लाई बीजगणित से प्रारंभ ${\mathfrak {g}}$, लूप बीजगणित पर विचार करता है, $L{\mathfrak {g}}$, द्वारा गठित ${\mathfrak {g}}$ बिंदुवार कम्यूटेटर के साथ वृत्त (बंद स्ट्रिंग के रूप में व्याख्या) पर मूल्यवान कार्य होता है। द एफ़िन लाई बीजगणित ${\hat {\mathfrak {g}}}$ लूप बीजगणित में अतिरिक्त आयाम जोड़कर और गैर-अल्प प्रकार से कम्यूटेटर को संशोधित करके प्राप्त किया जाता है, जिसे भौतिक विज्ञानी क्वांटम विसंगति कहते हैं (इस स्थिति में, WZW प्रारूप की विसंगति) और गणितज्ञ केंद्रीय विस्तार है। सामान्यतः अधिक, अगर σ साधारण लाई बीजगणित का automorphism है ${\mathfrak {g}}$ इसके डायनकिन आरेख, मुड़ लूप बीजगणित के ऑटोमोर्फिज्म से जुड़ा हुआ है $L_{\sigma }{\mathfrak {g}}$ के होते हैं ${\mathfrak {g}}$वास्तविक रेखा पर -मूल्यवान कार्य f जो संतुष्ट करते हैं मुड़ आवधिकता की स्थिति f(x + 2π) = σ f(x). उनके केंद्रीय विस्तार सटीक रूप से मुड़े हुए चक्कर वाले बीजगणित हैं। स्ट्रिंग थ्योरी के दृष्टिकोण से एफ़िन ले बीजगणित के कई गहरे गुणों को समझने में मदद मिलती है, जैसे तथ्य यह है कि उनके प्रतिनिधित्व के बीजगणितीय वर्ण मॉड्यूलर समूह के तहत आपस में बदलते हैं।

== Affine लाई बीजगणित सरल लाई बीजगणित == से

परिभाषा

अगर ${\mathfrak {g}}$ परिमित-आयामी सरल लाई बीजगणित है, संगत affine लाई बीजगणित ${\hat {\mathfrak {g}}}$ लूप बीजगणित के लाई बीजगणित विस्तार #Central के रूप में बनाया गया है ${\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]$, आयामी केंद्र के साथ $\mathbb {\mathbb {C} } c.$ सदिश स्थान के रूप में,

${\widehat {\mathfrak {g}}}={\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]\oplus \mathbb {\mathbb {C} } c,$

कहाँ $\mathbb {\mathbb {C} } [t,t^{-1}]$ अनिश्चित टी में लॉरेंट श्रृंखला का जटिल वेक्टर स्थान है। लाई ब्रैकेट सूत्र द्वारा परिभाषित किया गया है

$[a\otimes t^{n}+\alpha c,b\otimes t^{m}+\beta c]=[a,b]\otimes t^{n+m}+\langle a|b\rangle n\delta _{m+n,0}c$

सभी के लिए $a,b\in {\mathfrak {g}},\alpha ,\beta \in \mathbb {\mathbb {C} }$ और $n,m\in \mathbb {Z}$, कहाँ $[a,b]$ लाई बीजगणित में लाई ब्रैकेट है ${\mathfrak {g}}$ और $\langle \cdot |\cdot \rangle$ मारक रूप है|कार्टन-किलिंग फॉर्म चालू है ${\mathfrak {g}}.$ परिमित-आयामी अर्ध-सरल लाई बीजगणित के संगत एफ़िन लाई बीजगणित, एफ़िन लाई बीजगणित का सीधा योग है जो इसके सरल सारांश के अनुरूप है। द्वारा परिभाषित affine Lie बीजगणित की विशिष्ट व्युत्पत्ति है

$\delta (a\otimes t^{m}+\alpha c)=t{d \over dt}(a\otimes t^{m}).$

संबंधित affine Kac–Moody बीजगणित को अतिरिक्त जनरेटर d जोड़कर अर्ध-प्रत्यक्ष उत्पाद के रूप में परिभाषित किया गया है जो संतुष्ट करता है [d, A] = δ(A ).

डायकिन आरेखों का निर्माण

प्रत्येक एफ़िन लाई बीजगणित के डायनकिन आरेख में संबंधित सरल लाई बीजगणित और अतिरिक्त नोड होता है, जो काल्पनिक रूट के अतिरिक्त से मेल खाता है। बेशक, इस तरह के नोड को किसी भी स्थान पर डायनकिन आरेख से जोड़ा नहीं जा सकता है, लेकिन प्रत्येक साधारण लाई बीजगणित के लिए लाई बीजगणित के बाहरी ऑटोमोर्फिज्म समूह के समूह की प्रमुखता के बराबर कई संभावित अनुलग्नक मौजूद हैं। विशेष रूप से, इस समूह में हमेशा पहचान तत्व होता है, और संबंधित एफ़िन लाई बीजगणित को अनट्विस्टेड एफ़िन लाई बीजगणित कहा जाता है। जब साधारण बीजगणित ऑटोमोर्फिज़्म को स्वीकार करता है जो आंतरिक ऑटोमोर्फिज़्म नहीं हैं, तो कोई अन्य डायनकिन आरेख प्राप्त कर सकता है और ये ट्विस्टेड एफ़िन ले बीजगणित के अनुरूप होते हैं।

एफ़िन लाई एल्जेब्रस के लिए डाइनकिन डायग्राम

हरे रंग में जोड़े गए नोड्स के साथ विस्तारित (अनट्विस्टेड) ​​एफ़ाइन डाइकिन आरेखों का समूह

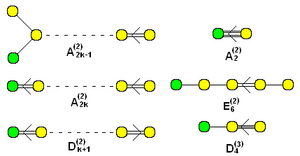"ट्विस्टेड" एफ़िन फॉर्म का नाम (2) या (3) सुपरस्क्रिप्ट के साथ रखा गया है। (k ग्राफ में नोड्स की संख्या है।)

केंद्रीय विस्तार का वर्गीकरण

इसी सरल लाई बीजगणित के डायनकिन आरेख के लिए अतिरिक्त नोड का लगाव निम्नलिखित निर्माण से मेल खाता है। affine Lie बीजगणित हमेशा समूह विस्तार के रूप में बनाया जा सकता है # संबंधित सरल लाई बीजगणित के पाश बीजगणित का केंद्रीय विस्तार। यदि कोई इसके बजाय अर्ध-सरल लाई बीजगणित के साथ शुरू करना चाहता है, तो उसे अर्ध-सरल बीजगणित के सरल घटकों की संख्या के बराबर तत्वों की संख्या से केंद्रीय रूप से विस्तार करने की आवश्यकता है। भौतिकी में, इसके बजाय अक्सर अर्ध-सरल बीजगणित और एबेलियन बीजगणित के प्रत्यक्ष योग पर विचार किया जाता है $\mathbb {\mathbb {C} } ^{n}$. इस मामले में n एबेलियन जनरेटर के लिए n और केंद्रीय तत्वों को जोड़ने की भी आवश्यकता है।

इसी सरल कॉम्पैक्ट लाई समूह के लूप समूह का दूसरा इंटीग्रल कोहोलॉजी पूर्णांकों के लिए आइसोमोर्फिक है। एकल जनरेटर द्वारा एफ़िन लाई समूह के केंद्रीय विस्तार इस मुक्त लूप समूह पर टोपोलॉजिकल रूप से सर्कल बंडल हैं, जिन्हें दो-श्रेणी द्वारा वर्गीकृत किया जाता है जिसे कंपन के पहले चेर्न वर्ग के रूप में जाना जाता है। इसलिए, एफ़िन ली ग्रुप के केंद्रीय एक्सटेंशन को पैरामीटर के द्वारा वर्गीकृत किया जाता है जिसे भौतिकी साहित्य में स्तर कहा जाता है, जहां यह पहली बार दिखाई देता है। Affine कॉम्पैक्ट समूहों का एकात्मक उच्चतम वजन प्रतिनिधित्व केवल तभी मौजूद होता है जब k प्राकृतिक संख्या हो। अधिक सामान्यतः, यदि कोई अर्ध-सरल बीजगणित पर विचार करता है, तो प्रत्येक साधारण घटक के लिए केंद्रीय शुल्क होता है।

संरचना

कार्टन-वील आधार

जैसा कि परिमित मामले में, कार्टन-वेइल आधार का निर्धारण एफ़िन लाई अलजेब्रस की संरचना का निर्धारण करने में महत्वपूर्ण कदम है।

परिमित-आयामी, सरल, जटिल लाई बीजगणित को ठीक करें ${\mathfrak {g}}$ यह सबलजेब्रा परीक्षण के साथ ${\mathfrak {h}}$ और विशेष जड़ प्रणाली $\Delta$. अंकन का परिचय $X_{n}=X\otimes t^{n},$, कोई कार्टन-वेइल आधार का विस्तार करने का प्रयास कर सकता है $\{H^{i}\}\cup \{E^{\alpha }|\alpha \in \Delta \}$ के लिए ${\mathfrak {g}}$ affine Lie बीजगणित के लिए एक, द्वारा दिया गया $\{H_{n}^{i}\}\cup \{c\}\cup \{E_{n}^{\alpha }\}$, साथ $\{H_{0}^{i}\}\cup \{c\}$ एबेलियन सबलजेब्रा बनाना।

के eigenvalues $ad(H_{0}^{i})$ और $ad(c)$ पर $E_{n}^{\alpha }$ हैं $\alpha ^{i}$ और $0$ क्रमशः और स्वतंत्र रूप से $n$. इसलिए जड़ $\alpha$ इस एबेलियन सबलजेब्रा के संबंध में असीम रूप से पतित है। एबेलियन सबलजेब्रा में ऊपर वर्णित व्युत्पत्ति को लागू करने से एबेलियन सबलजेब्रा एफ़िन लाई बीजगणित के लिए कार्टन सबलजेब्रा में बदल जाता है, ईगेनवैल्यू के साथ $(\alpha ^{1},\cdots ,\alpha ^{dim{\mathfrak {h}}},0,n)$ के लिए $E_{n}^{\alpha }.$

हत्या रूप

इसकी अचल संपत्ति का उपयोग करके हत्या का रूप लगभग पूरी तरह से निर्धारित किया जा सकता है। अंकन का उपयोग करना $B$ किलिंग फॉर्म के लिए ${\mathfrak {g}}$ और ${\hat {B}}$ एफिन केएसी-मूडी बीजगणित पर किलिंग फॉर्म के लिए,

$${\hat {B}}(X_{n},Y_{m})=B(X,Y)\delta _{n+m,0},$$

$${\hat {B}}(X_{n},c)=0,{\hat {B}}(X_{n},d)=0$$

$${\hat {B}}(c,c)=0,{\hat {B}}(c,d)=1,{\hat {B}}(d,d)=0,$$

जहां केवल अंतिम समीकरण को निश्चरता से तय नहीं किया जाता है और इसके बजाय सम्मेलन द्वारा चुना जाता है। विशेष रूप से, का प्रतिबंध ${\hat {B}}$ तक $c,d$ सबस्पेस हस्ताक्षर के साथ बिलिनियर फॉर्म देता है $(+,-)$.

से संबद्ध ऐफिन रूट लिखिए $E_{n}^{\alpha }$ जैसा ${\hat {\alpha }}=(\alpha ;0;n)$. परिभाषित $\delta =(0,0,1)$, इसे फिर से लिखा जा सकता है

$${\hat {\alpha }}=\alpha +n\delta .$$

जड़ों का पूरा सेट है

$${\hat {\Delta }}=\{\alpha +n\delta |n\in \mathbb {Z} ,\alpha \in \Delta \}\cup \{n\delta |n\in \mathbb {Z} ,n\neq 0\}.$$

तब $\delta$ असामान्य है क्योंकि इसकी लंबाई शून्य है: $(\delta ,\delta )=0$ कहाँ $(\cdot ,\cdot )$ किलिंग फॉर्म से प्रेरित जड़ों पर द्विरेखीय रूप है।

=== सरल रूट === एफ़िन करें एफ़िन बीजगणित के लिए सरल जड़ों का आधार प्राप्त करने के लिए, अतिरिक्त सरल जड़ को जोड़ा जाना चाहिए, और इसके द्वारा दिया गया है

$$\alpha _{0}=-\theta +\delta$$

कहाँ $\theta$ का उच्चतम मूल है ${\mathfrak {g}}$, रूट की ऊंचाई की सामान्य धारणा का उपयोग करते हुए। यह विस्तारित कार्टन मैट्रिक्स और विस्तारित डायनकिन आरेखों की परिभाषा की अनुमति देता है।

प्रतिनिधित्व सिद्धांत

एफ़िन लाई बीजगणित के लिए प्रतिनिधित्व सिद्धांत आमतौर पर वर्मा मॉड्यूल का उपयोग करके विकसित किया जाता है। अर्ध-सरल लाई बीजगणित के मामले में, ये उच्चतम वजन वाले मॉड्यूल हैं। कोई परिमित-आयामी निरूपण नहीं हैं; यह इस तथ्य से अनुसरण करता है कि परिमित-आयामी वर्मा मॉड्यूल के अशक्त वैक्टर आवश्यक रूप से शून्य हैं; जबकि affine लाई बीजगणित के लिए नहीं हैं। मोटे तौर पर, यह इस प्रकार है क्योंकि किलिंग फॉर्म लोरेंट्ज़ियन में है $c,\delta$ दिशा, इस प्रकार $(z,{\bar {z}})$ स्ट्रिंग पर कभी-कभी लाइटकोन निर्देशांक कहलाते हैं। रेडियल ऑर्डर किए गए वर्तमान बीजगणित उत्पादों को समय-समय पर सामान्य रूप से ऑर्डर करके समझा जा सकता है $z=\exp(\tau +i\sigma )$ साथ $\tau$ स्ट्रिंग विश्व पत्रक के साथ समय जैसी दिशा और $\sigma$ स्थानिक दिशा।

=== रैंक k === का निर्वात प्रतिनिधित्व अभ्यावेदन अधिक विस्तार से निम्नानुसार निर्मित किए गए हैं। लाई बीजगणित ठीक करें ${\mathfrak {g}}$ और आधार $\{J^{\rho }\}$. तब $\{J_{n}^{\rho }\}=\{J^{\rho }\otimes t^{n}\}$ संबंधित पाश बीजगणित के लिए आधार है, और $\{J_{n}^{\rho }\}\cup \{c\}$ affine लाई बीजगणित का आधार है ${\hat {\mathfrak {g}}}$.

रैंक का निर्वात प्रतिनिधित्व $k$, निरूपित $V_{k}({\mathfrak {g}})$ कहाँ $k\in \mathbb {C}$ आधार के साथ जटिल प्रतिनिधित्व है

$$\{v_{n_{1}\cdots n_{m}}^{\rho _{1}\cdots \rho _{m}}:n_{1}\geq \cdots \geq n_{m}\geq 1,\rho _{1}\leq \cdots \leq \rho _{m}\}\cup \{\Omega \}$$

और की क्रिया को परिभाषित करें ${\hat {\mathfrak {g}}}$ पर $V=V_{k}({\mathfrak {g}})$ द्वारा (के साथ $n>0$)

$$c=k{\text{id}}_{V},\,J_{n}^{\rho }\Omega =0,$$

$$J_{-n}^{\rho }\Omega =v_{n}^{\rho }\,J_{-n}^{\rho }v_{n_{1}\cdots n_{m}}^{\rho _{1}\cdots \rho _{m}}=v_{nn_{1}\cdots n_{m}}^{\rho \rho _{1}\cdots \rho _{m}}.$$

एफिन वर्टेक्स बीजगणित

See also: Vertex operator algebra § Example: WZW vacuum modules

वास्तव में निर्वात प्रतिनिधित्व शीर्ष बीजगणित संरचना से सुसज्जित किया जा सकता है, जिस स्थिति में इसे 'रैंक का एफ़िन वर्टेक्स बीजगणित' कहा जाता है $k$. एफ़िन लाई बीजगणित स्वाभाविक रूप से अंतर के साथ, काक-मूडी बीजगणित तक फैली हुई है $d$ अनुवाद ऑपरेटर द्वारा प्रतिनिधित्व किया $T$ शीर्ष बीजगणित में।

वेइल समूह और वर्ण

Main article: Weyl-Kac character formula

एफ़िन लाई बीजगणित के वेइल समूह को शून्य-मोड बीजगणित (लूप बीजगणित को लूप बीजगणित को परिभाषित करने के लिए उपयोग किया जाता है) और कोरूट जाली के वेइल समूह के अर्ध-प्रत्यक्ष उत्पाद के रूप में लिखा जा सकता है।

एफ़िन लाई बीजगणित के बीजगणितीय वर्णों का वेइल वर्ण सूत्र, वेइल-केएसी वर्ण सूत्र के लिए सामान्यीकरण करता है। इनमें से कई रोचक निर्माण अनुसरण करते हैं। कोई जैकोबी थीटा प्रकार्य के सामान्यीकरण का निर्माण कर सकता है। ये थीटा कार्य मॉड्यूलर समूह के अंतर्गत रूपांतरित होते हैं। अर्ध-सरल लाई बीजगणित की सामान्य भाजक पहचान भी सामान्यीकृत होती है; क्योंकि पात्रों को विकृतियों या उच्चतम वजन के क्यू-एनालॉग के रूप में लिखा जा सकता है, इसने कई नई संयोजक पहचानों को जन्म दिया, जिसमें डेडेकाइंड और फंक्शन के लिए कई पूर्व अज्ञात पहचान शामिल हैं। इन सामान्यीकरणों को लैंगलैंड्स कार्यक्रम के व्यावहारिक उदाहरण के रूप में देखा जा सकता है।

अनुप्रयोग

WZW मॉडल # सुगवारा निर्माण के कारण, किसी भी एफ़िन लाई बीजगणित के सार्वभौमिक लिफाफा बीजगणित में विरासोरो बीजगणित उपलजेब्रा के रूप में है। यह एफ़ाइन ले बीजगणित को द्वि-आयामी अनुरूप क्षेत्र सिद्धांत जैसे WZW मॉडल या कोसेट मॉडल के समरूपता बीजगणित के रूप में सेवा करने की अनुमति देता है। परिणामस्वरूप, स्ट्रिंग थ्योरी के वर्ल्डशीट विवरण में एफ़िन लाई बीजगणित भी दिखाई देते हैं।

उदाहरण

हाइजेनबर्ग बीजगणित जनरेटर द्वारा परिभाषित $a_{n},n\in \mathbb {Z}$ रूपांतरण संबंधों को संतोषजनक

$$[a_{m},a_{n}]=m\delta _{m+n,0}c$$

एफ़िन लाई बीजगणित ${\hat {\mathfrak {u}}}(1)$ के रूप में अनुभूत किया जा सकता है।

संदर्भ

• Fuchs, Jurgen (1992), Affine Lie Algebras and Quantum Groups, Cambridge University Press, ISBN 0-521-48412-X
• Goddard, Peter; Olive, David (1988), Kac-Moody and Virasoro algebras: A Reprint Volume for Physicists, Advanced Series in Mathematical Physics, vol. 3, World Scientific, ISBN 9971-5-0419-7
• Kac, Victor (1990), Infinite dimensional Lie algebras (3 ed.), Cambridge University Press, ISBN 0-521-46693-8
• Kohno, Toshitake (1998), Conformal Field Theory and Topology, American Mathematical Society, ISBN 0-8218-2130-X
• Pressley, Andrew; Segal, Graeme (1986), Loop groups, Oxford University Press, ISBN 0-19-853535-X