कोणीय व्यास: Difference between revisions
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
गोलाकार वस्तु <math>d_\mathrm{act}</math>के लिए जिसका वास्तविक व्यास समान होता है, और जहाँ <math>D</math> गोले के केंद्र की दूरी है, कोणीय व्यास निम्न सूत्र द्वारा पाया जा सकता है: | गोलाकार वस्तु <math>d_\mathrm{act}</math>के लिए जिसका वास्तविक व्यास समान होता है, और जहाँ <math>D</math> गोले के केंद्र की दूरी है, कोणीय व्यास निम्न सूत्र द्वारा पाया जा सकता है: | ||
:<math>\delta = 2\arcsin \left(\frac{d_\mathrm{act}}{2D}\right)</math> | :<math>\delta = 2\arcsin \left(\frac{d_\mathrm{act}}{2D}\right)</math> | ||
अंतर इस तथ्य के कारण है कि वृत्त के स्पष्ट किनारे इसके स्पर्श बिंदु हैं, जो वृत्त के केंद्र की तुलना में पर्यवेक्षक के निकट हैं। अंतर केवल बड़े कोणीय व्यास की गोलाकार वस्तुओं के लिए महत्वपूर्ण है, क्योंकि निम्नलिखित [[छोटे-कोण सन्निकटन]] छोटे मूल्यों <math>x</math> के लिए हैं:<ref>{{cite web |url=http://www.mathstat.concordia.ca/faculty/rhall/mc/arctan.pdf |title=कार्यकार्तान के लिए एक टेलर श्रृंखला|access-date=2015-01-23 |url-status=dead |archive-url=https://web.archive.org/web/20150218190328/http://www.mathstat.concordia.ca/faculty/rhall/mc/arctan.pdf |archive-date=2015-02-18 }}</ref> | अंतर इस तथ्य के कारण है कि वृत्त के स्पष्ट किनारे इसके स्पर्श बिंदु हैं, जो वृत्त के केंद्र की तुलना में पर्यवेक्षक के निकट होते हैं। अंतर केवल बड़े कोणीय व्यास की गोलाकार वस्तुओं के लिए महत्वपूर्ण होते है, क्योंकि निम्नलिखित [[छोटे-कोण सन्निकटन]] छोटे मूल्यों <math>x</math> के लिए हैं:<ref>{{cite web |url=http://www.mathstat.concordia.ca/faculty/rhall/mc/arctan.pdf |title=कार्यकार्तान के लिए एक टेलर श्रृंखला|access-date=2015-01-23 |url-status=dead |archive-url=https://web.archive.org/web/20150218190328/http://www.mathstat.concordia.ca/faculty/rhall/mc/arctan.pdf |archive-date=2015-02-18 }}</ref> | ||
:<math>\arcsin x \approx \arctan x \approx x.</math> | :<math>\arcsin x \approx \arctan x \approx x.</math> | ||
== हाथ से कोणीय व्यास का अनुमान लगाना == | == हाथ से कोणीय व्यास का अनुमान लगाना == | ||
Revision as of 20:10, 16 April 2023
कोणीय व्यास, आकार, स्पष्ट व्यास, या आकार ऐसी कोणीय दूरी है जो बताता है कि किसी दिए गए बिंदु से गोला या वृत्त कितना बड़ा दिखाई देता है। दृष्टि विज्ञान में, इसे दृश्य कोण कहा जाता है, और प्रकाशिकी में, इसे कोणीय छिद्र (लेंस का) कहा जाता है। कोणीय व्यास को कोणीय विस्थापन के रूप में माना जा सकता है जिसके माध्यम से आँख या कैमरे को स्पष्ट चक्र की ओर से विपरीत दिशा में देखने के लिए घूमना चाहिए। मनुष्य अपनी नग्न आंखों से लगभग 1 आर्कमिनट (लगभग 0.017° या 0.0003 रेडियन) तक के व्यास का समाधान कर सकते हैं।[1] यह 1 किमी की दूरी पर 0.3 मीटर से युग्मित होती है, या शुक्र को इष्टतम परिस्थितियों में डिस्क के रूप में देखने के अनुरूप होते है।
सूत्र
वृत्त का कोणीय व्यास जिसका तल विस्थापन सदिश के लंबवत होता है, और उक्त वृत्त के केंद्र के मध्य सूत्र का उपयोग करके गणना की जा सकती है[2]
जिसमें डिग्री में कोणीय व्यास है, और वस्तु का वास्तविक व्यास है, और वस्तु की दूरी है। जब , अपने निकट है, और प्राप्त परिणाम रेडियन में है।
गोलाकार वस्तु के लिए जिसका वास्तविक व्यास समान होता है, और जहाँ गोले के केंद्र की दूरी है, कोणीय व्यास निम्न सूत्र द्वारा पाया जा सकता है:
अंतर इस तथ्य के कारण है कि वृत्त के स्पष्ट किनारे इसके स्पर्श बिंदु हैं, जो वृत्त के केंद्र की तुलना में पर्यवेक्षक के निकट होते हैं। अंतर केवल बड़े कोणीय व्यास की गोलाकार वस्तुओं के लिए महत्वपूर्ण होते है, क्योंकि निम्नलिखित छोटे-कोण सन्निकटन छोटे मूल्यों के लिए हैं:[3]
हाथ से कोणीय व्यास का अनुमान लगाना
जैसा कि चित्र में दिखाया गया है, कोणीय व्यास का अनुमान हाथ को प्रत्येक प्रकार से विस्तारित भुजा समकोण पर प्राप्त किया जा सकता है।[4][5][6]
खगोल विज्ञान में प्रयोग
खगोल विज्ञान में, आकाशीय पिंडों के आकार प्रायः उनके वास्तविक आकार के अतिरिक्त पृथ्वी से देखे गए उनके कोणीय व्यास के संदर्भ में दिए जाते हैं। चूंकि ये कोणीय व्यास सामान्यतः छोटे होते हैं, इसलिए इन्हें आर्कसेकंड (″) में प्रस्तुत करना सामान्य है, एक आर्कसेकंड एक डिग्री (कोण) (1°) का 1/3600वाँ और रेडियन 180/π डिग्री का होता है। तो रेडियन समान 3,600 × 180/ आर्कसेकंड, जो लगभग 206,265 आर्कसेकंड (1 रेड ≈ 206,264.806247) है। इसलिए, D दूरी पर भौतिक व्यास d के साथ वस्तु का कोणीय व्यास, आर्कसेकेंड में व्यक्त किया गया है:[7]
- .
इन वस्तुओं का कोणीय व्यास 1″ है:
- 2.06 किमी की दूरी पर 1 सेमी व्यास की वस्तु होती है।
- 1 खगोलीय इकाई (एयू) की दूरी पर 725.27 किमी व्यास वाली वस्तु होती है।
- 1 प्रकाश-वर्ष पर 45 866 916 किमी व्यास वाली वस्तु होती है।
- 1 पारसेक (पीसी) की दूरी पर 1 एयू (149 597 871 किमी) व्यास की वस्तु होती है।
इस प्रकार, 1 पीसी की दूरी से देखने पर सूर्य के चारों ओर पृथ्वी की कक्षा का कोणीय व्यास 2″ है, क्योंकि 1 एयू पृथ्वी की कक्षा की माध्य त्रिज्या है।
प्रकाश वर्ष की दूरी से सूर्य का कोणीय व्यास 0.03″ और पृथ्वी का 0.0003″ है। ऊपर दिए गए सूर्य का कोणीय व्यास 0.03″ पृथ्वी के व्यास की दूरी पर मानव शरीर के समान है।
यह तालिका उल्लेखनीय खगोलीय पिंडों के कोणीय आकार को दर्शाती है जैसा कि पृथ्वी से देखा गया है:
| आकाशीय वस्तु | कोणीय व्यास या आकार | तुलनात्मक आकार |
|---|---|---|
| मैगेलैनिक स्ट्रीम | over 100° | |
| गम नेबुला | 36° | |
| आकाशगंगा | 30° (by 360°) | |
| विस्तारित हाथ की चौड़ाई | 20° | 1 किमी की दूरी पर 353 मीटर |
| सर्पेंस-अक्विला रिफ्ट | 20° by 10° | |
| कैनिस मेजर ओवरडेंसिटी | 12° by 12° | |
| स्मिथ का बादल | 11° | |
| बड़ा मैगेलैनिक बादल | 10.75° by 9.17° | ध्यान दें: रात के आकाश में मिल्की मार्ग की तुलना में सबसे चमकीली आकाशगंगा (0.9 स्पष्ट परिमाण (V)) |
| बरनार्ड का लूप | 10° | |
| ज़ेटा ओफियुची एसएच2-27 नेबुला | 10° | |
| हाथ के साथ मुट्ठी की चौड़ाई बाहर फैली हुई | 10° | 1 किमी की दूरी पर 175 मीटर |
| धनु बौना गोलाकार आकाशगंगा | 7.5° by 3.6° | |
| उत्तरी कोलसैक नेबुला | 7° by 5°[8] | |
| कोलसैक नेबुला | 7° by 5° | |
| सिग्नस OB7 | 4° by 7°[9] | |
| रो ओफ़ियुची बादल परिसर | 4.5° by 6.5° | |
| हयाडेस | 5°30′ | ध्यान दें: रात के आसमान में सबसे चमकीला तारा समूह, 0.5 स्पष्ट परिमाण (V) |
| छोटा मैगेलैनिक बादल | 5°20′ by 3°5′ | |
| एंड्रोमेडा आकाशगंगा | 3°10′ by 1° | सूर्य या चंद्रमा के आकार का लगभग छह गुना लंबी-एक्सपोज़र फ़ोटोग्राफ़ी के बिना अधिक छोटा कोर दिखाई देता है। |
| वैल नीहारिका | 3° | |
| हार्ट नेबुला | 2.5° by 2.5° | |
| वेस्टरहाउट 5 | 2.3° by 1.25° | |
| एसएच2-54 | 2.3° | |
| कैरिना नेबुला | 2° by 2° | ध्यान दें: रात के आसमान में सबसे चमकीला नेबुला, 1.0 स्पष्ट परिमाण (V) |
| उत्तरी अमेरिका नेबुला | 2° by 100′ | |
| ओरियन नेबुला | 1°5′ by 1° | |
| फैली हुई बांह के साथ छोटी उंगली की चौड़ाई | 1° | 1 किमी की दूरी पर 17.5 मीटर |
| चंद्रमा | 34′6″ – 29′20″ | शुक्र के लिए 32.5–28 गुना अधिकतम मूल्य (नीचे नारंगी पट्टी) / 2046–1760″ चंद्रमा का व्यास 3,474 किमी है। |
| सूर्य | 32′32″ – 31′27″ | शुक्र के लिए 31-30 गुना अधिकतम मूल्य (नीचे नारंगी पट्टी) / 1952-1887″ सूर्य का व्यास 1,391,400 किमी है। |
| हेलिक्स नेबुला | about 16′ by 28′ | |
| ईगल नेबुला में शिखर | 4′40″ | लंबाई 280″ है। |
| शुक्र | 1′6″ – 0′9.7″ | |
| अंतर्राष्ट्रीय अंतरिक्ष स्टेशन (आईएसएस) | 1′3″ | ;[10] आईएसएस की चौड़ाई लगभग 108 मीटर है। |
| मानव आँख द्वारा अधिकतम हल करने योग्य व्यास | 1′ | ;[11] 1 किमी की दूरी पर 0.3 मीटर[12] |
| चंद्रमा की सतह पर लगभग 100 किमी | 1′ | कोपरनिकस क्रेटर जैसे बड़े चंद्र क्रेटर जैसी सुविधाओं के आकार की तुलना में, ओसियनस प्रोसेलरम के पूर्वी भाग में एक प्रमुख चमकीला स्थान, घटती हुई ओर, या टाइको क्रेटर दक्षिण में उज्ज्वल क्षेत्र के अंदर, चंद्र के निकट की ओर है। |
| बृहस्पति | 50.1″ – 29.8″ | |
| मानव आंख द्वारा अधिकतम रिजोल्वेबल पॉइंट/गैप | 40″ | ;[11] निकट से देखने पर 0.04 मिमी अधिक पतले बालों की चौड़ाई[12] |
| मंगल | 25.1″ – 3.5″ | |
| शनि | 20.1″ – 14.5″ | |
| बुध | 13.0″ – 4.5″ | |
| अरुण | 4.1″ – 3.3″ | |
| नेपच्यून | 2.4″ – 2.2″ | |
| गेनीमेड | 1.8″ – 1.2″ | गैनीमीड का व्यास 5,268 किमी है। |
| 350 किमी की दूरी पर अंतरिक्ष यात्री (~1.7 मीटर),आईएसएस की औसत ऊंचाई | 1″ | |
| गैलीलियो गैलीली के सबसे बड़े 38 मिमी अपवर्तक टेलीस्कोप द्वारा अधिकतम रिजोल्वेबल व्यास | ~1″ | ;[13]ध्यान दें: 30x[14]आवर्धन, अधिक दृढ़ समकालीन स्थलीय दूरबीन के सामान है। |
| सायरस | 0.84″ – 0.33″ | |
| वेस्टा | 0.64″ – 0.20″ | |
| प्लूटो | 0.11″ – 0.06″ | |
| एरिस | 0.089″ – 0.034″ | |
| आर डोराडस | 0.062″ – 0.052″ | ध्यान दें: आर डोराडस को पृथ्वी से देखे जाने वाले सबसे बड़े स्पष्ट आकार के साथ एक्स्ट्रासोलर स्टार माना जाता है। |
| बेटेल्गेयूज़ | 0.060″ – 0.049″ | |
| एल्फ़र्ड | 0.00909″ | |
| अल्फा सेंटौरी ए | 0.007″ | |
| कैनॉपस | 0.006″ | |
| सिरियस | 0.005936″ | |
| अल्टेयर | 0.003″ | |
| डेनेब | 0.002″ | |
| प्रॉक्सिमा सेंटौरी | 0.001″ | |
| एल्निटैक | 0.0005″ | |
| प्रॉक्सिमा सेंटौरी बी | 0.00008″ | |
| M87आकाशगंगा के केंद्र में ब्लैक होल M87* का घटना क्षितिज, 2019 में इवेंट होराइज़न टेलीस्कोप द्वारा लिया गया चित्र। | 0.000025″
(2.5×10−5) |
चंद्रमा पर टेनिस बॉल के सामान है। |
| दूरी पर अलनीतक जैसा तारा जहां हबल स्पेस टेलीस्कोप इसे देख सकेगा।[15] | 6×10−10 आर्कसेकंड |


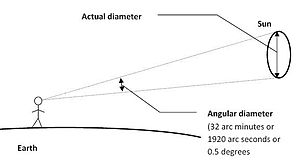
तालिका से ज्ञात होता है कि सूर्य का कोणीय व्यास, जब पृथ्वी से देखा जाता है, लगभग 32′ (1920″ या 0.53°) है, जैसा कि ऊपर दिखाया गया है।
इस प्रकार सूर्य का कोणीय व्यास सीरियस से लगभग 250,000 गुना अधिक है। (सीरियस का व्यास दो गुना है और इसकी दूरी 500,000 गुना अधिक है; सूर्य 1010 गुना अधिक उज्ज्वल है, 105 के कोणीय व्यास अनुपात के अनुरूप है, इसलिए सीरियस प्रति इकाई ठोस कोण के रूप में लगभग 6 गुना अधिक उज्ज्वल है।)
सूर्य का कोणीय व्यास भी अल्फा सेंटौरी ए के लगभग 250,000 गुना है (इसका व्यास लगभग समान है और दूरी 250,000 गुना अधिक है; सूर्य 4×1010 गुना उज्ज्वल है, जो 200,000 के कोणीय व्यास अनुपात के अनुरूप है, इसलिए अल्फा सेंटॉरी ए प्रति इकाई ठोस कोण से थोड़ा उज्जवल है)।
सूर्य का कोणीय व्यास लगभग चंद्रमा के समान है। (सूर्य का व्यास 400 गुना बड़ा है और इसकी दूरी भी; सूर्य पूर्ण चंद्रमा के रूप में 200,000 से 500,000 गुना उज्ज्वल है (आंकड़े भिन्न -भिन्न हैं), 450 से 700 के कोणीय व्यास अनुपात के अनुरूप है, इसलिए व्यास वाला खगोलीय पिंड 2.5-4″ का और समान चमक प्रति इकाई ठोस कोण में पूर्ण चंद्रमा के समान चमक होगी।)
भले ही प्लूटो शारीरिक रूप से सेरेस से बड़ा है, जब पृथ्वी से देखा जाता है (उदाहरण के लिए, हबल स्पेस टेलीस्कॉप के माध्यम से) सेरेस का स्पष्ट आकार अधिक बड़ा है।
डिग्री में मापे गए कोणीय आकार आकाश के बड़े पैच के लिए उपयोगी होते हैं। (उदाहरण के लिए, ओरियन के बेल्ट के तीन तारे लगभग 4.5° कोणीय आकार को कवर करते हैं।) यद्यपि, आकाशगंगाओं, नीहारिकाओं, या रात के आकाश की अन्य वस्तुओं के कोणीय आकार को मापने के लिए अधिक सूक्ष्म इकाइयों की आवश्यकता होती है।
इसलिए, डिग्रियों को इस प्रकार उपविभाजित किया गया है:
- पूर्ण वृत्त में 360 डिग्री (°) होती है।
- एक डिग्री में 60 आर्क-मिनट (′) होता है।
- एक आर्क-मिनट में 60 आर्क-सेकंड (″) होता है।
इसे परिप्रेक्ष्य में रखने के लिए, पृथ्वी से देखा जाने वाला पूर्ण चंद्रमा लगभग 1⁄2 °, या 30′ (या 1800″) है। पूर्ण आकाश में चंद्रमा की गति को कोणीय आकार में मापा जा सकता है: लगभग 15° प्रति घंटा, या 15″ प्रति सेकंड। चंद्रमा पर चित्रित एक मील लंबी रेखा पृथ्वी से लगभग 1″ लंबाई में दिखाई देगी।
खगोल विज्ञान में, सामान्यतः किसी वस्तु की दूरी को सीधे मापना कठिन होता है, फिर भी वस्तु का ज्ञात भौतिक आकार हो सकता है (संभवतः यह ज्ञात दूरी के साथ निकट वस्तु के समान है) और औसत श्रेणी का कोणीय व्यास है। उस स्थिति में, कोणीय व्यास सूत्र को दूर की वस्तुओं के रूप में कोणीय व्यास की दूरी प्राप्त करने के लिए विपरीत किया जा सकता है:
गैर-यूक्लिडियन अंतरिक्ष में, जैसे हमारे विस्तारित ब्रह्मांड में, कोणीय व्यास की दूरी की अनेक परिभाषाओं में से है, जिससे कि वस्तु के लिए भिन्न-भिन्न दूरी हो सकें। दूरी के उपाय (ब्रह्माण्ड विज्ञान) देखें।
गैर-परिपत्र वस्तुएं
आकाशगंगाओं और नीहारिकाओं जैसी अनेक गहरे आकाश की वस्तुएं गैर-गोलाकार दिखाई देती हैं और इस प्रकार सामान्यतः व्यास के दो माप दिए जाते हैं: जो प्रमुख अक्ष और लघु अक्ष हैं। उदाहरण के लिए, छोटे मैगेलैनिक बादल का दृश्य स्पष्ट व्यास 5° 20′ × 3° 5′ है।
प्रकाश का दोष
रोशनी का दोष किसी दिए गए पर्यवेक्षक द्वारा देखे गए खगोलीय पिंड के एकपक्षीय भाग की अधिकतम कोणीय चौड़ाई है। उदाहरण के लिए, यदि कोई वस्तु 40″ चाप की है, और 75% प्रकाशित है, तो रोशनी का दोष 10″ है।
यह भी देखें
- कोणीय व्यास दूरी
- कोणीय संकल्प
- ठोस कोण
- दृश्य तीक्ष्णता
- दृश्य कोण
- कथित दृश्य कोण
- हल की गई छवियों के साथ सितारों की सूची
- स्पष्ट परिमाण
संदर्भ
- ↑ Yanoff, Myron; Duker, Jay S. (2009). Ophthalmology 3rd Edition. MOSBY Elsevier. p. 54. ISBN 978-0444511416.
- ↑ This can be derived using the formula for the length of a cord found at "Circular Segment". Archived from the original on 2014-12-21. Retrieved 2015-01-23.
- ↑ "कार्यकार्तान के लिए एक टेलर श्रृंखला" (PDF). Archived from the original (PDF) on 2015-02-18. Retrieved 2015-01-23.
- ↑ "सिस्टम संयोजित करें". Archived from the original on 2015-01-21. Retrieved 2015-01-21.
- ↑ "छायांकन उपग्रह". 8 June 2013. Archived from the original on 21 January 2015.
- ↑ Wikiversity: Physics and Astronomy Labs/Angular size
- ↑ Michael A. Seeds; Dana E. Backman (2010). सितारे और आकाशगंगाएँ (7 ed.). Brooks Cole. p. 39. ISBN 978-0-538-73317-5.
- ↑ O'Meara, Stephen James (2019-08-06). "The coalsacks of Cygnus". Astronomy.com. Retrieved 2023-02-10.
- ↑ Dobashi, Kazuhito; Matsumoto, Tomoaki; Shimoikura, Tomomi; Saito, Hiro; Akisato, Ko; Ohashi, Kenjiro; Nakagomi, Keisuke (2014-11-24). "Colliding Filaments and a Massive Dense Core in the Cygnus Ob 7 Molecular Cloud". The Astrophysical Journal. American Astronomical Society. 797 (1): 58. doi:10.1088/0004-637x/797/1/58. ISSN 1538-4357. S2CID 118369651.
- ↑ "Problem 346: The International Space Station and a Sunspot: Exploring angular scales" (PDF). Space Math @ NASA !. 2018-08-19. Retrieved 2022-05-20.
- ↑ 11.0 11.1 Wong, Yan (2016-01-24). "How small can the naked eye see?". BBC Science Focus Magazine. Retrieved 2022-05-23.
- ↑ 12.0 12.1 "Sharp eyes: how well can we really see?". Science in School – scienceinschool.org. 2016-09-07. Retrieved 2022-05-23.
- ↑ Graney, Christopher M. (Dec 10, 2006). "The Accuracy of Galileo's Observations and the Early Search for Stellar Parallax". arXiv:physics/0612086. doi:10.1007/3-540-50906-2_2.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ "Galileo's telescope - How it works". Esposizioni on-line - Istituto e Museo di Storia della Scienza (in italiano). Retrieved May 21, 2022.
- ↑ 800 000 times smaller angular diameter than that of Alnitak as seen from Earth. Alnitak is a blue star so it gives off a lot of light for its size. If it were 800 000 times further away then it would be magnitude 31.5, at the limit of what Hubble can see.