क्षैतिज रेखा परीक्षण: Difference between revisions
No edit summary |
m (added Category:Vigyan Ready using HotCat) |
||
| Line 33: | Line 33: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 01/05/2023]] | [[Category:Created On 01/05/2023]] | ||
[[Category:Vigyan Ready]] | |||
Revision as of 15:07, 15 May 2023
गणित में, क्षैतिज रेखा परीक्षण, परीक्षण है जिसका उपयोग यह निर्धारित करने के लिए किया जाता है, कि कोई फलन (गणित) अंतःक्षेपी (अर्थात्, एक-से-एक) है या नहीं है।[1]
गणित में
क्षैतिज रेखा सीधी, समतल रेखा होती है, जो बाएं से दाएं जाती है। फलन (अर्थात वास्तविक संख्याओं से वास्तविक संख्याओं तक) दिया गया है, हम यह तय कर सकते हैं कि क्या यह क्षैतिज रेखाओं को देखकर अंतःक्षेपी है जो किसी फलन के ग्राफ़ को प्रतिच्छेदित करती है। यदि कोई क्षैतिज रेखा ग्राफ़ को एक से अधिक बिंदुओं पर प्रतिच्छेदित करती है, तो फलन अंतःक्षेपी नहीं है। इसे देखने के लिए, ध्यान दें कि प्रतिच्छेदन के बिंदुओं का समान y- मान है (क्योंकि वे रेखा पर स्थित हैं), लेकिन अलग-अलग x मान हैं, जिसका अर्थ है कि फलन अंतःक्षेपी नहीं हो सकता है।[1]
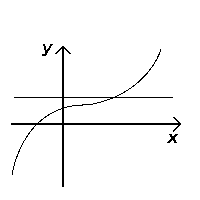 Passes the test (injective) |
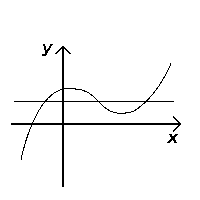 Fails the test (not injective) |
क्षैतिज रेखा परीक्षण की विविधताओं का उपयोग यह निर्धारित करने के लिए किया जा सकता है कि कोई फलन विशेषण या विशेषांक है:
- फलन f आच्छादक (अर्थात् आच्छादक) है, यदि और केवल यदि इसका ग्राफ किसी भी क्षैतिज रेखा को 'कम से कम' एक बार काटता है।
- f विशेषण है यदि और केवल यदि कोई क्षैतिज रेखा ग्राफ को ठीक एक बार काटती है।
समुच्चय सिद्धांत में
कार्टेशियन गुणन के उपसमुच्चय के रूप में इसके संबंधित ग्राफ के साथ फलन पर विचार करें। में क्षैतिज रेखाओं पर विचार करें: । फलन f अंतःक्षेपी है यदि और केवल यदि प्रत्येक क्षैतिज रेखा ग्राफ को अधिकतम एक बार काटती है। इस स्थिति में कहा जाता है कि ग्राफ क्षैतिज रेखा परीक्षण पास करता है। यदि कोई क्षैतिज रेखा ग्राफ़ को एक से अधिक बार काटती है, तो फलन क्षैतिज रेखा परीक्षण में विफल रहता है और अंतःक्षेपी नहीं होता है।[2]
यह भी देखें
- कार्यक्षेत्र रेखा परीक्षण
- उलटा काम करना
- मोनोटोनिक फलन
संदर्भ
- ↑ 1.0 1.1 Stewart, James (2003). Single Variable Calculus: Early Transcendentals (5th. ed.). Toronto ON: Brook/Cole. pp. 64. ISBN 0-534-39330-6. Retrieved 15 July 2012.
इसलिए, हमारे पास यह निर्धारित करने के लिए निम्न ज्यामितीय विधि है कि कोई फ़ंक्शन एक-से-एक है या नहीं।
- ↑ Zorn, Arnold Ostebee, Paul (2002). चित्रमय, संख्यात्मक और प्रतीकात्मक दृष्टिकोण से पथरी (2nd ed.). Australia: Brooks/Cole/Thomson Learning. p. 185. ISBN 0-03-025681-X.
No horizontal line crosses the f-graph more than once.
{{cite book}}: CS1 maint: multiple names: authors list (link)