कृत्रिम न्यूरॉन: Difference between revisions
(Created page with "{{short description|Mathematical function conceived as a crude model}} एक कृत्रिम न्यूरॉन एक क्रिया (गणित) है...") |
No edit summary |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Mathematical function conceived as a crude model}} | {{short description|Mathematical function conceived as a crude model}} | ||
कृत्रिम [[न्यूरॉन]] क्रिया है जिसे जैविक न्यूरॉन्स, [[तंत्रिका नेटवर्क]] के गणितीय मॉडल के रूप में माना जाता है। [[कृत्रिम तंत्रिका नेटवर्क]] में कृत्रिम न्यूरॉन्स प्राथमिक इकाइयां हैं।<ref>{{Cite journal|title=Neuromorphic Circuits With Neural Modulation Enhancing the Information Content of Neural Signaling {{!}} International Conference on Neuromorphic Systems 2020|language=EN|doi=10.1145/3407197.3407204|s2cid=220794387|doi-access=free}}</ref> कृत्रिम न्यूरॉन एक या एक से अधिक इनपुट प्राप्त करता है ([[उत्तेजक पोस्टसिनेप्टिक क्षमता]] और न्यूरल [[ डेन्ड्राइट |डेन्ड्राइट]] में [[निरोधात्मक पोस्टसिनेप्टिक क्षमता]] का प्रतिनिधित्व करता है) और उन्हें आउटपुट (या {{vanchor|सक्रियण}}, न्यूरॉन की क्रिया क्षमता का प्रतिनिधित्व करता है जो इसके अक्षतंतु के साथ संचरित होता है)। सामान्यतः प्रत्येक इनपुट अलग-अलग से [[भार|भारित]] किया जाता है, और योग को गैर-रैखिक फलन के माध्यम से पारित किया जाता है जिसे सक्रियण फलन या [[स्थानांतरण प्रकार्य]] के रूप में जाना जाता है। स्थानांतरण कार्यों में सामान्यतः [[सिग्मॉइड फ़ंक्शन|सिग्मॉइड फलन]] होता है, लेकिन वे अन्य गैर-रैखिक कार्यों, टुकड़े-टुकड़े रैखिक कार्यों या स्टेप फलन का रूप भी ले सकते हैं। वे अधिकांशतः [[मोनोटोनिक फ़ंक्शन|मोनोटोनिक फलन]], [[निरंतर कार्य]], [[विभेदक कार्य]] और [[परिबद्ध समारोह|परिबद्ध फलन]] भी होते हैं। कई शून्यों के साथ गैर-मोनोटोनिक, अनबाउंड और ऑसिलेटिंग एक्टिवेशन फलन जो कई कार्यों पर सिग्मोइडल और रीएलयू जैसे एक्टिवेशन फलन से अच्छा प्रदर्शन करते हैं, उन्हें भी हाल ही में खोजा गया है। थ्रेशोल्डिंग फलन ने बिल्डिंग [[ तर्क द्वार |लॉजिक गेट]] को थ्रेशोल्ड तर्क के रूप में संदर्भित करने के लिए प्रेरित किया है; मस्तिष्क प्रसंस्करण जैसी दिखने वाली [[तर्क सर्किट|तर्क परिपथ]] बनाने के लिए प्रयुक्त उदाहरण के लिए, हाल के दिनों में इस तरह के तर्क को विकसित करने के लिए [[memristor|मेमोरी स्टोर]] जैसे नए उपकरणों का बड़े पैमाने पर उपयोग किया गया है।<ref name=":0">{{Cite journal|last1=Maan|first1=A. K.|last2=Jayadevi|first2=D. A.|last3=James|first3=A. P.|date=1 January 2016|title=यादगार दहलीज तर्क सर्किट का एक सर्वेक्षण|journal=IEEE Transactions on Neural Networks and Learning Systems|volume=PP|issue=99|pages=1734–1746|doi=10.1109/TNNLS.2016.2547842|pmid=27164608|issn=2162-237X|arxiv=1604.07121|bibcode=2016arXiv160407121M|s2cid=1798273}}</ref> | |||
कृत्रिम न्यूरॉन | |||
कृत्रिम न्यूरॉन्स [[न्यूरोमॉर्फिक इंजीनियरिंग]] में [[कृत्रिम कोशिका]] | कृत्रिम न्यूरॉन स्थानांतरण फलन को रैखिक प्रणाली स्थानांतरण फलन के साथ भ्रमित नहीं होना चाहिए। | ||
कृत्रिम न्यूरॉन्स [[न्यूरोमॉर्फिक इंजीनियरिंग]] में [[कृत्रिम कोशिका|कृत्रिम कोशिकाओं]] को भी संदर्भित कर सकते हैं, जो प्राकृतिक भौतिक न्यूरॉन्स के समान हैं {{see below|नीचे देखें}}। | |||
== मूल संरचना == | == मूल संरचना == | ||
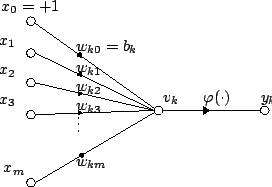
किसी दिए गए कृत्रिम न्यूरॉन k के लिए, | किसी दिए गए कृत्रिम न्यूरॉन k के लिए, माना ''x''<sub>0</sub> के माध्यम से ''x<sub>m</sub>'' और ''w<sub>k</sub>''<sub>0</sub> के माध्यम से ''w<sub>km</sub>'' के संकेतों के साथ m + 1 इनपुट हैं। सामान्यतः, ''x''<sub>0</sub> इनपुट को मान +1 असाइन किया गया है, जो इसे ''w<sub>k</sub>''<sub>0</sub> = ''b<sub>k</sub>'' के साथ पूर्वाग्रह इनपुट बनाता है यह न्यूरॉन के लिए केवल m वास्तविक इनपुट छोड़ता है: ''x''<sub>1</sub> से ''x<sub>m</sub>'' तक | ||
Kवाँ न्यूरॉन का आउटपुट है: | |||
:<math>y_k = \varphi \left( \sum_{j=0}^m w_{kj} x_j \right)</math> | :<math>y_k = \varphi \left( \sum_{j=0}^m w_{kj} x_j \right)</math> | ||
जहाँ <math>\varphi</math> (phi) स्थानांतरण फलन (सामान्यतः थ्रेशोल्ड फलन) है। | |||
[[File:artificial neuron.png]] | |||
आउटपुट जैविक न्यूरॉन के अक्षतंतु के अनुरूप होता है, और इसका मान अन्तर्ग्रथन के माध्यम से अगली परत के इनपुट तक फैलता है। यह संभवतः आउटपुट [[वेक्टर (गणित और भौतिकी)|सदिश (गणित और भौतिकी)]] के हिस्से के रूप में प्रणाली से बाहर निकल सकता है। | |||
इसकी कोई सीखने की प्रक्रिया नहीं है। इसके | इसकी कोई सीखने की प्रक्रिया नहीं है। इसके स्थानांतरण फलन वेट की गणना की जाती है और थ्रेशोल्ड वैल्यू पूर्व निर्धारित होती है। | ||
== प्रकार == | == प्रकार == | ||
{{main| | {{main|एनवी नेटवर्क}} | ||
उपयोग किए गए विशिष्ट मॉडल के आधार पर उन्हें सेमी- | उपयोग किए गए विशिष्ट मॉडल के आधार पर उन्हें सेमी-रेखीय इकाई, एनवी न्यूरॉन, बाइनरी न्यूरॉन, रेखीय थ्रेशोल्ड फलन या मैककुलोच-पिट्स (एमसीपी) न्यूरॉन कहा जा सकता है। | ||
सरल कृत्रिम न्यूरॉन्स, जैसे मैककुलोच-पिट्स मॉडल, को कभी-कभी कैरिकेचर मॉडल के रूप में वर्णित किया जाता है, क्योंकि उनका उद्देश्य एक या अधिक | सरल कृत्रिम न्यूरॉन्स, जैसे मैककुलोच-पिट्स मॉडल, को कभी-कभी कैरिकेचर मॉडल के रूप में वर्णित किया जाता है, क्योंकि उनका उद्देश्य एक या अधिक न्यूरोफिज़ियोतर्कल अवलोकनों को प्रतिबिंबित करना है, लेकिन यथार्थवाद के संबंध में होता है।<ref> | ||
{{cite book | {{cite book | ||
| author = F. C. Hoppensteadt and E. M. Izhikevich | | author = F. C. Hoppensteadt and E. M. Izhikevich | ||
| Line 30: | Line 34: | ||
| page = 4 | | page = 4 | ||
}}</ref> | }}</ref> | ||
== जैविक मॉडल == | == जैविक मॉडल == | ||
{{main| | {{main|जैविक न्यूरॉन मॉडल}} | ||
[[File:Neuron3.svg|thumb|right|400px|न्यूरॉन और मायेलिनेटेड एक्सॉन, डेन्ड्राइट्स पर इनपुट से अक्षतंतु टर्मिनलों पर आउटपुट के | [[File:Neuron3.svg|thumb|right|400px|न्यूरॉन और मायेलिनेटेड एक्सॉन, डेन्ड्राइट्स पर इनपुट से अक्षतंतु टर्मिनलों पर आउटपुट के संकेतिक प्रवाह के साथ]]कृत्रिम न्यूरॉन्स को उनके जैविक समकक्षों के पहलुओं की नकल करने के लिए डिज़ाइन किया गया है। चूँकि जैविक और कृत्रिम तंत्रिका नेटवर्क के बीच महत्वपूर्ण प्रदर्शन अंतर उपस्थित है। मानव मस्तिष्क में विशेष रूप से एकल जैविक न्यूरॉन्स में एक्सओआर फलन सीखने में सक्षम ऑसिलेटिंग एक्टिवेशन फलन के साथ खोजा गया है।<ref>{{Cite journal|last1=Gidon|first1=Albert|last2=Zolnik|first2=Timothy Adam|last3=Fidzinski|first3=Pawel|last4=Bolduan|first4=Felix|last5=Papoutsi|first5=Athanasia|last6=Poirazi|first6=Panayiota|author-link6=Panayiota Poirazi| last7=Holtkamp|first7=Martin|last8=Vida|first8=Imre|last9=Larkum|first9=Matthew Evan|date=2020-01-03|title=Dendritic action potentials and computation in human layer 2/3 cortical neurons|url=https://www.science.org/doi/10.1126/science.aax6239|journal=Science|volume=367|issue=6473|pages=83–87|doi=10.1126/science.aax6239|pmid=31896716|bibcode=2020Sci...367...83G|s2cid=209676937}}</ref> [[डेन्ड्राइट]] -जैविक न्यूरॉन में, डेन्ड्राइट इनपुट सदिश के रूप में कार्य करते हैं। ये डेन्ड्राइट कोशिका को पड़ोसी न्यूरॉन्स की बड़ी (>1000) संख्या से संकेत प्राप्त करने की अनुमति देते हैं। उपरोक्त गणितीय उपचार के अनुसार, प्रत्येक डेन्ड्राइट उस डेन्ड्राइट के वजन मान से गुणा करने में सक्षम होता है। सिनैप्टिक न्यूरोट्रांसमीटर के उत्तर में डेन्ड्राइट में प्रस्तुत किए गए संकेतिक रसायनों के लिए सिनैप्टिक न्यूरोट्रांसमीटर के अनुपात को बढ़ाकर या घटाकर गुणन पूरा किया जाता है। सिनैप्टिक न्यूरोट्रांसमीटर के स्वागत के उत्तर में डेंड्राइट के साथ संकेतिक इनहिबिटर (अर्थात् विपरीत आवेश आयन) को प्रेषित करके नकारात्मक गुणन प्रभाव प्राप्त किया जा सकता है। | ||
* [[सोमा (जीव विज्ञान)]] - | * [[सोमा (जीव विज्ञान)]] - जैविक न्यूरॉन में, सोम उपरोक्त गणितीय विवरण में देखे गए योग फलन के रूप में कार्य करता है। चूंकि सकारात्मक और नकारात्मक संकेत (रोमांचक और अवरोधक, क्रमशः) डेन्ड्राइट्स से सोमा में आते हैं, सकारात्मक और नकारात्मक आयन प्रभावी रूप से योग में जोड़े जाते हैं, सेल के शरीर के अंदर समाधान में साथ मिश्रित होने के सरल गुण से। | ||
* एक्सोन - अक्षतंतु अपना संकेत सोमा के अंदर होने वाले योग व्यवहार से प्राप्त करता है। अक्षतंतु का खुलना अनिवार्य रूप से सोमा के अंदर समाधान की विद्युत क्षमता का नमूना लेता है। एक बार सोमा | * एक्सोन - अक्षतंतु अपना संकेत सोमा के अंदर होने वाले योग व्यवहार से प्राप्त करता है। अक्षतंतु का खुलना अनिवार्य रूप से सोमा के अंदर समाधान की विद्युत क्षमता का नमूना लेता है। एक बार सोमा निश्चित क्षमता तक पहुंच जाता है, अक्षतंतु अपनी लंबाई के नीचे ऑल-इन संकेतिक पल्स संचारित करेगा। इस संबंध में, अक्षतंतु हमारे कृत्रिम न्यूरॉन को अन्य कृत्रिम न्यूरॉन्स से जोड़ने की क्षमता के रूप में व्यवहार करता है। | ||
चूँकि, अधिकांश कृत्रिम न्यूरॉन्स के विपरीत, जैविक न्यूरॉन्स असतत पल्सों में आग लगाते हैं। हर बार सोमा के अंदर विद्युत क्षमता निश्चित सीमा तक पहुँचती है, नाभिक अक्षतंतु के नीचे प्रेषित होती है। इस स्पंदन को निरंतर मूल्यों में अनुवादित किया जा सकता है। दर (प्रति सेकंड सक्रियता, आदि) जिस पर अक्षतंतु आग सीधे उस दर में परिवर्तित हो जाती है जिस पर पड़ोसी कोशिकाओं को संकेतिक आयन मिलते हैं। जितनी तीव्रता से जैविक न्यूरॉन प्रज्वलित होता है, उतनी ही तीव्रता से पास के न्यूरॉन्स विद्युत क्षमता एकत्र करते हैं (या विद्युत क्षमता खो देते हैं, डेन्ड्राइट के भार के आधार पर जो न्यूरॉन से जुड़ते हैं)। यह रूपांतरण है जो कंप्यूटर वैज्ञानिकों और गणितज्ञों को कृत्रिम न्यूरॉन्स का उपयोग करके जैविक तंत्रिका नेटवर्क का अनुकरण करने की अनुमति देता है जो अलग-अलग मान (अधिकांशतः -1 से 1 तक) का उत्पादन कर सकते हैं। | |||
=== एन्कोडिंग === | === एन्कोडिंग === | ||
शोध से पता चला है कि [[बर्डसॉन्ग]] प्रोडक्शन के लिए | शोध से पता चला है कि [[बर्डसॉन्ग]] प्रोडक्शन के लिए उत्तरदायी न्यूरल परिपथ में [[यूनरी कोडिंग]] का प्रयोग किया जाता है।<ref>{{cite book|editor1-last=Squire|editor1-first=L.|editor2-last=Albright|editor2-first=T.|editor3-last=Bloom|editor3-first=F.|editor4-last=Gage|editor4-first=F.|editor5-last=Spitzer|editor5-first=N.|title=बर्डसॉन्ग प्रोडक्शन, लर्निंग और कोडिंग के न्यूरल नेटवर्क मॉडल|date=October 2007|publisher=Elservier|location=New Encyclopedia of Neuroscience|url=https://clm.utexas.edu/fietelab/Papers/birdsong_review_topost.pdf|access-date=12 April 2015|archive-url=https://web.archive.org/web/20150412190625/https://clm.utexas.edu/fietelab/Papers/birdsong_review_topost.pdf|archive-date=2015-04-12}}</ref><ref>{{cite journal | last1 = Moore | first1 = J.M. | display-authors = etal | year = 2011| title = मोटर पाथवे अभिसरण ऑसीन पक्षियों में शब्दांश प्रदर्शनों के आकार की भविष्यवाणी करता है| journal = Proc. Natl. Acad. Sci. USA | volume = 108 | issue = 39| pages = 16440–16445 | doi = 10.1073/pnas.1102077108 | pmid = 21918109 | pmc = 3182746 | bibcode = 2011PNAS..10816440M | doi-access = free }}</ref> कोडिंग की अंतर्निहित सादगी के कारण जैविक नेटवर्क में यूनरी का उपयोग संभवतः है। अन्य योगदान कारक यह हो सकता है कि यूनरी कोडिंग त्रुटि सुधार की निश्चित डिग्री प्रदान करती है।<ref>{{cite arXiv|eprint=1411.7406|title=यूनरी कोडिंग की त्रुटि सुधार क्षमता|first=Pushpa Sree|last=Potluri|date=26 November 2014|class=cs.IT}}</ref> | ||
| Line 49: | Line 51: | ||
उदाहरण के लिए, कुछ कृत्रिम न्यूरॉन्स प्राप्त कर सकते हैं<ref name="knowablemagazineorganic">{{cite news |last1=Kleiner |first1=Kurt |title=कंप्यूटर चिप्स बनाना मस्तिष्क की कोशिकाओं की तरह अधिक कार्य करता है|url=https://knowablemagazine.org/article/technology/2022/making-computer-chips-act-more-like-brain-cells |access-date=23 September 2022 |work=Knowable Magazine {{!}} Annual Reviews |date=25 August 2022 |language=en |doi=10.1146/knowable-082422-1}}</ref><ref>{{cite journal |last1=Keene |first1=Scott T. |last2=Lubrano |first2=Claudia |last3=Kazemzadeh |first3=Setareh |last4=Melianas |first4=Armantas |last5=Tuchman |first5=Yaakov |last6=Polino |first6=Giuseppina |last7=Scognamiglio |first7=Paola |last8=Cinà |first8=Lucio |last9=Salleo |first9=Alberto |last10=van de Burgt |first10=Yoeri |last11=Santoro |first11=Francesca |title=न्यूरोट्रांसमीटर-मध्यस्थता प्लास्टिसिटी के साथ एक बायोहाइब्रिड सिनैप्स|journal=Nature Materials |date=September 2020 |volume=19 |issue=9 |pages=969–973 |doi=10.1038/s41563-020-0703-y |pmid=32541935 |bibcode=2020NatMa..19..969K |s2cid=219691307 |language=en |issn=1476-4660|url=https://research.tue.nl/nl/publications/ad3d2f99-23e6-4072-934d-2b058d800e42 }} | उदाहरण के लिए, कुछ कृत्रिम न्यूरॉन्स प्राप्त कर सकते हैं<ref name="knowablemagazineorganic">{{cite news |last1=Kleiner |first1=Kurt |title=कंप्यूटर चिप्स बनाना मस्तिष्क की कोशिकाओं की तरह अधिक कार्य करता है|url=https://knowablemagazine.org/article/technology/2022/making-computer-chips-act-more-like-brain-cells |access-date=23 September 2022 |work=Knowable Magazine {{!}} Annual Reviews |date=25 August 2022 |language=en |doi=10.1146/knowable-082422-1}}</ref><ref>{{cite journal |last1=Keene |first1=Scott T. |last2=Lubrano |first2=Claudia |last3=Kazemzadeh |first3=Setareh |last4=Melianas |first4=Armantas |last5=Tuchman |first5=Yaakov |last6=Polino |first6=Giuseppina |last7=Scognamiglio |first7=Paola |last8=Cinà |first8=Lucio |last9=Salleo |first9=Alberto |last10=van de Burgt |first10=Yoeri |last11=Santoro |first11=Francesca |title=न्यूरोट्रांसमीटर-मध्यस्थता प्लास्टिसिटी के साथ एक बायोहाइब्रिड सिनैप्स|journal=Nature Materials |date=September 2020 |volume=19 |issue=9 |pages=969–973 |doi=10.1038/s41563-020-0703-y |pmid=32541935 |bibcode=2020NatMa..19..969K |s2cid=219691307 |language=en |issn=1476-4660|url=https://research.tue.nl/nl/publications/ad3d2f99-23e6-4072-934d-2b058d800e42 }} | ||
* University press release: {{cite news |title=Researchers develop artificial synapse that works with living cells |url=https://medicalxpress.com/news/2020-06-artificial-synapse-cells.html |access-date=23 September 2022 |work=Stanford University via medicalxpress.com |language=en}}</ref> और [[डोपामाइन]] (विद्युत संकेतों के | * University press release: {{cite news |title=Researchers develop artificial synapse that works with living cells |url=https://medicalxpress.com/news/2020-06-artificial-synapse-cells.html |access-date=23 September 2022 |work=Stanford University via medicalxpress.com |language=en}}</ref> और [[डोपामाइन]] (विद्युत संकेतों के अतिरिक्त [[ स्नायुसंचारी |स्नायुसंचारी]] ) को छोड़ता है और मस्तिष्क-कंप्यूटर इंटरफेस/वेटवेयर कंप्यूटर भविष्य के अनुप्रयोगों में उपयोग की संभावना के साथ प्राकृतिक चूहे [[नरम रोबोट]] और [[मस्तिष्क कोशिका|मस्तिष्क कोशिकाओं]] के साथ संचार करता है।<ref>{{cite news |title=कृत्रिम न्यूरॉन वास्तविक की तरह चूहे के मस्तिष्क की कोशिकाओं के साथ डोपामाइन की अदला-बदली करता है|url=https://www.newscientist.com/article/2332554-artificial-neuron-swaps-dopamine-with-rat-brain-cells-like-a-real-one/ |access-date=16 September 2022 |work=New Scientist}}</ref><ref>{{cite journal |last1=Wang |first1=Ting |last2=Wang |first2=Ming |last3=Wang |first3=Jianwu |last4=Yang |first4=Le |last5=Ren |first5=Xueyang |last6=Song |first6=Gang |last7=Chen |first7=Shisheng |last8=Yuan |first8=Yuehui |last9=Liu |first9=Ruiqing |last10=Pan |first10=Liang |last11=Li |first11=Zheng |last12=Leow |first12=Wan Ru |last13=Luo |first13=Yifei |last14=Ji |first14=Shaobo |last15=Cui |first15=Zequn |last16=He |first16=Ke |last17=Zhang |first17=Feilong |last18=Lv |first18=Fengting |last19=Tian |first19=Yuanyuan |last20=Cai |first20=Kaiyu |last21=Yang |first21=Bowen |last22=Niu |first22=Jingyi |last23=Zou |first23=Haochen |last24=Liu |first24=Songrui |last25=Xu |first25=Guoliang |last26=Fan |first26=Xing |last27=Hu |first27=Benhui |last28=Loh |first28=Xian Jun |last29=Wang |first29=Lianhui |last30=Chen |first30=Xiaodong |title=रासायनिक रूप से मध्यस्थ कृत्रिम न्यूरॉन|journal=Nature Electronics |date=8 August 2022 |volume=5 |issue=9 |pages=586–595 |doi=10.1038/s41928-022-00803-0 |s2cid=251464760 |url=https://www.researchgate.net/publication/362561968 |language=en |issn=2520-1131|url-access=subscription}}</ref> | ||
कम-शक्ति वाले बायोकम्पैटिबल मेमिस्टर कृत्रिम न्यूरॉन्स के निर्माण को सक्षम कर सकते हैं जो जैविक क्रिया क्षमता के वोल्टेज पर कार्य करते हैं और [[न्यूरोमॉर्फिक कंप्यूटिंग]] और | |||
[[पॉलीमर]] से बने कार्बनिक न्यूरोमॉर्फिक | कम-शक्ति वाले बायोकम्पैटिबल मेमिस्टर कृत्रिम न्यूरॉन्स के निर्माण को सक्षम कर सकते हैं, जो जैविक क्रिया क्षमता के वोल्टेज पर कार्य करते हैं और [[न्यूरोमॉर्फिक कंप्यूटिंग]] और मस्तिष्क-कंप्यूटर इंटरफ़ेस के लिए [[बायोसेंसर]] को सीधे संसाधित करने के लिए उपयोग किया जा सकता है।<ref>{{cite news |title=वैज्ञानिक छोटे उपकरण बनाते हैं जो मानव मस्तिष्क की तरह काम करते हैं|url=https://www.independent.co.uk/life-style/gadgets-and-tech/news/brain-computing-memory-artificial-synapse-memristor-a9473671.html |access-date=May 17, 2020 |work=The Independent |date=April 20, 2020 |language=en |archive-date=April 24, 2020 |archive-url=https://web.archive.org/web/20200424110621/https://www.independent.co.uk/life-style/gadgets-and-tech/news/brain-computing-memory-artificial-synapse-memristor-a9473671.html |url-status=live }}</ref><ref>{{cite news |title=शोधकर्ताओं ने इलेक्ट्रॉनिक्स का खुलासा किया जो कुशल सीखने में मानव मस्तिष्क की नकल करता है|url=https://phys.org/news/2020-04-unveil-electronics-mimic-human-brain.html |access-date=May 17, 2020 |work=phys.org |language=en |archive-date=May 28, 2020 |archive-url=https://web.archive.org/web/20200528112833/https://phys.org/news/2020-04-unveil-electronics-mimic-human-brain.html |url-status=live }}</ref><ref>{{cite journal |last1=Fu |first1=Tianda |last2=Liu |first2=Xiaomeng |last3=Gao |first3=Hongyan |last4=Ward |first4=Joy E. |last5=Liu |first5=Xiaorong |last6=Yin |first6=Bing |last7=Wang |first7=Zhongrui |last8=Zhuo |first8=Ye |last9=Walker |first9=David J. F. |last10=Joshua Yang |first10=J. |last11=Chen |first11=Jianhan |last12=Lovley |first12=Derek R. |last13=Yao |first13=Jun |title=बायोइंस्पायर्ड बायो-वोल्टेज मेमिस्टर|journal=Nature Communications |date=April 20, 2020 |volume=11 |issue=1 |page=1861 |doi=10.1038/s41467-020-15759-y |pmid=32313096 |pmc=7171104 |bibcode=2020NatCo..11.1861F |doi-access=free }}</ref> | ||
[[पॉलीमर|बहुलक]] से बने कार्बनिक न्यूरोमॉर्फिक परिपथ, आयन-समृद्ध जेल के साथ लेपित, पदार्थ को न्यूरॉन जैसे इलेक्ट्रिक आवेश को ले जाने में सक्षम बनाने के लिए, रोबोट में बनाया गया है, जो इसे वास्तविक विश्व के अन्दर सेंसरिमोटरली सीखने में सक्षम बनाता है, अतिरिक्त सिमुलेशन या आभासी रूप से<ref name="sciame">{{cite news |last1=Bolakhe |first1=Saugat |title=कार्बनिक 'मस्तिष्क' के साथ लेगो रोबोट एक भूलभुलैया को नेविगेट करना सीखता है|url=https://www.scientificamerican.com/article/lego-robot-with-an-organic-brain-learns-to-navigate-a-maze/ |access-date=1 February 2022 |work=Scientific American |language=en}}</ref><ref>{{cite journal |last1=Krauhausen |first1=Imke |last2=Koutsouras |first2=Dimitrios A. |last3=Melianas |first3=Armantas |last4=Keene |first4=Scott T. |last5=Lieberth |first5=Katharina |last6=Ledanseur |first6=Hadrien |last7=Sheelamanthula |first7=Rajendar |last8=Giovannitti |first8=Alexander |last9=Torricelli |first9=Fabrizio |last10=Mcculloch |first10=Iain |last11=Blom |first11=Paul W. M. |last12=Salleo |first12=Alberto |last13=Burgt |first13=Yoeri van de |last14=Gkoupidenis |first14=Paschalis |title=सेंसरिमोटर एकीकरण और रोबोटिक्स में सीखने के लिए कार्बनिक न्यूरोमॉर्फिक इलेक्ट्रॉनिक्स|journal=Science Advances |date=December 2021 |volume=7 |issue=50 |pages=eabl5068 |doi=10.1126/sciadv.abl5068 |pmid=34890232 |pmc=8664264 |bibcode=2021SciA....7.5068K |hdl=10754/673986 |s2cid=245046482 |language=EN}}</ref> इसके अतिरिक्त, नरम पदार्थ (पॉलिमर) से बने कृत्रिम स्पाइकिंग न्यूरॉन्स जैविक रूप से प्रासंगिक वातावरण में काम कर सकते हैं और कृत्रिम और जैविक डोमेन के बीच तालमेल संचार को सक्षम कर सकते हैं।<ref>{{cite journal |last1=Sarkar |first1=Tanmoy |last2=Lieberth |first2=Katharina |last3=Pavlou |first3=Aristea |last4=Frank |first4=Thomas |last5=Mailaender |first5=Volker |last6=McCulloch |first6=Iain |last7=Blom |first7=Paul W. M. |last8=Torriccelli |first8=Fabrizio |last9=Gkoupidenis |first9=Paschalis |title=सीटू न्यूरोमॉर्फिक सेंसिंग और बायोइंटरफेसिंग के लिए एक कार्बनिक कृत्रिम स्पाइकिंग न्यूरॉन|journal=Nature Electronics |date=7 November 2022 |volume=5 |issue=11 |pages=774–783 |doi=10.1038/s41928-022-00859-y |s2cid=253413801 |language=en |issn=2520-1131|doi-access=free }}</ref><ref>{{cite journal |title=कृत्रिम न्यूरॉन्स सहक्रियात्मक संचालन को सक्षम करने के लिए जैविक समकक्षों का अनुकरण करते हैं|journal=Nature Electronics |date=10 November 2022 |volume=5 |issue=11 |pages=721–722 |doi=10.1038/s41928-022-00862-3 |s2cid=253469402 |url=https://www.nature.com/articles/s41928-022-00862-3 |language=en |issn=2520-1131}}</ref> | |||
== इतिहास == | == इतिहास == | ||
पहला कृत्रिम न्यूरॉन थ्रेसहोल्ड | पहला कृत्रिम न्यूरॉन थ्रेसहोल्ड तर्क इकाई (टीएलयू) या रेखीय थ्रेशोल्ड इकाई था,<ref name="Anthony2001">{{cite book|author=Martin Anthony|title=Discrete Mathematics of Neural Networks: Selected Topics|url=https://books.google.com/books?id=qOy4yLBqhFcC&pg=PA3|date=January 2001|publisher=SIAM|isbn=978-0-89871-480-7|pages=3–}}</ref> पहली बार 1943 में [[ वॉरेन मैककुलोच |वॉरेन मैककुलोच]] और [[वाल्टर पिट्स]] द्वारा प्रस्तावित किया गया था। मॉडल को विशेष रूप से मस्तिष्क में तंत्रिका जाल के कम्प्यूटेशनल मॉडल के रूप में लक्षित किया गया था।<ref name="Aggarwal2014">{{cite book|author=Charu C. Aggarwal|title=Data Classification: Algorithms and Applications|url=https://books.google.com/books?id=gJhBBAAAQBAJ&pg=PA209|date=25 July 2014|publisher=CRC Press|isbn=978-1-4665-8674-1|pages=209–}}</ref> स्थानांतरण फलन के रूप में, यह हेविसाइड चरण फलन का उपयोग करने के बराबर थ्रेसहोल्ड नियोजित करता है। प्रारंभ में, केवल साधारण मॉडल पर विचार किया गया था, बाइनरी इनपुट और आउटपुट के साथ, संभावित भार पर कुछ प्रतिबंध और अधिक लचीला थ्रेशोल्ड मान। प्रारंभ के बाद से यह पहले से ही देखा गया था कि किसी भी [[बूलियन समारोह|बूलियन फलन]] को ऐसे उपकरणों के नेटवर्क द्वारा कार्यान्वित किया जा सकता है, जो इस तथ्य से सरलता से देखा जा सकता है कि कोई एएनडी और ओआर फलन को कार्यान्वित कर सकता है, और उन्हें अलग-अलग सामान्य रूप या संयोजक सामान्य रूप में उपयोग कर सकता है . | ||
शोधकर्ताओं ने भी | |||
शोधकर्ताओं ने भी शीघ्र ही अनुभव किया कि चक्रीय नेटवर्क, न्यूरॉन्स के माध्यम से [[ प्रतिक्रिया |प्रतिक्रिया]] के साथ, गतिशील प्रणालियों को स्मृति के साथ परिभाषित कर सकते हैं, लेकिन अधिकांश शोध केंद्रित (और अभी भी) कठोरता से [[फीड-फॉरवर्ड नेटवर्क]] पर केंद्रित हैं क्योंकि वे छोटी कठिनाई प्रस्तुत करते हैं। | |||
महत्वपूर्ण और अग्रणी कृत्रिम तंत्रिका नेटवर्क जो रैखिक थ्रेशोल्ड फलन का उपयोग करता था, वह [[परसेप्ट्रॉन]] था, जिसे [[फ्रैंक रोसेनब्लैट]] द्वारा विकसित किया गया था। यह मॉडल पहले से ही न्यूरॉन्स में अधिक लचीले वजन मूल्यों पर विचार करता था, और अनुकूली क्षमताओं वाली मशीनों में उपयोग किया जाता था। 1960 में [[बर्नार्ड विड्रो]] द्वारा पूर्वाग्रह शब्द के रूप में सीमा मूल्यों का प्रतिनिधित्व प्रस्तुत किया गया था - [[ADALINE|एडलाइन]] देखें। | |||
1980 के दशक के उत्तरार्ध में, जब तंत्रिका नेटवर्क पर शोध फिर से कठोर हुआ, तो अधिक निरंतर आकार वाले न्यूरॉन्स पर विचार किया जाने लगा। सक्रियण फलन को अलग करने की संभावना वजन के समायोजन के लिए ढाल वंश और अन्य अनुकूलन कलनविधि के प्रत्यक्ष उपयोग की अनुमति देती है। तंत्रिका नेटवर्क भी सामान्य कार्य सन्निकटन मॉडल के रूप में उपयोग किए जाने लगे। सबसे प्रसिद्ध प्रशिक्षण कलनविधि जिसे [[backpropagation|बैकप्रोपैगेशन]] कहा जाता है, को कई बार फिर से खोजा गया है लेकिन इसका पहला विकास [[पॉल वर्बोस]] के काम पर वापस जाता है।<ref>[[Paul Werbos]], Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. PhD thesis, Harvard University, 1974</ref><ref>{{cite journal | last=Werbos | first=P.J. |author-link=Paul Werbos| title=Backpropagation through time: what it does and how to do it | journal=Proceedings of the IEEE | volume=78 | issue=10 | year=1990 | issn=0018-9219 | doi=10.1109/5.58337 | pages=1550–1560| s2cid=18470994 | url=https://zenodo.org/record/1262035 }}</ref> | |||
== स्थानांतरण कार्यों के प्रकार == | == स्थानांतरण कार्यों के प्रकार == | ||
{{Main| | {{Main|स्थानांतरण प्रकार्य}} | ||
न्यूरॉन के | |||
न्यूरॉन के स्थानांतरण फलन (सक्रियण फलन) को कई गुणों के लिए चुना जाता है जो न्यूरॉन युक्त नेटवर्क को बढ़ाते हैं या सरल करते हैं। महत्वपूर्ण रूप से, उदाहरण के लिए, किसी भी [[ बहुपरत परसेप्ट्रॉन |बहुपरत परसेप्ट्रॉन]] में रेखीय स्थानांतरण फलन का उपयोग करने के लिए समान एकल-परत नेटवर्क होता है; इसलिए बहु-परत नेटवर्क का लाभ प्राप्त करने के लिए गैर-रैखिक कार्य आवश्यक है। | |||
नीचे, | नीचे, ''u'' सभी स्थितियों में न्यूरॉन के सभी इनपुट के भारित योग को संदर्भित करता है, अर्थात ''n'' इनपुट के लिए, | ||
:<math> | :<math> | ||
u = \sum_{i = 1}^n w_i x_i | u = \sum_{i = 1}^n w_i x_i | ||
</math> | </math> | ||
जहां w 'सिनैप्टिक वेट' का | जहां w 'सिनैप्टिक वेट' का सदिश है और x इनपुट का सदिश है। | ||
=== स्टेप | === स्टेप फलन === | ||
इस | इस स्थानांतरण फलन का आउटपुट वाई बाइनरी है, यह इस बात पर निर्भर करता है कि इनपुट निर्दिष्ट सीमा, θ से मिलता है या नहीं मिलता है। संकेतिक भेजा जाता है, अर्थात् यदि सक्रियण थ्रेशोल्ड को पूरा करता है, तो आउटपुट पर सेट होता है। | ||
:<math>y = \begin{cases} 1 & \text{if }u \ge \theta \\ 0 & \text{if }u < \theta \end{cases}</math> | :<math>y = \begin{cases} 1 & \text{if }u \ge \theta \\ 0 & \text{if }u < \theta \end{cases}</math> | ||
यह | यह फलन परसेप्ट्रॉन में उपयोग किया जाता है और अधिकांशतः कई अन्य मॉडलों में दिखाई देता है। यह [[ hyperplane |हाइपरप्लेन]] द्वारा इनपुट के [[ सदिश स्थल |सदिश स्थल]] का विभाजन करता है। यह इनपुट के बाइनरी वर्गीकरण को करने के उद्देश्य से नेटवर्क की अंतिम परत में विशेष रूप से उपयोगी है। वज़न को बड़े मान निर्दिष्ट करके इसे अन्य सिग्मोइडल फलन से अनुमानित किया जा सकता है। | ||
=== रैखिक संयोजन === | === रैखिक संयोजन === | ||
इस | इस स्थितियों में, आउटपुट इकाई केवल इसके इनपुट का भारित योग और पूर्वाग्रह शब्द है। ऐसे कई रैखिक न्यूरॉन्स इनपुट सदिश के [[रैखिक परिवर्तन]] का प्रदर्शन करते हैं। यह सामान्यतः नेटवर्क की पहली परतों में अधिक उपयोगी होता है। [[हार्मोनिक विश्लेषण]] जैसे रैखिक मॉडल के आधार पर कई विश्लेषण उपकरण उपस्थित हैं, और वे सभी इस रैखिक न्यूरॉन के साथ तंत्रिका नेटवर्क में उपयोग किए जा सकते हैं। पूर्वाग्रह शब्द हमें डेटा के [[सजातीय निर्देशांक]] बनाने की अनुमति देता है। | ||
देखें: | देखें: रेखीय ट्रांसफॉर्मेशन, हार्मोनिक एनालिसिस,[[ रैखिक फ़िल्टर |रैखिक फ़िल्टर]],[[ छोटा लहर |छोटा लहर]], [[ प्रमुख कंपोनेंट विश्लेषण |प्रमुख कंपोनेंट विश्लेषण]], [[ स्वतंत्र घटक विश्लेषण |स्वतंत्र घटक विश्लेषण]], [[विखंडन]] | ||
=== सिग्मॉइड === | === सिग्मॉइड === | ||
{{See also| | {{See also|सिग्मॉइड फलन}} | ||
बहुत सरल गैर-रैखिक फलन, सिग्मॉइड फलन जैसे कि लॉजिस्टिक फलन में भी सरलता से परिकलित डेरिवेटिव होता है, जो नेटवर्क में वज़न अपडेट की गणना करते समय महत्वपूर्ण हो सकता है। इस प्रकार यह नेटवर्क को गणितीय रूप से अधिक सरलता से जोड़-तोड़ करने योग्य बनाता है, और प्रारंभिक कंप्यूटर वैज्ञानिकों के लिए आकर्षक था, जिन्हें अपने सिमुलेशन के कम्प्यूटेशनल लोड को कम करने की आवश्यकता थी। यह पहले सामान्यतः मल्टीपरत परसेप्ट्रॉन में देखा जाता था। चूँकि, हाल के काम ने सिग्मॉइड न्यूरॉन्स को रेक्टिफायर (तंत्रिका नेटवर्क) न्यूरॉन्स की तुलना में कम प्रभावी दिखाया है। कारण यह है कि पश्च प्रसार कलनविधि द्वारा गणना किए गए ग्रेडियेंट शून्य की ओर कम हो जाते हैं क्योंकि सक्रियण सिग्मोइडल न्यूरॉन्स की परतों के माध्यम से फैलता है, जिससे सिग्मोइडल न्यूरॉन्स की कई परतों का उपयोग करके तंत्रिका नेटवर्क को अनुकूलित करना कठिन हो जाता है। | |||
=== शुद्ध करनेवाला === | === शुद्ध करनेवाला === | ||
{{See also| | {{See also|शुद्ध करनेवाला (तंत्रिका नेटवर्क)}} | ||
कृत्रिम तंत्रिका नेटवर्क के संदर्भ में, रेक्टिफायर या | |||
कृत्रिम तंत्रिका नेटवर्क के संदर्भ में, रेक्टिफायर या रीएलयू (रेक्टीफाइड रेखीय इकाई) सक्रियण फलन है जिसे इसके तर्क के सकारात्मक भाग के रूप में परिभाषित किया गया है: | |||
: <math>f(x) = x^+ = \max(0, x),</math> | : <math>f(x) = x^+ = \max(0, x),</math> | ||
जहाँ x | जहाँ x न्यूरॉन का इनपुट है। इसे [[रैंप समारोह|रैंप फलन]] के रूप में भी जाना जाता है और इलेक्ट्रिकल इंजीनियरिंग में अर्ध-तरंग सुधार के समान है। इस एक्टिवेशन फलन को सबसे पहले हैनलोसर एट अल द्वारा डायनेमिक नेटवर्क में प्रस्तुत किया गया था। नेचर में 2000 के पेपर में<ref name="Hahnloser2000">{{cite journal | last1=Hahnloser | first1=Richard H. R. | last2=Sarpeshkar | first2=Rahul | last3=Mahowald | first3=Misha A. | last4=Douglas | first4=Rodney J. | last5=Seung | first5=H. Sebastian | title=डिजिटल चयन और एनालॉग प्रवर्धन कॉर्टेक्स-प्रेरित सिलिकॉन सर्किट में सह-अस्तित्व में हैं| journal=Nature | volume=405 | issue=6789 | year=2000 | issn=0028-0836 | doi=10.1038/35016072 | pmid=10879535 | pages=947–951| bibcode=2000Natur.405..947H | s2cid=4399014 }}</ref> कठोर [[जैविक]] प्रेरणा और गणितीय औचित्य के साथ<ref name="Hahnloser2001">{{cite conference |authors=R Hahnloser, H.S. Seung |year=2001 |title=सममित दहलीज-रैखिक नेटवर्क में अनुमत और निषिद्ध सेट|conference=NIPS 2001}}</ref> गहरे नेटवर्क के अच्छा प्रशिक्षण को सक्षम करने के लिए 2011 में पहली बार इसका प्रदर्शन किया गया है,<ref name="glorot2011">{{cite conference |authors=Xavier Glorot, Antoine Bordes and [[Yoshua Bengio]] |year=2011 |title=डीप विरल रेक्टिफायर न्यूरल नेटवर्क|conference=AISTATS |url=http://jmlr.org/proceedings/papers/v15/glorot11a/glorot11a.pdf}}</ref> 2011 से पहले व्यापक रूप से उपयोग किए जाने वाले सक्रियण कार्यों की तुलना में, अर्थात् [[लॉजिस्टिक फंक्शन|लॉजिस्टिक फलन]] (जो संभाव्यता सिद्धांत से प्रेरित है; [[ संभार तन्त्र परावर्तन |संभार तन्त्र परावर्तन]] देखें) और इसका अधिक व्यावहारिक<ref>{{cite encyclopedia |authors=[[Yann LeCun]], [[Leon Bottou]], Genevieve B. Orr and [[Klaus-Robert Müller]] |year=1998 |url=http://yann.lecun.com/exdb/publis/pdf/lecun-98b.pdf |title=कुशल बैकप्रॉप|editor=G. Orr |editor2=K. Müller |encyclopedia=Neural Networks: Tricks of the Trade |publisher=Springer}}</ref> समकक्ष, [[अतिशयोक्तिपूर्ण स्पर्शरेखा]] है। | ||
रीएलयू सक्रियण फलन का सामान्यतः उपयोग किया जाने वाला संस्करण लीकी रीएलयू है, जो इकाई के सक्रिय नहीं होने पर छोटे, सकारात्मक ढाल की अनुमति देता है: | |||
<math>f(x) = \begin{cases} | <math>f(x) = \begin{cases} | ||
| Line 104: | Line 119: | ||
ax & \text{otherwise}. | ax & \text{otherwise}. | ||
\end{cases}</math> | \end{cases}</math> | ||
जहाँ x न्यूरॉन का इनपुट है और a छोटा सकारात्मक स्थिरांक है (मूल पेपर में मान 0.01 का उपयोग a के लिए किया गया था)।<ref name="maas2014">Andrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014). [https://ai.stanford.edu/~amaas/papers/relu_hybrid_icml2013_final.pdf Rectifier Nonlinearities Improve Neural Network Acoustic Models].</ref> | |||
== [[स्यूडोकोड]] कलनविधि == | |||
निम्नलिखित एकल टीएलयू का सरल स्यूडोकोड कार्यान्वयन है, जो [[बूलियन डेटा प्रकार]] इनपुट (सही या गलत) लेता है, और सक्रिय होने पर एकल बूलियन आउटपुट देता है। [[ वस्तु के उन्मुख |वस्तु के उन्मुख]] ऑब्जेक्ट-ओरिएंटेड मॉडल का उपयोग किया जाता है। प्रशिक्षण का कोई विधि परिभाषित नहीं है, क्योंकि कई उपस्थित हैं। यदि विशुद्ध रूप से कार्यात्मक मॉडल का उपयोग किया गया था, तो नीचे दिए गए वर्ग टीएलयू को फलन टीएलयू के साथ परिवर्तित कर दिया जाएगा, जिसमें इनपुट पैरामीटर थ्रेशोल्ड, वज़न और इनपुट जो बूलियन मान लौटाते हैं।<syntaxhighlight> | |||
class TLU defined as: | |||
data member threshold : number | |||
data member weights : list of numbers of size X | |||
function member fire(inputs : list of booleans of size X) : boolean defined as: | |||
variable T : number | |||
T ← 0 | |||
for each i in 1 to X do | |||
if inputs(i) is true then | |||
T ← T + weights(i) | |||
end if | |||
end for each | |||
if T > threshold then | |||
return true | |||
else: | |||
return false | |||
end if | |||
end function | |||
end class | |||
</syntaxhighlight> | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 148: | Line 166: | ||
* [https://www.youtube.com/watch?v=NhTZnnJJP64 {{sic|nolink=y|Artifical}} neuron mimicks function of human cells] | * [https://www.youtube.com/watch?v=NhTZnnJJP64 {{sic|nolink=y|Artifical}} neuron mimicks function of human cells] | ||
* [http://www.mind.ilstu.edu/curriculum/modOverview.php?modGUI=212 McCulloch-Pitts Neurons (Overview)] | * [http://www.mind.ilstu.edu/curriculum/modOverview.php?modGUI=212 McCulloch-Pitts Neurons (Overview)] | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 errors]] | |||
[[Category:CS1 maint]] | |||
[[Category:Created On 02/05/2023]] | [[Category:Created On 02/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Pages with syntax highlighting errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:अमेरिकी आविष्कार]] | |||
[[Category:कृत्रिम तंत्रिका प्रसार]] | |||
Latest revision as of 20:13, 16 May 2023
कृत्रिम न्यूरॉन क्रिया है जिसे जैविक न्यूरॉन्स, तंत्रिका नेटवर्क के गणितीय मॉडल के रूप में माना जाता है। कृत्रिम तंत्रिका नेटवर्क में कृत्रिम न्यूरॉन्स प्राथमिक इकाइयां हैं।[1] कृत्रिम न्यूरॉन एक या एक से अधिक इनपुट प्राप्त करता है (उत्तेजक पोस्टसिनेप्टिक क्षमता और न्यूरल डेन्ड्राइट में निरोधात्मक पोस्टसिनेप्टिक क्षमता का प्रतिनिधित्व करता है) और उन्हें आउटपुट (या सक्रियण, न्यूरॉन की क्रिया क्षमता का प्रतिनिधित्व करता है जो इसके अक्षतंतु के साथ संचरित होता है)। सामान्यतः प्रत्येक इनपुट अलग-अलग से भारित किया जाता है, और योग को गैर-रैखिक फलन के माध्यम से पारित किया जाता है जिसे सक्रियण फलन या स्थानांतरण प्रकार्य के रूप में जाना जाता है। स्थानांतरण कार्यों में सामान्यतः सिग्मॉइड फलन होता है, लेकिन वे अन्य गैर-रैखिक कार्यों, टुकड़े-टुकड़े रैखिक कार्यों या स्टेप फलन का रूप भी ले सकते हैं। वे अधिकांशतः मोनोटोनिक फलन, निरंतर कार्य, विभेदक कार्य और परिबद्ध फलन भी होते हैं। कई शून्यों के साथ गैर-मोनोटोनिक, अनबाउंड और ऑसिलेटिंग एक्टिवेशन फलन जो कई कार्यों पर सिग्मोइडल और रीएलयू जैसे एक्टिवेशन फलन से अच्छा प्रदर्शन करते हैं, उन्हें भी हाल ही में खोजा गया है। थ्रेशोल्डिंग फलन ने बिल्डिंग लॉजिक गेट को थ्रेशोल्ड तर्क के रूप में संदर्भित करने के लिए प्रेरित किया है; मस्तिष्क प्रसंस्करण जैसी दिखने वाली तर्क परिपथ बनाने के लिए प्रयुक्त उदाहरण के लिए, हाल के दिनों में इस तरह के तर्क को विकसित करने के लिए मेमोरी स्टोर जैसे नए उपकरणों का बड़े पैमाने पर उपयोग किया गया है।[2]
कृत्रिम न्यूरॉन स्थानांतरण फलन को रैखिक प्रणाली स्थानांतरण फलन के साथ भ्रमित नहीं होना चाहिए।
कृत्रिम न्यूरॉन्स न्यूरोमॉर्फिक इंजीनियरिंग में कृत्रिम कोशिकाओं को भी संदर्भित कर सकते हैं, जो प्राकृतिक भौतिक न्यूरॉन्स के समान हैं ।
मूल संरचना
किसी दिए गए कृत्रिम न्यूरॉन k के लिए, माना x0 के माध्यम से xm और wk0 के माध्यम से wkm के संकेतों के साथ m + 1 इनपुट हैं। सामान्यतः, x0 इनपुट को मान +1 असाइन किया गया है, जो इसे wk0 = bk के साथ पूर्वाग्रह इनपुट बनाता है यह न्यूरॉन के लिए केवल m वास्तविक इनपुट छोड़ता है: x1 से xm तक
Kवाँ न्यूरॉन का आउटपुट है:
जहाँ (phi) स्थानांतरण फलन (सामान्यतः थ्रेशोल्ड फलन) है।
आउटपुट जैविक न्यूरॉन के अक्षतंतु के अनुरूप होता है, और इसका मान अन्तर्ग्रथन के माध्यम से अगली परत के इनपुट तक फैलता है। यह संभवतः आउटपुट सदिश (गणित और भौतिकी) के हिस्से के रूप में प्रणाली से बाहर निकल सकता है।
इसकी कोई सीखने की प्रक्रिया नहीं है। इसके स्थानांतरण फलन वेट की गणना की जाती है और थ्रेशोल्ड वैल्यू पूर्व निर्धारित होती है।
प्रकार
उपयोग किए गए विशिष्ट मॉडल के आधार पर उन्हें सेमी-रेखीय इकाई, एनवी न्यूरॉन, बाइनरी न्यूरॉन, रेखीय थ्रेशोल्ड फलन या मैककुलोच-पिट्स (एमसीपी) न्यूरॉन कहा जा सकता है।
सरल कृत्रिम न्यूरॉन्स, जैसे मैककुलोच-पिट्स मॉडल, को कभी-कभी कैरिकेचर मॉडल के रूप में वर्णित किया जाता है, क्योंकि उनका उद्देश्य एक या अधिक न्यूरोफिज़ियोतर्कल अवलोकनों को प्रतिबिंबित करना है, लेकिन यथार्थवाद के संबंध में होता है।[3]
जैविक मॉडल
कृत्रिम न्यूरॉन्स को उनके जैविक समकक्षों के पहलुओं की नकल करने के लिए डिज़ाइन किया गया है। चूँकि जैविक और कृत्रिम तंत्रिका नेटवर्क के बीच महत्वपूर्ण प्रदर्शन अंतर उपस्थित है। मानव मस्तिष्क में विशेष रूप से एकल जैविक न्यूरॉन्स में एक्सओआर फलन सीखने में सक्षम ऑसिलेटिंग एक्टिवेशन फलन के साथ खोजा गया है।[4] डेन्ड्राइट -जैविक न्यूरॉन में, डेन्ड्राइट इनपुट सदिश के रूप में कार्य करते हैं। ये डेन्ड्राइट कोशिका को पड़ोसी न्यूरॉन्स की बड़ी (>1000) संख्या से संकेत प्राप्त करने की अनुमति देते हैं। उपरोक्त गणितीय उपचार के अनुसार, प्रत्येक डेन्ड्राइट उस डेन्ड्राइट के वजन मान से गुणा करने में सक्षम होता है। सिनैप्टिक न्यूरोट्रांसमीटर के उत्तर में डेन्ड्राइट में प्रस्तुत किए गए संकेतिक रसायनों के लिए सिनैप्टिक न्यूरोट्रांसमीटर के अनुपात को बढ़ाकर या घटाकर गुणन पूरा किया जाता है। सिनैप्टिक न्यूरोट्रांसमीटर के स्वागत के उत्तर में डेंड्राइट के साथ संकेतिक इनहिबिटर (अर्थात् विपरीत आवेश आयन) को प्रेषित करके नकारात्मक गुणन प्रभाव प्राप्त किया जा सकता है।
- सोमा (जीव विज्ञान) - जैविक न्यूरॉन में, सोम उपरोक्त गणितीय विवरण में देखे गए योग फलन के रूप में कार्य करता है। चूंकि सकारात्मक और नकारात्मक संकेत (रोमांचक और अवरोधक, क्रमशः) डेन्ड्राइट्स से सोमा में आते हैं, सकारात्मक और नकारात्मक आयन प्रभावी रूप से योग में जोड़े जाते हैं, सेल के शरीर के अंदर समाधान में साथ मिश्रित होने के सरल गुण से।
- एक्सोन - अक्षतंतु अपना संकेत सोमा के अंदर होने वाले योग व्यवहार से प्राप्त करता है। अक्षतंतु का खुलना अनिवार्य रूप से सोमा के अंदर समाधान की विद्युत क्षमता का नमूना लेता है। एक बार सोमा निश्चित क्षमता तक पहुंच जाता है, अक्षतंतु अपनी लंबाई के नीचे ऑल-इन संकेतिक पल्स संचारित करेगा। इस संबंध में, अक्षतंतु हमारे कृत्रिम न्यूरॉन को अन्य कृत्रिम न्यूरॉन्स से जोड़ने की क्षमता के रूप में व्यवहार करता है।
चूँकि, अधिकांश कृत्रिम न्यूरॉन्स के विपरीत, जैविक न्यूरॉन्स असतत पल्सों में आग लगाते हैं। हर बार सोमा के अंदर विद्युत क्षमता निश्चित सीमा तक पहुँचती है, नाभिक अक्षतंतु के नीचे प्रेषित होती है। इस स्पंदन को निरंतर मूल्यों में अनुवादित किया जा सकता है। दर (प्रति सेकंड सक्रियता, आदि) जिस पर अक्षतंतु आग सीधे उस दर में परिवर्तित हो जाती है जिस पर पड़ोसी कोशिकाओं को संकेतिक आयन मिलते हैं। जितनी तीव्रता से जैविक न्यूरॉन प्रज्वलित होता है, उतनी ही तीव्रता से पास के न्यूरॉन्स विद्युत क्षमता एकत्र करते हैं (या विद्युत क्षमता खो देते हैं, डेन्ड्राइट के भार के आधार पर जो न्यूरॉन से जुड़ते हैं)। यह रूपांतरण है जो कंप्यूटर वैज्ञानिकों और गणितज्ञों को कृत्रिम न्यूरॉन्स का उपयोग करके जैविक तंत्रिका नेटवर्क का अनुकरण करने की अनुमति देता है जो अलग-अलग मान (अधिकांशतः -1 से 1 तक) का उत्पादन कर सकते हैं।
एन्कोडिंग
शोध से पता चला है कि बर्डसॉन्ग प्रोडक्शन के लिए उत्तरदायी न्यूरल परिपथ में यूनरी कोडिंग का प्रयोग किया जाता है।[5][6] कोडिंग की अंतर्निहित सादगी के कारण जैविक नेटवर्क में यूनरी का उपयोग संभवतः है। अन्य योगदान कारक यह हो सकता है कि यूनरी कोडिंग त्रुटि सुधार की निश्चित डिग्री प्रदान करती है।[7]
भौतिक कृत्रिम कोशिकाएं
भौतिक कृत्रिम न्यूरॉन्स - कार्बनिक और अकार्बनिक में अनुसंधान और विकास है।
उदाहरण के लिए, कुछ कृत्रिम न्यूरॉन्स प्राप्त कर सकते हैं[8][9] और डोपामाइन (विद्युत संकेतों के अतिरिक्त स्नायुसंचारी ) को छोड़ता है और मस्तिष्क-कंप्यूटर इंटरफेस/वेटवेयर कंप्यूटर भविष्य के अनुप्रयोगों में उपयोग की संभावना के साथ प्राकृतिक चूहे नरम रोबोट और मस्तिष्क कोशिकाओं के साथ संचार करता है।[10][11]
कम-शक्ति वाले बायोकम्पैटिबल मेमिस्टर कृत्रिम न्यूरॉन्स के निर्माण को सक्षम कर सकते हैं, जो जैविक क्रिया क्षमता के वोल्टेज पर कार्य करते हैं और न्यूरोमॉर्फिक कंप्यूटिंग और मस्तिष्क-कंप्यूटर इंटरफ़ेस के लिए बायोसेंसर को सीधे संसाधित करने के लिए उपयोग किया जा सकता है।[12][13][14]
बहुलक से बने कार्बनिक न्यूरोमॉर्फिक परिपथ, आयन-समृद्ध जेल के साथ लेपित, पदार्थ को न्यूरॉन जैसे इलेक्ट्रिक आवेश को ले जाने में सक्षम बनाने के लिए, रोबोट में बनाया गया है, जो इसे वास्तविक विश्व के अन्दर सेंसरिमोटरली सीखने में सक्षम बनाता है, अतिरिक्त सिमुलेशन या आभासी रूप से[15][16] इसके अतिरिक्त, नरम पदार्थ (पॉलिमर) से बने कृत्रिम स्पाइकिंग न्यूरॉन्स जैविक रूप से प्रासंगिक वातावरण में काम कर सकते हैं और कृत्रिम और जैविक डोमेन के बीच तालमेल संचार को सक्षम कर सकते हैं।[17][18]
इतिहास
पहला कृत्रिम न्यूरॉन थ्रेसहोल्ड तर्क इकाई (टीएलयू) या रेखीय थ्रेशोल्ड इकाई था,[19] पहली बार 1943 में वॉरेन मैककुलोच और वाल्टर पिट्स द्वारा प्रस्तावित किया गया था। मॉडल को विशेष रूप से मस्तिष्क में तंत्रिका जाल के कम्प्यूटेशनल मॉडल के रूप में लक्षित किया गया था।[20] स्थानांतरण फलन के रूप में, यह हेविसाइड चरण फलन का उपयोग करने के बराबर थ्रेसहोल्ड नियोजित करता है। प्रारंभ में, केवल साधारण मॉडल पर विचार किया गया था, बाइनरी इनपुट और आउटपुट के साथ, संभावित भार पर कुछ प्रतिबंध और अधिक लचीला थ्रेशोल्ड मान। प्रारंभ के बाद से यह पहले से ही देखा गया था कि किसी भी बूलियन फलन को ऐसे उपकरणों के नेटवर्क द्वारा कार्यान्वित किया जा सकता है, जो इस तथ्य से सरलता से देखा जा सकता है कि कोई एएनडी और ओआर फलन को कार्यान्वित कर सकता है, और उन्हें अलग-अलग सामान्य रूप या संयोजक सामान्य रूप में उपयोग कर सकता है .
शोधकर्ताओं ने भी शीघ्र ही अनुभव किया कि चक्रीय नेटवर्क, न्यूरॉन्स के माध्यम से प्रतिक्रिया के साथ, गतिशील प्रणालियों को स्मृति के साथ परिभाषित कर सकते हैं, लेकिन अधिकांश शोध केंद्रित (और अभी भी) कठोरता से फीड-फॉरवर्ड नेटवर्क पर केंद्रित हैं क्योंकि वे छोटी कठिनाई प्रस्तुत करते हैं।
महत्वपूर्ण और अग्रणी कृत्रिम तंत्रिका नेटवर्क जो रैखिक थ्रेशोल्ड फलन का उपयोग करता था, वह परसेप्ट्रॉन था, जिसे फ्रैंक रोसेनब्लैट द्वारा विकसित किया गया था। यह मॉडल पहले से ही न्यूरॉन्स में अधिक लचीले वजन मूल्यों पर विचार करता था, और अनुकूली क्षमताओं वाली मशीनों में उपयोग किया जाता था। 1960 में बर्नार्ड विड्रो द्वारा पूर्वाग्रह शब्द के रूप में सीमा मूल्यों का प्रतिनिधित्व प्रस्तुत किया गया था - एडलाइन देखें।
1980 के दशक के उत्तरार्ध में, जब तंत्रिका नेटवर्क पर शोध फिर से कठोर हुआ, तो अधिक निरंतर आकार वाले न्यूरॉन्स पर विचार किया जाने लगा। सक्रियण फलन को अलग करने की संभावना वजन के समायोजन के लिए ढाल वंश और अन्य अनुकूलन कलनविधि के प्रत्यक्ष उपयोग की अनुमति देती है। तंत्रिका नेटवर्क भी सामान्य कार्य सन्निकटन मॉडल के रूप में उपयोग किए जाने लगे। सबसे प्रसिद्ध प्रशिक्षण कलनविधि जिसे बैकप्रोपैगेशन कहा जाता है, को कई बार फिर से खोजा गया है लेकिन इसका पहला विकास पॉल वर्बोस के काम पर वापस जाता है।[21][22]
स्थानांतरण कार्यों के प्रकार
न्यूरॉन के स्थानांतरण फलन (सक्रियण फलन) को कई गुणों के लिए चुना जाता है जो न्यूरॉन युक्त नेटवर्क को बढ़ाते हैं या सरल करते हैं। महत्वपूर्ण रूप से, उदाहरण के लिए, किसी भी बहुपरत परसेप्ट्रॉन में रेखीय स्थानांतरण फलन का उपयोग करने के लिए समान एकल-परत नेटवर्क होता है; इसलिए बहु-परत नेटवर्क का लाभ प्राप्त करने के लिए गैर-रैखिक कार्य आवश्यक है।
नीचे, u सभी स्थितियों में न्यूरॉन के सभी इनपुट के भारित योग को संदर्भित करता है, अर्थात n इनपुट के लिए,
जहां w 'सिनैप्टिक वेट' का सदिश है और x इनपुट का सदिश है।
स्टेप फलन
इस स्थानांतरण फलन का आउटपुट वाई बाइनरी है, यह इस बात पर निर्भर करता है कि इनपुट निर्दिष्ट सीमा, θ से मिलता है या नहीं मिलता है। संकेतिक भेजा जाता है, अर्थात् यदि सक्रियण थ्रेशोल्ड को पूरा करता है, तो आउटपुट पर सेट होता है।
यह फलन परसेप्ट्रॉन में उपयोग किया जाता है और अधिकांशतः कई अन्य मॉडलों में दिखाई देता है। यह हाइपरप्लेन द्वारा इनपुट के सदिश स्थल का विभाजन करता है। यह इनपुट के बाइनरी वर्गीकरण को करने के उद्देश्य से नेटवर्क की अंतिम परत में विशेष रूप से उपयोगी है। वज़न को बड़े मान निर्दिष्ट करके इसे अन्य सिग्मोइडल फलन से अनुमानित किया जा सकता है।
रैखिक संयोजन
इस स्थितियों में, आउटपुट इकाई केवल इसके इनपुट का भारित योग और पूर्वाग्रह शब्द है। ऐसे कई रैखिक न्यूरॉन्स इनपुट सदिश के रैखिक परिवर्तन का प्रदर्शन करते हैं। यह सामान्यतः नेटवर्क की पहली परतों में अधिक उपयोगी होता है। हार्मोनिक विश्लेषण जैसे रैखिक मॉडल के आधार पर कई विश्लेषण उपकरण उपस्थित हैं, और वे सभी इस रैखिक न्यूरॉन के साथ तंत्रिका नेटवर्क में उपयोग किए जा सकते हैं। पूर्वाग्रह शब्द हमें डेटा के सजातीय निर्देशांक बनाने की अनुमति देता है।
देखें: रेखीय ट्रांसफॉर्मेशन, हार्मोनिक एनालिसिस,रैखिक फ़िल्टर,छोटा लहर, प्रमुख कंपोनेंट विश्लेषण, स्वतंत्र घटक विश्लेषण, विखंडन
सिग्मॉइड
बहुत सरल गैर-रैखिक फलन, सिग्मॉइड फलन जैसे कि लॉजिस्टिक फलन में भी सरलता से परिकलित डेरिवेटिव होता है, जो नेटवर्क में वज़न अपडेट की गणना करते समय महत्वपूर्ण हो सकता है। इस प्रकार यह नेटवर्क को गणितीय रूप से अधिक सरलता से जोड़-तोड़ करने योग्य बनाता है, और प्रारंभिक कंप्यूटर वैज्ञानिकों के लिए आकर्षक था, जिन्हें अपने सिमुलेशन के कम्प्यूटेशनल लोड को कम करने की आवश्यकता थी। यह पहले सामान्यतः मल्टीपरत परसेप्ट्रॉन में देखा जाता था। चूँकि, हाल के काम ने सिग्मॉइड न्यूरॉन्स को रेक्टिफायर (तंत्रिका नेटवर्क) न्यूरॉन्स की तुलना में कम प्रभावी दिखाया है। कारण यह है कि पश्च प्रसार कलनविधि द्वारा गणना किए गए ग्रेडियेंट शून्य की ओर कम हो जाते हैं क्योंकि सक्रियण सिग्मोइडल न्यूरॉन्स की परतों के माध्यम से फैलता है, जिससे सिग्मोइडल न्यूरॉन्स की कई परतों का उपयोग करके तंत्रिका नेटवर्क को अनुकूलित करना कठिन हो जाता है।
शुद्ध करनेवाला
कृत्रिम तंत्रिका नेटवर्क के संदर्भ में, रेक्टिफायर या रीएलयू (रेक्टीफाइड रेखीय इकाई) सक्रियण फलन है जिसे इसके तर्क के सकारात्मक भाग के रूप में परिभाषित किया गया है:
जहाँ x न्यूरॉन का इनपुट है। इसे रैंप फलन के रूप में भी जाना जाता है और इलेक्ट्रिकल इंजीनियरिंग में अर्ध-तरंग सुधार के समान है। इस एक्टिवेशन फलन को सबसे पहले हैनलोसर एट अल द्वारा डायनेमिक नेटवर्क में प्रस्तुत किया गया था। नेचर में 2000 के पेपर में[23] कठोर जैविक प्रेरणा और गणितीय औचित्य के साथ[24] गहरे नेटवर्क के अच्छा प्रशिक्षण को सक्षम करने के लिए 2011 में पहली बार इसका प्रदर्शन किया गया है,[25] 2011 से पहले व्यापक रूप से उपयोग किए जाने वाले सक्रियण कार्यों की तुलना में, अर्थात् लॉजिस्टिक फलन (जो संभाव्यता सिद्धांत से प्रेरित है; संभार तन्त्र परावर्तन देखें) और इसका अधिक व्यावहारिक[26] समकक्ष, अतिशयोक्तिपूर्ण स्पर्शरेखा है।
रीएलयू सक्रियण फलन का सामान्यतः उपयोग किया जाने वाला संस्करण लीकी रीएलयू है, जो इकाई के सक्रिय नहीं होने पर छोटे, सकारात्मक ढाल की अनुमति देता है:
जहाँ x न्यूरॉन का इनपुट है और a छोटा सकारात्मक स्थिरांक है (मूल पेपर में मान 0.01 का उपयोग a के लिए किया गया था)।[27]
स्यूडोकोड कलनविधि
निम्नलिखित एकल टीएलयू का सरल स्यूडोकोड कार्यान्वयन है, जो बूलियन डेटा प्रकार इनपुट (सही या गलत) लेता है, और सक्रिय होने पर एकल बूलियन आउटपुट देता है। वस्तु के उन्मुख ऑब्जेक्ट-ओरिएंटेड मॉडल का उपयोग किया जाता है। प्रशिक्षण का कोई विधि परिभाषित नहीं है, क्योंकि कई उपस्थित हैं। यदि विशुद्ध रूप से कार्यात्मक मॉडल का उपयोग किया गया था, तो नीचे दिए गए वर्ग टीएलयू को फलन टीएलयू के साथ परिवर्तित कर दिया जाएगा, जिसमें इनपुट पैरामीटर थ्रेशोल्ड, वज़न और इनपुट जो बूलियन मान लौटाते हैं।
class TLU defined as:
data member threshold : number
data member weights : list of numbers of size X
function member fire(inputs : list of booleans of size X) : boolean defined as:
variable T : number
T ← 0
for each i in 1 to X do
if inputs(i) is true then
T ← T + weights(i)
end if
end for each
if T > threshold then
return true
else:
return false
end if
end function
end class
यह भी देखें
संदर्भ
- ↑ "Neuromorphic Circuits With Neural Modulation Enhancing the Information Content of Neural Signaling | International Conference on Neuromorphic Systems 2020" (in English). doi:10.1145/3407197.3407204. S2CID 220794387.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Maan, A. K.; Jayadevi, D. A.; James, A. P. (1 January 2016). "यादगार दहलीज तर्क सर्किट का एक सर्वेक्षण". IEEE Transactions on Neural Networks and Learning Systems. PP (99): 1734–1746. arXiv:1604.07121. Bibcode:2016arXiv160407121M. doi:10.1109/TNNLS.2016.2547842. ISSN 2162-237X. PMID 27164608. S2CID 1798273.
- ↑ F. C. Hoppensteadt and E. M. Izhikevich (1997). Weakly connected neural networks. Springer. p. 4. ISBN 978-0-387-94948-2.
- ↑ Gidon, Albert; Zolnik, Timothy Adam; Fidzinski, Pawel; Bolduan, Felix; Papoutsi, Athanasia; Poirazi, Panayiota; Holtkamp, Martin; Vida, Imre; Larkum, Matthew Evan (2020-01-03). "Dendritic action potentials and computation in human layer 2/3 cortical neurons". Science. 367 (6473): 83–87. Bibcode:2020Sci...367...83G. doi:10.1126/science.aax6239. PMID 31896716. S2CID 209676937.
- ↑ Squire, L.; Albright, T.; Bloom, F.; Gage, F.; Spitzer, N., eds. (October 2007). बर्डसॉन्ग प्रोडक्शन, लर्निंग और कोडिंग के न्यूरल नेटवर्क मॉडल (PDF). New Encyclopedia of Neuroscience: Elservier. Archived from the original (PDF) on 2015-04-12. Retrieved 12 April 2015.
- ↑ Moore, J.M.; et al. (2011). "मोटर पाथवे अभिसरण ऑसीन पक्षियों में शब्दांश प्रदर्शनों के आकार की भविष्यवाणी करता है". Proc. Natl. Acad. Sci. USA. 108 (39): 16440–16445. Bibcode:2011PNAS..10816440M. doi:10.1073/pnas.1102077108. PMC 3182746. PMID 21918109.
- ↑ Potluri, Pushpa Sree (26 November 2014). "यूनरी कोडिंग की त्रुटि सुधार क्षमता". arXiv:1411.7406 [cs.IT].
- ↑ Kleiner, Kurt (25 August 2022). "कंप्यूटर चिप्स बनाना मस्तिष्क की कोशिकाओं की तरह अधिक कार्य करता है". Knowable Magazine | Annual Reviews (in English). doi:10.1146/knowable-082422-1. Retrieved 23 September 2022.
- ↑ Keene, Scott T.; Lubrano, Claudia; Kazemzadeh, Setareh; Melianas, Armantas; Tuchman, Yaakov; Polino, Giuseppina; Scognamiglio, Paola; Cinà, Lucio; Salleo, Alberto; van de Burgt, Yoeri; Santoro, Francesca (September 2020). "न्यूरोट्रांसमीटर-मध्यस्थता प्लास्टिसिटी के साथ एक बायोहाइब्रिड सिनैप्स". Nature Materials (in English). 19 (9): 969–973. Bibcode:2020NatMa..19..969K. doi:10.1038/s41563-020-0703-y. ISSN 1476-4660. PMID 32541935. S2CID 219691307.
- University press release: "Researchers develop artificial synapse that works with living cells". Stanford University via medicalxpress.com (in English). Retrieved 23 September 2022.
- ↑ "कृत्रिम न्यूरॉन वास्तविक की तरह चूहे के मस्तिष्क की कोशिकाओं के साथ डोपामाइन की अदला-बदली करता है". New Scientist. Retrieved 16 September 2022.
- ↑ Wang, Ting; Wang, Ming; Wang, Jianwu; Yang, Le; Ren, Xueyang; Song, Gang; Chen, Shisheng; Yuan, Yuehui; Liu, Ruiqing; Pan, Liang; Li, Zheng; Leow, Wan Ru; Luo, Yifei; Ji, Shaobo; Cui, Zequn; He, Ke; Zhang, Feilong; Lv, Fengting; Tian, Yuanyuan; Cai, Kaiyu; Yang, Bowen; Niu, Jingyi; Zou, Haochen; Liu, Songrui; Xu, Guoliang; Fan, Xing; Hu, Benhui; Loh, Xian Jun; Wang, Lianhui; Chen, Xiaodong (8 August 2022). "रासायनिक रूप से मध्यस्थ कृत्रिम न्यूरॉन". Nature Electronics (in English). 5 (9): 586–595. doi:10.1038/s41928-022-00803-0. ISSN 2520-1131. S2CID 251464760.
- ↑ "वैज्ञानिक छोटे उपकरण बनाते हैं जो मानव मस्तिष्क की तरह काम करते हैं". The Independent (in English). April 20, 2020. Archived from the original on April 24, 2020. Retrieved May 17, 2020.
- ↑ "शोधकर्ताओं ने इलेक्ट्रॉनिक्स का खुलासा किया जो कुशल सीखने में मानव मस्तिष्क की नकल करता है". phys.org (in English). Archived from the original on May 28, 2020. Retrieved May 17, 2020.
- ↑ Fu, Tianda; Liu, Xiaomeng; Gao, Hongyan; Ward, Joy E.; Liu, Xiaorong; Yin, Bing; Wang, Zhongrui; Zhuo, Ye; Walker, David J. F.; Joshua Yang, J.; Chen, Jianhan; Lovley, Derek R.; Yao, Jun (April 20, 2020). "बायोइंस्पायर्ड बायो-वोल्टेज मेमिस्टर". Nature Communications. 11 (1): 1861. Bibcode:2020NatCo..11.1861F. doi:10.1038/s41467-020-15759-y. PMC 7171104. PMID 32313096.
- ↑ Bolakhe, Saugat. "कार्बनिक 'मस्तिष्क' के साथ लेगो रोबोट एक भूलभुलैया को नेविगेट करना सीखता है". Scientific American (in English). Retrieved 1 February 2022.
- ↑ Krauhausen, Imke; Koutsouras, Dimitrios A.; Melianas, Armantas; Keene, Scott T.; Lieberth, Katharina; Ledanseur, Hadrien; Sheelamanthula, Rajendar; Giovannitti, Alexander; Torricelli, Fabrizio; Mcculloch, Iain; Blom, Paul W. M.; Salleo, Alberto; Burgt, Yoeri van de; Gkoupidenis, Paschalis (December 2021). "सेंसरिमोटर एकीकरण और रोबोटिक्स में सीखने के लिए कार्बनिक न्यूरोमॉर्फिक इलेक्ट्रॉनिक्स". Science Advances (in English). 7 (50): eabl5068. Bibcode:2021SciA....7.5068K. doi:10.1126/sciadv.abl5068. hdl:10754/673986. PMC 8664264. PMID 34890232. S2CID 245046482.
- ↑ Sarkar, Tanmoy; Lieberth, Katharina; Pavlou, Aristea; Frank, Thomas; Mailaender, Volker; McCulloch, Iain; Blom, Paul W. M.; Torriccelli, Fabrizio; Gkoupidenis, Paschalis (7 November 2022). "सीटू न्यूरोमॉर्फिक सेंसिंग और बायोइंटरफेसिंग के लिए एक कार्बनिक कृत्रिम स्पाइकिंग न्यूरॉन". Nature Electronics (in English). 5 (11): 774–783. doi:10.1038/s41928-022-00859-y. ISSN 2520-1131. S2CID 253413801.
- ↑ "कृत्रिम न्यूरॉन्स सहक्रियात्मक संचालन को सक्षम करने के लिए जैविक समकक्षों का अनुकरण करते हैं". Nature Electronics (in English). 5 (11): 721–722. 10 November 2022. doi:10.1038/s41928-022-00862-3. ISSN 2520-1131. S2CID 253469402.
- ↑ Martin Anthony (January 2001). Discrete Mathematics of Neural Networks: Selected Topics. SIAM. pp. 3–. ISBN 978-0-89871-480-7.
- ↑ Charu C. Aggarwal (25 July 2014). Data Classification: Algorithms and Applications. CRC Press. pp. 209–. ISBN 978-1-4665-8674-1.
- ↑ Paul Werbos, Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. PhD thesis, Harvard University, 1974
- ↑ Werbos, P.J. (1990). "Backpropagation through time: what it does and how to do it". Proceedings of the IEEE. 78 (10): 1550–1560. doi:10.1109/5.58337. ISSN 0018-9219. S2CID 18470994.
- ↑ Hahnloser, Richard H. R.; Sarpeshkar, Rahul; Mahowald, Misha A.; Douglas, Rodney J.; Seung, H. Sebastian (2000). "डिजिटल चयन और एनालॉग प्रवर्धन कॉर्टेक्स-प्रेरित सिलिकॉन सर्किट में सह-अस्तित्व में हैं". Nature. 405 (6789): 947–951. Bibcode:2000Natur.405..947H. doi:10.1038/35016072. ISSN 0028-0836. PMID 10879535. S2CID 4399014.
- ↑ R Hahnloser, H.S. Seung (2001). सममित दहलीज-रैखिक नेटवर्क में अनुमत और निषिद्ध सेट. NIPS 2001.
{{cite conference}}: CS1 maint: uses authors parameter (link) - ↑ Xavier Glorot, Antoine Bordes and Yoshua Bengio (2011). डीप विरल रेक्टिफायर न्यूरल नेटवर्क (PDF). AISTATS.
{{cite conference}}: CS1 maint: uses authors parameter (link) - ↑ Yann LeCun, Leon Bottou, Genevieve B. Orr and Klaus-Robert Müller (1998). "कुशल बैकप्रॉप" (PDF). In G. Orr; K. Müller (eds.). Neural Networks: Tricks of the Trade. Springer.
{{cite encyclopedia}}: CS1 maint: uses authors parameter (link) - ↑ Andrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014). Rectifier Nonlinearities Improve Neural Network Acoustic Models.
अग्रिम पठन
- McCulloch, Warren S.; Pitts, Walter (1943). "A logical calculus of the ideas immanent in nervous activity". Bulletin of Mathematical Biophysics. 5 (4): 115–133. doi:10.1007/bf02478259.
- Samardak, A.; Nogaret, A.; Janson, N. B.; Balanov, A. G.; Farrer, I.; Ritchie, D. A. (2009-06-05). "Noise-Controlled Signal Transmission in a Multithread Semiconductor Neuron". Physical Review Letters. 102 (22): 226802. Bibcode:2009PhRvL.102v6802S. doi:10.1103/physrevlett.102.226802. PMID 19658886. S2CID 11211062.