संगणना का सिद्धांत: Difference between revisions
(text) |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 47: | Line 47: | ||
==== औपचारिक भाषा सिद्धांत ==== | ==== औपचारिक भाषा सिद्धांत ==== | ||
{{main|औपचारिक भाषा}} | {{main|औपचारिक भाषा}} | ||
[[Image:Chomsky-hierarchy.svg|thumb|right|200px|alt=The Chomsky hierarchy|चॉम्स्की पदानुक्रम द्वारा वर्णित समावेशन | [[Image:Chomsky-hierarchy.svg|thumb|right|200px|alt=The Chomsky hierarchy|चॉम्स्की पदानुक्रम द्वारा वर्णित समावेशन निर्धारित करें]]भाषा सिद्धांत गणित की एक शाखा है जो वर्णमाला पर संचालन के एक समूह के रूप में भाषाओं का वर्णन करने से संबंधित है। यह ऑटोमेटा सिद्धांत से निकटता से जुड़ा हुआ है, क्योंकि ऑटोमेटा का उपयोग औपचारिक भाषाओं को उत्पन्न करने और पहचानने के लिए किया जाता है। औपचारिक भाषाओं के कई वर्ग हैं, जिनमें से प्रत्येक अपने से पहले की तुलना में अधिक जटिल भाषा विनिर्देशों की अनुमति देता है, अर्थात [[चॉम्स्की पदानुक्रम]],<ref>{{cite journal |last=[[Chomsky hierarchy]] |date=1956 |title=भाषा के वर्णन के लिए तीन मॉडल|journal=Information Theory, IRE Transactions on |publisher=IEEE |volume=2 |issue=3 |pages= 113–124|doi=10.1109/TIT.1956.1056813 }}</ref> और प्रत्येक ऑटोमेटा के एक वर्ग के अनुरूप है जो इसे पहचानता है। क्योंकि ऑटोमेटा का उपयोग गणना के लिए प्रारूप के रूप में किया जाता है, औपचारिक भाषाएं किसी भी समस्या के लिए विनिर्देशन का अधिमानित तरीका है जिसकी गणना की जानी चाहिए। | ||
=== कम्प्यूटेबिलिटी सिद्धांत === | === कम्प्यूटेबिलिटी सिद्धांत === | ||
| Line 74: | Line 74: | ||
====== [[लैम्ब्डा कैलकुलस]] ====== | ====== [[लैम्ब्डा कैलकुलस]] ====== | ||
एक गणना में प्रारंभिक लैम्ब्डा अभिव्यक्ति होती है (या यदि दो आप फ़ंक्शन और उसके इनपुट को अलग करना चाहते हैं ) प्लस लैम्ब्डा शर्तों का एक सीमित अनुक्रम, प्रत्येक बीटा कटौती के एक आवेदन द्वारा पूर्ववर्ती अवधि से घटाया जाता है। | एक गणना में प्रारंभिक लैम्ब्डा अभिव्यक्ति होती है (या यदि दो आप फ़ंक्शन और उसके इनपुट को अलग करना चाहते हैं ) प्लस लैम्ब्डा शर्तों का एक सीमित अनुक्रम, प्रत्येक बीटा कटौती के एक आवेदन द्वारा पूर्ववर्ती अवधि से घटाया जाता है। | ||
====== [[संयोजन तर्क]] ====== | ====== [[संयोजन तर्क]] ====== | ||
| Line 123: | Line 123: | ||
{{Computer science}} | {{Computer science}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Collapse templates]] | |||
[[Category: | |||
[[Category:Created On 07/05/2023]] | [[Category:Created On 07/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with empty portal template]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Portal-inline template with redlinked portals]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:संगणना का सिद्धांत| संगणना का सिद्धांत ]] | |||
Latest revision as of 12:04, 18 May 2023

सैद्धांतिक कंप्यूटर विज्ञान और गणित में, संगणना का सिद्धांत वह शाखा है जो संगणना के एक प्रारूप पर एक एल्गोरिथ्म का उपयोग करके हल की जा सकने वाली समस्याओं से संबंधित है, एल्गोरिदम का उपयोग करके, उन्हें कितनी कुशलता से हल किया जा सकता है या किस मात्रा तक (जैसे, अनुमानित समाधान या सटीक) हल किया जा सकता है। क्षेत्र को तीन प्रमुख शाखाओं में विभाजित किया गया है: ऑटोमेटा सिद्धांत और औपचारिक भाषाएं, संगणनीयता सिद्धांत और कम्प्यूटेशनल जटिलता सिद्धांत, जो इस प्रश्न से जुड़े हुए हैं: ''कंप्यूटर की मूलभूत क्षमताएं और सीमाएं क्या हैं?'' [1]
संगणना का यथार्थ अध्ययन करने के लिए, कंप्यूटर वैज्ञानिक संगणना का प्रारूप कहे जाने वाले कंप्यूटरों के गणितीय अमूर्तन के साथ काम करते हैं। उपयोग में कई प्रारूप हैं, लेकिन सबसे अधिक जांच की जाने वाली ट्यूरिंग मशीन है।[2] कंप्यूटर वैज्ञानिक ट्यूरिंग मशीन का अध्ययन करते हैं क्योंकि इसे प्रतिपादित करना आसान है, इसका विश्लेषण किया जा सकता है और परिणामों को सिद्ध करने के लिए उपयोग किया जा सकता है, और क्योंकि यह गणना के सबसे शक्तिशाली संभावित ''उचित'' प्रारूप का प्रतिनिधित्व करता है (चर्च-ट्यूरिंग थीसिस देखें)।[3] ऐसा लग सकता है कि संभावित रूप से अनंत मेमोरी क्षमता एक अवास्तविक विशेषता है, लेकिन ट्यूरिंग मशीन द्वारा हल की जाने वाली किसी भी निर्णायक समस्या[4] को हमेशा केवल एक सीमित मात्रा में मेमोरी की आवश्यकता होगी। तो सैद्धांतिक रूप में, कोई भी समस्या जिसे ट्यूरिंग मशीन द्वारा हल (निर्णित) किया जा सकता है, उस कंप्यूटर द्वारा हल किया जा सकता है जिसमें मेमोरी की सीमित मात्रा होती है।
इतिहास
संगणना के सिद्धांत को कंप्यूटर विज्ञान के क्षेत्र में सभी प्रकार के प्रारूपों का निर्माण माना जा सकता है। इसलिए गणितीय तर्क का प्रयोग किया जाता है। पिछली शताब्दी में यह एक स्वतंत्र शैक्षणिक विधा बन गया और गणित से अलग हो गया।
संगणना के सिद्धांत के कुछ अग्रदूत रेमन लुल्ल, अलोंजो चर्च, कर्ट गोडेल, एलन ट्यूरिंग, स्टीफन क्लेन, रोजसा पेटर, जॉन वॉन न्यूमैन और क्लाउड शैनन थे।
शाखाएँ
ऑटोमेटा सिद्धांत
| व्याकरण | भाषाएँ | स्वचल मशीन | उत्पादन नियम (बाधाएं) |
|---|---|---|---|
| प्रारूप-0 | पुनरावर्ती गणना योग्य | ट्यूरिंग मशीन | (कोई प्रतिबंध नहीं) |
| प्रारूप-1 | संदर्भ के प्रति संवेदनशील | रैखिक-सीमित गैर-नियतात्मक ट्यूरिंग मशीन | |
| प्रारूप-2 | विषय से मुक्त | गैर-नियतात्मक | |
| प्रारूप-3 | नियमित | परिमित स्थिति ऑटोमेटन | और |
ऑटोमेटा सिद्धांत अमूर्त मशीनों (या अधिक उचित रूप से, अमूर्त 'गणितीय' मशीन या सिस्टम) और इन मशीनों का उपयोग करके हल की जा सकने वाली कम्प्यूटेशनल समस्याओं का अध्ययन है। इन अमूर्त मशीनों को ऑटोमेटा कहा जाता है। ऑटोमेटा ग्रीक शब्द (Αυτόματα) से आया है जिसका अर्थ है कि कोई चीज अपने आप कुछ कर रही है। ऑटोमेटा सिद्धांत भी औपचारिक भाषा सिद्धांत से निकटता से संबंधित है,[5] जैसा कि ऑटोमेटा को प्रायः औपचारिक भाषाओं के वर्ग द्वारा वर्गीकृत किया जाता है जिसे वे पहचानने में सक्षम होते हैं। एक ऑटोमेटों(स्वचल मशीन) एक औपचारिक भाषा का परिमित प्रतिनिधित्व हो सकता है जो एक अनंत समूह हो सकता है। ऑटोमेटा का उपयोग कंप्यूटिंग मशीनों के लिए सैद्धांतिक मॉडल के रूप में किया जाता है, और कम्प्यूटेबिलिटी के प्रमाण के लिए उपयोग किया जाता है।
औपचारिक भाषा सिद्धांत
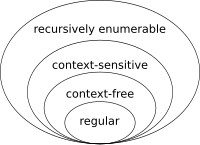
भाषा सिद्धांत गणित की एक शाखा है जो वर्णमाला पर संचालन के एक समूह के रूप में भाषाओं का वर्णन करने से संबंधित है। यह ऑटोमेटा सिद्धांत से निकटता से जुड़ा हुआ है, क्योंकि ऑटोमेटा का उपयोग औपचारिक भाषाओं को उत्पन्न करने और पहचानने के लिए किया जाता है। औपचारिक भाषाओं के कई वर्ग हैं, जिनमें से प्रत्येक अपने से पहले की तुलना में अधिक जटिल भाषा विनिर्देशों की अनुमति देता है, अर्थात चॉम्स्की पदानुक्रम,[6] और प्रत्येक ऑटोमेटा के एक वर्ग के अनुरूप है जो इसे पहचानता है। क्योंकि ऑटोमेटा का उपयोग गणना के लिए प्रारूप के रूप में किया जाता है, औपचारिक भाषाएं किसी भी समस्या के लिए विनिर्देशन का अधिमानित तरीका है जिसकी गणना की जानी चाहिए।
कम्प्यूटेबिलिटी सिद्धांत
कम्प्यूटेबिलिटी सिद्धांत मुख्य रूप से इस सवाल से संबंधित है कि कंप्यूटर पर किसी समस्या को किस सीमा तक हल किया जा सकता है। यह कथन कि हॉल्टिंग समस्या को ट्यूरिंग मशीन द्वारा हल नहीं किया जा सकता है[7] कम्प्यूटेबिलिटी सिद्धांत में सबसे महत्वपूर्ण परिणामों में से एक है, क्योंकि यह एक ठोस समस्या का एक उदाहरण है जिसे ट्यूरिंग मशीन का उपयोग करके हल करना आसान और असंभव दोनों है। अधिकांश कम्प्यूटेबिलिटी सिद्धांत हॉल्टिंग समस्या परिणाम पर आधारित है।
कम्प्यूटेबिलिटी सिद्धांत में एक और महत्वपूर्ण चरण राइस का प्रमेय था, जिसमें कहा गया है कि आंशिक कार्यों के सभी गैर-तुच्छ गुणों के लिए, यह अनिर्णीत है कि क्या एक ट्यूरिंग मशीन उस गुण के साथ एक आंशिक फ़ंक्शन की गणना करती है।[8]
संगणनीयता सिद्धांत गणितीय तर्क की शाखा से निकटता से संबंधित है जिसे पुनरावर्तन सिद्धांत कहा जाता है, जो गणना के केवल उन प्रारूपों का अध्ययन करने के प्रतिबंध को हटा देता है जो ट्यूरिंग प्रारूप के लिए कम हो जाते हैं।[9] कई गणितज्ञ और कम्प्यूटेशनल सिद्धांतकार जो पुनरावर्तन सिद्धांत का अध्ययन करते हैं, वे इसे कम्प्यूटेबिलिटी सिद्धांत के रूप में संदर्भित करेंगे।
कम्प्यूटेशनल जटिलता सिद्धांत
कम्प्यूटेशनल जटिलता सिद्धांत न केवल इस बात पर विचार करता है कि क्या किसी समस्या को कंप्यूटर पर हल किया जा सकता है, बल्कि यह भी कि समस्या को कितनी कुशलता से हल किया जा सकता है। दो प्रमुख पहलुओं पर विचार किया जाता है: समय की जटिलता और स्थान की जटिलता, जो क्रमशः एक संगणना करने में कितने चरण लगते हैं, और उस संगणना को करने के लिए कितनी मेमोरी की आवश्यकता होती है।
दिए गए एल्गोरिथम के लिए कितने समय और स्थान की आवश्यकता है, इसका विश्लेषण करने के लिए, कंप्यूटर वैज्ञानिक समस्या को हल करने के लिए आवश्यक समय या स्थान को इनपुट समस्या के आकार के कार्य के रूप में व्यक्त करते हैं। उदाहरण के लिए, संख्याओं की एक लंबी सूची में एक विशेष संख्या ढूँढना कठिन हो जाता है क्योंकि संख्याओं की सूची बड़ी हो जाती है। यदि हम कहते हैं कि सूची में n संख्याएँ हैं, तो यदि सूची को किसी भी तरह से क्रमबद्ध या अनुक्रमित नहीं किया गया है, तो हम जिस संख्या की तलाश कर रहे हैं, उसे खोजने के लिए हमें प्रत्येक संख्या को देखना पड़ सकता है। इस प्रकार हम कहते हैं कि इस समस्या को हल करने के लिए, कंप्यूटर को कई कदम उठाने की जरूरत है जो समस्या के आकार में रैखिक रूप से बढ़ते हैं।
इस समस्या को सरल बनाने के लिए, कंप्यूटर वैज्ञानिकों ने बिग ओ नोटेशन को अपनाया है, जो कार्यों की तुलना इस तरह से करने की अनुमति देता है जो यह सुनिश्चित करता है कि मशीन के निर्माण के विशेष पहलुओं पर विचार करने की आवश्यकता नहीं है, बल्कि समस्या के बड़े होने पर केवल स्पर्शोन्मुख व्यवहार पर विचार करने की आवश्यकता है। तो हमारे पिछले उदाहरण में, हम कह सकते हैं कि समस्या को हल करने के लिए चरणों की आवश्यकता है।
संभवतः कंप्यूटर विज्ञान में सबसे महत्वपूर्ण खुली समस्या यह सवाल है कि क्या एनपी को निरूपित समस्याओं के एक निश्चित व्यापक वर्ग को कुशलता से हल किया जा सकता है। इस पर आगे जटिलता पी और एनपी समस्या पर चर्चा की गई है, और पी बनाम एनपी समस्या 2000 में क्ले गणित संस्थान द्वारा बताए गए सात मिलेनियम पुरस्कार समस्याओं में से एक है। आधिकारिक समस्या विवरण ट्यूरिंग पुरस्कार विजेता स्टीफन कुक द्वारा दिया गया था।
गणना के मॉडल
एक ट्यूरिंग मशीन के अलावा, गणना के अन्य समकक्ष (देखें: चर्च-ट्यूरिंग थीसिस) मॉडल उपयोग में हैं।
लैम्ब्डा कैलकुलस
एक गणना में प्रारंभिक लैम्ब्डा अभिव्यक्ति होती है (या यदि दो आप फ़ंक्शन और उसके इनपुट को अलग करना चाहते हैं ) प्लस लैम्ब्डा शर्तों का एक सीमित अनुक्रम, प्रत्येक बीटा कटौती के एक आवेदन द्वारा पूर्ववर्ती अवधि से घटाया जाता है।
संयोजन तर्क
- एक अवधारणा है जिसमें कई समानताएं हैं -कैलकुलस, लेकिन महत्वपूर्ण अंतर भी निहित हैं (उदाहरण के लिए फिक्स्ड पॉइंट संयोजन वाई का संयोजन लॉजिक में सामान्य रूप है लेकिन इसमें -कैलकुलस नहीं है)। संयोजन तर्क को महान महत्वाकांक्षाओं के साथ विकसित किया गया था: विरोधाभासों की प्रकृति को समझना, गणित की नींव को अधिक आर्थिक (वैचारिक रूप से) बनाना, वेरिएबल्स की धारणा को समाप्त करना (इस प्रकार गणित में उनकी भूमिका को स्पष्ट करना)।
- μ-पुनरावर्ती फंक्शन्स
- एक संगणना में एक mu-पुनरावर्ती फ़ंक्शन होता है, अर्थात इसका परिभाषित क्रम, कोई भी इनपुट मान (एस) और पुनरावर्ती फंक्शन्स का एक क्रम इनपुट और आउटपुट के साथ परिभाषित अनुक्रम में दिखाई देता है। इस प्रकार, यदि पुनरावर्ती फ़ंक्शन के परिभाषित अनुक्रम में फ़ंक्शंस और प्रकट होते हैं, तो 'g(5)=7' या 'h(3,2)=10' रूप के पद प्रकट हो सकते हैं। इस क्रम में प्रत्येक प्रविष्टि को एक बुनियादी फ़ंक्शन का अनुप्रयोग होना चाहिए या फ़ंक्शन रचना, आदिम पुनरावर्तन या μ-पुनरावर्ती फ़ंक्शन का उपयोग करके ऊपर की प्रविष्टियों से अनुसरण करना चाहिए। उदाहरण के लिए अगर , फिर 'f(5)=3' के प्रकट होने के लिए, 'g(5)=6' और 'h(5,6)=3' जैसे शब्द ऊपर होने चाहिए। गणना तभी समाप्त होती है जब अंतिम शब्द इनपुट पर लागू पुनरावर्ती फ़ंक्शन का मान देता है।
मार्कोव एल्गोरिथम
एक स्ट्रिंग पुनर्लेखन प्रणाली जो प्रतीकों के स्ट्रिंग पर काम करने के लिए व्याकरण जैसे नियमों का उपयोग करती है।
रजिस्टर मशीन
- कंप्यूटर का एक सैद्धांतिक रूप से दिलचस्प आदर्शीकरण है। इसके कई प्रकार हैं। उनमें से अधिकांश में, प्रत्येक रजिस्टर में एक प्राकृतिक संख्या (असीमित आकार की) हो सकती है, और निर्देश सरल (और कुछ संख्या में) होते हैं, उदा केवल कमी (सशर्त पदोन्नति के साथ संयुक्त) और वृद्धि निहित है (और रोकना)। अनंत (या गतिशील रूप से बढ़ते) बाहरी स्टोर (ट्यूरिंग मशीनों पर देखा गया) की कमी को गोडेल नंबरिंग तकनीकों के साथ अपनी भूमिका को बदलकर समझा जा सकता है: तथ्य यह है कि प्रत्येक रजिस्टर में एक प्राकृतिक संख्या होती है जो एक जटिल चीज़ का प्रतिनिधित्व करने की संभावना की अनुमति देती है (उदाहरण के लिए एक अनुक्रम, या एक मैट्रिक्स आदि) एक उपयुक्त विशाल प्राकृतिक संख्या द्वारा - इन तकनीकों की संख्या सिद्धांत नींव द्वारा प्रतिनिधित्व और व्याख्या दोनों की अस्पष्टता स्थापित की जा सकती है।
सामान्य कम्प्यूटेशनल मॉडल के अतिरिक्त, कुछ सरल कम्प्यूटेशनल मॉडल विशेष, प्रतिबंधित अनुप्रयोगों के लिए उपयोगी होते हैं। नियमित अभिव्यक्तियाँ, उदाहरण के लिए, कार्यालय उत्पादकता सॉफ़्टवेयर से लेकर प्रोग्रामिंग भाषाओं तक, कई संदर्भों में स्ट्रिंग पैटर्न निर्दिष्ट करती हैं। गणितीय रूप से नियमित अभिव्यक्ति के समतुल्य एक अन्य औपचारिकता, परिमित स्वचल मशीनों का उपयोग सर्किट डिजाइन और कुछ प्रकार की समस्या-समाधान में किया जाता है। प्रसंग-मुक्त व्याकरण प्रोग्रामिंग भाषा सिंटैक्स निर्दिष्ट करते हैं। गैर-नियतात्मक पुशडाउन ऑटोमेटन संदर्भ-मुक्त व्याकरण के समकक्ष एक अन्य औपचारिकता है। आदिम पुनरावर्ती कार्य पुनरावर्ती कार्यों के एक परिभाषित उपवर्ग हैं।
गणना के विभिन्न मॉडलों में विभिन्न कार्यों को करने की क्षमता होती है। कम्प्यूटेशनल मॉडल की शक्ति को मापने का एक तरीका औपचारिक भाषाओं की कक्षा का अध्ययन करना है जो मॉडल उत्पन्न कर सकता है; इस तरह भाषाओं के चॉम्स्की पदानुक्रम को प्राप्त किया जाता है।
संदर्भ
- ↑ Michael Sipser (2013). Introduction to the Theory of Computation 3rd. Cengage Learning. ISBN 978-1-133-18779-0.
central areas of the theory of computation: automata, computability, and complexity. (Page 1)
- ↑ Hodges, Andrew (2012). Alan Turing: The Enigma (The Centenary ed.). Princeton University Press. ISBN 978-0-691-15564-7.
- ↑ Rabin, Michael O. (June 2012). Turing, Church, Gödel, Computability, Complexity and Randomization: A Personal View.
- ↑ Donald Monk (1976). गणितीय तर्क. Springer-Verlag. ISBN 9780387901701.
- ↑ Hopcroft, John E. and Jeffrey D. Ullman (2006). Introduction to Automata Theory, Languages, and Computation. 3rd ed. Reading, MA: Addison-Wesley. ISBN 978-0-321-45536-9.
- ↑ Chomsky hierarchy (1956). "भाषा के वर्णन के लिए तीन मॉडल". Information Theory, IRE Transactions on. IEEE. 2 (3): 113–124. doi:10.1109/TIT.1956.1056813.
- ↑ Alan Turing (1937). "Entscheidungsproblem के लिए एक आवेदन के साथ, संगणनीय संख्याओं पर". Proceedings of the London Mathematical Society. IEEE. 2 (42): 230–265. doi:10.1112/plms/s2-42.1.230. S2CID 73712. Retrieved 6 January 2015.
- ↑ Henry Gordon Rice (1953). "रिकर्सिवली एन्युमरेबल सेट्स की कक्षाएं और उनकी निर्णय समस्याएं". Transactions of the American Mathematical Society. American Mathematical Society. 74 (2): 358–366. doi:10.2307/1990888. JSTOR 1990888.
- ↑ Martin Davis (2004). The undecidable: Basic papers on undecidable propositions, unsolvable problems and computable functions (Dover Ed). Dover Publications. ISBN 978-0486432281.
अग्रिम पठन
- Textbooks aimed at computer scientists
(There are many textbooks in this area; this list is by necessity incomplete.)
- Hopcroft, John E., and Jeffrey D. Ullman (2006). Introduction to Automata Theory, Languages, and Computation. 3rd ed Reading, MA: Addison-Wesley. ISBN 978-0-321-45536-9 One of the standard references in the field.
- Linz P (2007). An introduction to formal language and automata. Narosa Publishing. ISBN 9788173197819.
- Michael Sipser (2013). Introduction to the Theory of Computation (3rd ed.). Cengage Learning. ISBN 978-1-133-18779-0.
- Eitan Gurari (1989). An Introduction to the Theory of Computation. Computer Science Press. ISBN 0-7167-8182-4. Archived from the original on 2007-01-07.
- Hein, James L. (1996) Theory of Computation. Sudbury, MA: Jones & Bartlett. ISBN 978-0-86720-497-1 A gentle introduction to the field, appropriate for second-year undergraduate computer science students.
- Taylor, R. Gregory (1998). Models of Computation and Formal Languages. New York: Oxford University Press. ISBN 978-0-19-510983-2 An unusually readable textbook, appropriate for upper-level undergraduates or beginning graduate students.
- Lewis, F. D. (2007). Essentials of theoretical computer science A textbook covering the topics of formal languages, automata and grammars. The emphasis appears to be on presenting an overview of the results and their applications rather than providing proofs of the results.
- Martin Davis, Ron Sigal, Elaine J. Weyuker, Computability, complexity, and languages: fundamentals of theoretical computer science, 2nd ed., Academic Press, 1994, ISBN 0-12-206382-1. Covers a wider range of topics than most other introductory books, including program semantics and quantification theory. Aimed at graduate students.
- Books on computability theory from the (wider) mathematical perspective
- Hartley Rogers, Jr (1987). Theory of Recursive Functions and Effective Computability, MIT Press. ISBN 0-262-68052-1
- S. Barry Cooper (2004). Computability Theory. Chapman and Hall/CRC. ISBN 1-58488-237-9..
- Carl H. Smith, A recursive introduction to the theory of computation, Springer, 1994, ISBN 0-387-94332-3. A shorter textbook suitable for graduate students in Computer Science.
- Historical perspective
- Richard L. Epstein and Walter A. Carnielli (2000). Computability: Computable Functions, Logic, and the Foundations of Mathematics, with Computability: A Timeline (2nd ed.). Wadsworth/Thomson Learning. ISBN 0-534-54644-7..
बाहरी संबंध
- Theory of Computation at MIT
- Theory of Computation at Harvard
- Computability Logic - A theory of interactive computation. The main web source on this subject.
{{Navbox
| name =गणित के क्षेत्र
|state = collapsed
| title =अंक शास्त्र | bodyclass = hlist
|above =
| group1 = नींव
| list1 =* श्रेणी सिद्धांत
| group2 =बीजगणित | list2 =* सार
| group3 = विश्लेषण | list3 =* पथरी
- वास्तविक विश्लेषण
- जटिल विश्लेषण
- हाइपरकम्प्लेक्स विश्लेषण
- अंतर समीकरण
- कार्यात्मक विश्लेषण
- हार्मोनिक विश्लेषण
- माप सिद्धांत
| group4 = असतत | list4 =* कॉम्बीनेटरिक्स
| group5 =ज्यामिति | list5 =* बीजगणितीय
| group6 =संख्या सिद्धांत | list6 =* अंकगणित
| group7 =टोपोलॉजी | list7 =* सामान्य
| group8 = लागू | list8 =* इंजीनियरिंग गणित
- गणितीय जीव विज्ञान
- गणितीय रसायन विज्ञान
- गणितीय अर्थशास्त्र
- गणितीय वित्त
- गणितीय भौतिकी
- गणितीय मनोविज्ञान
- गणितीय समाजशास्त्र
- गणितीय सांख्यिकी
- संभावना
- सांख्यिकी
- सिस्टम साइंस
| group9 = कम्प्यूटेशनल | list9 =* कंप्यूटर विज्ञान
| group10 = संबंधित विषय | list10 =* अनौपचारिक गणित
| below =* '
}}