सममित अंतर: Difference between revisions
(→गुण) |
No edit summary |
||
| (33 intermediate revisions by 3 users not shown) | |||
| Line 11: | Line 11: | ||
}} | }} | ||
गणित में, दो [[सेट (गणित)| | गणित में, दो [[सेट (गणित)|समुच्चयो (गणित)]] का सममित अंतर, जिसे वियोगात्मक संघ के रूप में भी जाना जाता है, उन तत्वों का समूह होता है जो किसी भी समुच्चय में होते हैं, लेकिन उनके प्रतिच्छेदन (समुच्चय सिद्धांत) में नहीं होते हैं। उदाहरण के लिए, समुच्चय का सममित अंतर <math>\{1,2,3\}</math> और <math>\{3,4\}</math> है <math>\{1,2,4\}</math>. | ||
समुच्चय A और B के सममितीय अंतर को सामान्यतया निरूपित किया जाता है <math>A \ominus B,</math> या <math>A\operatorname \triangle B.</math><ref name=":0">{{Cite web|last=Taylor|first=Courtney|date=March 31, 2019|title=What Is Symmetric Difference in Math?|url=https://www.thoughtco.com/what-is-the-symmetric-difference-3126594|access-date=2020-09-05|website=ThoughtCo|language=en}}</ref><ref>{{Cite web|last=Weisstein|first=Eric W.|title=सममित अंतर|url=https://mathworld.wolfram.com/SymmetricDifference.html|access-date=2020-09-05|website=mathworld.wolfram.com|language=en}}</ref><ref>https://en.wiktionary.org/wiki/symmetric_difference {{User-generated source|date=June 2022}}</ref> | समुच्चय A और B के सममितीय अंतर को सामान्यतया निरूपित किया जाता है <math>A \ominus B,</math> या <math>A\operatorname \triangle B.</math><ref name=":0">{{Cite web|last=Taylor|first=Courtney|date=March 31, 2019|title=What Is Symmetric Difference in Math?|url=https://www.thoughtco.com/what-is-the-symmetric-difference-3126594|access-date=2020-09-05|website=ThoughtCo|language=en}}</ref><ref>{{Cite web|last=Weisstein|first=Eric W.|title=सममित अंतर|url=https://mathworld.wolfram.com/SymmetricDifference.html|access-date=2020-09-05|website=mathworld.wolfram.com|language=en}}</ref><ref>https://en.wiktionary.org/wiki/symmetric_difference {{User-generated source|date=June 2022}}</ref> | ||
सममित अंतर के संचालन के तहत किसी भी | सममित अंतर के संचालन के तहत किसी भी समुच्चय का [[ सत्ता स्थापित |घात समुच्चय]] के [[तटस्थ तत्व]] के रूप में [[खाली सेट|रिक्त समुच्चय]] के साथ एक [[एबेलियन समूह|क्रमविनिमेय समूह]] बन जाता है और इस समूह में प्रत्येक तत्व का अपना व्युत्क्रम होता है। किसी भी समुच्चय का घात समुच्चय एक [[बूलियन रिंग]] बन जाता है, जिसमें रिंग के गुणन के रूप में रिंग और [[ चौराहा (सेट सिद्धांत) |प्रतिच्छेदन (समुच्चय सिद्धांत)]] के जोड़ के रूप में सममित अंतर होता है। | ||
== गुण == | == गुण == | ||
[[File:Venn 0110 1001.svg|thumb|का वेन आरेख <math>~(A \triangle B) \triangle C</math> | [[File:Venn 0110 1001.svg|thumb|का वेन आरेख <math>~(A \triangle B) \triangle C</math> | ||
{{nowrap|[[File:Venn 0110 0110.svg|40px]] <math>~\triangle~</math> [[File:Venn 0000 1111.svg|40px]]}} <math>~=~</math> [[File:Venn 0110 1001.svg|40px]]]]सममित अंतर दोनों [[पूरक (सेट सिद्धांत)]] के [[संघ (सेट सिद्धांत)]] के बराबर है, अर्थात:<ref name=":0" /> | {{nowrap|[[File:Venn 0110 0110.svg|40px]] <math>~\triangle~</math> [[File:Venn 0000 1111.svg|40px]]}} <math>~=~</math> [[File:Venn 0110 1001.svg|40px]]]]सममित अंतर दोनों [[पूरक (सेट सिद्धांत)|पूरक (समुच्चय सिद्धांत)]] के [[संघ (सेट सिद्धांत)|संघ (समुच्चय सिद्धांत)]] के बराबर होता है, अर्थात:<ref name=":0" /> | ||
:<math>A\,\triangle\,B = \left(A \setminus B\right) \cup \left(B \setminus A\right),</math> | :<math>A\,\triangle\,B = \left(A \setminus B\right) \cup \left(B \setminus A\right),</math> | ||
[[सेट-बिल्डर नोटेशन]] में दो | [[सेट-बिल्डर नोटेशन|समुच्चय-बिल्डर नोटेशन]] में दो समुच्चयों का वर्णन करने वाले [[विधेय (गणितीय तर्क)]] पर [[एकमात्र|एक्सक्लूसिव डिसजंक्शन एक तार्किक]] संचालन ⊕ का उपयोग करके सममित अंतर भी व्यक्त किया जा सकता है: | ||
:<math>A\mathbin{\triangle}B = \{x : (x \in A) \oplus (x \in B)\}.</math> | :<math>A\mathbin{\triangle}B = \{x : (x \in A) \oplus (x \in B)\}.</math> | ||
उसी तथ्य को संकेतक | उसी तथ्य को संकेतक फलन के रूप में कहा जा सकता है (यहाँ <math>\chi</math> द्वारा दर्शाया गया है ) सममित अंतर का, इसके दो तर्कों के संकेतक फलन का एक्सओआर (या अतिरिक्त [[मॉड्यूलर अंकगणित|मॉड्यूलर अंकगणितय प्रणाली]]) होना: <math>\chi_{(A\,\triangle\,B)} = \chi_A \oplus \chi_B</math> या [[आइवरसन ब्रैकेट]] नोटेशन का उपयोग करना <math>[x \in A\,\triangle\,B] = [x \in A] \oplus [x \in B]</math>. | ||
सममित अंतर को दो | सममित अंतर को दो समुच्चयो (गणित) के मिलन के रूप में भी व्यक्त किया जा सकता है, उनके प्रतिच्छेदन (समुच्चय सिद्धांत) को घटाकर: | ||
:<math>A\,\triangle\,B = (A \cup B) \setminus (A \cap B),</math><ref name=":0" /> | :<math>A\,\triangle\,B = (A \cup B) \setminus (A \cap B),</math><ref name=":0" /> | ||
विशेष रूप से, <math>A \mathbin{\triangle} B\subseteq A\cup B</math>; इस गैर-सख्त [[सबसेट]] में समानता तब होती है जब और केवल अगर <math>A</math> और <math>B</math> असंयुक्त समुच्चय हैं। इसके अलावा, निरूपण <math>D = A \mathbin{\triangle} B</math> और <math>I = A \cap B</math>, तब <math>D</math> और <math>I</math> हमेशा अलग होते हैं, इसलिए <math>D</math> और <math>I</math> [[एक सेट का विभाजन]] <math>A \cup B</math>. नतीजतन, | विशेष रूप से, <math>A \mathbin{\triangle} B\subseteq A\cup B</math>; इस गैर-सख्त [[सबसेट|उप-समूचय]] में समानता तब होती है जब और केवल अगर <math>A</math> और <math>B</math> असंयुक्त समुच्चय हैं। इसके अलावा, निरूपण <math>D = A \mathbin{\triangle} B</math> और <math>I = A \cap B</math>, तब <math>D</math> और <math>I</math> हमेशा अलग होते हैं, इसलिए <math>D</math> और <math>I</math> [[एक सेट का विभाजन|एक समुच्चय का विभाजन]] <math>A \cup B</math>. नतीजतन, प्रतिच्छेदन (समुच्चय सिद्धांत) और सममित अंतर को आदिम संचालन के रूप में मानते हुए, दो समुच्चयो के मिलन को समानता के दाईं ओर सममित अंतर के संदर्भ में अच्छी तरह से परिभाषित किया जा सकता है | ||
:<math>A\,\cup\,B = (A\,\triangle\,B)\,\triangle\,(A \cap B)</math>. | :<math>A\,\cup\,B = (A\,\triangle\,B)\,\triangle\,(A \cap B)</math>. | ||
सममित अंतर[[ क्रमविनिमेयता ]]और [[ संबद्धता |साहचर्य]] है: | सममित अंतर [[ क्रमविनिमेयता |क्रमविनिमेयता]] और [[ संबद्धता |साहचर्य]] है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 42: | Line 42: | ||
(A\,\triangle\,B)\,\triangle\,C &= A\,\triangle\,(B\,\triangle\,C). | (A\,\triangle\,B)\,\triangle\,C &= A\,\triangle\,(B\,\triangle\,C). | ||
\end{align}</math> | \end{align}</math> | ||
रिक्त समुच्चय [[पहचान तत्व]] होता है, और प्रत्येक | रिक्त समुच्चय [[पहचान तत्व]] होता है, और प्रत्येक समुच्चय का अपना व्युत्क्रम होता है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
A\,\triangle\,\varnothing &= A, \\ | A\,\triangle\,\varnothing &= A, \\ | ||
A\,\triangle\,A &= \varnothing. | A\,\triangle\,A &= \varnothing. | ||
\end{align}</math> | \end{align}</math> | ||
इस प्रकार, सममित अंतर | इस प्रकार, सममित अंतर संचालन के तहत किसी भी समुच्चय X का घात समुच्चय एक एबेलियन समूह बन जाता है। (अधिक सामान्यतः, समुच्चय का कोई भी क्षेत्र संक्रिया के रूप में सममितीय अंतर के साथ एक समूह बनाता है।) एक समूह जिसमें प्रत्येक तत्व का अपना व्युत्क्रम होता है (या, समतुल्य रूप से, जिसमें प्रत्येक तत्व का क्रम (समूह सिद्धांत) 2 होता है) को कभी-कभी [[बूलियन समूह]] कहा जाता है;<ref name="GivantHalmos2009">{{cite book |last1=Givant |first1=Steven |last2=Halmos |first2=Paul |author-link2=Paul Halmos |year=2009 |title=बूलियन बीजगणित का परिचय|publisher=Springer Science & Business Media |isbn=978-0-387-40293-2 |page=6}}</ref><ref name="Humberstone2011">{{cite book |last=Humberstone |first=Lloyd |year=2011 |title=कनेक्टिव्स|url=https://archive.org/details/connectives00humb |url-access=limited |publisher=MIT Press |isbn=978-0-262-01654-4 |page=[https://archive.org/details/connectives00humb/page/n800 782]}}</ref> सममित अंतर ऐसे समूहों का एक आदिरूप उदाहरण प्रदान करता है। कभी-कभी बूलियन समूह को वास्तव में समुच्चय पर सममित अंतर संचालन के रूप में परिभाषित किया जाता है।<ref name="Rotman2010">{{cite book |last=Rotman |first=Joseph J. |year=2010 |title=उन्नत आधुनिक बीजगणित|publisher=American Mathematical Soc. |isbn=978-0-8218-4741-1 |page=19}}</ref> ऐसे स्थितियों में जहां X में केवल दो तत्व हैं, इस प्रकार प्राप्त समूह [[क्लेन चार-समूह]] होता है। | ||
समतुल्य रूप से, एक बूलियन समूह एक [[प्राथमिक एबेलियन समूह | समतुल्य रूप से, एक बूलियन समूह एक [[प्राथमिक एबेलियन समूह|प्राथमिक एबेलियन 2-समूह]] है। नतीजतन, सममित अंतर से प्रेरित समूह वास्तव में 2 तत्वों '''Z'''<sub>2</sub> के साथ [[परिमित क्षेत्र]] पर एक सदिश स्थान है। यदि X परिमित है, तो [[सिंगलटन (गणित)]] इस सदिश स्थान का एक [[आधार (रैखिक बीजगणित)]] बनाते हैं, और इसका [[हेमल आयाम]] इसलिए X के तत्वों की संख्या के बराबर होता है। आरेख के [[चक्र स्थान]] को परिभाषित करने के लिए इस निर्माण का उपयोग [[ग्राफ सिद्धांत|आरेख सिद्धांत]] में किया जाता है। | ||
बूलियन समूह में व्युत्क्रम के गुण से, यह निम्नानुसार है कि दो दोहराए गए सममित अंतरों का सममित अंतर दो बहुसमुच्चय के जुड़ने से दोहराए गए सममित अंतर के बराबर होता है। जहां प्रत्येक दोहरे समुच्चय के लिए दोनों को हटाया जा सकता है। विशेष रूप से: | |||
:<math>(A\,\triangle\,B)\,\triangle\,(B\,\triangle\,C) = A\,\triangle\,C.</math> | :<math>(A\,\triangle\,B)\,\triangle\,(B\,\triangle\,C) = A\,\triangle\,C.</math> | ||
इसका तात्पर्य त्रिभुज असमानता है:<ref>{{cite book |last1=Rudin |first1=Walter |date=January 1, 1976 |title=गणितीय विश्लेषण के सिद्धांत|url=https://archive.org/details/principlesofmath00rudi |url-access=registration |edition=3rd |publisher=McGraw-Hill Education |isbn=978-0070542358 |page=[https://archive.org/details/principlesofmath00rudi/page/306 306]}}</ref> A और C का सममित अंतर A और B के सममित अंतर और B और C के सममित अंतर के मिलन में | इसका तात्पर्य त्रिभुज असमानता है:<ref>{{cite book |last1=Rudin |first1=Walter |date=January 1, 1976 |title=गणितीय विश्लेषण के सिद्धांत|url=https://archive.org/details/principlesofmath00rudi |url-access=registration |edition=3rd |publisher=McGraw-Hill Education |isbn=978-0070542358 |page=[https://archive.org/details/principlesofmath00rudi/page/306 306]}}</ref> A और C का सममित अंतर A और B के सममित अंतर और B और C के सममित अंतर के मिलन में समाहित है। | ||
सममित अंतर पर | प्रतिच्छेदन (समुच्चय सिद्धांत) सममित अंतर पर [[वितरण]] करता है: | ||
:<math>A \cap (B\,\triangle\,C) = (A \cap B)\,\triangle\,(A \cap C),</math> | :<math>A \cap (B\,\triangle\,C) = (A \cap B)\,\triangle\,(A \cap C),</math> | ||
और इससे पता चलता है कि X का पावर | और इससे पता चलता है कि X का पावर समुच्चय एक वलय (गणित में, बीजगणितीय संरचनाएँ) बन जाता है, जिसमें गुणा के रूप में जोड़ और प्रतिच्छेदन (समुच्चय सिद्धांत) के रूप में सममित अंतर होता है। यह बूलियन वलय का आदिरूप उदाहरण है। | ||
सममित अंतर के | सममित अंतर के गुणों में सम्मलित हैं: | ||
* <math>A \mathbin{\triangle} B = \emptyset</math> अगर और केवल अगर <math>A = B</math>. | * <math>A \mathbin{\triangle} B = \emptyset</math> अगर और केवल अगर <math>A = B</math>. | ||
* <math>A \mathbin{\triangle} B = A^c \mathbin{\triangle} B^c</math>, | * <math>A \mathbin{\triangle} B = A^c \mathbin{\triangle} B^c</math>, जहां <math>A^c</math>, <math>B^c</math> है <math>A</math> का पूरक, <math>B</math> का पूरक, क्रमशः, किसी भी (निश्चित) समुच्चय के सापेक्ष जिसमें दोनों सम्मलित हैं। | ||
* <math>\left(\bigcup_{\alpha\in\mathcal{I}}A_\alpha\right)\triangle\left(\bigcup_{\alpha\in\mathcal{I}}B_\alpha\right)\subseteq\bigcup_{\alpha\in\mathcal{I}}\left(A_\alpha \mathbin{\triangle} B_\alpha\right)</math>, | * <math>\left(\bigcup_{\alpha\in\mathcal{I}}A_\alpha\right)\triangle\left(\bigcup_{\alpha\in\mathcal{I}}B_\alpha\right)\subseteq\bigcup_{\alpha\in\mathcal{I}}\left(A_\alpha \mathbin{\triangle} B_\alpha\right)</math>, जहां <math>\mathcal{I}</math> एक इच्छानुसार अरिक्त सूचकांक समुच्चय है। | ||
* अगर <math>f : S \rightarrow T</math> कोई | * अगर <math>f : S \rightarrow T</math> कोई भी फलन है और <math>A, B \subseteq T</math> किसी भी समुच्चय में है <math>f</math> का कोडोमेन हैं, फिर <math>f^{-1}\left(A \mathbin{\triangle} B\right) = f^{-1}\left(A\right) \mathbin{\triangle} f^{-1}\left(B\right).</math> | ||
सममित अंतर को किसी भी [[बूलियन बीजगणित (संरचना)]] में लिखकर परिभाषित किया जा सकता है | सममित अंतर को किसी भी [[बूलियन बीजगणित (संरचना)]] में लिखकर परिभाषित किया जा सकता है | ||
:<math> x\,\triangle\,y = (x \lor y) \land \lnot(x \land y) = (x \land \lnot y) \lor (y \land \lnot x) = x \oplus y.</math> | :<math> x\,\triangle\,y = (x \lor y) \land \lnot(x \land y) = (x \land \lnot y) \lor (y \land \lnot x) = x \oplus y.</math> | ||
इस | इस संचालन में समुच्चय के सममित अंतर के समान गुण होते हैं। | ||
== एन-एरी सममित अंतर == | == एन-एरी सममित अंतर == | ||
दोहराए गए सममित अंतर एक अर्थ में समुच्चय के एक बहुसमुच्चय पर एक संचालन के बराबर है जो विषम संख्या में समुच्चय वाले तत्वों का एक समुच्चय देता है। | |||
ऊपर के रूप में, | ऊपर के रूप में, समुच्चय के संग्रह के सममित अंतर में केवल तत्व होते हैं जो संग्रह में समुच्चय की विषम संख्या में होते हैं:<math display="block">\triangle M = \left\{ a \in \bigcup M: \left|\{A \in M:a \in A\}\right| \text{ is odd}\right\}.</math>यह केवल तभी अच्छी तरह से परिभाषित होता है जब संघ के प्रत्येक तत्व <math display="inline">\bigcup M</math> के तत्वों की एक सीमित संख्या द्वारा योगदान दिया जाता है <math>M</math>. | ||
<math display="block">\triangle M = \left\{ a \in \bigcup M: \left|\{A \in M:a \in A\}\right| \text{ is odd}\right\}.</math> | |||
कल्पना करना <math>M = \left\{M_1, M_2, \ldots, M_n\right\}</math> एक | कल्पना करना <math>M = \left\{M_1, M_2, \ldots, M_n\right\}</math> एक बहुसमुच्चय है और <math>n \ge 2</math>. फिर इसके लिए एक सूत्र है <math>|\triangle M|</math>, में तत्वों की संख्या <math>\triangle M</math>, केवल तत्वों के प्रतिच्छेदन (समुच्चय सिद्धांत ) के संदर्भ में दिया गया है <math>M</math>:<math display="block">|\triangle M| = \sum_{l=1}^n (-2)^{l-1} \sum_{1 \leq i_1 < i_2 < \ldots < i_l \leq n} \left|M_{i_1} \cap M_{i_2} \cap \ldots \cap M_{i_l}\right|.</math> | ||
<math display="block">|\triangle M| = \sum_{l=1}^n (-2)^{l-1} \sum_{1 \leq i_1 < i_2 < \ldots < i_l \leq n} \left|M_{i_1} \cap M_{i_2} \cap \ldots \cap M_{i_l}\right|.</math> | |||
== माप रिक्त स्थान पर सममित अंतर == | |||
जब तक एक समुच्चय "कितना बड़ा" है, तब तक दो समुच्चयों के बीच सममित अंतर को एक उपाय माना जा सकता है कि वे कितने "दूर" हैं। | |||
पहले एक परिमित समुच्चय S पर विचार करें और उनके आकार द्वारा दिए गए उपसमुच्चय पर गिनती माप हैं। अब S के दो उपसमुच्चयों पर विचार करें और उनकी दूरी को उनके सममित अंतर के आकार के रूप में समुच्चय करें। यह दूरी वास्तव में एक [[मीट्रिक (गणित)]] है, जो एस के घात समुच्चय को एक [[मीट्रिक स्थान]] बनाती है। यदि S में n अवयव हैं, तो रिक्त समुच्चय से S तक की दूरी n है, और यह उपसमुच्चयों के किसी भी युग्म के लिए अधिकतम दूरी है <ref>Claude Flament (1963) ''Applications of Graph Theory to Group Structure'', page 16, [[Prentice-Hall]] {{mr|id=0157785}}</ref> | |||
[[माप सिद्धांत]] के विचारों का उपयोग करते हुए, मापने योग्य समुच्चयों के पृथक्करण को उनके सममित अंतर के माप के रूप में परिभाषित किया जा सकता है। यदि μ एक σ-सीमित माप है जो σ-बीजगणित Σ पर परिभाषित है, तो फलन | |||
[[माप सिद्धांत]] के विचारों का उपयोग करते हुए, मापने योग्य | |||
:<math>d_\mu(X, Y) = \mu(X\,\triangle\,Y)</math> | :<math>d_\mu(X, Y) = \mu(X\,\triangle\,Y)</math> | ||
Σ पर | Σ पर स्यूडोमेट्रिक स्थान है। ''d<sub>μ</sub>'' एक मीट्रिक स्थान बन जाता है अगर Σ को [[तुल्यता संबंध]] X ~ Y माना जाता है यदि और केवल यदि <math>\mu(X\,\triangle\,Y) = 0</math>. इसे कभी-कभी फ्रेचेट-निकोडीम मीट्रिक कहा जाता है। परिणामी मीट्रिक स्थान [[वियोज्य स्थान]] है यदि और केवल यदि L<sup>2</sup>(μ) वियोज्य है। | ||
अगर <math>\mu(X), \mu(Y) < \infty</math>, अपने पास: <math>|\mu(X) - \mu(Y)| \leq \mu(X\,\triangle\,Y)</math>. वास्तव में, | अगर <math>\mu(X), \mu(Y) < \infty</math>, अपने पास: <math>|\mu(X) - \mu(Y)| \leq \mu(X\,\triangle\,Y)</math>. वास्तव में, | ||
| Line 99: | Line 96: | ||
&= \mu\left(X\, \triangle \, Y\right) | &= \mu\left(X\, \triangle \, Y\right) | ||
\end{align}</math> | \end{align}</math> | ||
अगर <math>S = \left(\Omega, \mathcal{A},\mu\right)</math> एक माप स्थान है और <math>F, G \in \mathcal{A}</math> मापने योग्य | अगर <math>S = \left(\Omega, \mathcal{A},\mu\right)</math> एक माप स्थान है और <math>F, G \in \mathcal{A}</math> मापने योग्य समुच्चय हैं, तो उनका सममित अंतर भी मापने योग्य है: <math>F \triangle G \in \mathcal{A}</math>. मापने योग्य समुच्चयों पर एक समतुल्य संबंध को परिभाषित कर सकते हैं <math>F</math> और <math>G</math> संबंधित हो अगर <math>\mu\left(F \triangle G\right) = 0</math>. तो इस संबंध को दर्शाया गया है <math>F = G\left[\mathcal{A}, \mu\right]</math>. | ||
दिया गया <math>\mathcal{D}, \mathcal{E} \subseteq \mathcal{A}</math>, | दिया गया <math>\mathcal{D}, \mathcal{E} \subseteq \mathcal{A}</math>, को लिखते है <math>\mathcal{D}\subseteq\mathcal{E}\left[\mathcal{A}, \mu\right]</math> यदि प्रत्येक के लिए <math>D\in\mathcal{D}</math> कुछ <math>E \in \mathcal{E}</math> ऐसा है कि <math>D = E\left[\mathcal{A}, \mu\right]</math>. संबंध <math>\subseteq\left[\mathcal{A}, \mu\right]</math>के उपसमुच्चयों के परिवार पर एक आंशिक क्रम है <math>\mathcal{A}</math>. | ||
हम लिखते हैं <math>\mathcal{D} = \mathcal{E}\left[\mathcal{A}, \mu\right]</math> अगर <math>\mathcal{D}\subseteq\mathcal{E}\left[\mathcal{A}, \mu\right]</math> और <math>\mathcal{E} \subseteq \mathcal{D}\left[\mathcal{A}, \mu\right]</math>. | हम लिखते हैं <math>\mathcal{D} = \mathcal{E}\left[\mathcal{A}, \mu\right]</math> अगर <math>\mathcal{D}\subseteq\mathcal{E}\left[\mathcal{A}, \mu\right]</math> और <math>\mathcal{E} \subseteq \mathcal{D}\left[\mathcal{A}, \mu\right]</math>. संबंध<math>= \left[\mathcal{A}, \mu\right]</math> के उपसमुच्चयों के बीच एक तुल्यता संबंध है <math>\mathcal{A}</math>. | ||
का सममित समापन <math>\mathcal{D}</math> | का सममित समापन <math>\mathcal{D}</math> सभी का संग्रह है <math>\mathcal{A}</math>-मापने योग्य समुच्चय हैं जो <math>= \left[\mathcal{A}, \mu\right]</math> कुछ के लिए <math>D \in \mathcal{D}</math>. का सममित समापन <math>\mathcal{D}</math> में सम्मलित हैं <math>\mathcal{D}</math>. अगर <math>\mathcal{D}</math> एक उप है <math>\sigma</math>-बीजगणित का <math>\mathcal{A}</math>, तो सममित समापन है <math>\mathcal{D}</math>. | ||
<math>F = G\left[\mathcal{A}, \mu\right]</math> आईएफएफ <math>\left|\mathbf{1}_F - \mathbf{1}_G\right| = 0</math> <math>\left[\mathcal{A}, \mu\right]</math> [[लगभग हर जगह]]। | <math>F = G\left[\mathcal{A}, \mu\right]</math> आईएफएफ <math>\left|\mathbf{1}_F - \mathbf{1}_G\right| = 0</math> <math>\left[\mathcal{A}, \mu\right]</math> [[लगभग हर जगह]]। | ||
== हॉसडॉर्फ दूरी बनाम सममित अंतर == | == हॉसडॉर्फ दूरी बनाम सममित अंतर == | ||
[[File:HausdorffVsSymmetric.png|thumb|right]][[हॉसडॉर्फ दूरी]] और (क्षेत्र) सममित अंतर मापने योग्य ज्यामितीय आकृतियों के | [[File:HausdorffVsSymmetric.png|thumb|right]][[हॉसडॉर्फ दूरी]] और (क्षेत्र) सममित अंतर मापने योग्य ज्यामितीय आकृतियों के समुच्चय पर दोनों सूडो-मेट्रिक्स हैं। चूंकि, वे काफी अलग व्यवहार करते हैं। दाईं ओर का आंकड़ा आकृतियों के दो अनुक्रमों को दिखाता है, "लाल" और "लाल ∪ हरा"। जब उनके बीच हॉसडॉर्फ की दूरी कम हो जाती है, तो उनके बीच सममित अंतर का क्षेत्र बड़ा हो जाता है, और जो इसके विपरीत भी सम्भव हैं। इन अनुक्रमों को दोनों दिशाओं में जारी रखते हुए, दो अनुक्रम प्राप्त करना संभव है जैसे कि उनके बीच हॉसडॉर्फ की दूरी 0 में परिवर्तित हो जाती है और उनके बीच की सममित दूरी अलग हो जाती है, या जो इसके विपरीत भी सम्भव हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 136: | Line 133: | ||
== ग्रन्थसूची == | == ग्रन्थसूची == | ||
*{{cite book |last= | *{{cite book |last=हेल्मोस |first=पॉल आर. |author-link=हेल्मोस |year=1960 |title=[[नेव सेट थ्योरी (पुस्तक)|नेव सेट थ्योरी]] |series=स्नातक गणित में विश्वविद्यालय श्रृंखला |publisher=वैन नोस्ट्रैंड कंपनी |zbl=0087.04403}} | ||
*[http://www.encyclopediaofmath.org/index.php/Symmetric_difference_of_sets '' | *[http://www.encyclopediaofmath.org/index.php/Symmetric_difference_of_sets ''समुच्चय का सममित अंतर'']. In [[Encyclopaedia of Mathematics|गणित का विश्वकोश]] | ||
{{Set theory}} | {{Set theory}} | ||
[[Category: | [[Category:Accuracy disputes from June 2022]] | ||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 01/05/2023]] | [[Category:Created On 01/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:घटाव]] | |||
[[Category:सेट थ्योरी में बुनियादी अवधारणाएँ]] | |||
[[Category:सेट पर संचालन]] | |||
Latest revision as of 12:19, 18 May 2023
 | |
| Type | Set operation |
|---|---|
| Field | Set theory |
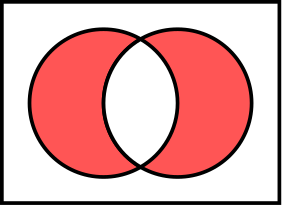
| Statement | The symmetric difference is the set of elements that are in either set, but not in the intersection. |
| Symbolic statement | |
गणित में, दो समुच्चयो (गणित) का सममित अंतर, जिसे वियोगात्मक संघ के रूप में भी जाना जाता है, उन तत्वों का समूह होता है जो किसी भी समुच्चय में होते हैं, लेकिन उनके प्रतिच्छेदन (समुच्चय सिद्धांत) में नहीं होते हैं। उदाहरण के लिए, समुच्चय का सममित अंतर और है .
समुच्चय A और B के सममितीय अंतर को सामान्यतया निरूपित किया जाता है या [1][2][3]
सममित अंतर के संचालन के तहत किसी भी समुच्चय का घात समुच्चय के तटस्थ तत्व के रूप में रिक्त समुच्चय के साथ एक क्रमविनिमेय समूह बन जाता है और इस समूह में प्रत्येक तत्व का अपना व्युत्क्रम होता है। किसी भी समुच्चय का घात समुच्चय एक बूलियन रिंग बन जाता है, जिसमें रिंग के गुणन के रूप में रिंग और प्रतिच्छेदन (समुच्चय सिद्धांत) के जोड़ के रूप में सममित अंतर होता है।
गुण
सममित अंतर दोनों पूरक (समुच्चय सिद्धांत) के संघ (समुच्चय सिद्धांत) के बराबर होता है, अर्थात:[1]
समुच्चय-बिल्डर नोटेशन में दो समुच्चयों का वर्णन करने वाले विधेय (गणितीय तर्क) पर एक्सक्लूसिव डिसजंक्शन एक तार्किक संचालन ⊕ का उपयोग करके सममित अंतर भी व्यक्त किया जा सकता है:
उसी तथ्य को संकेतक फलन के रूप में कहा जा सकता है (यहाँ द्वारा दर्शाया गया है ) सममित अंतर का, इसके दो तर्कों के संकेतक फलन का एक्सओआर (या अतिरिक्त मॉड्यूलर अंकगणितय प्रणाली) होना: या आइवरसन ब्रैकेट नोटेशन का उपयोग करना .
सममित अंतर को दो समुच्चयो (गणित) के मिलन के रूप में भी व्यक्त किया जा सकता है, उनके प्रतिच्छेदन (समुच्चय सिद्धांत) को घटाकर:
विशेष रूप से, ; इस गैर-सख्त उप-समूचय में समानता तब होती है जब और केवल अगर और असंयुक्त समुच्चय हैं। इसके अलावा, निरूपण और , तब और हमेशा अलग होते हैं, इसलिए और एक समुच्चय का विभाजन . नतीजतन, प्रतिच्छेदन (समुच्चय सिद्धांत) और सममित अंतर को आदिम संचालन के रूप में मानते हुए, दो समुच्चयो के मिलन को समानता के दाईं ओर सममित अंतर के संदर्भ में अच्छी तरह से परिभाषित किया जा सकता है
- .
सममित अंतर क्रमविनिमेयता और साहचर्य है:
रिक्त समुच्चय पहचान तत्व होता है, और प्रत्येक समुच्चय का अपना व्युत्क्रम होता है:
इस प्रकार, सममित अंतर संचालन के तहत किसी भी समुच्चय X का घात समुच्चय एक एबेलियन समूह बन जाता है। (अधिक सामान्यतः, समुच्चय का कोई भी क्षेत्र संक्रिया के रूप में सममितीय अंतर के साथ एक समूह बनाता है।) एक समूह जिसमें प्रत्येक तत्व का अपना व्युत्क्रम होता है (या, समतुल्य रूप से, जिसमें प्रत्येक तत्व का क्रम (समूह सिद्धांत) 2 होता है) को कभी-कभी बूलियन समूह कहा जाता है;[4][5] सममित अंतर ऐसे समूहों का एक आदिरूप उदाहरण प्रदान करता है। कभी-कभी बूलियन समूह को वास्तव में समुच्चय पर सममित अंतर संचालन के रूप में परिभाषित किया जाता है।[6] ऐसे स्थितियों में जहां X में केवल दो तत्व हैं, इस प्रकार प्राप्त समूह क्लेन चार-समूह होता है।
समतुल्य रूप से, एक बूलियन समूह एक प्राथमिक एबेलियन 2-समूह है। नतीजतन, सममित अंतर से प्रेरित समूह वास्तव में 2 तत्वों Z2 के साथ परिमित क्षेत्र पर एक सदिश स्थान है। यदि X परिमित है, तो सिंगलटन (गणित) इस सदिश स्थान का एक आधार (रैखिक बीजगणित) बनाते हैं, और इसका हेमल आयाम इसलिए X के तत्वों की संख्या के बराबर होता है। आरेख के चक्र स्थान को परिभाषित करने के लिए इस निर्माण का उपयोग आरेख सिद्धांत में किया जाता है।
बूलियन समूह में व्युत्क्रम के गुण से, यह निम्नानुसार है कि दो दोहराए गए सममित अंतरों का सममित अंतर दो बहुसमुच्चय के जुड़ने से दोहराए गए सममित अंतर के बराबर होता है। जहां प्रत्येक दोहरे समुच्चय के लिए दोनों को हटाया जा सकता है। विशेष रूप से:
इसका तात्पर्य त्रिभुज असमानता है:[7] A और C का सममित अंतर A और B के सममित अंतर और B और C के सममित अंतर के मिलन में समाहित है।
प्रतिच्छेदन (समुच्चय सिद्धांत) सममित अंतर पर वितरण करता है:
और इससे पता चलता है कि X का पावर समुच्चय एक वलय (गणित में, बीजगणितीय संरचनाएँ) बन जाता है, जिसमें गुणा के रूप में जोड़ और प्रतिच्छेदन (समुच्चय सिद्धांत) के रूप में सममित अंतर होता है। यह बूलियन वलय का आदिरूप उदाहरण है।
सममित अंतर के गुणों में सम्मलित हैं:
- अगर और केवल अगर .
- , जहां , है का पूरक, का पूरक, क्रमशः, किसी भी (निश्चित) समुच्चय के सापेक्ष जिसमें दोनों सम्मलित हैं।
- , जहां एक इच्छानुसार अरिक्त सूचकांक समुच्चय है।
- अगर कोई भी फलन है और किसी भी समुच्चय में है का कोडोमेन हैं, फिर
सममित अंतर को किसी भी बूलियन बीजगणित (संरचना) में लिखकर परिभाषित किया जा सकता है
इस संचालन में समुच्चय के सममित अंतर के समान गुण होते हैं।
एन-एरी सममित अंतर
दोहराए गए सममित अंतर एक अर्थ में समुच्चय के एक बहुसमुच्चय पर एक संचालन के बराबर है जो विषम संख्या में समुच्चय वाले तत्वों का एक समुच्चय देता है।
ऊपर के रूप में, समुच्चय के संग्रह के सममित अंतर में केवल तत्व होते हैं जो संग्रह में समुच्चय की विषम संख्या में होते हैं:
कल्पना करना एक बहुसमुच्चय है और . फिर इसके लिए एक सूत्र है , में तत्वों की संख्या , केवल तत्वों के प्रतिच्छेदन (समुच्चय सिद्धांत ) के संदर्भ में दिया गया है :
माप रिक्त स्थान पर सममित अंतर
जब तक एक समुच्चय "कितना बड़ा" है, तब तक दो समुच्चयों के बीच सममित अंतर को एक उपाय माना जा सकता है कि वे कितने "दूर" हैं।
पहले एक परिमित समुच्चय S पर विचार करें और उनके आकार द्वारा दिए गए उपसमुच्चय पर गिनती माप हैं। अब S के दो उपसमुच्चयों पर विचार करें और उनकी दूरी को उनके सममित अंतर के आकार के रूप में समुच्चय करें। यह दूरी वास्तव में एक मीट्रिक (गणित) है, जो एस के घात समुच्चय को एक मीट्रिक स्थान बनाती है। यदि S में n अवयव हैं, तो रिक्त समुच्चय से S तक की दूरी n है, और यह उपसमुच्चयों के किसी भी युग्म के लिए अधिकतम दूरी है [8]
माप सिद्धांत के विचारों का उपयोग करते हुए, मापने योग्य समुच्चयों के पृथक्करण को उनके सममित अंतर के माप के रूप में परिभाषित किया जा सकता है। यदि μ एक σ-सीमित माप है जो σ-बीजगणित Σ पर परिभाषित है, तो फलन
Σ पर स्यूडोमेट्रिक स्थान है। dμ एक मीट्रिक स्थान बन जाता है अगर Σ को तुल्यता संबंध X ~ Y माना जाता है यदि और केवल यदि . इसे कभी-कभी फ्रेचेट-निकोडीम मीट्रिक कहा जाता है। परिणामी मीट्रिक स्थान वियोज्य स्थान है यदि और केवल यदि L2(μ) वियोज्य है।
अगर , अपने पास: . वास्तव में,
अगर एक माप स्थान है और मापने योग्य समुच्चय हैं, तो उनका सममित अंतर भी मापने योग्य है: . मापने योग्य समुच्चयों पर एक समतुल्य संबंध को परिभाषित कर सकते हैं और संबंधित हो अगर . तो इस संबंध को दर्शाया गया है .
दिया गया , को लिखते है यदि प्रत्येक के लिए कुछ ऐसा है कि . संबंध के उपसमुच्चयों के परिवार पर एक आंशिक क्रम है .
हम लिखते हैं अगर और . संबंध के उपसमुच्चयों के बीच एक तुल्यता संबंध है .
का सममित समापन सभी का संग्रह है -मापने योग्य समुच्चय हैं जो कुछ के लिए . का सममित समापन में सम्मलित हैं . अगर एक उप है -बीजगणित का , तो सममित समापन है .
आईएफएफ लगभग हर जगह।
हॉसडॉर्फ दूरी बनाम सममित अंतर
हॉसडॉर्फ दूरी और (क्षेत्र) सममित अंतर मापने योग्य ज्यामितीय आकृतियों के समुच्चय पर दोनों सूडो-मेट्रिक्स हैं। चूंकि, वे काफी अलग व्यवहार करते हैं। दाईं ओर का आंकड़ा आकृतियों के दो अनुक्रमों को दिखाता है, "लाल" और "लाल ∪ हरा"। जब उनके बीच हॉसडॉर्फ की दूरी कम हो जाती है, तो उनके बीच सममित अंतर का क्षेत्र बड़ा हो जाता है, और जो इसके विपरीत भी सम्भव हैं। इन अनुक्रमों को दोनों दिशाओं में जारी रखते हुए, दो अनुक्रम प्राप्त करना संभव है जैसे कि उनके बीच हॉसडॉर्फ की दूरी 0 में परिवर्तित हो जाती है और उनके बीच की सममित दूरी अलग हो जाती है, या जो इसके विपरीत भी सम्भव हैं।
यह भी देखें
- सेट का बीजगणित
- बूलियन समारोह
- पूरक (सेट सिद्धांत)
- अंतर (सेट सिद्धांत)
- एकमात्र
- फजी सेट
- चौराहा (सेट सिद्धांत)
- जैकार्ड इंडेक्स
- निर्धारित पहचान और संबंधों की सूची
- तार्किक ग्राफ
- सिग्मा-बीजगणित # वियोज्य .CF.83-बीजगणित
- समुच्चय सिद्धान्त
- समरूपता
- संघ (सेट सिद्धांत)
- समावेश-बहिष्करण सिद्धांत
संदर्भ
- ↑ 1.0 1.1 1.2 Taylor, Courtney (March 31, 2019). "What Is Symmetric Difference in Math?". ThoughtCo (in English). Retrieved 2020-09-05.
- ↑ Weisstein, Eric W. "सममित अंतर". mathworld.wolfram.com (in English). Retrieved 2020-09-05.
- ↑ https://en.wiktionary.org/wiki/symmetric_difference[user-generated source]
- ↑ Givant, Steven; Halmos, Paul (2009). बूलियन बीजगणित का परिचय. Springer Science & Business Media. p. 6. ISBN 978-0-387-40293-2.
- ↑ Humberstone, Lloyd (2011). कनेक्टिव्स. MIT Press. p. 782. ISBN 978-0-262-01654-4.
- ↑ Rotman, Joseph J. (2010). उन्नत आधुनिक बीजगणित. American Mathematical Soc. p. 19. ISBN 978-0-8218-4741-1.
- ↑ Rudin, Walter (January 1, 1976). गणितीय विश्लेषण के सिद्धांत (3rd ed.). McGraw-Hill Education. p. 306. ISBN 978-0070542358.
- ↑ Claude Flament (1963) Applications of Graph Theory to Group Structure, page 16, Prentice-Hall MR0157785
ग्रन्थसूची
- हेल्मोस, पॉल आर. (1960). नेव सेट थ्योरी. स्नातक गणित में विश्वविद्यालय श्रृंखला. वैन नोस्ट्रैंड कंपनी. Zbl 0087.04403.
- समुच्चय का सममित अंतर. In गणित का विश्वकोश


