Line 368:
Line 368: ==बाहरी संबंध==
==बाहरी संबंध==
* [http://mathworld.wolfram.com/VectorSphericalHarmonic.html ''Vector Spherical Harmonics'' at Eric Weisstein's Mathworld]
* [http://mathworld.wolfram.com/VectorSphericalHarmonic.html ''Vector Spherical Harmonics'' at Eric Weisstein's Mathworld]
[[Category: वेक्टर पथरी]] [[Category: विशेष कार्य]] [[Category: विभेदक समीकरण]] [[Category: व्यावहारिक गणित]] [[Category: सैद्धांतिक भौतिकी]]
[[Category: Machine Translated Page]]
[[Category:Created On 12/05/2023]]
[[Category:Created On 12/05/2023]]
[[Category:Vigyan Ready]]
[[Category:Lua-based templates]]
[[Category:Machine Translated Page]]
[[Category:Pages with script errors]]
[[Category:Templates Vigyan Ready]]
[[Category:Templates that add a tracking category]]
[[Category:Templates that generate short descriptions]]
[[Category:Templates using TemplateData]]
[[Category:विभेदक समीकरण]]
[[Category:विशेष कार्य]]
[[Category:वेक्टर पथरी]]
[[Category:व्यावहारिक गणित]]
[[Category:सैद्धांतिक भौतिकी ]]
गणित में, सदिश गोलीय प्रसंवादी (वीएसएच) सदिश क्षेत्रों के उपयोग के लिए अदिश गोलीय प्रसंवादी का विस्तार है। वीएसएच के घटक गोलीय समन्वय प्रणाली में व्यक्त जटिल-मानित फलन हैं।
परिभाषा वीएसएच को परिभाषित करने के लिए कई परिपाटी का उपयोग किया गया है।[1] [2] [3] [4] [5] गोलीय प्रसंवादी Yℓm (θ , φ )
Y ℓ m = Y ℓ m r ^ , {\displaystyle \mathbf {Y} _{\ell m}=Y_{\ell m}{\hat {\mathbf {r} }},} Ψ ℓ m = r ∇ Y ℓ m , {\displaystyle \mathbf {\Psi } _{\ell m}=r\nabla Y_{\ell m},} Φ ℓ m = r × ∇ Y ℓ m , {\displaystyle \mathbf {\Phi } _{\ell m}=\mathbf {r} \times \nabla Y_{\ell m},} जिसमें r ^ {\displaystyle {\hat {\mathbf {r} }}} इकाई सदिश है और r {\displaystyle \mathbf {r} } r = r r ^ {\displaystyle \mathbf {r} =r{\hat {\mathbf {r} }}}
गोलीय निर्देशांक का उपयोग करते समय इन नवीन सदिश क्षेत्रों का हित त्रिज्यीय निर्भरता को कोणीय से अलग करना है, ताकि एक सदिश क्षेत्र बहुध्रुव विस्तार
E = ∑ ℓ = 0 ∞ ∑ m = − ℓ ℓ ( E ℓ m r ( r ) Y ℓ m + E ℓ m ( 1 ) ( r ) Ψ ℓ m + E ℓ m ( 2 ) ( r ) Φ ℓ m ) {\displaystyle \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left(E_{\ell m}^{r}(r)\mathbf {Y} _{\ell m}+E_{\ell m}^{(1)}(r)\mathbf {\Psi } _{\ell m}+E_{\ell m}^{(2)}(r)\mathbf {\Phi } _{\ell m}\right)} को स्वीकार कर सके।
घटकों पर लेबल यह दर्शाते हैं कि E ℓ m r {\displaystyle E_{\ell m}^{r}} E ℓ m ( 1 ) {\displaystyle E_{\ell m}^{(1)}} E ℓ m ( 2 ) {\displaystyle E_{\ell m}^{(2)}} r {\displaystyle \mathbf {r} }
मुख्य गुण समरूपता अदिश गोलीय प्रसंवादी के जैसे, वीएसएच
Y ℓ , − m = ( − 1 ) m Y ℓ m ∗ , Ψ ℓ , − m = ( − 1 ) m Ψ ℓ m ∗ , Φ ℓ , − m = ( − 1 ) m Φ ℓ m ∗ , {\displaystyle {\begin{aligned}\mathbf {Y} _{\ell ,-m}&=(-1)^{m}\mathbf {Y} _{\ell m}^{*},\\\mathbf {\Psi } _{\ell ,-m}&=(-1)^{m}\mathbf {\Psi } _{\ell m}^{*},\\\mathbf {\Phi } _{\ell ,-m}&=(-1)^{m}\mathbf {\Phi } _{\ell m}^{*},\end{aligned}}}
को संतुष्ट करता है जो स्वतंत्र फलनों की संख्या को लगभग आधा कर देता है। तारा जटिल संयुग्म को इंगित करता है।
लंबकोणीयता वीएसएच प्रत्येक बिंदु r {\displaystyle \mathbf {r} } लांबिक फलन हैं :
Y ℓ m ( r ) ⋅ Ψ ℓ m ( r ) = 0 , Y ℓ m ( r ) ⋅ Φ ℓ m ( r ) = 0 , Ψ ℓ m ( r ) ⋅ Φ ℓ m ( r ) = 0. {\displaystyle {\begin{aligned}\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Psi } _{\ell m}(\mathbf {r} )&=0,\\\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell m}(\mathbf {r} )&=0,\\\mathbf {\Psi } _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell m}(\mathbf {r} )&=0.\end{aligned}}}
वे हिल्बर्ट समष्टि में भी लांबिक हैं:
∫ Y ℓ m ⋅ Y ℓ ′ m ′ ∗ d Ω = δ ℓ ℓ ′ δ m m ′ , ∫ Ψ ℓ m ⋅ Ψ ℓ ′ m ′ ∗ d Ω = ℓ ( ℓ + 1 ) δ ℓ ℓ ′ δ m m ′ , ∫ Φ ℓ m ⋅ Φ ℓ ′ m ′ ∗ d Ω = ℓ ( ℓ + 1 ) δ ℓ ℓ ′ δ m m ′ , ∫ Y ℓ m ⋅ Ψ ℓ ′ m ′ ∗ d Ω = 0 , ∫ Y ℓ m ⋅ Φ ℓ ′ m ′ ∗ d Ω = 0 , ∫ Ψ ℓ m ⋅ Φ ℓ ′ m ′ ∗ d Ω = 0. {\displaystyle {\begin{aligned}\int \mathbf {Y} _{\ell m}\cdot \mathbf {Y} _{\ell 'm'}^{*}\,d\Omega &=\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {\Psi } _{\ell m}\cdot \mathbf {\Psi } _{\ell 'm'}^{*}\,d\Omega &=\ell (\ell +1)\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {\Phi } _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=\ell (\ell +1)\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {Y} _{\ell m}\cdot \mathbf {\Psi } _{\ell 'm'}^{*}\,d\Omega &=0,\\\int \mathbf {Y} _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=0,\\\int \mathbf {\Psi } _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=0.\end{aligned}}}
एकल
r {\displaystyle \mathbf {r} } पर अतिरिक्त परिणाम (बैरेरा एट अल, 1985 में रिपोर्ट नहीं किया गया) सभी
ℓ , m , ℓ ′ , m ′ {\displaystyle \ell ,m,\ell ',m'} ,
Y ℓ m ( r ) ⋅ Ψ ℓ ′ m ′ ( r ) = 0 , Y ℓ m ( r ) ⋅ Φ ℓ ′ m ′ ( r ) = 0 {\displaystyle {\begin{aligned}\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Psi } _{\ell 'm'}(\mathbf {r} )&=0,\\\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell 'm'}(\mathbf {r} )&=0\end{aligned}}} के लिए है।
सदिश बहुध्रुव आघूर्ण लंबकोणीयता संबंध किसी को सदिश क्षेत्र के गोलीय बहुध्रुव आघूर्ण को
E ℓ m r = ∫ E ⋅ Y ℓ m ∗ d Ω , E ℓ m ( 1 ) = 1 ℓ ( ℓ + 1 ) ∫ E ⋅ Ψ ℓ m ∗ d Ω , E ℓ m ( 2 ) = 1 ℓ ( ℓ + 1 ) ∫ E ⋅ Φ ℓ m ∗ d Ω {\displaystyle {\begin{aligned}E_{\ell m}^{r}&=\int \mathbf {E} \cdot \mathbf {Y} _{\ell m}^{*}\,d\Omega ,\\E_{\ell m}^{(1)}&={\frac {1}{\ell (\ell +1)}}\int \mathbf {E} \cdot \mathbf {\Psi } _{\ell m}^{*}\,d\Omega ,\\E_{\ell m}^{(2)}&={\frac {1}{\ell (\ell +1)}}\int \mathbf {E} \cdot \mathbf {\Phi } _{\ell m}^{*}\,d\Omega \end{aligned}}} के रूप में परिकलित करने की अनुमति देते हैं।
एक अदिश क्षेत्र की प्रवणता एक अदिश क्षेत्र
ϕ = ∑ ℓ = 0 ∞ ∑ m = − ℓ ℓ ϕ ℓ m ( r ) Y ℓ m ( θ , ϕ ) , {\displaystyle \phi =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\phi _{\ell m}(r)Y_{\ell m}(\theta ,\phi ),}
के बहुध्रुव विस्तार को देखते हुए, हम वीएसएच के संदर्भ में
∇ ϕ = ∑ ℓ = 0 ∞ ∑ m = − ℓ ℓ ( d ϕ ℓ m d r Y ℓ m + ϕ ℓ m r Ψ ℓ m ) {\displaystyle \nabla \phi =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {d\phi _{\ell m}}{dr}}\mathbf {Y} _{\ell m}+{\frac {\phi _{\ell m}}{r}}\mathbf {\Psi } _{\ell m}\right)} के रूप में इसकी प्रवणता व्यक्त कर सकते हैं।
विचलन किसी भी बहुध्रुवीय क्षेत्र के लिए हमारे निकट
∇ ⋅ ( f ( r ) Y ℓ m ) = ( d f d r + 2 r f ) Y ℓ m , ∇ ⋅ ( f ( r ) Ψ ℓ m ) = − ℓ ( ℓ + 1 ) r f Y ℓ m , ∇ ⋅ ( f ( r ) Φ ℓ m ) = 0 {\displaystyle {\begin{aligned}\nabla \cdot \left(f(r)\mathbf {Y} _{\ell m}\right)&=\left({\frac {df}{dr}}+{\frac {2}{r}}f\right)Y_{\ell m},\\\nabla \cdot \left(f(r)\mathbf {\Psi } _{\ell m}\right)&=-{\frac {\ell (\ell +1)}{r}}fY_{\ell m},\\\nabla \cdot \left(f(r)\mathbf {\Phi } _{\ell m}\right)&=0\end{aligned}}} है।
अधिस्थापन द्वारा हम किसी भी सदिश क्षेत्र का विचलन प्राप्त करते हैं:
∇ ⋅ E = ∑ ℓ = 0 ∞ ∑ m = − ℓ ℓ ( d E ℓ m r d r + 2 r E ℓ m r − ℓ ( ℓ + 1 ) r E ℓ m ( 1 ) ) Y ℓ m . {\displaystyle \nabla \cdot \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {dE_{\ell m}^{r}}{dr}}+{\frac {2}{r}}E_{\ell m}^{r}-{\frac {\ell (\ell +1)}{r}}E_{\ell m}^{(1)}\right)Y_{\ell m}.}
हम देखते हैं कि
Φ ℓm पर घटक सदैव
परिनालिकीय होता है।
कर्ल किसी भी बहुध्रुवीय क्षेत्र के लिए हमारे निकट
∇ × ( f ( r ) Y ℓ m ) = − 1 r f Φ ℓ m , ∇ × ( f ( r ) Ψ ℓ m ) = ( d f d r + 1 r f ) Φ ℓ m , ∇ × ( f ( r ) Φ ℓ m ) = − ℓ ( ℓ + 1 ) r f Y ℓ m − ( d f d r + 1 r f ) Ψ ℓ m {\displaystyle {\begin{aligned}\nabla \times \left(f(r)\mathbf {Y} _{\ell m}\right)&=-{\frac {1}{r}}f\mathbf {\Phi } _{\ell m},\\\nabla \times \left(f(r)\mathbf {\Psi } _{\ell m}\right)&=\left({\frac {df}{dr}}+{\frac {1}{r}}f\right)\mathbf {\Phi } _{\ell m},\\\nabla \times \left(f(r)\mathbf {\Phi } _{\ell m}\right)&=-{\frac {\ell (\ell +1)}{r}}f\mathbf {Y} _{\ell m}-\left({\frac {df}{dr}}+{\frac {1}{r}}f\right)\mathbf {\Psi } _{\ell m}\end{aligned}}} है।
अध्यारोपण द्वारा हम किसी सदिश क्षेत्र का कर्ल (गणित) प्राप्त करते हैं:
∇ × E = ∑ ℓ = 0 ∞ ∑ m = − ℓ ℓ ( − ℓ ( ℓ + 1 ) r E ℓ m ( 2 ) Y ℓ m − ( d E ℓ m ( 2 ) d r + 1 r E ℓ m ( 2 ) ) Ψ ℓ m + ( − 1 r E ℓ m r + d E ℓ m ( 1 ) d r + 1 r E ℓ m ( 1 ) ) Φ ℓ m ) . {\displaystyle \nabla \times \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left(-{\frac {\ell (\ell +1)}{r}}E_{\ell m}^{(2)}\mathbf {Y} _{\ell m}-\left({\frac {dE_{\ell m}^{(2)}}{dr}}+{\frac {1}{r}}E_{\ell m}^{(2)}\right)\mathbf {\Psi } _{\ell m}+\left(-{\frac {1}{r}}E_{\ell m}^{r}+{\frac {dE_{\ell m}^{(1)}}{dr}}+{\frac {1}{r}}E_{\ell m}^{(1)}\right)\mathbf {\Phi } _{\ell m}\right).}
लाप्लासियन लाप्लास प्रचालक Δ = ∇ ⋅ ∇ {\displaystyle \Delta =\nabla \cdot \nabla }
Δ ( f ( r ) Z ℓ m ) = ( 1 r 2 ∂ ∂ r r 2 ∂ f ∂ r ) Z ℓ m + f ( r ) Δ Z ℓ m , {\displaystyle \Delta \left(f(r)\mathbf {Z} _{\ell m}\right)=\left({\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}r^{2}{\frac {\partial f}{\partial r}}\right)\mathbf {Z} _{\ell m}+f(r)\Delta \mathbf {Z} _{\ell m},}
जहां
Z ℓ m = Y ℓ m , Ψ ℓ m , Φ ℓ m {\displaystyle \mathbf {Z} _{\ell m}=\mathbf {Y} _{\ell m},\mathbf {\Psi } _{\ell m},\mathbf {\Phi } _{\ell m}} और
Δ Y ℓ m = − 1 r 2 ( 2 + ℓ ( ℓ + 1 ) ) Y ℓ m + 2 r 2 Ψ ℓ m , Δ Ψ ℓ m = 2 r 2 ℓ ( ℓ + 1 ) Y ℓ m − 1 r 2 ℓ ( ℓ + 1 ) Ψ ℓ m , Δ Φ ℓ m = − 1 r 2 ℓ ( ℓ + 1 ) Φ ℓ m . {\displaystyle {\begin{aligned}\Delta \mathbf {Y} _{\ell m}&=-{\frac {1}{r^{2}}}(2+\ell (\ell +1))\mathbf {Y} _{\ell m}+{\frac {2}{r^{2}}}\mathbf {\Psi } _{\ell m},\\\Delta \mathbf {\Psi } _{\ell m}&={\frac {2}{r^{2}}}\ell (\ell +1)\mathbf {Y} _{\ell m}-{\frac {1}{r^{2}}}\ell (\ell +1)\mathbf {\Psi } _{\ell m},\\\Delta \mathbf {\Phi } _{\ell m}&=-{\frac {1}{r^{2}}}\ell (\ell +1)\mathbf {\Phi } _{\ell m}.\end{aligned}}}
यह भी ध्यान दें कि यह क्रिया
सममित आव्यूह हो जाती है, अर्थात उचित सामान्यीकृत वीएसएच के लिए अप विकर्ण गुणांक
2 r 2 ℓ ( ℓ + 1 ) {\textstyle {\frac {2}{r^{2}}}{\sqrt {\ell (\ell +1)}}} के बराबर हैं।
उदाहरण पहला सदिश गोलीय प्रसंवादी ℓ = 0 {\displaystyle \ell =0} Y 00 = 1 4 π r ^ , Ψ 00 = 0 , Φ 00 = 0 . {\displaystyle {\begin{aligned}\mathbf {Y} _{00}&={\sqrt {\frac {1}{4\pi }}}{\hat {\mathbf {r} }},\\\mathbf {\Psi } _{00}&=\mathbf {0} ,\\\mathbf {\Phi } _{00}&=\mathbf {0} .\end{aligned}}} ℓ = 1 {\displaystyle \ell =1} Y 10 = 3 4 π cos θ r ^ , Y 11 = − 3 8 π e i φ sin θ r ^ , {\displaystyle {\begin{aligned}\mathbf {Y} _{10}&={\sqrt {\frac {3}{4\pi }}}\cos \theta \,{\hat {\mathbf {r} }},\\\mathbf {Y} _{11}&=-{\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\sin \theta \,{\hat {\mathbf {r} }},\end{aligned}}} Ψ 10 = − 3 4 π sin θ θ ^ , Ψ 11 = − 3 8 π e i φ ( cos θ θ ^ + i φ ^ ) , {\displaystyle {\begin{aligned}\mathbf {\Psi } _{10}&=-{\sqrt {\frac {3}{4\pi }}}\sin \theta \,{\hat {\mathbf {\theta } }},\\\mathbf {\Psi } _{11}&=-{\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\left(\cos \theta \,{\hat {\mathbf {\theta } }}+i\,{\hat {\mathbf {\varphi } }}\right),\end{aligned}}} Φ 10 = − 3 4 π sin θ φ ^ , Φ 11 = 3 8 π e i φ ( i θ ^ − cos θ φ ^ ) . {\displaystyle {\begin{aligned}\mathbf {\Phi } _{10}&=-{\sqrt {\frac {3}{4\pi }}}\sin \theta \,{\hat {\mathbf {\varphi } }},\\\mathbf {\Phi } _{11}&={\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\left(i\,{\hat {\mathbf {\theta } }}-\cos \theta \,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}} ℓ = 2 {\displaystyle \ell =2} Y 20 = 1 4 5 π ( 3 cos 2 θ − 1 ) r ^ , Y 21 = − 15 8 π sin θ cos θ e i φ r ^ , Y 22 = 1 4 15 2 π sin 2 θ e 2 i φ r ^ . {\displaystyle {\begin{aligned}\mathbf {Y} _{20}&={\frac {1}{4}}{\sqrt {\frac {5}{\pi }}}\,(3\cos ^{2}\theta -1)\,{\hat {\mathbf {r} }},\\\mathbf {Y} _{21}&=-{\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,\cos \theta \,e^{i\varphi }\,{\hat {\mathbf {r} }},\\\mathbf {Y} _{22}&={\frac {1}{4}}{\sqrt {\frac {15}{2\pi }}}\,\sin ^{2}\theta \,e^{2i\varphi }\,{\hat {\mathbf {r} }}.\end{aligned}}} Ψ 20 = − 3 2 5 π sin θ cos θ θ ^ , Ψ 21 = − 15 8 π e i φ ( cos 2 θ θ ^ + i cos θ φ ^ ) , Ψ 22 = 15 8 π sin θ e 2 i φ ( cos θ θ ^ + i φ ^ ) . {\displaystyle {\begin{aligned}\mathbf {\Psi } _{20}&=-{\frac {3}{2}}{\sqrt {\frac {5}{\pi }}}\,\sin \theta \,\cos \theta \,{\hat {\mathbf {\theta } }},\\\mathbf {\Psi } _{21}&=-{\sqrt {\frac {15}{8\pi }}}\,e^{i\varphi }\,\left(\cos 2\theta \,{\hat {\mathbf {\theta } }}+i\cos \theta \,{\hat {\mathbf {\varphi } }}\right),\\\mathbf {\Psi } _{22}&={\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,e^{2i\varphi }\,\left(\cos \theta \,{\hat {\mathbf {\theta } }}+i\,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}} Φ 20 = − 3 2 5 π sin θ cos θ φ ^ , Φ 21 = 15 8 π e i φ ( i cos θ θ ^ − cos 2 θ φ ^ ) , Φ 22 = 15 8 π sin θ e 2 i φ ( − i θ ^ + cos θ φ ^ ) . {\displaystyle {\begin{aligned}\mathbf {\Phi } _{20}&=-{\frac {3}{2}}{\sqrt {\frac {5}{\pi }}}\sin \theta \,\cos \theta \,{\hat {\mathbf {\varphi } }},\\\mathbf {\Phi } _{21}&={\sqrt {\frac {15}{8\pi }}}\,e^{i\varphi }\,\left(i\cos \theta \,{\hat {\mathbf {\theta } }}-\cos 2\theta \,{\hat {\mathbf {\varphi } }}\right),\\\mathbf {\Phi } _{22}&={\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,e^{2i\varphi }\,\left(-i\,{\hat {\mathbf {\theta } }}+\cos \theta \,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}} सममिति संबंधों को लागू करके m के ऋणात्मक मानों के लिए व्यंजक प्राप्त किए जाते हैं।
अनुप्रयोग विद्युतगतिकी वीएसएच बहुध्रुव विकिरण क्षेत्रों के अध्ययन में विशेष रूप से उपयोगी है। उदाहरण के लिए, एक चुंबकीय बहुध्रुव कोणीय आवृत्ति ω {\displaystyle \omega }
J ^ = J ( r ) Φ ℓ m {\displaystyle {\hat {\mathbf {J} }}=J(r)\mathbf {\Phi } _{\ell m}}
के साथ एक दोलन धारा के कारण होते है, और संबंधित विद्युत और चुंबकीय क्षेत्र,
E ^ = E ( r ) Φ ℓ m , B ^ = B r ( r ) Y ℓ m + B ( 1 ) ( r ) Ψ ℓ m {\displaystyle {\begin{aligned}{\hat {\mathbf {E} }}&=E(r)\mathbf {\Phi } _{\ell m},\\{\hat {\mathbf {B} }}&=B^{r}(r)\mathbf {Y} _{\ell m}+B^{(1)}(r)\mathbf {\Psi } _{\ell m}\end{aligned}}} के रूप में लिखे जा सकते हैं।
मैक्सवेल समीकरणों में प्रतिस्थापित करने पर, गॉस का नियम स्वचालित रूप से
∇ ⋅ E ^ = 0 {\displaystyle \nabla \cdot {\hat {\mathbf {E} }}=0}
संतुष्ट हो जाता है, जबकि फैराडे का नियम
∇ × E ^ = − i ω B ^ ⇒ { ℓ ( ℓ + 1 ) r E = i ω B r , d E d r + E r = i ω B ( 1 ) {\displaystyle \nabla \times {\hat {\mathbf {E} }}=-i\omega {\hat {\mathbf {B} }}\quad \Rightarrow \quad {\begin{cases}{\dfrac {\ell (\ell +1)}{r}}E=i\omega B^{r},\\{\dfrac {dE}{dr}}+{\dfrac {E}{r}}=i\omega B^{(1)}\end{cases}}} के रूप में अलग हो जाते है।
चुंबकीय क्षेत्र के लिए गॉस के नियम का अर्थ है
∇ ⋅ B ^ = 0 ⇒ d B r d r + 2 r B r − ℓ ( ℓ + 1 ) r B ( 1 ) = 0 , {\displaystyle \nabla \cdot {\hat {\mathbf {B} }}=0\quad \Rightarrow \quad {\frac {dB^{r}}{dr}}+{\frac {2}{r}}B^{r}-{\frac {\ell (\ell +1)}{r}}B^{(1)}=0,}
और एम्पीयर-मैक्सवेल का समीकरण
∇ × B ^ = μ 0 J ^ + i μ 0 ε 0 ω E ^ ⇒ − B r r + d B ( 1 ) d r + B ( 1 ) r = μ 0 J + i ω μ 0 ε 0 E {\displaystyle \nabla \times {\hat {\mathbf {B} }}=\mu _{0}{\hat {\mathbf {J} }}+i\mu _{0}\varepsilon _{0}\omega {\hat {\mathbf {E} }}\quad \Rightarrow \quad -{\frac {B^{r}}{r}}+{\frac {dB^{(1)}}{dr}}+{\frac {B^{(1)}}{r}}=\mu _{0}J+i\omega \mu _{0}\varepsilon _{0}E} देता है।
इस प्रकार, आंशिक अवकल समीकरण साधारण अवकल समीकरणों के समुच्चय में रूपांतरित हो गए हैं।
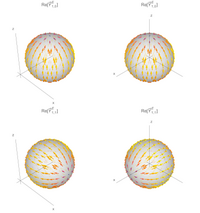
वैकल्पिक परिभाषा चुंबकीय और विद्युत सदिश गोलीय प्रसंवादी का कोणीय भाग। लाल और हरे तीर क्षेत्र की दिशा दिखाते हैं। अदिश फलन उत्पन्न करना भी प्रस्तुत किया जाता है, मात्र पहले तीन क्रम दिखाए जाते हैं (द्विध्रुवीय, चतुर्ध्रुवी, अष्टध्रुव)।
कई अनुप्रयोगों में, सदिश गोलीय प्रसंवादी को गोलीय निर्देशांक में सदिश हेल्महोल्त्ज़ समीकरण के हल के मौलिक समुच्चय के रूप में परिभाषित किया जाता है।[6] [7]
इस स्थिति में, सदिश गोलीय प्रसंवादी अदिश फलन द्वारा उत्पन्न होते हैं, जो तरंगसदिश k {\displaystyle \mathbf {k} }
ψ e m n = cos m φ P n m ( cos ϑ ) z n ( k r ) ψ o m n = sin m φ P n m ( cos ϑ ) z n ( k r ) {\displaystyle {\begin{array}{l}{\psi _{emn}=\cos m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}\\{\psi _{omn}=\sin m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}\end{array}}}
यहाँ
P n m ( cos θ ) {\displaystyle P_{n}^{m}(\cos \theta )} संबंधित लीजेंड्रे बहुपद हैं, और
z n ( k r ) {\displaystyle z_{n}({k}r)} कोई भी गोलीय बेसेल फलन हैं।
सदिश गोलीय प्रसंवादी को इस प्रकार परिभाषित किया गया है:
अनुदैर्ध्य प्रसंवादी
L o e m n = ∇ ψ o e m n {\displaystyle \mathbf {L} _{^{e}_{o}mn}=\mathbf {\nabla } \psi _{^{e}_{o}mn}} चुंबकीय प्रसंवादी
M o e m n = ∇ × ( r ψ o e m n ) {\displaystyle \mathbf {M} _{^{e}_{o}mn}=\nabla \times \left(\mathbf {r} \psi _{^{e}_{o}mn}\right)} विद्युतीय प्रसंवादी
N o e m n = ∇ × M o e m n k {\displaystyle \mathbf {N} _{^{e}_{o}mn}={\frac {\nabla \times \mathbf {M} _{^{e}_{o}mn}}{k}}} यहां हम प्रसंवादी वास्तविक-मानित कोणीय भाग का उपयोग करते हैं, जहां m ≥ 0 {\displaystyle m\geq 0}
आइए हम संकेतन ρ = k r {\displaystyle \rho =kr}
M e m n ( k , r ) = − m sin ( θ ) sin ( m φ ) P n m ( cos ( θ ) ) z n ( ρ ) e θ − cos ( m φ ) d P n m ( cos ( θ ) ) d θ z n ( ρ ) e φ {\displaystyle {\begin{aligned}{\mathbf {M} _{emn}(k,\mathbf {r} )=\qquad {{\frac {-m}{\sin(\theta )}}\sin(m\varphi )P_{n}^{m}(\cos(\theta ))}z_{n}(\rho )\mathbf {e} _{\theta }}\\{{}-\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}z_{n}(\rho )\mathbf {e} _{\varphi }\end{aligned}}} M o m n ( k , r ) = m sin ( θ ) cos ( m φ ) P n m ( cos ( θ ) ) z n ( ρ ) e θ − sin ( m φ ) d P n m ( cos ( θ ) ) d θ z n ( ρ ) e φ {\displaystyle {\begin{aligned}{\mathbf {M} _{omn}(k,\mathbf {r} )=\qquad {{\frac {m}{\sin(\theta )}}\cos(m\varphi )P_{n}^{m}(\cos(\theta ))}}z_{n}(\rho )\mathbf {e} _{\theta }\\{{}-\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}z_{n}(\rho )\mathbf {e} _{\varphi }}\end{aligned}}} N e m n ( k , r ) = z n ( ρ ) ρ cos ( m φ ) n ( n + 1 ) P n m ( cos ( θ ) ) e r + cos ( m φ ) d P n m ( cos ( θ ) ) d θ 1 ρ d d ρ [ ρ z n ( ρ ) ] e θ − m sin ( m φ ) P n m ( cos ( θ ) ) sin ( θ ) 1 ρ d d ρ [ ρ z n ( ρ ) ] e φ {\displaystyle {\begin{aligned}{\mathbf {N} _{emn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\cos(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }}\\{{}+\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{{}-m\sin(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}} N o m n ( k , r ) = z n ( ρ ) ρ sin ( m φ ) n ( n + 1 ) P n m ( cos ( θ ) ) e r + sin ( m φ ) d P n m ( cos ( θ ) ) d θ 1 ρ d d ρ [ ρ z n ( ρ ) ] e θ + m cos ( m φ ) P n m ( cos ( θ ) ) sin ( θ ) 1 ρ d d ρ [ ρ z n ( ρ ) ] e φ {\displaystyle {\begin{aligned}\mathbf {N} _{omn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\sin(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }\\{}+\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{}+{m\cos(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}
चुंबकीय प्रसंवादी के लिए कोई त्रिज्यीय भाग नहीं है। विद्युतीय प्रसंवादी के लिए, त्रिज्यीय भाग कोणीय से तीव्रता से घटता है, और बड़े
ρ {\displaystyle \rho } के लिए उपेक्षित किया जा सकता है। हम यह भी देख सकते हैं कि विद्युत और चुंबकीय प्रसंवादी के लिए ध्रुवीय और दिगंशीय इकाई सदिश के क्रमपरिवर्तन तक कोणीय भाग समान होते हैं, इसलिए बड़े
ρ {\displaystyle \rho } के लिए विद्युतीय और चुंबकीय प्रसंवादी सदिश एक दूसरे के मान और लंबवत के बराबर होते हैं।
अनुदैर्ध्य प्रसंवादी:
L o e m n ( k , r ) = ∂ ∂ r z n ( k r ) P n m ( cos θ ) sin cos m φ e r + 1 r z n ( k r ) ∂ ∂ θ P n m ( cos θ ) sin cos m φ e θ ∓ m r sin θ z n ( k r ) P n m ( cos θ ) cos sin m φ e φ {\displaystyle {\begin{aligned}\mathbf {L} _{^{e}_{o}{mn}}(k,\mathbf {r} ){}=\qquad &{\frac {\partial }{\partial r}}z_{n}(kr)P_{n}^{m}(\cos \theta ){^{\cos }_{\sin }}{m\varphi }\mathbf {e} _{r}\\{}+{}&{\frac {1}{r}}z_{n}(kr){\frac {\partial }{\partial \theta }}P_{n}^{m}(\cos \theta ){^{\cos }_{\sin }}m\varphi \mathbf {e} _{\theta }\\{}\mp {}&{\frac {m}{r\sin \theta }}z_{n}(kr)P_{n}^{m}(\cos \theta ){^{\sin }_{\cos }}m\varphi \mathbf {e} _{\varphi }\end{aligned}}}
लंबकोणीयता हेल्महोल्ट्ज़ सदिश समीकरण के हल निम्नलिखित लंबकोणीयता संबंधों का पालन करते हैं:[7]
∫ 0 2 π ∫ 0 π L o e m n ⋅ L o e m n sin ϑ d ϑ d φ = ( 1 + δ m , 0 ) 2 π ( 2 n + 1 ) 2 ( n + m ) ! ( n − m ) ! k 2 { n [ z n − 1 ( k r ) ] 2 + ( n + 1 ) [ z n + 1 ( k r ) ] 2 } ∫ 0 2 π ∫ 0 π M o e m n ⋅ M o e m n sin ϑ d ϑ d φ = ( 1 + δ m , 0 ) 2 π 2 n + 1 ( n + m ) ! ( n − m ) ! n ( n + 1 ) [ z n ( k r ) ] 2 ∫ 0 2 π ∫ 0 π
विभिन्न फलनों या विभिन्न सूचकांकों के साथ फलनों के बीच के कोणों पर अन्य सभी अभिन्न शून्य के बराबर हैं।
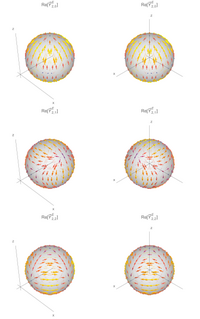
घूर्णन और व्युत्क्रमण घूर्णन के अंतर्गत सदिश गोलीय प्रसंवादी के परिवर्तन का चित्रण। कोई देख सकता है कि वे उसी प्रकार से रूपांतरित होते हैं जैसे संबंधित अदिश फलन।
घूर्णन के अंतर्गत, सदिश गोलीय प्रसंवादी एक दूसरे के माध्यम से उसी प्रकार से रूपांतरित होते हैं जैसे संबंधित गोलीय प्रसंवादी घूर्णन, जो एक विशिष्ट प्रकार के सदिश प्रसंवादी के लिए उत्पन्न होते हैं। उदाहरण के लिए, यदि उत्पादक फलन सामान्य गोलीय प्रसंवादी हैं, तो सदिश प्रसंवादी भी विग्नर डी-आव्यूह के माध्यम से रूपांतरित हो जाएंगे।[8] [9] [10]
D ^ ( α , β , γ ) Y J M ( s ) ( θ , φ ) = ∑ m ′ = − ℓ ℓ [ D M M ′ ( ℓ ) ( α , β , γ ) ] ∗ Y J M ′ ( s ) ( θ , φ ) , {\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )\mathbf {Y} _{JM}^{(s)}(\theta ,\varphi )=\sum _{m'=-\ell }^{\ell }[D_{MM'}^{(\ell )}(\alpha ,\beta ,\gamma )]^{*}\mathbf {Y} _{JM'}^{(s)}(\theta ,\varphi ),}
घूर्णन के अंतर्गत व्यवहार विद्युत, चुंबकीय और अनुदैर्ध्य प्रसंवादी के लिए समान है।
व्युत्क्रमण के अंतर्गत, विद्युत और अनुदैर्ध्य गोलीय प्रसंवादी उसी प्रकार व्यवहार करते हैं जैसे अदिश गोलीय फलन, अर्थात।
I ^ N J M ( θ , φ ) = ( − 1 ) J N J M ( θ , φ ) , {\displaystyle {\hat {I}}\mathbf {N} _{JM}(\theta ,\varphi )=(-1)^{J}\mathbf {N} _{JM}(\theta ,\varphi ),}
और चुंबकीय वाले विपरीत समानता रखते हैं:
I ^ M J M ( θ , φ ) = ( − 1 ) J + 1 M J M ( θ , φ ) , {\displaystyle {\hat {I}}\mathbf {M} _{JM}(\theta ,\varphi )=(-1)^{J+1}\mathbf {M} _{JM}(\theta ,\varphi ),}
द्रव गतिकी कर्षण के लिए स्टोक्स के नियम की गणना में कि एक श्यान द्रव एक छोटे गोलीय कण पर निकलते है, वेग वितरण जड़ता की उपेक्षा करते हुए नेवियर-स्टोक्स समीकरणों का पालन करते है, अर्थात।
0 = ∇ ⋅ v , 0 = − ∇ p + η ∇ 2 v , {\displaystyle {\begin{aligned}0&=\nabla \cdot \mathbf {v} ,\\\mathbf {0} &=-\nabla p+\eta \nabla ^{2}\mathbf {v} ,\end{aligned}}}
सीमा स्थितियों
v = { 0 r = a , − U 0 r → ∞ {\displaystyle \mathbf {v} ={\begin{cases}\mathbf {0} &r=a,\\-\mathbf {U} _{0}&r\to \infty \end{cases}}} के साथ।
जहाँ U, कण से दूर द्रव में कण का आपेक्षिक वेग है। गोलीय निर्देशांकों में अनंत पर इस वेग को
U 0 = U 0 ( cos θ r ^ − sin θ θ ^ ) = U 0 ( Y 10 + Ψ 10 ) {\displaystyle \mathbf {U} _{0}=U_{0}\left(\cos \theta \,{\hat {\mathbf {r} }}-\sin \theta \,{\hat {\mathbf {\theta } }}\right)=U_{0}\left(\mathbf {Y} _{10}+\mathbf {\Psi } _{10}\right)} के रूप में लिखा जा सकता है।
अंतिम अभिव्यक्ति तरल वेग और दाब
p = p ( r ) Y 10 , v = v r ( r ) Y 10 + v ( 1 ) ( r ) Ψ 10 {\displaystyle {\begin{aligned}p&=p(r)Y_{10},\\\mathbf {v} &=v^{r}(r)\mathbf {Y} _{10}+v^{(1)}(r)\mathbf {\Psi } _{10}\end{aligned}}} के लिए गोलीय प्रसंवादी में विस्तार का सुझाव देती है।
नेवियर-स्टोक्स समीकरणों में प्रतिस्थापन गुणांकों के लिए सामान्य अंतर समीकरणों के समुच्चय उत्पन्न करते है।
अभिन्न संबंध यहाँ निम्नलिखित परिभाषाओं का उपयोग किया जाता है:
Y e m n = cos m φ P n m ( cos θ ) Y o m n = sin m φ P n m ( cos θ ) {\displaystyle {\begin{aligned}Y_{emn}&=\cos m\varphi P_{n}^{m}(\cos \theta )\\Y_{omn}&=\sin m\varphi P_{n}^{m}(\cos \theta )\end{aligned}}} X o e m n ( k k ) = ∇ × ( k Y e o m n ( k k ) ) {\displaystyle \mathbf {X} _{^{e}_{o}mn}\left({\frac {\mathbf {k} }{k}}\right)=\nabla \times \left(\mathbf {k} Y_{^{o}_{e}mn}\left({\frac {\mathbf {k} }{k}}\right)\right)} Z e o m n ( k k ) = i k k × X o e m n ( k k ) {\displaystyle \mathbf {Z} _{^{o}_{e}mn}\left({\frac {\mathbf {k} }{k}}\right)=i{\frac {\mathbf {k} }{k}}\times \mathbf {X} _{^{e}_{o}mn}\left({\frac {\mathbf {k} }{k}}\right)}
स्थिति में, जब
z n {\displaystyle z_{n}} के अतिरिक्त गोलीय बेसेल फलन होते हैं, तो
समतल तरंग विस्तार की सहायता से निम्नलिखित अभिन्न संबंध प्राप्त किए जा सकते हैं:
[11]
N p m n ( k , r ) = i − n 4 π ∫ Z p m n ( k k ) e i k r d Ω k {\displaystyle \mathbf {N} _{pmn}(k,\mathbf {r} )={\frac {i^{-n}}{4\pi }}\int \mathbf {Z} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)e^{i\mathbf {k} \mathbf {r} }d\Omega _{k}} M p m n ( k , r ) = i − n 4 π ∫ X p m n ( k k ) e i k r d Ω k {\displaystyle \mathbf {M} _{pmn}(k,\mathbf {r} )={\frac {i^{-n}}{4\pi }}\int \mathbf {X} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)e^{i\mathbf {k} \mathbf {r} }d\Omega _{k}}
स्थिति में, जब
z n {\displaystyle z_{n}} गोलीय हैंकेल फलन होते हैं, तो विभिन्न सूत्रों का उपयोग करना चाहिए।
[12] [11] सदिश गोलीय प्रसंवादी के लिए निम्नलिखित संबंध प्राप्त होते हैं:
M p m n ( 3 ) ( k , r ) = i − n 2 π k ∬ − ∞ ∞ d k ‖ e i ( k x x + k y y ± k z z ) k z X p m n ( k k ) {\displaystyle \mathbf {M} _{pmn}^{(3)}(k,\mathbf {r} )={\frac {i^{-n}}{2\pi k}}\iint _{-\infty }^{\infty }dk_{\|}{\frac {e^{i\left(k_{x}x+k_{y}y\pm k_{z}z\right)}}{k_{z}}}\mathbf {X} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)} N p m n ( 3 ) ( k , r ) = i − n 2 π k ∬ − ∞ ∞ d k ‖ e i ( k x x + k y y ± k z z ) k z Z p m n ( k k ) {\displaystyle \mathbf {N} _{pmn}^{(3)}(k,\mathbf {r} )={\frac {i^{-n}}{2\pi k}}\iint _{-\infty }^{\infty }dk_{\|}{\frac {e^{i\left(k_{x}x+k_{y}y\pm k_{z}z\right)}}{k_{z}}}\mathbf {Z} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)}
जहां
k z = k 2 − k x 2 − k y 2 {\textstyle k_{z}={\sqrt {k^{2}-k_{x}^{2}-k_{y}^{2}}}} , अनुक्रमणिका
( 3 ) {\displaystyle (3)} का अर्थ है कि गोलीय हैंकेल फलनों का उपयोग किया जाता है।
यह भी देखें संदर्भ
↑ Barrera, R G; Estevez, G A; Giraldo, J (1985-10-01). "वेक्टर गोलाकार हार्मोनिक्स और मैग्नेटोस्टैटिक्स के लिए उनका अनुप्रयोग". European Journal of Physics . IOP Publishing. 6 (4): 287–294. Bibcode :1985EJPh....6..287B . CiteSeerX 10.1.1.718.2001 doi :10.1088/0143-0807/6/4/014 . ISSN 0143-0807 . S2CID 250894245 . ↑ Carrascal, B; Estevez, G A; Lee, Peilian; Lorenzo, V (1991-07-01). "वेक्टर गोलाकार हार्मोनिक्स और शास्त्रीय इलेक्ट्रोडायनामिक्स के लिए उनका अनुप्रयोग". European Journal of Physics . IOP Publishing. 12 (4): 184–191. Bibcode :1991EJPh...12..184C . doi :10.1088/0143-0807/12/4/007 . ISSN 0143-0807 . S2CID 250886412 . ↑ Hill, E. L. (1954). "वेक्टर गोलाकार हार्मोनिक्स का सिद्धांत" (PDF) . American Journal of Physics . American Association of Physics Teachers (AAPT). 22 (4): 211–214. Bibcode :1954AmJPh..22..211H . doi :10.1119/1.1933682 . ISSN 0002-9505 . S2CID 124182424 . Archived from the original (PDF) on 2020-04-12. ↑ Weinberg, Erick J. (1994-01-15). "मोनोपोल वेक्टर गोलाकार हार्मोनिक्स". Physical Review D . American Physical Society (APS). 49 (2): 1086–1092. arXiv :hep-th/9308054 Bibcode :1994PhRvD..49.1086W . doi :10.1103/physrevd.49.1086 . ISSN 0556-2821 . PMID 10017069 . S2CID 6429605 . ↑ P.M. Morse and H. Feshbach, Methods of Theoretical Physics, Part II , New York: McGraw-Hill, 1898-1901 (1953)
↑ Bohren, Craig F. and Donald R. Huffman, Absorption and scattering of light by small particles, New York : Wiley, 1998, 530 p., ISBN 0-471-29340-7 , ISBN 978-0-471-29340-8 (second edition)
↑ 7.0 7.1 Stratton, J. A. (1941). विद्युत चुम्बकीय सिद्धांत ↑ D. A. Varhalovich, A. N. Moskalev, and V. K. Khersonskii, Quantum Theory of Angular Momentum [in Russian], Nauka, Leningrad (1975)
↑ H. Zhang, Yi. Han, Addition theorem for the spherical vector wave functions and its application to the beam shape coeffcients. J. Opt. Soc. Am. B, 25(2):255-260, Feb 2008.
↑ S. Stein, Addition theorems for spherical wave functions , Quarterly of Applied Mathematics, 19(1):15-24, 1961.
↑ 11.0 11.1 B. Stout,Spherical harmonic lattice sums for gratings. In: Popov E, editor. Gratings: theory and numeric applications. Institut Fresnel, Universite d'Aix-Marseille 6 (2012). ↑ R. C. Wittmann, Spherical wave operators and the translation formulas, IEEE Transactions on Antennas and Propagation 36, 1078-1087 (1988)
बाहरी संबंध