वेक्टर क्षेत्र

सदिश क्षेत्र का एक भाग (sin y, sin x)

सदिश कलन और भौतिकी में, एक सदिश क्षेत्र (गणित) के उप-समूचय में प्रत्येक बिंदु पर एक सदिश (ज्यामिति) का कार्यभार है। उदाहरण के लिए, समतल (ज्यामिति) में एक सदिश क्षेत्र को दिए गए परिमाण और दिशा वाले तीरों के संग्रह के रूप में देखा जा सकता है, प्रत्येक विमान में एक बिंदु से जुड़ा हुआ है। सदिश क्षेत्र प्रायः प्रतिमान के लिए उपयोग किए जाते हैं, उदाहरण के लिए, पूरे अंतरिक्ष में एक गतिशील तरल पदार्थ की गति और दिशा, या चुंबकीय क्षेत्र या गुरुत्वाकर्षण बल जैसे किसी बल की ताकत और दिशा, क्योंकि यह एक बिंदु से दूसरे बिंदु पर बदलता है।

अंतर और अभिन्न कलन के तत्व स्वाभाविक रूप से सदिश क्षेत्रों तक विस्तरित हैं। जब एक सदिश क्षेत्र बल का प्रतिनिधित्व करता है, तो एक सदिश क्षेत्र की रेखा समाकलन एक पथ के साथ चलने वाले बल द्वारा किए गए कार्य (भौतिकी) का प्रतिनिधित्व करता है, और इस व्याख्या के तहत ऊर्जा के संरक्षण को कैलकुलस के मौलिक प्रमेय के एक विशेष घटनाओं के रूप में प्रदर्शित किया जाता है। सदिश क्षेत्रों को उपयोगी रूप से अंतरिक्ष में एक गतिमान प्रवाह के वेग का प्रतिनिधित्व करने के बारे में सोचा जा सकता है, और यह भौतिक अंतर्ज्ञान विचलन (जो प्रवाह की मात्रा के परिवर्तन की दर का प्रतिनिधित्व करता है) और कर्ल (गणित) (जो प्रतिनिधित्व करता है) जैसी धारणाओं की ओर जाता है। प्रवाह का घूर्णन)।

निर्देशांक प्रणाली में, n-आयामी यूक्लिडियन अंतरिक्ष में एक कार्यक्षेत्र पर एक सदिश क्षेत्र को एक सदिश-मूल्यवान कार्य के रूप में दर्शाया जा सकता है जो कार्यक्षेत्र के प्रत्येक बिंदु पर वास्तविक संख्याओं के एन-टपल को जोड़ता है। एक सदिश क्षेत्र का यह प्रतिनिधित्व समन्वय प्रणाली पर निर्भर करता है, और एक समन्वय प्रणाली से दूसरे में जाने में वैक्टरों का एक अच्छी तरह से परिभाषित सहप्रसरण और विरोधाभास है। सदिश क्षेत्र पर प्रायः यूक्लिडियन क्षेत्र के खुले सेट पर वार्तालाप की जाती है, लेकिन सतह (टोपोलॉजी) जैसे अन्य उप-समूचय पर भी समझ में आता है, जहां वे प्रत्येक बिंदु पर सतह पर एक तीर स्पर्शरेखा को जोड़ते हैं (वक्रों की एक विभेदक ज्यामिति)।

प्रायः, सदिश क्षेत्र को अलग-अलग कई गुना परिभाषित किया जाता है, जो ऐसे स्थान होते हैं जो छोटे पैमाने पर यूक्लिडियन क्षेत्र की तरह दिखते हैं, लेकिन बड़े पैमाने पर अधिक जटिल संरचना हो सकती है। इस सेटिंग में, एक सदिश क्षेत्र विविध के प्रत्येक बिंदु पर एक स्पर्शरेखा सदिश देता है (अर्थात, स्पर्शरेखा बंडल का एक खंड (फाइबर बंडल) के कई गुना)। सदिश क्षेत्र एक प्रकार का टेंसर क्षेत्र है।

परिभाषा

यूक्लिडियन अंतरिक्ष के उपसमुच्चय पर सदिश क्षेत्र

समान वेक्टर फ़ील्ड के दो प्रतिनिधित्व: v(x, y) = −r. एरो फ़ील्ड को असतत बिंदुओं पर दर्शाते हैं, हालाँकि, फ़ील्ड हर जगह मौजूद है।

एक उप-समूचय दिया गया S में Rⁿ, एक सदिश क्षेत्र एक सदिश-मूल्यवान कार्य द्वारा दर्शाया जाता है V: S → Rⁿ मानक कार्टेशियन निर्देशांक में (x₁, …, x_n). यदि का प्रत्येक घटक V निरंतर है, तो V एक सतत सदिश क्षेत्र है, और अधिक सामान्यतः V एक है C^k सदिश क्षेत्र यदि का प्रत्येक घटक V है k बार लगातार भिन्न।

एक सदिश क्षेत्र को एक n-आयामी अंतरिक्ष के भीतर अलग-अलग बिंदुओं पर एक सदिश निर्दिष्ट करने के रूप में देखा जा सकता है।

दिया गया दो C^k-सदिश क्षेत्र V, W पर परिभाषित S और एक वास्तविक मूल्यवान C^k- फ़ंक्शन f पर परिभाषित S, दो यंत्र का चालन अदिश गुणन और सदिश जोड़

$$(fV)(p):=f(p)V(p)$$

$$(V+W)(p):=V(p)+W(p)$$

के मॉड्यूल (गणित) को परिभाषित करें C^k-सदिश क्षेत्र्स ऑफ़ द रिंग (गणित) C^k-फ़ंक्शंस जहां फ़ंक्शंस के गुणन को बिंदुवार परिभाषित किया गया है (इसलिए, यह गुणक पहचान के साथ कम्यूटेटिव है f_id(p) := 1).

समन्वय परिवर्तन कानून

भौतिकी में, एक यूक्लिडियन सदिश को अतिरिक्त रूप से अलग किया जाता है कि जब एक अलग पृष्ठभूमि समन्वय प्रणाली के संबंध में एक ही सदिश को मापता है तो उसके निर्देशांक कैसे बदलते हैं। यूक्लिडियन सदिश, स्यूडोसदिश और परिवर्तन एक सदिश को एक ज्यामितीय रूप से अलग इकाई के रूप में अदिश्स की एक साधारण सूची से, या एक सह-सदिश से अलग करते हैं।

इस प्रकार, मान लीजिए कि (x₁, ..., x_n) कार्टेशियन निर्देशांक का एक विकल्प है, जिसके संदर्भ में सदिश के घटक V हैं

$$V_{x}=(V_{1,x},\dots ,V_{n,x})$$

और मान लीजिए कि (y₁,...,Y_n) x_i . के n फलन हैं एक अलग समन्वय प्रणाली को परिभाषित करना। फिर नए निर्देशांक में सदिश V के घटकों को परिवर्तन कानून को पूरा करने की आवश्यकता होती है

$$V_{i,y}=\sum _{j=1}^{n}{\frac {\partial y_{i}}{\partial x_{j}}}V_{j,x}.$$

(1)

इस तरह के परिवर्तन कानून को सहप्रसरण और सदिशों के विपरीत परिवर्तन कहा जाता है। एक समान परिवर्तन कानून भौतिकी में सदिश क्षेत्रों की विशेषता है: विशेष रूप से, एक सदिश क्षेत्र परिवर्तन कानून के अधीन प्रत्येक समन्वय प्रणाली में n कार्यों का एक विनिर्देश है (1) विभिन्न समन्वय प्रणालियों से संबंधित।

सदिश क्षेत्र इस प्रकार अदिश क्षेत्र के साथ विपरीत होते हैं, जो अंतरिक्ष में प्रत्येक बिंदु पर एक संख्या या अदिश को जोड़ते हैं, और अदिश क्षेत्र की सरल सूचियों के साथ भी विपरीत होते हैं, जो समन्वय परिवर्तनों के तहत परिवर्तित नहीं होते हैं।

कई गुना पर सदिश क्षेत्र

एक गोले पर एक सदिश क्षेत्र

एक अलग कई गुना दिया गया $M$, एक सदिश क्षेत्र पर $M$ में प्रत्येक बिंदु के लिए एक स्पर्शरेखा स्थान का कार्यभार है $M$. अधिक सटीक रूप से, एक सदिश क्षेत्र $F$ से एक चित् (गणित) है $M$ स्पर्शरेखा बंडल में $TM$ ताकि $p\circ F$ पहचान मानचित्रण है

जहाँ पर $p$ से प्रक्षेपण को दर्शाता है $TM$ प्रति $M$. दूसरे शब्दों में, एक सदिश क्षेत्र स्पर्शरेखा बंडल का एक खंड (फाइबर बंडल) है।

एक वैकल्पिक परिभाषा: एक सहज सदिश क्षेत्र $X$ कई गुना पर $M$ एक रैखिक नक्शा है $X:C^{\infty }(M)\to C^{\infty }(M)$ ऐसा है कि $X$ एक व्युत्पत्ति_(अंतर_बीजगणित) है: $X(fg)=fX(g)+X(f)g$ सभी के लिए $f,g\in C^{\infty }(M)$. अगर कई गुना $M$ सुचारू या विश्लेषणात्मक कार्य है - अर्थात, निर्देशांक का परिवर्तन सुचारू (विश्लेषणात्मक) है - तब कोई व्यक्ति चिकनी (विश्लेषणात्मक) सदिश क्षेत्रों की धारणा को समझ सकता है। एक चिकनी विविध प्रकार पर सभी चिकने सदिश क्षेत्रों का संग्रह $M$ प्रायः द्वारा निरूपित किया जाता है $\Gamma (TM)$ या $C^{\infty }(M,TM)$ (विशेषकर जब सदिश क्षेत्र को खंड (फाइबर बंडल) के रूप में सोचते हैं); सभी चिकने सदिश क्षेत्रों का संग्रह भी इसके द्वारा दर्शाया जाता है ${\textstyle {\mathfrak {X}}(M)}$ (एक फ्रैक्टूर (टाइपफेस उप-वर्गीकरण) X)।

उदाहरण

एक हवाई जहाज के चारों ओर प्रवाह क्षेत्र R . में एक सदिश क्षेत्र है³, यहाँ बुलबुले द्वारा देखे गए हैं जो एक विंगटिप भंवर दिखाते हुए स्ट्रीमलाइन्स, स्ट्रीकलाइन्स, और पथता का अनुसरण करते हैं।

सदिश क्षेत्र का उपयोग आमतौर पर कंप्यूटर ग्राफिक्स में पैटर्न बनाने के लिए किया जाता है। यहाँ: OpenSimplex शोर के साथ उत्पन्न एक सदिश क्षेत्र के बाद घटता की सार संरचना।

• पृथ्वी पर हवा की गति के लिए एक सदिश क्षेत्र पृथ्वी की सतह पर प्रत्येक बिंदु के लिए हवा की गति और उस बिंदु के लिए दिशा के साथ एक सदिश को जोड़ देगा। इसे हवा का प्रतिनिधित्व करने के लिए तीरों का उपयोग करके खींचा जा सकता है; तीर की लंबाई (परिमाण (गणित) ) हवा की गति का संकेत होगी। सामान्य बैरोमीटर के दबाव के मानचित्र पर एक उच्च तब एक स्रोत (दूर की ओर इशारा करते हुए तीर) के रूप में कार्य करेगा, और एक कम एक सिंक (तीर की ओर इशारा करते हुए) होगा, क्योंकि हवा उच्च दबाव वाले क्षेत्रों से कम दबाव वाले क्षेत्रों की ओर बढ़ती है।
• गतिमान द्रव का वेग क्षेत्र। इस घटनाये में, द्रव में प्रत्येक बिंदु से एक वेग सदिश जुड़ा होता है।
• स्ट्रीमलाइन, स्ट्रीकलाइन और पाथलाइन | स्ट्रीमलाइन, स्ट्रीकलाइन और पाथलाइन 3 प्रकार की लाइनें हैं जिन्हें (समय-निर्भर) सदिश क्षेत्र से बनाया जा सकता है। वे हैं:
  • रेखाएँ: विभिन्न समयों में एक विशिष्ट निश्चित बिंदु से निकलने वाले कणों द्वारा निर्मित रेखा
  • पाथलाइन्स: वह पथ दिखा रहा है जो एक दिया गया कण (शून्य द्रव्यमान का) अनुसरण करेगा।
  • स्ट्रीमलाइन (या फील्डलाइन): तात्कालिक क्षेत्र से प्रभावित कण का पथ (यानी, यदि क्षेत्र को स्थिर रखा जाता है तो कण का पथ)।
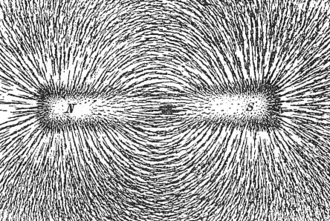
• चुंबकीय क्षेत्र, छोटे लोहे के बुरादे का उपयोग करके फील्डलाइनों को प्रकट किया जा सकता है।
• मैक्सवेल के समीकरण हमें यूक्लिडियन अंतरिक्ष में प्रत्येक बिंदु के लिए, उस बिंदु पर चार्ज परीक्षण कण द्वारा अनुभव किए गए बल के लिए एक परिमाण और दिशा निकालने के लिए प्रारंभिक और सीमा स्थितियों के दिए गए सेट का उपयोग करने की अनुमति देते हैं; परिणामी सदिश क्षेत्र विद्युत चुम्बकीय क्षेत्र है।
• किसी भी विशाल वस्तु द्वारा उत्पन्न गुरुत्वाकर्षण क्षेत्र भी एक सदिश क्षेत्र है। उदाहरण के लिए, गोलाकार रूप से सममित शरीर के लिए गुरुत्वाकर्षण क्षेत्र वैक्टर सभी क्षेत्र के केंद्र की ओर इशारा करते हैं, जिसमें शरीर से रेडियल दूरी बढ़ने पर वैक्टर की मात्रा कम हो जाती है।

यूक्लिडियन रिक्त स्थान में ढाल क्षेत्र

एक सदिश क्षेत्र जिसमें एक बिंदु के बारे में परिसंचरण होता है, उसे किसी कार्य के ग्रेडिएंट के रूप में नहीं लिखा जा सकता है।

Further information: ढाल

सदिश क्षेत्र को अदिश क्षेत्र से ढाल ऑपरेटर (डेल: द्वारा दर्शाया गया) का उपयोग करके बनाया जा सकता है।

एक खुले सेट s पर परिभाषित एक सदिश क्षेत्र वी को 'ग्रेडिएंट फील्ड' या ' रूढ़िवादी क्षेत्र ' कहा जाता है यदि s पर एक वास्तविक-मूल्यवान कार्य (एक अदिश क्षेत्र) f मौजूद है जैसे कि

$$V=\nabla f=\left({\frac {\partial f}{\partial x_{1}}},{\frac {\partial f}{\partial x_{2}}},{\frac {\partial f}{\partial x_{3}}},\dots ,{\frac {\partial f}{\partial x_{n}}}\right).$$

संबद्ध प्रवाह (गणित) को कहा जाता है ढाल प्रवाह, और ढाल वंश की विधि में प्रयोग किया जाता है।

रूढ़िवादी क्षेत्र में किसी भी बंद वक्र γ (γ(0) = γ(1)) के साथ अभिन्न रेखा शून्य है:

$$\oint _{\gamma }V(\mathbf {x} )\cdot \mathrm {d} \mathbf {x} =\oint _{\gamma }\nabla f(\mathbf {x} )\cdot \mathrm {d} \mathbf {x} =f(\gamma (1))-f(\gamma (0)).$$

यूक्लिडियन रिक्त स्थान में केंद्रीय क्षेत्र

C^∞-सदिश क्षेत्र खत्म Rⁿ \ {0} केंद्रीय क्षेत्र कहा जाता है यदि

$$V(T(p))=T(V(p))\qquad (T\in \mathrm {O} (n,\mathbb {R} ))$$

जहाँ पे O(n, R) ओर्थोगोनल समूह है। हम कहते हैं कि केंद्रीय क्षेत्र 0 के आसपास ऑर्थोगोनल मैट्रिक्स के तहत अपरिवर्तनीय (गणित) हैं।

बिंदु 0 को क्षेत्र का केंद्र कहा जाता है।

चूँकि ओर्थोगोनल परिवर्तन वास्तव में घूर्णन और परावर्तन हैं, अपरिवर्तनीय स्थितियों का अर्थ है कि एक केंद्रीय क्षेत्र के सदिश हमेशा 0 की ओर, या उससे दूर होते हैं; यह एक वैकल्पिक (और सरल) परिभाषा है। एक केंद्रीय क्षेत्र हमेशा एक ढाल क्षेत्र होता है, क्योंकि इसे एक अर्ध-अक्ष पर परिभाषित करना और एकीकृत करना एक विरोधी ढाल देता है।

सदिश क्षेत्रों पर संचालन

रेखा अभिन्न

Main article: रेखा अभिन्न

भौतिकी में एक सामान्य यांत्रिकी वक्रों की विभेदक ज्यामिति के साथ एक सदिश क्षेत्र को एकीकृत करना है, जिसे इसकी रेखा समाकलन का निर्धारण भी कहा जाता है। सहज रूप से यह वक्र के स्पर्शरेखा के अनुरूप सभी सदिश घटकों को जोड़ रहा है, जिसे उनके अदिश उत्पादों के रूप में व्यक्त किया जाता है। उदाहरण के लिए, एक बल क्षेत्र (जैसे गुरुत्वाकर्षण) में एक कण दिया गया है, जहां अंतरिक्ष में किसी बिंदु पर प्रत्येक सदिश कण पर अभिनय करने वाले बल का प्रतिनिधित्व करता है, एक निश्चित पथ के साथ अभिन्न रेखा कण पर किया गया कार्य है, जब वह यात्रा करता है इस रास्ते के साथ। सहज रूप से, यह बल सदिश के अदिश उत्पादों और वक्र के साथ प्रत्येक बिंदु में छोटे स्पर्शरेखा सदिश का योग है।

रेखा अभिन्न को रीमैन अभिन्न के अनुरूप बनाया गया है और यह मौजूद है यदि वक्र सुधार योग्य है (परिमित लंबाई है) और सदिश क्षेत्र निरंतर है।

एक सदिश क्षेत्र दिया गया V और एक वक्र γ, पैरामीट्रिक समीकरण द्वारा t में [a, b] (कहाँ पे a तथा b वास्तविक संख्या एँ हैं), रेखा समाकलन को इस प्रकार परिभाषित किया गया है:

$$\int _{\gamma }V(\mathbf {x} )\cdot \mathrm {d} \mathbf {x} =\int _{a}^{b}V(\gamma (t))\cdot {\dot {\gamma }}(t)\,\mathrm {d} t.$$

विचलन

Main article: विचलन

यूक्लिडियन अंतरिक्ष पर एक सदिश क्षेत्र का विचलन एक कार्य (या अदिश क्षेत्र) है। तीन आयामों में, विचलन द्वारा परिभाषित किया गया है

$$\operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial F_{1}}{\partial x}}+{\frac {\partial F_{2}}{\partial y}}+{\frac {\partial F_{3}}{\partial z}},$$

मनमाने आयामों के स्पष्ट सामान्यीकरण के साथ, एक बिंदु पर विचलन उस डिग्री का प्रतिनिधित्व करता है जिसमें बिंदु के चारों ओर एक छोटी मात्रा सदिश प्रवाह के लिए एक स्रोत या सिंक होती है, जिसके परिणामस्वरूप विचलन प्रमेय द्वारा सटीक बनाया जाता है।

विचलन को रीमैनियन विविध पर भी परिभाषित किया जा सकता है, जो कि रीमैनियन मीट्रिक के साथ कई गुना है जो वैक्टर की लंबाई को मापता है।

तीन आयामों में कर्ल

Main article: कर्ल (गणित)

कर्ल (गणित) एक यंत्र का चालन है जो एक सदिश क्षेत्र लेता है और एक और सदिश क्षेत्र उत्पन्न करता है। कर्ल को केवल तीन आयामों में परिभाषित किया गया है, लेकिन कर्ल के कुछ गुणों को बाहरी व्युत्पन्न के साथ उच्च आयामों में कैप्चर किया जा सकता है। तीन आयामों में, इसे द्वारा परिभाषित किया गया है

$$\operatorname {curl} \mathbf {F} =\nabla \times \mathbf {F} =\left({\frac {\partial F_{3}}{\partial y}}-{\frac {\partial F_{2}}{\partial z}}\right)\mathbf {e} _{1}-\left({\frac {\partial F_{3}}{\partial x}}-{\frac {\partial F_{1}}{\partial z}}\right)\mathbf {e} _{2}+\left({\frac {\partial F_{2}}{\partial x}}-{\frac {\partial F_{1}}{\partial y}}\right)\mathbf {e} _{3}.$$

कर्ल एक बिंदु पर सदिश प्रवाह के कोणीय गति के घनत्व को मापता है, अर्थात वह मात्रा जिसमें प्रवाह एक निश्चित अक्ष के चारों ओर घूमता है। यह सहज विवरण स्टोक्स के प्रमेय द्वारा सटीक बनाया गया है।

एक सदिश क्षेत्र का सूचकांक

एक सदिश क्षेत्र का सूचकांक एक पूर्णांक है जो एक पृथक शून्य (यानी, क्षेत्र की एक पृथक विलक्षणता) के आसपास एक सदिश क्षेत्र के व्यवहार का वर्णन करने में मदद करता है। समतल में, सूचकांक एक सैडल विलक्षणता पर −1 मान लेता है लेकिन स्रोत या सिंक विलक्षणता पर +1 करता है।

मान लीजिए कि विविध का आयाम जिस पर सदिश क्षेत्र परिभाषित किया गया है, n है। शून्य के चारों ओर एक छोटा गोला S लें ताकि कोई अन्य शून्य S के आंतरिक भाग में न हो। इस गोले से एक इकाई क्षेत्र के लिए एक नक्शा n − 1 इस गोले पर प्रत्येक सदिश को इसके द्वारा विभाजित करके बनाया जा सकता है लंबाई एक इकाई लंबाई सदिश बनाने के लिए, जो इकाई क्षेत्र पर एक बिंदु है Sⁿ⁻¹. यह S से Sⁿ⁻¹ तक एक सतत मानचित्र को परिभाषित करता है. बिंदु पर सदिश क्षेत्र का सूचकांक एक सतत मानचित्रण की डिग्री है, (इस मानचित्र की विभेदक टोपोलॉजी) यह दिखाया जा सकता है कि यह पूर्णांक S की पसंद पर निर्भर नहीं करता है, और इसलिए केवल सदिश क्षेत्र पर ही निर्भर करता है।

'सदिश क्षेत्र का सूचकांक' समग्र रूप से परिभाषित किया जाता है जब इसमें शून्य की सीमित संख्या होती है। इस घटनाये में, सभी शून्य अलग-थलग हैं, और सदिश क्षेत्र के सूचकांक को सभी शून्य पर सूचकांकों के योग के रूप में परिभाषित किया गया है।

सूचकांक किसी भी गैर-एकवचन बिंदु (यानी, एक बिंदु जहां सदिश गैर-शून्य है) पर परिभाषित नहीं किया गया है। यह एक स्रोत के आसपास +1 के बराबर है, और अधिक सामान्यतः (−1)^k के बराबर है एक सैडल के चारों ओर, जिसमें k संकुचन आयाम और n−k विस्तृत आयाम हैं। त्रि-आयामी अंतरिक्ष में एक साधारण (2-आयामी) क्षेत्र के लिए, यह दिखाया जा सकता है कि गोले पर किसी भी सदिश क्षेत्र का सूचकांक 2 होना चाहिए। इससे पता चलता है कि ऐसे प्रत्येक सदिश क्षेत्र में शून्य होना चाहिए। इसका तात्पर्य बालों वाली गेंद प्रमेय से है, जिसमें कहा गया है कि यदि 'R³' में एक सदिश इकाई क्षेत्र के प्रत्येक बिंदु को सौंपा गया है S² एक निरंतर विधि से, फिर बालों को समतल करना असंभव है, अर्थात, वैक्टर को निरंतर विधि से चुनना जैसे कि वे सभी गैर-शून्य और S के स्पर्श रेखा हों^{2</सुप>.}

शून्य की एक सीमित संख्या के साथ एक कॉम्पैक्ट विविध पर एक सदिश क्षेत्र के लिए, पोंकारे-हॉप प्रमेय कहता है कि सदिश क्षेत्र का सूचकांक विविध की यूलर विशेषता के बराबर है।

शारीरिक अंतर्ज्ञान

लोहे की छड़ की चुंबकत्व क्षेत्र रेखाएं (चुंबकीय द्विध्रुव )

माइकल फैराडे ने बल की रेखाओं की अपनी अवधारणा में इस बात पर बल दिया कि क्षेत्र ही अध्ययन का विषय होना चाहिए, जो कि क्षेत्र सिद्धांत (भौतिकी) के रूप में पूरे भौतिकी में बन गया है।

चुंबकीय क्षेत्र के अलावा, फैराडे द्वारा प्रतिमानिंग की गई अन्य घटनाओं में विद्युत क्षेत्र और प्रकाश क्षेत्र सम्मिलित हैं।

प्रवाह वक्र

Main article: अभिन्न वक्र

अंतरिक्ष के एक क्षेत्र के माध्यम से एक तरल पदार्थ के प्रवाह पर विचार करें। किसी भी समय, द्रव के किसी भी बिंदु के साथ एक विशेष वेग जुड़ा होता है; इस प्रकार किसी भी प्रवाह से जुड़ा एक सदिश क्षेत्र होता है। इसका विलोम भी सत्य है: प्रवाह को उस सदिश क्षेत्र से संबद्ध करना संभव है जिसमें उस सदिश क्षेत्र का वेग हो।

S पर परिभाषित एक सदिश क्षेत्र V को दिया गया है, कोई S पर वक्र γ(t) को इस प्रकार परिभाषित करता है कि प्रत्येक t के एक लिए अंतराल में,

$$\gamma '(t)=V(\gamma (t))\,.$$

पिकार्ड-लिंडेलोफ प्रमेय द्वारा, यदि वी लिप्सचिट्ज़ निरंतरता है तो एक अद्वितीय सी . है c¹-वक्र y_x प्रत्येक बिंदु x के लिए जो S पर है, कुछ ε > 0 के लिए,

$${\begin{aligned}\gamma _{x}(0)&=x\\\gamma '_{x}(t)&=V(\gamma _{x}(t))\qquad \forall t\in (-\varepsilon ,+\varepsilon )\subset \mathbb {R} .\end{aligned}}$$

वक्र_x सदिश क्षेत्र V के समाकलन वक्र या प्रक्षेप पथ (या कम सामान्यतः, प्रवाह रेखाएं) कहलाते हैं और तुल्यता वर्ग ों में विभाजन S कहलाते हैं। अंतराल का विस्तार करना हमेशा संभव नहीं होता है (−ε, +ε) पूर्ण वास्तविक संख्या रेखा तक। उदाहरण के लिए प्रवाह एक सीमित समय में S के किनारे तक पहुँच सकता है।

दो या तीन आयामों में कोई सदिश क्षेत्र को s पर प्रवाह (गणित) को जन्म देने के रूप में देख सकता है। यदि हम एक बिंदु पी पर इस प्रवाह में एक कण छोड़ते हैं तो यह वक्र के साथ आगे बढ़ेगा_p प्रवाह में प्रारंभिक बिंदु p पर निर्भर करता है। यदि p, V का एक स्थिर बिंदु है (अर्थात, सदिश क्षेत्र, बिंदु p पर शून्य सदिश के बराबर है), तो कण p पर ही रहेगा।

विशिष्ट अनुप्रयोग स्ट्रीमलाइन, स्ट्रीकलाइन, और द्रव प्रवाह, जियोडेसिक प्रवाह, और एक-पैरामीटर उपसमूह ों और झूठ समूह ों में घातीय मानचित्र (झूठ सिद्धांत) में पथरेखाएं हैं।

पूर्ण सदिश क्षेत्र

परिभाषा के अनुसार, एक सदिश क्षेत्र को पूर्ण कहा जाता है यदि उसका प्रत्येक प्रवाह वक्र सभी समय के लिए मौजूद हो। विशेष रूप से, कई गुना पर कॉम्पैक्ट समर्थन सदिश क्षेत्र पूर्ण हैं। यदि $X$ पर एक पूर्ण सदिश क्षेत्र है $M$, फिर प्रवाह द्वारा उत्पन्न भिन्नताओं का एक-पैरामीटर समूह $X$ सभी समय के लिए मौजूद है। सीमा के बिना एक कॉम्पैक्ट विविध पर, हर चिकना सदिश क्षेत्र पूरा होता है। अपूर्ण सदिश क्षेत्र का एक उदाहरण $V$ वास्तविक रेखा पर $\mathbb {R}$ द्वारा दिया गया है $V(x)=x^{2}$. के लिए, अवकल समीकरण ${\textstyle x'(t)=x^{2}}$, प्रारंभिक शर्त के साथ $x(0)=x_{0}$, इसका अनूठा समाधान है ${\textstyle x(t)={\frac {x_{0}}{1-tx_{0}}}}$ यदि $x_{0}\neq 0$ (तथा $x(t)=0$ सभी के लिए $t\in \mathbb {R}$ यदि $x_{0}=0$) इसलिए के लिए $x_{0}\neq 0$, $x(t)$ पर अपरिभाषित है ${\textstyle t={\frac {1}{x_{0}}}}$ इसलिए के सभी मूल्यों के लिए परिभाषित नहीं किया जा सकता है $t$.

f-संबंधितता

विविध्स के बीच एक सहज फलन को देखते हुए, f: M → N, व्युत्पन्न स्पर्शरेखा बंडलों पर एक प्रेरित मानचित्र है, f_* : टीएम → टीएन। दिए गए सदिश क्षेत्र V : M → TM और W : N → TN, हम कहते हैं कि W, V से संबंधित है यदि समीकरण W f = f_∗ वी रखती है।

अगर वी_i f-W से संबंधित है_i, i = 1, 2, फिर लेट ब्रैकेट [V₁, में₂] f से संबंधित है [W₁, में₂].

सामान्यीकरण

सदिशों को पी-सदिश|p-सदिश (पीटीएच वैक्टर की बाहरी शक्ति) द्वारा प्रतिस्थापित करने पर p-सदिश क्षेत्र प्राप्त होते हैं; दोहरे स्थान और बाहरी शक्तियों को लेने से अंतर रूप उत्पन्न होता है | विभेदक k - रूप, और इन पैदावार के संयोजन से सामान्य टेंसर क्षेत्र उत्पन्न होते हैं।

बीजगणितीय रूप से, सदिश क्षेत्रों को कई गुना चिकनी कार्यों के बीजगणित के व्युत्पन्न (अमूर्त बीजगणित) के रूप में वर्णित किया जा सकता है, जो बीजगणित पर एक व्युत्पत्ति के रूप में एक कम्यूटेटिव बीजगणित पर एक सदिश क्षेत्र को परिभाषित करने की ओर जाता है, जिसे अंतर कैलकुस के सिद्धांत में विकसित किया जाता है। कम्यूटेटिव बीजगणित पर।

यह भी देखें

• ईसेनबड-लेविन-खिम्शियाशविली हस्ताक्षर सूत्र
• फील्ड लाइन
• फील्ड की छमता
• संतुलित प्रवाह#वायुमंडलीय गतिकी में ढाल प्रवाह
• झूठ व्युत्पन्न
• अदिश क्षेत्र
• समय पर निर्भर वेक्टर क्षेत्र
• बेलनाकार और गोलाकार निर्देशांक में वेक्टर क्षेत्र
• टेंसर फ़ील्ड

ग्रन्थसूची

• हबर्ड, जे एच; हबर्ड, बी बी (1999). सदिश कलन, रेखीय बीजगणित और अवकलन रूप। एक एकीकृत दृष्टिकोण. अपर सैडल रिवर, एनजे: शागिर्द कक्ष. ISBN 0-13-657446-7.
• वार्नर, स्पष्टवादी (1983) [1971]. डिफरेंशियल मैनिफोल्ड्स और लाइ ग्रुप्स की नींव. न्यूयॉर्क-बर्लिन: स्प्रिंगर-वर्लाग. ISBN 0-387-90894-3.
• बूथबी, विलियम (1986). डिफरेंशियल मैनिफोल्ड्स और रीमैनियन ज्योमेट्री का परिचय. शुद्ध और अनुप्रयुक्त गणित, खंड 120 (दूसरा ed.). ऑरलैंडो, एफएल: अकादमिक प्रेस. ISBN 0-12-116053-X. {{cite book}}: Invalid |url-access=पंजीकरण (help)

बाहरी संबंध

Media related to वेक्टर क्षेत्र at Wikimedia Commons

• Online Vector Field Editor
• "वेक्टर क्षेत्र", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Vector field — मैथवर्ल्ड
• Vector field —प्लैनेटमैथ
• 3D Magnetic field viewer
• Vector fields and field lines
• Vector field simulation सदिश क्षेत्रों के प्रभाव दिखाने के लिए एक इंटरैक्टिव अनुप्रयोग