तरंग संकुल: Difference between revisions
m (Abhishek moved page वेव पैकेट to तरंग संकुल without leaving a redirect) |
No edit summary |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Short "burst" or "envelope" of restricted wave action that travels as a unit}} | {{short description|Short "burst" or "envelope" of restricted wave action that travels as a unit}} | ||
{{Redirect| | {{Redirect|लहर ट्रेन|गणित की अवधारणा|आवधिक यात्रा लहर}} | ||
{{distinguish| | {{distinguish|तरंग समूह}} | ||
[[File:Wave packet (no dispersion).gif|right|thumb|300px| | [[File:Wave packet (no dispersion).gif|right|thumb|300px|प्रसार के बिना एक तरंग संकुल (वास्तविक या काल्पनिक भाग)]] | ||
[[File:Wave packet (dispersion).gif|right|thumb|300px| | [[File:Wave packet (dispersion).gif|right|thumb|300px|प्रसार के साथ एक तरंग संकुल]]भौतिकी में '''तरंग संकुल''' स्थानीयकृत तरंग क्रिया की एक इकाई के रूप में यात्रा करता है। एक तरंग संकुल का विश्लेषण किया जा सकता है या विभिन्न तरंगों के घटक [[साइनसोइडल तरंग|साइनसोइडल तरंगों]] के एक अनंत सेट से संश्लेषित किया जाता है।<ref>{{harvnb|Manners|2000}}</ref> प्रत्येक घटक तरंग घटक और तरंग संकुल [[तरंग समीकरण|समीकरण]] के समाधान होता है। तरंग समीकरण के आधार पर तरंग संकुल की रूपरेखा स्थिर रहती है या प्रसार के दौरान यह बदल सकती है। | ||
प्रत्येक घटक तरंग | |||
[[क्वांटम यांत्रिकी]] तरंग | [[क्वांटम यांत्रिकी]] तरंग संकुल को एक विशेष महत्व देती है, इसे प्रायिकता आयाम के रूप में व्याख्यायित किया जाता है इसका मानक वर्ग संभाव्यता घनत्व का वर्णन करता है कि किसी विशेष अवस्था में एक कण या कण को दी गई स्थिति या गति के लिए मापा जाता है। लहर समीकरण इस स्थिति में श्रोडिंगर समीकरण होता है और इसके आवेदन के माध्यम से [[शास्त्रीय यांत्रिकी|मौलिक यांत्रिकी]] में [[हैमिल्टनियन यांत्रिकी]] औपचारिकता की प्रक्रिया के समान क्वांटम यांत्रिक प्रणाली के समय के विकास को कम करना संभव होता है। श्रोडिंगर समीकरण के समाधान के प्रसार चरित्र ने श्रोडिंगर समीकरण को खारिज करने में ऐतिहासिक पृष्ठभूमि और विकास श्रोडिंगर की मूल व्याख्या और बोर्न नियम को स्वीकार करने में महत्वपूर्ण भूमिका निभाई है। | ||
लहर के समन्वय प्रतिनिधित्व में | लहर के समन्वय प्रतिनिधित्व में भौतिक वस्तु की स्थानीय संभावना की स्थिति संकुल समाधान की स्थिति से निर्दिष्ट होती है। इसके अतिरिक्त स्थानिक तरंग संकुल जितना संकरा होता है उतनी तरंग संकुल की स्थिति बेहतर होती है उतना तरंग के संवेग में प्रसार उतना ही बड़ा होता है। स्थिति में प्रसार और [[गति]] में प्रसार के बीच यह [[वर्नर हाइजेनबर्ग]] अनिश्चितता सिद्धांत की एक विशेषता होती है। | ||
== ऐतिहासिक पृष्ठभूमि == | == ऐतिहासिक पृष्ठभूमि == | ||
1900 | 1900 के प्रारंभ में यह स्पष्ट हो गया कि क्लासिकल यांत्रिकी में कुछ बड़ी कमियां थी। [[आइजैक न्यूटन]] ने मूल रूप से इस विचार को प्रस्तावित किया था कि प्रकाश असतत संकुल में आता है जिसे उन्होंने कॉर्पसकल कहा था लेकिन कई प्रकाश घटनाओं के तरंग-समान व्यवहार ने वैज्ञानिकों को [[विद्युत]] चुंबकत्व के तरंग विवरण का पक्ष लेने के लिए प्रेरित किया था। यह 1930 के दशक तक नहीं था प्रकाश की कण प्रकृति को वास्तव में भौतिकी में व्यापक रूप से स्वीकार किया जाने लगा था। क्वांटम यांत्रिकी का विकास और भ्रमित करने वाले प्रायोगिक परिणामों की व्याख्या करने में इसकी सफलता, इसकी स्वीकृति के मूल में थी। इस प्रकार क्वांटम यांत्रिकी के निर्माण में बुनियादी अवधारणाओं में से एक यह है कि प्रकाश असतत बंडलों में आता है जिसे फोटॉन कहा जाता है। एक फोटॉन की ऊर्जा इसकी आवृत्ति होती है <ref>{{harvnb|Einstein|1905}}</ref> | ||
<math display="block"> E = h\nu.</math> | <math display="block"> E = h\nu.</math> | ||
फोटॉन की ऊर्जा [[प्लैंक स्थिरांक]] के गुणनफल के बराबर होती है | फोटॉन की ऊर्जा [[प्लैंक स्थिरांक]] के गुणनफल के बराबर होती है {{mvar|h}} और इसकी आवृत्ति होती है {{mvar|ν}}. यह मौलिक भौतिकी में एक समस्या का समाधान है। | ||
20वीं शताब्दी के दौरान क्वांटम यांत्रिकी के विचारों का विकास जारी | 20वीं शताब्दी के दौरान क्वांटम यांत्रिकी के विचारों का विकास जारी रहा था। जिसमें सभी घटनाएं और पदार्थ असतत कणों से बनते थे और परस्पर क्रिया करते थे, चूँकि इन कणों को प्रायिकता तरंग द्वारा वर्णित किया गया था। इन संभाव्यता आयामों की गणना के लिए परस्पर स्थान को कम किया जाता है। | ||
दुनिया की कण-जैसी प्रकृति की एक सदी से अधिक प्रयोग द्वारा पुष्टि की गई है | दुनिया की कण-जैसी प्रकृति की एक सदी से अधिक प्रयोग द्वारा पुष्टि की गई है जबकि तरंग जैसी घटना को क्वांटम कणों के तरंग संकुल पहलू के परिणाम के रूप में चित्रित किया गया है। संपूरकता के सिद्धांत के अनुसार तरंग-जैसी और कण-जैसी विशेषताएं कभी भी एक ही समय में अर्थात एक ही प्रयोग में प्रकट नहीं होती है। | ||
== मूल व्यवहार == | == मूल व्यवहार == | ||
[[File:Gaussian wavepacket tunneling in potential well.gif|thumbnail|right|एक केंद्रित संभावित दीवार में आवधिक क्वांटम टनलिंग का अनुभव करने वाले एक अनंत संभावित अच्छी तरह से फंसे एक प्रारंभिक गॉसियन | [[File:Gaussian wavepacket tunneling in potential well.gif|thumbnail|right|एक केंद्रित संभावित दीवार में आवधिक क्वांटम टनलिंग का अनुभव करने वाले एक अनंत संभावित अच्छी तरह से फंसे एक प्रारंभिक गॉसियन स्थिति की स्थिति स्पेस संभावना घनत्व।]] | ||
=== गैर- | === गैर-बड़ा होाने वाला === | ||
प्रसार के बिना प्रसार के एक उदाहरण के रूप में क्लासिकल भौतिकी से निम्न तरंग समीकरण के तरंग समाधान पर विचार करता है | |||
<math display="block">{ \partial^2 u \over \partial t^2 } = c^2 \, \nabla^2 u,</math> | <math display="block">{ \partial^2 u \over \partial t^2 } = c^2 \, \nabla^2 u,</math> | ||
जहाँ {{math|''c''}} किसी दिए गए माध्यम में तरंग के प्रसार की गति है। | |||
भौतिकी समय परिपाटी का उपयोग करते हुए | भौतिकी समय परिपाटी का उपयोग करते हुए {{math|''e''<sup>−''iωt''</sup>}} तरंग समीकरण के समतल-तरंग समाधान होता है | ||
<math display="block"> u(\mathbf{x},t) = e^{i{(\mathbf{k\cdot x}}-\omega t)},</math> | <math display="block"> u(\mathbf{x},t) = e^{i{(\mathbf{k\cdot x}}-\omega t)},</math> | ||
जहाँ | |||
<math display="block"> \omega^2 =|\mathbf{k}|^2 c^2,</math> और <math> |\mathbf{k}|^2 = k_x^2 + k_y^2+ k_z^2.</math> | <math display="block"> \omega^2 =|\mathbf{k}|^2 c^2,</math> और <math> |\mathbf{k}|^2 = k_x^2 + k_y^2+ k_z^2.</math> | ||
के बीच यह संबंध {{math|''ω''}} और {{math|'''k'''}} मान्य | के बीच यह संबंध है {{math|''ω''}} और {{math|'''k'''}} मान्य होता है जो कि समतल तरंग समीकरण का हल होता है। इसे [[फैलाव संबंध|प्रसार संबंध]] कहा जाता है। | ||
सरल बनाने के लिए | सरल बनाने के लिए केवल एक आयाम में बड़ा होने वाली तरंगों पर विचार करता है। तब सामान्य समाधान होता है | ||
<math display="block"> u(x,t)= A e^{i(kx-\omega t)} + B e^{-i(kx+\omega t)},</math> | <math display="block"> u(x,t)= A e^{i(kx-\omega t)} + B e^{-i(kx+\omega t)},</math> | ||
जिसमें हम ले सकते | जिसमें हम ले सकते है {{math|1=''ω ''='' kc''}}. पहला शब्द सकारात्मक में बड़ा होने वाली लहर का प्रतिनिधित्व करता है {{nowrap|{{math|''x''}}-दिशा}} चूंकि यह एक कार्य होता है {{math|''x ''−'' ct''}} केवल, दूसरा कार्यकाल का एक कार्य होता है {{math|''x'' + ''ct''}} ऋणात्मक में प्रसारित होने वाली तरंग का प्रतिनिधित्व करता है {{nowrap|{{math|''x''}}-दिशा}}. | ||
एक तरंग | एक तरंग संकुल एक स्थानीय गड़बड़ी होती है जो कई अलग-अलग [[तरंग रूप|तरंग रूपों]] के योग से उत्पन्न करता है। यदि संकुल दृढ़ता से स्थानीयकृत है तो स्थानीयकरण के क्षेत्र में रचनात्मक सुपरपोजिशन और क्षेत्र के बाहर विनाशकारी सुपरपोजिशन की अनुमति देने के लिए अधिक आवृत्तियों की आवश्यकता होती है। मूल समाधानों से एक आयाम में तरंग संकुल के एक सामान्य रूप को व्यक्त किया जाता है | ||
<math display="block"> u(x,t) = \frac{1}{\sqrt{2\pi}} \int^{\,\infty}_{-\infty} A(k) ~ e^{i(kx-\omega(k)t)} \, dk.</math> | <math display="block"> u(x,t) = \frac{1}{\sqrt{2\pi}} \int^{\,\infty}_{-\infty} A(k) ~ e^{i(kx-\omega(k)t)} \, dk.</math> | ||
जैसा कि प्लेन- | जैसा कि प्लेन-तरंग स्थिति में तरंग संकुल दाईं ओर जाता है {{math|1=''ω''(''k'') = ''kc''}} तब {{math|1=''u''(''x'', ''t'') = ''F''(''x'' − ''ct'')}} और बाईं ओर जाता है {{math|1=''ω''(''k'') = −''kc''}} तब {{math|1=''u''(''x'', ''t'') = ''F''(''x'' + ''ct'')}}. | ||
कारण {{frac|1|{{radical|2π}}}} [[फूरियर रूपांतरण]] कन्वेंशन से आता है। आयाम {{math|''A''(''k'')}} में समतल-तरंग समाधानों के रैखिक सुपरपोजिशन के गुणांक होते | इस कारण से {{frac|1|{{radical|2π}}}} [[फूरियर रूपांतरण]] कन्वेंशन से आता है। आयाम {{math|''A''(''k'')}} में समतल-तरंग समाधानों के रैखिक सुपरपोजिशन के गुणांक होते है। बदले में इन गुणांकों को एक कार्य के रूप में व्यक्त किया जा सकता है {{math|''u''(''x'', ''t'')}} पर मूल्यांकन किया गया {{math|1=''t'' = 0}} उपरोक्त फूरियर रूपांतरण संबंध को उल्टा करता है: | ||
<math display="block"> A(k) = \frac{1}{\sqrt{2\pi}} \int^{\,\infty}_{-\infty} u(x,0) ~ e^{-ikx} \, dx.</math> | <math display="block"> A(k) = \frac{1}{\sqrt{2\pi}} \int^{\,\infty}_{-\infty} u(x,0) ~ e^{-ikx} \, dx.</math> | ||
उदाहरण के लिए | उदाहरण के लिए चुनते है | ||
<math display="block"> u(x,0) = e^{-x^2 +ik_0x},</math> | <math display="block"> u(x,0) = e^{-x^2 +ik_0x},</math> | ||
हमे प्राप्त होता है | |||
<math display="block"> A(k) = \frac{1}{\sqrt{2}} e^{-\frac{(k-k_0)^2}{4}},</math> | <math display="block"> A(k) = \frac{1}{\sqrt{2}} e^{-\frac{(k-k_0)^2}{4}},</math> | ||
और अंत में | और अंत में | ||
| Line 55: | Line 53: | ||
&= e^{-(x-ct)^2} \left[\cos\left(2\pi \frac{x-ct}{\lambda}\right)+ i\sin\left(2\pi\frac{x-ct}{\lambda}\right)\right]. | &= e^{-(x-ct)^2} \left[\cos\left(2\pi \frac{x-ct}{\lambda}\right)+ i\sin\left(2\pi\frac{x-ct}{\lambda}\right)\right]. | ||
\end{align} </math> | \end{align} </math> | ||
उपरोक्त एनीमेशन में इस तरंग | उपरोक्त एनीमेशन में इस तरंग संकुल के वास्तविक या काल्पनिक भाग का नॉनडिस्पर्सिव प्रसार प्रस्तुत किया गया है। | ||
=== | === प्रसार वाला === | ||
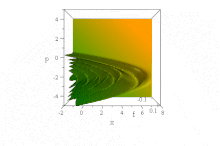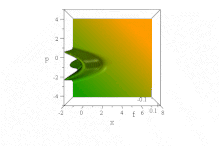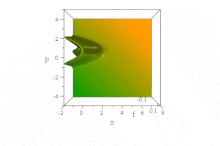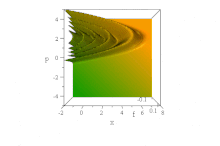
[[File:Guassian Dispersion.gif|360 px|अंगूठा|दाहिना|स्थान स्थान प्रायिकता घनत्व प्रारंभिक रूप से एक गाऊसी अवस्था में मुक्त स्थान में न्यूनतम अनिश्चित, स्थिर गति पर एक आयाम में गतिमान है।]]इसके विपरीत | [[File:Guassian Dispersion.gif|360 px|अंगूठा|दाहिना|स्थान स्थान प्रायिकता घनत्व प्रारंभिक रूप से एक गाऊसी अवस्था में मुक्त स्थान में न्यूनतम अनिश्चित, स्थिर गति पर एक आयाम में गतिमान है।]]इसके विपरीत प्रसार के एक उदाहरण के रूप में अब [[फैलाव (प्रकाशिकी)|प्रसार (प्रकाशिकी)]] के साथ के अतिरिक्त श्रोडिंगर समीकरण के समाधान पर विचार करता है (गैर-आयामी {{math|2Δ''x''}} {{mvar|m}} और ħ एक के बराबर सेट होता है) | ||
<math display="block">i{ \partial \psi \over \partial t } = -\frac{1}{2} { \nabla^2 \psi },</math> | <math display="block">i{ \partial \psi \over \partial t } = -\frac{1}{2} { \nabla^2 \psi },</math> | ||
प्रसार संबंध उत्पन्न करता है | |||
<math display="block"> \omega = \frac{1}{2}|\mathbf{k}|^2. </math> | <math display="block"> \omega = \frac{1}{2}|\mathbf{k}|^2. </math> | ||
एक बार फिर | एक बार फिर एक आयाम पर ध्यान केंद्रित करते हुए श्रोडिंगर समीकरण का समाधान प्रारंभिक स्थिति को संतुष्ट करता है <math display="inline"> \psi(x,0)= \sqrt[4]{2/\pi} \exp\left({-x^2 + ik_0 x}\right)</math> मूल स्थान पर स्थानीयकृत एक तरंग संकुल का प्रतिनिधित्व करते हुए देखा जाता है | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
\psi(x,t) &= \frac{ \sqrt[4]{2/\pi}}{\sqrt{1 + 2it}} e^{-\frac{1}{4}k_0^2} ~ e^{-\frac{1}{1 + 2it}\left(x - \frac{ik_0}{2}\right)^2}\\ | \psi(x,t) &= \frac{ \sqrt[4]{2/\pi}}{\sqrt{1 + 2it}} e^{-\frac{1}{4}k_0^2} ~ e^{-\frac{1}{1 + 2it}\left(x - \frac{ik_0}{2}\right)^2}\\ | ||
&= \frac{ \sqrt[4]{2/\pi}}{\sqrt{1 + 2it}} e^{-\frac{1}{1 + 4t^2}(x - k_0t)^2}~ e^{i \frac{1}{1 + 4t^2}\left((k_0 + 2tx)x - \frac{1}{2}tk_0^2\right)} ~. | &= \frac{ \sqrt[4]{2/\pi}}{\sqrt{1 + 2it}} e^{-\frac{1}{1 + 4t^2}(x - k_0t)^2}~ e^{i \frac{1}{1 + 4t^2}\left((k_0 + 2tx)x - \frac{1}{2}tk_0^2\right)} ~. | ||
\end{align} </math> | \end{align} </math> | ||
संभाव्यता घनत्व को देखकर इस तरंग | संभाव्यता घनत्व को देखकर इस तरंग संकुल के प्रसार वाले व्यवहार का आभास प्राप्त होता है: | ||
<math display="block">|\psi(x,t)|^2 = \frac{ \sqrt{2/\pi}}{\sqrt{1+4t^2}}~e^{-\frac{2(x-k_0t)^2}{1+4t^2}}~.</math> | <math display="block">|\psi(x,t)|^2 = \frac{ \sqrt{2/\pi}}{\sqrt{1+4t^2}}~e^{-\frac{2(x-k_0t)^2}{1+4t^2}}~.</math> | ||
यह स्पष्ट है कि निरंतर [[समूह वेग]] के साथ चलते हुए यह | यह स्पष्ट है कि निरंतर [[समूह वेग]] के साथ चलते हुए यह प्रसार तरंग संकुल होता है {{math|''k<sub>o</sub>''}} तेजी से डेलोकलाइज़ होता है: इसमें [[गाऊसी समारोह]] समय के साथ बढ़ता जाता है {{math|{{radical| 1 + 4''t''<sup>2</sup>}} → 2''t''}} तो अंततः यह असीमित क्षेत्र में बड़ा हो जाता है।<ref group=nb>By contrast, the introduction of ''interaction terms'' in dispersive equations, such as for the [[quantum harmonic oscillator]], may result in the emergence of envelope-non-dispersive, [[Coherent states#The wavefunction of a coherent state|classical-looking solutions]]—see [[coherent states]]: Such "minimum uncertainty states" do saturate the uncertainty principle permanently.</ref> | ||
गति | |||
गति रूपरेखा {{math|''A''(''k'')}} अपरिवर्तनीय होती है। प्रायिकता धारा होती है | |||
<math display="block">j=\rho v = \frac{1}{2i} (\psi^* \nabla \psi - \psi \nabla \psi^*)= \rho \left (k_0+\frac{4t(x-k_0 t)}{1+4t^2}\right ) . </math> | <math display="block">j=\rho v = \frac{1}{2i} (\psi^* \nabla \psi - \psi \nabla \psi^*)= \rho \left (k_0+\frac{4t(x-k_0 t)}{1+4t^2}\right ) . </math> | ||
== क्वांटम यांत्रिकी में गाऊसी तरंग संकुल == | |||
[[File:Wavepacket1.gif|thumb|right|1डी समतल तरंगों (नीला) का अध्यारोपण जो एक क्वांटम गॉसियन तरंग संकुल (लाल) बनाता है जो बड़ा होते समय दाईं ओर बड़ा होता है। नीले बिंदु प्रत्येक समतल तरंग के चरण वेग का अनुसरण करते है जबकि लाल रेखा केंद्रीय समूह वेग का अनुसरण करती है।]] | |||
[[File:Gaussian wavepacket tunneling in potential well.gif|thumbnail|right|एक केंद्रित संभावित दीवार में आवधिक क्वांटम टनलिंग का अनुभव करने वाले एक अनंत संभावित अच्छी तरह से फंस गए प्रारंभिक गॉसियन स्थिति की स्थिति स्पेस संभावना घनत्व।]] | |||
[[File:Gaussian wavepacket tunneling in potential well.gif|thumbnail|right|एक केंद्रित संभावित दीवार में आवधिक क्वांटम टनलिंग का अनुभव करने वाले एक अनंत संभावित अच्छी तरह से फंस गए प्रारंभिक गॉसियन | |||
[[File:Wavepacket-a2k4-en.gif|300px|thumb|1डी गॉसियन | [[File:Wavepacket-a2k4-en.gif|300px|thumb|1डी गॉसियन तरंग संकुल जटिल विमान में दिखाया गया है {{mvar|a}}=2 और {{mvar|k}}=4]]उपरोक्त बड़ा होाने वाला गॉसियन तरंग संकुल असामान्य और केवल मूल पर केंद्रित होता है इसके अतिरिक्त {{mvar|t}}=0 अब 3डी में लिखा जा सकता है और मानक इकाइयों में होता है:<ref>{{harvnb|Pauli|2000}}</ref><ref>{{harvnb|Abers|Pearson|2004}}</ref> | ||
<math display="block"> \psi(\mathbf{r},0) = e^{-\mathbf{r}\cdot\mathbf{r}/ 2a},</math> | <math display="block"> \psi(\mathbf{r},0) = e^{-\mathbf{r}\cdot\mathbf{r}/ 2a},</math> | ||
जहाँ {{mvar|a}} एक धनात्मक वास्तविक संख्या होती है और तरंग संकुल की चौड़ाई का वर्ग होता है | |||
<math display="block">a = 2\langle \mathbf r \cdot \mathbf r\rangle/3\langle 1\rangle = 2 (\Delta x)^2.</math> | <math display="block">a = 2\langle \mathbf r \cdot \mathbf r\rangle/3\langle 1\rangle = 2 (\Delta x)^2.</math> | ||
तरंग संख्या के संदर्भ में फूरियर रूपांतरण भी गॉसियन है | तरंग संख्या के संदर्भ में फूरियर रूपांतरण भी गॉसियन होता है {{mvar|t}}=0 के-वेक्टर उलटा होता है | ||
के-वेक्टर | |||
<math display="block">1/a = 2\langle\mathbf k\cdot \mathbf k\rangle/3\langle 1\rangle = 2 (\Delta p_x/\hbar)^2,</math> | <math display="block">1/a = 2\langle\mathbf k\cdot \mathbf k\rangle/3\langle 1\rangle = 2 (\Delta p_x/\hbar)^2,</math> | ||
जिससे कि | |||
<math display="block">\Delta x \Delta p_x = \hbar/2,</math> | <math display="block">\Delta x \Delta p_x = \hbar/2,</math> | ||
अर्थात यह अनिश्चितता के संबंध को संतृप्त करता है | |||
<math display="block"> \psi(\mathbf{k},0) = (2\pi a)^{3/2} e^{- a \mathbf{k}\cdot\mathbf{k}/2}.</math> | <math display="block"> \psi(\mathbf{k},0) = (2\pi a)^{3/2} e^{- a \mathbf{k}\cdot\mathbf{k}/2}.</math> | ||
प्रत्येक | प्रत्येक तरंग केवल समय में चरण-घूर्णन करती है जिससे कि समय पर निर्भर फूरियर-रूपांतरित समाधान होता है | ||
{{Equation box 1 | {{Equation box 1 | ||
|indent =: | |indent =: | ||
| Line 103: | Line 99: | ||
|border colour = #0073CF | |border colour = #0073CF | ||
|background colour=#F9FFF7}} | |background colour=#F9FFF7}} | ||
उलटा फूरियर रूपांतरण अभी भी गॉसियन है | उलटा फूरियर रूपांतरण अभी भी गॉसियन होता है लेकिन अब पैरामीटर है {{mvar|a}} जटिल हो जाता है और एक समग्र सामान्यीकरण कारक होता है।<ref>{{harvnb|Schiff|1968}}</ref> | ||
{{Equation box 1 | {{Equation box 1 | ||
|indent =: | |indent =: | ||
| Line 112: | Line 108: | ||
|background colour=#F9FFF7}} | |background colour=#F9FFF7}} | ||
इसका अभिन्न अंग {{math|Ψ}} सभी जगह अपरिवर्तनीय होता है क्योंकि यह आंतरिक उत्पाद होता है {{math|Ψ}} शून्य ऊर्जा की स्थिति के साथ जो अनंत तरंग दैर्ध्य वाली एक तरंग होती है जो निरंतर कार्य करती है। किसी भी स्वदेशी के लिए {{math|''η''(''x'')}} आंतरिक उत्पाद होता है | |||
<math display="block">\langle \eta | \psi \rangle = \int \eta(\mathbf{r}) \psi(\mathbf{r})d^3\mathbf{r},</math> | <math display="block">\langle \eta | \psi \rangle = \int \eta(\mathbf{r}) \psi(\mathbf{r})d^3\mathbf{r},</math> | ||
केवल समय में सरल | केवल समय में सरल विधि से परिवर्तन होता है: इसका चरण ऊर्जा द्वारा निर्धारित आवृत्ति के साथ घूमता है {{math|''η''}}. जब {{math|''η''}} में शून्य ऊर्जा होती है अनंत दैर्ध्य तरंग की तरह यह बिल्कुल भी नहीं बदलती है। | ||
अभिन्न {{math|∫ {{!}}Ψ{{!}}<sup>2</sup>''d''<sup>3</sup>''r''}} भी अपरिवर्तनीय है | अभिन्न {{math|∫ {{!}}Ψ{{!}}<sup>2</sup>''d''<sup>3</sup>''r''}} भी अपरिवर्तनीय होती है जो प्रायिकता के संरक्षण का कथन होती है। स्पष्ट रूप से | ||
{{Equation box 1 | {{Equation box 1 | ||
|indent =: | |indent =: | ||
| Line 124: | Line 120: | ||
|border colour = #0073CF | |border colour = #0073CF | ||
|background colour=#F9FFF7}} | |background colour=#F9FFF7}} | ||
जिसमें {{math|{{radic|''a''}}}} की चौड़ाई है {{math|''P''(''r'')}} पर {{math|1=''t'' = 0}} | जिसमें {{math|{{radic|''a''}}}} की चौड़ाई होती है {{math|''P''(''r'')}} पर {{math|1=''t'' = 0}}, {{math|''r''}} मूल बिंदु से दूरी होती है, कण की गति शून्य होती है, और समय मूल {{math|1=''t'' = 0}} मनमाने ढंग से चुनता है। | ||
गॉसियन की चौड़ाई | गॉसियन की चौड़ाई रोचक मात्रा होती है जिसे संभाव्यता घनत्व से पढ़ा जा सकता है {{math|{{!}}Ψ{{!}}<sup>2</sup>}} | ||
<math display="block"> \sqrt{a^2 + (\hbar t/m)^2 \over a}.</math> | <math display="block"> \sqrt{a^2 + (\hbar t/m)^2 \over a}.</math> | ||
यह चौड़ाई अंततः समय के साथ रैखिक रूप से बढ़ती है | यह चौड़ाई अंततः समय के साथ रैखिक रूप से बढ़ती है जैसे {{math|''ħt''/(''m''{{radic|''a''}})}} तरंग-संकुल प्रसार का संकेत देता है।<ref>Darwin, C. G. (1927). "Free motion in the wave mechanics", ''Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character'' '''117''' (776), 258-293.</ref> | ||
यह रैखिक वृद्धि | उदाहरण के लिए यदि एक इलेक्ट्रॉन तरंग संकुल प्रारंभ में परमाणु आयामों के क्षेत्र में स्थानीयकृत होता है (अर्थात {{math|10<sup>−10</sup>}} मी) तो संकुल की चौड़ाई लगभग दोगुनी हो जाती है {{math|10<sup>−16</sup>}}। स्पष्ट रूप से कण तरंग संकुल वास्तव में बहुत तेजी से बड़ा होता है:<ref>{{harvnb|Fitzpatrick}}</ref> उदाहरण के लिए {{math|1}} ms चौड़ाई लगभग एक किलोमीटर होती है। | ||
यह रैखिक वृद्धि गति अनिश्चितता का प्रतिबिंब होता है: तरंग संकुल एक संकीर्ण तक ही सीमित होता है {{math|1=Δ''x'' = {{radical|''a''/2}}}} और इसलिए एक गति होती है जो अनिश्चित होती है {{math|''ħ''/{{radical|2''a''}}}} इसके वेग में प्रसार {{math|''ħ/m''{{radical|2''a''}}}} और इस प्रकार भविष्य की स्थिति में {{math|''ħt /m''{{radical|2''a''}}}}. अनिश्चितता का संबंध तब एक सख्त असमानता होता है जब तक वास्तव में संतृप्ति से बहुत दूर नही होती है प्रारंभिक अनिश्चितता {{math|1=Δ''x''Δ''p'' = ''ħ''/2}} अब के गुणक से बढ़ जाता है {{math|''ħt/ma''}} (बड़े के लिए {{math|''t''}} होता है) | |||
== हवादार लहर ट्रेन == | == हवादार लहर ट्रेन == | ||
उपरोक्त गाऊसी तरंग | उपरोक्त गाऊसी तरंग संकुल के विपरीत यह देखा गया है<ref>{{harvnb|Berry|Balazs|1979}}</ref> कि वह एक विशेष लहर हवादार कार्यों के आधार पर आकार को बनाए रखते हुए प्रसार के बिना स्वतंत्र रूप से प्रचार करता है। यह एक बल क्षेत्र की अनुपस्थिति के बिना रुकता है: {{math|1=''ψ'' = Ai(''B''(''x'' − ''B''<sup>3</sup>''t''<sup>2</sup>)) exp(''iB''<sup>3</sup>''t''(''x'' − 2''B''<sup>3</sup>''t''<sup>2</sup>/3))}}. (सरलता के लिए {{math|1=''ħ'' = 1}} {{math|1=''m'' = 1/2}} और B एक स्थिरांक है cf. आयामीकरण।) | ||
हवादार कार्यों के आधार पर | |||
[[File:AiryFrontWF.gif|220px|thumb|के लिए समय विकास का छोटा दृश्य | [[File:AiryFrontWF.gif|220px|thumb|के लिए समय विकास का छोटा दृश्य | ||
फेज स्पेस में हवादार फ्रंट। (एनिमेट करने के लिए क्लिक करें।)]]फिर भी | फेज स्पेस में हवादार फ्रंट। (एनिमेट करने के लिए क्लिक करें।)]]फिर भी इस बल-मुक्त स्थिति में एरेनफेस्ट के प्रमेय के साथ कोई असंगति नही होतीं है क्योंकि स्थिति गैर-सामान्यीकरण योग्य होता है और एक अपरिभाषित (अनंत) होती है। इसे परिभाषित किया जा सकता है {{math|1=⟨''p''⟩ = 0}} | ||
[[ चरण स्थान ]] में | [[ चरण स्थान |चरण स्थान]] में यह इस तरंगट्रेन की [[शुद्ध अवस्था]] [[विग्नर क्वासिप्रोबेबिलिटी डिस्ट्रीब्यूशन|विग्नर क्वासिप्रोबेबिलिटी वितरण]] में स्पष्ट है जिसका x और p में आकार समय बढ़ने के साथ अपरिवर्तनीय होता है लेकिन जिनकी विशेषताएं परबोलस को तेज करने में दाईं ओर बढ़ती है {{math|1=''B''(''x'' − ''B''<sup>3</sup>''t''<sup>2</sup>) + (''p''/''B'' − ''tB''<sup>2</sup>)<sup>2</sup> = 0}} <ref>From a general pedagogy web-site by {{harvnb|Curtright}}.</ref> | ||
<math display="block">W(x,p;t) = W(x-B^3 t^2, p-B^3 t ;0) = {1\over 2^{1/3} \pi B} ~ \mathrm{Ai} \left(2^{2/3} \left(Bx + {p^2\over B^2}- 2Bpt\right)\right). </math> | <math display="block">W(x,p;t) = W(x-B^3 t^2, p-B^3 t ;0) = {1\over 2^{1/3} \pi B} ~ \mathrm{Ai} \left(2^{2/3} \left(Bx + {p^2\over B^2}- 2Bpt\right)\right). </math> | ||
सभी को एकीकृत करके प्राप्त संवेग वितरण पर ध्यान | सभी को एकीकृत करके प्राप्त संवेग वितरण पर ध्यान देता है {{mvar|x}} स्थिर रहता है। चूँकि यह विग्नर क्वासिप्रोबेबिलिटी वितरण गणितीय गुण होता है यह स्पष्ट होता है कि तरंग कार्य स्वयं सामान्य नही होती है। | ||
2018 में इज़राइली जर्मन और अमेरिकी विश्वविद्यालयों के शोधकर्ताओं के सहयोग से हवादार तरंग संकुलों को गति देने के क्यूबिक चरण का पहला प्रायोगिक अवलोकन प्राप्त किया गया था।<ref>{{cite journal|title=रैखिक विभव में वेव पैकेट का आयाम और चरण|year=2019 |url=https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.124302|publisher=American Physical Society, Phys. Rev. Lett.|doi=10.1103/PhysRevLett.122.124302 |last1=Rozenman |first1=Georgi Gary |last2=Zimmermann |first2=Matthias |last3=Efremov |first3=Maxim A. |last4=Schleich |first4=Wolfgang P. |last5=Shemer |first5=Lev |last6=Arie |first6=Ady |journal=Physical Review Letters |volume=122 |issue=12 |page=124302 |pmid=30978087 |bibcode=2019PhRvL.122l4302R |s2cid=111389900 }}</ref> | |||
== मुक्त प्रचारक == | == मुक्त प्रचारक == | ||
गाऊसी तरंग | गाऊसी तरंग संकुल समाधान की संकीर्ण-चौड़ाई सीमा पर चर्चा की गई मुक्त प्रचारक मुक्त कण और हार्मोनिक ऑसीलेटर का प्रचारकर्ता है {{mvar|K}}. अन्य अंतर समीकरणों के लिए इसे सामान्यतः ग्रीन का कार्य कहा जाता है <ref>{{harvnb|Jackson|1975}}</ref> लेकिन क्वांटम यांत्रिकी में फूरियर रूपांतरण के समय के लिए ग्रीन के कार्य का नाम आरक्षित करना पारंपरिक होता है {{mvar|K}}. | ||
सरलता के लिए एक आयाम पर | सरलता के लिए एक आयाम पर लौटता है m और ħ को एक के बराबर सेट करता है जब {{mvar|a}} अपरिमित मात्रा है {{mvar|ε}} गॉसियन प्रारंभिक स्थिति को पुनर्विभाजित करता है जिससे कि इसका अभिन्न होती है | ||
<math display="block"> \psi_0(x) = {1\over \sqrt{2\pi \varepsilon} } e^{-{x^2\over 2\varepsilon}} \,</math> | <math display="block"> \psi_0(x) = {1\over \sqrt{2\pi \varepsilon} } e^{-{x^2\over 2\varepsilon}} \,</math> | ||
एक डायराक डेल्टा | एक डायराक डेल्टा घटक बन जाता है {{math|''δ''(''x'')}} जिससे कि इसका समय विकास होता है | ||
<math display="block"> K_t(x) = {1\over \sqrt{2\pi (i t + \varepsilon)}} e^{ - x^2 \over 2it+\varepsilon }\,</math> | <math display="block"> K_t(x) = {1\over \sqrt{2\pi (i t + \varepsilon)}} e^{ - x^2 \over 2it+\varepsilon }\,</math> | ||
प्रचारक देता है। | प्रचारक देता है। | ||
एक बहुत ही संकीर्ण प्रारंभिक तरंग संकुल तुरन्त असीम रूप से चौड़ा हो जाता है लेकिन एक चरण के साथ जो x के बड़े मूल्यों पर अधिक तेजी से दोलनशील होता है। यह अजीब लग सकता है - समाधान एक बिंदु पर स्थानीय होने से बाद के समय में हर जगह होने के लिए जाता है लेकिन यह एक स्थानीयकृत कण के विशाल अनिश्चितता सिद्धांत का प्रतिबिंब होता है जैसा कि ऊपर बताया गया है। | |||
तरंग घटक का मानदंड अनंत होता है जो कि सही भी होता है क्योंकि [[डिराक डेल्टा समारोह]] का वर्ग उसी तरह भिन्न होता है। | |||
सम्मलित करने वाला कारक {{mvar|ε}} एक अतिसूक्ष्म मात्रा होती है जो यह सुनिश्चित करने के लिए होता है कि इंटीग्रल ओवर होता है {{mvar|K}} अच्छी तरह से परिभाषित होता है। उस सीमा में {{math|''ε'' → 0}} {{mvar|K}} विशुद्ध रूप से दोलनशील हो जाता है और अभिन्न अंग बन जाता है {{mvar|K}} बिल्कुल अभिसारी नही होता है। इस खंड के शेष भाग में इसे शून्य पर सेट किया जाता है लेकिन मध्यवर्ती स्थितियों पर सभी एकीकरणों को अच्छी तरह से परिभाषित करने के लिए सीमा ε→0 को केवल अंतिम स्थिति की गणना के बाद ही लिया जाता है। | |||
प्रोपेगेटर समय टी पर बिंदु x तक पहुंचने के लिए आयाम है | प्रोपेगेटर समय टी पर बिंदु x तक पहुंचने के लिए आयाम होता है जब मूल बिंदु x = 0 पर प्रारंभ होता है। अनुवाद व्युत्क्रम द्वारा बिंदु y पर प्रारंभ होने पर बिंदु x तक पहुँचने के लिए आयाम एक ही कार्य केवल अब अनुवादित होता है | ||
<math display="block"> K_t(x,y) = K_t(x-y) = {1\over \sqrt{2\pi it}} e^{i(x-y)^2 \over 2t} \, .</math> | <math display="block"> K_t(x,y) = K_t(x-y) = {1\over \sqrt{2\pi it}} e^{i(x-y)^2 \over 2t} \, .</math> | ||
सीमा में जब टी छोटा होता है | सीमा में जब टी छोटा होता है प्रचारक डेल्टा घटक में जाता है | ||
<math display="block"> \lim_{t \to 0} K_t(x-y) = \delta(x-y) ~,</math> | <math display="block"> \lim_{t \to 0} K_t(x-y) = \delta(x-y) ~,</math> | ||
लेकिन केवल [[वितरण (गणित)]] के अर्थ में: इस मात्रा का अभिन्न अंग एक मनमाने ढंग से विभेदित परीक्षण | लेकिन केवल [[वितरण (गणित)]] के अर्थ में: इस मात्रा का अभिन्न अंग एक मनमाने ढंग से विभेदित परीक्षण घटक से गुणा करके परीक्षण घटक का मान शून्य पर देता है। | ||
इसे देखने के लिए | इसे देखने के लिए सभी स्थान पर समाकल {{mvar|K}} हमेशा 1 के बराबर होता है | ||
<math display="block"> \int K_t(x) dx = 1 \, ,</math> | <math display="block"> \int K_t(x) dx = 1 \, ,</math> | ||
चूँकि यह समाकल एकसमान तरंग फलन के साथ K का आंतरिक-उत्पाद है। लेकिन एक्सपोनेंट में चरण कारक मूल को छोड़कर हर जगह एक गैर-स्थानिक स्थानिक व्युत्पन्न होता है | चूँकि यह समाकल एकसमान तरंग फलन के साथ K का आंतरिक-उत्पाद होता है। लेकिन एक्सपोनेंट में चरण कारक मूल को छोड़कर हर जगह एक गैर-स्थानिक स्थानिक व्युत्पन्न होता है और इसलिए जब समय छोटा होता है तो एक बिंदु पर तेजी से चरण रद्दीकरण होते है। यह सख्ती से सच होता है जब सीमा ε→0 को बिल्कुल अंत में लिया जाता है। | ||
तो प्रसार कर्नेल एक डेल्टा | तो प्रसार कर्नेल एक डेल्टा घटक का समय विकास होता है और यह निरंतर होता है एक अर्थ में यह छोटे समय में प्रारंभिक डेल्टा घटक में जाता है। यदि प्रारंभिक तरंग घटक स्थिति में एक असीम रूप से संकीर्ण होता है {{mvar|y}} | ||
<math display="block"> \psi_0(x) = \delta(x - y) \, ,</math> | <math display="block"> \psi_0(x) = \delta(x - y) \, ,</math> | ||
यह दोलनशील तरंग बन जाती है | यह दोलनशील तरंग बन जाती है | ||
<math display="block"> \psi_t(x) = {1\over \sqrt{2\pi i t}} e^{ i (x-y) ^2 /2t} \, .</math> | <math display="block"> \psi_t(x) = {1\over \sqrt{2\pi i t}} e^{ i (x-y) ^2 /2t} \, .</math> | ||
अब | अब चूँकि प्रत्येक फलन को इस तरह के संकीर्ण भारित योग के रूप में लिखा जा सकता है | ||
<math display="block"> \psi_0(x) = \int \psi_0(y) \delta(x-y) dy \, ,</math> | <math display="block"> \psi_0(x) = \int \psi_0(y) \delta(x-y) dy \, ,</math> | ||
हर | हर समय का विकास होता है {{mvar|ψ}}<sub>0</sub> इस प्रचार कर्नेल द्वारा निर्धारित किया जाता है {{mvar|K}} | ||
{{Equation box 1 | {{Equation box 1 | ||
|indent =: | |indent =: | ||
| Line 190: | Line 184: | ||
|bgcolor=#F9FFF7}} | |bgcolor=#F9FFF7}} | ||
इस प्रकार | इस प्रकार यह [[मौलिक समाधान]] या ''सामान्य समाधान'' को व्यक्त करने की एक औपचारिक विधि होती है। इस व्यंजक की व्याख्या यह है कि किसी बिंदु पर पाए जाने वाले कण का आयाम {{mvar|x}} समय पर {{mvar|t}} वह आयाम है जिस पर यह प्रारंभ हुआ था {{mvar|y}} उस आयाम का गुना जिससे वह गया था {{mvar|y}} को {{mvar|x}} सभी संभावित प्रारंभी बिंदुओं का योग होता है। दूसरे शब्दों में यह कर्नेल का [[कनवल्शन]] होता है {{mvar|K}} मनमानी प्रारंभिक स्थिति के साथ होता है {{math|''ψ''<sub>0</sub>}} | ||
<math display="block"> \psi_t = K * \psi_0 \, .</math> | <math display="block"> \psi_t = K * \psi_0 \, .</math> | ||
चूंकि आयाम से यात्रा करने के लिए {{mvar|x}} को {{mvar|y}} कुछ समय के बाद {{mvar|t}}+{{mvar|t}}' दो चरणों में माना जा सकता है | चूंकि आयाम से यात्रा करने के लिए {{mvar|x}} को {{mvar|y}} कुछ समय के बाद {{mvar|t}}+{{mvar|t}}' दो चरणों में माना जा सकता है प्रचारक रचना पहचान का पालन करता है | ||
<math display="block">\int K(x-y;t)K(y-z;t')dy = K(x-z;t+t')~ ,</math> | <math display="block">\int K(x-y;t)K(y-z;t')dy = K(x-z;t+t')~ ,</math> | ||
जिसकी व्याख्या इस प्रकार की जा सकती है: | जिसकी व्याख्या इस प्रकार की जा सकती है: जिसे आयाम से यात्रा करनी होती है {{mvar|x}} को {{mvar|z}} समय के भीतर {{mvar|t}}+{{mvar|t}}' से यात्रा करने के लिए आयाम का योग होता है {{mvar|x}} को {{mvar|y}} समय के भीतर {{mvar|t}} से यात्रा करने के लिए आयाम से गुणा {{mvar|y}} को {{mvar|z}} समय के भीतर {{mvar|t}}' सभी संभावित मध्यवर्ती स्थितियों y पर अभिव्यक्त करता है। यह एक मनमाना क्वांटम प्रणाली की एक संपत्ति होती है और समय को कई खंडों में विभाजित करता है यह समय के विकास को [[पथ अभिन्न सूत्रीकरण]] के रूप में व्यक्त करने की अनुमति देता है।<ref>{{harvnb|Feynman|Hibbs|1965}}</ref> | ||
== प्रसार के लिए विश्लेषणात्मक निरंतरता == | |||
{{See also|ऊष्मा समीकरण#मौलिक समाधान|गिरी गरम}} | |||
क्वांटम यांत्रिकी में तरंग संकुलों का [[प्रसार]] में संभाव्यता घनत्व के प्रसार से सीधे संबंधित होता है। एक कण के लिए जो यादृच्छिक चलता है किसी भी बिंदु पर संभाव्यता घनत्व समारोह [[प्रसार समीकरण]] को संतुष्ट करता है | |||
क्वांटम यांत्रिकी में तरंग | |||
<math display="block"> {\partial \over \partial t} \rho = {1\over 2} {\partial^2 \over \partial x^2 } \rho ~,</math> | <math display="block"> {\partial \over \partial t} \rho = {1\over 2} {\partial^2 \over \partial x^2 } \rho ~,</math> | ||
जहां 2 का कारक | जहां 2 का कारक जिसे समय या स्थान को फिर से स्केल करके हटाया जा सकता है केवल सुविधा के लिए होता है। | ||
इस समीकरण का एक समाधान प्रसार गॉसियन है | इस समीकरण का एक समाधान प्रसार गॉसियन होता है | ||
<math display="block"> \rho_t(x) = {1\over \sqrt{2\pi t}} e^{-x^2 \over 2t} ~,</math> | <math display="block"> \rho_t(x) = {1\over \sqrt{2\pi t}} e^{-x^2 \over 2t} ~,</math> | ||
और | और ρ<sub>t</sub> के अभिन्न अंग के बाद से स्थिर होता है जबकि चौड़ाई कम समय में संकीर्ण होता है यह घटक टी = 0 पर डेल्टा घटक तक पहुंचता है | ||
<math display="block"> \lim_{t \to 0} \rho_t(x) = \delta(x) </math> | <math display="block"> \lim_{t \to 0} \rho_t(x) = \delta(x) </math> | ||
फिर से केवल वितरण | फिर से केवल वितरण का अर्थ होता है जिससे कि | ||
<math display="block"> \lim_{t \to 0} \int_x f(x) \rho_t(x) = f(0) </math> | <math display="block"> \lim_{t \to 0} \int_x f(x) \rho_t(x) = f(0) </math> | ||
किसी भी सुचारू परीक्षण कार्य के लिए {{mvar|f}}. | किसी भी सुचारू परीक्षण कार्य के लिए {{mvar|f}}. | ||
प्रसार गाऊसी प्रसार समीकरण के लिए प्रसार कर्नेल है और यह कनवल्शन आइडेंटिटी का पालन करता है | प्रसार गाऊसी प्रसार समीकरण के लिए प्रसार कर्नेल होता है और यह कनवल्शन आइडेंटिटी का पालन करता है | ||
<math display="block"> K_{t+t'} = K_{t}*K_{t'} \, ,</math> | <math display="block"> K_{t+t'} = K_{t}*K_{t'} \, ,</math> | ||
जो प्रसार को पथ अभिन्न के रूप में व्यक्त करने की अनुमति देता है। प्रचारक एक ऑपरेटर का घातीय है {{mvar|H}} | जो प्रसार को पथ अभिन्न के रूप में व्यक्त करने की अनुमति देता है। प्रचारक एक ऑपरेटर का घातीय होता है {{mvar|H}} | ||
<math display="block"> K_t(x) = e^{-tH} \, ,</math> | <math display="block"> K_t(x) = e^{-tH} \, ,</math> | ||
जो कि अतिसूक्ष्म प्रसार संचालक होता है | |||
<math display="block"> H= -{\nabla^2\over 2} \, .</math> | <math display="block"> H= -{\nabla^2\over 2} \, .</math> | ||
एक मैट्रिक्स में दो सूचकांक होते | एक मैट्रिक्स में दो सूचकांक होते है जो निरंतर स्थान में इसे एक कार्य बनाते है {{mvar|x}} और {{mvar|x}}'। इस स्थिति में अनुवाद अपरिवर्तनीयता के कारण मैट्रिक्स तत्व {{mvar|K}} केवल स्थिति के अंतर पर निर्भर करता है और संकेतन का एक सुविधाजनक दुरुपयोग ऑपरेटर मैट्रिक्स तत्वों उसी नाम से संदर्भित करता है: | ||
<math display="block"> K_t(x,x') = K_t(x-x') \, .</math> | <math display="block"> K_t(x,x') = K_t(x-x') \, .</math> | ||
अनुवाद आक्रमण का अर्थ है कि निरंतर मैट्रिक्स गुणन | अनुवाद आक्रमण का अर्थ होता है कि निरंतर मैट्रिक्स गुणन होता है | ||
<math display="block"> C(x,x'') = \int_{x'} A(x,x')B(x',x'') \, ,</math> | <math display="block"> C(x,x'') = \int_{x'} A(x,x')B(x',x'') \, ,</math> | ||
अनिवार्य रूप से कनवल्शन है | अनिवार्य रूप से कनवल्शन होता है | ||
<math display="block"> C(\Delta) = C(x-x'') = \int_{x'} A(x-x') B(x'-x'') = \int_{y} A(\Delta-y)B(y) \, .</math> | <math display="block"> C(\Delta) = C(x-x'') = \int_{x'} A(x-x') B(x'-x'') = \int_{y} A(\Delta-y)B(y) \, .</math> | ||
एक्सपोनेंशियल को टीएस की एक सीमा पर परिभाषित किया जा सकता है जिसमें जटिल मान | एक्सपोनेंशियल को टीएस की एक सीमा पर परिभाषित किया जा सकता है जिसमें जटिल मान सम्मलित होता है जब तक प्रसार कर्नेल पर अभिन्न अभिसरण रहता है | ||
<math display="block"> K_z(x) = e^{-zH} \, .</math> | <math display="block"> K_z(x) = e^{-zH} \, .</math> | ||
जब तक | जब तक असली हिस्सा {{mvar|z}} सकारात्मक के बड़े मूल्यों के लिए {{mvar|x}} {{mvar|K}} तेजी से घट रहा होता है और अभिन्न खत्म हो जाता है {{mvar|K}} वास्तव में बिल्कुल अभिसारी होता है। | ||
इसके लिए इस अभिव्यक्ति की सीमा {{mvar|z}} शुद्ध काल्पनिक अक्ष के निकट आने वाला उपरोक्त श्रोडिंगर प्रचारक का सामना करता है | |||
<math display="block"> K_t^{\rm Schr} = K_{it+\varepsilon} = e^{-(it+\varepsilon)H} \, ,</math> | <math display="block"> K_t^{\rm Schr} = K_{it+\varepsilon} = e^{-(it+\varepsilon)H} \, ,</math> | ||
जो गौसियनों के उपरोक्त समय के विकास को दर्शाता है। | जो गौसियनों के उपरोक्त समय के विकास को दर्शाता है। | ||
घातांक | घातांक या पथ एकीकरण की मौलिक पहचान से | ||
<math display="block"> K_z * K_{z'} = K_{z+z'} \,</math> | <math display="block"> K_z * K_{z'} = K_{z+z'} \,</math> | ||
सभी जटिल जेड मूल्यों के लिए धारण करता है | सभी जटिल जेड मूल्यों के लिए धारण करता है जहां अभिन्न बिल्कुल अभिसरण होता है जिससे कि ऑपरेटरों को अच्छी तरह से परिभाषित किया जाता है। | ||
इस प्रकार | इस प्रकार गॉसियन का क्वांटम विकास जो जटिल प्रसार कर्नेल K होता है | ||
<math display="block"> \psi_0(x) = K_a(x) = K_a * \delta(x) \,</math> | <math display="block"> \psi_0(x) = K_a(x) = K_a * \delta(x) \,</math> | ||
समय विकसित | समय विकसित स्थिति के बराबर होता है | ||
<math display="block"> \psi_t = K_{it} * K_a = K_{a+it} \, .</math> | <math display="block"> \psi_t = K_{it} * K_a = K_{a+it} \, .</math> | ||
यह जटिल गाऊसी समाधानों के उपरोक्त विसरित रूप को दिखाता है | यह जटिल गाऊसी समाधानों के उपरोक्त विसरित रूप को दिखाता है | ||
<math display="block"> \psi_t(x) = {1\over \sqrt{2\pi (a+it)} } e^{- {x^2\over 2(a+it)} } \, .</math> | <math display="block"> \psi_t(x) = {1\over \sqrt{2\pi (a+it)} } e^{- {x^2\over 2(a+it)} } \, .</math> | ||
== यह भी देखें == | == यह भी देखें == | ||
{{div col|colwidth=28em}} | {{div col|colwidth=28em}} | ||
| Line 299: | Line 290: | ||
* {{Citation|first1=M. V.|last1=Berry|first2=N. L.|last2=Balazs|year=1979|title=Nonspreading wave packets|journal=Am J Phys|volume=47|issue= 3|pages=264–267|doi=10.1119/1.11855|bibcode = 1979AmJPh..47..264B }} | * {{Citation|first1=M. V.|last1=Berry|first2=N. L.|last2=Balazs|year=1979|title=Nonspreading wave packets|journal=Am J Phys|volume=47|issue= 3|pages=264–267|doi=10.1119/1.11855|bibcode = 1979AmJPh..47..264B }} | ||
* {{Citation|author-link=John David Jackson (physicist)|last=Jackson|first=J. D.|year=1975|title=Classical Electrodynamics|edition=2nd|location=New York|publisher=[[John Wiley & Sons]], Inc.|isbn=978-0-471-43132-9|url-access=registration|url=https://archive.org/details/classicalelectro00jack_0}} | * {{Citation|author-link=John David Jackson (physicist)|last=Jackson|first=J. D.|year=1975|title=Classical Electrodynamics|edition=2nd|location=New York|publisher=[[John Wiley & Sons]], Inc.|isbn=978-0-471-43132-9|url-access=registration|url=https://archive.org/details/classicalelectro00jack_0}} | ||
* {{Citation|author-link=Richard Feynman|last1=Feynman|first1=R. P.|last2=Hibbs|first2=A. R.|title=Quantum Mechanics and Path Integrals|location=New York|publisher=[[McGraw-Hill]]|year=1965|isbn=978-0-07-020650-2|url-access=registration|url=https://archive.org/details/quantummechanics0000feyn}} ([[Dover Publications|Dover]] | * {{Citation|author-link=Richard Feynman|last1=Feynman|first1=R. P.|last2=Hibbs|first2=A. R.|title=Quantum Mechanics and Path Integrals|location=New York|publisher=[[McGraw-Hill]]|year=1965|isbn=978-0-07-020650-2|url-access=registration|url=https://archive.org/details/quantummechanics0000feyn}} ([[Dover Publications|Dover]] 2010 {{ISBN|0-486-47722-3}}.) | ||
* {{Citation| last= Wheeler|first=Nicholas|year=2004|title=Remarks concerning the Energetics of a Gaussian wavepacket| | * {{Citation| last= Wheeler|first=Nicholas|year=2004|title=Remarks concerning the Energetics of a Gaussian wavepacket| | ||
url=https://www.reed.edu/physics/faculty/wheeler/documents/Quantum%20Mechanics/Miscellaneous%20Essays/Energetics%20of%20a%20Gaussian.pdf}} | url=https://www.reed.edu/physics/faculty/wheeler/documents/Quantum%20Mechanics/Miscellaneous%20Essays/Energetics%20of%20a%20Gaussian.pdf}} | ||
| Line 316: | Line 307: | ||
* [https://www.youtube.com/watch?v=s8RIqZgFbXA A simulation of a wave package in 2D (According to FOURIER-Synthesis in 2D)] | * [https://www.youtube.com/watch?v=s8RIqZgFbXA A simulation of a wave package in 2D (According to FOURIER-Synthesis in 2D)] | ||
* {{Citation|last=Curtright|first=T.L.|url=http://www.physics.miami.edu/~curtright/TimeDependentWignerFunctions.html|title=Time-dependent Wigner Functions}} | * {{Citation|last=Curtright|first=T.L.|url=http://www.physics.miami.edu/~curtright/TimeDependentWignerFunctions.html|title=Time-dependent Wigner Functions}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Created On 09/03/2023]] | [[Category:Created On 09/03/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Missing redirects]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:क्वांटम यांत्रिकी]] | |||
[[Category:तरंग यांत्रिकी]] | |||
Latest revision as of 13:11, 8 June 2023
भौतिकी में तरंग संकुल स्थानीयकृत तरंग क्रिया की एक इकाई के रूप में यात्रा करता है। एक तरंग संकुल का विश्लेषण किया जा सकता है या विभिन्न तरंगों के घटक साइनसोइडल तरंगों के एक अनंत सेट से संश्लेषित किया जाता है।[1] प्रत्येक घटक तरंग घटक और तरंग संकुल समीकरण के समाधान होता है। तरंग समीकरण के आधार पर तरंग संकुल की रूपरेखा स्थिर रहती है या प्रसार के दौरान यह बदल सकती है।
क्वांटम यांत्रिकी तरंग संकुल को एक विशेष महत्व देती है, इसे प्रायिकता आयाम के रूप में व्याख्यायित किया जाता है इसका मानक वर्ग संभाव्यता घनत्व का वर्णन करता है कि किसी विशेष अवस्था में एक कण या कण को दी गई स्थिति या गति के लिए मापा जाता है। लहर समीकरण इस स्थिति में श्रोडिंगर समीकरण होता है और इसके आवेदन के माध्यम से मौलिक यांत्रिकी में हैमिल्टनियन यांत्रिकी औपचारिकता की प्रक्रिया के समान क्वांटम यांत्रिक प्रणाली के समय के विकास को कम करना संभव होता है। श्रोडिंगर समीकरण के समाधान के प्रसार चरित्र ने श्रोडिंगर समीकरण को खारिज करने में ऐतिहासिक पृष्ठभूमि और विकास श्रोडिंगर की मूल व्याख्या और बोर्न नियम को स्वीकार करने में महत्वपूर्ण भूमिका निभाई है।
लहर के समन्वय प्रतिनिधित्व में भौतिक वस्तु की स्थानीय संभावना की स्थिति संकुल समाधान की स्थिति से निर्दिष्ट होती है। इसके अतिरिक्त स्थानिक तरंग संकुल जितना संकरा होता है उतनी तरंग संकुल की स्थिति बेहतर होती है उतना तरंग के संवेग में प्रसार उतना ही बड़ा होता है। स्थिति में प्रसार और गति में प्रसार के बीच यह वर्नर हाइजेनबर्ग अनिश्चितता सिद्धांत की एक विशेषता होती है।
ऐतिहासिक पृष्ठभूमि
1900 के प्रारंभ में यह स्पष्ट हो गया कि क्लासिकल यांत्रिकी में कुछ बड़ी कमियां थी। आइजैक न्यूटन ने मूल रूप से इस विचार को प्रस्तावित किया था कि प्रकाश असतत संकुल में आता है जिसे उन्होंने कॉर्पसकल कहा था लेकिन कई प्रकाश घटनाओं के तरंग-समान व्यवहार ने वैज्ञानिकों को विद्युत चुंबकत्व के तरंग विवरण का पक्ष लेने के लिए प्रेरित किया था। यह 1930 के दशक तक नहीं था प्रकाश की कण प्रकृति को वास्तव में भौतिकी में व्यापक रूप से स्वीकार किया जाने लगा था। क्वांटम यांत्रिकी का विकास और भ्रमित करने वाले प्रायोगिक परिणामों की व्याख्या करने में इसकी सफलता, इसकी स्वीकृति के मूल में थी। इस प्रकार क्वांटम यांत्रिकी के निर्माण में बुनियादी अवधारणाओं में से एक यह है कि प्रकाश असतत बंडलों में आता है जिसे फोटॉन कहा जाता है। एक फोटॉन की ऊर्जा इसकी आवृत्ति होती है [2]
20वीं शताब्दी के दौरान क्वांटम यांत्रिकी के विचारों का विकास जारी रहा था। जिसमें सभी घटनाएं और पदार्थ असतत कणों से बनते थे और परस्पर क्रिया करते थे, चूँकि इन कणों को प्रायिकता तरंग द्वारा वर्णित किया गया था। इन संभाव्यता आयामों की गणना के लिए परस्पर स्थान को कम किया जाता है।
दुनिया की कण-जैसी प्रकृति की एक सदी से अधिक प्रयोग द्वारा पुष्टि की गई है जबकि तरंग जैसी घटना को क्वांटम कणों के तरंग संकुल पहलू के परिणाम के रूप में चित्रित किया गया है। संपूरकता के सिद्धांत के अनुसार तरंग-जैसी और कण-जैसी विशेषताएं कभी भी एक ही समय में अर्थात एक ही प्रयोग में प्रकट नहीं होती है।
मूल व्यवहार
गैर-बड़ा होाने वाला
प्रसार के बिना प्रसार के एक उदाहरण के रूप में क्लासिकल भौतिकी से निम्न तरंग समीकरण के तरंग समाधान पर विचार करता है
भौतिकी समय परिपाटी का उपयोग करते हुए e−iωt तरंग समीकरण के समतल-तरंग समाधान होता है
सरल बनाने के लिए केवल एक आयाम में बड़ा होने वाली तरंगों पर विचार करता है। तब सामान्य समाधान होता है
एक तरंग संकुल एक स्थानीय गड़बड़ी होती है जो कई अलग-अलग तरंग रूपों के योग से उत्पन्न करता है। यदि संकुल दृढ़ता से स्थानीयकृत है तो स्थानीयकरण के क्षेत्र में रचनात्मक सुपरपोजिशन और क्षेत्र के बाहर विनाशकारी सुपरपोजिशन की अनुमति देने के लिए अधिक आवृत्तियों की आवश्यकता होती है। मूल समाधानों से एक आयाम में तरंग संकुल के एक सामान्य रूप को व्यक्त किया जाता है
इस कारण से 1⁄√2π फूरियर रूपांतरण कन्वेंशन से आता है। आयाम A(k) में समतल-तरंग समाधानों के रैखिक सुपरपोजिशन के गुणांक होते है। बदले में इन गुणांकों को एक कार्य के रूप में व्यक्त किया जा सकता है u(x, t) पर मूल्यांकन किया गया t = 0 उपरोक्त फूरियर रूपांतरण संबंध को उल्टा करता है:
प्रसार वाला
 इसके विपरीत प्रसार के एक उदाहरण के रूप में अब प्रसार (प्रकाशिकी) के साथ के अतिरिक्त श्रोडिंगर समीकरण के समाधान पर विचार करता है (गैर-आयामी 2Δx m और ħ एक के बराबर सेट होता है)
इसके विपरीत प्रसार के एक उदाहरण के रूप में अब प्रसार (प्रकाशिकी) के साथ के अतिरिक्त श्रोडिंगर समीकरण के समाधान पर विचार करता है (गैर-आयामी 2Δx m और ħ एक के बराबर सेट होता है)
गति रूपरेखा A(k) अपरिवर्तनीय होती है। प्रायिकता धारा होती है
क्वांटम यांत्रिकी में गाऊसी तरंग संकुल
उपरोक्त बड़ा होाने वाला गॉसियन तरंग संकुल असामान्य और केवल मूल पर केंद्रित होता है इसके अतिरिक्त t=0 अब 3डी में लिखा जा सकता है और मानक इकाइयों में होता है:[3][4]
उलटा फूरियर रूपांतरण अभी भी गॉसियन होता है लेकिन अब पैरामीटर है a जटिल हो जाता है और एक समग्र सामान्यीकरण कारक होता है।[5]
इसका अभिन्न अंग Ψ सभी जगह अपरिवर्तनीय होता है क्योंकि यह आंतरिक उत्पाद होता है Ψ शून्य ऊर्जा की स्थिति के साथ जो अनंत तरंग दैर्ध्य वाली एक तरंग होती है जो निरंतर कार्य करती है। किसी भी स्वदेशी के लिए η(x) आंतरिक उत्पाद होता है
अभिन्न ∫ |Ψ|2d3r भी अपरिवर्तनीय होती है जो प्रायिकता के संरक्षण का कथन होती है। स्पष्ट रूप से
जिसमें √a की चौड़ाई होती है P(r) पर t = 0, r मूल बिंदु से दूरी होती है, कण की गति शून्य होती है, और समय मूल t = 0 मनमाने ढंग से चुनता है।
गॉसियन की चौड़ाई रोचक मात्रा होती है जिसे संभाव्यता घनत्व से पढ़ा जा सकता है |Ψ|2
उदाहरण के लिए यदि एक इलेक्ट्रॉन तरंग संकुल प्रारंभ में परमाणु आयामों के क्षेत्र में स्थानीयकृत होता है (अर्थात 10−10 मी) तो संकुल की चौड़ाई लगभग दोगुनी हो जाती है 10−16। स्पष्ट रूप से कण तरंग संकुल वास्तव में बहुत तेजी से बड़ा होता है:[7] उदाहरण के लिए 1 ms चौड़ाई लगभग एक किलोमीटर होती है।
यह रैखिक वृद्धि गति अनिश्चितता का प्रतिबिंब होता है: तरंग संकुल एक संकीर्ण तक ही सीमित होता है Δx = √a/2 और इसलिए एक गति होती है जो अनिश्चित होती है ħ/√2a इसके वेग में प्रसार ħ/m√2a और इस प्रकार भविष्य की स्थिति में ħt /m√2a. अनिश्चितता का संबंध तब एक सख्त असमानता होता है जब तक वास्तव में संतृप्ति से बहुत दूर नही होती है प्रारंभिक अनिश्चितता ΔxΔp = ħ/2 अब के गुणक से बढ़ जाता है ħt/ma (बड़े के लिए t होता है)
हवादार लहर ट्रेन
उपरोक्त गाऊसी तरंग संकुल के विपरीत यह देखा गया है[8] कि वह एक विशेष लहर हवादार कार्यों के आधार पर आकार को बनाए रखते हुए प्रसार के बिना स्वतंत्र रूप से प्रचार करता है। यह एक बल क्षेत्र की अनुपस्थिति के बिना रुकता है: ψ = Ai(B(x − B3t2)) exp(iB3t(x − 2B3t2/3)). (सरलता के लिए ħ = 1 m = 1/2 और B एक स्थिरांक है cf. आयामीकरण।)
फिर भी इस बल-मुक्त स्थिति में एरेनफेस्ट के प्रमेय के साथ कोई असंगति नही होतीं है क्योंकि स्थिति गैर-सामान्यीकरण योग्य होता है और एक अपरिभाषित (अनंत) होती है। इसे परिभाषित किया जा सकता है ⟨p⟩ = 0
चरण स्थान में यह इस तरंगट्रेन की शुद्ध अवस्था विग्नर क्वासिप्रोबेबिलिटी वितरण में स्पष्ट है जिसका x और p में आकार समय बढ़ने के साथ अपरिवर्तनीय होता है लेकिन जिनकी विशेषताएं परबोलस को तेज करने में दाईं ओर बढ़ती है B(x − B3t2) + (p/B − tB2)2 = 0 [9]
2018 में इज़राइली जर्मन और अमेरिकी विश्वविद्यालयों के शोधकर्ताओं के सहयोग से हवादार तरंग संकुलों को गति देने के क्यूबिक चरण का पहला प्रायोगिक अवलोकन प्राप्त किया गया था।[10]
मुक्त प्रचारक
गाऊसी तरंग संकुल समाधान की संकीर्ण-चौड़ाई सीमा पर चर्चा की गई मुक्त प्रचारक मुक्त कण और हार्मोनिक ऑसीलेटर का प्रचारकर्ता है K. अन्य अंतर समीकरणों के लिए इसे सामान्यतः ग्रीन का कार्य कहा जाता है [11] लेकिन क्वांटम यांत्रिकी में फूरियर रूपांतरण के समय के लिए ग्रीन के कार्य का नाम आरक्षित करना पारंपरिक होता है K.
सरलता के लिए एक आयाम पर लौटता है m और ħ को एक के बराबर सेट करता है जब a अपरिमित मात्रा है ε गॉसियन प्रारंभिक स्थिति को पुनर्विभाजित करता है जिससे कि इसका अभिन्न होती है
एक बहुत ही संकीर्ण प्रारंभिक तरंग संकुल तुरन्त असीम रूप से चौड़ा हो जाता है लेकिन एक चरण के साथ जो x के बड़े मूल्यों पर अधिक तेजी से दोलनशील होता है। यह अजीब लग सकता है - समाधान एक बिंदु पर स्थानीय होने से बाद के समय में हर जगह होने के लिए जाता है लेकिन यह एक स्थानीयकृत कण के विशाल अनिश्चितता सिद्धांत का प्रतिबिंब होता है जैसा कि ऊपर बताया गया है।
तरंग घटक का मानदंड अनंत होता है जो कि सही भी होता है क्योंकि डिराक डेल्टा समारोह का वर्ग उसी तरह भिन्न होता है।
सम्मलित करने वाला कारक ε एक अतिसूक्ष्म मात्रा होती है जो यह सुनिश्चित करने के लिए होता है कि इंटीग्रल ओवर होता है K अच्छी तरह से परिभाषित होता है। उस सीमा में ε → 0 K विशुद्ध रूप से दोलनशील हो जाता है और अभिन्न अंग बन जाता है K बिल्कुल अभिसारी नही होता है। इस खंड के शेष भाग में इसे शून्य पर सेट किया जाता है लेकिन मध्यवर्ती स्थितियों पर सभी एकीकरणों को अच्छी तरह से परिभाषित करने के लिए सीमा ε→0 को केवल अंतिम स्थिति की गणना के बाद ही लिया जाता है।
प्रोपेगेटर समय टी पर बिंदु x तक पहुंचने के लिए आयाम होता है जब मूल बिंदु x = 0 पर प्रारंभ होता है। अनुवाद व्युत्क्रम द्वारा बिंदु y पर प्रारंभ होने पर बिंदु x तक पहुँचने के लिए आयाम एक ही कार्य केवल अब अनुवादित होता है
इसे देखने के लिए सभी स्थान पर समाकल K हमेशा 1 के बराबर होता है
तो प्रसार कर्नेल एक डेल्टा घटक का समय विकास होता है और यह निरंतर होता है एक अर्थ में यह छोटे समय में प्रारंभिक डेल्टा घटक में जाता है। यदि प्रारंभिक तरंग घटक स्थिति में एक असीम रूप से संकीर्ण होता है y
इस प्रकार यह मौलिक समाधान या सामान्य समाधान को व्यक्त करने की एक औपचारिक विधि होती है। इस व्यंजक की व्याख्या यह है कि किसी बिंदु पर पाए जाने वाले कण का आयाम x समय पर t वह आयाम है जिस पर यह प्रारंभ हुआ था y उस आयाम का गुना जिससे वह गया था y को x सभी संभावित प्रारंभी बिंदुओं का योग होता है। दूसरे शब्दों में यह कर्नेल का कनवल्शन होता है K मनमानी प्रारंभिक स्थिति के साथ होता है ψ0
प्रसार के लिए विश्लेषणात्मक निरंतरता
क्वांटम यांत्रिकी में तरंग संकुलों का प्रसार में संभाव्यता घनत्व के प्रसार से सीधे संबंधित होता है। एक कण के लिए जो यादृच्छिक चलता है किसी भी बिंदु पर संभाव्यता घनत्व समारोह प्रसार समीकरण को संतुष्ट करता है
इस समीकरण का एक समाधान प्रसार गॉसियन होता है
प्रसार गाऊसी प्रसार समीकरण के लिए प्रसार कर्नेल होता है और यह कनवल्शन आइडेंटिटी का पालन करता है
इसके लिए इस अभिव्यक्ति की सीमा z शुद्ध काल्पनिक अक्ष के निकट आने वाला उपरोक्त श्रोडिंगर प्रचारक का सामना करता है
घातांक या पथ एकीकरण की मौलिक पहचान से
इस प्रकार गॉसियन का क्वांटम विकास जो जटिल प्रसार कर्नेल K होता है
यह भी देखें
- लहर
- लहर प्रसार
- फूरियर विश्लेषण
- समूह वेग
- चरण वेग
- मुक्त कण
- सुसंगत राज्य
- तरंग
- तरंगिका
- पदार्थ तरंग
- पल्स (सिग्नल प्रोसेसिंग)
- नाड़ी (भौतिकी)
- श्रोडिंगर समीकरण
- क्वांटम यांत्रिकी का परिचय
- सॉलिटन
टिप्पणियाँ
- ↑ By contrast, the introduction of interaction terms in dispersive equations, such as for the quantum harmonic oscillator, may result in the emergence of envelope-non-dispersive, classical-looking solutions—see coherent states: Such "minimum uncertainty states" do saturate the uncertainty principle permanently.
टिप्पणियाँ
- ↑ Manners 2000
- ↑ Einstein 1905
- ↑ Pauli 2000
- ↑ Abers & Pearson 2004
- ↑ Schiff 1968
- ↑ Darwin, C. G. (1927). "Free motion in the wave mechanics", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 117 (776), 258-293.
- ↑ Fitzpatrick
- ↑ Berry & Balazs 1979
- ↑ From a general pedagogy web-site by Curtright.
- ↑ Rozenman, Georgi Gary; Zimmermann, Matthias; Efremov, Maxim A.; Schleich, Wolfgang P.; Shemer, Lev; Arie, Ady (2019). "रैखिक विभव में वेव पैकेट का आयाम और चरण". Physical Review Letters. American Physical Society, Phys. Rev. Lett. 122 (12): 124302. Bibcode:2019PhRvL.122l4302R. doi:10.1103/PhysRevLett.122.124302. PMID 30978087. S2CID 111389900.
- ↑ Jackson 1975
- ↑ Feynman & Hibbs 1965
संदर्भ
- Einstein, Albert (1905), "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (On a Heuristic Viewpoint Concerning the Production and Transformation of Light)" (PDF), Annalen der Physik, 17 (6): 132–148, Bibcode:1905AnP...322..132E, doi:10.1002/andp.19053220607 This annus mirabilis paper on the photoelectric effect was received by Annalen der Physik 18 March 1905.
- Schiff, Leonard I. (1968), Quantum mechanics (third ed.), London: McGraw-Hill
- Joy Manners (2000), Quantum Physics: An Introduction, CRC Press, pp. 53–56, ISBN 978-0-7503-0720-8
- Pauli, Wolfgang (2000), Wave Mechanics: Volume 5 of Pauli Lectures on Physics, Books on Physics, Dover Publications, ISBN 978-0-486-41462-1
- Abers, E.; Pearson, Ed (2004), Quantum Mechanics, Addison Wesley, Prentice-Hall Inc., ISBN 978-0-13-146100-0
- Richard Fitzpatrick, Oscillations and Waves
- Berry, M. V.; Balazs, N. L. (1979), "Nonspreading wave packets", Am J Phys, 47 (3): 264–267, Bibcode:1979AmJPh..47..264B, doi:10.1119/1.11855
- Jackson, J. D. (1975), Classical Electrodynamics (2nd ed.), New York: John Wiley & Sons, Inc., ISBN 978-0-471-43132-9
- Feynman, R. P.; Hibbs, A. R. (1965), Quantum Mechanics and Path Integrals, New York: McGraw-Hill, ISBN 978-0-07-020650-2 (Dover 2010 ISBN 0-486-47722-3.)
- Wheeler, Nicholas (2004), Remarks concerning the Energetics of a Gaussian wavepacket (PDF)
बाहरी संबंध
 Learning materials related to wave packet motion at Wikiversity
Learning materials related to wave packet motion at Wikiversity The dictionary definition of wave packet at Wiktionary
The dictionary definition of wave packet at Wiktionary- 1d Wave packet plot in Google
- 1d Wave train and probability density plot in Google
- 2d Wave packet plot in Google
- 2d Wave train plot in Google
- 2d probability density plot in Google
- Quantum physics online : Interactive simulation of a free wavepacket
- Web-Schrödinger: Interactive 2D wave packet dynamics simulation
- A simulation of a wave package in 2D (According to FOURIER-Synthesis in 2D)
- Curtright, T.L., Time-dependent Wigner Functions