विखंडन: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
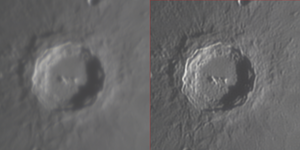
{{Short description|Reconstruction of a filtered signal}}{{Not to be confused with|Upsampling}}[[File:Deconvolution_of_an_astronomical_image.png|thumb|right|रिचर्डसन-लुसी डीकोनवोल्यूशन | रिचर्डसन-लुसी एल्गोरिथम का उपयोग करके चंद्र क्रेटर कोपरनिकस की एक छवि के विसंक्रमण से पहले और बाद में।]]गणित में, [[कनवल्शन]] का उलटा संक्रिया विसंक्रमण है। दोनों | {{Short description|Reconstruction of a filtered signal}}{{Not to be confused with|Upsampling}}[[File:Deconvolution_of_an_astronomical_image.png|thumb|right|रिचर्डसन-लुसी डीकोनवोल्यूशन | रिचर्डसन-लुसी एल्गोरिथम का उपयोग करके चंद्र क्रेटर कोपरनिकस की एक छवि के विसंक्रमण से पहले और बाद में।]]गणित में, [[कनवल्शन]] का उलटा संक्रिया विसंक्रमण है। दोनों संचालन [[ संकेत आगे बढ़ाना |संकेत प्रोसेसिंग]] और [[ मूर्ति प्रोद्योगिकी |इमेज प्रोसेसिंग]] में उपयोग किए जाते हैं। उदाहरण के लिए, निश्चित डिग्री स्पष्टता के साथ कनवल्शन विधि का उपयोग करके फ़िल्टर (कनवल्शन) के बाद मूल संकेत को पुनर्प्राप्त करना संभव हो सकता है।<ref>{{cite web |last=O'Haver |first=T. |title=सिग्नल प्रोसेसिंग का परिचय - डीकनवोल्यूशन|url=http://www.wam.umd.edu/~toh/spectrum/Deconvolution.html |publisher=University of Maryland at College Park |access-date=2007-08-15}}</ref> अभिलेख किए गए संकेत या छवि की माप त्रुटि के कारण, यह प्रदर्शित किया जा सकता है कि संकेत-टू-नॉइज़ अनुपात जितना व्यर्थ होगा, फिल्टर का उल्टा होना उतना ही व्यर्थ होगा | इसलिए, फ़िल्टर को उल्टा करना सदैव एक अच्छा समाधान नहीं होता है | क्योंकि त्रुटि बढ़ जाती है। कनवल्शन इस समस्या का समाधान प्रदान करता है। | ||
विसंक्रमण और समय-श्रृंखला विश्लेषण की नींव बड़े | विसंक्रमण और समय-श्रृंखला विश्लेषण की नींव बड़े मापदंड पर [[मैसाचुसेट्स की तकनीकी संस्था]] के [[नॉर्बर्ट वीनर]] ने अपनी पुस्तक एक्सट्रपलेशन, इंटरपोलेशन, और स्मूथिंग ऑफ़ स्टेशनरी टाइम सीरीज़ (1949) में रखी थी।<ref>{{cite book |last=Wiener |first=N. |title=एक्सट्रपलेशन, इंटरपोलेशन और स्टेशनरी टाइम सीरीज़ का स्मूथिंग|publisher=MIT Press |location=Cambridge, Mass |year=1964 |isbn=0-262-73005-7}}</ref> पुस्तक [[द्वितीय विश्व युद्ध]] के समय वीनर द्वारा किए गए कार्य पर आधारित थी | किन्तु उस समय इसे वर्गीकृत किया गया था। इन सिद्धांतों को प्रयुक्त करने के प्रारंभिक प्रयासों में से कुछ मौसम पूर्वानुमान और [[अर्थशास्त्र]] के क्षेत्र में थे। | ||
'''[[आवृत्ति डोमेन]] में, जहाँ <math>\omega</math> आवृत्ति चर है। यह मानते हुए कि परावर्तकता सफेद है, हम मान सकते हैं''' | '''[[आवृत्ति डोमेन]] में, जहाँ <math>\omega</math> आवृत्ति चर है। यह मानते हुए कि परावर्तकता सफेद है, हम मान सकते हैं''' | ||
== विवरण == | == विवरण == | ||
सामान्यतः, विसंक्रमण का उद्देश्य फॉर्म के कनवल्शन समीकरण के हल f को खोजना है | | |||
: <math>f * g = h \, </math> | : <math>f * g = h \, </math> | ||
सामान्यतः, h कुछ अभिलेख किया गया संकेत है, और f कुछ संकेत है | जिसे हम पुनर्प्राप्त करना चाहते हैं | किन्तु इसे अभिलेख करने से पहले फ़िल्टर या विरूपण फलन g के साथ सजाया गया है। सामान्यतः, h, f का विकृत संस्करण है और f के आकार को आँख या सरल समय-डोमेन संचालन द्वारा सरलता से पहचाना नहीं जा सकता है। फलन g उपकरण या ड्राइविंग बल की [[आवेग प्रतिक्रिया]] का प्रतिनिधित्व करता है | जिसे भौतिक प्रणाली पर प्रयुक्त किया गया था। यदि हम g को जानते हैं, या कम से कम g के रूप को जानते हैं, तो हम नियतात्मक विसंक्रमण कर सकते हैं। चूँकि, यदि हम g को पहले से नहीं जानते हैं, तो हमें इसका अनुमान लगाने की आवश्यकता है। यह सांख्यिकी आकलन सिद्धांत के विधियों का उपयोग करके या अंतर्निहित प्रणाली के भौतिक सिद्धांतों का निर्माण करके किया जा सकता है | जैसे विद्युत परिपथ समीकरण या प्रसार समीकरण है। | |||
माप त्रुटि और | माप त्रुटि और कनवल्शन मापदंडों की रूचि के आधार पर, कई कनवल्शन विधिया हैं। भौतिक माप में, स्थिति सामान्यतः के निकट होती है | | ||
: <math>(f * g) + \varepsilon = h \, </math> | : <math>(f * g) + \varepsilon = h \, </math> | ||
इस | इस स्थिति में ε [[शोर (भौतिकी)|ध्वनि (भौतिकी)]] है | जो हमारे अभिलेख किए गए संकेत में प्रवेश कर चुका है। यदि ध्वनि संकेत या छवि को नीरव माना जाता है, तो g का सांख्यिकीय अनुमान गलत होगा। बदले में, ƒ का अनुमान भी गलत होगा। संकेत-टू-ध्वनि अनुपात जितना कम होगा, विसंक्रमित संकेत का अनुमान उतना ही व्यर्थ होगा। यही कारण है कि प्रतिलोम फ़िल्टरिंग संकेत सामान्यतः अच्छा समाधान नहीं है। चूँकि, यदि डेटा में ध्वनि के प्रकार (उदाहरण के लिए, सफेद ध्वनि) के बारे में कम से कम कुछ ज्ञान उपस्थित है, तो ƒ के अनुमान को [[वीनर डीकोनोवोल्यूशन]] जैसी विधियों के माध्यम से सुधारा जा सकता है। | ||
जब माप त्रुटि बहुत कम होती है (आदर्श | जब माप त्रुटि बहुत कम होती है (आदर्श स्थिति) तो डीकोनोवोल्यूशन (कच्चा) फिल्टर में उलट जाता है। लाप्लास डोमेन में कच्चे विसंक्रमण का प्रदर्शन किया जा सकता है। अभिलेख किए गए संकेत एच और प्रणाली रिस्पांस फलन g के [[फूरियर रूपांतरण]] की गणना करके आपको [[ स्थानांतरण प्रकार्य ]] के रूप में g के साथ एच और g मिलते हैं। तो f के लिए हल करना | ||
: <math>F = H / G \, </math> | : <math>F = H / G \, </math> | ||
अंत में, | अंत में, फलन F के फूरियर व्युत्क्रम प्रमेय को अनुमानित विसंक्रमित संकेत f को खोजने के लिए लिया जाता है। ध्यान दें कि G भाजक पर है और यदि उपस्थित है तो त्रुटि मॉडल के तत्वों को बढ़ा सकता है। | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
| Line 25: | Line 25: | ||
=== [[भूकंप]] विज्ञान === | === [[भूकंप]] विज्ञान === | ||
प्रतिबिंब भूकम्प विज्ञान में डीकोनोवोल्यूशन की अवधारणा का प्रारंभिक अनुप्रयोग था। 1950 में, [[एंडर्स रॉबिन्सन]] एमआईटी में स्नातक छात्र थे। उन्होंने | प्रतिबिंब भूकम्प विज्ञान में डीकोनोवोल्यूशन की अवधारणा का प्रारंभिक अनुप्रयोग था। 1950 में, [[एंडर्स रॉबिन्सन]] एमआईटी में स्नातक छात्र थे। उन्होंने एमआईटी में दूसरों के [[साथ]] काम किया था | जैसे नॉर्बर्ट वीनर, [[नॉर्मन लेविंसन]], और अर्थशास्त्री [[पॉल सैमुएलसन]], ने परावर्तन [[सीस्मोग्राम]] के दृढ़ मॉडल को विकसित करने के लिए यह मॉडल मानता है कि अभिलेख किया गया सीस्मोग्राम s(t) पृथ्वी-परावर्तकता फलन e(t) और एक [[बिंदु स्रोत]] से भूकंपीय तरंगिका w(t) का कनवल्शन है | जहां t रिकॉर्डिंग समय का प्रतिनिधित्व करता है। इस प्रकार, हमारा कनवल्शन समीकरण है | | ||
:<math>s(t) = (e * w)(t). \, </math> | :<math>s(t) = (e * w)(t). \, </math> | ||
सीस्मोलॉजिस्ट | सीस्मोलॉजिस्ट e में रुचि रखता है, जिसमें पृथ्वी की संरचना के बारे में जानकारी होती है। [[कनवल्शन प्रमेय]] द्वारा, इस समीकरण को फूरियर में रूपांतरित किया जा सकता है | ||
: <math>S(\omega) = E(\omega)W(\omega) \, </math> | : <math>S(\omega) = E(\omega)W(\omega) \, </math> | ||
[[आवृत्ति डोमेन]] में, जहाँ <math>\omega</math> आवृत्ति चर है। यह मानते हुए कि परावर्तकता सफेद है | [[आवृत्ति डोमेन]] में, जहाँ <math>\omega</math> आवृत्ति चर है। यह मानते हुए कि परावर्तकता सफेद है | हम मान सकते हैं कि परावर्तकता का [[वर्णक्रमीय घनत्व]] स्थिर है, और सिस्मोग्राम का शक्ति स्पेक्ट्रम उस स्थिरांक से गुणा तरंगिका का स्पेक्ट्रम है। इस प्रकार, | ||
: <math>|S(\omega)| \approx k|W(\omega)|. \, </math> | : <math>|S(\omega)| \approx k|W(\omega)|. \, </math> | ||
यदि हम मानते हैं कि वेवलेट [[न्यूनतम चरण]] है, तो हम अभी पाए गए पावर स्पेक्ट्रम के सामान्य न्यूनतम चरण की गणना करके इसे पुनर्प्राप्त कर सकते हैं। [[डिराक डेल्टा समारोह|डिराक डेल्टा कार्य]] (अर्थात, स्पाइक) के लिए अनुमानित तरंगिका को आकार देने वाले [[विनीज़ फ़िल्टर]] को रचना और प्रयुक्त करके परावर्तकता को पुनर्प्राप्त किया जा सकता है। परिणाम को स्केल्ड, शिफ्ट किए गए डेल्टा कार्यों की श्रृंखला के रूप में देखा जा सकता है |(चूँकि यह गणितीय रूप से कठोर नहीं है) | |||
: <math>e(t)=\sum_{i=1}^N r_i\delta(t-\tau_i),</math> | : <math>e(t)=\sum_{i=1}^N r_i\delta(t-\tau_i),</math> | ||
जहाँ N परावर्तन घटनाओं की संख्या है | जहाँ N परावर्तन घटनाओं की संख्या है | <math>r_i</math> [[प्रतिबिंब गुणांक]] हैं | <math>t-\tau_i</math> प्रत्येक घटना के प्रतिबिंब समय हैं, और <math>\delta</math> डिराक डेल्टा फलन है। | ||
व्यवहार में, चूंकि हम | व्यवहार में, चूंकि हम ध्वनि, परिमित [[बैंडविड्थ (कंप्यूटिंग)]], परिमित लंबाई, [[नमूनाकरण (सिग्नल प्रोसेसिंग)|नमूनाकरण (संकेत प्रोसेसिंग)]] डेटासेट के साथ काम कर रहे हैं | उपरोक्त प्रक्रिया केवल डेटा को विखंडित करने के लिए आवश्यक फ़िल्टर का अनुमान देती है। चूँकि, समस्या को टोप्लेट्ज़ आव्यूह के समाधान के रूप में तैयार करके और लेविंसन पुनरावर्तन का उपयोग करके, हम सबसे छोटे माध्य चुकता त्रुटि के साथ अपेक्षाकृत जल्दी से फिल्टर का अनुमान लगा सकते हैं। हम आवृत्ति डोमेन में सीधे डीकोनवोल्यूशन भी कर सकते हैं और समान परिणाम प्राप्त कर सकते हैं। विधि [[रैखिक भविष्यवाणी]] से निकटता से संबंधित है। | ||
=== प्रकाशिकी और अन्य इमेजिंग === | === प्रकाशिकी और अन्य इमेजिंग === | ||
[[File:Depth Coded Phalloidin Stained Actin Filaments Cancer Cell.png|thumb|विसंक्रमित सूक्ष्मदर्शी छवि का उदाहरण|245x245px]] | [[File:Depth Coded Phalloidin Stained Actin Filaments Cancer Cell.png|thumb|विसंक्रमित सूक्ष्मदर्शी छवि का उदाहरण|245x245px]]प्रकाशिकी और इमेजिंग में, डिकॉन्वोल्यूशन शब्द विशेष रूप से प्रकाशीय प्रणाली में विचलन को उलटने की प्रक्रिया को संदर्भित करने के लिए प्रयोग किया जाता है | प्रकाशीय [[माइक्रोस्कोप]], [[ इलेक्ट्रॉन सूक्ष्मदर्शी ]], [[ दूरबीन ]], या अन्य इमेजिंग उपकरण में होने वाली छवि का विरूपण, इस प्रकार स्पष्ट छवियां बनाता है | यह सामान्यतः [[ माइक्रोस्कोप छवि प्रसंस्करण ]] विधियों के सूट के भाग के रूप में [[ सॉफ़्टवेयर ]] [[कलन विधि]] द्वारा डिजिटल डोमेन में किया जाता है। कनवल्शन उन छवियों को तेज करने के लिए भी व्यावहारिक है | जो कैप्चरिंग के समय तेज गति या झटकों से ग्रस्त हैं। प्रारंभिक [[हबल अंतरिक्ष सूक्ष्मदर्शी]] छवियों को हबल स्पेस टेलीस्कॉप त्रुटिपूर्ण दर्पण द्वारा विकृत किया गया था और डीकनवोल्यूशन द्वारा तेज किया गया था। | ||
सामान्य विधि यह मान लेना है कि उपकरण के माध्यम से | सामान्य विधि यह मान लेना है कि उपकरण के माध्यम से प्रकाशीय पथ वैकल्पिक रूप से सही है | बिंदु प्रसार कार्य (पीएसएफ) के साथ दृढ़ है | जो कि [[गणितीय कार्य]] है | जो मार्ग के संदर्भ में विरूपण का वर्णन करता है | प्रकाश का सैद्धांतिक बिंदु स्रोत (या) अन्य तरंगें) यंत्र के माध्यम से लेती हैं।<ref name=Pawley_2006>{{cite book |last=Cheng |first=P. C. |chapter =The Contrast Formation in Optical Microscopy |title=हैंडबुक ऑफ बायोलॉजिकल कॉन्फोकल माइक्रोस्कोपी|url=https://archive.org/details/handbookbiologic00pawl |url-access=limited |editor-last=Pawley |editor-first=J. B. |publisher=Springer |location=Berlin |year=2006 |pages= [https://archive.org/details/handbookbiologic00pawl/page/n214 189]–90 |edition=3rd |isbn=0-387-25921-X}}</ref> सामान्यतः, ऐसा बिंदु स्रोत अंतिम छवि में अस्पष्टता के छोटे से क्षेत्र का योगदान देता है। यदि यह फलन निर्धारित किया जा सकता है, तो यह उसके व्युत्क्रम फलन या पूरक फलन की गणना करने और उसके साथ अधिग्रहीत छवि को हल करने का विषय है। परिणाम मूल, अविकृत छवि है। | ||
व्यवहार में, वास्तविक | व्यवहार में, वास्तविक पीएसएफ को खोजना असंभव है, और सामान्यतः इसका अनुमान सैद्धांतिक रूप से गणना करके उपयोग किया जाता है या ज्ञात जांचों का उपयोग करके कुछ प्रयोगात्मक अनुमानों पर आधारित वास्तविक प्रकाशिकी में विभिन्न फोकल और स्थानिक स्थानों पर अलग-अलग पीएसएफ भी हो सकते हैं, और पीएसएफ गैर-रैखिक हो सकता है। पीएसएफ के सन्निकटन की स्पष्टता अंतिम परिणाम तय करेगी। अधिक कम्प्यूटेशनल रूप से गहन होने की कीमत पर उत्तम परिणाम देने के लिए विभिन्न एल्गोरिदम को नियोजित किया जा सकता है। चूंकि मूल कनवल्शन डेटा को छोड़ देता है | इसलिए कुछ एल्गोरिदम कुछ खोई हुई जानकारी को बनाने के लिए पास के फोकल पॉइंट्स पर प्राप्त अतिरिक्त डेटा का उपयोग करते हैं। पुनरावृत्त एल्गोरिदम में [[नियमितीकरण (गणित)]] (अपेक्षा-अधिकतमकरण एल्गोरिदम के रूप में) अवास्तविक समाधानों से बचने के लिए प्रयुक्त किया जा सकता है। | ||
जब पीएसएफ अज्ञात होता है, तो अलग-अलग संभावित पीएसएफ को व्यवस्थित रूप से आजमाकर और छवि में सुधार हुआ है या नहीं, इसका आकलन करके इसे निकालना संभव हो सकता है। इस प्रक्रिया को [[अंधा deconvolution]] कहा जाता है।<ref name=Pawley_2006 />ब्लाइंड डीकोनवोल्यूशन [[खगोल]] विज्ञान में अच्छी तरह से स्थापित [[छवि बहाली]] | जब पीएसएफ अज्ञात होता है, तो अलग-अलग संभावित पीएसएफ को व्यवस्थित रूप से आजमाकर और छवि में सुधार हुआ है या नहीं, इसका आकलन करके इसे निकालना संभव हो सकता है। इस प्रक्रिया को [[अंधा deconvolution|कनवल्शन]] कहा जाता है।<ref name=Pawley_2006 /> ब्लाइंड डीकोनवोल्यूशन [[खगोल]] विज्ञान में अच्छी तरह से स्थापित [[छवि बहाली]] विधि है | जहां फोटो खींची गई वस्तुओं की बिंदु प्रकृति पीएसएफ को उजागर करती है और इस प्रकार इसे और अधिक व्यवहार्य बनाती है। यह छवि बहाली के लिए [[प्रतिदीप्ति माइक्रोस्कोपी]] में भी प्रयोग किया जाता है, और कई अज्ञात [[ फ्लोरोफोरे ]] के वर्णक्रमीय पृथक्करण के लिए प्रतिदीप्ति [[वर्णक्रमीय इमेजिंग]] में इस उद्देश्य के लिए सबसे सामान्य [[ यात्रा ]] एल्गोरिथम रिचर्डसन-लुसी डीकोनवोल्यूशन एल्गोरिथम है | वीनर डीकोनवोल्यूशन (और सन्निकटन) सबसे सामान्य गैर-पुनरावृत्ति एल्गोरिदम हैं। | ||
[[File:High Resolution THz image.png|thumb|316x316px|उच्च रिज़ॉल्यूशन | [[File:High Resolution THz image.png|thumb|316x316px|उच्च रिज़ॉल्यूशन टीएचजे छवि टीएचजे छवि और गणितीय रूप से प्रतिरूपित टीएचजे पीएसएफ के विसंक्रमण द्वारा प्राप्त की जाती है। (ए) वृद्धि से पहले एकीकृत परिपथ (आईसी) की टीएचजे छवि; (बी) गणितीय रूप से तैयार किए गए टीएचजे पीएसएफ; (c) उच्च रिज़ॉल्यूशन टीएचजे छवि जो (a) में दिखाई गई टीएचजे छवि और (b) में दिखाई गई पीएसएफ के विखंडन के परिणामस्वरूप प्राप्त की जाती है; (डी) उच्च रिज़ॉल्यूशन एक्स-रे छवि मापा मूल्यों की स्पष्टता की पुष्टि करती है।<ref>{{Cite journal |last1=Ahi |first1=Kiarash |first2=Mehdi |last2=Anwar |editor3-first=Tariq |editor3-last=Manzur |editor2-first=Thomas W |editor2-last=Crowe |editor1-first=Mehdi F |editor1-last=Anwar |date=May 26, 2016 |title=टेराहर्ट्ज़ इमेजिंग समीकरण का विकास करना और डीकनवोल्यूशन का उपयोग करके टेराहर्ट्ज़ छवियों के रिज़ॉल्यूशन में वृद्धि करना|url=https://www.researchgate.net/publication/303563271 |journal=Proc. SPIE 9856, Terahertz Physics, Devices, and Systems X: Advanced Applications in Industry and Defense, 98560N |series=Terahertz Physics, Devices, and Systems X: Advanced Applications in Industry and Defense |volume=9856 |pages=98560N |doi=10.1117/12.2228680|bibcode=2016SPIE.9856E..0NA |s2cid=114994724 }}</ref>]]कुछ विशिष्ट इमेजिंग प्रणाली जैसे लेजर स्पंदित टेराहर्ट्ज प्रणाली के लिए, पीएसएफ को गणितीय रूप से तैयार किया जा सकता है।<ref>{{Cite book|title=चिकित्सा इमेजिंग में अनुप्रयोगों के लिए टेराहर्ट्ज़ इमेजिंग और रिमोट सेंसिंग डिज़ाइन|last=Sung |first=Shijun |publisher=UCLA Electronic Theses and Dissertations |year=2013}}</ref> परिणामस्वरूप, जैसा कि चित्र में दिखाया गया है | प्रतिरूपित पीएसएफ और टेराहर्ट्ज़ छवि का विसंक्रमण, टेराहर्ट्ज़ छवि का उच्च रिज़ॉल्यूशन प्रतिनिधित्व दे सकता है। | ||
=== [[रेडियो खगोल विज्ञान]] === | === [[रेडियो खगोल विज्ञान]] === | ||
रेडियो [[इंटरफेरोमेट्री]] में छवि संश्लेषण करते समय, विशिष्ट प्रकार की रेडियो खगोल विज्ञान, चरण में उत्पादित छवि को गंदे बीम के साथ विसंक्रमित करना होता है | रेडियो [[इंटरफेरोमेट्री]] में छवि संश्लेषण करते समय, विशिष्ट प्रकार की रेडियो खगोल विज्ञान, चरण में उत्पादित छवि को गंदे बीम के साथ विसंक्रमित करना होता है | जो बिंदु प्रसार कार्य के लिए अलग नाम है। सामान्यतः उपयोग की जाने वाली विधि [[स्वच्छ (एल्गोरिदम)]] है। | ||
=== जीव विज्ञान, शरीर विज्ञान और चिकित्सा उपकरण === | === जीव विज्ञान, शरीर विज्ञान और चिकित्सा उपकरण === | ||
ट्रेसर कैनेटीक्स में विसंक्रमण का विशिष्ट उपयोग है। उदाहरण के लिए, रक्त में हार्मोन की सांद्रता को मापते समय, इसके स्राव की दर का अनुमान विसंक्रमण द्वारा लगाया जा सकता है। एक अन्य उदाहरण मापा अंतरालीय ग्लूकोज से रक्त ग्लूकोज एकाग्रता का अनुमान है, जो वास्तविक रक्त ग्लूकोज के समय और आयाम में विकृत संस्करण है। <ref>{{cite journal |last1=Sparacino |first1=Giovanni |last2=Cobelli |first2=Claudio |title=Reconstruction of insulin secretion rate by deconvolution: domain of validity of a monoexponential C-peptide impulse response model|journal=Techno Health Care|volume=4 |issue=1 |pages=87–9511 |year=1996 |doi=10.3233/THC-1996-4110 |pmid=8773311}}</ref> | ट्रेसर कैनेटीक्स में विसंक्रमण का विशिष्ट उपयोग है। उदाहरण के लिए, रक्त में हार्मोन की सांद्रता को मापते समय, इसके स्राव की दर का अनुमान विसंक्रमण द्वारा लगाया जा सकता है। एक अन्य उदाहरण मापा अंतरालीय ग्लूकोज से रक्त ग्लूकोज एकाग्रता का अनुमान है, जो वास्तविक रक्त ग्लूकोज के समय और आयाम में विकृत संस्करण है। <ref>{{cite journal |last1=Sparacino |first1=Giovanni |last2=Cobelli |first2=Claudio |title=Reconstruction of insulin secretion rate by deconvolution: domain of validity of a monoexponential C-peptide impulse response model|journal=Techno Health Care|volume=4 |issue=1 |pages=87–9511 |year=1996 |doi=10.3233/THC-1996-4110 |pmid=8773311}}</ref> | ||
=== अवशोषण स्पेक्ट्रा === | === अवशोषण स्पेक्ट्रा === | ||
कनवल्शन बड़े मापदंड पर [[अवशोषण स्पेक्ट्रोस्कोपी]] के लिए प्रयुक्त किया गया है।<ref>{{cite book|last1=Blass|first1=W. E.|url=https://archive.org/details/deconvolutionofa0000blas|title=अवशोषण स्पेक्ट्रा का विसंक्रमण|last2=Halsey|first2=G. W.|publisher=Academic Press|year=1981|isbn=0121046508|url-access=registration}}</ref> :डी: वैन-सिटर्ट-डेकोनोवोल्यूशन (जर्मन में लेख) का उपयोग किया जा सकता है।<ref>{{cite journal|last=Wu|first=Chengqi|author2=Aissaoui, Idriss|author3=Jacquey, Serge|year=1994|title=एक सामान्य विश्राम कारक के साथ डीकोनवोल्यूशन के वैन सिटर्ट पुनरावृत्त विधि का बीजगणितीय विश्लेषण|journal=J. Opt. Soc. Am. A|volume=11|issue=11|pages=2804–2808|bibcode=1994JOSAA..11.2804X|doi=10.1364/JOSAA.11.002804}}</ref> | |||
=== फूरियर रूपांतरण | === फूरियर रूपांतरण स्पेक्ट === | ||
कनवल्शन फूरियर रूपांतरण में विभाजन के लिए मानचित्र फूरियर सह-डोमेन यह डीकोनवोल्यूशन को प्रयोगात्मक डेटा के साथ सरलता से प्रयुक्त करने की अनुमति देता है | जो फूरियर रूपांतरण के अधीन हैं। उदाहरण [[एनएमआर स्पेक्ट्रोस्कोपी]] है | जहां डेटा समय डोमेन में अंकित किया जाता है, किन्तु आवृत्ति डोमेन में विश्लेषण किया जाता है। घातीय कार्य द्वारा समय-डोमेन डेटा का विभाजन आवृत्ति डोमेन में लोरेंत्ज़ियन रेखाओ की चौड़ाई को कम करने का प्रभाव है। | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 65: | Line 65: | ||
* [[बिट प्लेन]] | * [[बिट प्लेन]] | ||
* [[डिजिटल फिल्टर]] | * [[डिजिटल फिल्टर]] | ||
* [[फ़िल्टर (सिग्नल प्रोसेसिंग)]] | * [[फ़िल्टर (सिग्नल प्रोसेसिंग)|फ़िल्टर (संकेत प्रोसेसिंग)]] | ||
* [[फिल्टर डिजाइन]] | * [[फिल्टर डिजाइन|फिल्टर रचना]] | ||
* न्यूनतम चरण | * न्यूनतम चरण | ||
* [[स्वतंत्र घटक विश्लेषण]] | * [[स्वतंत्र घटक विश्लेषण]] | ||
| Line 72: | Line 72: | ||
*रिचर्डसन-लुसी डीकोनोवोल्यूशन | *रिचर्डसन-लुसी डीकोनोवोल्यूशन | ||
* [[डिजिटल कक्ष सुधार]] | * [[डिजिटल कक्ष सुधार]] | ||
* [[नि: शुल्क deconvolution]] | * [[नि: शुल्क deconvolution|नि: शुल्क कनवल्शन]] | ||
* प्वाइंट स्प्रेड | * प्वाइंट स्प्रेड फलन | ||
* [[ डीब्लरिंग ]] | * [[ डीब्लरिंग ]] | ||
* [[अनशार्प मास्किंग]] | * [[अनशार्प मास्किंग]] | ||
Revision as of 12:41, 17 May 2023
गणित में, कनवल्शन का उलटा संक्रिया विसंक्रमण है। दोनों संचालन संकेत प्रोसेसिंग और इमेज प्रोसेसिंग में उपयोग किए जाते हैं। उदाहरण के लिए, निश्चित डिग्री स्पष्टता के साथ कनवल्शन विधि का उपयोग करके फ़िल्टर (कनवल्शन) के बाद मूल संकेत को पुनर्प्राप्त करना संभव हो सकता है।[1] अभिलेख किए गए संकेत या छवि की माप त्रुटि के कारण, यह प्रदर्शित किया जा सकता है कि संकेत-टू-नॉइज़ अनुपात जितना व्यर्थ होगा, फिल्टर का उल्टा होना उतना ही व्यर्थ होगा | इसलिए, फ़िल्टर को उल्टा करना सदैव एक अच्छा समाधान नहीं होता है | क्योंकि त्रुटि बढ़ जाती है। कनवल्शन इस समस्या का समाधान प्रदान करता है।
विसंक्रमण और समय-श्रृंखला विश्लेषण की नींव बड़े मापदंड पर मैसाचुसेट्स की तकनीकी संस्था के नॉर्बर्ट वीनर ने अपनी पुस्तक एक्सट्रपलेशन, इंटरपोलेशन, और स्मूथिंग ऑफ़ स्टेशनरी टाइम सीरीज़ (1949) में रखी थी।[2] पुस्तक द्वितीय विश्व युद्ध के समय वीनर द्वारा किए गए कार्य पर आधारित थी | किन्तु उस समय इसे वर्गीकृत किया गया था। इन सिद्धांतों को प्रयुक्त करने के प्रारंभिक प्रयासों में से कुछ मौसम पूर्वानुमान और अर्थशास्त्र के क्षेत्र में थे।
आवृत्ति डोमेन में, जहाँ आवृत्ति चर है। यह मानते हुए कि परावर्तकता सफेद है, हम मान सकते हैं
विवरण
सामान्यतः, विसंक्रमण का उद्देश्य फॉर्म के कनवल्शन समीकरण के हल f को खोजना है |
सामान्यतः, h कुछ अभिलेख किया गया संकेत है, और f कुछ संकेत है | जिसे हम पुनर्प्राप्त करना चाहते हैं | किन्तु इसे अभिलेख करने से पहले फ़िल्टर या विरूपण फलन g के साथ सजाया गया है। सामान्यतः, h, f का विकृत संस्करण है और f के आकार को आँख या सरल समय-डोमेन संचालन द्वारा सरलता से पहचाना नहीं जा सकता है। फलन g उपकरण या ड्राइविंग बल की आवेग प्रतिक्रिया का प्रतिनिधित्व करता है | जिसे भौतिक प्रणाली पर प्रयुक्त किया गया था। यदि हम g को जानते हैं, या कम से कम g के रूप को जानते हैं, तो हम नियतात्मक विसंक्रमण कर सकते हैं। चूँकि, यदि हम g को पहले से नहीं जानते हैं, तो हमें इसका अनुमान लगाने की आवश्यकता है। यह सांख्यिकी आकलन सिद्धांत के विधियों का उपयोग करके या अंतर्निहित प्रणाली के भौतिक सिद्धांतों का निर्माण करके किया जा सकता है | जैसे विद्युत परिपथ समीकरण या प्रसार समीकरण है।
माप त्रुटि और कनवल्शन मापदंडों की रूचि के आधार पर, कई कनवल्शन विधिया हैं। भौतिक माप में, स्थिति सामान्यतः के निकट होती है |
इस स्थिति में ε ध्वनि (भौतिकी) है | जो हमारे अभिलेख किए गए संकेत में प्रवेश कर चुका है। यदि ध्वनि संकेत या छवि को नीरव माना जाता है, तो g का सांख्यिकीय अनुमान गलत होगा। बदले में, ƒ का अनुमान भी गलत होगा। संकेत-टू-ध्वनि अनुपात जितना कम होगा, विसंक्रमित संकेत का अनुमान उतना ही व्यर्थ होगा। यही कारण है कि प्रतिलोम फ़िल्टरिंग संकेत सामान्यतः अच्छा समाधान नहीं है। चूँकि, यदि डेटा में ध्वनि के प्रकार (उदाहरण के लिए, सफेद ध्वनि) के बारे में कम से कम कुछ ज्ञान उपस्थित है, तो ƒ के अनुमान को वीनर डीकोनोवोल्यूशन जैसी विधियों के माध्यम से सुधारा जा सकता है।
जब माप त्रुटि बहुत कम होती है (आदर्श स्थिति) तो डीकोनोवोल्यूशन (कच्चा) फिल्टर में उलट जाता है। लाप्लास डोमेन में कच्चे विसंक्रमण का प्रदर्शन किया जा सकता है। अभिलेख किए गए संकेत एच और प्रणाली रिस्पांस फलन g के फूरियर रूपांतरण की गणना करके आपको स्थानांतरण प्रकार्य के रूप में g के साथ एच और g मिलते हैं। तो f के लिए हल करना
अंत में, फलन F के फूरियर व्युत्क्रम प्रमेय को अनुमानित विसंक्रमित संकेत f को खोजने के लिए लिया जाता है। ध्यान दें कि G भाजक पर है और यदि उपस्थित है तो त्रुटि मॉडल के तत्वों को बढ़ा सकता है।
अनुप्रयोग
भूकंप विज्ञान
प्रतिबिंब भूकम्प विज्ञान में डीकोनोवोल्यूशन की अवधारणा का प्रारंभिक अनुप्रयोग था। 1950 में, एंडर्स रॉबिन्सन एमआईटी में स्नातक छात्र थे। उन्होंने एमआईटी में दूसरों के साथ काम किया था | जैसे नॉर्बर्ट वीनर, नॉर्मन लेविंसन, और अर्थशास्त्री पॉल सैमुएलसन, ने परावर्तन सीस्मोग्राम के दृढ़ मॉडल को विकसित करने के लिए यह मॉडल मानता है कि अभिलेख किया गया सीस्मोग्राम s(t) पृथ्वी-परावर्तकता फलन e(t) और एक बिंदु स्रोत से भूकंपीय तरंगिका w(t) का कनवल्शन है | जहां t रिकॉर्डिंग समय का प्रतिनिधित्व करता है। इस प्रकार, हमारा कनवल्शन समीकरण है |
सीस्मोलॉजिस्ट e में रुचि रखता है, जिसमें पृथ्वी की संरचना के बारे में जानकारी होती है। कनवल्शन प्रमेय द्वारा, इस समीकरण को फूरियर में रूपांतरित किया जा सकता है
आवृत्ति डोमेन में, जहाँ आवृत्ति चर है। यह मानते हुए कि परावर्तकता सफेद है | हम मान सकते हैं कि परावर्तकता का वर्णक्रमीय घनत्व स्थिर है, और सिस्मोग्राम का शक्ति स्पेक्ट्रम उस स्थिरांक से गुणा तरंगिका का स्पेक्ट्रम है। इस प्रकार,
यदि हम मानते हैं कि वेवलेट न्यूनतम चरण है, तो हम अभी पाए गए पावर स्पेक्ट्रम के सामान्य न्यूनतम चरण की गणना करके इसे पुनर्प्राप्त कर सकते हैं। डिराक डेल्टा कार्य (अर्थात, स्पाइक) के लिए अनुमानित तरंगिका को आकार देने वाले विनीज़ फ़िल्टर को रचना और प्रयुक्त करके परावर्तकता को पुनर्प्राप्त किया जा सकता है। परिणाम को स्केल्ड, शिफ्ट किए गए डेल्टा कार्यों की श्रृंखला के रूप में देखा जा सकता है |(चूँकि यह गणितीय रूप से कठोर नहीं है)
जहाँ N परावर्तन घटनाओं की संख्या है | प्रतिबिंब गुणांक हैं | प्रत्येक घटना के प्रतिबिंब समय हैं, और डिराक डेल्टा फलन है।
व्यवहार में, चूंकि हम ध्वनि, परिमित बैंडविड्थ (कंप्यूटिंग), परिमित लंबाई, नमूनाकरण (संकेत प्रोसेसिंग) डेटासेट के साथ काम कर रहे हैं | उपरोक्त प्रक्रिया केवल डेटा को विखंडित करने के लिए आवश्यक फ़िल्टर का अनुमान देती है। चूँकि, समस्या को टोप्लेट्ज़ आव्यूह के समाधान के रूप में तैयार करके और लेविंसन पुनरावर्तन का उपयोग करके, हम सबसे छोटे माध्य चुकता त्रुटि के साथ अपेक्षाकृत जल्दी से फिल्टर का अनुमान लगा सकते हैं। हम आवृत्ति डोमेन में सीधे डीकोनवोल्यूशन भी कर सकते हैं और समान परिणाम प्राप्त कर सकते हैं। विधि रैखिक भविष्यवाणी से निकटता से संबंधित है।
प्रकाशिकी और अन्य इमेजिंग
प्रकाशिकी और इमेजिंग में, डिकॉन्वोल्यूशन शब्द विशेष रूप से प्रकाशीय प्रणाली में विचलन को उलटने की प्रक्रिया को संदर्भित करने के लिए प्रयोग किया जाता है | प्रकाशीय माइक्रोस्कोप, इलेक्ट्रॉन सूक्ष्मदर्शी , दूरबीन , या अन्य इमेजिंग उपकरण में होने वाली छवि का विरूपण, इस प्रकार स्पष्ट छवियां बनाता है | यह सामान्यतः माइक्रोस्कोप छवि प्रसंस्करण विधियों के सूट के भाग के रूप में सॉफ़्टवेयर कलन विधि द्वारा डिजिटल डोमेन में किया जाता है। कनवल्शन उन छवियों को तेज करने के लिए भी व्यावहारिक है | जो कैप्चरिंग के समय तेज गति या झटकों से ग्रस्त हैं। प्रारंभिक हबल अंतरिक्ष सूक्ष्मदर्शी छवियों को हबल स्पेस टेलीस्कॉप त्रुटिपूर्ण दर्पण द्वारा विकृत किया गया था और डीकनवोल्यूशन द्वारा तेज किया गया था।
सामान्य विधि यह मान लेना है कि उपकरण के माध्यम से प्रकाशीय पथ वैकल्पिक रूप से सही है | बिंदु प्रसार कार्य (पीएसएफ) के साथ दृढ़ है | जो कि गणितीय कार्य है | जो मार्ग के संदर्भ में विरूपण का वर्णन करता है | प्रकाश का सैद्धांतिक बिंदु स्रोत (या) अन्य तरंगें) यंत्र के माध्यम से लेती हैं।[3] सामान्यतः, ऐसा बिंदु स्रोत अंतिम छवि में अस्पष्टता के छोटे से क्षेत्र का योगदान देता है। यदि यह फलन निर्धारित किया जा सकता है, तो यह उसके व्युत्क्रम फलन या पूरक फलन की गणना करने और उसके साथ अधिग्रहीत छवि को हल करने का विषय है। परिणाम मूल, अविकृत छवि है।
व्यवहार में, वास्तविक पीएसएफ को खोजना असंभव है, और सामान्यतः इसका अनुमान सैद्धांतिक रूप से गणना करके उपयोग किया जाता है या ज्ञात जांचों का उपयोग करके कुछ प्रयोगात्मक अनुमानों पर आधारित वास्तविक प्रकाशिकी में विभिन्न फोकल और स्थानिक स्थानों पर अलग-अलग पीएसएफ भी हो सकते हैं, और पीएसएफ गैर-रैखिक हो सकता है। पीएसएफ के सन्निकटन की स्पष्टता अंतिम परिणाम तय करेगी। अधिक कम्प्यूटेशनल रूप से गहन होने की कीमत पर उत्तम परिणाम देने के लिए विभिन्न एल्गोरिदम को नियोजित किया जा सकता है। चूंकि मूल कनवल्शन डेटा को छोड़ देता है | इसलिए कुछ एल्गोरिदम कुछ खोई हुई जानकारी को बनाने के लिए पास के फोकल पॉइंट्स पर प्राप्त अतिरिक्त डेटा का उपयोग करते हैं। पुनरावृत्त एल्गोरिदम में नियमितीकरण (गणित) (अपेक्षा-अधिकतमकरण एल्गोरिदम के रूप में) अवास्तविक समाधानों से बचने के लिए प्रयुक्त किया जा सकता है।
जब पीएसएफ अज्ञात होता है, तो अलग-अलग संभावित पीएसएफ को व्यवस्थित रूप से आजमाकर और छवि में सुधार हुआ है या नहीं, इसका आकलन करके इसे निकालना संभव हो सकता है। इस प्रक्रिया को कनवल्शन कहा जाता है।[3] ब्लाइंड डीकोनवोल्यूशन खगोल विज्ञान में अच्छी तरह से स्थापित छवि बहाली विधि है | जहां फोटो खींची गई वस्तुओं की बिंदु प्रकृति पीएसएफ को उजागर करती है और इस प्रकार इसे और अधिक व्यवहार्य बनाती है। यह छवि बहाली के लिए प्रतिदीप्ति माइक्रोस्कोपी में भी प्रयोग किया जाता है, और कई अज्ञात फ्लोरोफोरे के वर्णक्रमीय पृथक्करण के लिए प्रतिदीप्ति वर्णक्रमीय इमेजिंग में इस उद्देश्य के लिए सबसे सामान्य यात्रा एल्गोरिथम रिचर्डसन-लुसी डीकोनवोल्यूशन एल्गोरिथम है | वीनर डीकोनवोल्यूशन (और सन्निकटन) सबसे सामान्य गैर-पुनरावृत्ति एल्गोरिदम हैं।

कुछ विशिष्ट इमेजिंग प्रणाली जैसे लेजर स्पंदित टेराहर्ट्ज प्रणाली के लिए, पीएसएफ को गणितीय रूप से तैयार किया जा सकता है।[5] परिणामस्वरूप, जैसा कि चित्र में दिखाया गया है | प्रतिरूपित पीएसएफ और टेराहर्ट्ज़ छवि का विसंक्रमण, टेराहर्ट्ज़ छवि का उच्च रिज़ॉल्यूशन प्रतिनिधित्व दे सकता है।
रेडियो खगोल विज्ञान
रेडियो इंटरफेरोमेट्री में छवि संश्लेषण करते समय, विशिष्ट प्रकार की रेडियो खगोल विज्ञान, चरण में उत्पादित छवि को गंदे बीम के साथ विसंक्रमित करना होता है | जो बिंदु प्रसार कार्य के लिए अलग नाम है। सामान्यतः उपयोग की जाने वाली विधि स्वच्छ (एल्गोरिदम) है।
जीव विज्ञान, शरीर विज्ञान और चिकित्सा उपकरण
ट्रेसर कैनेटीक्स में विसंक्रमण का विशिष्ट उपयोग है। उदाहरण के लिए, रक्त में हार्मोन की सांद्रता को मापते समय, इसके स्राव की दर का अनुमान विसंक्रमण द्वारा लगाया जा सकता है। एक अन्य उदाहरण मापा अंतरालीय ग्लूकोज से रक्त ग्लूकोज एकाग्रता का अनुमान है, जो वास्तविक रक्त ग्लूकोज के समय और आयाम में विकृत संस्करण है। [6]
अवशोषण स्पेक्ट्रा
कनवल्शन बड़े मापदंड पर अवशोषण स्पेक्ट्रोस्कोपी के लिए प्रयुक्त किया गया है।[7] :डी: वैन-सिटर्ट-डेकोनोवोल्यूशन (जर्मन में लेख) का उपयोग किया जा सकता है।[8]
फूरियर रूपांतरण स्पेक्ट
कनवल्शन फूरियर रूपांतरण में विभाजन के लिए मानचित्र फूरियर सह-डोमेन यह डीकोनवोल्यूशन को प्रयोगात्मक डेटा के साथ सरलता से प्रयुक्त करने की अनुमति देता है | जो फूरियर रूपांतरण के अधीन हैं। उदाहरण एनएमआर स्पेक्ट्रोस्कोपी है | जहां डेटा समय डोमेन में अंकित किया जाता है, किन्तु आवृत्ति डोमेन में विश्लेषण किया जाता है। घातीय कार्य द्वारा समय-डोमेन डेटा का विभाजन आवृत्ति डोमेन में लोरेंत्ज़ियन रेखाओ की चौड़ाई को कम करने का प्रभाव है।
यह भी देखें
- संक्रमण
- बिट प्लेन
- डिजिटल फिल्टर
- फ़िल्टर (संकेत प्रोसेसिंग)
- फिल्टर रचना
- न्यूनतम चरण
- स्वतंत्र घटक विश्लेषण
- वीनर डीकोनवोल्यूशन
- रिचर्डसन-लुसी डीकोनोवोल्यूशन
- डिजिटल कक्ष सुधार
- नि: शुल्क कनवल्शन
- प्वाइंट स्प्रेड फलन
- डीब्लरिंग
- अनशार्प मास्किंग
संदर्भ
- ↑ O'Haver, T. "सिग्नल प्रोसेसिंग का परिचय - डीकनवोल्यूशन". University of Maryland at College Park. Retrieved 2007-08-15.
- ↑ Wiener, N. (1964). एक्सट्रपलेशन, इंटरपोलेशन और स्टेशनरी टाइम सीरीज़ का स्मूथिंग. Cambridge, Mass: MIT Press. ISBN 0-262-73005-7.
- ↑ 3.0 3.1 Cheng, P. C. (2006). "The Contrast Formation in Optical Microscopy". In Pawley, J. B. (ed.). हैंडबुक ऑफ बायोलॉजिकल कॉन्फोकल माइक्रोस्कोपी (3rd ed.). Berlin: Springer. pp. 189–90. ISBN 0-387-25921-X.
- ↑ Ahi, Kiarash; Anwar, Mehdi (May 26, 2016). Anwar, Mehdi F; Crowe, Thomas W; Manzur, Tariq (eds.). "टेराहर्ट्ज़ इमेजिंग समीकरण का विकास करना और डीकनवोल्यूशन का उपयोग करके टेराहर्ट्ज़ छवियों के रिज़ॉल्यूशन में वृद्धि करना". Proc. SPIE 9856, Terahertz Physics, Devices, and Systems X: Advanced Applications in Industry and Defense, 98560N. Terahertz Physics, Devices, and Systems X: Advanced Applications in Industry and Defense. 9856: 98560N. Bibcode:2016SPIE.9856E..0NA. doi:10.1117/12.2228680. S2CID 114994724.
- ↑ Sung, Shijun (2013). चिकित्सा इमेजिंग में अनुप्रयोगों के लिए टेराहर्ट्ज़ इमेजिंग और रिमोट सेंसिंग डिज़ाइन. UCLA Electronic Theses and Dissertations.
- ↑ Sparacino, Giovanni; Cobelli, Claudio (1996). "Reconstruction of insulin secretion rate by deconvolution: domain of validity of a monoexponential C-peptide impulse response model". Techno Health Care. 4 (1): 87–9511. doi:10.3233/THC-1996-4110. PMID 8773311.
- ↑ Blass, W. E.; Halsey, G. W. (1981). अवशोषण स्पेक्ट्रा का विसंक्रमण. Academic Press. ISBN 0121046508.
- ↑ Wu, Chengqi; Aissaoui, Idriss; Jacquey, Serge (1994). "एक सामान्य विश्राम कारक के साथ डीकोनवोल्यूशन के वैन सिटर्ट पुनरावृत्त विधि का बीजगणितीय विश्लेषण". J. Opt. Soc. Am. A. 11 (11): 2804–2808. Bibcode:1994JOSAA..11.2804X. doi:10.1364/JOSAA.11.002804.