सूत्र: Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
Line 10: Line 10:
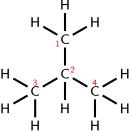
| alt2      = Isobutane
| alt2      = Isobutane
}}
}}
[[File:Edsger Dijkstra 1994.jpg|thumb|upright|[[ कंप्यूटर विज्ञान में अग्रदूतों की सूची ]] की गणना करने वाले सबसे प्रभावशाली आंकड़ों में से एक, [[ एडवर्ड डिजस्ट्रा ]] 1994 में [[ ईटीएच ज्यूरिख ]] में एक सम्मेलन के दौरान ब्लैकबोर्ड पर। डिजस्ट्रा के अपने शब्दों में, एक तस्वीर एक हजार शब्दों के लायक है, एक सूत्र एक हजार चित्रों के लायक है .<ref>[[Edsger Dijkstra|Dijkstra, E.W.]] (July 1996), ''[https://www.cs.utexas.edu/users/EWD/transcriptions/EWD12xx/EWD1239.html A first exploration of effective reasoning]'' [EWD896]. (E.W. Dijkstra Archive, Center for American History, [[University of Texas at Austin]])</ref>]][[ विज्ञान | विज्ञान]] में, सूत्र गणितीय सूत्र या ''[[ रासायनिक सूत्र ]]'' के रूप में प्रतीकात्मक रूप से जानकारी व्यक्त करने का एक संक्षिप्त विधि है। विज्ञान में [[ शब्दावली ]] ''सूत्र'' का अनौपचारिक उपयोग अनुरूपता (विज्ञान के दर्शन) को संदर्भित करता है।
[[File:Edsger Dijkstra 1994.jpg|thumb|upright|[[ कंप्यूटर विज्ञान में अग्रदूतों की सूची | कंप्यूटर विज्ञान में अग्रदूतों की सूची]] की गणना करने वाले सबसे प्रभावशाली आंकड़ों में से एक, [[ एडवर्ड डिजस्ट्रा |एडवर्ड डिजस्ट्रा]] 1994 में [[ ईटीएच ज्यूरिख |ईटीएच ज्यूरिख]] में एक सम्मेलन के दौरान ब्लैकबोर्ड पर। डिजस्ट्रा के अपने शब्दों में, एक तस्वीर एक हजार शब्दों के लायक है, एक सूत्र एक हजार चित्रों के लायक है .<ref>[[Edsger Dijkstra|Dijkstra, E.W.]] (July 1996), ''[https://www.cs.utexas.edu/users/EWD/transcriptions/EWD12xx/EWD1239.html A first exploration of effective reasoning]'' [EWD896]. (E.W. Dijkstra Archive, Center for American History, [[University of Texas at Austin]])</ref>]][[ विज्ञान | विज्ञान]] में, सूत्र गणितीय सूत्र या ''[[ रासायनिक सूत्र |रासायनिक सूत्र]]'' के रूप में प्रतीकात्मक रूप से जानकारी व्यक्त करने का एक संक्षिप्त विधि है। विज्ञान में [[ शब्दावली |शब्दावली]] ''सूत्र'' का अनौपचारिक उपयोग अनुरूपता (विज्ञान के दर्शन) को संदर्भित करता है।


''सूत्र'' का बहुवचन या तो ''सूत्र'' हो सकता है (सबसे समान्य अंग्रेजी बहुवचन या नियमित बहुवचन से) या, [[ वैज्ञानिक लैटिन ]]''सूत्र'' ([[ अंग्रेजी में लैटिन प्रभाव ]] से) के प्रभाव में है ।<ref name="oxford">{{OED|formula}}</ref>
''सूत्र'' का बहुवचन या तो ''सूत्र'' हो सकता है (सबसे समान्य अंग्रेजी बहुवचन या नियमित बहुवचन से) या, [[ वैज्ञानिक लैटिन |वैज्ञानिक लैटिन]] ''सूत्र'' ([[ अंग्रेजी में लैटिन प्रभाव | अंग्रेजी में लैटिन प्रभाव]] से) के प्रभाव में है ।<ref name="oxford">{{OED|formula}}</ref>
== गणित में ==
== गणित में ==
गणित में, एक सूत्र सामान्यतः एक [[ पहचान (गणित) ]] को संदर्भित करता है जो एक [[ गणितीय अभिव्यक्ति ]] को दूसरे के साथ जोड़ता है, जिसमें सबसे महत्वपूर्ण [[ गणितीय प्रमेय ]] है। वाक्यात्मक रूप से, एक सूत्र (अधिकांशतः एक [[ अच्छी तरह से गठित सूत्र ]] के रूप में संदर्भित) एक इकाई है जिसे किसी [[ औपचारिक भाषा ]] के प्रतीकों और गठन नियमों का उपयोग करके बनाया जाता है।<ref>{{Citation
गणित में, एक सूत्र सामान्यतः एक [[ पहचान (गणित) |पहचान (गणित)]] को संदर्भित करता है जो एक [[ गणितीय अभिव्यक्ति |गणितीय अभिव्यक्ति]] को दूसरे के साथ जोड़ता है, जिसमें सबसे महत्वपूर्ण [[ गणितीय प्रमेय |गणितीय प्रमेय]] है। वाक्यात्मक रूप से, एक सूत्र (अधिकांशतः एक [[ अच्छी तरह से गठित सूत्र |अच्छी तरह से गठित सूत्र]] के रूप में संदर्भित) एक इकाई है जिसे किसी [[ औपचारिक भाषा |औपचारिक भाषा]] के प्रतीकों और गठन नियमों का उपयोग करके बनाया जाता है।<ref>{{Citation
   |last=Rautenberg
   |last=Rautenberg
   |first=Wolfgang
   |first=Wolfgang
Line 25: Line 25:
   |isbn=978-1-4419-1220-6
   |isbn=978-1-4419-1220-6
   |year=2010
   |year=2010
}}</ref> उदाहरण के लिए, एक गोले का आयतन निर्धारित करने के लिए एक महत्वपूर्ण [[ मात्रा ]] में [[ समाकलन गणित ]] या इसके [[ ज्यामिति ]] एनालॉग, [[ थकावट की विधि |  निष्कासन विधि]] की आवश्यकता होती है।<ref>{{cite book
}}</ref> उदाहरण के लिए, एक गोले का आयतन निर्धारित करने के लिए एक महत्वपूर्ण [[ मात्रा |मात्रा]] में [[ समाकलन गणित |समाकलन गणित]] या इसके [[ ज्यामिति |ज्यामिति]] एनालॉग, [[ थकावट की विधि |  निष्कासन विधि]] की आवश्यकता होती है।<ref>{{cite book
  | last = Smith
  | last = Smith
  | first = David E.
  | first = David E.
Line 33: Line 33:
  | location = [[New York City|New York]]
  | location = [[New York City|New York]]
  | isbn = 0-486-20430-8
  | isbn = 0-486-20430-8
}}</ref> चूँकि एक बार कुछ [[ पैरामीटर ]] (उदाहरण के लिए त्रिज्या) के संदर्भ में ऐसा करने के बाद, गणितज्ञों ने इसकी त्रिज्या के संदर्भ में एक गोले के आयतन का वर्णन करने के लिए एक सूत्र तैयार किया है:
}}</ref> चूँकि एक बार कुछ [[ पैरामीटर |पैरामीटर]] (उदाहरण के लिए त्रिज्या) के संदर्भ में ऐसा करने के बाद, गणितज्ञों ने इसकी त्रिज्या के संदर्भ में एक गोले के आयतन का वर्णन करने के लिए एक सूत्र तैयार किया है:


: <math>V = \frac{4}{3} \pi r^3.</math>
: <math>V = \frac{4}{3} \pi r^3.</math>
Line 42: Line 42:
  |website    = [[Stackexchange.com|math.stackexchange.com]]
  |website    = [[Stackexchange.com|math.stackexchange.com]]
  |access-date = 31 December 2013
  |access-date = 31 December 2013
}}</ref> गणितीय सूत्र अधिकांशतः बीजगणितीय अभिव्यक्ति, [[ विश्लेषणात्मक अभिव्यक्ति ]] या बंद-रूप अभिव्यक्ति में होते हैं।<ref>{{cite web
}}</ref> गणितीय सूत्र अधिकांशतः बीजगणितीय अभिव्यक्ति, [[ विश्लेषणात्मक अभिव्यक्ति |विश्लेषणात्मक अभिव्यक्ति]] या बंद-रूप अभिव्यक्ति में होते हैं।<ref>{{cite web
  |url        = https://www.andlearning.org/math-formula/
  |url        = https://www.andlearning.org/math-formula/
  |title      = List of Mathematical formulas
  |title      = List of Mathematical formulas
Line 52: Line 52:


: <math>F = ma</math>
: <math>F = ma</math>
न्यूटन के गति के नियमों की अभिव्यक्ति है | न्यूटन का दूसरा नियम, और भौतिक स्थितियों की एक विस्तृत श्रृंखला पर प्रयुक्त होता है। किसी विशेष समस्या को हल करने के लिए अन्य सूत्र, जैसे कि एक [[ खाड़ी |बे]] में ज्वारीय गति को मॉडल करने के लिए [[ साइन वक्र | साइन वक्र]] के [[ समीकरण | समीकरण]] का उपयोग किया जा सकता है। चूँकि सभी स्थिति में, सूत्र गणना के लिए आधार बनाते हैं।
न्यूटन के गति के नियमों की अभिव्यक्ति है | न्यूटन का दूसरा नियम, और भौतिक स्थितियों की एक विस्तृत श्रृंखला पर प्रयुक्त होता है। किसी विशेष समस्या को हल करने के लिए अन्य सूत्र, जैसे कि एक [[ खाड़ी |बे]] में ज्वारीय गति को मॉडल करने के लिए [[ साइन वक्र |साइन वक्र]] के [[ समीकरण |समीकरण]] का उपयोग किया जा सकता है। चूँकि सभी स्थिति में, सूत्र गणना के लिए आधार बनाते हैं।


व्यंजक (गणित) सूत्रों से भिन्न हैं क्योंकि उनमें समान का चिह्न (=) नहीं हो सकता।<ref>{{Citation
व्यंजक (गणित) सूत्रों से भिन्न हैं क्योंकि उनमें समान का चिह्न (=) नहीं हो सकता।<ref>{{Citation
Line 62: Line 62:
   |edition=2nd
   |edition=2nd
   |isbn=978-0-521-36865-0
   |isbn=978-0-521-36865-0
   |year=1988}}</ref> भावों की तुलना [[ वाक्यांशों | वाक्यांशों]] से की जा सकती है उसी तरह सूत्रों की तुलना [[ वाक्य खंड संरचना | व्याकरणिक वाक्यों]] से की जा सकती है।
   |year=1988}}</ref> भावों की तुलना [[ वाक्यांशों |वाक्यांशों]] से की जा सकती है उसी तरह सूत्रों की तुलना [[ वाक्य खंड संरचना |व्याकरणिक वाक्यों]] से की जा सकती है।


== रासायनिक सूत्र ==
== रासायनिक सूत्र ==
{{main|रासायनिक सूत्र}}
{{main|रासायनिक सूत्र}}


रसायन विज्ञान या आधुनिक रसायन विज्ञान के सिद्धांतों में, एक रासायनिक सूत्र [[ परमाणु ]]ओं के अनुपात के बारे में जानकारी व्यक्त करने का एक विधि है जो रासायनिक [[ रासायनिक प्रतीक ]]संख्याओं और कभी-कभी अन्य प्रतीकों, जैसे कोष्ठक कोष्ठक और प्लस (+) और माइनस (-) संकेत।<ref>Atkins, P.W., Overton, T., Rourke, J., Weller, M. and Armstrong, F. ''Shriver and Atkins inorganic chemistry'' (4th edition) 2006 ([[Oxford University Press]]) {{isbn|0-19-926463-5}}</ref> उदाहरण के लिए, एच<sub>2</sub>O [[ पानी ]] का रासायनिक सूत्र है, यह निर्दिष्ट करता है कि प्रत्येक [[ अणु ]] में दो [[ हाइड्रोजन ]] (H) परमाणु और एक [[ ऑक्सीजन ]] (O) परमाणु होते हैं। इसी तरह, ओ{{sup sub|−|3}} एक [[ ओजोन ]] अणु को दर्शाता है जिसमें तीन ऑक्सीजन परमाणु होते हैं और एक शुद्ध नकारात्मक आवेश होता है।<ref>{{Cite web|url=http://www.chm.bris.ac.uk/motm/ozone/CHEM.htm|title=ओजोन रसायन|website=www.chm.bris.ac.uk|access-date=2019-11-26}}</ref>  
रसायन विज्ञान या आधुनिक रसायन विज्ञान के सिद्धांतों में, एक रासायनिक सूत्र [[ परमाणु |परमाणु]] ओं के अनुपात के बारे में जानकारी व्यक्त करने का एक विधि है जो रासायनिक [[ रासायनिक प्रतीक |रासायनिक प्रतीक]] संख्याओं और कभी-कभी अन्य प्रतीकों, जैसे कोष्ठक कोष्ठक और प्लस (+) और माइनस (-) संकेत।<ref>Atkins, P.W., Overton, T., Rourke, J., Weller, M. and Armstrong, F. ''Shriver and Atkins inorganic chemistry'' (4th edition) 2006 ([[Oxford University Press]]) {{isbn|0-19-926463-5}}</ref> उदाहरण के लिए, एच<sub>2</sub>O [[ पानी |पानी]] का रासायनिक सूत्र है, यह निर्दिष्ट करता है कि प्रत्येक [[ अणु |अणु]] में दो [[ हाइड्रोजन |हाइड्रोजन]] (H) परमाणु और एक [[ ऑक्सीजन |ऑक्सीजन]] (O) परमाणु होते हैं। इसी तरह, ओ{{sup sub|−|3}} एक [[ ओजोन |ओजोन]] अणु को दर्शाता है जिसमें तीन ऑक्सीजन परमाणु होते हैं और एक शुद्ध नकारात्मक आवेश होता है।<ref>{{Cite web|url=http://www.chm.bris.ac.uk/motm/ozone/CHEM.htm|title=ओजोन रसायन|website=www.chm.bris.ac.uk|access-date=2019-11-26}}</ref>  


एक रासायनिक सूत्र प्रत्येक घटक [[ रासायनिक तत्व ]] को उसके [[ रासायनिक प्रतीक ]] द्वारा पहचानता है, और प्रत्येक तत्व के परमाणुओं की आनुपातिक संख्या को इंगित करता है।
एक रासायनिक सूत्र प्रत्येक घटक [[ रासायनिक तत्व |रासायनिक तत्व]] को उसके [[ रासायनिक प्रतीक |रासायनिक प्रतीक]] द्वारा पहचानता है, और प्रत्येक तत्व के परमाणुओं की आनुपातिक संख्या को इंगित करता है।


[[ अनुभवजन्य सूत्र ]]में, ये अनुपात एक प्रमुख तत्व से प्रारंभ होते हैं और फिर यौगिक में अन्य तत्वों के परमाणुओं की संख्या को मुख्य तत्व के अनुपात के रूप में निर्दिष्ट करते हैं। आणविक यौगिकों के लिए, इन अनुपात संख्याओं को सदैव पूर्ण संख्याओं के रूप में व्यक्त किया जा सकता है। उदाहरण के लिए, [[ इथेनॉल ]] का अनुभवजन्य सूत्र C<sub>2</sub>H<sub>6</sub>O लिखा जा सकता है<ref>{{Cite web|url=https://pubchem.ncbi.nlm.nih.gov/compound/702|title=इथेनॉल|last=PubChem|website=pubchem.ncbi.nlm.nih.gov|language=en|access-date=2019-11-26}}</ref> क्योंकि इथेनॉल के सभी अणुओं में दो कार्बन परमाणु, छह हाइड्रोजन परमाणु और एक ऑक्सीजन परमाणु होते हैं। चूँकि, कुछ प्रकार के आयनिक यौगिकों को अनुभवजन्य सूत्रों के रूप में नहीं लिखा जा सकता है जिसमें केवल पूर्ण संख्याएँ होती हैं। एक उदाहरण [[ बोरॉन कार्बाइड ]] है, जिसका सूत्र CB<sub>n</sub> एक चर गैर-पूर्ण संख्या अनुपात है, जिसमें n 4 से अधिक से लेकर 6.5 से अधिक तक है।
[[ अनुभवजन्य सूत्र ]]में, ये अनुपात एक प्रमुख तत्व से प्रारंभ होते हैं और फिर यौगिक में अन्य तत्वों के परमाणुओं की संख्या को मुख्य तत्व के अनुपात के रूप में निर्दिष्ट करते हैं। आणविक यौगिकों के लिए, इन अनुपात संख्याओं को सदैव पूर्ण संख्याओं के रूप में व्यक्त किया जा सकता है। उदाहरण के लिए, [[ इथेनॉल |इथेनॉल]] का अनुभवजन्य सूत्र C<sub>2</sub>H<sub>6</sub>O लिखा जा सकता है<ref>{{Cite web|url=https://pubchem.ncbi.nlm.nih.gov/compound/702|title=इथेनॉल|last=PubChem|website=pubchem.ncbi.nlm.nih.gov|language=en|access-date=2019-11-26}}</ref> क्योंकि इथेनॉल के सभी अणुओं में दो कार्बन परमाणु, छह हाइड्रोजन परमाणु और एक ऑक्सीजन परमाणु होते हैं। चूँकि, कुछ प्रकार के आयनिक यौगिकों को अनुभवजन्य सूत्रों के रूप में नहीं लिखा जा सकता है जिसमें केवल पूर्ण संख्याएँ होती हैं। एक उदाहरण [[ बोरॉन कार्बाइड |बोरॉन कार्बाइड]] है, जिसका सूत्र CB<sub>n</sub> एक चर गैर-पूर्ण संख्या अनुपात है, जिसमें n 4 से अधिक से लेकर 6.5 से अधिक तक है।


जब सूत्र के रासायनिक यौगिक में सरल अणु होते हैं, तो रासायनिक सूत्र अधिकांशतः अणु की संरचना का सुझाव देने के विधियों का उपयोग करते हैं। इन सूत्रों के कई प्रकार हैं, जिनमें आणविक सूत्र और [[ संघनित सूत्र ]] सम्मिलित हैं। एक आणविक सूत्र अणु में उन परमाणुओं को प्रतिबिंबित करने के लिए परमाणुओं की संख्या की गणना करता है, जिससे [[ शर्करा ]] के लिए आणविक सूत्र C<sub>6</sub>H<sub>12</sub>O<sub>6</sub> हो ग्लूकोज अनुभवजन्य सूत्र के अतिरिक्त, जो CH<sub>2</sub>O है बहुत ही सरल पदार्थों को छोड़कर, आणविक रासायनिक सूत्रों में सामान्यतः आवश्यक संरचनात्मक जानकारी नहीं होती है, और अवसरों में अस्पष्ट भी हो सकती है।
जब सूत्र के रासायनिक यौगिक में सरल अणु होते हैं, तो रासायनिक सूत्र अधिकांशतः अणु की संरचना का सुझाव देने के विधियों का उपयोग करते हैं। इन सूत्रों के कई प्रकार हैं, जिनमें आणविक सूत्र और [[ संघनित सूत्र |संघनित सूत्र]] सम्मिलित हैं। एक आणविक सूत्र अणु में उन परमाणुओं को प्रतिबिंबित करने के लिए परमाणुओं की संख्या की गणना करता है, जिससे [[ शर्करा |शर्करा]] के लिए आणविक सूत्र C<sub>6</sub>H<sub>12</sub>O<sub>6</sub> हो ग्लूकोज अनुभवजन्य सूत्र के अतिरिक्त, जो CH<sub>2</sub>O है बहुत ही सरल पदार्थों को छोड़कर, आणविक रासायनिक सूत्रों में सामान्यतः आवश्यक संरचनात्मक जानकारी नहीं होती है, और अवसरों में अस्पष्ट भी हो सकती है।


एक संरचनात्मक सूत्र एक चित्र है जो प्रत्येक परमाणु के स्थान को दर्शाता है, और यह किन परमाणुओं से बंधता है।
एक संरचनात्मक सूत्र एक चित्र है जो प्रत्येक परमाणु के स्थान को दर्शाता है, और यह किन परमाणुओं से बंधता है।


== [[ कम्प्यूटिंग ]] में ==
== [[ कम्प्यूटिंग | कम्प्यूटिंग]] में ==
कंप्यूटिंग में, एक सूत्र सामान्यतः [[ गणना ]] का वर्णन करता है, जैसे कि जोड़, एक या अधिक चर पर किया जाना एक सूत्र अधिकांशतः एक [[ निर्देश (कंप्यूटर विज्ञान) ]] के रूप में निहित रूप से प्रदान किया जाता है जैसे।
कंप्यूटिंग में, एक सूत्र सामान्यतः [[ गणना |गणना]] का वर्णन करता है, जैसे कि जोड़, एक या अधिक चर पर किया जाना एक सूत्र अधिकांशतः एक [[ निर्देश (कंप्यूटर विज्ञान) |निर्देश (कंप्यूटर विज्ञान)]] के रूप में निहित रूप से प्रदान किया जाता है जैसे।


: डिग्री सेल्सियस = (5/9)*(डिग्री फारेनहाइट - 32)
: डिग्री सेल्सियस = (5/9)*(डिग्री फारेनहाइट - 32)


कंप्यूटर [[ स्प्रेडशीट ]] सॉफ़्टवेयर में, एक सूत्र जो यह दर्शाता है कि [[ सेल संदर्भ | सेल के मान]] के मान की गणना कैसे की जाती है, A3 को इस रूप में लिखा जा सकता है
कंप्यूटर [[ स्प्रेडशीट |स्प्रेडशीट]] सॉफ़्टवेयर में, एक सूत्र जो यह दर्शाता है कि [[ सेल संदर्भ |सेल के मान]] के मान की गणना कैसे की जाती है, A3 को इस रूप में लिखा जा सकता है


: ''=A1+A2''
: ''=A1+A2''
Line 91: Line 91:
विज्ञान में उपयोग किए जाने वाले सूत्रों को लगभग सदैव इकाइयों के चुनाव की आवश्यकता होती है।<ref name=":0">{{Cite book | isbn = 978-1466571143 | title = सीआरसी हैंडबुक ऑफ केमिस्ट्री एंड फिजिक्स, 94वां संस्करण| editor1-last = Haynes | editor1-first= William M. | year = 2013 | orig-year = 1914 | publisher = CRC Press | location = Boca Raton  }}</ref> सूत्रों का उपयोग विभिन्न मात्राओं के बीच संबंधों को व्यक्त करने के लिए किया जाता है, जैसे तापमान, द्रव्यमान या भौतिकी में आवेश; अर्थशास्त्र में आपूर्ति, लाभ या मांग; या अन्य विषयों में अन्य मात्राओं की एक विस्तृत श्रृंखला है।
विज्ञान में उपयोग किए जाने वाले सूत्रों को लगभग सदैव इकाइयों के चुनाव की आवश्यकता होती है।<ref name=":0">{{Cite book | isbn = 978-1466571143 | title = सीआरसी हैंडबुक ऑफ केमिस्ट्री एंड फिजिक्स, 94वां संस्करण| editor1-last = Haynes | editor1-first= William M. | year = 2013 | orig-year = 1914 | publisher = CRC Press | location = Boca Raton  }}</ref> सूत्रों का उपयोग विभिन्न मात्राओं के बीच संबंधों को व्यक्त करने के लिए किया जाता है, जैसे तापमान, द्रव्यमान या भौतिकी में आवेश; अर्थशास्त्र में आपूर्ति, लाभ या मांग; या अन्य विषयों में अन्य मात्राओं की एक विस्तृत श्रृंखला है।


विज्ञान में उपयोग किए जाने वाले सूत्र का एक उदाहरण बोल्ट्जमैन का [[ एन्ट्रापी ]] सूत्र है। [[ सांख्यिकीय ऊष्मप्रवैगिकी ]] में यह एक आदर्श गैस के एंट्रॉपी एस को मात्रा डब्ल्यू से संबंधित संभावना समीकरण है, जो किसी दिए गए [[ मैक्रोस्टेट ]] से संबंधित [[ माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) ]] की संख्या है:
विज्ञान में उपयोग किए जाने वाले सूत्र का एक उदाहरण बोल्ट्जमैन का [[ एन्ट्रापी |एन्ट्रापी]] सूत्र है। [[ सांख्यिकीय ऊष्मप्रवैगिकी |सांख्यिकीय ऊष्मप्रवैगिकी]] में यह एक आदर्श गैस के एंट्रॉपी एस को मात्रा डब्ल्यू से संबंधित संभावना समीकरण है, जो किसी दिए गए [[ मैक्रोस्टेट |मैक्रोस्टेट]] से संबंधित [[ माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) |माइक्रोस्टेट (सांख्यिकीय यांत्रिकी)]] की संख्या है:


:<math>S = k \cdot \log W </math> (1) S= k ln W
:<math>S = k \cdot \log W </math> (1) S= k ln W


जहाँ k बोल्ट्जमान स्थिरांक है | बोल्ट्जमान स्थिरांक 1.38062 x 10<sup>−23</sup> जूल/केल्विन के समान है और W दिए गए मैक्रोस्टेट के अनुरूप माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) की संख्या है।
जहाँ k बोल्ट्जमान स्थिरांक है | बोल्ट्जमान स्थिरांक 1.38062 x 10<sup>−23</sup> जूल/केल्विन के समान है और W दिए गए मैक्रोस्टेट के अनुरूप माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) की संख्या है।
'''ज्ञान में उपयोग किए जाने वाले सूत्रों को लगभग सदैव इकाइयों के चुनाव की आवश्यकता होती है।<ref name=":0" />'''
== यह भी देखें                                ==
== यह भी देखें                                ==
* [[ सूत्र संपादक ]]
* [[ सूत्र संपादक ]]

Revision as of 10:42, 19 May 2023

A sphere
Isobutane
On the left is a sphere, whose volume is given by the mathematical formula V = 4/3 π r3. On the right is the compound isobutane, which has chemical formula (CH3)3CH.
कंप्यूटर विज्ञान में अग्रदूतों की सूची की गणना करने वाले सबसे प्रभावशाली आंकड़ों में से एक, एडवर्ड डिजस्ट्रा 1994 में ईटीएच ज्यूरिख में एक सम्मेलन के दौरान ब्लैकबोर्ड पर। डिजस्ट्रा के अपने शब्दों में, एक तस्वीर एक हजार शब्दों के लायक है, एक सूत्र एक हजार चित्रों के लायक है .[1]

विज्ञान में, सूत्र गणितीय सूत्र या रासायनिक सूत्र के रूप में प्रतीकात्मक रूप से जानकारी व्यक्त करने का एक संक्षिप्त विधि है। विज्ञान में शब्दावली सूत्र का अनौपचारिक उपयोग अनुरूपता (विज्ञान के दर्शन) को संदर्भित करता है।

सूत्र का बहुवचन या तो सूत्र हो सकता है (सबसे समान्य अंग्रेजी बहुवचन या नियमित बहुवचन से) या, वैज्ञानिक लैटिन सूत्र ( अंग्रेजी में लैटिन प्रभाव से) के प्रभाव में है ।[2]

गणित में

गणित में, एक सूत्र सामान्यतः एक पहचान (गणित) को संदर्भित करता है जो एक गणितीय अभिव्यक्ति को दूसरे के साथ जोड़ता है, जिसमें सबसे महत्वपूर्ण गणितीय प्रमेय है। वाक्यात्मक रूप से, एक सूत्र (अधिकांशतः एक अच्छी तरह से गठित सूत्र के रूप में संदर्भित) एक इकाई है जिसे किसी औपचारिक भाषा के प्रतीकों और गठन नियमों का उपयोग करके बनाया जाता है।[3] उदाहरण के लिए, एक गोले का आयतन निर्धारित करने के लिए एक महत्वपूर्ण मात्रा में समाकलन गणित या इसके ज्यामिति एनालॉग, निष्कासन विधि की आवश्यकता होती है।[4] चूँकि एक बार कुछ पैरामीटर (उदाहरण के लिए त्रिज्या) के संदर्भ में ऐसा करने के बाद, गणितज्ञों ने इसकी त्रिज्या के संदर्भ में एक गोले के आयतन का वर्णन करने के लिए एक सूत्र तैयार किया है:

इस परिणाम को प्राप्त करने के बाद, किसी भी गोले के आयतन की गणना तब तक की जा सकती है जब तक कि उसकी त्रिज्या ज्ञात हो। यहां, ध्यान दें कि वॉल्यूम V और त्रिज्या r को शब्दों या वाक्यांशों के अतिरिक्त एकल अक्षरों के रूप में व्यक्त किया जाता है। यह सम्मेलन, जबकि अपेक्षाकृत सरल सूत्र में कम महत्वपूर्ण है, इसका अर्थ है कि गणितज्ञ उन सूत्रों में अधिक तेज़ी से हेरफेर कर सकते हैं जो बड़े और अधिक जटिल हैं।[5] गणितीय सूत्र अधिकांशतः बीजगणितीय अभिव्यक्ति, विश्लेषणात्मक अभिव्यक्ति या बंद-रूप अभिव्यक्ति में होते हैं।[6]

एक सामान्य संदर्भ में, सूत्र वास्तविक दुनिया की घटनाओं के लिए गणितीय मॉडल की एक अभिव्यक्ति हैं, और जैसे कि वास्तविक दुनिया की समस्याओं के समाधान (या अनुमानित समाधान) प्रदान करने के लिए उपयोग किया जा सकता है, कुछ दूसरों की तुलना में अधिक सामान्य हैं। उदाहरण के लिए, सूत्र

न्यूटन के गति के नियमों की अभिव्यक्ति है | न्यूटन का दूसरा नियम, और भौतिक स्थितियों की एक विस्तृत श्रृंखला पर प्रयुक्त होता है। किसी विशेष समस्या को हल करने के लिए अन्य सूत्र, जैसे कि एक बे में ज्वारीय गति को मॉडल करने के लिए साइन वक्र के समीकरण का उपयोग किया जा सकता है। चूँकि सभी स्थिति में, सूत्र गणना के लिए आधार बनाते हैं।

व्यंजक (गणित) सूत्रों से भिन्न हैं क्योंकि उनमें समान का चिह्न (=) नहीं हो सकता।[7] भावों की तुलना वाक्यांशों से की जा सकती है उसी तरह सूत्रों की तुलना व्याकरणिक वाक्यों से की जा सकती है।

रासायनिक सूत्र

Main article: रासायनिक सूत्र

रसायन विज्ञान या आधुनिक रसायन विज्ञान के सिद्धांतों में, एक रासायनिक सूत्र परमाणु ओं के अनुपात के बारे में जानकारी व्यक्त करने का एक विधि है जो रासायनिक रासायनिक प्रतीक संख्याओं और कभी-कभी अन्य प्रतीकों, जैसे कोष्ठक कोष्ठक और प्लस (+) और माइनस (-) संकेत।[8] उदाहरण के लिए, एच2O पानी का रासायनिक सूत्र है, यह निर्दिष्ट करता है कि प्रत्येक अणु में दो हाइड्रोजन (H) परमाणु और एक ऑक्सीजन (O) परमाणु होते हैं। इसी तरह, ओ−
3 एक ओजोन अणु को दर्शाता है जिसमें तीन ऑक्सीजन परमाणु होते हैं और एक शुद्ध नकारात्मक आवेश होता है।[9]

एक रासायनिक सूत्र प्रत्येक घटक रासायनिक तत्व को उसके रासायनिक प्रतीक द्वारा पहचानता है, और प्रत्येक तत्व के परमाणुओं की आनुपातिक संख्या को इंगित करता है।

अनुभवजन्य सूत्र में, ये अनुपात एक प्रमुख तत्व से प्रारंभ होते हैं और फिर यौगिक में अन्य तत्वों के परमाणुओं की संख्या को मुख्य तत्व के अनुपात के रूप में निर्दिष्ट करते हैं। आणविक यौगिकों के लिए, इन अनुपात संख्याओं को सदैव पूर्ण संख्याओं के रूप में व्यक्त किया जा सकता है। उदाहरण के लिए, इथेनॉल का अनुभवजन्य सूत्र C2H6O लिखा जा सकता है[10] क्योंकि इथेनॉल के सभी अणुओं में दो कार्बन परमाणु, छह हाइड्रोजन परमाणु और एक ऑक्सीजन परमाणु होते हैं। चूँकि, कुछ प्रकार के आयनिक यौगिकों को अनुभवजन्य सूत्रों के रूप में नहीं लिखा जा सकता है जिसमें केवल पूर्ण संख्याएँ होती हैं। एक उदाहरण बोरॉन कार्बाइड है, जिसका सूत्र CBn एक चर गैर-पूर्ण संख्या अनुपात है, जिसमें n 4 से अधिक से लेकर 6.5 से अधिक तक है।

जब सूत्र के रासायनिक यौगिक में सरल अणु होते हैं, तो रासायनिक सूत्र अधिकांशतः अणु की संरचना का सुझाव देने के विधियों का उपयोग करते हैं। इन सूत्रों के कई प्रकार हैं, जिनमें आणविक सूत्र और संघनित सूत्र सम्मिलित हैं। एक आणविक सूत्र अणु में उन परमाणुओं को प्रतिबिंबित करने के लिए परमाणुओं की संख्या की गणना करता है, जिससे शर्करा के लिए आणविक सूत्र C6H12O6 हो ग्लूकोज अनुभवजन्य सूत्र के अतिरिक्त, जो CH2O है बहुत ही सरल पदार्थों को छोड़कर, आणविक रासायनिक सूत्रों में सामान्यतः आवश्यक संरचनात्मक जानकारी नहीं होती है, और अवसरों में अस्पष्ट भी हो सकती है।

एक संरचनात्मक सूत्र एक चित्र है जो प्रत्येक परमाणु के स्थान को दर्शाता है, और यह किन परमाणुओं से बंधता है।

कम्प्यूटिंग में

कंप्यूटिंग में, एक सूत्र सामान्यतः गणना का वर्णन करता है, जैसे कि जोड़, एक या अधिक चर पर किया जाना एक सूत्र अधिकांशतः एक निर्देश (कंप्यूटर विज्ञान) के रूप में निहित रूप से प्रदान किया जाता है जैसे।

डिग्री सेल्सियस = (5/9)*(डिग्री फारेनहाइट - 32)

कंप्यूटर स्प्रेडशीट सॉफ़्टवेयर में, एक सूत्र जो यह दर्शाता है कि सेल के मान के मान की गणना कैसे की जाती है, A3 को इस रूप में लिखा जा सकता है

=A1+A2

जहाँ A1 और A2 स्प्रेडशीट के अंदर अन्य सेल (स्तम्भ A, पंक्ति 1 या 2) को संदर्भित करते हैं। यह पेपर रूप A3 = A1+A2 के लिए एक शॉर्टकट है, जहां परंपरा के अनुसार, A3 को छोड़ दिया गया है, क्योंकि परिणाम सदैव सेल में ही संग्रहीत होता है, जिससे नाम का विवरण निरर्थक हो जाता है।

इकाइयाँ

विज्ञान में उपयोग किए जाने वाले सूत्रों को लगभग सदैव इकाइयों के चुनाव की आवश्यकता होती है।[11] सूत्रों का उपयोग विभिन्न मात्राओं के बीच संबंधों को व्यक्त करने के लिए किया जाता है, जैसे तापमान, द्रव्यमान या भौतिकी में आवेश; अर्थशास्त्र में आपूर्ति, लाभ या मांग; या अन्य विषयों में अन्य मात्राओं की एक विस्तृत श्रृंखला है।

विज्ञान में उपयोग किए जाने वाले सूत्र का एक उदाहरण बोल्ट्जमैन का एन्ट्रापी सूत्र है। सांख्यिकीय ऊष्मप्रवैगिकी में यह एक आदर्श गैस के एंट्रॉपी एस को मात्रा डब्ल्यू से संबंधित संभावना समीकरण है, जो किसी दिए गए मैक्रोस्टेट से संबंधित माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) की संख्या है:

(1) S= k ln W

जहाँ k बोल्ट्जमान स्थिरांक है | बोल्ट्जमान स्थिरांक 1.38062 x 10−23 जूल/केल्विन के समान है और W दिए गए मैक्रोस्टेट के अनुरूप माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) की संख्या है।

यह भी देखें

संदर्भ

  1. ↑ Dijkstra, E.W. (July 1996), A first exploration of effective reasoning [EWD896]. (E.W. Dijkstra Archive, Center for American History, University of Texas at Austin)
  2. ↑ "formula". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
  3. ↑ Rautenberg, Wolfgang (2010), A Concise Introduction to Mathematical Logic (3rd ed.), New York, NY: Springer Science+Business Media, doi:10.1007/978-1-4419-1221-3, ISBN 978-1-4419-1220-6
  4. ↑ Smith, David E. (1958). गणित का इतिहास. New York: Dover Publications. ISBN 0-486-20430-8.
  5. ↑ "Why do mathematicians use single letter variables?". math.stackexchange.com. 28 February 2011. Retrieved 31 December 2013.
  6. ↑ "List of Mathematical formulas". andlearning.org. 24 August 2018.
  7. ↑ Hamilton, A. G. (1988), Logic for Mathematicians (2nd ed.), Cambridge: Cambridge University Press, ISBN 978-0-521-36865-0
  8. ↑ Atkins, P.W., Overton, T., Rourke, J., Weller, M. and Armstrong, F. Shriver and Atkins inorganic chemistry (4th edition) 2006 (Oxford University Press) ISBN 0-19-926463-5
  9. ↑ "ओजोन रसायन". www.chm.bris.ac.uk. Retrieved 2019-11-26.
  10. ↑ PubChem. "इथेनॉल". pubchem.ncbi.nlm.nih.gov (in English). Retrieved 2019-11-26.
  11. ↑ Haynes, William M., ed. (2013) [1914]. सीआरसी हैंडबुक ऑफ केमिस्ट्री एंड फिजिक्स, 94वां संस्करण. Boca Raton: CRC Press. ISBN 978-1466571143.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=सूत्र&oldid=182790’