प्रतिक्रिया प्रगति गतिज विश्लेषण: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|Methods for determining rate laws of chemical reactions and to elucidate their mechanisms}} | {{short description|Methods for determining rate laws of chemical reactions and to elucidate their mechanisms}} | ||
रसायन विज्ञान में, अभिक्रिया प्रगति काइनेटिक विश्लेषण (RPKA) रासायनिक अभिक्रियाओं के दर कानूनों को निर्धारित करने और अभिक्रिया तंत्र की व्याख्या में सहायता करने के लिए उपयोग की जाने वाली गतिज तकनीकों की एक विस्तृत श्रृंखला का एक उपवर्ग है। जबकि अभिक्रिया प्रगति काइनेटिक विश्लेषण का मार्गदर्शन करने वाली अवधारणाएं नई नहीं हैं, इस प्रक्रिया को 1990 के दशक के अंत में प्रोफेसर डोना ब्लैकमंड (वर्तमान में स्क्रिप्स रिसर्च इंस्टीट्यूट में) द्वारा औपचारिक रूप दिया गया था और तब से तेजी से व्यापक उपयोग देखा गया है।अधिक सामान्य छद्म-प्रथम-क्रम विश्लेषण के विपरीत, जिसमें ब्याज की एक प्रजाति के सापेक्ष एक या अधिक अभिकर्मकों की भारी मात्रा का उपयोग किया जाता है, RPKA कृत्रिम रूप से प्रासंगिक स्थितियों पर अभिक्रियाओं की जांच करता है (अर्थात सांद्रता और अभिकर्मक अनुपात के साथ जो अभिक्रिया में उपयोग किए जाने वाले समान होते हैं) दर कानून की खोज नहीं कर रहा है।) प्रायः, इस विश्लेषण में एक प्रणाली सम्मिलित होती है जिसमें अभिक्रिया के दौरान कई अभिकारकों की सांद्रता औसत रूप से बदल रही | रसायन विज्ञान में, अभिक्रिया प्रगति काइनेटिक विश्लेषण (RPKA) रासायनिक अभिक्रियाओं के दर कानूनों को निर्धारित करने और अभिक्रिया तंत्र की व्याख्या में सहायता करने के लिए उपयोग की जाने वाली गतिज तकनीकों की एक विस्तृत श्रृंखला का एक उपवर्ग है। जबकि अभिक्रिया प्रगति काइनेटिक विश्लेषण का मार्गदर्शन करने वाली अवधारणाएं नई नहीं हैं, इस प्रक्रिया को 1990 के दशक के अंत में प्रोफेसर डोना ब्लैकमंड (वर्तमान में स्क्रिप्स रिसर्च इंस्टीट्यूट में) द्वारा औपचारिक रूप दिया गया था और तब से तेजी से व्यापक उपयोग देखा गया है।अधिक सामान्य छद्म-प्रथम-क्रम विश्लेषण के विपरीत, जिसमें ब्याज की एक प्रजाति के सापेक्ष एक या अधिक अभिकर्मकों की भारी मात्रा का उपयोग किया जाता है, RPKA कृत्रिम रूप से प्रासंगिक स्थितियों पर अभिक्रियाओं की जांच करता है (अर्थात सांद्रता और अभिकर्मक अनुपात के साथ जो अभिक्रिया में उपयोग किए जाने वाले समान होते हैं) दर कानून की खोज नहीं कर रहा है।) प्रायः, इस विश्लेषण में एक प्रणाली सम्मिलित होती है जिसमें अभिक्रिया के दौरान कई अभिकारकों की सांद्रता औसत रूप से बदल रही है। जैसा कि तंत्र सम्मिलित प्रजातियों के सापेक्ष और पूर्ण सांद्रता के आधार पर भिन्न हो सकता है, यह दृष्टिकोण ऐसे परिणाम प्राप्त करता है जो पारंपरिक रणनीति की तुलना में प्रायः उपयोग की जाने वाली परिस्थितियों में अभिक्रिया व्यवहार के अधिक प्रतिनिधि होते हैं। इसके अतिरिक्त, समय के साथ अभिक्रिया के अवलोकन से प्राप्त जानकारी अप्रत्याशित व्यवहार जैसे प्रेरण अवधि, उत्प्रेरक निष्क्रियता, या तंत्र में परिवर्तन के बारे में अंतर्दृष्टि प्रदान कर सकती है।<ref name=Hartwig>{{cite book | ||
| last = Hartwig | first = J. F. | | last = Hartwig | first = J. F. | ||
| author-link= John Hartwig | | author-link= John Hartwig | ||
| Line 152: | Line 152: | ||
जहाँ q तात्क्षणिक ऊष्मा अंतरण है, ΔH अभिक्रिया का ज्ञात एन्थैल्पी परिवर्तन है, और V अभिक्रिया आयतन है। <ref name=Blackmond-2005/> | जहाँ q तात्क्षणिक ऊष्मा अंतरण है, ΔH अभिक्रिया का ज्ञात एन्थैल्पी परिवर्तन है, और V अभिक्रिया आयतन है। <ref name=Blackmond-2005/> | ||
अभिक्रिया प्रगति | अभिक्रिया प्रगति बलगति विज्ञान प्रयोगों से आंकड़ों भी प्रायः एक दर (v) बनाम कार्यद्रव्य सांद्रता ([S]) प्लॉट के माध्यम से प्रस्तुत किया जाता है। इसके लिए ऊपर वर्णित [S] बनाम t और v बनाम t दोनों प्लॉटों को प्राप्त करने और संयोजन करने की आवश्यकता है (ध्यान दें कि एक को दूसरे से सरल विभेदीकरण या एकीकरण द्वारा प्राप्त किया जा सकता है।)संयोजन घटता के एक मानक सेट की ओर जाता है जिसमें अभिक्रिया प्रगति को एक्स-अक्ष के साथ दाएं से बाएं और अभिक्रिया दर को वाई-अक्ष के साथ नीचे से ऊपर तक पढ़ा जाता है।<ref name=Blackmond-2005/>जबकि ये भूखंड प्रायः बुनियादी गतिज प्रवृत्तियों का एक नेत्रहीन सम्मोहक प्रदर्शन प्रदान करते हैं, संख्यात्मक दर स्थिरांक निकालने के लिए अंतर विधियां प्रायः बेहतर होती हैं। (नीचे देखें) | ||
=== कैटेलिटिक | === कैटेलिटिक बलगति विज्ञान और कैटलिस्ट रेस्टिंग स्टेट === | ||
उत्प्रेरक | उत्प्रेरक बलगति विज्ञान में, कई प्रणालियों के व्यवहार का वर्णन करने के लिए दो बुनियादी सन्निकटन उपयोगी होते हैं (विभिन्न परिस्थितियों में)। जिन स्थितियों में पूर्व-संतुलन और स्थिर-अवस्था सन्निकटन मान्य होते हैं, उन्हें प्रायः अभिक्रिया प्रगति गतिज विश्लेषण द्वारा अलग किया जा सकता है, और दो स्थितियां उत्प्रेरक की विश्राम अवस्था से निकटता से संबंधित होती हैं। | ||
=== स्थिर-अवस्था सन्निकटन === | === स्थिर-अवस्था सन्निकटन === | ||
[[File:Steady State 2.png|thumb|600px|ए) स्थिर अवस्था | [[File:Steady State 2.png|thumb|600px|ए) स्थिर अवस्था बलगति विज्ञान के सबसे सरल मामले में एक सब्सट्रेट उत्क्रमणीय रूप से उत्प्रेरक के साथ एक मध्यवर्ती परिसर (जिस पर स्थिर-अवस्था सन्निकटन लागू होता है) का निर्माण होता है, जिसके बाद अपरिवर्तनीय उत्पाद निर्माण होता है। बी) एक अधिक जटिल उदाहरण में, दो सबस्ट्रेट्स उत्प्रेरक को क्रमिक रूप से दो इंटरमीडिएट बनाने के लिए बांधते हैं (और स्थिर-अवस्था सन्निकटन दोनों पर लागू होता है) जिसके बाद अपरिवर्तनीय उत्पाद निर्माण होता है। ध्यान दें कि क्योंकि I2 काइनेटिक रूप से अदृश्य है, यह उस मामले के समान है जहां I1 सीधे मुक्त उत्पाद और उत्प्रेरक के पास जाता है। दोनों (ए) और (बी) के लिए, i) प्रासंगिक दर स्थिरांक और सांद्रता के साथ उत्प्रेरक चक्र का वर्णन करता है, ii) प्रतिक्रिया के दौरान उत्पाद और अभिकारक की एकाग्रता को प्रदर्शित करता है, iii) सब्सट्रेट के रूप में प्रतिक्रिया की दर का वर्णन करता है दाएँ से बाएँ उपभोग किया जाता है, और iv) दर्शाता है कि उत्प्रेरक विश्राम अवस्था पूरी तरह से मुक्त उत्प्रेरक है, जबकि मध्यवर्ती की सांद्रता छोटी रहती है और लगभग अपरिवर्तित रहती है क्योंकि सब्सट्रेट को दाएँ से बाएँ उपयोग किया जाता है।]]स्थिर-स्थिति स्थितियों के तहत, उत्प्रेरक और कार्यद्रव्य उत्क्रमणीय संघ से गुजरते हैं जिसके बाद उत्प्रेरक-कार्यद्रव्य परिसर की अपेक्षाकृत तेजी से खपत होती है (उत्पाद के लिए आगे की अभिक्रिया और आबंध उत्प्रेरक के लिए उत्क्रमणीय अभिक्रिया दोनों द्वारा)। उत्प्रेरक-कार्यद्रव्य परिसर समय के साथ नहीं बदल रहा है; इस परिसर की कुल सांद्रता कम रहती है क्योंकि इसे बनने के लगभग तुरंत बाद हटा दिया जाता है। एक स्थिर-अवस्था दर कानून में प्रारंभिक सामग्री से उत्पाद तक जाने के लिए आवश्यक सभी दर स्थिरांक और प्रजातियां सम्मिलित हैं, जबकि भाजक में स्थिर-अवस्था मध्यवर्ती की खपत करने वाली आगे और उत्क्रमणीय अभिक्रियाओं की सापेक्ष दरों का वर्णन करने वाले शब्दों का योग होता है। सबसे सरल मामले के लिए जहां एक कार्यद्रव्य एक उत्पाद के लिए एक मध्यवर्ती के माध्यम से जाता है: | ||
:{{sfrac|''d''[P]|''dt''}} = {{sfrac|''k''<sub>1</sub>''k''<sub>2</sub>[A][Cat]<sub>total</sub>|''k''<sub>−1</sub> + ''k''<sub>2</sub>}} | :{{sfrac|''d''[P]|''dt''}} = {{sfrac|''k''<sub>1</sub>''k''<sub>2</sub>[A][Cat]<sub>total</sub>|''k''<sub>−1</sub> + ''k''<sub>2</sub>}} | ||
| Line 181: | Line 181: | ||
=== पूर्व-संतुलन सन्निकटन === | === पूर्व-संतुलन सन्निकटन === | ||
[[File:Preequilibrium 2.png|thumb|600px|ए) पूर्व-संतुलन | [[File:Preequilibrium 2.png|thumb|600px|ए) पूर्व-संतुलन बलगति विज्ञान के सबसे सरल मामले में एक सब्सट्रेट "तेजी से" शामिल है और उत्क्रमणीय रूप से उत्प्रेरक के साथ एक मध्यवर्ती परिसर का निर्माण होता है, जिसके बाद अपरिवर्तनीय उत्पाद निर्माण होता है। बी) एक अधिक जटिल उदाहरण में, दो सबस्ट्रेट्स क्रमिक रूप से उत्प्रेरक को 'तेजी से' बांधते हैं और इसके बाद अपरिवर्तनीय उत्पाद निर्माण होता है। दोनों (ए) और (बी) के लिए, i) प्रासंगिक दर स्थिरांक और सांद्रता के साथ उत्प्रेरक चक्र का वर्णन करता है, ii) प्रतिक्रिया के दौरान उत्पाद और अभिकारक की एकाग्रता को प्रदर्शित करता है, iii) सब्सट्रेट के रूप में प्रतिक्रिया की दर का वर्णन करता है दाएँ से बाएँ उपभोग किया जाता है, और iv) दर्शाता है कि उत्प्रेरक विश्राम अवस्था मुक्त उत्प्रेरक और मध्यवर्ती का एक संतुलन वितरण है जहाँ वितरण को मुक्त उत्प्रेरक की ओर तेजी से स्थानांतरित किया जाता है क्योंकि सब्सट्रेट को दाएँ से बाएँ उपयोग किया जाता है।]]पूर्व-संतुलन स्थितियों के तहत, उत्प्रेरक और कार्यद्रव्य उत्पाद निर्माण और रिलीज के लिए अपेक्षाकृत धीमी गति से पहले तेजी से और प्रतिवर्ती जुड़ाव से गुजरते हैं। इन शर्तों के तहत, प्रणाली को "वन-प्लस" दर कानून द्वारा वर्णित किया जा सकता है जहां अंश में सभी दर स्थिरांक और प्रजातियां सम्मिलित होती हैं जो प्रारंभिक सामग्री से उत्पाद तक जाने के लिए आवश्यक होती हैं, और भाजक में प्रत्येक का वर्णन करने वाले शब्दों का योग होता है। जिन अवस्थाओं में उत्प्रेरक उपस्थित है।<ref name=Helfferich> | ||
{{cite journal | {{cite journal | ||
| last = Helfferich | first = F. G. | | last = Helfferich | first = F. G. | ||
| Line 200: | Line 200: | ||
ऊपर वर्णित सरल पूर्व-संतुलन स्थितियों के मामले में, उत्प्रेरक विश्राम अवस्था या तो पूरी तरह या आंशिक रूप से (संतुलन स्थिरांक के परिमाण के आधार पर) कार्यद्रव्य बंध परिसर है। | ऊपर वर्णित सरल पूर्व-संतुलन स्थितियों के मामले में, उत्प्रेरक विश्राम अवस्था या तो पूरी तरह या आंशिक रूप से (संतुलन स्थिरांक के परिमाण के आधार पर) कार्यद्रव्य बंध परिसर है। | ||
=== संतृप्ति | === संतृप्ति बलगति विज्ञान === | ||
{{main| | {{main|माइकलिस-मेंटेन बलगति विज्ञान}} | ||
संतृप्ति स्थितियों को पूर्व-संतुलन स्थितियों के एक विशेष कारको के रूप में देखा जा सकता है।कार्यद्रव्य की जांच की गई सांद्रता पर, उत्प्रेरक-कार्यद्रव्य परिसर का गठन तेजी से और अनिवार्य रूप से अपरिवर्तनीय है। उत्प्रेरक विश्राम अवस्था में पूरी तरह से बाध्य परिसर होते हैं, और [A] अब दर कानून में उपस्थित नहीं है; [A] बदलने से अभिक्रिया दर पर कोई प्रभाव नहीं पड़ेगा क्योंकि उत्प्रेरक पहले से ही पूरी तरह से बाध्य है और जितनी तेजी से के 2 अनुमति देता है उतनी तेजी से अभिक्रिया कर रहा है।यह संतृप्ति किनेटी का सबसे सरल मामला है जिसमे एंजाइम | |||
संतृप्ति स्थितियों को पूर्व-संतुलन स्थितियों के एक विशेष कारको के रूप में देखा जा सकता है।कार्यद्रव्य की जांच की गई सांद्रता पर, उत्प्रेरक-कार्यद्रव्य परिसर का गठन तेजी से और अनिवार्य रूप से अपरिवर्तनीय है। उत्प्रेरक विश्राम अवस्था में पूरी तरह से बाध्य परिसर होते हैं, और [A] अब दर कानून में उपस्थित नहीं है; [A] बदलने से अभिक्रिया दर पर कोई प्रभाव नहीं पड़ेगा क्योंकि उत्प्रेरक पहले से ही पूरी तरह से बाध्य है और जितनी तेजी से के 2 अनुमति देता है उतनी तेजी से अभिक्रिया कर रहा है।यह संतृप्ति किनेटी का सबसे सरल मामला है जिसमे एंजाइम बलगति विज्ञान के लिए अच्छी तरह से अध्ययन किया गया |[[माइकलिस-मेंटेन कैनेटीक्स|माइकलिस-मेंटेन बलगति विज्ञान]] माइकलिस-मेंटेन मॉडल है। | |||
=== उत्प्रेरक विश्राम अवस्था में परिवर्तन === | === उत्प्रेरक विश्राम अवस्था में परिवर्तन === | ||
[[File:Saturation Kinetics-2.png|thumb|400px|ए) संतृप्ति | [[File:Saturation Kinetics-2.png|thumb|400px|ए) संतृप्ति बलगति विज्ञान का सबसे सरल मामला पूर्व-संतुलन स्थिति से फैला हुआ है जिसमें उत्प्रेरक के साथ तेजी से सब्सट्रेट संकुलन के बाद उत्पाद का धीमा गठन होता है। बी) समय के साथ सब्सट्रेट एकाग्रता के लिए ग्राफ का सीधा हिस्सा अधिकांश प्रतिक्रिया के लिए सब्सट्रेट पर शून्य-क्रम निर्भरता का संकेत है, लेकिन कम [ए] पर वक्र (इस मामले में) पहले परिवर्तन का संकेत है [ए] पर आदेश निर्भरता। ग) सब्सट्रेट की उच्च सांद्रता पर उत्प्रेरक की संतृप्ति स्पष्ट है (जहां दर का [ए] पर कोई निर्भरता नहीं है, लेकिन जैसा कि सब्सट्रेट का सेवन किया जाता है, प्रतिक्रिया दर मूल से गुजरने के लिए [ए] पर पहले क्रम की निर्भरता के साथ गिर जाती है। डी) उत्प्रेरक आराम करने की स्थिति भी बदलती है, जहां यह लगभग पूरी तरह से सब्सट्रेट-बाउंड कॉम्प्लेक्स, कैट-ए, उच्च [ए] के रूप में मौजूद है, लेकिन तेजी से मुक्त उत्प्रेरक के रूप में, कैट, [ए] के दौरान घट जाती है प्रतिक्रिया।]] | ||
[[File:Rate vs Catalyst Loading at Multiple Conversion Points.png|thumb|300px|केटोन, A के सायनोसिलिलेशन में उत्पाद निर्माण की दर, उच्च उत्प्रेरक सांद्रता पर उत्प्रेरक लोडिंग पर मामूली गैर-रैखिक निर्भरता दर्शाती है। A) यह अवलोकन, दूसरों के बीच, निष्क्रिय उत्प्रेरक परिसरों के प्रतिवर्ती गठन के कारण होता है। बी) कई रूपांतरण बिंदुओं पर समान व्यवहार अभिक्रिया के पूरे पाठ्यक्रम पर काम करने वाले एक प्रमुख तंत्र के अनुरूप है।<ref>{{cite journal | last1 = Zuend | first1 = S. J. | last2 = Jacobsen | first2 = E. N. | year = 2007 | title = यंत्रवत योजना और गतिज डेटा को केटोन्स के अमीनो-थियोरिया उत्प्रेरित साइनोसिलिलेशन के लिए रिपोर्ट की गई दर और संतुलन स्थिरांक का उपयोग करके स्वतंत्र गतिज सिमुलेशन से अनुकूलित किया गया है।| journal = J. Am. Chem. Soc. | volume = 129 | issue = 51 | pages = 15872–15883 | doi=10.1021/ja0735352| pmid = 18052247 }}</ref>]]जबकि एक अभिक्रिया प्रारंभिक रूपांतरण पर गतिज व्यवहार का एक सेट प्रदर्शित कर सकती है, वह व्यवहार इसके कारण बदल सकता है | [[File:Rate vs Catalyst Loading at Multiple Conversion Points.png|thumb|300px|केटोन, A के सायनोसिलिलेशन में उत्पाद निर्माण की दर, उच्च उत्प्रेरक सांद्रता पर उत्प्रेरक लोडिंग पर मामूली गैर-रैखिक निर्भरता दर्शाती है। A) यह अवलोकन, दूसरों के बीच, निष्क्रिय उत्प्रेरक परिसरों के प्रतिवर्ती गठन के कारण होता है। बी) कई रूपांतरण बिंदुओं पर समान व्यवहार अभिक्रिया के पूरे पाठ्यक्रम पर काम करने वाले एक प्रमुख तंत्र के अनुरूप है।<ref>{{cite journal | last1 = Zuend | first1 = S. J. | last2 = Jacobsen | first2 = E. N. | year = 2007 | title = यंत्रवत योजना और गतिज डेटा को केटोन्स के अमीनो-थियोरिया उत्प्रेरित साइनोसिलिलेशन के लिए रिपोर्ट की गई दर और संतुलन स्थिरांक का उपयोग करके स्वतंत्र गतिज सिमुलेशन से अनुकूलित किया गया है।| journal = J. Am. Chem. Soc. | volume = 129 | issue = 51 | pages = 15872–15883 | doi=10.1021/ja0735352| pmid = 18052247 }}</ref>]]जबकि एक अभिक्रिया प्रारंभिक रूपांतरण पर गतिज व्यवहार का एक सेट प्रदर्शित कर सकती है, वह व्यवहार इसके कारण बदल सकता है | ||
* कार्यद्रव्य सांद्रता को बदलने से प्रभावित उत्प्रेरक स्थिर करने वाली अवस्था में परिवर्तन | * कार्यद्रव्य सांद्रता को बदलने से प्रभावित उत्प्रेरक स्थिर करने वाली अवस्था में परिवर्तन | ||
| Line 212: | Line 213: | ||
* उत्पाद निषेध | * उत्पाद निषेध | ||
* अपरिवर्तनीय (या प्रतिवर्ती) उत्प्रेरक मृत्यु | * अपरिवर्तनीय (या प्रतिवर्ती) उत्प्रेरक मृत्यु | ||
ऊपर वर्णित संतृप्ति | ऊपर वर्णित संतृप्ति बलगति विज्ञान के मामले में, बशर्ते कि [A] [B] के सापेक्ष बड़ी मात्रा में उपस्थित न हो, संतृप्ति की स्थिति केवल अभिक्रिया की शुरुआत में लागू होगी। जैसा कि कार्यद्रव्य का सेवन किया जाता है, सांद्रता कम हो जाती है और अंततः [A] अब पूरी तरह से डूबने के लिए पर्याप्त नहीं है। यह [A] में 0-ऑर्डर से कुछ उच्च (अर्थात 1, 2, आदि) क्रम में दर में क्रमिक परिवर्तन से प्रकट होता है। इसे उत्प्रेरक विश्राम अवस्था में परिवर्तन के रूप में भी वर्णित किया जा सकता है। | ||
अभिक्रिया को केवल धीमा करने के अतिरिक्त, अभिक्रिया के दौरान उत्प्रेरक आराम करने वाले अवस्था में बदलाव के परिणामस्वरूप प्रतिस्पर्धी पथ या प्रक्रियाएं हो सकती हैं। उत्पाद तक पहुंचने के लिए कई तंत्र उपस्थित हो सकते हैं, जिस स्थिति में अभिक्रिया में स्थिति या बिंदु के आधार पर उत्प्रेरक या कार्यद्रव्य में क्रम बदल सकता है। अभिक्रिया तंत्र में परिवर्तन के लिए एक विशेष रूप से उपयोगी जांच में सामान्यीकृत अभिक्रिया दर बनाम कई, निश्चित रूपांतरण बिंदुओं पर उत्प्रेरक लोडिंग की परीक्षा सम्मिलित है।। ध्यान दें कि सामान्यीकृत अभिक्रिया दर: | अभिक्रिया को केवल धीमा करने के अतिरिक्त, अभिक्रिया के दौरान उत्प्रेरक आराम करने वाले अवस्था में बदलाव के परिणामस्वरूप प्रतिस्पर्धी पथ या प्रक्रियाएं हो सकती हैं। उत्पाद तक पहुंचने के लिए कई तंत्र उपस्थित हो सकते हैं, जिस स्थिति में अभिक्रिया में स्थिति या बिंदु के आधार पर उत्प्रेरक या कार्यद्रव्य में क्रम बदल सकता है। अभिक्रिया तंत्र में परिवर्तन के लिए एक विशेष रूप से उपयोगी जांच में सामान्यीकृत अभिक्रिया दर बनाम कई, निश्चित रूपांतरण बिंदुओं पर उत्प्रेरक लोडिंग की परीक्षा सम्मिलित है।। ध्यान दें कि सामान्यीकृत अभिक्रिया दर: | ||
| Line 254: | Line 255: | ||
:[B]<sub>''t''</sub> = [A]<sub>''t''</sub> + e | :[B]<sub>''t''</sub> = [A]<sub>''t''</sub> + e | ||
उच्च क्रम स्टोइकोमेट्री के साथ अभिक्रियाओं के लिए एक समान सेट का निर्माण किया जा सकता है, जिसमें अभिक्रिया के दौरान अतिरिक्त रूप से भिन्न होता है। जबकि e कोई भी मूल्य हो सकता है (सकारात्मक, नकारात्मक, या शून्य)प्रायः कार्यद्रव्य के एक समकक्ष की तुलना में परिमाण में छोटे सकारात्मक या नकारात्मक मूल्यों का उपयोग अभिक्रिया प्रगति गतिज विश्लेषण में किया जाता है। (कोई यह नोट कर सकता है कि छद्म-शून्य-क्रम | उच्च क्रम स्टोइकोमेट्री के साथ अभिक्रियाओं के लिए एक समान सेट का निर्माण किया जा सकता है, जिसमें अभिक्रिया के दौरान अतिरिक्त रूप से भिन्न होता है। जबकि e कोई भी मूल्य हो सकता है (सकारात्मक, नकारात्मक, या शून्य)प्रायः कार्यद्रव्य के एक समकक्ष की तुलना में परिमाण में छोटे सकारात्मक या नकारात्मक मूल्यों का उपयोग अभिक्रिया प्रगति गतिज विश्लेषण में किया जाता है। (कोई यह नोट कर सकता है कि छद्म-शून्य-क्रम बलगति विज्ञान कार्यद्रव्य के एक समकक्ष की तुलना में परिमाण में बहुत अधिक मूल्यों का उपयोग करता है)। | ||
अतिरिक्त (e) के पैरामीटर को परिभाषित करने से समान-अतिरिक्त प्रयोगों के निर्माण की अनुमति मिलती है जिसमें विभिन्न प्रारंभिक सांद्रता के साथ गतिज प्रयोग के दो या दो से अधिक मान होते हैं, लेकिन समान-अतिरिक्त किसी भी बिंदु पर कृत्रिम रूप से अभिक्रिया दर्ज करने की अनुमति देता है। उत्प्रेरक अभिक्रियाओं के RPKA के लिए ये प्रयोग महत्वपूर्ण हैं, क्योंकि वे उत्प्रेरक सक्रियण (प्रेरण अवधि), उत्प्रेरक निष्क्रियता, और उत्पाद निषेध में वर्णित कई यंत्रवत संभावनाओं की जांच करने में सक्षम हैं।<ref name="Blackmond-2005" /><ref name="Blackmond-2006" /> | अतिरिक्त (e) के पैरामीटर को परिभाषित करने से समान-अतिरिक्त प्रयोगों के निर्माण की अनुमति मिलती है जिसमें विभिन्न प्रारंभिक सांद्रता के साथ गतिज प्रयोग के दो या दो से अधिक मान होते हैं, लेकिन समान-अतिरिक्त किसी भी बिंदु पर कृत्रिम रूप से अभिक्रिया दर्ज करने की अनुमति देता है। उत्प्रेरक अभिक्रियाओं के RPKA के लिए ये प्रयोग महत्वपूर्ण हैं, क्योंकि वे उत्प्रेरक सक्रियण (प्रेरण अवधि), उत्प्रेरक निष्क्रियता, और उत्पाद निषेध में वर्णित कई यंत्रवत संभावनाओं की जांच करने में सक्षम हैं।<ref name="Blackmond-2005" /><ref name="Blackmond-2006" /> | ||
| Line 309: | Line 310: | ||
| issue = 3 | | issue = 3 | ||
| pages = 658–666 | | pages = 658–666 | ||
| doi = 10.1021/ja01318a036}}</ref>जटिल वक्रों को फ़िट करने में सक्षम कंप्यूटिंग तकनीकों के आगमन से पहले रेखीकरण तकनीकों का विशेष महत्व था, और वे अपनी सहज सरल प्रस्तुति के कारण | | doi = 10.1021/ja01318a036}}</ref>जटिल वक्रों को फ़िट करने में सक्षम कंप्यूटिंग तकनीकों के आगमन से पहले रेखीकरण तकनीकों का विशेष महत्व था, और वे अपनी सहज सरल प्रस्तुति के कारण बलगति विज्ञान में एक प्रधान बने हुए हैं।<ref name=Blackmond-2005/>यह ध्यान रखना महत्वपूर्ण है कि रैखिककरण तकनीकों का उपयोग संख्यात्मक दर स्थिरांक निकालने के लिए नहीं किया जाना चाहिए क्योंकि वे वैकल्पिक संख्यात्मक तकनीकों के सापेक्ष बड़ी मात्रा में त्रुटि पेश करते हैं। ग्राफिकल दर कानून, यद्यपि, रैखिककृत आंकड़े की सहज प्रस्तुति को बनाए रखते हैं, जैसे कि प्लॉट का दृश्य निरीक्षण हाथ में अभिक्रिया के बारे में यंत्रवत अंतर्दृष्टि प्रदान कर सकता है। ग्राफिकल दर कानून का आधार दर (v) बनाम दर पर निर्भर करता है।कार्यद्रव्य सांद्रता ([S]) प्लॉट ऊपर चर्चा की। उदाहरण के लिए, सरल चक्र में विभिन्न-अतिरिक्त प्रयोगों के संबंध में चर्चा की गई है | ||
v/[A] बनाम [B] और उसके जुड़वां v/[B] बनाम [A] प्रत्येक अभिकर्मकों के क्रम के बारे में सहज अंतर्दृष्टि प्रदान कर सकता है। अगर प्लॉट्v/[A] बनाम [बी] विभिन्न-अतिरिक्त के साथ कई प्रयोगों के लिए ओवरले, डेटा [ए] पर पहले-क्रम की निर्भरता के अनुरूप हैं। के प्लॉट के लिए भी यही कहा जा सकता हैv/[B] बनाम [A];अधिचित्रित [B] पर पहले क्रम की निर्भरता के अनुरूप है। इन ग्राफिकल दर कानूनों के गैर- अधिचित्रित परिणाम संभव हैं और जांच किए गए कार्यद्रव्य पर उच्च आदेश निर्भरता का संकेत हैं। ब्लैकमंड ने ग्राफिकल दर समीकरणों की एक श्रृंखला के साथ विभिन्न-अतिरिक्त प्रयोगों के परिणामों को प्रस्तुत करने का प्रस्ताव दिया है (जो कि वह यहां अनुकूलित प्रवाह-चार्ट में प्रस्तुत करती है), लेकिन यह ध्यान रखना महत्वपूर्ण है कि उनकी प्रस्तावित विधि प्रदर्शित करने के कई संभावित तरीकों में से एक काइनेटिक संबंध है।इसके अतिरिक्त, जबकि ग्राफिकल दर कानूनों की प्रस्तुति को कभी-कभी जटिल गतिशील आंकड़े पेश करने के लिए एक दृष्टि से सरलीकृत तरीका माना जा सकता है, अंतर या अन्य कठोर संख्यात्मक तरीकों से विश्लेषण के लिए कच्चे गतिशील आंकड़ों को फिट करना सटीक और मात्रात्मक दर स्थिरांक और अभिक्रिया आदेश निकालने के लिए आवश्यक है। <ref name="Blackmond-2005" /><ref name="Blackmond-2006" /> | v/[A] बनाम [B] और उसके जुड़वां v/[B] बनाम [A] प्रत्येक अभिकर्मकों के क्रम के बारे में सहज अंतर्दृष्टि प्रदान कर सकता है। अगर प्लॉट्v/[A] बनाम [बी] विभिन्न-अतिरिक्त के साथ कई प्रयोगों के लिए ओवरले, डेटा [ए] पर पहले-क्रम की निर्भरता के अनुरूप हैं। के प्लॉट के लिए भी यही कहा जा सकता हैv/[B] बनाम [A];अधिचित्रित [B] पर पहले क्रम की निर्भरता के अनुरूप है। इन ग्राफिकल दर कानूनों के गैर- अधिचित्रित परिणाम संभव हैं और जांच किए गए कार्यद्रव्य पर उच्च आदेश निर्भरता का संकेत हैं। ब्लैकमंड ने ग्राफिकल दर समीकरणों की एक श्रृंखला के साथ विभिन्न-अतिरिक्त प्रयोगों के परिणामों को प्रस्तुत करने का प्रस्ताव दिया है (जो कि वह यहां अनुकूलित प्रवाह-चार्ट में प्रस्तुत करती है), लेकिन यह ध्यान रखना महत्वपूर्ण है कि उनकी प्रस्तावित विधि प्रदर्शित करने के कई संभावित तरीकों में से एक काइनेटिक संबंध है।इसके अतिरिक्त, जबकि ग्राफिकल दर कानूनों की प्रस्तुति को कभी-कभी जटिल गतिशील आंकड़े पेश करने के लिए एक दृष्टि से सरलीकृत तरीका माना जा सकता है, अंतर या अन्य कठोर संख्यात्मक तरीकों से विश्लेषण के लिए कच्चे गतिशील आंकड़ों को फिट करना सटीक और मात्रात्मक दर स्थिरांक और अभिक्रिया आदेश निकालने के लिए आवश्यक है। <ref name="Blackmond-2005" /><ref name="Blackmond-2006" /> | ||
| Line 317: | Line 318: | ||
=== यह भी देखें === | === यह भी देखें === | ||
* रासायनिक गतिकी | * रासायनिक गतिकी | ||
* [[एंजाइम कैनेटीक्स]] | * [[एंजाइम कैनेटीक्स|एंजाइम बलगति विज्ञान]] | ||
* पहाड़ी समीकरण (जैव रसायन) | * पहाड़ी समीकरण (जैव रसायन) | ||
* [[लैंगमुइर सोखना मॉडल]] | * [[लैंगमुइर सोखना मॉडल]] | ||
* माइकलिस-मेंटेन | * माइकलिस-मेंटेन बलगति विज्ञान | ||
* [[मोनोड समीकरण]] | * [[मोनोड समीकरण]] | ||
* [[दर समीकरण (रसायन विज्ञान)]] | * [[दर समीकरण (रसायन विज्ञान)]] | ||
Revision as of 17:52, 18 June 2023
रसायन विज्ञान में, अभिक्रिया प्रगति काइनेटिक विश्लेषण (RPKA) रासायनिक अभिक्रियाओं के दर कानूनों को निर्धारित करने और अभिक्रिया तंत्र की व्याख्या में सहायता करने के लिए उपयोग की जाने वाली गतिज तकनीकों की एक विस्तृत श्रृंखला का एक उपवर्ग है। जबकि अभिक्रिया प्रगति काइनेटिक विश्लेषण का मार्गदर्शन करने वाली अवधारणाएं नई नहीं हैं, इस प्रक्रिया को 1990 के दशक के अंत में प्रोफेसर डोना ब्लैकमंड (वर्तमान में स्क्रिप्स रिसर्च इंस्टीट्यूट में) द्वारा औपचारिक रूप दिया गया था और तब से तेजी से व्यापक उपयोग देखा गया है।अधिक सामान्य छद्म-प्रथम-क्रम विश्लेषण के विपरीत, जिसमें ब्याज की एक प्रजाति के सापेक्ष एक या अधिक अभिकर्मकों की भारी मात्रा का उपयोग किया जाता है, RPKA कृत्रिम रूप से प्रासंगिक स्थितियों पर अभिक्रियाओं की जांच करता है (अर्थात सांद्रता और अभिकर्मक अनुपात के साथ जो अभिक्रिया में उपयोग किए जाने वाले समान होते हैं) दर कानून की खोज नहीं कर रहा है।) प्रायः, इस विश्लेषण में एक प्रणाली सम्मिलित होती है जिसमें अभिक्रिया के दौरान कई अभिकारकों की सांद्रता औसत रूप से बदल रही है। जैसा कि तंत्र सम्मिलित प्रजातियों के सापेक्ष और पूर्ण सांद्रता के आधार पर भिन्न हो सकता है, यह दृष्टिकोण ऐसे परिणाम प्राप्त करता है जो पारंपरिक रणनीति की तुलना में प्रायः उपयोग की जाने वाली परिस्थितियों में अभिक्रिया व्यवहार के अधिक प्रतिनिधि होते हैं। इसके अतिरिक्त, समय के साथ अभिक्रिया के अवलोकन से प्राप्त जानकारी अप्रत्याशित व्यवहार जैसे प्रेरण अवधि, उत्प्रेरक निष्क्रियता, या तंत्र में परिवर्तन के बारे में अंतर्दृष्टि प्रदान कर सकती है।[1][2]
निगरानी प्रतिक्रिया प्रगति
अभिक्रिया प्रगति काइनेटिक विश्लेषण समय के साथ अभिक्रिया रूपांतरण की सटीक निगरानी करने की क्षमता पर निर्भर करता है। यह लक्ष्य कई तकनीकों द्वारा पूरा किया जा सकता है, जिनमें से सबसे आम नीचे वर्णित हैं। जबकि इन तकनीकों को कभी-कभी अंतर (समय के साथ निगरानी अभिक्रिया दर) या अभिन्न (समय के साथ कार्यद्रव्य और/या उत्पाद की मात्रा की निगरानी) के रूप में वर्गीकृत किया जाता है, सरल गणितीय हेरफेर (भेदभाव या एकीकरण) प्राप्त आंकड़े के अंतर-रूपांतरण की अनुमति देता है दोनों में से किसी के द्वारा प्राप्त किया गया।लागू की गई तकनीक के अतिरिक्त, एक अतिरिक्त स्वतंत्र विधि के साथ निगरानी करके ब्याज की प्रणाली में वैधता की पुष्टि करना प्रायः फायदेमंद होता है।[2]
प्रतिक्रिया प्रगति NMR
एनएमआर स्पेक्ट्रोस्कोपी प्रायः अभिक्रिया प्रगति की निगरानी के लिए पसंद की विधि होती है, जहां गैर-अभिक्रियाशील मानक के सापेक्ष शिखर एकीकरण के परिवर्तन से समय के साथ कार्यद्रव्य खपत और उत्पाद निर्माण देखा जा सकता है। सघनता आंकड़े से, समय के साथ अभिक्रिया की दर एक बहुपद के व्युत्पन्न को प्रयोगात्मक वक्र में फिट करके प्राप्त की जा सकती है।[3]अभिक्रिया प्रगति NMR को एक अभिन्न तकनीक के रूप में वर्गीकृत किया जा सकता है क्योंकि एकत्र किए गए प्राथमिक सांद्रता बनाम समय के समानुपाती होते हैं।[2]जबकि यह तकनीक विशिष्ट, पृथक उत्पाद और अभिक्रियाशील चोटियों के साथ स्पष्ट रूप से परिभाषित प्रणालियों के लिए बेहद सुविधाजनक है, इसमें एनएमआर नली में अभिक्रिया के लिए उत्तरदायी एक सजातीय प्रणाली की आवश्यकता की खामी है। जबकि एनएमआर अवलोकन अभिक्रिया मध्यवर्ती की पहचान के लिए अनुमति दे सकता है,अभिक्रिया के दौरान किसी भी प्रजाति की उपस्थिति जरूरी नहीं कि इसे उत्पादक प्रक्रिया में सम्मिलित किया जाए।[1]अभिक्रिया की प्रगति एनएमआर, यद्यपि,प्रायः चर तापमान पर चलाया जा सकता है, जिससे अभिक्रिया की दर को अवलोकन के लिए सुविधाजनक स्तर पर समायोजित किया जा सकता है।अभिक्रिया प्रगति एनएमआर के उपयोग के उदाहरण प्रचुर मात्रा में हैं, जिसमें बुचवाल्ड-हार्टविग अमिनेशन की जांच सहित उल्लेखनीय उदाहरण हैं (कोई यह ध्यान दे सकता है कि बुचवाल्ड-हार्टविग एमिनेशन के यंत्रवत विकास के सर्वोत्तम दृष्टिकोण को लेकर काफी बहस हुई, जैसा कि प्रकाशित कई विरोधाभासी और प्रतिस्पर्धी रिपोर्टों से संकेत मिलता है। थोड़े समय के लिए नामित लेख और उसमें संदर्भ देखें।)[4]
सीटू FT-IR में
n सीटू अवरक्त स्पेक्ट्रोस्कोपी का उपयोग अभिक्रिया के पाठ्यक्रम की निगरानी के लिए किया जा सकता है, बशर्ते एक अभिकर्मक या उत्पाद IR वर्णक्रमीय क्षेत्र में विशिष्ट अवशोषण दिखाता है।अभिक्रियाशील खपत और/या उत्पाद निर्माण की दर समय के साथ अवशोषण के परिवर्तन (बियर के कानून के आवेदन द्वारा) से अलग हो सकती है। यहां तक कि जब अभिकारक और उत्पाद स्पेक्ट्रा कुछ हद तक अतिव्यापैन प्रदर्शित करते हैं, तो आधुनिक इंस्ट्रूमेंटेशन सॉफ्टवेयर प्रायः वहां प्रदान किए गए सापेक्ष योगदानों को सटीक रूप से विखंडित करने में सक्षम होता है।सीटू IR को एक अभिन्न तकनीक के रूप में वर्गीकृत किया जा सकता है क्योंकि एकत्र किए गए प्राथमिक आंकड़े सांद्रता बनाम समय के समानुपाती होते हैं।।[2] इन आंकड़ों से, प्रारंभिक सामग्री या समय के साथ उत्पाद की सघनता प्रायोगिक वक्र के लिए एक बहुपद फिट के अभिन्न अंग को ले कर प्राप्त की जा सकती है।[3]सीटू निगरानी क्षमताओं के साथ स्पेक्ट्रोमीटर की उपलब्धता में वृद्धि के साथ, FT-IR ने हाल के वर्षों में उपयोग में वृद्धि देखी है। नोट के उदाहरणों में एमिडो-थी का यंत्रवत विश्लेषण सम्मिलित है।एमिडो-थियोरिया उत्प्रेरित असममित स्ट्रेकर अप्राकृतिक एमीनो अम्ल का संश्लेषण और लुईस क्षार उत्प्रेरित हैलोलैक्टोनाइजेशन और साइक्लोएथरिफिकेशन अभिक्रियाएं है।[5][6]
सीटू UV-विज़ में
ऊपर वर्णित सीटू IR प्रयोगों के अनुरूप, सीटू UV-दृश्य अवशोषक स्पेक्ट्रोस्कोपी में अभिक्रिया के पाठ्यक्रम की निगरानी के लिए उपयोग किया जा सकता है, बशर्ते एक अभिकर्मक या उत्पाद UV वर्णक्रमीय क्षेत्र में विशिष्ट अवशोषण दिखाता है। अभिक्रियाशील खपत और उत्पाद निर्माण की दर समय के साथ अवशोषण के परिवर्तन (बीयर के कानून के आवेदन द्वारा) से अमूर्त हो सकती है, फिर से एक अभिन्न तकनीक के रूप में वर्गीकरण के लिए अग्रणी हो सकती है।[2] उपयोग किए गए वर्णक्रमीय क्षेत्र के कारण,UV-विज़ तकनीकों का उपयोग विशुद्ध रूप से जैविक अभिक्रियाओं की तुलना में अकार्बनिक या ऑर्गोनोमेटेलिक प्रणाली पर अधिक किया जाता है, और उदाहरणों में समैरियम बारबियर अभिक्रिया की खोज सम्मिलित है।[7]
प्रतिक्रिया उष्मामिति
अभिक्रिया के पाठ्यक्रम की निगरानी के लिए कैलोरीमेट्री का उपयोग किया जा सकता है, क्योंकि अभिक्रिया के तात्कालिक गर्मी प्रवाह, जो अभिक्रिया के लिए एन्थैल्पी परिवर्तन से सीधे संबंधित है, की निगरानी की जाती है। अभिक्रिया कैलोरीमेट्री को एक विभेदक तकनीक के रूप में वर्गीकृत किया जा सकता है क्योंकि एकत्र किए गए प्राथमिक आंकड़े दर बनाम समय के समानुपाती होते हैं। इन आंकड़ों से, प्रारंभिक सामग्री या समय के साथ उत्पाद सांद्रता प्रयोगात्मक वक्र में बहुपद फिट का अभिन्न अंग लेकर प्राप्त किया जा सकता है।[2][8][9]जबकि कई अन्य तकनीकों की तुलना में अभिक्रिया कैलोरीमेट्री कम बार-बार नियोजित की जाती है, इसने उत्प्रेरक स्क्रीनिंग के लिए एक प्रभावी उपकरण के रूप में उपयोग पाया है।[10]अभिक्रिया कैलोरीमेट्री को व्यक्तिगत अभिक्रियाओं के यंत्रवत अध्ययन के लिए एक कुशल विधि के रूप में भी लागू किया गया है, जिसमें एल्डिहाइड के प्रोलिनेट-उत्प्रेरित α-एमिनेशन।[11] और पैलेडियम उत्प्रेरित बुक्वाल्ड-हार्टविग एमिनेशन अभिक्रिया सम्मिलित हैं।[4][12]
आगे की तकनीकें
जबकि गैस क्रोमैटोग्राफी, HPLC,और मास स्पेक्ट्रोमेट्री यौगिकों (और कभी-कभी प्रतिबिंबरूपता) के मिश्रण को अलग करने के लिए सभी उत्कृष्ट तकनीकें हैं, इन मापों का समय संकल्प ऊपर वर्णित तकनीकों की तुलना में कम सटीक है। भले ही, इन तकनीकों का अभी भी उपयोग देखा गया है, जैसे कि हेक अभिक्रिया की जांच में जहां अभिक्रिया की विषम प्रकृति ऊपर वर्णित तकनीकों के उपयोग को रोकती है।[13] और ऑर्गनोकैटलिस्ट्स द्वारा सोमो-सक्रियण [14] अपनी कमियों के बाद भी, ये तकनीकें उत्कृष्ट अंशांकन विधियों के रूप में काम कर सकती हैं।
डेटा हेरफेर और प्रस्तुति

अभिक्रिया प्रगति आंकड़े को प्रायः कार्यद्रव्य सांद्रता ([A] t) बनाम समय (t) या अंश रूपांतरण (F) बनाम समय (t) की साजिश के रूप में प्रस्तुत किया जा सकता है। उत्तरार्द्ध को आंशिक रूपांतरण (F) में सांद्रता / अवशोषण मूल्यों को परिवर्तित करने के लिए साधारण बीजगणितीय हेरफेर की आवश्यकता होती है:
- F = [A]0 − [A]t/[A]0
जहां [A] 0 प्रारंभिक रूप से उपस्थित कार्यद्रव्य की मात्रा, अवशोषण या सांद्रता है और [A] t t समय पर उस अभिकर्मक की मात्रा, अवशोषण या सांद्रता है।आंशिक रूपांतरण के लिए आंकड़े को सामान्य करना विशेष रूप से सहायक हो सकता है क्योंकि यह एक ही प्लॉट पर तुलना करने के लिए अलग-अलग निरपेक्ष मात्रा या सांद्रता के साथ चलने वाली कई अभिक्रियाओं की अनुमति देता है।
आंकड़ों को प्रायः अभिक्रिया दर (v) बनाम समय (t) के प्लॉट के रूप में भी प्रस्तुत किया जा सकता है। फिर से, सरल बीजगणितीय हेरफेर की आवश्यकता है; उदाहरण के लिए, कैलोरीमेट्रिक प्रयोग देते हैं:
- v = q/VΔH
जहाँ q तात्क्षणिक ऊष्मा अंतरण है, ΔH अभिक्रिया का ज्ञात एन्थैल्पी परिवर्तन है, और V अभिक्रिया आयतन है। [2]
अभिक्रिया प्रगति बलगति विज्ञान प्रयोगों से आंकड़ों भी प्रायः एक दर (v) बनाम कार्यद्रव्य सांद्रता ([S]) प्लॉट के माध्यम से प्रस्तुत किया जाता है। इसके लिए ऊपर वर्णित [S] बनाम t और v बनाम t दोनों प्लॉटों को प्राप्त करने और संयोजन करने की आवश्यकता है (ध्यान दें कि एक को दूसरे से सरल विभेदीकरण या एकीकरण द्वारा प्राप्त किया जा सकता है।)संयोजन घटता के एक मानक सेट की ओर जाता है जिसमें अभिक्रिया प्रगति को एक्स-अक्ष के साथ दाएं से बाएं और अभिक्रिया दर को वाई-अक्ष के साथ नीचे से ऊपर तक पढ़ा जाता है।[2]जबकि ये भूखंड प्रायः बुनियादी गतिज प्रवृत्तियों का एक नेत्रहीन सम्मोहक प्रदर्शन प्रदान करते हैं, संख्यात्मक दर स्थिरांक निकालने के लिए अंतर विधियां प्रायः बेहतर होती हैं। (नीचे देखें)
कैटेलिटिक बलगति विज्ञान और कैटलिस्ट रेस्टिंग स्टेट
उत्प्रेरक बलगति विज्ञान में, कई प्रणालियों के व्यवहार का वर्णन करने के लिए दो बुनियादी सन्निकटन उपयोगी होते हैं (विभिन्न परिस्थितियों में)। जिन स्थितियों में पूर्व-संतुलन और स्थिर-अवस्था सन्निकटन मान्य होते हैं, उन्हें प्रायः अभिक्रिया प्रगति गतिज विश्लेषण द्वारा अलग किया जा सकता है, और दो स्थितियां उत्प्रेरक की विश्राम अवस्था से निकटता से संबंधित होती हैं।
स्थिर-अवस्था सन्निकटन

स्थिर-स्थिति स्थितियों के तहत, उत्प्रेरक और कार्यद्रव्य उत्क्रमणीय संघ से गुजरते हैं जिसके बाद उत्प्रेरक-कार्यद्रव्य परिसर की अपेक्षाकृत तेजी से खपत होती है (उत्पाद के लिए आगे की अभिक्रिया और आबंध उत्प्रेरक के लिए उत्क्रमणीय अभिक्रिया दोनों द्वारा)। उत्प्रेरक-कार्यद्रव्य परिसर समय के साथ नहीं बदल रहा है; इस परिसर की कुल सांद्रता कम रहती है क्योंकि इसे बनने के लगभग तुरंत बाद हटा दिया जाता है। एक स्थिर-अवस्था दर कानून में प्रारंभिक सामग्री से उत्पाद तक जाने के लिए आवश्यक सभी दर स्थिरांक और प्रजातियां सम्मिलित हैं, जबकि भाजक में स्थिर-अवस्था मध्यवर्ती की खपत करने वाली आगे और उत्क्रमणीय अभिक्रियाओं की सापेक्ष दरों का वर्णन करने वाले शब्दों का योग होता है। सबसे सरल मामले के लिए जहां एक कार्यद्रव्य एक उत्पाद के लिए एक मध्यवर्ती के माध्यम से जाता है:
- d[P]/dt = k1k2[A][Cat]total/k−1 + k2
थोड़ी अधिक जटिल स्थिति में जहां दो कार्यद्रवो को अनुक्रम में बंधते हैं, जिसके बाद उत्पाद छूट जाता है:
- d[P]/dt = k1k2k3[A][B][Cat]total/k−1k−2 + k−1k3 + k2k3[B]
इस संदर्भ में वर्णित एल्गोरिथम के साथ तेजी से जटिल प्रणालियों का वर्णन किया जा सकता है।[15]
ऊपर वर्णित स्थिर-अवस्था स्थितियों में, उत्प्रेरक विश्राम अवस्था आबंध रूप में है (क्योंकि कार्यद्रव्य -बंध इंटरमीडिएट, परिभाषा के अनुसार, केवल न्यूनतम सांद्रता पर उपस्थित है।)[16]
पूर्व-संतुलन सन्निकटन

पूर्व-संतुलन स्थितियों के तहत, उत्प्रेरक और कार्यद्रव्य उत्पाद निर्माण और रिलीज के लिए अपेक्षाकृत धीमी गति से पहले तेजी से और प्रतिवर्ती जुड़ाव से गुजरते हैं। इन शर्तों के तहत, प्रणाली को "वन-प्लस" दर कानून द्वारा वर्णित किया जा सकता है जहां अंश में सभी दर स्थिरांक और प्रजातियां सम्मिलित होती हैं जो प्रारंभिक सामग्री से उत्पाद तक जाने के लिए आवश्यक होती हैं, और भाजक में प्रत्येक का वर्णन करने वाले शब्दों का योग होता है। जिन अवस्थाओं में उत्प्रेरक उपस्थित है।[17] सबसे सरल मामले के लिए जहां एक कार्यद्रव्य एक उत्पाद के लिए एक मध्यवर्ती के माध्यम से जाता है:
- d[P]/dt = K1k2[A][Cat]/1 + K1[A]
थोड़ी अधिक जटिल स्थिति में जहां दो कार्यद्रव्य अनुक्रम में बंधते हैं, जिसके बाद उत्पाद निकलता है:
- d[P]/dt = K1K2k3[A][B][Cat]/1 + K1[A] + K1K2[A][B]
ऊपर वर्णित सरल पूर्व-संतुलन स्थितियों के मामले में, उत्प्रेरक विश्राम अवस्था या तो पूरी तरह या आंशिक रूप से (संतुलन स्थिरांक के परिमाण के आधार पर) कार्यद्रव्य बंध परिसर है।
संतृप्ति बलगति विज्ञान
संतृप्ति स्थितियों को पूर्व-संतुलन स्थितियों के एक विशेष कारको के रूप में देखा जा सकता है।कार्यद्रव्य की जांच की गई सांद्रता पर, उत्प्रेरक-कार्यद्रव्य परिसर का गठन तेजी से और अनिवार्य रूप से अपरिवर्तनीय है। उत्प्रेरक विश्राम अवस्था में पूरी तरह से बाध्य परिसर होते हैं, और [A] अब दर कानून में उपस्थित नहीं है; [A] बदलने से अभिक्रिया दर पर कोई प्रभाव नहीं पड़ेगा क्योंकि उत्प्रेरक पहले से ही पूरी तरह से बाध्य है और जितनी तेजी से के 2 अनुमति देता है उतनी तेजी से अभिक्रिया कर रहा है।यह संतृप्ति किनेटी का सबसे सरल मामला है जिसमे एंजाइम बलगति विज्ञान के लिए अच्छी तरह से अध्ययन किया गया |माइकलिस-मेंटेन बलगति विज्ञान माइकलिस-मेंटेन मॉडल है।
उत्प्रेरक विश्राम अवस्था में परिवर्तन


जबकि एक अभिक्रिया प्रारंभिक रूपांतरण पर गतिज व्यवहार का एक सेट प्रदर्शित कर सकती है, वह व्यवहार इसके कारण बदल सकता है
- कार्यद्रव्य सांद्रता को बदलने से प्रभावित उत्प्रेरक स्थिर करने वाली अवस्था में परिवर्तन
- कार्यद्रव्य या उत्पाद सांद्रता से प्रभावित कई या बदलते तंत्र
- उत्प्रेरक सक्रियण (एक दीक्षा अवधि
- उत्पाद निषेध
- अपरिवर्तनीय (या प्रतिवर्ती) उत्प्रेरक मृत्यु
ऊपर वर्णित संतृप्ति बलगति विज्ञान के मामले में, बशर्ते कि [A] [B] के सापेक्ष बड़ी मात्रा में उपस्थित न हो, संतृप्ति की स्थिति केवल अभिक्रिया की शुरुआत में लागू होगी। जैसा कि कार्यद्रव्य का सेवन किया जाता है, सांद्रता कम हो जाती है और अंततः [A] अब पूरी तरह से डूबने के लिए पर्याप्त नहीं है। यह [A] में 0-ऑर्डर से कुछ उच्च (अर्थात 1, 2, आदि) क्रम में दर में क्रमिक परिवर्तन से प्रकट होता है। इसे उत्प्रेरक विश्राम अवस्था में परिवर्तन के रूप में भी वर्णित किया जा सकता है।
अभिक्रिया को केवल धीमा करने के अतिरिक्त, अभिक्रिया के दौरान उत्प्रेरक आराम करने वाले अवस्था में बदलाव के परिणामस्वरूप प्रतिस्पर्धी पथ या प्रक्रियाएं हो सकती हैं। उत्पाद तक पहुंचने के लिए कई तंत्र उपस्थित हो सकते हैं, जिस स्थिति में अभिक्रिया में स्थिति या बिंदु के आधार पर उत्प्रेरक या कार्यद्रव्य में क्रम बदल सकता है। अभिक्रिया तंत्र में परिवर्तन के लिए एक विशेष रूप से उपयोगी जांच में सामान्यीकृत अभिक्रिया दर बनाम कई, निश्चित रूपांतरण बिंदुओं पर उत्प्रेरक लोडिंग की परीक्षा सम्मिलित है।। ध्यान दें कि सामान्यीकृत अभिक्रिया दर:
- K = v/[A]t
अभिक्रिया के दौरान कार्यद्रव्य की खपत के लिए समायोजित करता है, इसलिए उत्प्रेरक लोडिंग के कारण केवल दर परिवर्तन देखा जाएगा। किसी दिए गए रूपांतरण के लिए उत्प्रेरक लोडिंग पर एक रैखिक निर्भरता उस रूपांतरण पर उत्प्रेरक पर पहले क्रम की निर्भरता का संकेत है, और इसी तरह उच्च आदेश निर्भरता से उत्पन्न गैर-रैखिक भूखंडों की कल्पना कर सकते हैं। रूपांतरण बिंदुओं के एक सेट से दूसरे में रैखिकता या गैर-रैखिकता में परिवर्तन निर्भरता में परिवर्तन का संकेत है।इसके विपरीत, कई रूपांतरण बिंदुओं (अर्थात 30, 50, और 70%) पर संरक्षित प्लॉट के क्षेत्रों की रैखिकता या गैर-रैखिकता में परिवर्तन पूर्ण उत्प्रेरक सांद्रता के आधार पर उत्प्रेरक पर निर्भरता में बदलाव का संकेत है।
एक अभिक्रिया मिश्रण के कई घटकों के साथ उत्प्रेरक की पारस्परिक क्रियाओं की एक जटिल गतिज निर्भरता को जन्म दे सकती है। जबकि ऑफ-साइकिल उत्प्रेरक-कार्यद्रव्य या उत्प्रेरक-उत्पाद पारस्परिक क्रिया को प्रायः प्रणाली के लिए "जहरीला" माना जाता है (निश्चित रूप से अपरिवर्तनीय जटिलता की स्थिति में) ऐसे मामले उपस्थित होते हैं जिनमें ऑफ-साइकल प्रजातियां वास्तव में उत्प्रेरक को स्थायी निष्क्रियता से बचाती हैं।[19][20]किसी भी मामले में, उत्प्रेरक आराम करने वाले अवस्था की भूमिका को समझना प्रायः आवश्यक होता है।[3][11]
समान-अतिरिक्त प्रयोग
अभिक्रिया प्रगति गतिज विश्लेषण में सबसे बड़ी रुचि का चर पैरामीटर एक कार्यद्रव्य के दूसरे पर अतिरिक्त (e) है, जो कि मोलरिटी की इकाइयों में दिया गया है। अभिक्रिया को दो प्रजातियों की प्रारंभिक सांद्रता द्वारा परिभाषित किया जा सकता है:
- [B]0 = [A]0 + e
और, एक-से-एक अभिक्रिया स्टोइकोमेट्री मानते हुए, कि एक कार्यद्रव्य की दूसरे पर अधिकता पूरी अभिक्रिया के दौरान मात्रात्मक रूप से संरक्षित होती है जैसे कि:[3]
- [B]t = [A]t + e
उच्च क्रम स्टोइकोमेट्री के साथ अभिक्रियाओं के लिए एक समान सेट का निर्माण किया जा सकता है, जिसमें अभिक्रिया के दौरान अतिरिक्त रूप से भिन्न होता है। जबकि e कोई भी मूल्य हो सकता है (सकारात्मक, नकारात्मक, या शून्य)प्रायः कार्यद्रव्य के एक समकक्ष की तुलना में परिमाण में छोटे सकारात्मक या नकारात्मक मूल्यों का उपयोग अभिक्रिया प्रगति गतिज विश्लेषण में किया जाता है। (कोई यह नोट कर सकता है कि छद्म-शून्य-क्रम बलगति विज्ञान कार्यद्रव्य के एक समकक्ष की तुलना में परिमाण में बहुत अधिक मूल्यों का उपयोग करता है)।
अतिरिक्त (e) के पैरामीटर को परिभाषित करने से समान-अतिरिक्त प्रयोगों के निर्माण की अनुमति मिलती है जिसमें विभिन्न प्रारंभिक सांद्रता के साथ गतिज प्रयोग के दो या दो से अधिक मान होते हैं, लेकिन समान-अतिरिक्त किसी भी बिंदु पर कृत्रिम रूप से अभिक्रिया दर्ज करने की अनुमति देता है। उत्प्रेरक अभिक्रियाओं के RPKA के लिए ये प्रयोग महत्वपूर्ण हैं, क्योंकि वे उत्प्रेरक सक्रियण (प्रेरण अवधि), उत्प्रेरक निष्क्रियता, और उत्पाद निषेध में वर्णित कई यंत्रवत संभावनाओं की जांच करने में सक्षम हैं।[2][3]
उत्प्रेरक टर्नओवर आवृत्ति का निर्धारण
आगे यंत्रवत जांच से पहले, उत्प्रेरक पर ब्याज की अभिक्रिया की गतिज निर्भरता निर्धारित करना महत्वपूर्ण है। उत्प्रेरक की टर्नओवर आवृत्ति (TOF) को उत्प्रेरक की सांद्रता के सामान्यीकृत अभिक्रिया दर के रूप में व्यक्त किया जा सकता है:
- TOF = v/[Cat]
यह TOF किसी भी दो या दो से अधिक समान-अतिरिक्त प्रयोगों को चलाकर निर्धारित किया जाता है जिसमें पूर्ण उत्प्रेरक सांद्रता भिन्न होती है। क्योंकि उत्प्रेरक की सघनता अभिक्रिया के दौरान स्थिर रहती है, परिणामी भूखंडों को एक अपरिवर्तनीय मान द्वारा सामान्यीकृत किया जाता है। यदि परिणामी प्लॉट पूरी तरह से ढक दिया जाता हैं, तो अभिक्रिया वास्तव में उत्प्रेरक में प्रथम-क्रम है। यदि अभिक्रिया ढकने में विफल रहती है, तो उच्च-क्रम प्रक्रियाएं काम कर रही हैं और यहां वर्णित की तुलना में अधिक विस्तृत विश्लेषण की आवश्यकता है।[3]यह भी ध्यान देने योग्य है कि यहाँ वर्णित सामान्यीकरण-ओवरले हेरफेर कच्चे आंकड़े की व्याख्या के लिए केवल एक दृष्टिकोण है। कृत्रिम दर कानूनों के लिए मनाए गए गतिशील व्यवहार को फिट करके समान रूप से वैध परिणाम प्राप्त किए जा सकते हैं।
उत्प्रेरक सक्रियण और निष्क्रियता की खोज

जैसा कि ऊपर वर्णित है, समान-अतिरिक्त प्रयोग दो या दो से अधिक प्रयोगों के साथ किए जाते हैं, जो कार्यद्रव्य की पूर्ण सांद्रता को बदलते हुए (e) स्थिर होते हैं (इस मामले में, उत्प्रेरक को कार्यद्रव्य के रूप में भी माना जाता है।) ध्यान दें कि यह निर्माण। समतुल्य की संख्या का कारण बनता है और इसलिए प्रत्येक अभिकर्मक/उत्प्रेरक का तिल प्रतिशत अभिक्रियाओं के बीच भिन्न होता है।[3]ये प्रयोग किसी भी बिंदु पर अभिक्रिया को कृत्रिम रूप से "प्रवेश" करने में सक्षम बनाते हैं, क्योंकि एक प्रयोग की प्रारंभिक सांद्रता (अवरोधन अभिक्रिया) को कुछ मध्यवर्ती समय, t, दूसरे (जनक अभिक्रिया) में प्रत्याशित सांद्रता पर सीधे मैप करने के लिए चुना जाता है।कोई अभिक्रिया की प्रगति की अपेक्षा करेगा, जो ऊपर वर्णित दर बनाम कार्यद्रव्य सांद्रताउस अवरोधन बिंदु से आगे एक दूसरे पर सीधे मैप करने के लिए भूखंडों द्वारा वर्णित है।यद्यपि, यह तभी सही होगा, जब उस अन्तर्रोधन से पहले सक्रिय कार्यद्रव्य /उत्प्रेरक सांद्रता (जैसे उत्प्रेरक सक्रियण, उत्प्रेरक निष्क्रियता, या उत्पाद अवरोध) में परिवर्तन से अभिक्रिया की दर में परिवर्तन नहीं होता है।[2][3]
समान-अतिरिक्त लेकिन विभिन्न प्रारंभिक कार्यद्रव्य लोडिंग के साथ कई प्रयोगों का एक सही आवरण बताता है कि अभिक्रिया के दौरान सक्रिय कार्यद्रव्य /उत्प्रेरक सांद्रता में कोई परिवर्तन नहीं होता है। ओवरले करने के लिए भूखंडों की विफलता प्रायः अभिक्रिया स्थितियों के तहत उत्प्रेरक सक्रियण, निष्क्रियता या उत्पाद अवरोध का संकेत है। इन मामलों को एक दूसरे के सापेक्ष अभिक्रिया प्रगति घटता की स्थिति से अलग किया जा सकता है।दर बनाम कार्यद्रव्य सांद्रता प्लॉट पर मूल अभिक्रियाएं (एक ही कार्यद्रव्य सांद्रता पर धीमी दर) नीचे पड़ी हुई अभिक्रियाओं को रोकना, अभिक्रिया स्थितियों के तहत उत्प्रेरक सक्रियण का संकेत है। ऊपर पड़ी हुई विच्छेदक अभिक्रियाएं (समान कार्यद्रव्य सांद्रता पर तेज दर) दर बनाम कार्यद्रव्य सांद्रता प्लॉट पर मूल अभिक्रियाएं, अभिक्रिया स्थितियों के तहत उत्प्रेरक निष्क्रियता का संकेत हैं; उत्पाद को अलग करने के लिए और प्रयोग आवश्यक है।[2]
विच्छेदक अभिक्रिया और ऊपर वर्णित जनक अभिक्रिया के बीच एक महत्वपूर्ण अंतर विच्छेदक बिंदु पर जनक अभिक्रिया में कुछ मात्रा में उत्पाद की उपस्थिति है। उत्पाद निषेध लंबे समय से कई प्रणालियों की उत्प्रेरक दक्षता को प्रभावित करने के लिए जाना जाता है, और समान-अतिरिक्त प्रयोगों के मामले में, यह अवरोधन और मूल अभिक्रियाओं को ओवरलेइंग से रोकता है। जबकि समान-अतिरिक्त प्रयोग जैसा कि ऊपर बताया गया है, किसी विशेष कारण के लिए उत्प्रेरक निष्क्रियता का श्रेय नहीं दे सकते हैं (उपस्थित होने की उम्मीद उत्पाद की मात्रा की नकल करने के लिए डिज़ाइन किया गया है) एक ही कार्यद्रव्य सांद्रता पर मूल अभिक्रिया में)। समान-अतिरिक्त-समान उत्पाद स्थितियों के तहत दर बनाम कार्यद्रव्य सांद्रता भूखंडों का एक सही ओवरले इंगित करता है कि उत्पाद अवरोध उपयोग की जाने वाली अभिक्रिया स्थितियों के तहत होता है। जबकि समान-अतिरिक्त-समान उत्पाद स्थितियों के तहत ओवरले करने के लिए दर बनाम कार्यद्रव्य सांद्रता भूखंडों की विफलता उत्पाद निषेध को नहीं रोकती है, यह कम से कम यह संकेत देती है कि अन्य उत्प्रेरक निष्क्रियता पथ भी सक्रिय होने चाहिए।
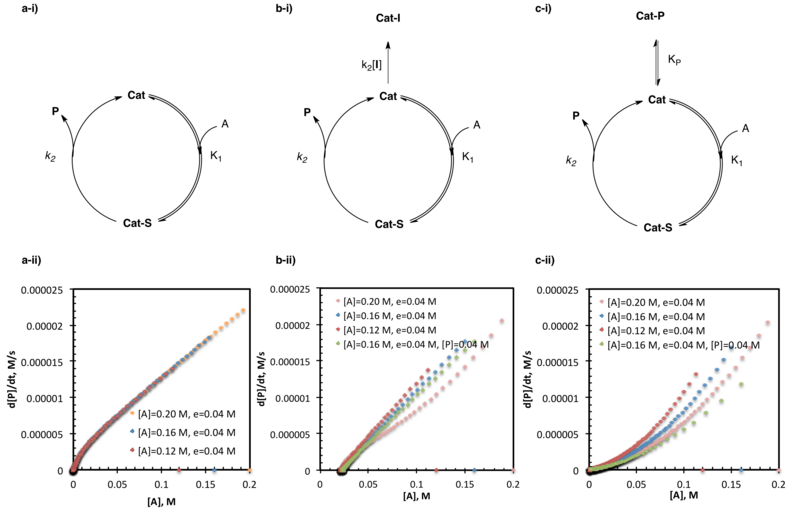
,उत्प्रेरक निष्क्रियता और उत्पाद निषेध की जांच करने वाले समान-अतिरिक्त प्रयोग अभिक्रिया प्रगति गतिज विश्लेषण के सबसे व्यापक रूप से उपयोग किए जाने वाले अनुप्रयोगों में से हैं। साहित्य में कई उदाहरणों में, कुछ में एल्डिहाइड के एमीनो एल्कोहल-उत्प्रेरित जस्ता क्षारीकरण की जांच सम्मिलित है[21] एमिडो-थियोरिया ने अप्राकृतिक एमीनो अम्ल के असममित स्ट्रेकर संश्लेषण को और [5]ऑर्गेनोकैटलिस्ट्स के SOMO-सक्रियण उत्प्रेरित किया।[14]
अभिक्रिया स्टोइकोमेट्री का निर्धारण
दर स्थिरांक निकालने के लिए विभेदक तरीके
समय के साथ अभिक्रिया प्रगति की निगरानी से उपलब्ध आंकड़ों की संपत्ति के साथ आधुनिक कंप्यूटिंग विधियों की शक्ति के साथ, यह दर कानून का संख्यात्मक रूप से मूल्यांकन करने के लिए यथोचित सरल हो गया है, समय के साथ अभिक्रिया प्रगति के एक फिट पर नकली अभिक्रियाएं पथों के एकीकृत दर कानूनों की मैपिंग त्रुटि के प्रसार के सिद्धांतों के कारण, दर स्थिरांक और दर कानूनों को इन अंतर विधियों द्वारा निर्माण की तुलना में काफी कम अनिश्चितता के साथ निर्धारित किया जा सकता है।[9]
अलग-अलग प्रयोग
जबकि RPKA पूरी अभिक्रिया के दौरान दरों के अवलोकन की अनुमति देता है, केवल समान-अतिरिक्त प्रयोग करने से संबंधित दर स्थिरांक के निर्धारण के लिए पर्याप्त जानकारी नहीं मिलती है। सभी अज्ञात दर स्थिरांकों को हल करने के लिए पर्याप्त स्वतंत्र संबंधों का निर्माण करने के लिए, विभिन्न-अतिरिक्त वाले प्रणाली की जांच करना आवश्यक है।
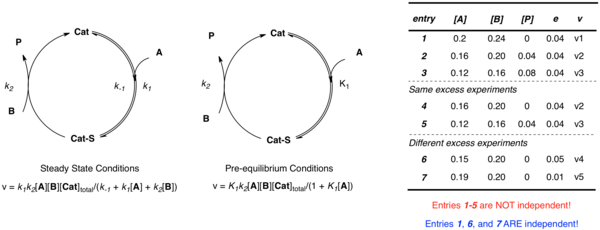
ऊपर चर्चा किए गए सरल उदाहरण पर फिर से विचार करें जहां उत्प्रेरक कार्यद्रव्य A के साथ जुड़ता है, जिसके बाद उत्पाद P और मुक्त उत्प्रेरक बनाने के लिए B के साथ अभिक्रिया होती है। लागू किए गए सन्निकटन के बाद भी, प्रणाली को परिभाषित करने के लिए कई स्वतंत्र पैरामीटर (पूर्व-संतुलन के मामले में k2 और K1; स्थिर-अवस्था के मामले में k1, k−1, और k2) की आवश्यकता होती है।जबकि कोई अलग-अलग सांद्रता पर अज्ञात का वर्णन करने के लिए कई समीकरणों के निर्माण की कल्पना कर सकता है, जब आंकड़ा समान-अतिरिक्त प्रयोग से प्राप्त होता है [A] और [B] स्वतंत्र नहीं होते हैं:
- e = [B] − [A]
प्रायोगिक दरों और सांद्रता के संदर्भ में कई स्वतंत्र दर स्थिरांक को परिभाषित करने वाले कई स्वतंत्र समीकरणों को स्थापित करने के लिए e के विभिन्न मूल्यों का उपयोग करने वाले कई प्रयोग आवश्यक हैं। गैर-रैखिक कम से कम वर्ग विश्लेषण तब उन समीकरणों के लिए अज्ञात दर स्थिरांक के सर्वोत्तम फिट मान प्राप्त करने के लिए नियोजित किया जा सकता है।
ग्राफिकल दर कानून
काइनेटिकिस्टों ने दर स्थिरांकों को बहिर्वेशन करने के लिए दर आंकड़ों के रैखिककरण पर ऐतिहासिक रूप से भरोसा किया है, शायद माइकलिस-मेंटेन समीकरण के मानक लाइनवीवर-बर्क रैखिककरण के व्यापक उपयोग द्वारा सबसे अच्छा प्रदर्शन किया है।[22]जटिल वक्रों को फ़िट करने में सक्षम कंप्यूटिंग तकनीकों के आगमन से पहले रेखीकरण तकनीकों का विशेष महत्व था, और वे अपनी सहज सरल प्रस्तुति के कारण बलगति विज्ञान में एक प्रधान बने हुए हैं।[2]यह ध्यान रखना महत्वपूर्ण है कि रैखिककरण तकनीकों का उपयोग संख्यात्मक दर स्थिरांक निकालने के लिए नहीं किया जाना चाहिए क्योंकि वे वैकल्पिक संख्यात्मक तकनीकों के सापेक्ष बड़ी मात्रा में त्रुटि पेश करते हैं। ग्राफिकल दर कानून, यद्यपि, रैखिककृत आंकड़े की सहज प्रस्तुति को बनाए रखते हैं, जैसे कि प्लॉट का दृश्य निरीक्षण हाथ में अभिक्रिया के बारे में यंत्रवत अंतर्दृष्टि प्रदान कर सकता है। ग्राफिकल दर कानून का आधार दर (v) बनाम दर पर निर्भर करता है।कार्यद्रव्य सांद्रता ([S]) प्लॉट ऊपर चर्चा की। उदाहरण के लिए, सरल चक्र में विभिन्न-अतिरिक्त प्रयोगों के संबंध में चर्चा की गई है
v/[A] बनाम [B] और उसके जुड़वां v/[B] बनाम [A] प्रत्येक अभिकर्मकों के क्रम के बारे में सहज अंतर्दृष्टि प्रदान कर सकता है। अगर प्लॉट्v/[A] बनाम [बी] विभिन्न-अतिरिक्त के साथ कई प्रयोगों के लिए ओवरले, डेटा [ए] पर पहले-क्रम की निर्भरता के अनुरूप हैं। के प्लॉट के लिए भी यही कहा जा सकता हैv/[B] बनाम [A];अधिचित्रित [B] पर पहले क्रम की निर्भरता के अनुरूप है। इन ग्राफिकल दर कानूनों के गैर- अधिचित्रित परिणाम संभव हैं और जांच किए गए कार्यद्रव्य पर उच्च आदेश निर्भरता का संकेत हैं। ब्लैकमंड ने ग्राफिकल दर समीकरणों की एक श्रृंखला के साथ विभिन्न-अतिरिक्त प्रयोगों के परिणामों को प्रस्तुत करने का प्रस्ताव दिया है (जो कि वह यहां अनुकूलित प्रवाह-चार्ट में प्रस्तुत करती है), लेकिन यह ध्यान रखना महत्वपूर्ण है कि उनकी प्रस्तावित विधि प्रदर्शित करने के कई संभावित तरीकों में से एक काइनेटिक संबंध है।इसके अतिरिक्त, जबकि ग्राफिकल दर कानूनों की प्रस्तुति को कभी-कभी जटिल गतिशील आंकड़े पेश करने के लिए एक दृष्टि से सरलीकृत तरीका माना जा सकता है, अंतर या अन्य कठोर संख्यात्मक तरीकों से विश्लेषण के लिए कच्चे गतिशील आंकड़ों को फिट करना सटीक और मात्रात्मक दर स्थिरांक और अभिक्रिया आदेश निकालने के लिए आवश्यक है। [2][3]
अभिक्रिया स्टोइकोमेट्री और प्रक्रिया
यह नोट करना महत्वपूर्ण है कि भले ही काइनेटिक विश्लेषण निचली स्थिति के सापेक्ष टर्न-ओवर सीमित संक्रमण अवस्था के स्टोइकोमेट्री का निर्धारण करने के लिए एक शक्तिशाली उपकरण है, लेकिन यह सभी यांत्रिक प्रश्नों का उत्तर नहीं दे सकता है। विशेष रूप से उत्प्रेरक स्थितियों के तहत, दो तंत्रों के लिए गतिशील रूप से अप्रभेद्य होना संभव है। किसी भी गहन यंत्रवत मूल्यांकन के लिए उत्प्रेरक प्रक्रिया और इसके व्यक्तिगत चरणों (जब संभव हो) दोनों का गतिज विश्लेषण करना आवश्यक है। दोनों का काइनेटिक विश्लेषण विश्लेषण के अन्य रूपों के साथ संगीत कार्यक्रम में जैसे कि रैखिक मुक्त ऊर्जा संबंधों का मूल्यांकन, आइसोटोप प्रभाव अध्ययन, कम्प्यूटेशनल विश्लेषण, या वैकल्पिक दृष्टिकोणों की संख्या। अंत में, यह ध्यान रखना महत्वपूर्ण है कि कोई यंत्रवत परिकल्पना कभी भी सिद्ध नहीं की जा सकती है; वैकल्पिक यंत्रवत परिकल्पना को केवल अप्रमाणित किया जा सकता है। इसलिए, परिकल्पना-चालित तरीके से किसी भी जांच का संचालन करना आवश्यक है। केवल प्रयोगात्मक रूप से उचित विकल्पों का खंडन करके ही किसी दिए गए का समर्थन किया जा सकता है।[23]
यह भी देखें
- रासायनिक गतिकी
- एंजाइम बलगति विज्ञान
- पहाड़ी समीकरण (जैव रसायन)
- लैंगमुइर सोखना मॉडल
- माइकलिस-मेंटेन बलगति विज्ञान
- मोनोड समीकरण
- दर समीकरण (रसायन विज्ञान)
- प्रतिक्रिया तंत्र
- स्थिर अवस्था (रसायन विज्ञान)
संदर्भ
- ↑ 1.0 1.1 Hartwig, J. F. (2010). Organotransition Metal Chemistry: From Bonding to Catalysis. Mill Valley, California: University Science Books. ISBN 978-1-891389-53-5.
- ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 Blackmond, D. G. (2005). "Reaction Progress Kinetic Analysis : A Powerful Methodology for Mechanistic Studies of Complex Catalytic Reactions". Angew. Chem. Int. Ed. 44 (28): 4302–4320. doi:10.1002/anie.200462544. PMID 15997457.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 Blackmond, D. G.; Ropic, M.; Stefinovic, M. (2006). "Kinetic Studies of the Asymmetric Transfer Hydrogenation of Imines with Formic Acid Catalyzed by Rh−Diamine Catalysts". Org. Process Res. Dev. 10 (3): 457–463. doi:10.1021/op060033k.
- ↑ 4.0 4.1 Shekhar, S.; Ryberg, P.; Hartwig, J. F.; Mathew, J. S.; Blackmond, D. G.; Strieter, E. R.; Buchwald, S. L. (2006). "Reevaluation of the Mechanism of the Amination of Aryl Halides Catalyzed by BINAP-Ligated Palladium Complexes". J. Am. Chem. Soc. 128 (11): 3584–3591. doi:10.1021/ja045533c. PMID 16536531.
- ↑ 5.0 5.1 Zuend, S. J.; Jacobsen, E. N. (2009). "Mechanism of Amido-Thiourea Catalyzed Enantioselective Imine Hydrocyanation: Transition State Stabilization via Multiple Non-Covalent Interactions". J. Am. Chem. Soc. 131 (42): 15358–15374. doi:10.1021/ja9058958. PMC 2783581. PMID 19778044.
- ↑ Denmark, S. D.; Burk, M. T. (2010). "Lewis base catalysis of bromo- and iodolactonization, and cycloetherification". Proc. Natl. Acad. Sci. 107 (48): 20655–20660. Bibcode:2010PNAS..10720655D. doi:10.1073/pnas.1005296107. PMC 2996424. PMID 20705900.
- ↑ Choquette, K. A.; Sadasivam, D. V.; Flowers, R. A. (2011). "Catalytic Ni(II) in Reactions of SmI2: Sm(II)- or Ni(0)-Based Chemistry?". J. Am. Chem. Soc. 133 (27): 10655–10661. doi:10.1021/ja204287n. PMID 21619012.
- ↑ Mathew, J. S.; Klussmann, M.; Iwamura, H.; Valera, F.; Futran, A; Emanuelsson, E. A. C.; Blackmond, D. G. (1999). "Investigations of Pd-Catalyzed ArX Coupling Reactions Informed by Reaction Progress Kinetic Analysis". J. Org. Chem. 71 (13): 4711–4722. doi:10.1021/jo052409i. PMID 16776495.
- ↑ 9.0 9.1 Steel, C.; Naquvi, K. R. (1991). "Differential method in chemical kinetics". J. Phys. Chem. 95 (26): 10703–10718. doi:10.1021/j100179a037.
- ↑ Blackmond, D. G.; Rosner, T.; Pfaltz, A. (1999). "Comprehensive Kinetic Screening of Catalysts Using Reaction Calorimetry". Org. Process Res. Dev. 3 (4): 275–280. doi:10.1021/op990024u.
- ↑ 11.0 11.1 Hein, J. E.; Armstrong, A.; Blackmond, D. G. (2011). "Kinetic Profiling of Prolinate-Catalyzed α-Amination of Aldehydes". Org. Lett. 13 (16): 4300–4303. doi:10.1021/ol201639z. PMID 21761822.
- ↑ Singh, U. K.; Strieter, E. R.; Blackmond, D. G.; Buchwald, S. L. (2002). "Mechanistic Insights into the Pd(BINAP)-Catalyzed Amination of Aryl Bromides: Kinetic Studies under Synthetically Relevant Conditions". J. Am. Chem. Soc. 124 (47): 14104–14114. doi:10.1021/ja026885r. PMID 12440909.
- ↑ Herrmann, W. A.; Brossmer, C.; Reisinger, C. P.; Riermeier, T. H.; Öfele, K.; Beller, M. (1997). "Palladacycles: Efficient New Catalysts for the Heck Vinylation of Aryl Halides". Chem. Eur. J. 3 (8): 1357–1364. doi:10.1002/chem.19970030823.
- ↑ 14.0 14.1 Devery, J. J.; Conrad, J. C.; MacMillan, D. W. C.; Flowers, R. A. (2010). "Mechanistic Complexity in Organo–SOMO Activation". Angew. Chem. Int. Ed. 49 (35): 6106–6110. doi:10.1002/anie.201001673. PMC 3065936. PMID 20632343.
- ↑ Gilbert, H. F. (1977). ""Rule of thumb" for deriving steady state rate equations". J. Chem. Educ. 54 (8): 492–493. Bibcode:1977JChEd..54..492G. doi:10.1021/ed054p492.
- ↑ "4.12: Steady-State Approximation". 22 July 2015.
- ↑ Helfferich, F. G. (1989). "Systematic approach to elucidation of multi-step reaction networks". J. Phys. Chem. 93 (18): 6676–6681. doi:10.1021/j100355a022.
- ↑ Zuend, S. J.; Jacobsen, E. N. (2007). "यंत्रवत योजना और गतिज डेटा को केटोन्स के अमीनो-थियोरिया उत्प्रेरित साइनोसिलिलेशन के लिए रिपोर्ट की गई दर और संतुलन स्थिरांक का उपयोग करके स्वतंत्र गतिज सिमुलेशन से अनुकूलित किया गया है।". J. Am. Chem. Soc. 129 (51): 15872–15883. doi:10.1021/ja0735352. PMID 18052247.
- ↑ List, B. (2002). "Proline-catalyzed asymmetric reactions". Tetrahedron. 58 (28): 5573–5590. doi:10.1016/S0040-4020(02)00516-1.
- ↑ Seebach, D.; Beck, A. K.; Badine, D. M.; Limbach, M.; Eschenmoser, A.; Treasurywala, A. M.; Hobi, R.; Prikoszovich, W. (2007). "Are Oxazolidinones Really Unproductive, Parasitic Species in Proline Catalysis? – Thoughts and Experiments Pointing to an Alternative View". Helv. Chim. Acta. 90 (3): 425–471. doi:10.1002/hlca.200790050.
- ↑ Rosner, T.; Sears, P.J.; Nugent, W. A.; Blackmond. D.G. (2000). "Kinetic Investigations of Product Inhibition in the Amino Alcohol-Catalyzed Asymmetric Alkylation of Benzaldehyde with Diethylzinc". Org. Lett. 2 (16): 2511–2513. doi:10.1021/ol006181r. PMID 10956534.
- ↑ Lineweaver, H.; Burke, D. (1934). "The determination of enzyme dissociation constants". J. Am. Chem. Soc. 56 (3): 658–666. doi:10.1021/ja01318a036.
- ↑ Platt, J. R. (1964). "प्रबल अनुमान". Science. 146 (3642): 347–353. Bibcode:1964Sci...146..347P. doi:10.1126/science.146.3642.347. PMID 17739513.
