तरंगिका रूपांतरण

JPEG2000 में उपयोग किए जाने वाले 2D असतत तरंगिका रूपांतरण का एक उदाहरण।

For broader coverage of this topic, see वेवलेट.

गणित में, एक तरंगिका श्रृंखला एक वर्ग-पूर्णांक (वास्तविक संख्या- या जटिल संख्या-मूल्यवान) फ़ंक्शन (गणित) का प्रतिनिधित्व करती है जो एक तरंगिका द्वारा उत्पन्न एक निश्चित ऑर्थोनॉर्मल श्रृंखला (गणित) द्वारा होती है। यह आलेख ऑर्थोनॉर्मल छोटा लहर और इंटीग्रल वेवलेट ट्रांसफ़ॉर्म की एक औपचारिक, गणितीय परिभाषा प्रदान करता है।

परिभाषा

एक समारोह $\psi \,\in \,L^{2}(\mathbb {R} )$ एक ऑर्थोनॉर्मल वेवलेट कहा जाता है यदि इसका उपयोग हिल्बर्ट अंतरिक्ष को परिभाषित करने के लिए किया जा सकता है#ऑर्थोनॉर्मल बेसिस, जो कि हिल्बर्ट स्पेस के लिए एक ऑर्थोनॉर्मल आधार है $L^{2}\left(\mathbb {R} \right)$ स्क्वायर-इंटीग्रेबल फ़ंक्शन फ़ंक्शन का।

हिल्बर्ट आधार का निर्माण कार्यों के परिवार के रूप में किया गया है $\{\psi _{jk}:\,j,\,k\,\in \,\mathbb {Z} \}$ डायाडिक परिवर्तन अनुवाद (ज्यामिति) और फैलाव (संचालक सिद्धांत) के माध्यम से $\psi \,$,

$\psi _{jk}(x)=2^{\frac {j}{2}}\psi \left(2^{j}x-k\right)\,$

पूर्णांकों के लिए $j,\,k\,\in \,\mathbb {Z}$.

यदि मानक आंतरिक उत्पाद के तहत $L^{2}\left(\mathbb {R} \right)$,

$\langle f,g\rangle =\int _{-\infty }^{\infty }f(x){\overline {g(x)}}dx$

यह परिवार ऑर्थोनॉर्मल है, यह एक ऑर्थोनॉर्मल सिस्टम है:

${\begin{aligned}\langle \psi _{jk},\psi _{lm}\rangle &=\int _{-\infty }^{\infty }\psi _{jk}(x){\overline {\psi _{lm}(x)}}dx\\&=\delta _{jl}\delta _{km}\end{aligned}}$

कहाँ $\delta _{jl}\,$ क्रोनकर डेल्टा है।

पूर्णता संतुष्ट है अगर हर समारोह $f\,\in \,L^{2}\left(\mathbb {R} \right)$ आधार पर विस्तारित किया जा सकता है

$f(x)=\sum _{j,k=-\infty }^{\infty }c_{jk}\psi _{jk}(x)$

श्रृंखला के अभिसरण के साथ मानक (गणित) # गुण समझा जाता है। F का ऐसा निरूपण 'तरंगिका श्रृंखला' के रूप में जाना जाता है। इसका तात्पर्य है कि एक ओर्थोनॉर्मल तरंगिका दोहरी तरंगिका है। स्व-दोहरी।

'इंटीग्रल वेवलेट ट्रांसफ़ॉर्म' अभिन्न परिवर्तन है जिसे परिभाषित किया गया है

$\left[W_{\psi }f\right](a,b)={\frac {1}{\sqrt {|a|}}}\int _{-\infty }^{\infty }{\overline {\psi \left({\frac {x-b}{a}}\right)}}f(x)dx\,$

तरंगिका गुणांक $c_{jk}$ इसके बाद दिया जाता है

$c_{jk}=\left[W_{\psi }f\right]\left(2^{-j},k2^{-j}\right)$

यहाँ, $a=2^{-j}$ बाइनरी डाइलेशन या डाइएडिक डाइलेशन कहा जाता है, और $b=k2^{-j}$ बाइनरी या डायाडिक स्थिति है।

सिद्धांत

वेवलेट ट्रांसफॉर्म का मूल विचार यह है कि परिवर्तन को केवल समय विस्तार में परिवर्तन की अनुमति देनी चाहिए, लेकिन आकार की नहीं। यह इसके लिए अनुमति देने वाले उपयुक्त आधार कार्यों को चुनकर प्राप्त किया जाता है। समय विस्तार में परिवर्तन के आधार समारोह की इसी विश्लेषण आवृत्ति के अनुरूप होने की उम्मीद है। अनिश्चितता सिद्धांत # सिग्नल प्रोसेसिंग के सिग्नल प्रोसेसिंग के आधार पर,

$\Delta t\Delta \omega \geq {\frac {1}{2}}$

कहाँ $t$ समय और का प्रतिनिधित्व करता है $\omega$ कोणीय आवृत्ति ($\omega =2\pi f$, कहाँ $f$ सामान्य आवृत्ति है)।

समय में आवश्यक रिज़ॉल्यूशन जितना अधिक होगा, फ़्रीक्वेंसी में रिज़ॉल्यूशन उतना ही कम होगा। विश्लेषण विंडो फंक्शन का जितना बड़ा विस्तार चुना जाता है, उतना बड़ा मान होता है $\Delta t$.

कब $\Delta t$ बड़ी है,

1. बुरे समय का संकल्प
2. अच्छा आवृत्ति संकल्प
3. कम आवृत्ति, बड़ा स्केलिंग कारक

कब $\Delta t$ छोटा है

1. शुभ समय संकल्प
2. खराब आवृत्ति संकल्प
3. उच्च आवृत्ति, छोटा स्केलिंग कारक

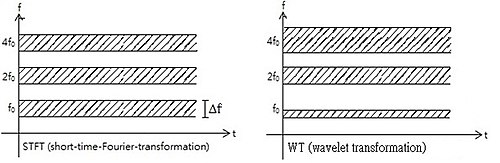
दूसरे शब्दों में, आधार कार्य $\psi$ एक प्रणाली की आवेग प्रतिक्रिया के रूप में माना जा सकता है जिसके साथ कार्य करता है $x(t)$ फ़िल्टर किया गया है। रूपांतरित संकेत समय और आवृत्ति के बारे में जानकारी प्रदान करता है। इसलिए, वेवलेट-ट्रांसफॉर्मेशन में [[शॉर्ट-टाइम फूरियर रूपांतरण]] के समान जानकारी होती है। फूरियर रूपांतरण और तरंगिका रूपांतरण के लिए आरोही आवृत्तियों पर समय संकल्प में अंतर नीचे दिखाया गया है। हालाँकि, ध्यान दें कि फ़्रीक्वेंसी रिज़ॉल्यूशन बढ़ने के लिए फ़्रीक्वेंसी रिज़ॉल्यूशन कम हो रहा है जबकि टेम्पोरल रिज़ॉल्यूशन बढ़ता है। फूरियर अनिश्चितता सिद्धांत का यह परिणाम चित्र में सही ढंग से प्रदर्शित नहीं होता है।

इससे पता चलता है कि उच्च आवृत्तियों के समय संकल्प में तरंगिका परिवर्तन अच्छा है, जबकि धीरे-धीरे भिन्न कार्यों के लिए, आवृत्ति संकल्प उल्लेखनीय है।

एक अन्य उदाहरण: तीन अध्यारोपित साइनसोइडल संकेतों का विश्लेषण $y(t)\;=\;\sin(2\pi f_{0}t)\;+\;\sin(4\pi f_{0}t)\;+\;\sin(8\pi f_{0}t)$ STFT और तरंगिका-परिवर्तन के साथ।

तरंगिका संपीड़न

See also: असतत वेवलेट परिवर्तन

तरंगिका संपीड़न छवि संपीड़न (कभी-कभी वीडियो संपीड़न और ऑडियो संपीड़न (डेटा)) के लिए उपयुक्त डेटा संपीड़न का एक रूप है। स्थिर छवियों के लिए जेपीईजी 2000, DjVu और ईसीडब्ल्यू (फ़ाइल प्रारूप), जेपीईजी एक्सएस, इस cineform और बीबीसी के डायराक (कोडेक) उल्लेखनीय कार्यान्वयन हैं। लक्ष्य छवि डेटा को कम्प्यूटर फाइल में यथासंभव कम जगह में संग्रहीत करना है। तरंगिका संपीड़न दोषरहित डेटा संपीड़न या हानिपूर्ण डेटा संपीड़न हो सकता है। वेवलेट ट्रांसफ़ॉर्म का उपयोग करते हुए, वेवलेट कंप्रेशन विधियाँ ट्रांसिएंट (ध्वनिकी) का प्रतिनिधित्व करने के लिए पर्याप्त हैं, जैसे कि ऑडियो में पर्क्यूशन ध्वनियाँ, या द्वि-आयामी छवियों में उच्च-आवृत्ति घटक, उदाहरण के लिए रात के आकाश में सितारों की छवि। इसका मतलब यह है कि डेटा सिग्नल के क्षणिक तत्वों को सूचना की एक छोटी मात्रा द्वारा दर्शाया जा सकता है, अगर कुछ अन्य परिवर्तन, जैसे कि अधिक व्यापक असतत कोसाइन परिवर्तन, का उपयोग किया गया हो।

इलेक्ट्रोकार्डियोग्राफ़ (ईसीजी) संकेतों के संपीड़न के लिए असतत तरंगिका परिवर्तन सफलतापूर्वक लागू किया गया है इस कार्य में, क्रमिक कार्डियक चक्रों के संकेतों के संबंधित तरंगिका गुणांकों के बीच उच्च सहसंबंध का उपयोग रैखिक भविष्यवाणी को नियोजित करने के लिए किया जाता है।

तरंगिका संपीड़न सभी प्रकार के डेटा के लिए प्रभावी नहीं होता है। वेवलेट संपीड़न क्षणिक संकेतों को अच्छी तरह से संभालता है। लेकिन सुचारू, आवधिक संकेतों को अन्य तरीकों का उपयोग करके बेहतर रूप से संकुचित किया जाता है, विशेष रूप से आवृत्ति डोमेन में फूरियर-संबंधित परिवर्तनों की सूची के साथ पारंपरिक हार्मोनिक विश्लेषण। फूरियर-संबंधित रूपांतरण। संपीडित डेटा जिसमें दोनों क्षणिक और आवधिक विशेषताएं हैं, हाइब्रिड तकनीकों के साथ किया जा सकता है जो पारंपरिक हार्मोनिक विश्लेषण के साथ तरंगों का उपयोग करते हैं। उदाहरण के लिए, Vorbis ऑडियो कोडेक मुख्य रूप से ऑडियो को संपीड़ित करने के लिए संशोधित असतत कोज्या परिवर्तन का उपयोग करता है (जो आम तौर पर चिकनी और आवधिक होता है), हालांकि ग्राहकों की बेहतर ध्वनि गुणवत्ता के लिए हाइब्रिड वेवलेट फ़िल्टर बैंक को जोड़ने की अनुमति देता है। देखें डायरी ऑफ एन x264 डेवलपर: वेवलेट्स के साथ समस्याएं (2010) के व्यावहारिक मुद्दों की चर्चा के लिए वीडियो संपीड़न के लिए तरंगों का उपयोग करने वाली वर्तमान विधियाँ।

विधि

सबसे पहले एक वेवलेट ट्रांसफॉर्म लागू किया जाता है। यह छवि में पिक्सेल के रूप में कई गुणांक उत्पन्न करता है (यानी, अभी तक कोई संपीड़न नहीं है क्योंकि यह केवल एक परिवर्तन है)। इन गुणांकों को तब अधिक आसानी से संकुचित किया जा सकता है क्योंकि जानकारी सांख्यिकीय रूप से केवल कुछ गुणांकों में केंद्रित होती है। इस सिद्धांत को कोडिंग बदलना कहा जाता है। उसके बाद, गुणांक परिमाणीकरण (सिग्नल प्रोसेसिंग) हैं और परिमाणित मान एन्ट्रापी एन्कोडिंग और/या रन-लेंथ एन्कोडिंग हैं।

तरंगिका संपीड़न के कुछ 1D और 2D अनुप्रयोग तरंगिका पदचिन्ह नामक तकनीक का उपयोग करते हैं।

मूल्यांकन

छवि संपीड़न के लिए आवश्यकता

अधिकांश प्राकृतिक छवियों के लिए, कम आवृत्ति का स्पेक्ट्रम घनत्व अधिक होता है। नतीजतन, कम आवृत्ति संकेत (संदर्भ संकेत) की जानकारी आम तौर पर संरक्षित होती है, जबकि विस्तार संकेत में जानकारी को छोड़ दिया जाता है। छवि संपीड़न और पुनर्निर्माण के दृष्टिकोण से, एक तरंगिका को छवि संपीड़न करते समय निम्नलिखित मानदंडों को पूरा करना चाहिए:

• अधिक मूल छवि को संदर्भ संकेत में बदलने में सक्षम होना।
• उच्चतम निष्ठा पुनर्निर्माण संदर्भ संकेत के आधार पर।
• अकेले संदर्भ संकेत से पुनर्निर्माण की गई छवि में कलाकृतियों का नेतृत्व नहीं करना चाहिए।

शिफ्ट विचरण और रिंगिंग व्यवहार के लिए आवश्यकता

वेवलेट इमेज कंप्रेशन सिस्टम में फिल्टर और डिकिमेशन शामिल है, इसलिए इसे एक लीनियर शिफ्ट-वेरिएंट सिस्टम के रूप में वर्णित किया जा सकता है। एक विशिष्ट तरंगिका परिवर्तन आरेख नीचे प्रदर्शित किया गया है:

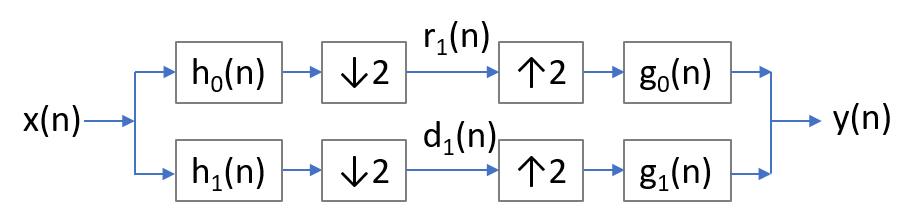परिवर्तन प्रणाली में दो विश्लेषण फ़िल्टर होते हैं (एक कम पास फ़िल्टर $h_{0}(n)$ और एक उच्च पास फिल्टर $h_{1}(n)$), एक क्षय प्रक्रिया, एक प्रक्षेप प्रक्रिया, और दो संश्लेषण फिल्टर ($g_{0}(n)$ और $g_{1}(n)$). संपीड़न और पुनर्निर्माण प्रणाली में आम तौर पर कम आवृत्ति वाले घटक शामिल होते हैं, जो विश्लेषण फ़िल्टर है $h_{0}(n)$ छवि संपीड़न और संश्लेषण फिल्टर के लिए $g_{0}(n)$ पुनर्निर्माण के लिए। ऐसी प्रणाली का मूल्यांकन करने के लिए, हम एक आवेग इनपुट कर सकते हैं $\delta (n-n_{i})$ और इसके पुनर्निर्माण का निरीक्षण करें $h(n-n_{i})$; इष्टतम वेवलेट वे हैं जो न्यूनतम शिफ्ट विचरण और साइडलोब लाते हैं $h(n-n_{i})$. भले ही सख्त बदलाव विचरण के साथ तरंगिका यथार्थवादी नहीं है, केवल मामूली बदलाव विचरण के साथ तरंगिका का चयन करना संभव है। उदाहरण के लिए, हम दो फ़िल्टरों के शिफ्ट वेरिएंस की तुलना कर सकते हैं:

Biorthogonal filters for wavelet image compression

		Length	Filter coefficients	Regularity
Wavelet filter 1	H0	9	.852699, .377402, -.110624, -.023849, .037828	1.068
	G0	7	.788486, .418092, -.040689, -.064539	1.701
Wavelet filter 2	H0	6	.788486, .047699, -.129078	0.701
	G0	10	.615051, .133389, -.067237, .006989, .018914	2.068

दो फ़िल्टरों की आवेग प्रतिक्रियाओं को देखकर, हम यह निष्कर्ष निकाल सकते हैं कि दूसरा फ़िल्टर इनपुट स्थान के प्रति कम संवेदनशील है (अर्थात यह कम बदलाव वाला संस्करण है)।

छवि संपीड़न और पुनर्निर्माण के लिए एक और महत्वपूर्ण मुद्दा सिस्टम का दोलन व्यवहार है, जो पुनर्निर्मित छवि में गंभीर अवांछित कलाकृतियों को जन्म दे सकता है। इसे प्राप्त करने के लिए, वेवलेट फिल्टर में साइडलोब अनुपात के लिए एक बड़ी चोटी होनी चाहिए।

अब तक हमने इमेज कंप्रेशन सिस्टम के एक आयामी परिवर्तन के बारे में चर्चा की है। इस मुद्दे को दो आयामों तक बढ़ाया जा सकता है, जबकि एक अधिक सामान्य शब्द - शिफ्टेबल मल्टीस्केल ट्रांसफॉर्म - प्रस्तावित है।

आवेग प्रतिक्रिया की व्युत्पत्ति

जैसा कि पहले उल्लेख किया गया है, छवि संपीड़न/पुनर्निर्माण प्रणाली का मूल्यांकन करने के लिए आवेग प्रतिक्रिया का उपयोग किया जा सकता है।

इनपुट अनुक्रम के लिए $x(n)=\delta (n-n_{i})$, संदर्भ संकेत $r_{1}(n)$ अपघटन के एक स्तर के बाद है $x(n)*h_{0}(n)$ दो के एक कारक द्वारा क्षय के माध्यम से चला जाता है, जबकि $h_{0}(n)$ एक कम पास फिल्टर है। इसी तरह, अगला संदर्भ संकेत $r_{2}(n)$ द्वारा प्राप्त किया जाता है $r_{1}(n)*h_{0}(n)$ दो के गुणक से क्षय से गुजरता है। अपघटन (और क्षय) के एल स्तरों के बाद, प्रत्येक में से एक को बनाए रखने के द्वारा विश्लेषण प्रतिक्रिया प्राप्त की जाती है $2^{L}$ नमूने: $h_{A}^{(L)}(n,n_{i})=f_{h0}^{(L)}(n-n_{i}/2^{L})$.

दूसरी ओर, सिग्नल एक्स (एन) के पुनर्निर्माण के लिए, हम एक संदर्भ सिग्नल पर विचार कर सकते हैं $r_{L}(n)=\delta (n-n_{j})$. यदि विवरण संकेत करता है $d_{i}(n)$ के लिए शून्य के बराबर हैं $1\leq i\leq L$, फिर पिछले चरण में संदर्भ संकेत ($L-1$ चरण) है $r_{L-1}(n)=g_{0}(n-2n_{j})$, जो प्रक्षेपित करके प्राप्त किया जाता है $r_{L}(n)$ और साथ उलझा हुआ $g_{0}(n)$. इसी तरह, संदर्भ संकेत प्राप्त करने के लिए प्रक्रिया को दोहराया जाता है $r(n)$ मंच पर $L-2,L-3,....,1$. एल पुनरावृत्तियों के बाद, संश्लेषण आवेग प्रतिक्रिया की गणना की जाती है: $h_{s}^{(L)}(n,n_{i})=f_{g0}^{(L)}(n/2^{L}-n_{j})$, जो संदर्भ संकेत से संबंधित है $r_{L}(n)$ और पुनर्निर्मित संकेत।

समग्र एल स्तर विश्लेषण/संश्लेषण प्रणाली प्राप्त करने के लिए, विश्लेषण और संश्लेषण प्रतिक्रियाओं को नीचे के रूप में संयोजित किया गया है:

$h_{AS}^{(L)}(n,n_{i})=\sum _{k}f_{h0}^{(L)}(k-n_{i}/2^{L})f_{g0}^{(L)}(n/2^{L}-k)$.

अंत में, पहले साइडलोब अनुपात का शिखर और समग्र आवेग प्रतिक्रिया का औसत दूसरा साइडलोब $h_{AS}^{(L)}(n,n_{i})$ तरंगिका छवि संपीड़न प्रदर्शन का मूल्यांकन करने के लिए इस्तेमाल किया जा सकता है।

फूरियर रूपांतरण और समय-आवृत्ति विश्लेषण के साथ तुलना

Transform	Representation	Input
Fourier transform	${\hat {X}}(f)=\int _{-\infty }^{\infty }x(t)e^{-i2\pi ft}\,dt$	$f$ : frequency
Time–frequency analysis	$X(t,f)$	$t$ time; $f$ frequency
Wavelet transform	$X(a,b)={\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }{\overline {\Psi \left({\frac {t-b}{a}}\right)}}x(t)\,dt$	$a$ scaling ; $b$ time shift factor

विशिष्ट आवृत्तियों की जांच करते समय कंप्यूटेशंस को कम करने में फूरियर रूपांतरणों पर वेवलेट्स के कुछ मामूली लाभ होते हैं। हालांकि, वे शायद ही कभी अधिक संवेदनशील होते हैं, और वास्तव में, सामान्य मोरलेट वेवलेट गणितीय रूप से गॉसियन विंडो फ़ंक्शन का उपयोग करके एक शॉर्ट-टाइम फूरियर रूपांतरण के समान है। अपवाद तब होता है जब एक ज्ञात, गैर-साइनसॉइडल आकार (जैसे, दिल की धड़कन) के संकेतों की खोज की जाती है; उस स्थिति में, मेल खाने वाली तरंगों का उपयोग मानक STFT/Morlet विश्लेषणों से बेहतर प्रदर्शन कर सकता है।

अन्य व्यावहारिक अनुप्रयोग

तरंगिका रूपांतरण हमें संकेतों की आवृत्ति और उन आवृत्तियों से जुड़ा समय प्रदान कर सकता है, जिससे यह कई क्षेत्रों में इसके अनुप्रयोग के लिए बहुत सुविधाजनक हो जाता है। उदाहरण के लिए, गति विश्लेषण के लिए त्वरण का सिग्नल प्रोसेसिंग, दोष का पता लगाने के लिए, कम शक्ति वाले पेसमेकर के डिजाइन के लिए और अल्ट्रा-वाइडबैंड (यूडब्ल्यूबी) बेतार संचार में भी।

1. Discretizing of the $c-\tau$ axis

   Applied the following discretization of frequency and time:

   ${\begin{aligned}c_{n}&=c_{0}^{n}\\\tau _{m}&=m\cdot T\cdot c_{0}^{n}\end{aligned}}$

   Leading to wavelets of the form, the discrete formula for the basis wavelet:

   $\Psi (k,n,m)={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \Psi \left[{\frac {k-mc_{0}^{n}}{c_{0}^{n}}}T\right]={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \Psi \left[\left({\frac {k}{c_{0}^{n}}}-m\right)T\right]$

   Such discrete wavelets can be used for the transformation:

   $Y_{DW}(n,m)={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \sum _{k=0}^{K-1}y(k)\cdot \Psi \left[\left({\frac {k}{c_{0}^{n}}}-m\right)T\right]$

2. Implementation via the FFT (fast Fourier transform)

   As apparent from wavelet-transformation representation (shown below)

   $Y_{W}(c,\tau )={\frac {1}{\sqrt {c}}}\cdot \int _{-\infty }^{\infty }y(t)\cdot \Psi \left({\frac {t-\tau }{c}}\right)\,dt$

   where $c$ is scaling factor, $\tau$ represents time shift factor

   and as already mentioned in this context, the wavelet-transformation corresponds to a convolution of a function $y(t)$ and a wavelet-function. A convolution can be implemented as a multiplication in the frequency domain. With this the following approach of implementation results into:

   • Fourier-transformation of signal $y(k)$ with the FFT
   • Selection of a discrete scaling factor $c_{n}$
   • Scaling of the wavelet-basis-function by this factor $c_{n}$ and subsequent FFT of this function
   • Multiplication with the transformed signal YFFT of the first step
   • Inverse transformation of the product into the time domain results in $Y_{W}(c,\tau )$ for different discrete values of $\tau$ and a discrete value of $c_{n}$
   • Back to the second step, until all discrete scaling values for $c_{n}$are processed
   There are many different types of wavelet transforms for specific purposes. See also a full list of wavelet-related transforms but the common ones are listed below: Mexican hat wavelet, Haar Wavelet, Daubechies wavelet, triangular wavelet.

समय-कारण तरंगें

वास्तविक समय में अस्थायी संकेतों को संसाधित करने के लिए, यह आवश्यक है कि तरंगिका फिल्टर भविष्य से सिग्नल मूल्यों तक न पहुंचें और साथ ही न्यूनतम अस्थायी विलंबता प्राप्त की जा सके। Szu et al द्वारा समय-कारण तरंगिकाओं का प्रतिनिधित्व विकसित किया गया है और लिंडबर्ग, बाद की विधि के साथ स्मृति-कुशल समय-पुनरावर्ती कार्यान्वयन भी शामिल है।

सिंक्रो-निचोड़ा हुआ परिवर्तन

सिंक्रो-स्क्वीज्ड ट्रांसफॉर्म पारंपरिक वेवलेट ट्रांसफॉर्म का उपयोग करके प्राप्त समय-आवृत्ति प्रतिनिधित्व के अस्थायी और आवृत्ति संकल्प को महत्वपूर्ण रूप से बढ़ा सकता है।

यह भी देखें

• निरंतर तरंगिका परिवर्तन
• असतत तरंगिका रूपांतरण
• जटिल तरंगिका रूपांतरण
• लगातार-क्यू परिवर्तन
• स्थिर तरंगिका रूपांतरण
• दोहरी तरंगिका
• कम से कम वर्ग वर्णक्रमीय विश्लेषण
• बहुविकल्पी विश्लेषण
• MrSID, लॉस अलामोस नेशनल लेबोरेटरी (LANL) में मूल तरंगिका संपीड़न अनुसंधान से विकसित छवि प्रारूप
• ECW (फ़ाइल स्वरूप), गति और प्रसंस्करण दक्षता के लिए डिज़ाइन किया गया एक तरंगिका-आधारित भू-स्थानिक छवि प्रारूप
• जेपीईजी 2000, एक वेवलेट-आधारित छवि संपीड़न मानक
• DjVu प्रारूप छवि संपीड़न के लिए वेवलेट-आधारित IW44 एल्गोरिथ्म का उपयोग करता है
• स्केलोग्राम, एक प्रकार का spectrogram जो थोड़े समय के फूरियर रूपांतरण के बजाय तरंगिकाओं का उपयोग करके उत्पन्न होता है

उसकी तरंगिका

• हर तरंगिका
• Daubechies तरंगिका
• द्विपद QMF (डौबेची तरंगिका के रूप में भी जाना जाता है)
• मोरलेट वेवलेट
• गेबर वेवलेट
• चिरपलेट रूपांतरण
• समय-आवृत्ति प्रतिनिधित्व
• एस परिवर्तन
• पदानुक्रमित पेड़ों में विभाजन सेट करें
• शॉर्ट-टाइम फूरियर रूपांतरण
• Biorthogonal लगभग coiflet आधार, जो दर्शाता है कि छवि संपीड़न के लिए तरंगिका लगभग coiflet (लगभग ओर्थोगोनल) भी हो सकती है।

बाहरी संबंध

• Amara Graps (June 1995). "An Introduction to Wavelets". IEEE Computational Science & Engineering. 2 (2): 50–61. doi:10.1109/99.388960.
• Robi Polikar (2001-01-12). "The Wavelet Tutorial".
• Concise Introduction to Wavelets by René Puschinger