मैट्रोइड: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Abstraction of linear independence of vectors}} | {{Short description|Abstraction of linear independence of vectors}} | ||
{{Distinguish| | {{Distinguish|मेट्रोइड|मेटोरॉइड }} | ||
[[साहचर्य]] में, गणित की शाखा, मैट्रोइड | [[साहचर्य]] में, गणित की शाखा, मैट्रोइड संरचना है जो सदिश स्थानों में [[रैखिक स्वतंत्रता]] की धारणा को अमूर्त और सामान्यीकृत करती है। मैट्रोइड को [[स्वयंसिद्ध प्रणाली]] के रूप में परिभाषित करने की कई समकक्ष विधि हैं, सबसे महत्वपूर्ण हैं: स्वतंत्र समुच्चय; आधार या परिपथ; पद फलन; बंद करने वाले ऑपरेटर; और बंद समुच्चय या फ्लैट है। आंशिक रूप से क्रमित समुच्चयों की भाषा में, परिमित सरल मैट्रोइड [[ज्यामितीय जाली]] के समान है। | ||
मैट्रोइड सिद्धांत बड़े पैमाने पर रैखिक बीजगणित और [[ग्राफ सिद्धांत]] दोनों की शब्दावली से उधार लेता है, मुख्यतः क्योंकि यह इन क्षेत्रों में केंद्रीय महत्व की विभिन्न धारणाओं का सार है। मैट्रोइड्स ने [[ज्यामिति]], [[टोपोलॉजी]], [[संयुक्त अनुकूलन]], [[नेटवर्क सिद्धांत]] और [[कोडिंग सिद्धांत]] में अनुप्रयोग पाया है।<ref name=Neel2009>{{cite journal|last1=Neel|first1=David L.|last2=Neudauer|first2=Nancy Ann|author2-link= Nancy Neudauer |title=मैट्रोइड्स को आप जानते होंगे|journal=Mathematics Magazine|date=2009|volume=82|issue=1|pages=26–41|url=http://www.maa.org/sites/default/files/pdf/shortcourse/2011/matroidsknown.pdf|access-date=4 October 2014|doi=10.4169/193009809x469020}}</ref><ref name=Kashyap2009>{{cite web|last1=Kashyap|first1=Navin|last2=Soljanin|first2=Emina|last3=Vontobel|first3=Pascal|title=सूचना और कोडिंग सिद्धांत के लिए मैट्रोइड सिद्धांत और संयोजन अनुकूलन के अनुप्रयोग|url=https://www.birs.ca/workshops/2009/09w5103/report09w5103.pdf|website=www.birs.ca|access-date=4 October 2014}}</ref> | मैट्रोइड सिद्धांत बड़े पैमाने पर रैखिक बीजगणित और [[ग्राफ सिद्धांत]] दोनों की शब्दावली से उधार लेता है, मुख्यतः क्योंकि यह इन क्षेत्रों में केंद्रीय महत्व की विभिन्न धारणाओं का सार है। मैट्रोइड्स ने [[ज्यामिति]], [[टोपोलॉजी]], [[संयुक्त अनुकूलन]], [[नेटवर्क सिद्धांत]] और [[कोडिंग सिद्धांत]] में अनुप्रयोग पाया है।<ref name=Neel2009>{{cite journal|last1=Neel|first1=David L.|last2=Neudauer|first2=Nancy Ann|author2-link= Nancy Neudauer |title=मैट्रोइड्स को आप जानते होंगे|journal=Mathematics Magazine|date=2009|volume=82|issue=1|pages=26–41|url=http://www.maa.org/sites/default/files/pdf/shortcourse/2011/matroidsknown.pdf|access-date=4 October 2014|doi=10.4169/193009809x469020}}</ref><ref name=Kashyap2009>{{cite web|last1=Kashyap|first1=Navin|last2=Soljanin|first2=Emina|last3=Vontobel|first3=Pascal|title=सूचना और कोडिंग सिद्धांत के लिए मैट्रोइड सिद्धांत और संयोजन अनुकूलन के अनुप्रयोग|url=https://www.birs.ca/workshops/2009/09w5103/report09w5103.pdf|website=www.birs.ca|access-date=4 October 2014}}</ref> | ||
== परिभाषा == | |||
(परिमित) मैट्रोइड को परिभाषित करने के लिए कई [[क्रिप्टोमोर्फिज्म]] विधि हैं।<ref name="oxley">A standard source for basic definitions and results about matroids is Oxley (1992). An older standard source is Welsh (1976). See Brylawski's appendix in White (1986), pp. 298–302, for a list of equivalent axiom systems.</ref> | |||
'''स्वतंत्र समुच्चय''' | |||
स्वतंत्रता की दृष्टि से, परिमित मैट्रोइड <math>M</math> जोड़ी है <math>(E,\mathcal{I})</math>, जहाँ <math>E</math> परिमित समुच्चय है (जिसे ग्राउंड समुच्चय कहा जाता है) और <math>\mathcal{I}</math> के उपसमुच्चय का सदस्य है <math>E</math> (स्वतंत्र समुच्चय कहा जाता है) निम्नलिखित गुणों के लिए निम्नलिखित है:<ref name="w7-9">{{harvtxt|Welsh|1976}}, Section 1.2, "Axiom Systems for a Matroid", pp. 7–9.</ref> | |||
* (I1) [[खाली सेट|रिक्त समुच्चय]] <math>\emptyset\in\mathcal{I}</math> स्वतंत्र है, | |||
* (I2) स्वतंत्र समुच्चय का प्रत्येक उपसमुच्चय स्वतंत्र होता है, अर्थात प्रत्येक के लिए <math>A'\subseteq A\subseteq E</math>, यदि <math>A\in\mathcal{I}</math> तब <math>A'\in\mathcal{I}</math> इसे कभी-कभी वंशानुगत गुण, या नीचे की ओर बंद गुण कहा जाता है। | |||
* (I3) यदि <math>A</math> और <math>B</math> दो स्वतंत्र समुच्चय हैं (अर्थात्, प्रत्येक समुच्चय स्वतंत्र है) और <math>A</math> में इससे अधिक तत्व हैं <math>B</math>, तो वहाँ उपस्तिथ है <math>x\in A \backslash B</math> ऐसा है कि <math>B \cup \{x\}</math> में है <math>\mathcal{I}</math> इसे कभी-कभी वृद्धि गुण या स्वतंत्र समुच्चय विनिमय गुण कहा जाता है। | |||
पसमाधाने दो गुण संयुक्त संरचना को परिभाषित करते हैं जिसे [[स्वतंत्रता प्रणाली]] (या अमूर्त सरलीकृत परिसर) के रूप में जाना जाता है। वास्तव में, (I2) मानते हुए, गुण (I1) इस तथ्य के समान है कि कम से कम उपसमुच्चय <math>E</math> स्वतंत्र है, अर्थात, <math>\mathcal{I}\neq\emptyset</math> है। | |||
स्वतंत्रता | |||
===आधार और परिपथ=== | |||
{{Main|मैट्रोइड का आधार}} | |||
ग्राउंड समुच्चय का उपसमुच्चय <math>E</math> जो स्वतंत्र नहीं है उसे आश्रित कहते हैं। अधिकतम स्वतंत्र समुच्चय—अर्थात स्वतंत्र समुच्चय जो किसी भी तत्व को जोड़ने पर निर्भर हो जाता है <math>E</math>-को मैट्रोइड के लिए आधार कहा जाता है। मैट्रोइड में परिपथ <math>M</math> का न्यूनतम आश्रित उपसमुच्चय है <math>E</math>- अर्थात, आश्रित समुच्चय जिसके सभी उचित उपसमुच्चय स्वतंत्र हैं। शब्दावली इसलिए उत्पन्न होती है क्योंकि [[ग्राफ़िक मैट्रोइड]] के परिपथ संबंधित ग्राफ़ में चक्र होते हैं।<ref name="w7-9" /> | |||
ग्राउंड | |||
मैट्रोइड के आश्रित | मैट्रोइड के आश्रित समुच्चय, आधार, या परिपथ पूर्ण रूप से मैट्रोइड की विशेषता बताते हैं: समुच्चय स्वतंत्र है यदि यह निर्भर नहीं है, यदि केवल आधार का उपसमुच्चय है, और यदि ऐसा होता है इसमें कोई परिपथ नहीं है, आश्रित समुच्चयों, आधारों और परिपथों के संग्रह में प्रत्येक में सरल गुण होते हैं जिन्हें मैट्रोइड के लिए सिद्धांतों के रूप में लिया जा सकता है। उदाहरण के लिए, कोई मैट्रोइड को परिभाषित कर सकता है <math>M</math> जोड़ी बनने के लिए <math>(E,\mathcal{B})</math>, जहाँ <math>E</math> पूर्व के जैसे परिमित समुच्चय है <math>\mathcal{B}</math> के उपसमुच्चय का संग्रह है <math>E</math>, जिसे निम्नलिखित गुणों के साथ आधार कहा जाता है:<ref name="w7-9" /> | ||
* (बी1) <math>\mathcal{B}</math> | * (बी1) <math>\mathcal{B}</math> अरिक्त है। | ||
* (बी2) यदि <math>A</math> और <math>B</math> के विशिष्ट सदस्य हैं <math>\mathcal{B}</math> और <math>a\in A\smallsetminus B</math>, तो वहां तत्व | * (बी2) यदि <math>A</math> और <math>B</math> के विशिष्ट सदस्य हैं <math>\mathcal{B}</math> और <math>a\in A\smallsetminus B</math>, तो वहां तत्व उपस्तिथ है <math>b\in B\smallsetminus A</math> ऐसा है कि <math>(A \smallsetminus \{ a \}) \cup \{b\} \in \mathcal{B}</math> इस गुण को आधार विनिमय गुण कहा जाता है। | ||
यह उस आधार विनिमय | यह उस आधार विनिमय गुण से चलता है जिसका कोई सदस्य नहीं है <math>\mathcal{B}</math> दूसरे का उचित उपसमुच्चय हो सकता है। | ||
=== | ===पद फलन=== | ||
यह मैट्रोइड सिद्धांत का मूल परिणाम है, जो | यह मैट्रोइड सिद्धांत का मूल परिणाम है, जो रैखिक बीजगणित में आधारों के समान प्रमेय के सरलता से अनुरूप है, कि मैट्रोइड के कोई भी दो आधार <math>M</math> तत्वों की संख्या समान है। इस संख्या को [[मैट्रोइड रैंक|मैट्रोइड पद]] कहा जाता है <math>M</math> यदि <math>M</math> मैट्रोइड प्रारंभ है <math>E</math>, और <math>A</math> का उपसमुच्चय है <math>E</math>, फिर मैट्रोइड प्रारंभ <math>A</math> के उपसमूह पर विचार करके परिभाषित किया जा सकता है <math>A</math> को स्वतंत्र होना चाहिए यदि <math>M</math> स्वतंत्र है यह हमें सबमैट्रोइड्स और किसी भी उपसमुच्चय के पद के बारे में बात करने की अनुमति देता है <math>E</math> उपसमुच्चय का पद <math>A</math> मैट्रोइड पद द्वारा दिया गया है <math>r(A)</math> मैट्रोइड का, जिसमें निम्नलिखित गुण हैं:<ref name="w7-9"/> | ||
के | (R1) पद फलन का मान सदैव अनकारात्मक [[पूर्णांक]] होता है। | ||
*(R2) किसी भी उपसमुच्चय के लिए <math>A\subset E</math>, अपने पास <math>r(A) \le |A|</math> है | |||
*(R3) किन्हीं दो उपसमुच्चयों के लिए <math>A, B\subset E</math>, अपने पास: <math>r(A\cup B)+r(A\cap B)\le r(A)+r(B)</math> अर्थात पद [[सबमॉड्यूलर फ़ंक्शन|सबमॉड्यूलर फलन]] है। | |||
*(R4) किसी भी समुच्चय के लिए <math>A</math> और तत्व <math>x</math>, अपने पास: <math>r(A)\le r(A\cup\{x\})\le r(A)+1</math> है, पसमाधानी असमानता से यह अधिक सामान्यतः इस प्रकार है कि, यदि <math>A\subseteq B\subseteq E</math>, तब <math>r(A)\leq r(B)\leq r(E)</math> अर्थात्, पद [[मोनोटोनिक फ़ंक्शन|मोनोटोनिक फलन]] है। | |||
इन गुणों का उपयोग परिमित मैट्रोइड की वैकल्पिक परिभाषाओं के रूप में किया जा सकता है: यदि <math>(E,r)</math> इन गुणों को संतुष्ट करता है, फिर मैट्रोइड के स्वतंत्र समुच्चय समाप्त हो जाते हैं <math>E</math> उन उपसमुच्चय के रूप में परिभाषित किया जा सकता है <math>A</math> का <math>E</math> के साथ <math>r(A)=|A|</math> आंशिक रूप से क्रमबद्ध समुच्चयों की भाषा में, ऐसी मैट्रोइड संरचना ज्यामितीय जाली के समान होती है जिसके तत्व उपसमुच्चय होते हैं <math>A\subset M</math> आंशिक रूप से समावेशन द्वारा क्रमबद्ध किया गया। | |||
<math>|A|-r(A)</math> का अंतर उपसमुच्चय की शून्यता कसमाधानाती है <math>A</math> यह उन तत्वों की न्यूनतम संख्या है जिन्हें विस्थापित किया जाना चाहिए <math>A</math> स्वतंत्र समुच्चय प्राप्त करने के लिए की अशक्तता <math>E</math> में <math>M</math> को शून्यता कहा जाता है <math>M</math> के अंतर <math>r(E)-r(A)</math> को कभी-कभी उपसमुच्चय <math>A</math> का कॉरैंक भी कहा जाता है। | |||
===क्लोजर ऑपरेटर=== | ===क्लोजर ऑपरेटर=== | ||
<math>M</math> परिमित समुच्चय पर मैट्रोइड को <math>E</math>, पद फलन के साथ <math>r</math> उपरोक्तानुसार समापन (या अवधि) <math>\operatorname{cl}(A)</math> उपसमुच्चय का <math>A</math> का <math>E</math> समुच्चय है। | |||
:<math>\operatorname{cl}(A) = \Bigl\{x\in E\mid r(A)=r\bigl(A\cup\{x\}\bigr)\Bigr\}. </math> | :<math>\operatorname{cl}(A) = \Bigl\{x\in E\mid r(A)=r\bigl(A\cup\{x\}\bigr)\Bigr\}. </math> | ||
यह [[ बंद करने वाला ऑपरेटर ]] को परिभाषित करता है <math>\operatorname{cl}: \mathcal{P}(E)\to \mathcal{P}(E)</math> | यह [[ बंद करने वाला ऑपरेटर |क्लोजर ऑपरेटर]] को परिभाषित करता है <math>\operatorname{cl}: \mathcal{P}(E)\to \mathcal{P}(E)</math> जहाँ <math>\mathcal{P}</math> निम्नलिखित गुणों के साथ [[ सत्ता स्थापित |पावर सेट]] को दर्शाता है: | ||
* ( | * (C1) सभी उपसमुच्चय के लिए <math>X</math> का <math>E</math>, <math>X\subseteq \operatorname{cl}(X)</math> है। | ||
* ( | * (C2) सभी उपसमुच्चय के लिए <math>X</math> का <math>E</math>, <math>\operatorname{cl}(X)= \operatorname{cl}(\operatorname{cl}(X))</math> है। | ||
* ( | * (C3) सभी उपसमुच्चय के लिए <math>X</math> और <math>Y</math> का <math>E</math> के साथ <math>X\subseteq Y</math>, <math>\operatorname{cl}(X)\subseteq \operatorname{cl}(Y)</math> है। | ||
* ( | * (C4) सभी तत्वों के लिए <math>a</math>, और <math>b</math> का <math>E</math> और सभी उपसमुच्चय <math>Y</math> का <math>E</math>, यदि <math>a\in\operatorname{cl}(Y\cup \{b\}) \smallsetminus \operatorname{cl}(Y)</math> तब <math>b\in\operatorname{cl}(Y\cup \{a\}) \smallsetminus \operatorname{cl}(Y)</math> है। | ||
इनमें से | इनमें से पसमाधाने तीन गुण क्लोजर ऑपरेटर के परिभाषित गुण हैं। चौथे को कभी-कभी मैक लेन-[[अर्नेस्ट स्टीनिट्ज़]] विनिमय गुण कहा जाता है। इन गुणों को मैट्रोइड की परिभाषा के रूप में लिया जा सकता है: प्रत्येक फलन <math>\operatorname{cl}: \mathcal{P}(E)\to \mathcal{P}(E)</math> जो इन गुणों का पालन करता है वह मैट्रोइड निर्धारित करता है।<ref name="w7-9"/> | ||
'''फ्लैट''' | |||
समुच्चय जिसका समापन स्वयं के समान होता है उसे बंद कहा जाता है, या मैट्रोइड का फ्लैट या उपस्थान है।<ref>{{harvtxt|Welsh|1976}}, Section 1.8, "Closed sets = Flats = Subspaces", pp. 21–22.</ref> समुच्चय को बंद कर दिया जाता है यदि वह अपनी पद के लिए [[अधिकतम तत्व]] है, जिसका अर्थ है कि समुच्चय में किसी अन्य तत्व को जोड़ने से पद में वृद्धि होगी। मैट्रोइड के बंद समुच्चय को कवरिंग विभाजन गुण की विशेषता होती है: | |||
* (F1) संपूर्ण बिंदु समुच्चय <math>E</math> बन्द है। | |||
* ( | * (F2) यदि <math>S</math> और <math>T</math> फ्लैट हैं <math>S\cap T</math> फ्लैट है। | ||
* (F2) यदि <math>S</math> और <math>T</math> | * (F3) यदि <math>S</math> समतल है, तो प्रत्येक तत्व <math>E\smallsetminus S</math> फ्लैट में है <math>T</math> वह [[ रिश्ते को कवर करना |कवर]] <math>S</math> (तात्पर्य है कि <math>T</math> ठीक से सम्मिलित करना है <math>S</math> किंतु कोई फ्लैट नहीं है <math>U</math> मध्य में <math>S</math> और <math>T</math>) है। | ||
* (F3) यदि <math>S</math> समतल है, तो प्रत्येक तत्व <math>E\smallsetminus S</math> | |||
कक्षा <math>\mathcal{L}(M)</math> | कक्षा समुच्चय समावेशन द्वारा आंशिक रूप से क्रमबद्ध सभी फ्लैटों का <math>\mathcal{L}(M)</math> मैट्रोइड जाली बनाता है। इसके विपरीत, प्रत्येक मैट्रोइड जाली <math>L</math> अपने समुच्चय पर मैट्रोइड बनाता है निम्नलिखित क्लोजर ऑपरेटर के अंतर्गत परमाणुओं के (ऑर्डर सिद्धांत) <math>E</math> समुच्चय के लिए <math>S</math> जुड़ने के साथ परमाणुओं का <math>\bigvee S</math> है: | ||
:<math>\operatorname{cl}(S) = \{ x\in E\mid x\le\bigvee S \}</math>. | :<math>\operatorname{cl}(S) = \{ x\in E\mid x\le\bigvee S \}</math>. | ||
इस मैट्रोइड के फ्लैट जाली के तत्वों के साथ | इस मैट्रोइड के फ्लैट जाली के तत्वों के साथ युग्मित होता हैं; जाली तत्व के अनुरूप फ्लैट <math>y</math> समुच्चय है: | ||
:<math>\{ x\in E\mid x\le y\}</math>. | :<math>\{ x\in E\mid x\le y\}</math>. | ||
इस प्रकार, इस मैट्रोइड के फ्लैटों की जाली स्वाभाविक रूप से | इस प्रकार, इस मैट्रोइड के फ्लैटों की जाली स्वाभाविक रूप से <math>L</math> आइसोमोर्फिक है। | ||
===हाइपरप्लेन=== | ===हाइपरप्लेन=== | ||
पद के मेट्रोइड में <math>r</math>, पद का फ्लैट <math>r-1</math> को हाइपरप्लेन कहा जाता है (हाइपरप्लेन को कोटम या सह-बिंदु भी कहा जाता है।) ये अधिकतम उचित फ्लैट हैं; अर्थात, हाइपरप्लेन का एकमात्र उप-समुच्चय जो फ्लैट भी है, समुच्चय मैट्रोइड के सभी तत्वों <math>E</math> की समतुल्य परिभाषा यह है कि कोटोम <math>E</math> का उपसमुच्चय है जो M तक नहीं विस्तारित है, किंतु ऐसा है कि इसमें कोई अन्य तत्व जोड़ने से स्पैनिंग समुच्चय बन जाता है।<ref name="w38-39">{{harvtxt|Welsh|1976}}, Section 2.2, "The Hyperplanes of a Matroid", pp. 38–39.</ref> | |||
*(H2) प्रत्येक के लिए <math>x\in E</math> और विशिष्ट <math>Y,Z\in\mathcal{H}</math> साथ <math>x\notin Y\cup Z</math>, वहां | सदस्य मैट्रोइड के हाइपरप्लेन के <math>\mathcal{H}</math> में निम्नलिखित गुण होते हैं, जिन्हें मैट्रोइड के स्वयंसिद्धीकरण के रूप में लिया जा सकता है:<ref name="w38-39" /> | ||
(H1) भिन्न-भिन्न समुच्चय उपस्तिथ नहीं हैं <math>X</math> और <math>Y</math> में <math>\mathcal{H}</math> के साथ <math>X\subseteq Y</math>. अर्थात्, हाइपरप्लेन [[स्पर्नर परिवार|स्पर्नर सदस्य]] बनाते हैं। | |||
*(H2) प्रत्येक के लिए <math>x\in E</math> और विशिष्ट <math>Y,Z\in\mathcal{H}</math> के साथ <math>x\notin Y\cup Z</math>, वहां उपस्तिथ है <math>X\in\mathcal{H}</math> साथ <math>(Y\cap Z)\cup\{x\}\subseteq X</math> है। | |||
===ग्राफोइड्स=== | ===ग्राफोइड्स=== | ||
जॉर्ज जे. मिन्टी (1966) ने ग्राफॉइड को त्रिक के रूप में परिभाषित किया <math>(L, C, D)</math> जिसमें <math>C</math> और <math>D</math> के | जॉर्ज जे. मिन्टी (1966) ने ग्राफॉइड को त्रिक के रूप में परिभाषित किया <math>(L, C, D)</math> जिसमें <math>C</math> और <math>D</math> के अरिक्त उपसमुच्चय की कक्षाएं हैं <math>L</math> ऐसा है कि | ||
*(G1) का कोई तत्व नहीं <math>C</math> (जिसे | *(G1) का कोई तत्व नहीं <math>C</math> (जिसे परिपथ कहा जाता है) में सम्मिलित है। | ||
*(G2) का कोई तत्व नहीं <math>D</math> (जिसे को- | *(G2) का कोई तत्व नहीं <math>D</math> (जिसे को-परिपथ कहा जाता है) में सम्मिलित है। | ||
*( | *(G3) कोई समुच्चय नहीं है <math>C</math> और समुच्चय करें <math>D</math> बिल्कुल तत्व में प्रतिच्छेद करता है, और | ||
*( | *(G4) जब भी <math>L</math> उपसमुच्चय के असंयुक्त संघ के रूप में दर्शाया गया है <math>R, G, B</math> के साथ <math>G=\{g\}</math> (सिंगलटन समुच्चय), फिर या तो <math>X \in C</math> का अस्तित्व इस प्रकार है <math>g \in X \subseteq R \cup G</math> या <math>Y \in D</math> ऐसे उपस्तिथ <math>g \in Y \subseteq B \cup G.</math> है। | ||
उन्होंने | उन्होंने सिद्ध कर दिया कि जिसके लिए मैट्रोइड है <math>C</math> परिपथ का वर्ग है और <math>D</math> सह-परिपथ का वर्ग है। इसके विपरीत, यदि <math>C</math> और <math>D</math> मैट्रोइड के परिपथ और सह-परिपथ वर्ग हैं ग्राउंड समुच्चय के साथ <math>M</math>, <math>E</math> तब <math>(E, C, D)</math> ग्राफ़ॉइड है. इस प्रकार, ग्राफ़ॉइड्स मैट्रोइड्स का स्व-दोहरा क्रिप्टोमोर्फिक स्वयंसिद्धीकरण देते हैं। | ||
== उदाहरण == | == उदाहरण == | ||
=== मुफ़्त मैट्रोइड === | === मुफ़्त मैट्रोइड === | ||
मान लीजिये <math>E</math> परिमित समुच्चय के सभी उपसमुच्चय का समुच्चय <math>E</math> मैट्रोइड के स्वतंत्र समुच्चय को परिभाषित करता है। इस <math>E</math> को [[मुफ़्त मैट्रोइड]] ओवर कहा जाता है। | |||
===यूनिफ़ॉर्म मैट्रिक्स=== | ===यूनिफ़ॉर्म मैट्रिक्स=== | ||
मान लीजिये <math>E</math> परिमित समुच्चय हो और <math>k</math> [[प्राकृतिक संख्या]] मैट्रोइड को परिभाषित कर सकता है <math>E</math> प्रत्येक को <math>k</math>-तत्व उपसमुच्चय <math>E</math> आधार बनाया जाता है, इसे पद के एकसमान मैट्रोइड के रूप में जाना जाता है <math>k</math> पद के साथ समान मैट्रोइड <math>k</math> के साथ <math>n</math> तत्वों को दर्शाया गया है <math>U_{k,n}</math> कम से कम 2 पद के सभी समान मैट्रोइड सरल हैं (देखें)। {{section link||अतिरिक्त शब्दावली}}) पद 2 की यूनिफार्म मैट्रोइड पर <math>n</math> अंक को कहा जाता है <math>n</math>-बिंदु रेखा मैट्रोइड के समान होती है यदि केवल तभी जब इसमें मैट्रोइड का पद प्लस से कम आकार का कोई परिपथ न हो। एकसमान मैट्रोइड्स के प्रत्यक्ष योग को [[विभाजन मैट्रोइड|विभाजन मैट्रोइड्स]] कहा जाता है। | |||
यूनिफार्म मेट्रोइड में <math>U_{0,n}</math>, प्रत्येक तत्व लूप है (ऐसा तत्व जो किसी स्वतंत्र समुच्चय से संबंधित नहीं है), और एकसमान मैट्रोइड में <math>U_{n,n}</math>, प्रत्येक तत्व कोलूप है (तत्व जो सभी आधारों से संबंधित है)। इन दो प्रकार के मैट्रोइड्स का सीधा योग विभाजन मैट्रोइड है जिसमें प्रत्येक तत्व लूप या कोलूप है; इसे असतत मैट्रोइड कहा जाता है। असतत मैट्रोइड की समतुल्य परिभाषा मैट्रोइड है जिसमें ग्राउंड समुच्चय का प्रत्येक उचित, अरिक्त उपसमुच्चय <math>E</math> विभाजक है। | |||
===रैखिक बीजगणित से मैट्रोइड्स=== | ===रैखिक बीजगणित से मैट्रोइड्स=== | ||
[[File:fano plane.svg|thumb|फ़ानो मैट्रोइड, फ़ानो विमान से प्राप्त हुआ। यह [[GF(2)]]-रैखिक है | [[File:fano plane.svg|thumb|फ़ानो मैट्रोइड, फ़ानो विमान से प्राप्त हुआ। यह [[GF(2)]]-रैखिक है किंतु वास्तविक-रैखिक नहीं है।]] | ||
[[File:Vamos matroid.svg|thumb|वामोस मैट्रोइड, किसी भी क्षेत्र पर रैखिक नहीं है]]मैट्रोइड सिद्धांत मुख्य रूप से वेक्टर स्थानों में स्वतंत्रता और आयाम के गुणों की गहन | [[File:Vamos matroid.svg|thumb|वामोस मैट्रोइड, किसी भी क्षेत्र पर रैखिक नहीं है]]मैट्रोइड सिद्धांत मुख्य रूप से वेक्टर स्थानों में स्वतंत्रता और आयाम के गुणों की गहन परिक्षण से विकसित हुआ। इस प्रकार परिभाषित मैट्रोइड्स को प्रस्तुत करने की दो विधि हैं: | ||
* | * यदि <math>E</math> सदिश समष्टि का कोई परिमित उपसमुच्चय <math>V</math> है, तो मैट्रोइड को परिभाषित कर सकते हैं <math>M</math> पर <math>E</math> के स्वतंत्र समुच्चय लेकर <math>M</math> का रैखिक रूप से स्वतंत्र उपसमुच्चय होना, <math>E</math> इस मैट्रोइड के लिए स्वतंत्र-समुच्चय स्वयंसिद्धों की वैधता [[स्टीनिट्ज़ एक्सचेंज लेम्मा]] से होती है। यदि <math>M</math> मैट्रोइड है जिसे इस प्रकार से परिभाषित किया जा सकता है, हम समुच्चय कहते हैं <math>E</math> [[मैट्रोइड प्रतिनिधित्व|प्रतिनिधित्व]] करता है, <math>M</math> इस प्रकार के [[मैट्रोइड प्रतिनिधित्व|मैट्रोइड्स]] को वेक्टर मैट्रोइड्स कहा जाता है। इस प्रकार से परिभाषित मैट्रोइड का महत्वपूर्ण उदाहरण फ़ानो मैट्रोइड से प्राप्त पद-तीन मैट्रोइड, सात बिंदुओं (मैट्रोइड के सात तत्व) और सात रेखाओं (मैट्रोइड के उचित गैर-तुच्छ फ्लैट) के साथ [[परिमित ज्यामिति]] मैट्रोइड) है। यह रैखिक मैट्रोइड है जिसके तत्वों को [[परिमित क्षेत्र]] GF(2) पर त्रि-आयामी वेक्टर अंतरिक्ष में सात गैर-शून्य बिंदुओं के रूप में वर्णित किया जा सकता है। चूँकि, GF(2) के स्थान पर [[वास्तविक संख्या|वास्तविक संख्याओं]] का उपयोग करके फ़ैनो मैट्रोइड के लिए समान प्रतिनिधित्व प्रदान करना संभव नहीं है। | ||
* [[मैट्रिक्स (गणित)]] | * [[मैट्रिक्स (गणित)]] किसी क्षेत्र (गणित) में प्रविष्टियों के साथ <math>A</math> मैट्रोइड को उत्पन्न करता है। इसके स्तंभों के समुच्चय पर <math>M</math> मैट्रोइड में स्तंभों के आश्रित समुच्चय वे होते हैं जो वैक्टर के रूप में रैखिक रूप से निर्भर होते हैं। इस मैट्रोइड को कॉलम मैट्रोइड कहा जाता है <math>A</math>, और <math>A</math> प्रतिनिधित्व करने के लिए कहा जाता है <math>M</math> उदाहरण के लिए, फ़ैनो मैट्रोइड को 3×7 (0,1)-मैट्रिक्स के रूप में इस प्रकार दर्शाया जा सकता है। कॉलम मैट्रोइड्स किसी अन्य नाम के अंतर्गत सिर्फ वेक्टर मैट्रोइड्स हैं, किंतु मैट्रिक्स प्रतिनिधित्व के पक्ष में प्रायः कारण होते हैं। (तकनीकी अंतर है: कॉलम मैट्रोइड में भिन्न-भिन्न तत्व हो सकते हैं जो वेक्टर होते हैं, किंतु जैसा कि ऊपर परिभाषित किया गया है वेक्टर मैट्रोइड में ऐसा नहीं हो सकता है। सामान्यतः यह अंतर महत्वहीन है और इसे उपेक्षा किया जा सकता है, किंतु अनुमति देकर <math>E</math> सदिशों का बहुसमूह हो, जो दो परिभाषाओं को पूर्ण सहमति में लाता है।) | ||
मैट्रोइड जो वेक्टर मैट्रोइड के समतुल्य है, | मैट्रोइड जो वेक्टर मैट्रोइड के समतुल्य है, चूँकि इसे भिन्न रूप से प्रस्तुत किया जा सकता है, प्रतिनिधित्व योग्य या रैखिक कहा जाता है। यदि <math>M</math> क्षेत्र पर वेक्टर मैट्रोइड के समान है (गणित) <math>F</math>, तो हम कहते हैं कि <math>M</math> प्रतिनिधित्व करने योग्य है {{nobreak|<math>F</math>;}} विशेष रूप से, <math>M</math>वास्तविक-प्रतिनिधित्व योग्य है यदि यह वास्तविक संख्याओं पर प्रतिनिधित्व योग्य है। उदाहरण के लिए, यद्यपि ग्राफिक मैट्रोइड (नीचे देखें) को ग्राफ के रूप में प्रस्तुत किया जाता है, यह किसी भी क्षेत्र में वैक्टर द्वारा भी प्रदर्शित किया जा सकता है। मैट्रोइड सिद्धांत में मूलभूत समस्या उन मैट्रोइड्स को चिह्नित करना है जिन्हें किसी दिए गए क्षेत्र में दर्शाया जा सकता है <math>F</math>; रोटा का अनुमान प्रत्येक परिमित क्षेत्र के लिए संभावित लक्षण वर्णन का वर्णन करता है। अब तक के मुख्य परिणाम डब्ल्यू.टी. टुटे (1950 के दशक) के कारण [[बाइनरी मैट्रोइड|बाइनरी मैट्रोइड्स]] (GF (2) पर प्रतिनिधित्व योग्य), रीड और बिक्सबी के कारण टर्नरी मैट्रोइड्स (3-तत्व क्षेत्र पर प्रतिनिधित्व योग्य) और भिन्न से सेमुर (1970 के दशक) के लक्षण वर्णन हैं।) और गिलेन, जेरार्ड्स और कपूर (2000) के कारण चतुर्धातुक मैट्रोइड्स (4-तत्व क्षेत्र पर प्रतिनिधित्व योग्य) यह अधिक ओपन क्षेत्र है। | ||
नियमित मैट्रोइड मैट्रोइड है जो सभी संभावित क्षेत्रों में प्रतिनिधित्व योग्य है। वामोस | नियमित मैट्रोइड ऐसा मैट्रोइड है जो सभी संभावित क्षेत्रों में प्रतिनिधित्व योग्य है। वामोस मैट्रोइड का सबसे सरल उदाहरण है जो किसी भी क्षेत्र में प्रदर्शित नहीं किया जा सकता है। | ||
===ग्राफ़ सिद्धांत से मैट्रोइड्स=== | ===ग्राफ़ सिद्धांत से मैट्रोइड्स=== | ||
मैट्रोइड्स के सिद्धांत का दूसरा मूल स्रोत ग्राफ़ सिद्धांत है। | मैट्रोइड्स के सिद्धांत का दूसरा मूल स्रोत ग्राफ़ सिद्धांत है। | ||
प्रत्येक परिमित ग्राफ (या [[मल्टीग्राफ]]) <math>G</math> मैट्रोइड को | प्रत्येक परिमित ग्राफ (या [[मल्टीग्राफ]]) <math>G</math> मैट्रोइड को उत्पन्न करता है <math>M(G)</math> इस प्रकार: के रूप में लीजिए <math>E</math> सभी किनारों का समुच्चय <math>G</math> और किनारों के समुच्चय को स्वतंत्र मानें यदि केवल यदि वह पेड़ है (ग्राफ़ सिद्धांत); अर्थात्, यदि इसमें कोई [[सरल चक्र]] न हो। तब <math>M(G)</math> को चक्र मैट्रोइड कहा जाता है। इस प्रकार से प्राप्त मैट्रोइड्स ग्राफिक मैट्रोइड्स हैं। प्रत्येक मैट्रोइड ग्राफिक नहीं है, किंतु तीन तत्वों पर सभी मैट्रोइड ग्राफिक हैं।<ref name=Ox13/>प्रत्येक ग्राफिक मैट्रोइड नियमित है। | ||
ग्राफ़ पर अन्य मैट्रोइड्स | ग्राफ़ पर अन्य मैट्रोइड्स पश्चात में परिक्षण किये गए: | ||
*ग्राफ के [[द्विवृत्ताकार मैट्रोइड]] को किनारों के | *ग्राफ के [[द्विवृत्ताकार मैट्रोइड]] को किनारों के समुच्चय को स्वतंत्र कहकर परिभाषित किया जाता है यदि प्रत्येक जुड़े उपसमुच्चय में अधिकतम चक्र होता है। | ||
*किसी भी निर्देशित या अप्रत्यक्ष ग्राफ़ में <math>G</math> | *किसी भी निर्देशित या अप्रत्यक्ष ग्राफ़ में <math>G</math> मान लीजिये <math>E</math> और <math>F</math> शीर्षों के दो विशिष्ट समुच्चय हैं। सेट में <math>E</math>, उपसमुच्चय परिभाषित करें यदि हैं तो स्वतंत्र रहें <math>|U|</math> शीर्ष-असंयुक्त पथ <math>F</math> पर <math>U</math> यह मैट्रोइड को परिभाषित करता है <math>E</math> को [[गैमॉइड]] कहा जाता है:<ref name=Ox115/>जटिल गैमॉइड वह है जिसके लिए समुच्चय <math>E</math> का संपूर्ण शीर्ष समुच्चय <math>G</math> है।<ref name=Ox100>{{harvnb|Oxley|1992|p=100}}</ref> | ||
*द्विपक्षीय ग्राफ़ में <math>G = (U,V,E)</math>, कोई मैट्रोइड बना सकता है जिसमें तत्व | *द्विपक्षीय ग्राफ़ में <math>G = (U,V,E)</math>, कोई मैट्रोइड बना सकता है जिसमें तत्व शीर्ष पर हैं, द्विविभाजन के <math>U</math>, और स्वतंत्र उपसमुच्चय ग्राफ के [[मिलान (ग्राफ सिद्धांत)|संयुग्मन (ग्राफ सिद्धांत)]] के अंतिम बिंदुओं के समुच्चय हैं। इसे ट्रांसवर्सल मैट्रोइड कहा जाता है,<ref name=Ox4648>{{harvnb|Oxley|1992|pp=46–48}}</ref><ref name=Wh877297>{{White|1987|pp=72–97}}</ref> और यह गैमॉइड की विशेष स्तिथि है।<ref name=Ox115>{{harvnb|Oxley|1992|pp=115}}</ref> ट्रांसवर्सल मैट्रोइड्स जटिल गैमॉइड्स के दोहरे मैट्रोइड्स हैं।<ref name=Ox100/> | ||
*ग्राफ़िक मैट्रोइड्स को [[हस्ताक्षरित ग्राफ]], [[ लाभ ग्राफ |गेन ग्राफ]] और [[पक्षपाती ग्राफ]] से मैट्रोइड्स में सामान्यीकृत किया गया है। ग्राफ <math>G</math> विशिष्ट रैखिक वर्ग के साथ चक्रों का <math>B</math>, जिसे पक्षपाती ग्राफ़ के रूप में जाना जाता है <math>(G, B)</math>, दो मैट्रोइड हैं, जिन्हें फ्रेम मैट्रोइड और बायस्ड ग्राफ के लिफ्ट मैट्रोइड के रूप में जाना जाता है। यदि प्रत्येक चक्र विशिष्ट वर्ग का है, तो ये मैट्रोइड्स चक्र मैट्रोइड के साथ युग्मित होते हैं <math>G</math> यदि कोई चक्र प्रतिष्ठित नहीं है, तो फ्रेम मैट्रोइड द्विवृत्ताकार मैट्रोइड है <math>G</math> हस्ताक्षरित ग्राफ, जिसके किनारों को संकेतों द्वारा लेबल किया जाता है, और लाभ ग्राफ, जो ऐसा ग्राफ है जिसके किनारों को समूह से उन्मुख रूप से लेबल किया जाता है, प्रत्येक पक्षपाती ग्राफ को उत्पन्न करता है और इसलिए इसमें फ्रेम और लिफ्ट मैट्रोइड होते हैं। | |||
*[[लमान ग्राफ]] द्वि-आयामी कठोरता मैट्रोइड का आधार बनाते हैं, जो [[संरचनात्मक कठोरता]] के सिद्धांत में परिभाषित मैट्रोइड है। | *[[लमान ग्राफ]] द्वि-आयामी कठोरता मैट्रोइड का आधार बनाते हैं, जो [[संरचनात्मक कठोरता]] के सिद्धांत में परिभाषित मैट्रोइड है। | ||
* | *मान लीजिये <math>G</math> कनेक्टेड ग्राफ है, और <math>E</math> इसका किनारा समुच्चय है <math>I</math> उपसमुच्चय का संग्रह हो <math>F</math> का <math>E</math> ऐसा है कि <math>G - F</math> अभी भी जुड़ा हुआ है। तब <math>M^*(G)</math>, जिसका तत्व <math>E</math> समुच्चय है इसके स्वतंत्र समुच्चयों के वर्ग के रूप में, मैट्रोइड है जिसे बॉन्ड मैट्रोइड कहा जाता है <math>G</math> पद फलन <math>r(F)</math> किनारे उपसमुच्चय पर प्रेरित उपग्राफ की [[चक्रीय संख्या]] है <math>F</math>, जो उस उपसमूह के अधिकतम जंगल के बाहर किनारों की संख्या और उसमें स्वतंत्र चक्रों की संख्या के समान है। | ||
=== | ===क्षेत्र एक्सटेंशन से मैट्रोइड्स=== | ||
मैट्रोइड सिद्धांत का तीसरा मूल स्रोत | मैट्रोइड सिद्धांत का तीसरा मूल स्रोत क्षेत्र सिद्धांत (गणित) है। | ||
किसी क्षेत्र का [[विस्तार क्षेत्र]] मैट्रोइड को | किसी [[विस्तार क्षेत्र|क्षेत्र]] का [[विस्तार क्षेत्र|विस्तार]] मैट्रोइड को उत्पन्न करता है। कल्पना करना <math>F</math> और <math>K</math> के साथ क्षेत्र हैं <math>K</math> युक्त <math>F</math> मान <math>E</math> का कोई परिमित उपसमुच्चय हो, <math>K</math> का उपसमुच्चय को परिभाषित करें। <math>S</math> यदि विस्तार क्षेत्र है तो <math>E</math> [[बीजगणितीय स्वतंत्रता|बीजगणितीय]] रूप से [[बीजगणितीय स्वतंत्रता|स्वतंत्र]] है, <math>F(S)</math> के पास ट्रान्सेंडेंस डिग्री <math>|S|</math> के समान है।<ref name=Ox215>{{harvnb|Oxley|1992|p=215}}</ref> | ||
== | मैट्रोइड जो इस प्रकार के मैट्रोइड के समान होता है उसे [[बीजगणितीय मैट्रोइड]] कहा जाता है।<ref name="Ox216">{{harvnb|Oxley|1992|p=216}}</ref>बीजगणितीय मैट्रोइड्स को चिह्नित करने की समस्या अत्यंत कठिन है; इसके बारे में अधिक कम जानकारी है, वैमोस मैट्रोइड का उदाहरण प्रदान करता है जो बीजगणितीय नहीं है। | ||
== मूलभूत निर्माण == | |||
प्राचीन मैट्रोइड से नए मैट्रोइड बनाने के कुछ मानक विधि हैं। | |||
===द्वैत=== | ===द्वैत=== | ||
यदि | यदि M परिमित मैट्रोइड है, तो हम उसी अंतर्निहित समुच्चय को लेकर 'ऑर्थोगोनल' या 'डुअल मैट्रोइड' M को परिभाषित कर सकते हैं और समुच्चय को M में आधार कह सकते हैं यदि केवल इसका पूरक M में आधार है। यह सत्यापित करना कठिन नहीं है वह M* मैट्रोइड है और M* का द्वैत M का द्वैत है।<ref name=Whi8632>{{harvnb|White|1986|p=32}}</ref> | ||
मैट्रोइड को परिभाषित करने की अन्य विधि के संदर्भ में दोहरे को समान रूप से वर्णित किया जा सकता है। उदाहरण के लिए: | |||
* M* में समुच्चय स्वतंत्र है यदि केवल उसका पूरक M तक विस्तारित हो। | |||
* समुच्चय M* का परिपथ है यदि केवल इसका पूरक M में कोटोम है। | |||
*डुअल का पद फलन <math>r^*(S) = |S|- r(M) + r\left(E\smallsetminus S\right)</math> है। | |||
'उदाहरण' | कुराटोस्की के प्रमेय के मैट्रोइड संस्करण के अनुसार, ग्राफिक मैट्रोइड M का दोहरा ग्राफिक मैट्रोइड है यदि केवल M [[समतलीय ग्राफ]] का मैट्रोइड है। इस स्तिथि में, M का द्वैत, G के द्वैत ग्राफ का मैट्रॉइड है।<ref name="Whi86105">{{harvnb|White|1986|p=105}}</ref> वेक्टर मैट्रोइड का द्वैत विशेष क्षेत्र F पर प्रदर्शित होता है, F पर भी प्रदर्शित होता है। ट्रांसवर्सल मैट्रोइड का द्वैत जटिल गैमॉइड इसके विपरीत है। | ||
'''उदाहरण''' | |||
किसी ग्राफ़ का चक्र मैट्रोइड उसके बांड मैट्रोइड का दोहरा मैट्रोइड है। | किसी ग्राफ़ का चक्र मैट्रोइड उसके बांड मैट्रोइड का दोहरा मैट्रोइड है। | ||
=== | ===माइनर्स=== | ||
{{Main| | {{Main|मैट्रोइड माइनर}} | ||
मैट्रोइड | यदि M तत्व समुच्चय E के साथ मैट्रोइड है, और S, E का उपसमुच्चय है, तो M से S का 'प्रतिबंध', जिसे M |S लिखा जाता है, समुच्चय S पर मैट्रोइड है जिसका स्वतंत्र समुच्चय M के स्वतंत्र समुच्चय हैं जो S में निहित हैं। इसके परिपथ M के परिपथ हैं जो S में निहित हैं और इसका पद फलन M का है जो S के उपसमुच्चय तक सीमित है। रैखिक बीजगणित में, यह S में वैक्टर द्वारा उत्पन्न उप-स्थान तक सीमित करने के अनुरूप है। समान रूप से यदि T = M−S इसे T का 'विलोपन' कहा जा सकता है, जिसे M\T या M−T लिखा जाता है। M के सबमैट्रोइड्स वास्तव में विलोपन के अनुक्रम के परिणाम हैं: क्रम अप्रासंगिक है।<ref name=Whi86131>{{harvnb|White|1986|p=131}}</ref><ref name=Whi86224>{{harvnb|White|1986|p=224}}</ref> | ||
प्रतिबंध की दोहरी क्रिया संकुचन है।<ref name="Whi866139">{{harvnb|White|1986|p=139}}</ref> यदि T, E का उपसमुच्चय है, तो T द्वारा M का 'संकुचन', जिसे M/T लिखा जाता है, अंतर्निहित समुच्चय E - T पर मैट्रोइड है जिसका पद फलन <math>r'(A) = r(A \cup T) - r(T).</math> है,<ref name="Whi86140">{{harvnb|White|1986|p=140}}</ref> रैखिक बीजगणित में, यह E-T में सदिशों की छवियों के साथ-साथ T में सदिशों द्वारा उत्पन्न रैखिक स्थान द्वारा भागफल स्थान को देखने से युग्मित होता है। | |||
मैट्रोइड N जो प्रतिबंध और संकुचन संचालन के अनुक्रम द्वारा M से प्राप्त किया जाता है, उसे M का [[मैथेरॉइड माइनर]] कहा जाता है।<ref name="Whi86224" /><ref name="Whi86150">{{harvnb|White|1986|p=150}}</ref> हम कहते हैं कि M में 'N' गौण है। मैट्रोइड्स के कई महत्वपूर्ण सदस्यों की विशेषता लघु-[[न्यूनतम तत्व|न्यूनतम मैट्रोइड्स]] से हो सकती है। जो सदस्य से संबंधित नहीं हैं; इन्हें निषिद्ध या बहिष्कृत अवयस्क कहा जाता है।<ref name="Whi861467">{{harvnb|White|1986|pp=146–147}}</ref> | |||
मैट्रोइड्स | |||
'''योग और संघ''' | |||
== अतिरिक्त शब्दावली == | मान लीजिए कि M तत्वों E के अंतर्निहित समुच्चय के साथ मैट्रॉइड है, और N को अंतर्निहित समुच्चय F पर और मैट्रॉइड होने दें। मैट्रोइड्स M और N का 'प्रत्यक्ष योग' वह मैट्रोइड है जिसका अंतर्निहित समुच्चय E और F का [[असंयुक्त संघ]] है, और जिसका स्वतंत्र समुच्चय M के स्वतंत्र समुच्चय का N के स्वतंत्र समुच्चय का असंयुक्त संघ है। | ||
मान लीजिए कि M मैट्रोइड है जिसमें E तत्वों का अंतर्निहित | |||
* E को M का 'ग्राउंड | M और N का 'संघ' वह मैट्रोइड है जिसका अंतर्निहित समुच्चय E और F का संघ (असंगठित संघ नहीं) है, और जिसका स्वतंत्र समुच्चय वे उपसमुच्चय हैं जो M में स्वतंत्र समुच्चय और N में का संघ हैं। सामान्यतः शब्द "संघ" तब प्रारम्भ होता है जब E = F होता है, किंतु यह धारणा आवश्यक नहीं है। यदि E और F असंयुक्त हैं, तो संघ सरल योग है। | ||
* E का उपसमुच्चय M को | |||
* | == अतिरिक्त शब्दावली == | ||
* तत्व जो | मान लीजिए कि M मैट्रोइड है जिसमें E तत्वों का अंतर्निहित समुच्चय है। | ||
* तत्व जो किसी | * E को M का 'ग्राउंड समुच्चय' कहा जा सकता है। इसके तत्वों को M का 'बिंदु' कहा जा सकता है। | ||
* | * E का उपसमुच्चय M को विस्तारित करता है यदि इसका समापन E है। समुच्चय को बंद समुच्चय K तक विस्तारित कहा जाता है यदि इसका समापन K है। | ||
* ''M'' का विभाजक ''E'' का उपसमुच्चय ''S'' इस प्रकार है <math>r(S) + r(E-S) = r(M)</math> | * मैट्रोइड का घेरा उसके सबसे छोटे परिपथ या आश्रित समुच्चय का आकार है। | ||
* मैट्रोइड जिसे दो | * तत्व जो M का एकल-तत्व परिपथ बनाता है उसे 'लूप' कहा जाता है। समान रूप से, तत्व लूप है यदि इसका कोई आधार नहीं है।<ref name=Ox13/><ref name=Wh86130>{{harvnb|White|1986|p=130}}</ref> | ||
* | * तत्व जो किसी परिपथ से संबंधित नहीं होता है उसे कोलूप या इस्थमस कहा जाता है। समान रूप से, तत्व कोलूप है यदि वह प्रत्येक आधार से संबंधित है। लूप और कोलूप परस्पर दोहरे हैं।<ref name=Wh86130/> | ||
* मैट्रोइड को [[फ़र्श विधि]] कहा जाता है यदि उसके सभी | *यदि दो-तत्व समुच्चय {f, g} M का परिपथ है, तो f और g,M में 'समानांतर' हैं।<ref name="Ox13" /> | ||
* [[मैट्रोइड पॉलीटोप]] <math>P_M</math> के आधारों के सूचक सदिशों का उत्तल | *मैट्रोइड को सरल कहा जाता है यदि इसमें 1 या 2 तत्वों से युक्त कोई परिपथ नहीं है। अर्थात्, इसमें कोई लूप नहीं है और कोई समानांतर तत्व नहीं है। संयोजक ज्यामिति शब्द का भी प्रयोग किया जाता है।<ref name="Ox13">{{harvnb|Oxley|1992|p=13}}</ref> सभी लूपों को विस्थापित करके और प्रत्येक 2-तत्व परिपथ न रह जाए, अन्य मैट्रॉइड M से प्राप्त साधारण मैट्रोइड को M का 'सरलीकरण' कहा जाता है।<ref name="Ox52">{{harvnb|Oxley|1992|p=52}}</ref> मैट्रोइड सह-सरल है यदि उसका दोहरा मैट्रोइड सरल है।<ref name="Ox347">{{harvnb|Oxley|1992|p=347}}</ref> | ||
* परिपथ के संघ को कभी-कभी M का चक्र कहा जाता है। इसलिए चक्र दोहरे मैट्रोइड के फ्लैट का पूरक है। (यह प्रयोग ग्राफ़ सिद्धांत में चक्र के सामान्य अर्थ के साथ विरोधाभास रखता है।) | |||
* ''M'' का विभाजक ''E'' का उपसमुच्चय ''S'' इस प्रकार है <math>r(S) + r(E-S) = r(M)</math> उचित या गैर-तुच्छ विभाजक है जो न तो E है और न ही रिक्त समुच्चय है।<ref name="Ox128">{{harvnb|Oxley|1992|p=128}}</ref> इरेड्यूसिबल विभाजक अरिक्त विभाजक है जिसमें कोई अन्य अरिक्त विभाजक नहीं होता है। इरेड्यूसिबल सेपरेटर ग्राउंड समुच्चय ''E'' को विभाजित करते हैं। | |||
* मैट्रोइड जिसे दो अरिक्त मैट्रोइड्स के प्रत्यक्ष योग के रूप में नहीं लिखा जा सकता है, या समकक्ष जिसमें कोई उचित विभाजक नहीं है, उसे कनेक्टेड या इरेड्यूसिबल कहा जाता है। मैट्रोइड तभी जुड़ा होता है जब उसका डुअल जुड़ा होता है।<ref name="Wh86110">{{harvnb|White|1986|p=110}}</ref> | |||
* M के अधिकतम इरेड्यूसिबल सबमैट्रोइड को M का 'घटक' कहा जाता है। घटक इरेड्यूसेबल विभाजक के लिए M का प्रतिबंध है, और इसके विपरीत, इरेड्यूसेबल विभाजक के लिए M का प्रतिबंध घटक है। विभाजक घटकों का संघ है।<ref name="Ox128" /> | |||
*मैट्रोइड M को 'फ्रेम मैट्रोइड' कहा जाता है यदि इसका, या जिस मैट्रोइड में यह सम्मिलित है, उसका आधार ऐसा है कि M के सभी बिंदु उन रेखाओं में समाहित हैं जो आधार तत्वों के जोड़े को जोड़ते हैं।<ref>{{cite journal | zbl=0797.05027 | last=Zaslavsky | first=Thomas | title=फ़्रेम मैट्रोइड्स और पक्षपाती ग्राफ़| journal=Eur. J. Comb. | volume=15 | number=3 | pages=303–307 | year=1994 | issn=0195-6698 | doi=10.1006/eujc.1994.1034| doi-access=free }}</ref> | |||
* मैट्रोइड को [[फ़र्श विधि|पेविंग मैट्रोइड]] कहा जाता है यदि उसके सभी परिपथ का आकार कम से कम उसके पद के समान हो।<ref name="Ox26">{{harvnb|Oxley|1992|p=26}}</ref> | |||
* [[मैट्रोइड पॉलीटोप]] <math>P_M</math> के आधारों के सूचक सदिशों का उत्तल <math>M</math> है। | |||
==एल्गोरिदम== | ==एल्गोरिदम== | ||
===[[लालची एल्गोरिदम]]=== | ===[[लालची एल्गोरिदम|ग्रेडी एल्गोरिदम]]=== | ||
[[भारित मैट्रोइड]] मैट्रोइड है जिसमें इसके तत्वों से लेकर | [[भारित मैट्रोइड]] ऐसा मैट्रोइड है जिसमें इसके तत्वों से लेकर अकारात्मक वास्तविक संख्याओं तक फलन होता है। तत्वों के उपसमूह के भार को उपसमूह में तत्वों के भार के योग के रूप में परिभाषित किया गया है। ग्रेडी एल्गोरिथ्म का उपयोग मैट्रोइड के अधिकतम-भार के आधार का परिक्षण करने के लिए किया जा सकता है, रिक्त समुच्चय से प्रारंभ करके और समय में तत्व को बार-बार जोड़कर, प्रत्येक चरण में उन तत्वों के मध्य अधिकतम-भार वाले तत्व का चयन किया जा सकता है जिनके अतिरिक्त स्वतंत्रता को संरक्षित किया जाएगा। संवर्धित समुच्चय का<ref name=Ox63>{{harvnb|Oxley|1992|p=63}}</ref>इस एल्गोरिदम को मैट्रोइड की परिभाषा के विवरण के बारे में कुछ भी जानने की आवश्यकता नहीं है, जब तक कि इसमें [[मैट्रोइड ओरेकल]] के माध्यम से मैट्रोइड तक पहुंच है, यह परीक्षण करने के लिए सबरूटीन है कि कोई समुच्चय स्वतंत्र है या नहीं। | ||
इस अनुकूलन एल्गोरिथ्म का उपयोग मैट्रोइड्स को चिह्नित करने के लिए किया जा सकता है: यदि | इस अनुकूलन एल्गोरिथ्म का उपयोग मैट्रोइड्स को चिह्नित करने के लिए किया जा सकता है: यदि समुच्चय का सदस्य F, जो सबसमुच्चय लेने के अंतर्गत बंद है, जिसमे गुण है कि, इससे कोई अंतर नहीं है कि समुच्चय कैसे भारित होते हैं, ग्रेडी एल्गोरिदम सदस्य में अधिकतम भार समुच्चय पाता है, फिर F मैट्रोइड के स्वतंत्र समुच्चयों का सदस्य होना चाहिए।<ref name=Ox64>{{harvnb|Oxley|1992|p=64}}</ref> | ||
अन्य प्रकार के | |||
अन्य प्रकार के समुच्चयों की अनुमति देने के लिए मैट्रोइड की धारणा को सामान्यीकृत किया गया है, जिस पर [[लालची|ग्रेडी]] एल्गोरिदम इष्टतम समाधान देता है; अधिक जानकारी के लिए ग्रीडॉइड और [[मैट्रोइड एम्बेडिंग]] देखें। | |||
===[[मैट्रोइड विभाजन]]=== | ===[[मैट्रोइड विभाजन]]=== | ||
मैट्रोइड विभाजन समस्या में मैट्रोइड के तत्वों को यथासंभव कुछ स्वतंत्र | मैट्रोइड विभाजन समस्या में मैट्रोइड के तत्वों को यथासंभव कुछ स्वतंत्र समुच्चयों में विभाजित करना है, और मैट्रोइड पैकिंग समस्या यथासंभव अधिक से अधिक असंयुक्त स्पैनिंग समुच्चय का परिक्षण करना है। दोनों को बहुपद समय में समाधान किया जा सकता है, और पद की गणना करने या मैट्रोइड योग में स्वतंत्र समुच्चय के परिक्षण की समस्या को सामान्यीकृत किया जा सकता है। | ||
===[[मैट्रोइड चौराहा]]=== | ===[[मैट्रोइड चौराहा|मैट्रोइड अंत:खंड]]=== | ||
दो या दो से अधिक मैट्रोइड्स का | दो या दो से अधिक मैट्रोइड्स का प्रतिच्छेदन समुच्चयों का सदस्य है जो प्रत्येक मैट्रोइड्स में साथ स्वतंत्र होते हैं। दो मैट्रोइड्स के प्रतिच्छेदन में सबसे बड़ा समुच्चय, या अधिकतम भारित समुच्चय का परिक्षण करने की समस्या बहुपद समय में पाई जा सकती है,<ref>{{Citation |last=Edmonds |first=Jack |title=Submodular Functions, Matroids, and Certain Polyhedra |date=2003 |url=https://doi.org/10.1007/3-540-36478-1_2 |work=Combinatorial Optimization — Eureka, You Shrink!: Papers Dedicated to Jack Edmonds 5th International Workshop Aussois, France, March 5–9, 2001 Revised Papers |series=Lecture Notes in Computer Science |volume=2570 |pages=11–26 |editor-last=Jünger |editor-first=Michael |place=Berlin, Heidelberg |publisher=Springer |language=en |doi=10.1007/3-540-36478-1_2 |isbn=978-3-540-36478-8 |access-date=2022-11-27 |editor2-last=Reinelt |editor2-first=Gerhard |editor3-last=Rinaldi |editor3-first=Giovanni}}</ref>{{Rp|location=(46)}} और कई अन्य महत्वपूर्ण संयोजन अनुकूलन समस्याओं का समाधान प्रदान करता है। उदाहरण के लिए, द्विदलीय ग्राफ़ में [[अधिकतम मिलान|अधिकतम संघ]] को दो विभाजन मैट्रोइड्स को प्रतिच्छेद करने की समस्या के रूप में व्यक्त किया जा सकता है। चूँकि, तीन या अधिक मैट्रोइड्स के प्रतिच्छेदन में सबसे बड़ा समुच्चय एनपी-पूर्ण है। | ||
===मैट्रोइड सॉफ़्टवेयर=== | ===मैट्रोइड सॉफ़्टवेयर=== | ||
मैट्रोइड्स के साथ गणना के लिए दो स्टैंडअलोन प्रणालियाँ | मैट्रोइड्स के साथ गणना के लिए दो स्टैंडअलोन प्रणालियाँ किंगन के [http://userhome.brooklyn.cuny.edu/skingan/software.html ओइड] और ह्लिननी के [http://www.fi.muni.cz/~hlineny/MACEK/ मेसेक] हैं। ये दोनों ओपन सोर्स पैकेज हैं। ओइड मैट्रोइड्स के साथ प्रयोग करने के लिए इंटरैक्टिव, एक्स्टेंसिबल सॉफ्टवेयर प्रणाली है। मैसेक विशेष सॉफ्टवेयर प्रणाली है जिसमें प्रतिनिधित्वयोग्य मैट्रोइड्स के साथ यथोचित कुशल संयोजन संगणना के लिए उपकरण और रूटीन हैं। | ||
दोनों ओपन सोर्स गणित सॉफ्टवेयर | दोनों ओपन सोर्स गणित सॉफ्टवेयर प्रणाली [[SageMath|सेग]] और [[Macaulay2|मैकाले2]] में मेट्रोइड पैकेज सम्मिलित हैं। | ||
==बहुपद अपरिवर्तनीय== | ==बहुपद अपरिवर्तनीय== | ||
ग्राउंड | ग्राउंड समुच्चय E पर परिमित मैट्रोइड M से जुड़े दो विशेष रूप से महत्वपूर्ण बहुपद हैं। प्रत्येक 'मैट्रोइड बहुपद' है, जिसका अर्थ है कि आइसोमोर्फिक मैट्रोइड्स में बहुपद होता है। | ||
===विशेषता बहुपद=== | ===विशेषता बहुपद=== | ||
''M'' का विशिष्ट बहुपद (जिसे कभी-कभी रंगीन बहुपद भी कहा जाता है,<ref name=Wh87127/> | ''M'' का विशिष्ट बहुपद (जिसे कभी-कभी रंगीन बहुपद भी कहा जाता है,<ref name=Wh87127/>चूँकि यह रंगों की गिनती नहीं करता), को परिभाषित किया गया है: | ||
:<math>p_M(\lambda) := \sum_{S \subseteq E} (-1)^{|S|}\lambda^{r(E)-r(S)},</math> | :<math>p_M(\lambda) := \sum_{S \subseteq E} (-1)^{|S|}\lambda^{r(E)-r(S)},</math> | ||
या समकक्ष (जब तक | या समकक्ष (जब तक रिक्त समुच्चय M में बंद है)। | ||
:<math>p_M(\lambda) := \sum_{A} \mu(\emptyset,A) \lambda^{r(E)-r(A)} \ ,</math> | :<math>p_M(\lambda) := \sum_{A} \mu(\emptyset,A) \lambda^{r(E)-r(A)} \ ,</math> | ||
जहां μ मैट्रोइड के ज्यामितीय जाली के मोबियस | जहां μ मैट्रोइड के ज्यामितीय जाली के मोबियस फलन (कॉम्बिनेटरिक्सको दर्शाता है और योग को मैट्रोइड के सभी फ्लैट्स A पर लिया जाता है।<ref name=Wh87120>{{harvnb|White|1987|p=120}}</ref> | ||
जब M, | जब M, ग्राफ G का चक्र मैट्रोइड M(G) है, तो विशेषता बहुपद [[रंगीन बहुपद]] का छोटा सा परिवर्तन है, जो χ<sub>''G''</sub> (λ) = λ<sup>c</sup>''p<sub>M</sub>''<sub>(''G'')</sub> (λ) द्वारा दिया गया है, जहां c, की संख्या है G से जुड़े घटक है। | ||
जब | जब M, ग्राफ़ G का बॉन्ड मैट्रोइड M*(G) है, तो विशेषता बहुपद, G के प्रवाह बहुपद के समान होता है। | ||
जब M ''''R'''<sup>''n''</sup>' (या Fn जहां F कोई क्षेत्र है) में रैखिक हाइपरप्लेन की व्यवस्था A का मैट्रोइड M(A) है, तो व्यवस्था का विशिष्ट बहुपद ''p<sub>A</sub>'' (λ) = λ<sup>''n''−''r''(''M'')</sup>''p<sub>M</sub>'' (λ) द्वारा दिया जाता है। | |||
====बीटा अपरिवर्तनीय==== | ====बीटा अपरिवर्तनीय==== | ||
[[हेनरी क्रैपो (गणितज्ञ)]] (1967) द्वारा प्रस्तुत मैट्रोइड के बीटा अपरिवर्तनीय को व्युत्पन्न के मूल्यांकन के रूप में विशेषता बहुपद | [[हेनरी क्रैपो (गणितज्ञ)]] (1967) द्वारा प्रस्तुत किए गए मैट्रोइड के बीटा अपरिवर्तनीय को व्युत्पन्न के मूल्यांकन के रूप में विशेषता बहुपद P के संदर्भ में व्यक्त किया जा सकता है।<ref name=Wh87123>{{harvnb|White|1987|p=123}}</ref> | ||
:<math> \beta(M) = (-1)^{r(M)-1} p_M'(1) \ </math> | :<math> \beta(M) = (-1)^{r(M)-1} p_M'(1) \ </math> | ||
या | या सरलता पूर्वक<ref name=Wh87124>{{harvnb|White|1987|p=124}}</ref> | ||
:<math> \beta(M) = (-1)^{r(M)} \sum_{X \subseteq E} (-1)^{|X|} r(X) \ . </math> | :<math> \beta(M) = (-1)^{r(M)} \sum_{X \subseteq E} (-1)^{|X|} r(X) \ . </math> | ||
बीटा अपरिवर्तनीय | बीटा अपरिवर्तनीय अनकारात्मक है, और शून्य है यदि केवल M डिस्कनेक्ट हो गया है, या रिक्त है, या लूप है। अन्यथा यह केवल M के फ्लैटों की जाली पर निर्भर करता है। यदि M में कोई लूप और कोलूप नहीं है तो β(M) = β(M)<sup>∗</sup>) होता है। <ref name=Wh87124/> | ||
'''व्हिटनी संख्या''' | |||
प्रथम प्रकार के M के व्हिटनी नंबर की शक्तियों के गुणांक हैं विशेषता बहुपद में <math>\lambda</math> विशेष रूप से, i-वें व्हिटनी संख्या <math>w_i(M)</math> का गुणांक है <math>\lambda^{r(M)-i}</math> और मोबियस फलन मानों का योग है: | |||
:<math>w_i(M) = \sum \{ \mu(\emptyset,A): r(A) = i \},</math> | :<math>w_i(M) = \sum \{ \mu(\emptyset,A): r(A) = i \},</math> | ||
उत्तम पद के फ्लैटों का सारांश दिया गया। ये संख्याएँ संकेत में वैकल्पिक होती हैं, जिससे <math>(-1)^i w_i(M) > 0</math> के लिए <math>0 \leq i \leq r(M).</math> है। | |||
दूसरे प्रकार के '' | |||
दूसरे प्रकार के ''M'' के व्हिटनी नंबर प्रत्येक पद के फ्लैटों की संख्या हैं। वह है, <math>W_i(M)</math> पद-I फ्लैट्स की संख्या है। | |||
दोनों प्रकार के व्हिटनी | दोनों प्रकार के व्हिटनी संख्याएं पहले और दूसरे प्रकार की [[ स्टर्लिंग संख्या |स्टर्लिंग संख्याओं]] को सामान्यीकृत करती हैं, जो पूर्ण ग्राफ के चक्र मैट्रोइड की व्हिटनी संख्याएं और विभाजन जाली के समकक्ष हैं। इनका नाम [[जियान-कार्लो रोटा]] द्वारा मैट्रोइड सिद्धांत के (सह) संस्थापक [[हस्लर व्हिटनी]] के नाम पर रखा गया था। नाम को परिमित श्रेणी वाले आंशिक रूप से क्रमित समुच्चयों के लिए समान संख्याओं तक बढ़ा दिया गया है। | ||
=== | ===टुट्टे बहुपद=== | ||
मैट्रोइड का | मैट्रोइड का टुट्टे बहुपद, ''T''<sub>''M''</sub>(x,y), विशेषता बहुपद को दो चरों के लिए सामान्यीकृत करता है। यह इसे अधिक संयोजनात्मक व्याख्याएँ देता है, और इसे द्वैत गुण भी देता है | ||
:<math>T_{M^*}(x,y) = T_M(y,x),</math> | :<math>T_{M^*}(x,y) = T_M(y,x),</math> | ||
जो | जो M के गुणों और M* के गुणों के मध्य कई द्वंद्वों को दर्शाता है। टुट्टे बहुपद की परिभाषा है: | ||
:<math>T_M(x,y) = \sum_{S \subseteq E} (x-1)^{r(M)-r(S)}(y-1)^{|S|-r(S)}.</math> | :<math>T_M(x,y) = \sum_{S \subseteq E} (x-1)^{r(M)-r(S)}(y-1)^{|S|-r(S)}.</math> | ||
यह | यह टुट्टे बहुपद को कॉपद-शून्यता या पद उत्पन्न करने वाले बहुपद के मूल्यांकन के रूप में व्यक्त करता है,<ref name="Wh87126">{{harvnb|White|1987|p=126}}</ref> | ||
:<math>R_M(u,v) = \sum_{S\subseteq E} u^{r(M)-r(S)}v^{|S|-r(S)}.</math> | :<math>R_M(u,v) = \sum_{S\subseteq E} u^{r(M)-r(S)}v^{|S|-r(S)}.</math> | ||
इस परिभाषा से यह देखना | इस परिभाषा से यह देखना सरल है कि विशेषता बहुपद, साधारण कारक तक, T<sub>''M''</sub> का मूल्यांकन है, विशेष रूप से, | ||
:<math>p_M(\lambda) = (-1)^{r(M)} T_M(1-\lambda,0). </math> | :<math>p_M(\lambda) = (-1)^{r(M)} T_M(1-\lambda,0). </math> | ||
अन्य परिभाषा आंतरिक और बाह्य गतिविधियों और आधारों के योग के संदर्भ में है, जो इस तथ्य को दर्शाती है कि T(1,1) आधारों की संख्या है।<ref name=Wh92188>{{harvnb|White|1992|p=188}}</ref> यह, जो कम उपसमुच्चय का योग है | अन्य परिभाषा आंतरिक और बाह्य गतिविधियों और आधारों के योग के संदर्भ में है, जो इस तथ्य को दर्शाती है कि T(1,1) आधारों की संख्या है।<ref name="Wh92188">{{harvnb|White|1992|p=188}}</ref> यह, जो कम उपसमुच्चय का योग है किंतु इसमें अधिक जटिल शब्द हैं, टुट्टे की मूल परिभाषा थी। | ||
विलोपन और संकुचन द्वारा पुनरावर्तन के संदर्भ में | विलोपन और संकुचन द्वारा पुनरावर्तन के संदर्भ में परिभाषा है।<ref name="Wh86260">{{harvnb|White|1986|p=260}}</ref> विलोपन-संकुचन की पहचान है: | ||
:<math>F(M) = F(M-e)+F(M/e)</math> कब <math>e</math> न तो लूप है और न ही कोलूप। | :<math>F(M) = F(M-e)+F(M/e)</math> कब <math>e</math> न तो लूप है और न ही कोलूप। | ||
मैट्रोइड्स का अपरिवर्तनीय ( | मैट्रोइड्स का अपरिवर्तनीय (अर्थात, फलन जो आइसोमोर्फिक मैट्रोइड्स पर समान मान लेता है) इस रिकर्सन और गुणक स्थिति को संतुष्ट करता है: | ||
:<math>F(M\oplus M') = F(M) F(M')</math> | :<math>F(M\oplus M') = F(M) F(M')</math> | ||
टुट्टे-ग्रोथेंडिक अपरिवर्तनीय | कहा जाता है कि यह टुट्टे-ग्रोथेंडिक अपरिवर्तनीय है।<ref name="Wh87126" />टुट्टे बहुपद इस प्रकार का सबसे सामान्य अपरिवर्तनीय है; अर्थात्, टुट्टे बहुपद टुट्टे-ग्रोथेंडिक अपरिवर्तनीय है और ऐसा प्रत्येक अपरिवर्तनीय टुट्टे बहुपद का मूल्यांकन है।<ref name="Wh87127">{{harvnb|White|1987|p=127}}</ref> | ||
टुट्टे बहुपद | |||
ग्राफ का टुट्टे बहुपद ''T<sub>G</sub>'' इसके चक्र मैट्रोइड का टुट्टे बहुपद ''T<sub>M</sub>''<sub>(''G'')</sub> है। | |||
== अनंत मैट्रोइड्स == | == अनंत मैट्रोइड्स == | ||
अनंत मैट्रोइड्स का सिद्धांत परिमित मैट्रोइड्स की तुलना में | अनंत मैट्रोइड्स का सिद्धांत परिमित मैट्रोइड्स की तुलना में अधिक जटिल है और इसका अपना विषय है। लंबे समय से, कठिनाई यह रही है कि कई उचित और उपयोगी परिभाषाएँ थीं, जिनमें से कोई भी परिमित मैट्रोइड सिद्धांत के सभी महत्वपूर्ण विषयों को पकड़ती नहीं थी। उदाहरण के लिए, अनंत मैट्रोइड्स की धारणा में आधार, परिपथ और द्वंद्व को साथ रखना कठिन प्रतीत होता है। | ||
अनंत मैट्रोइड की सबसे सरल परिभाषा परिमित | अनंत मैट्रोइड की सबसे सरल परिभाषा परिमित पद की आवश्यकता है; अर्थात्, E का पद परिमित है। यह सिद्धांत परिमित मैट्रोइड के समान है, इस तथ्य के कारण द्वैत की विफलता को छोड़कर कि परिमित पद के अनंत मैट्रोइड के दोहरे में परिमित पद नहीं है। परिमित-पद मैट्रोइड्स में परिमित-आयामी वेक्टर रिक्त स्थान और परिमित पारगमन डिग्री के क्षेत्र (गणित) विस्तार के किसी भी उपसमूह सम्मिलित हैं। | ||
अगला सरलतम अनंत सामान्यीकरण फ़िनिटरी मैट्रोइड्स है, जिसे [[प्रीजियोमेट्री (मॉडल सिद्धांत)]] के रूप में भी जाना जाता है। संभवतः अनंत ग्राउंड | अगला सरलतम अनंत सामान्यीकरण फ़िनिटरी मैट्रोइड्स है, जिसे [[प्रीजियोमेट्री (मॉडल सिद्धांत)]] के रूप में भी जाना जाता है। संभवतः अनंत ग्राउंड समुच्चय वाला मैट्रोइड परिमित होता है यदि उसमें वह गुण हो, | ||
:<math>x \in \operatorname{cl}(Y)\ \Leftrightarrow \ \text{ there is a finite set } Y' \subseteq Y \text{ such that } x \in \operatorname{cl}(Y').</math> | :<math>x \in \operatorname{cl}(Y)\ \Leftrightarrow \ \text{ there is a finite set } Y' \subseteq Y \text{ such that } x \in \operatorname{cl}(Y').</math> | ||
समान रूप से, प्रत्येक आश्रित समुच्चय में परिमित आश्रित समुच्चय होता है। | समान रूप से, प्रत्येक आश्रित समुच्चय में परिमित आश्रित समुच्चय होता है। उदाहरण अनंत-आयामी वेक्टर रिक्त स्थान के उपसमुच्चय की रैखिक निर्भरता हैं (किंतु हिल्बर्ट अंतरिक्ष और बानाच रिक्त स्थान क जैसे अनंत निर्भरता नहीं), और संभवतः अनंत पारगमन डिग्री के क्षेत्र विस्तार के उपसमुच्चय में [[बीजगणित|बीजगणितीय]] निर्भरता पुनः, फ़िनिटरी मैट्रोइड का वर्ग स्व-द्वैत नहीं है, क्योंकि फ़ाइनिटरी मैट्रोइड का द्वैत एकात्मक नहीं है।[[मॉडल सिद्धांत]] में फ़िनिटरी अनंत मैट्रोइड्स का अध्ययन किया जाता है, जो बीजगणित के साथ स्थिर संबंधों के साथ [[गणितीय तर्क]] की शाखा है। | ||
उदाहरण अनंत-आयामी वेक्टर रिक्त स्थान के | |||
[[मॉडल सिद्धांत]] में फ़िनिटरी अनंत मैट्रोइड्स का अध्ययन किया जाता है, जो बीजगणित के साथ | |||
1960 | 1960 दशक के अंत में मैट्रोइड सिद्धांतकारों ने अधिक सामान्य धारणा की आवश्यकता जो परिमित मैट्रोइड के विभिन्न विषयों को भागित करती है और उनके द्वंद्व को सामान्य बनाती है। इस अनुशय के उत्तर में अनंत मैट्रोइड्स की कई धारणाओं को परिभाषित किया गया, किंतु प्रश्न खुला रहा। डी.ए. द्वारा परिक्षण किये गए दृष्टिकोणों में से हिग्स को बी-मैट्रोइड्स के रूप में जाना जाने लगा और 1960 और 1970 दशक में हिग्स, ऑक्सले और अन्य लोगों द्वारा इसका अध्ययन किया गया। ब्रुहन, डायस्टेल और क्रिसेल एट अल के परिणाम के अनुसार (2013), यह समस्या का समाधान करता है: स्वतंत्र रूप से एक ही धारणा पर पहुंचते हुए, उन्होंने स्वतंत्रता, आधार, परिपथ, क्लोजर और पद के संदर्भ में स्वयंसिद्ध की पांच समकक्ष प्रणालियां प्रदान कीं। बी-मैट्रोइड्स का द्वंद्व उन द्वंद्वों को सामान्यीकृत करता है जिन्हें अनंत ग्राफ़ में देखा जा सकता है। | ||
स्वतंत्रता के सिद्धांत इस प्रकार हैं: | स्वतंत्रता के सिद्धांत इस प्रकार हैं: | ||
# | # रिक्त समुच्चय स्वतंत्र है। | ||
# स्वतंत्र समुच्चय का प्रत्येक उपसमुच्चय स्वतंत्र होता है। | # स्वतंत्र समुच्चय का प्रत्येक उपसमुच्चय स्वतंत्र होता है। | ||
# प्रत्येक अधिकतम | # प्रत्येक अधिकतम (समुच्चय समावेशन के अंतर्गत) स्वतंत्र समुच्चय I और अधिकतम स्वतंत्र समुच्चय J के लिए, वहाँ है <math>x\in J \smallsetminus I</math> ऐसा है कि <math>I\cup\{x\}</math> स्वतंत्र है। | ||
# आधार स्थान के प्रत्येक उपसमुच्चय X के लिए, X के प्रत्येक स्वतंत्र उपसमुच्चय I को X के अधिकतम स्वतंत्र उपसमुच्चय तक बढ़ाया जा सकता है। | # आधार स्थान के प्रत्येक उपसमुच्चय X के लिए, X के प्रत्येक स्वतंत्र उपसमुच्चय I को X के अधिकतम स्वतंत्र उपसमुच्चय तक बढ़ाया जा सकता है। | ||
| Line 255: | Line 269: | ||
==इतिहास== | ==इतिहास== | ||
मैट्रोइड सिद्धांत | मैट्रोइड सिद्धांत {{harvs|last=Whitney|first=Hassler|authorlink=हस्लर व्हिटनी|year=1935|txt}} द्वारा प्रस्तुत किया गया था। इसका परिक्षण भी [[ताकेओ नाकासावा]] ने स्वतंत्र रूप से की थी, जिनके कार्य को कई वर्षों तक भुला दिया गया था {{harv|निशिमुरा और|कुरोदा |2009}}। | ||
अपने मौलिक | अपने मौलिक दस्तावेज में, व्हिटनी ने स्वतंत्रता के लिए दो सिद्धांत प्रदान किए, और इन सिद्धांतों का पालन करने वाली किसी भी संरचना को मैट्रोइड के रूप में परिभाषित किया। (चूँकि यह संभवतः निहित था, उन्होंने स्वयंसिद्ध को सम्मिलित नहीं किया था जिसमें कम से कम उपसमुच्चय के स्वतंत्र होने की आवश्यकता थी।) उनका मुख्य अवलोकन यह था कि ये सिद्धांत स्वतंत्रता का अमूर्तन प्रदान करते हैं जो ग्राफ़ और मैट्रिक्स दोनों के लिए सामान्य है। इस कारण से, मैट्रोइड सिद्धांत में उपयोग किए गए कई शब्द रैखिक बीजगणित या ग्राफ सिद्धांत में उनके अनुरूप अवधारणाओं के समान हैं। | ||
( | |||
उनका मुख्य अवलोकन यह था कि ये सिद्धांत स्वतंत्रता का अमूर्तन प्रदान करते हैं जो ग्राफ़ और मैट्रिक्स दोनों के लिए सामान्य है। | |||
इस | |||
व्हिटनी द्वारा मैट्रोइड्स के बारे में | व्हिटनी द्वारा मैट्रोइड्स के बारे में प्रथम बार लिखने के लगभग पश्चात {{harvs|last=Mac Lane|first=Saunders|authorlink=Saunders Mac Lane|year=1936|txt}} द्वारा मैट्रोइड्स और [[प्रक्षेप्य ज्यामिति]] के संबंध पर महत्वपूर्ण लेख लिखा गया था। एक वर्ष पश्चात, {{harvs|last=van der Waerden|first=B. L.|authorlink=Bartel Leendert van der Waerden|year=1937|txt}} ने आधुनिक बीजगणित पर अपनी क्लासिक पाठ्यपुस्तक में बीजीय और रैखिक निर्भरता के मध्य समानताएं देखीं। | ||
1940 के दशक में [[रिचर्ड राडो]] ने [[ट्रांसवर्सल (कॉम्बिनेटरिक्स)]] को ध्यान में रखते हुए | 1940 के दशक में [[रिचर्ड राडो]] ने [[ट्रांसवर्सल (कॉम्बिनेटरिक्स)]] सिद्धांत को ध्यान में रखते हुए "स्वतंत्रता प्रणाली" के नाम से सिद्धांत विकसित किया, जहां विषय के लिए उनका नाम अभी भी कभी-कभी उपयोग किया जाता है। | ||
1950 के दशक में डब्ल्यू. टी. | 1950 के दशक में डब्ल्यू. टी. टुट्टे मैट्रोइड सिद्धांत में अग्रणी व्यक्ति बन गए, यह पद उन्होंने कई वर्षों तक स्थिर रखा। उनका योगदान प्रचुर मात्रा में था, जिसमें बहिष्कृत माइनर्स द्वारा बाइनरी, नियमित और ग्राफिक मैट्रोइड्स का लक्षण वर्णन सम्मिलित था; रेगुलर-मैट्रोइड अभ्यावेदन प्रमेय; श्रृंखला समूहों और उनके मैट्रोइड्स का सिद्धांत; और अपने कई परिणामों को सिद्ध करने के लिए उन्होंने जिन उपकरणों का उपयोग किया, पथ प्रमेय और टुट्टे होमोटॉपी प्रमेय (देखें, उदाहरण के लिए, {{harvnb|टुट्टे|1965}}), जो इतने जटिल हैं कि पश्चात के सिद्धांतकारों को उपयोग की आवश्यकता को समाप्त करने के लिए बड़ी परेशानी का सामना करना होता है उन्हें प्रमाणों में (उत्तम उदाहरण ए.एम.एच. जेरार्ड्स का टुट्टे के नियमित मैट्रोइड्स के लक्षण वर्णन का संक्षिप्त प्रमाण (1989) है।) | ||
{{harvs|first=Henry|last=Crapo|author-link= | {{harvs|first=Henry|last=Crapo|author-link=हेनरी क्रैपो (गणितज्ञ)|year=1969|txt}} और {{harvs|first=Thomas|last=Brylawski|author-link=Thomas H. Brylawski|year=1972|txt}} ने मैट्रोइड्स टुट्टे के "डाइक्रोमेट" को सामान्यीकृत किया, ग्राफिक बहुपद जिसे अब टुट्टे बहुपद (क्रैपो द्वारा नामित) के रूप में जाना जाता है। उनके कार्य के पश्चात वर्तमान में (विशेष रूप से 2000 के दशक में) कागजात की बाढ़ आ गई है- चूँकि ग्राफ के टुट्टे बहुपद के समान नहीं है। | ||
1976 में [[डोमिनिक वेल्श]] ने मैट्रोइड सिद्धांत पर | 1976 में [[डोमिनिक वेल्श]] ने मैट्रोइड सिद्धांत पर प्रथम व्यापक पुस्तक प्रकाशित की। | ||
नियमित मैट्रोइड्स के लिए पॉल सेमुर (गणितज्ञ) का अपघटन प्रमेय ( | नियमित मैट्रोइड्स के लिए पॉल सेमुर (गणितज्ञ) का अपघटन प्रमेय (1980) 1970 और 1980 के दशक का सबसे महत्वपूर्ण और प्रभावशाली कार्य था। {{harvtxt|Kahn|Kung|1982}} के अन्य मौलिक योगदान द्वारा दिखाया गया कि प्रोजेक्टिव ज्यामिति और [[ डाउलिंग ज्यामिति |डाउलिंग ज्यामिति]] मैट्रोइड सिद्धांत में इतनी महत्वपूर्ण भूमिका क्यों निभाते हैं। | ||
इस समय तक कई अन्य महत्वपूर्ण योगदानकर्ता थे, | इस समय तक कई अन्य महत्वपूर्ण योगदानकर्ता थे, किंतु टुट्टे के बाइनरी मैट्रोइड्स के लक्षण वर्णन के [[ज्योफ व्हिटल]] के टर्नरी मैट्रोइड्स के विस्तार का उल्लेख करना नहीं भूलना चाहिए जो कि तर्कसंगत {{harv|Whittle|1995}} पर प्रतिनिधित्व करने योग्य हैं, संभवतः 1990 के दशक का सबसे बड़ा एकल योगदान है। वर्तमान अवधि में (2000 के निकट से) [[जिम गिलेन]], जेरार्ड्स, व्हिटल और अन्य का मैट्रोइड माइनर्स प्रोजेक्ट, जो सीमित क्षेत्र में प्रतिनिधित्व करने योग्य मैट्रोइड्स का अनुसरण करने का प्रयास करता है, रॉबर्टसन-सेमुर ग्राफ माइनर्स प्रोजेक्ट की सफलता (रॉबर्टसन देखें) -सीमोर प्रमेय), ने मैट्रोइड्स के संरचना सिद्धांत में पर्याप्त प्रगति की है। कई अन्य लोगों ने भी मैट्रोइड सिद्धांत के उस भाग में योगदान दिया है, जो (21वीं दशक पहले और दूसरे दशकों में) प्रगति कर रहा है। | ||
==शोधकर्ता== | ==शोधकर्ता== | ||
मैट्रोइड्स के अध्ययन | मैट्रोइड्स के अध्ययन में अग्रणी गणितज्ञों में ताकेओ नाकासावा,{{sfnp|Nishimura|Kuroda|2009}} सॉन्डर्स मैक लेन, रिचर्ड राडो, डब्ल्यू. टी. टुट्टे, बी. एल. वैन डेर वेर्डन और हस्लर व्हिटनी सम्मिलित हैं। अन्य प्रमुख योगदानकर्ताओं में [[जैक एडमंड्स]], जिम गिलेन, [[यूजीन लॉलर]], लास्ज़लो लोवाज़, जियान-कार्लो रोटा, पी. डी. सेमुर और डोमिनिक वेल्श सम्मिलित हैं। | ||
अन्य प्रमुख योगदानकर्ताओं में [[जैक एडमंड्स]], जिम गिलेन, [[यूजीन लॉलर]], लास्ज़लो लोवाज़, जियान-कार्लो रोटा, | |||
==यह भी देखें== | ==यह भी देखें== | ||
*[[एंटीमैट्रोइड]] | *[[एंटीमैट्रोइड]] | ||
* [[कॉक्सेटर मैट्रोइड]] | * [[कॉक्सेटर मैट्रोइड|कॉक्समुच्चयर मैट्रोइड]] | ||
* [[ओरिएंटेड मैट्रोइड]] | * [[ओरिएंटेड मैट्रोइड]] | ||
* प्रीजियोमेट्री (मॉडल सिद्धांत) | * प्रीजियोमेट्री (मॉडल सिद्धांत) | ||
* [[पॉलीमेट्रोइड]] | * [[पॉलीमेट्रोइड]] | ||
* | * ग्रेडी | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
| Line 344: | Line 353: | ||
* {{SpringerEOM|title=Matroid}} | * {{SpringerEOM|title=Matroid}} | ||
* Kingan, Sandra : [http://userhome.brooklyn.cuny.edu/skingan/matroids/ | * Kingan, Sandra : [http://userhome.brooklyn.cuny.edu/skingan/matroids/ मेट्रोइड theory]. A large bibliography of मेट्रोइड papers, मेट्रोइड software, and links. | ||
* Locke, S. C. : [http://euler.math.fau.edu/locke/Greedy.htm Greedy Algorithms]. | * Locke, S. C. : [http://euler.math.fau.edu/locke/Greedy.htm Greedy Algorithms]. | ||
* Pagano, Steven R. : [http://www.math.binghamton.edu/zaslav/Pagano/Matridx.htm | * Pagano, Steven R. : [http://www.math.binghamton.edu/zaslav/Pagano/Matridx.htm मेट्रोइडs and Signed Graphs]. | ||
* Mark Hubenthal: [https://web.archive.org/web/20100812232232/http://www.math.washington.edu/~hubenjm/matroid2.pdf A Brief Look At | * Mark Hubenthal: [https://web.archive.org/web/20100812232232/http://www.math.washington.edu/~hubenjm/matroid2.pdf A Brief Look At मेट्रोइडs] ([[PDF]]) (contain proofs for statements of this article) | ||
* James Oxley : [https://www.math.lsu.edu/~oxley/survey4.pdf What is a | * James Oxley : [https://www.math.lsu.edu/~oxley/survey4.pdf What is a मेट्रोइड?] (PDF) | ||
* Neil White : [https://books.google.com/books?id=uD2H-RAcBpwC&dq=greedoid+theory&pg=PP1 | * Neil White : [https://books.google.com/books?id=uD2H-RAcBpwC&dq=greedoid+theory&pg=PP1 मेट्रोइड Applications] | ||
{{Authority control}} | {{Authority control}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:CS1]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:Created On 30/06/2023]] | [[Category:Created On 30/06/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Template SpringerEOM with broken ref|T]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:बंद करने वाले ऑपरेटर]] | |||
[[Category:मैट्रोइड सिद्धांत| मैट्रोइड सिद्धांत]] | |||
[[Category:सेट के परिवार]] | |||
Latest revision as of 18:02, 16 July 2023
साहचर्य में, गणित की शाखा, मैट्रोइड संरचना है जो सदिश स्थानों में रैखिक स्वतंत्रता की धारणा को अमूर्त और सामान्यीकृत करती है। मैट्रोइड को स्वयंसिद्ध प्रणाली के रूप में परिभाषित करने की कई समकक्ष विधि हैं, सबसे महत्वपूर्ण हैं: स्वतंत्र समुच्चय; आधार या परिपथ; पद फलन; बंद करने वाले ऑपरेटर; और बंद समुच्चय या फ्लैट है। आंशिक रूप से क्रमित समुच्चयों की भाषा में, परिमित सरल मैट्रोइड ज्यामितीय जाली के समान है।
मैट्रोइड सिद्धांत बड़े पैमाने पर रैखिक बीजगणित और ग्राफ सिद्धांत दोनों की शब्दावली से उधार लेता है, मुख्यतः क्योंकि यह इन क्षेत्रों में केंद्रीय महत्व की विभिन्न धारणाओं का सार है। मैट्रोइड्स ने ज्यामिति, टोपोलॉजी, संयुक्त अनुकूलन, नेटवर्क सिद्धांत और कोडिंग सिद्धांत में अनुप्रयोग पाया है।[1][2]
परिभाषा
(परिमित) मैट्रोइड को परिभाषित करने के लिए कई क्रिप्टोमोर्फिज्म विधि हैं।[3]
स्वतंत्र समुच्चय
स्वतंत्रता की दृष्टि से, परिमित मैट्रोइड जोड़ी है , जहाँ परिमित समुच्चय है (जिसे ग्राउंड समुच्चय कहा जाता है) और के उपसमुच्चय का सदस्य है (स्वतंत्र समुच्चय कहा जाता है) निम्नलिखित गुणों के लिए निम्नलिखित है:[4]
- (I1) रिक्त समुच्चय स्वतंत्र है,
- (I2) स्वतंत्र समुच्चय का प्रत्येक उपसमुच्चय स्वतंत्र होता है, अर्थात प्रत्येक के लिए , यदि तब इसे कभी-कभी वंशानुगत गुण, या नीचे की ओर बंद गुण कहा जाता है।
- (I3) यदि और दो स्वतंत्र समुच्चय हैं (अर्थात्, प्रत्येक समुच्चय स्वतंत्र है) और में इससे अधिक तत्व हैं , तो वहाँ उपस्तिथ है ऐसा है कि में है इसे कभी-कभी वृद्धि गुण या स्वतंत्र समुच्चय विनिमय गुण कहा जाता है।
पसमाधाने दो गुण संयुक्त संरचना को परिभाषित करते हैं जिसे स्वतंत्रता प्रणाली (या अमूर्त सरलीकृत परिसर) के रूप में जाना जाता है। वास्तव में, (I2) मानते हुए, गुण (I1) इस तथ्य के समान है कि कम से कम उपसमुच्चय स्वतंत्र है, अर्थात, है।
आधार और परिपथ
ग्राउंड समुच्चय का उपसमुच्चय जो स्वतंत्र नहीं है उसे आश्रित कहते हैं। अधिकतम स्वतंत्र समुच्चय—अर्थात स्वतंत्र समुच्चय जो किसी भी तत्व को जोड़ने पर निर्भर हो जाता है -को मैट्रोइड के लिए आधार कहा जाता है। मैट्रोइड में परिपथ का न्यूनतम आश्रित उपसमुच्चय है - अर्थात, आश्रित समुच्चय जिसके सभी उचित उपसमुच्चय स्वतंत्र हैं। शब्दावली इसलिए उत्पन्न होती है क्योंकि ग्राफ़िक मैट्रोइड के परिपथ संबंधित ग्राफ़ में चक्र होते हैं।[4]
मैट्रोइड के आश्रित समुच्चय, आधार, या परिपथ पूर्ण रूप से मैट्रोइड की विशेषता बताते हैं: समुच्चय स्वतंत्र है यदि यह निर्भर नहीं है, यदि केवल आधार का उपसमुच्चय है, और यदि ऐसा होता है इसमें कोई परिपथ नहीं है, आश्रित समुच्चयों, आधारों और परिपथों के संग्रह में प्रत्येक में सरल गुण होते हैं जिन्हें मैट्रोइड के लिए सिद्धांतों के रूप में लिया जा सकता है। उदाहरण के लिए, कोई मैट्रोइड को परिभाषित कर सकता है जोड़ी बनने के लिए , जहाँ पूर्व के जैसे परिमित समुच्चय है के उपसमुच्चय का संग्रह है , जिसे निम्नलिखित गुणों के साथ आधार कहा जाता है:[4]
- (बी1) अरिक्त है।
- (बी2) यदि और के विशिष्ट सदस्य हैं और , तो वहां तत्व उपस्तिथ है ऐसा है कि इस गुण को आधार विनिमय गुण कहा जाता है।
यह उस आधार विनिमय गुण से चलता है जिसका कोई सदस्य नहीं है दूसरे का उचित उपसमुच्चय हो सकता है।
पद फलन
यह मैट्रोइड सिद्धांत का मूल परिणाम है, जो रैखिक बीजगणित में आधारों के समान प्रमेय के सरलता से अनुरूप है, कि मैट्रोइड के कोई भी दो आधार तत्वों की संख्या समान है। इस संख्या को मैट्रोइड पद कहा जाता है यदि मैट्रोइड प्रारंभ है , और का उपसमुच्चय है , फिर मैट्रोइड प्रारंभ के उपसमूह पर विचार करके परिभाषित किया जा सकता है को स्वतंत्र होना चाहिए यदि स्वतंत्र है यह हमें सबमैट्रोइड्स और किसी भी उपसमुच्चय के पद के बारे में बात करने की अनुमति देता है उपसमुच्चय का पद मैट्रोइड पद द्वारा दिया गया है मैट्रोइड का, जिसमें निम्नलिखित गुण हैं:[4]
(R1) पद फलन का मान सदैव अनकारात्मक पूर्णांक होता है।
- (R2) किसी भी उपसमुच्चय के लिए , अपने पास है
- (R3) किन्हीं दो उपसमुच्चयों के लिए , अपने पास: अर्थात पद सबमॉड्यूलर फलन है।
- (R4) किसी भी समुच्चय के लिए और तत्व , अपने पास: है, पसमाधानी असमानता से यह अधिक सामान्यतः इस प्रकार है कि, यदि , तब अर्थात्, पद मोनोटोनिक फलन है।
इन गुणों का उपयोग परिमित मैट्रोइड की वैकल्पिक परिभाषाओं के रूप में किया जा सकता है: यदि इन गुणों को संतुष्ट करता है, फिर मैट्रोइड के स्वतंत्र समुच्चय समाप्त हो जाते हैं उन उपसमुच्चय के रूप में परिभाषित किया जा सकता है का के साथ आंशिक रूप से क्रमबद्ध समुच्चयों की भाषा में, ऐसी मैट्रोइड संरचना ज्यामितीय जाली के समान होती है जिसके तत्व उपसमुच्चय होते हैं आंशिक रूप से समावेशन द्वारा क्रमबद्ध किया गया।
का अंतर उपसमुच्चय की शून्यता कसमाधानाती है यह उन तत्वों की न्यूनतम संख्या है जिन्हें विस्थापित किया जाना चाहिए स्वतंत्र समुच्चय प्राप्त करने के लिए की अशक्तता में को शून्यता कहा जाता है के अंतर को कभी-कभी उपसमुच्चय का कॉरैंक भी कहा जाता है।
क्लोजर ऑपरेटर
परिमित समुच्चय पर मैट्रोइड को , पद फलन के साथ उपरोक्तानुसार समापन (या अवधि) उपसमुच्चय का का समुच्चय है।
यह क्लोजर ऑपरेटर को परिभाषित करता है जहाँ निम्नलिखित गुणों के साथ पावर सेट को दर्शाता है:
- (C1) सभी उपसमुच्चय के लिए का , है।
- (C2) सभी उपसमुच्चय के लिए का , है।
- (C3) सभी उपसमुच्चय के लिए और का के साथ , है।
- (C4) सभी तत्वों के लिए , और का और सभी उपसमुच्चय का , यदि तब है।
इनमें से पसमाधाने तीन गुण क्लोजर ऑपरेटर के परिभाषित गुण हैं। चौथे को कभी-कभी मैक लेन-अर्नेस्ट स्टीनिट्ज़ विनिमय गुण कहा जाता है। इन गुणों को मैट्रोइड की परिभाषा के रूप में लिया जा सकता है: प्रत्येक फलन जो इन गुणों का पालन करता है वह मैट्रोइड निर्धारित करता है।[4]
फ्लैट
समुच्चय जिसका समापन स्वयं के समान होता है उसे बंद कहा जाता है, या मैट्रोइड का फ्लैट या उपस्थान है।[5] समुच्चय को बंद कर दिया जाता है यदि वह अपनी पद के लिए अधिकतम तत्व है, जिसका अर्थ है कि समुच्चय में किसी अन्य तत्व को जोड़ने से पद में वृद्धि होगी। मैट्रोइड के बंद समुच्चय को कवरिंग विभाजन गुण की विशेषता होती है:
- (F1) संपूर्ण बिंदु समुच्चय बन्द है।
- (F2) यदि और फ्लैट हैं फ्लैट है।
- (F3) यदि समतल है, तो प्रत्येक तत्व फ्लैट में है वह कवर (तात्पर्य है कि ठीक से सम्मिलित करना है किंतु कोई फ्लैट नहीं है मध्य में और ) है।
कक्षा समुच्चय समावेशन द्वारा आंशिक रूप से क्रमबद्ध सभी फ्लैटों का मैट्रोइड जाली बनाता है। इसके विपरीत, प्रत्येक मैट्रोइड जाली अपने समुच्चय पर मैट्रोइड बनाता है निम्नलिखित क्लोजर ऑपरेटर के अंतर्गत परमाणुओं के (ऑर्डर सिद्धांत) समुच्चय के लिए जुड़ने के साथ परमाणुओं का है:
- .
इस मैट्रोइड के फ्लैट जाली के तत्वों के साथ युग्मित होता हैं; जाली तत्व के अनुरूप फ्लैट समुच्चय है:
- .
इस प्रकार, इस मैट्रोइड के फ्लैटों की जाली स्वाभाविक रूप से आइसोमोर्फिक है।
हाइपरप्लेन
पद के मेट्रोइड में , पद का फ्लैट को हाइपरप्लेन कहा जाता है (हाइपरप्लेन को कोटम या सह-बिंदु भी कहा जाता है।) ये अधिकतम उचित फ्लैट हैं; अर्थात, हाइपरप्लेन का एकमात्र उप-समुच्चय जो फ्लैट भी है, समुच्चय मैट्रोइड के सभी तत्वों की समतुल्य परिभाषा यह है कि कोटोम का उपसमुच्चय है जो M तक नहीं विस्तारित है, किंतु ऐसा है कि इसमें कोई अन्य तत्व जोड़ने से स्पैनिंग समुच्चय बन जाता है।[6]
सदस्य मैट्रोइड के हाइपरप्लेन के में निम्नलिखित गुण होते हैं, जिन्हें मैट्रोइड के स्वयंसिद्धीकरण के रूप में लिया जा सकता है:[6]
(H1) भिन्न-भिन्न समुच्चय उपस्तिथ नहीं हैं और में के साथ . अर्थात्, हाइपरप्लेन स्पर्नर सदस्य बनाते हैं।
- (H2) प्रत्येक के लिए और विशिष्ट के साथ , वहां उपस्तिथ है साथ है।
ग्राफोइड्स
जॉर्ज जे. मिन्टी (1966) ने ग्राफॉइड को त्रिक के रूप में परिभाषित किया जिसमें और के अरिक्त उपसमुच्चय की कक्षाएं हैं ऐसा है कि
- (G1) का कोई तत्व नहीं (जिसे परिपथ कहा जाता है) में सम्मिलित है।
- (G2) का कोई तत्व नहीं (जिसे को-परिपथ कहा जाता है) में सम्मिलित है।
- (G3) कोई समुच्चय नहीं है और समुच्चय करें बिल्कुल तत्व में प्रतिच्छेद करता है, और
- (G4) जब भी उपसमुच्चय के असंयुक्त संघ के रूप में दर्शाया गया है के साथ (सिंगलटन समुच्चय), फिर या तो का अस्तित्व इस प्रकार है या ऐसे उपस्तिथ है।
उन्होंने सिद्ध कर दिया कि जिसके लिए मैट्रोइड है परिपथ का वर्ग है और सह-परिपथ का वर्ग है। इसके विपरीत, यदि और मैट्रोइड के परिपथ और सह-परिपथ वर्ग हैं ग्राउंड समुच्चय के साथ , तब ग्राफ़ॉइड है. इस प्रकार, ग्राफ़ॉइड्स मैट्रोइड्स का स्व-दोहरा क्रिप्टोमोर्फिक स्वयंसिद्धीकरण देते हैं।
उदाहरण
मुफ़्त मैट्रोइड
मान लीजिये परिमित समुच्चय के सभी उपसमुच्चय का समुच्चय मैट्रोइड के स्वतंत्र समुच्चय को परिभाषित करता है। इस को मुफ़्त मैट्रोइड ओवर कहा जाता है।
यूनिफ़ॉर्म मैट्रिक्स
मान लीजिये परिमित समुच्चय हो और प्राकृतिक संख्या मैट्रोइड को परिभाषित कर सकता है प्रत्येक को -तत्व उपसमुच्चय आधार बनाया जाता है, इसे पद के एकसमान मैट्रोइड के रूप में जाना जाता है पद के साथ समान मैट्रोइड के साथ तत्वों को दर्शाया गया है कम से कम 2 पद के सभी समान मैट्रोइड सरल हैं (देखें)। § अतिरिक्त शब्दावली) पद 2 की यूनिफार्म मैट्रोइड पर अंक को कहा जाता है -बिंदु रेखा मैट्रोइड के समान होती है यदि केवल तभी जब इसमें मैट्रोइड का पद प्लस से कम आकार का कोई परिपथ न हो। एकसमान मैट्रोइड्स के प्रत्यक्ष योग को विभाजन मैट्रोइड्स कहा जाता है।
यूनिफार्म मेट्रोइड में , प्रत्येक तत्व लूप है (ऐसा तत्व जो किसी स्वतंत्र समुच्चय से संबंधित नहीं है), और एकसमान मैट्रोइड में , प्रत्येक तत्व कोलूप है (तत्व जो सभी आधारों से संबंधित है)। इन दो प्रकार के मैट्रोइड्स का सीधा योग विभाजन मैट्रोइड है जिसमें प्रत्येक तत्व लूप या कोलूप है; इसे असतत मैट्रोइड कहा जाता है। असतत मैट्रोइड की समतुल्य परिभाषा मैट्रोइड है जिसमें ग्राउंड समुच्चय का प्रत्येक उचित, अरिक्त उपसमुच्चय विभाजक है।
रैखिक बीजगणित से मैट्रोइड्स
मैट्रोइड सिद्धांत मुख्य रूप से वेक्टर स्थानों में स्वतंत्रता और आयाम के गुणों की गहन परिक्षण से विकसित हुआ। इस प्रकार परिभाषित मैट्रोइड्स को प्रस्तुत करने की दो विधि हैं:
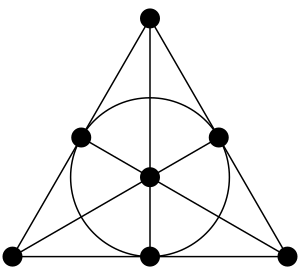
- यदि सदिश समष्टि का कोई परिमित उपसमुच्चय है, तो मैट्रोइड को परिभाषित कर सकते हैं पर के स्वतंत्र समुच्चय लेकर का रैखिक रूप से स्वतंत्र उपसमुच्चय होना, इस मैट्रोइड के लिए स्वतंत्र-समुच्चय स्वयंसिद्धों की वैधता स्टीनिट्ज़ एक्सचेंज लेम्मा से होती है। यदि मैट्रोइड है जिसे इस प्रकार से परिभाषित किया जा सकता है, हम समुच्चय कहते हैं प्रतिनिधित्व करता है, इस प्रकार के मैट्रोइड्स को वेक्टर मैट्रोइड्स कहा जाता है। इस प्रकार से परिभाषित मैट्रोइड का महत्वपूर्ण उदाहरण फ़ानो मैट्रोइड से प्राप्त पद-तीन मैट्रोइड, सात बिंदुओं (मैट्रोइड के सात तत्व) और सात रेखाओं (मैट्रोइड के उचित गैर-तुच्छ फ्लैट) के साथ परिमित ज्यामिति मैट्रोइड) है। यह रैखिक मैट्रोइड है जिसके तत्वों को परिमित क्षेत्र GF(2) पर त्रि-आयामी वेक्टर अंतरिक्ष में सात गैर-शून्य बिंदुओं के रूप में वर्णित किया जा सकता है। चूँकि, GF(2) के स्थान पर वास्तविक संख्याओं का उपयोग करके फ़ैनो मैट्रोइड के लिए समान प्रतिनिधित्व प्रदान करना संभव नहीं है।
- मैट्रिक्स (गणित) किसी क्षेत्र (गणित) में प्रविष्टियों के साथ मैट्रोइड को उत्पन्न करता है। इसके स्तंभों के समुच्चय पर मैट्रोइड में स्तंभों के आश्रित समुच्चय वे होते हैं जो वैक्टर के रूप में रैखिक रूप से निर्भर होते हैं। इस मैट्रोइड को कॉलम मैट्रोइड कहा जाता है , और प्रतिनिधित्व करने के लिए कहा जाता है उदाहरण के लिए, फ़ैनो मैट्रोइड को 3×7 (0,1)-मैट्रिक्स के रूप में इस प्रकार दर्शाया जा सकता है। कॉलम मैट्रोइड्स किसी अन्य नाम के अंतर्गत सिर्फ वेक्टर मैट्रोइड्स हैं, किंतु मैट्रिक्स प्रतिनिधित्व के पक्ष में प्रायः कारण होते हैं। (तकनीकी अंतर है: कॉलम मैट्रोइड में भिन्न-भिन्न तत्व हो सकते हैं जो वेक्टर होते हैं, किंतु जैसा कि ऊपर परिभाषित किया गया है वेक्टर मैट्रोइड में ऐसा नहीं हो सकता है। सामान्यतः यह अंतर महत्वहीन है और इसे उपेक्षा किया जा सकता है, किंतु अनुमति देकर सदिशों का बहुसमूह हो, जो दो परिभाषाओं को पूर्ण सहमति में लाता है।)
मैट्रोइड जो वेक्टर मैट्रोइड के समतुल्य है, चूँकि इसे भिन्न रूप से प्रस्तुत किया जा सकता है, प्रतिनिधित्व योग्य या रैखिक कहा जाता है। यदि क्षेत्र पर वेक्टर मैट्रोइड के समान है (गणित) , तो हम कहते हैं कि प्रतिनिधित्व करने योग्य है ; विशेष रूप से, वास्तविक-प्रतिनिधित्व योग्य है यदि यह वास्तविक संख्याओं पर प्रतिनिधित्व योग्य है। उदाहरण के लिए, यद्यपि ग्राफिक मैट्रोइड (नीचे देखें) को ग्राफ के रूप में प्रस्तुत किया जाता है, यह किसी भी क्षेत्र में वैक्टर द्वारा भी प्रदर्शित किया जा सकता है। मैट्रोइड सिद्धांत में मूलभूत समस्या उन मैट्रोइड्स को चिह्नित करना है जिन्हें किसी दिए गए क्षेत्र में दर्शाया जा सकता है ; रोटा का अनुमान प्रत्येक परिमित क्षेत्र के लिए संभावित लक्षण वर्णन का वर्णन करता है। अब तक के मुख्य परिणाम डब्ल्यू.टी. टुटे (1950 के दशक) के कारण बाइनरी मैट्रोइड्स (GF (2) पर प्रतिनिधित्व योग्य), रीड और बिक्सबी के कारण टर्नरी मैट्रोइड्स (3-तत्व क्षेत्र पर प्रतिनिधित्व योग्य) और भिन्न से सेमुर (1970 के दशक) के लक्षण वर्णन हैं।) और गिलेन, जेरार्ड्स और कपूर (2000) के कारण चतुर्धातुक मैट्रोइड्स (4-तत्व क्षेत्र पर प्रतिनिधित्व योग्य) यह अधिक ओपन क्षेत्र है।
नियमित मैट्रोइड ऐसा मैट्रोइड है जो सभी संभावित क्षेत्रों में प्रतिनिधित्व योग्य है। वामोस मैट्रोइड का सबसे सरल उदाहरण है जो किसी भी क्षेत्र में प्रदर्शित नहीं किया जा सकता है।
ग्राफ़ सिद्धांत से मैट्रोइड्स
मैट्रोइड्स के सिद्धांत का दूसरा मूल स्रोत ग्राफ़ सिद्धांत है।
प्रत्येक परिमित ग्राफ (या मल्टीग्राफ) मैट्रोइड को उत्पन्न करता है इस प्रकार: के रूप में लीजिए सभी किनारों का समुच्चय और किनारों के समुच्चय को स्वतंत्र मानें यदि केवल यदि वह पेड़ है (ग्राफ़ सिद्धांत); अर्थात्, यदि इसमें कोई सरल चक्र न हो। तब को चक्र मैट्रोइड कहा जाता है। इस प्रकार से प्राप्त मैट्रोइड्स ग्राफिक मैट्रोइड्स हैं। प्रत्येक मैट्रोइड ग्राफिक नहीं है, किंतु तीन तत्वों पर सभी मैट्रोइड ग्राफिक हैं।[7]प्रत्येक ग्राफिक मैट्रोइड नियमित है।
ग्राफ़ पर अन्य मैट्रोइड्स पश्चात में परिक्षण किये गए:
- ग्राफ के द्विवृत्ताकार मैट्रोइड को किनारों के समुच्चय को स्वतंत्र कहकर परिभाषित किया जाता है यदि प्रत्येक जुड़े उपसमुच्चय में अधिकतम चक्र होता है।
- किसी भी निर्देशित या अप्रत्यक्ष ग्राफ़ में मान लीजिये और शीर्षों के दो विशिष्ट समुच्चय हैं। सेट में , उपसमुच्चय परिभाषित करें यदि हैं तो स्वतंत्र रहें शीर्ष-असंयुक्त पथ पर यह मैट्रोइड को परिभाषित करता है को गैमॉइड कहा जाता है:[8]जटिल गैमॉइड वह है जिसके लिए समुच्चय का संपूर्ण शीर्ष समुच्चय है।[9]
- द्विपक्षीय ग्राफ़ में , कोई मैट्रोइड बना सकता है जिसमें तत्व शीर्ष पर हैं, द्विविभाजन के , और स्वतंत्र उपसमुच्चय ग्राफ के संयुग्मन (ग्राफ सिद्धांत) के अंतिम बिंदुओं के समुच्चय हैं। इसे ट्रांसवर्सल मैट्रोइड कहा जाता है,[10][11] और यह गैमॉइड की विशेष स्तिथि है।[8] ट्रांसवर्सल मैट्रोइड्स जटिल गैमॉइड्स के दोहरे मैट्रोइड्स हैं।[9]
- ग्राफ़िक मैट्रोइड्स को हस्ताक्षरित ग्राफ, गेन ग्राफ और पक्षपाती ग्राफ से मैट्रोइड्स में सामान्यीकृत किया गया है। ग्राफ विशिष्ट रैखिक वर्ग के साथ चक्रों का , जिसे पक्षपाती ग्राफ़ के रूप में जाना जाता है , दो मैट्रोइड हैं, जिन्हें फ्रेम मैट्रोइड और बायस्ड ग्राफ के लिफ्ट मैट्रोइड के रूप में जाना जाता है। यदि प्रत्येक चक्र विशिष्ट वर्ग का है, तो ये मैट्रोइड्स चक्र मैट्रोइड के साथ युग्मित होते हैं यदि कोई चक्र प्रतिष्ठित नहीं है, तो फ्रेम मैट्रोइड द्विवृत्ताकार मैट्रोइड है हस्ताक्षरित ग्राफ, जिसके किनारों को संकेतों द्वारा लेबल किया जाता है, और लाभ ग्राफ, जो ऐसा ग्राफ है जिसके किनारों को समूह से उन्मुख रूप से लेबल किया जाता है, प्रत्येक पक्षपाती ग्राफ को उत्पन्न करता है और इसलिए इसमें फ्रेम और लिफ्ट मैट्रोइड होते हैं।
- लमान ग्राफ द्वि-आयामी कठोरता मैट्रोइड का आधार बनाते हैं, जो संरचनात्मक कठोरता के सिद्धांत में परिभाषित मैट्रोइड है।
- मान लीजिये कनेक्टेड ग्राफ है, और इसका किनारा समुच्चय है उपसमुच्चय का संग्रह हो का ऐसा है कि अभी भी जुड़ा हुआ है। तब , जिसका तत्व समुच्चय है इसके स्वतंत्र समुच्चयों के वर्ग के रूप में, मैट्रोइड है जिसे बॉन्ड मैट्रोइड कहा जाता है पद फलन किनारे उपसमुच्चय पर प्रेरित उपग्राफ की चक्रीय संख्या है , जो उस उपसमूह के अधिकतम जंगल के बाहर किनारों की संख्या और उसमें स्वतंत्र चक्रों की संख्या के समान है।
क्षेत्र एक्सटेंशन से मैट्रोइड्स
मैट्रोइड सिद्धांत का तीसरा मूल स्रोत क्षेत्र सिद्धांत (गणित) है।
किसी क्षेत्र का विस्तार मैट्रोइड को उत्पन्न करता है। कल्पना करना और के साथ क्षेत्र हैं युक्त मान का कोई परिमित उपसमुच्चय हो, का उपसमुच्चय को परिभाषित करें। यदि विस्तार क्षेत्र है तो बीजगणितीय रूप से स्वतंत्र है, के पास ट्रान्सेंडेंस डिग्री के समान है।[12]
मैट्रोइड जो इस प्रकार के मैट्रोइड के समान होता है उसे बीजगणितीय मैट्रोइड कहा जाता है।[13]बीजगणितीय मैट्रोइड्स को चिह्नित करने की समस्या अत्यंत कठिन है; इसके बारे में अधिक कम जानकारी है, वैमोस मैट्रोइड का उदाहरण प्रदान करता है जो बीजगणितीय नहीं है।
मूलभूत निर्माण
प्राचीन मैट्रोइड से नए मैट्रोइड बनाने के कुछ मानक विधि हैं।
द्वैत
यदि M परिमित मैट्रोइड है, तो हम उसी अंतर्निहित समुच्चय को लेकर 'ऑर्थोगोनल' या 'डुअल मैट्रोइड' M को परिभाषित कर सकते हैं और समुच्चय को M में आधार कह सकते हैं यदि केवल इसका पूरक M में आधार है। यह सत्यापित करना कठिन नहीं है वह M* मैट्रोइड है और M* का द्वैत M का द्वैत है।[14]
मैट्रोइड को परिभाषित करने की अन्य विधि के संदर्भ में दोहरे को समान रूप से वर्णित किया जा सकता है। उदाहरण के लिए:
- M* में समुच्चय स्वतंत्र है यदि केवल उसका पूरक M तक विस्तारित हो।
- समुच्चय M* का परिपथ है यदि केवल इसका पूरक M में कोटोम है।
- डुअल का पद फलन है।
कुराटोस्की के प्रमेय के मैट्रोइड संस्करण के अनुसार, ग्राफिक मैट्रोइड M का दोहरा ग्राफिक मैट्रोइड है यदि केवल M समतलीय ग्राफ का मैट्रोइड है। इस स्तिथि में, M का द्वैत, G के द्वैत ग्राफ का मैट्रॉइड है।[15] वेक्टर मैट्रोइड का द्वैत विशेष क्षेत्र F पर प्रदर्शित होता है, F पर भी प्रदर्शित होता है। ट्रांसवर्सल मैट्रोइड का द्वैत जटिल गैमॉइड इसके विपरीत है।
उदाहरण
किसी ग्राफ़ का चक्र मैट्रोइड उसके बांड मैट्रोइड का दोहरा मैट्रोइड है।
माइनर्स
यदि M तत्व समुच्चय E के साथ मैट्रोइड है, और S, E का उपसमुच्चय है, तो M से S का 'प्रतिबंध', जिसे M |S लिखा जाता है, समुच्चय S पर मैट्रोइड है जिसका स्वतंत्र समुच्चय M के स्वतंत्र समुच्चय हैं जो S में निहित हैं। इसके परिपथ M के परिपथ हैं जो S में निहित हैं और इसका पद फलन M का है जो S के उपसमुच्चय तक सीमित है। रैखिक बीजगणित में, यह S में वैक्टर द्वारा उत्पन्न उप-स्थान तक सीमित करने के अनुरूप है। समान रूप से यदि T = M−S इसे T का 'विलोपन' कहा जा सकता है, जिसे M\T या M−T लिखा जाता है। M के सबमैट्रोइड्स वास्तव में विलोपन के अनुक्रम के परिणाम हैं: क्रम अप्रासंगिक है।[16][17]
प्रतिबंध की दोहरी क्रिया संकुचन है।[18] यदि T, E का उपसमुच्चय है, तो T द्वारा M का 'संकुचन', जिसे M/T लिखा जाता है, अंतर्निहित समुच्चय E - T पर मैट्रोइड है जिसका पद फलन है,[19] रैखिक बीजगणित में, यह E-T में सदिशों की छवियों के साथ-साथ T में सदिशों द्वारा उत्पन्न रैखिक स्थान द्वारा भागफल स्थान को देखने से युग्मित होता है।
मैट्रोइड N जो प्रतिबंध और संकुचन संचालन के अनुक्रम द्वारा M से प्राप्त किया जाता है, उसे M का मैथेरॉइड माइनर कहा जाता है।[17][20] हम कहते हैं कि M में 'N' गौण है। मैट्रोइड्स के कई महत्वपूर्ण सदस्यों की विशेषता लघु-न्यूनतम मैट्रोइड्स से हो सकती है। जो सदस्य से संबंधित नहीं हैं; इन्हें निषिद्ध या बहिष्कृत अवयस्क कहा जाता है।[21]
योग और संघ
मान लीजिए कि M तत्वों E के अंतर्निहित समुच्चय के साथ मैट्रॉइड है, और N को अंतर्निहित समुच्चय F पर और मैट्रॉइड होने दें। मैट्रोइड्स M और N का 'प्रत्यक्ष योग' वह मैट्रोइड है जिसका अंतर्निहित समुच्चय E और F का असंयुक्त संघ है, और जिसका स्वतंत्र समुच्चय M के स्वतंत्र समुच्चय का N के स्वतंत्र समुच्चय का असंयुक्त संघ है।
M और N का 'संघ' वह मैट्रोइड है जिसका अंतर्निहित समुच्चय E और F का संघ (असंगठित संघ नहीं) है, और जिसका स्वतंत्र समुच्चय वे उपसमुच्चय हैं जो M में स्वतंत्र समुच्चय और N में का संघ हैं। सामान्यतः शब्द "संघ" तब प्रारम्भ होता है जब E = F होता है, किंतु यह धारणा आवश्यक नहीं है। यदि E और F असंयुक्त हैं, तो संघ सरल योग है।
अतिरिक्त शब्दावली
मान लीजिए कि M मैट्रोइड है जिसमें E तत्वों का अंतर्निहित समुच्चय है।
- E को M का 'ग्राउंड समुच्चय' कहा जा सकता है। इसके तत्वों को M का 'बिंदु' कहा जा सकता है।
- E का उपसमुच्चय M को विस्तारित करता है यदि इसका समापन E है। समुच्चय को बंद समुच्चय K तक विस्तारित कहा जाता है यदि इसका समापन K है।
- मैट्रोइड का घेरा उसके सबसे छोटे परिपथ या आश्रित समुच्चय का आकार है।
- तत्व जो M का एकल-तत्व परिपथ बनाता है उसे 'लूप' कहा जाता है। समान रूप से, तत्व लूप है यदि इसका कोई आधार नहीं है।[7][22]
- तत्व जो किसी परिपथ से संबंधित नहीं होता है उसे कोलूप या इस्थमस कहा जाता है। समान रूप से, तत्व कोलूप है यदि वह प्रत्येक आधार से संबंधित है। लूप और कोलूप परस्पर दोहरे हैं।[22]
- यदि दो-तत्व समुच्चय {f, g} M का परिपथ है, तो f और g,M में 'समानांतर' हैं।[7]
- मैट्रोइड को सरल कहा जाता है यदि इसमें 1 या 2 तत्वों से युक्त कोई परिपथ नहीं है। अर्थात्, इसमें कोई लूप नहीं है और कोई समानांतर तत्व नहीं है। संयोजक ज्यामिति शब्द का भी प्रयोग किया जाता है।[7] सभी लूपों को विस्थापित करके और प्रत्येक 2-तत्व परिपथ न रह जाए, अन्य मैट्रॉइड M से प्राप्त साधारण मैट्रोइड को M का 'सरलीकरण' कहा जाता है।[23] मैट्रोइड सह-सरल है यदि उसका दोहरा मैट्रोइड सरल है।[24]
- परिपथ के संघ को कभी-कभी M का चक्र कहा जाता है। इसलिए चक्र दोहरे मैट्रोइड के फ्लैट का पूरक है। (यह प्रयोग ग्राफ़ सिद्धांत में चक्र के सामान्य अर्थ के साथ विरोधाभास रखता है।)
- M का विभाजक E का उपसमुच्चय S इस प्रकार है उचित या गैर-तुच्छ विभाजक है जो न तो E है और न ही रिक्त समुच्चय है।[25] इरेड्यूसिबल विभाजक अरिक्त विभाजक है जिसमें कोई अन्य अरिक्त विभाजक नहीं होता है। इरेड्यूसिबल सेपरेटर ग्राउंड समुच्चय E को विभाजित करते हैं।
- मैट्रोइड जिसे दो अरिक्त मैट्रोइड्स के प्रत्यक्ष योग के रूप में नहीं लिखा जा सकता है, या समकक्ष जिसमें कोई उचित विभाजक नहीं है, उसे कनेक्टेड या इरेड्यूसिबल कहा जाता है। मैट्रोइड तभी जुड़ा होता है जब उसका डुअल जुड़ा होता है।[26]
- M के अधिकतम इरेड्यूसिबल सबमैट्रोइड को M का 'घटक' कहा जाता है। घटक इरेड्यूसेबल विभाजक के लिए M का प्रतिबंध है, और इसके विपरीत, इरेड्यूसेबल विभाजक के लिए M का प्रतिबंध घटक है। विभाजक घटकों का संघ है।[25]
- मैट्रोइड M को 'फ्रेम मैट्रोइड' कहा जाता है यदि इसका, या जिस मैट्रोइड में यह सम्मिलित है, उसका आधार ऐसा है कि M के सभी बिंदु उन रेखाओं में समाहित हैं जो आधार तत्वों के जोड़े को जोड़ते हैं।[27]
- मैट्रोइड को पेविंग मैट्रोइड कहा जाता है यदि उसके सभी परिपथ का आकार कम से कम उसके पद के समान हो।[28]
- मैट्रोइड पॉलीटोप के आधारों के सूचक सदिशों का उत्तल है।
एल्गोरिदम
ग्रेडी एल्गोरिदम
भारित मैट्रोइड ऐसा मैट्रोइड है जिसमें इसके तत्वों से लेकर अकारात्मक वास्तविक संख्याओं तक फलन होता है। तत्वों के उपसमूह के भार को उपसमूह में तत्वों के भार के योग के रूप में परिभाषित किया गया है। ग्रेडी एल्गोरिथ्म का उपयोग मैट्रोइड के अधिकतम-भार के आधार का परिक्षण करने के लिए किया जा सकता है, रिक्त समुच्चय से प्रारंभ करके और समय में तत्व को बार-बार जोड़कर, प्रत्येक चरण में उन तत्वों के मध्य अधिकतम-भार वाले तत्व का चयन किया जा सकता है जिनके अतिरिक्त स्वतंत्रता को संरक्षित किया जाएगा। संवर्धित समुच्चय का[29]इस एल्गोरिदम को मैट्रोइड की परिभाषा के विवरण के बारे में कुछ भी जानने की आवश्यकता नहीं है, जब तक कि इसमें मैट्रोइड ओरेकल के माध्यम से मैट्रोइड तक पहुंच है, यह परीक्षण करने के लिए सबरूटीन है कि कोई समुच्चय स्वतंत्र है या नहीं।
इस अनुकूलन एल्गोरिथ्म का उपयोग मैट्रोइड्स को चिह्नित करने के लिए किया जा सकता है: यदि समुच्चय का सदस्य F, जो सबसमुच्चय लेने के अंतर्गत बंद है, जिसमे गुण है कि, इससे कोई अंतर नहीं है कि समुच्चय कैसे भारित होते हैं, ग्रेडी एल्गोरिदम सदस्य में अधिकतम भार समुच्चय पाता है, फिर F मैट्रोइड के स्वतंत्र समुच्चयों का सदस्य होना चाहिए।[30]
अन्य प्रकार के समुच्चयों की अनुमति देने के लिए मैट्रोइड की धारणा को सामान्यीकृत किया गया है, जिस पर ग्रेडी एल्गोरिदम इष्टतम समाधान देता है; अधिक जानकारी के लिए ग्रीडॉइड और मैट्रोइड एम्बेडिंग देखें।
मैट्रोइड विभाजन
मैट्रोइड विभाजन समस्या में मैट्रोइड के तत्वों को यथासंभव कुछ स्वतंत्र समुच्चयों में विभाजित करना है, और मैट्रोइड पैकिंग समस्या यथासंभव अधिक से अधिक असंयुक्त स्पैनिंग समुच्चय का परिक्षण करना है। दोनों को बहुपद समय में समाधान किया जा सकता है, और पद की गणना करने या मैट्रोइड योग में स्वतंत्र समुच्चय के परिक्षण की समस्या को सामान्यीकृत किया जा सकता है।
मैट्रोइड अंत:खंड
दो या दो से अधिक मैट्रोइड्स का प्रतिच्छेदन समुच्चयों का सदस्य है जो प्रत्येक मैट्रोइड्स में साथ स्वतंत्र होते हैं। दो मैट्रोइड्स के प्रतिच्छेदन में सबसे बड़ा समुच्चय, या अधिकतम भारित समुच्चय का परिक्षण करने की समस्या बहुपद समय में पाई जा सकती है,[31]: (46) और कई अन्य महत्वपूर्ण संयोजन अनुकूलन समस्याओं का समाधान प्रदान करता है। उदाहरण के लिए, द्विदलीय ग्राफ़ में अधिकतम संघ को दो विभाजन मैट्रोइड्स को प्रतिच्छेद करने की समस्या के रूप में व्यक्त किया जा सकता है। चूँकि, तीन या अधिक मैट्रोइड्स के प्रतिच्छेदन में सबसे बड़ा समुच्चय एनपी-पूर्ण है।
मैट्रोइड सॉफ़्टवेयर
मैट्रोइड्स के साथ गणना के लिए दो स्टैंडअलोन प्रणालियाँ किंगन के ओइड और ह्लिननी के मेसेक हैं। ये दोनों ओपन सोर्स पैकेज हैं। ओइड मैट्रोइड्स के साथ प्रयोग करने के लिए इंटरैक्टिव, एक्स्टेंसिबल सॉफ्टवेयर प्रणाली है। मैसेक विशेष सॉफ्टवेयर प्रणाली है जिसमें प्रतिनिधित्वयोग्य मैट्रोइड्स के साथ यथोचित कुशल संयोजन संगणना के लिए उपकरण और रूटीन हैं।
दोनों ओपन सोर्स गणित सॉफ्टवेयर प्रणाली सेग और मैकाले2 में मेट्रोइड पैकेज सम्मिलित हैं।
बहुपद अपरिवर्तनीय
ग्राउंड समुच्चय E पर परिमित मैट्रोइड M से जुड़े दो विशेष रूप से महत्वपूर्ण बहुपद हैं। प्रत्येक 'मैट्रोइड बहुपद' है, जिसका अर्थ है कि आइसोमोर्फिक मैट्रोइड्स में बहुपद होता है।
विशेषता बहुपद
M का विशिष्ट बहुपद (जिसे कभी-कभी रंगीन बहुपद भी कहा जाता है,[32]चूँकि यह रंगों की गिनती नहीं करता), को परिभाषित किया गया है:
या समकक्ष (जब तक रिक्त समुच्चय M में बंद है)।
जहां μ मैट्रोइड के ज्यामितीय जाली के मोबियस फलन (कॉम्बिनेटरिक्सको दर्शाता है और योग को मैट्रोइड के सभी फ्लैट्स A पर लिया जाता है।[33]
जब M, ग्राफ G का चक्र मैट्रोइड M(G) है, तो विशेषता बहुपद रंगीन बहुपद का छोटा सा परिवर्तन है, जो χG (λ) = λcpM(G) (λ) द्वारा दिया गया है, जहां c, की संख्या है G से जुड़े घटक है।
जब M, ग्राफ़ G का बॉन्ड मैट्रोइड M*(G) है, तो विशेषता बहुपद, G के प्रवाह बहुपद के समान होता है।
जब M 'Rn' (या Fn जहां F कोई क्षेत्र है) में रैखिक हाइपरप्लेन की व्यवस्था A का मैट्रोइड M(A) है, तो व्यवस्था का विशिष्ट बहुपद pA (λ) = λn−r(M)pM (λ) द्वारा दिया जाता है।
बीटा अपरिवर्तनीय
हेनरी क्रैपो (गणितज्ञ) (1967) द्वारा प्रस्तुत किए गए मैट्रोइड के बीटा अपरिवर्तनीय को व्युत्पन्न के मूल्यांकन के रूप में विशेषता बहुपद P के संदर्भ में व्यक्त किया जा सकता है।[34]
या सरलता पूर्वक[35]
बीटा अपरिवर्तनीय अनकारात्मक है, और शून्य है यदि केवल M डिस्कनेक्ट हो गया है, या रिक्त है, या लूप है। अन्यथा यह केवल M के फ्लैटों की जाली पर निर्भर करता है। यदि M में कोई लूप और कोलूप नहीं है तो β(M) = β(M)∗) होता है। [35]
व्हिटनी संख्या
प्रथम प्रकार के M के व्हिटनी नंबर की शक्तियों के गुणांक हैं विशेषता बहुपद में विशेष रूप से, i-वें व्हिटनी संख्या का गुणांक है और मोबियस फलन मानों का योग है:
उत्तम पद के फ्लैटों का सारांश दिया गया। ये संख्याएँ संकेत में वैकल्पिक होती हैं, जिससे के लिए है।
दूसरे प्रकार के M के व्हिटनी नंबर प्रत्येक पद के फ्लैटों की संख्या हैं। वह है, पद-I फ्लैट्स की संख्या है।
दोनों प्रकार के व्हिटनी संख्याएं पहले और दूसरे प्रकार की स्टर्लिंग संख्याओं को सामान्यीकृत करती हैं, जो पूर्ण ग्राफ के चक्र मैट्रोइड की व्हिटनी संख्याएं और विभाजन जाली के समकक्ष हैं। इनका नाम जियान-कार्लो रोटा द्वारा मैट्रोइड सिद्धांत के (सह) संस्थापक हस्लर व्हिटनी के नाम पर रखा गया था। नाम को परिमित श्रेणी वाले आंशिक रूप से क्रमित समुच्चयों के लिए समान संख्याओं तक बढ़ा दिया गया है।
टुट्टे बहुपद
मैट्रोइड का टुट्टे बहुपद, TM(x,y), विशेषता बहुपद को दो चरों के लिए सामान्यीकृत करता है। यह इसे अधिक संयोजनात्मक व्याख्याएँ देता है, और इसे द्वैत गुण भी देता है
जो M के गुणों और M* के गुणों के मध्य कई द्वंद्वों को दर्शाता है। टुट्टे बहुपद की परिभाषा है:
यह टुट्टे बहुपद को कॉपद-शून्यता या पद उत्पन्न करने वाले बहुपद के मूल्यांकन के रूप में व्यक्त करता है,[36]
इस परिभाषा से यह देखना सरल है कि विशेषता बहुपद, साधारण कारक तक, TM का मूल्यांकन है, विशेष रूप से,
अन्य परिभाषा आंतरिक और बाह्य गतिविधियों और आधारों के योग के संदर्भ में है, जो इस तथ्य को दर्शाती है कि T(1,1) आधारों की संख्या है।[37] यह, जो कम उपसमुच्चय का योग है किंतु इसमें अधिक जटिल शब्द हैं, टुट्टे की मूल परिभाषा थी।
विलोपन और संकुचन द्वारा पुनरावर्तन के संदर्भ में परिभाषा है।[38] विलोपन-संकुचन की पहचान है:
- कब न तो लूप है और न ही कोलूप।
मैट्रोइड्स का अपरिवर्तनीय (अर्थात, फलन जो आइसोमोर्फिक मैट्रोइड्स पर समान मान लेता है) इस रिकर्सन और गुणक स्थिति को संतुष्ट करता है:
कहा जाता है कि यह टुट्टे-ग्रोथेंडिक अपरिवर्तनीय है।[36]टुट्टे बहुपद इस प्रकार का सबसे सामान्य अपरिवर्तनीय है; अर्थात्, टुट्टे बहुपद टुट्टे-ग्रोथेंडिक अपरिवर्तनीय है और ऐसा प्रत्येक अपरिवर्तनीय टुट्टे बहुपद का मूल्यांकन है।[32]
ग्राफ का टुट्टे बहुपद TG इसके चक्र मैट्रोइड का टुट्टे बहुपद TM(G) है।
अनंत मैट्रोइड्स
अनंत मैट्रोइड्स का सिद्धांत परिमित मैट्रोइड्स की तुलना में अधिक जटिल है और इसका अपना विषय है। लंबे समय से, कठिनाई यह रही है कि कई उचित और उपयोगी परिभाषाएँ थीं, जिनमें से कोई भी परिमित मैट्रोइड सिद्धांत के सभी महत्वपूर्ण विषयों को पकड़ती नहीं थी। उदाहरण के लिए, अनंत मैट्रोइड्स की धारणा में आधार, परिपथ और द्वंद्व को साथ रखना कठिन प्रतीत होता है।
अनंत मैट्रोइड की सबसे सरल परिभाषा परिमित पद की आवश्यकता है; अर्थात्, E का पद परिमित है। यह सिद्धांत परिमित मैट्रोइड के समान है, इस तथ्य के कारण द्वैत की विफलता को छोड़कर कि परिमित पद के अनंत मैट्रोइड के दोहरे में परिमित पद नहीं है। परिमित-पद मैट्रोइड्स में परिमित-आयामी वेक्टर रिक्त स्थान और परिमित पारगमन डिग्री के क्षेत्र (गणित) विस्तार के किसी भी उपसमूह सम्मिलित हैं।
अगला सरलतम अनंत सामान्यीकरण फ़िनिटरी मैट्रोइड्स है, जिसे प्रीजियोमेट्री (मॉडल सिद्धांत) के रूप में भी जाना जाता है। संभवतः अनंत ग्राउंड समुच्चय वाला मैट्रोइड परिमित होता है यदि उसमें वह गुण हो,
समान रूप से, प्रत्येक आश्रित समुच्चय में परिमित आश्रित समुच्चय होता है। उदाहरण अनंत-आयामी वेक्टर रिक्त स्थान के उपसमुच्चय की रैखिक निर्भरता हैं (किंतु हिल्बर्ट अंतरिक्ष और बानाच रिक्त स्थान क जैसे अनंत निर्भरता नहीं), और संभवतः अनंत पारगमन डिग्री के क्षेत्र विस्तार के उपसमुच्चय में बीजगणितीय निर्भरता पुनः, फ़िनिटरी मैट्रोइड का वर्ग स्व-द्वैत नहीं है, क्योंकि फ़ाइनिटरी मैट्रोइड का द्वैत एकात्मक नहीं है।मॉडल सिद्धांत में फ़िनिटरी अनंत मैट्रोइड्स का अध्ययन किया जाता है, जो बीजगणित के साथ स्थिर संबंधों के साथ गणितीय तर्क की शाखा है।
1960 दशक के अंत में मैट्रोइड सिद्धांतकारों ने अधिक सामान्य धारणा की आवश्यकता जो परिमित मैट्रोइड के विभिन्न विषयों को भागित करती है और उनके द्वंद्व को सामान्य बनाती है। इस अनुशय के उत्तर में अनंत मैट्रोइड्स की कई धारणाओं को परिभाषित किया गया, किंतु प्रश्न खुला रहा। डी.ए. द्वारा परिक्षण किये गए दृष्टिकोणों में से हिग्स को बी-मैट्रोइड्स के रूप में जाना जाने लगा और 1960 और 1970 दशक में हिग्स, ऑक्सले और अन्य लोगों द्वारा इसका अध्ययन किया गया। ब्रुहन, डायस्टेल और क्रिसेल एट अल के परिणाम के अनुसार (2013), यह समस्या का समाधान करता है: स्वतंत्र रूप से एक ही धारणा पर पहुंचते हुए, उन्होंने स्वतंत्रता, आधार, परिपथ, क्लोजर और पद के संदर्भ में स्वयंसिद्ध की पांच समकक्ष प्रणालियां प्रदान कीं। बी-मैट्रोइड्स का द्वंद्व उन द्वंद्वों को सामान्यीकृत करता है जिन्हें अनंत ग्राफ़ में देखा जा सकता है।
स्वतंत्रता के सिद्धांत इस प्रकार हैं:
- रिक्त समुच्चय स्वतंत्र है।
- स्वतंत्र समुच्चय का प्रत्येक उपसमुच्चय स्वतंत्र होता है।
- प्रत्येक अधिकतम (समुच्चय समावेशन के अंतर्गत) स्वतंत्र समुच्चय I और अधिकतम स्वतंत्र समुच्चय J के लिए, वहाँ है ऐसा है कि स्वतंत्र है।
- आधार स्थान के प्रत्येक उपसमुच्चय X के लिए, X के प्रत्येक स्वतंत्र उपसमुच्चय I को X के अधिकतम स्वतंत्र उपसमुच्चय तक बढ़ाया जा सकता है।
इन सिद्धांतों के साथ, प्रत्येक मैट्रोइड में दोहरा होता है।
इतिहास
मैट्रोइड सिद्धांत Hassler Whitney (1935) द्वारा प्रस्तुत किया गया था। इसका परिक्षण भी ताकेओ नाकासावा ने स्वतंत्र रूप से की थी, जिनके कार्य को कई वर्षों तक भुला दिया गया था (निशिमुरा और & कुरोदा 2009)।
अपने मौलिक दस्तावेज में, व्हिटनी ने स्वतंत्रता के लिए दो सिद्धांत प्रदान किए, और इन सिद्धांतों का पालन करने वाली किसी भी संरचना को मैट्रोइड के रूप में परिभाषित किया। (चूँकि यह संभवतः निहित था, उन्होंने स्वयंसिद्ध को सम्मिलित नहीं किया था जिसमें कम से कम उपसमुच्चय के स्वतंत्र होने की आवश्यकता थी।) उनका मुख्य अवलोकन यह था कि ये सिद्धांत स्वतंत्रता का अमूर्तन प्रदान करते हैं जो ग्राफ़ और मैट्रिक्स दोनों के लिए सामान्य है। इस कारण से, मैट्रोइड सिद्धांत में उपयोग किए गए कई शब्द रैखिक बीजगणित या ग्राफ सिद्धांत में उनके अनुरूप अवधारणाओं के समान हैं।
व्हिटनी द्वारा मैट्रोइड्स के बारे में प्रथम बार लिखने के लगभग पश्चात Saunders Mac Lane (1936) द्वारा मैट्रोइड्स और प्रक्षेप्य ज्यामिति के संबंध पर महत्वपूर्ण लेख लिखा गया था। एक वर्ष पश्चात, B. L. van der Waerden (1937) ने आधुनिक बीजगणित पर अपनी क्लासिक पाठ्यपुस्तक में बीजीय और रैखिक निर्भरता के मध्य समानताएं देखीं।
1940 के दशक में रिचर्ड राडो ने ट्रांसवर्सल (कॉम्बिनेटरिक्स) सिद्धांत को ध्यान में रखते हुए "स्वतंत्रता प्रणाली" के नाम से सिद्धांत विकसित किया, जहां विषय के लिए उनका नाम अभी भी कभी-कभी उपयोग किया जाता है।
1950 के दशक में डब्ल्यू. टी. टुट्टे मैट्रोइड सिद्धांत में अग्रणी व्यक्ति बन गए, यह पद उन्होंने कई वर्षों तक स्थिर रखा। उनका योगदान प्रचुर मात्रा में था, जिसमें बहिष्कृत माइनर्स द्वारा बाइनरी, नियमित और ग्राफिक मैट्रोइड्स का लक्षण वर्णन सम्मिलित था; रेगुलर-मैट्रोइड अभ्यावेदन प्रमेय; श्रृंखला समूहों और उनके मैट्रोइड्स का सिद्धांत; और अपने कई परिणामों को सिद्ध करने के लिए उन्होंने जिन उपकरणों का उपयोग किया, पथ प्रमेय और टुट्टे होमोटॉपी प्रमेय (देखें, उदाहरण के लिए, टुट्टे 1965), जो इतने जटिल हैं कि पश्चात के सिद्धांतकारों को उपयोग की आवश्यकता को समाप्त करने के लिए बड़ी परेशानी का सामना करना होता है उन्हें प्रमाणों में (उत्तम उदाहरण ए.एम.एच. जेरार्ड्स का टुट्टे के नियमित मैट्रोइड्स के लक्षण वर्णन का संक्षिप्त प्रमाण (1989) है।)
Henry Crapo (1969) और Thomas Brylawski (1972) ने मैट्रोइड्स टुट्टे के "डाइक्रोमेट" को सामान्यीकृत किया, ग्राफिक बहुपद जिसे अब टुट्टे बहुपद (क्रैपो द्वारा नामित) के रूप में जाना जाता है। उनके कार्य के पश्चात वर्तमान में (विशेष रूप से 2000 के दशक में) कागजात की बाढ़ आ गई है- चूँकि ग्राफ के टुट्टे बहुपद के समान नहीं है।
1976 में डोमिनिक वेल्श ने मैट्रोइड सिद्धांत पर प्रथम व्यापक पुस्तक प्रकाशित की।
नियमित मैट्रोइड्स के लिए पॉल सेमुर (गणितज्ञ) का अपघटन प्रमेय (1980) 1970 और 1980 के दशक का सबसे महत्वपूर्ण और प्रभावशाली कार्य था। Kahn & Kung (1982) के अन्य मौलिक योगदान द्वारा दिखाया गया कि प्रोजेक्टिव ज्यामिति और डाउलिंग ज्यामिति मैट्रोइड सिद्धांत में इतनी महत्वपूर्ण भूमिका क्यों निभाते हैं।
इस समय तक कई अन्य महत्वपूर्ण योगदानकर्ता थे, किंतु टुट्टे के बाइनरी मैट्रोइड्स के लक्षण वर्णन के ज्योफ व्हिटल के टर्नरी मैट्रोइड्स के विस्तार का उल्लेख करना नहीं भूलना चाहिए जो कि तर्कसंगत (Whittle 1995) पर प्रतिनिधित्व करने योग्य हैं, संभवतः 1990 के दशक का सबसे बड़ा एकल योगदान है। वर्तमान अवधि में (2000 के निकट से) जिम गिलेन, जेरार्ड्स, व्हिटल और अन्य का मैट्रोइड माइनर्स प्रोजेक्ट, जो सीमित क्षेत्र में प्रतिनिधित्व करने योग्य मैट्रोइड्स का अनुसरण करने का प्रयास करता है, रॉबर्टसन-सेमुर ग्राफ माइनर्स प्रोजेक्ट की सफलता (रॉबर्टसन देखें) -सीमोर प्रमेय), ने मैट्रोइड्स के संरचना सिद्धांत में पर्याप्त प्रगति की है। कई अन्य लोगों ने भी मैट्रोइड सिद्धांत के उस भाग में योगदान दिया है, जो (21वीं दशक पहले और दूसरे दशकों में) प्रगति कर रहा है।
शोधकर्ता
मैट्रोइड्स के अध्ययन में अग्रणी गणितज्ञों में ताकेओ नाकासावा,[39] सॉन्डर्स मैक लेन, रिचर्ड राडो, डब्ल्यू. टी. टुट्टे, बी. एल. वैन डेर वेर्डन और हस्लर व्हिटनी सम्मिलित हैं। अन्य प्रमुख योगदानकर्ताओं में जैक एडमंड्स, जिम गिलेन, यूजीन लॉलर, लास्ज़लो लोवाज़, जियान-कार्लो रोटा, पी. डी. सेमुर और डोमिनिक वेल्श सम्मिलित हैं।
यह भी देखें
- एंटीमैट्रोइड
- कॉक्समुच्चयर मैट्रोइड
- ओरिएंटेड मैट्रोइड
- प्रीजियोमेट्री (मॉडल सिद्धांत)
- पॉलीमेट्रोइड
- ग्रेडी
टिप्पणियाँ
- ↑ Neel, David L.; Neudauer, Nancy Ann (2009). "मैट्रोइड्स को आप जानते होंगे" (PDF). Mathematics Magazine. 82 (1): 26–41. doi:10.4169/193009809x469020. Retrieved 4 October 2014.
- ↑ Kashyap, Navin; Soljanin, Emina; Vontobel, Pascal. "सूचना और कोडिंग सिद्धांत के लिए मैट्रोइड सिद्धांत और संयोजन अनुकूलन के अनुप्रयोग" (PDF). www.birs.ca. Retrieved 4 October 2014.
- ↑ A standard source for basic definitions and results about matroids is Oxley (1992). An older standard source is Welsh (1976). See Brylawski's appendix in White (1986), pp. 298–302, for a list of equivalent axiom systems.
- ↑ 4.0 4.1 4.2 4.3 4.4 Welsh (1976), Section 1.2, "Axiom Systems for a Matroid", pp. 7–9.
- ↑ Welsh (1976), Section 1.8, "Closed sets = Flats = Subspaces", pp. 21–22.
- ↑ 6.0 6.1 Welsh (1976), Section 2.2, "The Hyperplanes of a Matroid", pp. 38–39.
- ↑ 7.0 7.1 7.2 7.3 Oxley 1992, p. 13
- ↑ 8.0 8.1 Oxley 1992, pp. 115
- ↑ 9.0 9.1 Oxley 1992, p. 100
- ↑ Oxley 1992, pp. 46–48
- ↑ 1987
- ↑ Oxley 1992, p. 215
- ↑ Oxley 1992, p. 216
- ↑ White 1986, p. 32
- ↑ White 1986, p. 105
- ↑ White 1986, p. 131
- ↑ 17.0 17.1 White 1986, p. 224
- ↑ White 1986, p. 139
- ↑ White 1986, p. 140
- ↑ White 1986, p. 150
- ↑ White 1986, pp. 146–147
- ↑ 22.0 22.1 White 1986, p. 130
- ↑ Oxley 1992, p. 52
- ↑ Oxley 1992, p. 347
- ↑ 25.0 25.1 Oxley 1992, p. 128
- ↑ White 1986, p. 110
- ↑ Zaslavsky, Thomas (1994). "फ़्रेम मैट्रोइड्स और पक्षपाती ग्राफ़". Eur. J. Comb. 15 (3): 303–307. doi:10.1006/eujc.1994.1034. ISSN 0195-6698. Zbl 0797.05027.
- ↑ Oxley 1992, p. 26
- ↑ Oxley 1992, p. 63
- ↑ Oxley 1992, p. 64
- ↑ Edmonds, Jack (2003), Jünger, Michael; Reinelt, Gerhard; Rinaldi, Giovanni (eds.), "Submodular Functions, Matroids, and Certain Polyhedra", Combinatorial Optimization — Eureka, You Shrink!: Papers Dedicated to Jack Edmonds 5th International Workshop Aussois, France, March 5–9, 2001 Revised Papers, Lecture Notes in Computer Science (in English), Berlin, Heidelberg: Springer, vol. 2570, pp. 11–26, doi:10.1007/3-540-36478-1_2, ISBN 978-3-540-36478-8, retrieved 2022-11-27
- ↑ 32.0 32.1 White 1987, p. 127
- ↑ White 1987, p. 120
- ↑ White 1987, p. 123
- ↑ 35.0 35.1 White 1987, p. 124
- ↑ 36.0 36.1 White 1987, p. 126
- ↑ White 1992, p. 188
- ↑ White 1986, p. 260
- ↑ Nishimura & Kuroda (2009).
संदर्भ
- Bruhn, Henning; Diestel, Reinhard; Kriesell, Matthias; Pendavingh, Rudi; Wollan, Paul (2013), "Axioms for infinite matroids", Advances in Mathematics, 239: 18–46, arXiv:1003.3919, doi:10.1016/j.aim.2013.01.011, MR 3045140, S2CID 10436077.
- Bryant, Victor; Perfect, Hazel (1980), Independence Theory in Combinatorics, London and New York: Chapman and Hall, ISBN 978-0-412-22430-0.
- Brylawski, Thomas H. (1972), "A decomposition for combinatorial geometries", Transactions of the American Mathematical Society, 171: 235–282, doi:10.2307/1996381, JSTOR 1996381.
- Crapo, Henry H. (1969), "The Tutte polynomial", Aequationes Mathematicae, 3 (3): 211–229, doi:10.1007/BF01817442, S2CID 119602825.
- Crapo, Henry H.; Rota, Gian-Carlo (1970), On the Foundations of Combinatorial Theory: Combinatorial Geometries, Cambridge, Mass.: M.I.T. Press, ISBN 978-0-262-53016-3, MR 0290980.
- Geelen, Jim; Gerards, A. M. H.; Whittle, Geoff (2007), "Towards a matroid-minor structure theory", in Grimmett, Geoffrey; et al. (eds.), Combinatorics, Complexity, and Chance: A Tribute to Dominic Welsh, Oxford Lecture Series in Mathematics and its Applications, vol. 34, Oxford: Oxford University Press, pp. 72–82.
- Gerards, A. M. H. (1989), "A short proof of Tutte's characterization of totally unimodular matrices", Linear Algebra and Its Applications, 114/115: 207–212, doi:10.1016/0024-3795(89)90461-8.
- Kahn, Jeff; Kung, Joseph P. S. (1982), "Varieties of combinatorial geometries", Transactions of the American Mathematical Society, 271 (2): 485–499, doi:10.2307/1998894, JSTOR 1998894.
- Kingan, Robert; Kingan, Sandra (2005), "A software system for matroids", Graphs and Discovery, DIMACS Series in Discrete Mathematics and Theoretical Computer Science, pp. 287–296.
- Kung, Joseph P. S., ed. (1986), A Source Book in Matroid Theory, Boston: Birkhäuser, doi:10.1007/978-1-4684-9199-9, ISBN 978-0-8176-3173-4, MR 0890330.
- Mac Lane, Saunders (1936), "Some interpretations of abstract linear dependence in terms of projective geometry", American Journal of Mathematics, 58 (1): 236–240, doi:10.2307/2371070, JSTOR 2371070.
- Minty, George J. (1966), "On the axiomatic foundations of the theories of directed linear graphs, electrical networks and network-programming", Journal of Mathematics and Mechanics, 15: 485–520, MR 0188102.
- Nishimura, Hirokazu; Kuroda, Susumu, eds. (2009), A lost mathematician, Takeo Nakasawa. The forgotten father of matroid theory, Basel: Birkhäuser Verlag, doi:10.1007/978-3-7643-8573-6, ISBN 978-3-7643-8572-9, MR 2516551, Zbl 1163.01001.
- Oxley, James (1992), Matroid Theory, Oxford: Oxford University Press, ISBN 978-0-19-853563-8, MR 1207587, Zbl 0784.05002.
- Recski, András (1989), Matroid Theory and its Applications in Electric Network Theory and in Statics, Algorithms and Combinatorics, vol. 6, Berlin and Budapest: Springer-Verlag and Akademiai Kiado, doi:10.1007/978-3-662-22143-3, ISBN 978-3-540-15285-9, MR 1027839, S2CID 117772439.
- Sapozhenko, A.A. (2001) [1994], "मैट्रोइड", Encyclopedia of Mathematics, EMS Press
- Seymour, Paul D. (1980), "Decomposition of regular matroids", Journal of Combinatorial Theory, Series B, 28 (3): 305–359, doi:10.1016/0095-8956(80)90075-1, hdl:10338.dmlcz/101946, Zbl 0443.05027.
- Truemper, Klaus (1992), Matroid Decomposition, Boston: Academic Press, ISBN 978-0-12-701225-4, MR 1170126.
- Tutte, W. T. (1959), "Matroids and graphs", Transactions of the American Mathematical Society, 90 (3): 527–552, doi:10.2307/1993185, JSTOR 1993185, MR 0101527.
- Tutte, W. T. (1965), "Lectures on matroids", Journal of Research of the National Bureau of Standards Section B, 69: 1–47.
- Tutte, W.T. (1971), Introduction to the theory of matroids, Modern Analytic and Computational Methods in Science and Mathematics, vol. 37, New York: American Elsevier Publishing Company, Zbl 0231.05027.
- Vámos, Peter (1978), "The missing axiom of matroid theory is lost forever", Journal of the London Mathematical Society, 18 (3): 403–408, doi:10.1112/jlms/s2-18.3.403.
- van der Waerden, B. L. (1937), Moderne Algebra.
- Welsh, D. J. A. (1976), Matroid Theory, L.M.S. Monographs, vol. 8, Academic Press, ISBN 978-0-12-744050-7, Zbl 0343.05002.
- White, Neil, ed. (1986), Theory of Matroids, Encyclopedia of Mathematics and its Applications, vol. 26, Cambridge: Cambridge University Press, ISBN 978-0-521-30937-0, Zbl 0579.00001.
- White, Neil, ed. (1987), Combinatorial geometries, Encyclopedia of Mathematics and its Applications, vol. 29, Cambridge: Cambridge University Press, ISBN 978-0-521-33339-9, Zbl 0626.00007
- White, Neil, ed. (1992), Matroid Applications, Encyclopedia of Mathematics and its Applications, vol. 40, Cambridge: Cambridge University Press, ISBN 978-0-521-38165-9, Zbl 0742.00052.
- Whitney, Hassler (1935), "On the abstract properties of linear dependence", American Journal of Mathematics, 57 (3): 509–533, doi:10.2307/2371182, hdl:10338.dmlcz/100694, JSTOR 2371182, MR 1507091. Reprinted in Kung (1986), pp. 55–79.
- Whittle, Geoff (1995), "A characterization of the matroids representable over GF(3) and the rationals", Journal of Combinatorial Theory, Series B, 65 (2): 222–261, doi:10.1006/jctb.1995.1052.
बाहरी संबंध
- "Matroid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Kingan, Sandra : मेट्रोइड theory. A large bibliography of मेट्रोइड papers, मेट्रोइड software, and links.
- Locke, S. C. : Greedy Algorithms.
- Pagano, Steven R. : मेट्रोइडs and Signed Graphs.
- Mark Hubenthal: A Brief Look At मेट्रोइडs (PDF) (contain proofs for statements of this article)
- James Oxley : What is a मेट्रोइड? (PDF)
- Neil White : मेट्रोइड Applications
