ची वितरण: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Probability distribution| | संभाव्यता सिद्धांत और सांख्यिकी में, '''ची वितरण''' एक सतत संभाव्यता वितरण होता है। यह एक मानक [[सामान्य वितरण]] के पश्चात् स्वतंत्र यादृच्छिक चर के एक समूह के वर्गों के योग के धनात्मक वर्गमूल का वितरण, या समकक्ष, मूल से यादृच्छिक चर की [[यूक्लिडियन दूरी]] का वितरण होता है। इस प्रकार यह [[ची-वर्ग वितरण]] को स्वीकृति देने वाले एक चर के धनात्मक वर्गमूलों के वितरण का वर्णन करके ची-वर्ग वितरण से संबंधित होता है। | ||
यदि <math>Z_1, \ldots, Z_k</math> होता हैं तो <math>k</math> माध्य 0 और [[मानक विचलन]] 1 के साथ स्वतंत्र होता, सामान्य वितरण यादृच्छिक चर, फिर आँकड़ा निम्न प्रकार होता है | |||
:<math>Y = \sqrt{\sum_{i=1}^k Z_i^2} </math> | |||
जिसे ची वितरण के अनुसार वितरित किया जाता है। ची वितरण का एक पैरामीटर <math>k</math> होता है, जो [[स्वतंत्रता की डिग्री (सांख्यिकी)|स्वतंत्रता की डिग्री]] की संख्या को निर्दिष्ट करता है (अर्थात् यादृच्छिक चर की संख्या <math>Z_i</math> होती है)। {{Probability distribution| | |||
name =chi| | name =chi| | ||
type =density| | type =density| | ||
| Line 17: | Line 21: | ||
mgf =Complicated (see text)| | mgf =Complicated (see text)| | ||
char =Complicated (see text)| | char =Complicated (see text)| | ||
}} | }}सबसे परिचित उदाहरण [[रेले वितरण]] (स्वतंत्रता की दो डिग्री के साथ ची वितरण) और एक [[आदर्श गैस]] में आणविक गति का मैक्सवेल-बोल्ट्ज़मैन वितरण (स्वतंत्रता की तीन डिग्री के साथ ची वितरण) होता है। | ||
सबसे परिचित उदाहरण | |||
== परिभाषाएँ == | == परिभाषाएँ == | ||
=== संभाव्यता घनत्व | === संभाव्यता घनत्व फलन === | ||
ची-वितरण की संभाव्यता घनत्व | ची-वितरण की संभाव्यता घनत्व फलन (पीडीएफ) निम्न प्रकार है | ||
:<math>f(x;k) = \begin{cases} | :<math>f(x;k) = \begin{cases} | ||
\dfrac{x^{k-1}e^{-x^2/2}}{2^{k/2-1}\Gamma\left(\frac{k}{2}\right)}, & x\geq 0; \\ 0, & \text{otherwise}. | \dfrac{x^{k-1}e^{-x^2/2}}{2^{k/2-1}\Gamma\left(\frac{k}{2}\right)}, & x\geq 0; \\ 0, & \text{otherwise}. | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
जहाँ <math>\Gamma(z)</math> [[गामा फ़ंक्शन|गामा फलन]] होता है। | |||
===संचयी वितरण फलन=== | ===संचयी वितरण फलन=== | ||
संचयी वितरण | संचयी वितरण फलन निम्न प्रकार द्वारा दिया गया है: | ||
:<math>F(x;k)=P(k/2,x^2/2)\,</math> | :<math>F(x;k)=P(k/2,x^2/2)\,</math> | ||
जहाँ <math>P(k,x)</math> नियमित गामा फलन होता है। | |||
===कार्य उत्पन्न करना=== | ===कार्य उत्पन्न करना=== | ||
| Line 47: | Line 44: | ||
:<math>M(t)=M\left(\frac{k}{2},\frac{1}{2},\frac{t^2}{2}\right)+t\sqrt{2}\,\frac{\Gamma((k+1)/2)}{\Gamma(k/2)} M\left(\frac{k+1}{2},\frac{3}{2},\frac{t^2}{2}\right),</math> | :<math>M(t)=M\left(\frac{k}{2},\frac{1}{2},\frac{t^2}{2}\right)+t\sqrt{2}\,\frac{\Gamma((k+1)/2)}{\Gamma(k/2)} M\left(\frac{k+1}{2},\frac{3}{2},\frac{t^2}{2}\right),</math> | ||
जहाँ <math>M(a,b,z)</math> कुमेर का संगम हाइपरज्यामितीय फलन होता है। विशेषता फलन (संभावना सिद्धांत) द्वारा दिया गया है: | |||
:<math>\varphi(t;k)=M\left(\frac{k}{2},\frac{1}{2},\frac{-t^2}{2}\right) + it\sqrt{2}\,\frac{\Gamma((k+1)/2)}{\Gamma(k/2)} M\left(\frac{k+1}{2},\frac{3}{2},\frac{-t^2}{2}\right).</math> | :<math>\varphi(t;k)=M\left(\frac{k}{2},\frac{1}{2},\frac{-t^2}{2}\right) + it\sqrt{2}\,\frac{\Gamma((k+1)/2)}{\Gamma(k/2)} M\left(\frac{k+1}{2},\frac{3}{2},\frac{-t^2}{2}\right).</math> | ||
| Line 55: | Line 52: | ||
=== क्षण === | === क्षण === | ||
अपक्व [[क्षण (गणित)|क्षण]] तब निम्न प्रकार दिया जाता है: | |||
:<math>\mu_j = \int_0^\infty f(x;k) x^j \mathrm{d} x = 2^{j/2}\ \frac{\ \Gamma\left( \tfrac{1}{2}(k+j) \right)\ }{\Gamma\left( \tfrac{1}{2}k \right)}</math> | :<math>\mu_j = \int_0^\infty f(x;k) x^j \mathrm{d} x = 2^{j/2}\ \frac{\ \Gamma\left( \tfrac{1}{2}(k+j) \right)\ }{\Gamma\left( \tfrac{1}{2}k \right)}</math> | ||
जहाँ <math>\ \Gamma(z)\ </math>एक गामा फलन होता है। इस प्रकार पहले कुछ अपक्व क्षण निम्न प्रकार होता हैं: | |||
:<math>\mu_1 = \sqrt{2\ }\ \frac{\ \Gamma\left( \tfrac{1}{2}(k + 1) \right)\ }{\Gamma\left( \tfrac{1}{2}k \right)}</math> | :<math>\mu_1 = \sqrt{2\ }\ \frac{\ \Gamma\left( \tfrac{1}{2}(k + 1) \right)\ }{\Gamma\left( \tfrac{1}{2}k \right)}</math> | ||
| Line 65: | Line 62: | ||
:<math>\mu_5 = 4\sqrt{2\ }\ \frac{\ \Gamma\left( \tfrac{1}{2}(k\!+\!5) \right)\ }{\Gamma\left( \tfrac{1}{2}k \right)} = (k+1)(k+3)\ \mu_1\ ,</math> | :<math>\mu_5 = 4\sqrt{2\ }\ \frac{\ \Gamma\left( \tfrac{1}{2}(k\!+\!5) \right)\ }{\Gamma\left( \tfrac{1}{2}k \right)} = (k+1)(k+3)\ \mu_1\ ,</math> | ||
:<math> \mu_6 = (k)(k+2)(k+4)\ ,</math> | :<math> \mu_6 = (k)(k+2)(k+4)\ ,</math> | ||
जहाँ गामा फलन के लिए पुनरावृत्ति संबंध का उपयोग करके सबसे सही अभिव्यक्ति प्राप्त की जाती है: | |||
:<math> \Gamma(x+1) = x\ \Gamma(x) ~.</math> | :<math> \Gamma(x+1) = x\ \Gamma(x) ~.</math> | ||
इन अभिव्यक्तियों से हम निम्नलिखित संबंध प्राप्त कर सकते हैं: | इन अभिव्यक्तियों से हम निम्नलिखित संबंध प्राप्त कर सकते हैं: | ||
अर्थ: <math> \mu = \sqrt{2\ }\ \frac{\ \Gamma\left( \tfrac{1}{2}(k+1) \right)\ }{\Gamma\left( \tfrac{1}{2} k \right)}\ ,</math> जो | अर्थ: <math> \mu = \sqrt{2\ }\ \frac{\ \Gamma\left( \tfrac{1}{2}(k+1) \right)\ }{\Gamma\left( \tfrac{1}{2} k \right)}\ ,</math> जो <math> \sqrt{k - \tfrac{1}{2}\ }\ </math> बड़े {{mvar|k}} के समीप होता है। | ||
विचरण: <math> V = k - \mu^2\ ,</math> जो | विचरण: <math> V = k - \mu^2\ ,</math> जो जैसे {{mvar|k}} बढ़ती है वैसे ही <math>\ \tfrac{1}{2}\ </math>समीप आता है। | ||
विषमता: <math> \gamma_1 = \frac{\mu}{\ \sigma^3\ } \left(1 - 2 \sigma^2 \right) ~</math>होती है। | |||
कर्टोसिस की अधिकता: <math>\gamma_2 = \frac{2}{\ \sigma^2\ } \left(1 - \mu\ \sigma\ \gamma_1 - \sigma^2 \right) ~</math>होती है। | |||
===एंट्रॉपी=== | ===एंट्रॉपी=== | ||
एन्ट्रापी निम्न | एन्ट्रापी निम्न प्रकार दी जाती है: | ||
:<math>S=\ln(\Gamma(k/2))+\frac{1}{2}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi^0(k/2))</math> | :<math>S=\ln(\Gamma(k/2))+\frac{1}{2}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi^0(k/2))</math> | ||
जहाँ <math>\psi^0(z)</math> पलिगमी(बहुविवाह) फलन होता है। | |||
===बड़ा एन सन्निकटन=== | ===बड़ा एन सन्निकटन=== | ||
हम ची वितरण के माध्य और विचरण का बड़ा n=k+1 सन्निकटन | हम ची वितरण के माध्य और विचरण का बड़ा n=k+1 सन्निकटन प्राप्त करते हैं। इसमें एक एप्लिकेशन उपस्थित होती है उदा. सामान्य रूप से वितरित जनसंख्या के प्रतिरूप के मानक विचलन का वितरण ज्ञात करने में, जहाँ n प्रतिरूप आकार होता है। | ||
तब माध्य है: | तब माध्य निम्न प्रकार होता है: | ||
:<math>\mu = \sqrt{2}\,\,\frac{\Gamma(n/2)}{\Gamma((n-1)/2)}</math> | :<math>\mu = \sqrt{2}\,\,\frac{\Gamma(n/2)}{\Gamma((n-1)/2)}</math> | ||
हम लिखने के लिए | हम लिखने के लिए लीजेंड्रे दोहराव सूत्र का उपयोग करते हैं:: | ||
:<math>2^{n-2} \,\Gamma((n-1)/2)\cdot \Gamma(n/2) = \sqrt{\pi} \Gamma (n-1)</math>, | :<math>2^{n-2} \,\Gamma((n-1)/2)\cdot \Gamma(n/2) = \sqrt{\pi} \Gamma (n-1)</math>, | ||
जिससे: | |||
:<math>\mu = \sqrt{2/\pi}\,2^{n-2}\,\frac{(\Gamma(n/2))^2}{\Gamma(n-1)}</math> | :<math>\mu = \sqrt{2/\pi}\,2^{n-2}\,\frac{(\Gamma(n/2))^2}{\Gamma(n-1)}</math> | ||
गामा | गामा फलन के लिए स्टर्लिंग के सन्निकटन का उपयोग करते हुए, हमें माध्य के लिए निम्नलिखित अभिव्यक्ति प्राप्त होती है: | ||
:<math>\mu = \sqrt{2/\pi}\,2^{n-2}\,\frac{\left(\sqrt{2\pi}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot[1+\frac{1}{12(n/2-1)}+O(\frac{1}{n^2})]\right)^2}{\sqrt{2\pi}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+\frac{1}{12(n-2)}+O(\frac{1}{n^2})]}</math> | :<math>\mu = \sqrt{2/\pi}\,2^{n-2}\,\frac{\left(\sqrt{2\pi}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot[1+\frac{1}{12(n/2-1)}+O(\frac{1}{n^2})]\right)^2}{\sqrt{2\pi}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+\frac{1}{12(n-2)}+O(\frac{1}{n^2})]}</math> | ||
::<math> = (n-2)^{1/2}\,\cdot \left[1+\frac{1}{4n}+O(\frac{1}{n^2})\right] = \sqrt{n-1}\,(1-\frac{1}{n-1})^{1/2}\cdot \left[1+\frac{1}{4n}+O(\frac{1}{n^2})\right]</math> | ::<math> = (n-2)^{1/2}\,\cdot \left[1+\frac{1}{4n}+O(\frac{1}{n^2})\right] = \sqrt{n-1}\,(1-\frac{1}{n-1})^{1/2}\cdot \left[1+\frac{1}{4n}+O(\frac{1}{n^2})\right]</math> | ||
::<math> = \sqrt{n-1}\,\cdot \left[1-\frac{1}{2n}+O(\frac{1}{n^2})\right]\,\cdot \left[1+\frac{1}{4n}+O(\frac{1}{n^2})\right]</math> | ::<math> = \sqrt{n-1}\,\cdot \left[1-\frac{1}{2n}+O(\frac{1}{n^2})\right]\,\cdot \left[1+\frac{1}{4n}+O(\frac{1}{n^2})\right]</math> | ||
::<math> = \sqrt{n-1}\,\cdot \left[1-\frac{1}{4n}+O(\frac{1}{n^2})\right]</math> | ::<math> = \sqrt{n-1}\,\cdot \left[1-\frac{1}{4n}+O(\frac{1}{n^2})\right]</math> | ||
और इस प्रकार भिन्नता है: | और इस प्रकार भिन्नता निम्न प्रकार होती है: | ||
:<math>V=(n-1)-\mu^2\, = (n-1)\cdot \frac{1}{2n}\,\cdot \left[1+O(\frac{1}{n})\right]</math> | :<math>V=(n-1)-\mu^2\, = (n-1)\cdot \frac{1}{2n}\,\cdot \left[1+O(\frac{1}{n})\right]</math> | ||
==संबंधित वितरण== | ==संबंधित वितरण== | ||
* | *यदि <math>X \sim \chi_k</math> तब <math>X^2 \sim \chi^2_k</math> (ची-वर्ग वितरण) | ||
*<math> \lim_{k \to \infty}\tfrac{\chi_k-\mu_k}{\sigma_k} \xrightarrow{d}\ N(0,1) \,</math> (सामान्य वितरण) | *<math> \lim_{k \to \infty}\tfrac{\chi_k-\mu_k}{\sigma_k} \xrightarrow{d}\ N(0,1) \,</math> (सामान्य वितरण) | ||
* | *यदि <math> X \sim N(0,1)\,</math> तब <math>| X | \sim \chi_1 \,</math> | ||
* | *यदि <math>X \sim \chi_1\,</math> तब <math>\sigma X \sim HN(\sigma)\,</math> ([[अर्ध-सामान्य वितरण]]) किसी के लिए <math> \sigma > 0 \, </math> | ||
*<math> \chi_2 \sim \mathrm{Rayleigh}(1)\,</math> (रेले वितरण) | *<math> \chi_2 \sim \mathrm{Rayleigh}(1)\,</math> (रेले वितरण) | ||
*<math> \chi_3 \sim \mathrm{Maxwell}(1)\,</math> ([[मैक्सवेल वितरण]]) | *<math> \chi_3 \sim \mathrm{Maxwell}(1)\,</math> ([[मैक्सवेल वितरण]]) | ||
*<math> \|\boldsymbol{N}_{i=1,\ldots,k}{(0,1)}\|_2 \sim \chi_k </math>, | *<math> \|\boldsymbol{N}_{i=1,\ldots,k}{(0,1)}\|_2 \sim \chi_k </math>, बहुभिन्नरूपी सामान्य वितरण का मानक सामान्य यादृच्छिक सदिश साथ में <math>k</math> आयाम के साथ ची वितरण के अनुसार वितरित किया जाता है जहाँ <math> k </math> स्वतंत्रता की डिग्री होती है। | ||
*ची वितरण [[सामान्यीकृत गामा वितरण]] या [[नाकागामी वितरण]] या [[गैर-केंद्रीय ची वितरण]] का एक विशेष | *ची वितरण [[सामान्यीकृत गामा वितरण]] या [[नाकागामी वितरण]] या [[गैर-केंद्रीय ची वितरण]] का एक विशेष स्थति होती है। | ||
*ची वितरण का माध्य (वर्गमूल के आधार | *ची वितरण का माध्य (वर्गमूल के आधार <math>n-1</math> पर मापा गया) सामान्य वितरण के लिए मानक विचलन परिणामों के निष्पक्ष प्राक्लन में सुधार कारक उत्पन्न करता है। | ||
{| class="wikitable" style="margin: 1em auto;" | {| class="wikitable" style="margin: 1em auto;" | ||
|+ ''' | |+ '''विभिन्न ची और ची-वर्ग वितरणविभिन्न ची और ची-वर्ग वितरण''' | ||
|- | |- | ||
! | ! नाम !! सांख्यिकीय | ||
|- | |- | ||
| [[chi-squared distribution]] || <math>\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2</math> | | [[chi-squared distribution|ची-वर्ग वितरण]] || <math>\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2</math> | ||
|- | |- | ||
| [[noncentral chi-squared distribution]] || <math>\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2</math> | | [[noncentral chi-squared distribution|गैरकेंद्रीय ची-वर्ग वितरण]] || <math>\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2</math> | ||
|- | |- | ||
| | | ची वितरण || <math>\sqrt{\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2}</math> | ||
|- | |- | ||
| [[noncentral chi distribution]] || <math>\sqrt{\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2}</math> | | [[noncentral chi distribution|गैर-केंद्रीय ची वितरण]] || <math>\sqrt{\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2}</math> | ||
|} | |} | ||
| Line 141: | Line 140: | ||
{{ProbDistributions|continuous-semi-infinite}} | {{ProbDistributions|continuous-semi-infinite}} | ||
{{DEFAULTSORT:Chi Distribution}} | {{DEFAULTSORT:Chi Distribution}} | ||
[[Category: | [[Category:Collapse templates|Chi Distribution]] | ||
[[Category:Created On 07/07/2023]] | [[Category:Created On 07/07/2023|Chi Distribution]] | ||
[[Category:Machine Translated Page|Chi Distribution]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Chi Distribution]] | |||
[[Category:Pages with script errors|Chi Distribution]] | |||
[[Category:Sidebars with styles needing conversion|Chi Distribution]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Chi Distribution]] | |||
[[Category:Templates generating microformats|Chi Distribution]] | |||
[[Category:Templates that are not mobile friendly|Chi Distribution]] | |||
[[Category:Templates using TemplateData|Chi Distribution]] | |||
[[Category:Wikipedia metatemplates|Chi Distribution]] | |||
[[Category:घातीय पारिवारिक वितरण|Chi Distribution]] | |||
[[Category:निरंतर वितरण|Chi Distribution]] | |||
[[Category:सामान्य वितरण|Chi Distribution]] | |||
Latest revision as of 19:17, 21 July 2023
संभाव्यता सिद्धांत और सांख्यिकी में, ची वितरण एक सतत संभाव्यता वितरण होता है। यह एक मानक सामान्य वितरण के पश्चात् स्वतंत्र यादृच्छिक चर के एक समूह के वर्गों के योग के धनात्मक वर्गमूल का वितरण, या समकक्ष, मूल से यादृच्छिक चर की यूक्लिडियन दूरी का वितरण होता है। इस प्रकार यह ची-वर्ग वितरण को स्वीकृति देने वाले एक चर के धनात्मक वर्गमूलों के वितरण का वर्णन करके ची-वर्ग वितरण से संबंधित होता है।
यदि होता हैं तो माध्य 0 और मानक विचलन 1 के साथ स्वतंत्र होता, सामान्य वितरण यादृच्छिक चर, फिर आँकड़ा निम्न प्रकार होता है
जिसे ची वितरण के अनुसार वितरित किया जाता है। ची वितरण का एक पैरामीटर होता है, जो स्वतंत्रता की डिग्री की संख्या को निर्दिष्ट करता है (अर्थात् यादृच्छिक चर की संख्या होती है)।
|
Probability density function 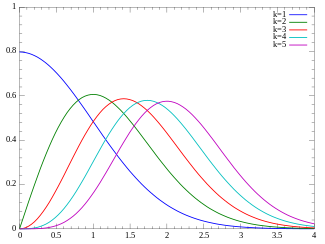 | |||
|
Cumulative distribution function 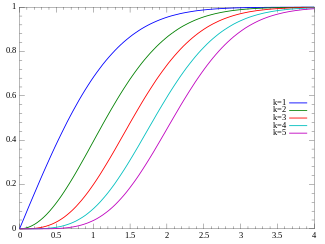 | |||
| Parameters | (degrees of freedom) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | for | ||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy |
| ||
| MGF | Complicated (see text) | ||
| CF | Complicated (see text) | ||
सबसे परिचित उदाहरण रेले वितरण (स्वतंत्रता की दो डिग्री के साथ ची वितरण) और एक आदर्श गैस में आणविक गति का मैक्सवेल-बोल्ट्ज़मैन वितरण (स्वतंत्रता की तीन डिग्री के साथ ची वितरण) होता है।
परिभाषाएँ
संभाव्यता घनत्व फलन
ची-वितरण की संभाव्यता घनत्व फलन (पीडीएफ) निम्न प्रकार है
जहाँ गामा फलन होता है।
संचयी वितरण फलन
संचयी वितरण फलन निम्न प्रकार द्वारा दिया गया है:
जहाँ नियमित गामा फलन होता है।
कार्य उत्पन्न करना
क्षण-उत्पन्न करने वाला कार्य इस प्रकार दिया गया है:
जहाँ कुमेर का संगम हाइपरज्यामितीय फलन होता है। विशेषता फलन (संभावना सिद्धांत) द्वारा दिया गया है:
गुण
क्षण
अपक्व क्षण तब निम्न प्रकार दिया जाता है:
जहाँ एक गामा फलन होता है। इस प्रकार पहले कुछ अपक्व क्षण निम्न प्रकार होता हैं:
- :
जहाँ गामा फलन के लिए पुनरावृत्ति संबंध का उपयोग करके सबसे सही अभिव्यक्ति प्राप्त की जाती है:
इन अभिव्यक्तियों से हम निम्नलिखित संबंध प्राप्त कर सकते हैं:
अर्थ: जो बड़े k के समीप होता है।
विचरण: जो जैसे k बढ़ती है वैसे ही समीप आता है।
विषमता: होती है।
कर्टोसिस की अधिकता: होती है।
एंट्रॉपी
एन्ट्रापी निम्न प्रकार दी जाती है:
जहाँ पलिगमी(बहुविवाह) फलन होता है।
बड़ा एन सन्निकटन
हम ची वितरण के माध्य और विचरण का बड़ा n=k+1 सन्निकटन प्राप्त करते हैं। इसमें एक एप्लिकेशन उपस्थित होती है उदा. सामान्य रूप से वितरित जनसंख्या के प्रतिरूप के मानक विचलन का वितरण ज्ञात करने में, जहाँ n प्रतिरूप आकार होता है।
तब माध्य निम्न प्रकार होता है:
हम लिखने के लिए लीजेंड्रे दोहराव सूत्र का उपयोग करते हैं::
- ,
जिससे:
गामा फलन के लिए स्टर्लिंग के सन्निकटन का उपयोग करते हुए, हमें माध्य के लिए निम्नलिखित अभिव्यक्ति प्राप्त होती है:
और इस प्रकार भिन्नता निम्न प्रकार होती है:
संबंधित वितरण
- यदि तब (ची-वर्ग वितरण)
- (सामान्य वितरण)
- यदि तब
- यदि तब (अर्ध-सामान्य वितरण) किसी के लिए
- (रेले वितरण)
- (मैक्सवेल वितरण)
- , बहुभिन्नरूपी सामान्य वितरण का मानक सामान्य यादृच्छिक सदिश साथ में आयाम के साथ ची वितरण के अनुसार वितरित किया जाता है जहाँ स्वतंत्रता की डिग्री होती है।
- ची वितरण सामान्यीकृत गामा वितरण या नाकागामी वितरण या गैर-केंद्रीय ची वितरण का एक विशेष स्थति होती है।
- ची वितरण का माध्य (वर्गमूल के आधार पर मापा गया) सामान्य वितरण के लिए मानक विचलन परिणामों के निष्पक्ष प्राक्लन में सुधार कारक उत्पन्न करता है।
| नाम | सांख्यिकीय |
|---|---|
| ची-वर्ग वितरण | |
| गैरकेंद्रीय ची-वर्ग वितरण | |
| ची वितरण | |
| गैर-केंद्रीय ची वितरण |
यह भी देखें
- नाकागामी वितरण
संदर्भ
- Martha L. Abell, James P. Braselton, John Arthur Rafter, John A. Rafter, Statistics with Mathematica (1999), 237f.
- Jan W. Gooch, Encyclopedic Dictionary of Polymers vol. 1 (2010), Appendix E, p. 972.