अर्ध-सामान्य वितरण
|
Probability density function  | |||
|
Cumulative distribution function 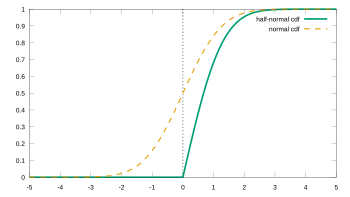 | |||
| Parameters | — (scale) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Quantile | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
संभाव्यता सिद्धांत और सांख्यिकी में, अर्ध-सामान्य वितरण मुड़े हुए सामान्य वितरण का विशेष स्थिति है।
माना सामान्य सामान्य वितरण का पालन करें, . तब, अर्ध-सामान्य वितरण का अनुसरण करता है। इस प्रकार, अर्ध-सामान्य वितरण माध्य शून्य के साथ सामान्य सामान्य वितरण के माध्य है।
गुण
सामान्य वितरण के पैरामीट्रिजेशन का उपयोग करते हुए, आधे-सामान्य की संभाव्यता घनत्व फलन (पीडीएफ) द्वारा दी गई है
जहाँ .
वैकल्पिक रूप से स्केल्ड परिशुद्धता (विचरण का व्युत्क्रम) पैरामीट्रिजेशन का उपयोग करना (यदि समस्याओं से बचने के लिए)। शून्य के निकट है), सेटिंग द्वारा प्राप्त किया गया था, संभाव्यता घनत्व फलन द्वारा दिया गया है
जहाँ .
संचयी वितरण फलन (सीडीएफ) द्वारा दिया गया है
परिवर्तन-परिवर्तन का उपयोग करना , सीडीएफ को इस प्रकार लिखा जा सकता है
जहां ईआरएफ त्रुटि फलन है, कई गणितीय सॉफ़्टवेयर पैकेजों में मानक फलन है।
क्वांटाइल फलन (या उलटा सीडीएफ) लिखा गया है:
जहाँ और व्युत्क्रम त्रुटि फलन व्युत्क्रम फलन है
अपेक्षा तब दी जाती है
विचरण द्वारा दिया गया है
चूँकि यह प्रसरण σX के समानुपाती है ,इस प्रकार σ2 को नए वितरण के स्केल मापदंड के रूप में देखा जा सकता है।
अर्ध-सामान्य वितरण की विभेदक एन्ट्रापी शून्य-माध्य सामान्य वितरण की अंतर एन्ट्रापी से ठीक बिट कम है, जिसका दूसरा क्षण लगभग 0 है। इसे सहज रूप से समझा जा सकता है क्योंकि परिमाण संचालक जानकारी को बिट कम कर देता है (यदि संभावना है इसके इनपुट पर वितरण सम है)। वैकल्पिक रूप से, चूंकि अर्ध-सामान्य वितरण सदैव धनात्मक होता है, मानक सामान्य यादृच्छिक चर धनात्मक (मान लीजिए, 1) या ऋणात्मक (मान लीजिए, 0) था या नहीं, यह रिकॉर्ड करने के लिए लगने वाला बिट अब आवश्यक नहीं है। इस प्रकार,
अनुप्रयोग
अर्ध-सामान्य वितरण का उपयोग सामान्यतः बायेसियन अनुमान अनुप्रयोगों में भिन्नता मापदंडों के लिए पूर्व संभाव्यता वितरण के रूप में किया जाता है।[1][2]
मापदंड अनुमान
दिए गए नंबर आधे-सामान्य वितरण से लिया गया था, अज्ञात मापदंड उस वितरण का अनुमान अधिकतम संभावना की विधि द्वारा दिया जा सकता है
पूर्वाग्रह सामान्य है
जो अधिकतम संभावना अनुमान उच्च-क्रम गुण या पूर्वाग्रह-संशोधित अधिकतम संभावना अनुमानक उत्पन्न करता है
संबंधित वितरण
- वितरण μ = 0 के साथ मुड़े हुए सामान्य वितरण का विशेष स्थिति है।
- यह नीचे से शून्य पर काटे गए शून्य-माध्य सामान्य वितरण से भी मेल खाता है (काटे गए सामान्य वितरण देखें)
- यदि Y का वितरण अर्ध-सामान्य है, तो (Y/σ)2 में 1 डिग्री की स्वतंत्रता के साथ ची वर्ग वितरण है, अर्थात Y/σ में 1 डिग्री की स्वतंत्रता के साथ ची वितरण है।
- अर्ध-सामान्य वितरण d = 1, p = 2, a = के साथ सामान्यीकृत गामा वितरण का विशेष स्थिति है.
- यदि Y का वितरण अर्ध-सामान्य है, तो Y-2 में लेवी वितरण है
- रेले वितरण आधे-सामान्य वितरण का क्षण-झुका हुआ और स्केल किया गया सामान्यीकरण है।
- संशोधित अर्ध-सामान्य वितरण [3] पीडीएफ के साथ के रूप में दिया गया है , जहाँ फॉक्स-राइट साई फलन को दर्शाता है।
यह भी देखें
- अर्ध-टी वितरण अर्ध-टी वितरण
- सामान्य वितरण को छोटा कर दिया गया
- फोल्डेड सामान्य वितरण
- संशोधित गाऊसी वितरण
संदर्भ
- ↑ Gelman, A. (2006), "Prior distributions for variance parameters in hierarchical models", Bayesian Analysis, 1 (3): 515–534, doi:10.1214/06-ba117a
- ↑ Röver, C.; Bender, R.; Dias, S.; Schmid, C.H.; Schmidli, H.; Sturtz, S.; Weber, S.; Friede, T. (2021), "On weakly informative prior distributions for the heterogeneity parameter in Bayesian random‐effects meta‐analysis", Research Synthesis Methods, 12 (4): 448–474, arXiv:2007.08352, doi:10.1002/jrsm.1475, PMID 33486828, S2CID 220546288
- ↑ Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 June 2021). "The Modified-Half-Normal distribution: Properties and an efficient sampling scheme". Communications in Statistics - Theory and Methods: 1–23. doi:10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.
अग्रिम पठन
- Leone, F. C.; Nelson, L. S.; Nottingham, R. B. (1961), "The folded normal distribution", Technometrics, 3 (4): 543–550, doi:10.2307/1266560, hdl:2027/mdp.39015095248541, JSTOR 1266560
बाहरी संबंध
- (note that MathWorld uses the parameter