क्यू-फलन: Difference between revisions
(Created page with "{{Short description|Statistics function}} {{For|the phase-space function representing a quantum state|Husimi Q representation}} Image:Q-function.png|thumb|right|400px|क्...") |
No edit summary |
||
| (19 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Statistics function}} | {{Short description|Statistics function}} | ||
{{For|the phase-space function representing a quantum state|Husimi Q representation}} | {{For|the phase-space function representing a quantum state|Husimi Q representation}} | ||
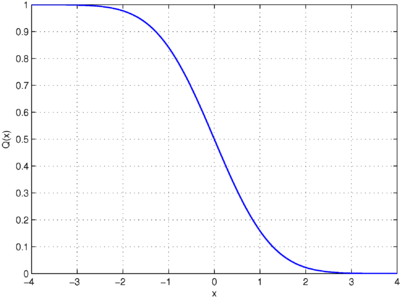
[[Image:Q-function.png|thumb|right|400px|क्यू- | [[Image:Q-function.png|thumb|right|400px|क्यू-फलन का प्लॉट]]आंकड़ों में, '''क्यू''-फलन''''' मानक सामान्य वितरण का संचयी वितरण फलन (पूंछ वितरण फलन) है।<ref>[http://cnx.org/content/m11537/latest/ The Q-function], from [[cnx.org]]</ref><ref name="jo">[http://www.eng.tau.ac.il/~jo/academic/Q.pdf Basic properties of the Q-function] {{webarchive |url=https://web.archive.org/web/20090325160012/http://www.eng.tau.ac.il/~jo/academic/Q.pdf |date=March 25, 2009 }}</ref> दूसरे शब्दों में <math>Q(x)</math> संभावना है कि एक सामान्य (गाऊसी) यादृच्छिक चर x मानक विचलन से बड़ा मान प्राप्त करेगा। समान रूप से <math>Q(x)</math> यह संभावना है कि एक मानक सामान्य यादृच्छिक चर <math>x</math> से बड़ा मान लेता है। | ||
अगर <math>Y</math> माध्य के साथ एक गाऊसी यादृच्छिक चर | अगर <math>Y</math> माध्य के साथ एक गाऊसी यादृच्छिक चर <math>\mu</math> हैं और विचरण <math>\sigma^2</math>, तो <math>X = \frac{Y-\mu}{\sigma}</math> मानक सामान्य वितरण हैं और | ||
:<math>P(Y > y) = P(X > x) = Q(x)</math> | :<math>P(Y > y) = P(X > x) = Q(x)</math> | ||
<math>x = \frac{y-\mu}{\sigma}</math> जहाँ | |||
क्यू- | '''क्यू-फलन''' की अन्य परिभाषाएँ, जो सभी सामान्य संचयी वितरण फलन के सरल परिवर्तन का भी कभी-कभी उपयोग किया जाता है।<ref>[http://mathworld.wolfram.com/NormalDistributionFunction.html Normal Distribution Function – from Wolfram MathWorld<!-- Bot generated title -->]</ref> | ||
सामान्य वितरण के संचयी वितरण | |||
सामान्य वितरण के संचयी वितरण फलन से इसके संबंध के कारण '''क्यू-फलन''' को [[त्रुटि फ़ंक्शन|त्रुटि फलन]] के संदर्भ में भी व्यक्त किया जा सकता है, जो लागू गणित और भौतिकी में एक महत्वपूर्ण फलन है। | |||
== परिभाषा और बुनियादी गुण == | == परिभाषा और बुनियादी गुण == | ||
औपचारिक रूप से, | औपचारिक रूप से, क्यू-फलन को इस प्रकार परिभाषित किया गया है | ||
:<math>Q(x) = \frac{1}{\sqrt{2\pi}} \int_x^\infty \exp\left(-\frac{u^2}{2}\right) \, du.</math> | :<math>Q(x) = \frac{1}{\sqrt{2\pi}} \int_x^\infty \exp\left(-\frac{u^2}{2}\right) \, du.</math> | ||
| Line 18: | Line 19: | ||
:<math>Q(x) = 1 - Q(-x) = 1 - \Phi(x)\,\!,</math> | :<math>Q(x) = 1 - Q(-x) = 1 - \Phi(x)\,\!,</math> | ||
जहाँ <math>\Phi(x)</math> मानक सामान्य गाऊसी वितरण का संचयी वितरण फलन है। | |||
क्यू- | क्यू-फलन को त्रुटि फलन या पूरक त्रुटि फलन के रूप में व्यक्त किया जा सकता है<ref name="jo"/> | ||
:<math> | :<math> | ||
| Line 29: | Line 30: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
क्यू- | क्यू-फलन का एक वैकल्पिक रूप जिसे इसके खोजकर्ता के नाम पर क्रेग के सूत्र के रूप में जाना जाता है, इस प्रकार व्यक्त किया गया है:<ref>{{cite book |doi=10.1109/MILCOM.1991.258319 |chapter-url=http://wsl.stanford.edu/~ee359/craig.pdf|chapter=A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations|title=MILCOM 91 - Conference record|pages=571–575|year=1991|last1=Craig|first1=J.W.|isbn=0-87942-691-8|s2cid=16034807}}</ref> | ||
:<math>Q(x) = \frac{1}{\pi} \int_0^{\frac{\pi}{2}} \exp \left( - \frac{x^2}{2 \sin^2 \theta} \right) d\theta.</math> | :<math>Q(x) = \frac{1}{\pi} \int_0^{\frac{\pi}{2}} \exp \left( - \frac{x^2}{2 \sin^2 \theta} \right) d\theta.</math> | ||
यह अभिव्यक्ति केवल x के सकारात्मक मानों के लिए मान्य है, लेकिन इसका उपयोग नकारात्मक मानों के लिए Q(x) प्राप्त करने के लिए Q(x) = 1 − Q(−x) के संयोजन में किया जा सकता है। यह रूप लाभप्रद है क्योंकि एकीकरण की सीमा निश्चित और सीमित है। | यह अभिव्यक्ति केवल x के सकारात्मक मानों के लिए मान्य है, लेकिन इसका उपयोग नकारात्मक मानों के लिए Q(x) प्राप्त करने के लिए Q(x) = 1 − Q(−x) के संयोजन में किया जा सकता है। यह रूप लाभप्रद है क्योंकि एकीकरण की सीमा निश्चित और सीमित है। | ||
क्रेग के | क्रेग के सूत्र को बाद में बेहनाद (2020) द्वारा <ref>{{cite journal |doi=10.1109/TCOMM.2020.2986209 |title=क्रेग के क्यू-फंक्शन फॉर्मूला का एक नया विस्तार और दोहरे-शाखा ईजीसी प्रदर्शन विश्लेषण में इसका अनुप्रयोग|journal=IEEE Transactions on Communications |volume=68|issue=7|pages=4117–4125|year=2020|last1=Behnad|first1=Aydin|s2cid=216500014}}</ref> दो गैर-नकारात्मक चर के योग के क्यू-फलन के लिए इस प्रकार बढ़ाया गया: | ||
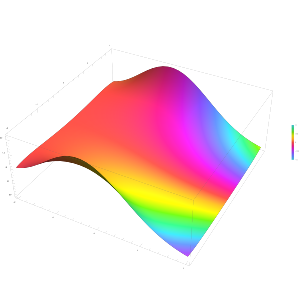
:[[File:Q function complex plot plotted with Mathematica 13.1 ComplexPlot3D.svg|alt=the Q- | :[[File:Q function complex plot plotted with Mathematica 13.1 ComplexPlot3D.svg|alt=the Q-function plotted in the complex plane|thumb|क्यू-फलन को सम्मिश्र सतह में प्लॉट किया गया]]<math>Q(x+y) = \frac{1}{\pi} \int_0^{\frac{\pi}{2}} \exp \left( - \frac{x^2}{2 \sin^2 \theta} - \frac{y^2}{2 \cos^2 \theta} \right) d\theta, \quad x,y \geqslant 0 .</math> | ||
==सीमाएँ और सन्निकटन== | ==सीमाएँ और सन्निकटन== | ||
*क्यू- | *क्यू-फलन कोई प्राथमिक फलन नहीं है। हालाँकि, बोरजेसन-सुंदरबर्ग सीमा जहाँ <math>\phi(x)</math> मानक सामान्य वितरण का घनत्व फलन है,<ref name = "Borjesson">{{Cite journal |doi = 10.1109/TCOM.1979.1094433|title = संचार अनुप्रयोगों के लिए त्रुटि फ़ंक्शन Q(x) का सरल अनुमान|journal = IEEE Transactions on Communications|volume = 27|issue = 3|pages = 639–643|year = 1979|last1 = Borjesson|first1 = P.|last2 = Sundberg|first2 = C.-E.}}</ref> | ||
::<math>\left (\frac{x}{1+x^2} \right ) \phi(x) < Q(x) < \frac{\phi(x)}{x}, \qquad x>0,</math> | ::<math>\left (\frac{x}{1+x^2} \right ) \phi(x) < Q(x) < \frac{\phi(x)}{x}, \qquad x>0,</math> | ||
:बड़े एक्स के लिए तेजी से तंग हो जाते हैं | :बड़े एक्स के लिए तेजी से तंग हो जाते हैं और अधिकतर उपयोगी होते हैं। | ||
:[[प्रतिस्थापन द्वारा एकीकरण]] | :[[प्रतिस्थापन द्वारा एकीकरण|प्रतिस्थापन]] v =u<sup>2</sup>/2 का उपयोग करके ऊपरी सीमा इस प्रकार प्राप्त की जाती है: | ||
::<math>Q(x) =\int_x^\infty\phi(u)\,du <\int_x^\infty\frac ux\phi(u)\,du =\int_{\frac{x^2}{2}}^\infty\frac{e^{-v}}{x\sqrt{2\pi}}\,dv=-\biggl.\frac{e^{-v}}{x\sqrt{2\pi}}\biggr|_{\frac{x^2}{2}}^\infty=\frac{\phi(x)}{x}.</math> | ::<math>Q(x) =\int_x^\infty\phi(u)\,du <\int_x^\infty\frac ux\phi(u)\,du =\int_{\frac{x^2}{2}}^\infty\frac{e^{-v}}{x\sqrt{2\pi}}\,dv=-\biggl.\frac{e^{-v}}{x\sqrt{2\pi}}\biggr|_{\frac{x^2}{2}}^\infty=\frac{\phi(x)}{x}.</math> | ||
:इसी प्रकार, | :इसी प्रकार, <math>\phi'(u) = - u \phi(u)</math> [[भागफल नियम|भागफल नियम का उपयोग करके]] | ||
::<math>\left(1+\frac1{x^2}\right)Q(x) =\int_x^\infty \left(1+\frac1{x^2}\right)\phi(u)\,du >\int_x^\infty \left(1+\frac1{u^2}\right)\phi(u)\,du =-\biggl.\frac{\phi(u)}u\biggr|_x^\infty | ::<math>\left(1+\frac1{x^2}\right)Q(x) =\int_x^\infty \left(1+\frac1{x^2}\right)\phi(u)\,du >\int_x^\infty \left(1+\frac1{u^2}\right)\phi(u)\,du =-\biggl.\frac{\phi(u)}u\biggr|_x^\infty | ||
| Line 52: | Line 63: | ||
:Q(x) को हल करने से निचली सीमा मिलती है। | :Q(x) को हल करने से निचली सीमा मिलती है। | ||
:ऊपरी और निचली सीमा का ज्यामितीय माध्य | :ऊपरी और निचली सीमा का ज्यामितीय माध्य <math>Q(x)</math> के लिए उपयुक्त सन्निकटन देता है: | ||
::<math>Q(x) \approx \frac{\phi(x)}{\sqrt{1 + x^2}}, \qquad x \geq 0. </math> | ::<math>Q(x) \approx \frac{\phi(x)}{\sqrt{1 + x^2}}, \qquad x \geq 0. </math> | ||
* | * निम्नलिखित अभिव्यक्ति को अनुकूलित करके <math>Q(x)</math> की सख्त सीमाएँ और सन्निकटन भी प्राप्त किए जा सकते हैं: <ref name = "Borjesson"/> | ||
:: <math> \tilde{Q}(x) = \frac{\phi(x)}{(1-a)x + a\sqrt{x^2 + b}}. </math> | :: <math> \tilde{Q}(x) = \frac{\phi(x)}{(1-a)x + a\sqrt{x^2 + b}}. </math> | ||
:के लिए <math>x \geq 0</math>, सर्वोत्तम ऊपरी सीमा किसके द्वारा दी गई है <math>a = 0.344</math> और <math>b = 5.334</math> 0.44% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ। इसी प्रकार, सर्वोत्तम सन्निकटन द्वारा दिया गया है <math>a = 0.339</math> और <math>b = 5.510</math> 0.27% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ। अंत में, सबसे अच्छी निचली सीमा दी गई है <math>a = 1/\pi</math> और <math>b = 2 \pi</math> 1.17% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ। | :के लिए <math>x \geq 0</math>, सर्वोत्तम ऊपरी सीमा किसके द्वारा दी गई है <math>a = 0.344</math> और <math>b = 5.334</math> 0.44% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ। इसी प्रकार, सर्वोत्तम सन्निकटन द्वारा दिया गया है <math>a = 0.339</math> और <math>b = 5.510</math> 0.27% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ। अंत में, सबसे अच्छी निचली सीमा दी गई है <math>a = 1/\pi</math> और <math>b = 2 \pi</math> 1.17% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ। | ||
* क्यू- | * क्यू-फलन का [[चेर्नॉफ़ बाध्य]] है | ||
::<math>Q(x)\leq e^{-\frac{x^2}{2}}, \qquad x>0</math> | ::<math>Q(x)\leq e^{-\frac{x^2}{2}}, \qquad x>0</math> | ||
*बेहतर घातीय सीमाएँ और | *बेहतर घातीय सीमाएँ और शुद्ध घातीय सन्निकटन हैं <ref>{{cite journal |url=http://campus.unibo.it/85943/1/mcddmsTranWIR2003.pdf |doi=10.1109/TWC.2003.814350|title=फ़ेडिंग चैनलों में त्रुटि संभावना की गणना के लिए नई घातीय सीमाएँ और सन्निकटन|journal=IEEE Transactions on Wireless Communications|volume=24|issue=5|pages=840–845|year=2003|last1=Chiani|first1=M.|last2=Dardari|first2=D.|last3=Simon|first3=M.K.}}</ref> | ||
::<math>Q(x)\leq \tfrac{1}{4}e^{-x^2}+\tfrac{1}{4}e^{-\frac{x^2}{2}} \leq \tfrac{1}{2}e^{-\frac{x^2}{2}}, \qquad x>0</math> | ::<math>Q(x)\leq \tfrac{1}{4}e^{-x^2}+\tfrac{1}{4}e^{-\frac{x^2}{2}} \leq \tfrac{1}{2}e^{-\frac{x^2}{2}}, \qquad x>0</math> | ||
:: <math>Q(x)\approx \frac{1}{12}e^{-\frac{x^2}{2}}+\frac{1}{4}e^{-\frac{2}{3} x^2}, \qquad x>0 </math> | :: <math>Q(x)\approx \frac{1}{12}e^{-\frac{x^2}{2}}+\frac{1}{4}e^{-\frac{2}{3} x^2}, \qquad x>0 </math> | ||
*उपरोक्त को तनाश और रिइहोनेन (2020) द्वारा सामान्यीकृत किया गया था,<ref>{{cite journal |doi=10.1109/TCOMM.2020.3006902|title=घातांक के योग द्वारा गॉसियन क्यू-फ़ंक्शन के लिए वैश्विक न्यूनतम अनुमान और सीमाएँ|journal=IEEE Transactions on Communications|year=2020|last1=Tanash|first1=I.M.|last2=Riihonen|first2=T.|volume=68|issue=10|pages=6514–6524|arxiv=2007.06939|s2cid=220514754}}</ref> | *उपरोक्त को तनाश और रिइहोनेन (2020) द्वारा सामान्यीकृत किया गया था,<ref>{{cite journal |doi=10.1109/TCOMM.2020.3006902|title=घातांक के योग द्वारा गॉसियन क्यू-फ़ंक्शन के लिए वैश्विक न्यूनतम अनुमान और सीमाएँ|journal=IEEE Transactions on Communications|year=2020|last1=Tanash|first1=I.M.|last2=Riihonen|first2=T.|volume=68|issue=10|pages=6514–6524|arxiv=2007.06939|s2cid=220514754}}</ref> जिन्होंने दिखाया कि <math>Q(x)</math> का उचित अनुमान लगाया जा सकता है या सीमाबद्ध किया जा सकता है | ||
::<math>\tilde{Q}(x) = \sum_{n=1}^N a_n e^{-b_n x^2}.</math> | ::<math>\tilde{Q}(x) = \sum_{n=1}^N a_n e^{-b_n x^2}.</math> | ||
:विशेष रूप से, उन्होंने संख्यात्मक गुणांकों को हल करने के लिए एक व्यवस्थित पद्धति प्रस्तुत की <math>\{(a_n,b_n)\}_{n=1}^N</math> जो एक न्यूनतम | :विशेष रूप से, उन्होंने संख्यात्मक गुणांकों को हल करने के लिए एक व्यवस्थित पद्धति प्रस्तुत की <math>\{(a_n,b_n)\}_{n=1}^N</math> जो एक न्यूनतम सन्निकटन या बाध्य उत्पन्न करता है: <math>Q(x) \approx \tilde{Q}(x)</math>, <math>Q(x) \leq \tilde{Q}(x)</math> या <math>Q(x) \geq \tilde{Q}(x)</math> के लिए <math>x\geq0</math>. लेख्य में सारणीबद्ध उदाहरण गुणांकों के साथ <math>N = 20</math> सापेक्ष और निरपेक्ष सन्निकटन त्रुटियाँ कम हैं <math>2.831 \cdot 10^{-6}</math> और <math>1.416 \cdot 10^{-6}</math> क्रमश से कम हैं। गुणांक <math>\{(a_n,b_n)\}_{n=1}^N</math> घातीय सन्निकटन और सीमा तक के कई रूपों के लिए <math>N = 25</math> एक व्यापक डेटासेट के रूप में विवृत अभिगम के लिए जारी किया गया है।<ref>{{cite journal |doi=10.5281/zenodo.4112978|title=Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]|url=https://zenodo.org/record/4112978|website=Zenodo|year=2020|last1=Tanash|first1=I.M.|last2=Riihonen|first2=T.}}</ref> | ||
* | *<math>Q(x)</math> के लिए <math>x \in [0,\infty)</math> का एक और सन्निकटन कारागियानिडिस और लिओमपास (2007) द्वारा दिया गया है,<ref>{{cite journal |doi=10.1109/LCOMM.2007.070470 |url=http://users.auth.gr/users/9/3/028239/public_html/pdf/Q_Approxim.pdf|title=गॉसियन क्यू-फ़ंक्शन के लिए एक बेहतर अनुमान|journal=IEEE Communications Letters|volume=11|issue=8|pages=644–646|year=2007|last1=Karagiannidis|first1=George|last2=Lioumpas|first2=Athanasios|s2cid=4043576}}</ref> जिन्होंने पैरामीटर्स के उचित चयन के लिए <math>\{A, B\}</math> प्रदर्शन किया | ||
:: <math>f(x; A, B) = \frac{\left(1 - e^{-Ax}\right)e^{-x^2}}{B\sqrt{\pi} x} \approx \operatorname{erfc} \left(x\right).</math> | :: <math>f(x; A, B) = \frac{\left(1 - e^{-Ax}\right)e^{-x^2}}{B\sqrt{\pi} x} \approx \operatorname{erfc} \left(x\right).</math> | ||
| Line 76: | Line 87: | ||
:: <math>\{A, B\} = \underset{\{A,B\}}{\arg \min} \frac{1}{R} \int_0^R | f(x; A, B) - \operatorname{erfc}(x) |dx.</math> | :: <math>\{A, B\} = \underset{\{A,B\}}{\arg \min} \frac{1}{R} \int_0^R | f(x; A, B) - \operatorname{erfc}(x) |dx.</math> | ||
: | : <math>R = 20</math> का उपयोग करते हुए और संख्यात्मक रूप से एकीकृत करने पर उन्होंने पाया कि न्यूनतम त्रुटि तब हुई जब <math>\{A, B\} = \{1.98, 1.135\},</math> जिसने इसके लिए एक अच्छा अनुमान <math>\forall x \ge 0.</math>दिया | ||
: इन मूल्यों को प्रतिस्थापित | : इन मूल्यों को प्रतिस्थापित करने और ऊपर से <math>Q(x)</math> और <math>\operatorname{erfc}(x)</math> के बीच संबंध का उपयोग करने से प्राप्त होता है | ||
:: <math> Q(x)\approx\frac{\left( 1-e^{\frac{-1.98x} {\sqrt{2}}}\right) e^{-\frac{x^{2}}{2}}}{1.135\sqrt{2\pi}x}, x \ge 0. </math> | :: <math> Q(x)\approx\frac{\left( 1-e^{\frac{-1.98x} {\sqrt{2}}}\right) e^{-\frac{x^{2}}{2}}}{1.135\sqrt{2\pi}x}, x \ge 0. </math> | ||
: किसी विशिष्ट अनुप्रयोग के लिए सटीकता को तैयार करने या इसे एक तंग सीमा में बदलने के लिए उपरोक्त 'कारागियानिडिस-लिओमपास सन्निकटन' के लिए वैकल्पिक गुणांक भी उपलब्ध हैं।<ref>{{cite journal |doi=10.1109/LCOMM.2021.3052257|title=Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function|journal=IEEE Communications Letters|year=2021|last1=Tanash|first1=I.M.|last2=Riihonen|first2=T.|volume=25|issue=5|pages=1468–1471|arxiv=2101.07631|s2cid=231639206}}</ref> | : किसी विशिष्ट अनुप्रयोग के लिए सटीकता को तैयार करने या इसे एक तंग सीमा में बदलने के लिए उपरोक्त 'कारागियानिडिस-लिओमपास सन्निकटन' के लिए वैकल्पिक गुणांक भी उपलब्ध हैं।<ref>{{cite journal |doi=10.1109/LCOMM.2021.3052257|title=Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function|journal=IEEE Communications Letters|year=2021|last1=Tanash|first1=I.M.|last2=Riihonen|first2=T.|volume=25|issue=5|pages=1468–1471|arxiv=2101.07631|s2cid=231639206}}</ref> | ||
*एक सख्त और अधिक सुव्यवस्थित सन्निकटन <math>Q(x)</math> सकारात्मक तर्कों के लिए <math>x \in [0,\infty)</math> लोपेज़-बेनिटेज़ और कैसादेवल द्वारा दिया गया है (2011)<ref>{{cite journal |doi=10.1109/TCOMM.2011.012711.100105 |url=http://www.lopezbenitez.es/journals/IEEE_TCOM_2011.pdf|title=गॉसियन क्यू-फ़ंक्शन के लिए बहुमुखी, सटीक और विश्लेषणात्मक रूप से ट्रैक्टेबल अनुमान|journal=IEEE Transactions on Communications|volume=59|issue=4|pages=917–922|year=2011|last1=Lopez-Benitez|first1=Miguel|last2=Casadevall|first2=Fernando|s2cid=1145101}}</ref> दूसरे क्रम के घातीय | *एक सख्त और अधिक सुव्यवस्थित सन्निकटन <math>Q(x)</math> सकारात्मक तर्कों के लिए <math>x \in [0,\infty)</math> लोपेज़-बेनिटेज़ और कैसादेवल द्वारा दिया गया है (2011)<ref>{{cite journal |doi=10.1109/TCOMM.2011.012711.100105 |url=http://www.lopezbenitez.es/journals/IEEE_TCOM_2011.pdf|title=गॉसियन क्यू-फ़ंक्शन के लिए बहुमुखी, सटीक और विश्लेषणात्मक रूप से ट्रैक्टेबल अनुमान|journal=IEEE Transactions on Communications|volume=59|issue=4|pages=917–922|year=2011|last1=Lopez-Benitez|first1=Miguel|last2=Casadevall|first2=Fernando|s2cid=1145101}}</ref> दूसरे क्रम के घातीय फलन के आधार पर: | ||
:: <math> Q(x) \approx e^{-ax^2-bx-c}, \qquad x \ge 0. </math> | :: <math> Q(x) \approx e^{-ax^2-bx-c}, \qquad x \ge 0. </math> | ||
: फिटिंग गुणांक <math> (a,b,c) </math> वर्ग त्रुटियों के योग को कम करने के लिए तर्कों की किसी भी वांछित सीमा पर अनुकूलित किया जा सकता है (<math>a = 0.3842</math>, <math>b = 0.7640</math>, <math>c = 0.6964</math> के लिए <math>x \in [0,20]</math>) या अधिकतम निरपेक्ष त्रुटि को कम करें (<math>a = 0.4920</math>, <math>b = 0.2887</math>, <math>c = 1.1893</math> | : फिटिंग गुणांक <math> (a,b,c) </math> वर्ग त्रुटियों के योग को कम करने के लिए तर्कों की किसी भी वांछित सीमा पर अनुकूलित किया जा सकता है (<math>a = 0.3842</math>, <math>b = 0.7640</math>, <math>c = 0.6964</math> के लिए <math>x \in [0,20]</math>) या अधिकतम निरपेक्ष त्रुटि को कम करें (<math>a = 0.4920</math>, <math>b = 0.2887</math>, <math>c = 1.1893</math> लिए <math>x \in [0,20]</math>). यह सन्निकटन कुछ लाभ प्रदान करता है जैसे सटीकता और विश्लेषणात्मक शिक्षणीयता के बीच एक अच्छा व्यापार-संवृत (उदाहरण के लिए, किसी भी मनमानी शक्ति का विस्तार) <math>Q(x)</math> तुच्छ है और सन्निकटन के बीजगणितीय रूप में परिवर्तन नहीं करता है)। | ||
== | ==विपरीत Q== | ||
व्युत्क्रम Q- | व्युत्क्रम Q-फलन व्युत्क्रम त्रुटि फलन से संबंधित हो सकता है: | ||
:<math>Q^{-1}(y) = \sqrt{2}\ \mathrm{erf}^{-1}(1-2y) = \sqrt{2}\ \mathrm{erfc}^{-1}(2y)</math> | :<math>Q^{-1}(y) = \sqrt{2}\ \mathrm{erf}^{-1}(1-2y) = \sqrt{2}\ \mathrm{erfc}^{-1}(2y)</math> | ||
फलन <math>Q^{-1}(y)</math> अंकीय संचार में अनुप्रयोग पाता है। इसे सामान्यतौर पर डेसीबल क्षेत्र मात्राओं और रूट-पावर मात्राओं में व्यक्त किया जाता है और सामान्यतौर पर इसे क्यू-फैक्टर कहा जाता है: | |||
:<math>\mathrm{Q\text{-}factor} = 20 \log_{10}\!\left(Q^{-1}(y)\right)\!~\mathrm{dB}</math> | :<math>\mathrm{Q\text{-}factor} = 20 \log_{10}\!\left(Q^{-1}(y)\right)\!~\mathrm{dB}</math> | ||
जहां y विश्लेषण के | जहां y विश्लेषण के अंतर्गत अंकीय रूप से संशोधित सिग्नल की बिट-त्रुटि दर (बीईआर) है। उदाहरण के लिए, योगात्मक सफेद गॉसियन शोर में चरण-शिफ्ट कुंजीयन क्वाड्रेचर चरण-शिफ्ट कुंजीयन (क्यूपीएसके) के लिए ऊपर परिभाषित क्यू-कारक सिग्नल-टू-शोर अनुपात डेसिबल के डीबी में मान के साथ मेल खाता है जो y के बराबर त्रुटि दर उत्पन्न करता है। | ||
[[File:Q-factor vs BER.png|thumb|none|400px|क्यू-फैक्टर बनाम बिट त्रुटि दर (बीईआर)।]] | [[File:Q-factor vs BER.png|thumb|none|400px|क्यू-फैक्टर बनाम बिट त्रुटि दर (बीईआर)।]] | ||
== मान == | == मान == | ||
क्यू- | क्यू-फलन अच्छी तरह से सारणीबद्ध है और अधिकांश गणितीय सॉफ़्टवेयर संकुल जैसे कि [[आर (प्रोग्रामिंग भाषा)]] और [[पायथन (प्रोग्रामिंग भाषा)]], मैटलैब और [[वोल्फ्राम मैथमैटिका]] में उपलब्ध संकुल में सीधे गणना की जा सकती है। क्यू-फलन के कुछ मान संदर्भ के लिए नीचे दिए गए हैं। | ||
<!-- This table was calculated in Matlab as follows: | <!-- This table was calculated in Matlab as follows: | ||
| Line 242: | Line 253: | ||
== उच्च आयामों का सामान्यीकरण == | == उच्च आयामों का सामान्यीकरण == | ||
क्यू-फलन को उच्च आयामों के लिए सामान्यीकृत किया जा सकता है:<ref>{{cite journal|last1=Savage|first1=I. R.|title=बहुभिन्नरूपी सामान्य वितरण के लिए मिल अनुपात|journal=Journal of Research of the National Bureau of Standards Section B|date=1962|volume=66|issue=3|pages=93–96|doi=10.6028/jres.066B.011|zbl=0105.12601|doi-access=free}}</ref> | |||
:<math>Q(\mathbf{x})= \mathbb{P}(\mathbf{X}\geq \mathbf{x}),</math> | :<math>Q(\mathbf{x})= \mathbb{P}(\mathbf{X}\geq \mathbf{x}),</math> | ||
जहाँ <math>\mathbf{X}\sim \mathcal{N}(\mathbf{0},\, \Sigma) </math> सहप्रसरण के साथ बहुभिन्नरूपी सामान्य वितरण का अनुसरण करता है <math>\Sigma </math> और दहलीज प्रकार की होती है | |||
<math>\mathbf{x}=\gamma\Sigma\mathbf{l}^*</math> कुछ सकारात्मक | <math>\mathbf{x}=\gamma\Sigma\mathbf{l}^*</math> कुछ सकारात्मक सदिश के लिए <math> \mathbf{l}^*>\mathbf{0}</math> और सकारात्मक स्थिरांक <math>\gamma>0</math>. जैसा कि एक आयामी स्थिति में क्यू-फलन के लिए कोई सरल विश्लेषणात्मक सूत्र नहीं है। फिर भी क्यू-फलन को [http://www.mathworks.com/matlabcentral/fileexchange/53796 अव्यवस्थित रूप से अनुमानित किया जा सकता है] <math>\gamma</math> बड़ा और बड़ा होता जाता है।<ref>{{cite journal|last1=Botev|first1=Z. I.|title=The normal law under linear restrictions: simulation and estimation via minimax tilting|journal=Journal of the Royal Statistical Society, Series B|volume=79|pages=125–148|date=2016|doi=10.1111/rssb.12162|arxiv=1603.04166|bibcode=2016arXiv160304166B|s2cid=88515228}}</ref><ref name="bmc17">{{cite book |chapter=Logarithmically efficient estimation of the tail of the multivariate normal distribution |last1=Botev |first1=Z. I. |last2=Mackinlay |first2=D. |last3=Chen |first3=Y.-L. |date=2017 |publisher=IEEE |isbn=978-1-5386-3428-8 |title= 2017 Winter Simulation Conference (WSC)|pages=1903–191 |doi= 10.1109/WSC.2017.8247926 |s2cid=4626481 }} | ||
</ref> | </ref> | ||
| Line 251: | Line 262: | ||
== संदर्भ == | == संदर्भ == | ||
<references /> | <references /> | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Created On 07/07/2023]] | [[Category:Created On 07/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors|Short description/doc]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Template documentation pages|Short description/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:प्रमाण युक्त लेख]] | |||
[[Category:विशेष कार्य]] | |||
[[Category:संभाव्यता वितरण से संबंधित कार्य]] | |||
[[Category:सामान्य वितरण]] | |||
Latest revision as of 16:09, 25 July 2023
आंकड़ों में, क्यू-फलन मानक सामान्य वितरण का संचयी वितरण फलन (पूंछ वितरण फलन) है।[1][2] दूसरे शब्दों में संभावना है कि एक सामान्य (गाऊसी) यादृच्छिक चर x मानक विचलन से बड़ा मान प्राप्त करेगा। समान रूप से यह संभावना है कि एक मानक सामान्य यादृच्छिक चर से बड़ा मान लेता है।
अगर माध्य के साथ एक गाऊसी यादृच्छिक चर हैं और विचरण , तो मानक सामान्य वितरण हैं और
जहाँ
क्यू-फलन की अन्य परिभाषाएँ, जो सभी सामान्य संचयी वितरण फलन के सरल परिवर्तन का भी कभी-कभी उपयोग किया जाता है।[3]
सामान्य वितरण के संचयी वितरण फलन से इसके संबंध के कारण क्यू-फलन को त्रुटि फलन के संदर्भ में भी व्यक्त किया जा सकता है, जो लागू गणित और भौतिकी में एक महत्वपूर्ण फलन है।
परिभाषा और बुनियादी गुण
औपचारिक रूप से, क्यू-फलन को इस प्रकार परिभाषित किया गया है
इस प्रकार,
जहाँ मानक सामान्य गाऊसी वितरण का संचयी वितरण फलन है।
क्यू-फलन को त्रुटि फलन या पूरक त्रुटि फलन के रूप में व्यक्त किया जा सकता है[2]
क्यू-फलन का एक वैकल्पिक रूप जिसे इसके खोजकर्ता के नाम पर क्रेग के सूत्र के रूप में जाना जाता है, इस प्रकार व्यक्त किया गया है:[4]
यह अभिव्यक्ति केवल x के सकारात्मक मानों के लिए मान्य है, लेकिन इसका उपयोग नकारात्मक मानों के लिए Q(x) प्राप्त करने के लिए Q(x) = 1 − Q(−x) के संयोजन में किया जा सकता है। यह रूप लाभप्रद है क्योंकि एकीकरण की सीमा निश्चित और सीमित है।
क्रेग के सूत्र को बाद में बेहनाद (2020) द्वारा [5] दो गैर-नकारात्मक चर के योग के क्यू-फलन के लिए इस प्रकार बढ़ाया गया:
:
सीमाएँ और सन्निकटन
- क्यू-फलन कोई प्राथमिक फलन नहीं है। हालाँकि, बोरजेसन-सुंदरबर्ग सीमा जहाँ मानक सामान्य वितरण का घनत्व फलन है,[6]
- बड़े एक्स के लिए तेजी से तंग हो जाते हैं और अधिकतर उपयोगी होते हैं।
- प्रतिस्थापन v =u2/2 का उपयोग करके ऊपरी सीमा इस प्रकार प्राप्त की जाती है:
- इसी प्रकार, भागफल नियम का उपयोग करके
- Q(x) को हल करने से निचली सीमा मिलती है।
- ऊपरी और निचली सीमा का ज्यामितीय माध्य के लिए उपयुक्त सन्निकटन देता है:
- निम्नलिखित अभिव्यक्ति को अनुकूलित करके की सख्त सीमाएँ और सन्निकटन भी प्राप्त किए जा सकते हैं: [6]
- के लिए , सर्वोत्तम ऊपरी सीमा किसके द्वारा दी गई है और 0.44% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ। इसी प्रकार, सर्वोत्तम सन्निकटन द्वारा दिया गया है और 0.27% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ। अंत में, सबसे अच्छी निचली सीमा दी गई है और 1.17% की अधिकतम पूर्ण सापेक्ष त्रुटि के साथ।
- क्यू-फलन का चेर्नॉफ़ बाध्य है
- बेहतर घातीय सीमाएँ और शुद्ध घातीय सन्निकटन हैं [7]
- उपरोक्त को तनाश और रिइहोनेन (2020) द्वारा सामान्यीकृत किया गया था,[8] जिन्होंने दिखाया कि का उचित अनुमान लगाया जा सकता है या सीमाबद्ध किया जा सकता है
- विशेष रूप से, उन्होंने संख्यात्मक गुणांकों को हल करने के लिए एक व्यवस्थित पद्धति प्रस्तुत की जो एक न्यूनतम सन्निकटन या बाध्य उत्पन्न करता है: , या के लिए . लेख्य में सारणीबद्ध उदाहरण गुणांकों के साथ सापेक्ष और निरपेक्ष सन्निकटन त्रुटियाँ कम हैं और क्रमश से कम हैं। गुणांक घातीय सन्निकटन और सीमा तक के कई रूपों के लिए एक व्यापक डेटासेट के रूप में विवृत अभिगम के लिए जारी किया गया है।[9]
- के लिए का एक और सन्निकटन कारागियानिडिस और लिओमपास (2007) द्वारा दिया गया है,[10] जिन्होंने पैरामीटर्स के उचित चयन के लिए प्रदर्शन किया
- के बीच पूर्ण त्रुटि और सीमा के ऊपर मूल्यांकन करके न्यूनतम किया जाता है
- का उपयोग करते हुए और संख्यात्मक रूप से एकीकृत करने पर उन्होंने पाया कि न्यूनतम त्रुटि तब हुई जब जिसने इसके लिए एक अच्छा अनुमान दिया
- इन मूल्यों को प्रतिस्थापित करने और ऊपर से और के बीच संबंध का उपयोग करने से प्राप्त होता है
- किसी विशिष्ट अनुप्रयोग के लिए सटीकता को तैयार करने या इसे एक तंग सीमा में बदलने के लिए उपरोक्त 'कारागियानिडिस-लिओमपास सन्निकटन' के लिए वैकल्पिक गुणांक भी उपलब्ध हैं।[11]
- एक सख्त और अधिक सुव्यवस्थित सन्निकटन सकारात्मक तर्कों के लिए लोपेज़-बेनिटेज़ और कैसादेवल द्वारा दिया गया है (2011)[12] दूसरे क्रम के घातीय फलन के आधार पर:
- फिटिंग गुणांक वर्ग त्रुटियों के योग को कम करने के लिए तर्कों की किसी भी वांछित सीमा पर अनुकूलित किया जा सकता है (, , के लिए ) या अधिकतम निरपेक्ष त्रुटि को कम करें (, , लिए ). यह सन्निकटन कुछ लाभ प्रदान करता है जैसे सटीकता और विश्लेषणात्मक शिक्षणीयता के बीच एक अच्छा व्यापार-संवृत (उदाहरण के लिए, किसी भी मनमानी शक्ति का विस्तार) तुच्छ है और सन्निकटन के बीजगणितीय रूप में परिवर्तन नहीं करता है)।
विपरीत Q
व्युत्क्रम Q-फलन व्युत्क्रम त्रुटि फलन से संबंधित हो सकता है:
फलन अंकीय संचार में अनुप्रयोग पाता है। इसे सामान्यतौर पर डेसीबल क्षेत्र मात्राओं और रूट-पावर मात्राओं में व्यक्त किया जाता है और सामान्यतौर पर इसे क्यू-फैक्टर कहा जाता है:
जहां y विश्लेषण के अंतर्गत अंकीय रूप से संशोधित सिग्नल की बिट-त्रुटि दर (बीईआर) है। उदाहरण के लिए, योगात्मक सफेद गॉसियन शोर में चरण-शिफ्ट कुंजीयन क्वाड्रेचर चरण-शिफ्ट कुंजीयन (क्यूपीएसके) के लिए ऊपर परिभाषित क्यू-कारक सिग्नल-टू-शोर अनुपात डेसिबल के डीबी में मान के साथ मेल खाता है जो y के बराबर त्रुटि दर उत्पन्न करता है।
मान
क्यू-फलन अच्छी तरह से सारणीबद्ध है और अधिकांश गणितीय सॉफ़्टवेयर संकुल जैसे कि आर (प्रोग्रामिंग भाषा) और पायथन (प्रोग्रामिंग भाषा), मैटलैब और वोल्फ्राम मैथमैटिका में उपलब्ध संकुल में सीधे गणना की जा सकती है। क्यू-फलन के कुछ मान संदर्भ के लिए नीचे दिए गए हैं।
|
|
|
|
उच्च आयामों का सामान्यीकरण
क्यू-फलन को उच्च आयामों के लिए सामान्यीकृत किया जा सकता है:[13]
जहाँ सहप्रसरण के साथ बहुभिन्नरूपी सामान्य वितरण का अनुसरण करता है और दहलीज प्रकार की होती है कुछ सकारात्मक सदिश के लिए और सकारात्मक स्थिरांक . जैसा कि एक आयामी स्थिति में क्यू-फलन के लिए कोई सरल विश्लेषणात्मक सूत्र नहीं है। फिर भी क्यू-फलन को अव्यवस्थित रूप से अनुमानित किया जा सकता है बड़ा और बड़ा होता जाता है।[14][15]
संदर्भ
- ↑ The Q-function, from cnx.org
- ↑ 2.0 2.1 Basic properties of the Q-function Archived March 25, 2009, at the Wayback Machine
- ↑ Normal Distribution Function – from Wolfram MathWorld
- ↑ Craig, J.W. (1991). "A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations" (PDF). MILCOM 91 - Conference record. pp. 571–575. doi:10.1109/MILCOM.1991.258319. ISBN 0-87942-691-8. S2CID 16034807.
- ↑ Behnad, Aydin (2020). "क्रेग के क्यू-फंक्शन फॉर्मूला का एक नया विस्तार और दोहरे-शाखा ईजीसी प्रदर्शन विश्लेषण में इसका अनुप्रयोग". IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ↑ 6.0 6.1 Borjesson, P.; Sundberg, C.-E. (1979). "संचार अनुप्रयोगों के लिए त्रुटि फ़ंक्शन Q(x) का सरल अनुमान". IEEE Transactions on Communications. 27 (3): 639–643. doi:10.1109/TCOM.1979.1094433.
- ↑ Chiani, M.; Dardari, D.; Simon, M.K. (2003). "फ़ेडिंग चैनलों में त्रुटि संभावना की गणना के लिए नई घातीय सीमाएँ और सन्निकटन" (PDF). IEEE Transactions on Wireless Communications. 24 (5): 840–845. doi:10.1109/TWC.2003.814350.
- ↑ Tanash, I.M.; Riihonen, T. (2020). "घातांक के योग द्वारा गॉसियन क्यू-फ़ंक्शन के लिए वैश्विक न्यूनतम अनुमान और सीमाएँ". IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ↑ Tanash, I.M.; Riihonen, T. (2020). "Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]". Zenodo. doi:10.5281/zenodo.4112978.
- ↑ Karagiannidis, George; Lioumpas, Athanasios (2007). "गॉसियन क्यू-फ़ंक्शन के लिए एक बेहतर अनुमान" (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ↑ Tanash, I.M.; Riihonen, T. (2021). "Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function". IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ↑ Lopez-Benitez, Miguel; Casadevall, Fernando (2011). "गॉसियन क्यू-फ़ंक्शन के लिए बहुमुखी, सटीक और विश्लेषणात्मक रूप से ट्रैक्टेबल अनुमान" (PDF). IEEE Transactions on Communications. 59 (4): 917–922. doi:10.1109/TCOMM.2011.012711.100105. S2CID 1145101.
- ↑ Savage, I. R. (1962). "बहुभिन्नरूपी सामान्य वितरण के लिए मिल अनुपात". Journal of Research of the National Bureau of Standards Section B. 66 (3): 93–96. doi:10.6028/jres.066B.011. Zbl 0105.12601.
- ↑ Botev, Z. I. (2016). "The normal law under linear restrictions: simulation and estimation via minimax tilting". Journal of the Royal Statistical Society, Series B. 79: 125–148. arXiv:1603.04166. Bibcode:2016arXiv160304166B. doi:10.1111/rssb.12162. S2CID 88515228.
- ↑ Botev, Z. I.; Mackinlay, D.; Chen, Y.-L. (2017). "Logarithmically efficient estimation of the tail of the multivariate normal distribution". 2017 Winter Simulation Conference (WSC). IEEE. pp. 1903–191. doi:10.1109/WSC.2017.8247926. ISBN 978-1-5386-3428-8. S2CID 4626481.