क्यू-फलन

For the phase-space function representing a quantum state, see Husimi Q representation.

File:Q-function.png

क्यू-फलन का प्लॉट

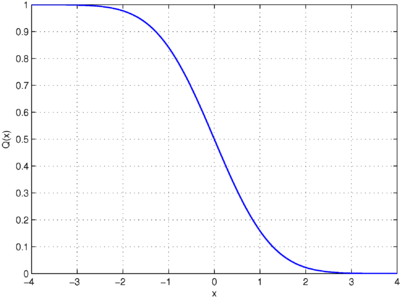
आंकड़ों में, क्यू-फलन मानक सामान्य वितरण का संचयी वितरण फलन (पूंछ वितरण फलन) है। दूसरे शब्दों में $Q(x)$ संभावना है कि एक सामान्य (गाऊसी) यादृच्छिक चर x मानक विचलन से बड़ा मान प्राप्त करेगा। समान रूप से $Q(x)$ यह संभावना है कि एक मानक सामान्य यादृच्छिक चर $x$ से बड़ा मान लेता है।

अगर $Y$ माध्य के साथ एक गाऊसी यादृच्छिक चर $\mu$ हैं और विचरण $\sigma ^{2}$, तो $X={\frac {Y-\mu }{\sigma }}$ मानक सामान्य वितरण हैं और

$P(Y>y)=P(X>x)=Q(x)$

$x={\frac {y-\mu }{\sigma }}$ जहाँ

क्यू-फलन की अन्य परिभाषाएँ, जो सभी सामान्य संचयी वितरण फलन के सरल परिवर्तन का भी कभी-कभी उपयोग किया जाता है।

सामान्य वितरण के संचयी वितरण फलन से इसके संबंध के कारण क्यू-फलन को त्रुटि फलन के संदर्भ में भी व्यक्त किया जा सकता है, जो लागू गणित और भौतिकी में एक महत्वपूर्ण फलन है।

परिभाषा और बुनियादी गुण

औपचारिक रूप से, क्यू-फलन को इस प्रकार परिभाषित किया गया है

$Q(x)={\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }\exp \left(-{\frac {u^{2}}{2}}\right)\,du.$

इस प्रकार,

$Q(x)=1-Q(-x)=1-\Phi (x)\,\!,$

जहाँ $\Phi (x)$ मानक सामान्य गाऊसी वितरण का संचयी वितरण फलन है।

क्यू-फलन को त्रुटि फलन या पूरक त्रुटि फलन के रूप में व्यक्त किया जा सकता है

${\begin{aligned}Q(x)&={\frac {1}{2}}\left({\frac {2}{\sqrt {\pi }}}\int _{x/{\sqrt {2}}}^{\infty }\exp \left(-t^{2}\right)\,dt\right)\\&={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)~~{\text{ -or-}}\\&={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right).\end{aligned}}$

क्यू-फलन का एक वैकल्पिक रूप जिसे इसके खोजकर्ता के नाम पर क्रेग के सूत्र के रूप में जाना जाता है, इस प्रकार व्यक्त किया गया है:

$Q(x)={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{2\sin ^{2}\theta }}\right)d\theta .$

यह अभिव्यक्ति केवल x के सकारात्मक मानों के लिए मान्य है, लेकिन इसका उपयोग नकारात्मक मानों के लिए Q(x) प्राप्त करने के लिए Q(x) = 1 − Q(−x) के संयोजन में किया जा सकता है। यह रूप लाभप्रद है क्योंकि एकीकरण की सीमा निश्चित और सीमित है।

क्रेग के सूत्र को बाद में बेहनाद (2020) द्वारा दो गैर-नकारात्मक चर के योग के क्यू-फलन के लिए इस प्रकार बढ़ाया गया:

 :

File:Q function complex plot plotted with Mathematica 13.1 ComplexPlot3D.svg

क्यू-फलन को सम्मिश्र सतह में प्लॉट किया गया

$Q(x+y)={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{2\sin ^{2}\theta }}-{\frac {y^{2}}{2\cos ^{2}\theta }}\right)d\theta ,\quad x,y\geqslant 0.$

सीमाएँ और सन्निकटन

• क्यू-फलन कोई प्राथमिक फलन नहीं है। हालाँकि, बोरजेसन-सुंदरबर्ग सीमा जहाँ $\phi (x)$ मानक सामान्य वितरण का घनत्व फलन है,

$\left({\frac {x}{1+x^{2}}}\right)\phi (x)<Q(x)<{\frac {\phi (x)}{x}},\qquad x>0,$

बड़े एक्स के लिए तेजी से तंग हो जाते हैं और अधिकतर उपयोगी होते हैं।

प्रतिस्थापन v =u²/2 का उपयोग करके ऊपरी सीमा इस प्रकार प्राप्त की जाती है:

$Q(x)={\int <!--\; \int \; -->}_x^{\mathrm{\infty <!--\; \infty \; -->}}\mathrm{\varphi <!--\; \varphi \; -->}(u)du<{\int <!--\; \int \; -->}_x^{\mathrm{\infty <!--\; \infty \; -->}}\frac{u}{x}\mathrm{\varphi <!--\; \varphi \; -->}(u)du=$