क्वांटम उलझाव: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
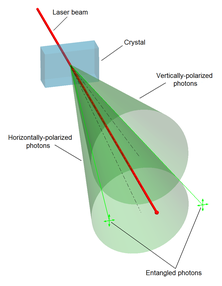
[[File:SPDC figure.png|thumb|286x286px|स्वतःस्फूर्त पैरामीट्रिक डाउन-रूपांतरण प्रक्रिया फोटॉनों को परस्पर लंबवत ध्रुवीकरण के साथ प्रकार II फोटॉन जोड़े में विभाजित कर सकती है।]] | [[File:SPDC figure.png|thumb|286x286px|स्वतःस्फूर्त पैरामीट्रिक डाउन-रूपांतरण प्रक्रिया फोटॉनों को परस्पर लंबवत ध्रुवीकरण के साथ प्रकार II फोटॉन जोड़े में विभाजित कर सकती है।]] | ||
{{Quantum mechanics|fundamentals}} | {{Quantum mechanics|fundamentals}} | ||
क्वांटम उलझाव वह घटना है जो तब घटित होती है जब [[कण|कणों]] का एक समूह उत्पन्न होता है, परस्पर क्रिया करता है, या स्थानिक निकटता को इस तरह से साझा करता है कि समूह के प्रत्येक कण की [[कितना राज्य|क्वांटम स्थिति]] को दूसरों की स्थिति से स्वतंत्र रूप से वर्णित नहीं किया जा सके, जिसमें कण बड़ी दूरी से अलग होने पर भी | '''क्वांटम उलझाव''' वह घटना है जो तब घटित होती है जब [[कण|कणों]] का एक समूह उत्पन्न होता है, परस्पर क्रिया करता है, या स्थानिक निकटता को इस तरह से साझा करता है कि समूह के प्रत्येक कण की [[कितना राज्य|क्वांटम स्थिति]] को दूसरों की स्थिति से स्वतंत्र रूप से वर्णित नहीं किया जा सके, जिसमें कण बड़ी दूरी से अलग होने पर भी सम्मलित हैं। क्वांटम उलझाव का विषय [[शास्त्रीय भौतिकी]] और [[क्वांटम भौतिकी]] के बीच असमानता के केंद्र में है: उलझाव क्वांटम यांत्रिकी की एक प्राथमिक विशेषता है जो शास्त्रीय यांत्रिकी में उपस्थित नहीं है।<ref name="NYT-20221010">{{cite news |last=Overbye |first=Dennis |author-link=Dennis Overbye |title=Black Holes May Hide a Mind-Bending Secret About Our Universe - Take gravity, add quantum mechanics, stir. What do you get? Just maybe, a holographic cosmos. |url=https://www.nytimes.com/2022/10/10/science/black-holes-cosmology-hologram.html |date=10 October 2022 |work=[[The New York Times]] |accessdate=10 October 2022 }}</ref> | ||
उलझे हुए कणों पर किए गए स्थिति, [[गति|संवेग]], [[स्पिन (भौतिकी)]], और [[ध्रुवीकरण (तरंगें)]] जैसे [[भौतिक गुण|भौतिक गुणों]] के माप, कुछ | उलझे हुए कणों पर किए गए स्थिति, [[गति|संवेग]], [[स्पिन (भौतिकी)]], और [[ध्रुवीकरण (तरंगें)]] जैसे [[भौतिक गुण|भौतिक गुणों]] के माप, कुछ स्थितियों में, पूरी तरह से [[सहसंबद्ध]] पाए जा सकते हैं। उदाहरण के लिए, यदि उलझे हुए कणों की एक जोड़ी इस प्रकार उत्पन्न होती है कि उनका कुल स्पिन शून्य माना जाता है, और एक कण को पहले अक्ष पर दक्षिणावर्त स्पिन पाया जाता है, तो दूसरे कण का स्पिन, उसी अक्ष पर मापा जाता है, वामावर्त पाया जाता है। चूंकि, यह व्यवहार प्रतीत होता है कि [[विरोधाभास|विरोधाभासी]] प्रभावों को जन्म देता है: किसी कण के गुणों के किसी भी माप के परिणामस्वरूप उस कण का एक स्पष्ट और अपरिवर्तनीय [[तरंग फ़ंक्शन पतन]] हो जाता है और मूल क्वांटम स्थिति बदल जाती है। उलझे हुए कणों के साथ, ऐसे माप उलझी हुई प्रणाली को समग्र रूप से प्रभावित करते हैं। | ||
ऐसी घटनाएँ 1935 में [[अल्बर्ट आइंस्टीन]], [[बोरिस पोडॉल्स्की]] और [[नाथन रोसेन]] के पेपर का विषय थीं,<ref name="Einstein1935"> | ऐसी घटनाएँ 1935 में [[अल्बर्ट आइंस्टीन]], [[बोरिस पोडॉल्स्की]] और [[नाथन रोसेन]] के पेपर का विषय थीं,<ref name="Einstein1935"> | ||
| Line 26: | Line 26: | ||
|doi=10.1103/PhysRev.47.777 | |doi=10.1103/PhysRev.47.777 | ||
|doi-access=free}} | |doi-access=free}} | ||
</ref> और इसके तुरंत | </ref> और इसके तुरंत पश्चात इरविन श्रोडिंगर के कई पेपर,<ref name="Schrödinger1935"> | ||
{{cite journal | {{cite journal | ||
|author=Schrödinger E | |author=Schrödinger E | ||
| Line 42: | Line 42: | ||
</ref> जिसमें वर्णन किया गया था कि [[ईपीआर विरोधाभास|ईपीआर विरोधाभा]] के रूप में जाना जाने लगा। आइंस्टीन और अन्य लोगों ने इस तरह के व्यवहार को असंभव माना, क्योंकि इसने कार्य-कारण के [[स्थानीय यथार्थवाद]] दृष्टिकोण का उल्लंघन किया था (आइंस्टीन ने इसे "दूरी पर डरावनी कार्रवाई" के रूप में संदर्भित किया था) और तर्क दिया कि इसलिए [[क्वांटम यांत्रिकी]] का स्वीकृत सूत्रीकरण अधूरा होना चाहिए। {{cite book |year=1987 |access-date=2014-06-14 |title=क्वांटम यांत्रिकी में बोलने योग्य और अकथनीय|first=J. S. |last=Bell |publisher=[[CERN]] |isbn=0521334950 |url=http://philosophyfaculty.ucsd.edu/faculty/wuthrich/GSSPP09/Files/BellJohnS1981Speakable_BertlmannsSocks.pdf |url-status=dead |archive-url=https://web.archive.org/web/20150412044550/http://philosophyfaculty.ucsd.edu/faculty/wuthrich/GSSPP09/Files/BellJohnS1981Speakable_BertlmannsSocks.pdf |archive-date=12 April 2015 |df=dmy-all }} | </ref> जिसमें वर्णन किया गया था कि [[ईपीआर विरोधाभास|ईपीआर विरोधाभा]] के रूप में जाना जाने लगा। आइंस्टीन और अन्य लोगों ने इस तरह के व्यवहार को असंभव माना, क्योंकि इसने कार्य-कारण के [[स्थानीय यथार्थवाद]] दृष्टिकोण का उल्लंघन किया था (आइंस्टीन ने इसे "दूरी पर डरावनी कार्रवाई" के रूप में संदर्भित किया था) और तर्क दिया कि इसलिए [[क्वांटम यांत्रिकी]] का स्वीकृत सूत्रीकरण अधूरा होना चाहिए। {{cite book |year=1987 |access-date=2014-06-14 |title=क्वांटम यांत्रिकी में बोलने योग्य और अकथनीय|first=J. S. |last=Bell |publisher=[[CERN]] |isbn=0521334950 |url=http://philosophyfaculty.ucsd.edu/faculty/wuthrich/GSSPP09/Files/BellJohnS1981Speakable_BertlmannsSocks.pdf |url-status=dead |archive-url=https://web.archive.org/web/20150412044550/http://philosophyfaculty.ucsd.edu/faculty/wuthrich/GSSPP09/Files/BellJohnS1981Speakable_BertlmannsSocks.pdf |archive-date=12 April 2015 |df=dmy-all }} | ||
चूंकि, पश्चात में, क्वांटम यांत्रिकी की प्रति-सहज ज्ञान युक्त भविष्यवाणियों को उन परीक्षणों में सत्यापित किया गया, जहां उलझे हुए कणों के ध्रुवीकरण या स्पिन को अलग-अलग स्थानों पर मापा गया था, जो सांख्यिकीय रूप से बेल की असमानता का उल्लंघन करता था। पहले के परीक्षणों में, इस बात से इंकार नहीं किया जा सकता था कि एक बिंदु पर परिणाम सूक्ष्मता से दूरस्थ बिंदु तक प्रेषित किया जा सकता था, जिससे दूसरे स्थान पर परिणाम प्रभावित हो सकता था। चूंकि, तथाकथित "लूपहोल-फ्री" बेल परीक्षण तब से किए गए हैं जहां स्थानों को पर्याप्त रूप से अलग किया गया था कि प्रकाश की गति से संचार में माप के बीच के अंतराल की समानता में अधिक समय लगेगा - एक स्थितियों में, 10,000 गुना अधिक। | |||
क्वांटम यांत्रिकी की कुछ व्याख्याओं के अनुसार, एक माप का प्रभाव तुरंत होता है। अन्य व्याख्याएँ जो [[वेवफ़ंक्शन पतन]] को नहीं पहचानती हैं, इस विवाद पर विवाद करती हैं कि इसका कोई "प्रभाव" है। | क्वांटम यांत्रिकी की कुछ व्याख्याओं के अनुसार, एक माप का प्रभाव तुरंत होता है। अन्य व्याख्याएँ जो [[वेवफ़ंक्शन पतन]] को नहीं पहचानती हैं, इस विवाद पर विवाद करती हैं कि इसका कोई "प्रभाव" है। चूंकि, सभी व्याख्याएँ इस बात से सहमत हैं कि उलझाव मापों के बीच सहसंबंध पैदा करता है, और उलझे हुए कणों के बीच पारस्परिक जानकारी का फायदा उठाया जा सकता है, लेकिन प्रकाश से भी तेज गति से सूचना का कोई भी प्रसारण असंभव है।<ref>[[Roger Penrose]], ''The Road to Reality: A Complete Guide to the Laws of the Universe'', London, 2004, p. 603.</ref><ref name="Griffiths2004">{{citation |author=Griffiths, David J.|title=Introduction to Quantum Mechanics (2nd ed.) |publisher=Prentice Hall |year=2004 |isbn= 978-0-13-111892-8}}</ref> | ||
क्वांटम उलझाव को फोटॉन,<ref name="Kocher1">{{cite journal |doi = 10.1103/PhysRevLett.18.575 |volume=18 |issue=15 |title=परमाणु कैस्केड में उत्सर्जित फोटॉनों का ध्रुवीकरण सहसंबंध|journal=Physical Review Letters |pages=575–577 |last1 = Kocher |first1 = CA |last2 = Commins |first2 = ED |year=1967 |url=http://www.escholarship.org/uc/item/1kb7660q |bibcode=1967PhRvL..18..575K }}</ref><ref name="Kocherphd">Carl A. Kocher, Ph.D. Thesis (University of California at Berkeley, 1967). ''[https://escholarship.org/uc/item/1kb7660q Polarization Correlation of Photons Emitted in an Atomic Cascade]''</ref> [[इलेक्ट्रॉन]],<ref name="NTR-20151021">{{cite journal |author=Hensen, B. |title=Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres |date=21 October 2015 |journal=[[Nature (journal)|Nature]] |doi=10.1038/nature15759 |display-authors=etal |volume=526 |issue=7575 |pages=682–686 |bibcode=2015Natur.526..682H |pmid=26503041 |arxiv=1508.05949 |hdl=2117/79298 |s2cid=205246446}} See also [http://www.nature.com/articles/nature15759.epdf?referrer_access_token=1QB20mTNTZW60nEXil0D79RgN0jAjWel9jnR3ZoTv0Pfu6MWINxm4Io03p2jIRZ8qX_3I3N0Kr-AlItuikCZOJrG8QbdRRghlecFwmixlbQpWuw1dtaib4Le5DQOG3u_aXHU85x1JEhOcQTa1sHi0yvW23bblxmEQZAmHL4G0gIVusG_6JWorroY5BprgbTl4FiaE8WltEgMoUMZfZBkEfbMcFDp5iR112TFx_x3ZRj88Wa23E2moEvTfKjtlued0&tracking_referrer=www.nytimes.com free online access version].</ref><ref name="NYT-20151021">{{cite news |last=Markoff |first=Jack |title=क्षमा करें, आइंस्टीन। क्वांटम अध्ययन से पता चलता है कि 'डरावनी कार्रवाई' वास्तविक है।|url=https://www.nytimes.com/2015/10/22/science/quantum-theory-experiment-said-to-prove-spooky-interactions.html |date=21 October 2015 |work=The New York Times |access-date=21 October 2015 }}</ref>और यहां तक कि छोटे हीरे के साथ प्रयोगात्मक रूप से प्रदर्शित किया गया है।<ref>{{cite journal |journal=Science |date=2 December 2011 |volume=334 |issue=6060 |pages=1253–1256 |doi=10.1126/science.1211914 |pmid=22144620 |title=कमरे के तापमान पर स्थूल हीरे को उलझाना|bibcode = 2011Sci...334.1253L |last1=Lee |first1=K. C. |last2=Sprague |first2=M. R. |last3=Sussman |first3=B. J. |last4=Nunn |first4=J. |last5=Langford |first5=N. K. |last6=Jin |first6=X.- M. |last7=Champion |first7=T. |last8=Michelberger |first8=P. |last9=Reim |first9=K. F. |last10=England |first10=D. |last11=Jaksch |first11=D. |last12=Walmsley |first12=I. A. |s2cid=206536690 }}</ref> [[क्वांटम संचार]], [[ क्वांटम कम्प्यूटिंग |क्वांटम कम्प्यूटिंग]] और [[राडार जितना|क्वांटम रडार]] में उलझाव का उपयोग अनुसंधान और विकास का एक बहुत ही सक्रिय क्षेत्र है। | क्वांटम उलझाव को फोटॉन,<ref name="Kocher1">{{cite journal |doi = 10.1103/PhysRevLett.18.575 |volume=18 |issue=15 |title=परमाणु कैस्केड में उत्सर्जित फोटॉनों का ध्रुवीकरण सहसंबंध|journal=Physical Review Letters |pages=575–577 |last1 = Kocher |first1 = CA |last2 = Commins |first2 = ED |year=1967 |url=http://www.escholarship.org/uc/item/1kb7660q |bibcode=1967PhRvL..18..575K }}</ref><ref name="Kocherphd">Carl A. Kocher, Ph.D. Thesis (University of California at Berkeley, 1967). ''[https://escholarship.org/uc/item/1kb7660q Polarization Correlation of Photons Emitted in an Atomic Cascade]''</ref> [[इलेक्ट्रॉन]],<ref name="NTR-20151021">{{cite journal |author=Hensen, B. |title=Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres |date=21 October 2015 |journal=[[Nature (journal)|Nature]] |doi=10.1038/nature15759 |display-authors=etal |volume=526 |issue=7575 |pages=682–686 |bibcode=2015Natur.526..682H |pmid=26503041 |arxiv=1508.05949 |hdl=2117/79298 |s2cid=205246446}} See also [http://www.nature.com/articles/nature15759.epdf?referrer_access_token=1QB20mTNTZW60nEXil0D79RgN0jAjWel9jnR3ZoTv0Pfu6MWINxm4Io03p2jIRZ8qX_3I3N0Kr-AlItuikCZOJrG8QbdRRghlecFwmixlbQpWuw1dtaib4Le5DQOG3u_aXHU85x1JEhOcQTa1sHi0yvW23bblxmEQZAmHL4G0gIVusG_6JWorroY5BprgbTl4FiaE8WltEgMoUMZfZBkEfbMcFDp5iR112TFx_x3ZRj88Wa23E2moEvTfKjtlued0&tracking_referrer=www.nytimes.com free online access version].</ref><ref name="NYT-20151021">{{cite news |last=Markoff |first=Jack |title=क्षमा करें, आइंस्टीन। क्वांटम अध्ययन से पता चलता है कि 'डरावनी कार्रवाई' वास्तविक है।|url=https://www.nytimes.com/2015/10/22/science/quantum-theory-experiment-said-to-prove-spooky-interactions.html |date=21 October 2015 |work=The New York Times |access-date=21 October 2015 }}</ref>और यहां तक कि छोटे हीरे के साथ प्रयोगात्मक रूप से प्रदर्शित किया गया है।<ref>{{cite journal |journal=Science |date=2 December 2011 |volume=334 |issue=6060 |pages=1253–1256 |doi=10.1126/science.1211914 |pmid=22144620 |title=कमरे के तापमान पर स्थूल हीरे को उलझाना|bibcode = 2011Sci...334.1253L |last1=Lee |first1=K. C. |last2=Sprague |first2=M. R. |last3=Sussman |first3=B. J. |last4=Nunn |first4=J. |last5=Langford |first5=N. K. |last6=Jin |first6=X.- M. |last7=Champion |first7=T. |last8=Michelberger |first8=P. |last9=Reim |first9=K. F. |last10=England |first10=D. |last11=Jaksch |first11=D. |last12=Walmsley |first12=I. A. |s2cid=206536690 }}</ref> [[क्वांटम संचार]], [[ क्वांटम कम्प्यूटिंग |क्वांटम कम्प्यूटिंग]] और [[राडार जितना|क्वांटम रडार]] में उलझाव का उपयोग अनुसंधान और विकास का एक बहुत ही सक्रिय क्षेत्र है। | ||
इसके विपरीत बहुत लोकप्रिय विचार के | इसके विपरीत बहुत लोकप्रिय विचार के अतिरिक्त, क्वांटम उलझाव का उपयोग [[प्रकाश से भी तेज़ संचार]] के लिए नहीं किया जा सकता है।<ref>{{Cite web |last=Siegel |first=Ethan |title=नहीं, हम अभी भी प्रकाश से भी तेज़ संचार करने के लिए क्वांटम एन्टैंगलमेंट का उपयोग नहीं कर सकते|url=https://www.forbes.com/sites/startswithabang/2020/01/02/no-we-still-cant-use-quantum-entanglement-to-communicate-faster-than-light/ |access-date=2023-01-06 |website=Forbes |language=en}}</ref> | ||
== इतिहास == | == इतिहास == | ||
{{Further|छिपा-परिवर्तनीय सिद्धांत}} | {{Further|छिपा-परिवर्तनीय सिद्धांत}} | ||
[[File:NYT May 4, 1935.jpg|right|thumb|268x268px|ईपीआर विरोधाभास के संबंध में लेख शीर्षक|द [[दी न्यू यौर्क टाइम्स]] मई, 1935 अंक में आइंस्टीन-पोडॉल्स्की-रोसेन (ईपीआर) विरोधाभास पेपर।]]1935 में, अल्बर्ट आइंस्टीन, बोरिस पोडॉल्स्की और नाथन रोसेन ने प्रति-सहज ज्ञान युक्त भविष्यवाणियों पर एक पेपर प्रकाशित किया था जो क्वांटम यांत्रिकी एक विशेष | [[File:NYT May 4, 1935.jpg|right|thumb|268x268px|ईपीआर विरोधाभास के संबंध में लेख शीर्षक|द [[दी न्यू यौर्क टाइम्स]] मई, 1935 अंक में आइंस्टीन-पोडॉल्स्की-रोसेन (ईपीआर) विरोधाभास पेपर।]]1935 में, अल्बर्ट आइंस्टीन, बोरिस पोडॉल्स्की और नाथन रोसेन ने प्रति-सहज ज्ञान युक्त भविष्यवाणियों पर एक पेपर प्रकाशित किया था जो क्वांटम यांत्रिकी एक विशेष ढंग से एक साथ प्रस्तुत की गई वस्तुओं के जोड़े के लिए बनाता है।<ref name="Einstein1935" /> इस अध्ययन में, तीनों ने आइंस्टीन-पोडॉल्स्की-रोसेन विरोधाभास (ईपीआर विरोधाभास) प्रस्तुत किया, एक विचार प्रयोग जिसने यह दिखाने का प्रयास किया कि तरंग कार्यों द्वारा दिया गया भौतिक वास्तविकता का [[ क्वांटम यांत्रिक |क्वांटम यांत्रिक]] विवरण पूरा नहीं है।<ref name="Einstein1935" />चूंकि, तीन वैज्ञानिकों ने उलझाव शब्द नहीं गढ़ा, न ही उन्होंने जिस क्वांटम अवस्था पर विचार किया उसके विशेष गुणों का सामान्यीकरण किया। ईपीआर पेपर के पश्चात, इरविन श्रोडिंगर ने [[जर्मन भाषा]] में आइंस्टीन को एक पत्र लिखा जिसमें उन्होंने दो कणों के बीच सहसंबंधों का वर्णन करने के लिए वर्स्क्रानकुंग (खुद द्वारा उलझाव के रूप में अनुवादित) शब्द का उपयोग किया, जो ईपीआर प्रयोग में बातचीत करते हैं और फिर अलग हो जाते हैं।<ref name=MK>Kumar, M., ''Quantum'', Icon Books, 2009, p. 313.</ref> | ||
इसके तुरंत | इसके तुरंत पश्चात श्रोडिंगर ने उलझाव की धारणा को परिभाषित करने और चर्चा करने वाला एक मौलिक पेपर प्रकाशित किया। पेपर में, उन्होंने अवधारणा के महत्व को पहचाना, और कहा:<ref name="Schrödinger1935"/> मैं इसे [उलझन] नहीं कहूंगा, बल्कि इसे क्वांटम यांत्रिकी का विशिष्ट गुण कहूंगा, जो कि [[शास्त्रीय यांत्रिकी]] के विचार से इसके संपूर्ण विचलन को क्रियान्वित करता है। आइंस्टीन की तरह, श्रोडिंगर उलझाव की अवधारणा से असंतुष्ट थे, क्योंकि यह [[सापेक्षता के सिद्धांत]] में निहित सूचना के प्रसारण पर गति सीमा का उल्लंघन करता प्रतीत होता था।<ref>Alisa Bokulich, Gregg Jaeger, ''Philosophy of Quantum Information and Entanglement'', Cambridge University Press, 2010, xv.</ref> आइंस्टीन ने पश्चात में उलझाव को "स्पुखाफ्टे फर्नविर्कुंग"<ref name="spukhafte">Letter from Einstein to Max Born, 3 March 1947; ''The Born-Einstein Letters; Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955'', Walker, New York, 1971. (cited in {{cite journal |title=Quantum Entanglement and Communication Complexity (1998) |journal=SIAM J. Comput. |volume=30 |issue=6 |citeseerx=10.1.1.20.8324 |author=M. P. Hobson |pages=1829–1841 |display-authors=etal |year=1998}})</ref> या "[[दूरी पर डरावनी कार्रवाई]]" कहकर प्रसिद्ध रूप से उपहास किया। | ||
ईपीआर पेपर ने भौतिकविदों के बीच महत्वपूर्ण रुचि पैदा की, जिसने क्वांटम यांत्रिकी की नींव और विशेष रूप से बोहम की व्याख्या के बारे में बहुत चर्चा को प्रेरित किया, लेकिन अपेक्षाकृत कम अन्य प्रकाशित कार्य किए गए। रुचि के | ईपीआर पेपर ने भौतिकविदों के बीच महत्वपूर्ण रुचि पैदा की, जिसने क्वांटम यांत्रिकी की नींव और विशेष रूप से बोहम की व्याख्या के बारे में बहुत चर्चा को प्रेरित किया, लेकिन अपेक्षाकृत कम अन्य प्रकाशित कार्य किए गए। रुचि के अतिरिक्त, ईपीआर के तर्क में कमजोर बिंदु की खोज 1964 तक नहीं की गई थी, जब [[जॉन स्टीवर्ट बेल]] ने सिद्ध करना किया कि उनकी प्रमुख धारणाओं में से एक, [[स्थानीयता का सिद्धांत]], जैसा कि ईपीआर द्वारा अपेक्षित छिपे हुए चर व्याख्या के प्रकार पर क्रियान्वित होता है, गणितीय रूप से असंगत था क्वांटम सिद्धांत की भविष्यवाणियों के साथ। | ||
विशेष रूप से, बेल ने स्थानीय यथार्थवाद का पालन करने वाले किसी भी सिद्धांत में उत्पन्न होने वाले सहसंबंधों की ताकत के संबंध में, बेल की असमानता में देखी गई एक ऊपरी सीमा का प्रदर्शन किया, और दिखाया कि क्वांटम सिद्धांत कुछ उलझी हुई प्रणालियों के लिए इस सीमा के उल्लंघन की भविष्यवाणी करता है।<ref>{{cite journal |author = J. S. Bell |title = आइंस्टीन-पोडॉल्स्की-रोसेन विरोधाभास पर|journal = Physics Physique Физика |volume = 1 |issue = 3 |pages = 195–200 |year = 1964|doi = 10.1103/PhysicsPhysiqueFizika.1.195 |doi-access = free }}</ref> उनकी असमानता प्रयोगात्मक रूप से परीक्षण योग्य है, और 1972 में [[स्टुअर्ट फ्रीडमैन]] और [[जॉन क्लॉसर]] के अग्रणी काम से शुरू होकर, कई [[बेल परीक्षण प्रयोग]] हुए हैं।<ref name="Clauser">{{cite journal|doi=10.1103/PhysRevLett.28.938|last1=Freedman|first1=Stuart J.|last2=Clauser|first2=John F.|title=स्थानीय छुपे-परिवर्तनीय सिद्धांतों का प्रायोगिक परीक्षण|journal=Physical Review Letters |volume=28 |issue=14 |pages=938–941|year=1972 |bibcode=1972PhRvL..28..938F|url=https://escholarship.org/uc/item/2f18n5nk}}</ref> और 1982 में [[एलेन पहलू]] के प्रयोग।<ref name="Aspect1982">{{cite journal | विशेष रूप से, बेल ने स्थानीय यथार्थवाद का पालन करने वाले किसी भी सिद्धांत में उत्पन्न होने वाले सहसंबंधों की ताकत के संबंध में, बेल की असमानता में देखी गई एक ऊपरी सीमा का प्रदर्शन किया, और दिखाया कि क्वांटम सिद्धांत कुछ उलझी हुई प्रणालियों के लिए इस सीमा के उल्लंघन की भविष्यवाणी करता है।<ref>{{cite journal |author = J. S. Bell |title = आइंस्टीन-पोडॉल्स्की-रोसेन विरोधाभास पर|journal = Physics Physique Физика |volume = 1 |issue = 3 |pages = 195–200 |year = 1964|doi = 10.1103/PhysicsPhysiqueFizika.1.195 |doi-access = free }}</ref> उनकी असमानता प्रयोगात्मक रूप से परीक्षण योग्य है, और 1972 में [[स्टुअर्ट फ्रीडमैन]] और [[जॉन क्लॉसर]] के अग्रणी काम से शुरू होकर, कई [[बेल परीक्षण प्रयोग]] हुए हैं।<ref name="Clauser">{{cite journal|doi=10.1103/PhysRevLett.28.938|last1=Freedman|first1=Stuart J.|last2=Clauser|first2=John F.|title=स्थानीय छुपे-परिवर्तनीय सिद्धांतों का प्रायोगिक परीक्षण|journal=Physical Review Letters |volume=28 |issue=14 |pages=938–941|year=1972 |bibcode=1972PhRvL..28..938F|url=https://escholarship.org/uc/item/2f18n5nk}}</ref> और 1982 में [[एलेन पहलू]] के प्रयोग।<ref name="Aspect1982">{{cite journal | ||
| Line 73: | Line 73: | ||
| doi-access = free }}</ref> | | doi-access = free }}</ref> | ||
प्रारंभिक प्रायोगिक सफलता कार्ल कोचर के कारण हुई,<ref name="Kocher1" /><ref name="Kocherphd" /> जिन्होंने 1967 में ही एक उपकरण प्रस्तुत किया था जिसमें कैल्शियम परमाणु से क्रमिक रूप से उत्सर्जित होने वाले दो फोटॉन को उलझते हुए दिखाया गया था - उलझे हुए दृश्य प्रकाश का पहला | प्रारंभिक प्रायोगिक सफलता कार्ल कोचर के कारण हुई,<ref name="Kocher1" /><ref name="Kocherphd" /> जिन्होंने 1967 में ही एक उपकरण प्रस्तुत किया था जिसमें कैल्शियम परमाणु से क्रमिक रूप से उत्सर्जित होने वाले दो फोटॉन को उलझते हुए दिखाया गया था - उलझे हुए दृश्य प्रकाश का पहला विषय। दो फोटॉन शास्त्रीय रूप से भविष्यवाणी की समानता में उच्च संभावना के साथ व्यासीय रूप से स्थित समानांतर ध्रुवीकरणकर्ताओं से गुजरे लेकिन क्वांटम यांत्रिक गणना के साथ मात्रात्मक समझौते में सहसंबंध थे। उन्होंने यह भी दिखाया कि ध्रुवीकरण समूहिंग्स के बीच कोण के वर्ग [[ज्या और कोज्या]] के रूप में सहसंबंध भिन्न होता है<ref name="Kocherphd" />और उत्सर्जित फोटॉन के बीच समय अंतराल के साथ तेजी से कमी आई।<ref name="Kocher2">{{cite journal | doi = 10.1016/0003-4916(71)90159-X | volume=65 | issue=1 | title=क्रमिक रूप से उत्सर्जित फोटॉन का पता लगाने में समय सहसंबंध| journal=Annals of Physics | pages=1–18 | last1 = Kocher | first1 = CA | year=1971| bibcode=1971AnPhy..65....1K }}</ref> कोचर का उपकरण, जो बेहतर ध्रुवीकरणकर्ताओं से सुसज्जित था, का उपयोग फ्रीडमैन और क्लॉसर द्वारा किया गया था जो कोसाइन-वर्ग निर्भरता की पुष्टि कर सकते थे और इसका उपयोग निश्चित कोणों के एक समूह के लिए बेल की असमानता के उल्लंघन को प्रदर्शित करने के लिए कर सकते थे।<ref name="Clauser" /> इन सभी प्रयोगों ने स्थानीय यथार्थवाद के सिद्धांत के अतिरिक्त क्वांटम यांत्रिकी के साथ सहमति दिखाई है। | ||
दशकों तक, प्रत्येक ने कम से कम एक खामी खुली रखी थी जिसके द्वारा परिणामों की वैधता पर सवाल उठाना संभव था। | दशकों तक, प्रत्येक ने कम से कम एक खामी खुली रखी थी जिसके द्वारा परिणामों की वैधता पर सवाल उठाना संभव था। चूंकि, 2015 में एक प्रयोग किया गया था जिसने एक साथ पता लगाने और इलाके की खामियों दोनों को संवृत कर दिया था, और इसे "खामियों से मुक्त" के रूप में प्रचारित किया गया था; इस प्रयोग ने निश्चितता के साथ स्थानीय यथार्थवाद सिद्धांतों के एक बड़े वर्ग को खारिज कर दिया।<ref name="hanson">{{cite journal|last1=Hanson|first1=Ronald|title=Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres|journal=Nature|volume=526|issue=7575|pages=682–686|doi=10.1038/nature15759|arxiv=1508.05949|bibcode = 2015Natur.526..682H|pmid=26503041|year=2015|s2cid=205246446}}</ref> पहलू लिखते हैं कि "... कोई भी प्रयोग ... पूरी तरह से खामियों से मुक्त नहीं कहा जा सकता है," लेकिन उनका कहना है कि प्रयोग "अंतिम संदेह को दूर करते हैं कि हमें स्थानीय छिपे हुए चर को त्याग देना चाहिए", और शेष खामियों के उदाहरणों को संदर्भित करता है "दूर की कौड़ी" होना और "भौतिकी में तर्क करने का सामान्य तरीका विदेशी होना।"<ref>{{cite journal |last=Aspect |first=Alain |date=December 16, 2015 |title=आइंस्टीन और बोह्र की क्वांटम बहस पर दरवाजा बंद करना|journal=[[Physics (magazine)|Physics]] |volume=8 |pages=123 |bibcode=2015PhyOJ...8..123A |doi=10.1103/Physics.8.123 |doi-access=free}}</ref> | ||
बेल के काम ने संचार के लिए एक संसाधन के रूप में इन सुपर-मजबूत सहसंबंधों का उपयोग करने की संभावना बढ़ा दी। इसके कारण 1984 में चार्ल्स एच. बेनेट (कंप्यूटर वैज्ञानिक) द्वारा [[क्वांटम कुंजी वितरण]] प्रोटोकॉल, सबसे प्रसिद्ध [[बीबी84]] की खोज हुई|चार्ल्स एच. बेनेट और [[गाइल्स ब्रासार्ड]]<ref>C. H. Bennett and G. Brassard. "Quantum cryptography: Public key distribution and coin tossing". In ''Proceedings of IEEE International Conference on Computers, Systems and Signal Processing'', volume 175, p. 8. New York, 1984. http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf {{Webarchive|url=https://web.archive.org/web/20200130165639/http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf |date=30 January 2020 }}</ref> और [[आर्थर एकर्ट]] द्वारा [[E91 प्रोटोकॉल]]।<ref>{{cite journal|last=Ekert|first=A.K.|author-link=Artur Ekert|title=बेल के प्रमेय पर आधारित क्वांटम क्रिप्टोग्राफी|journal=Phys. Rev. Lett.|volume=67|issue=6|year=1991|doi=10.1103/PhysRevLett.67.661|issn=0031-9007|bibcode = 1991PhRvL..67..661E|pmid=10044956|pages=661–663|s2cid=27683254 }}</ref> | बेल के काम ने संचार के लिए एक संसाधन के रूप में इन सुपर-मजबूत सहसंबंधों का उपयोग करने की संभावना बढ़ा दी। इसके कारण 1984 में चार्ल्स एच. बेनेट (कंप्यूटर वैज्ञानिक) द्वारा [[क्वांटम कुंजी वितरण]] प्रोटोकॉल, सबसे प्रसिद्ध [[बीबी84]] की खोज हुई|चार्ल्स एच. बेनेट और [[गाइल्स ब्रासार्ड]]<ref>C. H. Bennett and G. Brassard. "Quantum cryptography: Public key distribution and coin tossing". In ''Proceedings of IEEE International Conference on Computers, Systems and Signal Processing'', volume 175, p. 8. New York, 1984. http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf {{Webarchive|url=https://web.archive.org/web/20200130165639/http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf |date=30 January 2020 }}</ref> और [[आर्थर एकर्ट]] द्वारा [[E91 प्रोटोकॉल]]।<ref>{{cite journal|last=Ekert|first=A.K.|author-link=Artur Ekert|title=बेल के प्रमेय पर आधारित क्वांटम क्रिप्टोग्राफी|journal=Phys. Rev. Lett.|volume=67|issue=6|year=1991|doi=10.1103/PhysRevLett.67.661|issn=0031-9007|bibcode = 1991PhRvL..67..661E|pmid=10044956|pages=661–663|s2cid=27683254 }}</ref> चूंकि बीबी84 उलझाव का उपयोग नहीं करता है, एकर्ट का प्रोटोकॉल सुरक्षा के प्रमाण के रूप में बेल की असमानता के उल्लंघन का उपयोग करता है। | ||
2022 में, भौतिकी में नोबेल पुरस्कार एस्पेक्ट, क्लॉसर और [[एंटोन ज़िलिंगर]] को "उलझे हुए फोटॉन के साथ प्रयोगों, बेल असमानताओं के उल्लंघन की स्थापना और क्वांटम सूचना विज्ञान में अग्रणी" के लिए प्रदान किया गया था।<ref name="NobelPrize">{{cite press release |url=https://www.nobelprize.org/prizes/physics/2022/press-release/ |title=The Nobel Prize in Physics 2022 |date=October 4, 2022 |work=[[Nobel Prize]] |publisher=[[The Royal Swedish Academy of Sciences ]] |access-date=5 October 2022}}</ref> | 2022 में, भौतिकी में नोबेल पुरस्कार एस्पेक्ट, क्लॉसर और [[एंटोन ज़िलिंगर]] को "उलझे हुए फोटॉन के साथ प्रयोगों, बेल असमानताओं के उल्लंघन की स्थापना और क्वांटम सूचना विज्ञान में अग्रणी" के लिए प्रदान किया गया था।<ref name="NobelPrize">{{cite press release |url=https://www.nobelprize.org/prizes/physics/2022/press-release/ |title=The Nobel Prize in Physics 2022 |date=October 4, 2022 |work=[[Nobel Prize]] |publisher=[[The Royal Swedish Academy of Sciences ]] |access-date=5 October 2022}}</ref> | ||
| Line 83: | Line 83: | ||
=== उलझाव का अर्थ === | === उलझाव का अर्थ === | ||
एक उलझी हुई प्रणाली को उस प्रणाली के रूप में परिभाषित किया जाता है जिसकी क्वांटम स्थिति को उसके स्थानीय घटकों की स्थिति के उत्पाद के रूप में नहीं माना जा सकता है; कहने का तात्पर्य यह है कि, वे अलग-अलग कण नहीं हैं बल्कि एक अविभाज्य संपूर्ण हैं। उलझाव में, एक घटक को दूसरे पर विचार किए बिना पूरी तरह से वर्णित नहीं किया जा सकता है। एक समग्र प्रणाली की स्थिति | एक उलझी हुई प्रणाली को उस प्रणाली के रूप में परिभाषित किया जाता है जिसकी क्वांटम स्थिति को उसके स्थानीय घटकों की स्थिति के उत्पाद के रूप में नहीं माना जा सकता है; कहने का तात्पर्य यह है कि, वे अलग-अलग कण नहीं हैं बल्कि एक अविभाज्य संपूर्ण हैं। उलझाव में, एक घटक को दूसरे पर विचार किए बिना पूरी तरह से वर्णित नहीं किया जा सकता है। एक समग्र प्रणाली की स्थिति सदैव स्थानीय घटकों के स्थितिों के उत्पादों के योग या [[ जितना कि सुपरइम्पोज़िशन ]] के रूप में व्यक्त की जाती है; यह उलझा हुआ है यदि इस राशि को एकल उत्पाद पद के रूप में नहीं लिखा जा सकता है। | ||
क्वांटम [[भौतिक प्रणाली]] विभिन्न प्रकार की अंतःक्रियाओं के माध्यम से उलझ सकती है। प्रयोगात्मक उद्देश्यों के लिए उलझाव को किन | क्वांटम [[भौतिक प्रणाली]] विभिन्न प्रकार की अंतःक्रियाओं के माध्यम से उलझ सकती है। प्रयोगात्मक उद्देश्यों के लिए उलझाव को किन विधियों से प्राप्त किया जा सकता है, इसके लिए नीचे दिए गए तरीकों पर अनुभाग देखें। उलझाव तब टूटता है जब उलझे हुए कण पर्यावरण के साथ संपर्क के माध्यम से क्वांटम विघटन करते हैं; उदाहरण के लिए, जब माप किया जाता है।<ref name="Peres1993">Asher Peres, ''[[Quantum Theory: Concepts and Methods]]'', Kluwer, 1993; {{ISBN|0-7923-2549-4}} p. 115.</ref> | ||
उलझाव के उदाहरण के रूप में: एक उपपरमाण्विक कण कण अन्य कणों की उलझी हुई जोड़ी में क्षय हो जाता है। क्षय की घटनाएँ विभिन्न [[संरक्षण कानून|संरक्षण नियमो]] का पालन करती हैं, और परिणामस्वरूप, एक बेटी कण के माप परिणामों को दूसरे बेटी कण के माप परिणामों के साथ अत्यधिक सहसंबद्ध होना चाहिए ( | उलझाव के उदाहरण के रूप में: एक उपपरमाण्विक कण कण अन्य कणों की उलझी हुई जोड़ी में क्षय हो जाता है। क्षय की घटनाएँ विभिन्न [[संरक्षण कानून|संरक्षण नियमो]] का पालन करती हैं, और परिणामस्वरूप, एक बेटी कण के माप परिणामों को दूसरे बेटी कण के माप परिणामों के साथ अत्यधिक सहसंबद्ध होना चाहिए (जिससे कि कुल संवेग, कोणीय संवेग, ऊर्जा और इस प्रक्रिया से पहले और पश्चात में लगभग समान रहे)। उदाहरण के लिए, एक स्पिन-शून्य कण स्पिन-1/2 कणों की एक जोड़ी में क्षय हो सकता है। चूँकि इस क्षय से पहले और पश्चात में कुल स्पिन शून्य (कोणीय गति का संरक्षण) होना चाहिए, जब भी पहले कण को किसी अक्ष पर ऊपर की ओर घूमते हुए मापा जाता है, तो दूसरा, जब उसी अक्ष पर मापा जाता है, तो सदैव नीचे की ओर घूमता हुआ पाया जाता है। (इसे स्पिन विरोधी सहसंबद्ध मामला कहा जाता है; और यदि प्रत्येक स्पिन को मापने की पूर्व संभावनाएं बराबर हैं, तो जोड़ी को [[एकल अवस्था]] में कहा जाता है।) | ||
उपरोक्त परिणाम आश्चर्यजनक हो भी सकता है और नहीं भी। एक शास्त्रीय प्रणाली समान संपत्ति प्रदर्शित करेगी, और ऐसा करने के लिए निश्चित रूप से एक छिपे हुए चर सिद्धांत की आवश्यकता होगी, जो शास्त्रीय और क्वांटम यांत्रिकी में समान रूप से कोणीय गति के संरक्षण पर आधारित होगा। अंतर यह है कि एक शास्त्रीय प्रणाली में सभी अवलोकन योग्य वस्तुओं के लिए निश्चित मान होते हैं, जबकि क्वांटम प्रणाली में ऐसा नहीं होता है। नीचे चर्चा की जाने वाली अर्थ में, यहां माना गया क्वांटम | उपरोक्त परिणाम आश्चर्यजनक हो भी सकता है और नहीं भी। एक शास्त्रीय प्रणाली समान संपत्ति प्रदर्शित करेगी, और ऐसा करने के लिए निश्चित रूप से एक छिपे हुए चर सिद्धांत की आवश्यकता होगी, जो शास्त्रीय और क्वांटम यांत्रिकी में समान रूप से कोणीय गति के संरक्षण पर आधारित होगा। अंतर यह है कि एक शास्त्रीय प्रणाली में सभी अवलोकन योग्य वस्तुओं के लिए निश्चित मान होते हैं, जबकि क्वांटम प्रणाली में ऐसा नहीं होता है। नीचे चर्चा की जाने वाली अर्थ में, यहां माना गया क्वांटम प्रणाली पहले कण के माप पर दूसरे कण के किसी भी अक्ष के साथ स्पिन के माप के परिणाम के लिए संभाव्यता वितरण प्राप्त करता प्रतीत होता है। यह संभाव्यता वितरण सामान्यतः पहले कण के माप के बिना जो होगा उससे भिन्न है। स्थानिक रूप से अलग-अलग उलझे हुए कणों के स्थितियों में इसे निश्चित रूप से आश्चर्यजनक माना जा सकता है। | ||
===विरोधाभास=== | ===विरोधाभास=== | ||
विरोधाभास यह है कि किसी भी कण पर किया गया माप स्पष्ट रूप से पूरे उलझे हुए | विरोधाभास यह है कि किसी भी कण पर किया गया माप स्पष्ट रूप से पूरे उलझे हुए प्रणाली की स्थिति को ध्वस्त कर देता है - और ऐसा तुरंत होता है, इससे पहले कि माप परिणाम के बारे में कोई भी जानकारी दूसरे कण को संप्रेषित की जा सके (यह मानते हुए कि जानकारी प्रकाश से तेज गति से यात्रा नहीं कर सकती है) और इसलिए उलझे हुए जोड़े के दूसरे भाग के माप के उचित परिणाम का आश्वासन दिया गया है। [[कोपेनहेगन व्याख्या]] में, कणों में से एक पर स्पिन माप का परिणाम एक ऐसी स्थिति में पतन (तरंग फ़ंक्शन का) होता है। जिसमें प्रत्येक कण में माप की धुरी के साथ एक निश्चित स्पिन (या तो ऊपर या नीचे) होता है। परिणाम को यादृच्छिक माना जाता है, प्रत्येक संभावना की संभावना 50% होती है। चूंकि, यदि दोनों स्पिनों को एक ही अक्ष पर मापा जाता है, तो वे सहसंबद्ध विरोधी पाए जाते हैं। इसका तात्पर्य यह है कि एक कण पर किए गए माप का यादृच्छिक परिणाम दूसरे को प्रेषित किया गया लगता है, जिससे कि जब इसे भी मापा जाए तो वह सही विकल्प चुन सके।<ref>{{cite book|last1=Rupert W.|first1=Anderson|title=The Cosmic Compendium: Interstellar Travel|date=28 March 2015|publisher=The Cosmic Compendium|isbn=9781329022027|page=100|edition=First|url=https://books.google.com/books?id=JxauCQAAQBAJ&q=The+outcome+is+taken+to+be+random,+with+each+possibility+having+a+probability+of+50%25.+However,+if+both+spins+are+measured+along+the+same+axis,+they+are+found+to+be+anti-correlated.+This+means+that+the+random+outcome+of+the+measurement+made+on+one+particle+seems+to+have+been+transmitted+to+the+other,+so+that+it+can+make+the+%22right+choice%22+when+it+too+is+measured&pg=PA100}}</ref> | ||
(वास्तव में समान विरोधाभास उलझाव के बिना भी उत्पन्न हो सकते हैं: एक कण की स्थिति अंतरिक्ष में फैली हुई है, और दो अलग-अलग स्थानों में कण का पता लगाने का प्रयास करने वाले दो व्यापक रूप से अलग-अलग | माप की दूरी और समय को चुना जा सकता है जिससे कि दो मापों के बीच के अंतराल को अंतरिक्षीय बनाया जा सके, इसलिए, घटनाओं को जोड़ने वाले किसी भी कारण प्रभाव को प्रकाश की समानता में तेजी से यात्रा करनी होगी। [[विशेष सापेक्षता]] के सिद्धांतों के अनुसार, किसी भी जानकारी के लिए ऐसी दो मापने वाली घटनाओं के बीच यात्रा करना संभव नहीं है। यह कहना भी संभव नहीं है कि इनमें से कौन सा माप पहले आया। दो अंतरिक्षीय पृथक घटनाओं के लिए {{math|''x''<sub>1</sub>}} और {{math|''x''<sub>2</sub>}} जिसमें जड़त्वीय ढाँचे होते हैं {{math|''x''<sub>1</sub>}} प्रथम है तथा अन्य जिसमें {{math|''x''<sub>2</sub>}} प्रथम है। इसलिए, दो मापों के बीच सहसंबंध को इस प्रकार नहीं समझाया जा सकता है कि एक माप दूसरे को निर्धारित करता है: विभिन्न पर्यवेक्षक कारण और प्रभाव की भूमिका के बारे में असहमत होंगे। | ||
(वास्तव में समान विरोधाभास उलझाव के बिना भी उत्पन्न हो सकते हैं: एक कण की स्थिति अंतरिक्ष में फैली हुई है, और दो अलग-अलग स्थानों में कण का पता लगाने का प्रयास करने वाले दो व्यापक रूप से अलग-अलग संसूचकों को तत्काल उचित सहसंबंध प्राप्त करना होगा, जिससे कि वे दोनों का पता न लगा सकें कण।) | |||
=== छिपे हुए चर सिद्धांत === | === छिपे हुए चर सिद्धांत === | ||
| Line 105: | Line 106: | ||
| url = https://www.scientificamerican.com/article/cosmic-test-bolsters-einsteins-ldquo-spooky-action-at-a-distance-rdquo/ | | url = https://www.scientificamerican.com/article/cosmic-test-bolsters-einsteins-ldquo-spooky-action-at-a-distance-rdquo/ | ||
| year = 2017 | | year = 2017 | ||
}}</ref> मापे जा रहे कणों की स्थिति में कुछ छिपे हुए-परिवर्तनीय सिद्धांत | }}</ref> मापे जा रहे कणों की स्थिति में कुछ छिपे हुए-परिवर्तनीय सिद्धांत सम्मलित हैं, जिनके मान पृथक्करण के क्षण से ही प्रभावी ढंग से निर्धारित करते हैं कि स्पिन माप के परिणाम क्या होंगे। इसका तात्पर्य यह होगा कि प्रत्येक कण अपने साथ सभी आवश्यक जानकारी रखता है, और माप के समय एक कण से दूसरे तक कुछ भी प्रसारित करने की आवश्यकता नहीं होती है। आइंस्टीन और अन्य (पिछला भाग देखें) मूल रूप से मानते थे कि यह विरोधाभास से बाहर निकलने का एकमात्र तरीका था, और स्वीकृत क्वांटम यांत्रिक विवरण (यादृच्छिक माप परिणाम के साथ) अधूरा होना चाहिए। | ||
=== बेल की असमानता का उल्लंघन === | === बेल की असमानता का उल्लंघन === | ||
चूंकि, [[स्थानीय छिपा-चर सिद्धांत]] विफल हो जाता है, जब विभिन्न अक्षों के साथ उलझे हुए कणों के स्पिन के माप पर विचार किया जाता है। यदि ऐसे मापों के जोड़े बड़ी संख्या में बनाए जाते हैं (उलझे हुए कणों के जोड़े की बड़ी संख्या पर), तो सांख्यिकीय रूप से, यदि स्थानीय यथार्थवाद या छिपे हुए चर दृश्य सही थे, तो परिणाम सदैव बेल की असमानता को संतुष्ट करेंगे। बेल परीक्षण प्रयोगों ने व्यवहार में दिखाया है कि बेल की असमानता संतुष्ट नहीं है। चूंकि, 2015 से पहले, इन सभी में खामियों की समस्याएँ थीं जिन्हें भौतिकविदों के समुदाय द्वारा सबसे महत्वपूर्ण माना जाता था।<ref>{{citation |author1=I. Gerhardt |author2=Q. Liu |author3=A. Lamas-Linares |author4=J. Skaar |author5=V. Scarani |author6=V. Makarov |author7=C. Kurtsiefer |year=2011 |title=Experimentally faking the violation of Bell's inequalities |journal=Phys. Rev. Lett. |volume=107 |issue=17 |page=170404 |arxiv=1106.3224 |pmid=22107491 |doi=10.1103/PhysRevLett.107.170404 |bibcode=2011PhRvL.107q0404G |s2cid=16306493}}</ref><ref>{{cite journal |last1=Santos |first1=E |year=2004 |title=बेल की असमानता का खामियों से मुक्त परीक्षण करने में विफलता स्थानीय यथार्थवाद का समर्थन करती है|journal=Foundations of Physics |volume=34 |issue=11| pages=1643–1673 |doi=10.1007/s10701-004-1308-z |bibcode=2004FoPh...34.1643S |s2cid=123642560}}</ref> जब उलझे हुए कणों का माप गतिमान विशेष सापेक्षता संदर्भ फ्रेम में किया जाता है, जिसमें प्रत्येक माप (अपने स्वयं के सापेक्ष समय सीमा में) दूसरे से पहले होता है, तो माप परिणाम सहसंबद्ध रहते हैं।<ref>{{cite journal |author=H. Zbinden |author2=Gisin |author3=Tittel |display-authors=1 |title=सापेक्षतावादी विन्यास में गैर-स्थानीय क्वांटम सहसंबंधों का प्रायोगिक परीक्षण|journal=Phys. Rev. A |volume=63 |issue=2 |pages=22111 |doi=10.1103/PhysRevA.63.022111 |year=2001 |arxiv=quant-ph/0007009 |bibcode=2001PhRvA..63b2111Z |s2cid=44611890 |url=http://archive-ouverte.unige.ch/unige:37034}}</ref><ref name=LG>Some of the history of both referenced Zbinden, et al. experiments is provided in Gilder, L., ''The Age of Entanglement'', Vintage Books, 2008, pp. 321–324.</ref> | |||
विभिन्न अक्षों के साथ स्पिन को मापने के बारे में मूल मुद्दा यह है कि इन मापों में एक ही समय में निश्चित मान नहीं हो सकते हैं - वे इस अर्थ में असंगत अवलोकन योग्य हैं कि इन मापों की अधिकतम एक साथ सटीकता अनिश्चितता सिद्धांत द्वारा बाधित है। यह शास्त्रीय भौतिकी में पाए जाने वाले के विपरीत है, जहां किसी भी संख्या में गुणों को मनमानी सटीकता के साथ एक साथ मापा जा सकता है। यह गणितीय रूप से सिद्ध हो चुका है कि संगत माप बेल-असमानता-उल्लंघन सहसंबंध नहीं दिखा सकते हैं,<ref>{{cite journal|last1=Cirel'son|first1=B. S.|title=बेल की असमानता का क्वांटम सामान्यीकरण|journal=Letters in Mathematical Physics |volume=4|issue=2|pages=93–100| year=1980|doi=10.1007/BF00417500|bibcode=1980LMaPh...4...93C |s2cid=120680226}}</ref> और इस प्रकार उलझाव एक मौलिक रूप से गैर-शास्त्रीय घटना है। | विभिन्न अक्षों के साथ स्पिन को मापने के बारे में मूल मुद्दा यह है कि इन मापों में एक ही समय में निश्चित मान नहीं हो सकते हैं - वे इस अर्थ में असंगत अवलोकन योग्य हैं कि इन मापों की अधिकतम एक साथ सटीकता अनिश्चितता सिद्धांत द्वारा बाधित है। यह शास्त्रीय भौतिकी में पाए जाने वाले के विपरीत है, जहां किसी भी संख्या में गुणों को मनमानी सटीकता के साथ एक साथ मापा जा सकता है। यह गणितीय रूप से सिद्ध हो चुका है कि संगत माप बेल-असमानता-उल्लंघन सहसंबंध नहीं दिखा सकते हैं,<ref>{{cite journal|last1=Cirel'son|first1=B. S.|title=बेल की असमानता का क्वांटम सामान्यीकरण|journal=Letters in Mathematical Physics |volume=4|issue=2|pages=93–100| year=1980|doi=10.1007/BF00417500|bibcode=1980LMaPh...4...93C |s2cid=120680226}}</ref> और इस प्रकार उलझाव एक मौलिक रूप से गैर-शास्त्रीय घटना है। | ||
=== क्वांटम उलझाव को | === क्वांटम उलझाव को सिद्ध करना करने वाले उल्लेखनीय प्रयोगात्मक परिणाम === | ||
पहला प्रयोग जिसने दूरी (उलझाव) पर आइंस्टीन की डरावनी कार्रवाई को सत्यापित किया था, उसे 1949 में [[χ एन-शि यूएन जीडब्ल्यू यू|चिएन-शिउंग वू]] और सहयोगी आई. शाकनोव द्वारा एक प्रयोगशाला में सफलतापूर्वक पुष्टि की गई थी, और 1950 में नए साल के दिन प्रकाशित किया गया था। परिणाम ने विशेष रूप से क्वांटम सहसंबंधों को | पहला प्रयोग जिसने दूरी (उलझाव) पर आइंस्टीन की डरावनी कार्रवाई को सत्यापित किया था, उसे 1949 में [[χ एन-शि यूएन जीडब्ल्यू यू|चिएन-शिउंग वू]] और सहयोगी आई. शाकनोव द्वारा एक प्रयोगशाला में सफलतापूर्वक पुष्टि की गई थी, और 1950 में नए साल के दिन प्रकाशित किया गया था। परिणाम ने विशेष रूप से क्वांटम सहसंबंधों को सिद्ध करना किया फोटॉनों की एक जोड़ी का.<ref>{{cite journal |last1=Wu |first1=C. 's. |last2=Shaknov |first2=I. |year=1950 |title=बिखरे हुए विनाश विकिरण का कोणीय सहसंबंध|journal=[[Physical Review]] |volume=77 |issue=1 |pages=136 |bibcode=1950PhRv...77..136W |doi=10.1103/PhysRev.77.136}}</ref> 2012 और 2013 में प्रयोगों में, उन फोटॉनों के बीच ध्रुवीकरण सहसंबंध बनाया गया था जो समय में कभी सह-अस्तित्व में नहीं थे।<ref name="Xiao-song2012">{{cite journal |author1=Xiao-song Ma |author2=Stefan Zotter |author3=Johannes Kofler |author4=Rupert Ursin |author5=Thomas Jennewein |author6=Časlav Brukner |author7=Anton Zeilinger |title=प्रायोगिक विलंबित-विकल्प उलझाव स्वैपिंग|journal=Nature Physics |volume=8 |issue=6 |pages=480–485 |date=26 April 2012 |doi=10.1038/nphys2294|arxiv=1203.4834 |bibcode=2012NatPh...8..480M |s2cid=119208488}}</ref><ref>{{cite journal |last1=Megidish |first1=E. |last2=Halevy |first2=A. |last3=Shacham |first3=T. |last4=Dvir |first4=T. |last5=Dovrat |first5=L. |last6=Eisenberg |first6=H. S. |year=2013 |title=उन फोटॉनों के बीच उलझाव की अदला-बदली जो कभी एक साथ अस्तित्व में नहीं रहे|journal=Physical Review Letters |volume=110 |issue=21 |page=210403| doi=10.1103/physrevlett.110.210403 |arxiv=1209.4191 |bibcode=2013PhRvL.110u0403M |pmid=23745845 |s2cid=30063749}}</ref> लेखकों ने दावा किया कि यह परिणाम प्रारंभिक जोड़ी के एक फोटॉन के ध्रुवीकरण को मापने के पश्चात उलझे हुए फोटॉन के दो जोड़े के बीच क्वांटम टेलीपोर्टेशन एंटैंगलमेंट स्वैपिंग द्वारा प्राप्त किया गया था, और यह सिद्ध करना करता है कि क्वांटम गैर-स्थानीयता न केवल अंतरिक्ष पर बल्कि समय पर भी क्रियान्वित होती है। | ||
2013 में तीन स्वतंत्र प्रयोगों में, यह दिखाया गया कि शास्त्रीय भौतिकी की [[पृथक्करणीय अवस्था]] का उपयोग उलझी हुई अवस्थाओं को ले जाने के लिए किया जा सकता है।<ref>{{cite web |url=http://physicsworld.com/cws/article/news/2013/dec/11/classical-carrier-could-create-entanglement |title=शास्त्रीय वाहक उलझाव पैदा कर सकता है|publisher=physicsworld.com |access-date=2014-06-14 |date=2013-12-11 }}</ref> पहला लूपहोल-मुक्त बेल परीक्षण 2015 में [[डेल्फ़्ट प्रौद्योगिकी विश्वविद्यालय]] के [[ रोनाल्ड हैन्सन ]] द्वारा आयोजित किया गया था, जिसमें बेल असमानता के उल्लंघन की पुष्टि की गई थी।<ref>{{cite web |url=http://hansonlab.tudelft.nl/loophole-free-bell-test/ |title=Loophole-free Bell test | Ronald Hanson |access-date=24 October 2015 |url-status=dead |archive-date=4 July 2018 |archive-url=https://web.archive.org/web/20180704082456/http://hansonlab.tudelft.nl/loophole-free-bell-test/}}</ref> | 2013 में तीन स्वतंत्र प्रयोगों में, यह दिखाया गया कि शास्त्रीय भौतिकी की [[पृथक्करणीय अवस्था]] का उपयोग उलझी हुई अवस्थाओं को ले जाने के लिए किया जा सकता है।<ref>{{cite web |url=http://physicsworld.com/cws/article/news/2013/dec/11/classical-carrier-could-create-entanglement |title=शास्त्रीय वाहक उलझाव पैदा कर सकता है|publisher=physicsworld.com |access-date=2014-06-14 |date=2013-12-11 }}</ref> पहला लूपहोल-मुक्त बेल परीक्षण 2015 में [[डेल्फ़्ट प्रौद्योगिकी विश्वविद्यालय]] के [[ रोनाल्ड हैन्सन ]] द्वारा आयोजित किया गया था, जिसमें बेल असमानता के उल्लंघन की पुष्टि की गई थी।<ref>{{cite web |url=http://hansonlab.tudelft.nl/loophole-free-bell-test/ |title=Loophole-free Bell test | Ronald Hanson |access-date=24 October 2015 |url-status=dead |archive-date=4 July 2018 |archive-url=https://web.archive.org/web/20180704082456/http://hansonlab.tudelft.nl/loophole-free-bell-test/}}</ref> | ||
| Line 118: | Line 119: | ||
अगस्त 2014 में, ब्राज़ीलियाई शोधकर्ता गैब्रिएला बैरेटो लेमोस और टीम फोटॉनों का उपयोग करके उन वस्तुओं की तस्वीरें लेने में सक्षम थीं, जिन्होंने विषयों के साथ बातचीत नहीं की थी, लेकिन उन फोटॉनों से उलझ गए थे जो ऐसी वस्तुओं के साथ बातचीत करते थे। वियना विश्वविद्यालय के लेमोस को विश्वास है कि इस नई क्वांटम इमेजिंग तकनीक का उपयोग जैविक या चिकित्सा इमेजिंग जैसे क्षेत्रों में किया जा सकता है, जहां कम रोशनी में इमेजिंग अनिवार्य है।<ref>{{Cite journal |url=http://www.nature.com/news/entangled-photons-make-a-picture-from-a-paradox-1.15781 |title=उलझे हुए फोटॉन एक विरोधाभास से चित्र बनाते हैं|journal=Nature |access-date=2014-10-13 |doi=10.1038/nature.2014.15781 |year=2014 |last1=Gibney |first1=Elizabeth |s2cid=124976589|doi-access=free }}</ref> | अगस्त 2014 में, ब्राज़ीलियाई शोधकर्ता गैब्रिएला बैरेटो लेमोस और टीम फोटॉनों का उपयोग करके उन वस्तुओं की तस्वीरें लेने में सक्षम थीं, जिन्होंने विषयों के साथ बातचीत नहीं की थी, लेकिन उन फोटॉनों से उलझ गए थे जो ऐसी वस्तुओं के साथ बातचीत करते थे। वियना विश्वविद्यालय के लेमोस को विश्वास है कि इस नई क्वांटम इमेजिंग तकनीक का उपयोग जैविक या चिकित्सा इमेजिंग जैसे क्षेत्रों में किया जा सकता है, जहां कम रोशनी में इमेजिंग अनिवार्य है।<ref>{{Cite journal |url=http://www.nature.com/news/entangled-photons-make-a-picture-from-a-paradox-1.15781 |title=उलझे हुए फोटॉन एक विरोधाभास से चित्र बनाते हैं|journal=Nature |access-date=2014-10-13 |doi=10.1038/nature.2014.15781 |year=2014 |last1=Gibney |first1=Elizabeth |s2cid=124976589|doi-access=free }}</ref> | ||
2016 के | 2016 के पश्चात से, विभिन्न कंपनियों, उदाहरण के लिए आईबीएम और माइक्रोसॉफ्ट, ने क्वांटम कंप्यूटर बनाए हैं जो डेवलपर्स और तकनीकी उत्साही लोगों को क्वांटम उलझाव सहित क्वांटम यांत्रिकी की अवधारणाओं के साथ स्वतंत्र रूप से प्रयोग करने की अनुमति देते हैं।<ref>{{Cite journal|last=Rozatkar|first=Gaurav|date=2018-08-16|title=क्वांटम उलझाव का प्रदर्शन|url=https://osf.io/g8bpj/|journal=OSF|language=en}}</ref> | ||
=== समय का रहस्य === | === समय का रहस्य === | ||
समय की अवधारणा को एक उभरती हुई घटना के रूप में देखने के सुझाव दिए गए हैं जो क्वांटम उलझाव का एक दुष्प्रभाव है।<ref>{{Cite journal|title= Time from quantum entanglement: an experimental illustration|arxiv=1310.4691|bibcode = 2014PhRvA..89e2122M |doi = 10.1103/PhysRevA.89.052122|volume=89|issue= 5|pages=052122|journal=Physical Review A|year=2014 | last1 = Moreva | first1 = Ekaterina|s2cid=118638346}}</ref><ref>{{cite web | समय की अवधारणा को एक उभरती हुई घटना के रूप में देखने के सुझाव दिए गए हैं जो क्वांटम उलझाव का एक दुष्प्रभाव है।<ref>{{Cite journal|title= Time from quantum entanglement: an experimental illustration|arxiv=1310.4691|bibcode = 2014PhRvA..89e2122M |doi = 10.1103/PhysRevA.89.052122|volume=89|issue= 5|pages=052122|journal=Physical Review A|year=2014 | last1 = Moreva | first1 = Ekaterina|s2cid=118638346}}</ref><ref>{{cite web | ||
| Line 135: | Line 136: | ||
एडीएस/सीएफटी पत्राचार के आधार पर, [[मार्क वान रैम्स्डोंक]] ने सुझाव दिया कि [[ अंतरिक्ष समय |अंतरिक्ष समय]] स्वतंत्रता की क्वांटम डिग्री की एक उभरती हुई घटना के रूप में उभरता है जो उलझे हुए हैं और स्पेस-टाइम की सीमा में रहते हैं।<ref>{{Cite journal|last=Van Raamsdonk|first=Mark|date=2010-06-19|title=क्वांटम उलझाव के साथ स्पेसटाइम का निर्माण|journal=General Relativity and Gravitation|language=en|volume=42|issue=10|pages=2323–2329|doi=10.1007/s10714-010-1034-0|issn=0001-7701|arxiv=1005.3035|bibcode=2010GReGr..42.2323V|s2cid=189843725}}</ref> [[प्रेरित गुरुत्वाकर्षण]] उलझाव के पहले नियम से उभर सकता है<ref>{{Cite journal|last1=Lee|first1=Jae-Weon|last2=Kim|first2=Hyeong-Chan|last3=Lee|first3=Jungjai|date=2013|title=क्वांटम जानकारी से गुरुत्वाकर्षण|journal=Journal of the Korean Physical Society|language=en|volume=63|issue=5|pages=1094–1098|doi=10.3938/jkps.63.1094|issn=0374-4884|arxiv=1001.5445|bibcode=2013JKPS...63.1094L|s2cid=118494859}}</ref><ref>{{cite arXiv|last1=Swingle|first1=Brian|last2=Van Raamsdonk|first2=Mark|date=2014-05-12|title=उलझाव से गुरुत्वाकर्षण की सार्वभौमिकता|eprint=1405.2933 |class=hep-th}}</ref> | एडीएस/सीएफटी पत्राचार के आधार पर, [[मार्क वान रैम्स्डोंक]] ने सुझाव दिया कि [[ अंतरिक्ष समय |अंतरिक्ष समय]] स्वतंत्रता की क्वांटम डिग्री की एक उभरती हुई घटना के रूप में उभरता है जो उलझे हुए हैं और स्पेस-टाइम की सीमा में रहते हैं।<ref>{{Cite journal|last=Van Raamsdonk|first=Mark|date=2010-06-19|title=क्वांटम उलझाव के साथ स्पेसटाइम का निर्माण|journal=General Relativity and Gravitation|language=en|volume=42|issue=10|pages=2323–2329|doi=10.1007/s10714-010-1034-0|issn=0001-7701|arxiv=1005.3035|bibcode=2010GReGr..42.2323V|s2cid=189843725}}</ref> [[प्रेरित गुरुत्वाकर्षण]] उलझाव के पहले नियम से उभर सकता है<ref>{{Cite journal|last1=Lee|first1=Jae-Weon|last2=Kim|first2=Hyeong-Chan|last3=Lee|first3=Jungjai|date=2013|title=क्वांटम जानकारी से गुरुत्वाकर्षण|journal=Journal of the Korean Physical Society|language=en|volume=63|issue=5|pages=1094–1098|doi=10.3938/jkps.63.1094|issn=0374-4884|arxiv=1001.5445|bibcode=2013JKPS...63.1094L|s2cid=118494859}}</ref><ref>{{cite arXiv|last1=Swingle|first1=Brian|last2=Van Raamsdonk|first2=Mark|date=2014-05-12|title=उलझाव से गुरुत्वाकर्षण की सार्वभौमिकता|eprint=1405.2933 |class=hep-th}}</ref> | ||
== गैर-स्थानीयता और उलझाव == | == गैर-स्थानीयता और उलझाव == | ||
मीडिया और लोकप्रिय विज्ञान में, [[क्वांटम गैरस्थानीयता|क्वांटम गैर-स्थानीयता]] को | मीडिया और लोकप्रिय विज्ञान में, [[क्वांटम गैरस्थानीयता|क्वांटम गैर-स्थानीयता]] को अधिकांशतः उलझाव के बराबर चित्रित किया जाता है। चूंकि यह शुद्ध द्विदलीय क्वांटम अवस्थाओं के लिए सच है, सामान्यतः उलझाव केवल गैर-स्थानीय सहसंबंधों के लिए आवश्यक है, लेकिन मिश्रित उलझी हुई स्थितियाँ उपस्थित हैं जो ऐसे सहसंबंध उत्पन्न नहीं करती हैं।<ref name="Brunner-RMP2014">{{cite journal | ||
|title=Bell nonlocality | |title=Bell nonlocality | ||
| last1 = Brunner | | last1 = Brunner | ||
| Line 155: | Line 156: | ||
| arxiv=1303.2849 | | arxiv=1303.2849 | ||
| bibcode=2014RvMP...86..419B | | bibcode=2014RvMP...86..419B | ||
| s2cid=119194006 }}</ref> एक प्रसिद्ध उदाहरण [[वर्नर राज्य|वर्नर स्थिति]] है जो कुछ निश्चित मूल्यों के लिए उलझे हुए हैं <math>p_{sym}</math>, लेकिन | | s2cid=119194006 }}</ref> एक प्रसिद्ध उदाहरण [[वर्नर राज्य|वर्नर स्थिति]] है जो कुछ निश्चित मूल्यों के लिए उलझे हुए हैं <math>p_{sym}</math>, लेकिन सदैव स्थानीय छिपे हुए चर का उपयोग करके वर्णित किया जा सकता है।<ref name=werner1989>{{cite journal | last = Werner| first = R.F. | title = आइंस्टीन-पोडॉल्स्की-रोसेन सहसंबंध के साथ क्वांटम राज्य एक छिपे हुए-चर मॉडल को स्वीकार करते हैं| journal = [[Physical Review A]] | volume = 40| pages = 4277–4281 | year = 1989 |doi=10.1103/PhysRevA.40.4277 | pmid=9902666 | issue=8|bibcode = 1989PhRvA..40.4277W }}</ref> इसके अतिरिक्त, यह दिखाया गया कि, कणों की मनमानी संख्या के लिए, ऐसे स्थिति उपस्थित हैं जो वास्तव में उलझे हुए हैं लेकिन एक स्थानीय मॉडल को स्वीकार करते हैं।<ref name="Augusiak2015">{{cite journal | ||
| last1 = Augusiak | | last1 = Augusiak | ||
| first1 = R. | | first1 = R. | ||
| Line 177: | Line 178: | ||
| s2cid = 29758483 }}</ref> | | s2cid = 29758483 }}</ref> | ||
स्थानीय मॉडलों के अस्तित्व के बारे में उल्लिखित प्रमाण यह मानते हैं कि एक समय में क्वांटम स्थिति की केवल एक प्रति उपलब्ध है। यदि कणों को ऐसे स्थितिों की कई प्रतियों पर स्थानीय माप करने की अनुमति दी जाती है, तो कई स्पष्ट रूप से स्थानीय स्थितिों (उदाहरण के लिए, क्वबिट वर्नर स्थिति) को अब स्थानीय मॉडल द्वारा वर्णित नहीं किया जा सकता है। यह, विशेष रूप से, सभी [[उलझाव आसवन]] स्थितिों के लिए सच है। | स्थानीय मॉडलों के अस्तित्व के बारे में उल्लिखित प्रमाण यह मानते हैं कि एक समय में क्वांटम स्थिति की केवल एक प्रति उपलब्ध है। यदि कणों को ऐसे स्थितिों की कई प्रतियों पर स्थानीय माप करने की अनुमति दी जाती है, तो कई स्पष्ट रूप से स्थानीय स्थितिों (उदाहरण के लिए, क्वबिट वर्नर स्थिति) को अब स्थानीय मॉडल द्वारा वर्णित नहीं किया जा सकता है। यह, विशेष रूप से, सभी [[उलझाव आसवन]] स्थितिों के लिए सच है। चूंकि, यह एक विवृत प्रश्न बना हुआ है कि क्या पर्याप्त संख्या में प्रतियाँ दिए जाने पर सभी उलझे हुए स्थिति गैर-स्थानीय हो जाते हैं।<ref name="Vertesi2014">{{cite journal | ||
| last1 = Vértesi | | last1 = Vértesi | ||
| first1 = Tamás | | first1 = Tamás | ||
| Line 195: | Line 196: | ||
}}</ref> | }}</ref> | ||
संक्षेप में, दो कणों द्वारा साझा की गई अवस्था का उलझना आवश्यक है लेकिन उस अवस्था के गैर-स्थानीय होने के लिए पर्याप्त नहीं है। यह पहचानना महत्वपूर्ण है कि उलझाव को | संक्षेप में, दो कणों द्वारा साझा की गई अवस्था का उलझना आवश्यक है लेकिन उस अवस्था के गैर-स्थानीय होने के लिए पर्याप्त नहीं है। यह पहचानना महत्वपूर्ण है कि उलझाव को सामान्यतः एक बीजगणितीय अवधारणा के रूप में देखा जाता है, जो गैर-स्थानीयता के साथ-साथ [[क्वांटम टेलीपोर्टेशन]] और [[सुपरडेंस कोडिंग]] के लिए एक शर्त के रूप में जाना जाता है, जबकि गैर-स्थानीयता को प्रयोगात्मक आंकड़ों के अनुसार परिभाषित किया गया है और यह बहुत अधिक है [[क्वांटम नींव]] और क्वांटम यांत्रिकी की व्याख्याओं से जुड़े।<ref>In the literature "non-locality" is sometimes used to characterize concepts that differ from the non-existence of a local hidden variable model, e.g., whether states can be distinguished by local measurements and which can occur also for non-entangled states (see, e.g., {{cite journal |author1=Charles H. Bennett |author2=David P. DiVincenzo |author3=Christopher A. Fuchs |author4=Tal Mor |author5=Eric Rains |author6=Peter W. Shor |author7=John A. Smolin |author8=William K. Wootters |title=Quantum nonlocality without entanglement |journal=Phys. Rev. A |volume=59 |issue=2 |pages=1070–1091 |year=1999 |doi=10.1103/PhysRevA.59.1070 |arxiv=quant-ph/9804053 |bibcode=1999PhRvA..59.1070B |s2cid=15282650}}). This non-standard use of the term is not discussed here.</ref> | ||
==क्वांटम यांत्रिक ढांचा == | ==क्वांटम यांत्रिक ढांचा == | ||
निम्नलिखित उपखंड उन लोगों के लिए हैं जिनके पास क्वांटम यांत्रिकी के औपचारिक, गणितीय विवरण का अच्छा कार्यसाधक ज्ञान है, जिसमें लेखों में विकसित औपचारिकता और सैद्धांतिक ढांचे से परिचित होना | निम्नलिखित उपखंड उन लोगों के लिए हैं जिनके पास क्वांटम यांत्रिकी के औपचारिक, गणितीय विवरण का अच्छा कार्यसाधक ज्ञान है, जिसमें लेखों में विकसित औपचारिकता और सैद्धांतिक ढांचे से परिचित होना सम्मलित है: ब्रा-केट नोटेशन और [[क्वांटम यांत्रिकी का गणितीय सूत्रीकरण]]। | ||
=== शुद्ध अवस्थाएँ === | === शुद्ध अवस्थाएँ === | ||
दो | दो स्वेच्छाचारिता क्वांटम प्रणालियों पर विचार करें {{mvar|A}} और {{mvar|B}}, संबंधित हिल्बर्ट रिक्त स्थान के साथ {{mvar|H<sub>A</sub>}} और {{mvar|H<sub>B</sub>}}. मिश्रित प्रणाली का हिल्बर्ट स्थान [[टेंसर उत्पाद]] है | ||
: <math> H_A \otimes H_B.</math> | : <math> H_A \otimes H_B.</math> | ||
| Line 212: | Line 213: | ||
: <math>|\psi\rangle_{AB} = \sum_{i,j} c_{ij} |i\rangle_A \otimes |j\rangle_B</math>. | : <math>|\psi\rangle_{AB} = \sum_{i,j} c_{ij} |i\rangle_A \otimes |j\rangle_B</math>. | ||
यदि | यदि सदिश उपस्थित हैं तो यह स्थिति अलग की जा सकती है <math> [c^A_i], [c^B_j]</math> जिससे कि <math> c_{ij}= c^A_i c^B_j,</math> उपज <math display="inline"> |\psi\rangle_A = \sum_{i} c^A_{i} |i\rangle_A</math> और <math display="inline"> |\phi\rangle_B = \sum_{j} c^B_{j} |j\rangle_B.</math> यदि किसी सदिश के लिए यह अविभाज्य है <math> [c^A_i],[c^B_j]</math> कम से कम निर्देशांक की एक जोड़ी के लिए <math> c^A_i,c^B_j</math> अपने पास <math> c_{ij} \neq c^A_ic^B_j.</math> यदि कोई स्थिति अविभाज्य है, तो उसे 'उलझा हुआ स्थिति' कहा जाता है। | ||
उदाहरण के लिए, दो आधार | उदाहरण के लिए, दो आधार सदिश दिए गए हैं <math> \{|0\rangle_A, |1\rangle_A\}</math> का {{mvar|H<sub>A</sub>}} और दो आधार सदिश <math> \{|0\rangle_B, |1\rangle_B\}</math> का {{mvar|H<sub>B</sub>}}, निम्नलिखित एक उलझी हुई स्थिति है: | ||
: <math>\tfrac{1}{\sqrt{2}} \left ( |0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B \right ).</math> | : <math>\tfrac{1}{\sqrt{2}} \left ( |0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B \right ).</math> | ||
यदि समग्र प्रणाली इस स्थिति में है, तो किसी भी प्रणाली का श्रेय देना असंभव है {{mvar|A}} या | यदि समग्र प्रणाली इस स्थिति में है, तो किसी भी प्रणाली का श्रेय देना असंभव है {{mvar|A}} या प्रणाली {{mvar|B}} एक निश्चित [[शुद्ध अवस्था]]। इसे कहने का दूसरा विधि यह है कि जबकि पूरे स्थिति की [[वॉन न्यूमैन एन्ट्रापी]] शून्य है (जैसा कि यह किसी भी शुद्ध स्थिति के लिए है), उप-प्रणालियों की एन्ट्रॉपी शून्य से अधिक है। इस अर्थ में, प्रणालियाँ उलझी हुई हैं। इंटरफेरोमेट्री के लिए इसके विशिष्ट अनुभवजन्य प्रभाव हैं।<ref>{{cite journal |vauthors=Jaeger G, Shimony A, Vaidman L |title=दो इंटरफेरोमेट्रिक संपूरकताएँ|journal=Phys. Rev. |volume=51 |issue=1 |pages=54–67 |year=1995 |doi=10.1103/PhysRevA.51.54 |pmid=9911555 |bibcode=1995PhRvA..51...54J}}</ref> उपरोक्त उदाहरण चार बेल अवस्थाओं में से एक है, जो (अधिकतम) उलझी हुई शुद्ध अवस्थाएँ हैं {{math|''H<sub>A</sub>'' ⊗ ''H<sub>B</sub>''}} स्थान, लेकिन जिसे प्रत्येक की शुद्ध अवस्था में अलग नहीं किया जा सकता {{mvar|H<sub>A</sub>}} और {{mvar|H<sub>B</sub>}}). | ||
अब मान लीजिए कि ऐलिस | अब मान लीजिए कि ऐलिस प्रणाली का पर्यवेक्षक है {{mvar|A}}, और बॉब प्रणाली के लिए एक पर्यवेक्षक है {{mvar|B}}. यदि ऊपर दी गई उलझी हुई अवस्था में ऐलिस एक माप करती है <math> \{|0\rangle, |1\rangle\}</math> का अपना आधार {{mvar|A}}, समान संभावना के साथ घटित होने वाले दो संभावित परिणाम हैं:<ref>{{cite book| last1=Nielsen |first1=Michael A. |last2=Chuang |first2=Isaac L. |year=2000 |title=क्वांटम संगणना और क्वांटम सूचना|publisher=[[Cambridge University Press]] |pages=112–113| isbn=978-0-521-63503-5}}</ref> | ||
# ऐलिस का माप 0 है, और | # ऐलिस का माप 0 है, और प्रणाली की स्थिति ढह जाती है <math> |0\rangle_A |1\rangle_B</math>. | ||
# ऐलिस का माप 1 है, और | # ऐलिस का माप 1 है, और प्रणाली की स्थिति ढह जाती है <math> |1\rangle_A |0\rangle_B</math>. | ||
यदि पूर्व घटित होता है, तो उसी आधार पर बॉब द्वारा किया गया कोई भी | <nowiki>यदि पूर्व घटित होता है, तो उसी आधार पर बॉब द्वारा किया गया कोई भी पश्चात का माप सदैव 1 लौटाएगा। यदि पश्चात वाला घटित होता है, (ऐलिस माप 1) तो बॉब का माप निश्चितता के साथ 0 लौटाएगा। इस प्रकार, प्रणाली {{मावर|बी} ऐलिस द्वारा प्रणाली पर स्थानीय माप निष्पादित करके } को बदल दिया गया है </nowiki>{{mvar|A}}. यह तब भी सत्य रहता है, जब प्रणाली {{mvar|A}} और {{mvar|B}} स्थानिक रूप से अलग हो गए हैं। यह ईपीआर विरोधाभास की नींव है। | ||
ऐलिस के माप का परिणाम यादृच्छिक है। ऐलिस यह तय नहीं कर सकती कि समग्र | ऐलिस के माप का परिणाम यादृच्छिक है। ऐलिस यह तय नहीं कर सकती कि समग्र प्रणाली को किस स्थिति में ढहाया जाए, और इसलिए वह अपने प्रणाली पर कार्य करके बॉब को जानकारी प्रसारित नहीं कर सकती है। इस विशेष योजना में कार्य-कारण को इस प्रकार संरक्षित किया जाता है। सामान्य तर्क के लिए, [[नो-कम्युनिकेशन प्रमेय]] देखें। | ||
=== पहनावा === | === पहनावा === | ||
जैसा कि ऊपर बताया गया है, क्वांटम प्रणाली की स्थिति हिल्बर्ट स्पेस में एक यूनिट | जैसा कि ऊपर बताया गया है, क्वांटम प्रणाली की स्थिति हिल्बर्ट स्पेस में एक यूनिट सदिश द्वारा दी जाती है। सामान्यतः, यदि किसी के पास प्रणाली के बारे में कम जानकारी है, तो वह इसे 'एसेम्बल' कहता है और इसे [[घनत्व मैट्रिक्स|घनत्व आव्यूह]] द्वारा वर्णित करता है, जो एक सकारात्मक-अर्ध-निश्चित आव्यूह है, या एक [[ट्रेस क्लास]] है जब स्थिति स्थान अनंत-आयामी होता है, और इसमें ट्रेस 1 है। फिर से, [[वर्णक्रमीय प्रमेय]] द्वारा, ऐसा आव्यूह सामान्य रूप लेता है: | ||
: <math>\rho = \sum_i w_i |\alpha_i\rangle \langle\alpha_i|,</math> | : <math>\rho = \sum_i w_i |\alpha_i\rangle \langle\alpha_i|,</math> | ||
जहां डब्ल्यू<sub>i</sub> सकारात्मक-मूल्यवान संभावनाएं हैं (उनका योग 1 तक होता है), सदिश {{mvar| α<sub>i</sub>}} यूनिट | जहां डब्ल्यू<sub>i</sub> सकारात्मक-मूल्यवान संभावनाएं हैं (उनका योग 1 तक होता है), सदिश {{mvar| α<sub>i</sub>}} यूनिट सदिश हैं, और अनंत-आयामी स्थिति में, हम ट्रेस मानदंड में ऐसे स्थितिों को संवृत कर देंगे। हम व्याख्या कर सकते हैं {{mvar|ρ}} एक समूह का प्रतिनिधित्व करने के रूप में जहां <math> w_i </math> उस समूह का अनुपात है जिसके स्थिति हैं <math>|\alpha_i\rangle</math>. जब किसी मिश्रित स्थिति की रैंक 1 होती है, तो यह एक 'शुद्ध पहनावा' का वर्णन करता है। जब किसी क्वांटम प्रणाली की स्थिति के बारे में कुल जानकारी से कम होती है तो हमें स्थिति का प्रतिनिधित्व करने के लिए #कम घनत्व आव्यूह की आवश्यकता होती है। | ||
प्रायोगिक तौर पर, एक मिश्रित संयोजन को निम्नानुसार साकार किया जा सकता है। एक ब्लैक बॉक्स उपकरण पर विचार करें जो प्रेक्षक की ओर इलेक्ट्रॉन फेंकता है। इलेक्ट्रॉनों के हिल्बर्ट स्थान [[समान कण]] हैं। उपकरण ऐसे इलेक्ट्रॉन उत्पन्न कर सकता है जो सभी एक ही अवस्था में हों; इस | प्रायोगिक तौर पर, एक मिश्रित संयोजन को निम्नानुसार साकार किया जा सकता है। एक ब्लैक बॉक्स उपकरण पर विचार करें जो प्रेक्षक की ओर इलेक्ट्रॉन फेंकता है। इलेक्ट्रॉनों के हिल्बर्ट स्थान [[समान कण]] हैं। उपकरण ऐसे इलेक्ट्रॉन उत्पन्न कर सकता है जो सभी एक ही अवस्था में हों; इस स्थिति में, प्रेक्षक द्वारा प्राप्त इलेक्ट्रॉन एक शुद्ध समूह होते हैं। चूंकि, उपकरण विभिन्न अवस्थाओं में इलेक्ट्रॉन उत्पन्न कर सकता है। उदाहरण के लिए, यह इलेक्ट्रॉनों की दो आपश्चाती उत्पन्न कर सकता है: एक अवस्था के साथ <math>|\mathbf{z}+\rangle</math> स्पिन (भौतिकी) के साथ सकारात्मक में संरेखित {{math|'''z'''}}दिशा के साथ, और दूसरा स्थिति के साथ <math>|\mathbf{y}-\rangle</math> स्पिन के साथ नकारात्मक में संरेखित {{math|'''y'''}} दिशा। सामान्यतः, यह एक मिश्रित समूह है, क्योंकि इसमें किसी भी संख्या में आपश्चाती हो सकती है, प्रत्येक एक अलग स्थिति के अनुरूप है। | ||
उपरोक्त परिभाषा के अनुसार, एक द्विदलीय समग्र प्रणाली के लिए, मिश्रित अवस्थाएँ केवल घनत्व आव्यूह हैं {{math|''H<sub>A</sub>'' ⊗ ''H<sub>B</sub>''}}. अर्थात् इसका सामान्य स्वरूप है | उपरोक्त परिभाषा के अनुसार, एक द्विदलीय समग्र प्रणाली के लिए, मिश्रित अवस्थाएँ केवल घनत्व आव्यूह हैं {{math|''H<sub>A</sub>'' ⊗ ''H<sub>B</sub>''}}. अर्थात् इसका सामान्य स्वरूप है | ||
| Line 241: | Line 242: | ||
जहां डब्ल्यू<sub>i</sub> सकारात्मक रूप से मूल्यवान संभावनाएँ हैं, <math display="inline">\sum_j |c_{ij}|^2=1</math>, और सदिश इकाई सदिश हैं। यह स्व-संयुक्त और सकारात्मक है और इसमें ट्रेस 1 है। | जहां डब्ल्यू<sub>i</sub> सकारात्मक रूप से मूल्यवान संभावनाएँ हैं, <math display="inline">\sum_j |c_{ij}|^2=1</math>, और सदिश इकाई सदिश हैं। यह स्व-संयुक्त और सकारात्मक है और इसमें ट्रेस 1 है। | ||
शुद्ध | शुद्ध स्थितियों से पृथक्करण की परिभाषा का विस्तार करते हुए, हम कहते हैं कि एक मिश्रित अवस्था पृथक्करणीय है यदि इसे इस प्रकार लिखा जा सकता है<ref name=Laloe>{{citation|last=Laloe|first=Franck|year=2001|title=Do We Really Understand Quantum Mechanics|journal=American Journal of Physics |volume=69 |issue=6|pages=655–701 |arxiv=quant-ph/0209123 |bibcode=2001AmJPh..69..655L |doi=10.1119/1.1356698}}</ref>{{rp|131–132}} | ||
: <math>\rho = \sum_i w_i \rho_i^A \otimes \rho_i^B, </math> | : <math>\rho = \sum_i w_i \rho_i^A \otimes \rho_i^B, </math> | ||
जहां {{mvar|w<sub>i</sub>}} सकारात्मक रूप से मूल्यवान संभावनाएं हैं और <math>\rho_i^A</math>'रेत <math>\rho_i^B</math>उपप्रणालियों पर स्वयं मिश्रित अवस्थाएँ (घनत्व संचालक) हैं {{mvar|A}} और {{mvar|B}} क्रमश। दूसरे शब्दों में, एक स्थिति को अलग किया जा सकता है यदि यह असंबद्ध | जहां {{mvar|w<sub>i</sub>}} सकारात्मक रूप से मूल्यवान संभावनाएं हैं और <math>\rho_i^A</math>'रेत <math>\rho_i^B</math>उपप्रणालियों पर स्वयं मिश्रित अवस्थाएँ (घनत्व संचालक) हैं {{mvar|A}} और {{mvar|B}} क्रमश। दूसरे शब्दों में, एक स्थिति को अलग किया जा सकता है यदि यह असंबद्ध स्थिति, या उत्पाद स्थितिों पर संभाव्यता वितरण है। घनत्व आव्यूह को शुद्ध समुच्चय और विस्तार के योग के रूप में लिखकर, हम व्यापकता के नुकसान के बिना यह मान सकते हैं <math>\rho_i^A</math> और <math>\rho_i^B</math> वे स्वयं शुद्ध समूह हैं। एक स्थितियों को तब उलझा हुआ कहा जाता है यदि वह अलग करने योग्य नहीं है। | ||
सामान्यतः, यह पता लगाना मुश्किल माना जाता है कि मिश्रित स्थिति उलझी हुई है या नहीं। सामान्य द्विपक्षीय स्थितियों को [[ एनपी कठिन ]] दिखाया गया है।<ref>{{Cite book |vauthors=Gurvits L |title=Proceedings of the Thirty-Fifth ACM symposium on Theory of computing - STOC '03 |chapter=Classical deterministic complexity of Edmonds' Problem and quantum entanglement |journal=Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing |year=2003 |doi=10.1145/780542.780545 |page=10 |isbn=978-1-58113-674-6|arxiv=quant-ph/0303055 |s2cid=5745067 }}</ref> के लिए {{math|2 × 2}} और {{math|2 × 3}} स्थितियों में, पृथक्करण के लिए एक आवश्यक और पर्याप्त मानदंड प्रसिद्ध [[पेरेस-होरोडेकी मानदंड]]|पॉजिटिव आंशिक ट्रांसपोज़ (पीपीटी) स्थिति द्वारा दिया गया है।<ref>{{cite journal |vauthors=Horodecki M, Horodecki P, Horodecki R |title=Separability of mixed states: necessary and sufficient conditions |journal=Physics Letters A |volume=223 |issue=1 |page=210 |year=1996 |doi=10.1016/S0375-9601(96)00706-2 |bibcode=1996PhLA..223....1H|arxiv = quant-ph/9605038 |citeseerx=10.1.1.252.496 |s2cid=10580997 }}</ref> | |||
=== कम घनत्व आव्यूह === | === कम घनत्व आव्यूह === | ||
कम घनत्व आव्यूह का विचार 1930 में [[पॉल डिराक]] द्वारा पेश किया गया था।<ref name="Dirac1930">{{cite journal | कम घनत्व आव्यूह का विचार 1930 में [[पॉल डिराक]] द्वारा पेश किया गया था।<ref name="Dirac1930">{{cite journal | ||
| Line 267: | Line 266: | ||
: <math> |\Psi \rangle \in H_A \otimes H_B. </math> | : <math> |\Psi \rangle \in H_A \otimes H_B. </math> | ||
जैसा कि ऊपर बताया गया है, | जैसा कि ऊपर बताया गया है, सामान्यतः शुद्ध अवस्था को घटक प्रणाली से जोड़ने का कोई उपाए नहीं है {{mvar|A}}. चूंकि, घनत्व आव्यूह को संबद्ध करना अभी भी संभव है। | ||
: <math>\rho_T = |\Psi\rangle \; \langle\Psi|</math>. | : <math>\rho_T = |\Psi\rangle \; \langle\Psi|</math>. | ||
जो इस स्थिति पर प्रक्षेपण ऑपरेटर है। की स्थिति {{mvar|A}} का आंशिक निशान है {{mvar|ρ<sub>T</sub>}} | जो इस स्थिति पर प्रक्षेपण ऑपरेटर है। की स्थिति {{mvar|A}} का आंशिक निशान है {{mvar|ρ<sub>T</sub>}} प्रणाली के आधार पर {{mvar|B}}: | ||
: <math>\rho_A \ \stackrel{\mathrm{def}}{=}\ \sum_j^{N_B} \left( I_A \otimes \langle j|_B \right) \left( |\Psi\rangle \langle\Psi| \right)\left( I_A \otimes |j\rangle_B \right) = \hbox{Tr}_B \; \rho_T.</math> | : <math>\rho_A \ \stackrel{\mathrm{def}}{=}\ \sum_j^{N_B} \left( I_A \otimes \langle j|_B \right) \left( |\Psi\rangle \langle\Psi| \right)\left( I_A \otimes |j\rangle_B \right) = \hbox{Tr}_B \; \rho_T.</math> | ||
योग खत्म हो जाता है <math>N_B := \dim(H_B)</math> और <math>I_A</math> में पहचान ऑपरेटर <math>H_A</math>. {{mvar|ρ<sub>A</sub>}} को कभी-कभी कम घनत्व आव्यूह भी कहा जाता है {{mvar|ρ}} | योग खत्म हो जाता है <math>N_B := \dim(H_B)</math> और <math>I_A</math> में पहचान ऑपरेटर <math>H_A</math>. {{mvar|ρ<sub>A</sub>}} को कभी-कभी कम घनत्व आव्यूह भी कहा जाता है {{mvar|ρ}} सबप्रणाली पर {{mvar|A}}. बोलचाल की भाषा में हम प्रणाली का पता लगाते हैं {{mvar|B}} कम घनत्व आव्यूह प्राप्त करने के लिए {{mvar|A}}. | ||
उदाहरण के लिए, कम घनत्व आव्यूह {{mvar|A}} उलझी हुई अवस्था के लिए | उदाहरण के लिए, कम घनत्व आव्यूह {{mvar|A}} उलझी हुई अवस्था के लिए | ||
| Line 286: | Line 285: | ||
: <math>\rho_A = |\psi\rangle_A \langle\psi|_A</math>. | : <math>\rho_A = |\psi\rangle_A \langle\psi|_A</math>. | ||
सामान्यतः, एक द्विदलीय शुद्ध अवस्था ρ उलझ जाती है यदि और केवल तभी जब इसकी कम अवस्थाओं को शुद्ध के अतिरिक्त मिश्रित किया जाता है। | |||
=== दो अनुप्रयोग जो उनका उपयोग करते हैं === | === दो अनुप्रयोग जो उनका उपयोग करते हैं === | ||
कम घनत्व वाले आव्यूह की गणना अद्वितीय | कम घनत्व वाले आव्यूह की गणना अद्वितीय भू स्थिति के साथ विभिन्न स्पिन श्रृंखलाओं में स्पष्ट रूप से की गई थी। एक उदाहरण एक-आयामी एकेएलटी मॉडल है:<ref name="Fan2004">{{cite journal | doi = 10.1103/PhysRevLett.93.227203 | title = वैलेंस-बॉन्ड ठोस अवस्था में उलझाव| journal = Physical Review Letters | year = 2004 | first = H | last = Fan | page = 227203 |author2=Korepin V |author3=Roychowdhury V | volume = 93 | issue = 22 | pmid = 15601113 |arxiv=quant-ph/0406067 | bibcode=2004PhRvL..93v7203F| s2cid = 28587190 }}</ref> भू स्थिति को एक ब्लॉक और एक पर्यावरण में विभाजित किया जा सकता है। ब्लॉक का कम घनत्व आव्यूह एक प्रोजेक्टर के लिए किसी अन्य हैमिल्टनियन की विकृत जमीनी स्थिति के लिए [[आनुपातिकता (गणित)]] है। | ||
कम घनत्व आव्यूह का मूल्यांकन [[हाइजेनबर्ग मॉडल (क्वांटम)]] के लिए भी किया गया था, जहां इसकी पूर्ण रैंक है। यह | कम घनत्व आव्यूह का मूल्यांकन [[हाइजेनबर्ग मॉडल (क्वांटम)]] के लिए भी किया गया था, जहां इसकी पूर्ण रैंक है। यह सिद्ध करना हुआ कि थर्मोडायनामिक सीमा में, स्पिन के एक बड़े ब्लॉक के कम घनत्व आव्यूह का स्पेक्ट्रम इस स्थितियों का एक सटीक ज्यामितीय अनुक्रम है<ref>{{cite journal| doi=10.1007/s11128-010-0197-7|arxiv=1002.2931|title=एक आयाम में XY मॉडल के स्पिन के एक बड़े ''ब्लॉक'' के घनत्व मैट्रिक्स का स्पेक्ट्रम| year=2010|last1=Franchini|first1=F.|last2=Its|first2=A. R.| last3=Korepin|first3=V. E.|last4=Takhtajan|first4=L. A.|journal=Quantum Information Processing|volume=10|issue=3 |pages=325–341 |s2cid=6683370}}</ref> | ||
=== एक संसाधन के रूप में उलझाव === | === एक संसाधन के रूप में उलझाव === | ||
क्वांटम सूचना सिद्धांत में, उलझी हुई अवस्थाओं को एक 'संसाधन' माना जाता है, | क्वांटम सूचना सिद्धांत में, उलझी हुई अवस्थाओं को एक 'संसाधन' माना जाता है, अर्थात, उत्पादन करने के लिए कुछ महंगा और जो मूल्यवान परिवर्तनों को क्रियान्वित करने की अनुमति देता है।<ref name="Chitambar2019">{{cite journal | ||
| last1 = Chitambar | | last1 = Chitambar | ||
| first1 = Eric | | first1 = Eric | ||
| Line 324: | Line 323: | ||
| bibcode = 2022MPLB...3650101G | | bibcode = 2022MPLB...3650101G | ||
| s2cid = 250072286 | | s2cid = 250072286 | ||
}}</ref> जिस | }}</ref> जिस समूहिंग में यह परिप्रेक्ष्य सबसे अधिक स्पष्ट है, वह दूर की प्रयोगशालाओं की है, अर्थात, ए और बी लेबल वाले दो क्वांटम प्रणाली, जिनमें से प्रत्येक पर मनमाना क्वांटम संचालन किया जा सकता है, लेकिन जो यांत्रिक रूप से एक दूसरे [[क्वांटम ऑपरेशन|क्वांटम संचालन]] साथ बातचीत नहीं करते हैं। अनुमति दी गई एकमात्र परस्पर क्रिया शास्त्रीय जानकारी का आदान-प्रदान है, जो सबसे सामान्य स्थानीय क्वांटम संचालन के साथ मिलकर [[एलओसीसी]] (स्थानीय संचालन और शास्त्रीय संचार) नामक संचालन के वर्ग को जन्म देती है। ये संचालन प्रणाली ए और बी के बीच उलझे हुए स्थितिों के उत्पादन की अनुमति नहीं देते हैं। लेकिन यदि ए और बी को उलझे हुए स्थितिों की आपूर्ति प्रदान की जाती है, तो ये, एलओसीसी संचालन के साथ मिलकर परिवर्तनों के एक बड़े वर्ग को सक्षम कर सकते हैं। उदाहरण के लिए, A के क्वबिट और B के क्वबिट के बीच की बातचीत को पहले A के क्वबिट को B में टेलीपोर्ट करके, फिर उसे B के क्वबिट के साथ इंटरैक्ट करने की अनुमति देकर महसूस किया जा सकता है (जो अब एक एलओसीसी संचालन है, क्योंकि दोनों क्वबिट B की लैब में हैं) और फिर क्वबिट को वापस ए पर टेलीपोर्ट करना। इस प्रक्रिया में दो क्वबिट की दो अधिकतम उलझी हुई अवस्थाओं का उपयोग किया जाता है। इस प्रकार उलझे हुए स्थिति एक संसाधन हैं जो ऐसी समूहिंग में क्वांटम परस्पर क्रिया (या क्वांटम चैनल) की प्राप्ति को सक्षम बनाता है जहां केवल एलओसीसी उपलब्ध हैं, लेकिन प्रक्रिया में उनका उपभोग किया जाता है। ऐसे अन्य अनुप्रयोग हैं जहां उलझाव को एक संसाधन के रूप में देखा जा सकता है, उदाहरण के लिए, निजी संचार या क्वांटम अवस्थाओं को अलग करना।<ref name="horodecki2007" /> | ||
=== उलझाव का वर्गीकरण === | === उलझाव का वर्गीकरण === | ||
सभी क्वांटम अवस्थाएँ एक संसाधन के रूप में समान रूप से मूल्यवान नहीं हैं। इस मान को निर्धारित करने के लिए, विभिन्न उलझाव उपायों (नीचे देखें) का उपयोग किया जा सकता है, जो प्रत्येक क्वांटम स्थिति के लिए एक संख्यात्मक मान निर्दिष्ट करते हैं। | सभी क्वांटम अवस्थाएँ एक संसाधन के रूप में समान रूप से मूल्यवान नहीं हैं। इस मान को निर्धारित करने के लिए, विभिन्न उलझाव उपायों (नीचे देखें) का उपयोग किया जा सकता है, जो प्रत्येक क्वांटम स्थिति के लिए एक संख्यात्मक मान निर्दिष्ट करते हैं। चूंकि, क्वांटम अवस्थाओं की समानता करने के लिए मोटे तरीके से समझौता करना अधिकांशतः मनोहर होता है। यह विभिन्न वर्गीकरण योजनाओं को जन्म देता है। अधिकांश उलझाव वर्गों को इस आधार पर परिभाषित किया जाता है कि क्या एलओसीसी या इन परिचालनों के उपवर्ग का उपयोग करके स्थितिों को अन्य स्थितिों में परिवर्तित किया जा सकता है। अनुमत परिचालनों का समूह जितना छोटा होगा, वर्गीकरण उतना ही बेहतर होगा। महत्वपूर्ण उदाहरण हैं: | ||
* यदि दो स्थितिों को स्थानीय एकात्मक संचालन द्वारा एक दूसरे में परिवर्तित किया जा सकता है, तो उन्हें एक ही एलयू वर्ग में कहा जाता है। | * यदि दो स्थितिों को स्थानीय एकात्मक संचालन द्वारा एक दूसरे में परिवर्तित किया जा सकता है, तो उन्हें एक ही एलयू वर्ग में कहा जाता है। सामान्यतः मानी जाने वाली कक्षाओं में यह सबसे बेहतरीन है। एक ही एलयू वर्ग में दो स्थितिों में उलझाव के उपायों के लिए समान मूल्य और दूर-प्रयोगशाला समूहिंग में संसाधन के समान मूल्य होता है। विभिन्न एलयू वर्गों की अनंत संख्या है (शुद्ध अवस्था में दो क्वैबिट के सबसे सरल स्थितियों में भी)।<ref name="GRB1998">{{cite journal |author1=Grassl, M. |author2=Rötteler, M. |author3=Beth, T. |title=क्वांटम-बिट सिस्टम के स्थानीय अपरिवर्तनीयों की गणना|journal=Phys. Rev. A |volume=58 |issue=3 |pages=1833–1839 |year=1998 |doi=10.1103/PhysRevA.58.1833 |arxiv=quant-ph/9712040|bibcode=1998PhRvA..58.1833G |s2cid=15892529 }}</ref><ref name="Kraus2010">{{cite journal |author=B. Kraus |author-link=Barbara Kraus|title=बहुपक्षीय शुद्ध राज्यों की स्थानीय एकात्मक तुल्यता|journal=Phys. Rev. Lett. |volume=104 |issue=2 |page=020504 |year=2010 |arxiv=0909.5152 |doi=10.1103/PhysRevLett.104.020504|pmid=20366579 |bibcode=2010PhRvL.104b0504K|s2cid=29984499}}</ref> | ||
* यदि दो स्थितिों को 0 से अधिक संभावना वाले माप सहित स्थानीय संचालन द्वारा एक-दूसरे में परिवर्तित किया जा सकता है, तो उन्हें एक ही 'एसएलओसीसी वर्ग' (स्टोकेस्टिक एलओसीसी) में कहा जाता है। गुणात्मक रूप से, दो अवस्थाएँ <math>\rho_1</math> और <math>\rho_2</math> उसी एसएलओसीसी वर्ग में समान रूप से शक्तिशाली हैं (चूंकि मैं एक को दूसरे में बदल सकता हूं और फिर वह सब कुछ कर सकता हूं जो यह मुझे करने की अनुमति देता है), लेकिन परिवर्तनों के | * यदि दो स्थितिों को 0 से अधिक संभावना वाले माप सहित स्थानीय संचालन द्वारा एक-दूसरे में परिवर्तित किया जा सकता है, तो उन्हें एक ही 'एसएलओसीसी वर्ग' (स्टोकेस्टिक एलओसीसी) में कहा जाता है। गुणात्मक रूप से, दो अवस्थाएँ <math>\rho_1</math> और <math>\rho_2</math> उसी एसएलओसीसी वर्ग में समान रूप से शक्तिशाली हैं (चूंकि मैं एक को दूसरे में बदल सकता हूं और फिर वह सब कुछ कर सकता हूं जो यह मुझे करने की अनुमति देता है), लेकिन परिवर्तनों के पश्चात से <math>\rho_1\to\rho_2</math> और <math>\rho_2\to\rho_1</math> अलग-अलग संभावनाओं के साथ सफल हो सकते हैं, वे अब समान रूप से मूल्यवान नहीं हैं। उदाहरण के लिए, दो शुद्ध क्वैबिट के लिए केवल दो एसएलओसीसी वर्ग हैं: उलझी हुई अवस्थाएँ (जिसमें दोनों (अधिकतम उलझी हुई) बेल अवस्थाएँ और कमज़ोर उलझी हुई अवस्थाएँ सम्मलित हैं) <math>|00\rangle+0.01|11\rangle</math>) और अलग करने योग्य वाले (अर्थात, उत्पाद की स्थिति जैसे <math>|00\rangle</math>).<ref>{{cite journal |author=M. A. Nielsen |title=उलझाव परिवर्तनों के एक वर्ग के लिए शर्तें|journal=Phys. Rev. Lett. |volume=83 |issue=2 |page=436 |year=1999 |doi=10.1103/PhysRevLett.83.436 |arxiv=quant-ph/9811053 |bibcode=1999PhRvL..83..436N |s2cid=17928003}}</ref><ref name="GoWa2010">{{cite journal |author1=Gour, G. |author2=Wallach, N. R. |title=सभी परिमित आयामों के बहुपक्षीय उलझाव का वर्गीकरण|journal=Phys. Rev. Lett. |volume=111 |issue=6 |page=060502 |year=2013 |doi=10.1103/PhysRevLett.111.060502 |pmid=23971544 |arxiv=1304.7259 |bibcode=2013PhRvL.111f0502G |s2cid=1570745}}</ref> | ||
* किसी स्थिति की एकल प्रतियों के परिवर्तनों पर विचार करने के | * किसी स्थिति की एकल प्रतियों के परिवर्तनों पर विचार करने के अतिरिक्त (जैसे <math>\rho_1\to\rho_2</math>) कोई बहु-प्रतिलिपि परिवर्तनों की संभावना के आधार पर कक्षाओं को परिभाषित कर सकता है। उदाहरण के लिए, ऐसे उदाहरण हैं जब <math>\rho_1\to\rho_2</math> एलओसीसी द्वारा असंभव है, लेकिन <math>\rho_1\otimes\rho_1\to\rho_2</math> संभव है। एक बहुत ही महत्वपूर्ण (और बहुत मोटा) वर्गीकरण इस संपत्ति पर आधारित है कि क्या किसी स्थिति की स्वेच्छाचारिता ढंग से बड़ी संख्या में प्रतियों को बदलना संभव है <math>\rho</math> कम से कम एक शुद्ध उलझी हुई अवस्था में। जिन स्थितिों में यह गुण होता है उन्हें एन्टैंगलमेंट डिस्टिलेशन कहा जाता है। ये अवस्थाएँ सबसे उपयोगी क्वांटम अवस्थाएँ हैं, क्योंकि इनमें से पर्याप्त मात्रा में होने पर, इन्हें (स्थानीय संचालन के साथ) किसी भी उलझी हुई अवस्था में बदला जा सकता है और इसलिए सभी संभावित उपयोगों की अनुमति दी जा सकती है। प्रारंभ में यह आश्चर्य की बात थी कि सभी उलझी हुई अवस्थाएँ आसुत नहीं होती हैं, जो नहीं होती हैं उन्हें '[[बंधा हुआ उलझाव]]' कहा जाता है।<ref name="HHH97">{{cite journal |author1=Horodecki, M. |author2=Horodecki, P. |author3=Horodecki, R. |title=Mixed-state entanglement and distillation: Is there a ''bound'' entanglement in nature? |journal=Phys. Rev. Lett. |volume=80 |issue=1998 |pages=5239–5242 |year=1998 |arxiv=quant-ph/9801069|doi=10.1103/PhysRevLett.80.5239 |bibcode=1998PhRvL..80.5239H |s2cid=111379972 }}</ref><ref name="horodecki2007" /> | ||
एक अलग उलझाव वर्गीकरण इस पर आधारित है कि एक स्थिति में | एक अलग उलझाव वर्गीकरण इस पर आधारित है कि एक स्थिति में उपस्थित क्वांटम सहसंबंध ए और बी को क्या करने की अनुमति देते हैं: एक उलझे हुए स्थितिों के तीन उपसमूहों को अलग करता है: (1) गैर-स्थानीय राज्य, जो सहसंबंध उत्पन्न करते हैं जिन्हें स्थानीय छिपे हुए चर मॉडल द्वारा समझाया नहीं जा सकता है और इस प्रकार बेल असमानता का उल्लंघन होता है, (2) [[क्वांटम स्टीयरिंग]] में कहा गया है कि ए के लिए स्थानीय माप द्वारा बी की सशर्त कम स्थिति को इस तरह से संशोधित (संचालित) करने के लिए पर्याप्त सहसंबंध होते हैं, कि ए बी को सिद्ध करना कर सकता है कि वे जिस स्थिति में हैं स्वामित्व वास्तव में उलझा हुआ है, और अंत में (3) वे उलझी हुई स्थितियाँ जो न तो गैर-स्थानीय हैं और न ही नियंत्रित करने योग्य हैं। तीनों समूह गैर-रिक्त हैं।<ref name="WJD2007">{{cite journal |title=संचालन, उलझाव, गैर-स्थानीयता, और आइंस्टीन-पोडॉल्स्की-रोसेन विरोधाभास|author1=H. M. Wiseman |author2=S. J. Jones |author3=A. C. Doherty |journal=Phys. Rev. Lett. |volume=98 |issue=14 |page=140402 |year=2007 |doi=10.1103/PhysRevLett.98.140402 |pmid=17501251 |arxiv=quant-ph/0612147 |bibcode=2007PhRvL..98n0402W |s2cid=30078867}}</ref> | ||
===एंट्रॉपी === | ===एंट्रॉपी === | ||
इस खंड में, मिश्रित अवस्था की एन्ट्रापी पर चर्चा की गई है और साथ ही इसे क्वांटम उलझाव के माप के रूप में कैसे देखा जा सकता है। | इस खंड में, मिश्रित अवस्था की एन्ट्रापी पर चर्चा की गई है और साथ ही इसे क्वांटम उलझाव के माप के रूप में कैसे देखा जा सकता है। | ||
| Line 343: | Line 340: | ||
: <math>S(\rho) = - \hbox{Tr} \left( \rho \log_2 {\rho} \right).</math> | : <math>S(\rho) = - \hbox{Tr} \left( \rho \log_2 {\rho} \right).</math> | ||
सामान्यतः, कोई गैर-बहुपद फ़ंक्शन की गणना करने के लिए [[बोरेल कार्यात्मक कलन]] का उपयोग करता है {{math|log<sub>2</sub>(''ρ'')}}. यदि गैर-नकारात्मक ऑपरेटर {{mvar|ρ}} एक परिमित-आयामी हिल्बर्ट स्थान पर कार्य करता है और इसमें स्वदेशी मान हैं <math>\lambda_1, \cdots, \lambda_n</math>, {{math|log<sub>2</sub>(''ρ'')}} समान eigenvectors वाले ऑपरेटर से अधिक कुछ नहीं है, लेकिन eigenvalues <math>\log_2(\lambda_1), \cdots, \log_2(\lambda_n)</math>. शैनन एन्ट्रापी तब है: | |||
: <math>S(\rho) = - \hbox{Tr} \left( \rho \log_2 {\rho} \right) = - \sum_i \lambda_i \log_2 \lambda_i</math>. | : <math>S(\rho) = - \hbox{Tr} \left( \rho \log_2 {\rho} \right) = - \sum_i \lambda_i \log_2 \lambda_i</math>. | ||
| Line 350: | Line 347: | ||
:<math> \lim_{p \to 0} p \log p = 0,</math> | :<math> \lim_{p \to 0} p \log p = 0,</math> | ||
सम्मेलन {{math|0 log(0) {{=}} 0}} अपनाया गया है. यह अनंत-आयामी | सम्मेलन {{math|0 log(0) {{=}} 0}} अपनाया गया है. यह अनंत-आयामी स्थितियों तक भी विस्तारित है: यदि {{mvar|ρ}} में [[प्रक्षेपण-मूल्य माप]] है | ||
: <math> \rho = \int \lambda d P_{\lambda},</math> | : <math> \rho = \int \lambda d P_{\lambda},</math> | ||
| Line 356: | Line 353: | ||
: <math> \rho \log_2 \rho = \int \lambda \log_2 \lambda d P_{\lambda}.</math> | : <math> \rho \log_2 \rho = \int \lambda \log_2 \lambda d P_{\lambda}.</math> | ||
[[एन्ट्रापी]] की तरह, | [[एन्ट्रापी]] की तरह, प्रणाली में जितनी अधिक अनिश्चितता (माइक्रोस्टेट्स की संख्या) होनी चाहिए, एन्ट्रापी उतनी ही बड़ी होगी। उदाहरण के लिए, किसी भी शुद्ध अवस्था की एन्ट्रापी शून्य होती है, जो आश्चर्यजनक नहीं है क्योंकि शुद्ध अवस्था में किसी प्रणाली के बारे में कोई अनिश्चितता नहीं होती है। ऊपर चर्चा की गई उलझी हुई अवस्था की दो उप-प्रणालियों में से किसी की एन्ट्रापी है {{math|log(2)}} (जिसे अधिकतम एन्ट्रापी के रूप में दिखाया जा सकता है {{math|2 × 2}}मिश्रित अवस्थाएँ)। | ||
==== उलझाव के माप के रूप में ==== | ==== उलझाव के माप के रूप में ==== | ||
एन्ट्रॉपी एक उपकरण प्रदान करता है जिसका उपयोग उलझाव को मापने के लिए किया जा सकता है, | एन्ट्रॉपी एक उपकरण प्रदान करता है जिसका उपयोग उलझाव को मापने के लिए किया जा सकता है, चूंकि उलझाव के अन्य उपाय उपस्थित हैं।<ref name="Plenio">{{cite journal|last1=Plenio |first1=Martin B. |first2=Shashank |last2=Virmani|title=उलझाने के उपायों का परिचय|year=2007|pages=1–51|volume=1|journal=Quant. Inf. Comp. |arxiv=quant-ph/0504163|bibcode=2005quant.ph..4163P}}</ref><ref name="Vedral2002">{{cite journal | last = Vedral | first = Vlatko |author-link = Vlatko Vedral | doi = 10.1103/RevModPhys.74.197 | arxiv = quant-ph/0102094 | bibcode=2002RvMP...74..197V | volume=74 | issue = 1 | title=क्वांटम सूचना सिद्धांत में सापेक्ष एन्ट्रापी की भूमिका| year=2002 | journal=Reviews of Modern Physics | pages=197–234 | s2cid = 6370982 }}</ref> यदि समग्र प्रणाली शुद्ध है, तो एक उपप्रणाली की एन्ट्रापी का उपयोग अन्य उपप्रणालियों के साथ उसके उलझाव की डिग्री को मापने के लिए किया जा सकता है। द्विदलीय शुद्ध अवस्थाओं के लिए, कम अवस्थाओं की वॉन न्यूमैन एन्ट्रॉपी इस अर्थ में उलझाव का अद्वितीय माप है कि यह स्थितिों के परिवार पर एकमात्र कार्य है जो उलझाव माप के लिए आवश्यक कुछ सिद्धांतों को संतुष्ट करता है।<ref>{{cite journal |last1=Hill |first1=S |last2=Wootters |first2=W. K. |title=क्वांटम बिट्स की एक जोड़ी का उलझाव|journal=Phys. Rev. Lett. |arxiv=quant-ph/9703041 |doi =10.1103/PhysRevLett.78.5022 |year=1997 |volume=78 |issue=26 |pages=5022–5025 |bibcode=1997PhRvL..78.5022H |s2cid=9173232 }}</ref> | ||
यह एक शास्त्रीय परिणाम है कि शैनन एन्ट्रॉपी अपनी अधिकतम सीमा केवल और केवल समान संभाव्यता वितरण {1/n,...,1/n} पर प्राप्त करती है। अत: द्विदलीय शुद्ध अवस्था {{math|''ρ'' ∈ ''H''<sub>A</sub> ⊗ ''H''<sub>B</sub>}} को अधिकतम उलझी हुई स्थिति कहा जाता है यदि प्रत्येक उपप्रणाली की कम हुई स्थिति हो {{mvar|ρ}} विकर्ण आव्यूह है। | यह एक शास्त्रीय परिणाम है कि शैनन एन्ट्रॉपी अपनी अधिकतम सीमा केवल और केवल समान संभाव्यता वितरण {1/n,...,1/n} पर प्राप्त करती है। अत: द्विदलीय शुद्ध अवस्था {{math|''ρ'' ∈ ''H''<sub>A</sub> ⊗ ''H''<sub>B</sub>}} को अधिकतम उलझी हुई स्थिति कहा जाता है यदि प्रत्येक उपप्रणाली की कम हुई स्थिति हो {{mvar|ρ}} विकर्ण आव्यूह है। | ||
| Line 366: | Line 363: | ||
मिश्रित स्थितिों के लिए, कम वॉन न्यूमैन एन्ट्रॉपी एकमात्र उचित उलझाव उपाय नहीं है। | मिश्रित स्थितिों के लिए, कम वॉन न्यूमैन एन्ट्रॉपी एकमात्र उचित उलझाव उपाय नहीं है। | ||
एक तरफ, सूचना-सैद्धांतिक परिभाषा सांख्यिकीय यांत्रिकी के अर्थ में एन्ट्रापी (सांख्यिकीय विचार) से निकटता से संबंधित है<ref>{{cite book|first=Asher |last=Peres |title=Quantum Theory: Concepts and Methods |year=1993 |publisher=[[Kluwer]] |isbn=0-7923-2549-4 |oclc=28854083 |pages=260–270 |author-link=Asher Peres |title-link=Quantum Theory: Concepts and Methods}}</ref> (वर्तमान संदर्भ में दो परिभाषाओं की | एक तरफ, सूचना-सैद्धांतिक परिभाषा सांख्यिकीय यांत्रिकी के अर्थ में एन्ट्रापी (सांख्यिकीय विचार) से निकटता से संबंधित है<ref>{{cite book|first=Asher |last=Peres |title=Quantum Theory: Concepts and Methods |year=1993 |publisher=[[Kluwer]] |isbn=0-7923-2549-4 |oclc=28854083 |pages=260–270 |author-link=Asher Peres |title-link=Quantum Theory: Concepts and Methods}}</ref> (वर्तमान संदर्भ में दो परिभाषाओं की समानता करते हुए, [[बोल्ट्ज़मान स्थिरांक]] निर्धारित करने की प्रथा है {{math|''k'' {{=}} 1}}). उदाहरण के लिए, बोरेल कार्यात्मक कैलकुलस के गुणों से, हम इसे किसी भी एकात्मक ऑपरेटर के लिए देखते हैं {{mvar|U}}, | ||
: <math>S(\rho) = S \left (U \rho U^* \right).</math> | : <math>S(\rho) = S \left (U \rho U^* \right).</math> | ||
दरअसल, इस संपत्ति के बिना, वॉन न्यूमैन एन्ट्रॉपी को अच्छी तरह से परिभाषित नहीं किया जाएगा। | दरअसल, इस संपत्ति के बिना, वॉन न्यूमैन एन्ट्रॉपी को अच्छी तरह से परिभाषित नहीं किया जाएगा। | ||
विशेष रूप से, {{mvar|U}} | विशेष रूप से, {{mvar|U}} प्रणाली का समय विकास ऑपरेटर हो सकता है, अर्थात, | ||
: <math>U(t) = \exp \left(\frac{-i H t }{\hbar}\right),</math> | : <math>U(t) = \exp \left(\frac{-i H t }{\hbar}\right),</math> | ||
कहाँ {{mvar|H}} | कहाँ {{mvar|H}} प्रणाली का [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] है। यहां एन्ट्रापी अपरिवर्तित है। | ||
किसी प्रक्रिया की उत्क्रमणीयता परिणामी एन्ट्रापी परिवर्तन से जुड़ी होती है, | किसी प्रक्रिया की उत्क्रमणीयता परिणामी एन्ट्रापी परिवर्तन से जुड़ी होती है, अर्थात, एक प्रक्रिया तभी प्रतिवर्ती होती है, जब और केवल तभी, वह प्रणाली की एन्ट्रापी को अपरिवर्तनीय छोड़ देती है। इसलिए, [[थर्मोडायनामिक संतुलन]] की ओर समय के तीर का बढ़ना क्वांटम उलझाव का बढ़ता हुआ प्रसार मात्र है।<ref>{{cite news |url=https://www.wired.com/2014/04/quantum-theory-flow-time/ |title=नया क्वांटम सिद्धांत समय के प्रवाह को समझा सकता है|last1=Wolchover |first1=Natalie |date=25 April 2014 |website=www.wired.com |publisher=Quanta Magazine |access-date=27 April 2014}}</ref> | ||
यह [[क्वांटम सूचना सिद्धांत]] और [[ ऊष्मप्रवैगिकी | ऊष्मप्रवैगिकी]] के बीच संबंध प्रदान करता है। | यह [[क्वांटम सूचना सिद्धांत]] और [[ ऊष्मप्रवैगिकी | ऊष्मप्रवैगिकी]] के बीच संबंध प्रदान करता है। | ||
| Line 384: | Line 381: | ||
फिर भी, 23 जनवरी 2023 को, भौतिकविदों ने बताया कि, आख़िरकार, उलझाव हेरफेर का कोई दूसरा नियम नहीं है। शोधकर्ताओं के शब्दों में, ऊष्मागतिकी के दूसरे नियम का कोई प्रत्यक्ष समकक्ष स्थापित नहीं किया जा सकता है।<ref name="NP-20230123">{{cite journal |last1=Lami |first1=Ludovico |last2=Regula |first2=Bartosz |title=आख़िरकार उलझाव में हेराफेरी का कोई दूसरा नियम नहीं|url=https://www.nature.com/articles/s41567-022-01873-9 |date=23 January 2023 |journal=[[Nature Physics]] |volume=19 |issue=2 |pages=184–189 |doi=10.1038/s41567-022-01873-9 |bibcode=2023NatPh..19..184L |s2cid=242757348 |accessdate=17 February 2023 }}</ref> | फिर भी, 23 जनवरी 2023 को, भौतिकविदों ने बताया कि, आख़िरकार, उलझाव हेरफेर का कोई दूसरा नियम नहीं है। शोधकर्ताओं के शब्दों में, ऊष्मागतिकी के दूसरे नियम का कोई प्रत्यक्ष समकक्ष स्थापित नहीं किया जा सकता है।<ref name="NP-20230123">{{cite journal |last1=Lami |first1=Ludovico |last2=Regula |first2=Bartosz |title=आख़िरकार उलझाव में हेराफेरी का कोई दूसरा नियम नहीं|url=https://www.nature.com/articles/s41567-022-01873-9 |date=23 January 2023 |journal=[[Nature Physics]] |volume=19 |issue=2 |pages=184–189 |doi=10.1038/s41567-022-01873-9 |bibcode=2023NatPh..19..184L |s2cid=242757348 |accessdate=17 February 2023 }}</ref> | ||
=== उलझाव के उपाय === | === उलझाव के उपाय === | ||
उलझाव के उपाय एक ( | उलझाव के उपाय एक (अधिकांशतः द्विदलीय) क्वांटम अवस्था में उलझाव की मात्रा को मापते हैं। जैसा कि ऊपर बताया गया है, [[उलझाव की एन्ट्रापी]] शुद्ध अवस्थाओं के लिए उलझाव का मानक माप है (लेकिन अब मिश्रित अवस्थाओं के लिए उलझाव का माप नहीं है)। मिश्रित अवस्थाओं के लिए साहित्य में कुछ उलझाव के उपाय उपस्थित हैं<ref name="Plenio" />और कोई भी मानक नहीं है। | ||
*उलझाव लागत | *उलझाव लागत | ||
* उलझाव आसवन | * उलझाव आसवन | ||
| Line 391: | Line 388: | ||
* [[क्वांटम सापेक्ष एन्ट्रापी]] | * [[क्वांटम सापेक्ष एन्ट्रापी]] | ||
* [[कुचला हुआ उलझाव]] | * [[कुचला हुआ उलझाव]] | ||
* | * लघुगणकीय नकारात्मकता | ||
इनमें से अधिकांश (लेकिन सभी नहीं) उलझाव के उपाय शुद्ध अवस्थाओं के लिए उलझी हुई एन्ट्रापी को कम कर देते हैं, और मिश्रित अवस्थाओं के लिए गणना करना मुश्किल (एनपी-हार्ड) होता है क्योंकि उलझी हुई प्रणाली का आयाम बढ़ता है।<ref>{{cite journal|last1=Huang|first1=Yichen|title=क्वांटम कलह की गणना एनपी-पूर्ण है|journal=New Journal of Physics|date=21 March 2014|volume=16|issue=3|pages=033027|doi=10.1088/1367-2630/16/3/033027|bibcode=2014NJPh...16c3027H|arxiv = 1305.5941 |s2cid=118556793}}</ref> | इनमें से अधिकांश (लेकिन सभी नहीं) उलझाव के उपाय शुद्ध अवस्थाओं के लिए उलझी हुई एन्ट्रापी को कम कर देते हैं, और मिश्रित अवस्थाओं के लिए गणना करना मुश्किल (एनपी-हार्ड) होता है क्योंकि उलझी हुई प्रणाली का आयाम बढ़ता है।<ref>{{cite journal|last1=Huang|first1=Yichen|title=क्वांटम कलह की गणना एनपी-पूर्ण है|journal=New Journal of Physics|date=21 March 2014|volume=16|issue=3|pages=033027|doi=10.1088/1367-2630/16/3/033027|bibcode=2014NJPh...16c3027H|arxiv = 1305.5941 |s2cid=118556793}}</ref> | ||
=== [[क्वांटम क्षेत्र सिद्धांत]] === | === [[क्वांटम क्षेत्र सिद्धांत]] === | ||
| Line 402: | Line 399: | ||
उलझाव के सबसे प्रसिद्ध अनुप्रयोगों में सुपरडेंस कोडिंग और क्वांटम टेलीपोर्टेशन हैं।<ref>{{cite journal |last1=Bouwmeester |first1=Dik |last2=Pan |first2=Jian-Wei|last3=Mattle |first3=Klaus|last4=Eibl |first4=Manfred |last5=Weinfurter |first5=Harald|last6=Zeilinger |first6=Anton|year=1997 |title=प्रायोगिक क्वांटम टेलीपोर्टेशन|journal=Nature |volume=390 |issue=6660 |pages=575–579 |name-list-style=amp |url=http://qudev.ethz.ch/content/courses/QSIT06/pdfs/Bouwmeester97.pdf |doi=10.1038/37539|bibcode = 1997Natur.390..575B |arxiv=1901.11004 |s2cid=4422887 }}</ref> | उलझाव के सबसे प्रसिद्ध अनुप्रयोगों में सुपरडेंस कोडिंग और क्वांटम टेलीपोर्टेशन हैं।<ref>{{cite journal |last1=Bouwmeester |first1=Dik |last2=Pan |first2=Jian-Wei|last3=Mattle |first3=Klaus|last4=Eibl |first4=Manfred |last5=Weinfurter |first5=Harald|last6=Zeilinger |first6=Anton|year=1997 |title=प्रायोगिक क्वांटम टेलीपोर्टेशन|journal=Nature |volume=390 |issue=6660 |pages=575–579 |name-list-style=amp |url=http://qudev.ethz.ch/content/courses/QSIT06/pdfs/Bouwmeester97.pdf |doi=10.1038/37539|bibcode = 1997Natur.390..575B |arxiv=1901.11004 |s2cid=4422887 }}</ref> | ||
अधिकांश शोधकर्ताओं का मानना है कि [[ एक कंप्यूटर जितना | एक कंप्यूटर जितना]] को साकार करने के लिए उलझाव आवश्यक है ( | अधिकांश शोधकर्ताओं का मानना है कि [[ एक कंप्यूटर जितना | एक कंप्यूटर जितना]] को साकार करने के लिए उलझाव आवश्यक है (चूंकि इस पर कुछ लोगों द्वारा विवाद किया गया है)।<ref name="jozsa02">{{cite journal|author1=Richard Jozsa|author2=Noah Linden|doi=10.1098/rspa.2002.1097|title=क्वांटम कम्प्यूटेशनल स्पीड-अप में उलझाव की भूमिका पर|year=2002|journal=Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences|volume=459|issue=2036|pages=2011–2032|arxiv=quant-ph/0201143|bibcode = 2003RSPSA.459.2011J |citeseerx=10.1.1.251.7637|s2cid=15470259}}</ref> | ||
एंटैंगलमेंट का उपयोग [[क्वांटम क्रिप्टोग्राफी]] के कुछ प्रोटोकॉल में किया जाता है,<ref name="ekert91">{{cite journal |title=बेल के प्रमेय पर आधारित क्वांटम क्रिप्टोग्राफी|year=1991 |last1=Ekert |first1=Artur K. |journal=Physical Review Letters |volume=67 |issue=6 |pages=661–663 |doi=10.1103/PhysRevLett.67.661 |pmid=10044956 |bibcode=1991PhRvL..67..661E |s2cid=27683254}}</ref><ref name="horodecki10">{{cite journal |title=Entanglement-based secure quantum cryptography over 1,120 kilometres |author1=Juan Yin |author2=Yu-Huai Li |author3=Sheng-Kai Liao |author4=Meng Yang |author5=Yuan Cao |author6=Liang Zhang |author7=Ji-Gang Ren |author8=Wen-Qi Cai |author9=Wei-Yue Liu |author10=Shuang-Lin Li |author11=Rong Shu |author12=Yong-Mei Huang |author13=Lei Deng |author14=Li Li |author15=Qiang Zhang |author16=Nai-Le Liu |author17=Yu-Ao Chen |author18=Chao-Yang Lu |author19=Xiang-Bin Wang |author20=Feihu Xu |author21=Jian-Yu Wang |author22=Cheng-Zhi Peng |author23=Artur K. Ekert |author24=Jian-Wei Pan |journal=Nature |volume=582 |pages=501–505 |year=2020 |issue=7813 |doi=10.1038/s41586-020-2401-y|pmid=32541968 |bibcode=2020Natur.582..501Y |s2cid=219692094 }}</ref> लेकिन मानक मान्यताओं के तहत क्यूकेडी की सुरक्षा को | एंटैंगलमेंट का उपयोग [[क्वांटम क्रिप्टोग्राफी]] के कुछ प्रोटोकॉल में किया जाता है,<ref name="ekert91">{{cite journal |title=बेल के प्रमेय पर आधारित क्वांटम क्रिप्टोग्राफी|year=1991 |last1=Ekert |first1=Artur K. |journal=Physical Review Letters |volume=67 |issue=6 |pages=661–663 |doi=10.1103/PhysRevLett.67.661 |pmid=10044956 |bibcode=1991PhRvL..67..661E |s2cid=27683254}}</ref><ref name="horodecki10">{{cite journal |title=Entanglement-based secure quantum cryptography over 1,120 kilometres |author1=Juan Yin |author2=Yu-Huai Li |author3=Sheng-Kai Liao |author4=Meng Yang |author5=Yuan Cao |author6=Liang Zhang |author7=Ji-Gang Ren |author8=Wen-Qi Cai |author9=Wei-Yue Liu |author10=Shuang-Lin Li |author11=Rong Shu |author12=Yong-Mei Huang |author13=Lei Deng |author14=Li Li |author15=Qiang Zhang |author16=Nai-Le Liu |author17=Yu-Ao Chen |author18=Chao-Yang Lu |author19=Xiang-Bin Wang |author20=Feihu Xu |author21=Jian-Yu Wang |author22=Cheng-Zhi Peng |author23=Artur K. Ekert |author24=Jian-Wei Pan |journal=Nature |volume=582 |pages=501–505 |year=2020 |issue=7813 |doi=10.1038/s41586-020-2401-y|pmid=32541968 |bibcode=2020Natur.582..501Y |s2cid=219692094 }}</ref> लेकिन मानक मान्यताओं के तहत क्यूकेडी की सुरक्षा को सिद्ध करना करने के लिए उलझाव की आवश्यकता नहीं है।<ref>{{cite journal |title=QKD प्रोटोकॉल के लिए एक सूचना-सैद्धांतिक सुरक्षा प्रमाण|author1=R. Renner |author2=N. Gisin |author3=B. Kraus |journal=Phys. Rev. A |volume=72 |pages=012332 |year=2005 |doi=10.1103/PhysRevA.72.012332 |arxiv=quant-ph/0502064 |s2cid=119052621 }}</ref> चूंकि, क्यूकेडी की [[डिवाइस-स्वतंत्र क्वांटम क्रिप्टोग्राफी]] सुरक्षा को संचार भागीदारों के बीच उलझाव का फायदा उठाते हुए दिखाया गया है।<ref>{{cite journal |author1=S. Pirandola |author2=U. L. Andersen |author3=L. Banchi |author4=M. Berta |author5=D. Bunandar |author6=R. Colbeck |author7=D. Englund |author8=T. Gehring |author9=C. Lupo |author10=C. Ottaviani |author11=J. L. Pereira |author12=M. Razavi |author13=J. Shamsul Shaari |author14=M. Tomamichel |author15=V. C. Usenko |author16=G. Vallone |author17=P. Villoresi |author18=P. Wallden |year=2020 |title=क्वांटम क्रिप्टोग्राफी में प्रगति|journal=Adv. Opt. Photon. |volume=12 |issue=4 |pages=1012–1236 |arxiv=1906.01645 |bibcode=2020AdOP...12.1012P |doi=10.1364/AOP.361502 |s2cid=174799187}}</ref> | ||
=== उलझी हुई स्थितियाँ === | === उलझी हुई स्थितियाँ === | ||
ऐसी कई विहित उलझी हुई स्थितियाँ हैं जो | ऐसी कई विहित उलझी हुई स्थितियाँ हैं जो अधिकांशतः सिद्धांत और प्रयोगों में दिखाई देती हैं। | ||
दो क्विट के लिए, [[बेल अवस्था]]एँ हैं | दो क्विट के लिए, [[बेल अवस्था]]एँ हैं | ||
| Line 418: | Line 415: | ||
: <math>|\mathrm{GHZ}\rangle = \frac{|0\rangle^{\otimes M} + |1\rangle^{\otimes M}}{\sqrt{2}},</math> | : <math>|\mathrm{GHZ}\rangle = \frac{|0\rangle^{\otimes M} + |1\rangle^{\otimes M}}{\sqrt{2}},</math> | ||
जो बेल अवस्था तक कम हो जाता है <math>|\Phi^+\rangle</math> के लिए <math>M=2</math>. पारंपरिक GHZ स्थिति को परिभाषित किया गया था <math>M=3</math>. गीगा अवस्थाओं को कभी-कभी [[qudit|क्यूबिट]] तक विस्तारित किया जाता है, | जो बेल अवस्था तक कम हो जाता है <math>|\Phi^+\rangle</math> के लिए <math>M=2</math>. पारंपरिक GHZ स्थिति को परिभाषित किया गया था <math>M=3</math>. गीगा अवस्थाओं को कभी-कभी [[qudit|क्यूबिट]] तक विस्तारित किया जाता है, अर्थात, 2 आयामों के अतिरिक्त d की प्रणाली। | ||
इसके | इसके अतिरिक्त एम>2 क्विबिट्स के लिए, [[ स्पिन निचोड़ना ]] है, निचोड़े हुए सुसंगत स्थितिों का एक वर्ग जो स्पिन माप की अनिश्चितता पर कुछ प्रतिबंधों को संतुष्ट करता है, जो आवश्यक रूप से उलझे हुए हैं।<ref>{{cite journal | last1 = Kitagawa | first1 = Masahiro | last2 = Ueda | first2 = Masahito | year = 1993 | title = निचोड़ा हुआ स्पिन राज्य| journal = Phys. Rev. A | volume = 47 | issue = 6| pages = 5138–5143 | doi=10.1103/physreva.47.5138| pmid = 9909547 |bibcode = 1993PhRvA..47.5138K | hdl = 11094/77656 | url = https://ir.library.osaka-u.ac.jp/repo/ouka/all/77656/PhysRevA_47_06_005138.pdf | hdl-access = free }}</ref> क्वांटम उलझाव का उपयोग करके सटीक माप को बढ़ाने के लिए स्पिन निचोड़ा हुआ स्थिति अच्छे उम्मीदवार हैं।<ref>{{cite journal | last1 = Wineland | first1 = D. J. | last2 = Bollinger | first2 = J. J. | last3 = Itano | first3 = W. M. | last4 = Moore | first4 = F. L. | last5 = Heinzen | first5 = D. J. | year = 1992| title = स्पेक्ट्रोस्कोपी में स्पिन निचोड़ना और क्वांटम शोर कम करना| journal = Phys. Rev. A | volume = 46| issue = 11| pages = R6797–R6800| doi = 10.1103/PhysRevA.46.R6797 | pmid = 9908086 |bibcode = 1992PhRvA..46.6797W }}</ref> | ||
दो बोसोनिक मोड के लिए, एक नून अवस्था है | दो बोसोनिक मोड के लिए, एक नून अवस्था है | ||
| Line 427: | Line 424: | ||
यह बेल अवस्था की तरह है <math>|\Psi^+\rangle</math> आधार केट्स 0 और 1 को छोड़कर एन फोटॉन एक मोड में हैं और एन फोटॉन दूसरे मोड में हैं। | यह बेल अवस्था की तरह है <math>|\Psi^+\rangle</math> आधार केट्स 0 और 1 को छोड़कर एन फोटॉन एक मोड में हैं और एन फोटॉन दूसरे मोड में हैं। | ||
अंत में, बोसोनिक मोड के लिए [जुड़वां [[फॉक राज्य|फॉक स्थिति]]] भी | अंत में, बोसोनिक मोड के लिए [जुड़वां [[फॉक राज्य|फॉक स्थिति]]] भी उपस्थित हैं, जिन्हें एक फॉक स्थिति को दो भुजाओं में फीड करके बीम स्प्लिटर की ओर ले जाकर बनाया जा सकता है। वे नून स्थितिों के गुणकों का योग हैं, और उनका उपयोग हाइजेनबर्ग सीमा को प्राप्त करने के लिए किया जा सकता है।<ref>{{Cite journal |doi = 10.1103/PhysRevLett.71.1355|pmid = 10055519|title = हाइजेनबर्ग सीमा पर ऑप्टिकल चरण बदलाव का इंटरफेरोमेट्रिक पता लगाना|journal = Physical Review Letters|volume = 71|issue = 9|pages = 1355–1358|year = 1993|last1 = Holland|first1 = M. J|last2 = Burnett|first2 = K|bibcode = 1993PhRvL..71.1355H}}</ref> | ||
उलझाव के उचित रूप से चुने गए उपायों के लिए, बेल, जीएचजेड और एनओएन राज्य अधिकतम रूप से उलझे हुए हैं जबकि स्पिन निचोड़ा हुआ है और जुड़वां फॉक राज्य केवल आंशिक रूप से उलझे हुए हैं। आंशिक रूप से उलझी हुई अवस्थाओं को प्रयोगात्मक रूप से तैयार करना | उलझाव के उचित रूप से चुने गए उपायों के लिए, बेल, जीएचजेड और एनओएन राज्य अधिकतम रूप से उलझे हुए हैं जबकि स्पिन निचोड़ा हुआ है और जुड़वां फॉक राज्य केवल आंशिक रूप से उलझे हुए हैं। आंशिक रूप से उलझी हुई अवस्थाओं को प्रयोगात्मक रूप से तैयार करना सामान्यतः आसान होता है। | ||
=== उलझाव पैदा करने की विधियाँ === | === उलझाव पैदा करने की विधियाँ === | ||
उलझाव | उलझाव सामान्यतः उपपरमाण्विक कणों के बीच सीधे संपर्क से बनता है। ये अंतःक्रियाएँ अनेक रूप ले सकती हैं। ध्रुवीकरण में उलझे फोटॉनों की एक जोड़ी उत्पन्न करने के लिए सबसे अधिक उपयोग की जाने वाली विधियों में से एक सहज पैरामीट्रिक डाउन-रूपांतरण है।<ref name="horodecki2007">{{cite journal | ||
|last1 = Horodecki | |last1 = Horodecki | ||
|first1 = Ryszard | |first1 = Ryszard | ||
| Line 469: | Line 466: | ||
|last9=O'Brien | |last9=O'Brien | ||
|first9=J. L. | |first9=J. L. | ||
|title=पुन: कॉन्फ़िगर करने योग्य फोटोनिक सर्किट के साथ उलझाव और मिश्रण को उत्पन्न करना, हेरफेर करना और मापना|journal=Nature Photonics |arxiv=1108.3309 |doi=10.1038/nphoton.2011.283 |year=2012 |volume=6 |issue=1 |pages=45–59 |bibcode = 2012NaPho...6...45S |s2cid=56206588 }}</ref> अन्य | |title=पुन: कॉन्फ़िगर करने योग्य फोटोनिक सर्किट के साथ उलझाव और मिश्रण को उत्पन्न करना, हेरफेर करना और मापना|journal=Nature Photonics |arxiv=1108.3309 |doi=10.1038/nphoton.2011.283 |year=2012 |volume=6 |issue=1 |pages=45–59 |bibcode = 2012NaPho...6...45S |s2cid=56206588 }}</ref> अन्य ढंग में फोटॉन को सीमित करने और मिश्रित करने के लिए [[ फाइबर युग्मक ]] का उपयोग सम्मलित है, एक [[क्वांटम डॉट]] में द्वि-एक्सिटॉन के क्षय कैस्केड से उत्सर्जित फोटॉन,<ref>{{Cite journal|last=Akopian|first=N.|date=2006|title=सेमीकंडक्टर क्वांटम डॉट्स से उलझे हुए फोटॉन जोड़े|journal=Phys. Rev. Lett.|volume=96|issue=2|pages=130501|arxiv=quant-ph/0509060|bibcode=2006PhRvL..96b0501D|doi=10.1103/PhysRevLett.96.020501|pmid=16486553|s2cid=22040546}}</ref> होंग-ओउ-मंडेल प्रभाव आदि का उपयोग। एक प्राथमिक [[कण]] और उसके एंटीपार्टिकल, जैसे कि एक इलेक्ट्रॉन और एक [[पोजीट्रान]] का क्वांटम उलझाव, हार्डी के विरोधाभास में संबंधित क्वांटम तरंग कार्यों के आंशिक ओवरलैप द्वारा बनाया जा सकता है।<ref name="Hardy1992">{{cite journal | ||
| last = Hardy | | last = Hardy | ||
| first = Lucien | | first = Lucien | ||
| Line 498: | Line 495: | ||
}}</ref> | }}</ref> | ||
बेल के प्रमेय के | बेल के प्रमेय के प्रारंभी परीक्षणों में, उलझे हुए कण परमाणु कैस्केड का उपयोग करके उत्पन्न किए गए थे।<ref name="Clauser" /> | ||
एन्टैंगलमेंट स्वैपिंग के उपयोग के माध्यम से उन क्वांटम प्रणालियों के बीच उलझाव पैदा करना भी संभव है, जिन्होंने कभी सीधे संपर्क नहीं किया है। दो स्वतंत्र रूप से तैयार, समान कण भी उलझ सकते हैं यदि उनकी तरंग क्रियाएं केवल स्थानिक रूप से ओवरलैप होती हैं, कम से कम आंशिक रूप से।<ref>{{cite journal |first1=Rosario |last1=Lo Franco |first2=Giuseppe |last2=Compagno |title=क्वांटम सूचना प्रसंस्करण के लिए एक संसाधन के रूप में प्राथमिक प्रणालियों की अविभाज्यता|journal=Phys. Rev. Lett. |volume=120 |pages=240403 |date=14 June 2018 |issue=24 |doi=10.1103/PhysRevLett.120.240403 |pmid=29957003 |arxiv=1712.00706|bibcode=2018PhRvL.120x0403L |s2cid=49562954 }}</ref> | एन्टैंगलमेंट स्वैपिंग के उपयोग के माध्यम से उन क्वांटम प्रणालियों के बीच उलझाव पैदा करना भी संभव है, जिन्होंने कभी सीधे संपर्क नहीं किया है। दो स्वतंत्र रूप से तैयार, समान कण भी उलझ सकते हैं यदि उनकी तरंग क्रियाएं केवल स्थानिक रूप से ओवरलैप होती हैं, कम से कम आंशिक रूप से।<ref>{{cite journal |first1=Rosario |last1=Lo Franco |first2=Giuseppe |last2=Compagno |title=क्वांटम सूचना प्रसंस्करण के लिए एक संसाधन के रूप में प्राथमिक प्रणालियों की अविभाज्यता|journal=Phys. Rev. Lett. |volume=120 |pages=240403 |date=14 June 2018 |issue=24 |doi=10.1103/PhysRevLett.120.240403 |pmid=29957003 |arxiv=1712.00706|bibcode=2018PhRvL.120x0403L |s2cid=49562954 }}</ref> | ||
| Line 507: | Line 504: | ||
<math display="block">{\rho=\sum_j p_j \rho_j^{(A)}\otimes\rho_j^{(B)}}</math>साथ <math>1\ge p_j\ge 0</math> सम्भावनाएँ परिभाषा के अनुसार, कोई स्थिति उलझी हुई है यदि उसे अलग नहीं किया जा सकता है। | <math display="block">{\rho=\sum_j p_j \rho_j^{(A)}\otimes\rho_j^{(B)}}</math>साथ <math>1\ge p_j\ge 0</math> सम्भावनाएँ परिभाषा के अनुसार, कोई स्थिति उलझी हुई है यदि उसे अलग नहीं किया जा सकता है। | ||
2-क्यूबिट और क्यूबिट-क्यूट्रिट | 2-क्यूबिट और क्यूबिट-क्यूट्रिट प्रणाली (क्रमशः 2 × 2 और 2 × 3) के लिए सरल पेरेस-होरोडेकी मानदंड पृथक्करण के लिए एक आवश्यक और पर्याप्त मानदंड दोनों प्रदान करता है, और इस प्रकार - अपरिचित में - उलझाव का पता लगाने के लिए। चूंकि, सामान्य स्थितियों के लिए, पृथक्करण के लिए मानदंड केवल एक आवश्यक है, क्योंकि सामान्यीकृत होने पर समस्या एनपी-हार्ड हो जाती है।<ref name="NP-hard1">Gurvits, L., Classical deterministic complexity of Edmonds' problem and quantum entanglement, in Proceedings of the 35th ACM Symposium on Theory of Computing, ACM Press, New York, 2003.</ref><ref name="NP-hard2">{{cite journal |author=Sevag Gharibian |title=क्वांटम पृथक्करण समस्या की मजबूत एनपी-कठोरता|journal=Quantum Information and Computation |volume=10 |number=3&4 |pages=343–360 |year=2010 |doi=10.26421/QIC10.3-4-11 |arxiv=0810.4507|s2cid=621887}}</ref> अन्य पृथक्करण मानदंडों में [[सीमा मानदंड]], कमी मानदंड और अनिश्चितता संबंधों पर आधारित (लेकिन इन्हीं तक सीमित नहीं) सम्मलित हैं।<ref>{{cite journal |last1=Hofmann |first1=Holger F. |last2=Takeuchi |first2=Shigeki |title=उलझाव के हस्ताक्षर के रूप में स्थानीय अनिश्चितता संबंधों का उल्लंघन|journal=Physical Review A |date=22 September 2003 |volume=68 |issue=3 |page=032103 |doi=10.1103/PhysRevA.68.032103 |arxiv=quant-ph/0212090 |bibcode=2003PhRvA..68c2103H |s2cid=54893300 }}</ref><ref>{{cite journal |last1=Gühne |first1=Otfried |title=अनिश्चितता संबंधों के माध्यम से उलझाव की विशेषता|journal=Physical Review Letters |date=18 March 2004 |volume=92 |issue=11 |page=117903 |doi=10.1103/PhysRevLett.92.117903|pmid=15089173 |arxiv=quant-ph/0306194 |bibcode=2004PhRvL..92k7903G |s2cid=5696147 }}</ref><ref>{{cite journal |last1=Gühne |first1=Otfried |last2=Lewenstein |first2=Maciej |title=एंट्रोपिक अनिश्चितता संबंध और उलझाव|journal=Physical Review A |date=24 August 2004 |volume=70 |issue=2 |page=022316 |arxiv=quant-ph/0403219 |doi=10.1103/PhysRevA.70.022316 |bibcode=2004PhRvA..70b2316G |s2cid=118952931}}</ref><ref>{{cite journal |last1=Huang |first1=Yichen |title=अवतल-फ़ंक्शन अनिश्चितता संबंधों के माध्यम से उलझाव मानदंड|journal=Physical Review A |date=29 July 2010 |volume=82 |issue=1 |page=012335 |doi=10.1103/PhysRevA.82.012335 |bibcode=2010PhRvA..82a2335H }}</ref> रेफरी देखें।<ref>{{cite journal|last1=Gühne|first1=Otfried|last2=Tóth|first2=Géza| title=उलझाव का पता लगाना|journal=Physics Reports|volume=474|issue=1–6|pages=1–75|doi=10.1016/j.physrep.2009.02.004|arxiv=0811.2803 |bibcode=2009PhR...474....1G |year=2009|s2cid=119288569}}</ref> असतत-परिवर्तनीय प्रणालियों और संदर्भ में पृथक्करण मानदंड की समीक्षा के <ref name="FriisEtAl2019entanglement">{{Cite journal|last1= Friis |first1=Nicolai |last2= Vitagliano |first2=Giuseppe |last3=Malik |first3=Mehul |last4=Huber |first4=Marcus |date=2019 |title=सिद्धांत से प्रयोग तक उलझाव प्रमाणन|journal=Nature Reviews Physics |language=en|volume=1|issue=|pages=72–87|doi=10.1038/s42254-018-0003-5 |issn=2522-5820 |arxiv=1906.10929 |s2cid=125658647}}</ref> असतत-परिवर्तनीय प्रणालियों में प्रयोगात्मक उलझाव प्रमाणन में तकनीकों और चुनौतियों पर समीक्षा के लिए। | ||
समस्या के लिए एक संख्यात्मक दृष्टिकोण का सुझाव [[लीना में जॉन मैग्ने]], [[जान मिरहेम]] और [[एरिक ओवरम]] ने अपने पेपर जियोमेट्रिकल एस्पेक्ट्स ऑफ एन्टैंगलमेंट में दिया है।<ref>{{cite journal |last1=Leinaas| first1=Jon Magne| last2=Myrheim| first2=Jan| last3=Ovrum| first3=Eirik| year=2006| title=उलझाव के ज्यामितीय पहलू| journal=Physical Review A| volume=74| issue=1| page=012313| s2cid=119443360| doi=10.1103/PhysRevA.74.012313| arxiv=quant-ph/0605079| bibcode=2006PhRvA..74a2313L}}</ref> लीनास एट अल. एक संख्यात्मक दृष्टिकोण प्रदान करें, परीक्षण किए जाने वाले लक्ष्य स्थिति के प्रति अनुमानित अलग-अलग स्थिति को पुनरावृत्त रूप से परिष्कृत करें, और जांचें कि क्या लक्ष्य स्थिति तक वास्तव में पहुंचा जा सकता है। एल्गोरिदम का कार्यान्वयन (अंतर्निहित पेरेस-होरोडेकी मानदंड परीक्षण सहित) स्टेटसेपरेटर वेब-ऐप है। | समस्या के लिए एक संख्यात्मक दृष्टिकोण का सुझाव [[लीना में जॉन मैग्ने]], [[जान मिरहेम]] और [[एरिक ओवरम]] ने अपने पेपर जियोमेट्रिकल एस्पेक्ट्स ऑफ एन्टैंगलमेंट में दिया है।<ref>{{cite journal |last1=Leinaas| first1=Jon Magne| last2=Myrheim| first2=Jan| last3=Ovrum| first3=Eirik| year=2006| title=उलझाव के ज्यामितीय पहलू| journal=Physical Review A| volume=74| issue=1| page=012313| s2cid=119443360| doi=10.1103/PhysRevA.74.012313| arxiv=quant-ph/0605079| bibcode=2006PhRvA..74a2313L}}</ref> लीनास एट अल. एक संख्यात्मक दृष्टिकोण प्रदान करें, परीक्षण किए जाने वाले लक्ष्य स्थिति के प्रति अनुमानित अलग-अलग स्थिति को पुनरावृत्त रूप से परिष्कृत करें, और जांचें कि क्या लक्ष्य स्थिति तक वास्तव में पहुंचा जा सकता है। एल्गोरिदम का कार्यान्वयन (अंतर्निहित पेरेस-होरोडेकी मानदंड परीक्षण सहित) स्टेटसेपरेटर वेब-ऐप है। | ||
सतत परिवर्तनशील प्रणालियों में, पेरेस-होरोडेकी मानदंड भी | सतत परिवर्तनशील प्रणालियों में, पेरेस-होरोडेकी मानदंड भी क्रियान्वित होता है। विशेष रूप से, साइमन<ref>{{cite journal|last1=Simon|first1=R.|title=सतत परिवर्तनीय प्रणालियों के लिए पेरेस-होरोडेकी पृथक्करण मानदंड|journal=Physical Review Letters|volume=84|issue=12|pages=2726–2729|pmid=11017310 |doi=10.1103/PhysRevLett.84.2726|arxiv=quant-ph/9909044|bibcode=2000PhRvL..84.2726S|s2cid=11664720 |year=2000}}</ref> विहित ऑपरेटरों के दूसरे क्रम के क्षणों के संदर्भ में पेरेस-होरोडेकी मानदंड का एक विशेष संस्करण तैयार किया और दिखाया कि यह आवश्यक और पर्याप्त है <math> 1\oplus1 </math>-मोड गॉसियन स्थिति (संदर्भ देखें।<ref>{{cite journal|last1=Duan|first1=Lu-Ming |last2=Giedke|first2=G.|last3=Cirac|first3=J. I.|last4=Zoller|first4=P.|title=सतत परिवर्तनीय प्रणालियों के लिए अविभाज्यता मानदंड|journal=Physical Review Letters|volume=84|issue=12 |pages=2722–2725 |doi=10.1103/PhysRevLett.84.2722|pmid=11017309|arxiv=quant-ph/9908056|bibcode=2000PhRvL..84.2722D |year=2000|s2cid=9948874}}</ref> प्रतीत होता है कि भिन्न लेकिन अनिवार्य रूप से समतुल्य दृष्टिकोण के लिए)। यह पश्चात में पाया गया<ref>{{cite journal|last1=Werner|first1=R. F.|last2=Wolf|first2=M. M.|title=बंधे हुए उलझे हुए गॉसियन राज्य|journal=Physical Review Letters|volume=86|issue=16|pages=3658–3661|pmid=11328047 |arxiv=quant-ph/0009118 |doi=10.1103/PhysRevLett.86.3658|bibcode=2001PhRvL..86.3658W|year=2001 |s2cid=20897950}}</ref> साइमन की स्थिति भी आवश्यक और पर्याप्त है <math> 1\oplus n </math>-मोड गॉसियन स्थिति, लेकिन अब इसके लिए पर्याप्त नहीं है <math> 2\oplus2 </math>-मोड गॉसियन स्थिति। कैनोनिकल ऑपरेटरों के उच्च क्रम के क्षणों को ध्यान में रखकर साइमन की स्थिति को सामान्यीकृत किया जा सकता है<ref>{{cite journal|last1=Shchukin |first1=E.|last2=Vogel |first2=W. |title=सतत द्विदलीय क्वांटम अवस्थाओं के लिए अविभाज्यता मानदंड|journal=Physical Review Letters|volume=95|issue=23 |pages=230502|doi=10.1103/PhysRevLett.95.230502|pmid=16384285|bibcode=2005PhRvL..95w0502S |arxiv=quant-ph/0508132|year=2005|s2cid=28595936}}</ref><ref>{{cite journal| last1=Hillery|first1=Mark|last2=Zubairy |first2=M.Suhail|title=दो-मोड राज्यों के लिए उलझाव की स्थिति|journal=Physical Review Letters |volume=96|issue=5|page=050503|year=2006|doi=10.1103/PhysRevLett.96.050503|arxiv=quant-ph/0507168 |bibcode=2006PhRvL..96e0503H|pmid=16486912|s2cid=43756465}}</ref> या एन्ट्रोपिक उपायों का उपयोग करके।<ref>{{cite journal| last1=Walborn|first1=S.|last2=Taketani|first2=B.|last3=Salles|first3=A.|last4=Toscano |first4=F.|last5=de Matos Filho|first5=R.|title=सतत चर के लिए एंट्रोपिक एंटैंगलमेंट मानदंड|journal=Physical Review Letters |volume=103|issue=16|doi=10.1103/PhysRevLett.103.160505|arxiv=0909.0147 |bibcode=2009PhRvL.103p0505W|pmid=19905682|page=160505 |year=2009 |s2cid=10523704}}</ref><ref>{{cite journal |last1=Yichen Huang |title=Entanglement Detection: Complexity and Shannon Entropic Criteria |journal=IEEE Transactions on Information Theory |date=October 2013 |volume=59 |issue=10 |pages=6774–6778 |doi=10.1109/TIT.2013.2257936|s2cid=7149863}}</ref> | ||
2016 में, चीन ने दुनिया का पहला क्वांटम संचार उपग्रह | 2016 में, चीन ने दुनिया का पहला क्वांटम संचार उपग्रह प्रक्षेपण किया।<ref>{{cite web |url=https://physicsworld.com/a/china-launches-worlds-first-quantum-science-satellite/ |title=चीन ने दुनिया का पहला क्वांटम विज्ञान उपग्रह लॉन्च किया|date=2016-08-16 |work=physicsworld.com |access-date=2021-12-07}}</ref> $100m [[ अंतरिक्ष पैमाने पर क्वांटम प्रयोग | अंतरिक्ष पैमाने पर क्वांटम प्रयोग]] (क्यूयूईएसएस) उद्देश्य 16 अगस्त 2016 को स्थानीय समयानुसार 01:40 बजे उत्तरी चीन के जिउक्वान सैटेलाइट प्रक्षेपण सेंटर से प्रक्षेपण किया गया था। | ||
अगले दो वर्षों के लिए, शिल्प - जिसे प्राचीन चीनी दार्शनिक के नाम पर मिकियस नाम दिया गया है - क्वांटम की व्यवहार्यता का प्रदर्शन करेगा। | अगले दो वर्षों के लिए, शिल्प - जिसे प्राचीन चीनी दार्शनिक के नाम पर मिकियस नाम दिया गया है - क्वांटम की व्यवहार्यता का प्रदर्शन करेगा। | ||
| Line 522: | Line 519: | ||
== स्वाभाविक रूप से उलझी हुई प्रणालियाँ == | == स्वाभाविक रूप से उलझी हुई प्रणालियाँ == | ||
बहु-इलेक्ट्रॉन परमाणुओं के इलेक्ट्रॉन कोश | बहु-इलेक्ट्रॉन परमाणुओं के इलेक्ट्रॉन कोश सदैव उलझे हुए इलेक्ट्रॉनों से बने होते हैं। सही आयनीकरण ऊर्जा केवल इलेक्ट्रॉन उलझाव पर विचार करके [[कॉन्फ़िगरेशन इंटरैक्शन|कॉन्फ़िगरेशन परस्पर क्रिया]] हो सकती है।<ref>Frank Jensen: ''Introduction to Computational Chemistry.'' Wiley, 2007, {{ISBN|978-0-470-01187-4}}.</ref> | ||
== [[प्रकाश संश्लेषण]] == | == [[प्रकाश संश्लेषण]] == | ||
यह सुझाव दिया गया है कि प्रकाश संश्लेषण की प्रक्रिया में, प्रकाश-संचयन परिसरों और [[प्रकाश संश्लेषक प्रतिक्रिया केंद्र]] | यह सुझाव दिया गया है कि प्रकाश संश्लेषण की प्रक्रिया में, प्रकाश-संचयन परिसरों और [[प्रकाश संश्लेषक प्रतिक्रिया केंद्र|प्रकाश संश्लेषक प्रतिक्रिया केंद्रों]] के बीच ऊर्जा के हस्तांतरण में उलझाव सम्मलित होता है, जहां प्रत्येक अवशोषित फोटॉन की [[फोटॉन ऊर्जा]] रासायनिक ऊर्जा के रूप में एकत्रित होती है। ऐसी प्रक्रिया के बिना, प्रकाश के रासायनिक ऊर्जा में कुशल रूपांतरण की व्याख्या नहीं की जा सकती है। [<nowiki/>[[गुजरने]] स्पेक्ट्रोस्कोपी] का उपयोग करते हुए, [[ फेना-मैथ्यूज़-ओल्सन कॉम्प्लेक्स |फेना-मैथ्यूज़-ओल्सन कॉम्प्लेक्स]] में उलझाव की सुसंगतता को इस सिद्धांत को समर्थन प्रदान करते हुए सैकड़ों फेमटोसेकंड (इस संबंध में एक अपेक्षाकृत लंबा समय) में मापा गया था।<ref>Berkeley Lab Press Release: ''[http://newscenter.lbl.gov/feature-stories/2010/05/10/untangling-quantum-entanglement/ Untangling the Quantum Entanglement Behind Photosynthesis: Berkeley scientists shine new light on green plant secrets.]''</ref><ref>Mohan Sarovar, Akihito Ishizaki, Graham R. Fleming, K. Birgitta Whaley: ''Quantum entanglement in photosynthetic light harvesting complexes.'' {{arxiv|0905.3787}}</ref> | ||
चूंकि, महत्वपूर्ण अनुवर्ती अध्ययन इन परिणामों की व्याख्या पर सवाल उठाते हैं और क्रोमोफोर्स में परमाणु गतिशीलता या शारीरिक तापमान के अतिरिक्त क्रायोजेनिक पर किए जा रहे प्रयोगों के लिए इलेक्ट्रॉनिक क्वांटम सुसंगतता के रिपोर्ट किए गए हस्ताक्षरों को निर्दिष्ट करते हैं।<ref>{{cite journal | author = R. Tempelaar | author2 = T. L. C. Jansen | author3 = J. Knoester | title = एफएमओ लाइट-हार्वेस्टिंग कॉम्प्लेक्स में कंपन संबंधी धड़कनें इलेक्ट्रॉनिक सुसंगतता के साक्ष्य छिपाती हैं| journal = J. Phys. Chem. B | volume = 118 | issue = 45 | pages = 12865–12872 | date = 2014 | doi=10.1021/jp510074q| pmid = 25321492 }}</ref><ref>{{cite journal | author = N. Christenson | author2 = H. F. Kauffmann | author3 = T. Pullerits | author4 = T. Mancal | title = प्रकाश संचयन परिसरों में लंबे समय तक रहने वाले सामंजस्य की उत्पत्ति| journal = J. Phys. Chem. B | volume = 116 | issue = 25 | pages = 7449–7454 | date = 2012 | doi = 10.1021/jp304649c | pmid = 22642682 | pmc = 3789255 | bibcode = 2012arXiv1201.6325C | arxiv = 1201.6325 }}</ref><ref>{{cite journal | author = A. Kolli | author2 = E. J. O’Reilly | author3= G. D. Scholes | author4= A. Olaya-Castro | title = क्रिप्टोफाइट शैवाल द्वारा सुसंगत प्रकाश संचयन में परिमाणित कंपन की मौलिक भूमिका| journal = J. Chem. Phys. | volume = 137 | issue = 17 | pages = 174109 | date = 2012 | doi=10.1063/1.4764100| pmid = 23145719 | bibcode = 2012JChPh.137q4109K | arxiv = 1203.5056 | s2cid = 20156821 }}</ref><ref>{{cite journal | author = V. Butkus | author2 = D. Zigmantas | author3= L. Valkunas | author4= D. Abramavicius | title = Vibrational vs. electronic coherences in 2D spectrum of molecular systems| journal = Chem. Phys. Lett. | volume = 545 | issue = 30 | pages = 40–43 | date = 2012 | doi=10.1016/j.cplett.2012.07.014| arxiv = 1201.2753 | bibcode = 2012CPL...545...40B | s2cid = 96663719 }}</ref><ref>{{cite journal | author = V. Tiwari | author2 = W. K. Peters | author3= D. M. Jonas | title = सहसंबद्ध वर्णक कंपन के साथ इलेक्ट्रॉनिक अनुनाद रुद्धोष्म ढांचे के बाहर प्रकाश संश्लेषक ऊर्जा हस्तांतरण को संचालित करता है| journal = Proc. Natl. Acad. Sci. USA | volume = 110 | issue = 4 | pages = 1203–1208 | date = 2013 | doi=10.1073/pnas.1211157110| pmid = 23267114 | pmc = 3557059 | doi-access = free }}</ref><ref>{{cite journal | author = E. Thyrhaug | author2 = K. Zidek | author3 = J. Dostal | author4 = D. Bina | author5 = D. Zigmantas | title = Exciton Structure and Energy Transfer in the Fenna−Matthews− Olson Complex| journal = J. Phys. Chem. Lett. | volume = 7 | issue = 9 | pages = 1653–1660 | date = 2016 | doi=10.1021/acs.jpclett.6b00534| pmid = 27082631 | s2cid = 26355154 | url = https://lup.lub.lu.se/record/b1c8070b-60cf-4e41-8895-ea13faf95777 }}</ref><ref>{{cite journal | author = Y. Fujihashi | author2 = G. R. Fleming | author3= A. Ishizaki | title = Impact of environmentally induced fluctuations on quantum mechanically mixed electronic and vibrational pigment states in photosynthetic energy transfer and 2D electronic spectra| journal = J. Chem. Phys. | volume = 142 | issue = 21 | pages = 212403 | date = 2015 | doi=10.1063/1.4914302| pmid = 26049423 | arxiv = 1505.05281 | bibcode = 2015JChPh.142u2403F | s2cid = 1082742 }}</ref> | |||
== स्थूल वस्तुओं का उलझाव == | == स्थूल वस्तुओं का उलझाव == | ||
2020 में, शोधकर्ताओं ने एक गोलाकार झिल्ली के कंपन के बीच एक मिलीमीटर आकार के यांत्रिक थरथरानवाला की गति और परमाणुओं के एक | 2020 में, शोधकर्ताओं ने एक गोलाकार झिल्ली के कंपन के बीच एक मिलीमीटर आकार के यांत्रिक थरथरानवाला की गति और परमाणुओं के एक पश्चातल की एक असमान दूर स्पिन (भौतिकी) प्रणाली के बीच क्वांटम उलझाव की सूचना दी।<ref>{{cite news |title=दूर की बड़ी वस्तुओं के बीच क्वांटम उलझाव का एहसास हुआ|url=https://phys.org/news/2020-09-quantum-entanglement-distant-large.html |access-date=9 October 2020 |work=phys.org |language=en}}</ref><ref>{{cite journal |last1=Thomas |first1=Rodrigo A. |last2=Parniak |first2=Michał |last3=Østfeldt |first3=Christoffer |last4=Møller |first4=Christoffer B. |last5=Bærentsen |first5=Christian |last6=Tsaturyan |first6=Yeghishe |last7=Schliesser |first7=Albert |last8=Appel |first8=Jürgen |last9=Zeuthen |first9=Emil |last10=Polzik |first10=Eugene S. |title=दूरस्थ स्थूल यांत्रिक और स्पिन प्रणालियों के बीच उलझाव|journal=Nature Physics |date=21 September 2020 |volume=17 |issue=2 |pages=228–233 |doi=10.1038/s41567-020-1031-5 |arxiv=2003.11310 |s2cid=214641162 |url=https://www.nature.com/articles/s41567-020-1031-5 |access-date=9 October 2020 |language=en |issn=1745-2481}}</ref> पश्चात के कार्य ने दो यांत्रिक ऑसिलेटरों को क्वांटम-उलझाकर इस कार्य को पूरक बनाया।<ref>{{cite news |title=कंपन करने वाले ड्रमहेड यांत्रिक रूप से क्वांटम में उलझे हुए हैं|url=https://physicsworld.com/a/vibrating-drumheads-are-entangled-quantum-mechanically/ |access-date=14 June 2021 |work=Physics World |date=2021-05-17}}</ref><ref>{{cite journal |last1=Lépinay |first1=Laure Mercier de |last2=Ockeloen-Korppi |first2=Caspar F. |last3=Woolley |first3=Matthew J. |last4=Sillanpää |first4=Mika A. |title=Quantum mechanics–free subsystem with mechanical oscillators |journal=Science |date=2021-05-07 |volume=372 |issue=6542 |pages=625–629 |doi=10.1126/science.abf5389 |pmid=33958476 |arxiv=2009.12902 |bibcode=2021Sci...372..625M |s2cid=221971015 |url=https://www.science.org/doi/10.1126/science.abf5389 |access-date=14 June 2021 |language=en |issn=0036-8075}}</ref><ref>{{cite journal |last1=Kotler |first1=Shlomi |last2=Peterson |first2=Gabriel A. |last3=Shojaee |first3=Ezad |last4=Lecocq |first4=Florent |last5=Cicak |first5=Katarina |last6=Kwiatkowski |first6=Alex |last7=Geller |first7=Shawn |last8=Glancy |first8=Scott |last9=Knill |first9=Emanuel |last10=Simmonds |first10=Raymond W. |last11=Aumentado |first11=José |last12=Teufel |first12=John D. |title=नियतात्मक स्थूल उलझाव का प्रत्यक्ष अवलोकन|journal=Science |date=2021-05-07 |volume=372 |issue=6542 |pages=622–625 |doi=10.1126/science.abf2998 |pmid=33958475 |arxiv=2004.05515 |bibcode=2021Sci...372..622K |s2cid=233872863 |url=https://www.science.org/doi/10.1126/science.abf2998 |access-date=14 June 2021 |language=en |issn=0036-8075}}</ref> | ||
=== जीवित प्रणालियों के तत्वों का उलझाव === | === जीवित प्रणालियों के तत्वों का उलझाव === | ||
अक्टूबर 2018 में, भौतिकविदों ने जीवित जीवों का उपयोग करके क्वांटम उलझाव | अक्टूबर 2018 में, भौतिकविदों ने जीवित जीवों का उपयोग करके क्वांटम उलझाव उत्पन करने की सूचना दी, विशेष रूप से जीवित [[ जीवाणु |जीवाणु]] और फोटॉन के भीतर प्रकाश संश्लेषक अणुओं के बीच।<ref name="JPC-20181010">{{cite journal | ||
| last1=Marletto | | last1=Marletto | ||
| first1=C. | | first1=C. | ||
| Line 552: | Line 549: | ||
| s2cid=119236759 }}</ref><ref name="SA-20181029">{{cite web |last=O'Callaghan |first=Jonathan |title="Schrödinger's Bacterium" Could Be a Quantum Biology Milestone – A recent experiment may have placed living organisms in a state of quantum entanglement |url=https://www.scientificamerican.com/article/schroedingers-bacterium-could-be-a-quantum-biology-milestone/ |date=29 October 2018 |work=[[Scientific American]] |access-date=29 October 2018 }}</ref> | | s2cid=119236759 }}</ref><ref name="SA-20181029">{{cite web |last=O'Callaghan |first=Jonathan |title="Schrödinger's Bacterium" Could Be a Quantum Biology Milestone – A recent experiment may have placed living organisms in a state of quantum entanglement |url=https://www.scientificamerican.com/article/schroedingers-bacterium-could-be-a-quantum-biology-milestone/ |date=29 October 2018 |work=[[Scientific American]] |access-date=29 October 2018 }}</ref> | ||
जीवित जीवों (हरे सल्फर बैक्टीरिया) का मध्यस्थों के रूप में अध्ययन किया गया है जो अन्यथा गैर-अंतःक्रियात्मक प्रकाश मोड के बीच क्वांटम उलझाव पैदा करते हैं, जो प्रकाश और बैक्टीरिया मोड के बीच उच्च उलझाव दिखाते हैं, और कुछ | जीवित जीवों (हरे सल्फर बैक्टीरिया) का मध्यस्थों के रूप में अध्ययन किया गया है जो अन्यथा गैर-अंतःक्रियात्मक प्रकाश मोड के बीच क्वांटम उलझाव पैदा करते हैं, जो प्रकाश और बैक्टीरिया मोड के बीच उच्च उलझाव दिखाते हैं, और कुछ सीमा तक, बैक्टीरिया के भीतर भी उलझाव दिखाते हैं।<ref>{{cite journal | last1 = Krisnanda | first1 = T. | last2 = Marletto | first2 = C. | last3 = Vedral | first3 = V. | last4 = Paternostro | first4 = M. | last5 = Paterek | first5 = T. | year = 2018 | title = प्रकाश संश्लेषक जीवों की क्वांटम विशेषताओं की जांच करना| journal = npj Quantum Information | volume = 4 | page = 60 | doi = 10.1038/s41534-018-0110-2 | arxiv = 1711.06485 | bibcode = 2018npjQI...4...60K | doi-access = free }}</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
{{cols|colwidth=26em}} | {{cols|colwidth=26em}} | ||
| Line 642: | Line 639: | ||
{{authority control}} | {{authority control}} | ||
{{DEFAULTSORT:Quantum Entanglement}} | {{DEFAULTSORT:Quantum Entanglement}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page|Quantum Entanglement]] | ||
[[Category:Created On 26/07/2023]] | [[Category:Articles with invalid date parameter in template|Quantum Entanglement]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 errors|Quantum Entanglement]] | |||
[[Category:Collapse templates|Quantum Entanglement]] | |||
[[Category:Created On 26/07/2023|Quantum Entanglement]] | |||
[[Category:Lua-based templates|Quantum Entanglement]] | |||
[[Category:Machine Translated Page|Quantum Entanglement]] | |||
[[Category:Multi-column templates|Quantum Entanglement]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Quantum Entanglement]] | |||
[[Category:Pages using div col with small parameter|Quantum Entanglement]] | |||
[[Category:Pages with empty portal template|Quantum Entanglement]] | |||
[[Category:Pages with script errors|Quantum Entanglement]] | |||
[[Category:Portal templates with redlinked portals|Quantum Entanglement]] | |||
[[Category:Short description with empty Wikidata description|Quantum Entanglement]] | |||
[[Category:Sidebars with styles needing conversion|Quantum Entanglement]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi|Quantum Entanglement]] | |||
[[Category:Templates Vigyan Ready|Quantum Entanglement]] | |||
[[Category:Templates generating microformats|Quantum Entanglement]] | |||
[[Category:Templates that add a tracking category|Quantum Entanglement]] | |||
[[Category:Templates that are not mobile friendly|Quantum Entanglement]] | |||
[[Category:Templates that generate short descriptions|Quantum Entanglement]] | |||
[[Category:Templates using TemplateData|Quantum Entanglement]] | |||
[[Category:Templates using under-protected Lua modules|Quantum Entanglement]] | |||
[[Category:Use dmy dates from September 2016|Quantum Entanglement]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates|Quantum Entanglement]] | |||
[[Category:क्वांटम सूचना विज्ञान|Quantum Entanglement]] | |||
Latest revision as of 18:20, 8 August 2023
| के बारे में लेखों की एक श्रृंखला का हिस्सा |
| क्वांटम यांत्रिकी |
|---|
क्वांटम उलझाव वह घटना है जो तब घटित होती है जब कणों का एक समूह उत्पन्न होता है, परस्पर क्रिया करता है, या स्थानिक निकटता को इस तरह से साझा करता है कि समूह के प्रत्येक कण की क्वांटम स्थिति को दूसरों की स्थिति से स्वतंत्र रूप से वर्णित नहीं किया जा सके, जिसमें कण बड़ी दूरी से अलग होने पर भी सम्मलित हैं। क्वांटम उलझाव का विषय शास्त्रीय भौतिकी और क्वांटम भौतिकी के बीच असमानता के केंद्र में है: उलझाव क्वांटम यांत्रिकी की एक प्राथमिक विशेषता है जो शास्त्रीय यांत्रिकी में उपस्थित नहीं है।[1]
उलझे हुए कणों पर किए गए स्थिति, संवेग, स्पिन (भौतिकी), और ध्रुवीकरण (तरंगें) जैसे भौतिक गुणों के माप, कुछ स्थितियों में, पूरी तरह से सहसंबद्ध पाए जा सकते हैं। उदाहरण के लिए, यदि उलझे हुए कणों की एक जोड़ी इस प्रकार उत्पन्न होती है कि उनका कुल स्पिन शून्य माना जाता है, और एक कण को पहले अक्ष पर दक्षिणावर्त स्पिन पाया जाता है, तो दूसरे कण का स्पिन, उसी अक्ष पर मापा जाता है, वामावर्त पाया जाता है। चूंकि, यह व्यवहार प्रतीत होता है कि विरोधाभासी प्रभावों को जन्म देता है: किसी कण के गुणों के किसी भी माप के परिणामस्वरूप उस कण का एक स्पष्ट और अपरिवर्तनीय तरंग फ़ंक्शन पतन हो जाता है और मूल क्वांटम स्थिति बदल जाती है। उलझे हुए कणों के साथ, ऐसे माप उलझी हुई प्रणाली को समग्र रूप से प्रभावित करते हैं।
ऐसी घटनाएँ 1935 में अल्बर्ट आइंस्टीन, बोरिस पोडॉल्स्की और नाथन रोसेन के पेपर का विषय थीं,[2] और इसके तुरंत पश्चात इरविन श्रोडिंगर के कई पेपर,[3][4] जिसमें वर्णन किया गया था कि ईपीआर विरोधाभा के रूप में जाना जाने लगा। आइंस्टीन और अन्य लोगों ने इस तरह के व्यवहार को असंभव माना, क्योंकि इसने कार्य-कारण के स्थानीय यथार्थवाद दृष्टिकोण का उल्लंघन किया था (आइंस्टीन ने इसे "दूरी पर डरावनी कार्रवाई" के रूप में संदर्भित किया था) और तर्क दिया कि इसलिए क्वांटम यांत्रिकी का स्वीकृत सूत्रीकरण अधूरा होना चाहिए। Bell, J. S. (1987). क्वांटम यांत्रिकी में बोलने योग्य और अकथनीय (PDF). CERN. ISBN 0521334950. Archived from the original (PDF) on 12 April 2015. Retrieved 14 June 2014.
चूंकि, पश्चात में, क्वांटम यांत्रिकी की प्रति-सहज ज्ञान युक्त भविष्यवाणियों को उन परीक्षणों में सत्यापित किया गया, जहां उलझे हुए कणों के ध्रुवीकरण या स्पिन को अलग-अलग स्थानों पर मापा गया था, जो सांख्यिकीय रूप से बेल की असमानता का उल्लंघन करता था। पहले के परीक्षणों में, इस बात से इंकार नहीं किया जा सकता था कि एक बिंदु पर परिणाम सूक्ष्मता से दूरस्थ बिंदु तक प्रेषित किया जा सकता था, जिससे दूसरे स्थान पर परिणाम प्रभावित हो सकता था। चूंकि, तथाकथित "लूपहोल-फ्री" बेल परीक्षण तब से किए गए हैं जहां स्थानों को पर्याप्त रूप से अलग किया गया था कि प्रकाश की गति से संचार में माप के बीच के अंतराल की समानता में अधिक समय लगेगा - एक स्थितियों में, 10,000 गुना अधिक।
क्वांटम यांत्रिकी की कुछ व्याख्याओं के अनुसार, एक माप का प्रभाव तुरंत होता है। अन्य व्याख्याएँ जो वेवफ़ंक्शन पतन को नहीं पहचानती हैं, इस विवाद पर विवाद करती हैं कि इसका कोई "प्रभाव" है। चूंकि, सभी व्याख्याएँ इस बात से सहमत हैं कि उलझाव मापों के बीच सहसंबंध पैदा करता है, और उलझे हुए कणों के बीच पारस्परिक जानकारी का फायदा उठाया जा सकता है, लेकिन प्रकाश से भी तेज गति से सूचना का कोई भी प्रसारण असंभव है।[5][6]
क्वांटम उलझाव को फोटॉन,[7][8] इलेक्ट्रॉन,[9][10]और यहां तक कि छोटे हीरे के साथ प्रयोगात्मक रूप से प्रदर्शित किया गया है।[11] क्वांटम संचार, क्वांटम कम्प्यूटिंग और क्वांटम रडार में उलझाव का उपयोग अनुसंधान और विकास का एक बहुत ही सक्रिय क्षेत्र है।
इसके विपरीत बहुत लोकप्रिय विचार के अतिरिक्त, क्वांटम उलझाव का उपयोग प्रकाश से भी तेज़ संचार के लिए नहीं किया जा सकता है।[12]
इतिहास

1935 में, अल्बर्ट आइंस्टीन, बोरिस पोडॉल्स्की और नाथन रोसेन ने प्रति-सहज ज्ञान युक्त भविष्यवाणियों पर एक पेपर प्रकाशित किया था जो क्वांटम यांत्रिकी एक विशेष ढंग से एक साथ प्रस्तुत की गई वस्तुओं के जोड़े के लिए बनाता है।[2] इस अध्ययन में, तीनों ने आइंस्टीन-पोडॉल्स्की-रोसेन विरोधाभास (ईपीआर विरोधाभास) प्रस्तुत किया, एक विचार प्रयोग जिसने यह दिखाने का प्रयास किया कि तरंग कार्यों द्वारा दिया गया भौतिक वास्तविकता का क्वांटम यांत्रिक विवरण पूरा नहीं है।[2]चूंकि, तीन वैज्ञानिकों ने उलझाव शब्द नहीं गढ़ा, न ही उन्होंने जिस क्वांटम अवस्था पर विचार किया उसके विशेष गुणों का सामान्यीकरण किया। ईपीआर पेपर के पश्चात, इरविन श्रोडिंगर ने जर्मन भाषा में आइंस्टीन को एक पत्र लिखा जिसमें उन्होंने दो कणों के बीच सहसंबंधों का वर्णन करने के लिए वर्स्क्रानकुंग (खुद द्वारा उलझाव के रूप में अनुवादित) शब्द का उपयोग किया, जो ईपीआर प्रयोग में बातचीत करते हैं और फिर अलग हो जाते हैं।[13]
इसके तुरंत पश्चात श्रोडिंगर ने उलझाव की धारणा को परिभाषित करने और चर्चा करने वाला एक मौलिक पेपर प्रकाशित किया। पेपर में, उन्होंने अवधारणा के महत्व को पहचाना, और कहा:[3] मैं इसे [उलझन] नहीं कहूंगा, बल्कि इसे क्वांटम यांत्रिकी का विशिष्ट गुण कहूंगा, जो कि शास्त्रीय यांत्रिकी के विचार से इसके संपूर्ण विचलन को क्रियान्वित करता है। आइंस्टीन की तरह, श्रोडिंगर उलझाव की अवधारणा से असंतुष्ट थे, क्योंकि यह सापेक्षता के सिद्धांत में निहित सूचना के प्रसारण पर गति सीमा का उल्लंघन करता प्रतीत होता था।[14] आइंस्टीन ने पश्चात में उलझाव को "स्पुखाफ्टे फर्नविर्कुंग"[15] या "दूरी पर डरावनी कार्रवाई" कहकर प्रसिद्ध रूप से उपहास किया।
ईपीआर पेपर ने भौतिकविदों के बीच महत्वपूर्ण रुचि पैदा की, जिसने क्वांटम यांत्रिकी की नींव और विशेष रूप से बोहम की व्याख्या के बारे में बहुत चर्चा को प्रेरित किया, लेकिन अपेक्षाकृत कम अन्य प्रकाशित कार्य किए गए। रुचि के अतिरिक्त, ईपीआर के तर्क में कमजोर बिंदु की खोज 1964 तक नहीं की गई थी, जब जॉन स्टीवर्ट बेल ने सिद्ध करना किया कि उनकी प्रमुख धारणाओं में से एक, स्थानीयता का सिद्धांत, जैसा कि ईपीआर द्वारा अपेक्षित छिपे हुए चर व्याख्या के प्रकार पर क्रियान्वित होता है, गणितीय रूप से असंगत था क्वांटम सिद्धांत की भविष्यवाणियों के साथ।
विशेष रूप से, बेल ने स्थानीय यथार्थवाद का पालन करने वाले किसी भी सिद्धांत में उत्पन्न होने वाले सहसंबंधों की ताकत के संबंध में, बेल की असमानता में देखी गई एक ऊपरी सीमा का प्रदर्शन किया, और दिखाया कि क्वांटम सिद्धांत कुछ उलझी हुई प्रणालियों के लिए इस सीमा के उल्लंघन की भविष्यवाणी करता है।[16] उनकी असमानता प्रयोगात्मक रूप से परीक्षण योग्य है, और 1972 में स्टुअर्ट फ्रीडमैन और जॉन क्लॉसर के अग्रणी काम से शुरू होकर, कई बेल परीक्षण प्रयोग हुए हैं।[17] और 1982 में एलेन पहलू के प्रयोग।[18]
प्रारंभिक प्रायोगिक सफलता कार्ल कोचर के कारण हुई,[7][8] जिन्होंने 1967 में ही एक उपकरण प्रस्तुत किया था जिसमें कैल्शियम परमाणु से क्रमिक रूप से उत्सर्जित होने वाले दो फोटॉन को उलझते हुए दिखाया गया था - उलझे हुए दृश्य प्रकाश का पहला विषय। दो फोटॉन शास्त्रीय रूप से भविष्यवाणी की समानता में उच्च संभावना के साथ व्यासीय रूप से स्थित समानांतर ध्रुवीकरणकर्ताओं से गुजरे लेकिन क्वांटम यांत्रिक गणना के साथ मात्रात्मक समझौते में सहसंबंध थे। उन्होंने यह भी दिखाया कि ध्रुवीकरण समूहिंग्स के बीच कोण के वर्ग ज्या और कोज्या के रूप में सहसंबंध भिन्न होता है[8]और उत्सर्जित फोटॉन के बीच समय अंतराल के साथ तेजी से कमी आई।[19] कोचर का उपकरण, जो बेहतर ध्रुवीकरणकर्ताओं से सुसज्जित था, का उपयोग फ्रीडमैन और क्लॉसर द्वारा किया गया था जो कोसाइन-वर्ग निर्भरता की पुष्टि कर सकते थे और इसका उपयोग निश्चित कोणों के एक समूह के लिए बेल की असमानता के उल्लंघन को प्रदर्शित करने के लिए कर सकते थे।[17] इन सभी प्रयोगों ने स्थानीय यथार्थवाद के सिद्धांत के अतिरिक्त क्वांटम यांत्रिकी के साथ सहमति दिखाई है।
दशकों तक, प्रत्येक ने कम से कम एक खामी खुली रखी थी जिसके द्वारा परिणामों की वैधता पर सवाल उठाना संभव था। चूंकि, 2015 में एक प्रयोग किया गया था जिसने एक साथ पता लगाने और इलाके की खामियों दोनों को संवृत कर दिया था, और इसे "खामियों से मुक्त" के रूप में प्रचारित किया गया था; इस प्रयोग ने निश्चितता के साथ स्थानीय यथार्थवाद सिद्धांतों के एक बड़े वर्ग को खारिज कर दिया।[20] पहलू लिखते हैं कि "... कोई भी प्रयोग ... पूरी तरह से खामियों से मुक्त नहीं कहा जा सकता है," लेकिन उनका कहना है कि प्रयोग "अंतिम संदेह को दूर करते हैं कि हमें स्थानीय छिपे हुए चर को त्याग देना चाहिए", और शेष खामियों के उदाहरणों को संदर्भित करता है "दूर की कौड़ी" होना और "भौतिकी में तर्क करने का सामान्य तरीका विदेशी होना।"[21]
बेल के काम ने संचार के लिए एक संसाधन के रूप में इन सुपर-मजबूत सहसंबंधों का उपयोग करने की संभावना बढ़ा दी। इसके कारण 1984 में चार्ल्स एच. बेनेट (कंप्यूटर वैज्ञानिक) द्वारा क्वांटम कुंजी वितरण प्रोटोकॉल, सबसे प्रसिद्ध बीबी84 की खोज हुई|चार्ल्स एच. बेनेट और गाइल्स ब्रासार्ड[22] और आर्थर एकर्ट द्वारा E91 प्रोटोकॉल।[23] चूंकि बीबी84 उलझाव का उपयोग नहीं करता है, एकर्ट का प्रोटोकॉल सुरक्षा के प्रमाण के रूप में बेल की असमानता के उल्लंघन का उपयोग करता है।
2022 में, भौतिकी में नोबेल पुरस्कार एस्पेक्ट, क्लॉसर और एंटोन ज़िलिंगर को "उलझे हुए फोटॉन के साथ प्रयोगों, बेल असमानताओं के उल्लंघन की स्थापना और क्वांटम सूचना विज्ञान में अग्रणी" के लिए प्रदान किया गया था।[24]
संकल्पना
उलझाव का अर्थ
एक उलझी हुई प्रणाली को उस प्रणाली के रूप में परिभाषित किया जाता है जिसकी क्वांटम स्थिति को उसके स्थानीय घटकों की स्थिति के उत्पाद के रूप में नहीं माना जा सकता है; कहने का तात्पर्य यह है कि, वे अलग-अलग कण नहीं हैं बल्कि एक अविभाज्य संपूर्ण हैं। उलझाव में, एक घटक को दूसरे पर विचार किए बिना पूरी तरह से वर्णित नहीं किया जा सकता है। एक समग्र प्रणाली की स्थिति सदैव स्थानीय घटकों के स्थितिों के उत्पादों के योग या जितना कि सुपरइम्पोज़िशन के रूप में व्यक्त की जाती है; यह उलझा हुआ है यदि इस राशि को एकल उत्पाद पद के रूप में नहीं लिखा जा सकता है।
क्वांटम भौतिक प्रणाली विभिन्न प्रकार की अंतःक्रियाओं के माध्यम से उलझ सकती है। प्रयोगात्मक उद्देश्यों के लिए उलझाव को किन विधियों से प्राप्त किया जा सकता है, इसके लिए नीचे दिए गए तरीकों पर अनुभाग देखें। उलझाव तब टूटता है जब उलझे हुए कण पर्यावरण के साथ संपर्क के माध्यम से क्वांटम विघटन करते हैं; उदाहरण के लिए, जब माप किया जाता है।[25]
उलझाव के उदाहरण के रूप में: एक उपपरमाण्विक कण कण अन्य कणों की उलझी हुई जोड़ी में क्षय हो जाता है। क्षय की घटनाएँ विभिन्न संरक्षण नियमो का पालन करती हैं, और परिणामस्वरूप, एक बेटी कण के माप परिणामों को दूसरे बेटी कण के माप परिणामों के साथ अत्यधिक सहसंबद्ध होना चाहिए (जिससे कि कुल संवेग, कोणीय संवेग, ऊर्जा और इस प्रक्रिया से पहले और पश्चात में लगभग समान रहे)। उदाहरण के लिए, एक स्पिन-शून्य कण स्पिन-1/2 कणों की एक जोड़ी में क्षय हो सकता है। चूँकि इस क्षय से पहले और पश्चात में कुल स्पिन शून्य (कोणीय गति का संरक्षण) होना चाहिए, जब भी पहले कण को किसी अक्ष पर ऊपर की ओर घूमते हुए मापा जाता है, तो दूसरा, जब उसी अक्ष पर मापा जाता है, तो सदैव नीचे की ओर घूमता हुआ पाया जाता है। (इसे स्पिन विरोधी सहसंबद्ध मामला कहा जाता है; और यदि प्रत्येक स्पिन को मापने की पूर्व संभावनाएं बराबर हैं, तो जोड़ी को एकल अवस्था में कहा जाता है।)
उपरोक्त परिणाम आश्चर्यजनक हो भी सकता है और नहीं भी। एक शास्त्रीय प्रणाली समान संपत्ति प्रदर्शित करेगी, और ऐसा करने के लिए निश्चित रूप से एक छिपे हुए चर सिद्धांत की आवश्यकता होगी, जो शास्त्रीय और क्वांटम यांत्रिकी में समान रूप से कोणीय गति के संरक्षण पर आधारित होगा। अंतर यह है कि एक शास्त्रीय प्रणाली में सभी अवलोकन योग्य वस्तुओं के लिए निश्चित मान होते हैं, जबकि क्वांटम प्रणाली में ऐसा नहीं होता है। नीचे चर्चा की जाने वाली अर्थ में, यहां माना गया क्वांटम प्रणाली पहले कण के माप पर दूसरे कण के किसी भी अक्ष के साथ स्पिन के माप के परिणाम के लिए संभाव्यता वितरण प्राप्त करता प्रतीत होता है। यह संभाव्यता वितरण सामान्यतः पहले कण के माप के बिना जो होगा उससे भिन्न है। स्थानिक रूप से अलग-अलग उलझे हुए कणों के स्थितियों में इसे निश्चित रूप से आश्चर्यजनक माना जा सकता है।
विरोधाभास
विरोधाभास यह है कि किसी भी कण पर किया गया माप स्पष्ट रूप से पूरे उलझे हुए प्रणाली की स्थिति को ध्वस्त कर देता है - और ऐसा तुरंत होता है, इससे पहले कि माप परिणाम के बारे में कोई भी जानकारी दूसरे कण को संप्रेषित की जा सके (यह मानते हुए कि जानकारी प्रकाश से तेज गति से यात्रा नहीं कर सकती है) और इसलिए उलझे हुए जोड़े के दूसरे भाग के माप के उचित परिणाम का आश्वासन दिया गया है। कोपेनहेगन व्याख्या में, कणों में से एक पर स्पिन माप का परिणाम एक ऐसी स्थिति में पतन (तरंग फ़ंक्शन का) होता है। जिसमें प्रत्येक कण में माप की धुरी के साथ एक निश्चित स्पिन (या तो ऊपर या नीचे) होता है। परिणाम को यादृच्छिक माना जाता है, प्रत्येक संभावना की संभावना 50% होती है। चूंकि, यदि दोनों स्पिनों को एक ही अक्ष पर मापा जाता है, तो वे सहसंबद्ध विरोधी पाए जाते हैं। इसका तात्पर्य यह है कि एक कण पर किए गए माप का यादृच्छिक परिणाम दूसरे को प्रेषित किया गया लगता है, जिससे कि जब इसे भी मापा जाए तो वह सही विकल्प चुन सके।[26]
माप की दूरी और समय को चुना जा सकता है जिससे कि दो मापों के बीच के अंतराल को अंतरिक्षीय बनाया जा सके, इसलिए, घटनाओं को जोड़ने वाले किसी भी कारण प्रभाव को प्रकाश की समानता में तेजी से यात्रा करनी होगी। विशेष सापेक्षता के सिद्धांतों के अनुसार, किसी भी जानकारी के लिए ऐसी दो मापने वाली घटनाओं के बीच यात्रा करना संभव नहीं है। यह कहना भी संभव नहीं है कि इनमें से कौन सा माप पहले आया। दो अंतरिक्षीय पृथक घटनाओं के लिए x1 और x2 जिसमें जड़त्वीय ढाँचे होते हैं x1 प्रथम है तथा अन्य जिसमें x2 प्रथम है। इसलिए, दो मापों के बीच सहसंबंध को इस प्रकार नहीं समझाया जा सकता है कि एक माप दूसरे को निर्धारित करता है: विभिन्न पर्यवेक्षक कारण और प्रभाव की भूमिका के बारे में असहमत होंगे।
(वास्तव में समान विरोधाभास उलझाव के बिना भी उत्पन्न हो सकते हैं: एक कण की स्थिति अंतरिक्ष में फैली हुई है, और दो अलग-अलग स्थानों में कण का पता लगाने का प्रयास करने वाले दो व्यापक रूप से अलग-अलग संसूचकों को तत्काल उचित सहसंबंध प्राप्त करना होगा, जिससे कि वे दोनों का पता न लगा सकें कण।)
छिपे हुए चर सिद्धांत
विरोधाभास का एक संभावित समाधान यह मान लेना है कि क्वांटम सिद्धांत अधूरा है, और माप का परिणाम पूर्व निर्धारित छिपे हुए चर पर निर्भर करता है।[27] मापे जा रहे कणों की स्थिति में कुछ छिपे हुए-परिवर्तनीय सिद्धांत सम्मलित हैं, जिनके मान पृथक्करण के क्षण से ही प्रभावी ढंग से निर्धारित करते हैं कि स्पिन माप के परिणाम क्या होंगे। इसका तात्पर्य यह होगा कि प्रत्येक कण अपने साथ सभी आवश्यक जानकारी रखता है, और माप के समय एक कण से दूसरे तक कुछ भी प्रसारित करने की आवश्यकता नहीं होती है। आइंस्टीन और अन्य (पिछला भाग देखें) मूल रूप से मानते थे कि यह विरोधाभास से बाहर निकलने का एकमात्र तरीका था, और स्वीकृत क्वांटम यांत्रिक विवरण (यादृच्छिक माप परिणाम के साथ) अधूरा होना चाहिए।
बेल की असमानता का उल्लंघन
चूंकि, स्थानीय छिपा-चर सिद्धांत विफल हो जाता है, जब विभिन्न अक्षों के साथ उलझे हुए कणों के स्पिन के माप पर विचार किया जाता है। यदि ऐसे मापों के जोड़े बड़ी संख्या में बनाए जाते हैं (उलझे हुए कणों के जोड़े की बड़ी संख्या पर), तो सांख्यिकीय रूप से, यदि स्थानीय यथार्थवाद या छिपे हुए चर दृश्य सही थे, तो परिणाम सदैव बेल की असमानता को संतुष्ट करेंगे। बेल परीक्षण प्रयोगों ने व्यवहार में दिखाया है कि बेल की असमानता संतुष्ट नहीं है। चूंकि, 2015 से पहले, इन सभी में खामियों की समस्याएँ थीं जिन्हें भौतिकविदों के समुदाय द्वारा सबसे महत्वपूर्ण माना जाता था।[28][29] जब उलझे हुए कणों का माप गतिमान विशेष सापेक्षता संदर्भ फ्रेम में किया जाता है, जिसमें प्रत्येक माप (अपने स्वयं के सापेक्ष समय सीमा में) दूसरे से पहले होता है, तो माप परिणाम सहसंबद्ध रहते हैं।[30][31]
विभिन्न अक्षों के साथ स्पिन को मापने के बारे में मूल मुद्दा यह है कि इन मापों में एक ही समय में निश्चित मान नहीं हो सकते हैं - वे इस अर्थ में असंगत अवलोकन योग्य हैं कि इन मापों की अधिकतम एक साथ सटीकता अनिश्चितता सिद्धांत द्वारा बाधित है। यह शास्त्रीय भौतिकी में पाए जाने वाले के विपरीत है, जहां किसी भी संख्या में गुणों को मनमानी सटीकता के साथ एक साथ मापा जा सकता है। यह गणितीय रूप से सिद्ध हो चुका है कि संगत माप बेल-असमानता-उल्लंघन सहसंबंध नहीं दिखा सकते हैं,[32] और इस प्रकार उलझाव एक मौलिक रूप से गैर-शास्त्रीय घटना है।
क्वांटम उलझाव को सिद्ध करना करने वाले उल्लेखनीय प्रयोगात्मक परिणाम
पहला प्रयोग जिसने दूरी (उलझाव) पर आइंस्टीन की डरावनी कार्रवाई को सत्यापित किया था, उसे 1949 में चिएन-शिउंग वू और सहयोगी आई. शाकनोव द्वारा एक प्रयोगशाला में सफलतापूर्वक पुष्टि की गई थी, और 1950 में नए साल के दिन प्रकाशित किया गया था। परिणाम ने विशेष रूप से क्वांटम सहसंबंधों को सिद्ध करना किया फोटॉनों की एक जोड़ी का.[33] 2012 और 2013 में प्रयोगों में, उन फोटॉनों के बीच ध्रुवीकरण सहसंबंध बनाया गया था जो समय में कभी सह-अस्तित्व में नहीं थे।[34][35] लेखकों ने दावा किया कि यह परिणाम प्रारंभिक जोड़ी के एक फोटॉन के ध्रुवीकरण को मापने के पश्चात उलझे हुए फोटॉन के दो जोड़े के बीच क्वांटम टेलीपोर्टेशन एंटैंगलमेंट स्वैपिंग द्वारा प्राप्त किया गया था, और यह सिद्ध करना करता है कि क्वांटम गैर-स्थानीयता न केवल अंतरिक्ष पर बल्कि समय पर भी क्रियान्वित होती है।
2013 में तीन स्वतंत्र प्रयोगों में, यह दिखाया गया कि शास्त्रीय भौतिकी की पृथक्करणीय अवस्था का उपयोग उलझी हुई अवस्थाओं को ले जाने के लिए किया जा सकता है।[36] पहला लूपहोल-मुक्त बेल परीक्षण 2015 में डेल्फ़्ट प्रौद्योगिकी विश्वविद्यालय के रोनाल्ड हैन्सन द्वारा आयोजित किया गया था, जिसमें बेल असमानता के उल्लंघन की पुष्टि की गई थी।[37]
अगस्त 2014 में, ब्राज़ीलियाई शोधकर्ता गैब्रिएला बैरेटो लेमोस और टीम फोटॉनों का उपयोग करके उन वस्तुओं की तस्वीरें लेने में सक्षम थीं, जिन्होंने विषयों के साथ बातचीत नहीं की थी, लेकिन उन फोटॉनों से उलझ गए थे जो ऐसी वस्तुओं के साथ बातचीत करते थे। वियना विश्वविद्यालय के लेमोस को विश्वास है कि इस नई क्वांटम इमेजिंग तकनीक का उपयोग जैविक या चिकित्सा इमेजिंग जैसे क्षेत्रों में किया जा सकता है, जहां कम रोशनी में इमेजिंग अनिवार्य है।[38]
2016 के पश्चात से, विभिन्न कंपनियों, उदाहरण के लिए आईबीएम और माइक्रोसॉफ्ट, ने क्वांटम कंप्यूटर बनाए हैं जो डेवलपर्स और तकनीकी उत्साही लोगों को क्वांटम उलझाव सहित क्वांटम यांत्रिकी की अवधारणाओं के साथ स्वतंत्र रूप से प्रयोग करने की अनुमति देते हैं।[39]
समय का रहस्य
समय की अवधारणा को एक उभरती हुई घटना के रूप में देखने के सुझाव दिए गए हैं जो क्वांटम उलझाव का एक दुष्प्रभाव है।[40][41]
दूसरे शब्दों में, समय एक उलझी हुई घटना है, जो सभी समान घड़ी रीडिंग (सही ढंग से तैयार की गई घड़ियों, या घड़ियों के रूप में उपयोग करने योग्य किसी भी वस्तु) को एक ही इतिहास में रखती है। यह पहली बार 1983 में डॉन पेज (भौतिक विज्ञानी) और विलियम वूटर्स द्वारा पूरी तरह से सिद्धांतित किया गया था।[42]
व्हीलर-डेविट समीकरण जो सामान्य सापेक्षता और क्वांटम यांत्रिकी को जोड़ता है - समय को पूरी तरह से छोड़कर - 1960 के दशक में पेश किया गया था और इसे 1983 में फिर से लिया गया था, जब पेज और वूटर्स ने क्वांटम उलझाव के आधार पर एक समाधान बनाया था। पेज और वूटर्स ने तर्क दिया कि समय को मापने के लिए एन्टैंगलमेंट का उपयोग किया जा सकता है।[43]
आकस्मिक गुरुत्व
एडीएस/सीएफटी पत्राचार के आधार पर, मार्क वान रैम्स्डोंक ने सुझाव दिया कि अंतरिक्ष समय स्वतंत्रता की क्वांटम डिग्री की एक उभरती हुई घटना के रूप में उभरता है जो उलझे हुए हैं और स्पेस-टाइम की सीमा में रहते हैं।[44] प्रेरित गुरुत्वाकर्षण उलझाव के पहले नियम से उभर सकता है[45][46]
गैर-स्थानीयता और उलझाव
मीडिया और लोकप्रिय विज्ञान में, क्वांटम गैर-स्थानीयता को अधिकांशतः उलझाव के बराबर चित्रित किया जाता है। चूंकि यह शुद्ध द्विदलीय क्वांटम अवस्थाओं के लिए सच है, सामान्यतः उलझाव केवल गैर-स्थानीय सहसंबंधों के लिए आवश्यक है, लेकिन मिश्रित उलझी हुई स्थितियाँ उपस्थित हैं जो ऐसे सहसंबंध उत्पन्न नहीं करती हैं।[47] एक प्रसिद्ध उदाहरण वर्नर स्थिति है जो कुछ निश्चित मूल्यों के लिए उलझे हुए हैं , लेकिन सदैव स्थानीय छिपे हुए चर का उपयोग करके वर्णित किया जा सकता है।[48] इसके अतिरिक्त, यह दिखाया गया कि, कणों की मनमानी संख्या के लिए, ऐसे स्थिति उपस्थित हैं जो वास्तव में उलझे हुए हैं लेकिन एक स्थानीय मॉडल को स्वीकार करते हैं।[49]
स्थानीय मॉडलों के अस्तित्व के बारे में उल्लिखित प्रमाण यह मानते हैं कि एक समय में क्वांटम स्थिति की केवल एक प्रति उपलब्ध है। यदि कणों को ऐसे स्थितिों की कई प्रतियों पर स्थानीय माप करने की अनुमति दी जाती है, तो कई स्पष्ट रूप से स्थानीय स्थितिों (उदाहरण के लिए, क्वबिट वर्नर स्थिति) को अब स्थानीय मॉडल द्वारा वर्णित नहीं किया जा सकता है। यह, विशेष रूप से, सभी उलझाव आसवन स्थितिों के लिए सच है। चूंकि, यह एक विवृत प्रश्न बना हुआ है कि क्या पर्याप्त संख्या में प्रतियाँ दिए जाने पर सभी उलझे हुए स्थिति गैर-स्थानीय हो जाते हैं।[50]
संक्षेप में, दो कणों द्वारा साझा की गई अवस्था का उलझना आवश्यक है लेकिन उस अवस्था के गैर-स्थानीय होने के लिए पर्याप्त नहीं है। यह पहचानना महत्वपूर्ण है कि उलझाव को सामान्यतः एक बीजगणितीय अवधारणा के रूप में देखा जाता है, जो गैर-स्थानीयता के साथ-साथ क्वांटम टेलीपोर्टेशन और सुपरडेंस कोडिंग के लिए एक शर्त के रूप में जाना जाता है, जबकि गैर-स्थानीयता को प्रयोगात्मक आंकड़ों के अनुसार परिभाषित किया गया है और यह बहुत अधिक है क्वांटम नींव और क्वांटम यांत्रिकी की व्याख्याओं से जुड़े।[51]
क्वांटम यांत्रिक ढांचा
निम्नलिखित उपखंड उन लोगों के लिए हैं जिनके पास क्वांटम यांत्रिकी के औपचारिक, गणितीय विवरण का अच्छा कार्यसाधक ज्ञान है, जिसमें लेखों में विकसित औपचारिकता और सैद्धांतिक ढांचे से परिचित होना सम्मलित है: ब्रा-केट नोटेशन और क्वांटम यांत्रिकी का गणितीय सूत्रीकरण।
शुद्ध अवस्थाएँ
दो स्वेच्छाचारिता क्वांटम प्रणालियों पर विचार करें A और B, संबंधित हिल्बर्ट रिक्त स्थान के साथ HA और HB. मिश्रित प्रणाली का हिल्बर्ट स्थान टेंसर उत्पाद है
यदि पहली प्रणाली स्थिति में है और स्थिति में दूसरा , समग्र प्रणाली की स्थिति है
समग्र प्रणाली के जिन स्थितिों को इस रूप में दर्शाया जा सकता है उन्हें वियोज्य स्थिति या उत्पाद स्थिति कहा जाता है।
सभी स्थिति अलग-अलग स्थिति नहीं हैं (और इस प्रकार उत्पाद स्थिति भी हैं)। एक आधार तय करें (रैखिक बीजगणित) के लिए HA और एक आधार के लिए HB. में सबसे सामान्य अवस्था HA ⊗ HB रूप का है
- .
यदि सदिश उपस्थित हैं तो यह स्थिति अलग की जा सकती है जिससे कि उपज और यदि किसी सदिश के लिए यह अविभाज्य है कम से कम निर्देशांक की एक जोड़ी के लिए अपने पास यदि कोई स्थिति अविभाज्य है, तो उसे 'उलझा हुआ स्थिति' कहा जाता है।
उदाहरण के लिए, दो आधार सदिश दिए गए हैं का HA और दो आधार सदिश का HB, निम्नलिखित एक उलझी हुई स्थिति है:
यदि समग्र प्रणाली इस स्थिति में है, तो किसी भी प्रणाली का श्रेय देना असंभव है A या प्रणाली B एक निश्चित शुद्ध अवस्था। इसे कहने का दूसरा विधि यह है कि जबकि पूरे स्थिति की वॉन न्यूमैन एन्ट्रापी शून्य है (जैसा कि यह किसी भी शुद्ध स्थिति के लिए है), उप-प्रणालियों की एन्ट्रॉपी शून्य से अधिक है। इस अर्थ में, प्रणालियाँ उलझी हुई हैं। इंटरफेरोमेट्री के लिए इसके विशिष्ट अनुभवजन्य प्रभाव हैं।[52] उपरोक्त उदाहरण चार बेल अवस्थाओं में से एक है, जो (अधिकतम) उलझी हुई शुद्ध अवस्थाएँ हैं HA ⊗ HB स्थान, लेकिन जिसे प्रत्येक की शुद्ध अवस्था में अलग नहीं किया जा सकता HA और HB).
अब मान लीजिए कि ऐलिस प्रणाली का पर्यवेक्षक है A, और बॉब प्रणाली के लिए एक पर्यवेक्षक है B. यदि ऊपर दी गई उलझी हुई अवस्था में ऐलिस एक माप करती है का अपना आधार A, समान संभावना के साथ घटित होने वाले दो संभावित परिणाम हैं:[53]
- ऐलिस का माप 0 है, और प्रणाली की स्थिति ढह जाती है .
- ऐलिस का माप 1 है, और प्रणाली की स्थिति ढह जाती है .
यदि पूर्व घटित होता है, तो उसी आधार पर बॉब द्वारा किया गया कोई भी पश्चात का माप सदैव 1 लौटाएगा। यदि पश्चात वाला घटित होता है, (ऐलिस माप 1) तो बॉब का माप निश्चितता के साथ 0 लौटाएगा। इस प्रकार, प्रणाली {{मावर|बी} ऐलिस द्वारा प्रणाली पर स्थानीय माप निष्पादित करके } को बदल दिया गया है A. यह तब भी सत्य रहता है, जब प्रणाली A और B स्थानिक रूप से अलग हो गए हैं। यह ईपीआर विरोधाभास की नींव है।
ऐलिस के माप का परिणाम यादृच्छिक है। ऐलिस यह तय नहीं कर सकती कि समग्र प्रणाली को किस स्थिति में ढहाया जाए, और इसलिए वह अपने प्रणाली पर कार्य करके बॉब को जानकारी प्रसारित नहीं कर सकती है। इस विशेष योजना में कार्य-कारण को इस प्रकार संरक्षित किया जाता है। सामान्य तर्क के लिए, नो-कम्युनिकेशन प्रमेय देखें।
पहनावा
जैसा कि ऊपर बताया गया है, क्वांटम प्रणाली की स्थिति हिल्बर्ट स्पेस में एक यूनिट सदिश द्वारा दी जाती है। सामान्यतः, यदि किसी के पास प्रणाली के बारे में कम जानकारी है, तो वह इसे 'एसेम्बल' कहता है और इसे घनत्व आव्यूह द्वारा वर्णित करता है, जो एक सकारात्मक-अर्ध-निश्चित आव्यूह है, या एक ट्रेस क्लास है जब स्थिति स्थान अनंत-आयामी होता है, और इसमें ट्रेस 1 है। फिर से, वर्णक्रमीय प्रमेय द्वारा, ऐसा आव्यूह सामान्य रूप लेता है:
जहां डब्ल्यूi सकारात्मक-मूल्यवान संभावनाएं हैं (उनका योग 1 तक होता है), सदिश αi यूनिट सदिश हैं, और अनंत-आयामी स्थिति में, हम ट्रेस मानदंड में ऐसे स्थितिों को संवृत कर देंगे। हम व्याख्या कर सकते हैं ρ एक समूह का प्रतिनिधित्व करने के रूप में जहां उस समूह का अनुपात है जिसके स्थिति हैं . जब किसी मिश्रित स्थिति की रैंक 1 होती है, तो यह एक 'शुद्ध पहनावा' का वर्णन करता है। जब किसी क्वांटम प्रणाली की स्थिति के बारे में कुल जानकारी से कम होती है तो हमें स्थिति का प्रतिनिधित्व करने के लिए #कम घनत्व आव्यूह की आवश्यकता होती है।
प्रायोगिक तौर पर, एक मिश्रित संयोजन को निम्नानुसार साकार किया जा सकता है। एक ब्लैक बॉक्स उपकरण पर विचार करें जो प्रेक्षक की ओर इलेक्ट्रॉन फेंकता है। इलेक्ट्रॉनों के हिल्बर्ट स्थान समान कण हैं। उपकरण ऐसे इलेक्ट्रॉन उत्पन्न कर सकता है जो सभी एक ही अवस्था में हों; इस स्थिति में, प्रेक्षक द्वारा प्राप्त इलेक्ट्रॉन एक शुद्ध समूह होते हैं। चूंकि, उपकरण विभिन्न अवस्थाओं में इलेक्ट्रॉन उत्पन्न कर सकता है। उदाहरण के लिए, यह इलेक्ट्रॉनों की दो आपश्चाती उत्पन्न कर सकता है: एक अवस्था के साथ स्पिन (भौतिकी) के साथ सकारात्मक में संरेखित zदिशा के साथ, और दूसरा स्थिति के साथ स्पिन के साथ नकारात्मक में संरेखित y दिशा। सामान्यतः, यह एक मिश्रित समूह है, क्योंकि इसमें किसी भी संख्या में आपश्चाती हो सकती है, प्रत्येक एक अलग स्थिति के अनुरूप है।
उपरोक्त परिभाषा के अनुसार, एक द्विदलीय समग्र प्रणाली के लिए, मिश्रित अवस्थाएँ केवल घनत्व आव्यूह हैं HA ⊗ HB. अर्थात् इसका सामान्य स्वरूप है
जहां डब्ल्यूi सकारात्मक रूप से मूल्यवान संभावनाएँ हैं, , और सदिश इकाई सदिश हैं। यह स्व-संयुक्त और सकारात्मक है और इसमें ट्रेस 1 है।
शुद्ध स्थितियों से पृथक्करण की परिभाषा का विस्तार करते हुए, हम कहते हैं कि एक मिश्रित अवस्था पृथक्करणीय है यदि इसे इस प्रकार लिखा जा सकता है[54]: 131–132
जहां wi सकारात्मक रूप से मूल्यवान संभावनाएं हैं और 'रेत उपप्रणालियों पर स्वयं मिश्रित अवस्थाएँ (घनत्व संचालक) हैं A और B क्रमश। दूसरे शब्दों में, एक स्थिति को अलग किया जा सकता है यदि यह असंबद्ध स्थिति, या उत्पाद स्थितिों पर संभाव्यता वितरण है। घनत्व आव्यूह को शुद्ध समुच्चय और विस्तार के योग के रूप में लिखकर, हम व्यापकता के नुकसान के बिना यह मान सकते हैं और वे स्वयं शुद्ध समूह हैं। एक स्थितियों को तब उलझा हुआ कहा जाता है यदि वह अलग करने योग्य नहीं है।
सामान्यतः, यह पता लगाना मुश्किल माना जाता है कि मिश्रित स्थिति उलझी हुई है या नहीं। सामान्य द्विपक्षीय स्थितियों को एनपी कठिन दिखाया गया है।[55] के लिए 2 × 2 और 2 × 3 स्थितियों में, पृथक्करण के लिए एक आवश्यक और पर्याप्त मानदंड प्रसिद्ध पेरेस-होरोडेकी मानदंड|पॉजिटिव आंशिक ट्रांसपोज़ (पीपीटी) स्थिति द्वारा दिया गया है।[56]
कम घनत्व आव्यूह
कम घनत्व आव्यूह का विचार 1930 में पॉल डिराक द्वारा पेश किया गया था।[57] उपरोक्त प्रणालियों पर विचार करें A और B प्रत्येक हिल्बर्ट स्थान के साथ HA, HB. समग्र व्यवस्था की स्थिति रहने दीजिए
जैसा कि ऊपर बताया गया है, सामान्यतः शुद्ध अवस्था को घटक प्रणाली से जोड़ने का कोई उपाए नहीं है A. चूंकि, घनत्व आव्यूह को संबद्ध करना अभी भी संभव है।
- .
जो इस स्थिति पर प्रक्षेपण ऑपरेटर है। की स्थिति A का आंशिक निशान है ρT प्रणाली के आधार पर B:
योग खत्म हो जाता है और में पहचान ऑपरेटर . ρA को कभी-कभी कम घनत्व आव्यूह भी कहा जाता है ρ सबप्रणाली पर A. बोलचाल की भाषा में हम प्रणाली का पता लगाते हैं B कम घनत्व आव्यूह प्राप्त करने के लिए A.
उदाहरण के लिए, कम घनत्व आव्यूह A उलझी हुई अवस्था के लिए
ऊपर चर्चा की गई है
यह दर्शाता है कि, जैसा कि अपेक्षित था, एक उलझे हुए शुद्ध समूह के लिए कम घनत्व आव्यूह एक मिश्रित समूह है। यह भी आश्चर्य की बात नहीं है, का घनत्व आव्यूह Aशुद्ध उत्पाद अवस्था के लिए ऊपर चर्चा की गई है
- .
सामान्यतः, एक द्विदलीय शुद्ध अवस्था ρ उलझ जाती है यदि और केवल तभी जब इसकी कम अवस्थाओं को शुद्ध के अतिरिक्त मिश्रित किया जाता है।
दो अनुप्रयोग जो उनका उपयोग करते हैं
कम घनत्व वाले आव्यूह की गणना अद्वितीय भू स्थिति के साथ विभिन्न स्पिन श्रृंखलाओं में स्पष्ट रूप से की गई थी। एक उदाहरण एक-आयामी एकेएलटी मॉडल है:[58] भू स्थिति को एक ब्लॉक और एक पर्यावरण में विभाजित किया जा सकता है। ब्लॉक का कम घनत्व आव्यूह एक प्रोजेक्टर के लिए किसी अन्य हैमिल्टनियन की विकृत जमीनी स्थिति के लिए आनुपातिकता (गणित) है।
कम घनत्व आव्यूह का मूल्यांकन हाइजेनबर्ग मॉडल (क्वांटम) के लिए भी किया गया था, जहां इसकी पूर्ण रैंक है। यह सिद्ध करना हुआ कि थर्मोडायनामिक सीमा में, स्पिन के एक बड़े ब्लॉक के कम घनत्व आव्यूह का स्पेक्ट्रम इस स्थितियों का एक सटीक ज्यामितीय अनुक्रम है[59]
एक संसाधन के रूप में उलझाव
क्वांटम सूचना सिद्धांत में, उलझी हुई अवस्थाओं को एक 'संसाधन' माना जाता है, अर्थात, उत्पादन करने के लिए कुछ महंगा और जो मूल्यवान परिवर्तनों को क्रियान्वित करने की अनुमति देता है।[60][61] जिस समूहिंग में यह परिप्रेक्ष्य सबसे अधिक स्पष्ट है, वह दूर की प्रयोगशालाओं की है, अर्थात, ए और बी लेबल वाले दो क्वांटम प्रणाली, जिनमें से प्रत्येक पर मनमाना क्वांटम संचालन किया जा सकता है, लेकिन जो यांत्रिक रूप से एक दूसरे क्वांटम संचालन साथ बातचीत नहीं करते हैं। अनुमति दी गई एकमात्र परस्पर क्रिया शास्त्रीय जानकारी का आदान-प्रदान है, जो सबसे सामान्य स्थानीय क्वांटम संचालन के साथ मिलकर एलओसीसी (स्थानीय संचालन और शास्त्रीय संचार) नामक संचालन के वर्ग को जन्म देती है। ये संचालन प्रणाली ए और बी के बीच उलझे हुए स्थितिों के उत्पादन की अनुमति नहीं देते हैं। लेकिन यदि ए और बी को उलझे हुए स्थितिों की आपूर्ति प्रदान की जाती है, तो ये, एलओसीसी संचालन के साथ मिलकर परिवर्तनों के एक बड़े वर्ग को सक्षम कर सकते हैं। उदाहरण के लिए, A के क्वबिट और B के क्वबिट के बीच की बातचीत को पहले A के क्वबिट को B में टेलीपोर्ट करके, फिर उसे B के क्वबिट के साथ इंटरैक्ट करने की अनुमति देकर महसूस किया जा सकता है (जो अब एक एलओसीसी संचालन है, क्योंकि दोनों क्वबिट B की लैब में हैं) और फिर क्वबिट को वापस ए पर टेलीपोर्ट करना। इस प्रक्रिया में दो क्वबिट की दो अधिकतम उलझी हुई अवस्थाओं का उपयोग किया जाता है। इस प्रकार उलझे हुए स्थिति एक संसाधन हैं जो ऐसी समूहिंग में क्वांटम परस्पर क्रिया (या क्वांटम चैनल) की प्राप्ति को सक्षम बनाता है जहां केवल एलओसीसी उपलब्ध हैं, लेकिन प्रक्रिया में उनका उपभोग किया जाता है। ऐसे अन्य अनुप्रयोग हैं जहां उलझाव को एक संसाधन के रूप में देखा जा सकता है, उदाहरण के लिए, निजी संचार या क्वांटम अवस्थाओं को अलग करना।[62]
उलझाव का वर्गीकरण
सभी क्वांटम अवस्थाएँ एक संसाधन के रूप में समान रूप से मूल्यवान नहीं हैं। इस मान को निर्धारित करने के लिए, विभिन्न उलझाव उपायों (नीचे देखें) का उपयोग किया जा सकता है, जो प्रत्येक क्वांटम स्थिति के लिए एक संख्यात्मक मान निर्दिष्ट करते हैं। चूंकि, क्वांटम अवस्थाओं की समानता करने के लिए मोटे तरीके से समझौता करना अधिकांशतः मनोहर होता है। यह विभिन्न वर्गीकरण योजनाओं को जन्म देता है। अधिकांश उलझाव वर्गों को इस आधार पर परिभाषित किया जाता है कि क्या एलओसीसी या इन परिचालनों के उपवर्ग का उपयोग करके स्थितिों को अन्य स्थितिों में परिवर्तित किया जा सकता है। अनुमत परिचालनों का समूह जितना छोटा होगा, वर्गीकरण उतना ही बेहतर होगा। महत्वपूर्ण उदाहरण हैं:
- यदि दो स्थितिों को स्थानीय एकात्मक संचालन द्वारा एक दूसरे में परिवर्तित किया जा सकता है, तो उन्हें एक ही एलयू वर्ग में कहा जाता है। सामान्यतः मानी जाने वाली कक्षाओं में यह सबसे बेहतरीन है। एक ही एलयू वर्ग में दो स्थितिों में उलझाव के उपायों के लिए समान मूल्य और दूर-प्रयोगशाला समूहिंग में संसाधन के समान मूल्य होता है। विभिन्न एलयू वर्गों की अनंत संख्या है (शुद्ध अवस्था में दो क्वैबिट के सबसे सरल स्थितियों में भी)।[63][64]
- यदि दो स्थितिों को 0 से अधिक संभावना वाले माप सहित स्थानीय संचालन द्वारा एक-दूसरे में परिवर्तित किया जा सकता है, तो उन्हें एक ही 'एसएलओसीसी वर्ग' (स्टोकेस्टिक एलओसीसी) में कहा जाता है। गुणात्मक रूप से, दो अवस्थाएँ और उसी एसएलओसीसी वर्ग में समान रूप से शक्तिशाली हैं (चूंकि मैं एक को दूसरे में बदल सकता हूं और फिर वह सब कुछ कर सकता हूं जो यह मुझे करने की अनुमति देता है), लेकिन परिवर्तनों के पश्चात से और अलग-अलग संभावनाओं के साथ सफल हो सकते हैं, वे अब समान रूप से मूल्यवान नहीं हैं। उदाहरण के लिए, दो शुद्ध क्वैबिट के लिए केवल दो एसएलओसीसी वर्ग हैं: उलझी हुई अवस्थाएँ (जिसमें दोनों (अधिकतम उलझी हुई) बेल अवस्थाएँ और कमज़ोर उलझी हुई अवस्थाएँ सम्मलित हैं) ) और अलग करने योग्य वाले (अर्थात, उत्पाद की स्थिति जैसे ).[65][66]
- किसी स्थिति की एकल प्रतियों के परिवर्तनों पर विचार करने के अतिरिक्त (जैसे ) कोई बहु-प्रतिलिपि परिवर्तनों की संभावना के आधार पर कक्षाओं को परिभाषित कर सकता है। उदाहरण के लिए, ऐसे उदाहरण हैं जब एलओसीसी द्वारा असंभव है, लेकिन संभव है। एक बहुत ही महत्वपूर्ण (और बहुत मोटा) वर्गीकरण इस संपत्ति पर आधारित है कि क्या किसी स्थिति की स्वेच्छाचारिता ढंग से बड़ी संख्या में प्रतियों को बदलना संभव है कम से कम एक शुद्ध उलझी हुई अवस्था में। जिन स्थितिों में यह गुण होता है उन्हें एन्टैंगलमेंट डिस्टिलेशन कहा जाता है। ये अवस्थाएँ सबसे उपयोगी क्वांटम अवस्थाएँ हैं, क्योंकि इनमें से पर्याप्त मात्रा में होने पर, इन्हें (स्थानीय संचालन के साथ) किसी भी उलझी हुई अवस्था में बदला जा सकता है और इसलिए सभी संभावित उपयोगों की अनुमति दी जा सकती है। प्रारंभ में यह आश्चर्य की बात थी कि सभी उलझी हुई अवस्थाएँ आसुत नहीं होती हैं, जो नहीं होती हैं उन्हें 'बंधा हुआ उलझाव' कहा जाता है।[67][62]
एक अलग उलझाव वर्गीकरण इस पर आधारित है कि एक स्थिति में उपस्थित क्वांटम सहसंबंध ए और बी को क्या करने की अनुमति देते हैं: एक उलझे हुए स्थितिों के तीन उपसमूहों को अलग करता है: (1) गैर-स्थानीय राज्य, जो सहसंबंध उत्पन्न करते हैं जिन्हें स्थानीय छिपे हुए चर मॉडल द्वारा समझाया नहीं जा सकता है और इस प्रकार बेल असमानता का उल्लंघन होता है, (2) क्वांटम स्टीयरिंग में कहा गया है कि ए के लिए स्थानीय माप द्वारा बी की सशर्त कम स्थिति को इस तरह से संशोधित (संचालित) करने के लिए पर्याप्त सहसंबंध होते हैं, कि ए बी को सिद्ध करना कर सकता है कि वे जिस स्थिति में हैं स्वामित्व वास्तव में उलझा हुआ है, और अंत में (3) वे उलझी हुई स्थितियाँ जो न तो गैर-स्थानीय हैं और न ही नियंत्रित करने योग्य हैं। तीनों समूह गैर-रिक्त हैं।[68]
एंट्रॉपी
इस खंड में, मिश्रित अवस्था की एन्ट्रापी पर चर्चा की गई है और साथ ही इसे क्वांटम उलझाव के माप के रूप में कैसे देखा जा सकता है।
परिभाषा
शास्त्रीय सूचना सिद्धांत में H, शैनन एन्ट्रापी, संभाव्यता वितरण से संबंधित है, , इस अनुसार:[69]
चूँकि मिश्रित अवस्था है ρ एक समूह पर संभाव्यता वितरण है, यह स्वाभाविक रूप से वॉन न्यूमैन एन्ट्रॉपी की परिभाषा की ओर ले जाता है:
सामान्यतः, कोई गैर-बहुपद फ़ंक्शन की गणना करने के लिए बोरेल कार्यात्मक कलन का उपयोग करता है log2(ρ). यदि गैर-नकारात्मक ऑपरेटर ρ एक परिमित-आयामी हिल्बर्ट स्थान पर कार्य करता है और इसमें स्वदेशी मान हैं , log2(ρ) समान eigenvectors वाले ऑपरेटर से अधिक कुछ नहीं है, लेकिन eigenvalues . शैनन एन्ट्रापी तब है:
- .
चूँकि संभाव्यता 0 की घटना को एन्ट्रापी में योगदान नहीं देना चाहिए, और यह दिया गया है
सम्मेलन 0 log(0) = 0 अपनाया गया है. यह अनंत-आयामी स्थितियों तक भी विस्तारित है: यदि ρ में प्रक्षेपण-मूल्य माप है
गणना करते समय समान परिपाटी मान लें
एन्ट्रापी की तरह, प्रणाली में जितनी अधिक अनिश्चितता (माइक्रोस्टेट्स की संख्या) होनी चाहिए, एन्ट्रापी उतनी ही बड़ी होगी। उदाहरण के लिए, किसी भी शुद्ध अवस्था की एन्ट्रापी शून्य होती है, जो आश्चर्यजनक नहीं है क्योंकि शुद्ध अवस्था में किसी प्रणाली के बारे में कोई अनिश्चितता नहीं होती है। ऊपर चर्चा की गई उलझी हुई अवस्था की दो उप-प्रणालियों में से किसी की एन्ट्रापी है log(2) (जिसे अधिकतम एन्ट्रापी के रूप में दिखाया जा सकता है 2 × 2मिश्रित अवस्थाएँ)।
उलझाव के माप के रूप में
एन्ट्रॉपी एक उपकरण प्रदान करता है जिसका उपयोग उलझाव को मापने के लिए किया जा सकता है, चूंकि उलझाव के अन्य उपाय उपस्थित हैं।[70][71] यदि समग्र प्रणाली शुद्ध है, तो एक उपप्रणाली की एन्ट्रापी का उपयोग अन्य उपप्रणालियों के साथ उसके उलझाव की डिग्री को मापने के लिए किया जा सकता है। द्विदलीय शुद्ध अवस्थाओं के लिए, कम अवस्थाओं की वॉन न्यूमैन एन्ट्रॉपी इस अर्थ में उलझाव का अद्वितीय माप है कि यह स्थितिों के परिवार पर एकमात्र कार्य है जो उलझाव माप के लिए आवश्यक कुछ सिद्धांतों को संतुष्ट करता है।[72]
यह एक शास्त्रीय परिणाम है कि शैनन एन्ट्रॉपी अपनी अधिकतम सीमा केवल और केवल समान संभाव्यता वितरण {1/n,...,1/n} पर प्राप्त करती है। अत: द्विदलीय शुद्ध अवस्था ρ ∈ HA ⊗ HB को अधिकतम उलझी हुई स्थिति कहा जाता है यदि प्रत्येक उपप्रणाली की कम हुई स्थिति हो ρ विकर्ण आव्यूह है।
मिश्रित स्थितिों के लिए, कम वॉन न्यूमैन एन्ट्रॉपी एकमात्र उचित उलझाव उपाय नहीं है।
एक तरफ, सूचना-सैद्धांतिक परिभाषा सांख्यिकीय यांत्रिकी के अर्थ में एन्ट्रापी (सांख्यिकीय विचार) से निकटता से संबंधित है[73] (वर्तमान संदर्भ में दो परिभाषाओं की समानता करते हुए, बोल्ट्ज़मान स्थिरांक निर्धारित करने की प्रथा है k = 1). उदाहरण के लिए, बोरेल कार्यात्मक कैलकुलस के गुणों से, हम इसे किसी भी एकात्मक ऑपरेटर के लिए देखते हैं U,
दरअसल, इस संपत्ति के बिना, वॉन न्यूमैन एन्ट्रॉपी को अच्छी तरह से परिभाषित नहीं किया जाएगा।
विशेष रूप से, U प्रणाली का समय विकास ऑपरेटर हो सकता है, अर्थात,
कहाँ H प्रणाली का हैमिल्टनियन (क्वांटम यांत्रिकी) है। यहां एन्ट्रापी अपरिवर्तित है।
किसी प्रक्रिया की उत्क्रमणीयता परिणामी एन्ट्रापी परिवर्तन से जुड़ी होती है, अर्थात, एक प्रक्रिया तभी प्रतिवर्ती होती है, जब और केवल तभी, वह प्रणाली की एन्ट्रापी को अपरिवर्तनीय छोड़ देती है। इसलिए, थर्मोडायनामिक संतुलन की ओर समय के तीर का बढ़ना क्वांटम उलझाव का बढ़ता हुआ प्रसार मात्र है।[74]
यह क्वांटम सूचना सिद्धांत और ऊष्मप्रवैगिकी के बीच संबंध प्रदान करता है।
रेनी एन्ट्रॉपी का उपयोग उलझाव के माप के रूप में भी किया जा सकता है।
फिर भी, 23 जनवरी 2023 को, भौतिकविदों ने बताया कि, आख़िरकार, उलझाव हेरफेर का कोई दूसरा नियम नहीं है। शोधकर्ताओं के शब्दों में, ऊष्मागतिकी के दूसरे नियम का कोई प्रत्यक्ष समकक्ष स्थापित नहीं किया जा सकता है।[75]
उलझाव के उपाय
उलझाव के उपाय एक (अधिकांशतः द्विदलीय) क्वांटम अवस्था में उलझाव की मात्रा को मापते हैं। जैसा कि ऊपर बताया गया है, उलझाव की एन्ट्रापी शुद्ध अवस्थाओं के लिए उलझाव का मानक माप है (लेकिन अब मिश्रित अवस्थाओं के लिए उलझाव का माप नहीं है)। मिश्रित अवस्थाओं के लिए साहित्य में कुछ उलझाव के उपाय उपस्थित हैं[70]और कोई भी मानक नहीं है।
- उलझाव लागत
- उलझाव आसवन
- गठन का उलझाव
- सहमति (क्वांटम कंप्यूटिंग)
- क्वांटम सापेक्ष एन्ट्रापी
- कुचला हुआ उलझाव
- लघुगणकीय नकारात्मकता
इनमें से अधिकांश (लेकिन सभी नहीं) उलझाव के उपाय शुद्ध अवस्थाओं के लिए उलझी हुई एन्ट्रापी को कम कर देते हैं, और मिश्रित अवस्थाओं के लिए गणना करना मुश्किल (एनपी-हार्ड) होता है क्योंकि उलझी हुई प्रणाली का आयाम बढ़ता है।[76]
क्वांटम क्षेत्र सिद्धांत
क्वांटम क्षेत्र सिद्धांत के रीह-श्लीडर प्रमेय को कभी-कभी क्वांटम उलझाव के एक एनालॉग के रूप में देखा जाता है।
अनुप्रयोग
क्वांटम सूचना सिद्धांत में एंटैंगलमेंट के कई अनुप्रयोग हैं। उलझाव की सहायता से अन्यथा असंभव कार्य भी बन सकते हैं।
उलझाव के सबसे प्रसिद्ध अनुप्रयोगों में सुपरडेंस कोडिंग और क्वांटम टेलीपोर्टेशन हैं।[77]
अधिकांश शोधकर्ताओं का मानना है कि एक कंप्यूटर जितना को साकार करने के लिए उलझाव आवश्यक है (चूंकि इस पर कुछ लोगों द्वारा विवाद किया गया है)।[78]
एंटैंगलमेंट का उपयोग क्वांटम क्रिप्टोग्राफी के कुछ प्रोटोकॉल में किया जाता है,[79][80] लेकिन मानक मान्यताओं के तहत क्यूकेडी की सुरक्षा को सिद्ध करना करने के लिए उलझाव की आवश्यकता नहीं है।[81] चूंकि, क्यूकेडी की डिवाइस-स्वतंत्र क्वांटम क्रिप्टोग्राफी सुरक्षा को संचार भागीदारों के बीच उलझाव का फायदा उठाते हुए दिखाया गया है।[82]
उलझी हुई स्थितियाँ
ऐसी कई विहित उलझी हुई स्थितियाँ हैं जो अधिकांशतः सिद्धांत और प्रयोगों में दिखाई देती हैं।
दो क्विट के लिए, बेल अवस्थाएँ हैं
ये चार शुद्ध अवस्थाएँ अधिकतम रूप से उलझी हुई हैं (उलझाव की एन्ट्रापी के अनुसार) और दो क्वैबिट के हिल्बर्ट स्थान का एक ऑर्थोनॉर्मल आधार (रैखिक बीजगणित) बनाती हैं। वे बेल के प्रमेय में एक मौलिक भूमिका निभाते हैं।
M>2 क्यूबिट के लिए, ग्रीनबर्गर-हॉर्न-ज़ीलिंगर अवस्था है
जो बेल अवस्था तक कम हो जाता है के लिए . पारंपरिक GHZ स्थिति को परिभाषित किया गया था . गीगा अवस्थाओं को कभी-कभी क्यूबिट तक विस्तारित किया जाता है, अर्थात, 2 आयामों के अतिरिक्त d की प्रणाली।
इसके अतिरिक्त एम>2 क्विबिट्स के लिए, स्पिन निचोड़ना है, निचोड़े हुए सुसंगत स्थितिों का एक वर्ग जो स्पिन माप की अनिश्चितता पर कुछ प्रतिबंधों को संतुष्ट करता है, जो आवश्यक रूप से उलझे हुए हैं।[83] क्वांटम उलझाव का उपयोग करके सटीक माप को बढ़ाने के लिए स्पिन निचोड़ा हुआ स्थिति अच्छे उम्मीदवार हैं।[84]
दो बोसोनिक मोड के लिए, एक नून अवस्था है
यह बेल अवस्था की तरह है आधार केट्स 0 और 1 को छोड़कर एन फोटॉन एक मोड में हैं और एन फोटॉन दूसरे मोड में हैं।
अंत में, बोसोनिक मोड के लिए [जुड़वां फॉक स्थिति] भी उपस्थित हैं, जिन्हें एक फॉक स्थिति को दो भुजाओं में फीड करके बीम स्प्लिटर की ओर ले जाकर बनाया जा सकता है। वे नून स्थितिों के गुणकों का योग हैं, और उनका उपयोग हाइजेनबर्ग सीमा को प्राप्त करने के लिए किया जा सकता है।[85]
उलझाव के उचित रूप से चुने गए उपायों के लिए, बेल, जीएचजेड और एनओएन राज्य अधिकतम रूप से उलझे हुए हैं जबकि स्पिन निचोड़ा हुआ है और जुड़वां फॉक राज्य केवल आंशिक रूप से उलझे हुए हैं। आंशिक रूप से उलझी हुई अवस्थाओं को प्रयोगात्मक रूप से तैयार करना सामान्यतः आसान होता है।
उलझाव पैदा करने की विधियाँ
उलझाव सामान्यतः उपपरमाण्विक कणों के बीच सीधे संपर्क से बनता है। ये अंतःक्रियाएँ अनेक रूप ले सकती हैं। ध्रुवीकरण में उलझे फोटॉनों की एक जोड़ी उत्पन्न करने के लिए सबसे अधिक उपयोग की जाने वाली विधियों में से एक सहज पैरामीट्रिक डाउन-रूपांतरण है।[62][86] अन्य ढंग में फोटॉन को सीमित करने और मिश्रित करने के लिए फाइबर युग्मक का उपयोग सम्मलित है, एक क्वांटम डॉट में द्वि-एक्सिटॉन के क्षय कैस्केड से उत्सर्जित फोटॉन,[87] होंग-ओउ-मंडेल प्रभाव आदि का उपयोग। एक प्राथमिक कण और उसके एंटीपार्टिकल, जैसे कि एक इलेक्ट्रॉन और एक पोजीट्रान का क्वांटम उलझाव, हार्डी के विरोधाभास में संबंधित क्वांटम तरंग कार्यों के आंशिक ओवरलैप द्वारा बनाया जा सकता है।[88][89]
बेल के प्रमेय के प्रारंभी परीक्षणों में, उलझे हुए कण परमाणु कैस्केड का उपयोग करके उत्पन्न किए गए थे।[17]
एन्टैंगलमेंट स्वैपिंग के उपयोग के माध्यम से उन क्वांटम प्रणालियों के बीच उलझाव पैदा करना भी संभव है, जिन्होंने कभी सीधे संपर्क नहीं किया है। दो स्वतंत्र रूप से तैयार, समान कण भी उलझ सकते हैं यदि उनकी तरंग क्रियाएं केवल स्थानिक रूप से ओवरलैप होती हैं, कम से कम आंशिक रूप से।[90]
उलझाव के लिए एक प्रणाली का परीक्षण
एक घनत्व आव्यूह ρ को वियोज्य अवस्था कहा जाता है यदि इसे उत्पाद अवस्थाओं के उत्तल योग के रूप में लिखा जा सकता है, अर्थात्
2-क्यूबिट और क्यूबिट-क्यूट्रिट प्रणाली (क्रमशः 2 × 2 और 2 × 3) के लिए सरल पेरेस-होरोडेकी मानदंड पृथक्करण के लिए एक आवश्यक और पर्याप्त मानदंड दोनों प्रदान करता है, और इस प्रकार - अपरिचित में - उलझाव का पता लगाने के लिए। चूंकि, सामान्य स्थितियों के लिए, पृथक्करण के लिए मानदंड केवल एक आवश्यक है, क्योंकि सामान्यीकृत होने पर समस्या एनपी-हार्ड हो जाती है।[91][92] अन्य पृथक्करण मानदंडों में सीमा मानदंड, कमी मानदंड और अनिश्चितता संबंधों पर आधारित (लेकिन इन्हीं तक सीमित नहीं) सम्मलित हैं।[93][94][95][96] रेफरी देखें।[97] असतत-परिवर्तनीय प्रणालियों और संदर्भ में पृथक्करण मानदंड की समीक्षा के [98] असतत-परिवर्तनीय प्रणालियों में प्रयोगात्मक उलझाव प्रमाणन में तकनीकों और चुनौतियों पर समीक्षा के लिए।
समस्या के लिए एक संख्यात्मक दृष्टिकोण का सुझाव लीना में जॉन मैग्ने, जान मिरहेम और एरिक ओवरम ने अपने पेपर जियोमेट्रिकल एस्पेक्ट्स ऑफ एन्टैंगलमेंट में दिया है।[99] लीनास एट अल. एक संख्यात्मक दृष्टिकोण प्रदान करें, परीक्षण किए जाने वाले लक्ष्य स्थिति के प्रति अनुमानित अलग-अलग स्थिति को पुनरावृत्त रूप से परिष्कृत करें, और जांचें कि क्या लक्ष्य स्थिति तक वास्तव में पहुंचा जा सकता है। एल्गोरिदम का कार्यान्वयन (अंतर्निहित पेरेस-होरोडेकी मानदंड परीक्षण सहित) स्टेटसेपरेटर वेब-ऐप है।
सतत परिवर्तनशील प्रणालियों में, पेरेस-होरोडेकी मानदंड भी क्रियान्वित होता है। विशेष रूप से, साइमन[100] विहित ऑपरेटरों के दूसरे क्रम के क्षणों के संदर्भ में पेरेस-होरोडेकी मानदंड का एक विशेष संस्करण तैयार किया और दिखाया कि यह आवश्यक और पर्याप्त है -मोड गॉसियन स्थिति (संदर्भ देखें।[101] प्रतीत होता है कि भिन्न लेकिन अनिवार्य रूप से समतुल्य दृष्टिकोण के लिए)। यह पश्चात में पाया गया[102] साइमन की स्थिति भी आवश्यक और पर्याप्त है -मोड गॉसियन स्थिति, लेकिन अब इसके लिए पर्याप्त नहीं है -मोड गॉसियन स्थिति। कैनोनिकल ऑपरेटरों के उच्च क्रम के क्षणों को ध्यान में रखकर साइमन की स्थिति को सामान्यीकृत किया जा सकता है[103][104] या एन्ट्रोपिक उपायों का उपयोग करके।[105][106]
2016 में, चीन ने दुनिया का पहला क्वांटम संचार उपग्रह प्रक्षेपण किया।[107] $100m अंतरिक्ष पैमाने पर क्वांटम प्रयोग (क्यूयूईएसएस) उद्देश्य 16 अगस्त 2016 को स्थानीय समयानुसार 01:40 बजे उत्तरी चीन के जिउक्वान सैटेलाइट प्रक्षेपण सेंटर से प्रक्षेपण किया गया था।
अगले दो वर्षों के लिए, शिल्प - जिसे प्राचीन चीनी दार्शनिक के नाम पर मिकियस नाम दिया गया है - क्वांटम की व्यवहार्यता का प्रदर्शन करेगा।
पृथ्वी और अंतरिक्ष के बीच संचार, और अभूतपूर्व दूरी पर क्वांटम उलझाव का परीक्षण।
16 जून, 2017 के विज्ञान अंक में, यिन एट अल। रिपोर्ट में 1,203 किलोमीटर का एक नया क्वांटम उलझाव दूरी रिकॉर्ड स्थापित किया गया है, जो दो-फोटॉन जोड़ी के अस्तित्व को प्रदर्शित करता है और बेल असमानता का उल्लंघन करता है, सख्त आइंस्टीन इलाके की स्थितियों के तहत 2.37 ± 0.09 के सीएचएसएच मूल्यांकन तक पहुंचता है, माइकियस उपग्रह से लिजियन, युन्नान और डेलिंघा, क्विनहाई में अड्डों तक, परिमाण के क्रम से पूर्व फाइबरऑप्टिक प्रयोगों पर संचरण की दक्षता में वृद्धि।[108][109]
स्वाभाविक रूप से उलझी हुई प्रणालियाँ
बहु-इलेक्ट्रॉन परमाणुओं के इलेक्ट्रॉन कोश सदैव उलझे हुए इलेक्ट्रॉनों से बने होते हैं। सही आयनीकरण ऊर्जा केवल इलेक्ट्रॉन उलझाव पर विचार करके कॉन्फ़िगरेशन परस्पर क्रिया हो सकती है।[110]
प्रकाश संश्लेषण
यह सुझाव दिया गया है कि प्रकाश संश्लेषण की प्रक्रिया में, प्रकाश-संचयन परिसरों और प्रकाश संश्लेषक प्रतिक्रिया केंद्रों के बीच ऊर्जा के हस्तांतरण में उलझाव सम्मलित होता है, जहां प्रत्येक अवशोषित फोटॉन की फोटॉन ऊर्जा रासायनिक ऊर्जा के रूप में एकत्रित होती है। ऐसी प्रक्रिया के बिना, प्रकाश के रासायनिक ऊर्जा में कुशल रूपांतरण की व्याख्या नहीं की जा सकती है। [गुजरने स्पेक्ट्रोस्कोपी] का उपयोग करते हुए, फेना-मैथ्यूज़-ओल्सन कॉम्प्लेक्स में उलझाव की सुसंगतता को इस सिद्धांत को समर्थन प्रदान करते हुए सैकड़ों फेमटोसेकंड (इस संबंध में एक अपेक्षाकृत लंबा समय) में मापा गया था।[111][112]
चूंकि, महत्वपूर्ण अनुवर्ती अध्ययन इन परिणामों की व्याख्या पर सवाल उठाते हैं और क्रोमोफोर्स में परमाणु गतिशीलता या शारीरिक तापमान के अतिरिक्त क्रायोजेनिक पर किए जा रहे प्रयोगों के लिए इलेक्ट्रॉनिक क्वांटम सुसंगतता के रिपोर्ट किए गए हस्ताक्षरों को निर्दिष्ट करते हैं।[113][114][115][116][117][118][119]
स्थूल वस्तुओं का उलझाव
2020 में, शोधकर्ताओं ने एक गोलाकार झिल्ली के कंपन के बीच एक मिलीमीटर आकार के यांत्रिक थरथरानवाला की गति और परमाणुओं के एक पश्चातल की एक असमान दूर स्पिन (भौतिकी) प्रणाली के बीच क्वांटम उलझाव की सूचना दी।[120][121] पश्चात के कार्य ने दो यांत्रिक ऑसिलेटरों को क्वांटम-उलझाकर इस कार्य को पूरक बनाया।[122][123][124]
जीवित प्रणालियों के तत्वों का उलझाव
अक्टूबर 2018 में, भौतिकविदों ने जीवित जीवों का उपयोग करके क्वांटम उलझाव उत्पन करने की सूचना दी, विशेष रूप से जीवित जीवाणु और फोटॉन के भीतर प्रकाश संश्लेषक अणुओं के बीच।[125][126]
जीवित जीवों (हरे सल्फर बैक्टीरिया) का मध्यस्थों के रूप में अध्ययन किया गया है जो अन्यथा गैर-अंतःक्रियात्मक प्रकाश मोड के बीच क्वांटम उलझाव पैदा करते हैं, जो प्रकाश और बैक्टीरिया मोड के बीच उच्च उलझाव दिखाते हैं, और कुछ सीमा तक, बैक्टीरिया के भीतर भी उलझाव दिखाते हैं।[127]
यह भी देखें
- बंधा हुआ उलझाव
- सहमति (क्वांटम कंप्यूटिंग)
- नियंत्रित गेट नहीं
- आइंस्टीन के विचार प्रयोग
- उलझाव आसवन
- उलझाव का गवाह
- ईआर = ईपीआर
- प्रकाश से भी तेज़ संचार
- बहुपक्षीय उलझाव
- सामान्य रूप से वितरित और असंबद्ध का अर्थ स्वतंत्र नहीं है
- पाउली अपवर्जन सिद्धांत
- क्वांटम सुसंगति
- क्वांटम कम्प्यूटिंग
- क्वांटम कलह
- क्वांटम नेटवर्क
- क्वांटम चरण संक्रमण
- क्वांटम छद्म टेलीपैथी
- क्वांटम टेलीपोर्टेशन
- प्रतिकारणात्मकता
- वियोज्य अवस्था
- सहज पैरामीट्रिक डाउन-रूपांतरण
- कुचला हुआ उलझाव
- स्टर्न-गेरलाच प्रयोग
- जॉन क्लाइव वार्ड|वार्ड की संभाव्यता आयाम
संदर्भ
- ↑ Overbye, Dennis (10 October 2022). "Black Holes May Hide a Mind-Bending Secret About Our Universe - Take gravity, add quantum mechanics, stir. What do you get? Just maybe, a holographic cosmos". The New York Times. Retrieved 10 October 2022.
- ↑ 2.0 2.1 2.2 Einstein, Albert; Podolsky, Boris; Rosen, Nathan (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?". Phys. Rev. 47 (10): 777–780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777.
- ↑ 3.0 3.1 Schrödinger E (1935). "अलग-अलग प्रणालियों के बीच संभाव्यता संबंधों की चर्चा". Mathematical Proceedings of the Cambridge Philosophical Society. 31 (4): 555–563. Bibcode:1935PCPS...31..555S. doi:10.1017/S0305004100013554. S2CID 121278681.
- ↑ Schrödinger E. (1936). "अलग-अलग प्रणालियों के बीच संभाव्यता संबंध". Mathematical Proceedings of the Cambridge Philosophical Society. 32 (3): 446–452. Bibcode:1936PCPS...32..446S. doi:10.1017/S0305004100019137. S2CID 122822435.
- ↑ Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, London, 2004, p. 603.
- ↑ Griffiths, David J. (2004), Introduction to Quantum Mechanics (2nd ed.), Prentice Hall, ISBN 978-0-13-111892-8
- ↑ 7.0 7.1 Kocher, CA; Commins, ED (1967). "परमाणु कैस्केड में उत्सर्जित फोटॉनों का ध्रुवीकरण सहसंबंध". Physical Review Letters. 18 (15): 575–577. Bibcode:1967PhRvL..18..575K. doi:10.1103/PhysRevLett.18.575.
- ↑ 8.0 8.1 8.2 Carl A. Kocher, Ph.D. Thesis (University of California at Berkeley, 1967). Polarization Correlation of Photons Emitted in an Atomic Cascade
- ↑ Hensen, B.; et al. (21 October 2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. hdl:2117/79298. PMID 26503041. S2CID 205246446. See also free online access version.
- ↑ Markoff, Jack (21 October 2015). "क्षमा करें, आइंस्टीन। क्वांटम अध्ययन से पता चलता है कि 'डरावनी कार्रवाई' वास्तविक है।". The New York Times. Retrieved 21 October 2015.
- ↑ Lee, K. C.; Sprague, M. R.; Sussman, B. J.; Nunn, J.; Langford, N. K.; Jin, X.- M.; Champion, T.; Michelberger, P.; Reim, K. F.; England, D.; Jaksch, D.; Walmsley, I. A. (2 December 2011). "कमरे के तापमान पर स्थूल हीरे को उलझाना". Science. 334 (6060): 1253–1256. Bibcode:2011Sci...334.1253L. doi:10.1126/science.1211914. PMID 22144620. S2CID 206536690.
- ↑ Siegel, Ethan. "नहीं, हम अभी भी प्रकाश से भी तेज़ संचार करने के लिए क्वांटम एन्टैंगलमेंट का उपयोग नहीं कर सकते". Forbes (in English). Retrieved 6 January 2023.
- ↑ Kumar, M., Quantum, Icon Books, 2009, p. 313.
- ↑ Alisa Bokulich, Gregg Jaeger, Philosophy of Quantum Information and Entanglement, Cambridge University Press, 2010, xv.
- ↑ Letter from Einstein to Max Born, 3 March 1947; The Born-Einstein Letters; Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955, Walker, New York, 1971. (cited in M. P. Hobson; et al. (1998). "Quantum Entanglement and Communication Complexity (1998)". SIAM J. Comput. 30 (6): 1829–1841. CiteSeerX 10.1.1.20.8324.)
- ↑ J. S. Bell (1964). "आइंस्टीन-पोडॉल्स्की-रोसेन विरोधाभास पर". Physics Physique Физика. 1 (3): 195–200. doi:10.1103/PhysicsPhysiqueFizika.1.195.
- ↑ 17.0 17.1 17.2 Freedman, Stuart J.; Clauser, John F. (1972). "स्थानीय छुपे-परिवर्तनीय सिद्धांतों का प्रायोगिक परीक्षण". Physical Review Letters. 28 (14): 938–941. Bibcode:1972PhRvL..28..938F. doi:10.1103/PhysRevLett.28.938.
- ↑ Aspect, Alain; Grangier, Philippe; Roger, Gérard (1982). "Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell's Inequalities". Physical Review Letters. 49 (2): 91–94. Bibcode:1982PhRvL..49...91A. doi:10.1103/PhysRevLett.49.91.
- ↑ Kocher, CA (1971). "क्रमिक रूप से उत्सर्जित फोटॉन का पता लगाने में समय सहसंबंध". Annals of Physics. 65 (1): 1–18. Bibcode:1971AnPhy..65....1K. doi:10.1016/0003-4916(71)90159-X.
- ↑ Hanson, Ronald (2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. PMID 26503041. S2CID 205246446.
- ↑ Aspect, Alain (16 December 2015). "आइंस्टीन और बोह्र की क्वांटम बहस पर दरवाजा बंद करना". Physics. 8: 123. Bibcode:2015PhyOJ...8..123A. doi:10.1103/Physics.8.123.
- ↑ C. H. Bennett and G. Brassard. "Quantum cryptography: Public key distribution and coin tossing". In Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, volume 175, p. 8. New York, 1984. http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf Archived 30 January 2020 at the Wayback Machine
- ↑ Ekert, A.K. (1991). "बेल के प्रमेय पर आधारित क्वांटम क्रिप्टोग्राफी". Phys. Rev. Lett. 67 (6): 661–663. Bibcode:1991PhRvL..67..661E. doi:10.1103/PhysRevLett.67.661. ISSN 0031-9007. PMID 10044956. S2CID 27683254.
- ↑ "The Nobel Prize in Physics 2022". Nobel Prize (Press release). The Royal Swedish Academy of Sciences . 4 October 2022. Retrieved 5 October 2022.
- ↑ Asher Peres, Quantum Theory: Concepts and Methods, Kluwer, 1993; ISBN 0-7923-2549-4 p. 115.
- ↑ Rupert W., Anderson (28 March 2015). The Cosmic Compendium: Interstellar Travel (First ed.). The Cosmic Compendium. p. 100. ISBN 9781329022027.
- ↑ Gibney, Elizabeth (2017). "Cosmic Test Bolsters Einstein's "Spooky Action at a Distance"". Scientific American.
- ↑ I. Gerhardt; Q. Liu; A. Lamas-Linares; J. Skaar; V. Scarani; V. Makarov; C. Kurtsiefer (2011), "Experimentally faking the violation of Bell's inequalities", Phys. Rev. Lett., 107 (17): 170404, arXiv:1106.3224, Bibcode:2011PhRvL.107q0404G, doi:10.1103/PhysRevLett.107.170404, PMID 22107491, S2CID 16306493
- ↑ Santos, E (2004). "बेल की असमानता का खामियों से मुक्त परीक्षण करने में विफलता स्थानीय यथार्थवाद का समर्थन करती है". Foundations of Physics. 34 (11): 1643–1673. Bibcode:2004FoPh...34.1643S. doi:10.1007/s10701-004-1308-z. S2CID 123642560.
- ↑ H. Zbinden; et al. (2001). "सापेक्षतावादी विन्यास में गैर-स्थानीय क्वांटम सहसंबंधों का प्रायोगिक परीक्षण". Phys. Rev. A. 63 (2): 22111. arXiv:quant-ph/0007009. Bibcode:2001PhRvA..63b2111Z. doi:10.1103/PhysRevA.63.022111. S2CID 44611890.
- ↑ Some of the history of both referenced Zbinden, et al. experiments is provided in Gilder, L., The Age of Entanglement, Vintage Books, 2008, pp. 321–324.
- ↑ Cirel'son, B. S. (1980). "बेल की असमानता का क्वांटम सामान्यीकरण". Letters in Mathematical Physics. 4 (2): 93–100. Bibcode:1980LMaPh...4...93C. doi:10.1007/BF00417500. S2CID 120680226.
- ↑ Wu, C. 's.; Shaknov, I. (1950). "बिखरे हुए विनाश विकिरण का कोणीय सहसंबंध". Physical Review. 77 (1): 136. Bibcode:1950PhRv...77..136W. doi:10.1103/PhysRev.77.136.
- ↑ Xiao-song Ma; Stefan Zotter; Johannes Kofler; Rupert Ursin; Thomas Jennewein; Časlav Brukner; Anton Zeilinger (26 April 2012). "प्रायोगिक विलंबित-विकल्प उलझाव स्वैपिंग". Nature Physics. 8 (6): 480–485. arXiv:1203.4834. Bibcode:2012NatPh...8..480M. doi:10.1038/nphys2294. S2CID 119208488.
- ↑ Megidish, E.; Halevy, A.; Shacham, T.; Dvir, T.; Dovrat, L.; Eisenberg, H. S. (2013). "उन फोटॉनों के बीच उलझाव की अदला-बदली जो कभी एक साथ अस्तित्व में नहीं रहे". Physical Review Letters. 110 (21): 210403. arXiv:1209.4191. Bibcode:2013PhRvL.110u0403M. doi:10.1103/physrevlett.110.210403. PMID 23745845. S2CID 30063749.
- ↑ "शास्त्रीय वाहक उलझाव पैदा कर सकता है". physicsworld.com. 11 December 2013. Retrieved 14 June 2014.
- ↑ "Loophole-free Bell test | Ronald Hanson". Archived from the original on 4 July 2018. Retrieved 24 October 2015.
- ↑ Gibney, Elizabeth (2014). "उलझे हुए फोटॉन एक विरोधाभास से चित्र बनाते हैं". Nature. doi:10.1038/nature.2014.15781. S2CID 124976589. Retrieved 13 October 2014.
- ↑ Rozatkar, Gaurav (16 August 2018). "क्वांटम उलझाव का प्रदर्शन". OSF (in English).
- ↑ Moreva, Ekaterina (2014). "Time from quantum entanglement: an experimental illustration". Physical Review A. 89 (5): 052122. arXiv:1310.4691. Bibcode:2014PhRvA..89e2122M. doi:10.1103/PhysRevA.89.052122. S2CID 118638346.
- ↑ Aron, Jacob (25 October 2013). "Entangled toy universe shows time may be an illusion". Retrieved 8 January 2022.
- ↑ David Deutsch, The Beginning of infinity. Page 299
- ↑ "क्वांटम प्रयोग से पता चलता है कि उलझाव से समय कैसे 'उभरता' है". Medium. 23 October 2013. Retrieved 13 October 2014.
- ↑ Van Raamsdonk, Mark (19 June 2010). "क्वांटम उलझाव के साथ स्पेसटाइम का निर्माण". General Relativity and Gravitation (in English). 42 (10): 2323–2329. arXiv:1005.3035. Bibcode:2010GReGr..42.2323V. doi:10.1007/s10714-010-1034-0. ISSN 0001-7701. S2CID 189843725.
- ↑ Lee, Jae-Weon; Kim, Hyeong-Chan; Lee, Jungjai (2013). "क्वांटम जानकारी से गुरुत्वाकर्षण". Journal of the Korean Physical Society (in English). 63 (5): 1094–1098. arXiv:1001.5445. Bibcode:2013JKPS...63.1094L. doi:10.3938/jkps.63.1094. ISSN 0374-4884. S2CID 118494859.
- ↑ Swingle, Brian; Van Raamsdonk, Mark (12 May 2014). "उलझाव से गुरुत्वाकर्षण की सार्वभौमिकता". arXiv:1405.2933 [hep-th].
- ↑ Brunner, Nicolas; Cavalcanti, Daniel; Pironio, Stefano; Scarani, Valerio; Wehner, Stephanie (2014). "Bell nonlocality". Reviews of Modern Physics. 86 (2): 419–478. arXiv:1303.2849. Bibcode:2014RvMP...86..419B. doi:10.1103/RevModPhys.86.419. S2CID 119194006.
- ↑ Werner, R.F. (1989). "आइंस्टीन-पोडॉल्स्की-रोसेन सहसंबंध के साथ क्वांटम राज्य एक छिपे हुए-चर मॉडल को स्वीकार करते हैं". Physical Review A. 40 (8): 4277–4281. Bibcode:1989PhRvA..40.4277W. doi:10.1103/PhysRevA.40.4277. PMID 9902666.
- ↑ Augusiak, R.; Demianowicz, M.; Tura, J.; Acín, A. (2015). "Entanglement and nonlocality are inequivalent for any number of parties". Physical Review Letters. 115 (3): 030404. arXiv:1407.3114. Bibcode:2015PhRvL.115c0404A. doi:10.1103/PhysRevLett.115.030404. hdl:2117/78836. PMID 26230773. S2CID 29758483.
- ↑ Vértesi, Tamás; Brunner, Nicolas (2014). "Disproving the Peres conjecture by showing Bell nonlocality from bound entanglement". Nature Communications. 5 (1): 5297. arXiv:1405.4502. Bibcode:2014NatCo...5.5297V. doi:10.1038/ncomms6297. PMID 25370352. S2CID 5135148.
- ↑ In the literature "non-locality" is sometimes used to characterize concepts that differ from the non-existence of a local hidden variable model, e.g., whether states can be distinguished by local measurements and which can occur also for non-entangled states (see, e.g., Charles H. Bennett; David P. DiVincenzo; Christopher A. Fuchs; Tal Mor; Eric Rains; Peter W. Shor; John A. Smolin; William K. Wootters (1999). "Quantum nonlocality without entanglement". Phys. Rev. A. 59 (2): 1070–1091. arXiv:quant-ph/9804053. Bibcode:1999PhRvA..59.1070B. doi:10.1103/PhysRevA.59.1070. S2CID 15282650.). This non-standard use of the term is not discussed here.
- ↑ Jaeger G, Shimony A, Vaidman L (1995). "दो इंटरफेरोमेट्रिक संपूरकताएँ". Phys. Rev. 51 (1): 54–67. Bibcode:1995PhRvA..51...54J. doi:10.1103/PhysRevA.51.54. PMID 9911555.
- ↑ Nielsen, Michael A.; Chuang, Isaac L. (2000). क्वांटम संगणना और क्वांटम सूचना. Cambridge University Press. pp. 112–113. ISBN 978-0-521-63503-5.
- ↑ Laloe, Franck (2001), "Do We Really Understand Quantum Mechanics", American Journal of Physics, 69 (6): 655–701, arXiv:quant-ph/0209123, Bibcode:2001AmJPh..69..655L, doi:10.1119/1.1356698
- ↑ Gurvits L (2003). "Classical deterministic complexity of Edmonds' Problem and quantum entanglement". Proceedings of the Thirty-Fifth ACM symposium on Theory of computing - STOC '03. p. 10. arXiv:quant-ph/0303055. doi:10.1145/780542.780545. ISBN 978-1-58113-674-6. S2CID 5745067.
{{cite book}}:|journal=ignored (help) - ↑ Horodecki M, Horodecki P, Horodecki R (1996). "Separability of mixed states: necessary and sufficient conditions". Physics Letters A. 223 (1): 210. arXiv:quant-ph/9605038. Bibcode:1996PhLA..223....1H. CiteSeerX 10.1.1.252.496. doi:10.1016/S0375-9601(96)00706-2. S2CID 10580997.
- ↑ Dirac, Paul Adrien Maurice (1930). "Note on exchange phenomena in the Thomas atom" (PDF). Mathematical Proceedings of the Cambridge Philosophical Society. 26 (3): 376–385. Bibcode:1930PCPS...26..376D. doi:10.1017/S0305004100016108.
- ↑ Fan, H; Korepin V; Roychowdhury V (2004). "वैलेंस-बॉन्ड ठोस अवस्था में उलझाव". Physical Review Letters. 93 (22): 227203. arXiv:quant-ph/0406067. Bibcode:2004PhRvL..93v7203F. doi:10.1103/PhysRevLett.93.227203. PMID 15601113. S2CID 28587190.
- ↑ Franchini, F.; Its, A. R.; Korepin, V. E.; Takhtajan, L. A. (2010). "एक आयाम में XY मॉडल के स्पिन के एक बड़े ब्लॉक के घनत्व मैट्रिक्स का स्पेक्ट्रम". Quantum Information Processing. 10 (3): 325–341. arXiv:1002.2931. doi:10.1007/s11128-010-0197-7. S2CID 6683370.
- ↑ Chitambar, Eric; Gour, Gilad (2019). "Quantum resource theories". Reviews of Modern Physics. 91 (2): 025001. arXiv:1806.06107. Bibcode:2019RvMP...91b5001C. doi:10.1103/RevModPhys.91.025001. S2CID 119194947.
- ↑ Georgiev, Danko D.; Gudder, Stanley P. (2022). "Sensitivity of entanglement measures in bipartite pure quantum states". Modern Physics Letters B. 36 (22): 2250101–2250255. arXiv:2206.13180. Bibcode:2022MPLB...3650101G. doi:10.1142/S0217984922501019. S2CID 250072286.
- ↑ 62.0 62.1 62.2 Horodecki, Ryszard; Horodecki, Pawel; Horodecki, Michal; Horodecki, Karol (2009). "Quantum entanglement". Reviews of Modern Physics. 81 (2): 865–942. arXiv:quant-ph/0702225. Bibcode:2009RvMP...81..865H. doi:10.1103/RevModPhys.81.865. S2CID 59577352.
- ↑ Grassl, M.; Rötteler, M.; Beth, T. (1998). "क्वांटम-बिट सिस्टम के स्थानीय अपरिवर्तनीयों की गणना". Phys. Rev. A. 58 (3): 1833–1839. arXiv:quant-ph/9712040. Bibcode:1998PhRvA..58.1833G. doi:10.1103/PhysRevA.58.1833. S2CID 15892529.
- ↑ B. Kraus (2010). "बहुपक्षीय शुद्ध राज्यों की स्थानीय एकात्मक तुल्यता". Phys. Rev. Lett. 104 (2): 020504. arXiv:0909.5152. Bibcode:2010PhRvL.104b0504K. doi:10.1103/PhysRevLett.104.020504. PMID 20366579. S2CID 29984499.
- ↑ M. A. Nielsen (1999). "उलझाव परिवर्तनों के एक वर्ग के लिए शर्तें". Phys. Rev. Lett. 83 (2): 436. arXiv:quant-ph/9811053. Bibcode:1999PhRvL..83..436N. doi:10.1103/PhysRevLett.83.436. S2CID 17928003.
- ↑ Gour, G.; Wallach, N. R. (2013). "सभी परिमित आयामों के बहुपक्षीय उलझाव का वर्गीकरण". Phys. Rev. Lett. 111 (6): 060502. arXiv:1304.7259. Bibcode:2013PhRvL.111f0502G. doi:10.1103/PhysRevLett.111.060502. PMID 23971544. S2CID 1570745.
- ↑ Horodecki, M.; Horodecki, P.; Horodecki, R. (1998). "Mixed-state entanglement and distillation: Is there a bound entanglement in nature?". Phys. Rev. Lett. 80 (1998): 5239–5242. arXiv:quant-ph/9801069. Bibcode:1998PhRvL..80.5239H. doi:10.1103/PhysRevLett.80.5239. S2CID 111379972.
- ↑ H. M. Wiseman; S. J. Jones; A. C. Doherty (2007). "संचालन, उलझाव, गैर-स्थानीयता, और आइंस्टीन-पोडॉल्स्की-रोसेन विरोधाभास". Phys. Rev. Lett. 98 (14): 140402. arXiv:quant-ph/0612147. Bibcode:2007PhRvL..98n0402W. doi:10.1103/PhysRevLett.98.140402. PMID 17501251. S2CID 30078867.
- ↑ Cerf, Nicolas J.; Cleve, Richard. "क्वांटम त्रुटि-सुधार कोड की सूचना-सैद्धांतिक व्याख्या" (PDF).
- ↑ 70.0 70.1 Plenio, Martin B.; Virmani, Shashank (2007). "उलझाने के उपायों का परिचय". Quant. Inf. Comp. 1: 1–51. arXiv:quant-ph/0504163. Bibcode:2005quant.ph..4163P.
- ↑ Vedral, Vlatko (2002). "क्वांटम सूचना सिद्धांत में सापेक्ष एन्ट्रापी की भूमिका". Reviews of Modern Physics. 74 (1): 197–234. arXiv:quant-ph/0102094. Bibcode:2002RvMP...74..197V. doi:10.1103/RevModPhys.74.197. S2CID 6370982.
- ↑ Hill, S; Wootters, W. K. (1997). "क्वांटम बिट्स की एक जोड़ी का उलझाव". Phys. Rev. Lett. 78 (26): 5022–5025. arXiv:quant-ph/9703041. Bibcode:1997PhRvL..78.5022H. doi:10.1103/PhysRevLett.78.5022. S2CID 9173232.
- ↑ Peres, Asher (1993). Quantum Theory: Concepts and Methods. Kluwer. pp. 260–270. ISBN 0-7923-2549-4. OCLC 28854083.
- ↑ Wolchover, Natalie (25 April 2014). "नया क्वांटम सिद्धांत समय के प्रवाह को समझा सकता है". www.wired.com. Quanta Magazine. Retrieved 27 April 2014.
- ↑ Lami, Ludovico; Regula, Bartosz (23 January 2023). "आख़िरकार उलझाव में हेराफेरी का कोई दूसरा नियम नहीं". Nature Physics. 19 (2): 184–189. Bibcode:2023NatPh..19..184L. doi:10.1038/s41567-022-01873-9. S2CID 242757348. Retrieved 17 February 2023.
- ↑ Huang, Yichen (21 March 2014). "क्वांटम कलह की गणना एनपी-पूर्ण है". New Journal of Physics. 16 (3): 033027. arXiv:1305.5941. Bibcode:2014NJPh...16c3027H. doi:10.1088/1367-2630/16/3/033027. S2CID 118556793.
- ↑ Bouwmeester, Dik; Pan, Jian-Wei; Mattle, Klaus; Eibl, Manfred; Weinfurter, Harald & Zeilinger, Anton (1997). "प्रायोगिक क्वांटम टेलीपोर्टेशन" (PDF). Nature. 390 (6660): 575–579. arXiv:1901.11004. Bibcode:1997Natur.390..575B. doi:10.1038/37539. S2CID 4422887.
- ↑ Richard Jozsa; Noah Linden (2002). "क्वांटम कम्प्यूटेशनल स्पीड-अप में उलझाव की भूमिका पर". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 459 (2036): 2011–2032. arXiv:quant-ph/0201143. Bibcode:2003RSPSA.459.2011J. CiteSeerX 10.1.1.251.7637. doi:10.1098/rspa.2002.1097. S2CID 15470259.
- ↑ Ekert, Artur K. (1991). "बेल के प्रमेय पर आधारित क्वांटम क्रिप्टोग्राफी". Physical Review Letters. 67 (6): 661–663. Bibcode:1991PhRvL..67..661E. doi:10.1103/PhysRevLett.67.661. PMID 10044956. S2CID 27683254.
- ↑ Juan Yin; Yu-Huai Li; Sheng-Kai Liao; Meng Yang; Yuan Cao; Liang Zhang; Ji-Gang Ren; Wen-Qi Cai; Wei-Yue Liu; Shuang-Lin Li; Rong Shu; Yong-Mei Huang; Lei Deng; Li Li; Qiang Zhang; Nai-Le Liu; Yu-Ao Chen; Chao-Yang Lu; Xiang-Bin Wang; Feihu Xu; Jian-Yu Wang; Cheng-Zhi Peng; Artur K. Ekert; Jian-Wei Pan (2020). "Entanglement-based secure quantum cryptography over 1,120 kilometres". Nature. 582 (7813): 501–505. Bibcode:2020Natur.582..501Y. doi:10.1038/s41586-020-2401-y. PMID 32541968. S2CID 219692094.
- ↑ R. Renner; N. Gisin; B. Kraus (2005). "QKD प्रोटोकॉल के लिए एक सूचना-सैद्धांतिक सुरक्षा प्रमाण". Phys. Rev. A. 72: 012332. arXiv:quant-ph/0502064. doi:10.1103/PhysRevA.72.012332. S2CID 119052621.
- ↑ S. Pirandola; U. L. Andersen; L. Banchi; M. Berta; D. Bunandar; R. Colbeck; D. Englund; T. Gehring; C. Lupo; C. Ottaviani; J. L. Pereira; M. Razavi; J. Shamsul Shaari; M. Tomamichel; V. C. Usenko; G. Vallone; P. Villoresi; P. Wallden (2020). "क्वांटम क्रिप्टोग्राफी में प्रगति". Adv. Opt. Photon. 12 (4): 1012–1236. arXiv:1906.01645. Bibcode:2020AdOP...12.1012P. doi:10.1364/AOP.361502. S2CID 174799187.
- ↑ Kitagawa, Masahiro; Ueda, Masahito (1993). "निचोड़ा हुआ स्पिन राज्य" (PDF). Phys. Rev. A. 47 (6): 5138–5143. Bibcode:1993PhRvA..47.5138K. doi:10.1103/physreva.47.5138. hdl:11094/77656. PMID 9909547.
- ↑ Wineland, D. J.; Bollinger, J. J.; Itano, W. M.; Moore, F. L.; Heinzen, D. J. (1992). "स्पेक्ट्रोस्कोपी में स्पिन निचोड़ना और क्वांटम शोर कम करना". Phys. Rev. A. 46 (11): R6797–R6800. Bibcode:1992PhRvA..46.6797W. doi:10.1103/PhysRevA.46.R6797. PMID 9908086.
- ↑ Holland, M. J; Burnett, K (1993). "हाइजेनबर्ग सीमा पर ऑप्टिकल चरण बदलाव का इंटरफेरोमेट्रिक पता लगाना". Physical Review Letters. 71 (9): 1355–1358. Bibcode:1993PhRvL..71.1355H. doi:10.1103/PhysRevLett.71.1355. PMID 10055519.
- ↑ Shadbolt, P. J.; Verde, M. R.; Peruzzo, A.; Politi, A.; Laing, A.; Lobino, M.; Matthews, J. C. F.; Thompson, M. G.; O'Brien, J. L. (2012). "पुन: कॉन्फ़िगर करने योग्य फोटोनिक सर्किट के साथ उलझाव और मिश्रण को उत्पन्न करना, हेरफेर करना और मापना". Nature Photonics. 6 (1): 45–59. arXiv:1108.3309. Bibcode:2012NaPho...6...45S. doi:10.1038/nphoton.2011.283. S2CID 56206588.
- ↑ Akopian, N. (2006). "सेमीकंडक्टर क्वांटम डॉट्स से उलझे हुए फोटॉन जोड़े". Phys. Rev. Lett. 96 (2): 130501. arXiv:quant-ph/0509060. Bibcode:2006PhRvL..96b0501D. doi:10.1103/PhysRevLett.96.020501. PMID 16486553. S2CID 22040546.
- ↑ Hardy, Lucien (1992). "Quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories". Physical Review Letters. 68 (20): 2981–2984. Bibcode:1992PhRvL..68.2981H. doi:10.1103/PhysRevLett.68.2981. PMID 10045577.
- ↑ Georgiev, Danko; Cohen, Eliahu (2022). "Entanglement measures for two-particle quantum histories". Physical Review A. 106 (6): 062437. arXiv:2212.07502. Bibcode:2022PhRvA.106f2437G. doi:10.1103/PhysRevA.106.062437. S2CID 254685902.
- ↑ Lo Franco, Rosario; Compagno, Giuseppe (14 June 2018). "क्वांटम सूचना प्रसंस्करण के लिए एक संसाधन के रूप में प्राथमिक प्रणालियों की अविभाज्यता". Phys. Rev. Lett. 120 (24): 240403. arXiv:1712.00706. Bibcode:2018PhRvL.120x0403L. doi:10.1103/PhysRevLett.120.240403. PMID 29957003. S2CID 49562954.
- ↑ Gurvits, L., Classical deterministic complexity of Edmonds' problem and quantum entanglement, in Proceedings of the 35th ACM Symposium on Theory of Computing, ACM Press, New York, 2003.
- ↑ Sevag Gharibian (2010). "क्वांटम पृथक्करण समस्या की मजबूत एनपी-कठोरता". Quantum Information and Computation. 10 (3&4): 343–360. arXiv:0810.4507. doi:10.26421/QIC10.3-4-11. S2CID 621887.
- ↑ Hofmann, Holger F.; Takeuchi, Shigeki (22 September 2003). "उलझाव के हस्ताक्षर के रूप में स्थानीय अनिश्चितता संबंधों का उल्लंघन". Physical Review A. 68 (3): 032103. arXiv:quant-ph/0212090. Bibcode:2003PhRvA..68c2103H. doi:10.1103/PhysRevA.68.032103. S2CID 54893300.
- ↑ Gühne, Otfried (18 March 2004). "अनिश्चितता संबंधों के माध्यम से उलझाव की विशेषता". Physical Review Letters. 92 (11): 117903. arXiv:quant-ph/0306194. Bibcode:2004PhRvL..92k7903G. doi:10.1103/PhysRevLett.92.117903. PMID 15089173. S2CID 5696147.
- ↑ Gühne, Otfried; Lewenstein, Maciej (24 August 2004). "एंट्रोपिक अनिश्चितता संबंध और उलझाव". Physical Review A. 70 (2): 022316. arXiv:quant-ph/0403219. Bibcode:2004PhRvA..70b2316G. doi:10.1103/PhysRevA.70.022316. S2CID 118952931.
- ↑ Huang, Yichen (29 July 2010). "अवतल-फ़ंक्शन अनिश्चितता संबंधों के माध्यम से उलझाव मानदंड". Physical Review A. 82 (1): 012335. Bibcode:2010PhRvA..82a2335H. doi:10.1103/PhysRevA.82.012335.
- ↑ Gühne, Otfried; Tóth, Géza (2009). "उलझाव का पता लगाना". Physics Reports. 474 (1–6): 1–75. arXiv:0811.2803. Bibcode:2009PhR...474....1G. doi:10.1016/j.physrep.2009.02.004. S2CID 119288569.
- ↑ Friis, Nicolai; Vitagliano, Giuseppe; Malik, Mehul; Huber, Marcus (2019). "सिद्धांत से प्रयोग तक उलझाव प्रमाणन". Nature Reviews Physics (in English). 1: 72–87. arXiv:1906.10929. doi:10.1038/s42254-018-0003-5. ISSN 2522-5820. S2CID 125658647.
- ↑ Leinaas, Jon Magne; Myrheim, Jan; Ovrum, Eirik (2006). "उलझाव के ज्यामितीय पहलू". Physical Review A. 74 (1): 012313. arXiv:quant-ph/0605079. Bibcode:2006PhRvA..74a2313L. doi:10.1103/PhysRevA.74.012313. S2CID 119443360.
- ↑ Simon, R. (2000). "सतत परिवर्तनीय प्रणालियों के लिए पेरेस-होरोडेकी पृथक्करण मानदंड". Physical Review Letters. 84 (12): 2726–2729. arXiv:quant-ph/9909044. Bibcode:2000PhRvL..84.2726S. doi:10.1103/PhysRevLett.84.2726. PMID 11017310. S2CID 11664720.
- ↑ Duan, Lu-Ming; Giedke, G.; Cirac, J. I.; Zoller, P. (2000). "सतत परिवर्तनीय प्रणालियों के लिए अविभाज्यता मानदंड". Physical Review Letters. 84 (12): 2722–2725. arXiv:quant-ph/9908056. Bibcode:2000PhRvL..84.2722D. doi:10.1103/PhysRevLett.84.2722. PMID 11017309. S2CID 9948874.
- ↑ Werner, R. F.; Wolf, M. M. (2001). "बंधे हुए उलझे हुए गॉसियन राज्य". Physical Review Letters. 86 (16): 3658–3661. arXiv:quant-ph/0009118. Bibcode:2001PhRvL..86.3658W. doi:10.1103/PhysRevLett.86.3658. PMID 11328047. S2CID 20897950.
- ↑ Shchukin, E.; Vogel, W. (2005). "सतत द्विदलीय क्वांटम अवस्थाओं के लिए अविभाज्यता मानदंड". Physical Review Letters. 95 (23): 230502. arXiv:quant-ph/0508132. Bibcode:2005PhRvL..95w0502S. doi:10.1103/PhysRevLett.95.230502. PMID 16384285. S2CID 28595936.
- ↑ Hillery, Mark; Zubairy, M.Suhail (2006). "दो-मोड राज्यों के लिए उलझाव की स्थिति". Physical Review Letters. 96 (5): 050503. arXiv:quant-ph/0507168. Bibcode:2006PhRvL..96e0503H. doi:10.1103/PhysRevLett.96.050503. PMID 16486912. S2CID 43756465.
- ↑ Walborn, S.; Taketani, B.; Salles, A.; Toscano, F.; de Matos Filho, R. (2009). "सतत चर के लिए एंट्रोपिक एंटैंगलमेंट मानदंड". Physical Review Letters. 103 (16): 160505. arXiv:0909.0147. Bibcode:2009PhRvL.103p0505W. doi:10.1103/PhysRevLett.103.160505. PMID 19905682. S2CID 10523704.
- ↑ Yichen Huang (October 2013). "Entanglement Detection: Complexity and Shannon Entropic Criteria". IEEE Transactions on Information Theory. 59 (10): 6774–6778. doi:10.1109/TIT.2013.2257936. S2CID 7149863.
- ↑ "चीन ने दुनिया का पहला क्वांटम विज्ञान उपग्रह लॉन्च किया". physicsworld.com. 16 August 2016. Retrieved 7 December 2021.
- ↑ Yin, Juan; Cao, Yuan; Li, Yu-Huai; Liao, Sheng-Kai; Zhang, Liang; Ren, Ji-Gang; Cai, Wen-Qi; Liu, Wei-Yue; Li, Bo; Dai, Hui; Li, Guang-Bing; Lu, Qi-Ming; Gong, Yun-Hong; Xu, Yu; Li, Shuang-Lin; Li, Feng-Zhi; Yin, Ya-Yun; Jiang, Zi-Qing; Li, Ming; Jia, Jian-Jun; Ren, Ge; He, Dong; Zhou, Yi-Lin; Zhang, Xiao-Xiang; Wang, Na; Chang, Xiang; Zhu, Zhen-Cai; Liu, Nai-Le; Chen, Yu-Ao; Lu, Chao-Yang; Shu, Rong; Peng, Cheng-Zhi; Wang, Jian-Yu; Pan, Jian-Wei (2017). "Satellite-based entanglement distribution over 1200 kilometers". Science. 356 (6343): 1140–1144. arXiv:1707.01339. doi:10.1126/science.aan3211. PMID 28619937.
- ↑ "चीन के क्वांटम उपग्रह ने रिकॉर्ड दूरी पर हासिल की 'डरावनी कार्रवाई'". 14 June 2017.
- ↑ Frank Jensen: Introduction to Computational Chemistry. Wiley, 2007, ISBN 978-0-470-01187-4.
- ↑ Berkeley Lab Press Release: Untangling the Quantum Entanglement Behind Photosynthesis: Berkeley scientists shine new light on green plant secrets.
- ↑ Mohan Sarovar, Akihito Ishizaki, Graham R. Fleming, K. Birgitta Whaley: Quantum entanglement in photosynthetic light harvesting complexes. arXiv:0905.3787
- ↑ R. Tempelaar; T. L. C. Jansen; J. Knoester (2014). "एफएमओ लाइट-हार्वेस्टिंग कॉम्प्लेक्स में कंपन संबंधी धड़कनें इलेक्ट्रॉनिक सुसंगतता के साक्ष्य छिपाती हैं". J. Phys. Chem. B. 118 (45): 12865–12872. doi:10.1021/jp510074q. PMID 25321492.
- ↑ N. Christenson; H. F. Kauffmann; T. Pullerits; T. Mancal (2012). "प्रकाश संचयन परिसरों में लंबे समय तक रहने वाले सामंजस्य की उत्पत्ति". J. Phys. Chem. B. 116 (25): 7449–7454. arXiv:1201.6325. Bibcode:2012arXiv1201.6325C. doi:10.1021/jp304649c. PMC 3789255. PMID 22642682.
- ↑ A. Kolli; E. J. O’Reilly; G. D. Scholes; A. Olaya-Castro (2012). "क्रिप्टोफाइट शैवाल द्वारा सुसंगत प्रकाश संचयन में परिमाणित कंपन की मौलिक भूमिका". J. Chem. Phys. 137 (17): 174109. arXiv:1203.5056. Bibcode:2012JChPh.137q4109K. doi:10.1063/1.4764100. PMID 23145719. S2CID 20156821.
- ↑ V. Butkus; D. Zigmantas; L. Valkunas; D. Abramavicius (2012). "Vibrational vs. electronic coherences in 2D spectrum of molecular systems". Chem. Phys. Lett. 545 (30): 40–43. arXiv:1201.2753. Bibcode:2012CPL...545...40B. doi:10.1016/j.cplett.2012.07.014. S2CID 96663719.
- ↑ V. Tiwari; W. K. Peters; D. M. Jonas (2013). "सहसंबद्ध वर्णक कंपन के साथ इलेक्ट्रॉनिक अनुनाद रुद्धोष्म ढांचे के बाहर प्रकाश संश्लेषक ऊर्जा हस्तांतरण को संचालित करता है". Proc. Natl. Acad. Sci. USA. 110 (4): 1203–1208. doi:10.1073/pnas.1211157110. PMC 3557059. PMID 23267114.
- ↑ E. Thyrhaug; K. Zidek; J. Dostal; D. Bina; D. Zigmantas (2016). "Exciton Structure and Energy Transfer in the Fenna−Matthews− Olson Complex". J. Phys. Chem. Lett. 7 (9): 1653–1660. doi:10.1021/acs.jpclett.6b00534. PMID 27082631. S2CID 26355154.
- ↑ Y. Fujihashi; G. R. Fleming; A. Ishizaki (2015). "Impact of environmentally induced fluctuations on quantum mechanically mixed electronic and vibrational pigment states in photosynthetic energy transfer and 2D electronic spectra". J. Chem. Phys. 142 (21): 212403. arXiv:1505.05281. Bibcode:2015JChPh.142u2403F. doi:10.1063/1.4914302. PMID 26049423. S2CID 1082742.
- ↑ "दूर की बड़ी वस्तुओं के बीच क्वांटम उलझाव का एहसास हुआ". phys.org (in English). Retrieved 9 October 2020.
- ↑ Thomas, Rodrigo A.; Parniak, Michał; Østfeldt, Christoffer; Møller, Christoffer B.; Bærentsen, Christian; Tsaturyan, Yeghishe; Schliesser, Albert; Appel, Jürgen; Zeuthen, Emil; Polzik, Eugene S. (21 September 2020). "दूरस्थ स्थूल यांत्रिक और स्पिन प्रणालियों के बीच उलझाव". Nature Physics (in English). 17 (2): 228–233. arXiv:2003.11310. doi:10.1038/s41567-020-1031-5. ISSN 1745-2481. S2CID 214641162. Retrieved 9 October 2020.
- ↑ "कंपन करने वाले ड्रमहेड यांत्रिक रूप से क्वांटम में उलझे हुए हैं". Physics World. 17 May 2021. Retrieved 14 June 2021.
- ↑ Lépinay, Laure Mercier de; Ockeloen-Korppi, Caspar F.; Woolley, Matthew J.; Sillanpää, Mika A. (7 May 2021). "Quantum mechanics–free subsystem with mechanical oscillators". Science (in English). 372 (6542): 625–629. arXiv:2009.12902. Bibcode:2021Sci...372..625M. doi:10.1126/science.abf5389. ISSN 0036-8075. PMID 33958476. S2CID 221971015. Retrieved 14 June 2021.
- ↑ Kotler, Shlomi; Peterson, Gabriel A.; Shojaee, Ezad; Lecocq, Florent; Cicak, Katarina; Kwiatkowski, Alex; Geller, Shawn; Glancy, Scott; Knill, Emanuel; Simmonds, Raymond W.; Aumentado, José; Teufel, John D. (7 May 2021). "नियतात्मक स्थूल उलझाव का प्रत्यक्ष अवलोकन". Science (in English). 372 (6542): 622–625. arXiv:2004.05515. Bibcode:2021Sci...372..622K. doi:10.1126/science.abf2998. ISSN 0036-8075. PMID 33958475. S2CID 233872863. Retrieved 14 June 2021.
- ↑ Marletto, C.; Coles, D.M.; Farrow, T.; Vedral, V. (2018). "Entanglement between living bacteria and quantized light witnessed by Rabi splitting". Journal of Physics Communications. 2 (10): 101001. arXiv:1702.08075. Bibcode:2018JPhCo...2j1001M. doi:10.1088/2399-6528/aae224. S2CID 119236759.
- ↑ O'Callaghan, Jonathan (29 October 2018). ""Schrödinger's Bacterium" Could Be a Quantum Biology Milestone – A recent experiment may have placed living organisms in a state of quantum entanglement". Scientific American. Retrieved 29 October 2018.
- ↑ Krisnanda, T.; Marletto, C.; Vedral, V.; Paternostro, M.; Paterek, T. (2018). "प्रकाश संश्लेषक जीवों की क्वांटम विशेषताओं की जांच करना". npj Quantum Information. 4: 60. arXiv:1711.06485. Bibcode:2018npjQI...4...60K. doi:10.1038/s41534-018-0110-2.
अग्रिम पठन
- अल्बर्ट, David Z.; गैल्चेन, Rivka (2009). "क्या आइंस्टीन गलत थे?: विशेष सापेक्षता के लिए एक क्वांटम खतरा". अमेरिकी वैज्ञानिक. 300 (3): 32–39. doi:10.1038/scientificamerican0309-32. PMID 19253771.
- बेंग्टसन आई; ज़िक्ज़कोव्स्की के (2006). "क्वांटम अवस्थाओं की ज्यामिति". क्वांटम उलझाव का एक परिचय. कैंब्रिज: कैम्ब्रिज यूनिवर्सिटी प्रेस. second, revised edition (2017)
- बब, जेफरी (2019). "क्वांटम उलझाव और सूचना". स्टैनफोर्ड इनसाइक्लोपीडिया ऑफ फिलॉसफी. Stanford, California: स्टैनफोर्ड विश्वविद्यालय.
- क्रैमर जेजी (2015). क्वांटम हैंडशेक: उलझाव, गैर-स्थानीयता और लेनदेन. स्प्रिंगर वेरलाग. ISBN 978-3-319-24642-0.
{{cite book}}: Vancouver style error: name in name 1 (help) - डुआर्टे एफ.जे (2019). क्वांटम उलझाव के मूल सिद्धांत. Bristol, UK: भौतिकी संस्थान. ISBN 978-0-7503-2226-3.
{{cite book}}: Vancouver style error: punctuation in name 1 (help) - गुहने ओ, टोथ जी (2009). "Entanglement detection". भौतिकी रिपोर्ट. 474 (1–6): 1–75. arXiv:0811.2803. Bibcode:2009PhR...474....1G. doi:10.1016/j.physrep.2009.02.004. S2CID 119288569.
{{cite journal}}: Vancouver style error: name in name 1 (help) - भास्कर वी.एस., पाणिग्रही पी.के (2017). "लैग्रेंज की पहचान और वेज उत्पाद का उपयोग करके मल्टीपार्टिकल शुद्ध अवस्था उलझाव के विश्वसनीय परिमाणीकरण के लिए सामान्यीकृत सहमति उपाय". क्वांटम सूचना प्रसंस्करण. 16 (5): 118. arXiv:1607.00164. Bibcode:2017QuIP...16..118B. doi:10.1007/s11128-017-1568-0. S2CID 43754114.
{{cite journal}}: Vancouver style error: punctuation in name 1 (help) - स्वैन एसएन, भास्कर वीएस, पाणिग्रही पीके (2022). "सतत-परिवर्तनशील प्रणालियों के लिए सामान्यीकृत उलझाव माप". भौतिक. रेव्ह. ए. 105 (5): 052441. arXiv:1706.01448. Bibcode:2022PhRvA.105e2441S. doi:10.1103/PhysRevA.105.052441. S2CID 239885759.
{{cite journal}}: Vancouver style error: name in name 1 (help) - जैगर जी (2009). उलझाव, सूचना, और क्वांटम यांत्रिकी की व्याख्या. हाइडेलबर्ग: स्प्रिंगर. ISBN 978-3-540-92127-1.
{{cite book}}: Vancouver style error: name in name 1 (help) - स्टीवर्ड ई.जी (2008). क्वांटम यांत्रिकी: इसका प्रारंभिक विकास और उलझाव का मार्ग. इंपीरियल कॉलेज प्रेस. ISBN 978-1-86094-978-4.
{{cite book}}: Vancouver style error: punctuation in name 1 (help)
बाहरी संबंध
- आइंस्टीन ने ग़लत समझा, क्या आप बेहतर कर सकते हैं?
- क्वांटम उलझाव कैसे काम करता है
- साइंटिफिक अमेरिकन पत्रिका द्वारा व्याख्यात्मक वीडियो
- हैनसन लैब - लूपहोल-मुक्त बेल परीक्षण 'दूरी पर डरावना एक्शन', कोई धोखाधड़ी नहीं।
- अजीब क्वांटम उलझाव से जुड़े दो हीरे
- फोटॉन जोड़े के साथ उलझाव प्रयोग - इंटरैक्टिव
- वैज्ञानिक उलझाव की अदला-बदली की क्वांटम प्रकृति का प्रदर्शन करते हैं
- मैथपेज पर क्वांटम एन्टैंगलमेंट और बेल्स प्रमेय
- ऑडियो - कैन/गे (2009) एस्ट्रोनॉमी कास्ट एंटैंगलमेंट
- आयन ट्रैपिंग क्वांटम सूचना प्रसंस्करण
- आईईईई स्पेक्ट्रम ऑन-लाइन: ट्रैप तकनीक
- दूर से डरावनी हरकतें?: ओपेनहाइमर व्याख्यान, प्रोफेसर डेविड मर्मिन (कॉर्नेल विश्वविद्यालय) विश्वविद्यालय। कैलिफ़ोर्निया, बर्कले, 2008। यूट्यूब पर गैर-गणितीय लोकप्रिय व्याख्यान, मार्च 2008 को पोस्ट किया गया
- "क्वांटम उलझाव बनाम शास्त्रीय सहसंबंध" (इंटरैक्टिव प्रदर्शन)