डेटा आत्मसात्करण

डेटा एसिमिलेशन एक ऐसा गणितीय अनुशासन है जो अवलोकन के साथ सिद्धांत (सामान्यतः संख्यात्मक मॉडल के रूप में) को ठीक रूप से संयोजित करना चाहता है। कई अलग-अलग लक्ष्य हो सकते हैं - उदाहरण के लिए, किसी सिस्टम की इष्टतम स्थिति का अनुमान निर्धारित करना, संख्यात्मक पूर्वानुमान मॉडल के लिए प्रारंभिक स्थितियां निर्धारित करना, देखे जा रहे सिस्टम के ज्ञान (जैसे भौतिक) का उपयोग करके विरल अवलोकन डेटा को प्रक्षेपित करना, देखे गए डेटा से मॉडल को प्रशिक्षित करने के आधार पर संख्यात्मक पैरामीटर समूहित करना। इस प्रकार से लक्ष्य के आधार पर, विभिन्न हल विधियों का उपयोग किया जा सकता है। डेटा एसिमिलेशन को मशीन लर्निंग, प्रतिबिम्ब विश्लेषण और सांख्यिकीय विधियों के अन्य रूपों से अलग किया जाता है, क्योंकि यह विश्लेषण किए जा रहे सिस्टम के गतिशील मॉडल का उपयोग करता है।

डेटा सम्मिलन प्रारंभ में संख्यात्मक ऋतु पूर्वानुमान के क्षेत्र में विकसित हुआ। संख्यात्मक ऋतु पूर्वानुमान मॉडल वायुमंडल के गतिशील व्यवहार का वर्णन करने वाले समीकरण हैं, जिन्हें सामान्यतः कंप्यूटर प्रोग्राम में कोडित किया जाता है। इस प्रकार से पूर्वानुमान लगाने के लिए इन मॉडलों का उपयोग करने के लिए, मॉडल के लिए प्रारंभिक स्थितियों की आवश्यकता होती है जो वायुमंडल की वर्तमान स्थिति से अत्यधिक मिलती-जुलती हो। मात्र संख्यात्मक मॉडलों में बिंदुवार माप डालने से कोई संतोषजनक हल नहीं मिलता। वास्तविक संसार के मापों में उपकरण की गुणवत्ता और माप की स्थिति कितनी यथार्थ रूप से ज्ञात है, दोनों के कारण त्रुटियां होती हैं। ये त्रुटियां मॉडल में अस्थिरता उत्पन्न कर सकती हैं जो पूर्वानुमान में किसी भी स्तर के कौशल को समाप्त कर देती हैं। इस प्रकार, संख्यात्मक मॉडल में स्थिरता बनाए रखना सुनिश्चित करते हुए सभी उपलब्ध डेटा का उपयोग करके मॉडल को आरंभ करने के लिए अधिक परिष्कृत विधियों की आवश्यकता थी। इस प्रकार के डेटा में सामान्यतः माप के साथ-साथ पूर्व पूर्वानुमान भी सम्मिलित होते हैं जो माप किए जाने के समय मान्य होते हैं। यदि इसे पुनरावृत्त रूप से लागू किया जाए, तो यह प्रक्रिया पूर्व अवलोकनों से बाद के सभी पूर्वानुमानों में सूचना एकत्रित करना प्रारम्भ कर देती है।

क्योंकि डेटा सम्मिलन संख्यात्मक ऋतु पूर्वानुमान के क्षेत्र से विकसित हुआ, इसने प्रारम्भ में भूविज्ञान के बीच लोकप्रियता प्राप्त की थी। वस्तुतः, सभी भूविज्ञानों में सबसे अधिक उद्धृत प्रकाशनों में से वायुमंडल के देखे गए इतिहास के पुनर्निर्माण के लिए डेटा एसिमिलेशन का अनुप्रयोग है।

डेटा एसिमिलेशन प्रक्रिया का विवरण

इस प्रकार से शास्त्रीय रूप से, डेटा एसिमिलेशन को अव्यवस्थित गतिशील प्रणालियों पर लागू किया गया है, जिनकी सरल बहिर्वेशन विधियों का उपयोग करके पूर्वानुमान करना बहुत जटिल है। इस जटिलता का कारण यह है कि प्रारंभिक स्थितियों में छोटे बदलाव से पूर्वानुमान यथार्थता में बड़े बदलाव हो सकते हैं। अतः इसे कभी-कभी तितली प्रभाव के रूप में जाना जाता है - प्रारंभिक स्थितियों पर संवेदनशील निर्भरता जिसमें नियतात्मक गैर-रेखीय सिस्टम की स्थिति में छोटे से परिवर्तन के परिणामस्वरूप बाद की स्थिति में बड़े अंतर हो सकते हैं।

इस प्रकार से किसी भी अद्यतन समय पर, डेटा एसिमिलेशन सामान्यतः पूर्वानुमान लेता है (जिसे पहले अनुमान या पृष्ठभूमि सूचना के रूप में भी जाना जाता है) और देखे गए डेटा और अनुमानित त्रुटियों के समूह के आधार पर पूर्वानुमान में सुधार लागू करता है जो अवलोकन और पूर्वानुमान दोनों में स्थित होते हैं। अतः उस समय के पूर्वानुमान और टिप्पणियों के बीच के अंतर को प्रस्थान या नवाचार कहा जाता है (क्योंकि यह डेटा एसिमिलेशन प्रक्रिया को नवीन सूचना प्रदान करता है)। अवलोकनों से प्राप्त नवीन सूचना के आधार पर पूर्वानुमान में कितना सुधार किया जाना चाहिए, यह निर्धारित करने के लिए नवाचार पर भार कारक लागू किया जाता है। इस प्रकार से नवप्रवर्तन के गुणन कारक द्वारा निर्धारित पूर्वानुमान में सुधार के आधार पर सिस्टम की स्थिति का सबसे स्पष्ट अनुमान विश्लेषण कहा जाता है। विमा में, विश्लेषण की गणना करना पूर्वानुमानित और देखे गए मान का भारित औसत बनाने जितना सरल हो सकता है। अनेक विमाओं में समस्या अधिक जटिल हो जाती है। डेटा सम्मिलन में अधिकांश कार्य सिस्टम में त्रुटियों के जटिल ज्ञान के आधार पर उचित भार कारक का पर्याप्त अनुमान लगाने पर केंद्रित है।

इस प्रकार से माप सामान्यतः उस सिस्टम के मॉडल के अपूर्ण प्रतिनिधित्व के अतिरिक्त वास्तविक संसार सिस्टम से बने होते हैं, और इसलिए एक विशेष फलन, जिसे अवलोकन ऑपरेटर कहा जाता है (सामान्यतः गैर-रेखीय ऑपरेटर के लिए h() या इसके रैखिककरण के लिए H द्वारा दर्शाया जाता है) मॉडल किए गए चर को ऐसे रूप में प्रतिचित्रित करने की आवश्यकता है जिसकी तुलना प्रत्यक्षतः अवलोकन से की जा सके।

सांख्यिकीय अनुमान के रूप में डेटा एसिमिलेशन

सामान्य गणितीय दार्शनिक दृष्टिकोणों में से डेटा एसिमिलेशन को बायेसियन अनुमान समस्या के रूप में देखना है। इस दृष्टिकोण से, विश्लेषण चरण बेयस प्रमेय का अनुप्रयोग है और समग्र एसिमिलेशन प्रक्रिया पुनरावर्ती बायेसियन अनुमान का उदाहरण है। यद्यपि, संभाव्य विश्लेषण को सामान्यतः कम्प्यूटेशनल रूप से व्यवहार्य रूप में सरल बनाया जाता है। इस प्रकार से समय में संभाव्यता वितरण को आगे बढ़ाना सामान्य स्थिति में फोककर-प्लैंक समीकरण द्वारा किया जाएगा, परन्तु यह उच्च-विमीय प्रणालियों के लिए संभव नहीं है; इसलिए, इसके अतिरिक्त संभाव्यता वितरण के सरलीकृत प्रतिनिधित्व (गणित) पर कार्य करने वाले विभिन्न अनुमानों का उपयोग किया जाता है। प्रायः संभाव्यता वितरण को एक सामान्य वितरण माना जाता है ताकि उन्हें उनके माध्य और सहप्रसरण द्वारा दर्शाया जा सके, जो एक कलमन निस्यंदक को जन्म देता है।

कई विधियाँ मात्र माध्य द्वारा संभाव्यता वितरण का प्रतिनिधित्व करती हैं और कुछ पूर्व-गणना किए गए सहप्रसरण को इनपुट करती हैं। इस प्रकार से इसकी गणना करने के लिए प्रत्यक्ष (या अनुक्रमिक) विधि का उदाहरण इष्टतम सांख्यिकीय अंतर्वेशन, या मात्र इष्टतम अंतर्वेशन (ओआई) कहा जाता है। वैकल्पिक दृष्टिकोण लागत फलन को पुनरावृत्त रूप से हल करना है जो समान समस्या को हल करता है। इन्हें परिवर्तनशील विधियाँ कहा जाता है, जैसे कि 3डी-वार और 4डी-वार आदि। विशिष्ट न्यूनतमकरण एल्गोरिदम संयुग्म प्रवणता विधि या सामान्यीकृत न्यूनतम अवशिष्ट विधि हैं। अतः कल्मन निस्यंदक समवेत अनुक्रमिक एक ऐसी विधि है जो सिमुलेशन के समूह द्वारा गॉसियन संभाव्यता वितरण के माध्य और सहप्रसरण दोनों का अनुमान लगाने के लिए मोंटे कार्लो दृष्टिकोण का उपयोग करता है। वर्तमान में, समुच्चय दृष्टिकोण और परिवर्तनशील विधियों के संकर संयोजन अधिक लोकप्रिय हो गए हैं (उदाहरण के लिए इनका उपयोग मध्यम दूरी के ऋतु पूर्वानुमान के लिए यूरोपीय केंद्र (ईसीएमडब्ल्यूएफ) और एनओएए पर्यावरण पूर्वानुमान के लिए राष्ट्रीय केंद्र (एनसीईपी) दोनों में परिचालन पूर्वानुमान के लिए किया जाता है)।

ऋतु पूर्वानुमान अनुप्रयोग

इस प्रकार से संख्यात्मक ऋतु पूर्वानुमान अनुप्रयोगों में, संख्यात्मक पूर्वानुमान मॉडल को आरंभ करने के लिए पूर्व पूर्वानुमानों के साथ तापमान और वायुमंडलीय दाब जैसे ऋतु संबंधी चर के अवलोकनों को संयोजित करने की विधि के रूप में डेटा एसिमिलेशन को व्यापक रूप से जाना जाता है।

यह क्यों आवश्यक है

वातावरण तरल पदार्थ है। संख्यात्मक ऋतु पूर्वानुमान का विचार किसी निश्चित समय पर तरल पदार्थ की स्थिति का प्रतिदर्श लेना और भविष्य में किसी समय तरल पदार्थ की स्थिति का अनुमान लगाने के लिए तरल गतिशीलता और ऊष्मप्रवैगिकी के समीकरणों का उपयोग करना है। प्रारंभिक मान समस्या उत्पन्न करने के लिए मॉडल में अवलोकन डेटा दर्ज करने की प्रक्रिया को आरंभीकरण कहा जाता है। इस प्रकार से भूमि पर, विश्व स्तर पर 1 kilometer (0.6 mi) तक के विभेदन पर उपलब्ध भू-भाग प्रतिचित्रों का उपयोग असम स्थलाकृति वाले क्षेत्रों के भीतर वायुमंडलीय परिसंचरण को मॉडल करने में सहायता करने के लिए उपयोग किया जाता है, ताकि आने वाली सौर विकिरण को प्रभावित करने वाली ढलान वाली वायु, ली तरंगों और संबंधित बादलों जैसी विशेषताओं को ठीक रूप से चित्रित किया जा सके। देश-आधारित ऋतु सेवाओं के मुख्य इनपुट ऋतु गुब्बारों में उपकरणों (जिन्हें रेडियोसोंडे कहा जाता है) से अवलोकन हैं जो विभिन्न वायुमंडलीय मापदंडों को मापते हैं और उन्हें निश्चित ग्राही, साथ ही ऋतु उपग्रहों तक पहुंचाते हैं। विश्व ऋतु विज्ञान संगठन संसार भर में इन अवलोकनों के उपकरण, अवलोकन प्रथाओं और समय को मानकीकृत करने के लिए कार्य करता है। स्टेशन या तो प्रति घंटा मीटर रिपोर्ट में प्रति घंटा रिपोर्ट करते हैं, या साइनोप रिपोर्ट में प्रत्येक छह घंटे में रिपोर्ट करते हैं। ये अवलोकन अनियमित स्थान पर हैं, इसलिए उन्हें डेटा एसिमिलेशन और वस्तुनिष्ठ विश्लेषण विधियों द्वारा संसाधित किया जाता है, जो गुणवत्ता नियंत्रण करते हैं और मॉडल के गणितीय एल्गोरिदम द्वारा प्रयोग करने योग्य स्थानों पर मान प्राप्त करते हैं। इस प्रकार से कुछ वैश्विक मॉडल परिमित अंतरों का उपयोग करते हैं, जिसमें संसार को अक्षांश और देशांतर के नियमित रूप से दूरी वाले ग्रिड पर अलग-अलग बिंदुओं के रूप में दर्शाया जाता है; अन्य मॉडल वर्णक्रमीय विधियों का उपयोग करते हैं जो तरंग दैर्ध्य की श्रृंखला को हल करते हैं। फिर डेटा का उपयोग पूर्वानुमान के लिए प्रारंभिक बिंदु के रूप में मॉडल में किया जाता है।

अतः संख्यात्मक मॉडल में उपयोग के लिए अवलोकन संबंधी डेटा एकत्रित करने के लिए विभिन्न विधियों का उपयोग किया जाता है। साइटें ऋतु के गुब्बारों में रेडियोसॉन्डेस लॉन्च करती हैं जो क्षोभमंडल से होते हुए समतापमंडल में ऊपर उठती हैं। ऋतु उपग्रहों से सूचना का उपयोग वहां किया जाता है जहां पारंपरिक डेटा स्रोत उपलब्ध नहीं हैं। इस प्रकार से वाणिज्य विमान मार्गों पर पायलट रिपोर्ट और शिपिंग मार्गों पर जहाज रिपोर्ट प्रदान करता है। अनुसंधान परियोजनाएं उष्णकटिबंधीय चक्रवातों जैसी रुचि की ऋतु प्रणालियों में और उसके निकट उड़ान भरने के लिए ऋतु वीक्षण का उपयोग करती हैं। शीत ऋतु के समय वीक्षण विमान भी संवृत महासागरों के ऊपर सिस्टम में उड़ाए जाते हैं, जिससे पूर्वानुमान मार्गदर्शन में महत्वपूर्ण अनिश्चितता उत्पन्न होती है, या भविष्य में तीन से सात दिनों तक अनुप्रवाह महाद्वीप पर उच्च प्रभाव होने की अपेक्षा होती है। अतः 1971 में पूर्वानुमान मॉडल में समुद्री हिम का प्रारम्भ किया गया। प्रशांत महासागर के उच्च अक्षांशों में ऋतु को नियंत्रित करने में इसकी भूमिका के कारण मॉडल आरंभीकरण में समुद्री सतह के तापमान को सम्मिलित करने का प्रयास 1972 में प्रारम्भ हुआ।

इतिहास

लुईस फ्राई रिचर्डसन

इस प्रकार से 1922 में, लुईस फ्राई रिचर्डसन ने संख्यात्मक रूप से ऋतु की पूर्वानुमान करने का पहला प्रयास प्रकाशित किया। विल्हेम बर्कनेस के आदिम समीकरणों के जलस्थैतिक संतुलन भिन्नता का उपयोग करते हुए, रिचर्डसन ने मध्य यूरोप में दो बिंदुओं पर वातावरण की स्थिति के लिए हाथ से 6 घंटे का पूर्वानुमान तैयार किया, ऐसा करने में कम से कम छह सप्ताह लगे। उनके पूर्वानुमान ने गणना की कि सतह के दाब में परिवर्तन 145 millibars (4.3 inHg) होगा, जो परिमाण के दो क्रमों से अनुचित एक अवास्तविक मान है। बड़ी त्रुटि उनके विश्लेषण में प्रारंभिक स्थितियों के रूप में उपयोग किए गए दाब और वायु के वेग क्षेत्रों में असंतुलन के कारण हुई थी, जो डेटा एसिमिलेशन योजना की आवश्यकता को दर्शाता है।

अतः मूल रूप से व्यक्तिपरक विश्लेषण का उपयोग किया गया था जिसमें संख्यात्मक ऋतु पूर्वानुमान (एनडब्ल्यूपी) पूर्वानुमानों को ऋतु विज्ञानियों द्वारा अपनी परिचालन विशेषज्ञता का उपयोग करके समायोजित किया गया था। फिर स्वचालित डेटा सम्मिलन के लिए वस्तुनिष्ठ विश्लेषण (उदाहरण के लिए क्रेसमैन एल्गोरिदम) प्रस्तुत किया गया था। इस प्रकार से इन वस्तुनिष्ठ विधियों में सरल प्रक्षेप दृष्टिकोण का उपयोग किया गया, और इस प्रकार 3डीडीए (त्रि-विमीय डेटा एसिमिलेशन) विधियाँ थीं।

बाद में, 4डीडीए (चार-विमीय डेटा एसिमिलेशन) विधियाँ, जिन्हें नडिंग कहा जाता है, विकसित की गईं, जैसे कि एमएम5 (ऋतु मॉडल) मॉडल में। वे न्यूटोनियन श्रांति (न्यूटन का दूसरा सिद्धांत) के सरल विचार पर आधारित हैं। अतः वे मॉडल के गतिशील समीकरणों के दाहिने भाग में शब्द प्रस्तुत करते हैं जो गणना किए गए ऋतु संबंधी चर और देखे गए मान के अंतर के समानुपाती होता है। ऋणात्मक चिह्न वाला यह शब्द परिकलित अवस्था समष्टि (नियंत्रण) को प्रेक्षणों के निकट रखता है। इस प्रकार से नडिंग की व्याख्या कलमन-बुसी निस्यंदक (कलमन निस्यंदक का निरंतर समय संस्करण) के प्रकार के रूप में की जा सकती है, जिसमें सहप्रसरणों से प्राप्त लाभ आव्यूह के अतिरिक्त निर्धारित किया जाता है।

एल. गैंडिन (1963) द्वारा बड़ा विकास प्राप्त किया गया, जिन्होंने सांख्यिकीय अंतर्वेशन (या इष्टतम अंतर्वेशन) पद्धति की प्रारम्भ की थी, जिसने कोलमोगोरोव के पहले के विचारों को विकसित किया। यह 3डीडीए विधि है और प्रकार का प्रतिगमन विश्लेषण है जो पहले अनुमान क्षेत्र (पूर्व पूर्वानुमान) और उचित क्षेत्र की त्रुटियों के सहप्रसरण कार्यों के स्थानिक वितरण के विषय में सूचना का उपयोग करता है। ये फलन कभी ज्ञात नहीं होते है। यद्यपि, अलग-अलग अनुमान लगाए गए थे।

इष्टतम अंतर्वेशन एल्गोरिदम कलमन निस्यंदक (केएफ) एल्गोरिदम का छोटा संस्करण है और जिसमें सहप्रसरण आव्यूह की गणना गतिशील समीकरणों से नहीं की जाती है बल्कि पहले से पूर्व निर्धारित की जाती है।

एनडब्ल्यूपी मॉडल के लिए केएफ एल्गोरिदम को 4डीडीए टूल के रूप में प्रस्तुत करने का प्रयास बाद में हुआ। यद्यपि, यह जटिल कार्य था (और बना हुआ है) क्योंकि पूर्ण संस्करण के लिए भारी संख्या में अतिरिक्त समीकरणों (~N*N~10**12, जहां N=Nx*Ny*Nz अवस्था सदिश का आकार है, इसे Nx~100, Ny~100, Nz~100 - कम्प्यूटेशनल ग्रिड के विमा) के हल की आवश्यकता होती है। इस जटिलता को दूर करने के लिए, अनुमानित या उप-इष्टतम कलमैन निस्यंदक विकसित किए गए। इनमें समुच्चय कलमैन निस्यंदक और न्यूनीकृत-पद कलमैन निस्यंदक (आरआरएसक्यूआरटी) सम्मिलित हैं।

अतः 4डीडीए विधियों के विकास में और महत्वपूर्ण प्रगति जे.-एल के पूर्व कार्यों के आधार पर, ले डिमेट और टैलाग्रैंड (1986) के कार्यों में इष्टतम नियंत्रण सिद्धांत (परिवर्तनशील दृष्टिकोण) का उपयोग करना था। इस प्रकार से लायंस और जी. मार्चुक पर्यावरण मॉडलिंग में उस सिद्धांत को लागू करने वाले पहले व्यक्ति थे। परिवर्तनशील दृष्टिकोण का महत्वपूर्ण लाभ यह है कि ऋतु संबंधी क्षेत्र एनडब्ल्यूपी मॉडल के गतिशील समीकरणों को संतुष्ट करते हैं और साथ ही वे टिप्पणियों से उनके अंतर को दर्शाते हुए कार्यात्मकता को कम करते हैं। इस प्रकार, बाधित न्यूनतमकरण की समस्या हल हो जाती है। 3डीडीए परिवर्तनीय विधियाँ पहली बार सासाकी (1958) द्वारा विकसित की गईं।

जैसा कि लोरेंक (1986) द्वारा दिखाया गया था, उपरोक्त सभी 4डीडीए विधियां कुछ सीमा समतुल्य हैं, अर्थात कुछ मान्यताओं के अंतर्गत वे समान हानि फलन को कम करते हैं। यद्यपि, व्यावहारिक अनुप्रयोगों में ये धारणाएँ कभी पूर्ण नहीं होती हैं, अलग-अलग विधियाँ अलग-अलग प्रदर्शन करती हैं और सामान्यतः यह स्पष्ट नहीं है कि कौन सा दृष्टिकोण (कलमन निस्यंदक या विचरणी) ठीक है। इस प्रकार से उन्नत डीए तकनीकों के अनुप्रयोग में मूलभूत प्रश्न भी उठते हैं जैसे कि कम से कम की जाने वाली कार्यात्मकता के वैश्विक न्यूनतम तक कम्प्यूटेशनल पद्धति का अभिसरण है। उदाहरण के लिए, लागत फलन या वह समूह जिसमें हल मांगा गया है, उत्तल नहीं हो सकता है। 4DDA विधि जो वर्तमान में सबसे सफल है, हाइब्रिड वृद्धिशील 4डी-वार है, जहां डेटा एसिमिलेशन टाइम विंडो के प्रारम्भ में जलवायु संबंधी पृष्ठभूमि त्रुटि सहप्रसरण को बढ़ाने के लिए एक समूह का उपयोग किया जाता है, परन्तु एनडब्ल्यूपी पूर्वानुमान मॉडल के सरलीकृत संस्करण द्वारा समय विंडो के समय पृष्ठभूमि त्रुटि सहप्रसरण विकसित किए जाते हैं। इस डेटा सम्मिलन पद्धति का उपयोग ऋतु कार्यालय जैसे पूर्वानुमान केंद्रों पर परिचालन रूप से किया जाता है।

लागत फलन

अतः डेटा सम्मिलन में विश्लेषण बनाने की प्रक्रिया में प्रायः हानि फलन को कम करना सम्मिलित होता है। इस प्रकार से विशिष्ट लागत फलन अवलोकनों की यथार्थता द्वारा भारित अवलोकनों से विश्लेषण मानों के वर्ग विचलन का योग होगा, साथ ही पूर्वानुमान क्षेत्रों के वर्ग विचलन और पूर्वानुमान की यथार्थता द्वारा भारित विश्लेषण किए गए क्षेत्रों का योग होगा। इसका प्रभाव यह सुनिश्चित करना है कि विश्लेषण उन टिप्पणियों और पूर्वानुमानों से बहुत दूर नहीं जाता है जिन्हें सामान्यतः विश्वसनीय माना जाता है।

3डी-वार

$J(\mathbf {x} )=(\mathbf {x} -\mathbf {x} _{b})^{\mathrm {T} }\mathbf {B} ^{-1}(\mathbf {x} -\mathbf {x} _{b})+(\mathbf {y} -{\mathit {H}}[\mathbf {x} ])^{\mathrm {T} }\mathbf {R} ^{-1}(\mathbf {y} -{\mathit {H}}[\mathbf {x} ]),$

जहाँ $\mathbf {B}$ पृष्ठभूमि त्रुटि सहप्रसरण को दर्शाता है, $\mathbf {R}$ अवलोकन संबंधी त्रुटि सहप्रसरण को दर्शाता है।

$\nabla J(\mathbf {x} )=2\mathbf {B} ^{-1}(\mathbf {x} -\mathbf {x} _{b})-2{\mathit {H}}^{T}\mathbf {R} ^{-1}(\mathbf {y} -{\mathit {H}}[\mathbf {x} ])$

सीएचडी-वार

$J(\mathbf {x} )=(\mathbf {x} -\mathbf {x} _{b})^{\mathrm {T} }\mathbf {B} ^{-1}(\mathbf {x} -\mathbf {x} _{b})+\sum _{i=0}^{n}(\mathbf {y} _{i}-{\mathit {H}}_{i}[\mathbf {x} _{i}])^{\mathrm {T} }\mathbf {R} _{i}^{-1}(\mathbf {y} _{i}-{\mathit {H}}_{i}[\mathbf {x} _{i}])$

प्रदान किया गया कि ${\mathit {H}}$ एक रैखिक ऑपरेटर (आव्यूह) है।

भविष्य का विकास

इस प्रकार से एनडब्ल्यूपी मॉडल के लिए डेटा एसिमिलेशन विधियों के तीव्रता से विकास को चलाने वाले कारकों में सम्मिलित हैं:

• वर्तमान में अवलोकनों का उपयोग विभिन्न स्थानिक पैमानों (वैश्विक से अत्यधिक स्थानीय तक) और समय के पैमानों पर पूर्वानुमान कौशल में अपेक्षाजनक सुधार प्रदान करता है।
• विभिन्न प्रकार के उपलब्ध अवलोकनों (सोडार, राडार, उपग्रह) की संख्या तीव्रता से बढ़ रही है।

अन्य अनुप्रयोग

जल और ऊर्जा हस्तांतरण की देख रेख

सामान्य डेटा एसिमिलेशन आरेख (एल्पिल्स-रेसेडा)

1980 और 1990 के दशक में, मृदा, वनस्पति और वायुमंडल के बीच ऊर्जा हस्तांतरण की देख रेख के लिए कई हपेक्स (हाइड्रोलॉजिकल और वायुमंडलीय पायलट प्रयोग) परियोजनाओं में डेटा एसिमिलेशन का उपयोग किया गया है। इस प्रकार से उदाहरण के लिए:

- हपेक्स-मोबिलहाई, हपेक्स-साहेल,

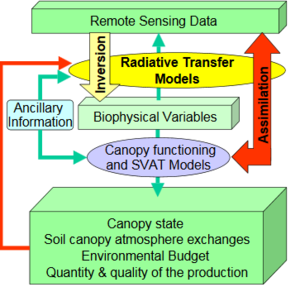
- एल्पिल्स-रेसेडा (रिमोट सेंसिंग डेटा एसिमिलेशन) प्रयोग, एफपी4-ईएनवी कार्यक्रम में यूरोपीय परियोजना जो फ्रांस के दक्षिण-पूर्व में एल्पिल्स क्षेत्र में (1996-97) हुआ था। अतः अनुक्रम चार्ट आरेख (दाएं), उस परियोजना की अंतिम रिपोर्ट से उद्धृत, यह दर्शाता है कि रिमोट सेंसिंग डेटा और सहायक सूचना से कैनोपी स्थिति, विकिरण प्रवाह, पर्यावरणीय बजट, मात्रा और गुणवत्ता में उत्पादन जैसे रुचि के चर का अनुमान कैसे लगाया जाए। उस आरेख में, छोटे नीले-हरे तीर मॉडल के वस्तुतः चलने के प्रत्यक्ष विधि को दर्शाते हैं।

अन्य पूर्वानुमान अनुप्रयोग

डेटा सम्मिलन विधियों का उपयोग वर्तमान में अन्य पर्यावरणीय पूर्वानुमान समस्याओं में भी किया जाता है, जैसे जल विज्ञान पूर्वानुमान में। भूस्खलन जैसे प्राकृतिक संकटों का आकलन करने के लिए डेटा एसिमिलेशन दृष्टिकोण में बायेसियन नेटवर्क का भी उपयोग किया जा सकता है।

इस प्रकार से सौर मंडल में अन्य ग्रहों के लिए अंतरिक्ष यान डेटा की प्रचुरता को देखते हुए, भौमेतर ग्रहों की वायुमंडलीय स्थिति का पुन: विश्लेषण प्राप्त करने के लिए डेटा एसिमिलेशन को अब पृथ्वी से परे भी लागू किया जाता है। मंगल एकमात्र भौमेतर ग्रह है जिस पर अब तक डेटा सम्मिलन लागू किया गया है। अतः उपलब्ध अंतरिक्ष यान डेटा में, विशेष रूप से, नासा के मंगल वैश्विक सर्वेक्षक पर तापीय उत्सर्जन स्पेक्ट्रोमीटर और नासा के मंगल वीक्षण कक्षित्र पर मंगल जलवायु ध्वनि से तापमान और धूल/जल/हिम प्रकाशिक मोटाई की पुनर्प्राप्ति सम्मिलित है। इन डेटासमूहों पर डेटा एसिमिलेशन करने की दो विधियाँ लागू की गई हैं: विश्लेषण सुधार योजना और दो समुच्चय कलमन निस्यंदक योजनाएँ, दोनों आगे के मॉडल के रूप में मंगल ग्रह के वातावरण के वैश्विक परिसंचरण मॉडल का उपयोग करते हैं। मंगल एनालिसिस करेक्शन डेटा एसिमिलेशन (मैकडा) डेटासमूह सार्वजनिक रूप से ब्रिटिश एटमॉस्फेरिक डेटा सेंटर से उपलब्ध है।

इस प्रकार से प्रत्येक पूर्वानुमान समस्या के लिए डेटा सम्मिलन आक्षेप का भाग है।

डेटा संकलन में पक्षपातपूर्ण डेटा से निपटना गंभीर आक्षेप है। पूर्वाग्रहों से निपटने के विधियों का और अधिक विकास विशेष रूप से उपयोगी होगा। यदि एक ही चर का अवलोकन करने वाले कई उपकरण हैं तो संभाव्यता घनत्व कार्यों का उपयोग करके उनकी परस्पर तुलना करना शिक्षाप्रद हो सकता है।

कम्प्यूटेशनल शक्ति में वृद्धि के कारण संख्यात्मक पूर्वानुमान मॉडल उच्च विभेदन के होते जा रहे हैं, परिचालन वायुमंडलीय मॉडल अब 1 किमी के क्रम के क्षैतिज विभेदन के साथ चल रहे हैं (उदाहरण के लिए जर्मन राष्ट्रीय ऋतु विज्ञान सेवा, ड्यूशर वेटरडिएंस्ट (डीडब्ल्यूडी) और यूके में ऋतु कार्यालय)। क्षैतिज विभेदन में यह वृद्धि गैर-रेखीय मॉडल की अधिक अव्यवस्थित विशेषताओं को हल करने की अनुमति देने लगी है, जैसे वायुमंडलीय मॉडल में ग्रिड स्तर या बादलों पर संवहन को हल करने के लिए। मॉडलों में बढ़ती गैर-रैखिकता और व्युत्क्रम समस्या डेटा एसिमिलेशन में नवीन समस्या उत्पन्न करती है। वर्तमान डेटा एसिमिलेशन करने के विधि जैसे कि समुच्चय कलमैन निस्यंदक के कई प्रकार और रैखिक या निकट-रेखीय मॉडल के साथ ठीक रूप से स्थापित वैरिएबल विधियों का मानांकन गैर-रेखीय मॉडल पर किया जा रहा है।

इस प्रकार से कई नवीन विधियाँ विकसित की जा रही हैं, उदा. उच्च-विमीय समस्याओं के लिए कण निस्यंदक, और हाइब्रिड डेटा एसिमिलेशन विधियाँ।

अतः अन्य उपयोगों में अपोलो कार्यक्रम, जीपीएस और ऑटोकेम के लिए प्रक्षेपवक्र अनुमान सम्मिलित हैं।

यह भी देखें

• अंशांकन (सांख्यिकी)

अग्रिम पठन

• Daley, R. (1991). Atmospheric Data Analysis. Cambridge University Press. ISBN 978-0-521-38215-1.
• "MM5 community model homepage".
• "ECMWF Data Assimilation Lecture notes".
• Ide, Kayo; Courtier, Philippe; Ghil, Michael; Lorenc, Andrew C (1997). "Unified Notation for Data Assimilation : Operational, Sequential and Variational (gtSpecial IssueltData Assimilation in Meteology and Oceanography: Theory and Practice)". Journal of the Meteorological Society of Japan. Ser. II. 75 (1B): 181–9. Bibcode:1997JMeSJ..75B.181I. doi:10.2151/jmsj1965.75.1B_181.
• "Understanding Data Assimilation". COMET module.
• Evensen, Geir (2009). Data Assimilation. The Ensemble Kalman Filter (Second ed.). Springer. ISBN 978-3-642-03710-8.
• Lewis, John M.; Lakshmivarahan, S.; Dhall, Sudarshan (2006). "Dynamic Data Assimilation : A Least Squares Approach". Encyclopedia of Mathematics and its Applications. Vol. 104. Cambridge University Press. ISBN 978-0-521-85155-8.
• Asch, Mark; Bocquet, Marc; Nodet, Maëlle (2016). Data Assimilation: Methods, Algorithms, and Applications. Society for Industrial and Applied Mathematics. ISBN 978-1-61197-453-9.
• Kalnay, Eugenia (2002). Atmospheric Modeling, Data Assimilation and Predictability. p. 364. Bibcode:2002amda.book.....K. ISBN 978-0-521-79179-3. {{cite book}}: |journal= ignored (help)
• Vetra-Carvalho, S.; van Leeuwen, P. J.; Nerger, L.; Barth, A.; Umer Altat, M.; Brasseur, P.; Kirchgessner, P.; Beckers, J-M. (2018). "State-of-the-art stochastic data assimilation methods for high-dimensional non-Gaussian problems". Tellus A: Dynamic Meteorology and Oceanography. 70 (1): 1445364. Bibcode:2018TellA..7045364V. doi:10.1080/16000870.2018.1445364.

बाहरी संबंध

Examples of how variational assimilation is implemented weather forecasting at:

• Data Assimilation. 2010. {{cite book}}: |work= ignored (help)
• "Data Assimilation". Met Office.

Other examples of assimilation:

• CDACentral (an example analysis from Chemical Data Assimilation)
• PDFCentral (using PDFs to examine biases and representativeness)
• OpenDA – Open Source Data Assimilation package
• PDAF – open-source Parallel Data Assimilation Framework
• SANGOMA New Data Assimilation techniques