टेलर प्रमेय: Difference between revisions
(Created page with "{{short description|Approximation of a function by a truncated power series}} File:Taylorspolynomialexbig.svg|thumb|right|300px|घातांकीय फलन <math disp...") |
No edit summary |
||
| Line 3: | Line 3: | ||
{{Calculus |Differential}} | {{Calculus |Differential}} | ||
[[ गणना ]] में, टेलर का प्रमेय एक अनुमान देता है <math display="inline">k</math>-डिग्री के [[बहुपद]] द्वारा किसी दिए गए बिंदु के चारों ओर बार-बार भिन्न-भिन्न कार्य <math display="inline">k</math>, इसको कॉल किया गया <math display="inline">k</math>-वें क्रम का टेलर बहुपद। एक सुचारु कार्य के लिए, टेलर बहुपद '' क्रम में काट-छाँट है<math display="inline">k</math>समारोह की [[टेलर श्रृंखला]] का। प्रथम-क्रम टेलर बहुपद | [[ गणना ]] में, टेलर का प्रमेय एक अनुमान देता है <math display="inline">k</math>-डिग्री के [[बहुपद]] द्वारा किसी दिए गए बिंदु के चारों ओर बार-बार भिन्न-भिन्न कार्य <math display="inline">k</math>, इसको कॉल किया गया <math display="inline">k</math>-वें क्रम का टेलर बहुपद। एक सुचारु कार्य के लिए, टेलर बहुपद '' क्रम में काट-छाँट है<math display="inline">k</math>समारोह की [[टेलर श्रृंखला]] का। प्रथम-क्रम टेलर बहुपद फलन का [[रैखिक सन्निकटन]] है, और दूसरे-क्रम टेलर बहुपद को प्रायः 'द्विघात सन्निकटन' के रूप में जाना जाता है।<ref>(2013). [http://www.math.ubc.ca/~sujatha/2013/103/week10-12/Linearapp.pdf"Linear and quadratic approximation"] Retrieved December 6, 2018</ref> टेलर के प्रमेय के कई संस्करण हैं, कुछ इसके टेलर बहुपद द्वारा फलन की सन्निकटन त्रुटि का स्पष्ट अनुमान देते हैं।'' | ||
टेलर के प्रमेय का नाम गणितज्ञ [[ब्रूक टेलर]] के नाम पर रखा गया है, जिन्होंने 1715 में इसका एक संस्करण बताया था,<ref>{{cite book|language=la|last=Taylor |first=Brook |title=वेतन वृद्धि की सीधी और उलटी विधि|url=https://archive.org/details/UFIE003454_TO0324_PNI-2529_000000|trans-title=Direct and Reverse Methods of Incrementation |location=London |date=1715 |at=p. 21–23 (Prop. VII, Thm. 3, Cor. 2)}} Translated into English in {{cite book|first=D. J. |last=Struik|title=A Source Book in Mathematics 1200–1800 |location=Cambridge, Massachusetts |publisher=Harvard University Press |date=1969 |pages= 329–332}}</ref> हालाँकि परिणाम के पहले संस्करण का उल्लेख 1671 में [[जेम्स ग्रेगरी (खगोलशास्त्री और गणितज्ञ)]] द्वारा विज्ञान में पहले ही किया जा चुका था।<ref>{{harvnb|Kline|1972|pp=442, 464}}.</ref> | टेलर के प्रमेय का नाम गणितज्ञ [[ब्रूक टेलर]] के नाम पर रखा गया है, जिन्होंने 1715 में इसका एक संस्करण बताया था,<ref>{{cite book|language=la|last=Taylor |first=Brook |title=वेतन वृद्धि की सीधी और उलटी विधि|url=https://archive.org/details/UFIE003454_TO0324_PNI-2529_000000|trans-title=Direct and Reverse Methods of Incrementation |location=London |date=1715 |at=p. 21–23 (Prop. VII, Thm. 3, Cor. 2)}} Translated into English in {{cite book|first=D. J. |last=Struik|title=A Source Book in Mathematics 1200–1800 |location=Cambridge, Massachusetts |publisher=Harvard University Press |date=1969 |pages= 329–332}}</ref> हालाँकि परिणाम के पहले संस्करण का उल्लेख 1671 में [[जेम्स ग्रेगरी (खगोलशास्त्री और गणितज्ञ)]] द्वारा विज्ञान में पहले ही किया जा चुका था।<ref>{{harvnb|Kline|1972|pp=442, 464}}.</ref> | ||
टेलर का प्रमेय परिचयात्मक-स्तर के कैलकुलस पाठ्यक्रमों में पढ़ाया जाता है और [[गणितीय विश्लेषण]] में केंद्रीय प्राथमिक उपकरणों में से एक है। यह घातांकीय फलन और [[त्रिकोणमितीय फलन]] जैसे कई पारलौकिक फलनों के मानों की सटीक गणना करने के लिए सरल अंकगणितीय सूत्र देता है। | टेलर का प्रमेय परिचयात्मक-स्तर के कैलकुलस पाठ्यक्रमों में पढ़ाया जाता है और [[गणितीय विश्लेषण]] में केंद्रीय प्राथमिक उपकरणों में से एक है। यह घातांकीय फलन और [[त्रिकोणमितीय फलन]] जैसे कई पारलौकिक फलनों के मानों की सटीक गणना करने के लिए सरल अंकगणितीय सूत्र देता है। | ||
यह [[विश्लेषणात्मक कार्य]]ों के अध्ययन का प्रारंभिक बिंदु है, और गणित के विभिन्न क्षेत्रों के साथ-साथ [[संख्यात्मक विश्लेषण]] और [[गणितीय भौतिकी]] में भी मौलिक है। टेलर का प्रमेय बहुभिन्नरूपी | यह [[विश्लेषणात्मक कार्य]]ों के अध्ययन का प्रारंभिक बिंदु है, और गणित के विभिन्न क्षेत्रों के साथ-साथ [[संख्यात्मक विश्लेषण]] और [[गणितीय भौतिकी]] में भी मौलिक है। टेलर का प्रमेय बहुभिन्नरूपी फलन और [[वेक्टर मूल्यवान फ़ंक्शन|आलेख मूल्यवान फलन]] फलन का भी सामान्यीकरण करता है। | ||
== प्रेरणा == | == प्रेरणा == | ||
का आलेख <math display="inline">f(x)=e^x</math> (नीला) इसके रैखिक सन्निकटन के साथ <math display="inline">P_1(x)=1+x</math> (लाल)पर <math display="inline">a=0</math>. | |||
यदि एक वास्तविक-मूल्यवान [[फ़ंक्शन (गणित)]] <math display="inline">f(x)</math> बिंदु पर व्युत्पन्न है <math display="inline">x=a</math>, तो इस बिंदु के निकट इसका एक रैखिक सन्निकटन होता है। इसका | यदि एक वास्तविक-मूल्यवान [[फ़ंक्शन (गणित)|फलन (गणित)]] <math display="inline">f(x)</math> बिंदु पर व्युत्पन्न है <math display="inline">x=a</math>, तो इस बिंदु के निकट इसका एक रैखिक सन्निकटन होता है। इसका अर्थ है कि एक फलन h उपस्थित है<sub>1</sub>(x) ऐसा कि | ||
<math display="block"> f(x) = f(a) + f'(a)(x - a) + h_1(x)(x - a), \quad \lim_{x \to a} h_1(x) = 0.</math> | <math display="block"> f(x) = f(a) + f'(a)(x - a) + h_1(x)(x - a), \quad \lim_{x \to a} h_1(x) = 0.</math> | ||
| Line 17: | Line 17: | ||
<math display="block">P_1(x) = f(a) + f'(a)(x - a)</math> | <math display="block">P_1(x) = f(a) + f'(a)(x - a)</math> | ||
का रैखिक सन्निकटन है <math display="inline">f(x)</math> बिंदु a के निकट x के लिए, जिसका | का रैखिक सन्निकटन है <math display="inline">f(x)</math> बिंदु a के निकट x के लिए, जिसका आलेख़ <math display="inline">y=P_1(x)</math> आलेख़ की [[स्पर्श रेखा]] है <math display="inline">y=f(x)</math> पर {{nowrap|1=''x'' = ''a''}}. सन्निकटन में त्रुटि है: | ||
<math display="block">R_1(x) = f(x) - P_1(x) = h_1(x)(x - a).</math> | <math display="block">R_1(x) = f(x) - P_1(x) = h_1(x)(x - a).</math> | ||
जैसे-जैसे x, a की ओर बढ़ता है, यह त्रुटि उससे कहीं अधिक | जैसे-जैसे x, a की ओर बढ़ता है, यह त्रुटि उससे कहीं अधिक तीव्रता से शून्य हो जाती है <math>f'(a)(x{-}a)</math>, बनाना <math>f(x)\approx P_1(x)</math> एक उपयोगी सन्निकटन. | ||
का आलेख <math display="inline">f(x)=e^x</math> (नीला) अपने द्विघात सन्निकटन के साथ <math>P_2(x) = 1 +x + \dfrac{x^2}{2}</math> (लाल)पर <math display="inline">a=0</math>. सन्निकटन में सुधार पर ध्यान दें. | |||
बेहतर सन्निकटन के लिए <math display="inline">f(x)</math>, हम एक रैखिक फलन के बजाय एक [[द्विघात बहुपद]] | बेहतर सन्निकटन के लिए <math display="inline">f(x)</math>, हम एक रैखिक फलन के बजाय एक [[द्विघात बहुपद]] उपयुक्त कर सकते हैं: | ||
<math display="block">P_2(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2}(x - a)^2.</math> | <math display="block">P_2(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2}(x - a)^2.</math> | ||
| Line 33: | Line 33: | ||
<math display="block">R_2(x) = f(x) - P_2(x) = h_2(x)(x - a)^2,</math> | <math display="block">R_2(x) = f(x) - P_2(x) = h_2(x)(x - a)^2,</math> | ||
जो, के सीमित व्यवहार को देखते हुए <math>h_2</math>की तुलना में | जो, के सीमित व्यवहार को देखते हुए <math>h_2</math>की तुलना में तीव्रता से शून्य पर चला जाता है <math>(x - a)^2</math> जैसे कि x, a की ओर प्रवृत्त होता है। | ||
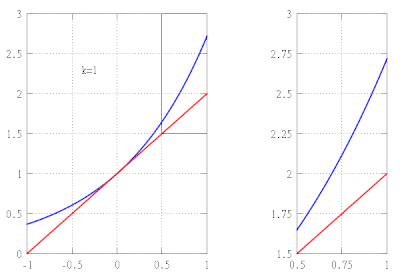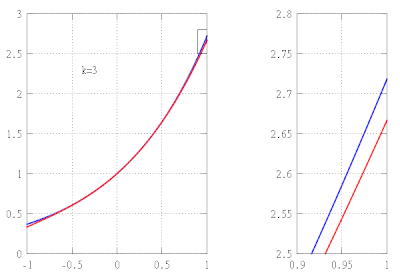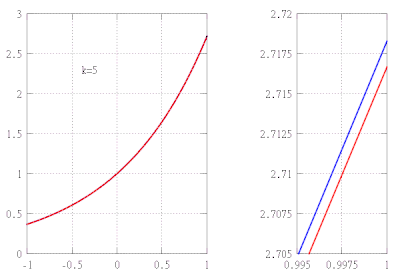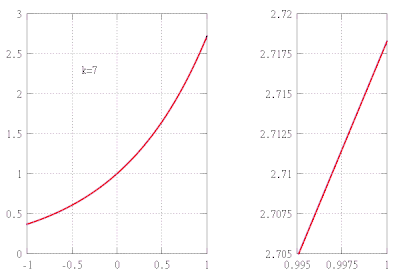
[[File:Tayloranimation.gif|thumb|360px|right|का अनुमान <math display="inline">f(x)= \dfrac{1}{1+x^2}</math> (नीला) इसके टेलर बहुपद द्वारा <math display="inline">P_k</math> आदेश की <math display="inline">k=1,\ldots,16</math> पर केन्द्रित <math display="inline">x=0</math> (लाल) और <math display="inline">x=1</math> (हरा)। बाहर अनुमानों में बिल्कुल भी सुधार नहीं होता <math>(-1,1)</math> और <math display="inline">(1-\sqrt{2}, 1+\sqrt{2})</math>, क्रमश।]]इसी प्रकार, यदि हम उच्च डिग्री के बहुपदों का उपयोग करते हैं तो हमें f के और भी बेहतर सन्निकटन प्राप्त हो सकते हैं, तब से हम चयनित आधार बिंदु पर f के साथ और भी अधिक व्युत्पन्नों का मिलान कर सकते हैं। | [[File:Tayloranimation.gif|thumb|360px|right|का अनुमान <math display="inline">f(x)= \dfrac{1}{1+x^2}</math> (नीला) इसके टेलर बहुपद द्वारा <math display="inline">P_k</math> आदेश की <math display="inline">k=1,\ldots,16</math> पर केन्द्रित <math display="inline">x=0</math> (लाल) और <math display="inline">x=1</math> (हरा)। बाहर अनुमानों में बिल्कुल भी सुधार नहीं होता <math>(-1,1)</math> और <math display="inline">(1-\sqrt{2}, 1+\sqrt{2})</math>, क्रमश।]]इसी प्रकार, यदि हम उच्च डिग्री के बहुपदों का उपयोग करते हैं तो हमें f के और भी बेहतर सन्निकटन प्राप्त हो सकते हैं, तब से हम चयनित आधार बिंदु पर f के साथ और भी अधिक व्युत्पन्नों का मिलान कर सकते हैं। | ||
सामान्य तौर पर, डिग्री k के बहुपद द्वारा किसी | सामान्य तौर पर, डिग्री k के बहुपद द्वारा किसी फलन का अनुमान लगाने में त्रुटि बहुत तीव्रता से शून्य हो जाएगी <math>(x-a)^k</math> जैसे कि x, a की ओर प्रवृत्त होता है। हालाँकि, ऐसे फलन हैं, यहां तक कि असीम रूप से भिन्न भी, जिनके लिए अनुमानित बहुपद की डिग्री बढ़ाने से सन्निकटन की सटीकता में वृद्धि नहीं होती है: हम कहते हैं कि ऐसा फलन x = a पर विश्लेषणात्मक फलन होने में विफल रहता है: यह (स्थानीय रूप से) इस बिंदु पर इसके अवकलज द्वारा निर्धारित नहीं होता है। | ||
टेलर का प्रमेय स्पर्शोन्मुख प्रकृति का है: यह हमें केवल यह बताता है कि त्रुटि हुई है <math display="inline">R_k</math> ए द्वारा एक अनुमान में <math display="inline">k</math>-वें क्रम का टेलर बहुपद पी<sub>k</sub>किसी भी गैर-शून्य की तुलना में | टेलर का प्रमेय स्पर्शोन्मुख प्रकृति का है: यह हमें केवल यह बताता है कि त्रुटि हुई है <math display="inline">R_k</math> ए द्वारा एक अनुमान में <math display="inline">k</math>-वें क्रम का टेलर बहुपद पी<sub>k</sub>किसी भी गैर-शून्य की तुलना में तीव्रता से शून्य हो जाता है <math display="inline">k</math>-वें डिग्री बहुपद के रूप में <math display="inline">x \to a</math>. यह हमें नहीं बताता कि विस्तार के केंद्र के किसी ठोस [[पड़ोस (गणित)]] में त्रुटि कितनी बड़ी है, लेकिन इस उद्देश्य के लिए शेष पद (नीचे दिए गए) के लिए स्पष्ट सूत्र हैं जो एफ पर कुछ अतिरिक्त नियमितता मान्यताओं के अंतर्गत मान्य हैं। टेलर के प्रमेय के ये उन्नत संस्करण आम तौर पर विस्तार के केंद्र के एक छोटे से पड़ोस में सन्निकटन त्रुटि के लिए एक समान अभिसरण की ओर ले जाते हैं, लेकिन अनुमान आवश्यक रूप से उन पड़ोस के लिए नहीं होते हैं जो बहुत बड़े हैं, भले ही फलन एफ विश्लेषणात्मक फलन हो। उस स्थिति में किसी को मूल फलन के विश्वसनीय टेलर-अनुमान प्राप्त करने के लिए विस्तार के विभिन्न केंद्रों के साथ कई टेलर बहुपदों का चयन करना पड़ सकता है (दाईं ओर एनीमेशन देखें।) | ||
ऐसे कई तरीके हैं जिनसे हम शेष पद का उपयोग कर सकते हैं: | ऐसे कई तरीके हैं जिनसे हम शेष पद का उपयोग कर सकते हैं: | ||
| Line 68: | Line 68: | ||
<math display="block">P_k(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k </math> | <math display="block">P_k(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k </math> | ||
बिंदु a पर फलन f का। टेलर बहुपद इस अर्थ में अद्वितीय स्पर्शोन्मुख सबसे उपयुक्त बहुपद है कि यदि कोई | बिंदु a पर फलन f का। टेलर बहुपद इस अर्थ में अद्वितीय स्पर्शोन्मुख सबसे उपयुक्त बहुपद है कि यदि कोई फलन उपस्थित है {{nowrap|''h<sub>k</sub>'' : '''R''' → '''R'''}} और ए <math display="inline">k</math>-वें क्रम का बहुपद p इस प्रकार है कि | ||
<math display="block"> f(x) = p(x) + h_k(x)(x-a)^k, \quad \lim_{x\to a} h_k(x) = 0 ,</math> | <math display="block"> f(x) = p(x) + h_k(x)(x-a)^k, \quad \lim_{x\to a} h_k(x) = 0 ,</math> | ||
| Line 81: | Line 81: | ||
=== शेषफल के लिए स्पष्ट सूत्र === | === शेषफल के लिए स्पष्ट सूत्र === | ||
एफ पर | एफ पर प्रबल नियमितता मान्यताओं के अंतर्गत शेष पद आर के लिए कई सटीक सूत्र हैं<sub>k</sub>टेलर बहुपद में से सबसे आम निम्नलिखित हैं। | ||
{{math theorem | {{math theorem | ||
| Line 98: | Line 98: | ||
}} | }} | ||
टेलर के प्रमेय के ये परिशोधन | टेलर के प्रमेय के ये परिशोधन सामान्यतः [[माध्य मान प्रमेय]] का उपयोग करके सिद्ध किए जाते हैं, जहां से यह नाम पड़ा है। इसके अतिरिक्त, ध्यान दें कि यह बिल्कुल माध्य मान प्रमेय है जब <math display="inline">k=0</math>. इसके अतिरिक्त अन्य समान अभिव्यक्तियाँ भी पाई जा सकती हैं। उदाहरण के लिए, यदि G(t) संवृत अंतराल पर निरंतर है और मध्य के विवृत अंतराल पर एक गैर-लुप्त व्युत्पन्न के साथ भिन्न है <math display=inline>a</math> और <math display=inline>x</math>, तब | ||
<math display="block"> R_k(x) = \frac{f^{(k+1)}(\xi)}{k!}(x-\xi)^k \frac{G(x)-G(a)}{G'(\xi)} </math> | <math display="block"> R_k(x) = \frac{f^{(k+1)}(\xi)}{k!}(x-\xi)^k \frac{G(x)-G(a)}{G'(\xi)} </math> | ||
कुछ संख्या के लिए <math display="inline">\xi</math> | कुछ संख्या के लिए <math display="inline">\xi</math> मध्य में <math display=inline>a</math> और <math display=inline>x</math>. यह संस्करण विशेष स्थितियों के रूप में शेष के लैग्रेंज और कॉची रूपों को सम्मिलित करता है, और नीचे माध्य मान प्रमेय#कॉची का माध्य मान प्रमेय|कॉची का माध्य मान प्रमेय का उपयोग करके सिद्ध किया गया है। लैग्रेंज फॉर्म लेने से प्राप्त होता है <math>G(t)=(x-t)^{k+1}</math> और कॉची रूप लेने से प्राप्त होता है <math>G(t)=t-a</math>. | ||
शेषफल के अभिन्न रूप के लिए बयान पिछले वाले की तुलना में अधिक उन्नत है, और पूर्ण व्यापकता के लिए लेबेसेग अभिन्न की समझ की आवश्यकता है। हालाँकि, यह [[ रीमैन अभिन्न ]] के अर्थ में भी | शेषफल के अभिन्न रूप के लिए बयान पिछले वाले की तुलना में अधिक उन्नत है, और पूर्ण व्यापकता के लिए लेबेसेग अभिन्न की समझ की आवश्यकता है। हालाँकि, यह [[ रीमैन अभिन्न ]] के अर्थ में भी अनुप्रयुक्त है, बशर्ते कि f का (k+1)वां व्युत्पन्न संवृत अंतराल [a,x] पर निरंतर हो। | ||
{{math theorem|name=Integral form of the remainder<ref>{{harvnb|Apostol|1967|loc=§7.5}}.</ref> |math_statement=Let <math display=inline>f^{(k)}</math> be [[absolutely continuous]] on the [[closed interval]] between <math display=inline>a</math> and <math display=inline>x</math>. Then | {{math theorem|name=Integral form of the remainder<ref>{{harvnb|Apostol|1967|loc=§7.5}}.</ref> |math_statement=Let <math display=inline>f^{(k)}</math> be [[absolutely continuous]] on the [[closed interval]] between <math display=inline>a</math> and <math display=inline>x</math>. Then | ||
| Line 111: | Line 111: | ||
}} | }} | ||
एफ के [[बिल्कुल निरंतर]] होने के कारण{{i sup|(''k'')}} के | एफ के [[बिल्कुल निरंतर]] होने के कारण{{i sup|(''k'')}} के मध्य [[बंद अंतराल|संवृत अंतराल]] पर <math display=inline>a</math> और <math display=inline>x</math>, इसका व्युत्पन्न एफ{{i sup|(''k''+1)}} एल के रूप में उपस्थित है{{i sup|1}}-फलन, और परिणाम को कैलकुलस के मौलिक प्रमेय और [[भागों द्वारा एकीकरण]] का उपयोग करके औपचारिक गणना द्वारा सिद्ध किया जा सकता है। | ||
===शेष के लिए अनुमान === | ===शेष के लिए अनुमान === | ||
टेलर सन्निकटन में दिखाई देने वाले शेष पद का अनुमान लगाने में सक्षम होना, इसके लिए एक सटीक सूत्र होने के बजाय, व्यवहार में | टेलर सन्निकटन में दिखाई देने वाले शेष पद का अनुमान लगाने में सक्षम होना, इसके लिए एक सटीक सूत्र होने के बजाय, व्यवहार में प्रायः उपयोगी होता है। मान लीजिए कि एफ है {{nowrap|(''k'' + 1)}}-अंतराल I में कई बार लगातार अंतर होता है जिसमें a होता है। मान लीजिए कि ऐसे वास्तविक स्थिरांक q और Q हैं | ||
<math display="block">q\le f^{(k+1)}(x)\le Q</math> | <math display="block">q\le f^{(k+1)}(x)\le Q</math> | ||
| Line 121: | Line 121: | ||
<math display="block">q\frac{(x-a)^{k+1}}{(k+1)!}\le R_k(x)\le Q\frac{(x-a)^{k+1}}{(k+1)!},</math> | <math display="block">q\frac{(x-a)^{k+1}}{(k+1)!}\le R_k(x)\le Q\frac{(x-a)^{k+1}}{(k+1)!},</math> | ||
यदि {{nowrap|''x'' > ''a''}}, और एक समान अनुमान यदि {{nowrap|''x'' < ''a''}}. यह शेषफल के लैग्रेंज रूप का एक सरल परिणाम है। विशेषकर, यदि | |||
<math display="block">|f^{(k+1)}(x)|\le M</math> | <math display="block">|f^{(k+1)}(x)|\le M</math> | ||
| Line 131: | Line 131: | ||
=== उदाहरण === | === उदाहरण === | ||
[[File:Expanimation.gif|thumb|400px|right|का अनुमान <math display="inline">e^x</math> (नीला) इसके टेलर बहुपद द्वारा <math>P_k</math> आदेश की <math display="inline">k=1,\ldots,7</math> पर केन्द्रित <math display="inline">x=0</math> (लाल)।]]मान लीजिए कि हम | [[File:Expanimation.gif|thumb|400px|right|का अनुमान <math display="inline">e^x</math> (नीला) इसके टेलर बहुपद द्वारा <math>P_k</math> आदेश की <math display="inline">k=1,\ldots,7</math> पर केन्द्रित <math display="inline">x=0</math> (लाल)।]]मान लीजिए कि हम फलन का अनुमानित मान ज्ञात करना चाहते हैं <math display="inline">f(x)=e^x</math> अंतराल पर <math display="inline">[-1,1]</math> यह सुनिश्चित करते हुए कि अनुमान में त्रुटि 10 से अधिक न हो<sup>−5</sup>. इस उदाहरण में हम दिखावा करते हैं कि हम घातीय फलन के केवल निम्नलिखित गुणों को जानते हैं: | ||
{{NumBlk|:|<math>e^0=1, \qquad \frac{d}{dx} e^x = e^x, \qquad e^x>0, \qquad x\in\R.</math>|{{EquationRef|★}}}} | {{NumBlk|:|<math>e^0=1, \qquad \frac{d}{dx} e^x = e^x, \qquad e^x>0, \qquad x\in\R.</math>|{{EquationRef|★}}}} | ||
| Line 138: | Line 138: | ||
<math display="block"> P_k(x) = 1+x+\frac{x^2}{2!}+\cdots+\frac{x^k}{k!}, \qquad R_k(x)=\frac{e^\xi}{(k+1)!}x^{k+1},</math> | <math display="block"> P_k(x) = 1+x+\frac{x^2}{2!}+\cdots+\frac{x^k}{k!}, \qquad R_k(x)=\frac{e^\xi}{(k+1)!}x^{k+1},</math> | ||
जहाँ <math display="inline">\xi</math> 0 और x के मध्य कोई संख्या है. चूँकि ई<sup>x</sup> बढ़ रहा है ({{EquationNote|★}}), हम बस उपयोग कर सकते हैं <math display="inline">e^x \leq 1</math> के लिए <math display="inline">x \in [-1,0]</math> उपअंतराल पर शेषफल का अनुमान लगाने के लिए <math>[-1,0]</math>. शेष के लिए ऊपरी सीमा प्राप्त करने के लिए <math>[0,1]</math>, हम गुणधर्म का उपयोग करते हैं <math display="inline">e^\xi <e^x</math> के लिए <math display="inline">0<\xi<x</math> अंदाज़ा लगाने के लिए | |||
<math display="block"> e^x = 1 + x + \frac{e^\xi}{2}x^2 < 1 + x + \frac{e^x}{2}x^2, \qquad 0 < x\leq 1 </math> | <math display="block"> e^x = 1 + x + \frac{e^\xi}{2}x^2 < 1 + x + \frac{e^x}{2}x^2, \qquad 0 < x\leq 1 </math> | ||
| Line 160: | Line 160: | ||
=== टेलर वास्तविक विश्लेषणात्मक कार्यों का विस्तार === | === टेलर वास्तविक विश्लेषणात्मक कार्यों का विस्तार === | ||
मान लीजिए I ⊂ 'R' एक [[खुला अंतराल]] है। परिभाषा के अनुसार, एक | मान लीजिए I ⊂ 'R' एक [[खुला अंतराल|विवृत अंतराल]] है। परिभाषा के अनुसार, एक फलन f: I → 'R' एक विश्लेषणात्मक फलन है यदि इसे स्थानीय रूप से एक अभिसरण शक्ति श्रृंखला द्वारा परिभाषित किया गया है। इसका अर्थ यह है कि प्रत्येक a ∈ I के लिए कुछ r > 0 और गुणांक c का एक क्रम उपस्थित होता है<sub>k</sub>∈ 'आर' ऐसे कि {{nowrap|(''a'' − ''r'', ''a'' + ''r'') ⊂ ''I''}} और | ||
<math display="block"> f(x) = \sum_{k=0}^\infty c_k(x-a)^k = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots, \qquad |x-a|<r. </math> | <math display="block"> f(x) = \sum_{k=0}^\infty c_k(x-a)^k = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots, \qquad |x-a|<r. </math> | ||
| Line 166: | Line 166: | ||
<math display="block"> \frac{1}{R} = \limsup_{k\to\infty}|c_k|^\frac{1}{k}. </math> | <math display="block"> \frac{1}{R} = \limsup_{k\to\infty}|c_k|^\frac{1}{k}. </math> | ||
यह परिणाम एक ज्यामितीय श्रृंखला के साथ तुलना पर आधारित है, और एक ही विधि से पता चलता है कि यदि किसी पर आधारित शक्ति श्रृंखला कुछ बी ∈ 'आर' के लिए अभिसरण करती है, तो उसे | यह परिणाम एक ज्यामितीय श्रृंखला के साथ तुलना पर आधारित है, और एक ही विधि से पता चलता है कि यदि किसी पर आधारित शक्ति श्रृंखला कुछ बी ∈ 'आर' के लिए अभिसरण करती है, तो उसे संवृत अंतराल पर एक समान अभिसरण अभिसरण करना होगा <math display="inline">[a-r_b,a+r_b]</math>, जहाँ <math display="inline">r_b=\left\vert b-a \right\vert</math>. यहां केवल शक्ति श्रृंखला के अभिसरण पर विचार किया गया है, और यह संभवतः ऐसा ही हो सकता है {{nowrap|(''a'' − ''R'',''a'' + ''R'')}} f के डोमेन I से आगे तक फैला हुआ है। | ||
वास्तविक विश्लेषणात्मक फलन f के टेलर बहुपद केवल परिमित | वास्तविक विश्लेषणात्मक फलन f के टेलर बहुपद केवल परिमित खंडन हैं | ||
<math display="block"> P_k(x) = \sum_{j=0}^k c_j(x-a)^j, \qquad c_j = \frac{f^{(j)}(a)}{j!}</math> | <math display="block"> P_k(x) = \sum_{j=0}^k c_j(x-a)^j, \qquad c_j = \frac{f^{(j)}(a)}{j!}</math> | ||
| Line 180: | Line 180: | ||
& h_k(x) = (x-a)\sum_{j=0}^\infty c_{k+1+j} \left(x - a\right)^j | & h_k(x) = (x-a)\sum_{j=0}^\infty c_{k+1+j} \left(x - a\right)^j | ||
\end{align}</math> | \end{align}</math> | ||
विश्लेषणात्मक भी हैं, क्योंकि उनकी परिभाषित शक्ति श्रृंखला में मूल श्रृंखला के समान अभिसरण की त्रिज्या है। ये मानते हुए {{nowrap|[''a'' − ''r'', ''a'' + ''r'']}} ⊂ I और r<R, ये सभी श्रृंखलाएं समान रूप से अभिसरित होती हैं {{nowrap|(''a'' − ''r'', ''a'' + ''r'')}}. स्वाभाविक रूप से, विश्लेषणात्मक कार्यों के | विश्लेषणात्मक भी हैं, क्योंकि उनकी परिभाषित शक्ति श्रृंखला में मूल श्रृंखला के समान अभिसरण की त्रिज्या है। ये मानते हुए {{nowrap|[''a'' − ''r'', ''a'' + ''r'']}} ⊂ I और r<R, ये सभी श्रृंखलाएं समान रूप से अभिसरित होती हैं {{nowrap|(''a'' − ''r'', ''a'' + ''r'')}}. स्वाभाविक रूप से, विश्लेषणात्मक कार्यों के स्थिति में कोई शेष पद का अनुमान लगा सकता है <math display="inline">R_k(x)</math> विस्तार के केंद्र में व्युत्पन्न f'(a) के अनुक्रम की पश्चभाग से, लेकिन [[जटिल विश्लेषण]] का उपयोग करने से एक और संभावना भी उत्पन्न होती है, जिसे टेलर के प्रमेय#विश्लेषणात्मकता से संबंध##जटिल विश्लेषण में टेलर के प्रमेय द्वारा वर्णित किया गया है। | ||
=== टेलर का प्रमेय और टेलर श्रृंखला का अभिसरण === | === टेलर का प्रमेय और टेलर श्रृंखला का अभिसरण === | ||
एफ की टेलर श्रृंखला कुछ अंतराल में अभिसरण करेगी जिसमें इसके सभी | एफ की टेलर श्रृंखला कुछ अंतराल में अभिसरण करेगी जिसमें इसके सभी अवकलज बंधे हुए हैं और बहुत तीव्रता से नहीं बढ़ते हैं क्योंकि के अनंत तक जाता है। (हालाँकि, भले ही टेलर श्रृंखला अभिसरण करती है, यह एफ में परिवर्तित नहीं हो सकती है, जैसा कि नीचे बताया गया है; तब एफ को गैर-विश्लेषणात्मक फलन कहा जाता है।) | ||
कोई टेलर श्रृंखला के | कोई टेलर श्रृंखला के विषय में विचार कर सकता है | ||
<math display="block"> f(x) \approx \sum_{k=0}^\infty c_k(x-a)^k = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots </math> | <math display="block"> f(x) \approx \sum_{k=0}^\infty c_k(x-a)^k = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots </math> | ||
एक अपरिमित रूप से अनेक बार अवकलनीय फलन f : 'R' → 'R' के अनंत क्रम टेलर बहुपद के रूप में। अब शेषफल के लिए टेलर के प्रमेय # अनुमान का अर्थ है कि यदि, किसी भी आर के लिए, एफ के व्युत्पन्न को (ए - आर, ए + आर) से घिरा हुआ माना जाता है, तो किसी भी क्रम के के लिए और किसी भी आर > 0 के लिए एक स्थिरांक | एक अपरिमित रूप से अनेक बार अवकलनीय फलन f : 'R' → 'R' के अनंत क्रम टेलर बहुपद के रूप में। अब शेषफल के लिए टेलर के प्रमेय # अनुमान का अर्थ है कि यदि, किसी भी आर के लिए, एफ के व्युत्पन्न को (ए - आर, ए + आर) से घिरा हुआ माना जाता है, तो किसी भी क्रम के के लिए और किसी भी आर > 0 के लिए एक स्थिरांक उपस्थित होता है {{nowrap|''M<sub>k,r</sub>'' > 0}} ऐसा है कि | ||
{{NumBlk|:|<math> |R_k(x)| \leq M_{k,r} \frac{|x-a|^{k+1}}{(k+1)!} </math>|{{EquationRef|★★}}}} | {{NumBlk|:|<math> |R_k(x)| \leq M_{k,r} \frac{|x-a|^{k+1}}{(k+1)!} </math>|{{EquationRef|★★}}}} | ||
प्रत्येक x ∈ (a − r,a + r) के लिए। कभी-कभी स्थिरांक {{nowrap|''M<sub>k,r</sub>''}} को इस तरह से चुना जा सकता है {{nowrap|''M<sub>k,r</sub>''}} निश्चित r और सभी k के लिए ऊपर परिबद्ध है। फिर कुछ विश्लेषणात्मक | प्रत्येक x ∈ (a − r,a + r) के लिए। कभी-कभी स्थिरांक {{nowrap|''M<sub>k,r</sub>''}} को इस तरह से चुना जा सकता है {{nowrap|''M<sub>k,r</sub>''}} निश्चित r और सभी k के लिए ऊपर परिबद्ध है। फिर कुछ विश्लेषणात्मक फलन के लिए एफ वर्दी अभिसरण की टेलर श्रृंखला | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 201: | Line 201: | ||
(किसी को अभिसरण भी मिलता है भले ही {{nowrap|''M<sub>k,r</sub>''}}जब तक यह धीरे-धीरे बढ़ता है तब तक ऊपर सीमित नहीं है।) | (किसी को अभिसरण भी मिलता है भले ही {{nowrap|''M<sub>k,r</sub>''}}जब तक यह धीरे-धीरे बढ़ता है तब तक ऊपर सीमित नहीं है।) | ||
सीमा समारोह {{nowrap|''T<sub>f</sub>''}} परिभाषा के अनुसार | सीमा समारोह {{nowrap|''T<sub>f</sub>''}} परिभाषा के अनुसार सदैव विश्लेषणात्मक होता है, लेकिन यह जरूरी नहीं कि मूल फलन f के बराबर हो, भले ही f असीम रूप से भिन्न हो। इस स्थिति में, हम कहते हैं कि f एक गैर-विश्लेषणात्मक सहज फलन है, उदाहरण के लिए एक [[समतल कार्य]]: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 216: | Line 216: | ||
0 & x \leq 0 | 0 & x \leq 0 | ||
\end{cases}</math> | \end{cases}</math> | ||
कुछ बहुपद पी के लिए<sub>k</sub>डिग्री 2(k − 1) की। कार्यक्रम <math>e^{-\frac{1}{x^2}}</math> किसी भी बहुपद की तुलना में | कुछ बहुपद पी के लिए<sub>k</sub>डिग्री 2(k − 1) की। कार्यक्रम <math>e^{-\frac{1}{x^2}}</math> किसी भी बहुपद की तुलना में तीव्रता से शून्य हो जाता है <math display="inline">x \to 0</math>, इसलिए f अपरिमित रूप से कई गुना भिन्न है और {{nowrap|1=''f''{{i sup|(''k'')}}(0) = 0}} प्रत्येक धनात्मक पूर्णांक k के लिए। उपरोक्त सभी परिणाम इस स्थिति में मान्य हैं: | ||
* एफ की टेलर श्रृंखला शून्य | * एफ की टेलर श्रृंखला शून्य फलन टी में समान रूप से परिवर्तित होती है<sub>f</sub>(x)=0, जो शून्य के बराबर सभी गुणांकों के साथ विश्लेषणात्मक है। | ||
* | * फलन f इस टेलर श्रृंखला के बराबर नहीं है, और इसलिए गैर-विश्लेषणात्मक है। | ||
* किसी भी क्रम k ∈ 'N' और त्रिज्या r > 0 के लिए M | * किसी भी क्रम k ∈ 'N' और त्रिज्या r > 0 के लिए M उपस्थित है<sub>k,r</sub>> 0 शेष सीमा को संतुष्ट करना ({{EquationNote|★★}}) ऊपर। | ||
हालाँकि, जैसे-जैसे k निश्चित r के लिए बढ़ता है, M का मान बढ़ता है<sub>k,r</sub>आर की तुलना में अधिक तेज़ी से बढ़ता है<sup>k</sup>, और त्रुटि शून्य पर नहीं जाती है। | हालाँकि, जैसे-जैसे k निश्चित r के लिए बढ़ता है, M का मान बढ़ता है<sub>k,r</sub>आर की तुलना में अधिक तेज़ी से बढ़ता है<sup>k</sup>, और त्रुटि शून्य पर नहीं जाती है। | ||
=== जटिल विश्लेषण में टेलर का प्रमेय === | === जटिल विश्लेषण में टेलर का प्रमेय === | ||
टेलर का प्रमेय फ़ंक्शंस f: 'C' → 'C' को सामान्यीकृत करता है जो [[जटिल विमान]] के एक | टेलर का प्रमेय फ़ंक्शंस f: 'C' → 'C' को सामान्यीकृत करता है जो [[जटिल विमान]] के एक विवृत उपसमुच्चय U ⊂ 'C' में जटिल रूप से भिन्न होते हैं। हालाँकि, जटिल विश्लेषण में इसकी उपयोगिता अन्य सामान्य प्रमेयों से कम है। अर्थात्, कॉची के अभिन्न सूत्र का उपयोग करके जटिल विभेदक कार्यों f : U → 'C' के लिए संबंधित परिणामों के प्रबल संस्करण निम्नानुसार निकाले जा सकते हैं। | ||
मान लीजिए r > 0 इस प्रकार है कि [[बंद डिस्क]] B(z,r) ∪S(z,r) U में समाहित है। फिर एक सकारात्मक पैरामीट्रिजेशन के साथ कॉची का अभिन्न सूत्र {{nowrap|1=''γ''(''t'') = ''z'' + ''re<sup>it</sup>''}} वृत्त S(z, r) के साथ <math>t \in [0,2 \pi]</math> देता है | मान लीजिए r > 0 इस प्रकार है कि [[बंद डिस्क|संवृत डिस्क]] B(z,r) ∪S(z,r) U में समाहित है। फिर एक सकारात्मक पैरामीट्रिजेशन के साथ कॉची का अभिन्न सूत्र {{nowrap|1=''γ''(''t'') = ''z'' + ''re<sup>it</sup>''}} वृत्त S(z, r) के साथ <math>t \in [0,2 \pi]</math> देता है | ||
<math display="block">f(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(w)}{w-z}\,dw, \quad f'(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(w)}{(w-z)^2} \, dw, \quad \ldots, \quad f^{(k)}(z) = \frac{k!}{2\pi i}\int_\gamma \frac{f(w)}{(w-z)^{k+1}} \, dw.</math> | <math display="block">f(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(w)}{w-z}\,dw, \quad f'(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(w)}{(w-z)^2} \, dw, \quad \ldots, \quad f^{(k)}(z) = \frac{k!}{2\pi i}\int_\gamma \frac{f(w)}{(w-z)^{k+1}} \, dw.</math> | ||
यहां सभी इंटीग्रैंड [[घेरा]] S(z,r) पर निरंतर हैं, जो | यहां सभी इंटीग्रैंड [[घेरा]] S(z,r) पर निरंतर हैं, जो समाकल चिह्न के अंतर्गत भेदभाव को उचित ठहराता है। विशेष रूप से, यदि विवृत समुच्चय U पर f एक बार जटिल अवकलनीय है, तो यह वास्तव में U पर अनंत बार जटिल अवकलनीय है। एक व्यक्ति कॉची के अनुमान भी प्राप्त करता है<ref>{{harvnb|Rudin|1987|loc=§10.26}}</ref> | ||
<math display="block"> |f^{(k)}(z)| \leq \frac{k!}{2\pi}\int_\gamma \frac{M_r}{|w-z|^{k+1}} \, dw = \frac{k!M_r}{r^k}, \quad M_r = \max_{|w-c|=r}|f(w)| </math> | <math display="block"> |f^{(k)}(z)| \leq \frac{k!}{2\pi}\int_\gamma \frac{M_r}{|w-z|^{k+1}} \, dw = \frac{k!M_r}{r^k}, \quad M_r = \max_{|w-c|=r}|f(w)| </math> | ||
| Line 236: | Line 236: | ||
<math display="block"> T_f(z) = \sum_{k=0}^\infty \frac{f^{(k)}(c)}{k!}(z-c)^k </math> | <math display="block"> T_f(z) = \sum_{k=0}^\infty \frac{f^{(k)}(c)}{k!}(z-c)^k </math> | ||
f का किसी भी खुली डिस्क पर समान रूप से अभिसरण होता है <math display="inline">B(c,r) \subset U</math> साथ <math display="inline">S(c,r) \subset U</math> किसी | f का किसी भी खुली डिस्क पर समान रूप से अभिसरण होता है <math display="inline">B(c,r) \subset U</math> साथ <math display="inline">S(c,r) \subset U</math> किसी फलन में टी<sub>f</sub>. इसके अतिरिक्त, अवकलज एफ के लिए समोच्च अभिन्न सूत्रों का उपयोग करना{{i sup|(''k'')}}(सी), | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 244: | Line 244: | ||
&= \frac{1}{2\pi i} \int_\gamma \frac{f(w)}{w-z} \, dw = f(z), | &= \frac{1}{2\pi i} \int_\gamma \frac{f(w)}{w-z} \, dw = f(z), | ||
\end{align}</math> | \end{align}</math> | ||
इसलिए किसी | इसलिए किसी विवृत समुच्चय U ⊂ 'C' में कोई भी [[जटिल व्युत्पन्न]] फलन f वास्तव में [[जटिल विश्लेषणात्मक]] है। वास्तविक विश्लेषणात्मक कार्यों के लिए जो कुछ भी कहा गया है टेलर का प्रमेय#विश्लेषणात्मकता से संबंध##विश्लेषणात्मक कार्यों का टेलर विस्तार जटिल विश्लेषणात्मक कार्यों के लिए भी अनुप्रयुक्त होता है, जिसमें विवृत अंतराल I को एक विवृत उपसमुच्चय U ∈ 'C' द्वारा प्रतिस्थापित किया जाता है और a-केंद्रित अंतराल (a − r, a +r) को C-केंद्रित डिस्क B(c,r) द्वारा प्रतिस्थापित किया जाता है। विशेष रूप से, टेलर विस्तार फॉर्म में है | ||
<math display="block"> f(z) = P_k(z) + R_k(z), \quad P_k(z) = \sum_{j=0}^k \frac{f^{(j)}(c)}{j!}(z-c)^j, </math> | <math display="block"> f(z) = P_k(z) + R_k(z), \quad P_k(z) = \sum_{j=0}^k \frac{f^{(j)}(c)}{j!}(z-c)^j, </math> | ||
| Line 250: | Line 250: | ||
<math display="block"> R_k(z) = \sum_{j=k+1}^\infty \frac{(z-c)^j}{2\pi i} \int_\gamma \frac{f(w)}{(w-c)^{j+1}} \, dw = \frac{(z-c)^{k+1}}{2\pi i} \int_\gamma \frac{f(w) \, dw}{(w-c)^{k+1}(w-z)} , \qquad z\in W. </math> | <math display="block"> R_k(z) = \sum_{j=k+1}^\infty \frac{(z-c)^j}{2\pi i} \int_\gamma \frac{f(w)}{(w-c)^{j+1}} \, dw = \frac{(z-c)^{k+1}}{2\pi i} \int_\gamma \frac{f(w) \, dw}{(w-c)^{k+1}(w-z)} , \qquad z\in W. </math> | ||
यहां महत्वपूर्ण विशेषता यह है कि क्षेत्र पर टेलर बहुपद द्वारा सन्निकटन की गुणवत्ता <math display="inline">W \subset U</math> सीमा पर स्वयं | यहां महत्वपूर्ण विशेषता यह है कि क्षेत्र पर टेलर बहुपद द्वारा सन्निकटन की गुणवत्ता <math display="inline">W \subset U</math> सीमा पर स्वयं फलन f के मानों का प्रभुत्व है <math display="inline">\partial W \subset U</math>. इसी प्रकार, कॉची के अनुमानों को शेष के लिए श्रृंखला अभिव्यक्ति पर अनुप्रयुक्त करने से, एक समान अनुमान प्राप्त होता है | ||
<math display="block"> |R_k(z)| | <math display="block"> |R_k(z)| | ||
| Line 266: | Line 266: | ||
& f(x) = \frac{1}{1+x^2} | & f(x) = \frac{1}{1+x^2} | ||
\end{align}</math> | \end{align}</math> | ||
विश्लेषणात्मक कार्य है, अर्थात स्थानीय रूप से इसकी टेलर श्रृंखला द्वारा निर्धारित किया जाता है। इस | विश्लेषणात्मक कार्य है, अर्थात स्थानीय रूप से इसकी टेलर श्रृंखला द्वारा निर्धारित किया जाता है। इस फलन को इस तथ्य को स्पष्ट करने के लिए टेलर के प्रमेय#प्रेरणा के अनुसार तैयार किया गया था कि कुछ प्राथमिक कार्यों को विस्तार के केंद्र के पड़ोस में टेलर बहुपद द्वारा अनुमानित नहीं किया जा सकता है जो बहुत बड़े हैं। इस प्रकार के व्यवहार को जटिल विश्लेषण के ढांचे में आसानी से समझा जा सकता है। अर्थात्, फलन f एक [[मेरोमोर्फिक फ़ंक्शन|मेरोमोर्फिक फलन]] में विस्तारित होता है | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 278: | Line 278: | ||
=== उच्च-क्रम भिन्नता === | === उच्च-क्रम भिन्नता === | ||
एक | एक फलन f: 'R'<sup>n</sup> → 'R', 'a' ∈'R' से व्युत्पन्न है<sup>n</sup> यदि और केवल यदि कोई [[रैखिक कार्यात्मक]] L उपस्थित है: 'R'<sup>n</sup> → 'R' और एक फलन h : 'R'<sup>n</sup> → 'R' ऐसा कि | ||
<math display="block"> f(\boldsymbol{x}) = f(\boldsymbol{a}) + L(\boldsymbol{x}-\boldsymbol{a}) + h(\boldsymbol{x})\lVert\boldsymbol{x}-\boldsymbol{a}\rVert, | <math display="block"> f(\boldsymbol{x}) = f(\boldsymbol{a}) + L(\boldsymbol{x}-\boldsymbol{a}) + h(\boldsymbol{x})\lVert\boldsymbol{x}-\boldsymbol{a}\rVert, | ||
\qquad \lim_{\boldsymbol{x}\to\boldsymbol{a}}h(\boldsymbol{x})=0. </math> | \qquad \lim_{\boldsymbol{x}\to\boldsymbol{a}}h(\boldsymbol{x})=0. </math> | ||
यदि यही बात है तो <math display="inline">L=df(\boldsymbol{a})</math> बिंदु 'ए' पर एफ के एक फलन का (विशिष्ट रूप से परिभाषित) अंतर है। इसके अतिरिक्त, f का आंशिक व्युत्पन्न 'a' पर उपस्थित है और f का अंतर 'a' पर दिया गया है | |||
<math display="block"> df( \boldsymbol{a} )( \boldsymbol{v} ) = \frac{\partial f}{\partial x_1}(\boldsymbol{a})v_1 + \cdots + \frac{\partial f}{\partial x_n}(\boldsymbol{a})v_n. </math> | <math display="block"> df( \boldsymbol{a} )( \boldsymbol{v} ) = \frac{\partial f}{\partial x_1}(\boldsymbol{a})v_1 + \cdots + \frac{\partial f}{\partial x_n}(\boldsymbol{a})v_n. </math> | ||
| Line 288: | Line 288: | ||
<math display="block"> |\alpha| = \alpha_1+\cdots+\alpha_n, \quad \alpha!=\alpha_1!\cdots\alpha_n!, \quad \boldsymbol{x}^\alpha=x_1^{\alpha_1}\cdots x_n^{\alpha_n} </math> | <math display="block"> |\alpha| = \alpha_1+\cdots+\alpha_n, \quad \alpha!=\alpha_1!\cdots\alpha_n!, \quad \boldsymbol{x}^\alpha=x_1^{\alpha_1}\cdots x_n^{\alpha_n} </math> | ||
α∈'N' के लिए<sup>n</sup> और 'x' ∈ 'R'<sup>n</sup>. यदि सभी <math display="inline">k</math>-वें क्रम का आंशिक व्युत्पन्न {{nowrap|''f'' : '''R'''<sup>''n''</sup> → '''R'''}} पर निरंतर हैं {{nowrap|'''''a''''' ∈ '''R'''<sup>''n''</sup>}}, फिर दूसरे | α∈'N' के लिए<sup>n</sup> और 'x' ∈ 'R'<sup>n</sup>. यदि सभी <math display="inline">k</math>-वें क्रम का आंशिक व्युत्पन्न {{nowrap|''f'' : '''R'''<sup>''n''</sup> → '''R'''}} पर निरंतर हैं {{nowrap|'''''a''''' ∈ '''R'''<sup>''n''</sup>}}, फिर दूसरे अवकलज की समरूपता द्वारा|क्लेरौट के प्रमेय, कोई ''ए'' पर मिश्रित अवकलज के क्रम को बदल सकता है, इसलिए संकेतन | ||
<math display="block"> D^\alpha f = \frac{\partial^{|\alpha|}f}{\partial x_1^{\alpha_1}\cdots \partial x_n^{\alpha_n}}, \qquad |\alpha|\leq k </math> | <math display="block"> D^\alpha f = \frac{\partial^{|\alpha|}f}{\partial x_1^{\alpha_1}\cdots \partial x_n^{\alpha_n}}, \qquad |\alpha|\leq k </math> | ||
उच्च क्रम के लिए आंशिक | उच्च क्रम के लिए आंशिक अवकलज इस स्थिति में उचित है। यही बात सत्य है यदि f के सभी (k − 1)-वें क्रम के आंशिक व्युत्पन्न 'a' के किसी पड़ोस में उपस्थित हैं और 'a' पर भिन्न हैं।<ref>This follows from iterated application of the theorem that if the partial derivatives of a function ''f'' exist in a neighborhood of '''''a''''' and are continuous at '''''a''''', then the function is differentiable at '''''a'''''. See, for instance, {{harvnb|Apostol|1974|loc=Theorem 12.11}}.</ref> तब हम कहते हैं कि f, k 'बिंदु a पर कई गुना भिन्न है'। | ||
=== बहुभिन्नरूपी कार्यों के लिए टेलर का प्रमेय === | === बहुभिन्नरूपी कार्यों के लिए टेलर का प्रमेय === | ||
पिछले अनुभाग के | पिछले अनुभाग के अंकन पद्धति का उपयोग करते हुए, निम्नलिखित प्रमेय प्राप्त होता है। | ||
{{math theorem|name=Multivariate version of Taylor's theorem<ref>Königsberger Analysis 2, p. 64 ff.</ref>|math_statement= Let {{nowrap|''f'' : '''R'''<sup>''n''</sup> → '''R'''}} be a ''k''-times [[continuously differentiable]] function at the point {{nowrap|'''''a''''' ∈ '''R'''<sup>''n''</sup>}}. Then there exist functions {{math|''h''<sub>''α''</sub> : '''R'''<sup>''n''</sup> → '''R'''}}, where <math>|\alpha|=k,</math> such that | {{math theorem|name=Multivariate version of Taylor's theorem<ref>Königsberger Analysis 2, p. 64 ff.</ref>|math_statement= Let {{nowrap|''f'' : '''R'''<sup>''n''</sup> → '''R'''}} be a ''k''-times [[continuously differentiable]] function at the point {{nowrap|'''''a''''' ∈ '''R'''<sup>''n''</sup>}}. Then there exist functions {{math|''h''<sub>''α''</sub> : '''R'''<sup>''n''</sup> → '''R'''}}, where <math>|\alpha|=k,</math> such that | ||
| Line 302: | Line 302: | ||
\end{align}</math>}} | \end{align}</math>}} | ||
यदि | यदि फलन {{nowrap|''f'' : '''R'''<sup>''n''</sup> → '''R'''}} एक [[बंद गेंद|संवृत गेंद]] में k + 1 बार [[लगातार भिन्न]] होता है <math>B = \{ \mathbf{y} \in \R^n : \left\|\mathbf{a}-\mathbf{y}\right\| \leq r\}</math> कुछ के लिए <math>r > 0</math>, तो कोई शेषफल के संदर्भ में एक सटीक सूत्र प्राप्त कर सकता है {{nowrap|(''k''+1)-th}} इस पड़ोस में f का आंशिक व्युत्पन्न ऑर्डर करें।<ref>https://sites.math.washington.edu/~folland/Math425/taylor2.pdf {{Bare URL PDF|date=March 2022}}</ref> अर्थात्, | ||
<math display="block"> \begin{align} | <math display="block"> \begin{align} | ||
| Line 309: | Line 309: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
इस | इस स्थिति में, [[कॉम्पैक्ट सेट|कॉम्पैक्ट समुच्चय]] बी में (k+1)-वें क्रम के आंशिक अवकलज के निरंतर कार्य के कारण, व्यक्ति को तुरंत एक समान अनुमान प्राप्त होता है | ||
<math display="block"> \left|R_\beta(\boldsymbol{x})\right| \leq \frac{1}{\beta!} \max_{|\alpha|=|\beta|} \max_{\boldsymbol{y}\in B} |D^\alpha f(\boldsymbol{y})|, \qquad \boldsymbol{x}\in B. </math> | <math display="block"> \left|R_\beta(\boldsymbol{x})\right| \leq \frac{1}{\beta!} \max_{|\alpha|=|\beta|} \max_{\boldsymbol{y}\in B} |D^\alpha f(\boldsymbol{y})|, \qquad \boldsymbol{x}\in B. </math> | ||
| Line 328: | Line 328: | ||
=== एक वास्तविक चर में टेलर के प्रमेय का प्रमाण === | === एक वास्तविक चर में टेलर के प्रमेय का प्रमाण === | ||
मान लीजिए<ref>{{harvnb|Stromberg|1981}}</ref> | |||
<math display="block"> h_k(x) = \begin{cases} | <math display="block"> h_k(x) = \begin{cases} | ||
| Line 341: | Line 341: | ||
<math display="block"> \lim_{x\to a} h_k(x) =0. </math> | <math display="block"> \lim_{x\to a} h_k(x) =0. </math> | ||
यहां प्रमाण एल'हॉपिटल के नियम के बार-बार | यहां प्रमाण एल'हॉपिटल के नियम के बार-बार अनुप्रयुक्त होने पर आधारित है। ध्यान दें, प्रत्येक के लिए <math display="inline">j=0,1,...,k-1</math>, <math>f^{(j)}(a)=P^{(j)}(a)</math>. इसलिए पहले में से प्रत्येक <math display="inline">k-1</math> अंश के व्युत्पन्न <math>h_k(x)</math> पर गायब हो जाता है <math>x=a</math>, और यही बात हर के बारे में भी सच है। इसके अतिरिक्त, शर्त यह है कि फलन <math display="inline">f</math> होना <math display="inline">k</math> एक बिंदु पर भिन्न-भिन्न समय के लिए क्रमानुसार भिन्नता की आवश्यकता होती है <math display="inline">k-1</math> उक्त बिंदु के पड़ोस में (यह सच है, क्योंकि भिन्नता के लिए एक बिंदु के पूरे पड़ोस में एक फलन को परिभाषित करने की आवश्यकता होती है), अंश और उसका <math display="inline">k-2</math> व्युत्पन्न पड़ोस में भिन्न होते हैं <math display="inline">a</math>. स्पष्ट रूप से, हर भी उक्त शर्त को पूरा करता है, और इसके अतिरिक्त, जब तक लुप्त नहीं होता है <math display="inline">x=a</math>, इसलिए एल'हॉपिटल के नियम के लिए आवश्यक सभी शर्तें पूरी की जाती हैं, और इसका उपयोग उचित है। इसलिए | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 352: | Line 352: | ||
=== एक वास्तविक चर में टेलर के प्रमेय के लिए वैकल्पिक प्रमाण === | === एक वास्तविक चर में टेलर के प्रमेय के लिए वैकल्पिक प्रमाण === | ||
मान लीजिए <math>f(x)</math> टेलर बहुपद द्वारा अनुमानित किया जाने वाला कोई भी वास्तविक-मूल्यवान, निरंतर, कार्य हो। | |||
चरण 1: चलो <math display="inline">F</math> और <math display="inline">G</math> कार्य हो. तय करना <math display="inline">F</math> और <math display="inline">G</math> होना | चरण 1: चलो <math display="inline">F</math> और <math display="inline">G</math> कार्य हो. तय करना <math display="inline">F</math> और <math display="inline">G</math> होना | ||
| Line 447: | Line 447: | ||
===शेषफल के माध्य मान रूपों की व्युत्पत्ति === | ===शेषफल के माध्य मान रूपों की व्युत्पत्ति === | ||
मान लीजिए कि G कोई वास्तविक-मूल्यवान | मान लीजिए कि G कोई वास्तविक-मूल्यवान फलन है, जो मध्य के संवृत अंतराल पर निरंतर है <math display=inline>a</math> और <math display=inline>x</math> और मध्य के विवृत अंतराल पर एक गैर-लुप्त होने वाले व्युत्पन्न के साथ भिन्न <math display=inline>a</math> और <math display=inline>x</math>, और परिभाषित करें | ||
<math display="block"> F(t) = f(t) + f'(t)(x-t) + \frac{f''(t)}{2!}(x-t)^2 + \cdots + \frac{f^{(k)}(t)}{k!}(x-t)^k. | <math display="block"> F(t) = f(t) + f'(t)(x-t) + \frac{f''(t)}{2!}(x-t)^2 + \cdots + \frac{f^{(k)}(t)}{k!}(x-t)^k. | ||
| Line 455: | Line 455: | ||
{{NumBlk|:|<math> \frac{F'(\xi)}{G'(\xi)} = \frac{F(x) - F(a)}{G(x) - G(a)}</math>|{{EquationRef|★★★}}}} | {{NumBlk|:|<math> \frac{F'(\xi)}{G'(\xi)} = \frac{F(x) - F(a)}{G(x) - G(a)}</math>|{{EquationRef|★★★}}}} | ||
कुछ के लिए <math display="inline">\xi</math> के | कुछ के लिए <math display="inline">\xi</math> के मध्य विवृत अंतराल पर <math display=inline>a</math> और <math display=inline>x</math>. ध्यान दें कि यहाँ अंश है <math display="inline">F(x)-F(a)=R_k(x)</math> टेलर बहुपद का बिल्कुल शेष भाग है <math display="inline">y=f(x)</math>. गणना करना | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 471: | Line 471: | ||
<math display="block"> G(t) = \int_a^t \frac{f^{(k+1)}(s)}{k!} (x-s)^k \, ds,</math> | <math display="block"> G(t) = \int_a^t \frac{f^{(k+1)}(s)}{k!} (x-s)^k \, ds,</math> | ||
लेकिन माध्य मान प्रमेय के उपयोग के लिए आवश्यक एफ की आवश्यकताएं बहुत | लेकिन माध्य मान प्रमेय के उपयोग के लिए आवश्यक एफ की आवश्यकताएं बहुत प्रबल हैं, यदि कोई इस स्थिति में दावे को साबित करने का लक्ष्य रखता है कि एफ{{i sup|(''k'')}} केवल पूर्णतया सतत है। हालाँकि, यदि कोई लेबेस्ग समाकल के बजाय रीमान समाकल का उपयोग करता है, तो धारणाओं को कमजोर नहीं किया जा सकता है। | ||
===शेषफल के पूर्णांक रूप की व्युत्पत्ति === | ===शेषफल के पूर्णांक रूप की व्युत्पत्ति === | ||
एफ के बिल्कुल निरंतर होने के कारण{{i sup|(''k'')}} के | एफ के बिल्कुल निरंतर होने के कारण{{i sup|(''k'')}} के मध्य संवृत अंतराल पर <math display=inline>a</math> और <math display=inline>x</math> इसका व्युत्पन्न एफ{{i sup|(''k''+1)}} एल के रूप में उपस्थित है<sup>1</sup>-फलन, और हम कलन के मौलिक प्रमेय और भागों द्वारा एकीकरण का उपयोग कर सकते हैं। यही प्रमाण रीमान समाकल के लिए अनुप्रयुक्त होता है, यह मानते हुए कि एफ{{i sup|(''k'')}} संवृत अंतराल पर निरंतर कार्य है और विवृत अंतराल पर अवकलनीय कार्य है <math display=inline>a</math> और <math display=inline>x</math>, और यह माध्य मान प्रमेय का उपयोग करने की तुलना में समान परिणाम की ओर ले जाता है। | ||
कैलकुलस का मौलिक प्रमेय यह बताता है | कैलकुलस का मौलिक प्रमेय यह बताता है | ||
| Line 487: | Line 487: | ||
&= f(a)+(x-a)f'(a)+\int_a^x \, (x-t)f''(t) \, dt, | &= f(a)+(x-a)f'(a)+\int_a^x \, (x-t)f''(t) \, dt, | ||
\end{align} </math> | \end{align} </math> | ||
जो बिल्कुल टेलर का प्रमेय है और k=1 | जो बिल्कुल टेलर का प्रमेय है और k=1 स्थिति में शेषफल अभिन्न रूप में है। सामान्य कथन को गणितीय प्रेरण का उपयोग करके सिद्ध किया जाता है। लगता है कि | ||
{{NumBlk|:|<math> f(x) = f(a) + \frac{f'(a)}{1!}(x - a) + \cdots + \frac{f^{(k)}(a)}{k!}(x - a)^k + \int_a^x \frac{f^{(k+1)} (t)}{k!} (x - t)^k \, dt. </math>|{{EquationRef|★★★★}}}} | {{NumBlk|:|<math> f(x) = f(a) + \frac{f'(a)}{1!}(x - a) + \cdots + \frac{f^{(k)}(a)}{k!}(x - a)^k + \int_a^x \frac{f^{(k+1)} (t)}{k!} (x - t)^k \, dt. </math>|{{EquationRef|★★★★}}}} | ||
| Line 500: | Line 500: | ||
=== बहुभिन्नरूपी टेलर बहुपदों के शेषफल के लिए व्युत्पत्ति === | === बहुभिन्नरूपी टेलर बहुपदों के शेषफल के लिए व्युत्पत्ति === | ||
हम विशेष | हम विशेष स्थिति सिद्ध करते हैं, जहां f : 'R'<sup>n</sup> → 'R' में केंद्र 'a' के साथ कुछ संवृत गेंद B में k+1 क्रम तक निरंतर आंशिक व्युत्पन्न होते हैं। प्रमाण की रणनीति टेलर के प्रमेय के एक-चर स्थिति को 'x' और 'a' से सटे रेखा खंड पर f के प्रतिबंध पर अनुप्रयुक्त करना है।<ref>{{harvnb|Hörmander|1976|pp=12–13}}</ref> ''a'' और ''x'' के मध्य रेखा खंड को ''u''(''t'') = द्वारा पैरामीट्रिज करें {{nowrap|'''''a''''' + ''t''('''''x''''' − '''''a''''').}} हम फलन पर टेलर के प्रमेय का एक-चर संस्करण अनुप्रयुक्त करते हैं {{nowrap|1=''g''(''t'') = ''f''('''''u'''''(''t''))}}: | ||
<math display="block"> f(\boldsymbol{x})=g(1)=g(0)+\sum_{j=1}^k\frac{1}{j!}g^{(j)}(0)\ +\ \int_0^1 \frac{(1-t)^k }{k!} g^{(k+1)}(t)\, dt.</math> | <math display="block"> f(\boldsymbol{x})=g(1)=g(0)+\sum_{j=1}^k\frac{1}{j!}g^{(j)}(0)\ +\ \int_0^1 \frac{(1-t)^k }{k!} g^{(k+1)}(t)\, dt.</math> | ||
कई चरों के लिए श्रृंखला नियम | कई चरों के लिए श्रृंखला नियम अनुप्रयुक्त करने से लाभ मिलता है | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 510: | Line 510: | ||
&= \sum_{|\alpha| =j} \left(\begin{matrix} j\\ \alpha\end{matrix} \right) (D^\alpha f) (\boldsymbol{a}+t(\boldsymbol{x}-\boldsymbol{a})) (\boldsymbol{x}-\boldsymbol{a})^\alpha | &= \sum_{|\alpha| =j} \left(\begin{matrix} j\\ \alpha\end{matrix} \right) (D^\alpha f) (\boldsymbol{a}+t(\boldsymbol{x}-\boldsymbol{a})) (\boldsymbol{x}-\boldsymbol{a})^\alpha | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ <math>\tbinom j \alpha</math> [[बहुपद गुणांक]] है. तब से <math>\tfrac{1}{j!}\tbinom j \alpha=\tfrac{1}{\alpha!}</math>, हम पाते हैं: | |||
<math display="block"> f(\mathbf x)= f(\mathbf a) + \sum_{1 \leq |\alpha| \leq k}\frac{1}{\alpha!} (D^\alpha f) (\mathbf a)(\mathbf x-\mathbf a)^\alpha+\sum_{|\alpha|=k+1}\frac{k+1}{\alpha!} | <math display="block"> f(\mathbf x)= f(\mathbf a) + \sum_{1 \leq |\alpha| \leq k}\frac{1}{\alpha!} (D^\alpha f) (\mathbf a)(\mathbf x-\mathbf a)^\alpha+\sum_{|\alpha|=k+1}\frac{k+1}{\alpha!} | ||
| Line 518: | Line 518: | ||
== यह भी देखें == | == यह भी देखें == | ||
{{Portal|Mathematics}} | {{Portal|Mathematics}} | ||
* {{annotated link| | * {{annotated link|हैडामर्ड लेम्मा}} | ||
* {{annotated link| | * {{annotated link|लॉरेंट शृंखला}} | ||
* {{annotated link| | * {{annotated link|पदे सन्निकट}} | ||
* {{annotated link| | * {{annotated link|न्यूटन शृंखला}} | ||
== फ़ुटनोट == | == फ़ुटनोट == | ||
Revision as of 17:18, 29 July 2023
| के बारे में लेखों की एक श्रृंखला का हिस्सा |
| पथरी |
|---|
गणना में, टेलर का प्रमेय एक अनुमान देता है -डिग्री के बहुपद द्वारा किसी दिए गए बिंदु के चारों ओर बार-बार भिन्न-भिन्न कार्य , इसको कॉल किया गया -वें क्रम का टेलर बहुपद। एक सुचारु कार्य के लिए, टेलर बहुपद क्रम में काट-छाँट हैसमारोह की टेलर श्रृंखला का। प्रथम-क्रम टेलर बहुपद फलन का रैखिक सन्निकटन है, और दूसरे-क्रम टेलर बहुपद को प्रायः 'द्विघात सन्निकटन' के रूप में जाना जाता है।[1] टेलर के प्रमेय के कई संस्करण हैं, कुछ इसके टेलर बहुपद द्वारा फलन की सन्निकटन त्रुटि का स्पष्ट अनुमान देते हैं।
टेलर के प्रमेय का नाम गणितज्ञ ब्रूक टेलर के नाम पर रखा गया है, जिन्होंने 1715 में इसका एक संस्करण बताया था,[2] हालाँकि परिणाम के पहले संस्करण का उल्लेख 1671 में जेम्स ग्रेगरी (खगोलशास्त्री और गणितज्ञ) द्वारा विज्ञान में पहले ही किया जा चुका था।[3] टेलर का प्रमेय परिचयात्मक-स्तर के कैलकुलस पाठ्यक्रमों में पढ़ाया जाता है और गणितीय विश्लेषण में केंद्रीय प्राथमिक उपकरणों में से एक है। यह घातांकीय फलन और त्रिकोणमितीय फलन जैसे कई पारलौकिक फलनों के मानों की सटीक गणना करने के लिए सरल अंकगणितीय सूत्र देता है। यह विश्लेषणात्मक कार्यों के अध्ययन का प्रारंभिक बिंदु है, और गणित के विभिन्न क्षेत्रों के साथ-साथ संख्यात्मक विश्लेषण और गणितीय भौतिकी में भी मौलिक है। टेलर का प्रमेय बहुभिन्नरूपी फलन और आलेख मूल्यवान फलन फलन का भी सामान्यीकरण करता है।
प्रेरणा
का आलेख (नीला) इसके रैखिक सन्निकटन के साथ (लाल)पर . यदि एक वास्तविक-मूल्यवान फलन (गणित) बिंदु पर व्युत्पन्न है , तो इस बिंदु के निकट इसका एक रैखिक सन्निकटन होता है। इसका अर्थ है कि एक फलन h उपस्थित है1(x) ऐसा कि
का आलेख (नीला) अपने द्विघात सन्निकटन के साथ (लाल)पर . सन्निकटन में सुधार पर ध्यान दें. बेहतर सन्निकटन के लिए , हम एक रैखिक फलन के बजाय एक द्विघात बहुपद उपयुक्त कर सकते हैं:
टेलर का प्रमेय यह सुनिश्चित करता है कि द्विघात सन्निकटन, पर्याप्त रूप से छोटे पड़ोस में है , रैखिक सन्निकटन से अधिक सटीक। विशेष रूप से,
इसी प्रकार, यदि हम उच्च डिग्री के बहुपदों का उपयोग करते हैं तो हमें f के और भी बेहतर सन्निकटन प्राप्त हो सकते हैं, तब से हम चयनित आधार बिंदु पर f के साथ और भी अधिक व्युत्पन्नों का मिलान कर सकते हैं।
सामान्य तौर पर, डिग्री k के बहुपद द्वारा किसी फलन का अनुमान लगाने में त्रुटि बहुत तीव्रता से शून्य हो जाएगी जैसे कि x, a की ओर प्रवृत्त होता है। हालाँकि, ऐसे फलन हैं, यहां तक कि असीम रूप से भिन्न भी, जिनके लिए अनुमानित बहुपद की डिग्री बढ़ाने से सन्निकटन की सटीकता में वृद्धि नहीं होती है: हम कहते हैं कि ऐसा फलन x = a पर विश्लेषणात्मक फलन होने में विफल रहता है: यह (स्थानीय रूप से) इस बिंदु पर इसके अवकलज द्वारा निर्धारित नहीं होता है।
टेलर का प्रमेय स्पर्शोन्मुख प्रकृति का है: यह हमें केवल यह बताता है कि त्रुटि हुई है ए द्वारा एक अनुमान में -वें क्रम का टेलर बहुपद पीkकिसी भी गैर-शून्य की तुलना में तीव्रता से शून्य हो जाता है -वें डिग्री बहुपद के रूप में . यह हमें नहीं बताता कि विस्तार के केंद्र के किसी ठोस पड़ोस (गणित) में त्रुटि कितनी बड़ी है, लेकिन इस उद्देश्य के लिए शेष पद (नीचे दिए गए) के लिए स्पष्ट सूत्र हैं जो एफ पर कुछ अतिरिक्त नियमितता मान्यताओं के अंतर्गत मान्य हैं। टेलर के प्रमेय के ये उन्नत संस्करण आम तौर पर विस्तार के केंद्र के एक छोटे से पड़ोस में सन्निकटन त्रुटि के लिए एक समान अभिसरण की ओर ले जाते हैं, लेकिन अनुमान आवश्यक रूप से उन पड़ोस के लिए नहीं होते हैं जो बहुत बड़े हैं, भले ही फलन एफ विश्लेषणात्मक फलन हो। उस स्थिति में किसी को मूल फलन के विश्वसनीय टेलर-अनुमान प्राप्त करने के लिए विस्तार के विभिन्न केंद्रों के साथ कई टेलर बहुपदों का चयन करना पड़ सकता है (दाईं ओर एनीमेशन देखें।)
ऐसे कई तरीके हैं जिनसे हम शेष पद का उपयोग कर सकते हैं:
- बहुपद P के लिए त्रुटि का अनुमान लगाएंk(x) डिग्री k का अनुमान लगाना किसी दिए गए अंतराल पर (ए - आर, ए + आर)। (अंतराल और डिग्री को देखते हुए, हम त्रुटि पाते हैं।)
- वह सबसे छोटी घात k ज्ञात कीजिए जिसके लिए बहुपद Pk(एक्स) अनुमानित किसी दिए गए अंतराल पर दी गई त्रुटि सहनशीलता के भीतर (ए - आर, ए + आर)। (अंतराल और त्रुटि सहनशीलता को देखते हुए, हम डिग्री पाते हैं।)
- सबसे बड़ा अंतराल (a − r, a + r) ज्ञात करें जिस पर Pk(एक्स) अनुमानित किसी दी गई त्रुटि सहनशीलता के भीतर। (डिग्री और त्रुटि सहनशीलता को देखते हुए, हम अंतराल पाते हैं।)
एक वास्तविक चर में टेलर का प्रमेय
प्रमेय का कथन
टेलर के प्रमेय के सबसे बुनियादी संस्करण का सटीक विवरण इस प्रकार है:
Taylor's theorem[4][5][6] — Let k ≥ 1 be an integer and let the function f : R → R be k times differentiable at the point a ∈ R. Then there exists a function hk : R → R such that
टेलर के प्रमेय में प्रदर्शित होने वाला बहुपद है-वें क्रम का टेलर बहुपद
शेषफल के लिए स्पष्ट सूत्र
एफ पर प्रबल नियमितता मान्यताओं के अंतर्गत शेष पद आर के लिए कई सटीक सूत्र हैंkटेलर बहुपद में से सबसे आम निम्नलिखित हैं।
Mean-value forms of the remainder — Let f : R → R be k + 1 times differentiable on the open interval with f(k) continuous on the closed interval between and .[7] Then
for some real number between and . This is the Lagrange form[8] of the remainder.
Similarly,
for some real number between and . This is the Cauchy form[9] of the remainder.
टेलर के प्रमेय के ये परिशोधन सामान्यतः माध्य मान प्रमेय का उपयोग करके सिद्ध किए जाते हैं, जहां से यह नाम पड़ा है। इसके अतिरिक्त, ध्यान दें कि यह बिल्कुल माध्य मान प्रमेय है जब . इसके अतिरिक्त अन्य समान अभिव्यक्तियाँ भी पाई जा सकती हैं। उदाहरण के लिए, यदि G(t) संवृत अंतराल पर निरंतर है और मध्य के विवृत अंतराल पर एक गैर-लुप्त व्युत्पन्न के साथ भिन्न है और , तब
शेषफल के अभिन्न रूप के लिए बयान पिछले वाले की तुलना में अधिक उन्नत है, और पूर्ण व्यापकता के लिए लेबेसेग अभिन्न की समझ की आवश्यकता है। हालाँकि, यह रीमैन अभिन्न के अर्थ में भी अनुप्रयुक्त है, बशर्ते कि f का (k+1)वां व्युत्पन्न संवृत अंतराल [a,x] पर निरंतर हो।
Integral form of the remainder[10] — Let be absolutely continuous on the closed interval between and . Then
एफ के बिल्कुल निरंतर होने के कारण(k) के मध्य संवृत अंतराल पर और , इसका व्युत्पन्न एफ(k+1) एल के रूप में उपस्थित है1-फलन, और परिणाम को कैलकुलस के मौलिक प्रमेय और भागों द्वारा एकीकरण का उपयोग करके औपचारिक गणना द्वारा सिद्ध किया जा सकता है।
शेष के लिए अनुमान
टेलर सन्निकटन में दिखाई देने वाले शेष पद का अनुमान लगाने में सक्षम होना, इसके लिए एक सटीक सूत्र होने के बजाय, व्यवहार में प्रायः उपयोगी होता है। मान लीजिए कि एफ है (k + 1)-अंतराल I में कई बार लगातार अंतर होता है जिसमें a होता है। मान लीजिए कि ऐसे वास्तविक स्थिरांक q और Q हैं
उदाहरण
मान लीजिए कि हम फलन का अनुमानित मान ज्ञात करना चाहते हैं अंतराल पर यह सुनिश्चित करते हुए कि अनुमान में त्रुटि 10 से अधिक न हो−5. इस उदाहरण में हम दिखावा करते हैं कि हम घातीय फलन के केवल निम्नलिखित गुणों को जानते हैं:
-
(★)
इन गुणों से यह निष्कर्ष निकलता है सभी के लिए , खास तरीके से, . इसलिए-वें क्रम का टेलर बहुपद पर और इसका शेष पद लैग्रेंज रूप में दिया गया है
विश्लेषणात्मकता से संबंध
टेलर वास्तविक विश्लेषणात्मक कार्यों का विस्तार
मान लीजिए I ⊂ 'R' एक विवृत अंतराल है। परिभाषा के अनुसार, एक फलन f: I → 'R' एक विश्लेषणात्मक फलन है यदि इसे स्थानीय रूप से एक अभिसरण शक्ति श्रृंखला द्वारा परिभाषित किया गया है। इसका अर्थ यह है कि प्रत्येक a ∈ I के लिए कुछ r > 0 और गुणांक c का एक क्रम उपस्थित होता हैk∈ 'आर' ऐसे कि (a − r, a + r) ⊂ I और
वास्तविक विश्लेषणात्मक फलन f के टेलर बहुपद केवल परिमित खंडन हैं
टेलर का प्रमेय और टेलर श्रृंखला का अभिसरण
एफ की टेलर श्रृंखला कुछ अंतराल में अभिसरण करेगी जिसमें इसके सभी अवकलज बंधे हुए हैं और बहुत तीव्रता से नहीं बढ़ते हैं क्योंकि के अनंत तक जाता है। (हालाँकि, भले ही टेलर श्रृंखला अभिसरण करती है, यह एफ में परिवर्तित नहीं हो सकती है, जैसा कि नीचे बताया गया है; तब एफ को गैर-विश्लेषणात्मक फलन कहा जाता है।)
कोई टेलर श्रृंखला के विषय में विचार कर सकता है
-
(★★)
प्रत्येक x ∈ (a − r,a + r) के लिए। कभी-कभी स्थिरांक Mk,r को इस तरह से चुना जा सकता है Mk,r निश्चित r और सभी k के लिए ऊपर परिबद्ध है। फिर कुछ विश्लेषणात्मक फलन के लिए एफ वर्दी अभिसरण की टेलर श्रृंखला
सीमा समारोह Tf परिभाषा के अनुसार सदैव विश्लेषणात्मक होता है, लेकिन यह जरूरी नहीं कि मूल फलन f के बराबर हो, भले ही f असीम रूप से भिन्न हो। इस स्थिति में, हम कहते हैं कि f एक गैर-विश्लेषणात्मक सहज फलन है, उदाहरण के लिए एक समतल कार्य:
- एफ की टेलर श्रृंखला शून्य फलन टी में समान रूप से परिवर्तित होती हैf(x)=0, जो शून्य के बराबर सभी गुणांकों के साथ विश्लेषणात्मक है।
- फलन f इस टेलर श्रृंखला के बराबर नहीं है, और इसलिए गैर-विश्लेषणात्मक है।
- किसी भी क्रम k ∈ 'N' और त्रिज्या r > 0 के लिए M उपस्थित हैk,r> 0 शेष सीमा को संतुष्ट करना (★★) ऊपर।
हालाँकि, जैसे-जैसे k निश्चित r के लिए बढ़ता है, M का मान बढ़ता हैk,rआर की तुलना में अधिक तेज़ी से बढ़ता हैk, और त्रुटि शून्य पर नहीं जाती है।
जटिल विश्लेषण में टेलर का प्रमेय
टेलर का प्रमेय फ़ंक्शंस f: 'C' → 'C' को सामान्यीकृत करता है जो जटिल विमान के एक विवृत उपसमुच्चय U ⊂ 'C' में जटिल रूप से भिन्न होते हैं। हालाँकि, जटिल विश्लेषण में इसकी उपयोगिता अन्य सामान्य प्रमेयों से कम है। अर्थात्, कॉची के अभिन्न सूत्र का उपयोग करके जटिल विभेदक कार्यों f : U → 'C' के लिए संबंधित परिणामों के प्रबल संस्करण निम्नानुसार निकाले जा सकते हैं।
मान लीजिए r > 0 इस प्रकार है कि संवृत डिस्क B(z,r) ∪S(z,r) U में समाहित है। फिर एक सकारात्मक पैरामीट्रिजेशन के साथ कॉची का अभिन्न सूत्र γ(t) = z + reit वृत्त S(z, r) के साथ देता है
उदाहरण
कार्यक्रम
टेलर के प्रमेय का सामान्यीकरण
उच्च-क्रम भिन्नता
एक फलन f: 'R'n → 'R', 'a' ∈'R' से व्युत्पन्न हैn यदि और केवल यदि कोई रैखिक कार्यात्मक L उपस्थित है: 'R'n → 'R' और एक फलन h : 'R'n → 'R' ऐसा कि
बहुभिन्नरूपी कार्यों के लिए टेलर का प्रमेय
पिछले अनुभाग के अंकन पद्धति का उपयोग करते हुए, निम्नलिखित प्रमेय प्राप्त होता है।
Multivariate version of Taylor's theorem[14] — Let f : Rn → R be a k-times continuously differentiable function at the point a ∈ Rn. Then there exist functions hα : Rn → R, where such that
यदि फलन f : Rn → R एक संवृत गेंद में k + 1 बार लगातार भिन्न होता है कुछ के लिए , तो कोई शेषफल के संदर्भ में एक सटीक सूत्र प्राप्त कर सकता है (k+1)-th इस पड़ोस में f का आंशिक व्युत्पन्न ऑर्डर करें।[15] अर्थात्,
दो आयामों में उदाहरण
उदाहरण के लिए, एक सुचारु फलन f: 'R' का तृतीय-क्रम टेलर बहुपद2 → 'R', 'x' को दर्शाता है − 'a' = 'v',
प्रमाण
एक वास्तविक चर में टेलर के प्रमेय का प्रमाण
मान लीजिए[16]
एक वास्तविक चर में टेलर के प्रमेय के लिए वैकल्पिक प्रमाण
मान लीजिए टेलर बहुपद द्वारा अनुमानित किया जाने वाला कोई भी वास्तविक-मूल्यवान, निरंतर, कार्य हो।
चरण 1: चलो और कार्य हो. तय करना और होना
होने देना और निरंतर कार्य चालू रहें . तब से इसलिए हम अंतराल के साथ काम कर सकते हैं . होने देना और पर भिन्न होना . मान लीजिए सभी के लिए . तभी अस्तित्व है ऐसा है कि
इसके लिए भी प्रदर्शन किया जा सकता है :
इससे एक विभाजन मिलता है :
शेषफल के माध्य मान रूपों की व्युत्पत्ति
मान लीजिए कि G कोई वास्तविक-मूल्यवान फलन है, जो मध्य के संवृत अंतराल पर निरंतर है और और मध्य के विवृत अंतराल पर एक गैर-लुप्त होने वाले व्युत्पन्न के साथ भिन्न और , और परिभाषित करें
-
(★★★)
कुछ के लिए के मध्य विवृत अंतराल पर और . ध्यान दें कि यहाँ अंश है टेलर बहुपद का बिल्कुल शेष भाग है . गणना करना
टिप्पणी। इस विधि का प्रयोग करके शेषफल का पूर्णांक रूप भी चुनकर प्राप्त किया जा सकता है
शेषफल के पूर्णांक रूप की व्युत्पत्ति
एफ के बिल्कुल निरंतर होने के कारण(k) के मध्य संवृत अंतराल पर और इसका व्युत्पन्न एफ(k+1) एल के रूप में उपस्थित है1-फलन, और हम कलन के मौलिक प्रमेय और भागों द्वारा एकीकरण का उपयोग कर सकते हैं। यही प्रमाण रीमान समाकल के लिए अनुप्रयुक्त होता है, यह मानते हुए कि एफ(k) संवृत अंतराल पर निरंतर कार्य है और विवृत अंतराल पर अवकलनीय कार्य है और , और यह माध्य मान प्रमेय का उपयोग करने की तुलना में समान परिणाम की ओर ले जाता है।
कैलकुलस का मौलिक प्रमेय यह बताता है
-
(★★★★)
शेष पद को भागों द्वारा एकीकृत करते हुए हम जिस पर पहुंचते हैं
बहुभिन्नरूपी टेलर बहुपदों के शेषफल के लिए व्युत्पत्ति
हम विशेष स्थिति सिद्ध करते हैं, जहां f : 'R'n → 'R' में केंद्र 'a' के साथ कुछ संवृत गेंद B में k+1 क्रम तक निरंतर आंशिक व्युत्पन्न होते हैं। प्रमाण की रणनीति टेलर के प्रमेय के एक-चर स्थिति को 'x' और 'a' से सटे रेखा खंड पर f के प्रतिबंध पर अनुप्रयुक्त करना है।[17] a और x के मध्य रेखा खंड को u(t) = द्वारा पैरामीट्रिज करें a + t(x − a). हम फलन पर टेलर के प्रमेय का एक-चर संस्करण अनुप्रयुक्त करते हैं g(t) = f(u(t)):
यह भी देखें
फ़ुटनोट
- ↑ (2013). "Linear and quadratic approximation" Retrieved December 6, 2018
- ↑ Taylor, Brook (1715). वेतन वृद्धि की सीधी और उलटी विधि [Direct and Reverse Methods of Incrementation] (in Latina). London. p. 21–23 (Prop. VII, Thm. 3, Cor. 2). Translated into English in Struik, D. J. (1969). A Source Book in Mathematics 1200–1800. Cambridge, Massachusetts: Harvard University Press. pp. 329–332.
- ↑ Kline 1972, pp. 442, 464.
- ↑ Genocchi, Angelo; Peano, Giuseppe (1884), Calcolo differenziale e principii di calcolo integrale, (N. 67, pp. XVII–XIX): Fratelli Bocca ed.
{{citation}}: CS1 maint: location (link) - ↑ Spivak, Michael (1994), Calculus (3rd ed.), Houston, TX: Publish or Perish, p. 383, ISBN 978-0-914098-89-8
- ↑ "Taylor formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- ↑ The hypothesis of f(k) being continuous on the closed interval between and is not redundant. Although f being k + 1 times differentiable on the open interval between and does imply that f(k) is continuous on the open interval between and , it does not imply that f(k) is continuous on the closed interval between and , i.e. it does not imply that f(k) is continuous at the endpoints of that interval. Consider, for example, the function f : [0,1] → R defined to equal on and with . This is not continuous at 0, but is continuous on . Moreover, one can show that this function has an antiderivative. Therefore that antiderivative is differentiable on , its derivative (the function f) is continuous on the open interval , but its derivative f is not continuous on the closed interval . So the theorem would not apply in this case.
- ↑ Kline 1998, §20.3; Apostol 1967, §7.7.
- ↑ Apostol 1967, §7.7.
- ↑ Apostol 1967, §7.5.
- ↑ Apostol 1967, §7.6
- ↑ Rudin 1987, §10.26
- ↑ This follows from iterated application of the theorem that if the partial derivatives of a function f exist in a neighborhood of a and are continuous at a, then the function is differentiable at a. See, for instance, Apostol 1974, Theorem 12.11.
- ↑ Königsberger Analysis 2, p. 64 ff.
- ↑ https://sites.math.washington.edu/~folland/Math425/taylor2.pdf[bare URL PDF]
- ↑ Stromberg 1981
- ↑ Hörmander 1976, pp. 12–13
संदर्भ
- Apostol, Tom (1967), Calculus, Wiley, ISBN 0-471-00005-1.
- Apostol, Tom (1974), Mathematical analysis, Addison–Wesley.
- Bartle, Robert G.; Sherbert, Donald R. (2011), Introduction to Real Analysis (4th ed.), Wiley, ISBN 978-0-471-43331-6.
- Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer, ISBN 978-3-540-00662-6.
- Kline, Morris (1972), Mathematical thought from ancient to modern times, Volume 2, Oxford University Press.
- Kline, Morris (1998), Calculus: An Intuitive and Physical Approach, Dover, ISBN 0-486-40453-6.
- Pedrick, George (1994), A First Course in Analysis, Springer, ISBN 0-387-94108-8.
- Stromberg, Karl (1981), Introduction to classical real analysis, Wadsworth, ISBN 978-0-534-98012-2.
- Rudin, Walter (1987), Real and complex analysis (3rd ed.), McGraw-Hill, ISBN 0-07-054234-1.
- Tao, Terence (2014), Analysis, Volume I (3rd ed.), Hindustan Book Agency, ISBN 978-93-80250-64-9.
- Proof of Taylor's Theorem (PDF), Chinese University of Hong Kong.
बाहरी संबंध
- टेलर प्रमेय at ProofWiki
- Taylor Series Approximation to Cosine at cut-the-knot
- Trigonometric Taylor Expansion interactive demonstrative applet
- Taylor Series Revisited at Holistic Numerical Methods Institute