योजक सफेद गाउसियन रव: Difference between revisions
(Created page with "{{Short description|Basic noise model used in information theory}} {{One source|date=February 2020}} एडिटिव व्हाइट गॉसियन शोर (AWGN)...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Basic noise model used in information theory}} | {{Short description|Basic noise model used in information theory}} | ||
{{One source|date=February 2020}} | {{One source|date=February 2020}} | ||
योजक सफेद गाउसियन रव (AWGN) एक बुनियादी रव मॉडल है जिसका उपयोग प्रकृति में होने वाली कई यादृच्छिक प्रक्रियाओं के प्रभाव की नकल करने के लिए [[सूचना सिद्धांत]] में किया जाता है। संशोधक विशिष्ट विशेषताओं को दर्शाते हैं: | |||
* ''एडिटिव'' क्योंकि यह किसी भी | * ''एडिटिव'' क्योंकि यह किसी भी रव में जोड़ा जाता है जो सूचना प्रणाली में अंतर्निहित हो सकता है। | ||
* ''व्हाइट'' इस विचार को संदर्भित करता है कि इसमें सूचना प्रणाली के लिए [[आवृत्ति]] बैंड में एक समान स्पेक्ट्रल घनत्व#पावर स्पेक्ट्रल घनत्व है। यह श्वेत#श्वेत प्रकाश का एक सादृश्य है जिसे दृश्य स्पेक्ट्रम में सभी आवृत्तियों पर समान उत्सर्जन द्वारा महसूस किया जा सकता है। | * ''व्हाइट'' इस विचार को संदर्भित करता है कि इसमें सूचना प्रणाली के लिए [[आवृत्ति]] बैंड में एक समान स्पेक्ट्रल घनत्व#पावर स्पेक्ट्रल घनत्व है। यह श्वेत#श्वेत प्रकाश का एक सादृश्य है जिसे दृश्य स्पेक्ट्रम में सभी आवृत्तियों पर समान उत्सर्जन द्वारा महसूस किया जा सकता है। | ||
* ''गाऊशियन'' क्योंकि इसका समय क्षेत्र में औसत समय डोमेन मान शून्य ([[गाऊसी प्रक्रिया]]) के साथ एक [[सामान्य वितरण]] है। | * ''गाऊशियन'' क्योंकि इसका समय क्षेत्र में औसत समय डोमेन मान शून्य ([[गाऊसी प्रक्रिया]]) के साथ एक [[सामान्य वितरण]] है। | ||
[[वाइडबैंड]] | [[वाइडबैंड]] रव कई प्राकृतिक रव स्रोतों से आता है, जैसे कंडक्टरों में परमाणुओं के थर्मल कंपन (थर्मल रव या जॉनसन-नाइक्विस्ट रव के रूप में जाना जाता है), शॉट रव, पृथ्वी और अन्य गर्म वस्तुओं से ब्लैक-बॉडी विकिरण, और सूर्य जैसे आकाशीय स्रोतों से। संभाव्यता सिद्धांत की [[केंद्रीय सीमा प्रमेय]] इंगित करती है कि कई यादृच्छिक प्रक्रियाओं के योग में गाऊसी या सामान्य नामक वितरण होगा। | ||
AWGN को अक्सर एक संचार चैनल के रूप में उपयोग किया जाता है जिसमें संचार में एकमात्र बाधा निरंतर [[वर्णक्रमीय घनत्व]] ([[बैंडविड्थ (सिग्नल प्रोसेसिंग)]] के प्रति [[ हेटर्स ]] [[वाट]] के रूप में व्यक्त) और आयाम के [[गाऊसी वितरण]] के साथ वाइडबैंड या सफेद | AWGN को अक्सर एक संचार चैनल के रूप में उपयोग किया जाता है जिसमें संचार में एकमात्र बाधा निरंतर [[वर्णक्रमीय घनत्व]] ([[बैंडविड्थ (सिग्नल प्रोसेसिंग)]] के प्रति [[ हेटर्स ]] [[वाट]] के रूप में व्यक्त) और आयाम के [[गाऊसी वितरण]] के साथ वाइडबैंड या सफेद रव का एक रैखिक जोड़ है। मॉडल [[लुप्त होती]], आवृत्ति चयनात्मकता, [[हस्तक्षेप (संचार)]], गैर-रैखिकता या [[फैलाव (प्रकाशिकी)]] को ध्यान में नहीं रखता है। हालाँकि, यह सरल और सुव्यवस्थित गणितीय मॉडल तैयार करता है जो इन अन्य घटनाओं पर विचार करने से पहले किसी प्रणाली के अंतर्निहित व्यवहार में अंतर्दृष्टि प्राप्त करने के लिए उपयोगी होते हैं। | ||
AWGN चैनल कई [[उपग्रह]] और गहरे अंतरिक्ष संचार लिंक के लिए एक अच्छा मॉडल है। मल्टीपाथ, भूभाग अवरोधन, हस्तक्षेप आदि के कारण अधिकांश स्थलीय लिंक के लिए यह एक अच्छा मॉडल नहीं है। हालाँकि, स्थलीय पथ मॉडलिंग के लिए, AWGN का उपयोग आमतौर पर मल्टीपाथ, भूभाग अवरोधन, हस्तक्षेप, जमीनी अव्यवस्था और स्वयं हस्तक्षेप के अलावा अध्ययन के तहत चैनल के पृष्ठभूमि | AWGN चैनल कई [[उपग्रह]] और गहरे अंतरिक्ष संचार लिंक के लिए एक अच्छा मॉडल है। मल्टीपाथ, भूभाग अवरोधन, हस्तक्षेप आदि के कारण अधिकांश स्थलीय लिंक के लिए यह एक अच्छा मॉडल नहीं है। हालाँकि, स्थलीय पथ मॉडलिंग के लिए, AWGN का उपयोग आमतौर पर मल्टीपाथ, भूभाग अवरोधन, हस्तक्षेप, जमीनी अव्यवस्था और स्वयं हस्तक्षेप के अलावा अध्ययन के तहत चैनल के पृष्ठभूमि रव का अनुकरण करने के लिए किया जाता है, जिसका सामना आधुनिक रेडियो सिस्टम स्थलीय संचालन में करते हैं। | ||
==चैनल क्षमता== | ==चैनल क्षमता== | ||
AWGN चैनल को आउटपुट की एक श्रृंखला द्वारा दर्शाया गया है <math>Y_i</math> असतत-समय घटना सूचकांक पर <math>i</math>. <math>Y_i</math> इनपुट का योग है <math>X_i</math> और | AWGN चैनल को आउटपुट की एक श्रृंखला द्वारा दर्शाया गया है <math>Y_i</math> असतत-समय घटना सूचकांक पर <math>i</math>. <math>Y_i</math> इनपुट का योग है <math>X_i</math> और रव, <math>Z_i</math>, कहाँ <math>Z_i</math> [[स्वतंत्र और समान रूप से वितरित यादृच्छिक चर]] है और भिन्नता के साथ शून्य-माध्य सामान्य वितरण से लिया गया है <math>N</math> (ये रव)। <math>Z_i</math> h> को आगे इसके साथ सहसंबद्ध नहीं माना जाता है <math>X_i</math>. | ||
:<math> | :<math> | ||
Z_i \sim \mathcal{N}(0, N) | Z_i \sim \mathcal{N}(0, N) | ||
| Line 20: | Line 20: | ||
Y_i = X_i + Z_i. | Y_i = X_i + Z_i. | ||
\,\!</math> | \,\!</math> | ||
जब तक | जब तक रव न हो, चैनल की क्षमता अनंत है <math>N</math> शून्येतर है, और <math>X_i</math> पर्याप्त रूप से प्रतिबंधित हैं. इनपुट पर सबसे आम बाधा तथाकथित पावर बाधा है, जिसके लिए कोडवर्ड की आवश्यकता होती है <math>(x_1, x_2, \dots , x_k)</math> चैनल के माध्यम से प्रसारित, हमारे पास है: | ||
:<math> | :<math> | ||
| Line 80: | Line 80: | ||
एक दर को प्राप्त करने योग्य कहा जाता है यदि कोड का अनुक्रम हो ताकि त्रुटि की अधिकतम संभावना शून्य हो जाए <math>n</math> अनंत तक पहुंचता है. क्षमता <math>C</math> उच्चतम प्राप्य दर है. | एक दर को प्राप्त करने योग्य कहा जाता है यदि कोड का अनुक्रम हो ताकि त्रुटि की अधिकतम संभावना शून्य हो जाए <math>n</math> अनंत तक पहुंचता है. क्षमता <math>C</math> उच्चतम प्राप्य दर है. | ||
लंबाई के एक कोडवर्ड पर विचार करें <math>n</math> | लंबाई के एक कोडवर्ड पर विचार करें <math>n</math> रव स्तर के साथ AWGN चैनल के माध्यम से भेजा गया <math>N</math>. प्राप्त होने पर, कोडवर्ड वेक्टर विचरण अब है <math>N</math>, और इसका माध्य भेजा गया कोडवर्ड है। वेक्टर के त्रिज्या के एक गोले में समाहित होने की बहुत संभावना है <math display=inline>\sqrt{n(N+\varepsilon)}</math> चारों ओर कोडवर्ड भेजा गया। यदि हम प्राप्त प्रत्येक संदेश को इस क्षेत्र के केंद्र में कोडवर्ड पर मैप करके डिकोड करते हैं, तो त्रुटि तभी होती है जब प्राप्त वेक्टर इस क्षेत्र के बाहर होता है, जो बहुत ही असंभव है। | ||
प्रत्येक कोडवर्ड वेक्टर में प्राप्त कोडवर्ड वैक्टर का एक संबद्ध क्षेत्र होता है जिसे इसमें डिकोड किया जाता है और ऐसे प्रत्येक क्षेत्र को एक कोडवर्ड पर विशिष्ट रूप से मैप किया जाना चाहिए। चूँकि इन गोले को एक दूसरे को नहीं काटना चाहिए, इसलिए हमें [[गोला पैकिंग]] की समस्या का सामना करना पड़ता है। हम अपने में कितने अलग-अलग कोडवर्ड पैक कर सकते हैं <math>n</math>-बिट कोडवर्ड वेक्टर? प्राप्त वैक्टर में अधिकतम ऊर्जा होती है <math>n(P+N)</math> और इसलिए उसे त्रिज्या का एक क्षेत्र घेरना चाहिए <math display=inline>\sqrt{n(P+N)}</math>. प्रत्येक कोडवर्ड गोले की त्रिज्या होती है <math>\sqrt{nN}</math>. एक n-आयामी गोले का आयतन सीधे आनुपातिक होता है <math>r^n</math>, इसलिए ट्रांसमिशन पावर पी के साथ हमारे क्षेत्र में पैक किए जा सकने वाले विशिष्ट डिकोडेबल क्षेत्रों की अधिकतम संख्या है: | प्रत्येक कोडवर्ड वेक्टर में प्राप्त कोडवर्ड वैक्टर का एक संबद्ध क्षेत्र होता है जिसे इसमें डिकोड किया जाता है और ऐसे प्रत्येक क्षेत्र को एक कोडवर्ड पर विशिष्ट रूप से मैप किया जाना चाहिए। चूँकि इन गोले को एक दूसरे को नहीं काटना चाहिए, इसलिए हमें [[गोला पैकिंग]] की समस्या का सामना करना पड़ता है। हम अपने में कितने अलग-अलग कोडवर्ड पैक कर सकते हैं <math>n</math>-बिट कोडवर्ड वेक्टर? प्राप्त वैक्टर में अधिकतम ऊर्जा होती है <math>n(P+N)</math> और इसलिए उसे त्रिज्या का एक क्षेत्र घेरना चाहिए <math display=inline>\sqrt{n(P+N)}</math>. प्रत्येक कोडवर्ड गोले की त्रिज्या होती है <math>\sqrt{nN}</math>. एक n-आयामी गोले का आयतन सीधे आनुपातिक होता है <math>r^n</math>, इसलिए ट्रांसमिशन पावर पी के साथ हमारे क्षेत्र में पैक किए जा सकने वाले विशिष्ट डिकोडेबल क्षेत्रों की अधिकतम संख्या है: | ||
| Line 142: | Line 142: | ||
P_i = \frac{1}{2^{nR}}\sum_{w}x^2_i(w) | P_i = \frac{1}{2^{nR}}\sum_{w}x^2_i(w) | ||
\,\!</math> | \,\!</math> | ||
जहां योग सभी इनपुट संदेशों से अधिक है <math>w</math>. <math>X_i</math> और <math>Z_i</math> स्वतंत्र हैं, अत: की शक्ति की अपेक्षा रखते हैं <math>Y_i</math> | जहां योग सभी इनपुट संदेशों से अधिक है <math>w</math>. <math>X_i</math> और <math>Z_i</math> स्वतंत्र हैं, अत: की शक्ति की अपेक्षा रखते हैं <math>Y_i</math> रव के स्तर के लिए है <math>N</math>: | ||
:<math> | :<math> | ||
| Line 178: | Line 178: | ||
==समय क्षेत्र में प्रभाव== | ==समय क्षेत्र में प्रभाव== | ||
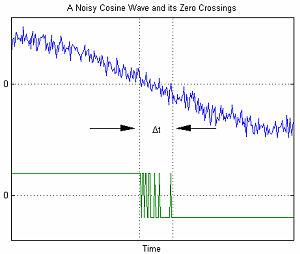
[[File:Zero crossing.jpg|thumb|300px| | [[File:Zero crossing.jpg|thumb|300px|रवगुल वाले कोसाइन का शून्य क्रॉसिंग]]सीरियल डेटा संचार में, AWGN गणितीय मॉडल का उपयोग यादृच्छिक [[ घबराना ]] (आरजे) के कारण होने वाली समय त्रुटि को मॉडल करने के लिए किया जाता है। | ||
दाईं ओर का ग्राफ़ AWGN से जुड़ी समय संबंधी त्रुटियों का एक उदाहरण दिखाता है। चर Δt शून्य क्रॉसिंग में अनिश्चितता का प्रतिनिधित्व करता है। जैसे-जैसे AWGN का आयाम बढ़ता है, सिग्नल-टू- | दाईं ओर का ग्राफ़ AWGN से जुड़ी समय संबंधी त्रुटियों का एक उदाहरण दिखाता है। चर Δt शून्य क्रॉसिंग में अनिश्चितता का प्रतिनिधित्व करता है। जैसे-जैसे AWGN का आयाम बढ़ता है, सिग्नल-टू-रव अनुपात कम हो जाता है। इसके परिणामस्वरूप अनिश्चितता बढ़ जाती है Δt।<ref name="rrd"/> | ||
जब AWGN से प्रभावित होता है, तो एक संकीर्ण बैंडपास फिल्टर के आउटपुट पर प्रति सेकंड सकारात्मक या नकारात्मक शून्य क्रॉसिंग की औसत संख्या होती है जब इनपुट साइन तरंग होता है | जब AWGN से प्रभावित होता है, तो एक संकीर्ण बैंडपास फिल्टर के आउटपुट पर प्रति सेकंड सकारात्मक या नकारात्मक शून्य क्रॉसिंग की औसत संख्या होती है जब इनपुट साइन तरंग होता है | ||
| Line 193: | Line 193: | ||
:<sub>0</sub> = फ़िल्टर की केंद्र आवृत्ति, | :<sub>0</sub> = फ़िल्टर की केंद्र आवृत्ति, | ||
: बी = फिल्टर बैंडविड्थ, | : बी = फिल्टर बैंडविड्थ, | ||
: एसएनआर = रैखिक शब्दों में सिग्नल-टू- | : एसएनआर = रैखिक शब्दों में सिग्नल-टू-रव शक्ति अनुपात। | ||
==फ़ेसर डोमेन में प्रभाव== | ==फ़ेसर डोमेन में प्रभाव== | ||
[[File:Noisy Phasor.jpg|thumb|300px|फेज़र डोमेन में AWGN का योगदान]]आधुनिक संचार प्रणालियों में, बैंडलिमिटेड AWGN को नजरअंदाज नहीं किया जा सकता है। जब फेज़र डोमेन में बैंडलिमिटेड AWGN की मॉडलिंग की जाती है, तो सांख्यिकीय विश्लेषण से पता चलता है कि वास्तविक और काल्पनिक योगदान के आयाम स्वतंत्र चर हैं जो गॉसियन वितरण मॉडल का पालन करते हैं। संयुक्त होने पर, परिणामी [[चरण]] का परिमाण एक [[रेले वितरण]] होता है | रेले-वितरित यादृच्छिक चर, जबकि चरण समान रूप से 0 से 2 तक वितरित होता है{{pi}}. | [[File:Noisy Phasor.jpg|thumb|300px|फेज़र डोमेन में AWGN का योगदान]]आधुनिक संचार प्रणालियों में, बैंडलिमिटेड AWGN को नजरअंदाज नहीं किया जा सकता है। जब फेज़र डोमेन में बैंडलिमिटेड AWGN की मॉडलिंग की जाती है, तो सांख्यिकीय विश्लेषण से पता चलता है कि वास्तविक और काल्पनिक योगदान के आयाम स्वतंत्र चर हैं जो गॉसियन वितरण मॉडल का पालन करते हैं। संयुक्त होने पर, परिणामी [[चरण]] का परिमाण एक [[रेले वितरण]] होता है | रेले-वितरित यादृच्छिक चर, जबकि चरण समान रूप से 0 से 2 तक वितरित होता है{{pi}}. | ||
दाईं ओर का ग्राफ़ एक उदाहरण दिखाता है कि बैंडलिमिटेड AWGN एक सुसंगत वाहक सिग्नल को कैसे प्रभावित कर सकता है। | दाईं ओर का ग्राफ़ एक उदाहरण दिखाता है कि बैंडलिमिटेड AWGN एक सुसंगत वाहक सिग्नल को कैसे प्रभावित कर सकता है। रव वेक्टर की तात्कालिक प्रतिक्रिया का सटीक अनुमान नहीं लगाया जा सकता है, हालांकि, इसकी समय-औसत प्रतिक्रिया का सांख्यिकीय रूप से अनुमान लगाया जा सकता है। जैसा कि ग्राफ में दिखाया गया है, हम विश्वासपूर्वक अनुमान लगाते हैं कि रव चरण 1σ सर्कल के अंदर लगभग 38% समय, 2σ सर्कल के अंदर लगभग 86% समय और 3σ सर्कल के अंदर लगभग 98% समय रहेगा।<ref name="rrd">{{citation | ||
| title = Radio Receiver Design | | title = Radio Receiver Design | ||
| first = Kevin | | first = Kevin | ||
| Line 208: | Line 208: | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[ज़मीन का उछाल]] | * [[ज़मीन का उछाल]] | ||
* [[शोर-चैनल कोडिंग प्रमेय]] | * [[शोर-चैनल कोडिंग प्रमेय|रव-चैनल कोडिंग प्रमेय]] | ||
* गाऊसी प्रक्रिया | * गाऊसी प्रक्रिया | ||
Revision as of 17:36, 28 July 2023
This article relies largely or entirely on a single source. (February 2020) |
योजक सफेद गाउसियन रव (AWGN) एक बुनियादी रव मॉडल है जिसका उपयोग प्रकृति में होने वाली कई यादृच्छिक प्रक्रियाओं के प्रभाव की नकल करने के लिए सूचना सिद्धांत में किया जाता है। संशोधक विशिष्ट विशेषताओं को दर्शाते हैं:
- एडिटिव क्योंकि यह किसी भी रव में जोड़ा जाता है जो सूचना प्रणाली में अंतर्निहित हो सकता है।
- व्हाइट इस विचार को संदर्भित करता है कि इसमें सूचना प्रणाली के लिए आवृत्ति बैंड में एक समान स्पेक्ट्रल घनत्व#पावर स्पेक्ट्रल घनत्व है। यह श्वेत#श्वेत प्रकाश का एक सादृश्य है जिसे दृश्य स्पेक्ट्रम में सभी आवृत्तियों पर समान उत्सर्जन द्वारा महसूस किया जा सकता है।
- गाऊशियन क्योंकि इसका समय क्षेत्र में औसत समय डोमेन मान शून्य (गाऊसी प्रक्रिया) के साथ एक सामान्य वितरण है।
वाइडबैंड रव कई प्राकृतिक रव स्रोतों से आता है, जैसे कंडक्टरों में परमाणुओं के थर्मल कंपन (थर्मल रव या जॉनसन-नाइक्विस्ट रव के रूप में जाना जाता है), शॉट रव, पृथ्वी और अन्य गर्म वस्तुओं से ब्लैक-बॉडी विकिरण, और सूर्य जैसे आकाशीय स्रोतों से। संभाव्यता सिद्धांत की केंद्रीय सीमा प्रमेय इंगित करती है कि कई यादृच्छिक प्रक्रियाओं के योग में गाऊसी या सामान्य नामक वितरण होगा।
AWGN को अक्सर एक संचार चैनल के रूप में उपयोग किया जाता है जिसमें संचार में एकमात्र बाधा निरंतर वर्णक्रमीय घनत्व (बैंडविड्थ (सिग्नल प्रोसेसिंग) के प्रति हेटर्स वाट के रूप में व्यक्त) और आयाम के गाऊसी वितरण के साथ वाइडबैंड या सफेद रव का एक रैखिक जोड़ है। मॉडल लुप्त होती, आवृत्ति चयनात्मकता, हस्तक्षेप (संचार), गैर-रैखिकता या फैलाव (प्रकाशिकी) को ध्यान में नहीं रखता है। हालाँकि, यह सरल और सुव्यवस्थित गणितीय मॉडल तैयार करता है जो इन अन्य घटनाओं पर विचार करने से पहले किसी प्रणाली के अंतर्निहित व्यवहार में अंतर्दृष्टि प्राप्त करने के लिए उपयोगी होते हैं।
AWGN चैनल कई उपग्रह और गहरे अंतरिक्ष संचार लिंक के लिए एक अच्छा मॉडल है। मल्टीपाथ, भूभाग अवरोधन, हस्तक्षेप आदि के कारण अधिकांश स्थलीय लिंक के लिए यह एक अच्छा मॉडल नहीं है। हालाँकि, स्थलीय पथ मॉडलिंग के लिए, AWGN का उपयोग आमतौर पर मल्टीपाथ, भूभाग अवरोधन, हस्तक्षेप, जमीनी अव्यवस्था और स्वयं हस्तक्षेप के अलावा अध्ययन के तहत चैनल के पृष्ठभूमि रव का अनुकरण करने के लिए किया जाता है, जिसका सामना आधुनिक रेडियो सिस्टम स्थलीय संचालन में करते हैं।
चैनल क्षमता
AWGN चैनल को आउटपुट की एक श्रृंखला द्वारा दर्शाया गया है असतत-समय घटना सूचकांक पर . इनपुट का योग है और रव, , कहाँ स्वतंत्र और समान रूप से वितरित यादृच्छिक चर है और भिन्नता के साथ शून्य-माध्य सामान्य वितरण से लिया गया है (ये रव)। h> को आगे इसके साथ सहसंबद्ध नहीं माना जाता है .
जब तक रव न हो, चैनल की क्षमता अनंत है शून्येतर है, और पर्याप्त रूप से प्रतिबंधित हैं. इनपुट पर सबसे आम बाधा तथाकथित पावर बाधा है, जिसके लिए कोडवर्ड की आवश्यकता होती है चैनल के माध्यम से प्रसारित, हमारे पास है:
कहाँ अधिकतम चैनल शक्ति का प्रतिनिधित्व करता है। इसलिए, बिजली-बाधित चैनल के लिए चैनल क्षमता इस प्रकार दी गई है:
कहाँ का वितरण है . बढ़ाना , इसे विभेदक एन्ट्रापी के संदर्भ में लिखना:
लेकिन और स्वतंत्र हैं, इसलिए:
गाऊसी की विभेदक एन्ट्रापी का मूल्यांकन करने पर यह मिलता है:
क्योंकि और स्वतंत्र हैं और उनका योग देता है :
इस सीमा से, हम अंतर एन्ट्रापी की एक संपत्ति से अनुमान लगाते हैं
इसलिए, चैनल क्षमता पारस्परिक जानकारी पर उच्चतम प्राप्य सीमा द्वारा दी गई है:
कहाँ अधिकतम तब होता है जब:
इस प्रकार चैनल क्षमता AWGN चैनल के लिए यह दिया गया है:
चैनल क्षमता और क्षेत्र पैकिंग
मान लीजिए कि हम सूचकांक वाले चैनल के माध्यम से संदेश भेज रहे हैं को , अलग-अलग संभावित संदेशों की संख्या। यदि हम एन्कोड करते हैं को संदेश बिट्स, फिर हम दर को परिभाषित करते हैं जैसा:
एक दर को प्राप्त करने योग्य कहा जाता है यदि कोड का अनुक्रम हो ताकि त्रुटि की अधिकतम संभावना शून्य हो जाए अनंत तक पहुंचता है. क्षमता उच्चतम प्राप्य दर है.
लंबाई के एक कोडवर्ड पर विचार करें रव स्तर के साथ AWGN चैनल के माध्यम से भेजा गया . प्राप्त होने पर, कोडवर्ड वेक्टर विचरण अब है , और इसका माध्य भेजा गया कोडवर्ड है। वेक्टर के त्रिज्या के एक गोले में समाहित होने की बहुत संभावना है चारों ओर कोडवर्ड भेजा गया। यदि हम प्राप्त प्रत्येक संदेश को इस क्षेत्र के केंद्र में कोडवर्ड पर मैप करके डिकोड करते हैं, तो त्रुटि तभी होती है जब प्राप्त वेक्टर इस क्षेत्र के बाहर होता है, जो बहुत ही असंभव है।
प्रत्येक कोडवर्ड वेक्टर में प्राप्त कोडवर्ड वैक्टर का एक संबद्ध क्षेत्र होता है जिसे इसमें डिकोड किया जाता है और ऐसे प्रत्येक क्षेत्र को एक कोडवर्ड पर विशिष्ट रूप से मैप किया जाना चाहिए। चूँकि इन गोले को एक दूसरे को नहीं काटना चाहिए, इसलिए हमें गोला पैकिंग की समस्या का सामना करना पड़ता है। हम अपने में कितने अलग-अलग कोडवर्ड पैक कर सकते हैं -बिट कोडवर्ड वेक्टर? प्राप्त वैक्टर में अधिकतम ऊर्जा होती है और इसलिए उसे त्रिज्या का एक क्षेत्र घेरना चाहिए . प्रत्येक कोडवर्ड गोले की त्रिज्या होती है . एक n-आयामी गोले का आयतन सीधे आनुपातिक होता है , इसलिए ट्रांसमिशन पावर पी के साथ हमारे क्षेत्र में पैक किए जा सकने वाले विशिष्ट डिकोडेबल क्षेत्रों की अधिकतम संख्या है:
इस तर्क से, दर R से अधिक नहीं हो सकती .
साध्यता
इस खंड में, हम अंतिम खंड से दर पर ऊपरी सीमा की प्राप्ति दर्शाते हैं।
एनकोडर और डिकोडर दोनों के लिए ज्ञात एक कोडबुक, लंबाई n, i.i.d. के कोडवर्ड का चयन करके तैयार की जाती है। विचरण के साथ गाऊसी और मतलब शून्य. बड़े n के लिए, कोडबुक का अनुभवजन्य विचरण इसके वितरण के विचरण के बहुत करीब होगा, जिससे संभावित रूप से शक्ति बाधा के उल्लंघन से बचा जा सकेगा।
प्राप्त संदेशों को कोडबुक में एक संदेश में डिकोड किया जाता है जो विशिष्ट रूप से संयुक्त रूप से विशिष्ट है। यदि ऐसा कोई संदेश नहीं है या यदि बिजली की कमी का उल्लंघन किया गया है, तो डिकोडिंग त्रुटि घोषित की जाती है।
होने देना संदेश के लिए कोडवर्ड बताएं , जबकि प्राप्त वेक्टर से पहले की तरह है। निम्नलिखित तीन घटनाओं को परिभाषित करें:
- आयोजन :प्राप्त संदेश की शक्ति इससे बड़ी है .
- आयोजन : प्रेषित और प्राप्त कोडवर्ड संयुक्त रूप से विशिष्ट नहीं हैं।
- आयोजन : में है , विशिष्ट सेट जहां , जिसका अर्थ यह है कि गलत कोडवर्ड प्राप्त वेक्टर के साथ संयुक्त रूप से विशिष्ट है।
इसलिए एक त्रुटि उत्पन्न होती है यदि , या इनमें से कोई भी घटित होना। बड़ी संख्या के नियम से, जैसे-जैसे n अनंत के करीब पहुंचता है, शून्य हो जाता है और संयुक्त स्पर्शोन्मुख समविभाजन संपत्ति द्वारा भी यही बात लागू होती है . इसलिए, पर्याप्त रूप से बड़े के लिए , दोनों और प्रत्येक से कम हैं . तब से और के लिए स्वतंत्र हैं , हमारे पास वह है और स्वतंत्र भी हैं. इसलिए, संयुक्त एईपी द्वारा, . यह हमें गणना करने की अनुमति देता है , त्रुटि की संभावना इस प्रकार है:
इसलिए, जैसे-जैसे n अनंत की ओर बढ़ता है, शून्य पर चला जाता है और . इसलिए, दर आर का एक कोड मनमाने ढंग से पहले प्राप्त क्षमता के करीब है।
कोडिंग प्रमेय का व्युत्क्रम
यहां हम दिखाते हैं कि दरें क्षमता से अधिक हैं प्राप्य नहीं हैं.
मान लीजिए कि कोडबुक के लिए बिजली की कमी पूरी हो गई है, और आगे यह भी मान लें कि संदेश एक समान वितरण का पालन करते हैं। होने देना इनपुट संदेश हो और आउटपुट संदेश. इस प्रकार जानकारी इस प्रकार प्रवाहित होती है:
फ़ानो की असमानता का उपयोग करने से मिलता है:
कहाँ जैसा होने देना कोडवर्ड इंडेक्स i का एन्कोडेड संदेश हो। तब:
होने देना सूचकांक i के कोडवर्ड की औसत शक्ति हो:
जहां योग सभी इनपुट संदेशों से अधिक है . और स्वतंत्र हैं, अत: की शक्ति की अपेक्षा रखते हैं रव के स्तर के लिए है :
और अगर सामान्य रूप से वितरित किया जाता है, हमारे पास वह है
इसलिए,
हम जेन्सेन की समानता को लागू कर सकते हैं , x का एक अवतल (नीचे की ओर) फ़ंक्शन, प्राप्त करने के लिए:
चूँकि प्रत्येक कोडवर्ड व्यक्तिगत रूप से शक्ति बाधा को संतुष्ट करता है, औसत भी शक्ति बाधा को संतुष्ट करता है। इसलिए,
जिसे हम उपरोक्त असमानता को सरल बनाने के लिए लागू कर सकते हैं और प्राप्त कर सकते हैं:
इसलिए, ऐसा होना ही चाहिए . इसलिए, आर को मनमाने ढंग से पहले प्राप्त क्षमता के करीब एक मूल्य से कम होना चाहिए .
समय क्षेत्र में प्रभाव
सीरियल डेटा संचार में, AWGN गणितीय मॉडल का उपयोग यादृच्छिक घबराना (आरजे) के कारण होने वाली समय त्रुटि को मॉडल करने के लिए किया जाता है।
दाईं ओर का ग्राफ़ AWGN से जुड़ी समय संबंधी त्रुटियों का एक उदाहरण दिखाता है। चर Δt शून्य क्रॉसिंग में अनिश्चितता का प्रतिनिधित्व करता है। जैसे-जैसे AWGN का आयाम बढ़ता है, सिग्नल-टू-रव अनुपात कम हो जाता है। इसके परिणामस्वरूप अनिश्चितता बढ़ जाती है Δt।[1]
जब AWGN से प्रभावित होता है, तो एक संकीर्ण बैंडपास फिल्टर के आउटपुट पर प्रति सेकंड सकारात्मक या नकारात्मक शून्य क्रॉसिंग की औसत संख्या होती है जब इनपुट साइन तरंग होता है
कहाँ
- 0 = फ़िल्टर की केंद्र आवृत्ति,
- बी = फिल्टर बैंडविड्थ,
- एसएनआर = रैखिक शब्दों में सिग्नल-टू-रव शक्ति अनुपात।
फ़ेसर डोमेन में प्रभाव
आधुनिक संचार प्रणालियों में, बैंडलिमिटेड AWGN को नजरअंदाज नहीं किया जा सकता है। जब फेज़र डोमेन में बैंडलिमिटेड AWGN की मॉडलिंग की जाती है, तो सांख्यिकीय विश्लेषण से पता चलता है कि वास्तविक और काल्पनिक योगदान के आयाम स्वतंत्र चर हैं जो गॉसियन वितरण मॉडल का पालन करते हैं। संयुक्त होने पर, परिणामी चरण का परिमाण एक रेले वितरण होता है | रेले-वितरित यादृच्छिक चर, जबकि चरण समान रूप से 0 से 2 तक वितरित होता हैπ.
दाईं ओर का ग्राफ़ एक उदाहरण दिखाता है कि बैंडलिमिटेड AWGN एक सुसंगत वाहक सिग्नल को कैसे प्रभावित कर सकता है। रव वेक्टर की तात्कालिक प्रतिक्रिया का सटीक अनुमान नहीं लगाया जा सकता है, हालांकि, इसकी समय-औसत प्रतिक्रिया का सांख्यिकीय रूप से अनुमान लगाया जा सकता है। जैसा कि ग्राफ में दिखाया गया है, हम विश्वासपूर्वक अनुमान लगाते हैं कि रव चरण 1σ सर्कल के अंदर लगभग 38% समय, 2σ सर्कल के अंदर लगभग 86% समय और 3σ सर्कल के अंदर लगभग 98% समय रहेगा।[1]
यह भी देखें
- ज़मीन का उछाल
- रव-चैनल कोडिंग प्रमेय
- गाऊसी प्रक्रिया