नर्नस्ट समीकरण: Difference between revisions
(Created page with "{{Short description|Physical law in electrochemistry}} {{Distinguish|Ernst equation}} इलेक्ट्रोकैमिस्ट्री में, नर्नस...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Physical law in electrochemistry}} | {{Short description|Physical law in electrochemistry}} | ||
{{Distinguish|Ernst equation}} | {{Distinguish|Ernst equation}} | ||
[[इलेक्ट्रोकैमिस्ट्री]] में, नर्नस्ट समीकरण | [[इलेक्ट्रोकैमिस्ट्री]] में, नर्नस्ट समीकरण थर्मोडायनामिक्स # रासायनिक थर्मोडायनामिक्स संबंध है जो [[मानक इलेक्ट्रोड क्षमता]], [[थर्मोडायनामिक तापमान]], [[रिडॉक्स]] में शामिल इलेक्ट्रॉनों की संख्या से प्रतिक्रिया ([[आधा सेल]] या [[विद्युत रासायनिक सेल]] प्रतिक्रिया) की कमी क्षमता की गणना की अनुमति देता है। क्रमशः कमी और [[ऑक्सीकरण]] से गुजरने वाली रासायनिक प्रजातियों की [[थर्मोडायनामिक गतिविधि]] (अक्सर सांद्रता द्वारा अनुमानित)। इसका नाम जर्मन [[भौतिक रसायनज्ञ]] [[वाल्थर नर्नस्ट]] के नाम पर रखा गया, जिन्होंने समीकरण तैयार किया था।<ref name="isbn0-8412-1572-3">{{cite book |last1=Orna |first1=Mary Virginia |last2=Stock |first2=John |title=Electrochemistry, past and present |publisher=American Chemical Society |location=Columbus, OH |year=1989 |isbn=978-0-8412-1572-6 |oclc= 19124885}}</ref><ref name=Wahl2005>{{Cite journal | last = Wahl | year = 2005 | title = A Short History of Electrochemistry | journal = Galvanotechtnik | volume = 96 | issue = 8 | pages = 1820–1828 }}</ref> | ||
| Line 8: | Line 8: | ||
===रासायनिक क्रियाओं के साथ सामान्य रूप === | ===रासायनिक क्रियाओं के साथ सामान्य रूप === | ||
जब | जब आक्सीकारक ({{Math|Ox}}) इलेक्ट्रॉनों की संख्या z स्वीकार करता है ({{e-}}) इसके कम रूप में परिवर्तित करने के लिए ({{Math|Red}}), आधी प्रतिक्रिया के रूप में व्यक्त किया गया है: | ||
: {{mvar|Ox}} + जेड {{e-}} → {{mvar|Red}} | : {{mvar|Ox}} + जेड {{e-}} → {{mvar|Red}} | ||
[[प्रतिक्रिया भागफल]] ({{Math|Q<sub>r</sub>}}), जिसे अक्सर आयन गतिविधि उत्पाद (आईएपी) भी कहा जाता है, [[रासायनिक गतिविधि]] (ए) के कम रूप ([[कम करना]],) के बीच का अनुपात है। {{Math|a<sub>Red</sub>}}) और ऑक्सीकृत रूप ([[ऑक्सीडेंट]], {{Math|a<sub>Ox</sub>}}). | [[प्रतिक्रिया भागफल]] ({{Math|Q<sub>r</sub>}}), जिसे अक्सर आयन गतिविधि उत्पाद (आईएपी) भी कहा जाता है, [[रासायनिक गतिविधि]] (ए) के कम रूप ([[कम करना]],) के बीच का अनुपात है। {{Math|a<sub>Red</sub>}}) और ऑक्सीकृत रूप ([[ऑक्सीडेंट]], {{Math|a<sub>Ox</sub>}}). विघटित प्रजाति की रासायनिक गतिविधि उच्च सांद्रता पर समाधान में मौजूद सभी आयनों के बीच विद्युतीय संबंधों को ध्यान में रखते हुए इसकी वास्तविक थर्मोडायनामिक [[एकाग्रता]] से मेल खाती है। किसी दी गई विघटित प्रजाति के लिए, इसकी रासायनिक गतिविधि (ए) इसकी मोलर सघनता (mol/L सॉल्यूशन), या [[मोलिटी]] (mol/kg पानी), सघनता (C) द्वारा इसकी [[गतिविधि गुणांक]] (γ) का उत्पाद है: a = γ सी। इसलिए, यदि ब्याज की सभी भंग प्रजातियों की एकाग्रता (सी, यहां नीचे वर्ग कोष्ठक [ ] के साथ भी दर्शाया गया है) पर्याप्त रूप से कम है और उनकी गतिविधि गुणांक एकता के करीब हैं, तो उनकी रासायनिक गतिविधियों को उनकी सांद्रता द्वारा अनुमानित किया जा सकता है आमतौर पर किया जाता है जब सरलीकृत, या आदर्शीकरण, उपचारात्मक उद्देश्यों के लिए प्रतिक्रिया: | ||
: <math>Q_r = \frac{a_\text{Red}}{a_\text{Ox}} = \frac{[Red]}{[Ox]}</math> | : <math>Q_r = \frac{a_\text{Red}}{a_\text{Ox}} = \frac{[Red]}{[Ox]}</math> | ||
| Line 20: | Line 20: | ||
<math display="block">\Delta G = \Delta G^{\ominus} + RT\ln Q_r</math> | <math display="block">\Delta G = \Delta G^{\ominus} + RT\ln Q_r</math> | ||
कहाँ {{math|''Q''<sub>r</sub>}} प्रतिक्रिया भागफल है। | कहाँ {{math|''Q''<sub>r</sub>}} प्रतिक्रिया भागफल है। | ||
सेल क्षमता {{mvar|E}} इलेक्ट्रोकेमिकल रिएक्शन से जुड़े गिब्स फ्री एनर्जी प्रति कूलॉम ऑफ चार्ज ट्रांसफर में कमी के रूप में परिभाषित किया गया है, जो रिश्ते की ओर जाता है <math display="block">\Delta G = -zFE.</math> अटल {{mvar|F}} ([[फैराडे स्थिरांक]]) | सेल क्षमता {{mvar|E}} इलेक्ट्रोकेमिकल रिएक्शन से जुड़े गिब्स फ्री एनर्जी प्रति कूलॉम ऑफ चार्ज ट्रांसफर में कमी के रूप में परिभाषित किया गया है, जो रिश्ते की ओर जाता है <math display="block">\Delta G = -zFE.</math> अटल {{mvar|F}} ([[फैराडे स्थिरांक]]) इकाई रूपांतरण कारक है {{math|1=''F'' = ''N''<sub>A</sub>''q''}}, कहाँ {{math|''N''<sub>A</sub>}} [[अवोगाद्रो स्थिरांक]] है और {{mvar|q}} मौलिक [[इलेक्ट्रॉन]] आवेश है। यह तुरंत नर्नस्ट समीकरण की ओर जाता है, जो विद्युत रासायनिक अर्ध-सेल के लिए है | ||
<math display="block">E_\text{red} = E^\ominus_\text{red} - \frac{RT}{zF} \ln Q_r=E^\ominus_\text{red} - \frac{RT}{zF} \ln\frac{a_\text{Red}}{a_\text{Ox}}.</math> | <math display="block">E_\text{red} = E^\ominus_\text{red} - \frac{RT}{zF} \ln Q_r=E^\ominus_\text{red} - \frac{RT}{zF} \ln\frac{a_\text{Red}}{a_\text{Ox}}.</math> | ||
पूर्ण विद्युत रासायनिक प्रतिक्रिया (पूर्ण सेल) के लिए, समीकरण को इस प्रकार लिखा जा सकता है | पूर्ण विद्युत रासायनिक प्रतिक्रिया (पूर्ण सेल) के लिए, समीकरण को इस प्रकार लिखा जा सकता है | ||
| Line 30: | Line 30: | ||
* {{math|''E''{{su|p=<s>o</s>|b=cell}}}} [[मानक सेल क्षमता]] है, | * {{math|''E''{{su|p=<s>o</s>|b=cell}}}} [[मानक सेल क्षमता]] है, | ||
* {{mvar|R}} [[सार्वभौमिक गैस स्थिरांक]] है: {{math|1=''R'' = {{val|8.31446261815324|u=J K<sup>−1</sup> mol<sup>−1</sup>}}}}, | * {{mvar|R}} [[सार्वभौमिक गैस स्थिरांक]] है: {{math|1=''R'' = {{val|8.31446261815324|u=J K<sup>−1</sup> mol<sup>−1</sup>}}}}, | ||
* {{mvar|T}} [[केल्विन]] में तापमान है | * {{mvar|T}} [[केल्विन]] में तापमान है, | ||
* {{mvar|z}} सेल प्रतिक्रिया या अर्ध-प्रतिक्रिया में स्थानांतरित इलेक्ट्रॉनों की संख्या है, | * {{mvar|z}} सेल प्रतिक्रिया या अर्ध-प्रतिक्रिया में स्थानांतरित इलेक्ट्रॉनों की संख्या है, | ||
* {{mvar|F}} फैराडे स्थिरांक है, इलेक्ट्रॉनों के प्रति मोल (इकाई) आवेश का परिमाण ([[कूलम्ब]] में): {{math|1=''F'' = {{val|96485.3321233100184|u=C mol<sup>−1</sup>}}}}, | * {{mvar|F}} फैराडे स्थिरांक है, इलेक्ट्रॉनों के प्रति मोल (इकाई) आवेश का परिमाण ([[कूलम्ब]] में): {{math|1=''F'' = {{val|96485.3321233100184|u=C mol<sup>−1</sup>}}}}, | ||
| Line 45: | Line 45: | ||
=== गतिविधि गुणांक और सांद्रता के साथ प्रपत्र === | === गतिविधि गुणांक और सांद्रता के साथ प्रपत्र === | ||
संतुलन स्थिरांक के समान, गतिविधियों को हमेशा मानक अवस्था के संबंध में मापा जाता है (विलेय के लिए 1 mol/L, गैसों के लिए 1 atm, और T = 298.15 K, यानी 25 °C या 77 °F)। | संतुलन स्थिरांक के समान, गतिविधियों को हमेशा मानक अवस्था के संबंध में मापा जाता है (विलेय के लिए 1 mol/L, गैसों के लिए 1 atm, और T = 298.15 K, यानी 25 °C या 77 °F)। प्रजाति की रासायनिक गतिविधि {{math|i}}, {{math|''a''<sub>i</sub>}}, मापा एकाग्रता से संबंधित है {{math|''C''<sub>i</sub>}} रिश्ते के माध्यम से {{math|1=''a''<sub>i</sub> = ''γ''<sub>i</sub> ''C''<sub>i</sub>}}, कहाँ {{math|''γ''<sub>i</sub>}} प्रजातियों का गतिविधि गुणांक है {{math|i}}. क्योंकि गतिविधि गुणांक कम सांद्रता पर एकता की ओर प्रवृत्त होते हैं, या मध्यम और उच्च सांद्रता पर अज्ञात या निर्धारित करने में कठिन होते हैं, नर्नस्ट समीकरण में गतिविधियों को अक्सर सरल सांद्रता से बदल दिया जाता है और फिर, औपचारिक मानक कमी क्षमता <math>E^{\ominus'}_\text{red}</math> इस्तेमाल किया गया। | ||
गतिविधि गुणांक को ध्यान में रखते हुए (<math>\gamma</math>) नर्नस्ट समीकरण बन जाता है: | गतिविधि गुणांक को ध्यान में रखते हुए (<math>\gamma</math>) नर्नस्ट समीकरण बन जाता है: | ||
| Line 54: | Line 54: | ||
<math display="block">E_\text{red} = \underbrace{\left(E^\ominus_\text{red} - \frac{RT}{zF} \ln\frac{\gamma_\text{Red}}{\gamma_\text{Ox}}\right)}_{E^{\ominus '}_\text{red}} - \frac{RT}{zF} \ln\frac{C_\text{Red}}{C_\text{Ox}}</math> | <math display="block">E_\text{red} = \underbrace{\left(E^\ominus_\text{red} - \frac{RT}{zF} \ln\frac{\gamma_\text{Red}}{\gamma_\text{Ox}}\right)}_{E^{\ominus '}_\text{red}} - \frac{RT}{zF} \ln\frac{C_\text{Red}}{C_\text{Ox}}</math> | ||
जहां गतिविधि गुणांक सहित पहला पद (<math>\gamma</math>) अंकित है <math>E^{\ominus '}_\text{red}</math> और औपचारिक मानक कमी क्षमता कहा जाता है, ताकि <math>E_\text{red}</math> के | जहां गतिविधि गुणांक सहित पहला पद (<math>\gamma</math>) अंकित है <math>E^{\ominus '}_\text{red}</math> और औपचारिक मानक कमी क्षमता कहा जाता है, ताकि <math>E_\text{red}</math> के समारोह के रूप में सीधे व्यक्त किया जा सकता है <math>E^{\ominus '}_\text{red}</math> और नर्नस्ट समीकरण के सरलतम रूप में सांद्रता: | ||
<math display="block">E_\text{red}=E^{\ominus '}_\text{red} - \frac{RT}{zF} \ln\frac{C_\text{Red}}{C_\text{Ox}}</math> | <math display="block">E_\text{red}=E^{\ominus '}_\text{red} - \frac{RT}{zF} \ln\frac{C_\text{Red}}{C_\text{Ox}}</math> | ||
| Line 67: | Line 67: | ||
और इसी तरह पूर्ण सेल अभिव्यक्ति के लिए। | और इसी तरह पूर्ण सेल अभिव्यक्ति के लिए। | ||
वेन्ज़ेल (2020) के अनुसार,<ref name="Wenzel_2020">{{Cite web |title=4. मानक राज्य विद्युत रासायनिक क्षमता की तालिका|last=Wenzel |first=Thomas |work=Chemistry LibreTexts |date=2020-06-09 |access-date=2021-11-24 |url= https://chem.libretexts.org/Bookshelves/Analytical_Chemistry/Supplemental_Modules_(Analytical_Chemistry)/Analytical_Sciences_Digital_Library/Active_Learning/In_Class_Activities/Electrochemical_Methods_of_Analysis/02_Text/4._Table_of_Standard_State_Electrochemical_Potentials}}</ref> | वेन्ज़ेल (2020) के अनुसार,<nowiki><ref name="Wenzel_2020"></nowiki>{{Cite web |title=4. मानक राज्य विद्युत रासायनिक क्षमता की तालिका|last=Wenzel |first=Thomas |work=Chemistry LibreTexts |date=2020-06-09 |access-date=2021-11-24 |url= https://chem.libretexts.org/Bookshelves/Analytical_Chemistry/Supplemental_Modules_(Analytical_Chemistry)/Analytical_Sciences_Digital_Library/Active_Learning/In_Class_Activities/Electrochemical_Methods_of_Analysis/02_Text/4._Table_of_Standard_State_Electrochemical_Potentials}}</ref> औपचारिक कटौती क्षमता <math>E^{\ominus '}_\text{red}</math> कमी की क्षमता है जो निर्दिष्ट शर्तों के सेट के तहत आधी प्रतिक्रिया पर लागू होती है, जैसे, [[पीएच]], आयनिक शक्ति, या [[जटिल एजेंट]]ों की एकाग्रता। | ||
औपचारिक कमी क्षमता <math>E^{\ominus '}_\text{red}</math> अक्सर | औपचारिक कमी क्षमता <math>E^{\ominus '}_\text{red}</math> अक्सर अधिक सुविधाजनक, लेकिन सशर्त, मानक कमी क्षमता का रूप होता है, जो प्रतिक्रिया के माध्यम की गतिविधि गुणांक और विशिष्ट स्थितियों की विशेषताओं को ध्यान में रखता है। इसलिए, इसका मूल्य सशर्त मूल्य है, अर्थात यह प्रायोगिक स्थितियों पर निर्भर करता है और क्योंकि आयनिक शक्ति गतिविधि गुणांक को प्रभावित करती है, <math>E^{\ominus '}_\text{red}</math> मध्यम से मध्यम भिन्न होगा।<ref name="Bard_Faultner" />औपचारिक कमी क्षमता की कई परिभाषाएँ साहित्य में पाई जा सकती हैं, जो अध्ययन किए गए उद्देश्य और अध्ययन प्रणाली द्वारा लगाए गए प्रयोगात्मक बाधाओं पर निर्भर करती हैं। की सामान्य परिभाषा <math>E^{\ominus '}_\text{red}</math> इसके मूल्य को संदर्भित करता है जब निर्धारित किया जाता है <math>\frac{C_\text{red}} {C_\text{ox}} = 1</math>. और विशेष मामला है जब <math>E^{\ominus '}_\text{red}</math> पीएच 7 पर भी निर्धारित किया जाता है, उदा। जैव रसायन या जैविक प्रणालियों में महत्वपूर्ण रेडॉक्स प्रतिक्रियाओं के लिए। | ||
==== औपचारिक मानक कमी क्षमता का निर्धारण जब {{mvar|{{sfrac|C<sub>red</sub>|C<sub>ox</sub>}}}} {{=}} 1==== | ==== औपचारिक मानक कमी क्षमता का निर्धारण जब {{mvar|{{sfrac|C<sub>red</sub>|C<sub>ox</sub>}}}} {{=}} 1==== | ||
| Line 79: | Line 79: | ||
जैसा, <math>E_\text{red} = E^{\ominus}_\text{red}</math>, कब <math>\frac{a_\text{red}} {a_\text{ox}} = 1</math>, | जैसा, <math>E_\text{red} = E^{\ominus}_\text{red}</math>, कब <math>\frac{a_\text{red}} {a_\text{ox}} = 1</math>, | ||
: <math>E_\text{red} = E^{\ominus'}_\text{red}</math>, कब <math>\frac{C_\text{red}} {C_\text{ox}} = 1</math>, | :<math>E_\text{red} = E^{\ominus'}_\text{red}</math>, कब <math>\frac{C_\text{red}} {C_\text{ox}} = 1</math>, | ||
क्योंकि <math>\ln{1} = 0</math>, और वह शब्द <math>\frac{\gamma_\text{red}} {\gamma_\text{ox}}</math> में शामिल है <math>E^{\ominus '}_\text{red}</math>. | क्योंकि <math>\ln{1} = 0</math>, और वह शब्द <math>\frac{\gamma_\text{red}} {\gamma_\text{ox}}</math> में शामिल है <math>E^{\ominus '}_\text{red}</math>. | ||
औपचारिक कमी की क्षमता मोलर सांद्रता (mol/L, M) या मोललता (mol/kg) के साथ अधिक आसानी से काम करना संभव बनाती है। {{H2O}}, एम) रासायनिक गतिविधि के स्थान पर सांद्रता। क्योंकि दाढ़ और मोलल सांद्रता को एक बार औपचारिक सांद्रता के रूप में संदर्भित किया गया था, यह अभिव्यक्ति औपचारिक क्षमता में औपचारिक विशेषण की उत्पत्ति की व्याख्या कर सकता है।{{cn|date= December 2021}} औपचारिक क्षमता इस प्रकार एक समाधान में डूबे हुए संतुलन पर एक इलेक्ट्रोड की प्रतिवर्ती क्षमता है जहां अभिकारक और उत्पाद इकाई एकाग्रता में हैं।<ref name="Freedictionary">{{Cite web |title=Formal potential |author= |work=TheFreeDictionary.com |date= |access-date=2021-12-06 |url= https://encyclopedia2.thefreedictionary.com/Formal+potential |language=English}}</ref> यदि क्षमता में कोई भी छोटा वृद्धिशील परिवर्तन प्रतिक्रिया की दिशा में परिवर्तन का कारण बनता है, अर्थात कमी से ऑक्सीकरण या इसके विपरीत, प्रणाली संतुलन के करीब है, प्रतिवर्ती है और अपनी औपचारिक क्षमता पर है। जब औपचारिक क्षमता को मानक स्थितियों के तहत मापा जाता है (अर्थात प्रत्येक विघटित प्रजाति की गतिविधि 1 mol/L, T = 298.15 K = 25 °C = 77 °F, {{mvar|P<sub>gas</sub>}} = 1 बार) तो यह वास्तव में | औपचारिक कमी की क्षमता मोलर सांद्रता (mol/L, M) या मोललता (mol/kg) के साथ अधिक आसानी से काम करना संभव बनाती है। {{H2O}}, एम) रासायनिक गतिविधि के स्थान पर सांद्रता। क्योंकि दाढ़ और मोलल सांद्रता को एक बार औपचारिक सांद्रता के रूप में संदर्भित किया गया था, यह अभिव्यक्ति औपचारिक क्षमता में औपचारिक विशेषण की उत्पत्ति की व्याख्या कर सकता है।{{cn|date= December 2021}} औपचारिक क्षमता इस प्रकार एक समाधान में डूबे हुए संतुलन पर एक इलेक्ट्रोड की प्रतिवर्ती क्षमता है जहां अभिकारक और उत्पाद इकाई एकाग्रता में हैं।<nowiki><ref name="Freedictionary"></nowiki>{{Cite web |title=Formal potential |author= |work=TheFreeDictionary.com |date= |access-date=2021-12-06 |url= https://encyclopedia2.thefreedictionary.com/Formal+potential |language=English}}</ref> यदि क्षमता में कोई भी छोटा वृद्धिशील परिवर्तन प्रतिक्रिया की दिशा में परिवर्तन का कारण बनता है, अर्थात कमी से ऑक्सीकरण या इसके विपरीत, प्रणाली संतुलन के करीब है, प्रतिवर्ती है और अपनी औपचारिक क्षमता पर है। जब औपचारिक क्षमता को मानक स्थितियों के तहत मापा जाता है (अर्थात प्रत्येक विघटित प्रजाति की गतिविधि 1 mol/L, T = 298.15 K = 25 °C = 77 °F, {{mvar|P<sub>gas</sub>}} = 1 बार) तो यह वास्तव में मानक विभव बन जाता है।<ref name="PalmSens">{{Cite web |title=Origins of electrochemical potentials — PalmSens |author=PalmSens |work=PalmSens |year=2021 |access-date=2021-12-06 |url=https://www.palmsens.com/knowledgebase-article/origins-of-electrochemical-potentials/}}</ref> <br />ब्राउन और स्विफ्ट (1949) के अनुसार: | ||
<blockquote> एक औपचारिक क्षमता को आधे सेल की क्षमता के रूप में परिभाषित किया जाता है, जिसे [[मानक हाइड्रोजन इलेक्ट्रोड]] के खिलाफ मापा जाता है, जब प्रत्येक ऑक्सीकरण राज्य की कुल एकाग्रता | <blockquote> एक औपचारिक क्षमता को आधे सेल की क्षमता के रूप में परिभाषित किया जाता है, जिसे [[मानक हाइड्रोजन इलेक्ट्रोड]] के खिलाफ मापा जाता है, जब प्रत्येक ऑक्सीकरण राज्य की कुल एकाग्रता औपचारिक एकाग्रता होती है।<ref name="Brown_1949">{{Cite journal| last1 = Brown| first1 = Raymond A.| last2 = Swift| first2 = Ernest H.| year = 1949| title = हाइड्रोक्लोरिक एसिड समाधान में एंटीमोनस-एंटीमोनिक आधा सेल की औपचारिक क्षमता| journal = Journal of the American Chemical Society| volume = 71| issue = 8| pages = 2719–2723| issn = 0002-7863|quote = <u>उद्धरण</u>: एक औपचारिक क्षमता को एक आधे सेल की क्षमता के रूप में परिभाषित किया जाता है, जिसे मानक हाइड्रोजन इलेक्ट्रोड के खिलाफ मापा जाता है, जब प्रत्येक ऑक्सीकरण अवस्था की कुल सांद्रता एक औपचारिक होती है।}}</Ref></blockquote> | ||
इस मामले में, मानक कमी क्षमता के लिए, भंग प्रजातियों की सांद्रता | इस मामले में, मानक कमी क्षमता के लिए, भंग प्रजातियों की सांद्रता मोलर सांद्रता (M) या मोलिटी (m) के बराबर रहती है, और इसलिए इसे औपचारिक सांद्रता (F) कहा जाता है। तो एकाग्रता व्यक्त कर रहे हैं {{mvar|C}} दाढ़ एकाग्रता में {{math|M}} (1 मोल / एल): | ||
: <math>\frac{C_\text{red}} {C_\text{ox}} = \frac{1 \, \mathrm{M}_\text{red}} {1 \, \mathrm{M}_\text{ox}} = 1</math> | : <math>\frac{C_\text{red}} {C_\text{ox}} = \frac{1 \, \mathrm{M}_\text{red}} {1 \, \mathrm{M}_\text{ox}} = 1</math> | ||
| Line 94: | Line 94: | ||
चक्रीय [[voltammetry]] में दो चोटियों के बीच औपचारिक क्षमता भी आधी पाई जाती है, जहां इस बिंदु पर इलेक्ट्रोड सतह पर ऑक्स (ऑक्सीडाइज्ड प्रजाति) और रेड (कम प्रजाति) की सांद्रता बराबर होती है। | चक्रीय [[voltammetry]] में दो चोटियों के बीच औपचारिक क्षमता भी आधी पाई जाती है, जहां इस बिंदु पर इलेक्ट्रोड सतह पर ऑक्स (ऑक्सीडाइज्ड प्रजाति) और रेड (कम प्रजाति) की सांद्रता बराबर होती है। | ||
गतिविधि गुणांक <math>\gamma_{red}</math> और <math>\gamma_{ox}</math> औपचारिक क्षमता में शामिल हैं <math>E^{\ominus '}_\text{red}</math>, और क्योंकि वे तापमान, आयनिक शक्ति और पीएच जैसी प्रायोगिक स्थितियों पर निर्भर करते हैं, <math>E^{\ominus '}_\text{red}</math> एक अपरिवर्तनीय मानक क्षमता के रूप में संदर्भित नहीं किया जा सकता है लेकिन प्रायोगिक स्थितियों के प्रत्येक विशिष्ट सेट के लिए व्यवस्थित रूप से निर्धारित करने की आवश्यकता है। | गतिविधि गुणांक <math>\gamma_{red}</math> और <math>\gamma_{ox}</math> औपचारिक क्षमता में शामिल हैं <math>E^{\ominus '}_\text{red}</math>, और क्योंकि वे तापमान, आयनिक शक्ति और पीएच जैसी प्रायोगिक स्थितियों पर निर्भर करते हैं, <math>E^{\ominus '}_\text{red}</math> एक अपरिवर्तनीय मानक क्षमता के रूप में संदर्भित नहीं किया जा सकता है लेकिन प्रायोगिक स्थितियों के प्रत्येक विशिष्ट सेट के लिए व्यवस्थित रूप से निर्धारित करने की आवश्यकता है। | ||
दी गई शर्तों और माप की व्याख्या के तहत एक मानी हुई प्रणाली की गणना को सरल बनाने के लिए औपचारिक कमी की क्षमता लागू की जाती है। प्रायोगिक स्थितियाँ जिनमें वे निर्धारित किए गए हैं और मानक कमी क्षमता के साथ उनके संबंध को स्पष्ट रूप से वर्णित किया जाना चाहिए ताकि उन्हें मानक कमी क्षमता के साथ भ्रमित करने से बचा जा सके। | दी गई शर्तों और माप की व्याख्या के तहत एक मानी हुई प्रणाली की गणना को सरल बनाने के लिए औपचारिक कमी की क्षमता लागू की जाती है। प्रायोगिक स्थितियाँ जिनमें वे निर्धारित किए गए हैं और मानक कमी क्षमता के साथ उनके संबंध को स्पष्ट रूप से वर्णित किया जाना चाहिए ताकि उन्हें मानक कमी क्षमता के साथ भ्रमित करने से बचा जा सके। | ||
| Line 102: | Line 102: | ||
औपचारिक मानक कमी क्षमता (<math>E^{\ominus '}_\text{red}</math>) आमतौर पर पीएच 7 पर मापी गई [[मानक कमी क्षमता]] के संदर्भ में जैव रसायन और कोशिका जीव विज्ञान में भी उपयोग किया जाता है, जो 0 के मानक राज्य पीएच की तुलना में अधिकांश शारीरिक और इंट्रासेल्युलर तरल पदार्थों के पीएच के करीब है। लाभ एक अधिक उपयुक्त रेडॉक्स को परिभाषित करना है। मानक स्थिति की तुलना में वास्तविक परिस्थितियों के अनुरूप बेहतर। औपचारिक मानक कमी क्षमता (<math>E^{\ominus '}_\text{red}</math>) अधिक आसानी से अनुमान लगाने की अनुमति दें कि क्या एक [[चयापचय प्रक्रिया]] में होने वाली रेडॉक्स प्रतिक्रिया या कुछ शर्तों के तहत माइक्रोबियल गतिविधि को बढ़ावा देना संभव है या नहीं। | औपचारिक मानक कमी क्षमता (<math>E^{\ominus '}_\text{red}</math>) आमतौर पर पीएच 7 पर मापी गई [[मानक कमी क्षमता]] के संदर्भ में जैव रसायन और कोशिका जीव विज्ञान में भी उपयोग किया जाता है, जो 0 के मानक राज्य पीएच की तुलना में अधिकांश शारीरिक और इंट्रासेल्युलर तरल पदार्थों के पीएच के करीब है। लाभ एक अधिक उपयुक्त रेडॉक्स को परिभाषित करना है। मानक स्थिति की तुलना में वास्तविक परिस्थितियों के अनुरूप बेहतर। औपचारिक मानक कमी क्षमता (<math>E^{\ominus '}_\text{red}</math>) अधिक आसानी से अनुमान लगाने की अनुमति दें कि क्या एक [[चयापचय प्रक्रिया]] में होने वाली रेडॉक्स प्रतिक्रिया या कुछ शर्तों के तहत माइक्रोबियल गतिविधि को बढ़ावा देना संभव है या नहीं। | ||
जबकि, मानक अपचयन विभव हमेशा मानक हाइड्रोजन इलेक्ट्रोड (SHE) को संदर्भित करते हैं, [के साथ]{{H+}}] = 1 एम पीएच 0 के अनुरूप, और <math>E^{\ominus}_\text{red H+}</math> कन्वेंशन द्वारा मनमाने ढंग से शून्य पर तय किया गया, यह अब 7 के पीएच पर मामला नहीं है। फिर, कमी की क्षमता <math>E_\text{red}</math> मानक हाइड्रोजन इलेक्ट्रोड (SHE) के संबंध में pH 7 पर संचालित हाइड्रोजन इलेक्ट्रोड का मान -0.413 V है।<ref name="Voet_2016">{{cite book |first1=Donald |last1=Voet |first2=Judith G. |last2=Voet |first3=Charlotte W. |last3=Pratt |title=बायोकैमिस्ट्री के मूल सिद्धांत: आणविक स्तर पर जीवन|chapter=Table 14-4 Standard Reduction Potentials for Some Biochemically Import Half-Reactions |chapter-url=https://books.google.com/books?id=9T7hCgAAQBAJ&pg=PA466 |date=2016 |publisher=Wiley |isbn=978-1-118-91840-1 |pages=466 |edition=5th}}</रेफरी> | जबकि, मानक अपचयन विभव हमेशा मानक हाइड्रोजन इलेक्ट्रोड (SHE) को संदर्भित करते हैं, [के साथ]{{H+}}] = 1 एम पीएच 0 के अनुरूप, और <math>E^{\ominus}_\text{red H+}</math> कन्वेंशन द्वारा मनमाने ढंग से शून्य पर तय किया गया, यह अब 7 के पीएच पर मामला नहीं है। फिर, कमी की क्षमता <math>E_\text{red}</math> मानक हाइड्रोजन इलेक्ट्रोड (SHE) के संबंध में pH 7 पर संचालित हाइड्रोजन इलेक्ट्रोड का मान -0.413 V है।<nowiki><ref name="Voet_2016"></nowiki>{{cite book |first1=Donald |last1=Voet |first2=Judith G. |last2=Voet |first3=Charlotte W. |last3=Pratt |title=बायोकैमिस्ट्री के मूल सिद्धांत: आणविक स्तर पर जीवन|chapter=Table 14-4 Standard Reduction Potentials for Some Biochemically Import Half-Reactions |chapter-url=https://books.google.com/books?id=9T7hCgAAQBAJ&pg=PA466 |date=2016 |publisher=Wiley |isbn=978-1-118-91840-1 |pages=466 |edition=5th}}</रेफरी> | ||
=== पीएच === के एक समारोह के रूप में नेर्नस्ट समीकरण की अभिव्यक्ति | === पीएच === के एक समारोह के रूप में नेर्नस्ट समीकरण की अभिव्यक्ति | ||
| Line 109: | Line 109: | ||
<math>E_h</math> h> और किसी विलयन का pH, Nernst समीकरण द्वारा संबंधित होते हैं, जैसा कि आमतौर पर एक Poorbaix आरेख द्वारा दर्शाया जाता है {{nowrap|(<math>E_h</math> – [[pH]] plot)}}. <math>E_h</math> स्पष्ट रूप से दर्शाता है <math>E_\text{red}</math> मानक हाइड्रोजन इलेक्ट्रोड (SHE) बनाम व्यक्त किया गया। आधे सेल समीकरण के लिए, पारंपरिक रूप से एक कमी प्रतिक्रिया के रूप में लिखा जाता है (यानी, बाईं ओर एक ऑक्सीडेंट द्वारा इलेक्ट्रॉनों को स्वीकार किया जाता है): | <math>E_h</math> h> और किसी विलयन का pH, Nernst समीकरण द्वारा संबंधित होते हैं, जैसा कि आमतौर पर एक Poorbaix आरेख द्वारा दर्शाया जाता है {{nowrap|(<math>E_h</math> – [[pH]] plot)}}. <math>E_h</math> स्पष्ट रूप से दर्शाता है <math>E_\text{red}</math> मानक हाइड्रोजन इलेक्ट्रोड (SHE) बनाम व्यक्त किया गया। आधे सेल समीकरण के लिए, पारंपरिक रूप से एक कमी प्रतिक्रिया के रूप में लिखा जाता है (यानी, बाईं ओर एक ऑक्सीडेंट द्वारा इलेक्ट्रॉनों को स्वीकार किया जाता है): | ||
: <math chem>a \, A + b \, B + h \, \ce{H+} + z \, e^{-} \quad \ce{<=>} \quad c \, C + d \, D</math> | :<math chem="">a \, A + b \, B + h \, \ce{H+} + z \, e^{-} \quad \ce{<=>} \quad c \, C + d \, D</math> | ||
आधा सेल मानक कमी क्षमता <math>E^{\ominus}_\text{red}</math> द्वारा दिया गया है | आधा सेल मानक कमी क्षमता <math>E^{\ominus}_\text{red}</math> द्वारा दिया गया है | ||
: <math>E^{\ominus}_\text{red} (\text{volt}) = -\frac{\Delta G^\ominus}{zF}</math> | :<math>E^{\ominus}_\text{red} (\text{volt}) = -\frac{\Delta G^\ominus}{zF}</math> | ||
कहाँ <math>\Delta G^\ominus</math> मानक गिब्स मुक्त ऊर्जा परिवर्तन है, {{mvar|z}} शामिल इलेक्ट्रॉनों की संख्या है, और {{mvar|F}} फैराडे स्थिरांक है। नर्नस्ट समीकरण पीएच और से संबंधित है <math>E_h</math> निम्नलिखित नुसार: | कहाँ <math>\Delta G^\ominus</math> मानक गिब्स मुक्त ऊर्जा परिवर्तन है, {{mvar|z}} शामिल इलेक्ट्रॉनों की संख्या है, और {{mvar|F}} फैराडे स्थिरांक है। नर्नस्ट समीकरण पीएच और से संबंधित है <math>E_h</math> निम्नलिखित नुसार: | ||
: <math>E_h = E_\text{red} = E^{\ominus}_\text{red} - \frac{0.05916}{z} \log\left(\frac{\{C\}^c\{D\}^d}{\{A\}^a\{B\}^b}\right) - \frac{0.05916\,h}{z} \text{pH}</math> {{cn|date=June 2020}} | :<math>E_h = E_\text{red} = E^{\ominus}_\text{red} - \frac{0.05916}{z} \log\left(\frac{\{C\}^c\{D\}^d}{\{A\}^a\{B\}^b}\right) - \frac{0.05916\,h}{z} \text{pH}</math> {{cn|date=June 2020}} | ||
जहां घुंघराले कोष्ठक गतिविधि (रसायन विज्ञान) को इंगित करते हैं, और घातांक पारंपरिक तरीके से दिखाए जाते हैं। यह समीकरण एक सीधी रेखा का समीकरण है <math>E_\text{red}</math> की ढलान के साथ पीएच के एक समारोह के रूप में <math>-0.05916\,\left(\frac{h}{z}\right)</math> वोल्ट (पीएच की कोई इकाई नहीं है)। | जहां घुंघराले कोष्ठक गतिविधि (रसायन विज्ञान) को इंगित करते हैं, और घातांक पारंपरिक तरीके से दिखाए जाते हैं। यह समीकरण एक सीधी रेखा का समीकरण है <math>E_\text{red}</math> की ढलान के साथ पीएच के एक समारोह के रूप में <math>-0.05916\,\left(\frac{h}{z}\right)</math> वोल्ट (पीएच की कोई इकाई नहीं है)। | ||
| Line 126: | Line 126: | ||
विभिन्न सम्मेलनों या अनुमानों (यानी, विभिन्न अंतर्निहित परिकल्पनाओं के साथ) का उपयोग करते हुए डेटा के विभिन्न स्रोतों को मिलाते समय समस्याएँ हो सकती हैं। अकार्बनिक और जैविक प्रक्रियाओं के बीच की सीमा पर काम करते समय (उदाहरण के लिए, भू-रसायन में अजैविक और जैविक प्रक्रियाओं की तुलना करते समय जब माइक्रोबियल गतिविधि भी सिस्टम में काम कर सकती है), इस बात का ध्यान रखा जाना चाहिए कि अनजाने में सीधे मानक कमी क्षमता बनाम SHE (pH) का मिश्रण न हो। = 0) औपचारिक कमी क्षमता (पीएच = 7) के साथ। परिभाषाओं को स्पष्ट रूप से व्यक्त किया जाना चाहिए और सावधानीपूर्वक नियंत्रित किया जाना चाहिए, विशेष रूप से यदि डेटा के स्रोत अलग-अलग हैं और विभिन्न क्षेत्रों से उत्पन्न होते हैं (उदाहरण के लिए, शास्त्रीय इलेक्ट्रोकैमिस्ट्री और माइक्रोबायोलॉजी पाठ्यपुस्तकों से डेटा चुनना और मिश्रित करना, विभिन्न सम्मेलनों पर ध्यान दिए बिना, जिस पर वे आधारित हैं)। | विभिन्न सम्मेलनों या अनुमानों (यानी, विभिन्न अंतर्निहित परिकल्पनाओं के साथ) का उपयोग करते हुए डेटा के विभिन्न स्रोतों को मिलाते समय समस्याएँ हो सकती हैं। अकार्बनिक और जैविक प्रक्रियाओं के बीच की सीमा पर काम करते समय (उदाहरण के लिए, भू-रसायन में अजैविक और जैविक प्रक्रियाओं की तुलना करते समय जब माइक्रोबियल गतिविधि भी सिस्टम में काम कर सकती है), इस बात का ध्यान रखा जाना चाहिए कि अनजाने में सीधे मानक कमी क्षमता बनाम SHE (pH) का मिश्रण न हो। = 0) औपचारिक कमी क्षमता (पीएच = 7) के साथ। परिभाषाओं को स्पष्ट रूप से व्यक्त किया जाना चाहिए और सावधानीपूर्वक नियंत्रित किया जाना चाहिए, विशेष रूप से यदि डेटा के स्रोत अलग-अलग हैं और विभिन्न क्षेत्रों से उत्पन्न होते हैं (उदाहरण के लिए, शास्त्रीय इलेक्ट्रोकैमिस्ट्री और माइक्रोबायोलॉजी पाठ्यपुस्तकों से डेटा चुनना और मिश्रित करना, विभिन्न सम्मेलनों पर ध्यान दिए बिना, जिस पर वे आधारित हैं)। | ||
==== पौरबैक्स आरेख के साथ उदाहरण ==== | ====पौरबैक्स आरेख के साथ उदाहरण==== | ||
{{Main|Pourbaix diagram}} | {{Main|Pourbaix diagram}} | ||
[[File:PourbaixWater.png|thumb|300px|right|[[मानक तापमान और दबाव]] (STP) पर पानी, ऑक्सीजन और हाइड्रोजन के लिए स्थिरता क्षेत्रों सहित पानी के लिए पौरबैक्स आरेख। वर्टिकल स्केल (ऑर्डिनेट) एक मानक हाइड्रोजन इलेक्ट्रोड इलेक्ट्रोड के सापेक्ष इलेक्ट्रोड क्षमता है। क्षैतिज पैमाने (एब्सिस्सा) इलेक्ट्रोलाइट का पीएच है (अन्यथा गैर-अंतःक्रियात्मक)। शीर्ष रेखा के ऊपर ऑक्सीजन इलेक्ट्रोड से तब तक बुदबुदाती रहेगी जब तक कि पानी पूरी तरह से समाप्त नहीं हो जाता। इसी तरह, नीचे की रेखा के नीचे हाइड्रोजन इलेक्ट्रोड से तब तक बुदबुदाएगा जब तक कि पानी पूरी तरह से खपत नहीं हो जाता।]]पीएच पर कमी की क्षमता की निर्भरता को स्पष्ट करने के लिए, कोई भी केवल दो रेडॉक्स पर विचार कर सकता है। पौरबैक्स आरेख में जल स्थिरता डोमेन का निर्धारण करने वाला ऑक्सीडो-कमी संतुलन {{nowrap|(E<sub>h</sub>–pH plot)}}. जब पानी में डूबे हुए दो [[इलेक्ट्रोड]]ों के बीच [[बिजली उत्पन्न करनेवाली सेल]] का पर्याप्त अंतर लगाकर [[पानी का इलेक्ट्रोलिसिस]] किया जाता है, तो [[कैथोड]] (पानी के प्रोटॉन में कमी) पर [[हाइड्रोजन]] का उत्पादन होता है, जबकि [[एनोड]] (जल [[ऑक्सीजन]] परमाणुओं का ऑक्सीकरण) पर ऑक्सीजन बनता है। ऐसा तब भी हो सकता है जब हाइड्रोजन से अधिक प्रबल अपचायक (जैसे, धात्विक Na) या ऑक्सीजन से अधिक प्रबल ऑक्सीकारक (जैसे, F)<sub>2</sub>) पानी के संपर्क में आता है और इसके साथ प्रतिक्रिया करता है। में {{nowrap|E<sub>h</sub>–pH plot}} इसके बगल में (पौरबैक्स आरेख का सबसे सरल संभव संस्करण), जल स्थिरता डोमेन (ग्रे सतह) को दो झुकी हुई लाल धराशायी रेखाओं द्वारा रेडॉक्स क्षमता के रूप में सीमांकित किया गया है: | [[File:PourbaixWater.png|thumb|300px|right|[[मानक तापमान और दबाव]] (STP) पर पानी, ऑक्सीजन और हाइड्रोजन के लिए स्थिरता क्षेत्रों सहित पानी के लिए पौरबैक्स आरेख। वर्टिकल स्केल (ऑर्डिनेट) एक मानक हाइड्रोजन इलेक्ट्रोड इलेक्ट्रोड के सापेक्ष इलेक्ट्रोड क्षमता है। क्षैतिज पैमाने (एब्सिस्सा) इलेक्ट्रोलाइट का पीएच है (अन्यथा गैर-अंतःक्रियात्मक)। शीर्ष रेखा के ऊपर ऑक्सीजन इलेक्ट्रोड से तब तक बुदबुदाती रहेगी जब तक कि पानी पूरी तरह से समाप्त नहीं हो जाता। इसी तरह, नीचे की रेखा के नीचे हाइड्रोजन इलेक्ट्रोड से तब तक बुदबुदाएगा जब तक कि पानी पूरी तरह से खपत नहीं हो जाता।]]पीएच पर कमी की क्षमता की निर्भरता को स्पष्ट करने के लिए, कोई भी केवल दो रेडॉक्स पर विचार कर सकता है। पौरबैक्स आरेख में जल स्थिरता डोमेन का निर्धारण करने वाला ऑक्सीडो-कमी संतुलन {{nowrap|(E<sub>h</sub>–pH plot)}}. जब पानी में डूबे हुए दो [[इलेक्ट्रोड]]ों के बीच [[बिजली उत्पन्न करनेवाली सेल]] का पर्याप्त अंतर लगाकर [[पानी का इलेक्ट्रोलिसिस]] किया जाता है, तो [[कैथोड]] (पानी के प्रोटॉन में कमी) पर [[हाइड्रोजन]] का उत्पादन होता है, जबकि [[एनोड]] (जल [[ऑक्सीजन]] परमाणुओं का ऑक्सीकरण) पर ऑक्सीजन बनता है। ऐसा तब भी हो सकता है जब हाइड्रोजन से अधिक प्रबल अपचायक (जैसे, धात्विक Na) या ऑक्सीजन से अधिक प्रबल ऑक्सीकारक (जैसे, F)<sub>2</sub>) पानी के संपर्क में आता है और इसके साथ प्रतिक्रिया करता है। में {{nowrap|E<sub>h</sub>–pH plot}} इसके बगल में (पौरबैक्स आरेख का सबसे सरल संभव संस्करण), जल स्थिरता डोमेन (ग्रे सतह) को दो झुकी हुई लाल धराशायी रेखाओं द्वारा रेडॉक्स क्षमता के रूप में सीमांकित किया गया है: | ||
* बहुत कम ई पर प्रोटॉन की कमी के कारण हाइड्रोजन गैस के विकास के साथ कम स्थिरता रेखा<sub>h</sub>: | *बहुत कम ई पर प्रोटॉन की कमी के कारण हाइड्रोजन गैस के विकास के साथ कम स्थिरता रेखा<sub>h</sub>: | ||
: {{math|{{chem2|2 H+ + 2 e- <-> H2}} }}(कैथोड: कमी) | :{{math|{{chem2|2 H+ + 2 e- <-> H2}} }}(कैथोड: कमी) | ||
* बहुत उच्च ई पर जल ऑक्सीजन ऑक्सीकरण के कारण ऑक्सीजन गैस के विकास के साथ उच्च स्थिरता रेखा<sub>h</sub>: | *बहुत उच्च ई पर जल ऑक्सीजन ऑक्सीकरण के कारण ऑक्सीजन गैस के विकास के साथ उच्च स्थिरता रेखा<sub>h</sub>: | ||
: {{math|{{chem2|2 H2O <-> O2 + 4 H+ + 4 e-}} }}(एनोड: ऑक्सीकरण) | :{{math|{{chem2|2 H2O <-> O2 + 4 H+ + 4 e-}} }}(एनोड: ऑक्सीकरण) | ||
प्रत्येक संबंधित कमी प्रतिक्रिया के लिए नर्नस्ट समीकरण को हल करते समय (ऑक्सीजन का उत्पादन करने वाले जल ऑक्सीकरण प्रतिक्रिया को वापस करने की आवश्यकता होती है), दोनों समीकरणों का एक समान रूप होता है क्योंकि प्रोटॉन की संख्या और प्रतिक्रिया में शामिल इलेक्ट्रॉनों की संख्या समान होती है और उनका अनुपात एक होता है (2{{H+}}/2{{e-}} एच के लिए<sub>2</sub> और 4{{H+}}/4{{e-}} साथ {{O2}} क्रमशः), इसलिए पीएच के एक समारोह के रूप में व्यक्त नर्नस्ट समीकरण को हल करते समय यह सरल हो जाता है। | प्रत्येक संबंधित कमी प्रतिक्रिया के लिए नर्नस्ट समीकरण को हल करते समय (ऑक्सीजन का उत्पादन करने वाले जल ऑक्सीकरण प्रतिक्रिया को वापस करने की आवश्यकता होती है), दोनों समीकरणों का एक समान रूप होता है क्योंकि प्रोटॉन की संख्या और प्रतिक्रिया में शामिल इलेक्ट्रॉनों की संख्या समान होती है और उनका अनुपात एक होता है (2{{H+}}/2{{e-}} एच के लिए<sub>2</sub> और 4{{H+}}/4{{e-}} साथ {{O2}} क्रमशः), इसलिए पीएच के एक समारोह के रूप में व्यक्त नर्नस्ट समीकरण को हल करते समय यह सरल हो जाता है। | ||
| Line 141: | Line 141: | ||
परिणाम को संख्यात्मक रूप से निम्नानुसार व्यक्त किया जा सकता है: | परिणाम को संख्यात्मक रूप से निम्नानुसार व्यक्त किया जा सकता है: | ||
: <math>E_\text{red} = E^{\ominus}_\text{red} - 0.05916 \ pH</math> | :<math>E_\text{red} = E^{\ominus}_\text{red} - 0.05916 \ pH</math> | ||
ध्यान दें कि दो जल स्थिरता डोमेन की ऊपरी और निचली रेखाओं के ढलान समान (-59.16 mV/pH इकाई) हैं, इसलिए वे पौरबैक्स आरेख पर समानांतर हैं। चूंकि ढलान नकारात्मक हैं, उच्च पीएच पर, हाइड्रोजन और ऑक्सीजन दोनों के विकास के लिए कम पीएच की तुलना में बहुत कम कमी की क्षमता की आवश्यकता होती है। | ध्यान दें कि दो जल स्थिरता डोमेन की ऊपरी और निचली रेखाओं के ढलान समान (-59.16 mV/pH इकाई) हैं, इसलिए वे पौरबैक्स आरेख पर समानांतर हैं। चूंकि ढलान नकारात्मक हैं, उच्च पीएच पर, हाइड्रोजन और ऑक्सीजन दोनों के विकास के लिए कम पीएच की तुलना में बहुत कम कमी की क्षमता की आवश्यकता होती है। | ||
एच की कमी के लिए<sup>+</sup> एच में<sub>2</sub> यहाँ ऊपर उल्लिखित रिश्ता बन जाता है: | एच की कमी के लिए<sup>+</sup> एच में<sub>2</sub> यहाँ ऊपर उल्लिखित रिश्ता बन जाता है: | ||
: <math>E_\text{red} = - 0.05916 \ pH</math> <br />क्योंकि परंपरा के अनुसार <math>E^{\ominus}_\text{red}</math> मानक हाइड्रोजन इलेक्ट्रोड के लिए = 0 V (SHE: pH = 1)। <br />इसलिए, pH = 7 पर, <math>E_\text{red}</math> = -0.414 वी प्रोटॉन की कमी के लिए। | :<math>E_\text{red} = - 0.05916 \ pH</math> <br />क्योंकि परंपरा के अनुसार <math>E^{\ominus}_\text{red}</math> मानक हाइड्रोजन इलेक्ट्रोड के लिए = 0 V (SHE: pH = 1)। <br />इसलिए, pH = 7 पर, <math>E_\text{red}</math> = -0.414 वी प्रोटॉन की कमी के लिए। | ||
ओ की कमी के लिए<sub>2</sub> 2 एच में<sub>2</sub>हे यहाँ उपर्युक्त संबंध बन जाता है: | ओ की कमी के लिए<sub>2</sub> 2 एच में<sub>2</sub>हे यहाँ उपर्युक्त संबंध बन जाता है: | ||
: <math>E_\text{red} = 1.229 - 0.05916 \ pH</math> <br />क्योंकि <math>E^{\ominus}_\text{red}</math> = +1.229 V मानक हाइड्रोजन इलेक्ट्रोड के संबंध में (SHE: pH = 1)। <br />इसलिए, pH = 7 पर, <math>E_\text{red}</math> = +0.815 वी ऑक्सीजन की कमी के लिए। | :<math>E_\text{red} = 1.229 - 0.05916 \ pH</math> <br />क्योंकि <math>E^{\ominus}_\text{red}</math> = +1.229 V मानक हाइड्रोजन इलेक्ट्रोड के संबंध में (SHE: pH = 1)। <br />इसलिए, pH = 7 पर, <math>E_\text{red}</math> = +0.815 वी ऑक्सीजन की कमी के लिए। | ||
ऑफ़सेट -414 mV in <math>E_\text{red}</math> दोनों कमी प्रतिक्रियाओं के लिए समान है क्योंकि वे पीएच के एक समारोह के समान रैखिक संबंध साझा करते हैं और उनकी रेखाओं की ढलान समान होती है। इसे पौरबैक्स आरेख पर सीधे सत्यापित किया जा सकता है। अन्य कमी प्रतिक्रियाओं के लिए, 7 के पीएच पर औपचारिक कमी की क्षमता का मान, जिसे आमतौर पर जैव रासायनिक प्रतिक्रियाओं के लिए संदर्भित किया जाता है, वह भी पौरबैक्स आरेख में संबंधित रेखा के ढलान पर निर्भर करता है अर्थात अनुपात पर{{frac|h|z}}की संख्या का {{H+}} की संख्या के लिए {{e-}} कमी प्रतिक्रिया में शामिल है, और इस प्रकार अर्ध-प्रतिक्रिया के [[स्तुईचिओमेटरी]] पर। किसी दिए गए जैव रासायनिक अर्ध-प्रतिक्रिया के लिए पीएच = 7 पर औपचारिक कमी क्षमता का निर्धारण करने के लिए पीएच के एक समारोह के रूप में संबंधित नर्नस्ट समीकरण के साथ इसकी गणना करने की आवश्यकता होती है। कोई ई पर -414 एमवी का ऑफसेट लागू नहीं कर सकता है<sub>h</sub> मूल्य (SHE) जब अनुपात{{frac|h|z}}1 से भिन्न है। | ऑफ़सेट -414 mV in <math>E_\text{red}</math> दोनों कमी प्रतिक्रियाओं के लिए समान है क्योंकि वे पीएच के एक समारोह के समान रैखिक संबंध साझा करते हैं और उनकी रेखाओं की ढलान समान होती है। इसे पौरबैक्स आरेख पर सीधे सत्यापित किया जा सकता है। अन्य कमी प्रतिक्रियाओं के लिए, 7 के पीएच पर औपचारिक कमी की क्षमता का मान, जिसे आमतौर पर जैव रासायनिक प्रतिक्रियाओं के लिए संदर्भित किया जाता है, वह भी पौरबैक्स आरेख में संबंधित रेखा के ढलान पर निर्भर करता है अर्थात अनुपात पर{{frac|h|z}}की संख्या का {{H+}} की संख्या के लिए {{e-}} कमी प्रतिक्रिया में शामिल है, और इस प्रकार अर्ध-प्रतिक्रिया के [[स्तुईचिओमेटरी]] पर। किसी दिए गए जैव रासायनिक अर्ध-प्रतिक्रिया के लिए पीएच = 7 पर औपचारिक कमी क्षमता का निर्धारण करने के लिए पीएच के एक समारोह के रूप में संबंधित नर्नस्ट समीकरण के साथ इसकी गणना करने की आवश्यकता होती है। कोई ई पर -414 एमवी का ऑफसेट लागू नहीं कर सकता है<sub>h</sub> मूल्य (SHE) जब अनुपात{{frac|h|z}}1 से भिन्न है। | ||
== जीव विज्ञान में अनुप्रयोग == | ==जीव विज्ञान में अनुप्रयोग== | ||
{{See also|Table of standard reduction potentials for half-reactions important in biochemistry}} | {{See also|Table of standard reduction potentials for half-reactions important in biochemistry}} | ||
बायोकैमिस्ट्री में महत्वपूर्ण अर्ध-प्रतिक्रियाओं के लिए मानक कमी क्षमता की तालिका के अलावा, एक प्रकार के [[आयन]] के संबंध में [[कोशिका झिल्ली]] की विद्युत क्षमता की गणना के लिए शरीर विज्ञान में नर्नस्ट समीकरण का भी उपयोग किया जाता है। इसे [[अम्ल पृथक्करण स्थिरांक]] से जोड़ा जा सकता है। | बायोकैमिस्ट्री में महत्वपूर्ण अर्ध-प्रतिक्रियाओं के लिए मानक कमी क्षमता की तालिका के अलावा, एक प्रकार के [[आयन]] के संबंध में [[कोशिका झिल्ली]] की विद्युत क्षमता की गणना के लिए शरीर विज्ञान में नर्नस्ट समीकरण का भी उपयोग किया जाता है। इसे [[अम्ल पृथक्करण स्थिरांक]] से जोड़ा जा सकता है। | ||
=== नर्नस्ट संभावित === | ===नर्नस्ट संभावित=== | ||
{{main|Reversal potential}} | {{main|Reversal potential}} | ||
आयन के आवेश की क्षमता की गणना करने के लिए उपयोग किए जाने पर नर्नस्ट समीकरण का एक शारीरिक अनुप्रयोग होता है {{math|''z''}} एक झिल्ली के पार। यह क्षमता कोशिका के अंदर और बाहर आयन की सांद्रता का उपयोग करके निर्धारित की जाती है: | आयन के आवेश की क्षमता की गणना करने के लिए उपयोग किए जाने पर नर्नस्ट समीकरण का एक शारीरिक अनुप्रयोग होता है {{math|''z''}} एक झिल्ली के पार। यह क्षमता कोशिका के अंदर और बाहर आयन की सांद्रता का उपयोग करके निर्धारित की जाती है: | ||
| Line 165: | Line 165: | ||
जब झिल्ली उष्मागतिक संतुलन में होती है (अर्थात्, आयनों का कोई शुद्ध प्रवाह नहीं), और यदि कोशिका केवल एक आयन के लिए पारगम्य है, तो [[झिल्ली क्षमता]] उस आयन के लिए नेर्नस्ट क्षमता के बराबर होनी चाहिए। | जब झिल्ली उष्मागतिक संतुलन में होती है (अर्थात्, आयनों का कोई शुद्ध प्रवाह नहीं), और यदि कोशिका केवल एक आयन के लिए पारगम्य है, तो [[झिल्ली क्षमता]] उस आयन के लिए नेर्नस्ट क्षमता के बराबर होनी चाहिए। | ||
=== गोल्डमैन समीकरण === | ===गोल्डमैन समीकरण=== | ||
{{main|Goldman equation}} | {{main|Goldman equation}} | ||
जब झिल्ली एक से अधिक आयनों के लिए पारगम्य होती है, जैसा कि अनिवार्य रूप से होता है, विश्राम क्षमता को गोल्डमैन समीकरण से निर्धारित किया जा सकता है, जो जीएचके फ्लक्स समीकरण का एक समाधान है। बल शून्य है: | जब झिल्ली एक से अधिक आयनों के लिए पारगम्य होती है, जैसा कि अनिवार्य रूप से होता है, विश्राम क्षमता को गोल्डमैन समीकरण से निर्धारित किया जा सकता है, जो जीएचके फ्लक्स समीकरण का एक समाधान है। बल शून्य है: | ||
| Line 172: | Line 172: | ||
कहाँ | कहाँ | ||
* {{math|''E''<sub>m</sub>}} झिल्ली क्षमता है ([[वाल्ट]] में, जूल प्रति कूलम्ब के बराबर), | *{{math|''E''<sub>m</sub>}} झिल्ली क्षमता है ([[वाल्ट]] में, जूल प्रति कूलम्ब के बराबर), | ||
* {{math|''P''<sub>ion</sub>}} उस आयन के लिए पारगम्यता है (मीटर प्रति सेकंड में), | *{{math|''P''<sub>ion</sub>}} उस आयन के लिए पारगम्यता है (मीटर प्रति सेकंड में), | ||
* {{math|[ion]<sub>out</sub>}} अन्य एसआई इकाइयों से मेल खाने के लिए उस आयन (मोल (यूनिट) प्रति घन मीटर में) की बाह्य एकाग्रता है, हालांकि इकाइयां सख्ती से कोई फर्क नहीं पड़ता, क्योंकि आयन एकाग्रता शब्द एक आयामहीन अनुपात बन जाते हैं), | *{{math|[ion]<sub>out</sub>}} अन्य एसआई इकाइयों से मेल खाने के लिए उस आयन (मोल (यूनिट) प्रति घन मीटर में) की बाह्य एकाग्रता है, हालांकि इकाइयां सख्ती से कोई फर्क नहीं पड़ता, क्योंकि आयन एकाग्रता शब्द एक आयामहीन अनुपात बन जाते हैं), | ||
* {{math|[ion]<sub>in</sub>}} उस आयन की इंट्रासेल्युलर सांद्रता है (मोल्स प्रति घन मीटर में), | *{{math|[ion]<sub>in</sub>}} उस आयन की इंट्रासेल्युलर सांद्रता है (मोल्स प्रति घन मीटर में), | ||
* {{mvar|R}} आदर्श गैस नियतांक है (जूल प्रति केल्विन प्रति मोल), | *{{mvar|R}} आदर्श गैस नियतांक है (जूल प्रति केल्विन प्रति मोल), | ||
* {{mvar|T}} केल्विन में तापमान है<!-- pluralized – see Kelvin#Usage conventions -->, | *{{mvar|T}} केल्विन में तापमान है<!-- pluralized – see Kelvin#Usage conventions -->, | ||
* {{mvar|F}} फैराडे स्थिरांक है | फैराडे स्थिरांक (कूलम्ब प्रति मोल)। | *{{mvar|F}} फैराडे स्थिरांक है | फैराडे स्थिरांक (कूलम्ब प्रति मोल)। | ||
कोशिका झिल्ली के पार की क्षमता जो झिल्ली के माध्यम से किसी विशेष आयन के शुद्ध प्रसार का बिल्कुल विरोध करती है, उस आयन के लिए नेर्नस्ट क्षमता कहलाती है। जैसा कि ऊपर देखा गया है, नेर्नस्ट क्षमता का परिमाण झिल्ली के दोनों किनारों पर उस विशिष्ट आयन की सांद्रता के अनुपात से निर्धारित होता है। यह अनुपात जितना अधिक होगा, आयन के एक दिशा में विसरित होने की प्रवृत्ति उतनी ही अधिक होगी, और इसलिए विसरण को रोकने के लिए आवश्यक नर्नस्ट क्षमता भी उतनी ही अधिक होगी। एक समान अभिव्यक्ति मौजूद है जिसमें शामिल है {{mvar|r}} (परिवहन अनुपात का पूर्ण मूल्य)। यह असमान एक्सचेंज वाले ट्रांसपोर्टरों को ध्यान में रखता है। देखें: [[सोडियम-पोटेशियम पंप]] जहां परिवहन अनुपात 2/3 होगा, इसलिए r नीचे दिए गए सूत्र में 1.5 के बराबर है। हम यहां एक कारक r = 1.5 क्यों डालते हैं इसका कारण विद्युत रासायनिक बल J द्वारा वर्तमान घनत्व है<sub>e.c.</sub>(वह<sup>+</sup>) + जे<sub>e.c.</sub>(क<sup>+</sup>) अब शून्य नहीं है, बल्कि J है<sub>e.c.</sub>(वह<sup>+</sup>) + 1.5M<sub>e.c.</sub>(क<sup>+</sup>) = 0 (विद्युत रासायनिक बल द्वारा दोनों आयनों के प्रवाह की भरपाई पंप द्वारा की जाती है, अर्थात J<sub>e.c.</sub> = -जे<sub>pump</sub>), GHK समीकरण को लागू करने के लिए बाधाओं को बदलना। अन्य चर ऊपर के समान हैं। निम्नलिखित उदाहरण में दो आयन शामिल हैं: पोटेशियम (के<sup>+</sup>) और सोडियम (Na<sup>+</sup>). क्लोराइड संतुलन में माना जाता है। | कोशिका झिल्ली के पार की क्षमता जो झिल्ली के माध्यम से किसी विशेष आयन के शुद्ध प्रसार का बिल्कुल विरोध करती है, उस आयन के लिए नेर्नस्ट क्षमता कहलाती है। जैसा कि ऊपर देखा गया है, नेर्नस्ट क्षमता का परिमाण झिल्ली के दोनों किनारों पर उस विशिष्ट आयन की सांद्रता के अनुपात से निर्धारित होता है। यह अनुपात जितना अधिक होगा, आयन के एक दिशा में विसरित होने की प्रवृत्ति उतनी ही अधिक होगी, और इसलिए विसरण को रोकने के लिए आवश्यक नर्नस्ट क्षमता भी उतनी ही अधिक होगी। एक समान अभिव्यक्ति मौजूद है जिसमें शामिल है {{mvar|r}} (परिवहन अनुपात का पूर्ण मूल्य)। यह असमान एक्सचेंज वाले ट्रांसपोर्टरों को ध्यान में रखता है। देखें: [[सोडियम-पोटेशियम पंप]] जहां परिवहन अनुपात 2/3 होगा, इसलिए r नीचे दिए गए सूत्र में 1.5 के बराबर है। हम यहां एक कारक r = 1.5 क्यों डालते हैं इसका कारण विद्युत रासायनिक बल J द्वारा वर्तमान घनत्व है<sub>e.c.</sub>(वह<sup>+</sup>) + जे<sub>e.c.</sub>(क<sup>+</sup>) अब शून्य नहीं है, बल्कि J है<sub>e.c.</sub>(वह<sup>+</sup>) + 1.5M<sub>e.c.</sub>(क<sup>+</sup>) = 0 (विद्युत रासायनिक बल द्वारा दोनों आयनों के प्रवाह की भरपाई पंप द्वारा की जाती है, अर्थात J<sub>e.c.</sub> = -जे<sub>pump</sub>), GHK समीकरण को लागू करने के लिए बाधाओं को बदलना। अन्य चर ऊपर के समान हैं। निम्नलिखित उदाहरण में दो आयन शामिल हैं: पोटेशियम (के<sup>+</sup>) और सोडियम (Na<sup>+</sup>). क्लोराइड संतुलन में माना जाता है। | ||
| Line 186: | Line 186: | ||
<math display="block">E_{m} = \frac{RT}{F} \ln{ \left( \frac{r P_{\mathrm{K}^+}\left[\mathrm{K}^+\right]_\mathrm{out} + P_{\mathrm{Na}^+}\left[\mathrm{Na}^+\right]_\mathrm{out} + P_{\mathrm{Cl}^-}\left[\mathrm{Cl}^-\right]_\mathrm{in}}{r P_{\mathrm{K}^+}\left[\mathrm{K}^+\right]_\mathrm{in} + P_{\mathrm{Na}^+}\left[\mathrm{Na}^+\right]_\mathrm{in} + P_{\mathrm{Cl}^-}\left[\mathrm{Cl}^-\right]_\mathrm{out}} \right) }.</math> | <math display="block">E_{m} = \frac{RT}{F} \ln{ \left( \frac{r P_{\mathrm{K}^+}\left[\mathrm{K}^+\right]_\mathrm{out} + P_{\mathrm{Na}^+}\left[\mathrm{Na}^+\right]_\mathrm{out} + P_{\mathrm{Cl}^-}\left[\mathrm{Cl}^-\right]_\mathrm{in}}{r P_{\mathrm{K}^+}\left[\mathrm{K}^+\right]_\mathrm{in} + P_{\mathrm{Na}^+}\left[\mathrm{Na}^+\right]_\mathrm{in} + P_{\mathrm{Cl}^-}\left[\mathrm{Cl}^-\right]_\mathrm{out}} \right) }.</math> | ||
==व्युत्पत्ति== | |||
== व्युत्पत्ति == | |||
===बोल्ट्जमैन फैक्टर का प्रयोग=== | ===बोल्ट्जमैन फैक्टर का प्रयोग=== | ||
सरलता के लिए, हम उन रेडॉक्स-सक्रिय अणुओं के विलयन पर विचार करेंगे जो एक-इलेक्ट्रॉन उत्क्रमणीय प्रतिक्रिया से गुजरते हैं | सरलता के लिए, हम उन रेडॉक्स-सक्रिय अणुओं के विलयन पर विचार करेंगे जो एक-इलेक्ट्रॉन उत्क्रमणीय प्रतिक्रिया से गुजरते हैं | ||
: {{math|Ox + e<sup>−</sup> {{eqm}} Red}} | :{{math|Ox + e<sup>−</sup> {{eqm}} Red}} | ||
और जिसमें शून्य की एक मानक क्षमता है, और जिसमें गतिविधियों को सांद्रता (यानी इकाई गतिविधि गुणांक) द्वारा अच्छी तरह से दर्शाया गया है। [[रासायनिक क्षमता]] {{math|''μ''<sub>c</sub>}} इस समाधान का अंतर, कार्यशील इलेक्ट्रोड से इलेक्ट्रॉनों को लेने और इलेक्ट्रॉनों को देने के लिए ऊर्जा बाधाओं के बीच का अंतर है जो समाधान की [[विद्युत रासायनिक क्षमता]] निर्धारित कर रहा है। ऑक्सीकृत और कम अणुओं का अनुपात, {{sfrac|[Ox]|[Red]}}, कम होने (इलेक्ट्रॉन लेने) की संभावना पर ऑक्सीकृत होने (इलेक्ट्रॉन देने) की संभावना के बराबर है, जिसे हम इन प्रक्रियाओं के लिए बोल्टज़मान कारक के संदर्भ में लिख सकते हैं: | और जिसमें शून्य की एक मानक क्षमता है, और जिसमें गतिविधियों को सांद्रता (यानी इकाई गतिविधि गुणांक) द्वारा अच्छी तरह से दर्शाया गया है। [[रासायनिक क्षमता]] {{math|''μ''<sub>c</sub>}} इस समाधान का अंतर, कार्यशील इलेक्ट्रोड से इलेक्ट्रॉनों को लेने और इलेक्ट्रॉनों को देने के लिए ऊर्जा बाधाओं के बीच का अंतर है जो समाधान की [[विद्युत रासायनिक क्षमता]] निर्धारित कर रहा है। ऑक्सीकृत और कम अणुओं का अनुपात, {{sfrac|[Ox]|[Red]}}, कम होने (इलेक्ट्रॉन लेने) की संभावना पर ऑक्सीकृत होने (इलेक्ट्रॉन देने) की संभावना के बराबर है, जिसे हम इन प्रक्रियाओं के लिए बोल्टज़मान कारक के संदर्भ में लिख सकते हैं: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 203: | Line 202: | ||
अगर {{math|''μ''<sub>c</sub> ≠ 0}} पर {{sfrac|[Ox]|[Red]}}= 1, हमें इस अतिरिक्त स्थिरांक में जोड़ने की आवश्यकता है: | अगर {{math|''μ''<sub>c</sub> ≠ 0}} पर {{sfrac|[Ox]|[Red]}}= 1, हमें इस अतिरिक्त स्थिरांक में जोड़ने की आवश्यकता है: | ||
<math display="block">\mu_\mathrm{c} = \mu_\mathrm{c}^\ominus + kT \ln \frac{[\mathrm{Red}]}{[\mathrm{Ox}]}.</math> | <math display="block">\mu_\mathrm{c} = \mu_\mathrm{c}^\ominus + kT \ln \frac{[\mathrm{Red}]}{[\mathrm{Ox}]}.</math> | ||
द्वारा समीकरण को विभाजित करना {{mvar|e}} रासायनिक क्षमता से इलेक्ट्रोड क्षमता में परिवर्तित करने के लिए, और उसे याद रखना {{math|1={{sfrac|''k''|''e''}} = {{sfrac|''R''|''F''}}}},<ref>{{math|1=''R'' = ''N''<sub>A</sub>''k''}}; see [[gas constant]]<br>{{math|1=''F'' = ''N''<sub>A</sub>''e''}}; see [[Faraday constant]]</ref> हम एक-इलेक्ट्रॉन प्रक्रिया के लिए नर्नस्ट समीकरण प्राप्त करते हैं {{math|{{nowrap|Ox + e<sup>−</sup> {{eqm}} Red}} }}: | द्वारा समीकरण को विभाजित करना {{mvar|e}} रासायनिक क्षमता से इलेक्ट्रोड क्षमता में परिवर्तित करने के लिए, और उसे याद रखना {{math|1={{sfrac|''k''|''e''}} = {{sfrac|''R''|''F''}}}},<nowiki><ref></nowiki>{{math|1=''R'' = ''N''<sub>A</sub>''k''}}; see [[gas constant]]<br>{{math|1=''F'' = ''N''<sub>A</sub>''e''}}; see [[Faraday constant]]</ref> हम एक-इलेक्ट्रॉन प्रक्रिया के लिए नर्नस्ट समीकरण प्राप्त करते हैं {{math|{{nowrap|Ox + e<sup>−</sup> {{eqm}} Red}} }}: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 212: | Line 211: | ||
=== ऊष्मप्रवैगिकी (रासायनिक क्षमता) का उपयोग === | === ऊष्मप्रवैगिकी (रासायनिक क्षमता) का उपयोग === | ||
यहाँ मात्राएँ प्रति अणु दी गई हैं, प्रति मोल (इकाई) नहीं, और इसलिए [[बोल्ट्जमैन स्थिरांक]] {{math|''k''}} और [[प्राथमिक शुल्क]] {{math|''e''}} [[गैस स्थिरांक]] के बजाय उपयोग किया जाता है {{math|''R''}} और फैराडे स्थिरांक | फैराडे स्थिरांक {{math|''F''}}. अधिकांश रसायन विज्ञान की पाठ्यपुस्तकों में दी गई दाढ़ मात्रा में परिवर्तित करने के लिए, अवोगाद्रो स्थिरांक से गुणा करना आवश्यक है: {{math|1 = ''R'' = ''kN''<sub>A</sub>}} और {{math|1 = ''F'' = ''eN''<sub>A</sub>}}. | यहाँ मात्राएँ प्रति अणु दी गई हैं, प्रति मोल (इकाई) नहीं, और इसलिए [[बोल्ट्जमैन स्थिरांक]] {{math|''k''}} और [[प्राथमिक शुल्क]] {{math|''e''}} [[गैस स्थिरांक]] के बजाय उपयोग किया जाता है {{math|''R''}} और फैराडे स्थिरांक | फैराडे स्थिरांक {{math|''F''}}. अधिकांश रसायन विज्ञान की पाठ्यपुस्तकों में दी गई दाढ़ मात्रा में परिवर्तित करने के लिए, अवोगाद्रो स्थिरांक से गुणा करना आवश्यक है: {{math|1 = ''R'' = ''kN''<sub>A</sub>}} और {{math|1 = ''F'' = ''eN''<sub>A</sub>}}. अणु की [[एन्ट्रापी]] को इस रूप में परिभाषित किया गया है | ||
<math display="block">S \ \stackrel{\mathrm{def}}{=}\ k \ln \Omega,</math> | <math display="block">S \ \stackrel{\mathrm{def}}{=}\ k \ln \Omega,</math> | ||
कहाँ {{math|Ω}} अणु के लिए उपलब्ध राज्यों की संख्या है। मात्रा के साथ राज्यों की संख्या रैखिक रूप से भिन्न होनी चाहिए {{math|''V''}} प्रणाली की (यहाँ बेहतर समझ के लिए | कहाँ {{math|Ω}} अणु के लिए उपलब्ध राज्यों की संख्या है। मात्रा के साथ राज्यों की संख्या रैखिक रूप से भिन्न होनी चाहिए {{math|''V''}} प्रणाली की (यहाँ बेहतर समझ के लिए आदर्श प्रणाली पर विचार किया जाता है, ताकि गतिविधियों को वास्तविक सांद्रता के बहुत करीब रखा जा सके। उल्लिखित रैखिकता का मौलिक सांख्यिकीय प्रमाण इस खंड के दायरे से परे है, लेकिन यह सच है यह देखने के लिए यह आसान है [[आदर्श गैस]] के लिए सामान्य इज़ोटेर्माल प्रक्रिया पर विचार करने के लिए जहाँ एन्ट्रापी का परिवर्तन होता है {{math|1=Δ''S'' = ''nR'' ln({{sfrac|''V''<sub>2</sub>|''V''<sub>1</sub>}})}} जगह लेता है। यह एन्ट्रापी की परिभाषा और स्थिर तापमान और गैस की मात्रा की स्थिति से अनुसरण करता है {{mvar|n}} कि राज्यों की संख्या में परिवर्तन मात्रा में सापेक्ष परिवर्तन के समानुपाती होना चाहिए {{math|{{sfrac|''V''<sub>2</sub>|''V''<sub>1</sub>}}}}. इस अर्थ में आदर्श गैस परमाणुओं के सांख्यिकीय गुणों में कोई अंतर नहीं है, जो समान गतिविधि गुणांक वाले समाधान की भंग प्रजातियों की तुलना में है: कण स्वतंत्र रूप से प्रदान की गई मात्रा को भरते हुए लटकते हैं), जो दाढ़ की एकाग्रता के व्युत्क्रमानुपाती होता है। {{mvar|c}}, इसलिए हम एंट्रॉपी को इस रूप में भी लिख सकते हैं | ||
<math display="block">S = k\ln \ (\mathrm{constant}\times V) = -k\ln \ (\mathrm{constant}\times c).</math> | <math display="block">S = k\ln \ (\mathrm{constant}\times V) = -k\ln \ (\mathrm{constant}\times c).</math> | ||
इसलिए किसी राज्य 1 से दूसरे राज्य 2 में एन्ट्रापी में परिवर्तन होता है | इसलिए किसी राज्य 1 से दूसरे राज्य 2 में एन्ट्रापी में परिवर्तन होता है | ||
| Line 221: | Line 220: | ||
ताकि राज्य 2 की एन्ट्रापी हो | ताकि राज्य 2 की एन्ट्रापी हो | ||
<math display="block">S_2 = S_1 - k \ln \frac{c_2}{c_1}.</math> | <math display="block">S_2 = S_1 - k \ln \frac{c_2}{c_1}.</math> | ||
यदि राज्य 1 मानक स्थितियों में है, जिसमें {{math|''c''<sub>1</sub>}} एकता है (उदाहरण के लिए, 1 एटीएम या 1 एम), यह केवल की इकाइयों को रद्द कर देगा {{math|''c''<sub>2</sub>}}. इसलिए, हम | यदि राज्य 1 मानक स्थितियों में है, जिसमें {{math|''c''<sub>1</sub>}} एकता है (उदाहरण के लिए, 1 एटीएम या 1 एम), यह केवल की इकाइयों को रद्द कर देगा {{math|''c''<sub>2</sub>}}. इसलिए, हम स्वेच्छ अणु A की एन्ट्रापी को इस प्रकार लिख सकते हैं | ||
<math display="block">S(\mathrm{A}) = S^\ominus(\mathrm{A}) - k \ln [\mathrm{A}],</math> | <math display="block">S(\mathrm{A}) = S^\ominus(\mathrm{A}) - k \ln [\mathrm{A}],</math> | ||
कहाँ <math>S^\ominus</math> मानक तापमान और दबाव पर एंट्रॉपी है और [ए] ए की एकाग्रता को दर्शाता है। प्रतिक्रिया के लिए एंट्रॉपी में परिवर्तन | कहाँ <math>S^\ominus</math> मानक तापमान और दबाव पर एंट्रॉपी है और [ए] ए की एकाग्रता को दर्शाता है। प्रतिक्रिया के लिए एंट्रॉपी में परिवर्तन | ||
| Line 233: | Line 232: | ||
हम अंतिम अवधि में अनुपात को प्रतिक्रिया भागफल के रूप में परिभाषित करते हैं: | हम अंतिम अवधि में अनुपात को प्रतिक्रिया भागफल के रूप में परिभाषित करते हैं: | ||
<math display="block">Q_r = \frac{\displaystyle\prod_j a_j^{\nu_j}}{\displaystyle\prod_i a_i^{\nu_i}} \approx \frac{[\mathrm{Z}]^z [\mathrm{Y}]^y}{[\mathrm{A}]^a [\mathrm{B}]^b},</math> | <math display="block">Q_r = \frac{\displaystyle\prod_j a_j^{\nu_j}}{\displaystyle\prod_i a_i^{\nu_i}} \approx \frac{[\mathrm{Z}]^z [\mathrm{Y}]^y}{[\mathrm{A}]^a [\mathrm{B}]^b},</math> | ||
जहां अंश प्रतिक्रिया उत्पाद थर्मोडायनामिक गतिविधि का उत्पाद है, {{math|''a<sub>j</sub>''}}, प्रत्येक को | जहां अंश प्रतिक्रिया उत्पाद थर्मोडायनामिक गतिविधि का उत्पाद है, {{math|''a<sub>j</sub>''}}, प्रत्येक को स्टोइकीओमेट्रिक गुणांक की शक्ति तक बढ़ाया जाता है, {{math|''ν<sub>j</sub>''}}, और भाजक प्रतिक्रियाशील गतिविधियों का समान उत्पाद है। सभी गतिविधियाँ समय को संदर्भित करती हैं {{math|''t''}}. कुछ परिस्थितियों में (रासायनिक संतुलन देखें) प्रत्येक गतिविधि शब्द जैसे {{math|''a{{su|b=j|p=ν<sub>j</sub>}}''}} एकाग्रता शब्द द्वारा प्रतिस्थापित किया जा सकता है, [ए]। इलेक्ट्रोकेमिकल सेल में, सेल की क्षमता {{math|''E''}} रेडॉक्स प्रतिक्रियाओं से उपलब्ध रासायनिक क्षमता है ({{math|1=''E'' = {{sfrac|''μ''<sub>c</sub>|''e''}}}}). {{math|''E''}} गिब्स मुक्त ऊर्जा परिवर्तन से संबंधित है {{math|Δ''G''}} केवल स्थिरांक द्वारा: | ||
{{math|1=Δ''G'' = −''zFE''}}, कहाँ {{math|''n''}} हस्तांतरित इलेक्ट्रॉनों की संख्या है और {{math|''F''}} फैराडे स्थिरांक है। | {{math|1=Δ''G'' = −''zFE''}}, कहाँ {{math|''n''}} हस्तांतरित इलेक्ट्रॉनों की संख्या है और {{math|''F''}} फैराडे स्थिरांक है। नकारात्मक संकेत है क्योंकि सहज प्रतिक्रिया में नकारात्मक गिब्स मुक्त ऊर्जा होती है {{math|Δ''G''}} और सकारात्मक क्षमता {{math|''E''}}. गिब्स मुक्त ऊर्जा किसके द्वारा एंट्रॉपी से संबंधित है? {{math|1=''G'' = ''H'' − ''TS''}}, कहाँ {{math|''H''}} [[तापीय धारिता]] और है {{math|''T''}} सिस्टम का तापमान है। इन संबंधों का उपयोग करके अब हम गिब्स मुक्त ऊर्जा में परिवर्तन लिख सकते हैं, | ||
<math display="block">\Delta G = \Delta H - T \Delta S = \Delta G^\ominus + kT \ln Q_r,</math> | <math display="block">\Delta G = \Delta H - T \Delta S = \Delta G^\ominus + kT \ln Q_r,</math> | ||
और सेल क्षमता, | और सेल क्षमता, | ||
| Line 248: | Line 247: | ||
&= E^\ominus - \frac{RT}{zF} \ln Q_r. | &= E^\ominus - \frac{RT}{zF} \ln Q_r. | ||
\end{align}</math> | \end{align}</math> | ||
मानक तापमान और दबाव (एसटीपी) पर सेल की क्षमता <math>E^\ominus</math> अक्सर औपचारिक क्षमता द्वारा प्रतिस्थापित किया जाता है <math>E^{\ominus'}</math>, जिसमें दिए गए प्रयोगात्मक स्थितियों (टी, पी, आयनिक शक्ति, पीएच, और जटिल एजेंट) के तहत भंग प्रजातियों के गतिविधि गुणांक शामिल हैं और यह वह क्षमता है जो वास्तव में | मानक तापमान और दबाव (एसटीपी) पर सेल की क्षमता <math>E^\ominus</math> अक्सर औपचारिक क्षमता द्वारा प्रतिस्थापित किया जाता है <math>E^{\ominus'}</math>, जिसमें दिए गए प्रयोगात्मक स्थितियों (टी, पी, आयनिक शक्ति, पीएच, और जटिल एजेंट) के तहत भंग प्रजातियों के गतिविधि गुणांक शामिल हैं और यह वह क्षमता है जो वास्तव में इलेक्ट्रोकेमिकल सेल में मापा जाता है। | ||
== रासायनिक संतुलन से संबंध == | == रासायनिक संतुलन से संबंध == | ||
मानक गिब्स मुक्त ऊर्जा <math>\Delta G^\ominus</math> संतुलन स्थिरांक से संबंधित है {{mvar|K}} निम्नलिखित नुसार:<ref name="Chem_Libre_Texts">{{Cite web| title = चित्र 20.5: गिब्स ऊर्जा और रेडॉक्स अभिक्रियाएँ| work = Chemistry LibreTexts| date = 2014-11-18| accessdate = 2021-12-06| url = https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/20%3A_Electrochemistry/20.5%3A_Gibbs_Energy_and_Redox_Reactions}}</रेफरी> | मानक गिब्स मुक्त ऊर्जा <math>\Delta G^\ominus</math> संतुलन स्थिरांक से संबंधित है {{mvar|K}} निम्नलिखित नुसार:<ref name="Chem_Libre_Texts">{{Cite web| title = चित्र 20.5: गिब्स ऊर्जा और रेडॉक्स अभिक्रियाएँ| work = Chemistry LibreTexts| date = 2014-11-18| accessdate = 2021-12-06| url = https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/20%3A_Electrochemistry/20.5%3A_Gibbs_Energy_and_Redox_Reactions}}</रेफरी> | ||
: <math>\Delta G^\ominus = -RT \ln{K}</math> | :<math>\Delta G^\ominus = -RT \ln{K}</math> | ||
एक ही समय पर, <math>\Delta G^\ominus</math> कुल शुल्क के उत्पाद के बराबर भी है ({{mvar|zF}}) प्रतिक्रिया और सेल क्षमता के दौरान स्थानांतरित (<math>E^\ominus_{cell}</math>): | एक ही समय पर, <math>\Delta G^\ominus</math> कुल शुल्क के उत्पाद के बराबर भी है ({{mvar|zF}}) प्रतिक्रिया और सेल क्षमता के दौरान स्थानांतरित (<math>E^\ominus_{cell}</math>): | ||
: <math>\Delta G^\ominus = -zF E^\ominus_{cell}</math> | :<math>\Delta G^\ominus = -zF E^\ominus_{cell}</math> | ||
संकेत नकारात्मक है, क्योंकि विचाराधीन प्रणाली कार्य करती है और इस प्रकार ऊर्जा जारी करती है। | संकेत नकारात्मक है, क्योंकि विचाराधीन प्रणाली कार्य करती है और इस प्रकार ऊर्जा जारी करती है। | ||
इसलिए, | इसलिए, | ||
: <math>-zFE^\ominus_{cell} = -RT \ln{K}</math> | :<math>-zFE^\ominus_{cell} = -RT \ln{K}</math> | ||
और इसलिए: | और इसलिए: | ||
: <math>E^\ominus_{cell} = \frac{RT} {zF} \ln{K}</math> | :<math>E^\ominus_{cell} = \frac{RT} {zF} \ln{K}</math> | ||
नेर्नस्ट समीकरण से शुरू करके, समान संबंध को विपरीत तरीके से भी प्रदर्शित किया जा सकता है। | नेर्नस्ट समीकरण से शुरू करके, समान संबंध को विपरीत तरीके से भी प्रदर्शित किया जा सकता है। | ||
रासायनिक संतुलन, या थर्मोडायनामिक संतुलन पर, विद्युत रासायनिक क्षमता {{math|1=(''E'') = 0}} और इसलिए प्रतिक्रिया भागफल ({{math|''Q<sub>r</sub>''}}) विशेष मूल्य प्राप्त करता है जिसे संतुलन स्थिरांक के रूप में जाना जाता है ({{math|''K''<sub>eq</sub>}}): | रासायनिक संतुलन, या थर्मोडायनामिक संतुलन पर, विद्युत रासायनिक क्षमता {{math|1=(''E'') = 0}} और इसलिए प्रतिक्रिया भागफल ({{math|''Q<sub>r</sub>''}}) विशेष मूल्य प्राप्त करता है जिसे संतुलन स्थिरांक के रूप में जाना जाता है ({{math|''K''<sub>eq</sub>}}): | ||
: {{math|1 = ''Q<sub>r</sub>'' = ''K''<sub>eq</sub>}} इसलिए, | :{{math|1 = ''Q<sub>r</sub>'' = ''K''<sub>eq</sub>}} इसलिए, | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 280: | Line 279: | ||
इस प्रकार हमने रेडॉक्स अभिक्रिया के मानक इलेक्ट्रोड विभव और साम्य स्थिरांक को संबंधित किया है। | इस प्रकार हमने रेडॉक्स अभिक्रिया के मानक इलेक्ट्रोड विभव और साम्य स्थिरांक को संबंधित किया है। | ||
== सीमाएं == | ==सीमाएं== | ||
तनु समाधानों में, नर्नस्ट समीकरण को सीधे सांद्रता के संदर्भ में व्यक्त किया जा सकता है (चूंकि गतिविधि गुणांक एकता के करीब हैं)। लेकिन उच्च सांद्रता पर, आयनों की वास्तविक गतिविधियों का उपयोग किया जाना चाहिए। यह नर्नस्ट समीकरण के उपयोग को जटिल बनाता है, क्योंकि आयनों की गैर-आदर्श गतिविधियों के आकलन के लिए आम तौर पर प्रयोगात्मक माप की आवश्यकता होती है। नर्नस्ट समीकरण भी केवल तभी लागू होता है जब इलेक्ट्रोड के माध्यम से कोई शुद्ध प्रवाह नहीं होता है। इलेक्ट्रोड सतह पर आयनों की गतिविधि [[विद्युत रासायनिक कैनेटीक्स]] को बदलती है, और अतिरिक्त अतिपरासारी और प्रतिरोधक हानि शर्तें हैं जो मापा क्षमता में योगदान करती हैं। | तनु समाधानों में, नर्नस्ट समीकरण को सीधे सांद्रता के संदर्भ में व्यक्त किया जा सकता है (चूंकि गतिविधि गुणांक एकता के करीब हैं)। लेकिन उच्च सांद्रता पर, आयनों की वास्तविक गतिविधियों का उपयोग किया जाना चाहिए। यह नर्नस्ट समीकरण के उपयोग को जटिल बनाता है, क्योंकि आयनों की गैर-आदर्श गतिविधियों के आकलन के लिए आम तौर पर प्रयोगात्मक माप की आवश्यकता होती है। नर्नस्ट समीकरण भी केवल तभी लागू होता है जब इलेक्ट्रोड के माध्यम से कोई शुद्ध प्रवाह नहीं होता है। इलेक्ट्रोड सतह पर आयनों की गतिविधि [[विद्युत रासायनिक कैनेटीक्स]] को बदलती है, और अतिरिक्त अतिपरासारी और प्रतिरोधक हानि शर्तें हैं जो मापा क्षमता में योगदान करती हैं। | ||
संभावित-निर्धारण करने वाले आयनों की बहुत कम सांद्रता पर, Nernst समीकरण द्वारा अनुमानित क्षमता की ओर रुख करती है {{math|±∞}}. यह शारीरिक रूप से अर्थहीन है, क्योंकि ऐसी परिस्थितियों में, विनिमय धारा घनत्व बहुत कम हो जाता है, और हो सकता है कि नर्नस्ट समीकरण को धारण करने के लिए कोई थर्मोडायनामिक संतुलन आवश्यक न हो। ऐसे मामले में इलेक्ट्रोड को अनपोइज़्ड कहा जाता है। अन्य प्रभाव प्रणाली के विद्युत रासायनिक व्यवहार को नियंत्रित करने की प्रवृत्ति रखते हैं, जैसे कि बिजली हस्तांतरण और इलेक्ट्रोड संतुलन में [[सॉल्वेटेड इलेक्ट्रॉन]] की भागीदारी, जैसा कि [[अलेक्जेंडर फ्रुमकिन]] और बी। दमस्किन द्वारा विश्लेषण किया गया है,<ref>[[J. Electroanal. Chem.]], 79 (1977), 259-266</ref> सर्जियो ट्रसत्ती, आदि। | संभावित-निर्धारण करने वाले आयनों की बहुत कम सांद्रता पर, Nernst समीकरण द्वारा अनुमानित क्षमता की ओर रुख करती है {{math|±∞}}. यह शारीरिक रूप से अर्थहीन है, क्योंकि ऐसी परिस्थितियों में, विनिमय धारा घनत्व बहुत कम हो जाता है, और हो सकता है कि नर्नस्ट समीकरण को धारण करने के लिए कोई थर्मोडायनामिक संतुलन आवश्यक न हो। ऐसे मामले में इलेक्ट्रोड को अनपोइज़्ड कहा जाता है। अन्य प्रभाव प्रणाली के विद्युत रासायनिक व्यवहार को नियंत्रित करने की प्रवृत्ति रखते हैं, जैसे कि बिजली हस्तांतरण और इलेक्ट्रोड संतुलन में [[सॉल्वेटेड इलेक्ट्रॉन]] की भागीदारी, जैसा कि [[अलेक्जेंडर फ्रुमकिन]] और बी। दमस्किन द्वारा विश्लेषण किया गया है,<nowiki><ref></nowiki>[[J. Electroanal. Chem.]], 79 (1977), 259-266</ref> सर्जियो ट्रसत्ती, आदि। | ||
=== क्षमता की समय निर्भरता === | === क्षमता की समय निर्भरता === | ||
| Line 290: | Line 289: | ||
== अन्य वैज्ञानिक क्षेत्रों में महत्व == | == अन्य वैज्ञानिक क्षेत्रों में महत्व == | ||
ठंडे संलयन के बारे में वैज्ञानिक विवाद में नर्नस्ट समीकरण शामिल रहा है। फ्लेक्समैन और पोंस ने दावा किया कि ठंड संलयन मौजूद हो सकता है, गणना की कि भारी पानी इलेक्ट्रोलिसिस सेल में डूबा हुआ [[दुर्ग]] कैथोड 10 तक प्राप्त कर सकता है।<sup>27</sup> कैथोड की धातु के [[क्रिस्टल लैटिस]] के भीतर दाब का वातावरण, सहज नाभिकीय संलयन पैदा करने के लिए पर्याप्त दाब। वास्तव में, केवल 10,000-20,000 वातावरण ही प्राप्त हुए थे। अमेरिकी भौतिकशास्त्री जॉन आर. हुइजेंगा ने दावा किया कि उनकी मूल गणना नर्नस्ट समीकरण की गलत व्याख्या से प्रभावित थी।<ref>{{cite book| last=Huizenga | first=John R. | author-link=John R. Huizenga | title=Cold Fusion: The Scientific Fiasco of the Century | edition=2 | location=Oxford and New York | publisher=Oxford University Press | year=1993 | pages=33, 47 | isbn=978-0-19-855817-0 }}</ref> उन्होंने पीडी-जेडआर मिश्र धातुओं के बारे में | ठंडे संलयन के बारे में वैज्ञानिक विवाद में नर्नस्ट समीकरण शामिल रहा है। फ्लेक्समैन और पोंस ने दावा किया कि ठंड संलयन मौजूद हो सकता है, गणना की कि भारी पानी इलेक्ट्रोलिसिस सेल में डूबा हुआ [[दुर्ग]] कैथोड 10 तक प्राप्त कर सकता है।<sup>27</sup> कैथोड की धातु के [[क्रिस्टल लैटिस]] के भीतर दाब का वातावरण, सहज नाभिकीय संलयन पैदा करने के लिए पर्याप्त दाब। वास्तव में, केवल 10,000-20,000 वातावरण ही प्राप्त हुए थे। अमेरिकी भौतिकशास्त्री जॉन आर. हुइजेंगा ने दावा किया कि उनकी मूल गणना नर्नस्ट समीकरण की गलत व्याख्या से प्रभावित थी।<ref>{{cite book| last=Huizenga | first=John R. | author-link=John R. Huizenga | title=Cold Fusion: The Scientific Fiasco of the Century | edition=2 | location=Oxford and New York | publisher=Oxford University Press | year=1993 | pages=33, 47 | isbn=978-0-19-855817-0 }}</ref> उन्होंने पीडी-जेडआर मिश्र धातुओं के बारे में पेपर का हवाला दिया।<ref name="Huot1989">{{cite journal|last1=Huot|first1=J. Y.|title=Electrolytic Hydrogenation and Amorphization of Pd-Zr Alloys|journal=Journal of the Electrochemical Society|volume=136|issue=3|year=1989|pages=630–635|issn=0013-4651|doi=10.1149/1.2096700}}</ref> | ||
नर्नस्ट समीकरण दो रेडॉक्स प्रणालियों के बीच प्रतिक्रिया की सीमा की गणना की अनुमति देता है और इसका उपयोग किया जा सकता है, उदाहरण के लिए, यह आकलन करने के लिए कि कोई विशेष प्रतिक्रिया पूरी होगी या नहीं। रासायनिक संतुलन में, दो आधे कोशिकाओं के इलेक्ट्रोमोटिव बल (ईएमएफ) बराबर होते हैं। यह संतुलन को स्थिर रखने की अनुमति देता है {{math|''K''}} गणना की जाने वाली प्रतिक्रिया और इसलिए प्रतिक्रिया की सीमा। | नर्नस्ट समीकरण दो रेडॉक्स प्रणालियों के बीच प्रतिक्रिया की सीमा की गणना की अनुमति देता है और इसका उपयोग किया जा सकता है, उदाहरण के लिए, यह आकलन करने के लिए कि कोई विशेष प्रतिक्रिया पूरी होगी या नहीं। रासायनिक संतुलन में, दो आधे कोशिकाओं के इलेक्ट्रोमोटिव बल (ईएमएफ) बराबर होते हैं। यह संतुलन को स्थिर रखने की अनुमति देता है {{math|''K''}} गणना की जाने वाली प्रतिक्रिया और इसलिए प्रतिक्रिया की सीमा। | ||
Revision as of 16:21, 10 July 2023
इलेक्ट्रोकैमिस्ट्री में, नर्नस्ट समीकरण थर्मोडायनामिक्स # रासायनिक थर्मोडायनामिक्स संबंध है जो मानक इलेक्ट्रोड क्षमता, थर्मोडायनामिक तापमान, रिडॉक्स में शामिल इलेक्ट्रॉनों की संख्या से प्रतिक्रिया (आधा सेल या विद्युत रासायनिक सेल प्रतिक्रिया) की कमी क्षमता की गणना की अनुमति देता है। क्रमशः कमी और ऑक्सीकरण से गुजरने वाली रासायनिक प्रजातियों की थर्मोडायनामिक गतिविधि (अक्सर सांद्रता द्वारा अनुमानित)। इसका नाम जर्मन भौतिक रसायनज्ञ वाल्थर नर्नस्ट के नाम पर रखा गया, जिन्होंने समीकरण तैयार किया था।[1][2]
अभिव्यक्ति
रासायनिक क्रियाओं के साथ सामान्य रूप
जब आक्सीकारक (Ox) इलेक्ट्रॉनों की संख्या z स्वीकार करता है ( e−) इसके कम रूप में परिवर्तित करने के लिए (Red), आधी प्रतिक्रिया के रूप में व्यक्त किया गया है:
- Ox + जेड e− → Red
प्रतिक्रिया भागफल (Qr), जिसे अक्सर आयन गतिविधि उत्पाद (आईएपी) भी कहा जाता है, रासायनिक गतिविधि (ए) के कम रूप (कम करना,) के बीच का अनुपात है। aRed) और ऑक्सीकृत रूप (ऑक्सीडेंट, aOx). विघटित प्रजाति की रासायनिक गतिविधि उच्च सांद्रता पर समाधान में मौजूद सभी आयनों के बीच विद्युतीय संबंधों को ध्यान में रखते हुए इसकी वास्तविक थर्मोडायनामिक एकाग्रता से मेल खाती है। किसी दी गई विघटित प्रजाति के लिए, इसकी रासायनिक गतिविधि (ए) इसकी मोलर सघनता (mol/L सॉल्यूशन), या मोलिटी (mol/kg पानी), सघनता (C) द्वारा इसकी गतिविधि गुणांक (γ) का उत्पाद है: a = γ सी। इसलिए, यदि ब्याज की सभी भंग प्रजातियों की एकाग्रता (सी, यहां नीचे वर्ग कोष्ठक [ ] के साथ भी दर्शाया गया है) पर्याप्त रूप से कम है और उनकी गतिविधि गुणांक एकता के करीब हैं, तो उनकी रासायनिक गतिविधियों को उनकी सांद्रता द्वारा अनुमानित किया जा सकता है आमतौर पर किया जाता है जब सरलीकृत, या आदर्शीकरण, उपचारात्मक उद्देश्यों के लिए प्रतिक्रिया:
रासायनिक संतुलन पर, अनुपातQrप्रतिक्रिया उत्पाद की गतिविधि (एRed) अभिकर्मक गतिविधि द्वारा (एOx) संतुलन स्थिरांक के बराबर हैKआधी प्रतिक्रिया की:
मानक ऊष्मप्रवैगिकी यह भी कहती है कि वास्तविक गिब्स मुक्त ऊर्जा है ΔG मानक स्थिति के तहत मुक्त ऊर्जा परिवर्तन से संबंधित है ΔGo
रिश्ते से:
- Ered ब्याज के तापमान पर आधा सेल कमी की क्षमता है,
- E
o
red मानक इलेक्ट्रोड क्षमता है | मानक आधा सेल कमी क्षमता, - Ecell ब्याज के तापमान पर सेल की क्षमता (वैद्युतवाहक बल) है,
- E
o
cell मानक सेल क्षमता है, - R सार्वभौमिक गैस स्थिरांक है: R = 8.31446261815324 J K−1 mol−1,
- T केल्विन में तापमान है,
- z सेल प्रतिक्रिया या अर्ध-प्रतिक्रिया में स्थानांतरित इलेक्ट्रॉनों की संख्या है,
- F फैराडे स्थिरांक है, इलेक्ट्रॉनों के प्रति मोल (इकाई) आवेश का परिमाण (कूलम्ब में): F = 96485.3321233100184 C mol−1,
- Qr सेल प्रतिक्रिया की प्रतिक्रिया भागफल है, और
- a प्रासंगिक प्रजातियों के लिए रासायनिक गतिविधि (रसायन विज्ञान) है, जहां aRed कम रूप की गतिविधि है और aOx ऑक्सीकृत रूप की गतिविधि है।
थर्मल वोल्टेज
कमरे के तापमान (25 डिग्री सेल्सियस) पर, थर्मल वोल्टेज लगभग 25.693 mV है। नेर्नस्ट समीकरण को प्राय: प्राकृतिक लघुगणक के बजाय आधार-10 लघुगणक (अर्थात्, सामान्य लघुगणक) के संदर्भ में व्यक्त किया जाता है, जिस स्थिति में यह लिखा जाता है:
गतिविधि गुणांक और सांद्रता के साथ प्रपत्र
संतुलन स्थिरांक के समान, गतिविधियों को हमेशा मानक अवस्था के संबंध में मापा जाता है (विलेय के लिए 1 mol/L, गैसों के लिए 1 atm, और T = 298.15 K, यानी 25 °C या 77 °F)। प्रजाति की रासायनिक गतिविधि i, ai, मापा एकाग्रता से संबंधित है Ci रिश्ते के माध्यम से ai = γi Ci, कहाँ γi प्रजातियों का गतिविधि गुणांक है i. क्योंकि गतिविधि गुणांक कम सांद्रता पर एकता की ओर प्रवृत्त होते हैं, या मध्यम और उच्च सांद्रता पर अज्ञात या निर्धारित करने में कठिन होते हैं, नर्नस्ट समीकरण में गतिविधियों को अक्सर सरल सांद्रता से बदल दिया जाता है और फिर, औपचारिक मानक कमी क्षमता इस्तेमाल किया गया।
गतिविधि गुणांक को ध्यान में रखते हुए () नर्नस्ट समीकरण बन जाता है:
औपचारिक मानक कमी क्षमता
गतिविधियों के स्थान पर सरल सांद्रता का उपयोग करने की इच्छा होने पर, लेकिन यह कि गतिविधि गुणांक एकता से बहुत दूर हैं और इसे अब उपेक्षित नहीं किया जा सकता है और अज्ञात या निर्धारित करने में बहुत मुश्किल है, तथाकथित मानक औपचारिक की धारणा को पेश करना सुविधाजनक हो सकता है कमी क्षमता () जो निम्नानुसार मानक कमी क्षमता से संबंधित है:[3] औपचारिक कटौती क्षमता कमी की क्षमता है जो निर्दिष्ट शर्तों के सेट के तहत आधी प्रतिक्रिया पर लागू होती है, जैसे, पीएच, आयनिक शक्ति, या जटिल एजेंटों की एकाग्रता।
औपचारिक कमी क्षमता अक्सर अधिक सुविधाजनक, लेकिन सशर्त, मानक कमी क्षमता का रूप होता है, जो प्रतिक्रिया के माध्यम की गतिविधि गुणांक और विशिष्ट स्थितियों की विशेषताओं को ध्यान में रखता है। इसलिए, इसका मूल्य सशर्त मूल्य है, अर्थात यह प्रायोगिक स्थितियों पर निर्भर करता है और क्योंकि आयनिक शक्ति गतिविधि गुणांक को प्रभावित करती है, मध्यम से मध्यम भिन्न होगा।[3]औपचारिक कमी क्षमता की कई परिभाषाएँ साहित्य में पाई जा सकती हैं, जो अध्ययन किए गए उद्देश्य और अध्ययन प्रणाली द्वारा लगाए गए प्रयोगात्मक बाधाओं पर निर्भर करती हैं। की सामान्य परिभाषा इसके मूल्य को संदर्भित करता है जब निर्धारित किया जाता है . और विशेष मामला है जब पीएच 7 पर भी निर्धारित किया जाता है, उदा। जैव रसायन या जैविक प्रणालियों में महत्वपूर्ण रेडॉक्स प्रतिक्रियाओं के लिए।
औपचारिक मानक कमी क्षमता का निर्धारण जब Cred/Cox = 1
औपचारिक मानक कमी क्षमता मापा कमी क्षमता के रूप में परिभाषित किया जा सकता है ऑक्सीकृत और कम प्रजातियों के एकता एकाग्रता अनुपात में आधी प्रतिक्रिया (यानी, जब Cred/Cox = 1) दी गई शर्तों के तहत।[4] यदि क्षमता में कोई भी छोटा वृद्धिशील परिवर्तन प्रतिक्रिया की दिशा में परिवर्तन का कारण बनता है, अर्थात कमी से ऑक्सीकरण या इसके विपरीत, प्रणाली संतुलन के करीब है, प्रतिवर्ती है और अपनी औपचारिक क्षमता पर है। जब औपचारिक क्षमता को मानक स्थितियों के तहत मापा जाता है (अर्थात प्रत्येक विघटित प्रजाति की गतिविधि 1 mol/L, T = 298.15 K = 25 °C = 77 °F, Pgas = 1 बार) तो यह वास्तव में मानक विभव बन जाता है।[5]
ब्राउन और स्विफ्ट (1949) के अनुसार:
एक औपचारिक क्षमता को आधे सेल की क्षमता के रूप में परिभाषित किया जाता है, जिसे मानक हाइड्रोजन इलेक्ट्रोड के खिलाफ मापा जाता है, जब प्रत्येक ऑक्सीकरण राज्य की कुल एकाग्रता औपचारिक एकाग्रता होती है।[6]
इस मामले में, मानक कमी क्षमता के लिए, भंग प्रजातियों की सांद्रता मोलर सांद्रता (M) या मोलिटी (m) के बराबर रहती है, और इसलिए इसे औपचारिक सांद्रता (F) कहा जाता है। तो एकाग्रता व्यक्त कर रहे हैं C दाढ़ एकाग्रता में M (1 मोल / एल):
औपचारिक एकाग्रता (एफ) शब्द को अब वर्तमान साहित्य में काफी हद तक नजरअंदाज कर दिया गया है और थर्मोडायनामिक गणनाओं के मामले में मोलर एकाग्रता (एम), या मोलिटी (एम) को आमतौर पर आत्मसात किया जा सकता है।[7] हम एक-इलेक्ट्रॉन प्रक्रिया के लिए नर्नस्ट समीकरण प्राप्त करते हैं Ox + e− ⇌ Red :
ऊष्मप्रवैगिकी (रासायनिक क्षमता) का उपयोग
यहाँ मात्राएँ प्रति अणु दी गई हैं, प्रति मोल (इकाई) नहीं, और इसलिए बोल्ट्जमैन स्थिरांक k और प्राथमिक शुल्क e गैस स्थिरांक के बजाय उपयोग किया जाता है R और फैराडे स्थिरांक | फैराडे स्थिरांक F. अधिकांश रसायन विज्ञान की पाठ्यपुस्तकों में दी गई दाढ़ मात्रा में परिवर्तित करने के लिए, अवोगाद्रो स्थिरांक से गुणा करना आवश्यक है: R = kNA और F = eNA. अणु की एन्ट्रापी को इस रूप में परिभाषित किया गया है
इसके बाद दिया जाता है
j एकाग्रता शब्द द्वारा प्रतिस्थापित किया जा सकता है, [ए]। इलेक्ट्रोकेमिकल सेल में, सेल की क्षमता E रेडॉक्स प्रतिक्रियाओं से उपलब्ध रासायनिक क्षमता है (E = μc/e). E गिब्स मुक्त ऊर्जा परिवर्तन से संबंधित है ΔG केवल स्थिरांक द्वारा:
ΔG = −zFE, कहाँ n हस्तांतरित इलेक्ट्रॉनों की संख्या है और F फैराडे स्थिरांक है। नकारात्मक संकेत है क्योंकि सहज प्रतिक्रिया में नकारात्मक गिब्स मुक्त ऊर्जा होती है ΔG और सकारात्मक क्षमता E. गिब्स मुक्त ऊर्जा किसके द्वारा एंट्रॉपी से संबंधित है? G = H − TS, कहाँ H तापीय धारिता और है T सिस्टम का तापमान है। इन संबंधों का उपयोग करके अब हम गिब्स मुक्त ऊर्जा में परिवर्तन लिख सकते हैं,
रेडॉक्स प्रतिक्रिया के लिए Ox + z e− → Red,
और हमारे पास है:
रासायनिक संतुलन से संबंध
मानक गिब्स मुक्त ऊर्जा संतुलन स्थिरांक से संबंधित है K निम्नलिखित नुसार:[8] सर्जियो ट्रसत्ती, आदि।
क्षमता की समय निर्भरता
काल निर्भरता की अभिव्यक्ति कारोग्लानॉफ द्वारा स्थापित की गई है।[9][10][11][12]
अन्य वैज्ञानिक क्षेत्रों में महत्व
ठंडे संलयन के बारे में वैज्ञानिक विवाद में नर्नस्ट समीकरण शामिल रहा है। फ्लेक्समैन और पोंस ने दावा किया कि ठंड संलयन मौजूद हो सकता है, गणना की कि भारी पानी इलेक्ट्रोलिसिस सेल में डूबा हुआ दुर्ग कैथोड 10 तक प्राप्त कर सकता है।27 कैथोड की धातु के क्रिस्टल लैटिस के भीतर दाब का वातावरण, सहज नाभिकीय संलयन पैदा करने के लिए पर्याप्त दाब। वास्तव में, केवल 10,000-20,000 वातावरण ही प्राप्त हुए थे। अमेरिकी भौतिकशास्त्री जॉन आर. हुइजेंगा ने दावा किया कि उनकी मूल गणना नर्नस्ट समीकरण की गलत व्याख्या से प्रभावित थी।[13] उन्होंने पीडी-जेडआर मिश्र धातुओं के बारे में पेपर का हवाला दिया।[14] नर्नस्ट समीकरण दो रेडॉक्स प्रणालियों के बीच प्रतिक्रिया की सीमा की गणना की अनुमति देता है और इसका उपयोग किया जा सकता है, उदाहरण के लिए, यह आकलन करने के लिए कि कोई विशेष प्रतिक्रिया पूरी होगी या नहीं। रासायनिक संतुलन में, दो आधे कोशिकाओं के इलेक्ट्रोमोटिव बल (ईएमएफ) बराबर होते हैं। यह संतुलन को स्थिर रखने की अनुमति देता है K गणना की जाने वाली प्रतिक्रिया और इसलिए प्रतिक्रिया की सीमा।
यह भी देखें
- एकाग्रता सेल
- न्यूनीकरण क्षमता#नर्न्स्ट समीकरण
- इलेक्ट्रोड क्षमता
- बिजली उत्पन्न करनेवाली सेल
- गोल्डमैन समीकरण
- झिल्ली क्षमता
- नर्नस्ट-प्लैंक समीकरण
- पौरबाइक्स आरेख
- कमी की संभावना
- सॉल्वेटेड इलेक्ट्रॉन
- मानक इलेक्ट्रोड क्षमता
- मानक इलेक्ट्रोड क्षमता (डेटा पृष्ठ)
- जैव रसायन में महत्वपूर्ण अर्ध-प्रतिक्रियाओं के लिए मानक कमी क्षमता की तालिका | पीएच 7 पर जैव रसायन में मानक स्पष्ट कमी क्षमता (डेटा पृष्ठ)
संदर्भ
- ↑ Orna, Mary Virginia; Stock, John (1989). Electrochemistry, past and present. Columbus, OH: American Chemical Society. ISBN 978-0-8412-1572-6. OCLC 19124885.
- ↑ Wahl (2005). "A Short History of Electrochemistry". Galvanotechtnik. 96 (8): 1820–1828.
- ↑ 3.0 3.1 Bard, Allen J.; Faulkner, Larry R. (2001). "Chapter 2. Potentials and Thermodynamics of Cells – See: 2.1.6 Formal Potentials". विद्युत रासायनिक विधियाँ: मूल तत्व और अनुप्रयोग (2 ed.). New York: John Wiley & Sons. p. 52.</रेफरी>
ताकि अर्ध-सेल प्रतिक्रिया के लिए नर्नस्ट समीकरण को औपचारिक रूप से सांद्रता के संदर्भ में सही ढंग से लिखा जा सके:और इसी तरह पूर्ण सेल अभिव्यक्ति के लिए। वेन्ज़ेल (2020) के अनुसार,<ref name="Wenzel_2020">Wenzel, Thomas (2020-06-09). "4. मानक राज्य विद्युत रासायनिक क्षमता की तालिका". Chemistry LibreTexts. Retrieved 2021-11-24.
- ↑ Kano, Kenji (2002). "जलीय घोलों में प्रोटीन और बायोइलेक्ट्रॉनिक रुचि के अन्य यौगिकों की रेडॉक्स क्षमता।". Review of Polarography. 48 (1): 29–46. doi:10.5189/revpolarography.48.29. eISSN 1884-7692. ISSN 0034-6691. Retrieved 2021-12-02.</रेफरी>
वास्तव में:
जैसा, , कब ,
- , कब ,
- ↑ PalmSens (2021). "Origins of electrochemical potentials — PalmSens". PalmSens. Retrieved 2021-12-06.
- ↑ Brown, Raymond A.; Swift, Ernest H. (1949). "हाइड्रोक्लोरिक एसिड समाधान में एंटीमोनस-एंटीमोनिक आधा सेल की औपचारिक क्षमता". Journal of the American Chemical Society. 71 (8): 2719–2723. ISSN 0002-7863.
उद्धरण: एक औपचारिक क्षमता को एक आधे सेल की क्षमता के रूप में परिभाषित किया जाता है, जिसे मानक हाइड्रोजन इलेक्ट्रोड के खिलाफ मापा जाता है, जब प्रत्येक ऑक्सीकरण अवस्था की कुल सांद्रता एक औपचारिक होती है।
- ↑ Harvey, David (2020-06-15). "2.2: एकाग्रता". Chemistry LibreTexts. Retrieved 2021-12-15.</रेफरी>
चक्रीय voltammetry में दो चोटियों के बीच औपचारिक क्षमता भी आधी पाई जाती है, जहां इस बिंदु पर इलेक्ट्रोड सतह पर ऑक्स (ऑक्सीडाइज्ड प्रजाति) और रेड (कम प्रजाति) की सांद्रता बराबर होती है।
गतिविधि गुणांक और औपचारिक क्षमता में शामिल हैं , और क्योंकि वे तापमान, आयनिक शक्ति और पीएच जैसी प्रायोगिक स्थितियों पर निर्भर करते हैं, एक अपरिवर्तनीय मानक क्षमता के रूप में संदर्भित नहीं किया जा सकता है लेकिन प्रायोगिक स्थितियों के प्रत्येक विशिष्ट सेट के लिए व्यवस्थित रूप से निर्धारित करने की आवश्यकता है।
दी गई शर्तों और माप की व्याख्या के तहत एक मानी हुई प्रणाली की गणना को सरल बनाने के लिए औपचारिक कमी की क्षमता लागू की जाती है। प्रायोगिक स्थितियाँ जिनमें वे निर्धारित किए गए हैं और मानक कमी क्षमता के साथ उनके संबंध को स्पष्ट रूप से वर्णित किया जाना चाहिए ताकि उन्हें मानक कमी क्षमता के साथ भ्रमित करने से बचा जा सके।
==== pH 7==== पर औपचारिक मानक कमी क्षमता
औपचारिक मानक कमी क्षमता () आमतौर पर पीएच 7 पर मापी गई मानक कमी क्षमता के संदर्भ में जैव रसायन और कोशिका जीव विज्ञान में भी उपयोग किया जाता है, जो 0 के मानक राज्य पीएच की तुलना में अधिकांश शारीरिक और इंट्रासेल्युलर तरल पदार्थों के पीएच के करीब है। लाभ एक अधिक उपयुक्त रेडॉक्स को परिभाषित करना है। मानक स्थिति की तुलना में वास्तविक परिस्थितियों के अनुरूप बेहतर। औपचारिक मानक कमी क्षमता () अधिक आसानी से अनुमान लगाने की अनुमति दें कि क्या एक चयापचय प्रक्रिया में होने वाली रेडॉक्स प्रतिक्रिया या कुछ शर्तों के तहत माइक्रोबियल गतिविधि को बढ़ावा देना संभव है या नहीं।
जबकि, मानक अपचयन विभव हमेशा मानक हाइड्रोजन इलेक्ट्रोड (SHE) को संदर्भित करते हैं, [के साथ] H+] = 1 एम पीएच 0 के अनुरूप, और कन्वेंशन द्वारा मनमाने ढंग से शून्य पर तय किया गया, यह अब 7 के पीएच पर मामला नहीं है। फिर, कमी की क्षमता मानक हाइड्रोजन इलेक्ट्रोड (SHE) के संबंध में pH 7 पर संचालित हाइड्रोजन इलेक्ट्रोड का मान -0.413 V है।<ref name="Voet_2016">Voet, Donald; Voet, Judith G.; Pratt, Charlotte W. (2016). "Table 14-4 Standard Reduction Potentials for Some Biochemically Import Half-Reactions". बायोकैमिस्ट्री के मूल सिद्धांत: आणविक स्तर पर जीवन (5th ed.). Wiley. p. 466. ISBN 978-1-118-91840-1.</रेफरी>
=== पीएच === के एक समारोह के रूप में नेर्नस्ट समीकरण की अभिव्यक्ति
h> और किसी विलयन का pH, Nernst समीकरण द्वारा संबंधित होते हैं, जैसा कि आमतौर पर एक Poorbaix आरेख द्वारा दर्शाया जाता है ( – pH plot). स्पष्ट रूप से दर्शाता है मानक हाइड्रोजन इलेक्ट्रोड (SHE) बनाम व्यक्त किया गया। आधे सेल समीकरण के लिए, पारंपरिक रूप से एक कमी प्रतिक्रिया के रूप में लिखा जाता है (यानी, बाईं ओर एक ऑक्सीडेंट द्वारा इलेक्ट्रॉनों को स्वीकार किया जाता है):
आधा सेल मानक कमी क्षमता द्वारा दिया गया है
कहाँ मानक गिब्स मुक्त ऊर्जा परिवर्तन है, z शामिल इलेक्ट्रॉनों की संख्या है, और F फैराडे स्थिरांक है। नर्नस्ट समीकरण पीएच और से संबंधित है निम्नलिखित नुसार:
जहां घुंघराले कोष्ठक गतिविधि (रसायन विज्ञान) को इंगित करते हैं, और घातांक पारंपरिक तरीके से दिखाए जाते हैं। यह समीकरण एक सीधी रेखा का समीकरण है की ढलान के साथ पीएच के एक समारोह के रूप में वोल्ट (पीएच की कोई इकाई नहीं है)।
यह समीकरण कम भविष्यवाणी करता है उच्च पीएच मान पर। यह ओ की कमी के लिए मनाया जाता है2 एच में2ओ, या ओह-, और H को कम करने के लिए+ एच में2. तब अक्सर के रूप में नोट किया जाता है यह इंगित करने के लिए कि यह मानक हाइड्रोजन इलेक्ट्रोड (एसएचई) को संदर्भित करता है जिसका = 0 मानक शर्तों के तहत सम्मेलन द्वारा (टी = 298.15 के = 25 डिग्री सेल्सियस = 77 एफ, पीgas = 1 एटीएम (1.013 बार), सांद्रता = 1 एम और इस प्रकार पीएच = 0)।
औपचारिक मानक कमी क्षमता को प्रभावित करने वाले मुख्य कारक
जैव रासायनिक या जैविक प्रक्रियाओं में औपचारिक कमी की क्षमता को प्रभावित करने वाला मुख्य कारक अक्सर पीएच होता है। औपचारिक कमी क्षमता के अनुमानित मूल्यों को निर्धारित करने के लिए, पहले दृष्टिकोण में आयनिक शक्ति के कारण गतिविधि गुणांक में परिवर्तन की उपेक्षा करते हुए, पीएच के एक समारोह के रूप में रिश्ते को पहले व्यक्त करने के लिए नर्नस्ट समीकरण को लागू किया जाना चाहिए। माना जाने वाला दूसरा कारक नर्नस्ट समीकरण में ध्यान में रखी गई सांद्रता के मूल्य हैं। एक जैव रासायनिक प्रतिक्रिया के लिए एक औपचारिक कमी क्षमता को परिभाषित करने के लिए, पीएच मान, सांद्रता मान और गतिविधि गुणांकों पर बनी परिकल्पनाओं को हमेशा स्पष्ट रूप से इंगित किया जाना चाहिए। उपयोग करते समय, या तुलना करते समय, कई औपचारिक कटौती क्षमताएँ उन्हें आंतरिक रूप से सुसंगत भी होना चाहिए।
विभिन्न सम्मेलनों या अनुमानों (यानी, विभिन्न अंतर्निहित परिकल्पनाओं के साथ) का उपयोग करते हुए डेटा के विभिन्न स्रोतों को मिलाते समय समस्याएँ हो सकती हैं। अकार्बनिक और जैविक प्रक्रियाओं के बीच की सीमा पर काम करते समय (उदाहरण के लिए, भू-रसायन में अजैविक और जैविक प्रक्रियाओं की तुलना करते समय जब माइक्रोबियल गतिविधि भी सिस्टम में काम कर सकती है), इस बात का ध्यान रखा जाना चाहिए कि अनजाने में सीधे मानक कमी क्षमता बनाम SHE (pH) का मिश्रण न हो। = 0) औपचारिक कमी क्षमता (पीएच = 7) के साथ। परिभाषाओं को स्पष्ट रूप से व्यक्त किया जाना चाहिए और सावधानीपूर्वक नियंत्रित किया जाना चाहिए, विशेष रूप से यदि डेटा के स्रोत अलग-अलग हैं और विभिन्न क्षेत्रों से उत्पन्न होते हैं (उदाहरण के लिए, शास्त्रीय इलेक्ट्रोकैमिस्ट्री और माइक्रोबायोलॉजी पाठ्यपुस्तकों से डेटा चुनना और मिश्रित करना, विभिन्न सम्मेलनों पर ध्यान दिए बिना, जिस पर वे आधारित हैं)।
पौरबैक्स आरेख के साथ उदाहरण
पीएच पर कमी की क्षमता की निर्भरता को स्पष्ट करने के लिए, कोई भी केवल दो रेडॉक्स पर विचार कर सकता है। पौरबैक्स आरेख में जल स्थिरता डोमेन का निर्धारण करने वाला ऑक्सीडो-कमी संतुलन (Eh–pH plot). जब पानी में डूबे हुए दो इलेक्ट्रोडों के बीच बिजली उत्पन्न करनेवाली सेल का पर्याप्त अंतर लगाकर पानी का इलेक्ट्रोलिसिस किया जाता है, तो कैथोड (पानी के प्रोटॉन में कमी) पर हाइड्रोजन का उत्पादन होता है, जबकि एनोड (जल ऑक्सीजन परमाणुओं का ऑक्सीकरण) पर ऑक्सीजन बनता है। ऐसा तब भी हो सकता है जब हाइड्रोजन से अधिक प्रबल अपचायक (जैसे, धात्विक Na) या ऑक्सीजन से अधिक प्रबल ऑक्सीकारक (जैसे, F)2) पानी के संपर्क में आता है और इसके साथ प्रतिक्रिया करता है। में Eh–pH plot इसके बगल में (पौरबैक्स आरेख का सबसे सरल संभव संस्करण), जल स्थिरता डोमेन (ग्रे सतह) को दो झुकी हुई लाल धराशायी रेखाओं द्वारा रेडॉक्स क्षमता के रूप में सीमांकित किया गया है: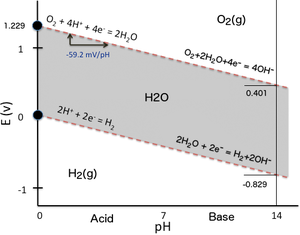 मानक तापमान और दबाव (STP) पर पानी, ऑक्सीजन और हाइड्रोजन के लिए स्थिरता क्षेत्रों सहित पानी के लिए पौरबैक्स आरेख। वर्टिकल स्केल (ऑर्डिनेट) एक मानक हाइड्रोजन इलेक्ट्रोड इलेक्ट्रोड के सापेक्ष इलेक्ट्रोड क्षमता है। क्षैतिज पैमाने (एब्सिस्सा) इलेक्ट्रोलाइट का पीएच है (अन्यथा गैर-अंतःक्रियात्मक)। शीर्ष रेखा के ऊपर ऑक्सीजन इलेक्ट्रोड से तब तक बुदबुदाती रहेगी जब तक कि पानी पूरी तरह से समाप्त नहीं हो जाता। इसी तरह, नीचे की रेखा के नीचे हाइड्रोजन इलेक्ट्रोड से तब तक बुदबुदाएगा जब तक कि पानी पूरी तरह से खपत नहीं हो जाता।
मानक तापमान और दबाव (STP) पर पानी, ऑक्सीजन और हाइड्रोजन के लिए स्थिरता क्षेत्रों सहित पानी के लिए पौरबैक्स आरेख। वर्टिकल स्केल (ऑर्डिनेट) एक मानक हाइड्रोजन इलेक्ट्रोड इलेक्ट्रोड के सापेक्ष इलेक्ट्रोड क्षमता है। क्षैतिज पैमाने (एब्सिस्सा) इलेक्ट्रोलाइट का पीएच है (अन्यथा गैर-अंतःक्रियात्मक)। शीर्ष रेखा के ऊपर ऑक्सीजन इलेक्ट्रोड से तब तक बुदबुदाती रहेगी जब तक कि पानी पूरी तरह से समाप्त नहीं हो जाता। इसी तरह, नीचे की रेखा के नीचे हाइड्रोजन इलेक्ट्रोड से तब तक बुदबुदाएगा जब तक कि पानी पूरी तरह से खपत नहीं हो जाता।- बहुत कम ई पर प्रोटॉन की कमी के कारण हाइड्रोजन गैस के विकास के साथ कम स्थिरता रेखाh:
- 2 H+ + 2 e− ⇌ H2 (कैथोड: कमी)
- बहुत उच्च ई पर जल ऑक्सीजन ऑक्सीकरण के कारण ऑक्सीजन गैस के विकास के साथ उच्च स्थिरता रेखाh:
- 2 H2O ⇌ O2 + 4 H+ + 4 e− (एनोड: ऑक्सीकरण)
प्रत्येक संबंधित कमी प्रतिक्रिया के लिए नर्नस्ट समीकरण को हल करते समय (ऑक्सीजन का उत्पादन करने वाले जल ऑक्सीकरण प्रतिक्रिया को वापस करने की आवश्यकता होती है), दोनों समीकरणों का एक समान रूप होता है क्योंकि प्रोटॉन की संख्या और प्रतिक्रिया में शामिल इलेक्ट्रॉनों की संख्या समान होती है और उनका अनुपात एक होता है (2 H+/2 e− एच के लिए2 और 4 H+/4 e− साथ O2 क्रमशः), इसलिए पीएच के एक समारोह के रूप में व्यक्त नर्नस्ट समीकरण को हल करते समय यह सरल हो जाता है।
परिणाम को संख्यात्मक रूप से निम्नानुसार व्यक्त किया जा सकता है:
ध्यान दें कि दो जल स्थिरता डोमेन की ऊपरी और निचली रेखाओं के ढलान समान (-59.16 mV/pH इकाई) हैं, इसलिए वे पौरबैक्स आरेख पर समानांतर हैं। चूंकि ढलान नकारात्मक हैं, उच्च पीएच पर, हाइड्रोजन और ऑक्सीजन दोनों के विकास के लिए कम पीएच की तुलना में बहुत कम कमी की क्षमता की आवश्यकता होती है।
एच की कमी के लिए+ एच में2 यहाँ ऊपर उल्लिखित रिश्ता बन जाता है:
-
क्योंकि परंपरा के अनुसार मानक हाइड्रोजन इलेक्ट्रोड के लिए = 0 V (SHE: pH = 1)।
इसलिए, pH = 7 पर, = -0.414 वी प्रोटॉन की कमी के लिए।
ओ की कमी के लिए2 2 एच में2हे यहाँ उपर्युक्त संबंध बन जाता है:
-
क्योंकि = +1.229 V मानक हाइड्रोजन इलेक्ट्रोड के संबंध में (SHE: pH = 1)।
इसलिए, pH = 7 पर, = +0.815 वी ऑक्सीजन की कमी के लिए।
ऑफ़सेट -414 mV in दोनों कमी प्रतिक्रियाओं के लिए समान है क्योंकि वे पीएच के एक समारोह के समान रैखिक संबंध साझा करते हैं और उनकी रेखाओं की ढलान समान होती है। इसे पौरबैक्स आरेख पर सीधे सत्यापित किया जा सकता है। अन्य कमी प्रतिक्रियाओं के लिए, 7 के पीएच पर औपचारिक कमी की क्षमता का मान, जिसे आमतौर पर जैव रासायनिक प्रतिक्रियाओं के लिए संदर्भित किया जाता है, वह भी पौरबैक्स आरेख में संबंधित रेखा के ढलान पर निर्भर करता है अर्थात अनुपात परh⁄zकी संख्या का H+ की संख्या के लिए e− कमी प्रतिक्रिया में शामिल है, और इस प्रकार अर्ध-प्रतिक्रिया के स्तुईचिओमेटरी पर। किसी दिए गए जैव रासायनिक अर्ध-प्रतिक्रिया के लिए पीएच = 7 पर औपचारिक कमी क्षमता का निर्धारण करने के लिए पीएच के एक समारोह के रूप में संबंधित नर्नस्ट समीकरण के साथ इसकी गणना करने की आवश्यकता होती है। कोई ई पर -414 एमवी का ऑफसेट लागू नहीं कर सकता हैh मूल्य (SHE) जब अनुपातh⁄z1 से भिन्न है।
जीव विज्ञान में अनुप्रयोग
बायोकैमिस्ट्री में महत्वपूर्ण अर्ध-प्रतिक्रियाओं के लिए मानक कमी क्षमता की तालिका के अलावा, एक प्रकार के आयन के संबंध में कोशिका झिल्ली की विद्युत क्षमता की गणना के लिए शरीर विज्ञान में नर्नस्ट समीकरण का भी उपयोग किया जाता है। इसे अम्ल पृथक्करण स्थिरांक से जोड़ा जा सकता है।
नर्नस्ट संभावित
आयन के आवेश की क्षमता की गणना करने के लिए उपयोग किए जाने पर नर्नस्ट समीकरण का एक शारीरिक अनुप्रयोग होता है z एक झिल्ली के पार। यह क्षमता कोशिका के अंदर और बाहर आयन की सांद्रता का उपयोग करके निर्धारित की जाती है:
जब झिल्ली उष्मागतिक संतुलन में होती है (अर्थात्, आयनों का कोई शुद्ध प्रवाह नहीं), और यदि कोशिका केवल एक आयन के लिए पारगम्य है, तो झिल्ली क्षमता उस आयन के लिए नेर्नस्ट क्षमता के बराबर होनी चाहिए।गोल्डमैन समीकरण
जब झिल्ली एक से अधिक आयनों के लिए पारगम्य होती है, जैसा कि अनिवार्य रूप से होता है, विश्राम क्षमता को गोल्डमैन समीकरण से निर्धारित किया जा सकता है, जो जीएचके फ्लक्स समीकरण का एक समाधान है। बल शून्य है:
कहाँ- Em झिल्ली क्षमता है (वाल्ट में, जूल प्रति कूलम्ब के बराबर),
- Pion उस आयन के लिए पारगम्यता है (मीटर प्रति सेकंड में),
- [ion]out अन्य एसआई इकाइयों से मेल खाने के लिए उस आयन (मोल (यूनिट) प्रति घन मीटर में) की बाह्य एकाग्रता है, हालांकि इकाइयां सख्ती से कोई फर्क नहीं पड़ता, क्योंकि आयन एकाग्रता शब्द एक आयामहीन अनुपात बन जाते हैं),
- [ion]in उस आयन की इंट्रासेल्युलर सांद्रता है (मोल्स प्रति घन मीटर में),
- R आदर्श गैस नियतांक है (जूल प्रति केल्विन प्रति मोल),
- T केल्विन में तापमान है,
- F फैराडे स्थिरांक है | फैराडे स्थिरांक (कूलम्ब प्रति मोल)।
कोशिका झिल्ली के पार की क्षमता जो झिल्ली के माध्यम से किसी विशेष आयन के शुद्ध प्रसार का बिल्कुल विरोध करती है, उस आयन के लिए नेर्नस्ट क्षमता कहलाती है। जैसा कि ऊपर देखा गया है, नेर्नस्ट क्षमता का परिमाण झिल्ली के दोनों किनारों पर उस विशिष्ट आयन की सांद्रता के अनुपात से निर्धारित होता है। यह अनुपात जितना अधिक होगा, आयन के एक दिशा में विसरित होने की प्रवृत्ति उतनी ही अधिक होगी, और इसलिए विसरण को रोकने के लिए आवश्यक नर्नस्ट क्षमता भी उतनी ही अधिक होगी। एक समान अभिव्यक्ति मौजूद है जिसमें शामिल है r (परिवहन अनुपात का पूर्ण मूल्य)। यह असमान एक्सचेंज वाले ट्रांसपोर्टरों को ध्यान में रखता है। देखें: सोडियम-पोटेशियम पंप जहां परिवहन अनुपात 2/3 होगा, इसलिए r नीचे दिए गए सूत्र में 1.5 के बराबर है। हम यहां एक कारक r = 1.5 क्यों डालते हैं इसका कारण विद्युत रासायनिक बल J द्वारा वर्तमान घनत्व हैe.c.(वह+) + जेe.c.(क+) अब शून्य नहीं है, बल्कि J हैe.c.(वह+) + 1.5Me.c.(क+) = 0 (विद्युत रासायनिक बल द्वारा दोनों आयनों के प्रवाह की भरपाई पंप द्वारा की जाती है, अर्थात Je.c. = -जेpump), GHK समीकरण को लागू करने के लिए बाधाओं को बदलना। अन्य चर ऊपर के समान हैं। निम्नलिखित उदाहरण में दो आयन शामिल हैं: पोटेशियम (के+) और सोडियम (Na+). क्लोराइड संतुलन में माना जाता है।
जब क्लोराइड (Cl−) को ध्यान में रखा जाता है,व्युत्पत्ति
बोल्ट्जमैन फैक्टर का प्रयोग
सरलता के लिए, हम उन रेडॉक्स-सक्रिय अणुओं के विलयन पर विचार करेंगे जो एक-इलेक्ट्रॉन उत्क्रमणीय प्रतिक्रिया से गुजरते हैं
- Ox + e− ⇌ Red
और जिसमें शून्य की एक मानक क्षमता है, और जिसमें गतिविधियों को सांद्रता (यानी इकाई गतिविधि गुणांक) द्वारा अच्छी तरह से दर्शाया गया है। रासायनिक क्षमता μc इस समाधान का अंतर, कार्यशील इलेक्ट्रोड से इलेक्ट्रॉनों को लेने और इलेक्ट्रॉनों को देने के लिए ऊर्जा बाधाओं के बीच का अंतर है जो समाधान की विद्युत रासायनिक क्षमता निर्धारित कर रहा है। ऑक्सीकृत और कम अणुओं का अनुपात, [Ox]/[Red], कम होने (इलेक्ट्रॉन लेने) की संभावना पर ऑक्सीकृत होने (इलेक्ट्रॉन देने) की संभावना के बराबर है, जिसे हम इन प्रक्रियाओं के लिए बोल्टज़मान कारक के संदर्भ में लिख सकते हैं:
दोनों पक्षों का प्राकृतिक लघुगणक लेने पर प्राप्त होता हैअगर μc ≠ 0 पर [Ox]/[Red]= 1, हमें इस अतिरिक्त स्थिरांक में जोड़ने की आवश्यकता है:द्वारा समीकरण को विभाजित करना e रासायनिक क्षमता से इलेक्ट्रोड क्षमता में परिवर्तित करने के लिए, और उसे याद रखना k/e = R/F,<ref>R = NAk; see gas constant
F = NAe; see Faraday constant - ↑ "चित्र 20.5: गिब्स ऊर्जा और रेडॉक्स अभिक्रियाएँ". Chemistry LibreTexts. 2014-11-18. Retrieved 2021-12-06.</रेफरी>
- Qr = Keq इसलिए,
या मानक स्थिति में,इस प्रकार हमने रेडॉक्स अभिक्रिया के मानक इलेक्ट्रोड विभव और साम्य स्थिरांक को संबंधित किया है।सीमाएं
तनु समाधानों में, नर्नस्ट समीकरण को सीधे सांद्रता के संदर्भ में व्यक्त किया जा सकता है (चूंकि गतिविधि गुणांक एकता के करीब हैं)। लेकिन उच्च सांद्रता पर, आयनों की वास्तविक गतिविधियों का उपयोग किया जाना चाहिए। यह नर्नस्ट समीकरण के उपयोग को जटिल बनाता है, क्योंकि आयनों की गैर-आदर्श गतिविधियों के आकलन के लिए आम तौर पर प्रयोगात्मक माप की आवश्यकता होती है। नर्नस्ट समीकरण भी केवल तभी लागू होता है जब इलेक्ट्रोड के माध्यम से कोई शुद्ध प्रवाह नहीं होता है। इलेक्ट्रोड सतह पर आयनों की गतिविधि विद्युत रासायनिक कैनेटीक्स को बदलती है, और अतिरिक्त अतिपरासारी और प्रतिरोधक हानि शर्तें हैं जो मापा क्षमता में योगदान करती हैं।
संभावित-निर्धारण करने वाले आयनों की बहुत कम सांद्रता पर, Nernst समीकरण द्वारा अनुमानित क्षमता की ओर रुख करती है ±∞. यह शारीरिक रूप से अर्थहीन है, क्योंकि ऐसी परिस्थितियों में, विनिमय धारा घनत्व बहुत कम हो जाता है, और हो सकता है कि नर्नस्ट समीकरण को धारण करने के लिए कोई थर्मोडायनामिक संतुलन आवश्यक न हो। ऐसे मामले में इलेक्ट्रोड को अनपोइज़्ड कहा जाता है। अन्य प्रभाव प्रणाली के विद्युत रासायनिक व्यवहार को नियंत्रित करने की प्रवृत्ति रखते हैं, जैसे कि बिजली हस्तांतरण और इलेक्ट्रोड संतुलन में सॉल्वेटेड इलेक्ट्रॉन की भागीदारी, जैसा कि अलेक्जेंडर फ्रुमकिन और बी। दमस्किन द्वारा विश्लेषण किया गया है,<ref>J. Electroanal. Chem., 79 (1977), 259-266
- ↑ Karaoglanoff, Z. (January 1906), "Über Oxydations- und Reduktionsvorgänge bei der Elektrolyse von Eisensaltzlösungen" [On Oxidation and Reduction Processes in the Electrolysis of Iron Salt Solutions], Zeitschrift für Elektrochemie (in Deutsch), 12 (1): 5–16, doi:10.1002/bbpc.19060120105
- ↑ Bard, Allen J.; Inzelt, György; Scholz, Fritz, eds. (2012-10-02), "Karaoglanoff equation", Electrochemical Dictionary, Springer, pp. 527–528, ISBN 9783642295515
- ↑ Zutshi, Kamala (2008), Introduction to Polarography and Allied Techniques, pp. 127–128, ISBN 9788122417913
- ↑ The Journal of Physical Chemistry, Volume 10, p 316. https://books.google.com/books?id=zCMSAAAAIAAJ&pg=PA316&lpg=PA316&hl=en&f=false
- ↑ Huizenga, John R. (1993). Cold Fusion: The Scientific Fiasco of the Century (2 ed.). Oxford and New York: Oxford University Press. pp. 33, 47. ISBN 978-0-19-855817-0.
- ↑ Huot, J. Y. (1989). "Electrolytic Hydrogenation and Amorphization of Pd-Zr Alloys". Journal of the Electrochemical Society. 136 (3): 630–635. doi:10.1149/1.2096700. ISSN 0013-4651.
बाहरी संबंध
- Nernst/Goldman Equation Simulator
- Nernst Equation Calculator
- Interactive Nernst/Goldman Java Applet
- DoITPoMS Teaching and Learning Package- "The Nernst Equation and Pourbaix Diagrams"
- "20.5: Gibbs energy and redox reactions". Chemistry LibreTexts. 2014-11-18. Retrieved 2021-12-06.