क्रमगुणित: Difference between revisions
No edit summary |
No edit summary |
||
| (18 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Product of numbers from 1 to n}} | {{Short description|Product of numbers from 1 to n}} | ||
{{about|क्रमागत पूर्णांकों का गुणनफल|मूल्यों के सभी संयोजनों पर सांख्यिकीय प्रयोग|तथ्यात्मक प्रयोग|स्वतंत्र घटकों द्वारा डेटा प्रतिनिधित्व| | {{about|क्रमागत पूर्णांकों का गुणनफल|मूल्यों के सभी संयोजनों पर सांख्यिकीय प्रयोग|तथ्यात्मक प्रयोग|स्वतंत्र घटकों द्वारा डेटा प्रतिनिधित्व|क्रमगुणित कोड}} | ||
{| class="wikitable" style="margin:0 0 0 1em; text-align:right; float:right;" | {| class="wikitable" style="margin:0 0 0 1em; text-align:right; float:right;" | ||
| Line 89: | Line 89: | ||
| [[googol|{{val|e=100}}]] ||10<sup>{{val|e=101.9981097754820}}</sup> | | [[googol|{{val|e=100}}]] ||10<sup>{{val|e=101.9981097754820}}</sup> | ||
|} | |} | ||
गणित में, | गणित में, गैर-ऋणात्मक पूर्णांक {{nowrap| <math>n</math>,}} का भाज्य है तथा {{nowrap| <math>n!</math>,}} द्वारा निरूपित {{nowrap|<math>n</math>.}} से कम या उसके समान सभी धनात्मक पूर्णांकों का गुणनफल है। अगले छोटे क्रमगुणित के साथ {{nowrap|<math>n</math>}} का भाज्य भी <math>n</math> के गुणनफल के समान होता है ) | ||
<math display="block"> | <math display="block"> | ||
\begin{align} | \begin{align} | ||
| Line 97: | Line 97: | ||
उदाहरण के लिए, | उदाहरण के लिए, | ||
<math display=block>5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. </math> | <math display=block>5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. </math> | ||
0 का मान | जहाँ 0 का मान [[खाली उत्पाद]] के लिए सम्मेलन के अनुसार 1 है।<ref name=gkp>{{cite book|first1=Ronald L.|last1=Graham|author1-link=Ronald Graham |first2=Donald E.|last2=Knuth|author2-link=Donald Knuth|first3=Oren|last3=Patashnik|author3-link=Oren Patashnik|date=1988|title=ठोस गणित|publisher=Addison-Wesley|location=Reading, MA|isbn=0-201-14236-8|title-link=ठोस गणित|page=111}}</ref> | ||
क्रमगुणित की खोज कई वर्ष पहले प्राचीन संस्कृतियों में की गई है, जिसे विशेष रूप से भारतीय गणित में जैन साहित्य के विहित कार्यों में, और यहूदी रहस्यवादियों द्वारा तल्मूडिक पुस्तक सेफ़र यत्ज़िराह में उपयोग किया जाता है। क्रमगुणित ऑपरेशन गणित के कई क्षेत्रों में पाया जाता है, विशेष रूप से कॉम्बिनेटरिक्स में, जहां इसका सबसे मूलभूत उपयोग संभावित विशिष्ट अनुक्रमों की गणना करता है। - क्रमपरिवर्तन - <math>n</math> अलग-अलग है जहाँ वस्तुओं के वहां {{nowrap|<math>n!</math>.}} गणितीय विश्लेषण में, क्रमगुणित का उपयोग किया जाता है तथा घातीय फलन और अन्य कार्यों के लिए शक्ति श्रृंखला, और उनके पास बीजगणित, तथा संख्या सिद्धांत, संभाव्यता सिद्धांत और कंप्यूटर विज्ञान में भी अनुप्रयोग हैं। | |||
18वीं सदी के अंत और 19वीं सदी की | 18वीं सदी के अंत तक और 19वीं सदी की प्रारम्भ में क्रमगुणित फलन का अधिकांश गणित कार्य विकसित किया गया था। स्टर्लिंग का सन्निकटन बड़ी संख्या के भाज्य के लिए स्पष्ट सन्निकटन प्रदान करता है, यह दर्शाता है कि यह घातीय वृद्धि की तुलना में यह अधिक तेज़ी से बढ़ता है। लेजेंड्रे का सूत्र भाज्यों के अभाज्य गुणनखंडन में अभाज्य संख्याओं के घातांकों का वर्णन करता है, और इसका उपयोग भाज्यों के अनुगामी शून्यों को गिनने के लिए किया जा सकता है। [[डेनियल बर्नौली]] और [[लियोनहार्ड यूलर]] ने ऋणात्मक पूर्णांक, (ऑफ़सेट) [[गामा समारोह|गामा कार्य]] को छोड़कर, [[सम्मिश्र संख्या]]ओं के निरंतर फलन के लिए क्रमगुणित फलन को किया गया । | ||
स्टर्लिंग का सन्निकटन बड़ी संख्या के भाज्य के लिए | |||
कई अन्य उल्लेखनीय कार्य और संख्या क्रम | कई अन्य उल्लेखनीय कार्य और संख्या क्रम क्रमगुणित से निकटता से संबंधित हैं, जिनमें [[द्विपद गुणांक]], [[डबल क्रमगुणित]], [[क्रमगुणित गिर रहा है]], [[मौलिक]] और [[सबक्रमगुणित]] सम्मिलित हैं। क्रमगुणित फलन के कार्यान्वयन सामान्यतः विभिन्न [[कंप्यूटर प्रोग्रामिंग]] शैलियों के उदाहरण के रूप में उपयोग किए जाते हैं, और वैज्ञानिक कैलकुलेटर और वैज्ञानिक कंप्यूटिंग सॉफ़्टवेयर लाइब्रेरी में सम्मिलित होते हैं। चूंकि उत्पाद सूत्र या पुनरावृत्ति का उपयोग करके सीधे बड़े क्रमगुणित की गणना करना कुशल नहीं है, जबकि तेज एल्गोरिदम ज्ञात हैं, समान संख्या वाले अंकों के लिए तेजी से गुणन एल्गोरिदम के लिए स्थिर कारक के अंदर मिलान करने का समय उपयोग किया जाता है | ||
== इतिहास == | == इतिहास == | ||
तथ्यात्मकता की अवधारणा कई संस्कृतियों में स्वतंत्र रूप से उत्पन्न हुई है: | तथ्यात्मकता की अवधारणा कई संस्कृतियों में स्वतंत्र रूप से उत्पन्न हुई है: | ||
*भारतीय गणित में, क्रमगुणों के सबसे पुराने ज्ञात विवरणों में से | *भारतीय गणित में, क्रमगुणों के सबसे पुराने ज्ञात विवरणों में से अनुयोगद्वार-सूत्र से आता है,<ref name=datta-singh/>जैन साहित्य के विहित कार्यों में से एक, जिसे 300 बीसीई से 400 सीई तक अलग-अलग तिथियां सौंपी गई हैं।<ref>{{cite journal | last = Jadhav | first = Dipak | date = August 2021 | doi = 10.18732/hssa67 | journal = History of Science in South Asia | pages = 209–231 | publisher = University of Alberta Libraries | title = एकता संख्या नहीं होने पर जैन विचार| volume = 9| s2cid = 238656716 }}. See discussion of dating on p. 211.</ref> तथा यह अन्य (मिश्रित) ऑर्डर से वस्तुओं के समुच्चय के सॉर्ट किए गए है और उलटे क्रम को अलग करता है, क्रमगुणित के लिए सामान्य उत्पाद सूत्र से दो घटाकर मिश्रित ऑर्डर की संख्या का मूल्यांकन करता है। क्रमचय के लिए गुणनफल नियम का वर्णन 6वीं शताब्दी के सीई जैन भिक्षु [[जिनभद्र]] ने भी किया था।<ref name=datta-singh>{{cite book | last1 = Datta | first1 = Bibhutibhusan | author1-link = Bibhutibhushan Datta | last2 = Singh | first2 = Awadhesh Narayan | editor1-last = Kolachana | editor1-first = Aditya | editor2-last = Mahesh | editor2-first = K. | editor3-last = Ramasubramanian | editor3-first = K. | contribution = Use of permutations and combinations in India | doi = 10.1007/978-981-13-7326-8_18 | pages = 356–376 | publisher = Springer Singapore | series = Sources and Studies in the History of Mathematics and Physical Sciences | title = भारतीय गणित और खगोल विज्ञान में अध्ययन: कृपा शंकर शुक्ल के चयनित लेख| year = 2019| s2cid = 191141516 }}. Revised by K. S. Shukla from a paper in ''[[Indian Journal of History of Science]]'' 27 (3): 231–249, 1992, {{MR|1189487}}. See p. 363.</ref> जिसे हिंदू विद्वान कम से कम 1150 से तथ्यात्मक सूत्रों का उपयोग कर रहे हैं, जब भास्कर द्वितीय ने अपनी कृति लीलावती में तथ्यात्मक सूत्रों का उल्लेख किया था, तथा इस समस्या के संबंध में कि विष्णु अपनी चार विशिष्ट वस्तुओं ( [[रेखावृत्त]], [[सुदर्शन चक्र]], [[कौमोदकी]] और पवित्र कमल) को कितने तरीकों से धारण कर सकते हैं। धार्मिक कला में) अपने चार हाथों में, और दस हाथ वाले भगवान के लिए समान समस्या है ।<ref>{{Cite journal |last=Biggs |first=Norman L. |author-link=Norman L. Biggs |date=May 1979 |title=कॉम्बिनेटरिक्स की जड़ें|journal=[[Historia Mathematica]] |volume=6 |issue=2 |pages=109–136 |doi=10.1016/0315-0860(79)90074-0 |doi-access=free | mr = 0530622 }}</ref> | ||
*मध्य पूर्व के गणित में, [[तल्मूड]] (200 से 500 ईसवी) से सृजन की हिब्रू रहस्यवादी पुस्तक सेफ़र यतिज़िराह, 7 तक के क्रमगुणों को सूचीबद्ध करती है! [[हिब्रू वर्णमाला]] से बनने वाले शब्दों की संख्या की जांच के हिस्से के रूप | *मध्य पूर्व के गणित में, [[तल्मूड]] (200 से 500 ईसवी) से सृजन की हिब्रू रहस्यवादी पुस्तक सेफ़र यतिज़िराह, 7 तक के क्रमगुणों को सूचीबद्ध करती है! [[हिब्रू वर्णमाला]] से बनने वाले शब्दों की संख्या की जांच के हिस्से के रूप में है ।<ref name=katz>{{cite journal | last = Katz | first = Victor J. | author-link = Victor J. Katz | date = June 1994 | issue = 2 | journal = [[For the Learning of Mathematics]] | jstor = 40248112 | pages = 26–30 | title = कक्षा में नृवंशविज्ञान| volume = 14}}</ref><ref>[https://en.wikisource.org/wiki/Sefer_Yetzirah#CHAPTER_IV Sefer Yetzirah at Wikisource], Chapter IV, Section 4</ref> इसी तरह के कारणों के लिए 8वीं शताब्दी के अरब व्याकरणविद [[अल-खलील इब्न अहमद अल-फ़राहिदी]] द्वारा क्रमगुणित का भी अध्ययन किया गया था।<ref name=katz/>अरब गणितज्ञ [[इब्न अल-हेथम]] (जिसे अल्हज़ेन के नाम से भी जाना जाता है, c.-965 - c.-1040) सबसे पहले विल्सन के प्रमेय को सूत्रबद्ध करने वाले थे, जो भाज्य संख्याओं को [[अभाज्य संख्या]]ओं से जोड़ते थे।<ref>{{cite journal | last = Rashed | first = Roshdi | author-link = Roshdi Rashed | doi = 10.1007/BF00717654 | issue = 4 | journal = [[Archive for History of Exact Sciences]] | language = fr | mr = 595903 | pages = 305–321 | title = इब्न अल-हेथम और विल्सन की प्रमेय| volume = 22 | year = 1980| s2cid = 120885025 }}</ref> | ||
*यूरोप में, चूंकि [[ग्रीक गणित]] में कुछ कॉम्बिनेटरिक्स सम्मिलित | *यूरोप में, चूंकि [[ग्रीक गणित]] में कुछ कॉम्बिनेटरिक्स सम्मिलित थे, और [[प्लेटो]] ने आदर्श समुदाय की आबादी के रूप में प्रसिद्ध रूप से 5040 ( क्रमगुणित) का उपयोग किया था, आंशिक रूप से इसकी विभाज्यता के गुणों के कारण,<ref>{{cite journal | last = Acerbi | first = F. | doi = 10.1007/s00407-003-0067-0 | issue = 6 | journal = [[Archive for History of Exact Sciences]] | jstor = 41134173 | mr = 2004966 | pages = 465–502 | title = हिप्पार्कस के कंधों पर: प्राचीन ग्रीक कॉम्बिनेटरिक्स का पुनर्मूल्यांकन| volume = 57 | year = 2003| s2cid = 122758966 }}</ref> क्रमगुणित के प्राचीन ग्रीक अध्ययन का कोई प्रत्यक्ष प्रमाण नहीं है। इसके बजाय, यूरोप में क्रमगुणित्स पर पहला काम यहूदी विद्वानों द्वारा किया गया था, जैसे कि [[शब्बीथाई डोनोलो]], सेफ़र यतिज़िरह मार्ग की खोज की ।<ref>{{cite book|editor1-last=Wilson|editor1-first=Robin|editor2-last=Watkins|editor2-first=John J.|title=कॉम्बिनेटरिक्स: प्राचीन और आधुनिक|publisher=[[Oxford University Press]]|date=2013|isbn=978-0-19-965659-2|first=Victor J.|last=Katz|author-link=Victor J. Katz|contribution=Chapter 4: Jewish combinatorics|pages=109–121}} See p. 111.</ref> 1677 में, ब्रिटिश लेखक [[फैबियन स्टेडमैन]] [[रिंगिंग बदलें]] को बदलने के लिए क्रमगुणित्स के अनुप्रयोग का वर्णन किया गया है , तथा संगीत कला जिसमें कई ट्यून्ड घंटियों की रिंगिंग सम्मिलित है।<ref>{{cite journal | last = Hunt | first = Katherine | date = May 2018 | doi = 10.1215/10829636-4403136 | issue = 2 | journal = Journal of Medieval and Early Modern Studies | pages = 387–412 | title = परिवर्तन की कला: बेल-रिंगिंग, विपर्यय, और सत्रहवीं शताब्दी इंग्लैंड में संयोजन की संस्कृति| volume = 48| url = https://ueaeprints.uea.ac.uk/id/eprint/83227/1/Accepted_Mnauscript.pdf }}</ref><ref>{{cite book|last=Stedman|first=Fabian|author-link=Fabian Stedman|title=कैम्पेनोलॉजी|year=1677|place=London|pages=6–9}} The publisher is given as "W.S." who may have been William Smith, possibly acting as agent for the [[Ancient Society of College Youths|Society of College Youths]], to which society the "Dedicatory" is addressed.</ref> | ||
15वीं शताब्दी के अंत से, | 15वीं शताब्दी के अंत से, क्रमगुणित पश्चिमी गणितज्ञों द्वारा अध्ययन का विषय बन गया। 1494 के ग्रंथ में, इतालवी गणितज्ञ [[लुका पैसिओली]] ने डाइनिंग टेबल व्यवस्था की समस्या के संबंध में 11 तक क्रमगुणित की गणना की।<ref>{{cite book|editor1-last=Wilson|editor1-first=Robin|editor2-last=Watkins|editor2-first=John J.|title=कॉम्बिनेटरिक्स: प्राचीन और आधुनिक|publisher=[[Oxford University Press]]|date=2013|isbn=978-0-19-965659-2|first=Eberhard|last=Knobloch|author-link=Eberhard Knobloch|contribution=Chapter 5: Renaissance combinatorics|pages=123–145}} See p. 126.</ref> [[क्रिस्टोफर की]] ने [[जोहान्स डी सैक्रोबोस्को]] के काम पर 1603 की टिप्पणी में क्रमगुणित्स पर चर्चा की, और 1640 के दशक में, फ्रांसीसी पोलीमैथ [[समुद्री मर्सेन]] ने क्लैवियस के काम के आधार पर क्रमगुणित्स की बड़ी (किन्तुपूरी तरह से सही नहीं) तालिकाएँ प्रकाशित कीं।{{sfn|Knobloch|2013|pages=130–133}} अपने गुणांकों के लिए क्रमगुणित के पारस्परिक के साथ घातीय कार्य के लिए शक्ति श्रृंखला, पहली बार 1676 में [[आइजैक न्यूटन]] द्वारा [[गॉटफ्रीड विल्हेम लीबनिज]] को पत्र में तैयार की गई थी।<ref name=exponential-series>{{cite book | last1 = Ebbinghaus | first1 = H.-D. | author1-link = Heinz-Dieter Ebbinghaus | last2 = Hermes | first2 = H. | author2-link = Hans Hermes | last3 = Hirzebruch | first3 = F. | author3-link = Friedrich Hirzebruch | last4 = Koecher | first4 = M. | author4-link = Max Koecher | last5 = Mainzer | first5 = K. | author5-link = Klaus Mainzer | last6 = Neukirch | first6 = J. | author6-link = Jürgen Neukirch | last7 = Prestel | first7 = A. | last8 = Remmert | first8 = R. | author8-link = Reinhold Remmert | doi = 10.1007/978-1-4612-1005-4 | isbn = 0-387-97202-1 | mr = 1066206 | page = 131 | publisher = Springer-Verlag | location = New York | series = Graduate Texts in Mathematics | title = नंबर| url = https://books.google.com/books?id=Z53SBwAAQBAJ&pg=PA131 | volume = 123 | year = 1990}}</ref> क्रमगुणित्स पर प्रारंभिक यूरोपीय गणित के अन्य महत्वपूर्ण कार्यों में [[जॉन वालिस]] द्वारा 1685 के ग्रंथ में व्यापक कवरेज सम्मिलित है, बड़े मूल्यों के लिए उनके अनुमानित मूल्यों का अध्ययन 1721 में [[अब्राहम डी मोइवरे]] द्वारा <math>n</math> , [[जेम्स स्टर्लिंग (गणितज्ञ)]] से डी मोइवर को 1729 का पत्र जिसमें कहा गया था कि स्टर्लिंग के सन्निकटन के रूप में जाना जाता है, और यही समय में डैनियल बर्नौली और लियोनहार्ड यूलर द्वारा गामा के लिए क्रमगुणित फलन के निरंतर विस्तार को तैयार करने का कार्य किया <ref>{{cite journal | last = Dutka | first = Jacques | doi = 10.1007/BF00389433 | issue = 3 | journal = [[Archive for History of Exact Sciences]] | jstor = 41133918 | mr = 1171521 | pages = 225–249 | title = क्रमगुणित फ़ंक्शन का प्रारंभिक इतिहास| volume = 43 | year = 1991| s2cid = 122237769 }}</ref> [[एड्रियन मैरी लीजेंड्रे]] ने संख्या सिद्धांत पर 1808 के पाठ में, प्रमुख शक्तियों में क्रमगुणित के [[पूर्णांक गुणनखंडन]] में एक्सपोनेंट्स का वर्णन करते हुए लीजेंड्रे के सूत्र को सम्मिलित किया।<ref>{{cite book|first=Leonard E.|last=Dickson|author-link=Leonard Eugene Dickson|title=संख्या के सिद्धांत का इतिहास|title-link=संख्या के सिद्धांत का इतिहास|volume=1|publisher=Carnegie Institution of Washington|year=1919|contribution=Chapter IX: Divisibility of factorials and multinomial coefficients|pages=263–278|contribution-url=https://archive.org/details/historyoftheoryo01dick/page/262}} See in particular p. 263.</ref> | ||
अंकन <math>n!</math> | अंकन <math>n!</math> क्रमगुणित के लिए 1808 में फ्रांसीसी गणितज्ञ [[क्रिश्चियन क्रैम्प]] द्वारा प्रस्तुत किया गया था।<ref name="cajori" />कई अन्य संकेतन भी उपयोग किए गए हैं। और बाद का अंकन, जिसमें क्रमगुणित का तर्क बॉक्स के बाईं ओर और नीचे की ओर आधा-संलग्न था, जो ब्रिटेन और अमेरिका में कुछ समय के लिए लोकप्रिय था, किन्तु उपयोग से बाहर हो गया था , संभवतः इसलिए कि इसे टाइप करना कठिनाई है।<ref name="cajori">{{cite book | last = Cajori | first = Florian | author-link = Florian Cajori | contribution = 448–449. Factorial "{{mvar|n}}" | contribution-url = https://archive.org/details/AHistoryOfMathematicalNotationVolII/page/n93 | pages = 71–77 | publisher = The Open Court Publishing Company | title = ए हिस्ट्री ऑफ़ मैथेमेटिकल नोटेशन्स, वॉल्यूम II: नोटेशन्स मेनली इन हायर मैथमेटिक्स| title-link = A History of Mathematical Notations | year = 1929}}</ref> जहाँ क्रमगुणित (मूल रूप से फ्रेंच: फैक्टोरिएल) शब्द का पहली बार उपयोग 1800 में लुइस फ्रांकोइस एंटोनी अर्बोगैस्ट द्वारा किया गया था,<ref>{{cite web|url=https://mathshistory.st-andrews.ac.uk/Miller/mathword/f/|title=गणित के कुछ शब्दों (एफ) के सबसे पहले ज्ञात उपयोग|work=[[MacTutor History of Mathematics archive]]|publisher=University of St Andrews|first=Jeff|last=Miller}}</ref> फा डि ब्रूनो के फार्मूले पर पहले काम में,<ref name="craik">{{cite journal | last = Craik | first = Alex D. D. | doi = 10.1080/00029890.2005.11920176 | issue = 2 | journal = [[The American Mathematical Monthly]] | jstor = 30037410 | mr = 2121322 | pages = 119–130 | title = फा डी ब्रूनो के फार्मूले का प्रागितिहास| volume = 112 | year = 2005| s2cid = 45380805 }}</ref> किन्तु [[अंकगणितीय प्रगति]] के उत्पादों की अधिक सामान्य अवधारणा का जिक्र करते हुए। यह नाम जिन कारकों को संदर्भित करता है, वे क्रमगुणित के लिए उत्पाद सूत्र की शर्तें हैं।<ref>{{cite book|title=व्युत्पत्ति गणना|last=Arbogast|first=Louis François Antoine|author-link=Louis François Antoine Arbogast|publisher=L'imprimerie de Levrault, frères|location=Strasbourg|year=1800|pages=364–365|url=https://archive.org/details/ducalculdesdri00arbouoft/page/364|language=fr}}</ref> | ||
== परिभाषा == | == परिभाषा == | ||
किसी धनात्मक पूर्णांक का क्रमगुणन फलन <math>n</math> से अधिक नहीं सभी | किसी धनात्मक पूर्णांक <math>n</math> का क्रमगुणन फलन <math>n</math> से अधिक नहीं सभी धनात्मक पूर्णांकों के उत्पाद द्वारा परिभाषित किया गया है <ref name=gkp/> | ||
<math display="block">n! = 1 \cdot 2 \cdot 3 \cdots (n-2) \cdot (n-1) \cdot n.</math> | <math display="block">n! = 1 \cdot 2 \cdot 3 \cdots (n-2) \cdot (n-1) \cdot n.</math> | ||
इसे अधिक संक्षेप में गुणन या कैपिटल पाई नोटेशन के रूप में लिखा जा सकता है<ref name="gkp" /> | इसे अधिक संक्षेप में गुणन या कैपिटल पाई नोटेशन के रूप में लिखा जा सकता है<ref name="gkp" /> | ||
<math display="block">n! = \prod_{i = 1}^n i.</math> | <math display="block">n! = \prod_{i = 1}^n i.</math> | ||
यदि यह उत्पाद सूत्र अंतिम शब्द को छोड़कर सभी को रखने के लिए बदल दिया जाता है, तो यह उसी रूप के उत्पाद को परिभाषित करेगा, | यदि यह उत्पाद सूत्र में अंतिम शब्द को छोड़कर सभी को रखने के लिए बदल दिया जाता है, तो यह उसी रूप के उत्पाद को परिभाषित करेगा,जिसे छोटे भाज्य के लिए। यह [[पुनरावृत्ति संबंध]] की ओर ले जाता है, जिसके अनुसार क्रमगुणित फलन के प्रत्येक मान को पिछले मान से उसको {{nowrap| <math>n</math>:<ref name=hamkins/>}} से गुणा करके प्राप्त किया जा सकता है | ||
<math display="block"> n! = n\cdot (n-1)!.</math> | <math display="block"> n! = n\cdot (n-1)!.</math> | ||
उदाहरण के लिए, {{nowrap|<math>5! = 5\cdot 4!=5\cdot 24=120</math>.}} | उदाहरण के लिए, {{nowrap|<math>5! = 5\cdot 4!=5\cdot 24=120</math>.}} | ||
| Line 128: | Line 126: | ||
=== शून्य का भाज्य === | === शून्य का भाज्य === | ||
तथ्यात्मक {{nowrap| | तथ्यात्मक {{nowrap|<math>0</math>}} {{nowrap|is <math>1</math>,}} या प्रतीकों में, {{nowrap|<math>0!=1</math>.}} इस परिभाषा के लिए कई प्रेरणाएँ हैं: | ||
* {{nowrap|<math>n=0</math>,}}के लिए <math>n!</math> की परिभाषा <math>n!</math> | * {{nowrap|<math>n=0</math>,}}के लिए <math>n!</math> की परिभाषा <math>n!</math> उत्पाद के रूप में बिना किसी संख्या के उत्पाद सम्मिलित है, और इसलिए व्यापक सम्मेलन का उदाहरण है कि खाली उत्पाद, बिना किसी कारक का उत्पाद गुणक पहचान के समान है।<ref>{{cite book|title=इंजीनियरिंग टेबल्स की सीआरसी हैंडबुक|first=Richard C.|last=Dorf|publisher=CRC Press|year=2003|page=5-5|contribution=Factorials|contribution-url=https://books.google.com/books?id=TCLOBgAAQBAJ&pg=SA5-PA5|isbn=978-0-203-00922-2}}</ref> | ||
*शून्य वस्तुओं का वास्तव में | *शून्य वस्तुओं का वास्तव में क्रमचय है: कुछ भी नहीं करने के लिए,होता है इसमें केवल पुनर्व्यवस्था कुछ भी नहीं करना है।<ref name="hamkins">{{cite book | last = Hamkins | first = Joel David | author-link = Joel David Hamkins | isbn = 978-0-262-53979-1 | location = Cambridge, Massachusetts | mr = 4205951 | page = 50 | publisher = MIT Press | title = सबूत और गणित की कला| url = https://books.google.com/books?id=Ns_tDwAAQBAJ&pg=PA50 | year = 2020}}</ref> | ||
* यह कन्वेंशन कॉम्बिनेटरिक्स में कई पहचानों को उनके मापदंडों के सभी मान्य विकल्पों के लिए मान्य बनाता है। उदाहरण के लिए, सभी को चुनने के | * यह कन्वेंशन कॉम्बिनेटरिक्स में कई पहचानों को उनके मापदंडों के सभी मान्य विकल्पों के लिए मान्य बनाता है। तथा उदाहरण के लिए, सभी को चुनने के विधियों की संख्या <math>n</math> के समुच्चय से तत्व <math>n</math> है <math display=inline>\tbinom{n}{n} = \tfrac{n!}{n!0!} = 1,</math> एक द्विपद गुणांक पहचान है जो केवल इसके {{nowrap| <math>0!=1</math>.<ref>{{cite journal | last1 = Goldenberg | first1 = E. Paul | last2 = Carter | first2 = Cynthia J. | date = October 2017 | doi = 10.5951/mathteacher.111.2.0104 | issue = 2 | journal = [[The Mathematics Teacher]] | jstor = 10.5951/mathteacher.111.2.0104 | pages = 104–110 | title = A student asks about (−5)! | volume = 111}}</ref>}} साथ मान्य होगी | | ||
* साथ {{nowrap|<math>0!=1</math>,}} | * 0 के साथ {{nowrap|<math>0!=1</math>,}} क्रमगुणित के लिए पुनरावृत्ति संबंध {{nowrap|<math>n=1</math>.}} पर वैध रहता है इसलिए, इस परिपाटी के साथ, क्रमगुणित की पुनरावर्ती संगणना में बेस केस ([[प्रत्यावर्तन]]) के रूप में शून्य के लिए केवल मान होना चाहिए, जिससे संगणना को सरल बनाना और अतिरिक्त विशेष स्थितियों की आवश्यकता से बचना।<ref>{{cite conference | last1 = Haberman | first1 = Bruria | last2 = Averbuch | first2 = Haim | editor1-last = Caspersen | editor1-first = Michael E. | editor2-last = Joyce | editor2-first = Daniel T. | editor3-last = Goelman | editor3-first = Don | editor4-last = Utting | editor4-first = Ian | contribution = The case of base cases: Why are they so difficult to recognize? Student difficulties with recursion | doi = 10.1145/544414.544441 | pages = 84–88 | publisher = Association for Computing Machinery | title = कंप्यूटर विज्ञान शिक्षा में नवाचार और प्रौद्योगिकी पर 7वें वार्षिक SIGCSE सम्मेलन की कार्यवाही, ITiCSE 2002, आरहस, डेनमार्क, 24-28 जून, 2002| year = 2002}}</ref> | ||
*स्थापना <math>0!=1</math> कई सूत्रों की कॉम्पैक्ट अभिव्यक्ति की अनुमति देता है, जैसे घातीय कार्य, | *स्थापना <math>0!=1</math> कई सूत्रों की कॉम्पैक्ट अभिव्यक्ति की अनुमति देता है, जैसे घातीय कार्य, शक्ति श्रृंखला के रूप में: {{nowrap|<math display=inline> e^x = \sum_{n = 0}^\infty \frac{x^n}{n!}.</math><ref name=exponential-series/>}} | ||
* यह विकल्प गामा | * यह विकल्प गामा फलन से मेल खाता है {{nowrap|<math>0! = \Gamma(0+1) = 1</math>,}} और गामा फलन का सतत फलन होने के लिए यह मान होना चाहिए।<ref>{{cite book|title=विश्लेषण में हल की गई समस्याएं: गामा, बीटा, लिजेंड्रे और बेसेल कार्यों के लिए लागू|series=Dover Books on Mathematics|first1=Orin J.|last1=Farrell|first2=Bertram|last2=Ross|publisher=Courier Corporation|year=1971|isbn=978-0-486-78308-6|page=10|url=https://books.google.com/books?id=fXPDAgAAQBAJ&pg=PA10}}</ref> | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
क्रमगुणित फलन के प्रारंभिक उपयोगों में गिनत:[[क्रमपरिवर्तन]] सम्मिलित हैं <math>n</math> अलग-अलग वस्तुओं को एक(nन) क्रम में व्यवस्थित करने के <math>n</math>! विभिन्न तरीके हैं।<ref name="ConwayGuy1998">{{Cite book |title=संख्याओं की पुस्तक|last1=Conway |first1=John H. |last2=Guy |first2=Richard |year=1998 |publisher=Springer Science & Business Media |isbn=978-0-387-97993-9 |language=en |author-link=John Horton Conway |author-link2=Richard K. Guy |pages=55–56|contribution=Factorial numbers}}</ref> कॉम्बिनेटरिक्स में कई फ़ार्मुलों में क्रमगुणित अधिक रूप से दिखाई देते हैं, जिनमे वस्तुओं के क्रमों के लिए खाते में होते है । उदाहरण के लिए द्विपद गुणांक <math>\tbinom{n}{k}</math> गिनती करो| {{nowrap|<math>k</math>-element}} संयोजन (के सबसेट {{nowrap|<math>k</math> elements)}} के साथ समुच्चय से {{nowrap|<math>n</math> elements,}} और सूत्र का उपयोग करके क्रमगुणित से गणना की जा सकती है{{sfn|Graham|Knuth|Patashnik|1988|p=156}} | |||
<math display="block">\binom{n}{k}=\frac{n!}{k!(n-k)!}.</math> | |||
प्रथम प्रकार की स्टर्लिंग संख्याएँ भाज्यों का योग करती हैं, और चक्रों की समान संख्या वाले उपसमुच्चय में समूहीकृत {{nowrap|<math>n</math>}} के क्रमपरिवर्तनों की गिनती करती हैं <ref>{{cite book | last = Riordan | first = John | author-link = John Riordan (mathematician) | mr = 0096594 | page = 76 | publisher = Chapman & Hall | series = Wiley Publications in Mathematical Statistics | title = कॉम्बिनेटरियल एनालिसिस का परिचय| url = https://books.google.com/books?id=Sbb_AwAAQBAJ&pg=PA76 | year = 1958| isbn = 9781400854332 }}</ref> अन्य संयोजी अनुप्रयोग अपंगताओं की गिनती में है, क्रमपरिवर्तन जो किसी भी तत्व को उसकी मूल स्थिति में नहीं छोड़ते हैं; <math>n</math> की अव्यवस्थाओं की संख्या {{nowrap|<math>n!/e</math>.}} आइटम [[गोलाई]] है| | |||
बीजगणित में, क्रमगुणित्स [[द्विपद प्रमेय]] के माध्यम से उत्पन्न होते हैं, जो राशियों की शक्तियों का विस्तार करने के लिए द्विपद गुणांक का उपयोग करता है।{{sfn|Graham|Knuth|Patashnik|1988|p=162}} वे बहुपदों के कुछ परिवारों को दूसरे से संबंधित करने के लिए उपयोग किए जाने वाले गुणांकों में भी होते हैं, उदाहरण के लिए [[सममित बहुपद]] के लिए न्यूटन की पहचान में है ।<ref>{{cite journal | last = Randić | first = Milan | doi = 10.1007/BF01205340 | issue = 1 | journal = Journal of Mathematical Chemistry | mr = 895533 | pages = 145–152 | title = सममित कार्य सिद्धांत के माध्यम से विशेषता बहुपद के मूल्यांकन पर| volume = 1 | year = 1987| s2cid = 121752631 }}</ref> क्रमपरिवर्तन की गणना में उनका उपयोग बीजगणितीय रूप से भी बहाल किया जा सकता है:और भाज्य परिमित [[सममित समूह]] के समूह का क्रम है।<ref>{{cite book|title=समूह और वर्ण|first=Victor E.|last=Hill|publisher=Chapman & Hall|year=2000|mr=1739394|isbn=978-1-351-44381-4|page=70|contribution=8.1 Proposition: Symmetric group {{math|''S''<sub>''n''</sub>}}|contribution-url=https://books.google.com/books?id=yjL3DwAAQBAJ&pg=PA70}}</ref> तथा कलन में, उच्च डेरिवेटिव की श्रृंखला के लिए फै डी ब्रूनो के सूत्र में क्रमगुणित होते हैं।<ref name="craik" />गणितीय विश्लेषण में, क्रमगुणित अधिकांशतः शक्ति श्रृंखला के denominators विशेष रूप से घातीय कार्य के लिए श्रृंखला में दिखाई देते हैं| <ref name="exponential-series" /> <math display="block">e^x=1+\frac{x}{1}+\frac{x^2}{2}+\frac{x^3}{6}+\cdots=\sum_{i=0}^{\infty}\frac{x^i}{i!},</math> | |||
और अन्य [[टेलर श्रृंखला]] के गुणांकों में (विशेष रूप से [[त्रिकोणमितीय कार्य]] और [[अतिशयोक्तिपूर्ण कार्य]] के), जहां वे ''<math>n!</math>'' कारकों को रद्द करते हैं {{nowrap|<math>x^n</math>.<ref>{{cite book|title=Complexity and Criticality|series=Advanced physics texts|volume=1|first1=Kim|last1=Christensen|first2=Nicholas R.|last2=Moloney|publisher=Imperial College Press|year=2005|isbn=978-1-86094-504-5|contribution=Appendix A: Taylor expansion|page=341|contribution-url=https://books.google.com/books?id=bAIM1_EoQu0C&pg=PA341}}</ref>}} के {{nowrap|<math>n</math>}} वें व्युत्पन्न से आ रहा है| पावर श्रृंखला में क्रमगुणित्स का यह उपयोग [[विश्लेषणात्मक संयोजन|वि]][[घातीय जनरेटिंग फ़ंक्शन|फ़ंक्शन]][[विश्लेषणात्मक संयोजन|षणात्मक संयोजन]] को [[घातीय जनरेटिंग फ़ंक्शन|घातीय जनरेटिंग फलन]] के माध्यम से जोड़ता है, जो आकार {{nowrap| <math>i</math>}} के <math>n_i</math> तत्वों के साथ एक कॉम्बिनेटर क्लास के लिए पावर श्रृंखला के रूप में परिभाषित किया गया है <math display="block">\sum_{i=0}^{\infty} \frac{x^i n_i}{i!}.</math> | |||
संख्या सिद्धांत में, क्रमगुणित की सबसे प्रमुख संपत्ति <math>n!</math> की विभाज्यता है {{nowrap| <math>n</math>,}}सभी धनात्मक पूर्णांकों द्वारा ऊपर लीजेंड्रे के सूत्र द्वारा प्रमुख कारकों के लिए अधिक स्पष्ट रूप से वर्णित होता है । यह इस प्रकार है कि इच्छानुसार से बड़ी अभाज्य संख्याएँ <math>n!\pm 1</math> संख्याओं के प्रमुख गुणनखंडों के रूप में पाई जा सकती हैं , यूक्लिड के प्रमेय के प्रमाण के लिए अग्रणी है कि अभाज्य संख्याओं की संख्या अनंत है।<ref>{{cite book | last = Ore | first = Øystein | author-link = Øystein Ore | location = New York | mr = 0026059 | page = 66 | publisher = McGraw-Hill | title = संख्या सिद्धांत और इसका इतिहास| url = https://books.google.com/books?id=Sl_6BPp7S0AC&pg=PA66 | year = 1948| isbn = 9780486656205 }}</ref> जब <math>n!\pm 1</math> स्वयं प्रधान है, इसे भाज्य अभाज्य कहा जाता है;<ref name="caldwell-gallot">{{cite journal | last1 = Caldwell | first1 = Chris K. | last2 = Gallot | first2 = Yves | doi = 10.1090/S0025-5718-01-01315-1 | issue = 237 | journal = [[Mathematics of Computation]] | mr = 1863013 | pages = 441–448 | title = <math>n!\pm1</math> और <math>2\times3\times5\times\dots\times p\pm1</math> की प्राथमिकता पर| volume = 71 | year = 2002}}</ref> संबंधित, ब्रोकार्ड की समस्या, जिसे [[श्रीनिवास रामानुजन]] ने भी प्रस्तुत किया है, प्रपत्र की [[वर्ग संख्या]]ओं के अस्तित्व से संबंधित है {{nowrap|<math>n!+1</math>.<ref>{{cite book | last = Guy | first = Richard K. | author-link = Richard K. Guy | contribution = D25: Equations involving factorial <math>n</math> | doi = 10.1007/978-0-387-26677-0 | edition = 3rd | isbn = 0-387-20860-7 | mr = 2076335 | pages = 301–302 | publisher = Springer-Verlag | location = New York | series = Problem Books in Mathematics | title = Unsolved Problems in Number Theory | year = 2004| volume = 1 }}</ref>}} इसके विपरीत, इच्छानुसार से बड़े [[प्रमुख अंतर]] के अस्तित्व को सिद्ध करते हुए सभी संख्याएँ <math>n!+2,n!+3,\dots n!+n</math> को समग्र होना चाहिए।<ref>{{cite book|title=गैप को बंद करना: अभाज्य संख्याओं को समझने की खोज|first=Vicky|last=Neale|author-link=Vicky Neale|publisher=Oxford University Press|year=2017|isbn=978-0-19-878828-7|pages=146–147|url=https://books.google.com/books?id=T7Q1DwAAQBAJ&pg=PA146}}</ref> {{nowrap| <math>[n,2n]</math>,}} के किसी भी अंतराल में प्राइम के अस्तित्व पर बर्ट्रेंड के अभिधारणा का प्राथमिक प्रमाण , पॉल एर्डोस के पहले परिणामों में से एक, क्रमगुणित के विभाज्यता गुणों पर आधारित था।<ref>{{cite journal | last = Erdős | first = Pál | author-link = Paul Erdős | journal = Acta Litt. Sci. Szeged | language = de | pages = 194–198 | title = चेबीशेव द्वारा एक प्रमेय का प्रमाण| trans-title = Proof of a theorem of Chebyshev | url = https://users.renyi.hu/~p_erdos/1932-01.pdf | volume = 5 | year = 1932 | zbl = 0004.10103}}</ref><ref>{{cite book | last = Chvátal | first = Vašek | author-link = Václav Chvátal | contribution = 1.5: Erdős's proof of Bertrand's postulate | contribution-url = https://books.google.com/books?id=_gVDEAAAQBAJ&pg=PA7 | doi = 10.1017/9781108912181 | isbn = 978-1-108-83183-3 | mr = 4282416 | pages = 7–10 | publisher = Cambridge University Press | location = Cambridge, England | title = पॉल एर्डोस का असतत गणितीय आकर्षण: एक सरल परिचय| year = 2021| s2cid = 242637862 }}</ref> [[भाज्य संख्या प्रणाली]] संख्याओं के लिए [[मिश्रित मूलांक]] संकेतन है जिसमें प्रत्येक अंक के स्थान मान भाज्य होते हैं।<ref>{{cite journal | last = Fraenkel | first = Aviezri S. | author-link = Aviezri Fraenkel | doi = 10.1080/00029890.1985.11971550 | issue = 2 | journal = [[The American Mathematical Monthly]] | jstor = 2322638 | mr = 777556 | pages = 105–114 | title = संख्या प्रणाली| volume = 92 | year = 1985}}</ref> | |||
संभाव्यता सिद्धांत में क्रमगुणित का व्यापक रूप से उपयोग किया जाता है, उदाहरण के लिए [[पॉसों वितरण]] में<ref>{{cite book | last = Pitman | first = Jim | contribution = 3.5: The Poisson distribution | doi = 10.1007/978-1-4612-4374-8 | pages = 222–236 | publisher = Springer | location = New York | title = संभावना| year = 1993| isbn = 978-0-387-94594-1 }}</ref> और [[यादृच्छिक क्रमपरिवर्तन]] की संभावनाओं में है ।{{sfn|Pitman|1993|p=153}} कंप्यूटर विज्ञान में, क्रमपरिवर्तन पर ब्रूट-फोर्स खोजों के विश्लेषण से परे है ,<ref>{{cite book|title=एल्गोरिथम डिजाइन|first1=Jon|last1=Kleinberg|author1-link=Jon Kleinberg|first2=Éva|last2=Tardos|author2-link=Éva Tardos|publisher=Addison-Wesley|year=2006|page=55}}</ref> <math>\log_2 n!=n\log_2n-O(n)</math> की निचली सीमा में भाज्य उत्पन्न होते हैं तुलना के समुच्चय को सॉर्ट करने के लिए आवश्यक तुलनाओं की संख्या पर <math>n</math> सामान,<ref name="knuth-sorting" />और श्रृंखलित [[हैश तालिका]]ओं के विश्लेषण में, जहां प्रति सेल चाबियों के वितरण को प्वासों वितरण द्वारा स्पष्ट रूप से अनुमानित किया जा सकता है।<ref>{{cite book|title=एल्गोरिदम|edition=4th|publisher=Addison-Wesley|first1=Robert|last1=Sedgewick|author1-link=Robert Sedgewick (computer scientist)|first2=Kevin|last2=Wayne|year=2011|isbn=978-0-13-276256-4|page=466|url=https://books.google.com/books?id=idUdqdDXqnAC&pg=PA466}}</ref> इसके अतिरिक्त, क्रमगुणित स्वाभाविक रूप से [[क्वांटम यांत्रिकी]] और [[सांख्यिकीय भौतिकी]] के सूत्रों में दिखाई देते हैं, जहां अधिकांशतः कणों के समुच्चय के सभी संभावित क्रमपरिवर्तनों पर विचार किया जाता है। [[सांख्यिकीय यांत्रिकी]] में, [[एन्ट्रापी]] की गणना जैसे कि बोल्ट्जमैन का एंट्रॉपी फॉर्मूला या सैकुर-टेट्रोड समीकरण को [[गिब्स विरोधाभास]] से बचने के लिए प्रत्येक प्रकार के [[समान कण]] की संख्या के भाज्य द्वारा विभाजित करके [[माइक्रोस्टेट (सांख्यिकीय यांत्रिकी)]] की गिनती को सही करना चाहिए। क्वांटम भौतिकी अंतर्निहित कारण प्रदान करती है कि ये सुधार क्यों आवश्यक हैं।<ref>{{cite book|first=Mehran |last=Kardar |author-link=Mehran Kardar |title=कणों का सांख्यिकीय भौतिकी|title-link=कणों का सांख्यिकीय भौतिकी|year=2007 |publisher=[[Cambridge University Press]] |isbn=978-0-521-87342-0 |oclc=860391091 |pages=107–110, 181–184}}</ref> | |||
संभाव्यता सिद्धांत में क्रमगुणित का व्यापक रूप से उपयोग किया जाता है, उदाहरण के लिए [[पॉसों वितरण]] में<ref>{{cite book | last = Pitman | first = Jim | contribution = 3.5: The Poisson distribution | doi = 10.1007/978-1-4612-4374-8 | pages = 222–236 | publisher = Springer | location = New York | title = संभावना| year = 1993| isbn = 978-0-387-94594-1 }}</ref> और [[यादृच्छिक क्रमपरिवर्तन]] की संभावनाओं | |||
| Line 152: | Line 156: | ||
[[File:Mplwp factorial stirling loglog2.svg|thumb|भाज्य की तुलना, स्टर्लिंग का सन्निकटन और सरल सन्निकटन {{nowrap|<math>(n/e)^n</math>,}} दोहरे लघुगणकीय पैमाने पर]] | [[File:Mplwp factorial stirling loglog2.svg|thumb|भाज्य की तुलना, स्टर्लिंग का सन्निकटन और सरल सन्निकटन {{nowrap|<math>(n/e)^n</math>,}} दोहरे लघुगणकीय पैमाने पर]] | ||
[[File:Stirling series relative error.svg|thumb|upright=1.6|छोटी स्टर्लिंग श्रृंखला बनाम शब्दों की संख्या में सापेक्ष त्रुटि]] | [[File:Stirling series relative error.svg|thumb|upright=1.6|छोटी स्टर्लिंग श्रृंखला बनाम शब्दों की संख्या में सापेक्ष त्रुटि]] | ||
{{main| | {{main|स्टर्लिंग का अनुमान}} | ||
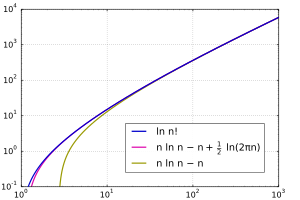
<math display=block>\ln n! = \sum_{x=1}^n \ln x \approx \int_1^n\ln x\, dx=n\ln n-n+1.</math> | {{nowrap|<math>n</math>,}} कार्य के रूप में क्रमगुणित में एक्सपोनेंशियल ग्रोथ की तुलना में तेज है, किन्तु [[दोहरा घातीय कार्य]] की तुलना में धीरे-धीरे बढ़ता है।<ref>{{cite book | last = Cameron | first = Peter J. | author-link = Peter Cameron (mathematician) | contribution = 2.4: Orders of magnitude | isbn = 978-0-521-45133-8 | pages = 12–14 | publisher = Cambridge University Press | title = कॉम्बिनेटरिक्स: विषय, तकनीक, एल्गोरिदम| year = 1994}}</ref> इसकी विकास {{nowrap| <math>n^n</math>,}} दर समान है किन्तु एक घातीय कारक द्वारा धीमा है। इस परिणाम तक पहुँचने का विधि क्रमगुणित का [[प्राकृतिक]] लघुगणक लेना है, जो इसके उत्पाद सूत्र को योग में बदल देता है, और फिर अभिन्न द्वारा योग का अनुमान लगाता है: | ||
परिणाम को एक्सपोनेंट करना (और नगण्य | <math display="block">\ln n! = \sum_{x=1}^n \ln x \approx \int_1^n\ln x\, dx=n\ln n-n+1.</math> | ||
ट्रैपेज़ॉइड नियम का उपयोग करते हुए, अधिक ध्यान से ऊपर और नीचे दोनों को | |||
<math display=block>n!\sim\sqrt{2\pi n}\left(\frac{n}{e}\right)^n\,.</math> | परिणाम को एक्सपोनेंट करना (और नगण्य <math>+1</math> को अनदेखा करना टर्म) <math>n!</math> अनुमानित है जैसा {{nowrap|<math>(n/e)^n</math>.<ref>{{cite book | last = Magnus | first = Robert | contribution = 11.10: Stirling's approximation | contribution-url = https://books.google.com/books?id=5hvxDwAAQBAJ&pg=PA391 | doi = 10.1007/978-3-030-46321-2 | isbn = 978-3-030-46321-2 | location = Cham | mr = 4178171 | page = 391 | publisher = Springer | series = Springer Undergraduate Mathematics Series | title = Fundamental Mathematical Analysis | year = 2020| s2cid = 226465639 }}</ref>}} ट्रैपेज़ॉइड नियम का उपयोग करते हुए, अधिक ध्यान से ऊपर और नीचे दोनों को इंटीग्रल से जोड़ना, यह दर्शाता है कि इस अनुमान {{nowrap| <math>\sqrt n</math>.}} के लिए आनुपातिक सुधार कारक की आवश्यकता है {{nowrap| <math>\sqrt n</math>.}} इस सुधार के लिए आनुपातिकता का स्थिरांक वालिस उत्पाद से पाया जा सकता है, जो <math>\pi</math> क्रमगुणित और दो की शक्तियों के सीमित अनुपात के रूप में व्यक्त करता है । इन सुधारों का परिणाम स्टर्लिंग का सन्निकटन है:<ref>{{cite book | last = Palmer | first = Edgar M. | contribution = Appendix II: Stirling's formula | isbn = 0-471-81577-2 | location = Chichester | mr = 795795 | pages = 127–128 | publisher = John Wiley & Sons | series = Wiley-Interscience Series in Discrete Mathematics | title = ग्राफिकल इवोल्यूशन: रैंडम ग्राफ के सिद्धांत का परिचय| year = 1985}}</ref> | ||
यहां ही <math>\sim</math> प्रतीक का अर्थ है कि, जैसा <math>n</math> अनंत तक जाता है, बाएँ और दाएँ पक्षों के बीच का अनुपात [[सीमा (गणित)]] में | <math display="block">n!\sim\sqrt{2\pi n}\left(\frac{n}{e}\right)^n\,.</math> | ||
स्टर्लिंग का सूत्र | |||
<math display=block> | यहां ही <math>\sim</math> प्रतीक का अर्थ है कि, जैसा <math>n</math> अनंत तक जाता है, बाएँ और दाएँ पक्षों के बीच का अनुपात [[सीमा (गणित)]] में के करीब पहुँचता है। स्टर्लिंग का सूत्र [[स्पर्शोन्मुख श्रृंखला]] में पहला शब्द प्रदान करता है जो अधिक संख्या में पदों पर ले जाने पर और भी स्पष्ट हो जाता है:<ref name="asymptotic">{{cite journal | last1 = Chen | first1 = Chao-Ping | last2 = Lin | first2 = Long | doi = 10.1016/j.aml.2012.06.025 | issue = 12 | journal = Applied Mathematics Letters | mr = 2967837 | pages = 2322–2326 | title = गामा फ़ंक्शन के लिए स्पर्शोन्मुख विस्तार पर टिप्पणी| volume = 25 | year = 2012}}</ref> | ||
<math display="block"> | |||
n! \sim \sqrt{2\pi n}\left(\frac{n}{e}\right)^n \left(1 +\frac{1}{12n}+\frac{1}{288n^2} - \frac{139}{51840n^3} -\frac{571}{2488320n^4}+ \cdots \right).</math> | n! \sim \sqrt{2\pi n}\left(\frac{n}{e}\right)^n \left(1 +\frac{1}{12n}+\frac{1}{288n^2} - \frac{139}{51840n^3} -\frac{571}{2488320n^4}+ \cdots \right).</math> | ||
वैकल्पिक संस्करण सुधार शर्तों में केवल विषम घातांक का उपयोग करता है:<ref name=asymptotic/> | वैकल्पिक संस्करण सुधार शर्तों में केवल विषम घातांक का उपयोग करता है:<ref name=asymptotic/> | ||
| Line 167: | Line 172: | ||
श्रीनिवास रामानुजन, [[बिल गोस्पर]] और अन्य लोगों द्वारा इन सूत्रों के कई अन्य रूपों को भी विकसित किया गया है।<ref name=asymptotic/> | श्रीनिवास रामानुजन, [[बिल गोस्पर]] और अन्य लोगों द्वारा इन सूत्रों के कई अन्य रूपों को भी विकसित किया गया है।<ref name=asymptotic/> | ||
तुलना छँटाई का विश्लेषण करने के लिए उपयोग किए जाने वाले | तुलना छँटाई का विश्लेषण करने के लिए उपयोग किए जाने वाले क्रमगुणित के [[द्विआधारी लघुगणक]] का स्टर्लिंग के सन्निकटन का उपयोग करके बहुत स्पष्ट अनुमान लगाया जा सकता है। नीचे दिए गए सूत्र में <math>O(1)</math> टर्म [[बिग ओ नोटेशन]] को आमंत्रित करता है।<ref name=knuth-sorting>{{cite book|title=कंप्यूटर प्रोग्रामिंग की कला, खंड 3: छँटाई और खोज|first=Donald E.|last=Knuth|author-link=Donald Knuth|edition=2nd|publisher=Addison-Wesley|year=1998|isbn=978-0-321-63578-5|page=182|url=https://books.google.com/books?id=cYULBAAAQBAJ&pg=PA182}}</ref> | ||
<math display=block>\log_2 n! = n\log_2 n-(\log_2 e)n + \frac12\log_2 n + O(1).</math> | |||
<math display="block">\log_2 n! = n\log_2 n-(\log_2 e)n + \frac12\log_2 n + O(1).</math> | |||
=== विभाज्यता और अंक === | === विभाज्यता और अंक === | ||
{{main| | {{main|लीजेंड्रे का सूत्र}} | ||
क्रमगुणित के लिए उत्पाद सूत्र का तात्पर्य है <math>n!</math> पर होने वाली सभी अ[[भाज्य]] {{nowrap|<math>n</math>,}}संख्याओं से विभाज्य है और कोई बड़ी अभाज्य संख्या नहीं।<ref name=beiler>{{cite book|title=संख्या के सिद्धांत में मनोरंजन: गणित की रानी मनोरंजन करती है|series=Dover Recreational Math Series|first=Albert H.|last=Beiler|publisher=Courier Corporation|year=1966|edition=2nd|isbn=978-0-486-21096-4|page=49|url=https://books.google.com/books?id=NbbbL9gMJ88C&pg=PA49}}</ref> इसकी विभाज्यता के बारे में अधिक स्पष्ट जानकारी लीजेंड्रे के सूत्र द्वारा दी गई है, जो <math>n!</math> के प्रधान गुणनखंड में प्रत्येक अभाज्य <math>p</math> का प्रतिपादक देता है <ref>{{harvnb|Chvátal|2021}}. "1.4: Legendre's formula". pp. 6–7.</ref><ref name="padic">{{cite book | last = Robert | first = Alain M. | author-link = Alain M. Robert | contribution = 3.1: The {{nowrap|<math>p</math>-adic}} valuation of a factorial | doi = 10.1007/978-1-4757-3254-2 | isbn = 0-387-98669-3 | mr = 1760253 | pages = 241–242 | publisher = Springer-Verlag | location = New York | series = [[Graduate Texts in Mathematics]] | title = {{nowrap|<math>p</math>-adic}} Analysis | volume = 198 | year = 2000}}</ref> | |||
<math display=block>\sum_{i=1}^\infty \left \lfloor \frac n {p^i} \right \rfloor=\frac{n - s_p(n)}{p - 1}.</math> | <math display="block">\sum_{i=1}^\infty \left \lfloor \frac n {p^i} \right \rfloor=\frac{n - s_p(n)}{p - 1}.</math> | ||
यहां <math>s_p(n)</math> | |||
यहां <math>s_p(n)</math>, {{nowrap|<math>n</math>,}} के आधार {{nowrap|<math>p</math>}} अंक योग को दर्शाता है और इस सूत्र द्वारा दिए गए प्रतिपादक की व्याख्या उन्नत गणित में {{nowrap|<math>p</math>}}-adic वैल्यूएशन के रूप में भी की जा सकती है भाज्य का मूल्यांकन।<ref name="padic" /> द्विपद गुणांकों के उत्पाद सूत्र के लिए लीजेंड्रे के सूत्र को प्रयुक्त करने से कम्मर प्रमेय उत्पन्न होता है, द्विपद गुणांक के गुणनखंड में प्रत्येक अभाज्य के घातांक पर समान परिणाम।<ref>{{cite book | last1 = Peitgen | author1-link=Heinz-Otto Peitgen | first1 = Heinz-Otto | last2 = Jürgens | first2 = Hartmut | author2-link = Hartmut Jürgens | last3 = Saupe | first3 = Dietmar | author3-link = Dietmar Saupe | contribution = Kummer's result and Legendre's identity | doi = 10.1007/b97624 | location = New York | pages = 399–400 | publisher = Springer | title = कैओस एंड फ्रैक्टल्स: न्यू फ्रंटियर्स ऑफ साइंस| year = 2004| isbn=978-1-4684-9396-2 }}</ref> क्रमगुणित के प्रमुख कारकों को अलग-अलग तरीकों से प्रमुख शक्तियों में समूहीकृत करने से [[क्रमगुणित के गुणक विभाजन]] उत्पन्न होते हैं।<ref>{{Cite journal|last1=Alladi|first1=Krishnaswami|last2=Grinstead|first2=Charles|authorlink1=Krishnaswami Alladi |title=N के अपघटन पर! प्रमुख शक्तियों में|url=http://linkinghub.elsevier.com/retrieve/pii/0022314X77900063|journal=[[Journal of Number Theory]]|year=1977 |language=en|volume=9|issue=4|pages=452–458|doi=10.1016/0022-314x(77)90006-3}}</ref> | |||
<math>p=5</math> लीजेंड्रे के फार्मूले का विशेष स्थितिया भाज्य के दशमलव निरूपण में अनुगामी शून्य या क्रमगुणित की संख्या देता है।<ref name="koshy" /> इस सूत्र के अनुसार के <math>n</math> से <math>n</math> आधार-5 अंकों को घटाकर शून्यों की संख्या प्राप्त की जा सकती है और परिणाम को चार से विभाजित करना।<ref>{{cite OEIS|A027868|Number of trailing zeros in n!; highest power of 5 dividing n!}}</ref> लीजेंड्रे के सूत्र का अर्थ है कि अभाज्य का प्रतिपादक <math>p=2</math> के घातांक से {{nowrap|<math>p=5</math>,}} सदैव बड़ा होता है {{nowrap|<math>p=5</math>,}} इसलिए इन अनुगामी शून्यों में से इस का उत्पादन करने के लिए पांच के प्रत्येक कारक को दो '''के''' कारक के साथ जोड़ा जा सकता है।<ref name="koshy">{{cite book|title=प्राथमिक संख्या सिद्धांत अनुप्रयोगों के साथ|first=Thomas|last=Koshy|edition=2nd|publisher=Elsevier|year=2007|isbn=978-0-08-054709-1|contribution=Example 3.12|page=178|contribution-url=https://books.google.com/books?id=d5Z5I3gnFh0C&pg=PA178}}</ref> क्रमगुणित के प्रमुख अंक बेनफोर्ड के नियम के अनुसार वितरित किए जाते हैं।<ref>{{cite journal | last = Diaconis | first = Persi | author-link = Persi Diaconis | doi = 10.1214/aop/1176995891 | issue = 1 | journal = [[Annals of Probability]] | mr = 422186 | pages = 72–81 | title = प्रमुख अंकों का वितरण और समान वितरण मोड 1| volume = 5 | year = 1977}}</ref> अंकों का प्रत्येक अनुक्रम, किसी भी आधार में, उस आधार में किसी भाज्य संख्या के आरंभिक अंकों का क्रम होता है।<ref>{{cite journal|last=Bird|first=R. S.|author-link=Richard Bird (computer scientist)|doi=10.1080/00029890.1972.11993051|journal=[[The American Mathematical Monthly]]|jstor=2978087|mr=302553|pages=367–370|title=दिए गए आरंभिक अंकों के साथ पूर्णांक|volume=79|year=1972|issue=4}}</ref> | |||
क्रमगुणित्स की विभाज्यता पर और परिणाम, विल्सन के प्रमेय में कहा गया है कि <math>(n-1)!+1</math>, <math>n</math> से विभाज्य है यदि और केवल यदि <math>n</math> अभाज्य संख्या है।<ref name="beiler" /> किसी दिए गए के लिए {{nowrap|integer <math>x</math>,}} [[केम्पनर समारोह|केम्पनर कार्य]] कार्य <math>x</math> सबसे छोटा <math>n</math> दिया जाता है <math>n</math> जिसके लिए <math>x</math> {{nowrap|<math>n!</math>.}}विभाजित करता है तथा लगभग सभी संख्याओं के लिए (शून्य [[स्पर्शोन्मुख घनत्व]] वाले अपवादों के उपसमुच्चय को छोड़कर), यह सबसे बड़े अभाज्य गुणक {{nowrap|<math>x</math>.}} के साथ मेल खाता है | |||
दो क्रमगुणित का उत्पाद, {{nowrap|<math>m!\cdot n!</math>,}} सदैव {{nowrap|<math>(m+n)!</math>.}} समान रूप से विभाजित करता है असीम रूप से कई क्रमगुणित हैं जो अन्य क्रमगुणित के उत्पाद के समान हैं: यदि <math>n</math> तब स्वयं क्रमगुणित का कोई उत्पाद है <math>n!</math> उसी उत्पाद को और भाज्य से गुणा करने के समान है, {{nowrap|<math>(n-1)!</math>.}} क्रमगुणित के एकमात्र ज्ञात उदाहरण जो अन्य क्रमगुणित के उत्पाद हैं किन्तु इस तुच्छ रूप के नहीं हैं {{nowrap|<math>9!=7!\cdot 3!\cdot 3!\cdot 2!</math>,}} {{nowrap|<math>10!=7!\cdot 6!=7!\cdot 5!\cdot 3!</math>,}} और {{nowrap|<math>16!=14!\cdot 5!\cdot 2!</math>.<ref>{{harvnb|Guy|2004}}. "B23: Equal products of factorials". p. 123.</ref>}} यह एबीसी अनुमान से अनुसरण करेगा {{mvar|abc}} अनुमान है कि केवल बहुत से गैर-तुच्छ उदाहरण हैं।<ref>{{cite journal | last = Luca | first = Florian | author-link = Florian Luca | doi = 10.1017/S0305004107000308 | issue = 3 | journal = [[Mathematical Proceedings of the Cambridge Philosophical Society]] | mr = 2373957 | pages = 533–542 | title = क्रमगुणित पर जो क्रमगुणित के उत्पाद हैं| volume = 143 | year = 2007| bibcode = 2007MPCPS.143..533L | s2cid = 120875316 }}</ref> | |||
आदिम भाग और डिग्री की सामग्री के मूल्यों का सबसे बड़ा सामान्य विभाजक <math>d</math> पूर्णांकों पर समान रूप से {{nowrap|<math>d!</math>.}} विभाजित होता है | |||
The product of two factorials, {{nowrap|<math>m!\cdot n!</math>,}} always evenly divides {{nowrap|<math>(m+n)!</math>.<ref name=bhargava/>}} There are infinitely many factorials that equal the product of other factorials: if <math>n</math> is itself any product of factorials, then <math>n!</math> equals that same product multiplied by one more factorial, {{nowrap|<math>(n-1)!</math>.}} The only known examples of factorials that are products of other factorials but are not of this "trivial" form are {{nowrap|<math>9!=7!\cdot 3!\cdot 3!\cdot 2!</math>,}} {{nowrap|<math>10!=7!\cdot 6!=7!\cdot 5!\cdot 3!</math>,}} and {{nowrap|<math>16!=14!\cdot 5!\cdot 2!</math>.<ref>{{harvnb|Guy|2004}}. "B23: Equal products of factorials". p. 123.</ref>}} It would follow from the [[abc conjecture|{{mvar|abc}} conjecture]] that there are only finitely many nontrivial examples.<ref>{{cite journal | last = Luca | first = Florian | author-link = Florian Luca | doi = 10.1017/S0305004107000308 | issue = 3 | journal = [[Mathematical Proceedings of the Cambridge Philosophical Society]] | mr = 2373957 | pages = 533–542 | title = On factorials which are products of factorials | volume = 143 | year = 2007| bibcode = 2007MPCPS.143..533L | s2cid = 120875316 }}</ref> | |||
The [[greatest common divisor]] of the values of a [[Primitive part and content|primitive polynomial]] of degree <math>d</math> over the integers evenly divides {{nowrap|<math>d!</math>.<ref name=bhargava>{{cite journal | last = Bhargava | first = Manjul | author-link = Manjul Bhargava | url = https://www.maa.org/programs/maa-awards/writing-awards/the-factorial-function-and-generalizations | title = The factorial function and generalizations | journal = [[The American Mathematical Monthly]] | volume = 107 | year = 2000 | pages = 783–799 | doi = 10.2307/2695734 | issue = 9 | jstor = 2695734 | citeseerx = 10.1.1.585.2265 | |||
}}</ref>}} | }}</ref>}} | ||
=== सतत | |||
[[File:Generalized factorial function more infos.svg|thumb|upright=1.6|गामा | |||
[[File:Gamma abs 3D.png|thumb|गैर- | |||
{{Main| | |||
=== सतत इंटरपोलेशनफ़ंक्शनगैर-पूर्णांक सामान्यीकरण === | |||
[[File:Generalized factorial function more infos.svg|thumb|upright=1.6|गामा फलन (फ़ैक्टोरियल्स से मिलान करने के लिए इकाई को छोड़ दिया गया है) क्रमगुणित को गैर-पूर्णांक मानों में निरंतर प्रक्षेपित करता है]] | |||
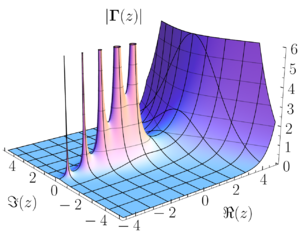
[[File:Gamma abs 3D.png|thumb|गैर-धनात्मक पूर्णांकों फलन ध्रुवों को दिखाते हुए, सम्मिश्र गामा फलन के निरपेक्ष मान]] | |||
{{Main|गामा फलन }} | |||
क्रमगुणित को निरंतर कार्य करने के लिए असीमित रूप से कई तरीके हैं।<ref name=davis/> इनमें से सबसे अधिक व्फ़ंक्शन रूप से उपयोग किया जाता है<ref name=borwein-corless/> गामा फलन का उपयोग करता है, जिसे [[अभिन्न]] के रूप में धनात्मक वास्तविक संख्याओं के लिए पफ़ंक्शनषित किया जा सकता है | |||
<math display=block> \Gamma(z) = \int_0^\infty x^{z-1} e^{-x}\,dx.</math> | <math display=block> \Gamma(z) = \int_0^\infty x^{z-1} e^{-x}\,dx.</math> | ||
परिणामी | परिणामी फलन <math>n</math> समीकरण द्वारा गैर-नकारात्मक पूर्णांक के भाज्य से संबंधित है | ||
<math display=block> n!=\Gamma(n+1),</math> | <math display=block> n!=\Gamma(n+1),</math> | ||
जिसका उपयोग गैर-पूर्णांक तर्कों के लिए भाज्य की परिभाषा के रूप में किया जा सकता है। | जिसका उपयोग गैर-पूर्णांक तर्कों के लिए भाज्य की परिभाषा के रूप में किया जा सकता है। हर कीमत पर <math>x</math> जिसके लफ़ंक्शनोनों <math>\Gamma(x)</math> और <math>\Gamma(x-1)</math> परिभाषित हैं, गामा फलन [[कार्यात्मक समीकरण]] का पालन करता है | ||
हर कीमत पर <math>x</math> जिसके | |||
<math display=block> \Gamma(n)=(n-1)\Gamma(n-1),</math> | <math display=block> \Gamma(n)=(n-1)\Gamma(n-1),</math> | ||
क्रमगुणित के लिए पुनरावृत्ति संबंध को सामान्य बनाना।<ref name=davis>{{cite journal | last = Davis | first = Philip J. | author-link = Philip J. Davis | doi = 10.1080/00029890.1959.11989422 | journal = [[The American Mathematical Monthly]] | jstor = 2309786 | mr = 106810 | pages = 849–869 | title = लियोनहार्ड यूलर का अभिन्न: गामा फ़ंक्शन का एक ऐतिहासिक प्रोफ़ाइल| url = https://www.maa.org/programs/maa-awards/writing-awards/leonhard-eulers-integral-an-historical-profile-of-the-gamma-function | volume = 66 | year = 1959| issue = 10 }}</ref> | |||
समान समाकल किसी सम्मिश्र संख्या के लिए अधिक सामान्य रूप से अभिसरित होता है <math>z</math> जिसका वास्तविक भाग धनात्मक होता है। इसे यूलर के परावर्तन सूत्र को हल करके बाकी | |||
<math display=block>\Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin\pi z}.</math> | समान समाकल किसी सम्मिश्र संख्या के लिए अधिक सामान्य रूप से अभिसरित होता है <math>z</math> जिसका वास्तविक भाग धनात्मक होता है। इसे यूलर के परावर्तन सूत्र को हल करके बाकी सम्मिश्र तल में गैर-पूर्णांक बिंदुओं तक बढ़ाया जा सकता है | ||
चूँकि, इस सूत्र का उपयोग पूर्णांकों पर नहीं किया जा सकता है, क्योंकि उनके लिए, <math>\sin\pi z</math> अवधि शून्य से | <math display="block">\Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin\pi z}.</math> | ||
गामा फलन की | चूँकि, इस सूत्र का उपयोग पूर्णांकों पर नहीं किया जा सकता है, क्योंकि उनके लिए, <math>\sin\pi z</math> अवधि शून्य से विभाजन का उत्पादन करेगी। इस विस्तार प्रक्रिया का फ़ंक्शनाम [[विश्लेषणात्मक कार्य]] है, गामा फलन के अभिन्न सूत्र की [[विश्लेषणात्मक निरंतरता]]। गैर-धनात्मक पूर्णांकों को छोड़कर जहां इसमें शून्य और ध्रुव होते हैं, सभी सम्मिश्र संख्याओं में इसका शून्येतर मान होता है। इसलिए , यह ऋणात्मक पूर्णांकों के अतिरिक्त अन्य सभी सम्मिश्र संख्याओं पर क्रमगुणन की परिभाषा प्रदान करता है।<ref name="borwein-corless">{{cite journal | last1 = Borwein | first1 = Jonathan M. | author1-link = Jonathan Borwein | last2 = Corless | first2 = Robert M. | doi = 10.1080/00029890.2018.1420983 | issue = 5 | journal = [[The American Mathematical Monthly]] | mr = 3785875 | pages = 400–424 | title = ''मासिक'' में गामा और क्रमगुणित| volume = 125 | year = 2018| arxiv = 1703.05349 | s2cid = 119324101 }}</ref> गामा फलन की संपत्ति, इसे भाज्य के अन्य निरंतर प्रक्षेपों से अलग करती है, बोह्र-मोलेरुप प्रमेय द्वारा दी गई है, जिसमें कहा गया है कि गामा फलन ( द्वारा ऑफसेट) धनात्मक वास्तविक संख्याओं पर एकमात्र [[लॉग-उत्तल]] कार्य है जो क्रमगुणित्स को प्रक्षेपित करता है और समान कार्यात्मक समीकरण का पालन करता है। [[हेल्मुट विलैंड्ट]] के संबंधित अद्वितीयतफ़ंक्शनरमेय में कहा गया है कि सम्मिश्र गामा फलन और इसके स्केलर गुणक धनात्मक जट[[होलोमॉर्फिक फ़ंक्शन|फ़ंक्शन]]र्ध-विमान पर एकमात्र [[होलोमॉर्फिक फ़ंक्शन|होलोमॉर्फिक फलन]] हैं जो कार्यात्मक समीकरण का पालन करते हैं और 1 और 2 के बीच वास्तविक भाग के साथ सम्मिश्र संख्याओं के लिए बंधे रहते हैं।<ref>{{cite journal | last = Remmert | first = Reinhold | author-link = Reinhold Remmert | doi = 10.1080/00029890.1996.12004726 | issue = 3 | journal = [[The American Mathematical Monthly]] | jstor = 2975370 | mr = 1376175 | pages = 214–220 | title = {{nowrap|<math>\Gamma</math>-function}} | volume = 103 | year = 1996}}</ref> | ||
अन्य | |||
</ref><ref>{{cite journal | last = Alzer | first = Horst | doi = 10.1007/s12188-008-0009-5 | issue = 1 | journal = Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg | mr = 2541340 | pages = 11–23 | title = हैडमर्ड के गामा फ़ंक्शन का एक सुपरएडिटिव गुण| volume = 79 | year = 2009| s2cid = 123691692 }}</ref> पी- | अन्य सम्मिश्र कार्य जो तथ्यात्मक मूल्यों को प्रक्षेप फलन करते हैं, उनमें हैडमार्ड का गामा फलन सम्मिलित है, जो गैर-धनात्मक पूर्णांकों सहित सभी सम्मिश्र संख्याओं पर संपूर्ण कार्य है।<ref>{{cite book|first=J.|last=Hadamard|author-link=Jacques Hadamard|chapter=Sur l'expression du produit {{math|1·2·3· · · · ·(''n''−1)}} par une fonction entière|title=जैक्स हैडमार्ड द्वारा काम करता है|publisher=Centre National de la Recherche Scientifiques|location=Paris|date=1968|chapter-url=http://www.luschny.de/math/factorial/hadamard/HadamardFactorial.pdf|orig-date=1894|language=fr}} | ||
</ref><ref>{{cite journal | last = Alzer | first = Horst | doi = 10.1007/s12188-008-0009-5 | issue = 1 | journal = Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg | mr = 2541340 | pages = 11–23 | title = हैडमर्ड के गामा फ़ंक्शन का एक सुपरएडिटिव गुण| volume = 79 | year = 2009| s2cid = 123691692 }}</ref> पी-एडिफ़ंक्शनबर में {{mvar|p}}-ऐडिक नंबर, क्रमगुणित फलन को सीधे इंटरपोलेट करना संभव नहीं है, क्योंकि बड़े पूर्णांक के क्रमगुणित ( सघन उपसमुच्चय) {{mvar|p}}-adics) लीजेंड्रे के सूत्रों के अनुसार शून्य में परिवर्तित हो जाते हैं, किसी भी निरंतर कार्य को विवस कर देते हैं जो उनके मूल्यों के करीब हर स्थान शून्यफ़ंक्शनजाता है। इसके बफ़ंक्शन पी-एडिक गामा फलन {{mvar|p}}-एडिक गामा फलन क्रमगुणित के संशोधित रूप का निरंतर प्रक्षेप प्रदान करता है, जो क्रमगुणित में उन कारकों को छोड़ देता है जो {{mvar|p}} फलन हैं .<ref>{{harvnb|Robert|2000}}. "7.1: The gamma function {{nowrap|<math>\Gamma_p</math>".}} pp. 366–385.</ref> | |||
डिगामा फलन गामा फलन का लघुगणकीय व्युत्पन्न है।जिस तरह गामा फलन क्रमगुणित्स का निरंतर प्रक्षेप प्रदान करता है, के फलन ऑफसेट होता है, उसी तरह डिगामा फलन [[हार्मोनिक संख्या]]ओं का निरंतर प्रक्षेप प्रदान करता है, जो यूलर-मास्चेरोनी स्थिरांक द्वारा ऑफसेट होता है।<ref>{{cite journal | last = Ross | first = Bertram | doi = 10.1080/0025570X.1978.11976704 | issue = 3 | journal = [[Mathematics Magazine]] | jstor = 2689999 | mr = 1572267 | pages = 176–179 | title = साई समारोह| volume = 51 | year = 1978}}</ref> | |||
=== संगणना === | === संगणना === | ||
[[File:Vintage Texas Instruments Model SR-50A Handheld LED Electronic Calculator, Made in the USA, Price Was $109.50 in 1975 (8715012843).jpg|thumb|TI SR-50A, | [[File:Vintage Texas Instruments Model SR-50A Handheld LED Electronic Calculator, Made in the USA, Price Was $109.50 in 1975 (8715012843).jpg|thumb|TI SR-50A, 1975 का कैलकुलेटर जिसमें क्रमगुणित कुंजी है (तीसरी पंक्फ़ंक्शनबीच में दाहिनी ओर)]]क्रमगुणित फलन वैज्ञानिक कैलकुलेटर में सामान्य विशेषता है।<ref>{{cite book|title=समझने योग्य सांख्यिकी: अवधारणाएं और तरीके|first1=Charles Henry|last1=Brase|first2=Corrinne Pellillo|last2=Brase|edition=11th|publisher=Cengage Learning|year=2014|isbn=978-1-305-14290-9|page=182|url=https://books.google.com/books?id=a8OiAgAAQBAJ&pg=PA182}}</ref> यह वैज्ञानिक प्रोग्रामिंग पुस्तकालयों जैसे कि [[पायथन (प्रोग्रामिंग भाषा)]] गणितीय कार्य मॉड्यूल में भी सम्मिलित है<ref>{{cite web|url=https://docs.python.org/3/library/math.html|title=गणित - गणितीय कार्य|work=Python 3 Documentation: The Python Standard Library|access-date=2021-12-21}}</ref> और बूस्ट (सी++ लाइब्रेरी)|<ref>{{cite web|url=https://www.boost.org/doc/libs/1_78_0/libs/math/doc/html/math_toolkit/factorials/sf_factorial.html| title=कारख़ाने का|work=Boost 1.78.0 Documentation: Math Special Functions|access-date=2021-12-21}}</ref> यदि दक्षता चिंता का विषय नहीं है, तो क्रमगुणित की गणना तुच्छ है: बस {{nowrap|<math>1</math>}} से क्रमिक रूप से चर को {{nowrap|<math>n</math>.}} आरंभिक रूप से गुणा करें ऊपर पूर्णांकों द्वारा इस संगणना की सरलता इसे विभिन्न कंप्यूटर प्रोग्रामिंग शैलियों और विधियों के उपयोग में सामान्य उदाहरण बनाती है।<ref>{{cite book|title=आरेखण कार्यक्रम: योजनाबद्ध कार्यात्मक प्रोग्रामिंग का सिद्धांत और अभ्यास|first1=Tom|last1=Addis|first2=Jan|last2=Addis|publisher=Springer| year=2009| isbn=978-1-84882-618-2| pages=149–150|url=https://books.google.com/books?id=cWM7ZBfEl_0C&pg=PA149}}</ref> | ||
जिसे <math>n!</math> की गणना पुनरावृति का उपयोग करके [[स्यूडोकोड]] में व्यक्त किया जा सकता है<ref>{{cite book|title=इंजीनियरों के लिए MATLAB प्रोग्रामिंग|first=Stephen J.|last=Chapman|edition=6th|publisher=Cengage Learning|year=2019| isbn=978-0-357-03052-3| page=215|contribution=Example 5.2: The factorial function|contribution-url=https://books.google.com/books?id=jVEzEAAAQBAJ&pg=PA215}}</ref> | |||
क्रमगुणित परिभाषित करें (N): | |||
च:= 1 | |||
i := 1, 2, 3, ..., n के लिए: | |||
च�:= च × मैं | |||
वापसी च | |||
या पुनरावर्तन (कंप्यूटर विज्ञान) का उपयोग करना<ref>{{cite book|title=द कम्प्यूटिंग यूनिवर्स: ए जर्नी थ्रू ए रेवोल्यूशन|first1=Tony|last1=Hey|first2=Gyuri|last2=Pápay|publisher=Cambridge University Press|year=2014|isbn=9781316123225|page=64|url=https://books.google.com/books?id=q4FIBQAAQBAJ&pg=PA64}}</ref> इसके पुनरावृत्ति संबंध के आधार पर | या पुनरावर्तन (कंप्यूटर विज्ञान) का उपयोग करना<ref>{{cite book|title=द कम्प्यूटिंग यूनिवर्स: ए जर्नी थ्रू ए रेवोल्यूशन|first1=Tony|last1=Hey|first2=Gyuri|last2=Pápay|publisher=Cambridge University Press|year=2014|isbn=9781316123225|page=64|url=https://books.google.com/books?id=q4FIBQAAQBAJ&pg=PA64}}</ref> इसके पुनरावृत्ति संबंध के आधार पर | ||
क्रमगुणित परिभाषित करें (एन): | |||
यदि एन = 0 वापसी 1 | |||
वापसी n × भाज्य (n − 1) | |||
इसकी गणना के लिए उपयुक्त अन्य विधियों में [[memoization]],<ref>{{cite book|title=C++ के साथ हैंड्स-ऑन फंक्शनल प्रोग्रामिंग: C++17 और C++20 का उपयोग करके त्वरित कार्यात्मक कोड लिखने के लिए एक प्रभावी गाइड| first=Alexandru|last=Bolboaca | publisher=Packt Publishing|year=2019|isbn=978-1-78980-921-3|page=188|url=https://books.google.com/books?id=GwSgDwAAQBAJ&pg=PA188}}</ref> [[गतिशील प्रोग्रामिंग]],<ref>{{cite book|title=मास्टरिंग मैथमैटिका: प्रोग्रामिंग के तरीके और अनुप्रयोग| first=John W.|last=Gray|publisher=Academic Press|year=2014|isbn=978-1-4832-1403-0|pages=233–234| url=https://books.google.com/books?id=a4riBQAAQBAJ&pg=PA233}}</ref> और [[कार्यात्मक प्रोग्रामिंग]]।<ref>{{cite book|title=एक कार्यात्मक प्रोग्रामिंग परिप्रेक्ष्य से स्काला: प्रोग्रामिंग भाषा का एक परिचय|volume=9980|series=Lecture Notes in Computer Science| first=Vicenç| last=Torra| publisher=Springer|year=2016|isbn=978-3-319-46481-7|page=96|url=https://books.google.com/books?id=eMwcDQAAQBAJ&pg=PA96}}</ref> इन एल्गोरिदम की कम्प्यूटेशनल | इसकी गणना के लिए उपयुक्त अन्य विधियों में [[memoization|मेमोइज़ेशन,]] ,<ref>{{cite book|title=C++ के साथ हैंड्स-ऑन फंक्शनल प्रोग्रामिंग: C++17 और C++20 का उपयोग करके त्वरित कार्यात्मक कोड लिखने के लिए एक प्रभावी गाइड| first=Alexandru|last=Bolboaca | publisher=Packt Publishing|year=2019|isbn=978-1-78980-921-3|page=188|url=https://books.google.com/books?id=GwSgDwAAQBAJ&pg=PA188}}</ref> [[गतिशील प्रोग्रामिंग|डायनेमिक प्रोग्रामिंग,]],<ref>{{cite book|title=मास्टरिंग मैथमैटिका: प्रोग्रामिंग के तरीके और अनुप्रयोग| first=John W.|last=Gray|publisher=Academic Press|year=2014|isbn=978-1-4832-1403-0|pages=233–234| url=https://books.google.com/books?id=a4riBQAAQBAJ&pg=PA233}}</ref> और [[कार्यात्मक प्रोग्रामिंग]]।<ref>{{cite book|title=एक कार्यात्मक प्रोग्रामिंग परिप्रेक्ष्य से स्काला: प्रोग्रामिंग भाषा का एक परिचय|volume=9980|series=Lecture Notes in Computer Science| first=Vicenç| last=Torra| publisher=Springer|year=2016|isbn=978-3-319-46481-7|page=96|url=https://books.google.com/books?id=eMwcDQAAQBAJ&pg=PA96}}</ref> इन एल्गोरिदम की कम्प्यूटेशनल सम्मिश्रता का विश्लेषण गणना के यूनिट-कॉस्ट [[रैंडम-एक्सेस मशीन]] मॉडल का उपयोग करके किया जा सकता है, जिसमें प्रत्येक अंकगणितीय ऑपरेशन में निरंतर समय लगता है और प्रत्येक संख्या स्टोरेज स्पेस की निरंतर मात्रा का उपयोग करती है। इस मॉडल में, ये विधियाँ <math>n!</math> गणना कर सकती हैं जिससे समय {{nowrap|<math>O(n)</math>,}} के अंदर और पुनरावृत्त संस्करण स्थान {{nowrap|<math>O(1)</math>.}} का उपयोग करता है जब तक [[पूंछ पुनरावर्तन]] के लिए अनुकूलित नहीं किया जाता है, पुनरावर्ती संस्करण अपने [[कॉल स्टैक]] को संग्रहीत करने के लिए रैखिक स्थान लेता है।<ref>{{cite book|title=कार्यात्मक प्रोग्रामिंग और इसके अनुप्रयोग: एक उन्नत पाठ्यक्रम| publisher=Cambridge University Press|series=CREST Advanced Courses|contribution=LISP, programming, and implementation| first=Gerald Jay|last=Sussman|author-link=Gerald Jay Sussman|year=1982|pages=29–72|isbn=978-0-521-24503-6}} See in particular [https://books.google.com/books?id=O_M8AAAAIAAJ&pg=PA34 p. 34].</ref> चूँकि, गणना का यह मॉडल तभी उपयुक्त है जब <math>n</math> अनुमति देने के लिए अधिक छोटा है <math>n!</math> [[मशीन शब्द]] में फिट होने के लिए।<ref>{{cite journal | last = Chaudhuri | first = Ranjan | date = June 2003 | doi = 10.1145/782941.782977 | issue = 2 | journal = ACM SIGCSE Bulletin | pages = 43–44 | publisher = Association for Computing Machinery | title = क्या अंकगणितीय परिचालन वास्तव में निरंतर समय में निष्पादित होते हैं?| volume = 35| s2cid = 13629142 }}</ref> मान 12! और 20! सबसे बड़े क्रमगुणित हैं जिन्हें क्रमशः [[32-बिट कंप्यूटिंग]] | 32-बिट में संग्रहीत किया जा सकता है<ref name=fateman/> and [[64-bit computing|64-bit]] [[Integer (computer science)|integers]].<ref name=sigplan>{{cite journal | last1 = Winkler | first1 = Jürgen F. H. | last2 = Kauer | first2 = Stefan | date = March 1997 | doi = 10.1145/251634.251638 | issue = 3 | journal = ACM SIGPLAN Notices | pages = 38–41 | publisher = Association for Computing Machinery | title = Proving assertions is also useful | volume = 32| s2cid = 17347501 | doi-access = free }}</ref> [[Floating point]] can represent larger factorials, but approximately rather than exactly, and will still overflow for factorials larger than {{nowrap|<math>170!</math>.<ref name=fateman>{{cite web| url=http://people.eecs.berkeley.edu/~fateman/papers/factorial.pdf|title=Comments on Factorial Programs|date=April 11, 2006| publisher=University of California, Berkeley|first=Richard J.|last=Fateman|author-link=Richard Fateman}}</ref>}} | ||
बड़े | बड़े क्रमगुणित की स्पष्ट गणना में क्रमगुणित या ग्रोथ_एंड_प्रॉक्सिमेशन और [[पूर्णांक अतिप्रवाह]] के कारण इच्छानुसार से स्पष्ट अंकगणित सम्मिलित है। परिणाम में अंकों या बिट्स की संख्या के कार्य के रूप में गणना के समय का विश्लेषण किया जा सकता है।<ref name="sigplan" /> स्टर्लिंग के सूत्र से, <math>n!</math> है <math>b = O(n\log n)</math> बिट्स।<ref name="borwein" /> शॉनहेज-स्ट्रैसन एल्गोरिथम उत्पादन कर सकता है {{nowrap|<math>O(b\log b\log\log b)</math>,}} में {{nowrap|<math>b</math>-bit}} उत्पादन कर सकता है और <math>O(b\log b)</math> समय तेज गुणन एल्गोरिदम में समय लगता है जाने जाते हैं।<ref>{{cite journal | last1 = Harvey | first1 = David | last2 = van der Hoeven | first2 = Joris | author2-link = Joris van der Hoeven | doi = 10.4007/annals.2021.193.2.4 | issue = 2 | journal = [[Annals of Mathematics]] | mr = 4224716 | pages = 563–617 | series = Second Series | title = समय में पूर्णांक गुणन <math>O(n \log n)</math>| volume = 193 | year = 2021| s2cid = 109934776 | url = https://hal.archives-ouvertes.fr/hal-02070778/file/nlogn.pdf }}</ref> चूंकि, क्रमगुणित की गणना में एकल गुणन के अतिरिक्त बार-बार उत्पाद सम्मिलित होते हैं, इसलिए ये समय सीमाएं सीधे प्रयुक्त नहीं होती हैं। इस सेटिंग में, कंप्यूटिंग <math>n!</math> 1 से {{nowrap| <math>n</math>}} संख्याओं का गुणा करके क्रम में अक्षम है, क्योंकि इसमें <math>n</math> सम्मिलित है गुणन, जिसका निरंतर अंश <math>O(n\log^2 n)</math> समय लेता है प्रत्येक, कुल समय {{nowrap|<math>O(n^2\log^2 n)</math>.}} दे रहा है गुणा-और-जीत एल्गोरिदम के रूप में गुणा करने का नियमविधि है जो अनुक्रम को गुणा करता है <math>i</math> संख्याओं को इसके दो क्रमों में विभाजित करके <math>i/2</math> संख्याएँ, प्रत्येक अनुक्रम को गुणा करती हैं, और परिणामों को अंतिम गुणन के साथ जोड़ती हैं। क्रमगुणित के इस दृष्टिकोण में कुल समय लगता है {{nowrap|<math>O(n\log^3 n)</math>:}} लघुगणक क्रमगुणित में बिट्स की संख्या से आता है, दूसरा गुणन एल्गोरिथ्म से आता है, और तीसरा फूट डालो और जीतो से आता है।<ref>{{cite book|last=Arndt|first=Jörg| title=मामले कम्प्यूटेशनल: विचार, एल्गोरिदम, स्रोत कोड|publisher=Springer|year=2011|url=http://jjj.de/fxt/fxtbook.pdf| contribution=34.1.1.1: Computation of the factorial|pages=651–652}} See also "34.1.5: Performance", pp. 655–656.</ref> | ||
कंप्यूटिंग द्वारा और भी नियमदक्षता प्राप्त की जाती है {{math|''n''!}} इसके प्रधान गुणनखंड से, इस सिद्धांत पर आधारित है कि वर्ग करके घातांक | |||
{{math|''n''!}} कंप्यूटिंग द्वारा और भी नियमदक्षता प्राप्त की जाती है {{math|''n''!}} इसके प्रधान गुणनखंड से, इस सिद्धांत पर आधारित है कि वर्ग करके घातांक उत्पाद में घातांक का विस्तार करने की तुलना में तेज़ है।<ref name="borwein">{{cite journal | last = Borwein | first = Peter B. | author-link = Peter Borwein | doi = 10.1016/0196-6774(85)90006-9 | issue = 3 | journal = [[Journal of Algorithms]] | mr = 800727 | pages = 376–380 | title = क्रमगुणित की गणना की सम्मिश्रता पर| volume = 6 | year = 1985}}</ref><ref name="schonhage">{{cite book|first=Arnold|last=Schönhage|year=1994|title=फास्ट एल्गोरिदम: एक मल्टीटेप ट्यूरिंग मशीन कार्यान्वयन|publisher=B.I. Wissenschaftsverlag|page=226}}</ref> अर्नोल्ड शॉनहेज द्वारा इसके लिए एल्गोरिदम प्राइम अप की सूची ढूंढकर प्रारंभिक होता है उदाहरण के लिए [[एराटोस्थनीज की चालनित्र]] का उपयोग करके,{{nowrap| <math>n</math>,}} और प्रत्येक अभाज्य के लिए प्रतिपादक की गणना करने के लिए लीजेंड्रे के सूत्र का उपयोग करता है। फिर यह पुनरावर्ती एल्गोरिथम का उपयोग करते हुए, इन घातांकों के साथ प्रमुख शक्तियों के उत्पाद की गणना करता है:: | |||
* उन अभाज्य संख्याओं के गुणनफल की गणना करने के लिए विभाजित करें और जीतें जिनका घातांक विषम हैं | * उन अभाज्य संख्याओं के गुणनफल की गणना करने के लिए विभाजित करें और जीतें जिनका घातांक विषम हैं | ||
* सभी घातांकों को दो से विभाजित करें ( पूर्णांक तक नीचे की ओर), इन छोटे घातांकों के साथ प्रमुख शक्तियों के उत्पाद की पुनरावर्ती गणना करें, और परिणाम का वर्ग करें | * सभी घातांकों को दो से विभाजित करें ( पूर्णांक तक नीचे की ओर), इन छोटे घातांकों के साथ प्रमुख शक्तियों के उत्पाद की पुनरावर्ती गणना करें, और परिणाम का वर्ग करें | ||
* पिछले दो चरणों के परिणामों को | * पिछले दो चरणों के परिणामों को साथ गुणा करें | ||
<math>n</math> तक सभी अभाज्य संख्याओं का गुणनफल <math>O(n)</math>-बिट संख्या, अभाज्य संख्या प्रमेय द्वारा, तो पहले चरण के लिए समय <math>O(n\log^2 n)</math> है , जिसमें लघुगणक विभाजित और अधीन करना आता है और दूसरा गुणा एल्गोरिथम से आता है। एल्गोरिथ्म के पुनरावर्ती कॉल में, प्रधान संख्या प्रमेय को फिर से यह सिद्ध करने के लिए प्रयुक्त किया जा सकता है कि संबंधित उत्पादों में बिट्स की संख्या पुनरावर्तन के प्रत्येक स्तर पर स्थिर कारक से घट जाती है, इसलिए पुनरावर्तन के सभी स्तरों पर इन चरणों के लिए कुल समय {{nowrap| <math>O(n\log^2 n)</math>.}} ज्यामितीय श्रृंखला में जोड़ता है दूसरे चरण में वर्ग करने और तीसरे चरण में गुणा करने का समय फिर से है {{nowrap|<math>O(n\log^2 n)</math>,}} क्योंकि प्रत्येक <math>O(n\log n)</math> बिट्स। संख्या का एकल गुणन है । फिर से, पुनरावर्तन के प्रत्येक स्तर पर सम्मिलित संख्याओं में कई बिट्स के रूप में निरंतर अंश होता है (क्योंकि अन्यथा बार-बार उन्हें चुकता करने से अंतिम परिणाम बहुत बड़ा होगा) इसलिए फिर से पुनरावर्ती कॉल में इन चरणों के लिए समय की मात्रा ज्यामितीय श्रृंखला में जोड़ती है {{nowrap| <math>O(n\log^2 n)</math>.}} परिणाम स्वरुप , पूरा एल्गोरिदम लेता है {{nowrap|<math>O(n\log^2 n)</math>,}} इसके परिणाम में बिट्स की समान संख्या के साथ एकल गुणन के समानुपाती।<ref name=schonhage/> | |||
== संबंधित अनुक्रम और कार्य == | == संबंधित अनुक्रम और कार्य == | ||
{{main| | {{main|भाज्य और द्विपद विषयों की सूची}} | ||
कई अन्य पूर्णांक क्रम | कई अन्य पूर्णांक क्रम क्रमगुणित के समान या उससे संबंधित हैं: | ||
[[वैकल्पिक योग]] | [[वैकल्पिक योग]] क्रमगुणित | ||
:प्रत्यावर्ती भाज्य पहले | :प्रत्यावर्ती भाज्य पहले <math>n</math> के क्रमगुणित, {{nowrap|<math display=inline>\sum_{i = 1}^n (-1)^{n - i}i!</math>.}} प्रत्यावर्ती योग का निरपेक्ष मान है इनका मुख्य रूप से उनकी आदिमता के संबंध में अध्ययन किया गया है; उनमें से बहुत से ही प्रधान हो सकते हैं, किन्तुइस रूप के अभाज्यों की पूरी सूची ज्ञात नहीं है।<ref>{{harvnb|Guy|2004}}. "B43: Alternating sums of factorials". pp. 152–153.</ref> | ||
;[[भार्गव | : | ||
: भार्गव | ;[[भार्गव क्रमगुणित]] | ||
: कुछ विषम धनात्मक तक सभी विषम पूर्णांकों का गुणनफल {{nowrap| | : भार्गव क्रमगुणित, [[मंजुल भार्गव]] द्वारा परिभाषित पूर्णांक अनुक्रमों का परिवार है, जिसमें क्रमगुणित्स के समान संख्या-सैद्धांतिक गुण हैं, जिसमें क्रमगुणित्स स्वयं विशेष स्थितियोंके रूप में सम्मिलित हैं।<ref name=bhargava/>डबल क्रमगुणित | ||
: कुछ विषम धनात्मक तक सभी विषम {{nowrap|<math>n</math>}} पूर्णांकों का गुणनफल {{nowrap|<math>n</math>,}} डबल क्रमगुणित कहा जाता है और {{nowrap|<math>n!!</math>.}} द्वारा दर्शाया गया वह है, | |||
:<math display="block">(2k-1)!! = \prod_{i=1}^k (2i-1) = \frac{(2k)!}{2^k k!}.</math> उदाहरण के लिए, {{nowrap|1=9!! = 1 × 3 × 5 × 7 × 9 = 945}}. [[त्रिकोणमितीय कार्यों के इंटीग्रल की सूची]] में डबल क्रमगुणित का उपयोग कफ़ंक्शनजाता है,<ref name="callan">{{cite arXiv|title=A combinatorial survey of identities for the double factorial|first=David|last=Callan|eprint=0906.1317|year=2009|class=math.CO}}</ref>}} That is, <math display=block>(2k-1)!! = \prod_{i=1}^k (2i-1) = \frac{(2k)!}{2^k k!}.</math> For example, {{nowrap|1=9!! = 1 × 3 × 5 × 7 × 9 = 945}}. Double factorials are used in [[List of integrals of trigonometric functions|trigonometric integrals]],<ref>{{cite journal | |||
| last = Meserve | first = B. E. | | last = Meserve | first = B. E. | ||
| doi = 10.2307/2306136 | | doi = 10.2307/2306136 | ||
| Line 240: | Line 271: | ||
| mr = 1527019 | | mr = 1527019 | ||
| pages = 425–426 | | pages = 425–426 | ||
| title = | | title = Classroom Notes: Double Factorials | ||
| volume = 55 | |||
| year = 1948| jstor = 2306136 | | year = 1948| jstor = 2306136 | ||
}} | }}</ref> | ||
;घातीय भाज्य | ;घातीय भाज्य | ||
: जिस प्रकार त्रिभुजाकार संख्याओं से संख्याओं का योग होता है <math>1</math> {{nowrap| | : जिस प्रकार त्रिभुजाकार संख्याओं <math>1</math> से {{nowrap|<math>n</math>,}} संख्याओं का योग होता है <math>1</math> {{nowrap|<math>n</math>,}} और क्रमगुणित उनके उत्पाद को लेते हैं, [[घातीय भाज्य]] एक्सपोनेंटियेट्स। घातीय क्रमगुणन को पुनरावर्ती रूप से परिभाषित किया गया है {{nowrap|as <math>a_0 = 1,\ a_n = n^{a_{n - 1}}</math>.}} उदाहरण के लिए, 4 का चरघातांकी भाज्य है | ||
:ये संख्याएँ नियमित क्रमगुणित्स की तुलना में बहुत अधिक तेज़ी से बढ़ती हैं।<ref>{{cite journal | last1 = Luca | first1 = Florian | author1-link = Florian Luca | last2 = Marques | first2 = Diego | issue = 3 | journal = [[Journal de Théorie des Nombres de Bordeaux]] | mr = 2769339 | pages = 703–718 | title = पावर टावर के सारांश कार्य में पूर्ण शक्तियाँ| url = http://jtnb.cedram.org/item?id=JTNB_2010__22_3_703_0 | volume = 22 | year = 2010| doi = 10.5802/jtnb.740 }}</ref> | |||
: | क्रमगुणित गिरना | ||
[[hyperactorial]] | : अंकन <math>(x)_{n}</math> या <math>x^{\underline n}</math> का उपयोग कभी-कभी {{nowrap|<math>x!/(x-n)!</math>.}} के समान और {{nowrap| <math>x</math>,}}सहित <math>n</math> पूर्णांकों की गिनती और उनके गुणनफल को दर्शाने के लिए किया जाता है। इसे फ़ॉलिंग फ़ैक्टोरियल या बैकवर्ड फ़ैक्टोरियल के रूप में भी जाना जाता है, और <math>(x)_{n}</math> अंकन एक पोचहैमर प्रतीक है। [96] गिरते क्रमगुणित एन अलग-अलग वस्तुओं के विभिन्न अनुक्रमों की संख्या की गणना करते हैं जिन्हें एक्स वस्तुओं के ब्रह्मांड से खींचा जा सकता है। [97] वे बहुपदों के उच्च व्युत्पन्नों में गुणांक के रूप में होते हैं, [98] और यादृच्छिक चर के तथ्यात्मक क्षणों में। [99] | ||
: का | [[hyperactorial|हाइपरएक्टोरियल]] | ||
: का हाइपरक्रमगुणित <math>n</math> उत्पाद है <math>1^1\cdot 2^2\cdots n^n</math>. ये संख्याएँ [[हर्मिट बहुपद]] के [[विभेदक]] का निर्माण करती हैं।<ref>{{cite OEIS | 1=A002109 | 2=Hyperfactorials: Product_{k = 1..n} k^k}}</ref> उन्हें ''K'' [[कश्मीर समारोह|कार्य]] द्वारा निरंतर प्रक्षेपित किया जा सकता है,<ref>{{cite journal | last = Kinkelin | first = H. | author-link = Hermann Kinkelin | doi = 10.1515/crll.1860.57.122 | journal = [[Crelle's Journal | Journal für die reine und angewandte Mathematik]] | language = de | pages = 122–138 | title = गामा फलन से संबंधित एक पारलौकिक पर और समाकलन कलन में इसका अनुप्रयोग| trans-title = On a transcendental variation of the gamma function and its application to the integral calculus | volume = 1860 | year = 1860| issue = 57 | s2cid = 120627417 }}</ref> और स्टर्लिंग के सूत्र के अनुरूपों का पालन करें<ref>{{cite journal | last = Glaisher | first = J. W. L. | author-link = James Whitbread Lee Glaisher | journal = [[Messenger of Mathematics]] | pages = 43–47 | title = उत्पाद पर {{math|1<sup>1</sup>.2<sup>2</sup>.3<sup>3</sup>...''n''<sup>''n''</sup>}} | url = https://archive.org/details/messengermathem01glaigoog/page/n56 | volume = 7 | year = 1877}}</ref> और विल्सन की प्रमेय।<ref>{{cite journal | last1 = Aebi | first1 = Christian | last2 = Cairns | first2 = Grant | doi = 10.4169/amer.math.monthly.122.5.433 | issue = 5 | journal = [[The American Mathematical Monthly]] | jstor = 10.4169/amer.math.monthly.122.5.433 | mr = 3352802 | pages = 433–443 | title = डबल-, हाइपर-, सब- और सुपरक्रमगुणित्स के लिए विल्सन के प्रमेय का सामान्यीकरण| volume = 122 | year = 2015| s2cid = 207521192 }}</ref> | |||
;जॉर्डन-पोल्या नंबर | ;जॉर्डन-पोल्या नंबर | ||
:जॉर्डन-पोल्या नंबर | :जॉर्डन-पोल्या नंबर क्रमगुणित के उत्पाद हैं, जो दोहराव की अनुमति देते हैं। प्रत्येक ट्री (ग्राफ सिद्धांत) में [[समरूपता समूह]] होता है जिसकी समरूपता की संख्या जॉर्डन-पोल्या संख्या होती है, और प्रत्येक जॉर्डन-पोल्या संख्या किसी ट्री की समरूपता की गणना करती है।<ref>{{cite OEIS|A001013|Jordan-Polya numbers: products of factorial numbers}}</ref> | ||
प्राथमिक | प्राथमिक | ||
: आदिम <math>n\#</math> | : आदिम <math>n\#</math> {{nowrap| <math>n</math>;}} कम या समान अभाज्य संख्याओं का गुणनफल है यह निर्माण उन्हें क्रमगुणित्स के लिए कुछ समान विभाज्यता गुण देता है,<ref name=caldwell-gallot/> किन्तु क्रमगुणित के विपरीत वर्गमुक्त हैं।<ref>{{cite book | last = Nelson | first = Randolph | doi = 10.1007/978-3-030-37861-5 | isbn = 978-3-030-37861-5 | location = Cham | mr = 4297795 | page = 127 | publisher = Springer | title = असतत गणित में एक संक्षिप्त यात्रा| url = https://books.google.com/books?id=m8PPDwAAQBAJ&pg=PA127 | year = 2020| s2cid = 213895324 }}</ref> क्रमगुणित प्राइम्स {{nowrap|<math>n!\pm 1</math>,}} की तरह शोधकर्ताओं ने प्राथमिक अभाज्यताओं {{nowrap|<math>n\#\pm 1</math>.<ref name=caldwell-gallot/>}} का अध्ययन किया है | ||
सबक्रमगुणित | |||
: | : सबक्रमगुणित <math>n</math> समुच्चय के विचलन की संख्या उत्पन्न करता है वस्तुओं। इसे कभी-कभी <math>!n</math> निरूपित किया जाता है {{nowrap|<math>n!/e</math>.{{sfn|Graham|Knuth|Patashnik|1988|p=195}}}} और निकटतम पूर्णांक के समान है | ||
[[superactorial]] | [[superactorial|सुपरएक्टोरियल]] | ||
: | : <math>n</math> का सुपरक्रमगुणित पहले <math>n</math>का उत्पाद है भाज्य। [[बार्न्स जी-फंक्शन|बार्न्स जी-कार्य]] द्वारा सुपरक्रमगुणित्स को निरंतर प्रक्षेपित किया जाता है।<ref>{{cite journal|last=Barnes|first=E. W.|author-link=Ernest Barnes|jfm=30.0389.02|journal=[[The Quarterly Journal of Pure and Applied Mathematics]]|pages=264–314|title={{मवर|G}}-function|url=https://gdz.sub.uni-goettingen.de/id/PPN600494829_0031?tify={%22pages%22:[268],%22view%22:%22toc%22}|volume=31|year=1900}}</ref> | ||
| Line 273: | Line 297: | ||
==बाहरी कड़ियाँ== | ==बाहरी कड़ियाँ== | ||
{{Portal|Arithmetic|Mathematics}} | {{Portal|Arithmetic|Mathematics}} | ||
| Line 339: | Line 312: | ||
[[श्रेणी: एकात्मक संचालन]] | [[श्रेणी: एकात्मक संचालन]] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category: | [[Category:CS1 Deutsch-language sources (de)]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 errors]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:Collapse templates]] | |||
[[Category:Commons category link is locally defined]] | |||
[[Category:Created On 02/01/2023]] | [[Category:Created On 02/01/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with empty portal template]] | |||
[[Category:Pages with maths render errors]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Portal templates with redlinked portals]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
Latest revision as of 12:38, 30 August 2023
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432902008176640000 |
| 25 | 1.551121004×1025 |
| 50 | 3.041409320×1064 |
| 70 | 1.197857167×10100 |
| 100 | 9.332621544×10157 |
| 450 | 1.733368733×101000 |
| 1000 | 4.023872601×102567 |
| 3249 | 6.412337688×1010000 |
| 10000 | 2.846259681×1035659 |
| 25206 | 1.205703438×10100000 |
| 100000 | 2.824229408×10456573 |
| 205023 | 2.503898932×101000004 |
| 1000000 | 8.263931688×105565708 |
| 10100 | 1010101.9981097754820 |
गणित में, गैर-ऋणात्मक पूर्णांक , का भाज्य है तथा , द्वारा निरूपित . से कम या उसके समान सभी धनात्मक पूर्णांकों का गुणनफल है। अगले छोटे क्रमगुणित के साथ का भाज्य भी के गुणनफल के समान होता है )
क्रमगुणित की खोज कई वर्ष पहले प्राचीन संस्कृतियों में की गई है, जिसे विशेष रूप से भारतीय गणित में जैन साहित्य के विहित कार्यों में, और यहूदी रहस्यवादियों द्वारा तल्मूडिक पुस्तक सेफ़र यत्ज़िराह में उपयोग किया जाता है। क्रमगुणित ऑपरेशन गणित के कई क्षेत्रों में पाया जाता है, विशेष रूप से कॉम्बिनेटरिक्स में, जहां इसका सबसे मूलभूत उपयोग संभावित विशिष्ट अनुक्रमों की गणना करता है। - क्रमपरिवर्तन - अलग-अलग है जहाँ वस्तुओं के वहां . गणितीय विश्लेषण में, क्रमगुणित का उपयोग किया जाता है तथा घातीय फलन और अन्य कार्यों के लिए शक्ति श्रृंखला, और उनके पास बीजगणित, तथा संख्या सिद्धांत, संभाव्यता सिद्धांत और कंप्यूटर विज्ञान में भी अनुप्रयोग हैं।
18वीं सदी के अंत तक और 19वीं सदी की प्रारम्भ में क्रमगुणित फलन का अधिकांश गणित कार्य विकसित किया गया था। स्टर्लिंग का सन्निकटन बड़ी संख्या के भाज्य के लिए स्पष्ट सन्निकटन प्रदान करता है, यह दर्शाता है कि यह घातीय वृद्धि की तुलना में यह अधिक तेज़ी से बढ़ता है। लेजेंड्रे का सूत्र भाज्यों के अभाज्य गुणनखंडन में अभाज्य संख्याओं के घातांकों का वर्णन करता है, और इसका उपयोग भाज्यों के अनुगामी शून्यों को गिनने के लिए किया जा सकता है। डेनियल बर्नौली और लियोनहार्ड यूलर ने ऋणात्मक पूर्णांक, (ऑफ़सेट) गामा कार्य को छोड़कर, सम्मिश्र संख्याओं के निरंतर फलन के लिए क्रमगुणित फलन को किया गया ।
कई अन्य उल्लेखनीय कार्य और संख्या क्रम क्रमगुणित से निकटता से संबंधित हैं, जिनमें द्विपद गुणांक, डबल क्रमगुणित, क्रमगुणित गिर रहा है, मौलिक और सबक्रमगुणित सम्मिलित हैं। क्रमगुणित फलन के कार्यान्वयन सामान्यतः विभिन्न कंप्यूटर प्रोग्रामिंग शैलियों के उदाहरण के रूप में उपयोग किए जाते हैं, और वैज्ञानिक कैलकुलेटर और वैज्ञानिक कंप्यूटिंग सॉफ़्टवेयर लाइब्रेरी में सम्मिलित होते हैं। चूंकि उत्पाद सूत्र या पुनरावृत्ति का उपयोग करके सीधे बड़े क्रमगुणित की गणना करना कुशल नहीं है, जबकि तेज एल्गोरिदम ज्ञात हैं, समान संख्या वाले अंकों के लिए तेजी से गुणन एल्गोरिदम के लिए स्थिर कारक के अंदर मिलान करने का समय उपयोग किया जाता है
इतिहास
तथ्यात्मकता की अवधारणा कई संस्कृतियों में स्वतंत्र रूप से उत्पन्न हुई है:
- भारतीय गणित में, क्रमगुणों के सबसे पुराने ज्ञात विवरणों में से अनुयोगद्वार-सूत्र से आता है,[2]जैन साहित्य के विहित कार्यों में से एक, जिसे 300 बीसीई से 400 सीई तक अलग-अलग तिथियां सौंपी गई हैं।[3] तथा यह अन्य (मिश्रित) ऑर्डर से वस्तुओं के समुच्चय के सॉर्ट किए गए है और उलटे क्रम को अलग करता है, क्रमगुणित के लिए सामान्य उत्पाद सूत्र से दो घटाकर मिश्रित ऑर्डर की संख्या का मूल्यांकन करता है। क्रमचय के लिए गुणनफल नियम का वर्णन 6वीं शताब्दी के सीई जैन भिक्षु जिनभद्र ने भी किया था।[2] जिसे हिंदू विद्वान कम से कम 1150 से तथ्यात्मक सूत्रों का उपयोग कर रहे हैं, जब भास्कर द्वितीय ने अपनी कृति लीलावती में तथ्यात्मक सूत्रों का उल्लेख किया था, तथा इस समस्या के संबंध में कि विष्णु अपनी चार विशिष्ट वस्तुओं ( रेखावृत्त, सुदर्शन चक्र, कौमोदकी और पवित्र कमल) को कितने तरीकों से धारण कर सकते हैं। धार्मिक कला में) अपने चार हाथों में, और दस हाथ वाले भगवान के लिए समान समस्या है ।[4]
- मध्य पूर्व के गणित में, तल्मूड (200 से 500 ईसवी) से सृजन की हिब्रू रहस्यवादी पुस्तक सेफ़र यतिज़िराह, 7 तक के क्रमगुणों को सूचीबद्ध करती है! हिब्रू वर्णमाला से बनने वाले शब्दों की संख्या की जांच के हिस्से के रूप में है ।[5][6] इसी तरह के कारणों के लिए 8वीं शताब्दी के अरब व्याकरणविद अल-खलील इब्न अहमद अल-फ़राहिदी द्वारा क्रमगुणित का भी अध्ययन किया गया था।[5]अरब गणितज्ञ इब्न अल-हेथम (जिसे अल्हज़ेन के नाम से भी जाना जाता है, c.-965 - c.-1040) सबसे पहले विल्सन के प्रमेय को सूत्रबद्ध करने वाले थे, जो भाज्य संख्याओं को अभाज्य संख्याओं से जोड़ते थे।[7]
- यूरोप में, चूंकि ग्रीक गणित में कुछ कॉम्बिनेटरिक्स सम्मिलित थे, और प्लेटो ने आदर्श समुदाय की आबादी के रूप में प्रसिद्ध रूप से 5040 ( क्रमगुणित) का उपयोग किया था, आंशिक रूप से इसकी विभाज्यता के गुणों के कारण,[8] क्रमगुणित के प्राचीन ग्रीक अध्ययन का कोई प्रत्यक्ष प्रमाण नहीं है। इसके बजाय, यूरोप में क्रमगुणित्स पर पहला काम यहूदी विद्वानों द्वारा किया गया था, जैसे कि शब्बीथाई डोनोलो, सेफ़र यतिज़िरह मार्ग की खोज की ।[9] 1677 में, ब्रिटिश लेखक फैबियन स्टेडमैन रिंगिंग बदलें को बदलने के लिए क्रमगुणित्स के अनुप्रयोग का वर्णन किया गया है , तथा संगीत कला जिसमें कई ट्यून्ड घंटियों की रिंगिंग सम्मिलित है।[10][11]
15वीं शताब्दी के अंत से, क्रमगुणित पश्चिमी गणितज्ञों द्वारा अध्ययन का विषय बन गया। 1494 के ग्रंथ में, इतालवी गणितज्ञ लुका पैसिओली ने डाइनिंग टेबल व्यवस्था की समस्या के संबंध में 11 तक क्रमगुणित की गणना की।[12] क्रिस्टोफर की ने जोहान्स डी सैक्रोबोस्को के काम पर 1603 की टिप्पणी में क्रमगुणित्स पर चर्चा की, और 1640 के दशक में, फ्रांसीसी पोलीमैथ समुद्री मर्सेन ने क्लैवियस के काम के आधार पर क्रमगुणित्स की बड़ी (किन्तुपूरी तरह से सही नहीं) तालिकाएँ प्रकाशित कीं।[13] अपने गुणांकों के लिए क्रमगुणित के पारस्परिक के साथ घातीय कार्य के लिए शक्ति श्रृंखला, पहली बार 1676 में आइजैक न्यूटन द्वारा गॉटफ्रीड विल्हेम लीबनिज को पत्र में तैयार की गई थी।[14] क्रमगुणित्स पर प्रारंभिक यूरोपीय गणित के अन्य महत्वपूर्ण कार्यों में जॉन वालिस द्वारा 1685 के ग्रंथ में व्यापक कवरेज सम्मिलित है, बड़े मूल्यों के लिए उनके अनुमानित मूल्यों का अध्ययन 1721 में अब्राहम डी मोइवरे द्वारा , जेम्स स्टर्लिंग (गणितज्ञ) से डी मोइवर को 1729 का पत्र जिसमें कहा गया था कि स्टर्लिंग के सन्निकटन के रूप में जाना जाता है, और यही समय में डैनियल बर्नौली और लियोनहार्ड यूलर द्वारा गामा के लिए क्रमगुणित फलन के निरंतर विस्तार को तैयार करने का कार्य किया [15] एड्रियन मैरी लीजेंड्रे ने संख्या सिद्धांत पर 1808 के पाठ में, प्रमुख शक्तियों में क्रमगुणित के पूर्णांक गुणनखंडन में एक्सपोनेंट्स का वर्णन करते हुए लीजेंड्रे के सूत्र को सम्मिलित किया।[16]
अंकन क्रमगुणित के लिए 1808 में फ्रांसीसी गणितज्ञ क्रिश्चियन क्रैम्प द्वारा प्रस्तुत किया गया था।[17]कई अन्य संकेतन भी उपयोग किए गए हैं। और बाद का अंकन, जिसमें क्रमगुणित का तर्क बॉक्स के बाईं ओर और नीचे की ओर आधा-संलग्न था, जो ब्रिटेन और अमेरिका में कुछ समय के लिए लोकप्रिय था, किन्तु उपयोग से बाहर हो गया था , संभवतः इसलिए कि इसे टाइप करना कठिनाई है।[17] जहाँ क्रमगुणित (मूल रूप से फ्रेंच: फैक्टोरिएल) शब्द का पहली बार उपयोग 1800 में लुइस फ्रांकोइस एंटोनी अर्बोगैस्ट द्वारा किया गया था,[18] फा डि ब्रूनो के फार्मूले पर पहले काम में,[19] किन्तु अंकगणितीय प्रगति के उत्पादों की अधिक सामान्य अवधारणा का जिक्र करते हुए। यह नाम जिन कारकों को संदर्भित करता है, वे क्रमगुणित के लिए उत्पाद सूत्र की शर्तें हैं।[20]
परिभाषा
किसी धनात्मक पूर्णांक का क्रमगुणन फलन से अधिक नहीं सभी धनात्मक पूर्णांकों के उत्पाद द्वारा परिभाषित किया गया है [1]
इसे अधिक संक्षेप में गुणन या कैपिटल पाई नोटेशन के रूप में लिखा जा सकता है[1]
शून्य का भाज्य
तथ्यात्मक is , या प्रतीकों में, . इस परिभाषा के लिए कई प्रेरणाएँ हैं:
- ,के लिए की परिभाषा उत्पाद के रूप में बिना किसी संख्या के उत्पाद सम्मिलित है, और इसलिए व्यापक सम्मेलन का उदाहरण है कि खाली उत्पाद, बिना किसी कारक का उत्पाद गुणक पहचान के समान है।[22]
- शून्य वस्तुओं का वास्तव में क्रमचय है: कुछ भी नहीं करने के लिए,होता है इसमें केवल पुनर्व्यवस्था कुछ भी नहीं करना है।[21]
- यह कन्वेंशन कॉम्बिनेटरिक्स में कई पहचानों को उनके मापदंडों के सभी मान्य विकल्पों के लिए मान्य बनाता है। तथा उदाहरण के लिए, सभी को चुनने के विधियों की संख्या के समुच्चय से तत्व है एक द्विपद गुणांक पहचान है जो केवल इसके .[23] साथ मान्य होगी |
- 0 के साथ , क्रमगुणित के लिए पुनरावृत्ति संबंध . पर वैध रहता है इसलिए, इस परिपाटी के साथ, क्रमगुणित की पुनरावर्ती संगणना में बेस केस (प्रत्यावर्तन) के रूप में शून्य के लिए केवल मान होना चाहिए, जिससे संगणना को सरल बनाना और अतिरिक्त विशेष स्थितियों की आवश्यकता से बचना।[24]
- स्थापना कई सूत्रों की कॉम्पैक्ट अभिव्यक्ति की अनुमति देता है, जैसे घातीय कार्य, शक्ति श्रृंखला के रूप में: [14]
- यह विकल्प गामा फलन से मेल खाता है , और गामा फलन का सतत फलन होने के लिए यह मान होना चाहिए।[25]
अनुप्रयोग
क्रमगुणित फलन के प्रारंभिक उपयोगों में गिनत:क्रमपरिवर्तन सम्मिलित हैं अलग-अलग वस्तुओं को एक(nन) क्रम में व्यवस्थित करने के ! विभिन्न तरीके हैं।[26] कॉम्बिनेटरिक्स में कई फ़ार्मुलों में क्रमगुणित अधिक रूप से दिखाई देते हैं, जिनमे वस्तुओं के क्रमों के लिए खाते में होते है । उदाहरण के लिए द्विपद गुणांक गिनती करो| -element संयोजन (के सबसेट elements) के साथ समुच्चय से elements, और सूत्र का उपयोग करके क्रमगुणित से गणना की जा सकती है[27]
प्रथम प्रकार की स्टर्लिंग संख्याएँ भाज्यों का योग करती हैं, और चक्रों की समान संख्या वाले उपसमुच्चय में समूहीकृत के क्रमपरिवर्तनों की गिनती करती हैं [28] अन्य संयोजी अनुप्रयोग अपंगताओं की गिनती में है, क्रमपरिवर्तन जो किसी भी तत्व को उसकी मूल स्थिति में नहीं छोड़ते हैं; की अव्यवस्थाओं की संख्या . आइटम गोलाई है|
बीजगणित में, क्रमगुणित्स द्विपद प्रमेय के माध्यम से उत्पन्न होते हैं, जो राशियों की शक्तियों का विस्तार करने के लिए द्विपद गुणांक का उपयोग करता है।[29] वे बहुपदों के कुछ परिवारों को दूसरे से संबंधित करने के लिए उपयोग किए जाने वाले गुणांकों में भी होते हैं, उदाहरण के लिए सममित बहुपद के लिए न्यूटन की पहचान में है ।[30] क्रमपरिवर्तन की गणना में उनका उपयोग बीजगणितीय रूप से भी बहाल किया जा सकता है:और भाज्य परिमित सममित समूह के समूह का क्रम है।[31] तथा कलन में, उच्च डेरिवेटिव की श्रृंखला के लिए फै डी ब्रूनो के सूत्र में क्रमगुणित होते हैं।[19]गणितीय विश्लेषण में, क्रमगुणित अधिकांशतः शक्ति श्रृंखला के denominators विशेष रूप से घातीय कार्य के लिए श्रृंखला में दिखाई देते हैं| [14]
संभाव्यता सिद्धांत में क्रमगुणित का व्यापक रूप से उपयोग किया जाता है, उदाहरण के लिए पॉसों वितरण में[40] और यादृच्छिक क्रमपरिवर्तन की संभावनाओं में है ।[41] कंप्यूटर विज्ञान में, क्रमपरिवर्तन पर ब्रूट-फोर्स खोजों के विश्लेषण से परे है ,[42] की निचली सीमा में भाज्य उत्पन्न होते हैं तुलना के समुच्चय को सॉर्ट करने के लिए आवश्यक तुलनाओं की संख्या पर सामान,[43]और श्रृंखलित हैश तालिकाओं के विश्लेषण में, जहां प्रति सेल चाबियों के वितरण को प्वासों वितरण द्वारा स्पष्ट रूप से अनुमानित किया जा सकता है।[44] इसके अतिरिक्त, क्रमगुणित स्वाभाविक रूप से क्वांटम यांत्रिकी और सांख्यिकीय भौतिकी के सूत्रों में दिखाई देते हैं, जहां अधिकांशतः कणों के समुच्चय के सभी संभावित क्रमपरिवर्तनों पर विचार किया जाता है। सांख्यिकीय यांत्रिकी में, एन्ट्रापी की गणना जैसे कि बोल्ट्जमैन का एंट्रॉपी फॉर्मूला या सैकुर-टेट्रोड समीकरण को गिब्स विरोधाभास से बचने के लिए प्रत्येक प्रकार के समान कण की संख्या के भाज्य द्वारा विभाजित करके माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) की गिनती को सही करना चाहिए। क्वांटम भौतिकी अंतर्निहित कारण प्रदान करती है कि ये सुधार क्यों आवश्यक हैं।[45]
गुण
विकास और सन्निकटन
, कार्य के रूप में क्रमगुणित में एक्सपोनेंशियल ग्रोथ की तुलना में तेज है, किन्तु दोहरा घातीय कार्य की तुलना में धीरे-धीरे बढ़ता है।[46] इसकी विकास , दर समान है किन्तु एक घातीय कारक द्वारा धीमा है। इस परिणाम तक पहुँचने का विधि क्रमगुणित का प्राकृतिक लघुगणक लेना है, जो इसके उत्पाद सूत्र को योग में बदल देता है, और फिर अभिन्न द्वारा योग का अनुमान लगाता है:
परिणाम को एक्सपोनेंट करना (और नगण्य को अनदेखा करना टर्म) अनुमानित है जैसा .[47] ट्रैपेज़ॉइड नियम का उपयोग करते हुए, अधिक ध्यान से ऊपर और नीचे दोनों को इंटीग्रल से जोड़ना, यह दर्शाता है कि इस अनुमान . के लिए आनुपातिक सुधार कारक की आवश्यकता है . इस सुधार के लिए आनुपातिकता का स्थिरांक वालिस उत्पाद से पाया जा सकता है, जो क्रमगुणित और दो की शक्तियों के सीमित अनुपात के रूप में व्यक्त करता है । इन सुधारों का परिणाम स्टर्लिंग का सन्निकटन है:[48]
यहां ही प्रतीक का अर्थ है कि, जैसा अनंत तक जाता है, बाएँ और दाएँ पक्षों के बीच का अनुपात सीमा (गणित) में के करीब पहुँचता है। स्टर्लिंग का सूत्र स्पर्शोन्मुख श्रृंखला में पहला शब्द प्रदान करता है जो अधिक संख्या में पदों पर ले जाने पर और भी स्पष्ट हो जाता है:[49]
तुलना छँटाई का विश्लेषण करने के लिए उपयोग किए जाने वाले क्रमगुणित के द्विआधारी लघुगणक का स्टर्लिंग के सन्निकटन का उपयोग करके बहुत स्पष्ट अनुमान लगाया जा सकता है। नीचे दिए गए सूत्र में टर्म बिग ओ नोटेशन को आमंत्रित करता है।[43]
विभाज्यता और अंक
क्रमगुणित के लिए उत्पाद सूत्र का तात्पर्य है पर होने वाली सभी अभाज्य ,संख्याओं से विभाज्य है और कोई बड़ी अभाज्य संख्या नहीं।[50] इसकी विभाज्यता के बारे में अधिक स्पष्ट जानकारी लीजेंड्रे के सूत्र द्वारा दी गई है, जो के प्रधान गुणनखंड में प्रत्येक अभाज्य का प्रतिपादक देता है [51][52]
यहां , , के आधार अंक योग को दर्शाता है और इस सूत्र द्वारा दिए गए प्रतिपादक की व्याख्या उन्नत गणित में -adic वैल्यूएशन के रूप में भी की जा सकती है भाज्य का मूल्यांकन।[52] द्विपद गुणांकों के उत्पाद सूत्र के लिए लीजेंड्रे के सूत्र को प्रयुक्त करने से कम्मर प्रमेय उत्पन्न होता है, द्विपद गुणांक के गुणनखंड में प्रत्येक अभाज्य के घातांक पर समान परिणाम।[53] क्रमगुणित के प्रमुख कारकों को अलग-अलग तरीकों से प्रमुख शक्तियों में समूहीकृत करने से क्रमगुणित के गुणक विभाजन उत्पन्न होते हैं।[54]
लीजेंड्रे के फार्मूले का विशेष स्थितिया भाज्य के दशमलव निरूपण में अनुगामी शून्य या क्रमगुणित की संख्या देता है।[55] इस सूत्र के अनुसार के से आधार-5 अंकों को घटाकर शून्यों की संख्या प्राप्त की जा सकती है और परिणाम को चार से विभाजित करना।[56] लीजेंड्रे के सूत्र का अर्थ है कि अभाज्य का प्रतिपादक के घातांक से , सदैव बड़ा होता है , इसलिए इन अनुगामी शून्यों में से इस का उत्पादन करने के लिए पांच के प्रत्येक कारक को दो के कारक के साथ जोड़ा जा सकता है।[55] क्रमगुणित के प्रमुख अंक बेनफोर्ड के नियम के अनुसार वितरित किए जाते हैं।[57] अंकों का प्रत्येक अनुक्रम, किसी भी आधार में, उस आधार में किसी भाज्य संख्या के आरंभिक अंकों का क्रम होता है।[58]
क्रमगुणित्स की विभाज्यता पर और परिणाम, विल्सन के प्रमेय में कहा गया है कि , से विभाज्य है यदि और केवल यदि अभाज्य संख्या है।[50] किसी दिए गए के लिए integer , केम्पनर कार्य कार्य सबसे छोटा दिया जाता है जिसके लिए .विभाजित करता है तथा लगभग सभी संख्याओं के लिए (शून्य स्पर्शोन्मुख घनत्व वाले अपवादों के उपसमुच्चय को छोड़कर), यह सबसे बड़े अभाज्य गुणक . के साथ मेल खाता है
दो क्रमगुणित का उत्पाद, , सदैव . समान रूप से विभाजित करता है असीम रूप से कई क्रमगुणित हैं जो अन्य क्रमगुणित के उत्पाद के समान हैं: यदि तब स्वयं क्रमगुणित का कोई उत्पाद है उसी उत्पाद को और भाज्य से गुणा करने के समान है, . क्रमगुणित के एकमात्र ज्ञात उदाहरण जो अन्य क्रमगुणित के उत्पाद हैं किन्तु इस तुच्छ रूप के नहीं हैं , , और .[59] यह एबीसी अनुमान से अनुसरण करेगा abc अनुमान है कि केवल बहुत से गैर-तुच्छ उदाहरण हैं।[60]
आदिम भाग और डिग्री की सामग्री के मूल्यों का सबसे बड़ा सामान्य विभाजक पूर्णांकों पर समान रूप से . विभाजित होता है
The product of two factorials, , always evenly divides .[61] There are infinitely many factorials that equal the product of other factorials: if is itself any product of factorials, then equals that same product multiplied by one more factorial, . The only known examples of factorials that are products of other factorials but are not of this "trivial" form are , , and .[62] It would follow from the [[abc conjecture|abc conjecture]] that there are only finitely many nontrivial examples.[63]
The greatest common divisor of the values of a primitive polynomial of degree over the integers evenly divides .[61]
सतत इंटरपोलेशनफ़ंक्शनगैर-पूर्णांक सामान्यीकरण
क्रमगुणित को निरंतर कार्य करने के लिए असीमित रूप से कई तरीके हैं।[64] इनमें से सबसे अधिक व्फ़ंक्शन रूप से उपयोग किया जाता है[65] गामा फलन का उपयोग करता है, जिसे अभिन्न के रूप में धनात्मक वास्तविक संख्याओं के लिए पफ़ंक्शनषित किया जा सकता है
समान समाकल किसी सम्मिश्र संख्या के लिए अधिक सामान्य रूप से अभिसरित होता है जिसका वास्तविक भाग धनात्मक होता है। इसे यूलर के परावर्तन सूत्र को हल करके बाकी सम्मिश्र तल में गैर-पूर्णांक बिंदुओं तक बढ़ाया जा सकता है
अन्य सम्मिश्र कार्य जो तथ्यात्मक मूल्यों को प्रक्षेप फलन करते हैं, उनमें हैडमार्ड का गामा फलन सम्मिलित है, जो गैर-धनात्मक पूर्णांकों सहित सभी सम्मिश्र संख्याओं पर संपूर्ण कार्य है।[67][68] पी-एडिफ़ंक्शनबर में p-ऐडिक नंबर, क्रमगुणित फलन को सीधे इंटरपोलेट करना संभव नहीं है, क्योंकि बड़े पूर्णांक के क्रमगुणित ( सघन उपसमुच्चय) p-adics) लीजेंड्रे के सूत्रों के अनुसार शून्य में परिवर्तित हो जाते हैं, किसी भी निरंतर कार्य को विवस कर देते हैं जो उनके मूल्यों के करीब हर स्थान शून्यफ़ंक्शनजाता है। इसके बफ़ंक्शन पी-एडिक गामा फलन p-एडिक गामा फलन क्रमगुणित के संशोधित रूप का निरंतर प्रक्षेप प्रदान करता है, जो क्रमगुणित में उन कारकों को छोड़ देता है जो p फलन हैं .[69]
डिगामा फलन गामा फलन का लघुगणकीय व्युत्पन्न है।जिस तरह गामा फलन क्रमगुणित्स का निरंतर प्रक्षेप प्रदान करता है, के फलन ऑफसेट होता है, उसी तरह डिगामा फलन हार्मोनिक संख्याओं का निरंतर प्रक्षेप प्रदान करता है, जो यूलर-मास्चेरोनी स्थिरांक द्वारा ऑफसेट होता है।[70]
संगणना
क्रमगुणित फलन वैज्ञानिक कैलकुलेटर में सामान्य विशेषता है।[71] यह वैज्ञानिक प्रोग्रामिंग पुस्तकालयों जैसे कि पायथन (प्रोग्रामिंग भाषा) गणितीय कार्य मॉड्यूल में भी सम्मिलित है[72] और बूस्ट (सी++ लाइब्रेरी)|[73] यदि दक्षता चिंता का विषय नहीं है, तो क्रमगुणित की गणना तुच्छ है: बस से क्रमिक रूप से चर को . आरंभिक रूप से गुणा करें ऊपर पूर्णांकों द्वारा इस संगणना की सरलता इसे विभिन्न कंप्यूटर प्रोग्रामिंग शैलियों और विधियों के उपयोग में सामान्य उदाहरण बनाती है।[74]
जिसे की गणना पुनरावृति का उपयोग करके स्यूडोकोड में व्यक्त किया जा सकता है[75]
क्रमगुणित परिभाषित करें (N):
च:= 1
i := 1, 2, 3, ..., n के लिए:
च�:= च × मैं
वापसी च
या पुनरावर्तन (कंप्यूटर विज्ञान) का उपयोग करना[76] इसके पुनरावृत्ति संबंध के आधार पर
क्रमगुणित परिभाषित करें (एन): यदि एन = 0 वापसी 1 वापसी n × भाज्य (n − 1)
इसकी गणना के लिए उपयुक्त अन्य विधियों में मेमोइज़ेशन, ,[77] डायनेमिक प्रोग्रामिंग,,[78] और कार्यात्मक प्रोग्रामिंग।[79] इन एल्गोरिदम की कम्प्यूटेशनल सम्मिश्रता का विश्लेषण गणना के यूनिट-कॉस्ट रैंडम-एक्सेस मशीन मॉडल का उपयोग करके किया जा सकता है, जिसमें प्रत्येक अंकगणितीय ऑपरेशन में निरंतर समय लगता है और प्रत्येक संख्या स्टोरेज स्पेस की निरंतर मात्रा का उपयोग करती है। इस मॉडल में, ये विधियाँ गणना कर सकती हैं जिससे समय , के अंदर और पुनरावृत्त संस्करण स्थान . का उपयोग करता है जब तक पूंछ पुनरावर्तन के लिए अनुकूलित नहीं किया जाता है, पुनरावर्ती संस्करण अपने कॉल स्टैक को संग्रहीत करने के लिए रैखिक स्थान लेता है।[80] चूँकि, गणना का यह मॉडल तभी उपयुक्त है जब अनुमति देने के लिए अधिक छोटा है मशीन शब्द में फिट होने के लिए।[81] मान 12! और 20! सबसे बड़े क्रमगुणित हैं जिन्हें क्रमशः 32-बिट कंप्यूटिंग | 32-बिट में संग्रहीत किया जा सकता है[82] and 64-bit integers.[83] Floating point can represent larger factorials, but approximately rather than exactly, and will still overflow for factorials larger than .[82] बड़े क्रमगुणित की स्पष्ट गणना में क्रमगुणित या ग्रोथ_एंड_प्रॉक्सिमेशन और पूर्णांक अतिप्रवाह के कारण इच्छानुसार से स्पष्ट अंकगणित सम्मिलित है। परिणाम में अंकों या बिट्स की संख्या के कार्य के रूप में गणना के समय का विश्लेषण किया जा सकता है।[83] स्टर्लिंग के सूत्र से, है बिट्स।[84] शॉनहेज-स्ट्रैसन एल्गोरिथम उत्पादन कर सकता है , में -bit उत्पादन कर सकता है और समय तेज गुणन एल्गोरिदम में समय लगता है जाने जाते हैं।[85] चूंकि, क्रमगुणित की गणना में एकल गुणन के अतिरिक्त बार-बार उत्पाद सम्मिलित होते हैं, इसलिए ये समय सीमाएं सीधे प्रयुक्त नहीं होती हैं। इस सेटिंग में, कंप्यूटिंग 1 से संख्याओं का गुणा करके क्रम में अक्षम है, क्योंकि इसमें सम्मिलित है गुणन, जिसका निरंतर अंश समय लेता है प्रत्येक, कुल समय . दे रहा है गुणा-और-जीत एल्गोरिदम के रूप में गुणा करने का नियमविधि है जो अनुक्रम को गुणा करता है संख्याओं को इसके दो क्रमों में विभाजित करके संख्याएँ, प्रत्येक अनुक्रम को गुणा करती हैं, और परिणामों को अंतिम गुणन के साथ जोड़ती हैं। क्रमगुणित के इस दृष्टिकोण में कुल समय लगता है : लघुगणक क्रमगुणित में बिट्स की संख्या से आता है, दूसरा गुणन एल्गोरिथ्म से आता है, और तीसरा फूट डालो और जीतो से आता है।[86]
n! कंप्यूटिंग द्वारा और भी नियमदक्षता प्राप्त की जाती है n! इसके प्रधान गुणनखंड से, इस सिद्धांत पर आधारित है कि वर्ग करके घातांक उत्पाद में घातांक का विस्तार करने की तुलना में तेज़ है।[84][87] अर्नोल्ड शॉनहेज द्वारा इसके लिए एल्गोरिदम प्राइम अप की सूची ढूंढकर प्रारंभिक होता है उदाहरण के लिए एराटोस्थनीज की चालनित्र का उपयोग करके, , और प्रत्येक अभाज्य के लिए प्रतिपादक की गणना करने के लिए लीजेंड्रे के सूत्र का उपयोग करता है। फिर यह पुनरावर्ती एल्गोरिथम का उपयोग करते हुए, इन घातांकों के साथ प्रमुख शक्तियों के उत्पाद की गणना करता है::
- उन अभाज्य संख्याओं के गुणनफल की गणना करने के लिए विभाजित करें और जीतें जिनका घातांक विषम हैं
- सभी घातांकों को दो से विभाजित करें ( पूर्णांक तक नीचे की ओर), इन छोटे घातांकों के साथ प्रमुख शक्तियों के उत्पाद की पुनरावर्ती गणना करें, और परिणाम का वर्ग करें
- पिछले दो चरणों के परिणामों को साथ गुणा करें
तक सभी अभाज्य संख्याओं का गुणनफल -बिट संख्या, अभाज्य संख्या प्रमेय द्वारा, तो पहले चरण के लिए समय है , जिसमें लघुगणक विभाजित और अधीन करना आता है और दूसरा गुणा एल्गोरिथम से आता है। एल्गोरिथ्म के पुनरावर्ती कॉल में, प्रधान संख्या प्रमेय को फिर से यह सिद्ध करने के लिए प्रयुक्त किया जा सकता है कि संबंधित उत्पादों में बिट्स की संख्या पुनरावर्तन के प्रत्येक स्तर पर स्थिर कारक से घट जाती है, इसलिए पुनरावर्तन के सभी स्तरों पर इन चरणों के लिए कुल समय . ज्यामितीय श्रृंखला में जोड़ता है दूसरे चरण में वर्ग करने और तीसरे चरण में गुणा करने का समय फिर से है , क्योंकि प्रत्येक बिट्स। संख्या का एकल गुणन है । फिर से, पुनरावर्तन के प्रत्येक स्तर पर सम्मिलित संख्याओं में कई बिट्स के रूप में निरंतर अंश होता है (क्योंकि अन्यथा बार-बार उन्हें चुकता करने से अंतिम परिणाम बहुत बड़ा होगा) इसलिए फिर से पुनरावर्ती कॉल में इन चरणों के लिए समय की मात्रा ज्यामितीय श्रृंखला में जोड़ती है . परिणाम स्वरुप , पूरा एल्गोरिदम लेता है , इसके परिणाम में बिट्स की समान संख्या के साथ एकल गुणन के समानुपाती।[87]
संबंधित अनुक्रम और कार्य
कई अन्य पूर्णांक क्रम क्रमगुणित के समान या उससे संबंधित हैं:
वैकल्पिक योग क्रमगुणित
- प्रत्यावर्ती भाज्य पहले के क्रमगुणित, . प्रत्यावर्ती योग का निरपेक्ष मान है इनका मुख्य रूप से उनकी आदिमता के संबंध में अध्ययन किया गया है; उनमें से बहुत से ही प्रधान हो सकते हैं, किन्तुइस रूप के अभाज्यों की पूरी सूची ज्ञात नहीं है।[88]
- भार्गव क्रमगुणित
- भार्गव क्रमगुणित, मंजुल भार्गव द्वारा परिभाषित पूर्णांक अनुक्रमों का परिवार है, जिसमें क्रमगुणित्स के समान संख्या-सैद्धांतिक गुण हैं, जिसमें क्रमगुणित्स स्वयं विशेष स्थितियोंके रूप में सम्मिलित हैं।[61]डबल क्रमगुणित
- कुछ विषम धनात्मक तक सभी विषम पूर्णांकों का गुणनफल , डबल क्रमगुणित कहा जाता है और . द्वारा दर्शाया गया वह है,
- उदाहरण के लिए, 9!! = 1 × 3 × 5 × 7 × 9 = 945. त्रिकोणमितीय कार्यों के इंटीग्रल की सूची में डबल क्रमगुणित का उपयोग कफ़ंक्शनजाता है,[89]}} That is,For example, 9!! = 1 × 3 × 5 × 7 × 9 = 945. Double factorials are used in trigonometric integrals,[90]
- घातीय भाज्य
- जिस प्रकार त्रिभुजाकार संख्याओं से , संख्याओं का योग होता है , और क्रमगुणित उनके उत्पाद को लेते हैं, घातीय भाज्य एक्सपोनेंटियेट्स। घातीय क्रमगुणन को पुनरावर्ती रूप से परिभाषित किया गया है as . उदाहरण के लिए, 4 का चरघातांकी भाज्य है
- ये संख्याएँ नियमित क्रमगुणित्स की तुलना में बहुत अधिक तेज़ी से बढ़ती हैं।[91]
क्रमगुणित गिरना
- अंकन या का उपयोग कभी-कभी . के समान और ,सहित पूर्णांकों की गिनती और उनके गुणनफल को दर्शाने के लिए किया जाता है। इसे फ़ॉलिंग फ़ैक्टोरियल या बैकवर्ड फ़ैक्टोरियल के रूप में भी जाना जाता है, और अंकन एक पोचहैमर प्रतीक है। [96] गिरते क्रमगुणित एन अलग-अलग वस्तुओं के विभिन्न अनुक्रमों की संख्या की गणना करते हैं जिन्हें एक्स वस्तुओं के ब्रह्मांड से खींचा जा सकता है। [97] वे बहुपदों के उच्च व्युत्पन्नों में गुणांक के रूप में होते हैं, [98] और यादृच्छिक चर के तथ्यात्मक क्षणों में। [99]
- का हाइपरक्रमगुणित उत्पाद है . ये संख्याएँ हर्मिट बहुपद के विभेदक का निर्माण करती हैं।[92] उन्हें K कार्य द्वारा निरंतर प्रक्षेपित किया जा सकता है,[93] और स्टर्लिंग के सूत्र के अनुरूपों का पालन करें[94] और विल्सन की प्रमेय।[95]
- जॉर्डन-पोल्या नंबर
- जॉर्डन-पोल्या नंबर क्रमगुणित के उत्पाद हैं, जो दोहराव की अनुमति देते हैं। प्रत्येक ट्री (ग्राफ सिद्धांत) में समरूपता समूह होता है जिसकी समरूपता की संख्या जॉर्डन-पोल्या संख्या होती है, और प्रत्येक जॉर्डन-पोल्या संख्या किसी ट्री की समरूपता की गणना करती है।[96]
प्राथमिक
- आदिम ; कम या समान अभाज्य संख्याओं का गुणनफल है यह निर्माण उन्हें क्रमगुणित्स के लिए कुछ समान विभाज्यता गुण देता है,[34] किन्तु क्रमगुणित के विपरीत वर्गमुक्त हैं।[97] क्रमगुणित प्राइम्स , की तरह शोधकर्ताओं ने प्राथमिक अभाज्यताओं .[34] का अध्ययन किया है
सबक्रमगुणित
- सबक्रमगुणित समुच्चय के विचलन की संख्या उत्पन्न करता है वस्तुओं। इसे कभी-कभी निरूपित किया जाता है .[98] और निकटतम पूर्णांक के समान है
- का सुपरक्रमगुणित पहले का उत्पाद है भाज्य। बार्न्स जी-कार्य द्वारा सुपरक्रमगुणित्स को निरंतर प्रक्षेपित किया जाता है।[99]
संदर्भ
- ↑ 1.0 1.1 1.2 Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1988). ठोस गणित. Reading, MA: Addison-Wesley. p. 111. ISBN 0-201-14236-8.
- ↑ 2.0 2.1 Datta, Bibhutibhusan; Singh, Awadhesh Narayan (2019). "Use of permutations and combinations in India". In Kolachana, Aditya; Mahesh, K.; Ramasubramanian, K. (eds.). भारतीय गणित और खगोल विज्ञान में अध्ययन: कृपा शंकर शुक्ल के चयनित लेख. Sources and Studies in the History of Mathematics and Physical Sciences. Springer Singapore. pp. 356–376. doi:10.1007/978-981-13-7326-8_18. S2CID 191141516.. Revised by K. S. Shukla from a paper in Indian Journal of History of Science 27 (3): 231–249, 1992, MR1189487. See p. 363.
- ↑ Jadhav, Dipak (August 2021). "एकता संख्या नहीं होने पर जैन विचार". History of Science in South Asia. University of Alberta Libraries. 9: 209–231. doi:10.18732/hssa67. S2CID 238656716.. See discussion of dating on p. 211.
- ↑ Biggs, Norman L. (May 1979). "कॉम्बिनेटरिक्स की जड़ें". Historia Mathematica. 6 (2): 109–136. doi:10.1016/0315-0860(79)90074-0. MR 0530622.
- ↑ 5.0 5.1 Katz, Victor J. (June 1994). "कक्षा में नृवंशविज्ञान". For the Learning of Mathematics. 14 (2): 26–30. JSTOR 40248112.
- ↑ Sefer Yetzirah at Wikisource, Chapter IV, Section 4
- ↑ Rashed, Roshdi (1980). "इब्न अल-हेथम और विल्सन की प्रमेय". Archive for History of Exact Sciences (in français). 22 (4): 305–321. doi:10.1007/BF00717654. MR 0595903. S2CID 120885025.
- ↑ Acerbi, F. (2003). "हिप्पार्कस के कंधों पर: प्राचीन ग्रीक कॉम्बिनेटरिक्स का पुनर्मूल्यांकन". Archive for History of Exact Sciences. 57 (6): 465–502. doi:10.1007/s00407-003-0067-0. JSTOR 41134173. MR 2004966. S2CID 122758966.
- ↑ Katz, Victor J. (2013). "Chapter 4: Jewish combinatorics". In Wilson, Robin; Watkins, John J. (eds.). कॉम्बिनेटरिक्स: प्राचीन और आधुनिक. Oxford University Press. pp. 109–121. ISBN 978-0-19-965659-2. See p. 111.
- ↑ Hunt, Katherine (May 2018). "परिवर्तन की कला: बेल-रिंगिंग, विपर्यय, और सत्रहवीं शताब्दी इंग्लैंड में संयोजन की संस्कृति" (PDF). Journal of Medieval and Early Modern Studies. 48 (2): 387–412. doi:10.1215/10829636-4403136.
- ↑ Stedman, Fabian (1677). कैम्पेनोलॉजी. London. pp. 6–9. The publisher is given as "W.S." who may have been William Smith, possibly acting as agent for the Society of College Youths, to which society the "Dedicatory" is addressed.
- ↑ Knobloch, Eberhard (2013). "Chapter 5: Renaissance combinatorics". In Wilson, Robin; Watkins, John J. (eds.). कॉम्बिनेटरिक्स: प्राचीन और आधुनिक. Oxford University Press. pp. 123–145. ISBN 978-0-19-965659-2. See p. 126.
- ↑ Knobloch 2013, pp. 130–133.
- ↑ 14.0 14.1 14.2 Ebbinghaus, H.-D.; Hermes, H.; Hirzebruch, F.; Koecher, M.; Mainzer, K.; Neukirch, J.; Prestel, A.; Remmert, R. (1990). नंबर. Graduate Texts in Mathematics. Vol. 123. New York: Springer-Verlag. p. 131. doi:10.1007/978-1-4612-1005-4. ISBN 0-387-97202-1. MR 1066206.
- ↑ Dutka, Jacques (1991). "क्रमगुणित फ़ंक्शन का प्रारंभिक इतिहास". Archive for History of Exact Sciences. 43 (3): 225–249. doi:10.1007/BF00389433. JSTOR 41133918. MR 1171521. S2CID 122237769.
- ↑ Dickson, Leonard E. (1919). "Chapter IX: Divisibility of factorials and multinomial coefficients". संख्या के सिद्धांत का इतिहास. Vol. 1. Carnegie Institution of Washington. pp. 263–278. See in particular p. 263.
- ↑ 17.0 17.1 Cajori, Florian (1929). "448–449. Factorial "n[[Category: Templates Vigyan Ready]]"". ए हिस्ट्री ऑफ़ मैथेमेटिकल नोटेशन्स, वॉल्यूम II: नोटेशन्स मेनली इन हायर मैथमेटिक्स. The Open Court Publishing Company. pp. 71–77.
{{cite book}}: URL–wikilink conflict (help) - ↑ Miller, Jeff. "गणित के कुछ शब्दों (एफ) के सबसे पहले ज्ञात उपयोग". MacTutor History of Mathematics archive. University of St Andrews.
- ↑ 19.0 19.1 Craik, Alex D. D. (2005). "फा डी ब्रूनो के फार्मूले का प्रागितिहास". The American Mathematical Monthly. 112 (2): 119–130. doi:10.1080/00029890.2005.11920176. JSTOR 30037410. MR 2121322. S2CID 45380805.
- ↑ Arbogast, Louis François Antoine (1800). व्युत्पत्ति गणना (in français). Strasbourg: L'imprimerie de Levrault, frères. pp. 364–365.
- ↑ 21.0 21.1 Hamkins, Joel David (2020). सबूत और गणित की कला. Cambridge, Massachusetts: MIT Press. p. 50. ISBN 978-0-262-53979-1. MR 4205951.
- ↑ Dorf, Richard C. (2003). "Factorials". इंजीनियरिंग टेबल्स की सीआरसी हैंडबुक. CRC Press. p. 5-5. ISBN 978-0-203-00922-2.
- ↑ Goldenberg, E. Paul; Carter, Cynthia J. (October 2017). "A student asks about (−5)!". The Mathematics Teacher. 111 (2): 104–110. doi:10.5951/mathteacher.111.2.0104. JSTOR 10.5951/mathteacher.111.2.0104.
- ↑ Haberman, Bruria; Averbuch, Haim (2002). "The case of base cases: Why are they so difficult to recognize? Student difficulties with recursion". In Caspersen, Michael E.; Joyce, Daniel T.; Goelman, Don; Utting, Ian (eds.). कंप्यूटर विज्ञान शिक्षा में नवाचार और प्रौद्योगिकी पर 7वें वार्षिक SIGCSE सम्मेलन की कार्यवाही, ITiCSE 2002, आरहस, डेनमार्क, 24-28 जून, 2002. Association for Computing Machinery. pp. 84–88. doi:10.1145/544414.544441.
- ↑ Farrell, Orin J.; Ross, Bertram (1971). विश्लेषण में हल की गई समस्याएं: गामा, बीटा, लिजेंड्रे और बेसेल कार्यों के लिए लागू. Dover Books on Mathematics. Courier Corporation. p. 10. ISBN 978-0-486-78308-6.
- ↑ Conway, John H.; Guy, Richard (1998). "Factorial numbers". संख्याओं की पुस्तक (in English). Springer Science & Business Media. pp. 55–56. ISBN 978-0-387-97993-9.
- ↑ Graham, Knuth & Patashnik 1988, p. 156.
- ↑ Riordan, John (1958). कॉम्बिनेटरियल एनालिसिस का परिचय. Wiley Publications in Mathematical Statistics. Chapman & Hall. p. 76. ISBN 9781400854332. MR 0096594.
- ↑ Graham, Knuth & Patashnik 1988, p. 162.
- ↑ Randić, Milan (1987). "सममित कार्य सिद्धांत के माध्यम से विशेषता बहुपद के मूल्यांकन पर". Journal of Mathematical Chemistry. 1 (1): 145–152. doi:10.1007/BF01205340. MR 0895533. S2CID 121752631.
- ↑ Hill, Victor E. (2000). "8.1 Proposition: Symmetric group Sn[[Category: Templates Vigyan Ready]]". समूह और वर्ण. Chapman & Hall. p. 70. ISBN 978-1-351-44381-4. MR 1739394.
{{cite book}}: URL–wikilink conflict (help) - ↑ Christensen, Kim; Moloney, Nicholas R. (2005). "Appendix A: Taylor expansion". Complexity and Criticality. Advanced physics texts. Vol. 1. Imperial College Press. p. 341. ISBN 978-1-86094-504-5.
- ↑ Ore, Øystein (1948). संख्या सिद्धांत और इसका इतिहास. New York: McGraw-Hill. p. 66. ISBN 9780486656205. MR 0026059.
- ↑ 34.0 34.1 34.2 Caldwell, Chris K.; Gallot, Yves (2002). " और की प्राथमिकता पर". Mathematics of Computation. 71 (237): 441–448. doi:10.1090/S0025-5718-01-01315-1. MR 1863013.
- ↑ Guy, Richard K. (2004). "D25: Equations involving factorial ". Unsolved Problems in Number Theory. Problem Books in Mathematics. Vol. 1 (3rd ed.). New York: Springer-Verlag. pp. 301–302. doi:10.1007/978-0-387-26677-0. ISBN 0-387-20860-7. MR 2076335.
- ↑ Neale, Vicky (2017). गैप को बंद करना: अभाज्य संख्याओं को समझने की खोज. Oxford University Press. pp. 146–147. ISBN 978-0-19-878828-7.
- ↑ Erdős, Pál (1932). "चेबीशेव द्वारा एक प्रमेय का प्रमाण" [Proof of a theorem of Chebyshev] (PDF). Acta Litt. Sci. Szeged (in Deutsch). 5: 194–198. Zbl 0004.10103.
- ↑ Chvátal, Vašek (2021). "1.5: Erdős's proof of Bertrand's postulate". पॉल एर्डोस का असतत गणितीय आकर्षण: एक सरल परिचय. Cambridge, England: Cambridge University Press. pp. 7–10. doi:10.1017/9781108912181. ISBN 978-1-108-83183-3. MR 4282416. S2CID 242637862.
- ↑ Fraenkel, Aviezri S. (1985). "संख्या प्रणाली". The American Mathematical Monthly. 92 (2): 105–114. doi:10.1080/00029890.1985.11971550. JSTOR 2322638. MR 0777556.
- ↑ Pitman, Jim (1993). "3.5: The Poisson distribution". संभावना. New York: Springer. pp. 222–236. doi:10.1007/978-1-4612-4374-8. ISBN 978-0-387-94594-1.
- ↑ Pitman 1993, p. 153.
- ↑ Kleinberg, Jon; Tardos, Éva (2006). एल्गोरिथम डिजाइन. Addison-Wesley. p. 55.
- ↑ 43.0 43.1 Knuth, Donald E. (1998). कंप्यूटर प्रोग्रामिंग की कला, खंड 3: छँटाई और खोज (2nd ed.). Addison-Wesley. p. 182. ISBN 978-0-321-63578-5.
- ↑ Sedgewick, Robert; Wayne, Kevin (2011). एल्गोरिदम (4th ed.). Addison-Wesley. p. 466. ISBN 978-0-13-276256-4.
- ↑ Kardar, Mehran (2007). कणों का सांख्यिकीय भौतिकी. Cambridge University Press. pp. 107–110, 181–184. ISBN 978-0-521-87342-0. OCLC 860391091.
- ↑ Cameron, Peter J. (1994). "2.4: Orders of magnitude". कॉम्बिनेटरिक्स: विषय, तकनीक, एल्गोरिदम. Cambridge University Press. pp. 12–14. ISBN 978-0-521-45133-8.
- ↑ Magnus, Robert (2020). "11.10: Stirling's approximation". Fundamental Mathematical Analysis. Springer Undergraduate Mathematics Series. Cham: Springer. p. 391. doi:10.1007/978-3-030-46321-2. ISBN 978-3-030-46321-2. MR 4178171. S2CID 226465639.
- ↑ Palmer, Edgar M. (1985). "Appendix II: Stirling's formula". ग्राफिकल इवोल्यूशन: रैंडम ग्राफ के सिद्धांत का परिचय. Wiley-Interscience Series in Discrete Mathematics. Chichester: John Wiley & Sons. pp. 127–128. ISBN 0-471-81577-2. MR 0795795.
- ↑ 49.0 49.1 49.2 Chen, Chao-Ping; Lin, Long (2012). "गामा फ़ंक्शन के लिए स्पर्शोन्मुख विस्तार पर टिप्पणी". Applied Mathematics Letters. 25 (12): 2322–2326. doi:10.1016/j.aml.2012.06.025. MR 2967837.
- ↑ 50.0 50.1 Beiler, Albert H. (1966). संख्या के सिद्धांत में मनोरंजन: गणित की रानी मनोरंजन करती है. Dover Recreational Math Series (2nd ed.). Courier Corporation. p. 49. ISBN 978-0-486-21096-4.
- ↑ Chvátal 2021. "1.4: Legendre's formula". pp. 6–7.
- ↑ 52.0 52.1 Robert, Alain M. (2000). "3.1: The -adic valuation of a factorial". -adic Analysis. Graduate Texts in Mathematics. Vol. 198. New York: Springer-Verlag. pp. 241–242. doi:10.1007/978-1-4757-3254-2. ISBN 0-387-98669-3. MR 1760253.
- ↑ Peitgen, Heinz-Otto; Jürgens, Hartmut; Saupe, Dietmar (2004). "Kummer's result and Legendre's identity". कैओस एंड फ्रैक्टल्स: न्यू फ्रंटियर्स ऑफ साइंस. New York: Springer. pp. 399–400. doi:10.1007/b97624. ISBN 978-1-4684-9396-2.
- ↑ Alladi, Krishnaswami; Grinstead, Charles (1977). "N के अपघटन पर! प्रमुख शक्तियों में". Journal of Number Theory (in English). 9 (4): 452–458. doi:10.1016/0022-314x(77)90006-3.
- ↑ 55.0 55.1 Koshy, Thomas (2007). "Example 3.12". प्राथमिक संख्या सिद्धांत अनुप्रयोगों के साथ (2nd ed.). Elsevier. p. 178. ISBN 978-0-08-054709-1.
- ↑ Sloane, N. J. A. (ed.). "Sequence A027868 (Number of trailing zeros in n!; highest power of 5 dividing n!)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Diaconis, Persi (1977). "प्रमुख अंकों का वितरण और समान वितरण मोड 1". Annals of Probability. 5 (1): 72–81. doi:10.1214/aop/1176995891. MR 0422186.
- ↑ Bird, R. S. (1972). "दिए गए आरंभिक अंकों के साथ पूर्णांक". The American Mathematical Monthly. 79 (4): 367–370. doi:10.1080/00029890.1972.11993051. JSTOR 2978087. MR 0302553.
- ↑ Guy 2004. "B23: Equal products of factorials". p. 123.
- ↑ Luca, Florian (2007). "क्रमगुणित पर जो क्रमगुणित के उत्पाद हैं". Mathematical Proceedings of the Cambridge Philosophical Society. 143 (3): 533–542. Bibcode:2007MPCPS.143..533L. doi:10.1017/S0305004107000308. MR 2373957. S2CID 120875316.
- ↑ 61.0 61.1 61.2 Bhargava, Manjul (2000). "The factorial function and generalizations". The American Mathematical Monthly. 107 (9): 783–799. CiteSeerX 10.1.1.585.2265. doi:10.2307/2695734. JSTOR 2695734.
- ↑ Guy 2004. "B23: Equal products of factorials". p. 123.
- ↑ Luca, Florian (2007). "On factorials which are products of factorials". Mathematical Proceedings of the Cambridge Philosophical Society. 143 (3): 533–542. Bibcode:2007MPCPS.143..533L. doi:10.1017/S0305004107000308. MR 2373957. S2CID 120875316.
- ↑ 64.0 64.1 Davis, Philip J. (1959). "लियोनहार्ड यूलर का अभिन्न: गामा फ़ंक्शन का एक ऐतिहासिक प्रोफ़ाइल". The American Mathematical Monthly. 66 (10): 849–869. doi:10.1080/00029890.1959.11989422. JSTOR 2309786. MR 0106810.
- ↑ 65.0 65.1 Borwein, Jonathan M.; Corless, Robert M. (2018). "मासिक में गामा और क्रमगुणित". The American Mathematical Monthly. 125 (5): 400–424. arXiv:1703.05349. doi:10.1080/00029890.2018.1420983. MR 3785875. S2CID 119324101.
- ↑ Remmert, Reinhold (1996). "-function". The American Mathematical Monthly. 103 (3): 214–220. doi:10.1080/00029890.1996.12004726. JSTOR 2975370. MR 1376175.
- ↑ Hadamard, J. (1968) [1894]. "Sur l'expression du produit 1·2·3· · · · ·(n−1)[[Category: Templates Vigyan Ready]] par une fonction entière" (PDF). जैक्स हैडमार्ड द्वारा काम करता है (in français). Paris: Centre National de la Recherche Scientifiques.
{{cite book}}: URL–wikilink conflict (help) - ↑ Alzer, Horst (2009). "हैडमर्ड के गामा फ़ंक्शन का एक सुपरएडिटिव गुण". Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 79 (1): 11–23. doi:10.1007/s12188-008-0009-5. MR 2541340. S2CID 123691692.
- ↑ Robert 2000. "7.1: The gamma function ". pp. 366–385.
- ↑ Ross, Bertram (1978). "साई समारोह". Mathematics Magazine. 51 (3): 176–179. doi:10.1080/0025570X.1978.11976704. JSTOR 2689999. MR 1572267.
- ↑ Brase, Charles Henry; Brase, Corrinne Pellillo (2014). समझने योग्य सांख्यिकी: अवधारणाएं और तरीके (11th ed.). Cengage Learning. p. 182. ISBN 978-1-305-14290-9.
- ↑ "गणित - गणितीय कार्य". Python 3 Documentation: The Python Standard Library. Retrieved 2021-12-21.
- ↑ "कारख़ाने का". Boost 1.78.0 Documentation: Math Special Functions. Retrieved 2021-12-21.
- ↑ Addis, Tom; Addis, Jan (2009). आरेखण कार्यक्रम: योजनाबद्ध कार्यात्मक प्रोग्रामिंग का सिद्धांत और अभ्यास. Springer. pp. 149–150. ISBN 978-1-84882-618-2.
- ↑ Chapman, Stephen J. (2019). "Example 5.2: The factorial function". इंजीनियरों के लिए MATLAB प्रोग्रामिंग (6th ed.). Cengage Learning. p. 215. ISBN 978-0-357-03052-3.
- ↑ Hey, Tony; Pápay, Gyuri (2014). द कम्प्यूटिंग यूनिवर्स: ए जर्नी थ्रू ए रेवोल्यूशन. Cambridge University Press. p. 64. ISBN 9781316123225.
- ↑ Bolboaca, Alexandru (2019). C++ के साथ हैंड्स-ऑन फंक्शनल प्रोग्रामिंग: C++17 और C++20 का उपयोग करके त्वरित कार्यात्मक कोड लिखने के लिए एक प्रभावी गाइड. Packt Publishing. p. 188. ISBN 978-1-78980-921-3.
- ↑ Gray, John W. (2014). मास्टरिंग मैथमैटिका: प्रोग्रामिंग के तरीके और अनुप्रयोग. Academic Press. pp. 233–234. ISBN 978-1-4832-1403-0.
- ↑ Torra, Vicenç (2016). एक कार्यात्मक प्रोग्रामिंग परिप्रेक्ष्य से स्काला: प्रोग्रामिंग भाषा का एक परिचय. Lecture Notes in Computer Science. Vol. 9980. Springer. p. 96. ISBN 978-3-319-46481-7.
- ↑ Sussman, Gerald Jay (1982). "LISP, programming, and implementation". कार्यात्मक प्रोग्रामिंग और इसके अनुप्रयोग: एक उन्नत पाठ्यक्रम. CREST Advanced Courses. Cambridge University Press. pp. 29–72. ISBN 978-0-521-24503-6. See in particular p. 34.
- ↑ Chaudhuri, Ranjan (June 2003). "क्या अंकगणितीय परिचालन वास्तव में निरंतर समय में निष्पादित होते हैं?". ACM SIGCSE Bulletin. Association for Computing Machinery. 35 (2): 43–44. doi:10.1145/782941.782977. S2CID 13629142.
- ↑ 82.0 82.1 Fateman, Richard J. (April 11, 2006). "Comments on Factorial Programs" (PDF). University of California, Berkeley.
- ↑ 83.0 83.1 Winkler, Jürgen F. H.; Kauer, Stefan (March 1997). "Proving assertions is also useful". ACM SIGPLAN Notices. Association for Computing Machinery. 32 (3): 38–41. doi:10.1145/251634.251638. S2CID 17347501.
- ↑ 84.0 84.1 Borwein, Peter B. (1985). "क्रमगुणित की गणना की सम्मिश्रता पर". Journal of Algorithms. 6 (3): 376–380. doi:10.1016/0196-6774(85)90006-9. MR 0800727.
- ↑ Harvey, David; van der Hoeven, Joris (2021). "समय में पूर्णांक गुणन " (PDF). Annals of Mathematics. Second Series. 193 (2): 563–617. doi:10.4007/annals.2021.193.2.4. MR 4224716. S2CID 109934776.
- ↑ Arndt, Jörg (2011). "34.1.1.1: Computation of the factorial". मामले कम्प्यूटेशनल: विचार, एल्गोरिदम, स्रोत कोड (PDF). Springer. pp. 651–652. See also "34.1.5: Performance", pp. 655–656.
- ↑ 87.0 87.1 Schönhage, Arnold (1994). फास्ट एल्गोरिदम: एक मल्टीटेप ट्यूरिंग मशीन कार्यान्वयन. B.I. Wissenschaftsverlag. p. 226.
- ↑ Guy 2004. "B43: Alternating sums of factorials". pp. 152–153.
- ↑ Callan, David (2009). "A combinatorial survey of identities for the double factorial". arXiv:0906.1317 [math.CO].
- ↑ Meserve, B. E. (1948). "Classroom Notes: Double Factorials". The American Mathematical Monthly. 55 (7): 425–426. doi:10.2307/2306136. JSTOR 2306136. MR 1527019.
- ↑ Luca, Florian; Marques, Diego (2010). "पावर टावर के सारांश कार्य में पूर्ण शक्तियाँ". Journal de Théorie des Nombres de Bordeaux. 22 (3): 703–718. doi:10.5802/jtnb.740. MR 2769339.
- ↑ Sloane, N. J. A. (ed.). "Sequence A002109 (Hyperfactorials: Product_{k = 1..n} k^k)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Kinkelin, H. (1860). "गामा फलन से संबंधित एक पारलौकिक पर और समाकलन कलन में इसका अनुप्रयोग" [On a transcendental variation of the gamma function and its application to the integral calculus]. Journal für die reine und angewandte Mathematik (in Deutsch). 1860 (57): 122–138. doi:10.1515/crll.1860.57.122. S2CID 120627417.
- ↑ Glaisher, J. W. L. (1877). "उत्पाद पर 11.22.33...nn[[Category: Templates Vigyan Ready]]". Messenger of Mathematics. 7: 43–47.
{{cite journal}}: URL–wikilink conflict (help) - ↑ Aebi, Christian; Cairns, Grant (2015). "डबल-, हाइपर-, सब- और सुपरक्रमगुणित्स के लिए विल्सन के प्रमेय का सामान्यीकरण". The American Mathematical Monthly. 122 (5): 433–443. doi:10.4169/amer.math.monthly.122.5.433. JSTOR 10.4169/amer.math.monthly.122.5.433. MR 3352802. S2CID 207521192.
- ↑ Sloane, N. J. A. (ed.). "Sequence A001013 (Jordan-Polya numbers: products of factorial numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Nelson, Randolph (2020). असतत गणित में एक संक्षिप्त यात्रा. Cham: Springer. p. 127. doi:10.1007/978-3-030-37861-5. ISBN 978-3-030-37861-5. MR 4297795. S2CID 213895324.
- ↑ Graham, Knuth & Patashnik 1988, p. 195.
- ↑ Barnes, E. W. (1900). "[[:Template:मवर]]-function". The Quarterly Journal of Pure and Applied Mathematics. 31: 264–314. JFM 30.0389.02.
{{cite journal}}: URL–wikilink conflict (help)
बाहरी कड़ियाँ
- OEIS sequence A000142 (Factorial numbers)
- "Factorial". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- Weisstein, Eric W. "Factorial". MathWorld.
श्रेणी: संयोजन विज्ञान श्रेणी:गामा और संबंधित कार्य श्रेणी: क्रमगुणित और द्विपद विषय श्रेणी: एकात्मक संचालन