स्टेट-स्पेस प्रतिनिधित्व: Difference between revisions
No edit summary |
m (Abhishekkshukla moved page राज्य-अंतरिक्ष प्रतिनिधित्व to स्टेट-स्पेस प्रतिनिधित्व without leaving a redirect) |
(No difference)
| |
Revision as of 16:11, 13 September 2023
नियंत्रण इंजीनियरिंग में, एक स्टेट-स्पेस प्रतिनिधित्व एक भौतिक प्रणाली का एक गणितीय मॉडल है जो इनपुट, आउटपुट और चर (गणित) के एक समूह के रूप में निर्दिष्ट है, जो पहले-क्रम (दूसरा डेरिवेटिव सम्मिलित नहीं) अंतर समीकरण या अंतर समीकरणों से संबंधित है। इस तरह के वेरिएबल्स, जिन्हें 'स्टेट वेरिएबल्स' कहा जाता है, समय के साथ इस तरह से विकसित होते हैं जो किसी दिए गए तत्काल और इनपुट वैरिएबल के बाहरी रूप से लगाए गए मानों पर निर्भर करते हैं। आउटपुट चर के मान स्टेट चर के मान पर निर्भर करते हैं।
स्टेट स्पेस या चरण स्थान ज्यामितीय स्थान है जिसमें अक्षों पर चर स्टेट चर होते हैं। प्रणाली की स्थिति को वेक्टर (गणित), स्टेट स्पेस के अंदर स्टेट वेक्टर के रूप में दर्शाया जा सकता है।
यदि गतिशील प्रणाली रैखिक, समय-अपरिवर्तनीय और परिमित-आयामी है, तो अंतर और बीजगणितीय समीकरण आव्यूह (गणित) रूप में लिखे जा सकते हैं।[1][2] स्टेट-स्पेस पद्धति को सामान्य प्रणाली सिद्धांत के महत्वपूर्ण बीजगणित द्वारा वर्णित किया जाता है, जो क्रोनकर वेक्टर-आव्यूह संरचनाओं का उपयोग करना संभव बनाता है। इन संरचनाओं की क्षमता को मॉडुलन के साथ या इसके बिना अनुसंधान प्रणालियों पर कुशलतापूर्वक प्रयुक्त किया जा सकता है।[3] स्टेट-स्पेस प्रतिनिधित्व ( समय क्षेत्र दृष्टिकोण के रूप में भी जाना जाता है) कई इनपुट और आउटपुट के साथ प्रणाली को मॉडल और विश्लेषण करने के लिए एक सुविधाजनक और कॉम्पैक्ट विधि प्रदान करता है। इनपुट और आउटपुट के साथ हमें प्रणाली के बारे में सभी जानकारी को एनकोड करने के लिए लाप्लास ट्रांसफॉर्म को लिखना होगा। आवृत्ति डोमेन दृष्टिकोण के विपरीत, स्टेट-स्पेस प्रतिनिधित्व का उपयोग रैखिक घटकों और शून्य प्रारंभिक स्थितियों वाले प्रणाली तक सीमित नहीं है।
स्टेट-स्पेस मॉडल को अर्थशास्त्र जैसे विषयों में प्रयुक्त किया जा सकता है,[4] सांख्यिकी,[5] कंप्यूटर विज्ञान और इलेक्ट्रिकल इंजीनियरिंग,[6] और तंत्रिका विज्ञान।[7] अर्थमिति में, उदाहरण के लिए, स्टेट-स्पेस मॉडल का उपयोग समय श्रृंखला को प्रवृत्ति और चक्र में विघटित करने के लिए किया जा सकता है, व्यक्तिगत संकेतकों को एक समग्र सूचकांक में बना सकता है,[8] व्यापार चक्र के मोड़ बिंदुओं की पहचान करें, और गुप्त और अप्रमाणित के समय श्रृंखला का उपयोग करके सकल घरेलू उत्पाद का अनुमान लगाएं।[9][10] कई अनुप्रयोग अपने पिछले अवलोकनों का उपयोग करके वर्तमान अज्ञात स्थिति चर के अनुमानों का उत्पादन करने के लिए कलमन फिल्टर पर भरोसा करते हैं।[11][12]
स्टेट चर
आंतरिक स्टेट चर प्रणाली चर का सबसे छोटा संभव उपसमुच्चय है जो किसी भी समय प्रणाली की संपूर्ण स्थिति का प्रतिनिधित्व कर सकता है।[13] किसी दिए गए प्रणाली का प्रतिनिधित्व करने के लिए आवश्यक स्टेट चर की न्यूनतम संख्या, , सामान्यतः प्रणाली के परिभाषित अंतर समीकरण के क्रम के सामान्य होता है, किन्तु आवश्यक नहीं है। यदि प्रणाली को स्थानांतरण कार्य प्रपत्र में दर्शाया गया है, तो स्टेट चर की न्यूनतम संख्या स्थानांतरण कार्य के भाजक के क्रम के सामान्य होती है, इसे एक उचित अंश में घटा दिया जाता है। यह समझना महत्वपूर्ण है कि एक स्टेट-स्पेस प्राप्ति को स्थानांतरण कार्य फॉर्म में परिवर्तित करने से प्रणाली के बारे में कुछ आंतरिक जानकारी खो सकती है, और एक प्रणाली का विवरण प्रदान कर सकता है जो स्थिर है, जब स्टेट -स्थान की प्राप्ति कुछ बिंदुओं पर अस्थिर होती है। इलेक्ट्रिक परिपथ में, स्टेट चर की संख्या अधिकांशतः होती है, चूंकि सदैव नहीं, परिपथ में ऊर्जा भंडारण तत्वों की संख्या जैसे संधारित्र और प्रारंभ करनेवाला के समान होती है। परिभाषित स्टेट चर रैखिक रूप से स्वतंत्र होने चाहिए, अर्थात, किसी भी स्टेट चर को अन्य स्टेट चर के रैखिक संयोजन के रूप में नहीं लिखा जा सकता है, या प्रणाली को हल नहीं किया जा सकता है।
रैखिक प्रणाली
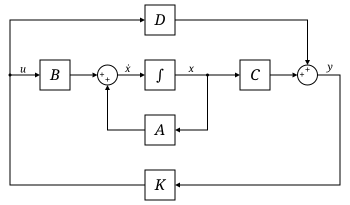
सबसे सामान्य स्टेट-स्पेस प्रतिनिधित्व के साथ एक रैखिक प्रणाली का इनपुट्स, आउटपुट और स्टेट चर निम्नलिखित रूप में लिखे गए हैं:[14]
जहाँ :
- स्टेट वेक्टर कहा जाता है, ;
- आउटपुट वेक्टर कहा जाता है, ;
- इनपुट (या नियंत्रण) वेक्टर कहा जाता है, ;
- स्टेट (या प्रणाली ) आव्यूह है, ,
- इनपुट आव्यूह है, ,
- आउटपुट आव्यूह है, ,
- फीडथ्रू (या फीडफॉरवर्ड) आव्यूह है (ऐसे स्थितियों में जहां प्रणाली मॉडल में डायरेक्ट फीडथ्रू नहीं है, शून्य आव्यूह है), ,
- .
इस सामान्य सूत्रीकरण में, सभी आव्यूहों को समय-भिन्न होने की अनुमति है (अर्थात उनके तत्व समय पर निर्भर हो सकते हैं); चूंकि , सामान्य एलटीआई प्रणाली स्थितियों में, मैट्रिसेस समय अपरिवर्तनीय होंगे। समय परिवर्तनशील निरंतर हो सकता है (उदा। ) या असतत (उदा. ). बाद के स्थितियों में, समय चर का उपयोग सामान्यतः अतिरिक्त किया जाता है . हाइब्रिड प्रणाली समय डोमेन के लिए अनुमति देता है जिसमें निरंतर और असतत दोनों भाग होते हैं। की गई मान्यताओं के आधार पर, स्टेट-स्पेस मॉडल प्रतिनिधित्व निम्नलिखित रूपों को ग्रहण कर सकता है:
| प्रणाली प्रकार | स्टेट-स्पेस मॉडल |
| निरंतर समय-परिवर्तनशील | |
| निरंतर समय-भिन्न | |
| स्पष्ट असतत समय-परिवर्तनशील | |
| स्पष्ट असतत समय-भिन्न | |
| लाप्लास का डोमेन
निरंतर समय-अपरिवर्तनीय |
|
| Z-डोमेन का
असतत समय-अपरिवर्तनीय |
उदाहरण: निरंतर समय एलटीआई स्थिति
एक निरंतर-समय एलटीआई प्रणाली की स्थिरता और प्राकृतिक प्रतिक्रिया विशेषताओं (अर्थात, मैट्रिसेस के साथ रैखिक जो समय के संबंध में स्थिर हैं) का अध्ययन आव्यूह के आइजन वैल्यूज से किया जा सकता है एक समय-अपरिवर्तनीय स्टेट-स्पेस मॉडल की स्थिरता को कारक रूप में प्रणाली के स्थानांतरण कार्य को देखकर निर्धारित किया जा सकता है। तब यह कुछ ऐसा दिखाई देगा:
स्थानांतरण कार्य का भाजक के निर्धारक को लेकर प्राप्त विशेषता बहुपद के सामान्य है ,
इस बहुपद (ईजेनवेल्यूज) की जड़ें प्रणाली स्थानांतरण कार्य के जटिल ध्रुव हैं (अर्थात, गणितीय विलक्षणता जहां स्थानांतरण कार्य की परिमाण अबाधित है)। इन ध्रुवों का विश्लेषण करने के लिए उपयोग किया जा सकता है कि प्रणाली घातीय स्थिरता या सीमांत स्थिरता है या नहीं। स्थिरता का निर्धारण करने के लिए एक वैकल्पिक दृष्टिकोण, जिसमें आइजन वैल्यूज की गणना सम्मिलित नहीं है, प्रणाली की लाइपुनोव स्थिरता का विश्लेषण करना है।
के अंश में पाए जाने वाले शून्य इसी तरह यह निर्धारित करने के लिए उपयोग किया जा सकता है कि प्रणाली न्यूनतम चरण है या नहीं।
प्रणाली अभी भी इनपुट-आउटपुट स्थिर हो सकता है (बीआईबीओ स्थिरता देखें) तथापि यह आंतरिक रूप से स्थिर न हो। यह स्थिति हो सकता है कि यदि अस्थिर ध्रुवों को शून्य से रद्द कर दिया जाता है (अर्थात, यदि स्थानांतरण कार्य में उन विलक्षणताओं को हटाने योग्य विलक्षणता है)।
नियंत्रणीयता
स्टेट नियंत्रणीयता की स्थिति का तात्पर्य है कि यह संभव है - स्वीकार्य इनपुट्स द्वारा - स्थिति किसी भी प्रारंभिक मान से कुछ सीमित समय के अंदर किसी भी अंतिम मान तक ले जाने के लिए। एक निरंतर समय-अपरिवर्तनीय रैखिक स्टेट-स्पेस मॉडल नियंत्रणीय है यदि
जहां रैंक (रैखिक बीजगणित) एक आव्यूह में रैखिक रूप से स्वतंत्र पंक्तियों की संख्या है, और जहां n स्टेट चर की संख्या है।
अवलोकनीयता
प्रेक्षणीयता एक उपाय है कि बाहरी आउटपुट के ज्ञान से प्रणाली के आंतरिक स्टेट को कितनी अच्छी तरह अनुमान लगाया जा सकता है। एक प्रणाली की अवलोकनीयता और नियंत्रणीयता गणितीय दोहरी होती है (अर्थात्, नियंत्रणीयता प्रदान करती है कि एक इनपुट उपलब्ध है जो किसी भी वांछित अंतिम स्थिति में प्रारंभिक अवस्था लाता है, अवलोकनीयता प्रदान करती है कि एक आउटपुट प्रक्षेपवक्र जानने से प्रणाली की प्रारंभिक स्थिति की भविष्यवाणी करने के लिए पर्याप्त जानकारी मिलती है ).
एक निरंतर समय-अपरिवर्तनीय रैखिक स्टेट-स्पेस मॉडल देखने योग्य है यदि और केवल यदि
स्थानांतरण कार्य
निरंतर समय-अपरिवर्तनीय रैखिक स्टेट-स्पेस मॉडल का स्थानांतरण कार्य निम्न विधि से प्राप्त किया जा सकता है:
सबसे पहले, का लाप्लास रूपांतरण लेना
उत्पन्न
अगला, हम देने के लिए सरल करते हैं
और इस तरह
को आउटपुट समीकरण में प्रतिस्थापित करना
दे रही है
शून्य प्रारंभिक स्थितियों को मानते हुए और एक सिंगल-इनपुट सिंगल-आउटपुट (एसआईएसओ) प्रणाली , स्थानांतरण कार्य को आउटपुट और इनपुट के अनुपात के रूप में परिभाषित किया गया है . एमआईएमओ| बहु-इनपुट बहु-आउटपुट (एमआईएमओ) प्रणाली के लिए, चूंकि , यह अनुपात परिभाषित नहीं है। इसलिए, शून्य प्रारंभिक स्थितियों को मानते हुए, स्थानांतरण कार्य आव्यूह से लिया गया है
गुणकों को समान करने की विधि का उपयोग करना जो उपज देता है
- .
फलस्वरूप, आयाम के साथ एक आव्यूह है जिसमें प्रत्येक इनपुट आउटपुट संयोजन के लिए स्थानांतरण कार्य सम्मिलित हैं। इस आव्यूह संकेतन की सादगी के कारण, स्टेट-स्पेस प्रतिनिधित्व सामान्यतः बहु-इनपुट, बहु-आउटपुट प्रणाली के लिए उपयोग किया जाता है। रोसेनब्रॉक प्रणाली आव्यूह स्टेट-स्पेस प्रतिनिधित्व और इसके हस्तांतरण कार्य के बीच एक पुल प्रदान करता है।
प्रामाणिक अहसास
किसी दिए गए स्थानांतरण कार्य को जो सख्ती से उचित है, आसानी से निम्नलिखित दृष्टिकोण से स्टेट -स्पेस में स्थानांतरित किया जा सकता है (यह उदाहरण 4-आयामी, सिंगल-इनपुट, सिंगल-आउटपुट प्रणाली के लिए है):
स्थानांतरण कार्य दिया गया है, अंश और भाजक दोनों में सभी गुणांक प्रकट करने के लिए इसका विस्तार करें। इसका परिणाम निम्न रूप में होना चाहिए:
गुणांक अब निम्नलिखित दृष्टिकोण से सीधे स्टेट-स्पेस मॉडल में डाला जा सकता है:
इस स्टेट-स्पेस की प्राप्ति को नियंत्रणीय विहित रूप कहा जाता है क्योंकि परिणामी मॉडल को नियंत्रित करने की अस्वासन दी जाती है (अर्थात, क्योंकि नियंत्रण एकीकृत करने की एक श्रृंखला में प्रवेश करता है, इसमें हर स्टेट को स्थानांतरित करने की क्षमता होती है)।
स्थानांतरण कार्य गुणांक का उपयोग दूसरे प्रकार के विहित रूप के निर्माण के लिए भी किया जा सकता है
इस स्टेट-स्पेस की प्राप्ति को अवलोकनीय विहित रूप कहा जाता है क्योंकि परिणामी मॉडल को देखने योग्य होने की अस्वासन है (अर्थात, क्योंकि आउटपुट एकीकृत करने की एक श्रृंखला से बाहर निकलता है, प्रत्येक स्टेट का आउटपुट पर प्रभाव पड़ता है)।
उचित स्थानांतरण कार्य
स्थानांतरण कार्य जो केवल उचित स्थानांतरण कार्य हैं (और सख्ती से उचित नहीं हैं) को भी अधिक आसानी से अनुभूत किया जा सकता है। यहां उचित स्थानांतरण कार्य को दो भागों में अलग करने के लिए है: एक कड़ाई से उचित भाग और एक स्थिरांक है।
वास्तव में उचित हस्तांतरण कार्य को ऊपर दिखाए गए विधि का उपयोग करके एक विहित स्टेट-स्पेस प्राप्ति में परिवर्तित किया जा सकता है। निरंतर की स्थिति-स्थान की प्राप्ति तुच्छ रूप से है | साथ में हम एक साथ स्टेट -स्थान की प्राप्ति प्राप्त करते हैं, आव्यूह A, B और C के साथ सख्ती से उचित भाग और मैट्रिक्स D द्वारा निरंतर निर्धारित किया जाता है।
यहाँ चीजों को थोड़ा स्पष्ट करने के लिए एक उदाहरण है:
जो निम्नलिखित नियंत्रणीय अहसास उत्पन्न करता है
ध्यान दें कि आउटपुट सीधे इनपुट पर कैसे निर्भर करता है। यह स्थानांतरण कार्य स्थिरांक के कारण है।
प्रतिक्रिया
प्रतिक्रिया के लिए एक सामान्य विधि है आउटपुट को आव्यूह K से गुणा करना और इसे प्रणाली के इनपुट के रूप में समूह करना: .
चूँकि K के मान अप्रतिबंधित हैं, ऋणात्मक प्रतिक्रिया के लिए मानो को आसानी से नकारा जा सकता है।
एक ऋणात्मक चिह्न (सामान्य संकेतन) की उपस्थिति केवल एक अंकन है और इसकी अनुपस्थिति का अंतिम परिणामों पर कोई प्रभाव नहीं पड़ता है।
हो जाता है
के लिए आउटपुट समीकरण को हल करना और स्टेट समीकरण में प्रतिस्थापित करने का परिणाम होता है
इसका लाभ यह है कि A के आइजन वैल्यूज के आइजन अपघटन के माध्यम से K को उचित रूप से स्थित करके नियंत्रित किया जा सकता है .
यह मानता है कि बंद-लूप प्रणाली नियंत्रणीय है या ए के अस्थिर आइजन वैल्यूज को के उचित विकल्प के माध्यम से स्थिर बनाया जा सकता है।
उदाहरण
वास्तव में उचित प्रणाली के लिए डी शून्य के सामान्य है। एक और अधिक सामान्य स्थिति है जब सभी स्टेट आउटपुट होते हैं, अर्थात y = x, जो C = I, शिनाख्त सांचा देता है। इसके परिणामस्वरूप सरल समीकरण होंगे
यह आवश्यक आइजन अपघटन को कम कर देता है .
निर्दिष्ट बिंदू (संदर्भ) इनपुट के साथ प्रतिक्रिया
 प्रतिक्रिया के अतिरिक्त , एक इनपुट, , इस तरह जोड़ा जा सकता है .
प्रतिक्रिया के अतिरिक्त , एक इनपुट, , इस तरह जोड़ा जा सकता है .
हो जाता है
के लिए आउटपुट समीकरण को हल करना और स्टेट समीकरण में प्रतिस्थापन करने का परिणाम होता है
इस प्रणाली के लिए एक अधिक सामान्य सरलीकरण D को हटा रहा है, जो समीकरणों को कम कर देता है
चलती वस्तु का उदाहरण
एक मौलिक रैखिक प्रणाली एक वस्तु (जैसे, एक कार्ट) के एक आयामी आंदोलन की है।
एक विमान पर क्षैतिज रूप से चलती हुई वस्तु के लिए न्यूटन के गति के नियम और एक स्प्रिंग वाली दीवार से जुड़ी:
जहाँ
- स्थिति है; वेग है; त्वरण है
- एक अनुप्रयुक्त बल है
- चिपचिपा घर्षण गुणांक है
- वसंत स्थिरांक है
- वस्तु का द्रव्यमान है
इसके बाद स्टेट का समीकरण बन जाएगा
जहाँ
- वस्तु की स्थिति का प्रतिनिधित्व करता है
- वस्तु का वेग है
- वस्तु का त्वरण है
- उत्पादन वस्तु की स्थिति है
नियंत्रणीयता परीक्षण तब है
जिसमें सभी के लिए फुल श्रेणी है और . इसका कारण यह है, कि यदि प्रणाली की प्रारंभिक अवस्था ज्ञात है (, , ), और यदि और स्थिर हैं, तो एक बल है जो कार्ट को प्रणाली में किसी अन्य स्थिति में ले जा सकता है।
अवलोकन परीक्षण तब है
जिसकी भी पूरी श्रेणी है। इसलिए, यह प्रणाली नियंत्रणीय और अवलोकनीय दोनों है।
अरेखीय प्रणालियाँ
स्टेट-स्पेस मॉडल का अधिक सामान्य रूप दो कार्यों के रूप में लिखा जा सकता है।
पहला स्टेट समीकरण है और बाद वाला आउटपुट समीकरण है।
यदि कार्य स्टेट और इनपुट का एक रैखिक संयोजन है तो समीकरणों को ऊपर की तरह आव्यूह नोटेशन में लिखा जा सकता है। h> कार्य के तर्क को छोड़ दिया जा सकता है यदि प्रणाली अनफोर्स्ड है (अर्थात, इसमें कोई इनपुट नहीं है)।
पेंडुलम उदाहरण
एक क्लासिक अरेखीय प्रणाली एक साधारण अप्रत्याशित पेंडुलम है
जहाँ
- गुरुत्वाकर्षण की दिशा के संबंध में पेंडुलम का कोण है
- पेंडुलम का द्रव्यमान है (पेंडुलम रॉड का द्रव्यमान शून्य माना जाता है)
- गुरुत्वीय त्वरण है
- धुरी बिंदु पर घर्षण का गुणांक है
- पेंडुलम की त्रिज्या है (द्रव्यमान के गुरुत्वाकर्षण के केंद्र में )
स्टेट के समीकरण हैं
जहाँ
- पेंडुलम का कोण है
- पेंडुलम का घूर्णी वेग है
- पेंडुलम का घूर्णी त्वरण है
इसके अतिरिक्त, स्टेट समीकरण को सामान्य रूप में लिखा जा सकता है
एक प्रणाली के यांत्रिक संतुलन/स्थिर बिंदु हैं जब और इसलिए एक पेंडुलम के संतुलन बिंदु वे हैं जो संतुष्ट करते हैं
पूर्णांक n के लिए।
यह भी देखें
- नियंत्रण इंजीनियरिंग
- नियंत्रण सिद्धांत
- स्टेट पर्यवेक्षक
- अवलोकनीयता
- नियंत्रणीयता
- स्टेट -स्पेस मॉडल का विवेक
- भौतिकी और गणित में चरण अवस्था (जैसेस्टेट -स्पेस ) के बारे में जानकारी के लिए चरण स्थान।
- कंप्यूटर विज्ञान में असतत राज्यों के साथ स्टेट -स्पेस के बारे में जानकारी के लिए राज्य स्थान।
- भौतिकी में राज्य अंतरिक्ष के बारे में जानकारी के लिए स्टेट -स्पेस (भौतिकी)।
- सांख्यिकीय अनुप्रयोग के लिए कलमन छनन ।
संदर्भ
- ↑ Katalin M. Hangos; R. Lakner & M. Gerzson (2001). Intelligent Control Systems: An Introduction with Examples. Springer. p. 254. ISBN 978-1-4020-0134-5.
- ↑ Katalin M. Hangos; József Bokor & Gábor Szederkényi (2004). Analysis and Control of Nonlinear Process Systems. Springer. p. 25. ISBN 978-1-85233-600-4.
- ↑ Vasilyev A.S.; Ushakov A.V. (2015). "क्रोनकर वेक्टर-मैट्रिक्स प्रतिनिधित्व के माध्यम से मॉड्यूलेशन के साथ गतिशील प्रणालियों की मॉडलिंग।". Scientific and Technical Journal of Information Technologies, Mechanics and Optics. 15 (5): 839–848. doi:10.17586/2226-1494-2015-15-5-839-848.
- ↑ Stock, J.H.; Watson, M.W. (2016), "Dynamic Factor Models, Factor-Augmented Vector Autoregressions, and Structural Vector Autoregressions in Macroeconomics", Handbook of Macroeconomics (in English), Elsevier, vol. 2, pp. 415–525, doi:10.1016/bs.hesmac.2016.04.002, ISBN 978-0-444-59487-7
- ↑ Durbin, James; Koopman, Siem Jan (2012). राज्य अंतरिक्ष विधियों द्वारा समय श्रृंखला विश्लेषण. Oxford University Press. ISBN 978-0-19-964117-8. OCLC 794591362.
- ↑ Roesser, R. (1975). "लीनियर इमेज प्रोसेसिंग के लिए एक डिस्क्रीट स्टेट-स्पेस मॉडल". IEEE Transactions on Automatic Control. 20 (1): 1–10. doi:10.1109/tac.1975.1100844. ISSN 0018-9286.
- ↑ Smith, Anne C.; Brown, Emery N. (2003). "प्वाइंट प्रोसेस ऑब्जर्वेशन से स्टेट-स्पेस मॉडल का अनुमान लगाना". Neural Computation. 15 (5): 965–991. doi:10.1162/089976603765202622. ISSN 0899-7667. PMID 12803953. S2CID 10020032.
- ↑ James H. Stock & Mark W. Watson, 1989. "New Indexes of Coincident and Leading Economic Indicators," NBER Chapters, in: NBER Macroeconomics Annual 1989, Volume 4, pages 351-409, National Bureau of Economic Research, Inc.
- ↑ Bańbura, Marta; Modugno, Michele (2012-11-12). "मिसिंग डेटा के मनमाने पैटर्न के साथ डेटासेट पर फैक्टर मॉडल का अधिकतम संभावना अनुमान". Journal of Applied Econometrics. 29 (1): 133–160. doi:10.1002/jae.2306. hdl:10419/153623. ISSN 0883-7252. S2CID 14231301.
- ↑ "State-Space Models with Markov Switching and Gibbs-Sampling", State-Space Models with Regime Switching, The MIT Press, 2017, doi:10.7551/mitpress/6444.003.0013, ISBN 978-0-262-27711-2
- ↑ Kalman, R. E. (1960-03-01). "रेखीय छानने और भविष्यवाणी की समस्याओं के लिए एक नया दृष्टिकोण". Journal of Basic Engineering (in English). 82 (1): 35–45. doi:10.1115/1.3662552. ISSN 0021-9223.
- ↑ Harvey, Andrew C. (1990). Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge: Cambridge University Press. doi:10.1017/CBO9781107049994
- ↑ Nise, Norman S. (2010). नियंत्रण प्रणाली इंजीनियरिंग (6th ed.). John Wiley & Sons, Inc. ISBN 978-0-470-54756-4.
- ↑ Brogan, William L. (1974). आधुनिक नियंत्रण सिद्धांत (1st ed.). Quantum Publishers, Inc. p. 172.
अग्रिम पठन
- Antsaklis, P. J.; Michel, A. N. (2007). A Linear Systems Primer. Birkhauser. ISBN 978-0-8176-4460-4.
- Chen, Chi-Tsong (1999). Linear System Theory and Design (3rd ed.). Oxford University Press. ISBN 0-19-511777-8.
- Khalil, Hassan K. (2001). Nonlinear Systems (3rd ed.). Prentice Hall. ISBN 0-13-067389-7.
- Hinrichsen, Diederich; Pritchard, Anthony J. (2005). Mathematical Systems Theory I, Modelling, State Space Analysis, Stability and Robustness. Springer. ISBN 978-3-540-44125-0.
- Sontag, Eduardo D. (1999). Mathematical Control Theory: Deterministic Finite Dimensional Systems (PDF) (2nd ed.). Springer. ISBN 0-387-98489-5. Retrieved June 28, 2012.
- Friedland, Bernard (2005). Control System Design: An Introduction to State-Space Methods. Dover. ISBN 0-486-44278-0.
- Zadeh, Lotfi A.; Desoer, Charles A. (1979). Linear System Theory. Krieger Pub Co. ISBN 978-0-88275-809-1.
- On the applications of state-space models in econometrics
- Durbin, J.; Koopman, S. (2001). Time series analysis by state space methods. Oxford, UK: Oxford University Press. ISBN 978-0-19-852354-3.
बाहरी संबंध
- Wolfram language functions for linear state-space models, affine state-space models, and nonlinear state-space models.