मोनोटोन संभावना अनुपात

वितरण में संभावना अनुपात $f(x)$ और $g(x)$

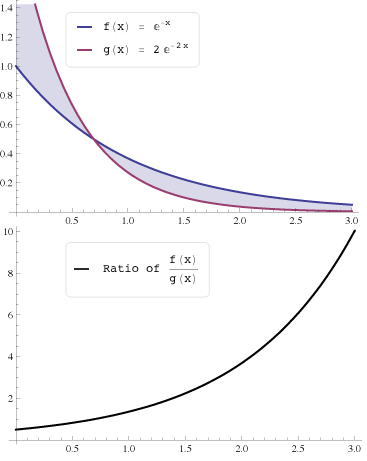
उपरोक्त संभाव्यता घनत्व फलन का अनुपात पैरामीटर में बढ़ रहा है $x$, इसलिए $f(x)/g(x)$ मोनोटोन संभावना अनुपात संपत्ति को संतुष्ट करता है।

आंकड़ों में, मोनोटोन संभावना अनुपात संपत्ति दो संभाव्यता घनत्व कार्यों (पीडीएफ) के अनुपात की संपत्ति है। औपचारिक रूप से, वितरण ƒ(x) और g(x) गुण धारण करते हैं यदि

${\text{for every}}x_{1}>x_{0},\quad {\frac {f(x_{1})}{g(x_{1})}}\geq {\frac {f(x_{0})}{g(x_{0})}}$

अर्थात, यदि तर्क में अनुपात घटता नहीं है $x$.

यदि कार्य भिन्न-भिन्न हैं, तो संपत्ति को कभी-कभी ${\frac {\partial }{\partial x}}\left({\frac {f(x)}{g(x)}}\right)\geq 0$ कहा जा सकता है।

दो वितरणों के लिए जो कुछ तर्क x के संबंध में परिभाषा को संतुष्ट करते हैं, उनके पास x में MLRP है। वितरण के सदस्य के लिए जो सभी कुछ आंकड़े T(X) के संबंध में परिभाषा को पूरा करते हैं, हम कहते हैं कि उनके पास T(X) में एमएलआर है।

अंतर्ज्ञान

MLRP का उपयोग डेटा-जनरेटिंग प्रक्रिया का प्रतिनिधित्व करने के लिए किया जाता है जो कुछ प्रेक्षित चर के परिमाण और इसके द्वारा प्राप्त वितरण के मध्य सीधा संबंध प्राप्त करता है। यदि $f(x)$ के संबंध में MLRP को $g(x)$ संतुष्ट करता है, प्रेक्षित संख्या जितनी अधिक होगी $x$, अधिक संभावना यह वितरण से खींची गई थी $f$ इसके बजाय $g$. मोनोटोनिक संबंधों के लिए संभावना अनुपात की मोनोटोनिकिटी आँकड़ों में कार्य आती है, विशेषकर जब अधिकतम संभावना अनुमान का उपयोग किया जाता है। इसके अतिरिक्त, एमएलआर वाले वितरण सदस्यों में कई अच्छे स्टोचैस्टिक गुण होते हैं, जैसे प्रथम-क्रम स्टोकेस्टिक प्रभुत्व और बढ़ते जोखिम अनुपात है। दुर्भाग्य से, जैसा कि सदैव होता है, इस धारणा का बल यथार्थवाद के मूल्य पर आतापर आती है। दुनिया में कई प्रक्रियाएं इनपुट और आउटपुट के मध्य मोनोटोनिक पत्राचार प्रदर्शित नहीं करती हैं।

उदाहरण: कड़ी मेहनत करना या आलसी होना

विचार कीजिए की आप किसी प्रोजेक्ट पर कार्य कर रहे हैं, और आप या तो कड़ी मेहनत कर सकते हैं या सुस्त हो सकते हैं। अपनी पसंद के प्रयास $e$ और परिणामी परियोजना की गुणवत्ता $q$ है, यदि एमएलआरपी आपके प्रयास $e$ पर सशर्त के वितरण के लिए है , गुणवत्ता q जितनी अधिक होगी, आपके द्वारा कड़ी मेहनत करने की संभावना उतनी ही अधिक होगी। इसके विपरीत, गुणवत्ता जितनी कम होगी, आपके सुस्त होने की संभावना उतनी ही अधिक होगी।

1. प्रयास $e\in \{H,L\}$ जहां H का तात्पर्य हाई और L का तात्पर्य लो है
2. अवलोकन करना $q$ से खींचा $f(q\mid e)$. बेयस के कानून द्वारा समान पूर्व के साथ,

   $\Pr[e=H\mid q]={\frac {f(q\mid H)}{f(q\mid H)+f(q\mid L)}}$

3. कल्पना करना $f(q\mid e)$ एमएलआरपी को संतुष्ट करता है। पुनर्व्यवस्थित करने पर, कार्यकर्ता द्वारा कठिन परिश्रम करने की प्रायिकता

${\frac {1}{1+f(q\mid L)/f(q\mid H)}}$ है ।

जो, एमएलआरपी के लिए नीरस रूप से $q$ बढ़ रहा है (क्योंकि $f(q\mid L)/f(q\mid H)$ में $q$ घट रहा है ), इसलिए यदि कोई नियोक्ता प्रदर्शन की समीक्षा कर रहा है तो वह अपने कर्मचारी के व्यवहार को उसके कार्य की योग्यता से अनुमान लगा सकता है।

एमएलआर को संतुष्ट करने वाले वितरण के सदस्य

सांख्यिकीय मॉडल प्रायः मानते हैं कि डेटा वितरण के कुछ सदस्य से वितरण द्वारा उत्पन्न होते हैं और उस वितरण को निर्धारित करना चाहते हैं। यह कार्य सरल हो जाता है यदि सदस्य के पास मोनोटोन संभावना अनुपात संपत्ति (एमएलआरपी) है।

घनत्व कार्यों का सदस्य $\{f_{\theta }(x)\}_{\theta \in \Theta }$ पैरामीटर द्वारा अनुक्रमित $\theta$ आदेशित सेट में मान लेना $\Theta$ कहा जाता है कि आँकड़ों में मोनोटोन संभावना अनुपात (एमएलआर) $T(X)$ है, यदि किसी के लिए $\theta _{1}<\theta _{2}$,

${\frac {f_{\theta _{2}}(X=x_{1},x_{2},x_{3},\dots )}{f_{\theta _{1}}(X=x_{1},x_{2},x_{3},\dots )}}$का गैर-घटता कार्य $T(X)$ है।

अतः हम कहते हैं कि वितरण के सदस्य में एमएलआर $T(X)$ है।

सदस्यों की सूची

Family	$T(X)$  in which $f_{\theta }(X)$ has the MLR
Exponential$[\lambda ]$	$\sum x_{i}$ observations
Binomial$[n,p]$	$\sum x_{i}$ observations
Poisson$[\lambda ]$	$\sum x_{i}$ observations
Normal$[\mu ,\sigma ]$	if $\sigma$ known, $\sum x_{i}$ observations

परिकल्पना परीक्षण

यदि यादृच्छिक चर के सदस्य में MLRP $T(X)$ है, परिकल्पना के लिए समान रूप से सबसे शक्तिशाली परीक्षण $H_{0}:\theta \leq \theta _{0}$ बनाम $H_{1}:\theta >\theta _{0}$ सरलता से निर्धारित किया जा सकता है।

उदाहरण: प्रयास और आउटपुट

उदाहरण: $e$ स्टोकेस्टिक प्रौद्यिगिकी में इनपुट बनें कार्यकर्ता का प्रयास है, उदाहरण के लिए $y$ इसका आउटपुट है, जिसकी संभावना प्रायिकता घनत्व फलन$f(y;e)$ द्वारा वर्णित है। सदस्य की मोनोटोन संभावना अनुपात संपत्ति (एमएलआरपी) $f$ निम्नानुसार व्यक्त किया गया है: किसी के लिए $e_{1},e_{2}$, यह तथ्य कि $e_{2}>e_{1}$ तात्पर्य है कि अनुपात $f(y;e_{2})/f(y;e_{1})$ में $y$ बढ़ रहा है। .

अन्य सांख्यिकीय गुणों से संबंध

मोनोटोन संभावनाएं सांख्यिकीय सिद्धांत के कई क्षेत्रों में उपयोग की जाती हैं, जिसमें बिंदु अनुमान और परिकल्पना परीक्षण, साथ ही संभाव्यता मॉडल भी सम्मिलित हैं।

घातीय सदस्य

पैरामीटर एक्सपोनेंशियल फैमिली में मोनोटोन संभावना-कार्य होते हैं। विशेष रूप से, संभाव्यता घनत्व कार्यों या संभाव्यता द्रव्यमान कार्यों के आयामी घातीय सदस्य के साथ

$f_{\theta }(x)=c(\theta )h(x)\exp(\pi (\theta )T(x))$

पर्याप्तता (सांख्यिकी) T(x) में मोनोटोन अन्य-घटती संभावना अनुपात है, परन्तु $\pi (\theta )$ घटता नहीं है।

समान रूप से सबसे शक्तिशाली परीक्षण: कार्लिन-रुबिन प्रमेय

कार्लिन-रुबिन प्रमेय के अनुसार, मोनोटोन संभावना कार्यों का उपयोग समान रूप से सबसे शक्तिशाली परीक्षणों के निर्माण के लिए किया जाता है। स्केलर मापन पर विचार करें जिसमें स्केलर पैरामीटर θ द्वारा प्राचलित प्रायिकता घनत्व फलन होता है, और $\ell (x)=f_{\theta _{1}}(x)/f_{\theta _{0}}(x)$ संभावना अनुपात को परिभाषित करता है। यदि $\ell (x)$ मोनोटोन अन्य-घटता है, में $x$, किसी भी जोड़ी के लिए $\theta _{1}\geq \theta _{0}$ (जिसका अर्थ है कि बड़ा $x$ है, अधिक सम्भावना $H_{1}$ है), तो परीक्षण:

$\varphi (x)={\begin{cases}1&{\text{if }}x>x_{0}\\0&{\text{if }}x<x_{0}\end{cases}}$ है,

जहाँ $x_{0}$ इसलिए चयन किया जाता है जिससे $\operatorname {E} _{\theta _{0}}\varphi (X)=\alpha$ है

परीक्षण के लिए आकार α का UMP परीक्षण $H_{0}:\theta \leq \theta _{0}{\text{ vs. }}H_{1}:\theta >\theta _{0}$है, ध्यान दें कि ठीक यही परीक्षण $H_{0}:\theta =\theta _{0}{\text{ vs. }}H_{1}:\theta >\theta _{0}$परीक्षण के लिए UMP भी है।

माध्य निष्पक्ष अनुमान

मोनोटोन संभावना-कार्यों का उपयोग मध्य-निष्पक्ष आकलनकर्ताओं के निर्माण के लिए किया जाता है, जोहान फनज़ागल और अन्य द्वारा निर्दिष्ट विधियों का उपयोग करते हुए। ऐसी ही प्रक्रिया राव-ब्लैकवेल प्रमेय का एनालॉग है। समान रूप से न्यूनतम-विचरण निष्पक्ष अनुमानक के लिए राव-ब्लैकवेल प्रक्रिया|मीन-निष्पक्ष अनुमानक: प्रक्रिया माध्य के लिए राव-ब्लैकवेल प्रक्रिया की उपेक्षा में संभाव्यता वितरण के छोटे वर्ग के लिए है- निष्पक्ष अनुमान परन्तु नुकसान कार्यों के बड़े वर्ग के लिए है।

आजीवन विश्लेषण: उत्तरजीविता विश्लेषण और विश्वसनीयता

यदि वितरण का सदस्य $f_{\theta }(x)$ में मोनोटोन संभावना अनुपात गुण $T(X)$ है ,

1. सदस्य में मोनोटोन घटती खतरे की दर $\theta$ (परन्तु जरूरी नहीं कि अंदर $T(X)$) है।
2. सदस्य पूर्व क्रम (और इसलिए दूसरे क्रम) में स्टोकास्टिक प्रभुत्व प्रदर्शित करता है $x$, और का सबसे उचित बायेसियन अपडेट $\theta$ में $T(X)$ बढ़ रहा है। .

परन्तु इसके विपरीत नहीं: न तो मोनोटोन खतरे की दर और न ही स्टोकेस्टिक प्रभुत्व एमएलआरपी को प्रभावित करते हैं।

प्रमाण

वितरण सदस्य चलो $f_{\theta }$ एक्स में एमएलआर को संतुष्ट करें, ताकि के लिए $\theta _{1}>\theta _{0}$ और $x_{1}>x_{0}$:

${\frac {f_{\theta _{1}}(x_{1})}{f_{\theta _{0}}(x_{1})}}\geq {\frac {f_{\theta _{1}}(x_{0})}{f_{\theta _{0}}(x_{0})}},$

या समकक्ष:

$f_{\theta _{1}}(x_{1})f_{\theta _{0}}(x_{0})\geq f_{\theta _{1}}(x_{0})f_{\theta _{0}}(x_{1}).\,$

इस अभिव्यक्ति को दो बार एकीकृत करना, हम प्राप्त करते हैं:

1. To $x_{1}$ with respect to $x_{0}$ ${\begin{aligned}&\int _{\min _{x}\in X}^{x_{1}}f_{\theta _{1}}(x_{1})f_{\theta _{0}}(x_{0})\,dx_{0}\\[6pt]\geq {}&\int _{\min _{x}\in X}^{x_{1}}f_{\theta _{1}}(x_{0})f_{\theta _{0}}(x_{1})\,dx_{0}\end{aligned}}$ integrate and rearrange to obtain ${\frac {f_{\theta _{1}}}{f_{\theta _{0}}}}(x)\geq {\frac {F_{\theta _{1}}}{F_{\theta _{0}}}}(x)$		2. From $x_{0}$ with respect to $x_{1}$ ${\begin{aligned}&\int _{x_{0}}^{\max _{x}\in X}f_{\theta _{1}}(x_{1})f_{\theta _{0}}(x_{0})\,dx_{1}\\[6pt]\geq {}&\int _{x_{0}}^{\max _{x}\in X}f_{\theta _{1}}(x_{0})f_{\theta _{0}}(x_{1})\,dx_{1}\end{aligned}}$ integrate and rearrange to obtain ${\frac {1-F_{\theta _{1}}(x)}{1-F_{\theta _{0}}(x)}}\geq {\frac {f_{\theta _{1}}}{f_{\theta _{0}}}}(x)$

पूर्व क्रम का स्टोकेस्टिक प्रभुत्व

प्रथम क्रम प्रभुत्व प्राप्त करने के लिए उपरोक्त दो असमानताओं को मिलाएं:

$F_{\theta _{1}}(x)\leq F_{\theta _{0}}(x)\ \forall x$

मोनोटोन खतरा दर

मोनोटोन खतरा दर प्राप्त करने के लिए केवल ऊपर दी गई दूसरी असमानता का उपयोग करें:

${\frac {f_{\theta _{1}}(x)}{1-F_{\theta _{1}}(x)}}\leq {\frac {f_{\theta _{0}}(x)}{1-F_{\theta _{0}}(x)}}\ \forall x$

उपयोग करता है

अर्थशास्त्र

एमएलआर तंत्र डिजाइन और सूचना के अर्थशास्त्र में एजेंटों के प्रकार वितरण पर एक महत्वपूर्ण शर्त है, जहां एमएलआर के परिणाम के रूप में पॉल मिलग्रोम ने संकेतों की अनुकूलता (स्टोकेस्टिक प्रभुत्व के संदर्भ में) को परिभाषित किया। तंत्र डिजाइन मॉडल के अधिकांश समाधान ऐसे वितरणों को मानते हैं जो समाधान विधियों का लाभ लेने के लिए एमएलआर को संतुष्ट करते हैं जो कि लागू करना और व्याख्या करना आसान हो सकता है।