फ़ेज़-शिफ्ट कुंजीयन: Difference between revisions
No edit summary |
No edit summary |
||
| (6 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{Modulation techniques}} | ||
'''फेज-शिफ्ट कुंजीयन (पीएसके)''' एक डिजिटल मॉड्यूलेशन प्रक्रिया है जो निरंतर[[ आवृत्ति ]] संदर्भ सिग्नल([[ वाहक लहर | वाहक तरंग]] ) के चरण को बदलकर(मॉड्यूलेट) करके [[ डेटा (कंप्यूटिंग) | डेटा]] सम्पादित करती है। सही समय पर [[ साइन तरंग | ज्या तरंग]] और [[ कोज्या तरंग ]] इनपुट को परिवर्तित कर मॉड्यूलेशन पूरा किया जाता है। यह व्यापक रूप से [[ वायरलेस लेन | वायरलेस लैन]] , [[ आरएफआईडी ]] और [[ ब्लूटूथ ]] संचार के लिए उपयोग किया जाता है। | '''फेज-शिफ्ट कुंजीयन (पीएसके)''' एक डिजिटल मॉड्यूलेशन प्रक्रिया है जो निरंतर[[ आवृत्ति ]] संदर्भ सिग्नल([[ वाहक लहर | वाहक तरंग]] ) के चरण को बदलकर(मॉड्यूलेट) करके [[ डेटा (कंप्यूटिंग) | डेटा]] सम्पादित करती है। सही समय पर [[ साइन तरंग | ज्या तरंग]] और [[ कोज्या तरंग ]] इनपुट को परिवर्तित कर मॉड्यूलेशन पूरा किया जाता है। यह व्यापक रूप से [[ वायरलेस लेन | वायरलेस लैन]] , [[ आरएफआईडी ]] और [[ ब्लूटूथ ]] संचार के लिए उपयोग किया जाता है। | ||
| Line 24: | Line 24: | ||
==बाइनरी चरण-शिफ्ट कुंजीयन (बीपीएसके)== | ==बाइनरी चरण-शिफ्ट कुंजीयन (बीपीएसके)== | ||
[[File:BPSK Gray Coded.svg|200px|right|thumb|बीपीएसके के लिए नक्षत्र आरेख उदाहरण]] | [[File:BPSK Gray Coded.svg|200px|right|thumb|बीपीएसके के लिए नक्षत्र आरेख उदाहरण]] | ||
बीपीएसके (जिसे कभी-कभी पीआरके, फेज़ रिवर्सल कुंजीयन या 2पीएसके भी कहा जाता है) फेज़ शिफ्ट कीइंग (पीएसके) का सबसे सरल रूप है। यह दो चरणों का उपयोग करता है जो 180 ° से अलग होते हैं और इसलिए इसे 2-पीएसके भी कहा जा सकता है। यह विशेष रूप से बिल्कुल मायने नहीं रखता है कि नक्षत्र बिंदु | बीपीएसके (जिसे कभी-कभी पीआरके, फेज़ रिवर्सल कुंजीयन या 2पीएसके भी कहा जाता है) फेज़ शिफ्ट कीइंग (पीएसके) का सबसे सरल रूप है। यह दो चरणों का उपयोग करता है जो 180 ° से अलग होते हैं और इसलिए इसे 2-पीएसके भी कहा जा सकता है। यह विशेष रूप से बिल्कुल मायने नहीं रखता है कि नक्षत्र बिंदु जहाँ स्थित हैं, और इस आंकड़े में उन्हें वास्तविक अक्ष पर 0 ° और 180 ° पर दिखाया गया है। इसलिए, यह डिमोडुलेटर के गलत निर्णय पर पहुंचने से पहले उच्चतम रव स्तर या विकृति को संभालता है। यह इसे सभी पीएसके में सबसे मजबूत बनाता है। हालांकि, यह केवल 1 बिट/प्रतीक (जैसा कि चित्र में देखा गया है) पर मॉड्यूलेट करने में सक्षम है और इसलिए उच्च डेटा-दर अनुप्रयोगों के लिए अनुपयुक्त है। फिर भी इस बिट/प्रतीक को विस्तारित करने की संभावना है, मॉड्यूलेटर प्रतीक एन्क्रिप्शन/डिक्रिप्शन तर्क प्रणाली को देखते हुए। | ||
[[ संचार चैनल ]] द्वारा शुरू की गई मनमानी चरण-शिफ्ट की उपस्थिति में, डिमोडुलेटर (देखें, जैसे [[ कोस्टास लूप ]]) यह बताने में असमर्थ है कि कौन सा नक्षत्र बिंदु है। फलस्वरूप, डेटा | [[ संचार चैनल ]] द्वारा शुरू की गई मनमानी चरण-शिफ्ट की उपस्थिति में, डिमोडुलेटर (देखें, जैसे [[ कोस्टास लूप ]]) यह बताने में असमर्थ है कि कौन सा नक्षत्र बिंदु है। फलस्वरूप, डेटा प्रायः मॉडुलन से पहले अलग-अलग एन्कोड किया जाता है। | ||
बीपीएसके कार्यात्मक रूप से समकक्ष 2-क्यूएएम मॉड्यूलेशन के बराबर है। | बीपीएसके कार्यात्मक रूप से समकक्ष 2-क्यूएएम मॉड्यूलेशन के बराबर है। | ||
| Line 34: | Line 34: | ||
:<math>s_n(t) = \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f t + \pi(1-n )),\quad n = 0,1. </math> | :<math>s_n(t) = \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f t + \pi(1-n )),\quad n = 0,1. </math> | ||
इससे दो चरण प्राप्त होते हैं, 0 और विशिष्ट रूप में, बाइनरी डेटा को | इससे दो चरण प्राप्त होते हैं, 0 और विशिष्ट रूप में, बाइनरी डेटा को प्रायः निम्नलिखित संकेतों से अवगत कराया जाता है{{citation needed|date=June 2019}} | ||
:<math>s_0(t) = \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f t + \pi ) | :<math>s_0(t) = \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f t + \pi ) | ||
= - \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f t)</math> बाइनरी 0 . के लिए | = - \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f t)</math> बाइनरी 0 . के लिए | ||
| Line 41: | Line 41: | ||
जहाँ f बेस बैंड की आवृत्ति है। | जहाँ f बेस बैंड की आवृत्ति है। | ||
इसलिए, सिग्नल स्पेस को सिंगल [[ आधार समारोह ]] द्वारा दर्शाया जा सकता है | इसलिए, सिग्नल स्पेस को सिंगल [[ आधार समारोह | आधार फलन]] द्वारा दर्शाया जा सकता है | ||
:<math>\phi(t) = \sqrt{\frac{2}{T_b}} \cos(2 \pi f t) </math> | :<math>\phi(t) = \sqrt{\frac{2}{T_b}} \cos(2 \pi f t) </math> | ||
| Line 49: | Line 49: | ||
=== [[ बिट त्रुटि दर ]] === | === [[ बिट त्रुटि दर ]] === | ||
[[ योज्य सफेद गाऊसी शोर | योगशील सफेद गाऊसी | [[ योज्य सफेद गाऊसी शोर | योगशील सफेद गाऊसी रव]] (एडब्ल्यूजीएन) के तहत बीपीएसके की बिट एरर रेट (बीईआर) की गणना इस प्रकार की जा सकती है<ref>Communications Systems, H. Stern & S. Mahmoud, Pearson Prentice Hall, 2004, p. 283.</ref> | ||
:<math>P_b = Q\left(\sqrt{\frac{2 E_b}{N_0}}\right)</math> या <math>P_e = \frac{1}{2} \operatorname{erfc} \left( \sqrt{\frac{E_b}{N_0}}\right)</math> | :<math>P_b = Q\left(\sqrt{\frac{2 E_b}{N_0}}\right)</math> या <math>P_e = \frac{1}{2} \operatorname{erfc} \left( \sqrt{\frac{E_b}{N_0}}\right)</math> | ||
चूंकि प्रति प्रतीक केवल एक बिट है, यह भी प्रतीक त्रुटि दर है। | चूंकि प्रति प्रतीक केवल एक बिट है, यह भी प्रतीक त्रुटि दर है। | ||
| Line 57: | Line 57: | ||
कभी-कभी इसे क्वाड्रिफेज पीएसके, 4-पीएसके, या 4-[[ क्यूएएम ]] के रूप में जाना जाता है। (हालांकि क्यूपीएसके और 4-क्यूएएम की मूल अवधारणाएं अलग हैं, परिणामी संशोधित रेडियो तरंगें बिल्कुल समान हैं।) क्यूपीएसके नक्षत्र आरेख पर चार बिंदुओं का उपयोग करता है, जो एक सर्कल के चारों ओर समान होता है। चार चरणों के साथ, क्यूपीएसके बिट त्रुटि दर (बीईआर) को कम करने के लिए ग्रे कोडिंग के साथ आरेख में दिखाए गए प्रति प्रतीक दो बिट्स को एन्कोड कर सकता है। कभी-कभी बीपीएसके के दोगुने बीईआर के रूप में गलत समझा जाता है। | कभी-कभी इसे क्वाड्रिफेज पीएसके, 4-पीएसके, या 4-[[ क्यूएएम ]] के रूप में जाना जाता है। (हालांकि क्यूपीएसके और 4-क्यूएएम की मूल अवधारणाएं अलग हैं, परिणामी संशोधित रेडियो तरंगें बिल्कुल समान हैं।) क्यूपीएसके नक्षत्र आरेख पर चार बिंदुओं का उपयोग करता है, जो एक सर्कल के चारों ओर समान होता है। चार चरणों के साथ, क्यूपीएसके बिट त्रुटि दर (बीईआर) को कम करने के लिए ग्रे कोडिंग के साथ आरेख में दिखाए गए प्रति प्रतीक दो बिट्स को एन्कोड कर सकता है। कभी-कभी बीपीएसके के दोगुने बीईआर के रूप में गलत समझा जाता है। | ||
गणितीय विश्लेषण से पता चलता है कि सिग्नल के समान [[ बैंडविड्थ (सिग्नल प्रोसेसिंग) ]] को बनाए रखते हुए, या बीपीएसके की डेटा-दर को बनाए रखने के लिए, लेकिन आवश्यक बैंडविड्थ को आधा करने के लिए क्यूपीएसके का उपयोग या तो बीपीएसके प्रणाली की तुलना में डेटा दर को दोगुना करने के लिए किया जा सकता है। इस | गणितीय विश्लेषण से पता चलता है कि सिग्नल के समान [[ बैंडविड्थ (सिग्नल प्रोसेसिंग) ]] को बनाए रखते हुए, या बीपीएसके की डेटा-दर को बनाए रखने के लिए, लेकिन आवश्यक बैंडविड्थ को आधा करने के लिए क्यूपीएसके का उपयोग या तो बीपीएसके प्रणाली की तुलना में डेटा दर को दोगुना करने के लिए किया जा सकता है। इस परिस्थिति के बाद में, बीपीएसके का बीईआर बिल्कुल बीपीएसके के बीईआर के समान है - और बीपीएसके पर विचार या वर्णन करते समय अलग-अलग तरह से विश्वास करना एक सामान्य भ्रम है। प्रेषित वाहक कई चरण परिवर्तनों से गुजर सकता है। | ||
यह देखते हुए कि रेडियो संचार चैनल [[ संघीय संचार आयोग ]] जैसी एजेंसियों द्वारा निर्धारित (अधिकतम) बैंडविड्थ देने के लिए आवंटित किए जाते हैं, बीपीएसके पर क्यूपीएसके का लाभ स्पष्ट हो जाता है क्यूपीएसके बीपीएसके की तुलना में दिए गए बैंडविड्थ में दो बार डेटा दर प्रसारित करता है - उसी बीईआर पर इंजीनियरिंग जुर्माना जो भुगतान किया जाता है वह यह है कि क्यूपीएसके ट्रांसमीटर और रिसीवर बीपीएसके के लिए अधिक जटिल हैं। हालांकि, आधुनिक [[ इलेक्ट्रानिक्स ]] प्रौद्योगिकी के साथ, लागत दंड बहुत कम है। | यह देखते हुए कि रेडियो संचार चैनल [[ संघीय संचार आयोग ]] जैसी एजेंसियों द्वारा निर्धारित (अधिकतम) बैंडविड्थ देने के लिए आवंटित किए जाते हैं, बीपीएसके पर क्यूपीएसके का लाभ स्पष्ट हो जाता है क्यूपीएसके बीपीएसके की तुलना में दिए गए बैंडविड्थ में दो बार डेटा दर प्रसारित करता है - उसी बीईआर पर इंजीनियरिंग जुर्माना जो भुगतान किया जाता है वह यह है कि क्यूपीएसके ट्रांसमीटर और रिसीवर बीपीएसके के लिए अधिक जटिल हैं। हालांकि, आधुनिक [[ इलेक्ट्रानिक्स ]] प्रौद्योगिकी के साथ, लागत दंड बहुत कम है। | ||
बीपीएसके के साथ, प्राप्त करने वाले अंत में चरण अस्पष्टता की समस्याएं हैं, और विशेषक एन्कोडिंग क्यूपीएसके | बीपीएसके के साथ, प्राप्त करने वाले अंत में चरण अस्पष्टता की समस्याएं हैं, और विशेषक एन्कोडिंग क्यूपीएसके प्रायः अभ्यास में प्रयोग किया जाता है। | ||
===कार्यान्वयन === | ===कार्यान्वयन === | ||
| Line 106: | Line 106: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
यदि सिग्नल-टू- | यदि सिग्नल-टू-रव अनुपात अधिक है (जैसा कि व्यावहारिक क्यूपीएसके प्रणाली के लिए आवश्यक है) प्रतीक त्रुटि की संभावना का अनुमान लगाया जा सकता है | ||
:<math>P_s \approx 2 Q \left( \sqrt{\frac{E_s}{N_0}} \right ) = \operatorname{erfc} \left( \sqrt{\frac{E_s}{2N_0}} \right) = \operatorname{erfc} \left( \sqrt{\frac{E_b}{N_0}} \right)</math> | :<math>P_s \approx 2 Q \left( \sqrt{\frac{E_s}{N_0}} \right ) = \operatorname{erfc} \left( \sqrt{\frac{E_s}{2N_0}} \right) = \operatorname{erfc} \left( \sqrt{\frac{E_b}{N_0}} \right)</math> | ||
| Line 168: | Line 168: | ||
:<math>P_s = 1 - \int_{-\pi/M}^{\pi/M} p_{\theta_r}\left(\theta_r\right)d\theta_r,</math> | :<math>P_s = 1 - \int_{-\pi/M}^{\pi/M} p_{\theta_r}\left(\theta_r\right)d\theta_r,</math> | ||
जहाँ पे | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 212: | Line 212: | ||
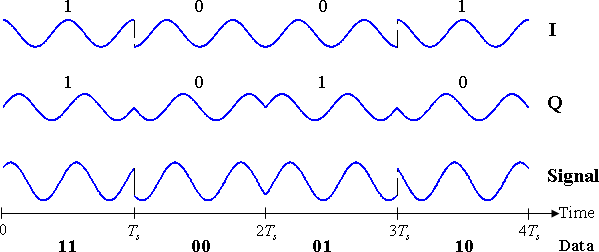
[[File:DBQPSK timing diag fixed.png|center|thumb|600px|डीबीपीएसके और डीक्यूपीएसके के लिए समय आरेख। बाइनरी डेटा स्ट्रीम डीबीपीएसके सिग्नल के ऊपर है। डीबीपीएसके सिग्नल के अलग-अलग बिट्स को डीक्यूपीएसके सिग्नल के लिए जोड़े में बांटा गया है, जो केवल हर ''T<sub>s</sub>''= 2''T<sub>b</sub>''.]] | [[File:DBQPSK timing diag fixed.png|center|thumb|600px|डीबीपीएसके और डीक्यूपीएसके के लिए समय आरेख। बाइनरी डेटा स्ट्रीम डीबीपीएसके सिग्नल के ऊपर है। डीबीपीएसके सिग्नल के अलग-अलग बिट्स को डीक्यूपीएसके सिग्नल के लिए जोड़े में बांटा गया है, जो केवल हर ''T<sub>s</sub>''= 2''T<sub>b</sub>''.]] | ||
विश्लेषण से पता चलता है कि अलग-अलग एन्कोडिंग सामान्य एम-पीएसके की तुलना में त्रुटि दर को लगभग दोगुना कर देता है लेकिन इसे <math>E_b/N_0</math> में केवल एक छोटी सी वृद्धि से दूर किया जा सकता है इसके अलावा, यह विश्लेषण (और नीचे दिए गए चित्रमय परिणाम) एक ऐसी प्रणाली पर आधारित हैं जिसमें एकमात्र भ्रष्टाचार योगात्मक सफेद गाऊसी | विश्लेषण से पता चलता है कि अलग-अलग एन्कोडिंग सामान्य एम-पीएसके की तुलना में त्रुटि दर को लगभग दोगुना कर देता है लेकिन इसे <math>E_b/N_0</math> में केवल एक छोटी सी वृद्धि से दूर किया जा सकता है इसके अलावा, यह विश्लेषण (और नीचे दिए गए चित्रमय परिणाम) एक ऐसी प्रणाली पर आधारित हैं जिसमें एकमात्र भ्रष्टाचार योगात्मक सफेद गाऊसी रव (एडब्ल्यूजीएन) है। यद्यपि, संचार प्रणाली में ट्रांसमीटर और रिसीवर के बीच एक भौतिक चैनल भी होगा। यह चैनल, सामान्य रूप से, पीएसके संकेत के लिए एक अज्ञात चरण-शिफ्ट पेश करेगा इन मामलों में अंतर योजनाएँ सामान्य योजनाओं की तुलना में बेहतर त्रुटि-दर प्राप्त कर सकती हैं जो सटीक चरण की जानकारी पर निर्भर करती हैं। | ||
डीपीएसके के सबसे लोकप्रिय अनुप्रयोगों में से एक ब्लूटूथ कार्यान्वयन है जहां <math>\pi/4</math>-डीक्यूपीएसके और 8-डीपीएसके लागू किए गए। | डीपीएसके के सबसे लोकप्रिय अनुप्रयोगों में से एक ब्लूटूथ कार्यान्वयन है जहां <math>\pi/4</math>-डीक्यूपीएसके और 8-डीपीएसके लागू किए गए। | ||
=== विमॉडुलन === | === विमॉडुलन === | ||
[[File:DPSK BER curves.svg|thumb|right|280px|डीबीपीएसके, डीक्यूपीएसके और उनके गैर-विभेदक रूपों के बीच बीईआर की तुलना ग्रे कोडिंग का उपयोग करके और सफेद | [[File:DPSK BER curves.svg|thumb|right|280px|डीबीपीएसके, डीक्यूपीएसके और उनके गैर-विभेदक रूपों के बीच बीईआर की तुलना ग्रे कोडिंग का उपयोग करके और सफेद रव में संचालन]] | ||
एक संकेत के लिए जिसे अलग-अलग एन्कोड किया गया है, डिमॉड्यूलेशन की एक स्पष्ट वैकल्पिक विधि है। हमेशा की तरह डिमॉड्यूलेट करने और वाहक-चरण अस्पष्टता को अनदेखा करने के बजाय, दो लगातार प्राप्त प्रतीकों के बीच के चरण की तुलना की जाती है और यह निर्धारित करने के लिए उपयोग किया जाता है कि डेटा क्या होना चाहिए था। जब इस तरह से अलग-अलग एन्कोडिंग का उपयोग किया जाता है, तो स्कीम को अलग-अलग फेज-शिफ्ट कुंजीयन (डीपीएसके) के रूप में जाना जाता है। ध्यान दें कि यह केवल अलग-अलग एन्कोडेड पीएसके से अलग है, क्योंकि रिसेप्शन पर, प्राप्त प्रतीकों को एक-एक करके तारामंडल बिंदुओं पर डीकोड नहीं किया जाता है बल्कि इसके बजाय सीधे एक दूसरे से तुलना की जाती है। | एक संकेत के लिए जिसे अलग-अलग एन्कोड किया गया है, डिमॉड्यूलेशन की एक स्पष्ट वैकल्पिक विधि है। हमेशा की तरह डिमॉड्यूलेट करने और वाहक-चरण अस्पष्टता को अनदेखा करने के बजाय, दो लगातार प्राप्त प्रतीकों के बीच के चरण की तुलना की जाती है और यह निर्धारित करने के लिए उपयोग किया जाता है कि डेटा क्या होना चाहिए था। जब इस तरह से अलग-अलग एन्कोडिंग का उपयोग किया जाता है, तो स्कीम को अलग-अलग फेज-शिफ्ट कुंजीयन (डीपीएसके) के रूप में जाना जाता है। ध्यान दें कि यह केवल अलग-अलग एन्कोडेड पीएसके से अलग है, क्योंकि रिसेप्शन पर, प्राप्त प्रतीकों को एक-एक करके तारामंडल बिंदुओं पर डीकोड नहीं किया जाता है बल्कि इसके बजाय सीधे एक दूसरे से तुलना की जाती है। | ||
प्राप्त प्रतीक को <math>k</math><sup>वें</sup> टाइमलॉट में कॉल करें और इसे चरण <math>\phi_k</math> होने दें व्यापकता की हानि के बिना मान लें कि वाहक तरंग का चरण शून्य है। योज्य सफेद गाऊसी | प्राप्त प्रतीक को <math>k</math><sup>वें</sup> टाइमलॉट में कॉल करें और इसे चरण <math>\phi_k</math> होने दें व्यापकता की हानि के बिना मान लें कि वाहक तरंग का चरण शून्य है। योज्य सफेद गाऊसी रव (एडब्ल्यूजीएन) शब्द को <math>n_k</math> के रूप में निरूपित करें। फिर | ||
:<math>r_k = \sqrt{E_s}e^{j\phi_k} + n_k.</math> | :<math>r_k = \sqrt{E_s}e^{j\phi_k} + n_k.</math> | ||
| Line 226: | Line 226: | ||
:<math>r_kr_{k-1}^* = E_se^{j\left(\varphi_k - \varphi_{k-1}\right)} + \sqrt{E_s}e^{j\varphi_k}n_{k-1}^* + \sqrt{E_s}e^{-j\varphi_{k-1}}n_k + n_kn_{k-1}^*</math> | :<math>r_kr_{k-1}^* = E_se^{j\left(\varphi_k - \varphi_{k-1}\right)} + \sqrt{E_s}e^{j\varphi_k}n_{k-1}^* + \sqrt{E_s}e^{-j\varphi_{k-1}}n_k + n_kn_{k-1}^*</math> | ||
जहां सुपरस्क्रिप्ट * [[ जटिल संयुग्मन ]] को दर्शाता है। | जहां सुपरस्क्रिप्ट * [[ जटिल संयुग्मन ]] को दर्शाता है। रव की अनुपस्थिति में, इसका चरण है <math>\phi_{k}-\phi_{k-1}</math>, दो प्राप्त संकेतों के बीच चरण-शिफ्ट जिसका उपयोग प्रेषित डेटा को निर्धारित करने के लिए किया जा सकता है। | ||
डीपीएसके के लिए त्रुटि की संभावना की सामान्य रूप से गणना करना मुश्किल है, लेकिन, डीबीपीके के | डीपीएसके के लिए त्रुटि की संभावना की सामान्य रूप से गणना करना मुश्किल है, लेकिन, डीबीपीके के परिस्थिति में यह है: | ||
:<math>P_b = \frac{1}{2}e^{-\frac{E_b}{N_0}},</math><ref>G.L. Stüber, “Soft Decision Direct-Sequence DPSK Receivers,” IEEE Transactions on Vehicular Technology, vol. 37, no. 3, pp. 151–157, August 1988.</ref> | :<math>P_b = \frac{1}{2}e^{-\frac{E_b}{N_0}},</math><ref>G.L. Stüber, “Soft Decision Direct-Sequence DPSK Receivers,” IEEE Transactions on Vehicular Technology, vol. 37, no. 3, pp. 151–157, August 1988.</ref> | ||
| Line 235: | Line 235: | ||
डीपीएसके का उपयोग करने से एक सटीक चरण अनुमान प्रदान करने के लिए संभावित जटिल वाहक-वसूली योजनाओं की आवश्यकता से बचा जाता है और यह सामान्य पीएसके के लिए एक आकर्षक विकल्प हो सकता है। | डीपीएसके का उपयोग करने से एक सटीक चरण अनुमान प्रदान करने के लिए संभावित जटिल वाहक-वसूली योजनाओं की आवश्यकता से बचा जाता है और यह सामान्य पीएसके के लिए एक आकर्षक विकल्प हो सकता है। | ||
[[ ऑप्टिकल संचार ]] में, डेटा को एक लेजर के चरण में भिन्न तरीके से संशोधित किया जा सकता है। मॉड्यूलेशन [[ लेज़र ]] है जो एक [[ निरंतर तरंग ]] का उत्सर्जन करता है, और एक मच-ज़ेन्डर मॉड्यूलेटर जो विद्युत बाइनरी डेटा प्राप्त करता है। बीपीएसके के | [[ ऑप्टिकल संचार ]] में, डेटा को एक लेजर के चरण में भिन्न तरीके से संशोधित किया जा सकता है। मॉड्यूलेशन [[ लेज़र ]] है जो एक [[ निरंतर तरंग ]] का उत्सर्जन करता है, और एक मच-ज़ेन्डर मॉड्यूलेटर जो विद्युत बाइनरी डेटा प्राप्त करता है। बीपीएसके के परिस्थिति में, लेजर बाइनरी '1' के लिए अपरिवर्तित क्षेत्र को प्रसारित करता है, और '0' के लिए रिवर्स पोलरिटी के साथ। डिमोडुलेटर में एक [[ विलंब रेखा व्यतिकरणमापी ]] होता है जो एक बिट्स की देरी करता है, इसलिए एक समय में दो बिट्स की तुलना की जा सकती है। आगे की प्रक्रिया में, [[ ऑप्टिकल क्षेत्र ]] को विद्युत प्रवाह में बदलने के लिए एक [[ फोटोडायोड ]] का उपयोग किया जाता है, इसलिए सूचना को उसकी मूल स्थिति में वापस बदल दिया जाता है। | ||
डीबीपीएसके और डीक्यूपीएसके की बिट-त्रुटि दर की तुलना ग्राफ में उनके गैर-अंतर समकक्षों से की जाती है। डीबीपीएससी का उपयोग करने का नुकसान जटिलता में कमी की तुलना में काफी छोटा है जिसका उपयोग | डीबीपीएसके और डीक्यूपीएसके की बिट-त्रुटि दर की तुलना ग्राफ में उनके गैर-अंतर समकक्षों से की जाती है। डीबीपीएससी का उपयोग करने का नुकसान जटिलता में कमी की तुलना में काफी छोटा है जिसका उपयोग प्रायः संचार प्रणालियों में किया जाता है जो अन्यथा बीपीएसके का उपयोग करेंगे। यद्यपि डीक्यूपीएसके के लिए, सामान्य क्यूपीएसके की तुलना में प्रदर्शन में नुकसान बड़ा है और प्रणाली डिजाइनर को इसे जटिलता में कमी के खिलाफ संतुलित करना चाहिए। | ||
=== उदाहरण: अलग-अलग एन्कोडेड बीपीएसके === | === उदाहरण: अलग-अलग एन्कोडेड बीपीएसके === | ||
| Line 246: | Line 246: | ||
जहां पे <math>\oplus{}</math> बाइनरी या [[ मॉड्यूलर अंकगणित | मॉड्यूलर जोड़ -2]] को इंगित करता है | | जहां पे <math>\oplus{}</math> बाइनरी या [[ मॉड्यूलर अंकगणित | मॉड्यूलर जोड़ -2]] को इंगित करता है | | ||
[[File:Diff enc BPSK BER curves.svg|thumb|right|280px|बीपीएसके के बीच बीईआर तुलना और सफेद | [[File:Diff enc BPSK BER curves.svg|thumb|right|280px|बीपीएसके के बीच बीईआर तुलना और सफेद रव में काम कर रहे बीपीएसके के अंतर एन्कोडेड बीपीएसके]] | ||
इसलिए <math>e_k</math> केवल स्थिति बदलता है (बाइनरी "0" से बाइनरी "1" या बाइनरी "1" से बाइनरी "0" में) अगर <math>b_k</math> एक बाइनरी "1" है। अन्यथा यह अपनी पूर्व अवस्था में ही रहता है। यह ऊपर दिए गए डिफरेंशियल एनकोडेड बीपीएसके का विवरण है। | इसलिए <math>e_k</math> केवल स्थिति बदलता है (बाइनरी "0" से बाइनरी "1" या बाइनरी "1" से बाइनरी "0" में) अगर <math>b_k</math> एक बाइनरी "1" है। अन्यथा यह अपनी पूर्व अवस्था में ही रहता है। यह ऊपर दिए गए डिफरेंशियल एनकोडेड बीपीएसके का विवरण है। | ||
| Line 258: | Line 258: | ||
अन्य पीएसके मॉड्यूलेशन के लिए डिफरेंशियल स्कीमें समान तर्ज पर तैयार की जा सकती हैं। डीपीएसके के लिए वेवफॉर्म ऊपर दिए गए डिफरेंशियल एनकोडेड पीएसके के समान हैं क्योंकि दोनों योजनाओं के बीच एकमात्र परिवर्तन रिसीवर पर है। | अन्य पीएसके मॉड्यूलेशन के लिए डिफरेंशियल स्कीमें समान तर्ज पर तैयार की जा सकती हैं। डीपीएसके के लिए वेवफॉर्म ऊपर दिए गए डिफरेंशियल एनकोडेड पीएसके के समान हैं क्योंकि दोनों योजनाओं के बीच एकमात्र परिवर्तन रिसीवर पर है। | ||
'''इस''' उदाहरण के लिए बीईआर वक्र की तुलना दाईं ओर साधारण बीपीएसके से की जाती है। जैसा कि ऊपर उल्लेख किया गया है, जबकि त्रुटि दर लगभग दोगुनी है, इसमें वृद्धि की आवश्यकता है <math>E_b/N_0</math> इस पर काबू पाने के लिए वृद्धि कम है। <math>E_b/N_0</math> कोडित प्रणालियों में अंतर मॉडुलन को दूर करने के लिए आवश्यक है, हालांकि, बड़ा है{{snd}} सामान्य लगभग 3 डीबी। प्रदर्शन में गिरावट गैर-सुसंगत संचरण का परिणाम है{{snd}} इस | '''इस''' उदाहरण के लिए बीईआर वक्र की तुलना दाईं ओर साधारण बीपीएसके से की जाती है। जैसा कि ऊपर उल्लेख किया गया है, जबकि त्रुटि दर लगभग दोगुनी है, इसमें वृद्धि की आवश्यकता है <math>E_b/N_0</math> इस पर काबू पाने के लिए वृद्धि कम है। <math>E_b/N_0</math> कोडित प्रणालियों में अंतर मॉडुलन को दूर करने के लिए आवश्यक है, हालांकि, बड़ा है{{snd}} सामान्य लगभग 3 डीबी। प्रदर्शन में गिरावट गैर-सुसंगत संचरण का परिणाम है{{snd}} इस परिस्थिति में यह इस तथ्य को संदर्भित करता है कि चरण की ट्रैकिंग को पूरी तरह से अनदेखा किया जाता है। | ||
===परिभाषाएं === | ===परिभाषाएं === | ||
| Line 267: | Line 267: | ||
* <math>T_b</math>, [[ बिट दर ]] | * <math>T_b</math>, [[ बिट दर ]] | ||
* <math>T_s</math>, प्रतिक दर | * <math>T_s</math>, प्रतिक दर | ||
* <math>\frac{1}{2}N_0</math>, [[ संकेत शोर ]] [[ वर्णक्रमीय घनत्व ]] ([[ वाट ]]/[[ हेटर्स ]]) | * <math>\frac{1}{2}N_0</math>, [[ संकेत शोर | संकेत रव]] [[ वर्णक्रमीय घनत्व ]] ([[ वाट ]]/[[ हेटर्स ]]) | ||
* <math>P_b</math>, बिट-त्रुटि की [[ संभावना ]] | * <math>P_b</math>, बिट-त्रुटि की [[ संभावना ]] | ||
* <math>P_s</math>, प्रतीक-त्रुटि की संभावना | * <math>P_s</math>, प्रतीक-त्रुटि की संभावना | ||
| Line 275: | Line 275: | ||
: <math>Q(x) = \frac{1}{\sqrt{2\pi}}\int_x^\infty e^{-\frac{1}{2}t^2} \,dt = \frac{1}{2} \operatorname{erfc}\left(\frac{x}{\sqrt{2}}\right),\ x \geq 0</math>. | : <math>Q(x) = \frac{1}{\sqrt{2\pi}}\int_x^\infty e^{-\frac{1}{2}t^2} \,dt = \frac{1}{2} \operatorname{erfc}\left(\frac{x}{\sqrt{2}}\right),\ x \geq 0</math>. | ||
यहां उद्धृत त्रुटि दर योज्य सफेद गाऊसी | यहां उद्धृत त्रुटि दर योज्य सफेद गाऊसी रव (एडब्ल्यूजीएन) में हैं। ये त्रुटि दर [[ लुप्त होती चैनल ]] में गणना की तुलना में कम हैं, इसलिए, तुलना करने के लिए एक अच्छा सैद्धांतिक बेंचमार्क है। | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
| Line 290: | Line 290: | ||
ऐतिहासिक रूप से, बेल 201, 208, और 209 और सीसीआईटीटी वी.26, वी.27, वी.29, वी.32 और वी.34 जैसे वॉयस-बैंड सिंक्रोनस [[ मोडेम | मोडेम]] पीएसके का इस्तेमाल करते थे।<ref>{{Cite web |title=Local and Remote Modems |url=http://www.blackbox.com/resource/files/productdetails/19558.PDF |url-status=dead |archive-url=https://web.archive.org/web/20151222112409/http://www.blackbox.com/resource/files/productdetails/19558.PDF |archive-date=December 22, 2015 |access-date=December 20, 2015 |website=Black Box |publisher=Black Box Network Services}}</ref> | ऐतिहासिक रूप से, बेल 201, 208, और 209 और सीसीआईटीटी वी.26, वी.27, वी.29, वी.32 और वी.34 जैसे वॉयस-बैंड सिंक्रोनस [[ मोडेम | मोडेम]] पीएसके का इस्तेमाल करते थे।<ref>{{Cite web |title=Local and Remote Modems |url=http://www.blackbox.com/resource/files/productdetails/19558.PDF |url-status=dead |archive-url=https://web.archive.org/web/20151222112409/http://www.blackbox.com/resource/files/productdetails/19558.PDF |archive-date=December 22, 2015 |access-date=December 20, 2015 |website=Black Box |publisher=Black Box Network Services}}</ref> | ||
== योगात्मक सफेद गाऊसी | == योगात्मक सफेद गाऊसी रव के साथ पारस्परिक जानकारी == | ||
[[File:PSK Mutual Information in AWGN.svg|300px|right|thumb|AWGN चैनल पर PSK की पारस्परिक जानकारी]] | [[File:PSK Mutual Information in AWGN.svg|300px|right|thumb|AWGN चैनल पर PSK की पारस्परिक जानकारी]] | ||
पीएसके की पारस्परिक जानकारी का मूल्यांकन इसकी परिभाषा के [[ संख्यात्मक एकीकरण ]] द्वारा योगात्मक सफेद गाऊसी | पीएसके की पारस्परिक जानकारी का मूल्यांकन इसकी परिभाषा के [[ संख्यात्मक एकीकरण ]] द्वारा योगात्मक सफेद गाऊसी रव में किया जा सकता है।<ref name=Blahut1988>{{cite book|last1=Blahut|first1=R. E.|title=Principles and Practice of Information Theory|date=1988|publisher=Addison Wesley Publishing Company|location=Boston, MA, USA|isbn=0-201-10709-0}}</ref> पारस्परिक सूचना के वक्र रव अनुपात के अनंत संकेत की सीमा में प्रत्येक प्रतीक द्वारा किए गए बिट्स की संख्या से संतृप्त होते हैं <math>E_s/N_0</math>. इसके विपरीत, रव अनुपात के लिए छोटे सिग्नल की सीमा में आपसी जानकारी एडब्ल्यूजीएन चैनल क्षमता प्रमेय तक पहुंचती है, जो कि प्रतीक सांख्यिकीय वितरण के सभी संभावित विकल्पों में सर्वोच्च है। | ||
रव अनुपात के संकेत के मध्यवर्ती मूल्यों पर पारस्परिक सूचना (एमआई) अच्छी तरह से अनुमानित है<ref name=Blahut1988 /> | |||
:<math>\textrm{MI} \simeq \log_2\left(\sqrt{\frac{4\pi}{e}\frac{E_s}{N_0}}\right).</math> | :<math>\textrm{MI} \simeq \log_2\left(\sqrt{\frac{4\pi}{e}\frac{E_s}{N_0}}\right).</math> | ||
| Line 324: | Line 324: | ||
[[Category:Machine Translated Page]] | |||
[[Category:All articles with unsourced statements|Phase-Shift Keying]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page|Phase-Shift Keying]] | |||
[[Category:Articles with invalid date parameter in template|Phase-Shift Keying]] | |||
[[Category:Articles with short description|Phase-Shift Keying]] | |||
[[Category:Articles with unsourced statements from June 2019|Phase-Shift Keying]] | |||
[[Category:CS1|Phase-Shift Keying]] | |||
[[Category:Commons category link is locally defined|Phase-Shift Keying]] | |||
[[Category:Exclude in print|Phase-Shift Keying]] | |||
[[Category:Interwiki category linking templates|Phase-Shift Keying]] | |||
[[Category:Interwiki link templates|Phase-Shift Keying]] | |||
[[Category:Pages with script errors|Phase-Shift Keying]] | |||
[[Category:Pages with template loops|Phase-Shift Keying]] | |||
[[Category:Short description with empty Wikidata description|Phase-Shift Keying]] | |||
[[Category:Templates that add a tracking category|Phase-Shift Keying]] | |||
[[Category:Templates using TemplateData|Phase-Shift Keying]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:Wikimedia Commons templates|Phase-Shift Keying]] | |||
Latest revision as of 13:17, 19 October 2023
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
फेज-शिफ्ट कुंजीयन (पीएसके) एक डिजिटल मॉड्यूलेशन प्रक्रिया है जो निरंतरआवृत्ति संदर्भ सिग्नल( वाहक तरंग ) के चरण को बदलकर(मॉड्यूलेट) करके डेटा सम्पादित करती है। सही समय पर ज्या तरंग और कोज्या तरंग इनपुट को परिवर्तित कर मॉड्यूलेशन पूरा किया जाता है। यह व्यापक रूप से वायरलेस लैन , आरएफआईडी और ब्लूटूथ संचार के लिए उपयोग किया जाता है।
कोई भी डिजिटल मॉडुलन योजना डिजिटल डेटा का प्रतिनिधित्व करने के लिए सीमित संख्या में विशिष्ट संकेतों का उपयोग करती है। पीएसके चरणों की सीमित संख्या का उपयोग करता है, प्रत्येक को द्विआधारी अंकों का एक अनूठा स्वरूप सौंपा गया है। प्रायः, प्रत्येक चरण समान संख्या में बिट्स को एन्कोड करता है। बिट्स का प्रत्येक स्वरूप उस प्रतीक का निर्माण करता है जिसे विशेष चरण द्वारा दर्शाया जाता है। डिमोडुलेटर, जिसे विशेष रूप से मॉड्यूलेटर द्वारा उपयोग किए जाने वाले प्रतीक-सेट के लिए डिज़ाइन किया गया है, प्राप्त सिग्नल के चरण को निर्धारित करता है और इसे उस प्रतीक पर वापस मैप करता है जो इसे दर्शाता है, इस प्रकार मूल डेटा को पुनर्प्राप्त करता है। इसके लिए रिसीवर को प्राप्त सिग्नल के चरण की तुलना संदर्भ सिग्नल से करने में सक्षम होना चाहिए – ऐसी प्रणाली को सुसंगत (और सीपीएसके के रूप में संदर्भित) कहा जाता है।
सीपीएसके को एक जटिल डिमोडुलेटर की आवश्यकता होती है, क्योंकि इसे प्राप्त सिग्नल से संदर्भ तरंग निकालना चाहिए और प्रत्येक नमूने की तुलना करने के लिए इसका ट्रैक रखना चाहिए। वैकल्पिक रूप से, भेजे गए प्रत्येक प्रतीक के चरण बदलाव को पिछले भेजे गए प्रतीक के चरण के संबंध में मापा जा सकता है। चूंकि प्रतीकों को क्रमिक नमूनों के बीच चरण के अंतर में एन्कोड किया गया है, इसे अंतर चरण-शिफ्ट कुंजीयन (डीपीएसके) कहा जाता है। डीपीएसके सामान्य पीएसके की तुलना में लागू करने के लिए काफी सरल हो सकता है, क्योंकि यह 'गैर-सुसंगत' योजना है, संदर्भ तरंग का ट्रैक रखने के लिए डिमोडुलेटर की कोई आवश्यकता नहीं है। ट्रेड-ऑफ यह है कि इसमें अधिक डिमॉड्यूलेशन अशुद्धियाँ हैं।
परिचय
डिजिटल रूप से प्रस्तुत डेटा के प्रसारण के लिए उपयोग की जाने वाली डिजिटल मॉड्यूलेशन तकनीकों के तीन प्रमुख वर्ग हैं:
- आयाम-शिफ्ट कुंजीयन (एएसके - एम्पलीट्यूड शिफ्ट कीइंग)
- आवृत्ति-शिफ्ट कुंजीयन (एफएसके - फ्रीक्वेंसी शिफ्ट कीइंग)
- चरण-शिफ्ट कुंजीयन (पीएसके - फेज शिफ्ट कीइंग)
सभी डेटा सिग्नल के जवाब में सभी बेस सिग्नल के कुछ पहलू, वाहक तरंग (प्रायः ज्या तरंग) को बदलकर डेटा देते हैं। पीएसके की स्थिति में, डेटा सिग्नल का प्रतिनिधित्व करने के लिए चरण बदल दिया जाता है। इस तरह से सिग्नल के चरण का उपयोग करने के दो मूलभूत तरीके हैं:
- सूचना को संप्रेषित करने के रूप में चरण को देखकर, जिस स्थिति में प्राप्त संकेत के चरण की तुलना करने के लिए डिमोडुलेटर के पास एक संदर्भ संकेत होना चाहिए।
- सूचना देने के रूप में चरण में परिवर्तन को देखकर – डिफरेंशियल एनकोडिंग स्कीम, डिफरेंशियल फेज-शिफ्ट कुंजीयन जिनमें से किसी निर्देश वाहक(निश्चित सीमा तक) की जरूरत नहीं है।
पीएसके योजनाओं का प्रतिनिधित्व करने की एक सुविधाजनक युक्ति नक्षत्र आरेख पर है। यह जटिल तल में उन बिंदुओं को दर्शाता है जहां, इस संदर्भ में, वास्तविक संख्या और काल्पनिक संख्या अक्षों को उनके 90° पृथक्करण के कारण क्रमशः चरण और चतुर्भुज अक्ष कहा जाता है। लंबवत अक्षों पर इस तरह का प्रतिनिधित्व सीधे कार्यान्वयन के लिए उधार देता है। इन-फेज अक्ष के साथ प्रत्येक बिंदु का आयाम कोज्या (या ज्या) तरंग और ज्या (या कोज्या) तरंग को संशोधित करने के लिए चतुर्भुज अक्ष के साथ आयाम को संशोधित करने के लिए उपयोग किया जाता है। पद्यति के अनुसार, इन-फेज कोज्या को संशोधित करता है और चतुर्भुज चिन्ह को मॉड्यूलेट करता है।
पीएसके में, चुने गए नक्षत्र आरेख को प्रायः वृत्त के चारों ओर एकसमान कोणीय रिक्ति के साथ स्थित किया जाता है। यह आसन्न बिंदुओं के बीच अधिकतम चरण-पृथक्करण देता है और इस प्रकार भ्रष्टाचार के लिए सर्वोत्तम प्रतिरक्षा प्रदान करता है। उन्हें एक वृत्त पर रखा जाता है ताकि उन सभी को एक ही ऊर्जा से संचरित किया जा सके। इस तरह, वे जिन सम्मिश्र संख्याओं का प्रतिनिधित्व करते हैं, उनका मापक समान होगा और इस प्रकार कोज्या और ज्या तरंगों के लिए आवश्यक आयाम भी होंगे। दो सामान्य उदाहरण "द्विआधारी चरण-शिफ्ट कुंजीयन" (बीपीएसके) जो दो चरणों का उपयोग करते हैं, और "चतुर्भुज चरण-शिफ्ट कुंजीयन" (क्यूपीएसके) जो चार चरणों का उपयोग करता है, हालांकि कोई भी संख्या में चरणों का उपयोग किया जा सकता है। चूंकि प्रेषित किए जाने वाले डेटा प्रायः द्विआधारी होते हैं, पीएसके योजना सामान्यत दो की शक्ति होने वाले नक्षत्र बिंदुओं की संख्या के साथ तैयार की जाती है।
बाइनरी चरण-शिफ्ट कुंजीयन (बीपीएसके)
बीपीएसके (जिसे कभी-कभी पीआरके, फेज़ रिवर्सल कुंजीयन या 2पीएसके भी कहा जाता है) फेज़ शिफ्ट कीइंग (पीएसके) का सबसे सरल रूप है। यह दो चरणों का उपयोग करता है जो 180 ° से अलग होते हैं और इसलिए इसे 2-पीएसके भी कहा जा सकता है। यह विशेष रूप से बिल्कुल मायने नहीं रखता है कि नक्षत्र बिंदु जहाँ स्थित हैं, और इस आंकड़े में उन्हें वास्तविक अक्ष पर 0 ° और 180 ° पर दिखाया गया है। इसलिए, यह डिमोडुलेटर के गलत निर्णय पर पहुंचने से पहले उच्चतम रव स्तर या विकृति को संभालता है। यह इसे सभी पीएसके में सबसे मजबूत बनाता है। हालांकि, यह केवल 1 बिट/प्रतीक (जैसा कि चित्र में देखा गया है) पर मॉड्यूलेट करने में सक्षम है और इसलिए उच्च डेटा-दर अनुप्रयोगों के लिए अनुपयुक्त है। फिर भी इस बिट/प्रतीक को विस्तारित करने की संभावना है, मॉड्यूलेटर प्रतीक एन्क्रिप्शन/डिक्रिप्शन तर्क प्रणाली को देखते हुए।
संचार चैनल द्वारा शुरू की गई मनमानी चरण-शिफ्ट की उपस्थिति में, डिमोडुलेटर (देखें, जैसे कोस्टास लूप ) यह बताने में असमर्थ है कि कौन सा नक्षत्र बिंदु है। फलस्वरूप, डेटा प्रायः मॉडुलन से पहले अलग-अलग एन्कोड किया जाता है।
बीपीएसके कार्यात्मक रूप से समकक्ष 2-क्यूएएम मॉड्यूलेशन के बराबर है।
कार्यान्वयन
बीपीएसके के लिए सामान्य रूप इस समीकरण का अनुसरण करता है:
इससे दो चरण प्राप्त होते हैं, 0 और विशिष्ट रूप में, बाइनरी डेटा को प्रायः निम्नलिखित संकेतों से अवगत कराया जाता है[citation needed]
- बाइनरी 0 . के लिए
- बाइनरी 1 . के लिए
जहाँ f बेस बैंड की आवृत्ति है।
इसलिए, सिग्नल स्पेस को सिंगल आधार फलन द्वारा दर्शाया जा सकता है
जहाँ 1 को द्वारा दर्शाया जाता है और 0 को द्वारा दर्शाया गया है . यह अज्यामेंट मनमाना है।
इस आधार फ़ंक्शन का यह उपयोग सिग्नल टाइमिंग आरेख में दिखाया गया है। सबसे ऊपरी संकेत एक बीपीएसके-संग्राहक कोज्या तरंग है जो बीपीएसके न्यूनाधिक उत्पन्न करेगा। इस आउटपुट का कारण बनने वाली बिट-स्ट्रीम सिग्नल के ऊपर दिखाई जाती है (इस आंकड़े के अन्य भाग केवल क्यूपीएसके के लिए प्रासंगिक हैं)। मॉडुलन के बाद, बेस बैंड सिग्नल को से गुणा करके उच्च आवृत्ति बैंड में ले जाया जाएगा
बिट त्रुटि दर
योगशील सफेद गाऊसी रव (एडब्ल्यूजीएन) के तहत बीपीएसके की बिट एरर रेट (बीईआर) की गणना इस प्रकार की जा सकती है[1]
- या
चूंकि प्रति प्रतीक केवल एक बिट है, यह भी प्रतीक त्रुटि दर है।
चतुर्भुज चरण-शिफ्ट कुंजीयन (क्यूपीएसके)

कभी-कभी इसे क्वाड्रिफेज पीएसके, 4-पीएसके, या 4-क्यूएएम के रूप में जाना जाता है। (हालांकि क्यूपीएसके और 4-क्यूएएम की मूल अवधारणाएं अलग हैं, परिणामी संशोधित रेडियो तरंगें बिल्कुल समान हैं।) क्यूपीएसके नक्षत्र आरेख पर चार बिंदुओं का उपयोग करता है, जो एक सर्कल के चारों ओर समान होता है। चार चरणों के साथ, क्यूपीएसके बिट त्रुटि दर (बीईआर) को कम करने के लिए ग्रे कोडिंग के साथ आरेख में दिखाए गए प्रति प्रतीक दो बिट्स को एन्कोड कर सकता है। कभी-कभी बीपीएसके के दोगुने बीईआर के रूप में गलत समझा जाता है।
गणितीय विश्लेषण से पता चलता है कि सिग्नल के समान बैंडविड्थ (सिग्नल प्रोसेसिंग) को बनाए रखते हुए, या बीपीएसके की डेटा-दर को बनाए रखने के लिए, लेकिन आवश्यक बैंडविड्थ को आधा करने के लिए क्यूपीएसके का उपयोग या तो बीपीएसके प्रणाली की तुलना में डेटा दर को दोगुना करने के लिए किया जा सकता है। इस परिस्थिति के बाद में, बीपीएसके का बीईआर बिल्कुल बीपीएसके के बीईआर के समान है - और बीपीएसके पर विचार या वर्णन करते समय अलग-अलग तरह से विश्वास करना एक सामान्य भ्रम है। प्रेषित वाहक कई चरण परिवर्तनों से गुजर सकता है।
यह देखते हुए कि रेडियो संचार चैनल संघीय संचार आयोग जैसी एजेंसियों द्वारा निर्धारित (अधिकतम) बैंडविड्थ देने के लिए आवंटित किए जाते हैं, बीपीएसके पर क्यूपीएसके का लाभ स्पष्ट हो जाता है क्यूपीएसके बीपीएसके की तुलना में दिए गए बैंडविड्थ में दो बार डेटा दर प्रसारित करता है - उसी बीईआर पर इंजीनियरिंग जुर्माना जो भुगतान किया जाता है वह यह है कि क्यूपीएसके ट्रांसमीटर और रिसीवर बीपीएसके के लिए अधिक जटिल हैं। हालांकि, आधुनिक इलेक्ट्रानिक्स प्रौद्योगिकी के साथ, लागत दंड बहुत कम है।
बीपीएसके के साथ, प्राप्त करने वाले अंत में चरण अस्पष्टता की समस्याएं हैं, और विशेषक एन्कोडिंग क्यूपीएसके प्रायः अभ्यास में प्रयोग किया जाता है।
कार्यान्वयन
क्यूपीएसके का कार्यान्वयन बीपीएसके की तुलना में अधिक सामान्य है और उच्च-क्रम पीएसके के कार्यान्वयन को भी ठीक करता है। नक्षत्र आरेख में प्रतीकों को ज्या और कोज्या तरंगों के संदर्भ में लिखना जो उन्हें प्रसारित करते हैं:
यह चार चरणों / 4, 3π/4, 5π/4 और 7π/4 को आवश्यकतानुसार प्राप्त करता है।
इसका परिणाम इकाई आधार कार्यों के साथ द्वि-आयामी सिग्नल स्थान में होता है
पहला बेस फंक्शन सिग्नल के इन-फेज कंपोनेंट के रूप में और दूसरा सिगनल के क्वाड्रैचर कंपोनेंट के रूप में उपयोग किया जाता है।
इसलिए, संकेत तारामंडल में संकेत-स्पेस 4 बिंदु होते हैं
1/2 के गुणनखंड इंगित करते हैं कि कुल शक्ति दो वाहकों के बीच समान रूप से विभाजित है।
बीपीएसके के लिए इन आधार कार्यों की तुलना स्पष्ट रूप से दिखाती है कि क्यूपीएसके को दो स्वतंत्र बीपीएसके संकेतों के रूप में कैसे देखा जा सकता है। ध्यान दें कि बीपीएसके के लिए सिग्नल-स्पेस बिंदु को बीपीएसके तारामंडल आरेख में दिखाई गई योजना में दो वाहकों पर प्रतीक (बिट) ऊर्जा को विभाजित करने की आवश्यकता नहीं है।
क्यूपीएसके प्रणाली को कई तरीकों से लागू किया जा सकता है। ट्रांसमीटर और रिसीवर संरचना के प्रमुख घटकों का एक उदाहरण नीचे दिखाया गया है।

त्रुटि की संभावना
यद्यपि क्यूपीएसके को चतुर्धातुक मॉडुलन के रूप में देखा जा सकता है, इसे दो स्वतंत्र रूप से संग्राहक चतुर्भुज वाहक के रूप में देखना आसान है। इस व्याख्या के साथ, सम (या विषम) बिट्स का उपयोग वाहक के इन-फेज घटक को संशोधित करने के लिए किया जाता है, जबकि विषम (या सम) बिट्स का उपयोग वाहक के चतुर्भुज-चरण घटक को संशोधित करने के लिए किया जाता है। बीपीएसके का उपयोग दोनों वाहकों पर किया जाता है और उन्हें स्वतंत्र रूप से डिमॉड्यूलेट किया जा सकता है।
परिणामस्वरूप, क्यूपीएसके के लिए बिट-त्रुटि की संभावना बीपीएसके के समान ही है,
यद्यपि, बीपीएसके के समान बिट-त्रुटि संभावना को प्राप्त करने के लिए, क्यूपीएसके दो बार शक्ति का उपयोग करता है (चूंकि दो बिट्स एक साथ प्रसारित होते हैं)।
प्रतीक त्रुटि दर द्वारा दिया जाता है,
यदि सिग्नल-टू-रव अनुपात अधिक है (जैसा कि व्यावहारिक क्यूपीएसके प्रणाली के लिए आवश्यक है) प्रतीक त्रुटि की संभावना का अनुमान लगाया जा सकता है
अनियमित बाइनरी डेटा-स्ट्रीम के एक छोटे खंड के लिए संशोधित संकेत नीचे दिखाया गया है। दो वाहक तरंगें एक कोज्या तरंग और एक ज्या लहर हैं, जैसा कि ऊपर सिग्नल-स्पेस विश्लेषण द्वारा दर्शाया गया है। यहां, विषम-संख्या वाले बिट्स को इन-फेज घटक और सम-संख्या वाले बिट्स को क्वाडरेचर घटक (पहले बिट को नंबर 1 के रूप में लेते हुए) को सौंपा गया है। कुल संकेत – दो घटकों का योग – नीचे दिखाया गया है। चरण में कूदता देखा जा सकता है क्योंकि पीएसके प्रत्येक बिट-अवधि की शुरुआत में प्रत्येक घटक पर चरण बदलता है। सबसे ऊपरी तरंग अकेले ऊपर बीपीएसके के लिए दिए गए विवरण से मेल खाती है।
बाइनरी डेटा जो इस तरंग द्वारा व्यक्त किया जाता है वह है: 11000110.
- विषम बिट्स, यहां हाइलाइट किए गए, इन-फेज घटक में योगदान करते हैं 1 1 0 0 0 1 1 0
- यहां पर प्रकाश डाला गया सम बिट्स, चतुर्भुज-फेज घटक में योगदान करते हैं 1 1 0 0 0 1 1 0
वेरिएंट
ऑफसेट क्यूपीएसके (ओक्यूपीएसके)
ऑफसेट क्वाड्रेचर फेज-शिफ्ट कुंजीयन (ओक्यूपीएसके) फेज-शिफ्ट कीइंग मॉडुलन का एक प्रकार है, जो चरण के चार अलग-अलग मूल्यों को संचारित करने के लिए उपयोग करता है। इसे कभी-कभी कंपित चतुर्भुज चरण-शिफ्ट कुंजीयन (एसक्यूपीएसके) कहा जाता है।
क्यूपीएसके प्रतीक के निर्माण के लिए एक समय में चरण के चार मान (दो बिट्स) लेने से संकेत के चरण को एक बार में 180° तक कूदने की अनुमति मिल सकती है। जब सिग्नल कम-पास फ़िल्टर किया जाता है (जैसा कि ट्रांसमीटर में विशिष्ट होता है), इन चरण-शिफ्टों के परिणामस्वरूप बड़े आयाम में उतार-चढ़ाव होता है, संचार प्रणालियों में एक अवांछनीय गुणवत्ता। विषम और सम बिट्स के समय को एक बिट-अवधि, या आधे प्रतीक-अवधि से ऑफसेट करके, चरण और चतुर्भुज घटक एक ही समय में कभी नहीं बदलेंगे। दाईं ओर दिखाए गए तारामंडल आरेख में, यह देखा जा सकता है कि यह चरण-शिफ्ट को एक बार में 90° से अधिक तक नहीं सीमित कर देगा। यह गैर-ऑफ़सेट क्यूपीएसके की तुलना में बहुत कम आयाम में उतार-चढ़ाव पैदा करता है और कभी-कभी व्यवहार में इसे पसंद किया जाता है।
दाईं ओर की तस्वीर साधारण क्यूपीएसके और ओक्यूपीएसके के बीच के चरण के व्यवहार में अंतर दिखाती है। यह देखा जा सकता है कि पहले प्लॉट में फेज एक बार में 180° तक बदल सकता है, जबकि ओक्यूपीएसके में परिवर्तन कभी भी 90° से अधिक नहीं होते हैं।
अनियमित बाइनरी डेटा-स्ट्रीम के एक छोटे खंड के लिए संशोधित संकेत नीचे दिखाया गया है। दो घटक तरंगों के बीच आधे प्रतीक-अवधि ऑफसेट पर ध्यान दें। क्यूपीएसके के लिए अचानक चरण-शिफ्ट लगभग दो बार होती है (क्योंकि सिग्नल अब एक साथ नहीं बदलते हैं), लेकिन वे कम गंभीर होते हैं। दूसरे शब्दों में, क्यूपीएसके की तुलना में ओक्यूपीएसके में छलांग का परिमाण छोटा होता है।
एसओक्यूपीएसके
लाइसेंस-मुक्त पल्स शेपिंग -ऑफसेट क्यूपीएसके (एसओक्यूपीएसके) फेहर-पेटेंट क्यूपीएसके (एफक्यूपीएसके) के साथ इंटरऑपरेबल है, इस अर्थ में कि एक एकीकृत और-डंप ऑफसेट क्यूपीएसके डिटेक्टर समान आउटपुट का उत्पादन करता है, चाहे किसी भी प्रकार के ट्रांसमीटर का उपयोग किया जाए।[2] ये मॉड्यूलेशन और क्यू तरंगों को सावधानीपूर्वक आकार देते हैं जैसे कि वे बहुत आसानी से बदलते हैं, और सिग्नल संक्रमण के दौरान भी सिग्नल स्थिर-आयाम रहता है। (एक प्रतीक से दूसरे प्रतीक या यहां तक कि रैखिक रूप से यात्रा करने के बजाय, यह एक प्रतीक से दूसरे प्रतीक तक निरंतर-आयाम वृत्त के चारों ओर आसानी से यात्रा करता है।) एसओक्यूपीएसके मॉड्यूलेशन को क्यूपीएसके और न्यूनतम-शिफ्ट कुंजीयन के संकर के रूप में दर्शाया जा सकता है एसओक्यूपीएसके है क्यूपीएसके के समान सिग्नल तारामंडल, हालाँकि एसओक्यूपीएसके का चरण हमेशा स्थिर रहता है।[3][4]
एसओक्यूपीएसके-टीजी के मानक विवरण में टर्नरी सिग्नल शामिल है।[5] एसओक्यूपीएसके निम्न पृथ्वी की कक्षा उपग्रह संचार के लिए आवेदन में सबसे अधिक प्रसार मॉड्यूलेशन योजनाओं में से एक है।[6]
π/4-क्यूपीएसके
क्यूपीएसके का यह दो प्रकार के समान तारामंडल का उपयोग करता है जो 45 डिग्री घुमाए जाते हैं इसलिए ( रेडियन,) एक दूसरे के संबंध में प्रायः, या तो सम या विषम प्रतीकों का उपयोग किसी एक तारामंडल से बिंदुओं का चयन करने के लिए किया जाता है और अन्य प्रतीकों का उपयोग दूसरे तारामंडल से बिंदुओं का चयन करने के लिए किया जाता है। यह चरण-शिफ्ट को अधिकतम 180 ° से कम करता है, लेकिन केवल अधिकतम 135 ° तक और इसलिए -क्यूपीएसके के आयाम में उतार-चढ़ाव ओक्यूपीएसके और नॉन-ऑफ़सेट क्यूपीएसके के बीच होते हैं।
इस मॉडुलन योजना की संपत्ति यह है कि यदि संग्राहक संकेत को जटिल डोमेन में दर्शाया जाता है, तो प्रतीकों के बीच संक्रमण कभी भी 0 से नहीं गुजरता है। दूसरे शब्दों में, संकेत मूल से नहीं गुजरता है। यह सिग्नल में उतार-चढ़ाव की गतिशील सीमा को कम करता है जो इंजीनियरिंग संचार संकेतों के दौरान वांछनीय है।
दूसरी ओर, -क्यूपीएसके खुद को आसान डिमॉड्यूलेशन के लिए उधार देता है और उदाहरण के लिए टाइम-डिवीजन मल्टीपल एक्सेस सेलुलर टेलीफोन प्रणाली इसे उपयोग के लिए अपनाया गया है।
अनियमित बाइनरी डेटा-स्ट्रीम के एक छोटे खंड के लिए संशोधित संकेत नीचे दिखाया गया है। निर्माण सामान्य क्यूपीएसके के लिए ऊपर जैसा ही है। आरेख में दिखाए गए दो तारामंडल से क्रमिक प्रतीक लिए गए हैं। इस प्रकार, पहला प्रतीक (11) नीले तारामंडल से लिया गया है और दूसरा प्रतीक (0 0) हरे तारामंडल से लिया गया है। ध्यान दें कि दो घटक तरंगों के परिमाण बदलते हैं क्योंकि वे तारामंडल के बीच स्विच करते हैं, लेकिन कुल सिग्नल का परिमाण स्थिर रहता है (निरंतर लिफाफा )। चरण-शिफ्ट दो पिछले समय-आरेखों के बीच हैं।
डीपीक्यूपीएसके
दोहरी-ध्रुवीकरण चतुर्भुज फेज शिफ्ट कुंजीयन (डीपीक्यूपीएसके) या दोहरी-ध्रुवीकरण क्यूपीएसके - में दो अलग-अलग क्यूपीएसके सिग्नलों का ध्रुवीकरण मल्टीप्लेक्सिंग शामिल है, इस प्रकार 2 के कारक द्वारा वर्णक्रमीय दक्षता में सुधार होता है। यह 16-एसके का उपयोग करने के लिए एक लागत प्रभावी विकल्प है, वर्णक्रमीय दक्षता को दोगुना करने के लिए क्यूपीएसके के बजाय
उच्च क्रम पीएसके
पीएसके तारामंडल के निर्माण के लिए कितने भी चरणों का उपयोग किया जा सकता है, लेकिन 8-पीएसके प्रायः तैनात उच्चतम क्रम पीएसके तारामंडल है। 8 से अधिक चरणों के साथ, त्रुटि-दर बहुत अधिक हो जाती है और बेहतर होते हैं, हालांकि अधिक जटिल, मॉड्यूलेशन उपलब्ध होते हैं जैसे कि चतुर्भुज आयाम मॉडुलन (क्यूएएम)। यद्यपि किसी भी संख्या में चरणों का उपयोग किया जा सकता है, तथ्य यह है कि तारामंडल को प्रायः बाइनरी डेटा से निपटना चाहिए, इसका मतलब है कि प्रतीकों की संख्या प्रायः प्रति प्रतीक बिट्स की पूर्णांक संख्या की अनुमति देने के लिए 2 की शक्ति है।
बिट त्रुटि दर
सामान्य एम-पीएसके के लिए प्रतीक-त्रुटि प्रायिकता के लिए कोई सरल व्यंजक नहीं है यदि . दुर्भाग्य से, यह केवल से प्राप्त किया जा सकता है
जहाँ पे
तथा तथा प्रत्येक गाऊसी यादृच्छिक चर हैं।
यह उच्च के लिए अनुमानित किया जा सकता है और उच्च द्वारा:
के लिए बिट-त्रुटि संभावना -पीएसके केवल बिट-मैपिंग ज्ञात होने के बाद ही निर्धारित किया जा सकता है। हालाँकि, जब ग्रे कोडिंग का उपयोग किया जाता है, तो एक प्रतीक से दूसरे में सबसे संभावित त्रुटि केवल बिट-त्रुटि उत्पन्न करती है और
(ग्रे कोडिंग का उपयोग करने से हमें डीकोडेड बिटस्ट्रीम में त्रुटियों की हैमिंग दूरी के रूप में त्रुटियों की ली दूरी का अनुमान लगाने की अनुमति मिलती है, जो हार्डवेयर में लागू करना आसान है।)
दाईं ओर का ग्राफ बीपीएसके, क्यूपीएसके (जो ऊपर बताए गए अनुसार समान हैं), 8-पीएसके और 16-पीएसके की बिट-एरर दरों की तुलना करता है। यह देखा गया है कि उच्च-क्रम मॉडुलन उच्च त्रुटि-दर प्रदर्शित करते हैं बदले में हालांकि वे एक उच्च कच्ची डेटा दर प्रदान करते हैं।
विभिन्न डिजिटल मॉडुलन योजनाओं की त्रुटि दरों पर सीमाओं की गणना सिग्नल तारामंडल से बंधे संघ के आवेदन के साथ की जा सकती है।
वर्णक्रमीय दक्षता
एम-पीएसके मॉडुलन योजनाओं की बैंडविड्थ (या वर्णक्रमीय) दक्षता मॉडुलन क्रम एम के बढ़ने के साथ बढ़ जाती है (उदाहरण के लिए, एम-एफएसके एकाधिक आवृत्ति-शिफ्ट कुंजीयन | [7]
एम-क्यूएएम के लिए भी यही संबंध सही है।[8]
डिफरेंशियल फेज-शिफ्ट कुंजीयन (डीपीएसके)
डिफरेंशियल एन्कोडिंग
डिफरेंशियल फेज शिफ्ट कुंजीयन (डीपीएसके) फेज मॉडुलन का एक सामान्य रूप है जो कैरियर वेव के फेज को बदलकर डेटा पहुंचाता है। जैसा कि बीपीएसके और क्यूपीएसके के लिए उल्लेख किया गया है, चरण की अस्पष्टता है यदि तारामंडल संचार चैनल में किसी प्रभाव से घुमाया जाता है जिसके माध्यम से सिग्नल गुजरता है। चरण निर्धारित करने के बजाय डेटा को बदलने के लिए उपयोग करके इस समस्या को दूर किया जा सकता है।
उदाहरण के लिए, अलग-अलग एन्कोडेड बीपीएसके में बाइनरी "1" को वर्तमान चरण में 180 डिग्री और वर्तमान चरण में 0 डिग्री जोड़कर एक बाइनरी "0" जोड़कर प्रेषित किया जा सकता है। डीपीएसके का एक अन्य प्रकार सममित विभेदक चरण शिफ्ट कुंजीयन, एसडीपीएसके है, जहां "1" के लिए एन्कोडिंग +90° और "0" के लिए -90° होगा।
अलग-अलग एनकोडेड क्यूपीएसके (डीक्यूपीएसके) में, फेज़-शिफ्ट 0°, 90°, 180°, -90° डेटा "00", "01", "11", "10" के अनुरूप हैं। इस तरह के एन्कोडिंग को उसी तरह से डिमोड्यूलेट किया जा सकता है जैसे गैर-अंतर पीएसके के लिए लेकिन चरण अस्पष्टताओं को अनदेखा किया जा सकता है। इस प्रकार, प्रत्येक प्राप्त प्रतीक को में से किसी एक के लिए डिमॉड्यूलेट किया जाता है तारामंडल में एम अंक और एक तुलनित्र तब इस प्राप्त संकेत और पिछले एक के बीच के अंतर की गणना करता है। अंतर ऊपर वर्णित अनुसार डेटा को एन्कोड करता है। सममित अंतर क्वाड्रैचर फेज शिफ्ट कुंजीयन (एसडीक्यूपीएसके) डीक्यूपीएसके की तरह है, लेकिन −135°, −45°, +45° और +135° के फेज शिफ्ट मानों का उपयोग करते हुए एन्कोडिंग सममित है।
जैसा कि ऊपर वर्णित है, डीबीपीएसके और डीक्यूपीएसके दोनों के लिए संशोधित संकेत नीचे दिखाया गया है। आकृति में, यह माना जाता है कि संकेत शून्य चरण से शुरू होता है, और इसलिए दोनों संकेतों में एक चरण बदलाव होता है .
विश्लेषण से पता चलता है कि अलग-अलग एन्कोडिंग सामान्य एम-पीएसके की तुलना में त्रुटि दर को लगभग दोगुना कर देता है लेकिन इसे में केवल एक छोटी सी वृद्धि से दूर किया जा सकता है इसके अलावा, यह विश्लेषण (और नीचे दिए गए चित्रमय परिणाम) एक ऐसी प्रणाली पर आधारित हैं जिसमें एकमात्र भ्रष्टाचार योगात्मक सफेद गाऊसी रव (एडब्ल्यूजीएन) है। यद्यपि, संचार प्रणाली में ट्रांसमीटर और रिसीवर के बीच एक भौतिक चैनल भी होगा। यह चैनल, सामान्य रूप से, पीएसके संकेत के लिए एक अज्ञात चरण-शिफ्ट पेश करेगा इन मामलों में अंतर योजनाएँ सामान्य योजनाओं की तुलना में बेहतर त्रुटि-दर प्राप्त कर सकती हैं जो सटीक चरण की जानकारी पर निर्भर करती हैं।
डीपीएसके के सबसे लोकप्रिय अनुप्रयोगों में से एक ब्लूटूथ कार्यान्वयन है जहां -डीक्यूपीएसके और 8-डीपीएसके लागू किए गए।
विमॉडुलन
एक संकेत के लिए जिसे अलग-अलग एन्कोड किया गया है, डिमॉड्यूलेशन की एक स्पष्ट वैकल्पिक विधि है। हमेशा की तरह डिमॉड्यूलेट करने और वाहक-चरण अस्पष्टता को अनदेखा करने के बजाय, दो लगातार प्राप्त प्रतीकों के बीच के चरण की तुलना की जाती है और यह निर्धारित करने के लिए उपयोग किया जाता है कि डेटा क्या होना चाहिए था। जब इस तरह से अलग-अलग एन्कोडिंग का उपयोग किया जाता है, तो स्कीम को अलग-अलग फेज-शिफ्ट कुंजीयन (डीपीएसके) के रूप में जाना जाता है। ध्यान दें कि यह केवल अलग-अलग एन्कोडेड पीएसके से अलग है, क्योंकि रिसेप्शन पर, प्राप्त प्रतीकों को एक-एक करके तारामंडल बिंदुओं पर डीकोड नहीं किया जाता है बल्कि इसके बजाय सीधे एक दूसरे से तुलना की जाती है।
प्राप्त प्रतीक को वें टाइमलॉट में कॉल करें और इसे चरण होने दें व्यापकता की हानि के बिना मान लें कि वाहक तरंग का चरण शून्य है। योज्य सफेद गाऊसी रव (एडब्ल्यूजीएन) शब्द को के रूप में निरूपित करें। फिर
के लिए निर्णय चर वें प्रतीक और वें प्रतीक के बीच चरण अंतर है तथा . यानी अगर पर प्रक्षेपित है , परिणामी सम्मिश्र संख्या के चरण पर निर्णय लिया जाता है।
जहां सुपरस्क्रिप्ट * जटिल संयुग्मन को दर्शाता है। रव की अनुपस्थिति में, इसका चरण है , दो प्राप्त संकेतों के बीच चरण-शिफ्ट जिसका उपयोग प्रेषित डेटा को निर्धारित करने के लिए किया जा सकता है।
डीपीएसके के लिए त्रुटि की संभावना की सामान्य रूप से गणना करना मुश्किल है, लेकिन, डीबीपीके के परिस्थिति में यह है:
जो, जब संख्यात्मक रूप से मूल्यांकन किया जाता है, तो सामान्य बीपीएसके की तुलना में केवल थोड़ा ही खराब होता है, विशेष रूप से उच्चतर मूल्य पर।
डीपीएसके का उपयोग करने से एक सटीक चरण अनुमान प्रदान करने के लिए संभावित जटिल वाहक-वसूली योजनाओं की आवश्यकता से बचा जाता है और यह सामान्य पीएसके के लिए एक आकर्षक विकल्प हो सकता है।
ऑप्टिकल संचार में, डेटा को एक लेजर के चरण में भिन्न तरीके से संशोधित किया जा सकता है। मॉड्यूलेशन लेज़र है जो एक निरंतर तरंग का उत्सर्जन करता है, और एक मच-ज़ेन्डर मॉड्यूलेटर जो विद्युत बाइनरी डेटा प्राप्त करता है। बीपीएसके के परिस्थिति में, लेजर बाइनरी '1' के लिए अपरिवर्तित क्षेत्र को प्रसारित करता है, और '0' के लिए रिवर्स पोलरिटी के साथ। डिमोडुलेटर में एक विलंब रेखा व्यतिकरणमापी होता है जो एक बिट्स की देरी करता है, इसलिए एक समय में दो बिट्स की तुलना की जा सकती है। आगे की प्रक्रिया में, ऑप्टिकल क्षेत्र को विद्युत प्रवाह में बदलने के लिए एक फोटोडायोड का उपयोग किया जाता है, इसलिए सूचना को उसकी मूल स्थिति में वापस बदल दिया जाता है।
डीबीपीएसके और डीक्यूपीएसके की बिट-त्रुटि दर की तुलना ग्राफ में उनके गैर-अंतर समकक्षों से की जाती है। डीबीपीएससी का उपयोग करने का नुकसान जटिलता में कमी की तुलना में काफी छोटा है जिसका उपयोग प्रायः संचार प्रणालियों में किया जाता है जो अन्यथा बीपीएसके का उपयोग करेंगे। यद्यपि डीक्यूपीएसके के लिए, सामान्य क्यूपीएसके की तुलना में प्रदर्शन में नुकसान बड़ा है और प्रणाली डिजाइनर को इसे जटिलता में कमी के खिलाफ संतुलित करना चाहिए।
उदाहरण: अलग-अलग एन्कोडेड बीपीएसके
पर वें टाइम-स्लॉट पर बिट को मॉड्यूलेट करने के लिए कॉल करें , विभेदित रूप से एन्कोडेड बिट और परिणामी संग्राहक संकेत . मान लें कि तारामंडल आरेख प्रतीकों को ±1 (जो कि बीपीएसके है) पर रखता है। डिफरेंशियल एनकोडर पैदा करता है
जहां पे बाइनरी या मॉड्यूलर जोड़ -2 को इंगित करता है |
इसलिए केवल स्थिति बदलता है (बाइनरी "0" से बाइनरी "1" या बाइनरी "1" से बाइनरी "0" में) अगर एक बाइनरी "1" है। अन्यथा यह अपनी पूर्व अवस्था में ही रहता है। यह ऊपर दिए गए डिफरेंशियल एनकोडेड बीपीएसके का विवरण है।
प्राप्त संकेत उपज के लिए डिमोड्यूलेट किया गया है और फिर डिफरेंशियल डिकोडर एन्कोडिंग प्रक्रिया को उलट देता है और उत्पादन करता है
चूंकि बाइनरी घटाव बाइनरी जोड़ के समान है।
इसलिए, यदि तथा भिन्न और अगर वे समान हैं। इसलिए, यदि दोनों तथा उलटे हैं, अभी भी सही ढंग से डीकोड किया जाएगा। इस प्रकार, 180° चरण की अस्पष्टता कोई मायने नहीं रखती।
अन्य पीएसके मॉड्यूलेशन के लिए डिफरेंशियल स्कीमें समान तर्ज पर तैयार की जा सकती हैं। डीपीएसके के लिए वेवफॉर्म ऊपर दिए गए डिफरेंशियल एनकोडेड पीएसके के समान हैं क्योंकि दोनों योजनाओं के बीच एकमात्र परिवर्तन रिसीवर पर है।
इस उदाहरण के लिए बीईआर वक्र की तुलना दाईं ओर साधारण बीपीएसके से की जाती है। जैसा कि ऊपर उल्लेख किया गया है, जबकि त्रुटि दर लगभग दोगुनी है, इसमें वृद्धि की आवश्यकता है इस पर काबू पाने के लिए वृद्धि कम है। कोडित प्रणालियों में अंतर मॉडुलन को दूर करने के लिए आवश्यक है, हालांकि, बड़ा है – सामान्य लगभग 3 डीबी। प्रदर्शन में गिरावट गैर-सुसंगत संचरण का परिणाम है – इस परिस्थिति में यह इस तथ्य को संदर्भित करता है कि चरण की ट्रैकिंग को पूरी तरह से अनदेखा किया जाता है।
परिभाषाएं
गणितीय रूप से त्रुटि-दर निर्धारित करने के लिए, कुछ परिभाषाओं की आवश्यकता होगी
- , ऊर्जा प्रति बिट
- , n बिट्स के साथ प्रति प्रतीक ऊर्जा
- , बिट दर
- , प्रतिक दर
- , संकेत रव वर्णक्रमीय घनत्व (वाट /हेटर्स )
- , बिट-त्रुटि की संभावना
- , प्रतीक-त्रुटि की संभावना
संभावना देगा कि शून्य-माध्य और इकाई-विचरण के साथ अनियमित प्रक्रिया से लिया गया एक नमूना सामान्य वितरण अधिक या बराबर होगा . यह त्रुटि फ़ंक्शन का एक छोटा रूप है:
- .
यहां उद्धृत त्रुटि दर योज्य सफेद गाऊसी रव (एडब्ल्यूजीएन) में हैं। ये त्रुटि दर लुप्त होती चैनल में गणना की तुलना में कम हैं, इसलिए, तुलना करने के लिए एक अच्छा सैद्धांतिक बेंचमार्क है।
अनुप्रयोग
पीएसके की सादगी के कारण, विशेष रूप से जब इसकी प्रतिस्पर्धी क्वाड्रेचर एम्पलीट्यूड मॉड्यूलेशन के साथ तुलना की जाती है, तो इसका व्यापक रूप से मौजूदा प्रौद्योगिकियों में उपयोग किया जाता है।
वायरलेस लैन मानक, आईईई 802.11 बी-1999,[10][11] आवश्यक डेटा दर के आधार पर विभिन्न पीएसके का उपयोग करता है। 1 एमबिट/एस की मूल दर पर, यह डीबीपीएससी (अंतर बीपीएसके) का उपयोग करता है। 2 एमबिट/एस की विस्तारित दर प्रदान करने के लिए , डीक्यूपीएसके का उपयोग किया जाता है। 5.5 एमबिट/एस और 11 एमबिट/एस की पूर्ण दर तक पहुँचने में, क्यूपीएसके कार्यरत है, लेकिन इसे पूरक कोड कुंजीयन के साथ जोड़ा जाना है। उच्च गति वायरलेस लैन मानक, आईईई 802.11g-2003,[10][12] आठ डेटा दरें हैं 6, 9, 12, 18, 24, 36, 48 और 54 एमबिट/एस। 6 और 9 एमबिट/एस मोड समकोणकार आवृति विभाजन बहुसंकेतन मॉडुलन का उपयोग करते हैं जहाँ प्रत्येक उप-वाहक बीपीएसके संग्राहक होता है। 12 और 18 एमबिट/एस मोड क्यूपीएसके के साथ ओएफडीएम का उपयोग करते हैं। सबसे तेज़ चार मोड चतुर्भुज आयाम मॉडुलन के रूपों के साथ ओएफडीएम का उपयोग करते हैं।
इसकी सादगी के कारण, बीपीएसके कम लागत वाले निष्क्रिय ट्रांसमीटरों के लिए उपयुक्त है, और आरएफआईडी मानकों जैसे आईएसओ / आईसी 14443 में उपयोग किया जाता है जिसे बॉयोमीट्रिक पासपोर्ट , अमेरिकन एक्सप्रेस के एक्सप्रेसपे जैसे क्रेडिट कार्ड और कई अन्य अनुप्रयोगों के लिए अपनाया गया है।[13]
ब्लूटूथ 2 का उपयोग करता है -डीक्यूपीएसके इसकी कम दर पर (2 एमबिट/एस) और 8-बीपीएसके इसकी उच्च दर (3 एमबिट/एस) पर जब दो उपकरणों के बीच की लिंक पर्याप्त रूप से मजबूत होता है। ब्लूटूथ 1 गाऊसी न्यूनतम-शिफ्ट कुंजीयन के साथ मॉड्यूलेट करता है | एक द्विआधारी योजना, इसलिए संस्करण 2 में या तो मॉड्यूलेशन विकल्प उच्च डेटा-दर प्राप्त करेगा। एक समान तकनीक, आईईई 802.15.4 (ज़िगबी द्वारा उपयोग किया जाने वाला वायरलेस मानक) भी दो आवृत्ति बैंडों का उपयोग करके पीएसके पर निर्भर करता है बीपीएसके के साथ 868–915 मेगाहर्ट्ज़ और ओक्यूपीएसके के साथ 2.4 गीगाहर्ट्ज़ पर।
क्यूपीएसके और 8 पीएसके दोनों का व्यापक रूप से उपग्रह प्रसारण में उपयोग किया जाता है। क्यूपीएसके अभी भी एसडी उपग्रह चैनलों और कुछ एचडी चैनलों की स्ट्रीमिंग में व्यापक रूप से उपयोग किया जाता है। एचडी वीडियो के उच्च बिटरेट और उपग्रह बैंडविड्थ की उच्च लागत के कारण उच्च परिभाषा प्रोग्रामिंग लगभग विशेष रूप से 8पीएसके में वितरित की जाती है।[14] डीवीबी-एस 2 मानक को क्यूपीएसके और 8पीएसके दोनों के लिए समर्थन की आवश्यकता है। नए उपग्रह सेट टॉप बॉक्स में प्रयुक्त चिपसेट, जैसे कि ब्रॉडकॉम की 7000 श्रृंखला 8पीएसके का समर्थन करते हैं और पुराने मानक के साथ पिछड़े संगत हैं।[15]
ऐतिहासिक रूप से, बेल 201, 208, और 209 और सीसीआईटीटी वी.26, वी.27, वी.29, वी.32 और वी.34 जैसे वॉयस-बैंड सिंक्रोनस मोडेम पीएसके का इस्तेमाल करते थे।[16]
योगात्मक सफेद गाऊसी रव के साथ पारस्परिक जानकारी
पीएसके की पारस्परिक जानकारी का मूल्यांकन इसकी परिभाषा के संख्यात्मक एकीकरण द्वारा योगात्मक सफेद गाऊसी रव में किया जा सकता है।[17] पारस्परिक सूचना के वक्र रव अनुपात के अनंत संकेत की सीमा में प्रत्येक प्रतीक द्वारा किए गए बिट्स की संख्या से संतृप्त होते हैं . इसके विपरीत, रव अनुपात के लिए छोटे सिग्नल की सीमा में आपसी जानकारी एडब्ल्यूजीएन चैनल क्षमता प्रमेय तक पहुंचती है, जो कि प्रतीक सांख्यिकीय वितरण के सभी संभावित विकल्पों में सर्वोच्च है।
रव अनुपात के संकेत के मध्यवर्ती मूल्यों पर पारस्परिक सूचना (एमआई) अच्छी तरह से अनुमानित है[17]
एडब्ल्यूजीएन चैनल पर पीएसके की पारस्परिक जानकारी सामान्य क्यूएएम मॉड्यूलेशन प्रारूपों की तुलना में एडब्ल्यूजीएन चैनल क्षमता से अधिक दूर है।
यह भी देखें
- बाइनरी ऑफ़सेट कैरियर मॉडुलन
- विशेषक कोडिंग
- मॉड्यूलेशन – सभी मॉडुलन योजनाओं के अवलोकन के लिए
- चरण मॉडुलन (पीएम) – पीएसके के एनालॉग समकक्ष
- ध्रुवीय मॉडुलन
- पीएसके31
- पीएसके63
टिप्पणियाँ
- ↑ Communications Systems, H. Stern & S. Mahmoud, Pearson Prentice Hall, 2004, p. 283.
- ↑ Tom Nelson, Erik Perrins, and Michael Rice. "Common detectors for Tier 1 modulations" Archived 2012-09-17 at the Wayback Machine. T. Nelson, E. Perrins, M. Rice. "Common detectors for shaped offset QPSK (SOQPSK) and Feher-patented QPSK (FQPSK)" Nelson, T.; Perrins, E.; Rice, M. (2005). "Common detectors for shaped offset QPSK (SOQPSK) and Feher-patented QPSK (FQPSK)". GLOBECOM '05. IEEE Global Telecommunications Conference, 2005. pp. 5 pp. doi:10.1109/GLOCOM.2005.1578470. ISBN 0-7803-9414-3. S2CID 11020777. ISBN 0-7803-9414-3
- ↑ Hill, Terrance J. "A non-proprietary, constant envelope, variant of shaped offset QPSK (SOQPSK) for improved spectral containment and detection efficiency." MILCOM 2000. 21st Century Military Communications Conference Proceedings. Vol. 1. IEEE, 2000.
- ↑ Li, Lifang, and M. K. Simon. "Performance of coded offset quadrature phase-shift keying (OQPSK) and MIL-STD shaped OQPSK (SOQPSK) with iterative decoding." Interplanetary Network Prog. Rep. 42 (2004).
- ↑ Sahin, C. and Perrins, E., 2011, November. The capacity of SOQPSK-TG. In 2011-MILCOM 2011 Military Communications Conference (pp. 555-560). IEEE.
- ↑ Saeed, N., Elzanaty, A., Almorad, H., Dahrouj, H., Al-Naffouri, T.Y. and Alouini, M.S., 2020. Cubesat communications: Recent advances and future challenges. IEEE Communications Surveys & Tutorials.
- ↑ Haykin, S., 2001. Communication Systems, John Wiley&Sons. Inc. - p. 368
- ↑ Link Budget Analysis: Digital Modulation, Part 3 (www.AtlantaRF.com)
- ↑ G.L. Stüber, “Soft Decision Direct-Sequence DPSK Receivers,” IEEE Transactions on Vehicular Technology, vol. 37, no. 3, pp. 151–157, August 1988.
- ↑ 10.0 10.1 IEEE Std 802.11-1999: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications – the overarching IEEE 802.11 specification. Archived August 28, 2007, at the Wayback Machine
- ↑ IEEE Std 802.11b-1999 (R2003) – the IEEE 802.11b specification.
- ↑ IEEE Std 802.11g-2003 – the IEEE 802.11g specification.
- ↑ Understanding the Requirements of ISO/IEC 14443 for Type B Proximity Contactless Identification Cards, Application Note, Rev. 2056B–RFID–11/05, 2005, ATMEL.
- ↑ "How Communications Satellites Work". Planet Fox. 2014.
- ↑ "Low-Cost Satellite Set-top Box SoC - BCM7325 | Broadcom". Archived from the original on 2015-09-15. Retrieved 2015-09-08.
- ↑ "Local and Remote Modems" (PDF). Black Box. Black Box Network Services. Archived from the original (PDF) on December 22, 2015. Retrieved December 20, 2015.
- ↑ 17.0 17.1 Blahut, R. E. (1988). Principles and Practice of Information Theory. Boston, MA, USA: Addison Wesley Publishing Company. ISBN 0-201-10709-0.
संदर्भ
The notation and theoretical results in this article are based on material presented in the following sources:
- Proakis, John G. (1995). Digital Communications. Singapore: McGraw Hill. ISBN 0-07-113814-5.
- Couch, Leon W. II (1997). Digital and Analog Communications. Upper Saddle River, NJ: Prentice-Hall. ISBN 0-13-081223-4.
- Haykin, Simon (1988). Digital Communications. Toronto, Canada: John Wiley & Sons. ISBN 0-471-62947-2.