समूह सिद्धांत: Difference between revisions
No edit summary |
|||
| (35 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Branch of mathematics that studies the properties of groups}} | {{short description|Branch of mathematics that studies the properties of groups}}[[Image:Rubik's cube.svg|thumb|1974 में अर्नो रूबिक द्वारा आविष्कार की गई लोकप्रिय पहेली रूबिक क्यूब का उपयोग [[क्रमपरिवर्तन समूह|क्रमपरिवर्तन समूहों]] के उदाहरण के रूप में किया गया है। रुबिक का घन समूह देखें।]] | ||
[[Image:Rubik's cube.svg|thumb|1974 में अर्नो रूबिक द्वारा आविष्कार की गई लोकप्रिय पहेली रूबिक क्यूब का उपयोग [[क्रमपरिवर्तन समूह|क्रमपरिवर्तन समूहों]] के उदाहरण के रूप में किया गया है। रुबिक का घन समूह देखें।]] | |||
{{Group theory sidebar}} | {{Group theory sidebar}} | ||
अमूर्त बीजगणित में, '''समूह सिद्धांत''' [[समूह (गणित)|समूह]] के रूप में ज्ञात [[बीजगणितीय संरचना]]ओं का अध्ययन करता है। एक समूह की अवधारणा सार बीजगणित के लिए केंद्रीय है: अन्य प्रसिद्ध बीजगणितीय संरचनाएं, जैसे कि छल्ले (गणित), क्षेत्र (गणित), और सदिश रिक्त स्थान, सभी को अतिरिक्त संचालन (गणित) और [[स्वयंसिद्ध|स्वयंसिद्धों]] से संपन्न समूहों के रूप में देखा जा सकता है। पूरे गणित में समूह की पुनरावृत्ति होती है, और समूह सिद्धांत के उपायों ने बीजगणित के कई हिस्सों को प्रभावित किया है। रेखीय बीजगणितीय समूह और लाई समूह सिद्धांत की दो शाखाएँ हैं जिन्होंने प्रगति का अनुभव किया है और अपने आप में विषय क्षेत्र बन गए हैं। | |||
एक समूह की अवधारणा सार बीजगणित के लिए केंद्रीय है: अन्य प्रसिद्ध बीजगणितीय संरचनाएं, जैसे कि छल्ले (गणित), क्षेत्र (गणित), और सदिश रिक्त स्थान, सभी को अतिरिक्त संचालन (गणित) और [[स्वयंसिद्ध|स्वयंसिद्धों]] से संपन्न समूहों के रूप में देखा जा सकता है। | |||
विभिन्न भौतिक प्रणालियाँ, जैसे कि [[क्रिस्टल]] और [[हाइड्रोजन परमाणु]], और [[मानक मॉडल]] ब्रह्मांड में ज्ञात मौलिक बल, [[समरूपता समूह|समरूपता समूहों]] द्वारा प्रतिरूपित किए जा सकते हैं। इस प्रकार समूह सिद्धांत और निकट से संबंधित [[प्रतिनिधित्व सिद्धांत]] के भौतिकी, [[रसायन विज्ञान]] और सामग्री विज्ञान में कई महत्वपूर्ण अनुप्रयोग हैं। सार्वजनिक कुंजी क्रिप्टोग्राफ़ी के लिए समूह सिद्धांत भी केंद्रीय है। | विभिन्न भौतिक प्रणालियाँ, जैसे कि [[क्रिस्टल]] और [[हाइड्रोजन परमाणु]], और [[मानक मॉडल]] ब्रह्मांड में ज्ञात मौलिक बल, [[समरूपता समूह|समरूपता समूहों]] द्वारा प्रतिरूपित किए जा सकते हैं। इस प्रकार समूह सिद्धांत और निकट से संबंधित [[प्रतिनिधित्व सिद्धांत]] के भौतिकी, [[रसायन विज्ञान]] और सामग्री विज्ञान में कई महत्वपूर्ण अनुप्रयोग हैं। सार्वजनिक कुंजी क्रिप्टोग्राफ़ी के लिए समूह सिद्धांत भी केंद्रीय है। | ||
समूह सिद्धांत का प्रारंभिक इतिहास 19वीं | समूह सिद्धांत का प्रारंभिक इतिहास 19वीं दशक का है। 20वीं दशक की सबसे महत्वपूर्ण गणितीय उपलब्धियों में से एक<ref>{{citation|last=Elwes|first=Richard|url=http://plus.maths.org/issue41/features/elwes/index.html|title=An enormous theorem: the classification of finite simple groups|journal=[[Plus Magazine]]|issue=41|date=December 2006|access-date=2011-12-20|archive-date=2009-02-02|archive-url=https://web.archive.org/web/20090202092008/http://plus.maths.org/issue41/features/elwes/index.html|url-status=dead}}</ref> सहयोगात्मक प्रयास था, जिसमें 10,000 से अधिक जर्नल पेज सम्मिलित थे और अधिकतर 1960 और 2004 के बीच प्रकाशित हुए थे, जिसकी परिणति परिमित सरल समूहों के पूर्ण वर्गीकरण में हुई। | ||
== इतिहास == | == इतिहास == | ||
{{Main| | {{Main|समूह सिद्धांत का इतिहास}} | ||
समूह सिद्धांत के तीन मुख्य ऐतिहासिक स्रोत हैं: [[संख्या सिद्धांत]], [[बीजगणितीय समीकरण|बीजगणितीय समीकरणों]] का सिद्धांत और [[ज्यामिति]]। संख्या-सैद्धांतिक किनारा [[लियोनहार्ड यूलर]] द्वारा प्रारभ्म किया गया था, और कार्ल फ्रेडरिक गॉस द्वारा विकसित किया गया था। क्वाड्रेटिक क्षेत्रों से संबंधित [[मॉड्यूलर अंकगणित]] और योगात्मक और गुणात्मक समूहों पर गॉस का काम। उच्च स्तर के [[बहुपद समीकरण|बहुपद समीकरणों]] के सामान्य समाधान के लिए अपनी खोज में [[जोसेफ लुइस लाग्रेंज]], पाओलो रफ़िनी (गणितज्ञ), और [[नील्स हेनरिक एबेल]] द्वारा क्रमचय समूहों के बारे में प्रारंभिक परिणाम प्राप्त किए गए थे। इवरिस्ट गैलोइस ने समूह शब्द गढ़ा और एक संबंध स्थापित किया, जिसे अब गैलोज़ सिद्धांत के रूप में जाना जाता है, समूहों और [[क्षेत्र सिद्धांत (गणित)]] के नवजात सिद्धांत के बीच। ज्यामिति में, समूह पहले [[प्रक्षेपी ज्यामिति]] और बाद में, | |||
समूह सिद्धांत के तीन मुख्य ऐतिहासिक स्रोत हैं: [[संख्या सिद्धांत]], [[बीजगणितीय समीकरण|बीजगणितीय समीकरणों]] का सिद्धांत और [[ज्यामिति]]। संख्या-सैद्धांतिक किनारा [[लियोनहार्ड यूलर]] द्वारा प्रारभ्म किया गया था, और कार्ल फ्रेडरिक गॉस द्वारा विकसित किया गया था। क्वाड्रेटिक क्षेत्रों से संबंधित [[मॉड्यूलर अंकगणित]] और योगात्मक और गुणात्मक समूहों पर गॉस का काम। उच्च स्तर के [[बहुपद समीकरण|बहुपद समीकरणों]] के सामान्य समाधान के लिए अपनी खोज में [[जोसेफ लुइस लाग्रेंज]], पाओलो रफ़िनी (गणितज्ञ), और [[नील्स हेनरिक एबेल]] द्वारा क्रमचय समूहों के बारे में प्रारंभिक परिणाम प्राप्त किए गए थे। इवरिस्ट गैलोइस ने समूह शब्द गढ़ा और एक संबंध स्थापित किया, जिसे अब गैलोज़ सिद्धांत के रूप में जाना जाता है, समूहों और [[क्षेत्र सिद्धांत (गणित)]] के नवजात सिद्धांत के बीच। ज्यामिति में, समूह पहले [[प्रक्षेपी ज्यामिति]] और बाद में, गैर-[[यूक्लिडियन ज्यामिति]] में महत्वपूर्ण हो गए। [[फेलिक्स क्लेन]] के [[एर्लांगेन कार्यक्रम]] ने समूह सिद्धांत को ज्यामिति के आयोजन सिद्धांत के रूप में घोषित किया। | |||
1830 के दशक में इवरिस्ट गैलोइस, बहुपद समीकरणों की विलेयता निर्धारित करने के लिए समूहों को नियुक्त करने वाले पहले व्यक्ति थे। [[आर्थर केली]] और [[ऑगस्टिन लुइस कॉची]] ने क्रमचय समूहों के सिद्धांत को बनाकर इन जांचों को आगे बढ़ाया। समूहों के लिए दूसरा ऐतिहासिक स्रोत ज्यामिति स्थितियों से उपजा है। समूह सिद्धांत का उपयोग करते हुए संभावित ज्यामिति (जैसे यूक्लिडियन ज्यामिति, [[अतिशयोक्तिपूर्ण ज्यामिति]] या प्रक्षेपी ज्यामिति) के साथ पकड़ में आने के प्रयास में, फेलिक्स क्लेन ने एर्लांगेन कार्यक्रम की शुरुआत की। 1884 में [[सोफस झूठ|सोफस लाइ]] ने [[विश्लेषण (गणित)]] की समस्याओं से जुड़े समूहों (अब लाई समूह कहा जाता है) का उपयोग करना प्रारभ्म कर दिया। तीसरे, समूह, पहले अप्रत्यक्ष रूप से और बाद में स्पष्ट रूप से, [[बीजगणितीय संख्या सिद्धांत]] में उपयोग किए गए थे। | 1830 के दशक में इवरिस्ट गैलोइस, बहुपद समीकरणों की विलेयता निर्धारित करने के लिए समूहों को नियुक्त करने वाले पहले व्यक्ति थे। [[आर्थर केली]] और [[ऑगस्टिन लुइस कॉची]] ने क्रमचय समूहों के सिद्धांत को बनाकर इन जांचों को आगे बढ़ाया। समूहों के लिए दूसरा ऐतिहासिक स्रोत ज्यामिति स्थितियों से उपजा है। समूह सिद्धांत का उपयोग करते हुए संभावित ज्यामिति (जैसे यूक्लिडियन ज्यामिति, [[अतिशयोक्तिपूर्ण ज्यामिति]] या प्रक्षेपी ज्यामिति) के साथ पकड़ में आने के प्रयास में, फेलिक्स क्लेन ने एर्लांगेन कार्यक्रम की शुरुआत की। 1884 में [[सोफस झूठ|सोफस लाइ]] ने [[विश्लेषण (गणित)]] की समस्याओं से जुड़े समूहों (अब लाई समूह कहा जाता है) का उपयोग करना प्रारभ्म कर दिया। तीसरे, समूह, पहले अप्रत्यक्ष रूप से और बाद में स्पष्ट रूप से, [[बीजगणितीय संख्या सिद्धांत]] में उपयोग किए गए थे। | ||
इन प्रारंभिक स्रोतों के | इन प्रारंभिक स्रोतों के भिन्न -भिन्न सीमा के परिणामस्वरूप समूहों की भिन्न -भिन्न धारणाएँ बनीं। 1880 के आसपास समूहों के सिद्धांत को एकीकृत किया गया था। तब से, समूह सिद्धांत का प्रभाव लगातार बढ़ रहा है, 20 वीं दशक के प्रारभ्म में अमूर्त बीजगणित, प्रतिनिधित्व सिद्धांत और कई और प्रभावशाली स्पिन-ऑफ डोमेन को जन्म दे रहा है। परिमित सरल समूहों का वर्गीकरण 20वीं दशक के मध्य से काम का एक विशाल निकाय है, जो सभी [[परिमित सेट|परिमित समुच्चय]] सरल समूहों को वर्गीकृत करता है। | ||
== समूहों के मुख्य वर्ग == | == समूहों के मुख्य वर्ग == | ||
{{Main| | {{Main|समूह (गणित) | ||
जिन समूहों पर विचार किया जा रहा है, उनकी सीमा धीरे-धीरे परिमित क्रमपरिवर्तन समूहों और [[मैट्रिक्स समूह|आव्यूह समूहों]] के विशेष उदाहरणों से अमूर्त समूहों तक विस्तारित हो गई है, जिन्हें समूह और [[बाइनरी संबंध]] के | }} | ||
जिन समूहों पर विचार किया जा रहा है, उनकी सीमा धीरे-धीरे परिमित क्रमपरिवर्तन समूहों और [[मैट्रिक्स समूह|आव्यूह समूहों]] के विशेष उदाहरणों से अमूर्त समूहों तक विस्तारित हो गई है, जिन्हें समूह और [[बाइनरी संबंध]] के उत्पादक समूह द्वारा समूह की प्रस्तुति के माध्यम से निर्दिष्ट किया जा सकता है। | |||
=== क्रमपरिवर्तन समूह === | === क्रमपरिवर्तन समूह === | ||
एक व्यवस्थित अध्ययन से गुजरने वाले समूहों का प्रथम [[वर्ग (सेट सिद्धांत)|वर्ग (समूह सिद्धांत)]] क्रमचय समूह था। किसी भी समूह X और अपने आप में X के [[द्विभाजन|द्विभाजनों]] का एक संग्रह G दिया गया है (जिसे क्रमपरिवर्तन के रूप में जाना जाता है) जो रचनाओं और व्युत्क्रमों के अनुसार बंद है, G, X पर एक | एक व्यवस्थित अध्ययन से गुजरने वाले समूहों का प्रथम [[वर्ग (सेट सिद्धांत)|वर्ग (समूह सिद्धांत)]] क्रमचय समूह था। किसी भी समूह X और अपने आप में X के [[द्विभाजन|द्विभाजनों]] का एक संग्रह G दिया गया है (जिसे क्रमपरिवर्तन के रूप में जाना जाता है) जो रचनाओं और व्युत्क्रमों के अनुसार बंद है, G, X पर एक [[समूह क्रिया (गणित)]] है। यदि X में n तत्व सम्मिलित हैं और G में सभी सम्मिलित हैं क्रमपरिवर्तन, जी [[सममित समूह]] S<sub>''n''</sub> है; सामान्य तौर पर, कोई भी क्रमपरिवर्तन समूह G, X के सममित समूह का एक [[उपसमूह]] है। आर्थर केली के कारण एक प्रारंभिक निर्माण ने किसी भी समूह को एक क्रमचय समूह के रूप में प्रदर्शित किया, जो({{nowrap|1=''X'' = ''G''}}) बाएं [[नियमित प्रतिनिधित्व]] के माध्यम से स्वयं पर कार्य करता है । | ||
कई स्थितियों में, क्रमचय समूह की संरचना का संबंधित समूह पर | कई स्थितियों में, क्रमचय समूह की संरचना का संबंधित समूह पर इसके कार्य के गुणों का उपयोग करके अध्ययन किया जा सकता है। उदाहरण के लिए, इस प्रकार से यह सिद्ध होता है कि {{nowrap|''n'' ≥ 5}} के लिए, [[वैकल्पिक समूह]] A<sub>''n''</sub> सरल समूह है, अर्थात किसी उचित [[सामान्य उपसमूह]] को स्वीकार नहीं करता है। यह तथ्य एबेल-रफ़िनी प्रमेय में एक महत्वपूर्ण भूमिका निभाता है | डिग्री के एक सामान्य बीजगणितीय समीकरण को समाधान करने की असंभवता {{nowrap|''n'' ≥ 5}} रेडिकल्स में है। | ||
=== आव्यूह समूह === | === आव्यूह समूह === | ||
समूहों का अगला महत्वपूर्ण वर्ग आव्यूह समूहों, या [[रैखिक समूह|रैखिक समूहों]] द्वारा दिया जाता है। यहाँ G एक समूह है जिसमें एक क्षेत्र (गणित) K पर दिए गए क्रम n के व्युत्क्रमणीय [[मैट्रिक्स (गणित)|आव्यूह (गणित)]] होते हैं जो उत्पादों और व्युत्क्रमों के | समूहों का अगला महत्वपूर्ण वर्ग आव्यूह समूहों, या [[रैखिक समूह|रैखिक समूहों]] द्वारा दिया जाता है। यहाँ G एक समूह है जिसमें एक क्षेत्र (गणित) K पर दिए गए क्रम n के व्युत्क्रमणीय [[मैट्रिक्स (गणित)|आव्यूह (गणित)]] होते हैं जो उत्पादों और व्युत्क्रमों के अंतर्गत बंद होते हैं। ऐसा समूह n-आयामी सदिश समष्टि K पर कार्य करता है<sup>n</sup> [[रैखिक परिवर्तन|रैखिक रूपांतरणों]] द्वारा। यह क्रिया आव्यूह समूहों को संकल्पनात्मक रूप से क्रमचय समूहों के समान बनाती है, और समूह G के गुणों को स्थापित करने के लिए क्रिया की ज्यामिति का उपयोगी उपयोग किया जा सकता है। | ||
=== [[परिवर्तन समूह]] === | === [[परिवर्तन समूह]] === | ||
| Line 38: | Line 35: | ||
=== सार समूह === | === सार समूह === | ||
समूह सिद्धांत के विकास के पहले चरण में माने जाने वाले अधिकांश समूह ठोस थे, जिन्हें संख्याओं, क्रमपरिवर्तन या आव्यूहों के माध्यम से महसूस किया गया था। यह उन्नीसवीं | समूह सिद्धांत के विकास के पहले चरण में माने जाने वाले अधिकांश समूह ठोस थे, जिन्हें संख्याओं, क्रमपरिवर्तन या आव्यूहों के माध्यम से महसूस किया गया था। यह उन्नीसवीं दशक के उत्तरार्ध तक नहीं था कि एक सार समूह का विचार एक समूह के रूप में संचालन के साथ एक निश्चित प्रणाली को संतुष्ट करता है। एक सार समूह को निर्दिष्ट करने का एक विशिष्ट उपाय जनरेटर और संबंधों द्वारा समूह की प्रस्तुति के माध्यम से होता है, | ||
: <math> G = \langle S|R\rangle. </math> | : <math> G = \langle S|R\rangle. </math> | ||
अमूर्त समूहों का एक महत्वपूर्ण स्रोत एक सामान्य उपसमूह | अमूर्त समूहों का एक महत्वपूर्ण स्रोत एक सामान्य उपसमूह H द्वारा एक समूह जी के एक कारक समूह, या [[भागफल समूह]], G/H के निर्माण द्वारा दिया जाता है। [[बीजगणितीय संख्या क्षेत्र|बीजगणितीय संख्या क्षेत्रों]] के [[वर्ग समूह]], कारक समूहों के प्रारंभिक उदाहरणों में से थे। संख्या सिद्धांत में बहुत रुचि। यदि समूह G समूह X पर एक क्रमचय समूह है, तो कारक समूह G/H अब X पर कार्य नहीं कर रहा है; लेकिन एक सार समूह का विचार इस विसंगति के बारे में चिंता न करने की अनुमति देता है। | ||
ठोस से अमूर्त समूहों के दृष्टिकोण में परिवर्तन से उन समूहों के गुणों पर विचार करना स्वाभाविक हो जाता है जो किसी विशेष बोध से स्वतंत्र हैं, या आधुनिक भाषा में, समरूपतावाद के अनुसार अपरिवर्तनीय हैं, साथ ही इस प्रकार की संपत्ति वाले समूह के वर्ग: [[परिमित समूह]], [[आवधिक समूह]], सरल समूह, [[हल करने योग्य समूह|समाधान करने योग्य समूह]], और इसी तरह। एक व्यक्तिगत समूह के गुणों की खोज करने के अतिरिक्त, ऐसे परिणाम स्थापित करने का प्रयास किया जाता है जो समूहों के एक पूरे वर्ग पर लागू होते हैं। नया प्रतिमान गणित के विकास के लिए सर्वोपरि था: इसने [[डेविड हिल्बर्ट]], [[एमिल आर्टिन]], [[एमी नोथेर]] और उनके स्कूल के गणितज्ञों के कार्यों में अमूर्त बीजगणित के निर्माण का पूर्वाभास कराया।{{citation needed|date=June 2012}} | |||
=== अतिरिक्त संरचना वाले समूह === | === अतिरिक्त संरचना वाले समूह === | ||
एक समूह की अवधारणा का एक महत्वपूर्ण विस्तार तब होता है जब | एक समूह की अवधारणा का एक महत्वपूर्ण विस्तार तब होता है जब G अतिरिक्त संरचना के साथ संपन्न होता है, विशेष रूप से, एक [[टोपोलॉजिकल स्पेस|संस्थानिक स्थान]], भिन्न -भिन्न कई गुना, या बीजगणितीय विविधता। यदि समूह संचालन एम (गुणा) और आई (उलटा), | ||
: <math> m: G\times G\to G, (g,h)\mapsto gh, \quad i:G\to G, g\mapsto g^{-1}, </math> | : <math> m: G\times G\to G, (g,h)\mapsto gh, \quad i:G\to G, g\mapsto g^{-1}, </math> | ||
इस संरचना के साथ संगत हैं, अर्थात, वे निरंतर मानचित्र, चिकने मानचित्र या नियमित मानचित्र (बीजगणितीय ज्यामिति) (बीजगणितीय ज्यामिति के अर्थ में) मानचित्र हैं, तो G एक सामयिक समूह, एक | इस संरचना के साथ संगत हैं, अर्थात, वे निरंतर मानचित्र, चिकने मानचित्र या नियमित मानचित्र (बीजगणितीय ज्यामिति) (बीजगणितीय ज्यामिति के अर्थ में) मानचित्र हैं, तो G एक सामयिक समूह, एक लाई समूह या एक [[बीजगणितीय समूह]] है।<ref>This process of imposing extra structure has been formalized through the notion of a [[group object]] in a suitable [[category (mathematics)|category]]. Thus Lie groups are group objects in the category of differentiable manifolds and affine algebraic groups are group objects in the category of affine algebraic varieties.</ref> | ||
अतिरिक्त संरचना की उपस्थिति इस प्रकार के समूहों को अन्य गणितीय विषयों से जोड़ती है और इसका | अतिरिक्त संरचना की उपस्थिति इस प्रकार के समूहों को अन्य गणितीय विषयों से जोड़ती है और इसका अर्थ है कि उनके अध्ययन में अधिक उपकरण उपलब्ध हैं। सांस्थितिक समूह अमूर्त हार्मोनिक विश्लेषण के लिए एक प्राकृतिक डोमेन बनाते हैं, जबकि लाई समूह (प्रायः परिवर्तन समूहों के रूप में महसूस किए जाते हैं) अंतर ज्यामिति और एकात्मक प्रतिनिधित्व सिद्धांत के मुख्य आधार हैं। कुछ वर्गीकरण प्रश्न जिन्हें सामान्य रूप से समाधान नहीं किया जा सकता है, समूहों के विशेष उपवर्गों के लिए संपर्क किया जा सकता है और समाधान किया जा सकता है। इस प्रकार, सघन लाइ समूह को पूरी प्रकार से वर्गीकृत किया गया है। अनंत अमूर्त समूहों और सामयिक समूहों के बीच एक उपयोगी संबंध है: जब भी एक समूह Γ को एक सांस्थितिक समूह G में एक [[जाली (असतत उपसमूह)]] के रूप में महसूस किया जा सकता है, G से संबंधित ज्यामिति और विश्लेषण Γ के बारे में महत्वपूर्ण परिणाम देते हैं। परिमित समूहों के सिद्धांत में एक तुलनात्मक रूप से हाल की प्रवृत्ति सघन सांस्थितिक समूहों ([[अनंत समूह|अनंत समूहों]]) के साथ उनके संबंधों का लाभ उठाती है: उदाहरण के लिए, एक शक्तिशाली P-समूह | विभिन्न आदेशों के पी-समूह, और G के गुण इसके परिमित भागफल के गुणों में अनुवाद करते हैं। | ||
== समूह सिद्धांत की शाखाएँ == | == समूह सिद्धांत की शाखाएँ == | ||
=== परिमित समूह सिद्धांत === | === परिमित समूह सिद्धांत === | ||
{{Main| | {{Main|परिमित समूह | ||
}} | |||
बीसवीं | बीसवीं दशक के समय, गणितज्ञों ने परिमित समूहों के सिद्धांत के कुछ पहलुओं की बहुत गहराई से जाँच की, विशेष रूप से परिमित समूहों के [[स्थानीय विश्लेषण]] और समाधान करने योग्य समूह और [[निलपोटेंट समूह|नगण्य समूहों]] के सिद्धांत की।{{citation needed|date=December 2013|reason=In who's opinion?}} परिणामस्वरूप, परिमित सरल समूहों का पूर्ण वर्गीकरण प्राप्त किया गया, जिसका अर्थ है कि वे सभी सरल समूह जिनसे सभी परिमित समूह बनाए जा सकते हैं, अब ज्ञात हैं। | ||
गणितीय या की [[समरूपता]] पर विचार करते समय | |||
बीसवीं दशक के उत्तरार्ध के समय, [[क्लाउड चेवेली]] और [[रॉबर्ट स्टाइनबर्ग]] जैसे गणितज्ञों ने [[शास्त्रीय समूह|शास्त्रीय]] [[निलपोटेंट समूह|समूहों]] और अन्य संबंधित समूहों के परिमित एनालॉग्स की हमारी समझ को भी बढ़ाया। समूहों का ऐसा ही एक परिवार [[परिमित क्षेत्र|परिमित क्षेत्रों]] पर सामान्य रेखीय समूहों का परिवार है। | |||
जिसे [[निरंतर समरूपता]] से निपटने के रूप में देखा जा सकता है, संबद्ध [[वेइल समूह]] | परिमित समूह प्रायः गणितीय या भौतिक वस्तुओं की [[समरूपता]] पर विचार करते समय होते हैं | ||
, जब वे वस्तुएँ संरचना-संरक्षण परिवर्तनों की एक सीमित संख्या को स्वीकार करती हैं। लाई समूहों का सिद्धांत, | |||
जिसे [[निरंतर समरूपता]] से निपटने के रूप में देखा जा सकता है, संबद्ध [[वेइल समूह|वेइल समूहों]] द्वारा दृढ़ता से प्रभावित होता है। ये परिमित समूह हैं जो प्रतिबिंबों द्वारा उत्पन्न होते हैं जो परिमित-आयामी [[यूक्लिडियन अंतरिक्ष]] पर कार्य करते हैं। परिमित समूहों के गुण इस प्रकार [[सैद्धांतिक भौतिकी]] और रसायन विज्ञान जैसे विषयों में भूमिका निभा सकते हैं। | |||
=== समूहों का प्रतिनिधित्व === | === समूहों का प्रतिनिधित्व === | ||
{{Main| | {{Main|प्रतिनिधित्व सिद्धांत | ||
यह कहना कि एक | }} | ||
यह कहना कि एक समूह X पर एक समूह G समूह क्रिया (गणित) का अर्थ है कि G का प्रत्येक तत्व समूह संरचना के साथ संगत उपाय से समूह X पर एक विशेषण मानचित्र को परिभाषित करता है। जब X की संरचना अधिक होती है, तो इस धारणा को और सीमित करना उपयोगी होता है: सदिश समष्टि V पर G का निरूपण एक [[समूह समरूपता]] है: | |||
:<math>\rho:G \to \operatorname{GL}(V),</math> | :<math>\rho:G \to \operatorname{GL}(V),</math> | ||
जहां सामान्य रैखिक समूह ( | जहां सामान्य रैखिक समूह (V) में V के उलटा [[रैखिक नक्शा|रैखिक परिवर्तन]] होता है। दूसरे शब्दों में, प्रत्येक समूह तत्व G को एक [[automorphism|ऑटोमोर्फिज्म]] ρ(g) नियुक्त किया जाता है जैसे कि {{nowrap|1=''ρ''(''g'') ∘ ''ρ''(''h'') = ''ρ''(''gh'')}} जी में किसी भी H के लिए। | ||
इस परिभाषा को दो दिशाओं में समझा जा सकता है, दोनों ही गणित के संपूर्ण नए क्षेत्रों को जन्म देती हैं।<ref>Such as [[group cohomology]] or [[Equivariant algebraic K-theory|equivariant K-theory]].</ref> एक ओर, यह समूह G के बारे में नई जानकारी दे सकता है: | इस परिभाषा को दो दिशाओं में समझा जा सकता है, दोनों ही गणित के संपूर्ण नए क्षेत्रों को जन्म देती हैं।<ref>Such as [[group cohomology]] or [[Equivariant algebraic K-theory|equivariant K-theory]].</ref> एक ओर, यह समूह G के बारे में नई जानकारी दे सकता है: प्रायः, G में समूह संचालन अमूर्त रूप से दिया जाता है, लेकिन ρ के माध्यम से, यह [[मैट्रिक्स गुणन|आव्यूहों गुणन]] से मेल खाता है, जो बहुत स्पष्ट है।<ref>In particular, if the representation is [[faithful representation|faithful]].</ref> दूसरी ओर, एक जटिल वस्तु पर अभिनय करने वाले एक सुविचारित समूह को देखते हुए, यह प्रश्न में वस्तु के अध्ययन को सरल करता है। उदाहरण के लिए, यदि G परिमित है, तो यह ज्ञात है कि V ऊपर अप्रासंगिक प्रतिनिधित्व में विघटित हो जाता है (माशके प्रमेय देखें)। बदले में, ये हिस्से पूरे वी (शूर के लेम्मा के माध्यम से) की तुलना में अधिक आसानी से प्रबंधनीय होते हैं। | ||
एक समूह | एक समूह G को देखते हुए, प्रतिनिधित्व सिद्धांत तब पूछता है कि जी के क्या प्रतिनिधित्व सम्मिलित हैं। कई समायोजन हैं, और नियोजित उपाय और प्राप्त परिणाम हर स्थिति में भिन्न -भिन्न हैं: [[परिमित समूहों का प्रतिनिधित्व सिद्धांत]] और लाई समूहों का प्रतिनिधित्व सिद्धांत के दो मुख्य उप डोमेन हैं। अभ्यावेदन की समग्रता समूह के [[चरित्र सिद्धांत]] द्वारा नियंत्रित होती है। उदाहरण के लिए, फूरियर श्रृंखला को [[एकात्मक समूह]] के पात्रों के रूप में व्याख्या किया जा सकता है। U(1), LP स्थान पर अभिनय करने वाले पूर्ण मूल्य 1 की जटिल संख्याओं का समूह। L<sup>2</sup>- आवधिक कार्यों का स्थान। | ||
=== | === लाई सिद्धांत === | ||
{{main| | {{main|लाई सिद्धांत | ||
एक | }} | ||
एक लाई समूह एक ऐसा समूह (गणित) है जो एक भिन्न -भिन्न कई गुना है, इस संपत्ति के साथ कि समूह के संचालन [[विभेदक संरचना]] के साथ संगत हैं। लाई समूहों का नाम सोफस लाइ के नाम पर रखा गया है, जिन्होंने निरंतर परिवर्तन समूहों के सिद्धांत की नींव रखी। ग्रुप्स डी लाइ शब्द पहली बार फ्रेंच में 1893 में ली के छात्र [[आर्थर ब्रेडेड]] की थीसिस, पृष्ठ 3 में दिखाई दिया।<ref>{{citation |title= Sur les invariants différentiels des groupes continus de transformations | author= Arthur Tresse |journal=Acta Mathematica|volume=18|year=1893|pages=1–88 |doi=10.1007/bf02418270|url=https://zenodo.org/record/2273334|doi-access=free}}</ref> | |||
लाई समूह [[गणितीय वस्तु]]ओं और [[गणितीय संरचना]] की निरंतर समरूपता के सर्वोत्तम विकसित सिद्धांत का प्रतिनिधित्व करते हैं, जो उन्हें समकालीन गणित के कई हिस्सों के साथ-साथ आधुनिक सैद्धांतिक भौतिकी के लिए अनिवार्य उपकरण बनाता है। वे [[विभेदक समीकरण|विभेदक समीकरणों]] की निरंतर समरूपता के विश्लेषण के लिए एक प्राकृतिक ढांचा प्रदान करते हैं (अंतर गैलोज़ सिद्धांत), ठीक उसी प्रकार जैसे क्रमपरिवर्तन समूहों का उपयोग गैलोज़ सिद्धांत में [[बीजगणितीय समीकरण|बीजगणितीय समीकरणों]] की असतत समरूपता का विश्लेषण करने के लिए किया जाता है। निरंतर समरूपता समूहों के मामले में गैलोज़ सिद्धांत का विस्तार लाइ की प्रमुख प्रेरणाओं में से एक था। | |||
=== संयोजन और ज्यामितीय समूह सिद्धांत === | === संयोजन और ज्यामितीय समूह सिद्धांत === | ||
{{main| | {{main|ज्यामितीय समूह सिद्धांत | ||
समूहों को विभिन्न | }} | ||
समूहों को विभिन्न उपायों से वर्णित किया जा सकता है। परिमित समूहों को सभी संभावित गुणन वाली [[समूह तालिका]] लिखकर वर्णित किया जा सकता है {{nowrap|''g'' • ''h''}}. एक समूह को परिभाषित करने का एक अधिक संक्षिप्त उपाय जनरेटर और संबंधों द्वारा होता है, जिसे समूह की प्रस्तुति भी कहा जाता है। जनरेटर के किसी भी समूह F को देखते हुए <math>\{g_i\}_{i\in I}</math>, F द्वारा उत्पन्न [[मुक्त समूह]] समूह G पर आरोपित करता है। इस मानचित्र के कर्नेल को संबंधों का उपसमूह कहा जाता है, जो कुछ उपसमुच्चय D द्वारा उत्पन्न होता है। प्रस्तुति को सामान्यतः निरूपित किया जाता है <math>\langle F \mid D\rangle.</math> उदाहरण के लिए, समूह प्रस्तुति <math>\langle a,b\mid aba^{-1}b^{-1}\rangle</math> एक समूह का वर्णन करता है जो आइसोमोर्फिक है <math>\mathbb{Z}\times\mathbb{Z}.</math> जनरेटर प्रतीकों और उनके व्युत्क्रमों से युक्त एक स्ट्रिंग को एक शब्द कहा जाता है। | |||
संयोजी समूह सिद्धांत जनरेटर और संबंधों के दृष्टिकोण से समूहों का अध्ययन करता है।<ref>{{harvnb|Schupp|Lyndon|2001}}</ref> यह विशेष रूप से उपयोगी है जहां परिमितता धारणाएं संतुष्ट होती हैं, उदाहरण के लिए सूक्ष्म रूप से उत्पन्न समूह, या सूक्ष्म रूप से प्रस्तुत समूह (अर्थात इसके | संयोजी समूह सिद्धांत जनरेटर और संबंधों के दृष्टिकोण से समूहों का अध्ययन करता है।<ref>{{harvnb|Schupp|Lyndon|2001}}</ref> यह विशेष रूप से उपयोगी है जहां परिमितता धारणाएं संतुष्ट होती हैं, उदाहरण के लिए सूक्ष्म रूप से उत्पन्न समूह, या सूक्ष्म रूप से प्रस्तुत समूह (अर्थात इसके अतिरिक्त संबंध परिमित हैं)। क्षेत्र अपने [[मौलिक समूह|मौलिक समूहों]] के माध्यम से [[ग्राफ (असतत गणित)|रेखांकन (असतत गणित)]] के संबंध का उपयोग करता है। उदाहरण के लिए, कोई दिखा सकता है कि मुक्त समूह का प्रत्येक उपसमूह निःशुल्क है। | ||
किसी समूह को उसकी प्रस्तुति द्वारा देने से कई स्वाभाविक प्रश्न उत्पन्न होते हैं। [[समूहों के लिए शब्द समस्या]] पूछती है कि क्या दो शब्द प्रभावी रूप से एक ही समूह तत्व हैं। समस्या को [[ट्यूरिंग मशीन]] | किसी समूह को उसकी प्रस्तुति द्वारा देने से कई स्वाभाविक प्रश्न उत्पन्न होते हैं। [[समूहों के लिए शब्द समस्या]] पूछती है कि क्या दो शब्द प्रभावी रूप से एक ही समूह तत्व हैं। समस्या को [[ट्यूरिंग मशीन]] से संबंधित करके, कोई दिखा सकता है कि सामान्य रूप से इस कार्य को समाधान करने वाला कोई [[कलन विधि]] नहीं है। एक और, सामान्यतः कठिन, एल्गोरिदमिक रूप से अघुलनशील समस्या [[समूह समरूपता समस्या]] है, जो पूछती है कि क्या भिन्न -भिन्न प्रस्तुतियों द्वारा दिए गए दो समूह वास्तव में समरूप हैं। उदाहरण के लिए, प्रस्तुति वाला समूह <math>\langle x,y \mid xyxyx = e \rangle,</math> पूर्णांकों के योज्य समूह Z के लिए समरूपी है, चूंकि यह तुरंत स्पष्ट नहीं हो सकता है। (लिख रहे हैं <math>z=xy</math>, किसी के पास <math>G \cong \langle z,y \mid z^3 = y\rangle \cong \langle z\rangle.</math>) | ||
[[File:Cayley graph of F2.svg|right|150px|thumb|〈 x, y ∣ 〉, रैंक 2 के मुक्त समूह का केली ग्राफ।]][[ज्यामितीय समूह सिद्धांत]] इन समस्याओं पर एक ज्यामितीय दृष्टिकोण से | [[File:Cayley graph of F2.svg|right|150px|thumb|〈 x, y ∣ 〉, रैंक 2 के मुक्त समूह का केली ग्राफ।]][[ज्यामितीय समूह सिद्धांत]] इन समस्याओं पर एक ज्यामितीय दृष्टिकोण से आक्रमण करता है, या तो समूहों को ज्यामितीय वस्तुओं के रूप में देखकर, या उपयुक्त ज्यामितीय वस्तुओं को ढूंढकर एक समूह कार्य करता है।<ref>{{harvnb|La Harpe|2000}}</ref> पहले विचार को [[केली ग्राफ|केली रेखांकन]] के माध्यम से सटीक बनाया गया है, जिसका शिखर समूह तत्वों के अनुरूप है और किनारे समूह में सही गुणन के अनुरूप हैं। दो तत्वों को देखते हुए, तत्वों के बीच न्यूनतम पथ की लंबाई द्वारा दिए गए [[शब्द मीट्रिक]] का निर्माण करता है। [[जॉन मिल्नोर]] और स्वार्क का एक प्रमेय तब कहता है कि एक समूह जी को एक [[मीट्रिक स्थान]] X पर उचित उपाय से कार्य करने के लिए दिया जाता है, उदाहरण के लिए एक [[कॉम्पैक्ट कई गुना|सघन कई गुना]], तो जी अर्ध-सममिति है। अर्ध-सममितीय (यानी दूरी से समान दिखता है) अंतरिक्ष एक्स. | ||
== समूहों और समरूपता का संबंध == | == समूहों और समरूपता का संबंध == | ||
{{main| | {{main|समरूपता समूह | ||
किसी भी प्रकार की एक संरचित वस्तु X को देखते हुए, एक समरूपता उस वस्तु का मानचित्रण है जो संरचना को संरक्षित करती है। यह कई | }} | ||
*यदि | किसी भी प्रकार की एक संरचित वस्तु X को देखते हुए, एक समरूपता उस वस्तु का मानचित्रण है जो संरचना को संरक्षित करती है। यह कई स्थितियों में होता है, उदाहरण के लिए | ||
*यदि | *यदि X बिना किसी अतिरिक्त संरचना के एक समूह है, तो एक समरूपता क्रमपरिवर्तन समूहों को जन्म देने के लिए समूह से ही एक आक्षेप मानचित्र है। | ||
* यदि इसके | *यदि विषय X अपनी [[मीट्रिक (गणित)]] संरचना या किसी अन्य मीट्रिक स्थान के साथ समतल में बिंदुओं का एक समूह है, तो एक समरूपता समूह का एक आक्षेप है जो बिंदुओं के प्रत्येक जोड़े (एक [[आइसोमेट्री]]) के बीच की दूरी को संरक्षित करता है। संबंधित समूह को X का [[आइसोमेट्री समूह]] कहा जाता है। | ||
*समरूपता केवल ज्यामितीय वस्तुओं तक ही सीमित नहीं है, बल्कि इसमें बीजगणितीय वस्तुएँ भी | * यदि इसके अतिरिक्त [[कोण|कोणों]] को संरक्षित रखा जाता है, तो अनुरूप मानचित्रों की बात की जाती है। उदाहरण के लिए, अनुरूप मानचित्र [[क्लेनियन समूह|क्लेनियन समूहों]] को जन्म देते हैं। | ||
*समरूपता केवल ज्यामितीय वस्तुओं तक ही सीमित नहीं है, बल्कि इसमें बीजगणितीय वस्तुएँ भी सम्मिलित हैं। उदाहरण के लिए, समीकरण <math>x^2-3=0</math> दो उपाय हैं <math>\sqrt{3}</math> तथा <math>-\sqrt{3}</math>. इस स्थिति में, वह समूह जो दो जड़ों का आदान-प्रदान करता है, समीकरण से संबंधित गैलोज़ समूह है। एक चर में प्रत्येक बहुपद समीकरण में गैलोइस समूह होता है, जो इसकी जड़ों पर एक निश्चित क्रमचय समूह होता है। | |||
एक समूह के स्वयंसिद्ध समरूपता के आवश्यक पहलुओं को औपचारिक रूप देते हैं। समरूपता एक समूह बनाती है: वे बंद (गणित) हैं क्योंकि यदि आप किसी वस्तु की समरूपता लेते हैं, और फिर दूसरी समरूपता लागू करते हैं, तो परिणाम अभी भी समरूपता होगा। वस्तु को स्थिर रखने वाली पहचान हमेशा वस्तु की समरूपता होती है। समरूपता को पूर्ववत करके व्युत्क्रमों के अस्तित्व की गारंटी दी जाती है और साहचर्य इस तथ्य से आता है कि समरूपता एक स्थान पर कार्य करती है, और कार्यों की संरचना साहचर्य है। | एक समूह के स्वयंसिद्ध समरूपता के आवश्यक पहलुओं को औपचारिक रूप देते हैं। समरूपता एक समूह बनाती है: वे बंद (गणित) हैं क्योंकि यदि आप किसी वस्तु की समरूपता लेते हैं, और फिर दूसरी समरूपता लागू करते हैं, तो परिणाम अभी भी समरूपता होगा। वस्तु को स्थिर रखने वाली पहचान हमेशा वस्तु की समरूपता होती है। समरूपता को पूर्ववत करके व्युत्क्रमों के अस्तित्व की गारंटी दी जाती है और साहचर्य इस तथ्य से आता है कि समरूपता एक स्थान पर कार्य करती है, और कार्यों की संरचना साहचर्य है। | ||
फ्रूच की प्रमेय कहती है कि प्रत्येक समूह किसी न किसी | फ्रूच की प्रमेय कहती है कि प्रत्येक समूह किसी न किसी रेखांकन (असतत गणित) का सममिति समूह है। इसलिए प्रत्येक अमूर्त समूह वास्तव में किसी स्पष्ट वस्तु की सममिति है। | ||
किसी [[श्रेणी (गणित)]] में काम करके किसी वस्तु की संरचना को संरक्षित करने की कहावत को सटीक बनाया जा सकता है। संरचना को संरक्षित करने वाले | किसी [[श्रेणी (गणित)]] में काम करके किसी वस्तु की संरचना को संरक्षित करने की कहावत को सटीक बनाया जा सकता है। संरचना को संरक्षित करने वाले मानचित्र तब आकारिकी होते हैं, और समरूपता समूह प्रश्न में वस्तु का ऑटोमोर्फिज़्म समूह होता है। | ||
== समूह सिद्धांत के अनुप्रयोग ==<!--this section is linked at from [[Applications of group theory]]--> | == समूह सिद्धांत के अनुप्रयोग ==<!--this section is linked at from [[Applications of group theory]]--> | ||
समूह सिद्धांत के अनुप्रयोग | समूह सिद्धांत के अनुप्रयोग आवश्यक हैं।अमूर्त बीजगणित में लगभग सभी संरचनाएं समूहों के विशेष मामले हैं। अंगूठी (गणित), उदाहरण के लिए, एक दूसरे संचालन (गुणन के अनुरूप) के साथ [[एबेलियन समूह|एबेलियन समूहों]] (जोड़ के अनुरूप) के रूप में देखा जा सकता है। इसलिए, समूह सैद्धांतिक तर्क उन संस्थाओं के सिद्धांत के बड़े हिस्से को रेखांकित करते हैं। | ||
===गैलोइस सिद्धांत=== | ===गैलोइस सिद्धांत=== | ||
{{main| | {{main|गाल्वा सिद्धांत | ||
गैलोज़ सिद्धांत एक बहुपद की जड़ों की समरूपता का वर्णन करने के लिए समूहों का उपयोग करता है (या अधिक सटीक रूप से इन जड़ों द्वारा उत्पन्न बीजगणित के ऑटोमोर्फिज़्म)। गैलोज़ सिद्धांत का मौलिक प्रमेय [[बीजगणितीय क्षेत्र विस्तार]] और समूह सिद्धांत के बीच एक कड़ी प्रदान करता है। यह संबंधित गैलोज़ समूह की घुलनशीलता के संदर्भ में बहुपद समीकरणों की विलेयता के लिए एक प्रभावी मानदंड देता है। उदाहरण के लिए | }} | ||
गैलोज़ सिद्धांत एक बहुपद की जड़ों की समरूपता का वर्णन करने के लिए समूहों का उपयोग करता है (या अधिक सटीक रूप से इन जड़ों द्वारा उत्पन्न बीजगणित के ऑटोमोर्फिज़्म)। गैलोज़ सिद्धांत का मौलिक प्रमेय [[बीजगणितीय क्षेत्र विस्तार]] और समूह सिद्धांत के बीच एक कड़ी प्रदान करता है। यह संबंधित गैलोज़ समूह की घुलनशीलता के संदर्भ में बहुपद समीकरणों की विलेयता के लिए एक प्रभावी मानदंड देता है। उदाहरण के लिए, 5 तत्वों में सममित समूह, समाधान करने योग्य नहीं है जिसका अर्थ है कि सामान्य क्विंटिक समीकरण को रेडिकल्स द्वारा कम डिग्री के समीकरणों के उपाय से समाधान नहीं किया जा सकता है। सिद्धांत, समूह सिद्धांत की ऐतिहासिक जड़ों में से एक होने के नाते, [[वर्ग क्षेत्र सिद्धांत]] जैसे क्षेत्रों में नए परिणाम प्राप्त करने के लिए अभी भी उपयोगी रूप से लागू किया जाता है। | |||
=== बीजगणितीय | === बीजगणितीय सांस्थिति === | ||
{{main| | {{main|बीजगणितीय टोपोलॉजी | ||
[[बीजगणितीय टोपोलॉजी]] एक अन्य डोमेन है जो सिद्धांत में रुचि रखने वाली वस्तुओं के समूहों को प्रमुखता से कार्य करता है। वहां, समूहों का उपयोग | }} | ||
[[बीजगणितीय टोपोलॉजी|बीजगणितीय सांस्थिति]] एक अन्य डोमेन है जो सिद्धांत में रुचि रखने वाली वस्तुओं के समूहों को प्रमुखता से कार्य करता है। वहां, समूहों का उपयोग सांस्थितिक रिक्त स्थान के कुछ आविष्कारों का वर्णन करने के लिए किया जाता है। उन्हें अपरिवर्तनीय कहा जाता है क्योंकि उन्हें इस प्रकार से परिभाषित किया जाता है कि यदि अंतरिक्ष कुछ होमोमोर्फिज्म के अधीन है तो वे नहीं बदलते हैं। उदाहरण के लिए, मूलभूत समूह गणना करता है कि अंतरिक्ष में कितने पथ अनिवार्य रूप से भिन्न हैं। [[त्वरित पेरेलमैन]] द्वारा 2002/2003 में सिद्ध किया गया पॉइंकेयर अनुमान, इस विचार का एक प्रमुख अनुप्रयोग है। चूंकि प्रभाव एकदिशीय नहीं है। उदाहरण के लिए, बीजगणितीय सांस्थिति ईलेनबर्ग-मैकलेन रिक्त स्थान का उपयोग करती है जो निर्धारित [[होमोटॉपी समूह|होमोटॉपी समूहों]] के साथ रिक्त स्थान हैं। इसी प्रकार [[बीजगणितीय के-सिद्धांत]] एक तरह से समूहों के रिक्त स्थान को वर्गीकृत करने पर निर्भर करता है। अंत में, अनंत समूह के मरोड़ वाले उपसमूह का नाम समूह सिद्धांत में सांस्थिति की विरासत को दर्शाता है। | |||
[[File:Torus.png|thumb|right|200px|एक टोरस। इसकी एबेलियन समूह संरचना मानचित्र से प्रेरित है {{nowrap|'''C''' → '''C'''/('''Z''' + ''τ'''''Z''')}}, जहां τ ऊपरी आधे विमान में रहने वाला एक पैरामीटर है।]] | [[File:Torus.png|thumb|right|200px|एक टोरस। इसकी एबेलियन समूह संरचना मानचित्र से प्रेरित है {{nowrap|'''C''' → '''C'''/('''Z''' + ''τ'''''Z''')}}, जहां τ ऊपरी आधे विमान में रहने वाला एक पैरामीटर है।]] | ||
=== बीजगणितीय ज्यामिति === | === बीजगणितीय ज्यामिति === | ||
{{main| | {{main|बीजगणितीय ज्यामिति | ||
}} | |||
बीजगणितीय ज्यामिति इसी प्रकार कई तरह से समूह सिद्धांत का उपयोग करती है। एबेलियन किस्म को ऊपर दर्शाया गया है। समूह संचालन की उपस्थिति से अतिरिक्त जानकारी मिलती है जो इन किस्मों को विशेष रूप से सुलभ बनाती है। वे प्रायः नए अनुमानों के लिए एक परीक्षण के रूप में भी काम करते हैं। (उदाहरण के लिए [[हॉज अनुमान]] (कुछ स्थितियों में)।) एक आयामी स्थिति, अर्थात् [[अण्डाकार वक्र|अण्डाकार वक्रों]] का विशेष विस्तार से अध्ययन किया जाता है। वे दोनों सैद्धांतिक और व्यावहारिक रूप से कठिन हैं।<ref>See the [[Birch and Swinnerton-Dyer conjecture]], one of the [[millennium problem]]s</ref> एक अन्य दिशा में, टोरिक प्रकार बीजगणितीय विविधता है जो एक [[टोरस्र्स]] द्वारा कार्य करती है। टोरॉयडल एम्बेडिंग ने हाल ही में बीजगणितीय ज्यामिति में प्रगति की है, विशेष रूप से एकवचन के संकल्प में।<ref>{{Citation | last1=Abramovich | first1=Dan | last2=Karu | first2=Kalle | last3=Matsuki | first3=Kenji | last4=Wlodarczyk | first4=Jaroslaw | title=Torification and factorization of birational maps | mr=1896232 | year=2002 | journal=[[Journal of the American Mathematical Society]] | volume=15 | issue=3 | pages=531–572 | doi=10.1090/S0894-0347-02-00396-X| arxiv=math/9904135 | s2cid=18211120 }}</ref> | |||
===बीजगणितीय संख्या सिद्धांत=== | ===बीजगणितीय संख्या सिद्धांत=== | ||
{{main| | {{main|बीजगणितीय संख्या सिद्धांत | ||
बीजगणितीय संख्या सिद्धांत कुछ महत्वपूर्ण अनुप्रयोगों के लिए समूहों का उपयोग करता है। उदाहरण के लिए, | }} | ||
बीजगणितीय संख्या सिद्धांत कुछ महत्वपूर्ण अनुप्रयोगों के लिए समूहों का उपयोग करता है। उदाहरण के लिए, यूलर का उत्पाद सूत्र, | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 130: | Line 140: | ||
\end{align} | \end{align} | ||
\!</math> | \!</math> | ||
अंकगणित के मौलिक प्रमेय को पकड़ता है कि कोई भी पूर्णांक [[अभाज्य संख्या]] में एक अनोखे | अंकगणित के मौलिक प्रमेय को पकड़ता है कि कोई भी पूर्णांक [[अभाज्य संख्या]] में एक अनोखे उपाय से विघटित होता है। [[डेडेकाइंड रिंग|अधिक सामान्य छल्लों]] के लिए इस कथन की विफलता वर्ग समूहों और नियमित अभाज्य संख्या को जन्म देती है, जो अर्न्स्ट कुमेर | कुमेर द्वारा फ़र्मेट की अंतिम प्रमेय के उपचार में दिखाई देती है। | ||
=== हार्मोनिक विश्लेषण === | === हार्मोनिक विश्लेषण === | ||
{{main| | {{main|हार्मोनिक विश्लेषण | ||
}} | |||
लाई समूहों और कुछ अन्य समूहों पर विश्लेषण को हार्मोनिक विश्लेषण कहा जाता है। हार उपाय, यानी, लाई समूह में अनुवाद के अनुसार अभिन्न अंग, स्वरूप पहचान और अन्य छवि प्रसंस्करण तकनीकों के लिए उपयोग किए जाते हैं।<ref>{{Citation | last1=Lenz | first1=Reiner | title=Group theoretical methods in image processing | publisher=[[Springer-Verlag]] | location=Berlin, New York | series=Lecture Notes in Computer Science | isbn=978-0-387-52290-6 | year=1990 | volume=413 | url=https://archive.org/details/grouptheoretical0000lenz | doi=10.1007/3-540-52290-5 | s2cid=2738874 | url-access=registration }}</ref> | |||
=== | === साहचर्य === | ||
साहचर्य में, क्रमचय समूह की धारणा और समूह क्रिया की अवधारणा का उपयोगप्रायः वस्तुओं के एक समूह की गिनती को आसान बनाने के लिए किया जाता है; विशेष रूप से बर्नसाइड लेम्मा देखें। | |||
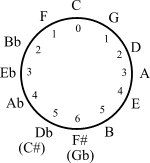
[[File:Fifths.png|right|thumb|150px|पांचवें चक्र को चक्रीय समूह संरचना के साथ संपन्न किया जा सकता है]] | [[File:Fifths.png|right|thumb|150px|पांचवें चक्र को चक्रीय समूह संरचना के साथ संपन्न किया जा सकता है]] | ||
=== संगीत === | === संगीत === | ||
पंचम के घेरे में 12-आवधिक समूह की उपस्थिति | पंचम के घेरे में 12-आवधिक समूह की उपस्थिति समूह सिद्धांत (संगीत) में [[प्राथमिक समूह सिद्धांत]] के अनुप्रयोगों को उत्पन्न करती है। [[परिवर्तनकारी सिद्धांत]] एक गणितीय समूह के तत्वों के रूप में संगीत परिवर्तन को मॉडल करता है। | ||
===भौतिकी === | ===भौतिकी === | ||
भौतिकी में, समूह महत्वपूर्ण हैं क्योंकि वे समरूपता का वर्णन करते हैं जो कि भौतिकी के नियमों का पालन करते हैं। नोएदर के प्रमेय के अनुसार, भौतिक प्रणाली की प्रत्येक निरंतर समरूपता प्रणाली के एक | भौतिकी में, समूह महत्वपूर्ण हैं क्योंकि वे समरूपता का वर्णन करते हैं जो कि भौतिकी के नियमों का पालन करते हैं। नोएदर के प्रमेय के अनुसार, भौतिक प्रणाली की प्रत्येक निरंतर समरूपता प्रणाली के एक संरक्षण कानून (भौतिकी) से मेल खाती है। भौतिक विज्ञानी समूह अभ्यावेदन में बहुत रुचि रखते हैं, विशेष रूप से लाई समूहों में, क्योंकि ये अभ्यावेदन प्रायः संभावित भौतिक सिद्धांतों के मार्ग को संकेत करते हैं। भौतिकी में समूहों के उपयोग के उदाहरणों में मानक मॉडल, [[गेज सिद्धांत]], [[लोरेंत्ज़ समूह]] और पॉइनकेयर समूह सम्मिलित हैं। | ||
[[योशिय्याह विलार्ड गिब्स]] द्वारा विकसित यांत्रिकी की सांख्यिकीय व्याख्याओं की अपूर्णता को समाधान करने के लिए समूह सिद्धांत का उपयोग किया जा सकता है, जो एक सार्थक समाधान प्राप्त करने के लिए अनंत संख्या की संभावनाओं के योग से संबंधित है।<ref>[[Norbert Wiener]], Cybernetics: Or Control and Communication in the Animal and the Machine, {{ISBN|978-0262730099}}, Ch 2</ref> | |||
===रसायन विज्ञान और सामग्री विज्ञान=== | ===रसायन विज्ञान और सामग्री विज्ञान=== | ||
{{main| | {{main|आणविक समरूपता | ||
रसायन विज्ञान और सामग्री विज्ञान में, [[बिंदु समूह]] | }} | ||
रसायन विज्ञान और सामग्री विज्ञान में, [[बिंदु समूह|बिंदु समूहों]] का उपयोग नियमित पॉलीहेड्रा, और [[आणविक समरूपता]] और [[अंतरिक्ष समूह|अंतरिक्ष समूहों]] को क्रिस्टल संरचनाओं को वर्गीकृत करने के लिए किया जाता है। समर्पित किए गए समूहों का उपयोग तब भौतिक गुणों (जैसे कि [[रासायनिक ध्रुवीयता]] और दाहिनी ओर(रसायन विज्ञान)), स्पेक्ट्रोस्कोपिक गुणों (विशेष रूप से [[रमन स्पेक्ट्रोस्कोपी]], [[अवरक्त स्पेक्ट्रोस्कोपी]], वृत्ताकार द्वैतवाद स्पेक्ट्रोस्कोपी, चुंबकीय वृत्ताकार द्वैतवाद स्पेक्ट्रोस्कोपी, UVविज़ स्पेक्ट्रोस्कोपी, और के लिए उपयोगी) को निर्धारित करने के लिए किया जा सकता है। प्रतिदीप्ति स्पेक्ट्रोस्कोपी), और आणविक कक्षाओं का निर्माण करने के लिए। | |||
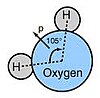
आणविक समरूपता यौगिकों के कई भौतिक और स्पेक्ट्रोस्कोपिक गुणों के लिए | आणविक समरूपता यौगिकों के कई भौतिक और स्पेक्ट्रोस्कोपिक गुणों के लिए उत्तरदायित्व है और रासायनिक प्रतिक्रियाएं कैसे होती हैं, इसके बारे में प्रासंगिक जानकारी प्रदान करती है। किसी दिए गए अणु के लिए एक बिंदु समूह निर्दिष्ट करने के लिए, उस पर उपस्थित समरूपता संक्रियाओं के समूह को खोजना आवश्यक है। समरूपता संक्रिया एक क्रिया है, जैसे अक्ष के चारों ओर घूमना या दर्पण तल के माध्यम से प्रतिबिंब। दूसरे शब्दों में, यह एक संक्रिया है जो अणु को इस प्रकार गतिमान करती है कि यह मूल विन्यास से अप्रभेद्य है। समूह सिद्धांत में, घूर्णन कुल्हाड़ियों और दर्पण तलों को समरूपता तत्व कहा जाता है। ये तत्व एक बिंदु, रेखा या समतल हो सकते हैं जिसके संबंध में सममिति संक्रिया की जाती है। एक अणु की समरूपता संचालन इस अणु के लिए विशिष्ट बिंदु समूह निर्धारित करता है। | ||
[[File:Miri2.jpg|thumb|100px|समरूपता अक्ष के साथ जल अणु]]रसायन विज्ञान में, पाँच महत्वपूर्ण सममिति संक्रियाएँ हैं। वे | [[File:Miri2.jpg|thumb|100px|समरूपता अक्ष के साथ जल अणु]]रसायन विज्ञान में, पाँच महत्वपूर्ण सममिति संक्रियाएँ हैं। वे पहचान ऑपरेशन (ई), रोटेशन ऑपरेशन या उचित रोटेशन (C<sub>''n''</sub>), प्रतिबिंब ऑपरेशन (σ), उलटा (i) और रोटेशन प्रतिबिंब ऑपरेशन या अनुचित रोटेशन (S<sub>''n''</sub>). पहचान संक्रिया (E) में अणु को उसी रूप में छोड़ना सम्मिलित है। यह किसी भी अक्ष के चारों ओर पूर्ण घुमावों की संख्या के बराबर है। यह सभी अणुओं की एक समरूपता है, जबकि [[chiral|चिरल]] अणु के समरूपता समूह में केवल पहचान संक्रिया होती है। एक पहचान संक्रिया प्रत्येक अणु की एक विशेषता है, भले ही इसमें कोई समरूपता न हो। अक्ष के चारों ओर घूमना (C<sub>''n''</sub>) एक विशिष्ट अक्ष के चारों ओर एक विशिष्ट कोण से अणु को घुमाने के होते हैं। यह 360°/''n'' कोण के माध्यम से घूर्णन है, जहां ''n'' एक पूर्णांक है, घूर्णन अक्ष के बारे में। उदाहरण के लिए, यदि एक [[पानी]] का अणु उस अक्ष के चारों ओर 180° घूमता है जो [[ऑक्सीजन]] परमाणु से होकर गुजरता है और [[हाइड्रोजन]] परमाणुओं के बीच होता है, तो यह उसी विन्यास में होता है जैसे यह प्रारभ्म हुआ था। इस स्थिति में, {{nowrap|1=''n'' = 2}}, क्योंकि इसे दो बार लगाने से पहचान ऑपरेशन उत्पन्न होता है। एक से अधिक रोटेशन अक्ष वाले अणुओं में, C<sub>n</sub> n का सबसे बड़ा मान रखने वाली धुरी उच्चतम क्रम रोटेशन अक्ष या प्रमुख अक्ष है। उदाहरण के लिए [[बोरॉन ट्राइफ्लोराइड]] (BF<sub>3</sub>), घूर्णन अक्ष का उच्चतम क्रम C<sub>3</sub> है, इसलिए घूर्णन का मुख्य अक्ष C<sub>3</sub> हैI. | ||
परावर्तन संक्रिया (σ) में कई अणुओं में दर्पण तल होते हैं, | परावर्तन संक्रिया (σ) में कई अणुओं में दर्पण तल होते हैं, चूंकि वे स्पष्ट नहीं हो सकते हैं। प्रतिबिंब ऑपरेशन बाएं और दाएं का आदान-प्रदान करता है, जैसे कि प्रत्येक बिंदु विमान के माध्यम से लंबवत रूप से उस स्थिति में चला गया हो, जब वह शुरू हुआ था। जब तल घूर्णन के मुख्य अक्ष के लंबवत होता है, तो इसे σ कहा जाता है<sub>''h''</sub>(क्षैतिज)। अन्य तल, जिनमें घूर्णन का मुख्य अक्ष होता है, को लंबवत (σ<sub>''v''</sub>) या डायहेड्रल (σ<sub>''d''</sub>). | ||
व्युत्क्रम (i) एक अधिक जटिल संक्रिया है। प्रत्येक बिंदु अणु के केंद्र के माध्यम से मूल स्थिति के विपरीत स्थिति में और केंद्रीय बिंदु से जहां से शुरू हुआ था, वहां तक जाता है। कई अणु जो पहली नज़र में उलटा केंद्र रखते हैं, ऐसा नहीं है; उदाहरण के लिए, [[मीथेन]] और अन्य [[चतुर्पाश्वीय]] अणुओं में व्युत्क्रम समरूपता का अभाव होता है। इसे देखने के लिए, एक मीथेन मॉडल को दाईं ओर ऊर्ध्वाधर तल में दो हाइड्रोजन परमाणुओं और बाईं ओर क्षैतिज तल में दो हाइड्रोजन परमाणुओं के साथ पकड़ें। व्युत्क्रमण के परिणामस्वरूप दाहिनी ओर क्षैतिज तल में दो हाइड्रोजन परमाणु और बाईं ओर ऊर्ध्वाधर तल में दो हाइड्रोजन परमाणु होते हैं। उलटा इसलिए मीथेन का समरूपता ऑपरेशन नहीं है, क्योंकि उलटा ऑपरेशन के बाद अणु का उन्मुखीकरण मूल अभिविन्यास से भिन्न होता है। और अंतिम ऑपरेशन अनुचित रोटेशन या रोटेशन | व्युत्क्रम (i) एक अधिक जटिल संक्रिया है। प्रत्येक बिंदु अणु के केंद्र के माध्यम से मूल स्थिति के विपरीत स्थिति में और केंद्रीय बिंदु से जहां से शुरू हुआ था, वहां तक जाता है। कई अणु जो पहली नज़र में उलटा केंद्र रखते हैं, ऐसा नहीं है; उदाहरण के लिए, [[मीथेन]] और अन्य [[चतुर्पाश्वीय]] अणुओं में व्युत्क्रम समरूपता का अभाव होता है। इसे देखने के लिए, एक मीथेन मॉडल को दाईं ओर ऊर्ध्वाधर तल में दो हाइड्रोजन परमाणुओं और बाईं ओर क्षैतिज तल में दो हाइड्रोजन परमाणुओं के साथ पकड़ें। व्युत्क्रमण के परिणामस्वरूप दाहिनी ओर क्षैतिज तल में दो हाइड्रोजन परमाणु और बाईं ओर ऊर्ध्वाधर तल में दो हाइड्रोजन परमाणु होते हैं। उलटा इसलिए मीथेन का समरूपता ऑपरेशन नहीं है, क्योंकि उलटा ऑपरेशन के बाद अणु का उन्मुखीकरण मूल अभिविन्यास से भिन्न होता है। और अंतिम ऑपरेशन अनुचित रोटेशन या रोटेशन प्रतिबिंब ऑपरेशन (S<sub>''n''</sub>) को 360°/''n'' घुमाने की ज़रूरत होती है, इसके बाद रोटेशन की धुरी के लम्बवत् तल से परावर्तन होता है। | ||
=== क्रिप्टोग्राफी === | === क्रिप्टोग्राफी === | ||
[[File:Caesar3.svg|thumb|[[चक्रीय समूह]] Z<sub>26</sub> सीज़र के सिफर को रेखांकित करता है।]]अण्डाकार [[सार्वजनिक कुंजी क्रिप्टोग्राफी]] में निर्मित | [[File:Caesar3.svg|thumb|[[चक्रीय समूह]] Z<sub>26</sub> सीज़र के सिफर को रेखांकित करता है।]]अण्डाकार [[सार्वजनिक कुंजी क्रिप्टोग्राफी]] में निर्मित प्रधान क्रम के बहुत बड़े समूह सार्वजनिक-कुंजी क्रिप्टोग्राफी के लिए काम करते हैं। इस क्रम के क्रिप्टोग्राफ़िक उपाय ज्यामितीय वस्तुओं के लचीलेपन से लाभान्वित होते हैं, इसलिए उनकी समूह संरचनाएँ, इन समूहों की जटिल संरचना के साथ मिलकर, [[असतत लघुगणक]] की गणना करना बहुत कठिन बना देती हैं। जल्द से जल्द कूटलेखन प्रोटोकॉल में से एक, सीज़र सिफर | सीज़र का सिफर, को एक (बहुत आसान) समूह ऑपरेशन के रूप में भी व्याख्या किया जा सकता है। अधिकांश क्रिप्टोग्राफ़िक योजनाएँ किसी न किसी रूप में समूहों का उपयोग करती हैं। विशेष रूप से डिफी-हेलमैन कुंजी लेन देन परिमित चक्रीय समूहों का उपयोग करता है। इसलिए समूह-आधारित क्रिप्टोग्राफी शब्द अधिकतर क्रिप्टोग्राफ़िक प्रोटोकॉल को संदर्भित करता है जो अनंत अविश्वासी समूहों जैसे ब्रैड समूह का उपयोग करता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 195: | Line 205: | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
* [http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/Abstract_groups.html History of the abstract group concept] | * [http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/Abstract_groups.html History of the abstract group concept] | ||
* [https://archive.today/20120723235509/http://www.bangor.ac.uk/r.brown/hdaweb2.htm Higher dimensional group theory] This presents a view of group theory as level one of a theory that extends in all dimensions, and has applications in homotopy theory and to higher dimensional nonabelian methods for local-to-global problems. | * [https://archive.today/20120723235509/http://www.bangor.ac.uk/r.brown/hdaweb2.htm Higher dimensional group theory] This presents a view of group theory as level one of a theory that extends in all dimensions, and has applications in homotopy theory and to higher dimensional nonabelian methods for local-to-global problems. | ||
* [http://plus.maths.org/issue48/package/index.html Plus teacher and student package: Group Theory] This package brings together all the articles on group theory from ''Plus'', the online mathematics magazine produced by the Millennium Mathematics Project at the University of Cambridge, exploring applications and recent breakthroughs, and giving explicit definitions and examples of groups. | * [http://plus.maths.org/issue48/package/index.html Plus teacher and student package: Group Theory] This package brings together all the articles on group theory from ''Plus'', the online mathematics magazine produced by the Millennium Mathematics Project at the University of Cambridge, exploring applications and recent breakthroughs, and giving explicit definitions and examples of groups. | ||
* {{Cite EB1911|wstitle=Groups, Theory of|volume=12|pages=626–636|first=William|last=Burnside|author-link=William Burnside|mode=cs2}} This is a detailed exposition of contemporaneous understanding of Group Theory by an early researcher in the field. | * {{Cite EB1911|wstitle=Groups, Theory of|volume=12|pages=626–636|first=William|last=Burnside|author-link=William Burnside|mode=cs2}} This is a detailed exposition of contemporaneous understanding of Group Theory by an early researcher in the field. | ||
{{Authority control}} | {{Authority control}} | ||
[[Category:All articles with unsourced statements]] | |||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:Articles with short description]] | |||
[[Category:Articles with unsourced statements from December 2013]] | |||
[[Category:Articles with unsourced statements from June 2012]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:Created On 29/11/2022]] | [[Category:Created On 29/11/2022]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Mathematics sidebar templates]] | |||
[[Category:Physics sidebar templates]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Wikipedia articles incorporating a citation from the 1911 Encyclopaedia Britannica with Wikisource reference]] | |||
[[Category:समूह सिद्धांत| ]] | |||
Latest revision as of 12:52, 27 October 2023

| बीजगणितीय संरचना → 'समूह सिद्धांत' समूह सिद्धांत |
|---|
 |
अमूर्त बीजगणित में, समूह सिद्धांत समूह के रूप में ज्ञात बीजगणितीय संरचनाओं का अध्ययन करता है। एक समूह की अवधारणा सार बीजगणित के लिए केंद्रीय है: अन्य प्रसिद्ध बीजगणितीय संरचनाएं, जैसे कि छल्ले (गणित), क्षेत्र (गणित), और सदिश रिक्त स्थान, सभी को अतिरिक्त संचालन (गणित) और स्वयंसिद्धों से संपन्न समूहों के रूप में देखा जा सकता है। पूरे गणित में समूह की पुनरावृत्ति होती है, और समूह सिद्धांत के उपायों ने बीजगणित के कई हिस्सों को प्रभावित किया है। रेखीय बीजगणितीय समूह और लाई समूह सिद्धांत की दो शाखाएँ हैं जिन्होंने प्रगति का अनुभव किया है और अपने आप में विषय क्षेत्र बन गए हैं।
विभिन्न भौतिक प्रणालियाँ, जैसे कि क्रिस्टल और हाइड्रोजन परमाणु, और मानक मॉडल ब्रह्मांड में ज्ञात मौलिक बल, समरूपता समूहों द्वारा प्रतिरूपित किए जा सकते हैं। इस प्रकार समूह सिद्धांत और निकट से संबंधित प्रतिनिधित्व सिद्धांत के भौतिकी, रसायन विज्ञान और सामग्री विज्ञान में कई महत्वपूर्ण अनुप्रयोग हैं। सार्वजनिक कुंजी क्रिप्टोग्राफ़ी के लिए समूह सिद्धांत भी केंद्रीय है।
समूह सिद्धांत का प्रारंभिक इतिहास 19वीं दशक का है। 20वीं दशक की सबसे महत्वपूर्ण गणितीय उपलब्धियों में से एक[1] सहयोगात्मक प्रयास था, जिसमें 10,000 से अधिक जर्नल पेज सम्मिलित थे और अधिकतर 1960 और 2004 के बीच प्रकाशित हुए थे, जिसकी परिणति परिमित सरल समूहों के पूर्ण वर्गीकरण में हुई।
इतिहास
समूह सिद्धांत के तीन मुख्य ऐतिहासिक स्रोत हैं: संख्या सिद्धांत, बीजगणितीय समीकरणों का सिद्धांत और ज्यामिति। संख्या-सैद्धांतिक किनारा लियोनहार्ड यूलर द्वारा प्रारभ्म किया गया था, और कार्ल फ्रेडरिक गॉस द्वारा विकसित किया गया था। क्वाड्रेटिक क्षेत्रों से संबंधित मॉड्यूलर अंकगणित और योगात्मक और गुणात्मक समूहों पर गॉस का काम। उच्च स्तर के बहुपद समीकरणों के सामान्य समाधान के लिए अपनी खोज में जोसेफ लुइस लाग्रेंज, पाओलो रफ़िनी (गणितज्ञ), और नील्स हेनरिक एबेल द्वारा क्रमचय समूहों के बारे में प्रारंभिक परिणाम प्राप्त किए गए थे। इवरिस्ट गैलोइस ने समूह शब्द गढ़ा और एक संबंध स्थापित किया, जिसे अब गैलोज़ सिद्धांत के रूप में जाना जाता है, समूहों और क्षेत्र सिद्धांत (गणित) के नवजात सिद्धांत के बीच। ज्यामिति में, समूह पहले प्रक्षेपी ज्यामिति और बाद में, गैर-यूक्लिडियन ज्यामिति में महत्वपूर्ण हो गए। फेलिक्स क्लेन के एर्लांगेन कार्यक्रम ने समूह सिद्धांत को ज्यामिति के आयोजन सिद्धांत के रूप में घोषित किया।
1830 के दशक में इवरिस्ट गैलोइस, बहुपद समीकरणों की विलेयता निर्धारित करने के लिए समूहों को नियुक्त करने वाले पहले व्यक्ति थे। आर्थर केली और ऑगस्टिन लुइस कॉची ने क्रमचय समूहों के सिद्धांत को बनाकर इन जांचों को आगे बढ़ाया। समूहों के लिए दूसरा ऐतिहासिक स्रोत ज्यामिति स्थितियों से उपजा है। समूह सिद्धांत का उपयोग करते हुए संभावित ज्यामिति (जैसे यूक्लिडियन ज्यामिति, अतिशयोक्तिपूर्ण ज्यामिति या प्रक्षेपी ज्यामिति) के साथ पकड़ में आने के प्रयास में, फेलिक्स क्लेन ने एर्लांगेन कार्यक्रम की शुरुआत की। 1884 में सोफस लाइ ने विश्लेषण (गणित) की समस्याओं से जुड़े समूहों (अब लाई समूह कहा जाता है) का उपयोग करना प्रारभ्म कर दिया। तीसरे, समूह, पहले अप्रत्यक्ष रूप से और बाद में स्पष्ट रूप से, बीजगणितीय संख्या सिद्धांत में उपयोग किए गए थे।
इन प्रारंभिक स्रोतों के भिन्न -भिन्न सीमा के परिणामस्वरूप समूहों की भिन्न -भिन्न धारणाएँ बनीं। 1880 के आसपास समूहों के सिद्धांत को एकीकृत किया गया था। तब से, समूह सिद्धांत का प्रभाव लगातार बढ़ रहा है, 20 वीं दशक के प्रारभ्म में अमूर्त बीजगणित, प्रतिनिधित्व सिद्धांत और कई और प्रभावशाली स्पिन-ऑफ डोमेन को जन्म दे रहा है। परिमित सरल समूहों का वर्गीकरण 20वीं दशक के मध्य से काम का एक विशाल निकाय है, जो सभी परिमित समुच्चय सरल समूहों को वर्गीकृत करता है।
समूहों के मुख्य वर्ग
जिन समूहों पर विचार किया जा रहा है, उनकी सीमा धीरे-धीरे परिमित क्रमपरिवर्तन समूहों और आव्यूह समूहों के विशेष उदाहरणों से अमूर्त समूहों तक विस्तारित हो गई है, जिन्हें समूह और बाइनरी संबंध के उत्पादक समूह द्वारा समूह की प्रस्तुति के माध्यम से निर्दिष्ट किया जा सकता है।
क्रमपरिवर्तन समूह
एक व्यवस्थित अध्ययन से गुजरने वाले समूहों का प्रथम वर्ग (समूह सिद्धांत) क्रमचय समूह था। किसी भी समूह X और अपने आप में X के द्विभाजनों का एक संग्रह G दिया गया है (जिसे क्रमपरिवर्तन के रूप में जाना जाता है) जो रचनाओं और व्युत्क्रमों के अनुसार बंद है, G, X पर एक समूह क्रिया (गणित) है। यदि X में n तत्व सम्मिलित हैं और G में सभी सम्मिलित हैं क्रमपरिवर्तन, जी सममित समूह Sn है; सामान्य तौर पर, कोई भी क्रमपरिवर्तन समूह G, X के सममित समूह का एक उपसमूह है। आर्थर केली के कारण एक प्रारंभिक निर्माण ने किसी भी समूह को एक क्रमचय समूह के रूप में प्रदर्शित किया, जो(X = G) बाएं नियमित प्रतिनिधित्व के माध्यम से स्वयं पर कार्य करता है ।
कई स्थितियों में, क्रमचय समूह की संरचना का संबंधित समूह पर इसके कार्य के गुणों का उपयोग करके अध्ययन किया जा सकता है। उदाहरण के लिए, इस प्रकार से यह सिद्ध होता है कि n ≥ 5 के लिए, वैकल्पिक समूह An सरल समूह है, अर्थात किसी उचित सामान्य उपसमूह को स्वीकार नहीं करता है। यह तथ्य एबेल-रफ़िनी प्रमेय में एक महत्वपूर्ण भूमिका निभाता है | डिग्री के एक सामान्य बीजगणितीय समीकरण को समाधान करने की असंभवता n ≥ 5 रेडिकल्स में है।
आव्यूह समूह
समूहों का अगला महत्वपूर्ण वर्ग आव्यूह समूहों, या रैखिक समूहों द्वारा दिया जाता है। यहाँ G एक समूह है जिसमें एक क्षेत्र (गणित) K पर दिए गए क्रम n के व्युत्क्रमणीय आव्यूह (गणित) होते हैं जो उत्पादों और व्युत्क्रमों के अंतर्गत बंद होते हैं। ऐसा समूह n-आयामी सदिश समष्टि K पर कार्य करता हैn रैखिक रूपांतरणों द्वारा। यह क्रिया आव्यूह समूहों को संकल्पनात्मक रूप से क्रमचय समूहों के समान बनाती है, और समूह G के गुणों को स्थापित करने के लिए क्रिया की ज्यामिति का उपयोगी उपयोग किया जा सकता है।
परिवर्तन समूह
क्रमचय समूह और आव्यूह समूह परिवर्तन समूहों की विशेष स्थिति हैं: समूह जो एक निश्चित स्थान X पर अपनी अंतर्निहित संरचना को संरक्षित करते हैं। क्रमचय समूहों की स्थिति में, X एक समुच्चय है; आव्यूह समूहों के लिए, X एक सदिश स्थान है। एक परिवर्तन समूह की अवधारणा समरूपता समूह की अवधारणा से निकटता से संबंधित है: परिवर्तन समूहों में प्रायः सभी परिवर्तन होते हैं जो एक निश्चित संरचना को संरक्षित करते हैं।
परिवर्तन समूहों का सिद्धांत अंतर ज्यामिति के साथ समूह सिद्धांत को जोड़ने वाला एक पुल बनाता है। सोफस ली और फेलिक्स क्लेन के साथ प्रारभ्म होने वाले शोध की एक लंबी श्रृंखला होमियोमोर्फिज्म या डिफियोमोर्फिज्म द्वारा कई गुना समूह क्रियाओं पर विचार करती है। समूह स्वयं असतत समूह या निरंतर समूह हो सकते हैं।
सार समूह
समूह सिद्धांत के विकास के पहले चरण में माने जाने वाले अधिकांश समूह ठोस थे, जिन्हें संख्याओं, क्रमपरिवर्तन या आव्यूहों के माध्यम से महसूस किया गया था। यह उन्नीसवीं दशक के उत्तरार्ध तक नहीं था कि एक सार समूह का विचार एक समूह के रूप में संचालन के साथ एक निश्चित प्रणाली को संतुष्ट करता है। एक सार समूह को निर्दिष्ट करने का एक विशिष्ट उपाय जनरेटर और संबंधों द्वारा समूह की प्रस्तुति के माध्यम से होता है,
अमूर्त समूहों का एक महत्वपूर्ण स्रोत एक सामान्य उपसमूह H द्वारा एक समूह जी के एक कारक समूह, या भागफल समूह, G/H के निर्माण द्वारा दिया जाता है। बीजगणितीय संख्या क्षेत्रों के वर्ग समूह, कारक समूहों के प्रारंभिक उदाहरणों में से थे। संख्या सिद्धांत में बहुत रुचि। यदि समूह G समूह X पर एक क्रमचय समूह है, तो कारक समूह G/H अब X पर कार्य नहीं कर रहा है; लेकिन एक सार समूह का विचार इस विसंगति के बारे में चिंता न करने की अनुमति देता है।
ठोस से अमूर्त समूहों के दृष्टिकोण में परिवर्तन से उन समूहों के गुणों पर विचार करना स्वाभाविक हो जाता है जो किसी विशेष बोध से स्वतंत्र हैं, या आधुनिक भाषा में, समरूपतावाद के अनुसार अपरिवर्तनीय हैं, साथ ही इस प्रकार की संपत्ति वाले समूह के वर्ग: परिमित समूह, आवधिक समूह, सरल समूह, समाधान करने योग्य समूह, और इसी तरह। एक व्यक्तिगत समूह के गुणों की खोज करने के अतिरिक्त, ऐसे परिणाम स्थापित करने का प्रयास किया जाता है जो समूहों के एक पूरे वर्ग पर लागू होते हैं। नया प्रतिमान गणित के विकास के लिए सर्वोपरि था: इसने डेविड हिल्बर्ट, एमिल आर्टिन, एमी नोथेर और उनके स्कूल के गणितज्ञों के कार्यों में अमूर्त बीजगणित के निर्माण का पूर्वाभास कराया।[citation needed]
अतिरिक्त संरचना वाले समूह
एक समूह की अवधारणा का एक महत्वपूर्ण विस्तार तब होता है जब G अतिरिक्त संरचना के साथ संपन्न होता है, विशेष रूप से, एक संस्थानिक स्थान, भिन्न -भिन्न कई गुना, या बीजगणितीय विविधता। यदि समूह संचालन एम (गुणा) और आई (उलटा),
इस संरचना के साथ संगत हैं, अर्थात, वे निरंतर मानचित्र, चिकने मानचित्र या नियमित मानचित्र (बीजगणितीय ज्यामिति) (बीजगणितीय ज्यामिति के अर्थ में) मानचित्र हैं, तो G एक सामयिक समूह, एक लाई समूह या एक बीजगणितीय समूह है।[2] अतिरिक्त संरचना की उपस्थिति इस प्रकार के समूहों को अन्य गणितीय विषयों से जोड़ती है और इसका अर्थ है कि उनके अध्ययन में अधिक उपकरण उपलब्ध हैं। सांस्थितिक समूह अमूर्त हार्मोनिक विश्लेषण के लिए एक प्राकृतिक डोमेन बनाते हैं, जबकि लाई समूह (प्रायः परिवर्तन समूहों के रूप में महसूस किए जाते हैं) अंतर ज्यामिति और एकात्मक प्रतिनिधित्व सिद्धांत के मुख्य आधार हैं। कुछ वर्गीकरण प्रश्न जिन्हें सामान्य रूप से समाधान नहीं किया जा सकता है, समूहों के विशेष उपवर्गों के लिए संपर्क किया जा सकता है और समाधान किया जा सकता है। इस प्रकार, सघन लाइ समूह को पूरी प्रकार से वर्गीकृत किया गया है। अनंत अमूर्त समूहों और सामयिक समूहों के बीच एक उपयोगी संबंध है: जब भी एक समूह Γ को एक सांस्थितिक समूह G में एक जाली (असतत उपसमूह) के रूप में महसूस किया जा सकता है, G से संबंधित ज्यामिति और विश्लेषण Γ के बारे में महत्वपूर्ण परिणाम देते हैं। परिमित समूहों के सिद्धांत में एक तुलनात्मक रूप से हाल की प्रवृत्ति सघन सांस्थितिक समूहों (अनंत समूहों) के साथ उनके संबंधों का लाभ उठाती है: उदाहरण के लिए, एक शक्तिशाली P-समूह | विभिन्न आदेशों के पी-समूह, और G के गुण इसके परिमित भागफल के गुणों में अनुवाद करते हैं।
समूह सिद्धांत की शाखाएँ
परिमित समूह सिद्धांत
बीसवीं दशक के समय, गणितज्ञों ने परिमित समूहों के सिद्धांत के कुछ पहलुओं की बहुत गहराई से जाँच की, विशेष रूप से परिमित समूहों के स्थानीय विश्लेषण और समाधान करने योग्य समूह और नगण्य समूहों के सिद्धांत की।[citation needed] परिणामस्वरूप, परिमित सरल समूहों का पूर्ण वर्गीकरण प्राप्त किया गया, जिसका अर्थ है कि वे सभी सरल समूह जिनसे सभी परिमित समूह बनाए जा सकते हैं, अब ज्ञात हैं।
बीसवीं दशक के उत्तरार्ध के समय, क्लाउड चेवेली और रॉबर्ट स्टाइनबर्ग जैसे गणितज्ञों ने शास्त्रीय समूहों और अन्य संबंधित समूहों के परिमित एनालॉग्स की हमारी समझ को भी बढ़ाया। समूहों का ऐसा ही एक परिवार परिमित क्षेत्रों पर सामान्य रेखीय समूहों का परिवार है। परिमित समूह प्रायः गणितीय या भौतिक वस्तुओं की समरूपता पर विचार करते समय होते हैं , जब वे वस्तुएँ संरचना-संरक्षण परिवर्तनों की एक सीमित संख्या को स्वीकार करती हैं। लाई समूहों का सिद्धांत, जिसे निरंतर समरूपता से निपटने के रूप में देखा जा सकता है, संबद्ध वेइल समूहों द्वारा दृढ़ता से प्रभावित होता है। ये परिमित समूह हैं जो प्रतिबिंबों द्वारा उत्पन्न होते हैं जो परिमित-आयामी यूक्लिडियन अंतरिक्ष पर कार्य करते हैं। परिमित समूहों के गुण इस प्रकार सैद्धांतिक भौतिकी और रसायन विज्ञान जैसे विषयों में भूमिका निभा सकते हैं।
समूहों का प्रतिनिधित्व
यह कहना कि एक समूह X पर एक समूह G समूह क्रिया (गणित) का अर्थ है कि G का प्रत्येक तत्व समूह संरचना के साथ संगत उपाय से समूह X पर एक विशेषण मानचित्र को परिभाषित करता है। जब X की संरचना अधिक होती है, तो इस धारणा को और सीमित करना उपयोगी होता है: सदिश समष्टि V पर G का निरूपण एक समूह समरूपता है:
जहां सामान्य रैखिक समूह (V) में V के उलटा रैखिक परिवर्तन होता है। दूसरे शब्दों में, प्रत्येक समूह तत्व G को एक ऑटोमोर्फिज्म ρ(g) नियुक्त किया जाता है जैसे कि ρ(g) ∘ ρ(h) = ρ(gh) जी में किसी भी H के लिए।
इस परिभाषा को दो दिशाओं में समझा जा सकता है, दोनों ही गणित के संपूर्ण नए क्षेत्रों को जन्म देती हैं।[3] एक ओर, यह समूह G के बारे में नई जानकारी दे सकता है: प्रायः, G में समूह संचालन अमूर्त रूप से दिया जाता है, लेकिन ρ के माध्यम से, यह आव्यूहों गुणन से मेल खाता है, जो बहुत स्पष्ट है।[4] दूसरी ओर, एक जटिल वस्तु पर अभिनय करने वाले एक सुविचारित समूह को देखते हुए, यह प्रश्न में वस्तु के अध्ययन को सरल करता है। उदाहरण के लिए, यदि G परिमित है, तो यह ज्ञात है कि V ऊपर अप्रासंगिक प्रतिनिधित्व में विघटित हो जाता है (माशके प्रमेय देखें)। बदले में, ये हिस्से पूरे वी (शूर के लेम्मा के माध्यम से) की तुलना में अधिक आसानी से प्रबंधनीय होते हैं।
एक समूह G को देखते हुए, प्रतिनिधित्व सिद्धांत तब पूछता है कि जी के क्या प्रतिनिधित्व सम्मिलित हैं। कई समायोजन हैं, और नियोजित उपाय और प्राप्त परिणाम हर स्थिति में भिन्न -भिन्न हैं: परिमित समूहों का प्रतिनिधित्व सिद्धांत और लाई समूहों का प्रतिनिधित्व सिद्धांत के दो मुख्य उप डोमेन हैं। अभ्यावेदन की समग्रता समूह के चरित्र सिद्धांत द्वारा नियंत्रित होती है। उदाहरण के लिए, फूरियर श्रृंखला को एकात्मक समूह के पात्रों के रूप में व्याख्या किया जा सकता है। U(1), LP स्थान पर अभिनय करने वाले पूर्ण मूल्य 1 की जटिल संख्याओं का समूह। L2- आवधिक कार्यों का स्थान।
लाई सिद्धांत
एक लाई समूह एक ऐसा समूह (गणित) है जो एक भिन्न -भिन्न कई गुना है, इस संपत्ति के साथ कि समूह के संचालन विभेदक संरचना के साथ संगत हैं। लाई समूहों का नाम सोफस लाइ के नाम पर रखा गया है, जिन्होंने निरंतर परिवर्तन समूहों के सिद्धांत की नींव रखी। ग्रुप्स डी लाइ शब्द पहली बार फ्रेंच में 1893 में ली के छात्र आर्थर ब्रेडेड की थीसिस, पृष्ठ 3 में दिखाई दिया।[5] लाई समूह गणितीय वस्तुओं और गणितीय संरचना की निरंतर समरूपता के सर्वोत्तम विकसित सिद्धांत का प्रतिनिधित्व करते हैं, जो उन्हें समकालीन गणित के कई हिस्सों के साथ-साथ आधुनिक सैद्धांतिक भौतिकी के लिए अनिवार्य उपकरण बनाता है। वे विभेदक समीकरणों की निरंतर समरूपता के विश्लेषण के लिए एक प्राकृतिक ढांचा प्रदान करते हैं (अंतर गैलोज़ सिद्धांत), ठीक उसी प्रकार जैसे क्रमपरिवर्तन समूहों का उपयोग गैलोज़ सिद्धांत में बीजगणितीय समीकरणों की असतत समरूपता का विश्लेषण करने के लिए किया जाता है। निरंतर समरूपता समूहों के मामले में गैलोज़ सिद्धांत का विस्तार लाइ की प्रमुख प्रेरणाओं में से एक था।
संयोजन और ज्यामितीय समूह सिद्धांत
समूहों को विभिन्न उपायों से वर्णित किया जा सकता है। परिमित समूहों को सभी संभावित गुणन वाली समूह तालिका लिखकर वर्णित किया जा सकता है g • h. एक समूह को परिभाषित करने का एक अधिक संक्षिप्त उपाय जनरेटर और संबंधों द्वारा होता है, जिसे समूह की प्रस्तुति भी कहा जाता है। जनरेटर के किसी भी समूह F को देखते हुए , F द्वारा उत्पन्न मुक्त समूह समूह G पर आरोपित करता है। इस मानचित्र के कर्नेल को संबंधों का उपसमूह कहा जाता है, जो कुछ उपसमुच्चय D द्वारा उत्पन्न होता है। प्रस्तुति को सामान्यतः निरूपित किया जाता है उदाहरण के लिए, समूह प्रस्तुति एक समूह का वर्णन करता है जो आइसोमोर्फिक है जनरेटर प्रतीकों और उनके व्युत्क्रमों से युक्त एक स्ट्रिंग को एक शब्द कहा जाता है।
संयोजी समूह सिद्धांत जनरेटर और संबंधों के दृष्टिकोण से समूहों का अध्ययन करता है।[6] यह विशेष रूप से उपयोगी है जहां परिमितता धारणाएं संतुष्ट होती हैं, उदाहरण के लिए सूक्ष्म रूप से उत्पन्न समूह, या सूक्ष्म रूप से प्रस्तुत समूह (अर्थात इसके अतिरिक्त संबंध परिमित हैं)। क्षेत्र अपने मौलिक समूहों के माध्यम से रेखांकन (असतत गणित) के संबंध का उपयोग करता है। उदाहरण के लिए, कोई दिखा सकता है कि मुक्त समूह का प्रत्येक उपसमूह निःशुल्क है।
किसी समूह को उसकी प्रस्तुति द्वारा देने से कई स्वाभाविक प्रश्न उत्पन्न होते हैं। समूहों के लिए शब्द समस्या पूछती है कि क्या दो शब्द प्रभावी रूप से एक ही समूह तत्व हैं। समस्या को ट्यूरिंग मशीन से संबंधित करके, कोई दिखा सकता है कि सामान्य रूप से इस कार्य को समाधान करने वाला कोई कलन विधि नहीं है। एक और, सामान्यतः कठिन, एल्गोरिदमिक रूप से अघुलनशील समस्या समूह समरूपता समस्या है, जो पूछती है कि क्या भिन्न -भिन्न प्रस्तुतियों द्वारा दिए गए दो समूह वास्तव में समरूप हैं। उदाहरण के लिए, प्रस्तुति वाला समूह पूर्णांकों के योज्य समूह Z के लिए समरूपी है, चूंकि यह तुरंत स्पष्ट नहीं हो सकता है। (लिख रहे हैं , किसी के पास )
ज्यामितीय समूह सिद्धांत इन समस्याओं पर एक ज्यामितीय दृष्टिकोण से आक्रमण करता है, या तो समूहों को ज्यामितीय वस्तुओं के रूप में देखकर, या उपयुक्त ज्यामितीय वस्तुओं को ढूंढकर एक समूह कार्य करता है।[7] पहले विचार को केली रेखांकन के माध्यम से सटीक बनाया गया है, जिसका शिखर समूह तत्वों के अनुरूप है और किनारे समूह में सही गुणन के अनुरूप हैं। दो तत्वों को देखते हुए, तत्वों के बीच न्यूनतम पथ की लंबाई द्वारा दिए गए शब्द मीट्रिक का निर्माण करता है। जॉन मिल्नोर और स्वार्क का एक प्रमेय तब कहता है कि एक समूह जी को एक मीट्रिक स्थान X पर उचित उपाय से कार्य करने के लिए दिया जाता है, उदाहरण के लिए एक सघन कई गुना, तो जी अर्ध-सममिति है। अर्ध-सममितीय (यानी दूरी से समान दिखता है) अंतरिक्ष एक्स.
समूहों और समरूपता का संबंध
किसी भी प्रकार की एक संरचित वस्तु X को देखते हुए, एक समरूपता उस वस्तु का मानचित्रण है जो संरचना को संरक्षित करती है। यह कई स्थितियों में होता है, उदाहरण के लिए
- यदि X बिना किसी अतिरिक्त संरचना के एक समूह है, तो एक समरूपता क्रमपरिवर्तन समूहों को जन्म देने के लिए समूह से ही एक आक्षेप मानचित्र है।
- यदि विषय X अपनी मीट्रिक (गणित) संरचना या किसी अन्य मीट्रिक स्थान के साथ समतल में बिंदुओं का एक समूह है, तो एक समरूपता समूह का एक आक्षेप है जो बिंदुओं के प्रत्येक जोड़े (एक आइसोमेट्री) के बीच की दूरी को संरक्षित करता है। संबंधित समूह को X का आइसोमेट्री समूह कहा जाता है।
- यदि इसके अतिरिक्त कोणों को संरक्षित रखा जाता है, तो अनुरूप मानचित्रों की बात की जाती है। उदाहरण के लिए, अनुरूप मानचित्र क्लेनियन समूहों को जन्म देते हैं।
- समरूपता केवल ज्यामितीय वस्तुओं तक ही सीमित नहीं है, बल्कि इसमें बीजगणितीय वस्तुएँ भी सम्मिलित हैं। उदाहरण के लिए, समीकरण दो उपाय हैं तथा . इस स्थिति में, वह समूह जो दो जड़ों का आदान-प्रदान करता है, समीकरण से संबंधित गैलोज़ समूह है। एक चर में प्रत्येक बहुपद समीकरण में गैलोइस समूह होता है, जो इसकी जड़ों पर एक निश्चित क्रमचय समूह होता है।
एक समूह के स्वयंसिद्ध समरूपता के आवश्यक पहलुओं को औपचारिक रूप देते हैं। समरूपता एक समूह बनाती है: वे बंद (गणित) हैं क्योंकि यदि आप किसी वस्तु की समरूपता लेते हैं, और फिर दूसरी समरूपता लागू करते हैं, तो परिणाम अभी भी समरूपता होगा। वस्तु को स्थिर रखने वाली पहचान हमेशा वस्तु की समरूपता होती है। समरूपता को पूर्ववत करके व्युत्क्रमों के अस्तित्व की गारंटी दी जाती है और साहचर्य इस तथ्य से आता है कि समरूपता एक स्थान पर कार्य करती है, और कार्यों की संरचना साहचर्य है।
फ्रूच की प्रमेय कहती है कि प्रत्येक समूह किसी न किसी रेखांकन (असतत गणित) का सममिति समूह है। इसलिए प्रत्येक अमूर्त समूह वास्तव में किसी स्पष्ट वस्तु की सममिति है।
किसी श्रेणी (गणित) में काम करके किसी वस्तु की संरचना को संरक्षित करने की कहावत को सटीक बनाया जा सकता है। संरचना को संरक्षित करने वाले मानचित्र तब आकारिकी होते हैं, और समरूपता समूह प्रश्न में वस्तु का ऑटोमोर्फिज़्म समूह होता है।
समूह सिद्धांत के अनुप्रयोग
समूह सिद्धांत के अनुप्रयोग आवश्यक हैं।अमूर्त बीजगणित में लगभग सभी संरचनाएं समूहों के विशेष मामले हैं। अंगूठी (गणित), उदाहरण के लिए, एक दूसरे संचालन (गुणन के अनुरूप) के साथ एबेलियन समूहों (जोड़ के अनुरूप) के रूप में देखा जा सकता है। इसलिए, समूह सैद्धांतिक तर्क उन संस्थाओं के सिद्धांत के बड़े हिस्से को रेखांकित करते हैं।
गैलोइस सिद्धांत
गैलोज़ सिद्धांत एक बहुपद की जड़ों की समरूपता का वर्णन करने के लिए समूहों का उपयोग करता है (या अधिक सटीक रूप से इन जड़ों द्वारा उत्पन्न बीजगणित के ऑटोमोर्फिज़्म)। गैलोज़ सिद्धांत का मौलिक प्रमेय बीजगणितीय क्षेत्र विस्तार और समूह सिद्धांत के बीच एक कड़ी प्रदान करता है। यह संबंधित गैलोज़ समूह की घुलनशीलता के संदर्भ में बहुपद समीकरणों की विलेयता के लिए एक प्रभावी मानदंड देता है। उदाहरण के लिए, 5 तत्वों में सममित समूह, समाधान करने योग्य नहीं है जिसका अर्थ है कि सामान्य क्विंटिक समीकरण को रेडिकल्स द्वारा कम डिग्री के समीकरणों के उपाय से समाधान नहीं किया जा सकता है। सिद्धांत, समूह सिद्धांत की ऐतिहासिक जड़ों में से एक होने के नाते, वर्ग क्षेत्र सिद्धांत जैसे क्षेत्रों में नए परिणाम प्राप्त करने के लिए अभी भी उपयोगी रूप से लागू किया जाता है।
बीजगणितीय सांस्थिति
बीजगणितीय सांस्थिति एक अन्य डोमेन है जो सिद्धांत में रुचि रखने वाली वस्तुओं के समूहों को प्रमुखता से कार्य करता है। वहां, समूहों का उपयोग सांस्थितिक रिक्त स्थान के कुछ आविष्कारों का वर्णन करने के लिए किया जाता है। उन्हें अपरिवर्तनीय कहा जाता है क्योंकि उन्हें इस प्रकार से परिभाषित किया जाता है कि यदि अंतरिक्ष कुछ होमोमोर्फिज्म के अधीन है तो वे नहीं बदलते हैं। उदाहरण के लिए, मूलभूत समूह गणना करता है कि अंतरिक्ष में कितने पथ अनिवार्य रूप से भिन्न हैं। त्वरित पेरेलमैन द्वारा 2002/2003 में सिद्ध किया गया पॉइंकेयर अनुमान, इस विचार का एक प्रमुख अनुप्रयोग है। चूंकि प्रभाव एकदिशीय नहीं है। उदाहरण के लिए, बीजगणितीय सांस्थिति ईलेनबर्ग-मैकलेन रिक्त स्थान का उपयोग करती है जो निर्धारित होमोटॉपी समूहों के साथ रिक्त स्थान हैं। इसी प्रकार बीजगणितीय के-सिद्धांत एक तरह से समूहों के रिक्त स्थान को वर्गीकृत करने पर निर्भर करता है। अंत में, अनंत समूह के मरोड़ वाले उपसमूह का नाम समूह सिद्धांत में सांस्थिति की विरासत को दर्शाता है।
बीजगणितीय ज्यामिति
बीजगणितीय ज्यामिति इसी प्रकार कई तरह से समूह सिद्धांत का उपयोग करती है। एबेलियन किस्म को ऊपर दर्शाया गया है। समूह संचालन की उपस्थिति से अतिरिक्त जानकारी मिलती है जो इन किस्मों को विशेष रूप से सुलभ बनाती है। वे प्रायः नए अनुमानों के लिए एक परीक्षण के रूप में भी काम करते हैं। (उदाहरण के लिए हॉज अनुमान (कुछ स्थितियों में)।) एक आयामी स्थिति, अर्थात् अण्डाकार वक्रों का विशेष विस्तार से अध्ययन किया जाता है। वे दोनों सैद्धांतिक और व्यावहारिक रूप से कठिन हैं।[8] एक अन्य दिशा में, टोरिक प्रकार बीजगणितीय विविधता है जो एक टोरस्र्स द्वारा कार्य करती है। टोरॉयडल एम्बेडिंग ने हाल ही में बीजगणितीय ज्यामिति में प्रगति की है, विशेष रूप से एकवचन के संकल्प में।[9]
बीजगणितीय संख्या सिद्धांत
बीजगणितीय संख्या सिद्धांत कुछ महत्वपूर्ण अनुप्रयोगों के लिए समूहों का उपयोग करता है। उदाहरण के लिए, यूलर का उत्पाद सूत्र,
अंकगणित के मौलिक प्रमेय को पकड़ता है कि कोई भी पूर्णांक अभाज्य संख्या में एक अनोखे उपाय से विघटित होता है। अधिक सामान्य छल्लों के लिए इस कथन की विफलता वर्ग समूहों और नियमित अभाज्य संख्या को जन्म देती है, जो अर्न्स्ट कुमेर | कुमेर द्वारा फ़र्मेट की अंतिम प्रमेय के उपचार में दिखाई देती है।
हार्मोनिक विश्लेषण
लाई समूहों और कुछ अन्य समूहों पर विश्लेषण को हार्मोनिक विश्लेषण कहा जाता है। हार उपाय, यानी, लाई समूह में अनुवाद के अनुसार अभिन्न अंग, स्वरूप पहचान और अन्य छवि प्रसंस्करण तकनीकों के लिए उपयोग किए जाते हैं।[10]
साहचर्य
साहचर्य में, क्रमचय समूह की धारणा और समूह क्रिया की अवधारणा का उपयोगप्रायः वस्तुओं के एक समूह की गिनती को आसान बनाने के लिए किया जाता है; विशेष रूप से बर्नसाइड लेम्मा देखें।
संगीत
पंचम के घेरे में 12-आवधिक समूह की उपस्थिति समूह सिद्धांत (संगीत) में प्राथमिक समूह सिद्धांत के अनुप्रयोगों को उत्पन्न करती है। परिवर्तनकारी सिद्धांत एक गणितीय समूह के तत्वों के रूप में संगीत परिवर्तन को मॉडल करता है।
भौतिकी
भौतिकी में, समूह महत्वपूर्ण हैं क्योंकि वे समरूपता का वर्णन करते हैं जो कि भौतिकी के नियमों का पालन करते हैं। नोएदर के प्रमेय के अनुसार, भौतिक प्रणाली की प्रत्येक निरंतर समरूपता प्रणाली के एक संरक्षण कानून (भौतिकी) से मेल खाती है। भौतिक विज्ञानी समूह अभ्यावेदन में बहुत रुचि रखते हैं, विशेष रूप से लाई समूहों में, क्योंकि ये अभ्यावेदन प्रायः संभावित भौतिक सिद्धांतों के मार्ग को संकेत करते हैं। भौतिकी में समूहों के उपयोग के उदाहरणों में मानक मॉडल, गेज सिद्धांत, लोरेंत्ज़ समूह और पॉइनकेयर समूह सम्मिलित हैं।
योशिय्याह विलार्ड गिब्स द्वारा विकसित यांत्रिकी की सांख्यिकीय व्याख्याओं की अपूर्णता को समाधान करने के लिए समूह सिद्धांत का उपयोग किया जा सकता है, जो एक सार्थक समाधान प्राप्त करने के लिए अनंत संख्या की संभावनाओं के योग से संबंधित है।[11]
रसायन विज्ञान और सामग्री विज्ञान
रसायन विज्ञान और सामग्री विज्ञान में, बिंदु समूहों का उपयोग नियमित पॉलीहेड्रा, और आणविक समरूपता और अंतरिक्ष समूहों को क्रिस्टल संरचनाओं को वर्गीकृत करने के लिए किया जाता है। समर्पित किए गए समूहों का उपयोग तब भौतिक गुणों (जैसे कि रासायनिक ध्रुवीयता और दाहिनी ओर(रसायन विज्ञान)), स्पेक्ट्रोस्कोपिक गुणों (विशेष रूप से रमन स्पेक्ट्रोस्कोपी, अवरक्त स्पेक्ट्रोस्कोपी, वृत्ताकार द्वैतवाद स्पेक्ट्रोस्कोपी, चुंबकीय वृत्ताकार द्वैतवाद स्पेक्ट्रोस्कोपी, UVविज़ स्पेक्ट्रोस्कोपी, और के लिए उपयोगी) को निर्धारित करने के लिए किया जा सकता है। प्रतिदीप्ति स्पेक्ट्रोस्कोपी), और आणविक कक्षाओं का निर्माण करने के लिए।
आणविक समरूपता यौगिकों के कई भौतिक और स्पेक्ट्रोस्कोपिक गुणों के लिए उत्तरदायित्व है और रासायनिक प्रतिक्रियाएं कैसे होती हैं, इसके बारे में प्रासंगिक जानकारी प्रदान करती है। किसी दिए गए अणु के लिए एक बिंदु समूह निर्दिष्ट करने के लिए, उस पर उपस्थित समरूपता संक्रियाओं के समूह को खोजना आवश्यक है। समरूपता संक्रिया एक क्रिया है, जैसे अक्ष के चारों ओर घूमना या दर्पण तल के माध्यम से प्रतिबिंब। दूसरे शब्दों में, यह एक संक्रिया है जो अणु को इस प्रकार गतिमान करती है कि यह मूल विन्यास से अप्रभेद्य है। समूह सिद्धांत में, घूर्णन कुल्हाड़ियों और दर्पण तलों को समरूपता तत्व कहा जाता है। ये तत्व एक बिंदु, रेखा या समतल हो सकते हैं जिसके संबंध में सममिति संक्रिया की जाती है। एक अणु की समरूपता संचालन इस अणु के लिए विशिष्ट बिंदु समूह निर्धारित करता है।
रसायन विज्ञान में, पाँच महत्वपूर्ण सममिति संक्रियाएँ हैं। वे पहचान ऑपरेशन (ई), रोटेशन ऑपरेशन या उचित रोटेशन (Cn), प्रतिबिंब ऑपरेशन (σ), उलटा (i) और रोटेशन प्रतिबिंब ऑपरेशन या अनुचित रोटेशन (Sn). पहचान संक्रिया (E) में अणु को उसी रूप में छोड़ना सम्मिलित है। यह किसी भी अक्ष के चारों ओर पूर्ण घुमावों की संख्या के बराबर है। यह सभी अणुओं की एक समरूपता है, जबकि चिरल अणु के समरूपता समूह में केवल पहचान संक्रिया होती है। एक पहचान संक्रिया प्रत्येक अणु की एक विशेषता है, भले ही इसमें कोई समरूपता न हो। अक्ष के चारों ओर घूमना (Cn) एक विशिष्ट अक्ष के चारों ओर एक विशिष्ट कोण से अणु को घुमाने के होते हैं। यह 360°/n कोण के माध्यम से घूर्णन है, जहां n एक पूर्णांक है, घूर्णन अक्ष के बारे में। उदाहरण के लिए, यदि एक पानी का अणु उस अक्ष के चारों ओर 180° घूमता है जो ऑक्सीजन परमाणु से होकर गुजरता है और हाइड्रोजन परमाणुओं के बीच होता है, तो यह उसी विन्यास में होता है जैसे यह प्रारभ्म हुआ था। इस स्थिति में, n = 2, क्योंकि इसे दो बार लगाने से पहचान ऑपरेशन उत्पन्न होता है। एक से अधिक रोटेशन अक्ष वाले अणुओं में, Cn n का सबसे बड़ा मान रखने वाली धुरी उच्चतम क्रम रोटेशन अक्ष या प्रमुख अक्ष है। उदाहरण के लिए बोरॉन ट्राइफ्लोराइड (BF3), घूर्णन अक्ष का उच्चतम क्रम C3 है, इसलिए घूर्णन का मुख्य अक्ष C3 हैI.
परावर्तन संक्रिया (σ) में कई अणुओं में दर्पण तल होते हैं, चूंकि वे स्पष्ट नहीं हो सकते हैं। प्रतिबिंब ऑपरेशन बाएं और दाएं का आदान-प्रदान करता है, जैसे कि प्रत्येक बिंदु विमान के माध्यम से लंबवत रूप से उस स्थिति में चला गया हो, जब वह शुरू हुआ था। जब तल घूर्णन के मुख्य अक्ष के लंबवत होता है, तो इसे σ कहा जाता हैh(क्षैतिज)। अन्य तल, जिनमें घूर्णन का मुख्य अक्ष होता है, को लंबवत (σv) या डायहेड्रल (σd).
व्युत्क्रम (i) एक अधिक जटिल संक्रिया है। प्रत्येक बिंदु अणु के केंद्र के माध्यम से मूल स्थिति के विपरीत स्थिति में और केंद्रीय बिंदु से जहां से शुरू हुआ था, वहां तक जाता है। कई अणु जो पहली नज़र में उलटा केंद्र रखते हैं, ऐसा नहीं है; उदाहरण के लिए, मीथेन और अन्य चतुर्पाश्वीय अणुओं में व्युत्क्रम समरूपता का अभाव होता है। इसे देखने के लिए, एक मीथेन मॉडल को दाईं ओर ऊर्ध्वाधर तल में दो हाइड्रोजन परमाणुओं और बाईं ओर क्षैतिज तल में दो हाइड्रोजन परमाणुओं के साथ पकड़ें। व्युत्क्रमण के परिणामस्वरूप दाहिनी ओर क्षैतिज तल में दो हाइड्रोजन परमाणु और बाईं ओर ऊर्ध्वाधर तल में दो हाइड्रोजन परमाणु होते हैं। उलटा इसलिए मीथेन का समरूपता ऑपरेशन नहीं है, क्योंकि उलटा ऑपरेशन के बाद अणु का उन्मुखीकरण मूल अभिविन्यास से भिन्न होता है। और अंतिम ऑपरेशन अनुचित रोटेशन या रोटेशन प्रतिबिंब ऑपरेशन (Sn) को 360°/n घुमाने की ज़रूरत होती है, इसके बाद रोटेशन की धुरी के लम्बवत् तल से परावर्तन होता है।
क्रिप्टोग्राफी

अण्डाकार सार्वजनिक कुंजी क्रिप्टोग्राफी में निर्मित प्रधान क्रम के बहुत बड़े समूह सार्वजनिक-कुंजी क्रिप्टोग्राफी के लिए काम करते हैं। इस क्रम के क्रिप्टोग्राफ़िक उपाय ज्यामितीय वस्तुओं के लचीलेपन से लाभान्वित होते हैं, इसलिए उनकी समूह संरचनाएँ, इन समूहों की जटिल संरचना के साथ मिलकर, असतत लघुगणक की गणना करना बहुत कठिन बना देती हैं। जल्द से जल्द कूटलेखन प्रोटोकॉल में से एक, सीज़र सिफर | सीज़र का सिफर, को एक (बहुत आसान) समूह ऑपरेशन के रूप में भी व्याख्या किया जा सकता है। अधिकांश क्रिप्टोग्राफ़िक योजनाएँ किसी न किसी रूप में समूहों का उपयोग करती हैं। विशेष रूप से डिफी-हेलमैन कुंजी लेन देन परिमित चक्रीय समूहों का उपयोग करता है। इसलिए समूह-आधारित क्रिप्टोग्राफी शब्द अधिकतर क्रिप्टोग्राफ़िक प्रोटोकॉल को संदर्भित करता है जो अनंत अविश्वासी समूहों जैसे ब्रैड समूह का उपयोग करता है।
यह भी देखें
टिप्पणियाँ
- ↑ Elwes, Richard (December 2006), "An enormous theorem: the classification of finite simple groups", Plus Magazine (41), archived from the original on 2009-02-02, retrieved 2011-12-20
- ↑ This process of imposing extra structure has been formalized through the notion of a group object in a suitable category. Thus Lie groups are group objects in the category of differentiable manifolds and affine algebraic groups are group objects in the category of affine algebraic varieties.
- ↑ Such as group cohomology or equivariant K-theory.
- ↑ In particular, if the representation is faithful.
- ↑ Arthur Tresse (1893), "Sur les invariants différentiels des groupes continus de transformations", Acta Mathematica, 18: 1–88, doi:10.1007/bf02418270
- ↑ Schupp & Lyndon 2001
- ↑ La Harpe 2000
- ↑ See the Birch and Swinnerton-Dyer conjecture, one of the millennium problems
- ↑ Abramovich, Dan; Karu, Kalle; Matsuki, Kenji; Wlodarczyk, Jaroslaw (2002), "Torification and factorization of birational maps", Journal of the American Mathematical Society, 15 (3): 531–572, arXiv:math/9904135, doi:10.1090/S0894-0347-02-00396-X, MR 1896232, S2CID 18211120
- ↑ Lenz, Reiner (1990), Group theoretical methods in image processing, Lecture Notes in Computer Science, vol. 413, Berlin, New York: Springer-Verlag, doi:10.1007/3-540-52290-5, ISBN 978-0-387-52290-6, S2CID 2738874
- ↑ Norbert Wiener, Cybernetics: Or Control and Communication in the Animal and the Machine, ISBN 978-0262730099, Ch 2
संदर्भ
- Borel, Armand (1991), Linear algebraic groups, Graduate Texts in Mathematics, vol. 126 (2nd ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-0941-6, ISBN 978-0-387-97370-8, MR 1102012
- Carter, Nathan C. (2009), Visual group theory, Classroom Resource Materials Series, Mathematical Association of America, ISBN 978-0-88385-757-1, MR 2504193
- Cannon, John J. (1969), "Computers in group theory: A survey", Communications of the ACM, 12: 3–12, doi:10.1145/362835.362837, MR 0290613, S2CID 18226463
- Frucht, R. (1939), "Herstellung von Graphen mit vorgegebener abstrakter Gruppe", Compositio Mathematica, 6: 239–50, ISSN 0010-437X, archived from the original on 2008-12-01
- Golubitsky, Martin; Stewart, Ian (2006), "Nonlinear dynamics of networks: the groupoid formalism", Bull. Amer. Math. Soc. (N.S.), 43 (3): 305–364, doi:10.1090/S0273-0979-06-01108-6, MR 2223010 Shows the advantage of generalising from group to groupoid.
- Judson, Thomas W. (1997), Abstract Algebra: Theory and Applications An introductory undergraduate text in the spirit of texts by Gallian or Herstein, covering groups, rings, integral domains, fields and Galois theory. Free downloadable PDF with open-source GFDL license.
- Kleiner, Israel (1986), "The evolution of group theory: a brief survey", Mathematics Magazine, 59 (4): 195–215, doi:10.2307/2690312, ISSN 0025-570X, JSTOR 2690312, MR 0863090
- La Harpe, Pierre de (2000), Topics in geometric group theory, University of Chicago Press, ISBN 978-0-226-31721-2
- Livio, M. (2005), The Equation That Couldn't Be Solved: How Mathematical Genius Discovered the Language of Symmetry, Simon & Schuster, ISBN 0-7432-5820-7 Conveys the practical value of group theory by explaining how it points to symmetries in physics and other sciences.
- Mumford, David (1970), Abelian varieties, Oxford University Press, ISBN 978-0-19-560528-0, OCLC 138290
- Ronan M., 2006. Symmetry and the Monster. Oxford University Press. ISBN 0-19-280722-6. For lay readers. Describes the quest to find the basic building blocks for finite groups.
- Rotman, Joseph (1994), An introduction to the theory of groups, New York: Springer-Verlag, ISBN 0-387-94285-8 A standard contemporary reference.
- Schupp, Paul E.; Lyndon, Roger C. (2001), Combinatorial group theory, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41158-1
- Scott, W. R. (1987) [1964], Group Theory, New York: Dover, ISBN 0-486-65377-3 Inexpensive and fairly readable, but somewhat dated in emphasis, style, and notation.
- Shatz, Stephen S. (1972), Profinite groups, arithmetic, and geometry, Princeton University Press, ISBN 978-0-691-08017-8, MR 0347778
- Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38, Cambridge University Press, ISBN 978-0-521-55987-4, MR 1269324, OCLC 36131259
बाहरी संबंध
- History of the abstract group concept
- Higher dimensional group theory This presents a view of group theory as level one of a theory that extends in all dimensions, and has applications in homotopy theory and to higher dimensional nonabelian methods for local-to-global problems.
- Plus teacher and student package: Group Theory This package brings together all the articles on group theory from Plus, the online mathematics magazine produced by the Millennium Mathematics Project at the University of Cambridge, exploring applications and recent breakthroughs, and giving explicit definitions and examples of groups.
- Burnside, William (1911), , in Chisholm, Hugh (ed.), Encyclopædia Britannica (in English), vol. 12 (11th ed.), Cambridge University Press, pp. 626–636 This is a detailed exposition of contemporaneous understanding of Group Theory by an early researcher in the field.