वीन ब्रिज दोलक: Difference between revisions
No edit summary |
No edit summary |
||
| (44 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Wien Bridge Oscillator.png|right|thumb|300px| | [[File:Wien Bridge Oscillator.png|right|thumb|300px|दोलक के इस संस्करण में, Rb छोटा तपित दीपक है। सामान्यतः R1 = R2 = R और C1 = C2 = C है। सामान्य ऑपरेशन में, Rb स्वयं उस बिंदु तक गर्म होता है जहां इसका प्रतिरोध Rf/2 है।]]'''वीन ब्रिज दोलक''' ऐसा [[इलेक्ट्रॉनिक थरथरानवाला|इलेक्ट्रॉनिक दोलक]] है जो साइन वेव्स उत्पन्न करता है। यह [[आवृत्तियों]] की बड़ी श्रृंखला उत्पन्न कर सकता है। दोलक [[ब्रिज सर्किट|ब्रिज]] परिपथ पर आधारित है जिसे मूल रूप से 1891 में [[मैक्स वियना]] द्वारा [[विद्युत प्रतिबाधा]] के मापन के लिए विकसित किया गया था।<ref>{{Harvnb|Wien|1891}}</ref> | ||
[[वीन ब्रिज]] में चार प्रतिरोधक और दो [[ संधारित्र ]] होते हैं। | [[वीन ब्रिज]] में चार प्रतिरोधक और दो [[ संधारित्र |संधारित्र]] होते हैं। दोलक भी सकारात्मक प्रतिक्रिया प्रदान करता है कि[[ बंदपास छननी | बैंडपास फिल्टर]] के साथ संयुक्त सकारात्मक लाभ प्रवर्धक के रूप में देखा जा सकता है। स्वत: लाभ नियंत्रण, निश्चयपूर्वक अन्य-रैखिकता और आकस्मिक अन्य-रैखिकता दोलक के विभिन्न कार्यान्वयन में आउटपुट आयाम को सीमित करती है। | ||
दाईं ओर दिखाया गया परिपथ | दाईं ओर दिखाया गया परिपथ तपित दीपक का उपयोग करके स्वत: लाभ नियंत्रण के साथ, दोलक के सामान्य कार्यान्वयन को दर्शाता है। नियम के अनुसार है कि R<sub>1</sub>= R<sub>2</sub>= R और C<sub>1</sub>= C<sub>2</sub>=C, दोलन की आवृत्ति द्वारा दी गई है: | ||
<math>f_{hz}=\frac{1}{2 \pi R C}</math> | <math>f_{hz}=\frac{1}{2 \pi R C}</math> | ||
और स्थिर दोलन की स्थिति इसके द्वारा दी गई है | और स्थिर दोलन की स्थिति इसके द्वारा दी गई है: | ||
<math>R_b = \frac {R_f} {2} </math> | <math>R_b = \frac {R_f} {2} </math> | ||
== पृष्ठभूमि == | == पृष्ठभूमि == | ||
1930 के दशक में | 1930 के दशक में दोलक को उत्तम बनाने के लिए अनेक प्रयास किए गए हैं। रैखिकता को महत्वपूर्ण माना गया है। प्रतिरोध-स्थिर दोलक समायोज्य प्रतिक्रिया रोकनेवाला था; उस अवरोधक को व्यस्थापित किया जाएगा जिससे कि दोलक प्रारंभ हो जाए (इस प्रकार लूप लाभ को मात्र एकता पर व्यस्थापित करना)। दोलन तब तक होगा जब तक कि वैक्यूम ट्यूब का ग्रिड धारा का संचालन प्रारंभ नहीं कर देता, जिससे हानि बढ़ जाती है, और आउटपुट आयाम सीमित हो जाता है।<ref>{{harvnb|Terman|1933}}</ref><ref>{{harvnb|Terman|1935|pp=283–289}}</ref><ref>{{harvnb|Terman|1937|pp=371–372}}</ref> स्वचालित आयाम नियंत्रण का परिक्षण किया गया।<ref>{{harvnb|Arguimbau|1933}}</ref><ref>{{harvnb|Groszkowski|1934}}</ref> [[फ्रेडरिक टर्मन]] कहते हैं, किसी भी सामान्य दोलक की आवृत्ति स्थिरता और तरंग-आकार के रूप को सभी परिस्थितियों में स्थिर दोलनों के आयाम को बनाए रखने के लिए स्वचालित-आयाम-नियंत्रण व्यवस्था का उपयोग करके संशोधन किया जा सकता है।<ref>{{harvnb|Terman|1937|p=370}}</ref> | ||
1937 में, लारेड मेचम ने ब्रिज दोलक में स्वत: लाभ नियंत्रण के लिए फिलामेंट लैंप का उपयोग करने का वर्णन किया।<ref>{{harvnb|Meacham|1939}}</ref><ref name="Meacham 1938">{{Harvnb|Meacham|1938}}</ref> | |||
इसके अतिरिक्त 1937 में, [[हेर्मोन होस्मर स्कॉट]] ने वीन ब्रिज सहित विभिन्न ब्रिजों पर आधारित ऑडियो दोलक का वर्णन किया।<ref>{{harvnb|Scott|1939}}</ref><ref>{{harvnb|Scott|1938}}</ref> | |||
[[स्टैनफोर्ड विश्वविद्यालय]] में टरमन, नकारात्मक प्रतिक्रिया पर [[हेरोल्ड स्टीफन ब्लैक]] के कार्य में रुचि रखते थे,<ref>{{harvnb|Black|1934a}}</ref><ref>{{harvnb|Black|1934b}}</ref> इसलिए उन्होंने नकारात्मक प्रतिक्रिया पर स्नातक संगोष्ठी आयोजित की।<ref>{{harvnb|HP|2002}}</ref> [[बिल हेवलेट]] ने सेमिनार में भाग लिया। संगोष्ठी के समय स्कॉट का फरवरी 1938 का दोलक पेपर निकला। यहाँ टरमन द्वारा स्मरण है:<ref>{{harvnb|Sharpe|n.d.}}</ref> | |||
:फ्रेड टर्मन बताते हैं: स्टैनफोर्ड में अभियांत्रिक की डिग्री की आवश्यकताओं को पूर्ण करने के लिए बिल को थीसिस तत्पर करनी पड़ी। उस समय मैंने अपने स्नातक संगोष्ठी का पूर्ण चौथाई 'नकारात्मक प्रतिक्रिया' के विषय में समर्पित करने का निर्णय लिया था, मुझे इस तत्कालीन नई प्रौद्योगिक में रूचि हो गई थी क्योंकि ऐसा लगता था कि इसमें अनेक उपयोगी चीजें करने की अधिक संभावनाएं हैं। मैं नकारात्मक प्रतिक्रिया पर विचार किए गए कुछ अनुप्रयोगों पर रिपोर्ट करूंगा, जिनके विषय में मैंने सोचा था, और लड़के वर्तमान के लेख पढ़ेंगे और वर्तमान विकास पर एक-दूसरे को रिपोर्ट करेंगे। यह संगोष्ठी अभी उत्तम प्रकार से प्रारंभ हुई थी जब पेपर निकला जो मुझे रोचक लगा। यह जनरल रेडियो के व्यक्ति द्वारा किया गया था और निश्चित-आवृत्ति ऑडियो दोलक से समाधान किया गया था जिसमें आवृत्ति को प्रतिरोध-संधारित्र नेटवर्क द्वारा नियंत्रित किया गया था, और पुश-बटन के माध्यम से परिवर्तित कर दिया गया था। नकारात्मक प्रतिक्रिया के सरल अनुप्रयोग द्वारा दोलन प्राप्त किए गए थे। | |||
जून 1938 में, टर्मन, आर.आर. बस, हेवलेट और एफ.सी. काहिल ने न्यूयॉर्क में आईआरइ (IRE) कन्वेंशन में नकारात्मक प्रतिक्रिया के विषय में प्रस्तुति दी; अगस्त 1938 में, पोर्टलैंड, ओआर (OR) में आईआरइ (IRE) पैसिफिक कोस्ट कन्वेंशन में दूसरी प्रस्तुति हुई; प्रस्तुति आईआरइ (IRE) पेपर बन गई।<ref>{{harvnb|Terman|Buss|Hewlett|Cahill|1939}}</ref> विषय वीन ब्रिज दोलक में आयाम नियंत्रण था। दोलक पोर्टलैंड में प्रदर्शित किया गया था।<ref>{{harvnb|Sharpe|n.d.|p=???}}{{page needed|date=November 2015}}; Packard remembers first demonstration of the 200A in Portland.</ref> हेवलेट, [[डेविड पैकर्ड]] के साथ, [[हेवलेट पैकर्ड]] की सह-स्थापना की, और हेवलेट-पैकर्ड का प्रथम उत्पाद [[HP200A]] था, जो त्रुटिहीन वीन ब्रिज दोलक था। प्रथम बिक्री जनवरी 1939 में हुई थी।<ref>{{harvnb|Sharpe|n.d.|p=xxx}}{{page needed|date=November 2015}}</ref> | |||
हेवलेट के जून 1939 के अभियांत्रिक की डिग्री थीसिस ने वीन ब्रिज दोलक के आयाम को नियंत्रित करने के लिए दीपक का उपयोग किया।<ref>{{harvtxt|Williams|1991|p=46}} states, "Hewlett may have adapted this technique from Meacham, who published it in 1938 as a way to stabilize a quartz crystal oscillator. Meacham's paper, "The Bridge Stabilized Oscillator," is in reference number five in Hewlett's thesis."</ref> हेवलेट के दोलक स्थिर आयाम और अल्प [[विरूपण]] के साथ साइनसोइडल आउटपुट का उत्पादन करता है।<ref>{{Harvnb|Hewlett|1942}}</ref><ref>{{Harvnb|Williams|1991|pp=46–47}}</ref> | |||
=== स्वचालित लाभ नियंत्रण के बिना दोलक === | |||
[[File:Wien Bridge Oscillator with diode limiting.png|right|thumb|300px|आयाम को नियंत्रित करने के लिए डायोड का उपयोग करने वाले वीन ब्रिज दोलक योजनाबद्ध होते हैं। यह परिपथ सामान्यतः 1-5% की सीमा में कुल हार्मोनिक विरूपण उत्पन्न करता है, यह इस विषय पर निर्भर करता है कि इसे कितनी सावधानी से पृथक किया जाता है।]]पारंपरिक दोलक परिपथ को इस प्रकार डिज़ाइन किया गया है कि यह दोलन (स्टार्ट अप) करना प्रारंभ कर देगा और इसका आयाम नियंत्रित हो जाएगा। | |||
एम्पलीफायर आउटपुट में नियंत्रित संपीड़न जोड़ने के लिए दाईं ओर दोलक डायोड का उपयोग करता है। यह 1-5% की सीमा में कुल हार्मोनिक विरूपण उत्पन्न कर सकता है, यह इस विषय पर निर्भर करता है कि इसे कितनी सावधानी से विभक्त किया जाता है।<ref name="Graeme">{{cite book |last1=Graeme |first1=Jerald G. |last2=Tobey |first2=Gene E. |last3=Huelsman |first3=Lawrence P. |year=1971 |title=परिचालन प्रवर्धक, डिजाइन और अनुप्रयोग|url=https://archive.org/details/operationalampli00grae/page/383 |url-access=registration |edition=1st |publisher=McGraw-Hill |isbn=0-07-064917-0 |pages=[https://archive.org/details/operationalampli00grae/page/383 383–385] }}</ref> | |||
=== | |||
दोलन करने के लिए रैखिक परिपथ के लिए, इसे बार्कहाउज़ेन स्थिरता मानदंड को पूर्ण करना चाहिए: इसका लूप लाभ होना चाहिए और लूप के चारों ओर चरण 360 डिग्री का पूर्णांक होना चाहिए। रैखिक दोलक सिद्धांत यह नहीं बताता है कि दोलक कैसे प्रारंभ होता है या आयाम कैसे निर्धारित होता है। रैखिक दोलक किसी भी आयाम का समर्थन कर सकता है। | |||
व्यवहार में, पाश लाभ प्रारंभ में एकता से बड़ा होता है। यादृच्छिक व्यग्रता सभी परिपथों में उपस्थित होता है, और उस व्यग्रता में से कुछ वांछित आवृत्ति के निकट होगा। लूप लाभ से अधिक आवृत्ति के आयाम को प्रत्येक बार तीव्रता से बढ़ाने की अनुमति देता है। अधिक लूप लाभ के साथ, दोलक प्रारंभ हो जाएगा। | |||
आदर्श रूप से, लूप लाभ को थोड़ा बड़ा होना चाहिए, किन्तु व्यवहार में, यह प्रायः अत्यधिक होता है। बड़ा लूप लाभ दोलक को शीघ्रता से प्रारंभ करता है। बड़ा लूप लाभ तापमान के साथ भिन्नता और ट्यून करने योग्य दोलक की वांछित आवृत्ति के लिए भी क्षतिपूर्ति करता है। दोलक प्रारंभ करने के लिए, पाश लाभ सभी संभव परिस्थितियों में से अधिक होना चाहिए। | |||
अधिक लूप लाभ का नकारात्मक पक्ष होता है। सिद्धांत रूप में, दोलक आयाम बिना सीमा के बढ़ेगा। व्यवहार में, आयाम तब तक बढ़ेगा जब तक आउटपुट कुछ सीमित कारक जैसे कि विद्युत आपूर्ति वोल्टेज (एम्पलीफायर आउटपुट आपूर्ति रेल में चलता है) या एम्पलीफायर आउटपुट वर्तमान सीमा में चलता है। सीमित करने से एम्पलीफायर का प्रभावी लाभ अल्प हो जाता है (प्रभाव को लाभ संपीड़न कहा जाता है)। स्थिर दोलक में, औसत पाश लाभ होगा। | |||
हेवलेट की थीसिस ने निम्नलिखित निष्कर्ष | चूँकि सीमित क्रिया आउटपुट वोल्टेज को स्थिर करती है, इसके दो महत्वपूर्ण प्रभाव हैं: यह हार्मोनिक विरूपण का परिचय देती है और दोलक की आवृत्ति स्थिरता को प्रभावित करती है। | ||
: अभी वर्णित प्रकार का | विरूपण की मात्रा स्टार्टअप के लिए उपयोग किए जाने वाले अतिरिक्त लूप लाभ से संबंधित है। यदि छोटे आयामों पर अत्यधिक अतिरिक्त लूप लाभ होता है, तो उच्च तात्कालिक आयामों पर लाभ में और अल्पता आनी चाहिए। अर्थात अधिक विकृति होनी चाहिए। | ||
विरूपण की मात्रा दोलन के अंतिम आयाम से भी संबंधित होती है। चूँकि एम्पलीफायर का लाभ आदर्श रूप से रैखिक है, व्यवहार में यह अरैखिक है। नॉनलाइनियर ट्रांसफर फ़ंक्शन को [[टेलर श्रृंखला]] के रूप में व्यक्त किया जा सकता है। छोटे आयामों के लिए, उच्च क्रम का नियम अधिक अल्प प्रभाव डालती हैं। बड़े आयामों के लिए, अन्य-रैखिकता का उच्चारण किया जाता है। परिणामस्वरूप, अल्प विरूपण के लिए, दोलक का आउटपुट आयाम एम्पलीफायर की गतिशील श्रृंखला का छोटा अंश होना चाहिए। | |||
=== मेचम का ब्रिज स्थिर दोलक === | |||
[[File:Meachams bridge oscillator schematic.png|thumb|300px|बेल प्रणाली टेक्निकल जर्नल, अक्टूबर 1938 में प्रकाशित मीचम ब्रिज दोलक का सरलीकृत योजनाबद्ध अचिह्नित कैपेसिटर में सिग्नल आवृत्ति पर शॉर्ट परिपथ माने जाने के लिए पर्याप्त कैपेसिटेंस होता है। वैक्यूम ट्यूब को बायस करने और लोड करने के लिए अचिह्नित प्रतिरोधों और प्रारंभ करनेवाला को उपयुक्त मान माना जाता है। इस चित्र में नोड लेबल प्रकाशन में उपस्थित नहीं हैं।]] | |||
लारेड मेचम ने 1938 में दाईं ओर दिखाए गए ब्रिज दोलक परिपथ का विवरण किया। परिपथ को अधिक उच्च आवृत्ति स्थिरता और अधिक शुद्ध साइनसोइडल आउटपुट के रूप में वर्णित किया गया था।<ref name="Meacham 1938"/> आयाम को नियंत्रित करने के लिए ट्यूब ओवरलोडिंग का उपयोग करने के अतिरिक्त, मेचम ने परिपथ प्रस्तावित किया जो लूप लाभ को एकता में व्यस्थापित करता है जबकि एम्पलीफायर अपने रैखिक क्षेत्र में होता है। मेचम के परिपथ में क्वार्ट्ज क्रिस्टल दोलक और [[ व्हीटस्टोन पुल |व्हीटस्टोन]] ब्रिज में लैंप सम्मिलित था। | |||
मेचम के परिपथ में, आवृत्ति निर्धारण घटक ब्रिज की नकारात्मक फ़ीड बैक शाखा और लाभ नियंत्रण तत्व सकारात्मक फ़ीड बैक शाखा में हैं। क्रिस्टल, Z<sub>4</sub>, श्रृंखला अनुनाद में संचालित होता है। इस प्रकार यह अनुनाद पर नकारात्मक प्रतिक्रिया को अल्प करता है। विशेष क्रिस्टल ने अनुनाद पर 114 ohms का वास्तविक प्रतिरोध प्रदर्शित किया। अनुनाद के नीचे आवृत्तियों पर, क्रिस्टल कैपेसिटिव होता है और नकारात्मक प्रतिक्रिया शाखा के लाभ में नकारात्मक चरण परिवर्तित होता है। प्रतिध्वनि से ऊपर की आवृत्तियों पर, क्रिस्टल आगमनात्मक होता है और नकारात्मक प्रतिक्रिया शाखा के लाभ में सकारात्मक चरण परिवर्तित होता है। आवृत्ति पर चरण परिवर्तित शून्य से निकलता है। जैसे ही दीपक गर्म होता है, यह सकारात्मक प्रतिक्रिया को अल्प करता है। मेचम के परिपथ में क्रिस्टल का Q 104,000 के रूप में दिया गया है। आवृत्ति से क्रिस्टल की बैंडविड्थ के छोटे से अधिक आवृत्ति पर, नकारात्मक प्रतिक्रिया शाखा लूप लाभ पर आच्छादित होती है और क्रिस्टल की संकीर्ण बैंडविड्थ के अतिरिक्त कोई आत्मनिर्भर दोलन नहीं हो सकता है। | |||
1944 में (हेवलेट के डिजाइन के पश्चात), जे. के. क्लैप ने ब्रिज को चलाने के लिए ट्रांसफॉर्मर के अतिरिक्त वैक्यूम ट्यूब फेज इन्वर्टर का उपयोग करने के लिए मेचम के परिपथ को संशोधित किया।<ref>{{harvnb|Clapp|1944a}}</ref><ref>{{harvnb|Clapp|1944b}}</ref> संशोधित मेचम दोलक क्लैप के चरण इन्वर्टर का उपयोग करता है किन्तु टंगस्टन लैंप के लिए डायोड लिमिटर को प्रतिस्थापित करता है।<ref>{{harvnb|Matthys|1992|pp=53–57}}</ref> | |||
=== हेवलेट का दोलक === | |||
[[File:Wien bridge oscillator schematic from Hewletts US patent.png|thumb|300px|हेवलेट के यूएस पेटेंट 2,268,872 से वीन ब्रिज दोलक का सरलीकृत योजनाबद्ध अचिह्नित कैपेसिटर में सिग्नल आवृत्ति पर शॉर्ट परिपथ माने जाने के लिए पर्याप्त कैपेसिटेंस होता है। वैक्यूम ट्यूबों को बायसिंग और लोड करने के लिए अचिह्नित प्रतिरोधों को उपयुक्त मान माना जाता है। इस आंकड़े में नोड लेबल और संदर्भ डिज़ाइनर पेटेंट में उपयोग किए जाने वाले समान नहीं हैं। हेवलेट के पेटेंट में संकेतित वैक्यूम ट्यूब यहां दिखाए गए ट्रायोड के अतिरिक्त पेंटोड थे।]]विलियम आर हेवलेट के वीन ब्रिज दोलक को अंतर एम्पलीफायर और वीन ब्रिज को संयोजन के रूप में माना जा सकता है, जो एम्पलीफायर आउटपुट और अंतर इनपुट के मध्य सकारात्मक प्रतिक्रिया पाश में जुड़ा हुआ है। दोलन आवृत्ति पर, ब्रिज लगभग संतुलित होता है और इसका अंतरण अनुपात अधिक अल्प होता है। [[पाश लाभ]] अधिक उच्च एम्पलीफायर लाभ और अधिक अल्प ब्रिज अनुपात का उत्पाद है।<ref name="Schilling">{{Harvnb|Schilling|Belove|1968|pp=612–614}}</ref> हेवलेट के परिपथ में, एम्पलीफायर को दो वैक्यूम ट्यूबों द्वारा कार्यान्वित किया जाता है। एम्पलीफायर का इन्वर्टिंग इनपुट ट्यूब V<sub>1</sub> का कैथोड है और नॉन-इनवर्टिंग इनपुट ट्यूब V<sub>2</sub> का कंट्रोल ग्रिड है। विश्लेषण को सरल बनाने के लिए, R<sub>1</sub>, R<sub>2</sub>, C<sub>1</sub> और C<sub>2</sub> के अतिरिक्त अन्य सभी घटकों को 1+R<sub>f</sub>/R<sub>b</sub> के लाभ और उच्च इनपुट प्रतिबाधा के साथ अन्य-इनवर्टिंग एम्पलीफायर के रूप में तत्पर किया जा सकता है। R<sub>1</sub>, R<sub>2</sub>, C<sub>1</sub> और C<sub>2</sub> बैंडपास फिल्टर बनाएं जो दोलन की आवृत्ति पर सकारात्मक प्रतिक्रिया प्रदान करने के लिए जुड़ा हो। R<sub>b</sub> स्वयं गर्म होता है और नकारात्मक प्रतिक्रिया को बढ़ाता है जो एम्पलीफायर लाभ को अल्प करता है जब तक कि बिंदु तक नहीं पहुंच जाता है कि एम्पलीफायर को चलाए बिना साइनसोइडल दोलन को बनाए रखने के लिए पर्याप्त लाभ होता है। यदि R<sub>1</sub> = R<sub>2</sub> और C<sub>1</sub> = C<sub>2</sub> फिर संतुलन पर R<sub>f</sub>/R<sub>b</sub> = 2 और एम्पलीफायर का लाभ 3 है। जब परिपथ प्रथम बार सक्रिय होता है, तो दीपक ठंडा होता है और परिपथ का लाभ 3 से अधिक होता है जो स्टार्ट अप सुनिश्चित करता है। वैक्यूम ट्यूब V1 का dc बायस धारा भी लैंप से होकर प्रवाहित होता है। यह परिपथ के संचालन के सिद्धांतों को परिवर्तित नहीं करता है, किन्तु यह संतुलन पर आउटपुट के आयाम को अल्प करता है क्योंकि पूर्वाग्रह वर्तमान दीपक के ताप का भाग प्रदान करता है। | |||
हेवलेट की थीसिस ने निम्नलिखित निष्कर्ष दिया है:<ref>{{harvnb|Hewlett|1939|p=13}}</ref> | |||
: अभी वर्णित प्रकार का प्रतिरोध-क्षमता दोलक प्रयोगशाला सेवा के लिए उपयुक्त होना चाहिए। इसमें बीट-आवृत्ति दोलक को संभालने में सरलता होती है और फिर भी इसकी कुछ हानि हैं। प्रथम विषय तो यह है कि बीट-आवृत्ति प्रकार की स्पर्धा अल्प आवृत्तियों पर स्थिरता अधिक उत्तम होती है। छोटे तापमान परिवर्तनों को सुनिश्चित करने के लिए घटकों के महत्वपूर्ण प्लेसमेंट की आवश्यकता नहीं होती है, न ही दोलक के इंटरलॉकिंग को रोकने के लिए सावधानीपूर्वक डिज़ाइन किए गए डिटेक्टर परिपथ होते हैं। इसके परिणामस्वरूप, दोलक का समग्र भार अल्प से अल्प रखा जा सकता है। तुलनीय प्रदर्शन के सामान्य रेडियो बीट-आवृत्ति दोलक के लिए 93 पाउंड के विपरीत, 1 वाट एम्पलीफायर और विद्युत की आपूर्ति सहित इस प्रकार के दोलक का वजन केवल 18 पाउंड था। आउटपुट की विकृति और स्थिरता उपलब्ध सर्वोत्तम बीट-आवृत्ति दोलक के साथ अनुकूल रूप से तुलना करती है। अंत में, इस प्रकार के दोलक को वाणिज्यिक प्रसारण रिसीवर के समान आधार पर बनाया जा सकता है, किन्तु बनाने के लिए अल्प समायोजन की आवश्कयता होती है। इस प्रकार यह आदर्श प्रयोगशाला दोलक देने के लिए अल्प व्यय के साथ प्रदर्शन की गुणवत्ता को जोड़ती है। | |||
== वीन ब्रिज == | == वीन ब्रिज == | ||
{{Main article| | {{Main article|वीन ब्रिज}} | ||
ब्रिज | ब्रिज परिपथ घटक के ज्ञात मूल्यों से तुलना करके मापने का सामान्य प्रकार था। प्रायः अज्ञात घटक को ब्रिज की भुजा में रखा जाता है, और फिर अन्य भुजाओं को समायोजित करके या वोल्टेज स्रोत की आवृत्ति को परिवर्तित करके ब्रिज को अशक्त कर दिया जाता है (देखें, उदाहरण के लिए, व्हीटस्टोन ब्रिज)। | ||
वीन | वीन ब्रिज अनेक सामान्य ब्रिज में से है।<ref>{{Harvnb|Terman|1943|p=904}}</ref> प्रतिरोध और आवृत्ति की स्थिति में संधारित्र के त्रुटिहीन माप के लिए वीन के ब्रिज का उपयोग किया जाता है।<ref>{{Harvnb|Terman|1943|p=904}} citing {{Harvnb|Ferguson|Bartlett|1928}}</ref> इसका उपयोग ऑडियो आवृत्तियों को मापने के लिए भी किया जाता था। | ||
वीन ब्रिज को | वीन ब्रिज को ''R'' या ''C'' के समान मूल्यों की आवश्यकता नहीं होती है। V<sub>out</sub> पर सिग्नल के सापेक्ष V<sub>p</sub> पर सिग्नल का चरण लगभग 90° से भिन्न होता है, जो निम्न आवृत्ति पर लगभग 90° पश्चगामी उच्च आवृत्ति पर होता है। कुछ मध्यवर्ती आवृत्ति पर, चरण परिवर्तन शून्य होगा। उस आवृत्ति पर Z<sub>1</sub> से Z<sub>2</sub> का अनुपात विशुद्ध रूप से वास्तविक (शून्य काल्पनिक भाग) होगा। यदि R<sub>b</sub> से R<sub>f</sub> के अनुपात को उसी अनुपात में समायोजित किया जाता है, तो ब्रिज संतुलित होता है और परिपथ दोलन को बनाए रख सकता है। भले ही R<sub>b</sub>/R<sub>f</sub> छोटा फेज शिफ्ट है और भले ही एम्पलीफायर के इनवर्टिंग और नॉन-इनवर्टिंग इनपुट में भिन्न-भिन्न फेज शिफ्ट हों। सदैव आवृत्ति होगी जिस पर ब्रिज की प्रत्येक शाखा का कुल चरण परिवर्तन समान होगा। यदि ''R''<sub>b</sub>/''R''<sub>f</sub> कोई फेज शिफ्ट नहीं है और एम्पलीफायरों के इनपुट का फेज शिफ्ट शून्य है तो ब्रिज संतुलित है जब:<ref>{{Harvnb|Terman|1943|p=905}}</ref> | ||
:<math>\omega^2 = {1 \over R_1 R_2 C_1 C_2}</math> और | :<math>\omega^2 = {1 \over R_1 R_2 C_1 C_2}</math> और <math> {R_f \over R_b} = {C_1 \over C_2} + {R_2 \over R_1} </math> | ||
जहां ω रेडियन आवृत्ति है। | जहां ω रेडियन आवृत्ति है। | ||
यदि कोई | यदि कोई ''R<sub>1</sub>'' = ''R''<sub>2</sub> और ''C''<sub>1</sub>= ''C''<sub>2</sub> चयन करता है, तो ''R''<sub>f</sub>= 2 ''R''<sub>b</sub> होता है। | ||
व्यवहार में, R और C के मान कभी भी बिल्कुल समान नहीं होंगे, | व्यवहार में, R और C के मान कभी भी बिल्कुल समान नहीं होंगे, किन्तु ऊपर दिए गए समीकरणों से ज्ञात होता है कि Z<sub>1</sub> और Z<sub>2</sub> प्रतिबाधाओं में निश्चित मानों के लिए, ब्रिज कुछ ω और R<sub>b</sub>/R<sub>f</sub> के कुछ अनुपात पर संतुलित होगा। | ||
== विश्लेषण == | == विश्लेषण == | ||
=== लूप | === लूप लाभ से विश्लेषण किया गया === | ||
शिलिंग के अनुसार,<ref name="Schilling"/>वीन ब्रिज | शिलिंग के अनुसार,<ref name="Schilling" />वीन ब्रिज दोलक का लूप गेन, इस नियम के अनुसार है कि R<sub>1</sub>= R<sub>2</sub>= R और C<sub>1</sub>= C<sub>2</sub>= C, द्वारा दिया गया है: | ||
:<math>T = \left( \frac { R C s } {R^2 C^2 s^2 + 3RCs +1 } - \frac {R_b} {R_b + R_f } \right) A_0 \,</math> | :<math>T = \left( \frac { R C s } {R^2 C^2 s^2 + 3RCs +1 } - \frac {R_b} {R_b + R_f } \right) A_0 \,</math> | ||
जहाँ <math> A_0 \,</math>ऑप-एम्प का आवृत्ति-निर्भर लाभ है (ध्यान दें, शिलिंग में घटक नामों को पूर्व चित्र में घटक नामों से परिवर्तित कर दिया गया है)। | |||
शिलिंग आगे कहता है कि दोलन की स्थिति T = 1 है, जो संतुष्ट है | शिलिंग आगे कहता है कि दोलन की स्थिति T = 1 है, जो संतुष्ट है: | ||
:<math> \omega = \frac {1} {R C} \rightarrow f = \frac {1} {2 \pi R C}\,</math> | :<math> \omega = \frac {1} {R C} \rightarrow f = \frac {1} {2 \pi R C}\,</math> | ||
और | और | ||
:<math> \frac {R_f} {R_b} = \frac {2 A_0 + 3} {A_0 - 3} \,</math> साथ <math>\lim_{A_0\rightarrow \infin} \frac {R_f} {R_b} = 2 \, </math> | :<math> \frac {R_f} {R_b} = \frac {2 A_0 + 3} {A_0 - 3} \,</math> साथ <math>\lim_{A_0\rightarrow \infin} \frac {R_f} {R_b} = 2 \, </math> | ||
अन्य विश्लेषण, विशेष रूप से आवृत्ति स्थिरता और चयनात्मकता के संदर्भ में, | अन्य विश्लेषण, विशेष रूप से आवृत्ति स्थिरता और चयनात्मकता के संदर्भ में, {{Harvtxt|स्ट्रास|1970|p=671}} और {{Harvtxt|हैमिल्टन|2003|p=449}} है। | ||
=== आवृत्ति निर्धारण नेटवर्क === | === आवृत्ति निर्धारण नेटवर्क === | ||
| Line 84: | Line 90: | ||
:<math> H(s) = \frac { s C_2 R_1 } {s C_2 R_1 + (1 + s C_1 R_1) (s C_2 R_2 + 1 )} </math> | :<math> H(s) = \frac { s C_2 R_1 } {s C_2 R_1 + (1 + s C_1 R_1) (s C_2 R_2 + 1 )} </math> | ||
:<math> H(s) = \frac { s C_2 R_1 } {C_1 C_2 R_1 R_2 s^2 + (C_2 R_1 + C_2 R_2 + C_1 R_1) s + 1 } </math> | :<math> H(s) = \frac { s C_2 R_1 } {C_1 C_2 R_1 R_2 s^2 + (C_2 R_1 + C_2 R_2 + C_1 R_1) s + 1 } </math> | ||
माना R = R<sub>1</sub>= R<sub>2</sub> और C = C<sub>1</sub>= C<sub>2</sub> | |||
:<math> H(s) = \frac { s C R } {C^2 R^2 s^2 + 3 C R s + 1 } </math> | :<math> H(s) = \frac { s C R } {C^2 R^2 s^2 + 3 C R s + 1 } </math> | ||
''CR'' = 1 को सामान्य करें। | |||
:<math> H(s) = \frac { s } {s^2 + 3 s + 1 } </math> | :<math> H(s) = \frac { s } {s^2 + 3 s + 1 } </math> | ||
इस प्रकार आवृत्ति निर्धारण नेटवर्क में 0 पर शून्य और ध्रुव पर | इस प्रकार आवृत्ति निर्धारण नेटवर्क में 0 पर शून्य और ध्रुव पर <math>-1.5\plusmn \frac{\sqrt{5}}{2}</math> या -2.6180 और -0.38197 होता है। | ||
== आयाम स्थिरीकरण == | == आयाम स्थिरीकरण == | ||
वीन ब्रिज | वीन ब्रिज दोलक के अल्प विरूपण दोलन की कुंजी आयाम स्थिरीकरण विधि है जो क्लिपिंग का उपयोग नहीं करती है। आयाम स्थिरीकरण के लिए ब्रिज विन्यास में दीपक का उपयोग करने का विचार 1938 में मीचम द्वारा प्रकाशित किया गया था।<ref>{{Harvnb|Meacham|1938}}. {{Harvnb|Meacham1938a}}. Meacham presented his work at the Thirteenth Annual Convention of the Institute of Radio Engineers, New York City, June 16, 1938 and published in ''Proc. IRE'' October 1938. Hewlett's patent (filed July 11, 1939) does not mention Meacham.</ref> [[क्लिपिंग (सिग्नल प्रोसेसिंग)|क्लिपिंग]] या अन्य लाभ (इलेक्ट्रॉनिक्स) सीमा तक पहुंचने के लिए इलेक्ट्रॉनिक दोलक का आयाम बढ़ जाता है। इससे उच्च हार्मोनिक विरूपण होता है, जो प्रायः अवांछनीय होता है। | ||
हेवलेट ने आउटपुट आयाम को नियंत्रित करने के लिए | हेवलेट ने आउटपुट आयाम को नियंत्रित करने के लिए दोलक फीडबैक पथ में पावर डिटेक्टर, लो पास फिल्टर और लाभ कंट्रोल एलिमेंट के रूप में तापदीप्त बल्ब का उपयोग किया। प्रकाश बल्ब फिलामेंट का प्रतिरोध (प्रतिरोधकता लेख देखें) बढ़ता है। फिलामेंट के तापमान में विस्तारित हुई शक्ति और कुछ अन्य कारकों पर निर्भर करता है। यदि दोलक की अवधि (इसकी आवृत्ति का व्युत्क्रम) फिलामेंट के थर्मल समय स्थिरांक से अधिक अल्प है, तो फिलामेंट का तापमान चक्र पर अधिक सीमा तक स्थिर रहेगा। फिलामेंट प्रतिरोध तब आउटपुट सिग्नल के आयाम को निर्धारित करेगा। यदि आयाम बढ़ता है, तो फिलामेंट गर्म हो जाता है और इसका प्रतिरोध बढ़ जाता है। परिपथ को डिज़ाइन किया गया है जिससे कि बड़ा फिलामेंट प्रतिरोध लूप लाभ को अल्प कर दे, जो विपरीत में आउटपुट आयाम को अल्प कर देगा। परिणामस्वरूप नकारात्मक प्रतिक्रिया प्रणाली वह है जो आउटपुट आयाम को स्थिर मूल्य पर स्थिर करता है। आयाम नियंत्रण के इस रूप के साथ, दोलक निकट आदर्श रैखिक प्रणाली के रूप में कार्य करता है और अधिक अल्प विरूपण आउटपुट सिग्नल प्रदान करता है। दोलक जो आयाम नियंत्रण के लिए सीमित करने का उपयोग करते हैं, उनमें प्रायः महत्वपूर्ण हार्मोनिक विरूपण होता है। अल्प आवृत्तियों पर, जैसे-जैसे वीन ब्रिज दोलक की समयावधि [[गरमागरम बल्ब|तपित बल्ब]] के तापीय समय स्थिरांक तक पहुँचती है, परिपथ का संचालन अधिक अरैखिक हो जाता है, और आउटपुट विरूपण अधिक बढ़ जाता है। | ||
वीन ब्रिज दोलक में लाभ नियंत्रण तत्वों के रूप में उपयोग किए जाने पर प्रकाश बल्बों की अपनी हानि होती हैं, विशेष रूप से बल्ब के [[microphonics|माइक्रोफ़ोनिक]] प्रकृति आयाम मॉडुलन दोलक आउटपुट के कारण कंपन के लिए अत्यधिक उच्च संवेदनशीलता, कॉइल की आगमनात्मक प्रकृति के कारण उच्च आवृत्ति प्रतिक्रिया में सीमा फिलामेंट, और वर्तमान आवश्यकताएं जो अनेक ऑप-एम्प्स की क्षमता से अधिक हैं। आधुनिक वीन ब्रिज दोलक ने प्रकाश बल्बों के स्थान पर आयाम स्थिरीकरण के लिए [[डायोड]], [[ thermistor |थर्मिस्टर्स]] [[ फील्ड इफ़ेक्ट ट्रांजिस्टर |फील्ड इफ़ेक्ट ट्रांजिस्टर]] , या फोटोकल्स जैसे अन्य अरेखीय तत्वों का उपयोग किया है। हेवलेट के लिए अनुपलब्ध आधुनिक घटकों के साथ 0.0003% (3 ppm) जितना अल्प विरूपण प्राप्त किया जा सकता है।<ref>{{Harvnb|Williams|1990|pp=32–33}}</ref> | |||
थर्मिस्टर्स का उपयोग करने वाले वीन ब्रिज दोलक तपित दीपक की तुलना में थर्मिस्टर के अल्प परिचालन तापमान के कारण परिवेश के तापमान के प्रति अत्यधिक संवेदनशीलता प्रदर्शित करते हैं।<ref>{{Harvnb|Strauss|1970|p=710}}, stating "For acceptable amplitude stability, some form of temperature compensation would be necessary."</ref> | |||
== स्वचालित लाभ नियंत्रण गतिकी == | == स्वचालित लाभ नियंत्रण गतिकी == | ||
[[File:Root Locus.png|thumb|400px| | [[File:Root Locus.png|thumb|400px|R<sub>1</sub> = R<sub>2</sub> = 1 और C<sub>1</sub> = C<sub>2</sub> =1 बनाम K = (R<sub>b</sub> + R<sub>f</sub>)/R<sub>b</sub> के लिए वीन ब्रिज दोलक पोल पोजिशन का रूट लोकस प्लॉट है। K के संख्यात्मक मान बैंगनी फ़ॉन्ट में दिखाए जाते हैं। K=3 के लिए ध्रुवों का प्रक्षेपवक्र काल्पनिक (β) अक्ष के लंबवत है। K >> 5 के लिए, ध्रुव मूल की ओर और दूसरा K की ओर पहुंचता है।<ref>{{Harvnb|Strauss|1970|p=667}}</ref>]]R<sub>b</sub> के मूल्य में छोटे क्षोभ प्रमुख ध्रुवों को jω (काल्पनिक) अक्ष पर आगे और पीछे जाने का कारण बनता है। यदि ध्रुव बाएँ आधे तल में चले जाते हैं, तो दोलन घातीय रूप से शून्य हो जाता है। यदि ध्रुव दाहिने आधे तल में चले जाते हैं, तो दोलन तीव्रता से बढ़ता है जब तक कि कुछ इसे सीमित न कर दे। यदि क्षोभ अधिक छोटा है, तो समतुल्य Q का परिमाण इतना बड़ा है कि आयाम धीरे-धीरे परिवर्तित होता है। यदि क्षोभ छोटा है और थोड़े समय के पश्चात विपरीत हो जाती है, तो एनवेलप रैंप का अनुसरण करता है। एनवेलप लगभग क्षोभ का अभिन्न अंग है। एनवेलप ट्रांसफर फंक्शन में क्षोभ 6 dB/ऑक्टेव पर रोल ऑफ होती है और -90° फेज शिफ्ट का कारण बनती है। | ||
प्रकाश बल्ब में ऊष्मीय जड़ता होती है | प्रकाश बल्ब में ऊष्मीय जड़ता होती है जिससे कि प्रतिरोध हस्तांतरण फंक्शन की शक्ति एकल पोल लो पास फिल्टर प्रदर्शित करते हैं। एनवेलप ट्रांसफर फंक्शन और बल्ब ट्रांसफर फंक्शन कैस्केड में प्रभावी रूप से होते हैं, जिससे कंट्रोल लूप में प्रभावी रूप से लो पास पोल और शून्य पर पोल लगभग -180° का नेट फेज शिफ्ट होता है। यह अल्प [[ चरण मार्जिन |चरण मार्जिन]] के कारण नियंत्रण पाश में खराब क्षणिक प्रतिक्रिया का कारण बनेगा। आउटपुट [[निचोड़ना|न्यूनतम]] प्रदर्शित कर सकता है। बर्नार्ड एम ओलिवर<ref>{{harvnb|Oliver|1960}}</ref> में दिखाया गया है कि एम्पलीफायर द्वारा लाभ का सामान्य संपीड़न एनवेलप स्थानांतरण फ़ंक्शन को अल्प करता है जिससे कि अधिकांश दोलक उत्तम क्षणिक प्रतिक्रिया दिखाते हैं, जो दुर्लभ स्थिति को त्यागकर [[ वेक्यूम - ट्यूब |वेक्यूम ट्यूबों]] में अन्य-रैखिकता दूसरे को असामान्य रूप से रैखिक एम्पलीफायर का उत्पादन करती है। | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 145: | Line 150: | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
* [http://www.hp.com/hpinfo/abouthp/histnfacts/museum/earlyinstruments/0002/index.html Model 200A Audio Oscillator, 1939], HP Virtual Museum. | * [http://www.hp.com/hpinfo/abouthp/histnfacts/museum/earlyinstruments/0002/index.html Model 200A Audio Oscillator, 1939], HP Virtual Museum. | ||
* [http://www.ecircuitcenter.com/Circuits/opwien/opwien.htm Wien Bridge Oscillator], including SPICE simulation. The "Wien bridge oscillator" in the simulation is not a low distortion design with amplitude stabilization; it is a more conventional oscillator with a diode limiter. | * [http://www.ecircuitcenter.com/Circuits/opwien/opwien.htm Wien Bridge Oscillator], including SPICE simulation. The "Wien bridge oscillator" in the simulation is not a low distortion design with amplitude stabilization; it is a more conventional oscillator with a diode limiter. | ||
* {{Citation |last1=Aigrain |first1=P. R. |last2=Williams |first2=E. M. |title=Theory of Amplitude-Stabilized Oscillators |date=January 1948 |journal=Proceedings of the IRE |volume=36 |issue=1 |pages=16–19 |doi=10.1109/JRPROC.1948.230539 |s2cid=51640873 |ref=none}} | * {{Citation |last1=Aigrain |first1=P. R. |last2=Williams |first2=E. M. |title=Theory of Amplitude-Stabilized Oscillators |date=January 1948 |journal=Proceedings of the IRE |volume=36 |issue=1 |pages=16–19 |doi=10.1109/JRPROC.1948.230539 |s2cid=51640873 |ref=none}} | ||
* [http://www.cirvirlab.com/simulation/op_amp_wien_bridge_oscillator_online.php Online Simulator of | * [http://www.cirvirlab.com/simulation/op_amp_wien_bridge_oscillator_online.php Online Simulator of Wien Bridge Oscillator] – Gives online simulation of Wien bridge oscillator. | ||
* [http://www.cliftonlaboratories.com/Bill%20Hewlett%20and%20his%20Magic%20Lamp.htm Bill Hewlett and his Magic Lamp], Clifton Laboratories | * [http://www.cliftonlaboratories.com/Bill%20Hewlett%20and%20his%20Magic%20Lamp.htm Bill Hewlett and his Magic Lamp], Clifton Laboratories | ||
* {{citation |date=October 1939 |journal=Proceedings of the IRE |volume=27 |issue=10 |pages=649–655 |first1=F. E. |last1=Terman |first2=R. R. |last2=Buss |first3=W. R. |last3=Hewlett |first4=F. C. |last4=Cahill |url=http://www.hparchive.com/Manuals/HP-200-IRE-Article.pdf |title=Some Applications of Negative Feedback with Particular Reference to Laboratory Equipment |doi=10.1109/JRPROC.1939.228752|s2cid=51642790 }} (Acks Edward L. Ginzton at end of paper.) (Presented 16 June 1938 at 13th Annual Convention, Manuscript received 22 November 1938, abridged 1 August 1939); Meacham presented at 13th Annual Convention on 16 June 1938, too. See BSTJ. Also presented at Pacific Coast Convention, Portland, OR, 11 August 1938. | * {{citation |date=October 1939 |journal=Proceedings of the IRE |volume=27 |issue=10 |pages=649–655 |first1=F. E. |last1=Terman |first2=R. R. |last2=Buss |first3=W. R. |last3=Hewlett |first4=F. C. |last4=Cahill |url=http://www.hparchive.com/Manuals/HP-200-IRE-Article.pdf |title=Some Applications of Negative Feedback with Particular Reference to Laboratory Equipment |doi=10.1109/JRPROC.1939.228752|s2cid=51642790 }} (Acks Edward L. Ginzton at end of paper.) (Presented 16 June 1938 at 13th Annual Convention, Manuscript received 22 November 1938, abridged 1 August 1939); Meacham presented at 13th Annual Convention on 16 June 1938, too. See BSTJ. Also presented at Pacific Coast Convention, Portland, OR, 11 August 1938. | ||
| Line 160: | Line 164: | ||
* {{US patent|2303485}} Later (31 December 1940) Meacham patent about multi-frequency bridge-stabilized oscillators using series resonant circuits. | * {{US patent|2303485}} Later (31 December 1940) Meacham patent about multi-frequency bridge-stabilized oscillators using series resonant circuits. | ||
{{DEFAULTSORT:Wien Bridge Oscillator}} | |||
{{DEFAULTSORT:Wien Bridge Oscillator}} | |||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page|Wien Bridge Oscillator]] | ||
[[Category:Created On 23/03/2023]] | [[Category:Articles with invalid date parameter in template]] | ||
[[Category:CS1 Deutsch-language sources (de)|Wien Bridge Oscillator]] | |||
[[Category:Collapse templates|Wien Bridge Oscillator]] | |||
[[Category:Commons category link is locally defined|Wien Bridge Oscillator]] | |||
[[Category:Created On 23/03/2023|Wien Bridge Oscillator]] | |||
[[Category:Machine Translated Page|Wien Bridge Oscillator]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Wien Bridge Oscillator]] | |||
[[Category:Pages with script errors|Wien Bridge Oscillator]] | |||
[[Category:Sidebars with styles needing conversion|Wien Bridge Oscillator]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Wien Bridge Oscillator]] | |||
[[Category:Templates generating microformats|Wien Bridge Oscillator]] | |||
[[Category:Templates that are not mobile friendly|Wien Bridge Oscillator]] | |||
[[Category:Templates using TemplateData|Wien Bridge Oscillator]] | |||
[[Category:Wikipedia articles needing page number citations from November 2015]] | |||
[[Category:Wikipedia metatemplates|Wien Bridge Oscillator]] | |||
[[Category:इलेक्ट्रॉनिक ऑसिलेटर्स|Wien Bridge Oscillator]] | |||
[[Category:इलेक्ट्रॉनिक परीक्षण उपकरण|Wien Bridge Oscillator]] | |||
[[Category:एनालॉग सर्किट|Wien Bridge Oscillator]] | |||
Latest revision as of 12:45, 30 October 2023
वीन ब्रिज दोलक ऐसा इलेक्ट्रॉनिक दोलक है जो साइन वेव्स उत्पन्न करता है। यह आवृत्तियों की बड़ी श्रृंखला उत्पन्न कर सकता है। दोलक ब्रिज परिपथ पर आधारित है जिसे मूल रूप से 1891 में मैक्स वियना द्वारा विद्युत प्रतिबाधा के मापन के लिए विकसित किया गया था।[1]
वीन ब्रिज में चार प्रतिरोधक और दो संधारित्र होते हैं। दोलक भी सकारात्मक प्रतिक्रिया प्रदान करता है कि बैंडपास फिल्टर के साथ संयुक्त सकारात्मक लाभ प्रवर्धक के रूप में देखा जा सकता है। स्वत: लाभ नियंत्रण, निश्चयपूर्वक अन्य-रैखिकता और आकस्मिक अन्य-रैखिकता दोलक के विभिन्न कार्यान्वयन में आउटपुट आयाम को सीमित करती है।
दाईं ओर दिखाया गया परिपथ तपित दीपक का उपयोग करके स्वत: लाभ नियंत्रण के साथ, दोलक के सामान्य कार्यान्वयन को दर्शाता है। नियम के अनुसार है कि R1= R2= R और C1= C2=C, दोलन की आवृत्ति द्वारा दी गई है:
और स्थिर दोलन की स्थिति इसके द्वारा दी गई है:
पृष्ठभूमि
1930 के दशक में दोलक को उत्तम बनाने के लिए अनेक प्रयास किए गए हैं। रैखिकता को महत्वपूर्ण माना गया है। प्रतिरोध-स्थिर दोलक समायोज्य प्रतिक्रिया रोकनेवाला था; उस अवरोधक को व्यस्थापित किया जाएगा जिससे कि दोलक प्रारंभ हो जाए (इस प्रकार लूप लाभ को मात्र एकता पर व्यस्थापित करना)। दोलन तब तक होगा जब तक कि वैक्यूम ट्यूब का ग्रिड धारा का संचालन प्रारंभ नहीं कर देता, जिससे हानि बढ़ जाती है, और आउटपुट आयाम सीमित हो जाता है।[2][3][4] स्वचालित आयाम नियंत्रण का परिक्षण किया गया।[5][6] फ्रेडरिक टर्मन कहते हैं, किसी भी सामान्य दोलक की आवृत्ति स्थिरता और तरंग-आकार के रूप को सभी परिस्थितियों में स्थिर दोलनों के आयाम को बनाए रखने के लिए स्वचालित-आयाम-नियंत्रण व्यवस्था का उपयोग करके संशोधन किया जा सकता है।[7]
1937 में, लारेड मेचम ने ब्रिज दोलक में स्वत: लाभ नियंत्रण के लिए फिलामेंट लैंप का उपयोग करने का वर्णन किया।[8][9]
इसके अतिरिक्त 1937 में, हेर्मोन होस्मर स्कॉट ने वीन ब्रिज सहित विभिन्न ब्रिजों पर आधारित ऑडियो दोलक का वर्णन किया।[10][11]
स्टैनफोर्ड विश्वविद्यालय में टरमन, नकारात्मक प्रतिक्रिया पर हेरोल्ड स्टीफन ब्लैक के कार्य में रुचि रखते थे,[12][13] इसलिए उन्होंने नकारात्मक प्रतिक्रिया पर स्नातक संगोष्ठी आयोजित की।[14] बिल हेवलेट ने सेमिनार में भाग लिया। संगोष्ठी के समय स्कॉट का फरवरी 1938 का दोलक पेपर निकला। यहाँ टरमन द्वारा स्मरण है:[15]
- फ्रेड टर्मन बताते हैं: स्टैनफोर्ड में अभियांत्रिक की डिग्री की आवश्यकताओं को पूर्ण करने के लिए बिल को थीसिस तत्पर करनी पड़ी। उस समय मैंने अपने स्नातक संगोष्ठी का पूर्ण चौथाई 'नकारात्मक प्रतिक्रिया' के विषय में समर्पित करने का निर्णय लिया था, मुझे इस तत्कालीन नई प्रौद्योगिक में रूचि हो गई थी क्योंकि ऐसा लगता था कि इसमें अनेक उपयोगी चीजें करने की अधिक संभावनाएं हैं। मैं नकारात्मक प्रतिक्रिया पर विचार किए गए कुछ अनुप्रयोगों पर रिपोर्ट करूंगा, जिनके विषय में मैंने सोचा था, और लड़के वर्तमान के लेख पढ़ेंगे और वर्तमान विकास पर एक-दूसरे को रिपोर्ट करेंगे। यह संगोष्ठी अभी उत्तम प्रकार से प्रारंभ हुई थी जब पेपर निकला जो मुझे रोचक लगा। यह जनरल रेडियो के व्यक्ति द्वारा किया गया था और निश्चित-आवृत्ति ऑडियो दोलक से समाधान किया गया था जिसमें आवृत्ति को प्रतिरोध-संधारित्र नेटवर्क द्वारा नियंत्रित किया गया था, और पुश-बटन के माध्यम से परिवर्तित कर दिया गया था। नकारात्मक प्रतिक्रिया के सरल अनुप्रयोग द्वारा दोलन प्राप्त किए गए थे।
जून 1938 में, टर्मन, आर.आर. बस, हेवलेट और एफ.सी. काहिल ने न्यूयॉर्क में आईआरइ (IRE) कन्वेंशन में नकारात्मक प्रतिक्रिया के विषय में प्रस्तुति दी; अगस्त 1938 में, पोर्टलैंड, ओआर (OR) में आईआरइ (IRE) पैसिफिक कोस्ट कन्वेंशन में दूसरी प्रस्तुति हुई; प्रस्तुति आईआरइ (IRE) पेपर बन गई।[16] विषय वीन ब्रिज दोलक में आयाम नियंत्रण था। दोलक पोर्टलैंड में प्रदर्शित किया गया था।[17] हेवलेट, डेविड पैकर्ड के साथ, हेवलेट पैकर्ड की सह-स्थापना की, और हेवलेट-पैकर्ड का प्रथम उत्पाद HP200A था, जो त्रुटिहीन वीन ब्रिज दोलक था। प्रथम बिक्री जनवरी 1939 में हुई थी।[18]
हेवलेट के जून 1939 के अभियांत्रिक की डिग्री थीसिस ने वीन ब्रिज दोलक के आयाम को नियंत्रित करने के लिए दीपक का उपयोग किया।[19] हेवलेट के दोलक स्थिर आयाम और अल्प विरूपण के साथ साइनसोइडल आउटपुट का उत्पादन करता है।[20][21]
स्वचालित लाभ नियंत्रण के बिना दोलक
पारंपरिक दोलक परिपथ को इस प्रकार डिज़ाइन किया गया है कि यह दोलन (स्टार्ट अप) करना प्रारंभ कर देगा और इसका आयाम नियंत्रित हो जाएगा।
एम्पलीफायर आउटपुट में नियंत्रित संपीड़न जोड़ने के लिए दाईं ओर दोलक डायोड का उपयोग करता है। यह 1-5% की सीमा में कुल हार्मोनिक विरूपण उत्पन्न कर सकता है, यह इस विषय पर निर्भर करता है कि इसे कितनी सावधानी से विभक्त किया जाता है।[22]
दोलन करने के लिए रैखिक परिपथ के लिए, इसे बार्कहाउज़ेन स्थिरता मानदंड को पूर्ण करना चाहिए: इसका लूप लाभ होना चाहिए और लूप के चारों ओर चरण 360 डिग्री का पूर्णांक होना चाहिए। रैखिक दोलक सिद्धांत यह नहीं बताता है कि दोलक कैसे प्रारंभ होता है या आयाम कैसे निर्धारित होता है। रैखिक दोलक किसी भी आयाम का समर्थन कर सकता है।
व्यवहार में, पाश लाभ प्रारंभ में एकता से बड़ा होता है। यादृच्छिक व्यग्रता सभी परिपथों में उपस्थित होता है, और उस व्यग्रता में से कुछ वांछित आवृत्ति के निकट होगा। लूप लाभ से अधिक आवृत्ति के आयाम को प्रत्येक बार तीव्रता से बढ़ाने की अनुमति देता है। अधिक लूप लाभ के साथ, दोलक प्रारंभ हो जाएगा।
आदर्श रूप से, लूप लाभ को थोड़ा बड़ा होना चाहिए, किन्तु व्यवहार में, यह प्रायः अत्यधिक होता है। बड़ा लूप लाभ दोलक को शीघ्रता से प्रारंभ करता है। बड़ा लूप लाभ तापमान के साथ भिन्नता और ट्यून करने योग्य दोलक की वांछित आवृत्ति के लिए भी क्षतिपूर्ति करता है। दोलक प्रारंभ करने के लिए, पाश लाभ सभी संभव परिस्थितियों में से अधिक होना चाहिए।
अधिक लूप लाभ का नकारात्मक पक्ष होता है। सिद्धांत रूप में, दोलक आयाम बिना सीमा के बढ़ेगा। व्यवहार में, आयाम तब तक बढ़ेगा जब तक आउटपुट कुछ सीमित कारक जैसे कि विद्युत आपूर्ति वोल्टेज (एम्पलीफायर आउटपुट आपूर्ति रेल में चलता है) या एम्पलीफायर आउटपुट वर्तमान सीमा में चलता है। सीमित करने से एम्पलीफायर का प्रभावी लाभ अल्प हो जाता है (प्रभाव को लाभ संपीड़न कहा जाता है)। स्थिर दोलक में, औसत पाश लाभ होगा।
चूँकि सीमित क्रिया आउटपुट वोल्टेज को स्थिर करती है, इसके दो महत्वपूर्ण प्रभाव हैं: यह हार्मोनिक विरूपण का परिचय देती है और दोलक की आवृत्ति स्थिरता को प्रभावित करती है। विरूपण की मात्रा स्टार्टअप के लिए उपयोग किए जाने वाले अतिरिक्त लूप लाभ से संबंधित है। यदि छोटे आयामों पर अत्यधिक अतिरिक्त लूप लाभ होता है, तो उच्च तात्कालिक आयामों पर लाभ में और अल्पता आनी चाहिए। अर्थात अधिक विकृति होनी चाहिए।
विरूपण की मात्रा दोलन के अंतिम आयाम से भी संबंधित होती है। चूँकि एम्पलीफायर का लाभ आदर्श रूप से रैखिक है, व्यवहार में यह अरैखिक है। नॉनलाइनियर ट्रांसफर फ़ंक्शन को टेलर श्रृंखला के रूप में व्यक्त किया जा सकता है। छोटे आयामों के लिए, उच्च क्रम का नियम अधिक अल्प प्रभाव डालती हैं। बड़े आयामों के लिए, अन्य-रैखिकता का उच्चारण किया जाता है। परिणामस्वरूप, अल्प विरूपण के लिए, दोलक का आउटपुट आयाम एम्पलीफायर की गतिशील श्रृंखला का छोटा अंश होना चाहिए।
मेचम का ब्रिज स्थिर दोलक

लारेड मेचम ने 1938 में दाईं ओर दिखाए गए ब्रिज दोलक परिपथ का विवरण किया। परिपथ को अधिक उच्च आवृत्ति स्थिरता और अधिक शुद्ध साइनसोइडल आउटपुट के रूप में वर्णित किया गया था।[9] आयाम को नियंत्रित करने के लिए ट्यूब ओवरलोडिंग का उपयोग करने के अतिरिक्त, मेचम ने परिपथ प्रस्तावित किया जो लूप लाभ को एकता में व्यस्थापित करता है जबकि एम्पलीफायर अपने रैखिक क्षेत्र में होता है। मेचम के परिपथ में क्वार्ट्ज क्रिस्टल दोलक और व्हीटस्टोन ब्रिज में लैंप सम्मिलित था।
मेचम के परिपथ में, आवृत्ति निर्धारण घटक ब्रिज की नकारात्मक फ़ीड बैक शाखा और लाभ नियंत्रण तत्व सकारात्मक फ़ीड बैक शाखा में हैं। क्रिस्टल, Z4, श्रृंखला अनुनाद में संचालित होता है। इस प्रकार यह अनुनाद पर नकारात्मक प्रतिक्रिया को अल्प करता है। विशेष क्रिस्टल ने अनुनाद पर 114 ohms का वास्तविक प्रतिरोध प्रदर्शित किया। अनुनाद के नीचे आवृत्तियों पर, क्रिस्टल कैपेसिटिव होता है और नकारात्मक प्रतिक्रिया शाखा के लाभ में नकारात्मक चरण परिवर्तित होता है। प्रतिध्वनि से ऊपर की आवृत्तियों पर, क्रिस्टल आगमनात्मक होता है और नकारात्मक प्रतिक्रिया शाखा के लाभ में सकारात्मक चरण परिवर्तित होता है। आवृत्ति पर चरण परिवर्तित शून्य से निकलता है। जैसे ही दीपक गर्म होता है, यह सकारात्मक प्रतिक्रिया को अल्प करता है। मेचम के परिपथ में क्रिस्टल का Q 104,000 के रूप में दिया गया है। आवृत्ति से क्रिस्टल की बैंडविड्थ के छोटे से अधिक आवृत्ति पर, नकारात्मक प्रतिक्रिया शाखा लूप लाभ पर आच्छादित होती है और क्रिस्टल की संकीर्ण बैंडविड्थ के अतिरिक्त कोई आत्मनिर्भर दोलन नहीं हो सकता है।
1944 में (हेवलेट के डिजाइन के पश्चात), जे. के. क्लैप ने ब्रिज को चलाने के लिए ट्रांसफॉर्मर के अतिरिक्त वैक्यूम ट्यूब फेज इन्वर्टर का उपयोग करने के लिए मेचम के परिपथ को संशोधित किया।[23][24] संशोधित मेचम दोलक क्लैप के चरण इन्वर्टर का उपयोग करता है किन्तु टंगस्टन लैंप के लिए डायोड लिमिटर को प्रतिस्थापित करता है।[25]
हेवलेट का दोलक

विलियम आर हेवलेट के वीन ब्रिज दोलक को अंतर एम्पलीफायर और वीन ब्रिज को संयोजन के रूप में माना जा सकता है, जो एम्पलीफायर आउटपुट और अंतर इनपुट के मध्य सकारात्मक प्रतिक्रिया पाश में जुड़ा हुआ है। दोलन आवृत्ति पर, ब्रिज लगभग संतुलित होता है और इसका अंतरण अनुपात अधिक अल्प होता है। पाश लाभ अधिक उच्च एम्पलीफायर लाभ और अधिक अल्प ब्रिज अनुपात का उत्पाद है।[26] हेवलेट के परिपथ में, एम्पलीफायर को दो वैक्यूम ट्यूबों द्वारा कार्यान्वित किया जाता है। एम्पलीफायर का इन्वर्टिंग इनपुट ट्यूब V1 का कैथोड है और नॉन-इनवर्टिंग इनपुट ट्यूब V2 का कंट्रोल ग्रिड है। विश्लेषण को सरल बनाने के लिए, R1, R2, C1 और C2 के अतिरिक्त अन्य सभी घटकों को 1+Rf/Rb के लाभ और उच्च इनपुट प्रतिबाधा के साथ अन्य-इनवर्टिंग एम्पलीफायर के रूप में तत्पर किया जा सकता है। R1, R2, C1 और C2 बैंडपास फिल्टर बनाएं जो दोलन की आवृत्ति पर सकारात्मक प्रतिक्रिया प्रदान करने के लिए जुड़ा हो। Rb स्वयं गर्म होता है और नकारात्मक प्रतिक्रिया को बढ़ाता है जो एम्पलीफायर लाभ को अल्प करता है जब तक कि बिंदु तक नहीं पहुंच जाता है कि एम्पलीफायर को चलाए बिना साइनसोइडल दोलन को बनाए रखने के लिए पर्याप्त लाभ होता है। यदि R1 = R2 और C1 = C2 फिर संतुलन पर Rf/Rb = 2 और एम्पलीफायर का लाभ 3 है। जब परिपथ प्रथम बार सक्रिय होता है, तो दीपक ठंडा होता है और परिपथ का लाभ 3 से अधिक होता है जो स्टार्ट अप सुनिश्चित करता है। वैक्यूम ट्यूब V1 का dc बायस धारा भी लैंप से होकर प्रवाहित होता है। यह परिपथ के संचालन के सिद्धांतों को परिवर्तित नहीं करता है, किन्तु यह संतुलन पर आउटपुट के आयाम को अल्प करता है क्योंकि पूर्वाग्रह वर्तमान दीपक के ताप का भाग प्रदान करता है।
हेवलेट की थीसिस ने निम्नलिखित निष्कर्ष दिया है:[27]
- अभी वर्णित प्रकार का प्रतिरोध-क्षमता दोलक प्रयोगशाला सेवा के लिए उपयुक्त होना चाहिए। इसमें बीट-आवृत्ति दोलक को संभालने में सरलता होती है और फिर भी इसकी कुछ हानि हैं। प्रथम विषय तो यह है कि बीट-आवृत्ति प्रकार की स्पर्धा अल्प आवृत्तियों पर स्थिरता अधिक उत्तम होती है। छोटे तापमान परिवर्तनों को सुनिश्चित करने के लिए घटकों के महत्वपूर्ण प्लेसमेंट की आवश्यकता नहीं होती है, न ही दोलक के इंटरलॉकिंग को रोकने के लिए सावधानीपूर्वक डिज़ाइन किए गए डिटेक्टर परिपथ होते हैं। इसके परिणामस्वरूप, दोलक का समग्र भार अल्प से अल्प रखा जा सकता है। तुलनीय प्रदर्शन के सामान्य रेडियो बीट-आवृत्ति दोलक के लिए 93 पाउंड के विपरीत, 1 वाट एम्पलीफायर और विद्युत की आपूर्ति सहित इस प्रकार के दोलक का वजन केवल 18 पाउंड था। आउटपुट की विकृति और स्थिरता उपलब्ध सर्वोत्तम बीट-आवृत्ति दोलक के साथ अनुकूल रूप से तुलना करती है। अंत में, इस प्रकार के दोलक को वाणिज्यिक प्रसारण रिसीवर के समान आधार पर बनाया जा सकता है, किन्तु बनाने के लिए अल्प समायोजन की आवश्कयता होती है। इस प्रकार यह आदर्श प्रयोगशाला दोलक देने के लिए अल्प व्यय के साथ प्रदर्शन की गुणवत्ता को जोड़ती है।
वीन ब्रिज
ब्रिज परिपथ घटक के ज्ञात मूल्यों से तुलना करके मापने का सामान्य प्रकार था। प्रायः अज्ञात घटक को ब्रिज की भुजा में रखा जाता है, और फिर अन्य भुजाओं को समायोजित करके या वोल्टेज स्रोत की आवृत्ति को परिवर्तित करके ब्रिज को अशक्त कर दिया जाता है (देखें, उदाहरण के लिए, व्हीटस्टोन ब्रिज)।
वीन ब्रिज अनेक सामान्य ब्रिज में से है।[28] प्रतिरोध और आवृत्ति की स्थिति में संधारित्र के त्रुटिहीन माप के लिए वीन के ब्रिज का उपयोग किया जाता है।[29] इसका उपयोग ऑडियो आवृत्तियों को मापने के लिए भी किया जाता था।
वीन ब्रिज को R या C के समान मूल्यों की आवश्यकता नहीं होती है। Vout पर सिग्नल के सापेक्ष Vp पर सिग्नल का चरण लगभग 90° से भिन्न होता है, जो निम्न आवृत्ति पर लगभग 90° पश्चगामी उच्च आवृत्ति पर होता है। कुछ मध्यवर्ती आवृत्ति पर, चरण परिवर्तन शून्य होगा। उस आवृत्ति पर Z1 से Z2 का अनुपात विशुद्ध रूप से वास्तविक (शून्य काल्पनिक भाग) होगा। यदि Rb से Rf के अनुपात को उसी अनुपात में समायोजित किया जाता है, तो ब्रिज संतुलित होता है और परिपथ दोलन को बनाए रख सकता है। भले ही Rb/Rf छोटा फेज शिफ्ट है और भले ही एम्पलीफायर के इनवर्टिंग और नॉन-इनवर्टिंग इनपुट में भिन्न-भिन्न फेज शिफ्ट हों। सदैव आवृत्ति होगी जिस पर ब्रिज की प्रत्येक शाखा का कुल चरण परिवर्तन समान होगा। यदि Rb/Rf कोई फेज शिफ्ट नहीं है और एम्पलीफायरों के इनपुट का फेज शिफ्ट शून्य है तो ब्रिज संतुलित है जब:[30]
- और
जहां ω रेडियन आवृत्ति है।
यदि कोई R1 = R2 और C1= C2 चयन करता है, तो Rf= 2 Rb होता है।
व्यवहार में, R और C के मान कभी भी बिल्कुल समान नहीं होंगे, किन्तु ऊपर दिए गए समीकरणों से ज्ञात होता है कि Z1 और Z2 प्रतिबाधाओं में निश्चित मानों के लिए, ब्रिज कुछ ω और Rb/Rf के कुछ अनुपात पर संतुलित होगा।
विश्लेषण
लूप लाभ से विश्लेषण किया गया
शिलिंग के अनुसार,[26]वीन ब्रिज दोलक का लूप गेन, इस नियम के अनुसार है कि R1= R2= R और C1= C2= C, द्वारा दिया गया है:
जहाँ ऑप-एम्प का आवृत्ति-निर्भर लाभ है (ध्यान दें, शिलिंग में घटक नामों को पूर्व चित्र में घटक नामों से परिवर्तित कर दिया गया है)।
शिलिंग आगे कहता है कि दोलन की स्थिति T = 1 है, जो संतुष्ट है:
और
- साथ
अन्य विश्लेषण, विशेष रूप से आवृत्ति स्थिरता और चयनात्मकता के संदर्भ में, स्ट्रास (1970, p. 671) और हैमिल्टन (2003, p. 449) है।
आवृत्ति निर्धारण नेटवर्क
माना R = R1= R2 और C = C1= C2
CR = 1 को सामान्य करें।
इस प्रकार आवृत्ति निर्धारण नेटवर्क में 0 पर शून्य और ध्रुव पर या -2.6180 और -0.38197 होता है।
आयाम स्थिरीकरण
वीन ब्रिज दोलक के अल्प विरूपण दोलन की कुंजी आयाम स्थिरीकरण विधि है जो क्लिपिंग का उपयोग नहीं करती है। आयाम स्थिरीकरण के लिए ब्रिज विन्यास में दीपक का उपयोग करने का विचार 1938 में मीचम द्वारा प्रकाशित किया गया था।[31] क्लिपिंग या अन्य लाभ (इलेक्ट्रॉनिक्स) सीमा तक पहुंचने के लिए इलेक्ट्रॉनिक दोलक का आयाम बढ़ जाता है। इससे उच्च हार्मोनिक विरूपण होता है, जो प्रायः अवांछनीय होता है।
हेवलेट ने आउटपुट आयाम को नियंत्रित करने के लिए दोलक फीडबैक पथ में पावर डिटेक्टर, लो पास फिल्टर और लाभ कंट्रोल एलिमेंट के रूप में तापदीप्त बल्ब का उपयोग किया। प्रकाश बल्ब फिलामेंट का प्रतिरोध (प्रतिरोधकता लेख देखें) बढ़ता है। फिलामेंट के तापमान में विस्तारित हुई शक्ति और कुछ अन्य कारकों पर निर्भर करता है। यदि दोलक की अवधि (इसकी आवृत्ति का व्युत्क्रम) फिलामेंट के थर्मल समय स्थिरांक से अधिक अल्प है, तो फिलामेंट का तापमान चक्र पर अधिक सीमा तक स्थिर रहेगा। फिलामेंट प्रतिरोध तब आउटपुट सिग्नल के आयाम को निर्धारित करेगा। यदि आयाम बढ़ता है, तो फिलामेंट गर्म हो जाता है और इसका प्रतिरोध बढ़ जाता है। परिपथ को डिज़ाइन किया गया है जिससे कि बड़ा फिलामेंट प्रतिरोध लूप लाभ को अल्प कर दे, जो विपरीत में आउटपुट आयाम को अल्प कर देगा। परिणामस्वरूप नकारात्मक प्रतिक्रिया प्रणाली वह है जो आउटपुट आयाम को स्थिर मूल्य पर स्थिर करता है। आयाम नियंत्रण के इस रूप के साथ, दोलक निकट आदर्श रैखिक प्रणाली के रूप में कार्य करता है और अधिक अल्प विरूपण आउटपुट सिग्नल प्रदान करता है। दोलक जो आयाम नियंत्रण के लिए सीमित करने का उपयोग करते हैं, उनमें प्रायः महत्वपूर्ण हार्मोनिक विरूपण होता है। अल्प आवृत्तियों पर, जैसे-जैसे वीन ब्रिज दोलक की समयावधि तपित बल्ब के तापीय समय स्थिरांक तक पहुँचती है, परिपथ का संचालन अधिक अरैखिक हो जाता है, और आउटपुट विरूपण अधिक बढ़ जाता है।
वीन ब्रिज दोलक में लाभ नियंत्रण तत्वों के रूप में उपयोग किए जाने पर प्रकाश बल्बों की अपनी हानि होती हैं, विशेष रूप से बल्ब के माइक्रोफ़ोनिक प्रकृति आयाम मॉडुलन दोलक आउटपुट के कारण कंपन के लिए अत्यधिक उच्च संवेदनशीलता, कॉइल की आगमनात्मक प्रकृति के कारण उच्च आवृत्ति प्रतिक्रिया में सीमा फिलामेंट, और वर्तमान आवश्यकताएं जो अनेक ऑप-एम्प्स की क्षमता से अधिक हैं। आधुनिक वीन ब्रिज दोलक ने प्रकाश बल्बों के स्थान पर आयाम स्थिरीकरण के लिए डायोड, थर्मिस्टर्स फील्ड इफ़ेक्ट ट्रांजिस्टर , या फोटोकल्स जैसे अन्य अरेखीय तत्वों का उपयोग किया है। हेवलेट के लिए अनुपलब्ध आधुनिक घटकों के साथ 0.0003% (3 ppm) जितना अल्प विरूपण प्राप्त किया जा सकता है।[32]
थर्मिस्टर्स का उपयोग करने वाले वीन ब्रिज दोलक तपित दीपक की तुलना में थर्मिस्टर के अल्प परिचालन तापमान के कारण परिवेश के तापमान के प्रति अत्यधिक संवेदनशीलता प्रदर्शित करते हैं।[33]
स्वचालित लाभ नियंत्रण गतिकी
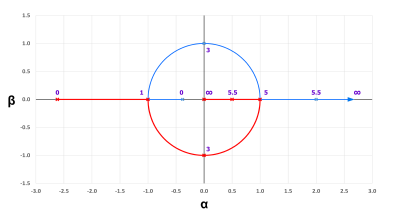
Rb के मूल्य में छोटे क्षोभ प्रमुख ध्रुवों को jω (काल्पनिक) अक्ष पर आगे और पीछे जाने का कारण बनता है। यदि ध्रुव बाएँ आधे तल में चले जाते हैं, तो दोलन घातीय रूप से शून्य हो जाता है। यदि ध्रुव दाहिने आधे तल में चले जाते हैं, तो दोलन तीव्रता से बढ़ता है जब तक कि कुछ इसे सीमित न कर दे। यदि क्षोभ अधिक छोटा है, तो समतुल्य Q का परिमाण इतना बड़ा है कि आयाम धीरे-धीरे परिवर्तित होता है। यदि क्षोभ छोटा है और थोड़े समय के पश्चात विपरीत हो जाती है, तो एनवेलप रैंप का अनुसरण करता है। एनवेलप लगभग क्षोभ का अभिन्न अंग है। एनवेलप ट्रांसफर फंक्शन में क्षोभ 6 dB/ऑक्टेव पर रोल ऑफ होती है और -90° फेज शिफ्ट का कारण बनती है।
प्रकाश बल्ब में ऊष्मीय जड़ता होती है जिससे कि प्रतिरोध हस्तांतरण फंक्शन की शक्ति एकल पोल लो पास फिल्टर प्रदर्शित करते हैं। एनवेलप ट्रांसफर फंक्शन और बल्ब ट्रांसफर फंक्शन कैस्केड में प्रभावी रूप से होते हैं, जिससे कंट्रोल लूप में प्रभावी रूप से लो पास पोल और शून्य पर पोल लगभग -180° का नेट फेज शिफ्ट होता है। यह अल्प चरण मार्जिन के कारण नियंत्रण पाश में खराब क्षणिक प्रतिक्रिया का कारण बनेगा। आउटपुट न्यूनतम प्रदर्शित कर सकता है। बर्नार्ड एम ओलिवर[35] में दिखाया गया है कि एम्पलीफायर द्वारा लाभ का सामान्य संपीड़न एनवेलप स्थानांतरण फ़ंक्शन को अल्प करता है जिससे कि अधिकांश दोलक उत्तम क्षणिक प्रतिक्रिया दिखाते हैं, जो दुर्लभ स्थिति को त्यागकर वेक्यूम ट्यूबों में अन्य-रैखिकता दूसरे को असामान्य रूप से रैखिक एम्पलीफायर का उत्पादन करती है।
संदर्भ
- ↑ Wien 1891
- ↑ Terman 1933
- ↑ Terman 1935, pp. 283–289
- ↑ Terman 1937, pp. 371–372
- ↑ Arguimbau 1933
- ↑ Groszkowski 1934
- ↑ Terman 1937, p. 370
- ↑ Meacham 1939
- ↑ 9.0 9.1 Meacham 1938
- ↑ Scott 1939
- ↑ Scott 1938
- ↑ Black 1934a
- ↑ Black 1934b
- ↑ HP 2002
- ↑ Sharpe n.d.
- ↑ Terman et al. 1939
- ↑ Sharpe n.d., p. ???[page needed]; Packard remembers first demonstration of the 200A in Portland.
- ↑ Sharpe n.d., p. xxx[page needed]
- ↑ Williams (1991, p. 46) states, "Hewlett may have adapted this technique from Meacham, who published it in 1938 as a way to stabilize a quartz crystal oscillator. Meacham's paper, "The Bridge Stabilized Oscillator," is in reference number five in Hewlett's thesis."
- ↑ Hewlett 1942
- ↑ Williams 1991, pp. 46–47
- ↑ Graeme, Jerald G.; Tobey, Gene E.; Huelsman, Lawrence P. (1971). परिचालन प्रवर्धक, डिजाइन और अनुप्रयोग (1st ed.). McGraw-Hill. pp. 383–385. ISBN 0-07-064917-0.
- ↑ Clapp 1944a
- ↑ Clapp 1944b
- ↑ Matthys 1992, pp. 53–57
- ↑ 26.0 26.1 Schilling & Belove 1968, pp. 612–614
- ↑ Hewlett 1939, p. 13
- ↑ Terman 1943, p. 904
- ↑ Terman 1943, p. 904 citing Ferguson & Bartlett 1928
- ↑ Terman 1943, p. 905
- ↑ Meacham 1938. Meacham1938a. Meacham presented his work at the Thirteenth Annual Convention of the Institute of Radio Engineers, New York City, June 16, 1938 and published in Proc. IRE October 1938. Hewlett's patent (filed July 11, 1939) does not mention Meacham.
- ↑ Williams 1990, pp. 32–33
- ↑ Strauss 1970, p. 710, stating "For acceptable amplitude stability, some form of temperature compensation would be necessary."
- ↑ Strauss 1970, p. 667
- ↑ Oliver 1960
अन्य संदर्भ
- Arguimbau, L. B. (January 1933), "An Oscillator Having a Linear Operating Characteristic", Proceedings of the I.R.E., 21: 14
- Bauer, Brunton (November 1949a), "Design Notes on the Resistance-Capacity Oscillator Circuit (Part I)" (PDF), Hewlett-Packard Journal, Hewlett-Packard Company, 1 (3)
- Bauer, Brunton (December 1949b), "Design Notes on the Resistance-Capacity Oscillator Circuit (Part II)" (PDF), Hewlett-Packard Journal, Hewlett-Packard Company, 1 (4)
- Black, H. S. (January 1934a), "Stabilized feedback amplifier", Radio Engineer, 53: 114–120
- Black, H. S. (January 1934b), "Stabilized feedback amplifier", Bell System Technical Journal, 13 (1): 1–18, doi:10.1002/j.1538-7305.1934.tb00652.x
- Ferguson, J. G.; Bartlett, B. W. (July 1928), "The Measurement of Capacitance in Terms of Resistance and Frequency" (PDF), Bell System Technical Journal, 7 (3): 420–437, doi:10.1002/j.1538-7305.1928.tb01234.x
- Clapp, J. K. (April 1944a), "A Bridge-Controlled Oscillator" (PDF), The General Radio Experimenter, XVIII (11): 1–4
- Clapp, J. K. (May 1944b), "An Analysis of the Bridge-Controlled Oscillator" (PDF), The General Radio Experimenter, XVIII (12): 6–8
- Groszkowski, Janusz (February 1934), "Oscillators with Automatic Control of the Threshold of Regenerations", Proceedings of the I.R.E., 22: 145
- Hamilton, Scott (2003), An Analog Electronics Companion: basic circuit design for engineers and scientists, Cambridge University Press, ISBN 978-0-521-79838-9
- Hamilton, Scott (2007), An Analog Electronics Companion: basic circuit design for engineers and scientists and introduction to SPICE simulation, Cambridge University Press, ISBN 978-0-521-68780-5
- Hewlett, William Redington (June 1939), A New Type Resistance-Capacity Oscillator, Engineer's Thesis, Stanford University
- US 2268872, Hewlett, William R., "चर आवृत्ति दोलन जनरेटर", published July 11, 1939, issued January 6, 1942
- HP (22 January 2002), A real gem: HP's audio oscillator patent turns 60, HP; ब्लैक द्वारा टरमन की प्रेरणा और 1930 के दशक के उत्तरार्ध में नकारात्मक प्रतिक्रिया और फिक्स्ड-फ्रीक्वेंसी ऑडियो ऑसिलेटर्स के बारे में उनकी स्नातक संगोष्ठी; हेवलेट फिनिशिंग मास्टर्स और इंजीनियर थीसिस की तलाश; 1939 में सैन फ्रांसिस्को पेटेंट अटॉर्नी को काम पर रखना।
- Meacham, L. A. (October 1938a), "The Bridge Stabilized Oscillator", Proc. IRE, 26 (10): 1278–1294, doi:10.1109/jrproc.1938.228725, S2CID 51651042
- Meacham, L. A. (October 1938), "The Bridge Stabilized Oscillator", Bell System Technical Journal, 17 (4): 574–591, doi:10.1002/j.1538-7305.1938.tb00799.x. ट्यूब ओवरलोडिंग के बिना एक ऑसीलेटर की आवृत्ति और आयाम स्थिरीकरण। पुल को संतुलित करने के लिए टंगस्टन लैंप का उपयोग करता है।
- US 2163403, Meacham, Larned A., "स्थिर थरथरानवाला", published 2 July 1937, issued 20 June 1939, assigned to Bell Telephone Laboratories
- Matthys, Robert J. (1992), Crystal Oscillator Circuits (revised ed.), Malabar, Florida: Krieger Publishing Company, pp. 53–57
- Oliver, Bernard M. (April–June 1960), "The Effect of μ-Circuit Non-Linearity on the Amplitude Stability of RC Oscillators" (PDF), Hewlett-Packard Journal, 11 (8–10): 1–8. दिखाता है कि वीन ब्रिज ऑसिलेटर के तेज आयाम के निपटान के लिए एम्पलीफायर गैर-रैखिकता की आवश्यकता है।
- Schilling, Donald; Belove, Charles (1968), Electronic Circuits: Discrete and Integrated, McGraw-Hill
- Scott, H. H. (February 1938), "A new type of selective circuit and some applications", Proc. IRE, 26 (2): 226–235, doi:10.1109/JRPROC.1938.228287, S2CID 51674762
- US 2173427, Scott, Hermon Hosner, "इलेक्ट्रिक ऑसिलेटर", published 30 August 1937, issued 19 September 1939, assigned to General Radio Company; वीन, ब्रिज-टी, ट्विन-टी ऑसिलेटर
- Sharpe, Ed (n.d.), Hewlett-Packard, The Early Years; हेवलेट ने स्टैनफोर्ड से स्नातक किया और शोध करते हुए एक वर्ष बिताया; फिर वह अपने आकाओं को पाने के लिए MIT जाता है। हेवलेट सेना में शामिल हो गए, लेकिन 1936 में छुट्टी दे दी गई।
- Strauss, Leonard (1970), Wave Generation and Shaping (2nd ed.), McGraw-Hill, ISBN 978-0-07-062161-9
- Terman, Frederick (July 1933), "Resistance-stabilized Oscillators", Electronics, 6: 190
- Terman, Frederick (1935), Measurements in Radio Engineering, New York, NY: McGraw-Hill, pp. 283–289, ASIN B001KZ1IFK, OCLC 180980 (डायोड लिमिटिंग)
- Terman, Frederick (1937), Radio Engineering, McGraw-Hill
- Terman, Frederick (1943), Radio Engineers' Handbook, McGraw-Hill
- Wien, M. (1891), "Messung der Inductionsconstanten mit dem "optischen Telephon"" [Measurement of Inductive Constants with the "Optical Telephone"], Annalen der Physik und Chemie (in Deutsch), 280 (12): 689–712, Bibcode:1891AnP...280..689W, doi:10.1002/andp.18912801208
- Williams, Jim (June 1990), Bridge Circuits: Marrying Gain and Balance (PDF), Application Note, vol. 43, Linear Technology Inc, pp. 29–33, 43
- Williams, Jim (1991), "Max Wien, Mr. Hewlett, and a Rainy Sunday Afternoon", in Williams, Jim (ed.), Analog Circuit Design, Art, Science, and Personalities, Butterworth Heinemann, pp. 43–58, ISBN 0-7506-9640-0
बाहरी संबंध
- Model 200A Audio Oscillator, 1939, HP Virtual Museum.
- Wien Bridge Oscillator, including SPICE simulation. The "Wien bridge oscillator" in the simulation is not a low distortion design with amplitude stabilization; it is a more conventional oscillator with a diode limiter.
- Aigrain, P. R.; Williams, E. M. (January 1948), "Theory of Amplitude-Stabilized Oscillators", Proceedings of the IRE, 36 (1): 16–19, doi:10.1109/JRPROC.1948.230539, S2CID 51640873
- Online Simulator of Wien Bridge Oscillator – Gives online simulation of Wien bridge oscillator.
- Bill Hewlett and his Magic Lamp, Clifton Laboratories
- Terman, F. E.; Buss, R. R.; Hewlett, W. R.; Cahill, F. C. (October 1939), "Some Applications of Negative Feedback with Particular Reference to Laboratory Equipment" (PDF), Proceedings of the IRE, 27 (10): 649–655, doi:10.1109/JRPROC.1939.228752, S2CID 51642790 (Acks Edward L. Ginzton at end of paper.) (Presented 16 June 1938 at 13th Annual Convention, Manuscript received 22 November 1938, abridged 1 August 1939); Meacham presented at 13th Annual Convention on 16 June 1938, too. See BSTJ. Also presented at Pacific Coast Convention, Portland, OR, 11 August 1938.
- Terman et al. (1939, pp. 653–654), §Resistance-stabilized Oscillators Employing Negative Feedback, state "For a discussion of ordinary resistance-stabilized oscillators see pages 283–289 of F. E. Terman, 'Measurements in Radio Engineering,' McGraw-Hill Book Company, New York, N.Y., (1935)." OCLC 180980 ASIN B001KZ1IFK (diode limiting)
- Terman et al. (1939, p. 654) state, "This oscillator [Hewlett's] somewhat resembles that described by H. H. Scott, in the paper 'A new type of selective circuit and some applications,' Proc. I.R.E., vol 26, pp. 226–236; February, (1938), although differing in a number of respects, such as being provided with amplitude control and having the frequency adjusted by variable condensers rather than variable resistors. The latter feature makes the impedance from a to ground constant as the capacitance is varied to change the frequency, and so greatly simplifies the design of the amplifier circuits."
- US 2319965, Wise, Raymond O., "Variable Frequency Bridge Stabilized Oscillator", published 14 June 1941, issued 25 May 1943, assigned to Bell Telephone Laboratories
- US 2343539, Edson, William A., "Stabilized Oscillator", published 16 January 1942, issued 7 March 1944, assigned to Bell Telephone Laboratories
- http://www.radiomuseum.org/forum/single_pentode_wien_bridge_oscillator.html
- http://www.americanradiohistory.com/Archive-Bell-Laboratories-Record/40s/Bell-Laboratories-Record-1945-12.pdf has Black bio; "Stabilized feedback amplifier" won prize in 1934.
- U.S. Patent 2,303,485 Later (31 December 1940) Meacham patent about multi-frequency bridge-stabilized oscillators using series resonant circuits.

